Computational studies of the metal-free [3+2] cycloaddition reaction of azide with enaminone for the synthesis of 1,2,3-triazoles

Abstract

In this study, we investigated the mechanism of [3+2] cycloaddition (32CA) reaction between phenyl azide and phenyl enaminone using the M06-2X/6-31+G(d,p) level of theory for the first time. Computational results indicate that the metal-free azide-enaminone 32CA reaction for the selective synthesis of 1,2,3-triazoles in toluene proceeds along the 1,4- and 1,5-pathway, with the corresponding activation free energies (ΔG) of about 30.3 and 39.5 kcal mol⁻¹, respectively, corresponding to the 32CA step. The alternative mechanism for this reaction in the presence of a catalyst and water as the solvent is proposed. The solvents studied displayed similar effects on activation energies (E^#) and ΔG. The results of our computational study on the effect of phenyl azide substituents are consistent with the experimental observations in terms of reaction yield. The global and local nucleophilic and electrophilic indices of reagents and non-covalent interactions (NCI) are analyzed to determine the selectivity of the reaction and elucidate the most stable transition state structures.

---

1. Introduction

Heterocyclic compounds containing 1,2,3-triazole rings have garnered significant attention due to their broad applications and importance in the fields of chemistry, medicine, and biology.^1–7 Copper-catalyzed [3+2] azide–alkyne cycloaddition (CuAAC) reactions are the most common in the synthesis of these heterocycles in the field of click chemistry.^8–15 However, due to the toxicity of transition metals, these reactions are not suitable for biological applications. Recently, organocatalytic [3+2] cycloaddition (32CA) reactions of azides with aldehydes and ketones for the synthesis of triazole derivatives have received wide attention in applied and theoretical fields.^16–23 Moreover, metal-free strategies have been designed to synthesize fully substituted triazoles.^24–27 Novel synthetic strategies for the synthesis of α-ketotriazoles (4-acyl-1,2,3-triazoles), which exhibit diverse medicinal and biological properties,^28–43 have been reported. Thomas et al.⁴⁴ developed a new metal-free selective strategy for synthesizing α-ketotriazoles based on the recognition that enaminones, prepared via the condensation reaction of enolizable ketones with N,N-dimethylformamide dimethyl acetal,^45–50 (Scheme 1) can undergo 32CA reaction with azides to form specific α-ketotriazoles. Recently, enaminones with good stability and easy availability have been employed as starting materials to synthesize NH-1,2,3-triazoles with various functional groups.^51,52 These reactions proceed without the need for a catalyst or any additional reagents. Scheme 2 illustrates the proposed mechanism for the 32CA reaction of azides with enaminones.

Scheme 1 Preparation of enaminones and their 32CA reaction with azides in toluene.

Scheme 2 Proposed mechanism for the 32CA reaction of azide with enaminone.⁴⁴

The reaction starts with 32CA reaction of azide with enaminone (A) to form the intermediate triazoline B, via the 1,4- or 1,5-pathway, which undergoes aromatization via spontaneous elimination of dimethylamine, resulting in the synthesis of corresponding α-ketotriazoles. However, experimental observations and theoretical studies on enaminone-mediated 32CA reactions with tosyl or sulfonyl azides for the synthesis of NH-1,2,3-triazoles^51,52 suggest that water, used as a catalyst, promotes the elimination of dimethylamine. Therefore, the 32CA reaction of azides and enaminones can be alternatively performed in the presence of water, which serves as both the solvent and catalyst, instead of using toluene as a solvent.

Furthermore, recent theoretical studies on 32CA reactions of three-atom-compound (TAC) have demonstrated a relationship between their electronic structure and reactivity.^53–56 Thus, 32CA reactions are classified into pseudodiradical, pseudoradical, carbenoid, and zwitterionic reactions depending on the electronic structure of TACs.⁵⁴ A recent MEDT study of the poor reactivity of azides in 32CA reactions showed that they react efficiently with only strongly nucleophilic ethylene.⁵⁵

In this work, we investigate the quantum mechanical mechanism of the 32CA reaction of phenyl azide with phenyl enaminone, study the effect of solvents, as well as the phenyl azide substituents and verify the alternative mechanism in the presence of water as solvent and catalyst. Furthermore, we analyze the global and local electrophilic and nucleophilic indices of the reactants^57–59 and perform the NCI (non-covalent interaction) index analysis, which is of great importance for revealing the covalent and non-covalent interactions in molecular systems.^60–62

2. Computational details

The M06-2X/6-31+G(d,p) level of theory⁶³ was used to investigate the 32CA reaction mechanism of phenyl azide with phenyl enaminone in the gas phase and in the presence of toluene as a solvent. The PCM (continuous polarization method)⁶⁴ was used to optimize the energies of the mechanism components in the presence of various solvents using the higher M06-2X/6-311+G(d,p) level of theory. All calculations were performed using the Gaussian 16 program.⁶⁵ The NCI and AIM topographies were visualized using the NCI plot,⁶² VMD,⁶⁶ and Multiwfn⁶⁷ programs. The global and local nucleophilic and electrophilic indices were calculated according to the relationships in ref. 58. The ESI† includes the component energies of both pathways and their Cartesian coordinates.

3. Results and discussion

3.1. Classical Huisgen cycloaddition reaction of azides with alkenes

α-Ketotriazoles can be synthesized by the Huisgen 32CA reaction of azide with the corresponding alkyne via the mechanism shown in Fig. 1, which involves 1,4- and 1,5-pathways, leading to products (1,4- and 1,5-P), respectively. We chose 1-phenylprop-2-yn-1-one to form α-ketotriazoles to compare the 32CA reactions of azide and enaminone. Fig. 2 shows the optimized transition state structures (TSs) for both 1,4- and 1,5-pathways determined using the M06-2X functional with a diagram of the Gibbs free energy changes along both pathways. As illustrated in Fig. 2, the conventional Huisgen 32CA reaction of azide with an alkyne lacks selectivity, with both paths encountering similar free energy barriers.

Fig. 1 Mechanism of the classical Huisgen 32CA reaction of azide and alkyne.

Fig. 2 Structures of 1,4- and 1,5-TS, and plots of Gibbs free energy changes along the 1,4-and 1,5-pathways. The purple sphere represents the phenyl ring. The solvent used is toluene.

3.2. 32CA reaction of phenyl azide and phenyl enaminone

In this subsection, we discuss the computational results related to the 32CA reaction of phenyl azide with phenyl enaminone, as well as the influence of solvents on the reaction mechanism. Fig. 3 shows the geometries of the 1,4- and 1,5-pathway components determined by the M06-2X functional with the basis set 6-31+g(d,p) in the gas phase. Fig. 4 shows the ΔG energies along the two pathways studied.

Fig. 3 Structures of the reaction components along the two pathways optimized by the M06-2X functional in the gas phase. Bond lengths are in angstroms (Å).

Fig. 4 Gibbs free energy changes along the catalytic cycle via the 1,4- and 1,5 pathways for the 32CA reaction of phenyl azide with phenyl enaminone in the gas phase and in the presence of the toluene solvent.

As shown in Fig. 3, the N1–C1 distance is longer than the N3–C2 distance in the 1,4-TS, while these two distances in the 1,5-TS (similar to the cycloaddition of azide with an alkyne; see Fig. 2) are close, which means that the 1,5-TS is synchronous, while 1.4-TS is asynchronous, and the last state is expected to be more stable than 1,5-TS. Based on our previous results for the organo-catalyzed 32CA reaction of azide with saturated aldehydes,²¹ in terms of the energy barriers or activation energy of 1,4-TS-H and 1,4-TS-H, we note from Fig. 4 that the 1,4-pathway encounters a lower free energy barrier of about 10.2 kcal mol⁻¹ compared to 1,5-pathway. For the previous reaction,²¹ this value is about ΔG = 8.9 kcal mol⁻¹.²¹ However, due to the high strain associated with the four-membered TS, the intramolecular 1,3-hydrogen shifts are involved in the tautomerization steps and have very high activation energies. These steps always involve an acid/base species.⁶⁸ The 32CA step is, therefore, the rate-determining step. Thus, we can see from Fig. 4 that the energy barrier for 1,4-TS is about 9.2 kcal mol⁻¹ lower than that of 1,5-TS in the toluene solvent and that the 32CA reaction of azide with enaminone is efficient and selective without any catalysts.

We selected some of the most commonly used solvents in 32CA reactions to study their effects. As shown in Fig. 5, solvents show similar effects of the activation free energy barrier (ΔG) and activation energy (E^#), and the lowest energy barriers for the 32CA step (1,4-TS) and for the 1,3-hydrogen shift (1,4-TS-H) are related to the toluene solvent (30.3 and 34.7 kcal mol⁻¹, respectively).

Fig. 5 ΔG energies of transition state structures (1,4-TS-H and 1,4-TS) and activation energies depending on the solvents used.

3.3. Water-catalyzed 32CA reaction of phenyl azide and phenyl enaminone

We display here the results of our study of the alternative mechanism of azide reaction with enaminone in the presence of water as solvent and catalyst. Fig. 6 shows the optimized structures of the components of the catalytic cycle according to the mechanism shown in Scheme 2 but with the inclusion of a water molecule starting from the 1,4- and 1,5-TS related to the 1,4- and 1,5-pathways. Table 1 shows some characteristics of the transition state structures in the gas phase.

Fig. 6 Optimized structures of some components of the two pathways studied in the presence of water as a catalyst. Bond lengths are in angstroms (Å).

Table 1 Some characteristics of the transition state structures (TS) of 1,4- and 1,5-pathways of the 32CA reaction of phenyl azide with phenyl enaminone in the gas phase^a

TS	Water as solvent	Water as catalyst
a The imaginary frequency is in cm^−1, and the distance is in Å.
1,4-TS (imag. freq.)	364.3i	371.1i
N1–C1	2.408	2.356
N3–C2	1.960	1.985
1,4-TS-H (imag. freq.)	1654.4i	1509.8i
C–H	1.435	1.360
N–H	1.339	1.220
1,5-TS (imag. freq.)	503.5i	486.1i
N3–C1	2.108	2.090
N1–C2	2.046	2.127
1,5-TS-H (imag. freq.)	1655.4i	1308.0i
C–H	1.505	1.363
N–H	1.284	1.106

---

We notice from Fig. 6 that the water molecule in 1,5-TS-H provides a hydrogen atom to nitrogen so that it is located at a shorter distance (N–H = 1.106 Å) than in 1,4-TS-H (N–H = 1.220 Å), and this requires higher Gibbs free energy to remove hydrogen from the water molecule. From this result, it is expected that the Gibbs free energy of 1,5-TS-H will be higher than that of 1,4-TS-H. Our results are consistent with those obtained by Shafran et al. for the water-mediated 32CA reaction of sulfonyl azide with enaminone to synthesize NH-1,2,3-triazoles.⁵²

The computational results shown in Fig. 7 indicate that water as a catalyst increases the ΔG of 1,4- and 1,5-TS and decreases the ΔG of 1,4- and 1,5-TS-H so that 1,4- and 1,5-TS become the rate-determining steps of the 32CA reaction for both pathways. Thus, water promotes the elimination of dimethylamine and α-hydrogen of the acyl group to form a selective product via1,4-TS-H. However, as we mentioned earlier, these steps always need the participation of other acid/base molecules⁶⁸ due to the high strain associated with the four-membered TS. In this context, we studied the 32CA reaction in the presence of methanol instead of water as a catalyst to confirm the role of water as a catalyst in the presence of water and toluene as a solvent for the dominant pathway 1. Fig. 8 shows the geometries structures of the corresponding transition state structures in the presence of methanol (Fig. 8A) and water (Fig. 8B) molecules. The computational results presented in Fig. 9 indicates that methanol exhibits a similar effect to water as a catalyst because it leads to a decrease in the energy barrier of the 1,3-hydrogen shift and an increase in the energy barriers of the cycloaddition step so that it becomes the rate-determining step of the 32CA reaction.

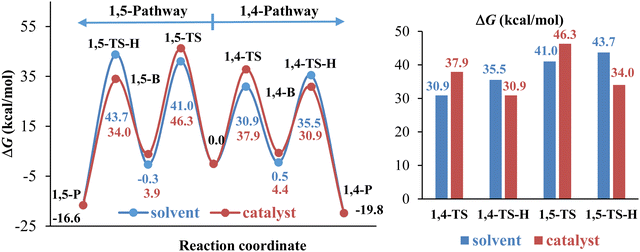Fig. 7 Gibbs free energy changes along the 1,4- and 1,5-pathways for the 32CA reaction of phenyl azide with phenyl enaminone in the presence of water as solvent (blue), and solvent/catalyst (red).

Fig. 8 Optimized structures of some components of the two pathways studied in the presence of (A) methanol and (B) water as a catalyst. Bond lengths are in angstroms (Å).

Fig. 9 A graph showing the Gibbs free energy changes of the transition states associated with the 1,4 pathway and the activation energies in the presence of water and methanol as a catalyst where M, T, and W represent methanol, toluene, and water, respectively.

3.4. Effect of phenyl azide substituents

Experimental observations indicate that phenyl azide substituents influence the region-selectivity of the reaction, and we select some substituents to illustrate this. Table 2 shows some characteristics of the 1,4- and 1,5-TS together with the corresponding 1,4- and 1,5-TS-H related to both studied pathways, while Fig. 10 shows optimized structures of 1,4- and 1,5-TS in the gas phase.

Table 2 Values of some transition state structure characteristics relevant to the 1,4- and 1,5-pathway for phenyl azide substituents^a

TS	H	4-NO2	4-COOEt
a The imaginary frequency is in cm^−1, and the distance is in Å.
1,4-TS (imag. freq.)	364.3i	363.5i	362.7i
N1–C1	2.408	2.415	2.515
N3–C2	1.960	1.959	1.986
1,4-TS-H (imag. freq.)	1654.4i	1653.8i	1649.9i
C–H	1.435	1.437	1.438
N–H	1.339	1.337	1.333
1,5-TS (imag. freq.)	503.5i	502.3i	495.1i
N3–C1	2.108	2.108	2.116
N1–C2	2.046	2.052	2.060
1,5-TS-H (imag. freq.)	1655.4i	1648.0i	−1687.7i
C–H	1.505	1.507	1.489
N–H	1.284	1.282	1.299

---

Fig. 10 Optimized structures of the 1,4- and 1,5-TS in the gas phase. Bond lengths are in angstroms (Å).

It is noted from Fig. 10 that the N1–C1 distance (2.408 Å) for 1,4-TS in the case of R = 4-NO₂ is longer than that for the other substituents, which means that the 4-NO₂ substituent increases the non-synchronicity of the N–C bond formation, and the energy of 1,4-TS for R = 4-NO₂ is lower than that of the other cases, while 1,5-TSs for almost all substituents leading to N–C bond formation are almost synchronous. Table 3 shows the calculated ΔG values for the components of the 1,4- and 1,5-pathways in the toluene solvent. Fig. 11 illustrates the plots of the free energy barriers for all the transition state structures corresponding to the activation energies for the studied phenyl azide substituents. As shown in Fig. 11, the 1,4-pathway is the dominant or most likely pathway for the 32CA reaction of all phenyl azide substituents with enaminone.

Table 3 Calculated ΔG values for the components related to 1,4- and 1,5-pathways for phenyl azide substituents in toluene solvent

Components	H	4-NO2	4-COOEt
a Values are taken from ref. 44.
Reagents	0.0	0.0	0.0
1,4-TS	30.3	27.0	28.8
1,4-B	−1.3	−2.3	−1.7
1,4-TS-H	34.7	33.2	34.3
1,4-P	−20.5	−19.0	−19.2
1,5-TS	39.5	38.9	39.4
1,5-B	−1.4	−3.4	−2.2
1,5-TS-H	45.0	42.7	44.1
1,5-P	−21.3	−15.0	−15.8
1,4-E^#	36.1	35.5	36.0
1,5-E^#	46.4	46.1	46.3
Product yield^a	86%	89%	82%

---

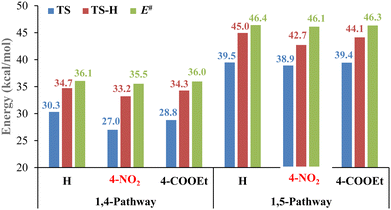Fig. 11 Plot of transition state Gibbs free energy changes and activation energies for the 1,4- and 1,5-pathways for phenyl azide substituents.

We note from Table 3 and Fig. 11 that the Gibbs free energy (27.0 kcal mol⁻¹) for 1,4-TS in case R = 4-NO₂ is lower than in the other cases. However, the ΔG of 1,4-TS in case R = 4-COOEt is lower than that in case R = H by about 1.5 kcal mol⁻¹. Thus, the reaction efficiency can be arranged according to the substituent as follows: 4-NO₂ > 4-COOEt > H.

3.5. Analysis of global and local electrophilic and nucleophilic indices of reactants

The electrophilic and nucleophilic indices of the reagents were determined according to the relationships given in ref. 58 The calculated global nucleophilic and electrophilic indices of the enaminone and phenyl azide substituents (Fig. 12) in the gas state are shown in Table 4. The results in Table 4 indicate that enaminone and phenyl azide exhibit similar chemical potentials, −3.83 eV and −3.94 eV, respectively; therefore, the 32CA reactions of these two molecules are expected to be non-polar.⁵⁸ The presence of the 4-NO₂ and 4-COOEt substituents reduces the chemical potential to −5.17 eV and −4.42 eV, respectively, increasing the polarity of the 32CA reaction towards the azide. Thus, for these substituents, the electron density flow occurs from the enaminone molecule with the highest μ value to the azide molecule with the lowest μ value. This result agrees with the global electron density transfer (GEDT)⁵⁷ values calculated for 1,4-TS. The GEDT values for 1,5-TS show that the 32CA reaction of substituted and unsubstituted azide with enaminones is non-polar.⁵⁸ Furthermore, the large difference between the GEDT values for the 1,4- and 1,5-TS indicates an increased non-synchronicity of N–C bond formation across the 1,4-TS. This result agrees with the optimized TSs for phenyl azide substituents (see Fig. 5). We also note from Table 4 that enaminone has a higher nucleophilic index (N = 3.71 eV) than azide (N = 3.11 eV for R = H), and it is classified among strong nucleophiles.⁵⁸ Moreover, the 4-NO₂ substituent increases ω by about 1.00 eV, while the 4-COOEt substituent increases its value by a smaller amount (0.36 eV). Consequently, the 4-NO₂ substituent activates azide to a greater extent than the 4-COOEt substituent, which agrees with the previously calculated activation energies for these two substituents and experimental observations. The local nucleophilic and electrophilic indices of the phenyl azide substituents and enaminone were calculated using the Parr functions⁵⁹ to illustrate the regioselectivity in these 32CA reactions (see Table 5).

Fig. 12 Structures of enaminone and phenyl azide substituents.

Table 4 Global electrophilic and nucleophilic indices (in eV) of the reagents and global electronic density transfer values (GEDT) for phenyl enaminone and phenyl azide substituents (R)

R	μ	η	ω	N	GEDT
					1,4-TS	1,5-TS
H	−3.94	7.51	1.03	3.11	0.31	0.08
4-NO2	−5.17	6.60	2.03	2.33	0.35	0.13
4-COOEt	−4.42	7.01	1.39	2.88	0.33	0.10
Enaminone	−3.83	6.53	1.12	3.71	—	—

---

Table 5 Local electrophilic and nucleophilic indices (eV) of substituted phenyl azides and enaminone

Indices	No atom	Parr function		Electrophilic	Nucleophilic
R		Pk^+	Pk^−	ω k	N k
H	N1	−0.06	0.21	−0.06	0.65
	N2	0.20	−0.06	0.21	−0.17
	N3	0.22	0.23	0.23	0.72
4-NO2	N1	−0.07	0.26	−0.15	0.60
	N2	0.07	−0.07	0.15	−0.16
	N3	0.08	0.24	0.17	0.56
4-COOEt	N1	−0.09	0.21	−0.13	0.60
	N2	0.14	−0.05	0.19	−0.15
	N3	0.14	0.22	0.19	0.63
Enaminone	C1	0.31	−0.16	0.34	−0.59
	C2	−0.10	0.71	−0.12	2.64

---

As shown in Table 5, the high value of the nucleophilic indices is related to the C2 center of enaminone and the high value of the electrophilic indices in azide is related to the N3 center. Thus, the most favorable two-center interaction is between the C2 carbon of the enaminone and the N3 nitrogen of the phenyl azide, which is consistent with the lower energy 1,4-TS (dominant). This result confirms that the 32CA reaction is regioselective.

3.6. Analysis of non-covalent interaction indices (NCIs)

Fig. 13 and 14 show the NCI analysis and RDG plot of the relevant 1,4- and 1,5-TS structures of the 32CA reaction of phenyl azide with enaminone in the gas phase. It is worth noting that the green, blue, and red regions are due to van der Waals interactions, attractive interactions or hydrogen bonding, and repulsive interactions, respectively.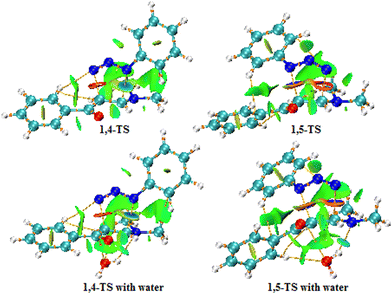

Fig. 13 NCI and AIM plots of the 1,4- and 1,5-TS structures for uncatalyzed (top) and water-catalyzed (bottom) reactions (isovalue = 0.55).

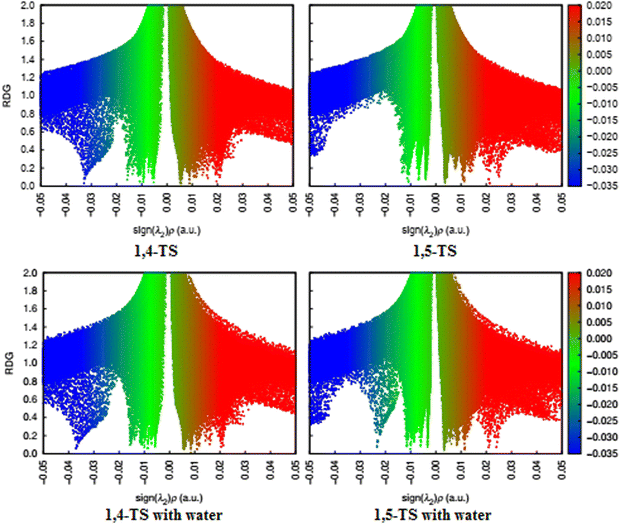Fig. 14 RDG diagrams of the 1,4- and 1,5-TS for uncatalyzed (top) and water-catalyzed (bottom) reactions.

Previous studies have suggested that the non-covalent interactions may be the main factor responsible for the selectivity of 32CA reactions,^69–72 thus revealing the preferred structure analysis of the 1,4- and 1,5-TS. From the NCI plot of the 1,4-TS state, we can see that one hydrogen atom in the phenyl ring of enaminone is located at a distance of 2.530 Å from the N3 nitrogen atom of phenyl azide, so a hydrogen bond (HB) formed between these two atoms enhances the stability of 1,4-TS. Moreover, the green surface is visible between the azide and part of the enaminone (bonding region, precisely between the nitrogen atom N2 of azide and the carbon atom C1 of enaminone). This surface is not observed in the bonding region for 1,5-TS, and the green surfaces are more widespread in 1,4-TS. It is also noted that the blue surfaces in the RDG diagram associated with the mutually attractive interactions are more widespread in 1,4-TS, especially between N1 of azide and C1 of enaminone, which makes 1,4-TS more stable than 1,5-TS. This is in agreement with the results of our calculations of the Gibbs free energies for these two cases (ΔΔG = 9.2 kcal mol⁻¹ in toluene solvent). In the presence of water as a catalyst, it is noted from the RDG plot that the green regions are more widespread for both 1,4- and 1,5-TS due to the formation of hydrogen bonds between the oxygen atom of water and the hydrogen atom in the α position of the enaminone, which increases the stability of both 1,4- and 1,5-TS. Furthermore, we notice the appearance of a blue region near −0.02 in the RDG of 1,5-TS, which enhances its stability, but 1,4-TS remains more stable than 1,5-TS.

4. Conclusions and recommendations

The mechanism of the 32CA reaction of phenyl azide with enaminone was investigated for the first time using the M06-2X functional with the 6-31+G(d,p) basis set. The results of our computational study are summarized in the following main points:

1. The classical 32CA reaction of azide with the alkene phenylprop-2-yn-1-one lacks regioselectivity due to the coincidence of the two pathways, leading to 1,4- and 1,5-regioisomer with identical Gibbs free energy barriers.

2. The azide–enaminone 32CA reaction occurs via the 1,4- and 1,5-pathway and leads to the formation of the 1,4-regioisomer selectively.

3. Studied solvents exhibit similar effects on ΔG and E^#.

4. A computational study of the alternative mechanism of the reaction of azide–enaminone 32CA with water as a solvent and catalyst indicates that the presence of water as a catalyst leads to a decrease in the activation energy of about 8.5 kcal mol⁻¹ compared to the presence of water as a solvent only. However, due to the high strain associated with the four-membered TS, the intramolecular 1,3-hydrogen shifts always require the participation of other acid/base molecules.

5. The analysis of the electrophilic and electrophilic indices agrees with our calculation of the Gibbs free energy for transition state structures and experimental observations.

6. Analysis of the AIM + NCI and the RDG plots indicate that 1,4-TS is more stable than 1,5-TS within the gas phase.

We recommend studying the effect of the electron-donating and electron-accepting substituents of enaminone on the efficiency and selectivity of the free metal 32CA reaction of azide with enaminone.

Data availability

All required data are available in the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. W. J. Evans, E. Montalvo, T. M. Champagne, J. W. Ziller, A. G. DiPasquale and A. L. Rheingold, J. Am. Chem. Soc., 2008, 130, 16.
2. P. Thirumurugan, D. Matosiuk and K. Jozwiak, Chem. Rev., 2013, 113, 4905.
3. Y.-C. Li, C. Qi, S.-H. Li, H.-J. Zhang, C.-H. Sun, Y.-Z. Yu and S.-P. Pang, J. Am. Chem. Soc., 2010, 132, 12172.
4. R. J. Thibault, K. Takizawa, P. Lowenheilm, B. Helms, J. L. Mynar, J. M. J. Frechet and C. J. Hawker, J. Am. Chem. Soc., 2006, 128, 12084.
5. R. Subbaraman, H. Ghassemi and T. A. Zawodzinski, J. Am. Chem. Soc., 2007, 129, 2238.
6. C. Ornelas, J. R. Aranzaes, E. Cloutet, S. Alves and D. Astruc, Angew. Chem., Int. Ed., 2007, 46, 872.
7. A. Lauria, R. Delisi, F. Mingoia, A. Terenzi, A. Martorana, G. Barone and A. M. Almerico, Eur. J. Org. Chem., 2014, 3289.
8. V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., 2002, 114, 2708.
9. C. W. Tornøe, C. Christensen and M. Meldal, J. Org. Chem., 2002, 67, 3057.
10. S. S. van Berkel, S. Brauch, L. Gabriel, M. Henze, S. Stark, D. Vasilev and B. Westermann, Angew. Chem., Int. Ed., 2012, 22, 5343.
11. Z. Chen, Q. Yan, Z. Liu and Y. Zhang, Chem. – Eur. J., 2014, 20, 17635.
12. Z. J. Cai, X. M. Lu, Y. Zi, C. Yang, L. J. Shen, J. Li and S. Ji, J. Org. Lett., 2014, 16, 5108.
13. J. P. Wan, D. Hu, Y. Liu and S. Sheng, ChemCatChem, 2015, 7, 875.
14. J. P. Wan, S. Cao and Y. Liu, J. Org. Chem., 2015, 80, 9028.
15. S. Ahamad, R. Kant and K. Mohanan, Org. Lett., 2016, 18(2), 280.
16. L. J. T. Danence, Y. Gao, M. Li, Y. Huang and J. Wang, Chem. – Eur. J., 2011, 13, 3584.
17. L. Wang, S. Peng, L. J. T. Danence, Y. Gao and J. Wang, Chem. – Eur. J., 2012, 18, 6088.
18. D. B. Ramachary, A. B. Shashank and S. Karthik, Angew. Chem., Int. Ed., 2014, 53, 10420.
19. C. G. Lima, A. Ali, S. S. van Berkel, B. Westermann and M. W. Paixão, Chem. Commun., 2015, 51, 10784.
20. J. John, J. Thomas and W. Dehaen, Chem. Commun., 2015, 51, 10797.
21. M. A. A. H. Badawi, Comput. Theor. Chem., 2022, 1209, 113593.
22. M. A. Al-Hakim Badawi, M. I. Al-Zaben and R. Thomas, Catal. Lett., 2024, 154, 1134.
23. A. Ali, A. G. Corrêa, D. Alves, J. Zukerman-Schpector, B. Westermann, M. A. Ferreira and M. W. Paixão, Chem. Commun., 2014, 50, 11926.
24. W. Li and J. Wang, Angew. Chem., In. Ed., 2014, 53, 14186.
25. J. Thomas, J. John and N. Parekh, & Dehaen, W, Angew. Chem., 2014, 126, 10319.
26. J. John, J. Thomas, N. Parekh and W. Dehaen, Eur. J. Org. Chem., 2015, 4922.
27. J. Thomas, S. Jana, J. John, S. Liekens and W. Dehaen, Chem. Commun., 2016, 52, 2885.
28. F. Friscourt and G. Boons, J. Org. Lett., 2010, 12, 4936.
29. S. Hwang, H. Bae and S. Kim, Tetrahedron, 2012, 68, 1460.
30. C. Menendez, S. Gau, S. Ladeira, C. Lherbet and M. Baltas, Eur. J. Org. Chem., 2012, 409.
31. P. M. Diz, A. Coelho, A. El Maatougui, J. Azuaje, O. Caamano, A. Gil and E. Sotelo, J. Org. Chem., 2013, 78, 6540.
32. S. Nawratil, M. Grypioti, C. Menendez, S. Mallet-Ladeira, C. Lherbet and M. Baltas, Eur. J. Org. Chem., 2014, 654.
33. V. Calderone, I. Giorgi, O. Livi, E. Martinotti, E. Mantuano, A. Martelli and A. Nardi, Eur. J. Med. Chem., 2005, 40, 521.
34. R. V. Somu, H. Boshoff, C. Qiao, E. M. Bennett, C. E. Barry III and C. C. Aldrich, J. Med. Chem., 2006, 49, 31.
35. J. Xie and C. T. Seto, Bioorg. Med. Chem., 2007, 15, 458.
36. C. Pardin, I. Roy, W. D. Lubell and J. W. Keillor, Chem. Biol. Drug Des., 2008, 72, 189.
37. O. Mesenzani, A. Massarotti, M. Giustiniano, T. Pirali, V. Bevilacqua, A. Caldarelli, P. Canonico, G. Sorba, E. Novellino, A. A. Genazzani and G. C. Tron, Bioorg. Med. Chem. Lett., 2011, 21, 764.
38. S. P. Sau and P. J. Hrdlicka, J. Org. Chem., 2012, 77, 5.
39. K. V. Praveen Kumar, R. R. Gajendra, D. D. Vo, S. Chakravarty, S. Chandrasekhar and R. Gree, Bioorg. Med. Chem. Lett., 2012, 22, 1439.
40. S. Xu, X. Zhuang, X. Pan, Z. Zhang, L. Duan, Y. Liu, L. Zhang, X. Ren and K. Ding, J. Med. Chem., 2013, 56, 4631.
41. C. Menendez, F. Rodriguez, A. L. de Jesus Lopez Ribeiro, F. Zara, C. Frongia, V. Lobjois, N. Saffon, M. R. C. Pasca, L. Herbet and M. Baltas, Eur. J. Med. Chem., 2013, 69, 167.
42. T. Srinivasa Reddy, H. Kulhari, V. G. Reddy, A. V. S. Rao, V. Bansal, A. Kamal and R. Shukl, Org. Biomol. Chem., 2015, 13, 10136.
43. L. da SM Forezi, C. G. Lima, A. A. Amaral, P. G. Ferreira, M. C. B. de Souza, A. C. Cunha and V. F. Ferreira, Chem. Rec., 2021, 21, 2782–2807.
44. J. Thomas, V. Goyvaerts, S. Liekens and W. Dehaen, Chem. – Eur. J., 2016, 22, 9966.
45. V. A. Bakulev, I. V. Efimov, N. A. Belyaev, Y. A. Rozin, N. NVolkova and O. S. El'tsov, Chem. Heterocycl. Compd., 2012, 47, 1593.
46. I. Efimov, V. Bakulev, N. Beliaev, T. Beryozkina, U. Knippschild, J. Leban, F. Zhi-Jin, O. Eltsov, P. Slepukhin, M. Ezhikova and W. Dehaen, Eur. J. Org. Chem., 2014, 3684.
47. B. Stanovnik and J. Svete, Synlett, 2000, 1077.
48. A.-K. Pleier, E. Herdtweck, S. A. Mason and W. R. Thiel, Eur. J. Org. Chem., 2003, 499.
49. B. Stanovnik and J. Svete, Chem. Rev., 2004, 104, 2433.
50. S. Hernμndez, I. Moreno, R. SanMartin, G. Gómez, M. T. Herrero and E. Domínguez, J. Org. Chem., 2010, 75, 434.
51. L. Yang, Y. Wu, Y. Yang, C. Wen and J. P. Wan, Beilstein. J. Org. Chem., 2018, 14, 2348.
52. Y. M. Shafran, A. A. Hussein, N. A. Beliaev, V. A. Shevyrin, S. Shityakov, T. V. Beryozkina and V. A. Bakulev, ACS Omega, 2022, 7, 5008.
53. H. B. El Ayouchia, B. Lahoucine, H. Anane, M. Ríos-Gutiérrez, L. R. Domingo and S. E. Stiriba, ChemistrySelect, 2018, 3, 1215.
54. M. Ríos-Gutiérrez and L. R. Euro Domingo, J. Org. Chem., 2019, 267.
55. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Org. Chem. Front., 2023, 10, 5579.
56. L. R. Domingo and M. Ríos-Gutiérrez, Molecules, 2017, 22, 750.
57. L. R. Domingo, RSC Adv., 2014, 4, 32415.
58. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748.
59. L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486.
60. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, J. Cohen and A. W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
61. J. R. Lane, J. Contreras-Garcia, J. P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263.
62. J. E. Contreras-Garcia, R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625.
63. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364.
64. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman and D. J. Fox, Gaussian 16 revision a.03, Gaussian Inc., Wallingford, 2016.
66. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33.
67. T. Lu and F. Chen, Multiwfn: A multifunctional wave function analyzer, J. Comput. Chem., 2011, 33, 580.
68. S. R. Emamian, L. R. Domingo and S. F. Tayyari, J. Mol. Graph. Model., 2014, 49, 47.
69. A. K. Nacereddine, C. Sobhi, A. Djerourou, M. Ríos-Gutiérrez and L. R. Domingo, RSC Adv., 2015, 5, 99299.
70. C. Sobhi, A. Khorief Nacereddine, A. Djerourou, M. Ríos-Gutiérrez and L. R. Domingo, J. Phys. Org. Chem., 2017, 30, e3637.
71. Z. Lachtar, A. Khorief Nacereddine and A. Djerourou, Struct. Chem., 2020, 31, 253.
72. F. Chafaa, A. Khorief Nacereddine and A. Djerourou, Theor. Chem. Acc., 2019, 138, 1.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj04341c

---