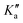Open Access Article
Open Access ArticleHigh resolution infrared spectroscopy of monodeutero-oxirane (c-C2H3DO) and analysis of two fundamentals between 820 and 950 cm−1†
Sieghard
Albert
a,
Ziqiu
Chen
 ab,
Karen
Keppler
ab,
Karen
Keppler
 a,
Gunther
Wichmann
a,
Gunther
Wichmann
 a,
Martin
Quack
a,
Martin
Quack
 *a,
Jürgen
Stohner
*a,
Jürgen
Stohner
 c,
Volker
Schurig
d and
Oliver
Trapp
c,
Volker
Schurig
d and
Oliver
Trapp
 e
e
aDepartment of Chemistry and Applied Biosciences, ETH Zürich, CH-8093 Zürich, Switzerland. E-mail: martin@quack.ch; Web: https://www.ir.ETHz.CH
bCollege of Chemistry and Chemical Engineering, Lanzhou University, Lanzhou 730000, China
cInstitute for Chemistry and Biotechnology ICBT, Zürich University of Applied Sciences ZHAW, Campus Reidbach, CH-8820 Wädenswil, Switzerland
dInstitut für Organische Chemie, Universität Tübingen, D-72076 Tübingen, Germany
eDepartment of Chemistry, Ludwig Maximilians University, D-80539 Munich, Germany
First published on 23rd May 2025
Abstract
We report the analysis of the infrared (IR) spectrum of monodeutero-oxirane (c-CH2CHDO), measured at room temperature at a self-apodized instrumental resolution of 0.0015 cm−1 with the Bruker IFS 125 HR Zürich Prototype spectrometer (ZP 2001), in the range of the ring deformation fundamental ν12 centered at 896.025 cm−1 and the wagging fundamental ν13 centered at 837.36 cm−1. A total of more than 1100 transitions were analyzed and fitted with an effective Hamiltonian which represents the data accurately, within 0.001 cm−1 for ν12 and 0.004 cm−1 for most transitions of ν13. We also report ab initio calculations including parity violation and an extended analysis with a substantial number of further assigned lines in our previously measured pure rotational spectra in the GHz and far infrared range. In combination with ground state combination differences from the IR spectra and further available results, we provide a critical analysis and improved spectroscopic parameters for the vibrational ground state based on more than 3300 assigned rotational transitions. The results are discussed as they pertain to isotopic chirality, molecular parity violation and the astrophysical observation of this isotopomer.
1 Introduction
The concept of isotopic chirality is of fundamental interest because it introduces a completely new isotope effect arising from the parity violating weak nuclear force.1–5 Because of the different weak charge of isotopes with different numbers of neutrons, the enantiomers of molecules which become chiral by isotopic substitution are predicted to have different ground state energies, separated by a parity violating energy difference ΔpvE, which can in principle be measured in special experiments,6 although no successful experiment has been reported to date despite ongoing efforts reviewed previously.4 ΔpvE would be exactly zero by symmetry for the symmetric “parent” molecule.Isotopic chirality also has possible astrophysical implications. In this context we have initiated, some time ago, a project to provide high resolution spectroscopic analyses for chiral isotopomers of the achiral cyclic molecule oxirane, 12C2H416O, which had been detected by astrophysical spectroscopy starting already in 19977 followed by several further observations.8–11 Oxirane might also be the carrier of some of the unidentified infrared bands in astrophysical spectroscopy.12,13
Oxirane has a total of four achiral deutero isotopomers C2H4O, C2D4O, CH2CD2O, and cis-CHDCHDO. It also has a total of 6 chiral isotopomers, R-C2H3DO, S-C2H3DO, R-C2HD3O, R-C2HD3O, R-trans-CHDCHDO, and S-trans-CHDCHDO. We have previously reported the analyses of high-resolution rotational spectra of the isotopomers C2H3DO, and trans-CHDCHDO which are the most likely ones to be detected by astrophysical spectroscopy.14,15 In our previous work we suggested explicitly with predictions from our analysis of the rotational spectra for the 300 to 370 GHz range that this molecule might lead to the first detection of an isotopically chiral molecule by astrophysical spectroscopy, because in this range undeuterated oxirane had been detected in the low mass protostar IRAS-2422 using the Atacama Large Millimeter/Submillimeter Array (ALMA).11,16 Following our predictions, Müller et al. were, indeed, very recently able to identify the corresponding lines of c-C2H3DO towards IRAS 16293-2422B.17
With the recent successful launch of the James Webb Space Telescope18–21 there is a new path toward the astrophysical observation of molecules by infrared spectroscopy. In this context there exists the tantalizing possibility of detecting a very strong signature of extraterrestrial life by means of infrared spectroscopy using vibrational circular dichroism to search for a possible consistent extraterrestrial homochirality as suggested in ref. 22. We therefore have also studied high resolution infrared spectra of C2H3DO and report here the results of the corresponding analysis.
Monodeutero-oxirane (c-C2H3DO or monodeutero-ethylene oxide), shown in Fig. 1, lends itself well to investigation as a simple, isotopically chiral molecule. As mentioned above, the parent species c-C2H4O has been detected in a variety of interstellar environments.7–11,23 Also detected have been vinyl alcohol24 and acetaldehyde,25 of which c-C2H4O is a kinetically stable isomer. It has been predicted to exist in the atmosphere of Titan as well,26 which is particularly interesting because the chemistry of Titan's atmosphere might provide information about the formation of terrestrial prebiotic compounds.27 It has also been proposed as a carrier for the Unidentified Infrared Bands (UIBs).12 The molecule and its isotopomers have been the subject of theoretical studies by Puzzarini et al.,28 who have investigated not only the main species c-C2H4O, but also the singly deuterated isotopomer c-C2H3DO.
Oxirane and its isotopomers have been the subject of many experimental infrared,29–35 microwave,36–38 and submillimeter wave39 studies. In addition to the older studies, there have been several recent investigations of the spectrum of the undeuterated oxirane, including the work on the ν15, ν12, ν5, ν10 and ν2 bands in the infrared at high resolution by Flaud et al.29 and Kwabia Tchana et al.40 The ν3 band at 1270.4 cm−1 has been examined by Russell and Wesendrup35 and by Ngom et al.41 The ν1 fundamental at 3018.3 cm−1 has been studied by W. J. Lafferty et al.42 Undeuterated oxirane has been examined in the ground state by Pan et al.39 and by Medcraft et al.30 There is less information available in the literature thus far about the spectrum of the isotopomers. Experimental investigations in the microwave region were conducted by Hirose43 and in the infrared at limited resolution by Nakanaga33,34 more than 40 years ago. The calculated band centers and intensities of infrared bands have been published by Puzzarini et al.28 Müller et al. have recently published a study of the doubly deuterated c-CD2CH2O and its tentative detection toward IRAS 16293-2422B.17,44
We had previously reported the analysis of the THz and GHz spectrum of c-C2H3DO in the vibrational ground state.14 For that study, the GHz spectrum of c-C2H3DO was recorded using our GHz setup at the ETH Zürich45 and the THz spectrum was recorded using our ETH-protoype FTS (Fourier Transform Spectrometer) at the Swiss Light Source (SLS) with a best resolution close to 0.0005 cm−1.13 In the meantime, we have been able to assign more than 1000 further lines in the THz spectra in the range of 0.75–1.84 THz and have noted that inadvertently in our previous publication, pre-final tables appeared in print, including uncorrected misprints. Also, most recently, Müller et al. have provided additional rotational lines in the submm (GHz) range, together with an analysis including our previous data.17 In order to provide an optimal starting point for our new analysis of the vibrational spectra, we have therefore re-examined the rotational spectra of the ground state, conducting a global analysis of all currently available data including combination differences from the IR-spectra. We have used these new molecular parameters obtained for the ground state to conduct the first rovibrational high-resolution analysis of the mid-infrared spectrum of c-C2H3DO. We are able to completely resolve the rovibrational structure of the far and mid infrared spectra of substituted oxiranes with our Bruker prototype spectrometer IFS 125 HR (ZP 2001)46,47 (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 0.0007 cm−1). Due to the resolution with which it is possible to measure infrared spectra in our laboratory, we can not only nearly fully assign the infrared spectrum in this region but can also characterize interactions between the rovibrational states of c-C2H3DO, thus providing insight into the structure and dynamics of this molecule.
= 0.0007 cm−1). Due to the resolution with which it is possible to measure infrared spectra in our laboratory, we can not only nearly fully assign the infrared spectrum in this region but can also characterize interactions between the rovibrational states of c-C2H3DO, thus providing insight into the structure and dynamics of this molecule.
The bands for which the analysis is presented here, ν12 (ring deformation) and ν13 (CHD wag), are the strongest absorption bands in this part of the spectrum of the singly deuterated (and singly fluorinated31) species. The need of using the sextic constants in the analysis of the ν12 transitions when they are fit independently of the ν13 transitions indicates that there exists a strong interaction between the ν12 and several other nearby states. The interaction has already been reported by Nakanaga33 in lower resolution studies of the undeuterated and fully deuterated species of oxirane. The existence of a Coriolis-type resonance has also been proposed by Russell and Wesendrup35 in their high-resolution study of the ν3 state of the main species. Coriolis resonances have been examined between the ν2 and ν10 states in the spectrum of the undeuterated oxirane by Kwabia Tchana et al.48 as well.
The present publication is organized as follows: in Section 2 we briefly summarize the synthesis of c-C2H3DO and the FTIR measurements. In Section 3 we provide a short summary of theoretical results including ab initio calculations of the harmonic and anharmonic vibrational frequencies and fundamental transitions, as well as some theoretical results on parity violation in this molecule. We also provide a very brief summary of the basic theoretical background and definitions for the effective Hamiltonians used in the analysis of the spectra. In Section 4 we present the new critical analysis of the vibrational ground state. Section 5 describes the assignment of the infrared spectra and the corresponding results of the analysis. In Section 6 we conclude with a discussion of the results and an outlook. Some preliminary results of our work have previously been reported.49–52
2 Experimental
2.1 Synthesis
The singly deuterated isotopomer of C2H4O was synthesized as a racemate according to the procedure briefly described elsewhere14 and summarized here in Fig. 2. In a protective atmosphere, vinyl magnesium chloride solution in THF was quenched with deuterium oxide and the monodeuteroethane produced was introduced into a freshly prepared solution of acetylhypobromide (from silver acetate and bromine) in anhydrous tetrachloromethane. After the reaction was completed, the solution was washed with 10% sodium hydrogen sulfate and dried over magnesium sulfate, and the solvent was removed. The crude product (1-acetoxy-2-bromo[2H]ethane) was distilled under vacuum (60 °C at 30 torr, yield 80%). 1-Acetoxy-2-bromo[2H]ethane and 25% sodium hydroxide in solution were combined in a flask equipped with a condenser filled with a molecular sieve (3 Å) and a nitrogen gas inlet. The flask was heated to 100 °C and monodeutero-oxirane was condensed in a cryogenic trap. The product was redistilled at 10.7 °C (yield 68%). The product was identified by NMR and mass spectrometry and the identity and purity were also obvious from the GHz and THz spectra obtained.14 Here, as seen in the survey spectrum in the spectral region examined in this work (Fig. 3), carbon tetrachloride CCl4 and methylene chloride CH2Cl2 were present as impurities. However, this did not adversely affect the analysis of the spectrum at high resolution. | ||
| Fig. 2 Synthesis of C2H3DO (described in more detail in ref. 14). | ||
 | ||
| Fig. 3 Overview spectrum of C2H3DO as recorded for this study. (T = 295 K, P ≈ 1.8 mbar, resolution = 0.0015 cm−1, l = 18 cm). Decadic absorbance lg(I0/I) is shown (partial pressure, see text). | ||
2.2 FTIR spectrum
We have recorded the infrared spectrum of monodeutero-oxirane in the region from 600 to 1000 cm−1 and beyond, and in particular 800 to 960 cm−1 at 295 K at a nominal instrumental resolution of 0.0015 cm−1 given by 0.9/dMOPD (Maximum Optical Path Difference),47 slightly less than the Doppler width of C2H3DO spectra in this region at room temperature (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) D = 0.0018 cm−1). An absorbance path length l = 18 cm in a glass cell equipped with KBr windows and several sample pressures were chosen (aperture 1.3 mm, spectrum self-apodized). The spectrum used for this analysis was measured with a pressure of 1.8 mbar, the partial pressure of C2H3DO being uncertain, however, due to composition. A Globar source was used with an MCT detector and Ge:KBr beam splitters. The spectrometer used was the Bruker IFS 125 HR Zürich Prototype (ZP 2001).46,47 The final spectrum was obtained by the co-addition of 160 scans and was analyzed in absorbance. Peak positions were determined using the OPUS software supplied by Bruker. The line positions were calibrated (Δ
D = 0.0018 cm−1). An absorbance path length l = 18 cm in a glass cell equipped with KBr windows and several sample pressures were chosen (aperture 1.3 mm, spectrum self-apodized). The spectrum used for this analysis was measured with a pressure of 1.8 mbar, the partial pressure of C2H3DO being uncertain, however, due to composition. A Globar source was used with an MCT detector and Ge:KBr beam splitters. The spectrometer used was the Bruker IFS 125 HR Zürich Prototype (ZP 2001).46,47 The final spectrum was obtained by the co-addition of 160 scans and was analyzed in absorbance. Peak positions were determined using the OPUS software supplied by Bruker. The line positions were calibrated (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) rms = 0.00006 cm−1) using 41 transitions in the ν2 fundamental of CO253 present in parts of the spectrum. The calibration shift was small and about constant (Δ
rms = 0.00006 cm−1) using 41 transitions in the ν2 fundamental of CO253 present in parts of the spectrum. The calibration shift was small and about constant (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) shift =
shift = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp −
exp − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) reference = 0.00005 cm−1), which is very small and also consistent with results of a wavenumber calibration performed using a proportional factor. The data in the supplementary publication are presented as calibrated line wavenumbers (
reference = 0.00005 cm−1), which is very small and also consistent with results of a wavenumber calibration performed using a proportional factor. The data in the supplementary publication are presented as calibrated line wavenumbers (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) obs =
obs = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp − Δ
exp − Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) shift).
shift).
3 Theory
3.1 Ab initio calculations
The fully optimized geometry of oxirane has been determined by ab initio calculations using Møller–Plesset perturbation theory to second order (MP2) with Gaussian 03 (and subsequent releases)54 using an augmented, correlation consistent triple-zeta basis set (aug-cc-pVTZ). The vibrational frequencies at the stationary points were all real. Table 1 provides the harmonic ωi and anharmonic![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i fundamentals (in cm−1) for monodeutero-oxirane. The anharmonic analysis is based on second order perturbation theory and obtained from the quartic force field computed with the software from ref. 54. All anharmonic constants are reported in the corresponding table in the ESI.† We also report intensities (calculated in the double harmonic approximation as well as with approximate anharmonic corrections) listed as integrated cross sections Gi/(pm)2 related to the IR intensity Ai/(km mol−1)55 by eqn (1):
i fundamentals (in cm−1) for monodeutero-oxirane. The anharmonic analysis is based on second order perturbation theory and obtained from the quartic force field computed with the software from ref. 54. All anharmonic constants are reported in the corresponding table in the ESI.† We also report intensities (calculated in the double harmonic approximation as well as with approximate anharmonic corrections) listed as integrated cross sections Gi/(pm)2 related to the IR intensity Ai/(km mol−1)55 by eqn (1):| Gi/(pm2) ≈ 16.60540·(Ai/km mol−1)(ωi/cm−1) | (1) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i, as well as Gi (in pm2). Calculations are carried out at the MP2 level with an aug-cc-pVTZ basis set (compared also with the calculated results reported by Puzzarini et al. in ref. 28)
i, as well as Gi (in pm2). Calculations are carried out at the MP2 level with an aug-cc-pVTZ basis set (compared also with the calculated results reported by Puzzarini et al. in ref. 28)
| Fundamental i | ω i /cm−1 (this work) | A i /km mol−1 (this work) | G i /pm2 (this work) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i
/cm−1 (this work)
i
/cm−1 (this work) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i
/cm−1 CC(VQZ)28
i
/cm−1 CC(VQZ)28 |
A i /km mol−1 (ref. 28) | G i /pm2 (ref. 28) |
|---|---|---|---|---|---|---|---|
| 1 | 3253.318 | 13.506 | 0.069 | 3109.374 | 3065.3 | 23.34 | 0.126 |
| 2 | 3205.911 | 12.538 | 0.065 | 3070.223 | 3029.6 | 9.89 | 0.054 |
| 3 | 3152.067 | 18.862 | 0.100 | 3047.255 | 3012.2 | 23.25 | 0.128 |
| 4 | 2354.197 | 10.263 | 0.072 | 2276.243 | 2251.3 | 2.78 | 0.021 |
| 5 | 1534.503 | 1.166 | 0.013 | 1487.890 | 1475.4 | 0.46 | 0.005 |
| 6 | 1406.279 | 2.159 | 0.026 | 1368.916 | 1358.4 | 1.91 | 0.023 |
| 7 | 1284.669 | 8.873 | 0.115 | 1256.018 | 1246.7 | 10.54 | 0.140 |
| 8 | 1170.365 | 1.543 | 0.022 | 1148.945 | 1146.4 | 2.00 | 0.029 |
| 9 | 1157.065 | 0.424 | 0.006 | 1130.548 | 1131.8 | 0.07 | 0.001 |
| 10 | 1104.401 | 1.259 | 0.019 | 1080.160 | 1079.1 | 1.14 | 0.018 |
| 11 | 1060.128 | 1.474 | 0.023 | 1039.569 | 1039.6 | 2.18 | 0.035 |
| 12 | 916.301 | 40.817 | 0.740 | 894.734 | 891.7 | 39.80 | 0.741 |
| 13 | 853.563 | 21.433 | 0.417 | 836.304 | 831.4 | 32.37 | 0.647 |
| 14 | 840.512 | 10.010 | 0.198 | 817.003 | 816.7 | 11.28 | 0.229 |
| 15 | 714.490 | 2.545 | 0.059 | 704.655 | 701.2 | 2.76 | 0.065 |
The summary in Table 2 anticipates some of our experimental results, agreeing relatively well with our theoretical results, in which anharmonic corrections are considered in the fundamentals. The agreement is slightly better than for the results of Puzzarini et al.28
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i) from this work and from ref. 28 and experimentally determined band centers for the fundamentals of monodeuterated oxirane in this spectral region, in cm−1
i) from this work and from ref. 28 and experimentally determined band centers for the fundamentals of monodeuterated oxirane in this spectral region, in cm−1
| Band | A i /km mol−1 this work (calc.) | A i /A12 (harmonic) (this work) | A i /A12 (anharmonic) (this work) | A i /km mol−1 (ref. 28) | A i /A12 (ref. 28) | ω i /cm−1 this work |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc/cm−1 (ref. 28)
calc/cm−1 (ref. 28) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i
/cm−1 this work (calc.)
i
/cm−1 this work (calc.) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp/cm−1 this work
exp/cm−1 this work |
||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Harmonic | Anharmonic | ||||||||||
| ν 12 | Ring deform | 40.817 | 37.226 | 1.000 | 1.000 | 39.80 | 1.000 | 916.301 | 891.7 | 894.734 | 896.025 |
| ν 13 | CHD twist | 21.433 | 29.204 | 0.525 | 0.785 | 32.37 | 0.813 | 853.563 | 831.4 | 836.304 | 837.363 |
| ν 14 | Ring deform | 10.010 | 9.917 | 0.245 | 0.266 | 11.28 | 0.283 | 840.512 | 816.7 | 817.003 | — |
| ν 15 | CHD rock | 2.545 | 2.629 | 0.062 | 0.071 | 2.76 | 0.0693 | 714.490 | 701.2 | 704.655 | — |
Monodeutero-oxirane is chiral by isotopic substitution, and with one of three distinct isotope effects relevant in high- and ultra-high-resolution spectroscopy,1,2,5 the parity violating energy difference ΔpvE between the isotopically chiral enantiomers arises largely from the electroweak interaction between nucleons and electrons.56,57 Parity-violating potentials Vpv have been calculated using the parity violating contribution Hpv with the dominant term to the Hamiltonian following56–58
 | (2) |
QA ≈ ZA (1 − 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΘW) − NA ΘW) − NA | (3) |
V pv is in principle a multidimensional potential hypersurface depending on the 3N − 6 internal coordinates. The parity violating energy difference ΔpvEel = 2|Vpv| at the equilibrium position (q = 0) is about hc·2.1 × 10−16 cm−1. Within the separable harmonic adiabatic approximation (SHAA) the relative frequency shift for the fundamental ν12 can be estimated from the calculated Δω/ω ≈ 69 × 10−20 whereas a one-dimensional anharmonic approximation (SAAA) gives Δν/ν ≈ 64 × 10−20.57,58 Within this approximation and taking only ν12 into account one can estimate the ground state energy difference ΔpvE0. From extensive earlier investigations56,59,60 it is well established that anharmonic effects on observables influenced by parity violation are most important for stretching vibrations and it is often sufficient to consider anharmonic effects only for the parity conserving potential. Here, the vibrations under consideration are a ring deformation (ν12) and a wagging mode (ν13). In comparison with other molecules for which spectroscopic observables under the influence of parity violation have been investigated,56,57,61 monodeutero-oxirane shows a rather small relative frequency shift and ground state energy difference arising from parity violation. We report the results here because of their current theoretical interest although they are clearly not detectable in the present spectroscopic experiments.
3.2 Rovibrational Hamiltonian
The rovibrational analysis has been carried out with Watson's A-reduced effective Hamiltonian in the Ir representation up to sextic centrifugal distortion constants,62,63 with .
. | (4) |
 | (5) |
 | (6) |
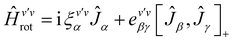 | (7) |
The rotational constants A, B, C, the quartic centrifugal distortion constants ΔvJ, ΔvJK, ΔvK, δvJ and δvK and the sextic centrifugal distortion constants ϕvJ, ϕvJK, ϕvKJ, ϕvK, ηvJ, ηvJK and ηvK depend upon the vibrational level v. Here, [,]+ is the anticommutator and [,]− is the commutator. We prefer the notation with the Greek η here, because the also quite commonly used lower case Greek phi ϕ can be confused with the upper case phi (Φ). The spectroscopic data have been analyzed with a least squares fit using the WANG program, described in detail in ref. 64. Extensive background information on the applications of WANG is also available in the literature.47,63,65 For comparison, we have also used the program SPFIT developed later by Pickett,66 and for some of the graphics PGOPHER.67 When used with the same effective Hamiltonians, the two programs give almost identical results, with occasional small numerical differences of no physical significance.
4 Vibrational ground state of c-C2H3DO revisited
In the course of the present work on the spectra of excited vibrational states of c-C2H3DO, we have extended substantially the assignment of rotational transitions in the FT-THz spectra measured with our spectrometer at the Swiss Light Source (SLS) in our previous work.14We were able to assign about 1000 further transitions in these spectra in the range from 0.75 to 1.84 THz in addition to the 398 previous assignments in this range.14 We have noted that inadvertently in the previous publication some uncorrected tables with misprints and results from preliminary pre-converged fits of the data were represented. While this does not affect the original spectra and corresponding data and conclusions, as the changes are not large, in general, we reproduce here in the ESI† a set of the corresponding corrected tables (labeled as C1 and C2 (2019) for the tables in the main text part and Table CS1, CS2, CS3 (2019) for the supplementary tables (ESI†) also Fig. S1, S2, S3, S4 (2019)), although the changes in these are hardly visible. In the previous supplementary tables (ESI†) we also had truncated the wavenumber data for the observed lines presented in cm−1 units at the 5th digit after the decimal point (i.e. to 0.00001 cm−1). While this precision would be adequate for the FT-THz values, it may not be adequate for further use of the GHz data, which are actually more precise. Thus, in the corrected tables we report all the previously observed line data in MHz to four digits after the decimal point (i.e. 0.1 kHz), which is well below the experimental uncertainty of the data and sufficiently numerically precise for most purposes. These experimental data are now given in Table CS2 (ESI†) (the data truncated in cm−1 as before would be the same as in S2(2019)). Recently the work of Müller et al.17 has also added more than one thousand newly measured lines in the submm range (0.491 to 1.06 THz) to the data set for the vibrational ground state of c-C2H3DO.
Table 3 provides a survey of all currently available data for this state, as well as various previous and present analyses and fits of these data, with relative weights assigned according to the reciprocal of the estimated uncertainty of the corresponding experimental data. Müller et al.17 have already provided a combined fit of their new and our previous data (communicated by us to them at higher precision than given by the truncated values in the previously published tables). We have reproduced their fit using their selected combined dataset, which included our 2019 results. We give the result of this fit in column 3 of Table 4. The result agrees perfectly except for deviations in one unit of the last digit for a few parameters, far below the uncertainty, below one tenth of the 1σ uncertainty, resulting from small numerical effects and not physically significant. In their analysis, Müller et al.17 recalibrated our previous FT-THz results with an average recalibration factor of 1.0000037 leading to a very slight shift of our original data. We have in our own final global analysis not used such a recalibration but rather used our original FT-THz values as they were calibrated in a standard way using water lines appearing in situ in our spectra.68 This calibration shift in any case is very small, ranging from 0.00007 at 25 cm−1 to 0.00010 at 50 cm−1. With the most recent data from the HITRAN data set69 one would obtain different shifts, but it is not clear whether this would provide an improvement. The uncertainty in the calibration data is estimated to be about 0.0001 cm−1, although it may actually be larger. Müller et al.17 have also argued that an effective Hamiltonian using Watson's S-reduction and the IIIl representation gives a better fit than the use of the A-reduction with the Ir-representation as used by us before. While we were able to reproduce their IIIl fit as well, in essence, the minimal improvement occurs only in the GHz and MW data and disappears when all data are considered. Indeed, c-C2H3DO is a highly asymmetric rotor with an asymmetry parameter κ = 0.20470 which is closer to zero than it is to +1 (oblate limit) or to −1 (prolate limit). The choice of reduction and representation is not a priori obvious and is rather arbitrary. In any case, the parameters of the effective Hamiltonians do not have much physical significance in terms of a simple model interpretation. They are “effective parameters” in the proper sense of the word (see also the discussion in ref. 63).
| Range/GHz | N trans | N freq | K a,max | K c,max | J max | Rel. weight | Ref. |
|---|---|---|---|---|---|---|---|
| a Number of transitions used in the fit. b Number of distinct frequencies used in the fit. c Combination differences from rovibrational analyses of IR spectra in the range of 800–950 cm−1. d The FT-THz data of 2019 were reanalyzed and combined with the new data set of 2023 for the selected data set in the final fit. e This is the data set which was selected in our final fit combining data from all sources, but not retaining all of them in the final fit, see text. f Hirose, 1974.43 g Albert et al., 2019.14 h Müller et al., 2023.17 | |||||||
| 10–60 (MW) | 20 | 20 | 5 | 4 | 8 | 20 | [Hirose]f |
| 60–120 (GHz) | 112 | 112 | 14 | 10 | 23 | 200 | [Albert et al.]g |
| 750–2090 (FT-THz) | 398 | 398 | 40 | 58 | 58 | 0.42 | [Albert et al.]g |
| 491–1060 (submm) | 1506 | 1091 | 58 | 43 | 55 | 33.3–200 | [Müller et al.]h |
| 41–297 (IR GSCD) | 325c | 310 | 30 | 41 | 42 | 0.21 | This work |
| 750–1840 (FT-THz) | 1409d | 848 | 38 | 57 | 57 | 0.42 | This work |
| 10–1840 (global) | 3370e | 2379 | 58 | 43 | 57 | This work | |
| MW, GHz, THz combineda C2019 | MW, GHz, sub-mm, THz combinedd MNRAS2023 | All rotational transitionse global fit (SPFIT) LP | All rotational transitionse global fit (WANG) SP | |
|---|---|---|---|---|
| This work | This work | |||
| a Based on spectra reported in Albert et al.14 in 2019 (as corrected here as C2019). b Values in parenthesis indicate uncertainties as 1σ in units of the last digits given. Rotational constants in C2019 were held fixed to the respective values of the ground state obtained by fitting only transitions in the GHz region of this study, to which the uncertainties given correspond. c Fixed at the ab initio estimate from Puzzarini et al.28 d Reproduced from data reported in Müller et al.17 as MNRAS2023. e All FT-THz transition wavenumbers were converted to frequencies in MHz in the data set. LP: large parameter set; SP: small parameter set, see also discussion in the text. | ||||
| A/MHz | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.6477(44)b 252.6477(44)b |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.647815(44) 252.647815(44) |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.647835(43) 252.647835(43) |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.64570(15) 252.64570(15) |
| B/MHz | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.5213(44) 905.5213(44) |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.523291(40) 905.523291(40) |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.523330(39) 905.523330(39) |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.52270(20) 905.52270(20) |
| C/MHz | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.5813(44) 327.5813(44) |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.583649(53) 327.583649(53) |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.583701(52) 327.583701(52) |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327.58370(16) 327.58370(16) |
| Δ J /kHz | 17.0779(35) | 17.04198(11) | 17.04211(11) | 17.04117(26) |
| Δ K /kHz | 25.458(19) | 25.46266(18) | 25.46261(18) | 25.45675(24) |
| Δ JK /kHz | 17.275(19) | 17.25673(12) | 17.25667(12) | 17.25473(26) |
| δ j /kHz | 4.7418(17) | 4.742161(17) | 4.742156(17) | 4.741796(42) |
| δ k /kHz | 13.2423(85) | 13.231691(56) | 13.231664(55) | 13.23277(11) |
| ϕ J /mHz | 13.9(12) | 12.36(10) | 12.50(10) | 11.697(95) |
| ϕ JK /mHz | 219(15) | 141.97(15) | 141.92(15) | 138.67(17) |
| ϕ KJ /mHz | −1006(37) | −835.25(36) | −835.38(35) | −829.84(22) |
| ϕ K /mHz | 910(29) | 808.08(30) | 808.11(30) | 797.41(14) |
| η J /mHz | 2.2c | 4.797(13) | 4.794(13) | 4.602(15) |
| η JK /mHz | 81.1c | 62.667(69) | 62.640(68) | 62.056(62) |
| η K /mHz | 61.7c | 30.21(10) | 30.17(10) | 33.301(74) |
| L K /Hz | — | −9.13(24) | −9.15(24) | — |
| L KKJ /Hz | — | 6.51(27) | 6.52(27) | — |
| L JK /Hz | — | 1.55(19) | 1.61(19) | — |
| L JJK /Hz | — | −2.099(64) | −2.087(63) | — |
| L J /Hz | — | −0.169(30) | −0.212(30) | — |
| l K /Hz | — | −4.571(60) | −4.587(59) | — |
| l KJ /Hz | — | 2.243(41) | 2.262(40) | — |
| l JK /Hz | — | −1.191(24) | −1.183(24) | — |
| l J /10−3 Hz | — | −34.7(36) | −34.5(35) | — |
| P K /10−3 Hz | — | 1.30(10) | 1.27(10) | — |
| P KKJ /10−3 Hz | — | −1.94(17) | −1.87(17) | — |
| P KJ /10−3 Hz | — | 0.851(99) | 0.798(98) | — |
| d rms/MHz | 2.290 | 2.405 | 2.6797 | 2.501 |
| n data | 530 | 2418 | 3370 | 3370 |
Indeed, we are able to provide an adequate fit of all current data, including also our new data, using an A-reduced Hamiltonian in the Ir representation using a small parameter set including only up to sextic constants as we used it before.14 The result of our new global analysis, which includes more than 1000 newly assigned rotational transitions and almost 400 combination differences obtained from the analyses of the vibrational spectra discussed in detail below, are shown in columns 4 and 5 of Table 4 obtained with a large parameter set (LP) and a small parameter set (SP). We thus consider the result in the last column (5) in Table 4 to be a best compromise choice. These parameters for the vibrational ground state provide a good starting point in the analysis of the spectra of excited vibrational states. This effective Hamiltonian incorporates effects from the omitted higher order parameters in the low order parameters, which therefore differ slightly between the LP and the SP Hamiltonians. However, such an effective Hamiltonian with a small number of parameters, while not providing the highest precision for all data, provides more stability in predictions, being less sensitive to artifacts arising when extrapolating with many high order parameters of non-negligible uncertainties. We note that the apparent contradiction of a slightly larger root mean square deviation drms for LP and SP on the same data set (see columns 4 and 5) arises from the actual weighting of the data in the fit, whereas drms is calculated here as an unweighted result. We have also found that the program SPFIT66 converges apparently on a slightly less favourable minimum in the fit than WANG64 (see also supplementary tables, ESI†). The slight differences have no physical significance (as described elsewhere63,71). We note that slight differences in the parameters arise even with a use of the same program, when changing the input for transitions from cm−1 to Hz units by multiplication with the speed of light. While physically identical by definition, the results of the fits are not numerically identical, with small differences, which have no physical significance.
In our final new global fits we did not retain all lines of the previous data set, but excluded those which have relatively large uncertainties when they arise from blended or very weak lines. For instance, the new data set of 1409 original FT-THz transitions includes many but not all of the 2019 FT-THz data (398). The actually selected data set of 3370 assigned transitions is apparent from the table in the ESI.† The last line in Table 3 thus does not simply arise as a sum of the values in the lines above it. In order to characterize further the quality of the parameter adjustment in representing the data globally, we note the absolute values of the maximum deviations of observed and calculated lines (0.026 MHz for the GHz data,14 0.646 MHz for the GHz data,17 8.96 MHz for the FT-THz, and 23.9 MHz for the GSCD which have the largest uncertainty).
Of the 3370 transitions, only 55 FT-THz deviate by more than |Δν| = 5 MHz and 123 for the ground state combination differences (GSCD, none for GHz and MW). Deviations larger than 10 MHz occur only for the GSCD data. As an example of a comparison of experimental primary data and simulations we show in Fig. 4 a small region of the experimental FT-THz spectrum compared with several simulations. The agreement is very good and similar for all three simulations (extra lines arise from other isotopomers, hot bands, and impurities as discussed before14). In the ESI,† we show further examples of experimental and simulated spectra with similar conclusions. For completeness, we show here in Table 5 the predicted frequencies for the lines identified by Müller et al.17 in the astrophysical spectra. The column “Identified” provides the predicted frequencies of the Hamiltonian of Müller et al. identified in the astrophysical observations. The other columns give the predictions from the 2019 data (C2019) and current results using the large parameter set (LP2025) and the small parameter set (SP2025). The differences are very small, usually below 0.1 MHz and always below 1 MHz, thus not really significant for this application.
 | ||
Fig. 4 A comparison of the THz spectrum of monodeutero-oxirane (from top to bottom): (1) observed spectrum; (2) simulated spectrum based on the global analysis of this study (Table 4, column 4); (3) simulated spectrum reproduced using data in Albert et al.14 (Table 5, column 1); (4) simulated spectrum reproduced using data in Müller et al.17 (Table 5, column 2). Quantum numbers of transitions are arranged in the form of 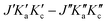 . Absorbance is shown in relative units for illustration. . Absorbance is shown in relative units for illustration. | ||
| J′ | J′′ | Identified | Predicted frequencies | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MNRAS2023a | C2019b | LP2025 | SP2025 | ||||||
| a Müller et al., 202317 b Albert et al. 2019.14 | |||||||||
| 5 | 5 | 1 | 4 | 4 | 0 | 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.99 180.99 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.966 180.966 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.993 180.993 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.977 180.977 |
| 22 | 8 | 14 | 22 | 7 | 15 | 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.43 190.43 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.334 190.334 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.428 190.428 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.421 190.421 |
| 22 | 9 | 14 | 22 | 8 | 15 | 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200.38 200.38 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200.288 200.288 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200.382 200.382 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200.375 200.375 |
| 5 | 5 | 0 | 4 | 4 | 1 | 235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965.82 965.82 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965.795 965.795 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965.823 965.823 |
235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965.807 965.807 |
| 9 | 5 | 5 | 8 | 4 | 4 | 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.82 568.82 |
331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.679 568.679 |
331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.820 568.820 |
331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568.805 568.805 |
| 10 | 5 | 5 | 9 | 6 | 4 | 332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130.07 130.07 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129.880 129.880 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130.068 130.068 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130.080 130.080 |
| 7 | 7 | 1 | 6 | 6 | 0 | 332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.25 520.25 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.181 520.181 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.251 520.251 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.232 520.232 |
| 7 | 7 | 0 | 6 | 6 | 1 | 332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594.25 594.25 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594.177 594.177 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594.248 594.248 |
332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 594.229 594.229 |
| 11 | 2 | 9 | 10 | 3 | 8 | 335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611.61 611.61 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611.599 611.599 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611.835 611.835 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611.835 611.835 |
| 11 | 3 | 9 | 10 | 2 | 8 | 335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620.97 620.97 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620.737 620.737 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620.973 620.973 |
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620.972 620.972 |
| 7 | 4 | 3 | 6 | 3 | 4 | 337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191.43 191.43 |
337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191.354 191.354 |
337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191.432 191.432 |
337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191.420 191.420 |
| 10 | 4 | 6 | 9 | 5 | 5 | 338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717.98 717.98 |
338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717.793 717.793 |
338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717.979 717.979 |
338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717.979 717.979 |
| 12 | 1 | 11 | 11 | 2 | 10 | 345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236.98 236.98 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236.689 236.689 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236.984 236.984 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236.985 236.985 |
| 12 | 2 | 11 | 11 | 1 | 10 | 345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.01 237.01 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236.717 236.717 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.013 237.013 |
345![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.014 237.014 |
| 8 | 6 | 3 | 7 | 5 | 2 | 346![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.07 866.07 |
346![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865.973 865.973 |
346![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.075 866.075 |
346![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866.056 866.056 |
| 10 | 5 | 6 | 9 | 4 | 5 | 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.77 271.77 |
350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.581 271.581 |
350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.767 271.767 |
350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.757 271.757 |
| 11 | 3 | 8 | 10 | 4 | 7 | 352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.86 688.86 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.627 688.627 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.864 688.864 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688.863 688.863 |
| 11 | 4 | 8 | 10 | 3 | 7 | 352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.91 939.91 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.678 939.678 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.915 939.915 |
352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.913 939.913 |
| 10 | 6 | 5 | 10 | 7 | 4 | 353![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.70 520.70 |
353![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.462 520.462 |
353![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.698 520.698 |
353![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.718 520.718 |
| 13 | 1 | 13 | 12 | 0 | 12 | 354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.73 922.73 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.366 922.366 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.732 922.732 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.734 922.734 |
| 13 | 0 | 13 | 12 | 1 | 12 | 354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.73 922.73 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.366 922.366 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.732 922.732 |
354![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.734 922.734 |
| 8 | 6 | 2 | 7 | 5 | 3 | 358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772.79 772.79 |
358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772.683 772.683 |
358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772.790 772.790 |
358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772.774 772.774 |
| 12 | 2 | 10 | 11 | 3 | 9 | 362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.22 232.22 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.924 231.924 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.220 232.220 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.220 232.220 |
| 12 | 3 | 10 | 11 | 2 | 9 | 362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233.93 233.93 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233.635 233.635 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233.930 233.930 |
362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 233.931 233.931 |
5 Assignment for excited vibrational states and results
The assignment of over 1100 rovibrational transitions belonging to particular subbands of ν12 and ν13 consisting of P and R branches has been carried out efficiently with the interactive Giessen Loomis-Wood assignment program72 and with the Zürich program LOOM4WANG.63 The Loomis-Wood method, previously extensively used for the assignment of linear molecules,73 has been used successfully for several asymmetric top molecules CH35Cl2F,74 CDBrClF46 and CHClF275 because these molecules display symmetric top behavior (no observable asymmetry splitting) at higher J levels. An extensive overview of the development and current use of Loomis-Wood programs is available in ref. 63.The assignments were confirmed using combination differences (GSCD) and the ground state energy level values available from Section 4. The overwhelming majority of the ν12 and ν13 transitions observed here were from unresolved doublets with degenerate Ka values (Ka = J − Kc and Ka = J − Kc + 1) or Kc values (Kc = J − Ka and Kc = J − Ka + 1). The transitions belonging to the ν12 band were fit initially, including up to the quartic centrifugal distortion constants, initially using J < 20 transitions (ν12: 325 transitions) to determine molecular parameters for the molecule as outlined above. The observed minus calculated values Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) =
= ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) obs −
obs − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc for the line positions are shown in Fig. 5. The fit was then extended to fit the entire 825 transitions assigned for ν12. The deviations between observed and calculated transitions for higher J and Ka quantum numbers increased with increasing J and Ka values.
calc for the line positions are shown in Fig. 5. The fit was then extended to fit the entire 825 transitions assigned for ν12. The deviations between observed and calculated transitions for higher J and Ka quantum numbers increased with increasing J and Ka values.
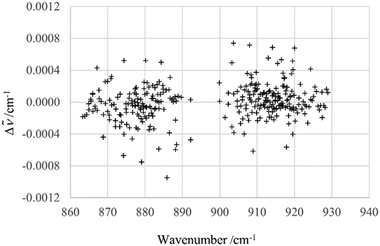 | ||
Fig. 5 Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) obs − obs − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc for ν12 transitions (J < 20). Calculated values were obtained using the effective Hamiltonian described in the text. calc for ν12 transitions (J < 20). Calculated values were obtained using the effective Hamiltonian described in the text. | ||
This behavior indicated a possible Coriolis resonance between the ν12 and nearby states, particularly the ν13 state at 837 cm−1. The transitions associated with the ν13 band were then assigned and included in the fit. Initially, the 230 ν13 transitions with J < 20 were analyzed separately, before including higher J value transitions in the fit. The presence of interactions between ν13 and other states was already indicated in the diagrams of the observed-calculated line positions for lines with J < 20 (Fig. 6).
 | ||
Fig. 6 Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) obs − obs − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc for ν13 transitions (J < 20). Calculated values were obtained using the effective Hamiltonian described in more detail in the text. calc for ν13 transitions (J < 20). Calculated values were obtained using the effective Hamiltonian described in more detail in the text. | ||
The analysis was then carried out for both bands simultaneously using all assigned transitions: (ν12: 825 transitions and ν13: 323 transitions, total = 1148 transitions), providing a better estimate of molecular parameters for ν12 and ν13 and providing an estimate of the Coriolis interaction between the two upper states. The difference Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) =
= ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) observed −
observed − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calculated between the observed spectrum and a spectrum calculated using the molecular parameters in Table 6 is shown in Fig. 7.
calculated between the observed spectrum and a spectrum calculated using the molecular parameters in Table 6 is shown in Fig. 7.
| Parameter | Fit separately, no interaction included | Coriolis interaction included | Ground statea | ||
|---|---|---|---|---|---|
| ν 12 (separate) | ν 13 (separate) | ν 12 | ν 13 | ||
| a Fixed (see Table 4). | |||||
| ν 0/cm−1 | 896.025095(45) | 837.36315(65) | 896.02513(17) | 837.36303(36) | — |
| A/cm−1 | 0.80716728(40) | 0.808361(12) | 0.80694(14) | 0.80859(14) | 0.808981182 |
| B/cm−1− | 0.66274527(84) | 0.663813(20) | 0.6627467(33) | 0.663822(11) | 0.663976767 |
| C/cm−1 | 0.449280716(23) | 0.4530818(76) | 0.4492788(14) | 0.4530821(42) | 0.44456034 |
| Δ J /10−6 cm−1 | 0.8004(18) | 3.292(73) | 0.8021(67) | 3.398(39) | 0.568432245 |
| Δ K /10−6 cm−1 | 1.08060(42) | 4.17(24) | 1.082(16) | 4.44(13) | 0.849145778 |
| Δ JK /10−6 cm−1 | 0.0286(60) | −5.99(29) | 0.034(23) | −6.36(16) | 0.576555584 |
| δ j /10−6 cm−1 | 0.03073(88) | −1.159(36) | 0.0326(35) | −1.110(19) | 0.158169289 |
| δ k /10−6 cm−1 | 0.7022(15) | 3.977(96) | 0.6953(73) | 4.105(50) | 0.441397695 |
| ϕ J /10−12 cm−1 | 18(2) | 990(190) | 18(8) | 1534(69) | 0.390169922 |
| ϕ JK /10−12 cm−1 | −67(7) | −3570(880) | −74(28) | −5070(450) | 4.62553331 |
| ϕ KJ /10−12 cm−1 | 118(5) | 4800(120) | 139(21) | 3910(600) | −27.6804829 |
| ϕ K /10−12 cm−1 | −70(4) | −2650(800) | −83(16) | −790(260) | 26.5987345 |
| η J /10−12 cm−1 | −12(1) | −650(93) | −11(4) | −381(33) | 0.153506197 |
| η JK /10−12 cm−1 | 50(1) | 2600(270) | 50(5) | 2880(140) | 2.06996535 |
| η K /10−12 cm−1 | −94(5) | −3700(740) | −103(21) | −1540(200) | 1.11080179 |
| ξ z /cm−1 | — | — | 0.116(34) | — | |
| n data | 825 | 323 | 1148 | — | |
| d rms/cm−1 | 0.0003101 | 0.002132 | 0.001176 | — | |
The reduced term values were calculated and examined for further insight into the resonance between ν13 and an as yet unassigned resonance partner, possibly ν14 (predicted to be near 817 cm−1). The reduced term values were calculated by first finding the energy of the upper vibrational level (the transition plus the ground state energy level for  ) and then subtracting the energy of the ground state energy level with
) and then subtracting the energy of the ground state energy level with  . It is apparent that the higher Ka = n states (n = 1, 2, 3) are perturbed, even at low J. This explains the difficulties encountered even while fitting only the lower J value transitions of this band, and the large residuals observed for the ν13 transitions in Fig. 6 and 7. In addition, the calculated relative intensity values (anharmonic vs. harmonic) differ significantly for ν12 and ν13 (Table 2): this is as would be expected in light of the interactions present. Illustrated in Fig. 8 and 9 are direct comparisons between the observed spectrum (black) and the spectrum as calculated (red) using the effective Hamiltonian and the parameters in Table 6 (columns 4–6) (bottom trace). Fig. 8 shows a section of the ν12P-branch region, with the assignments for the Ka and Kc series indicated on the combs above the spectrum. A detailed view of part of the ν12P-branch region, including assignments, is shown in Fig. 9, see also the overview in Fig. 10.
. It is apparent that the higher Ka = n states (n = 1, 2, 3) are perturbed, even at low J. This explains the difficulties encountered even while fitting only the lower J value transitions of this band, and the large residuals observed for the ν13 transitions in Fig. 6 and 7. In addition, the calculated relative intensity values (anharmonic vs. harmonic) differ significantly for ν12 and ν13 (Table 2): this is as would be expected in light of the interactions present. Illustrated in Fig. 8 and 9 are direct comparisons between the observed spectrum (black) and the spectrum as calculated (red) using the effective Hamiltonian and the parameters in Table 6 (columns 4–6) (bottom trace). Fig. 8 shows a section of the ν12P-branch region, with the assignments for the Ka and Kc series indicated on the combs above the spectrum. A detailed view of part of the ν12P-branch region, including assignments, is shown in Fig. 9, see also the overview in Fig. 10.
 | ||
Fig. 9 Comparison of an extended section of the measured P branch transitions (top trace, T = 295 K, l = 18 cm, P ≈ 1.8 mbar, nominal instrumental resolution 0.0015 cm−1) in the ν12 fundamental of c-C2H3DO with a spectrum calculated using the molecular parameters in Table 6 (columns 4–6) and a Gaussian line width with Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc(FWHM) = 0.0015 cm−1. The effective linewidth Δ calc(FWHM) = 0.0015 cm−1. The effective linewidth Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) FWHM ≈ 0.0025 cm−1, typically, for isolated lines in the spectrum. The assignments of the transitions are indicated in the figure. Decadic absorbance lg(I0/I) is shown. FWHM ≈ 0.0025 cm−1, typically, for isolated lines in the spectrum. The assignments of the transitions are indicated in the figure. Decadic absorbance lg(I0/I) is shown. | ||
 | ||
Fig. 10 Overview spectrum of the ν12 fundamental illustrating the calculated (red, top traces) and experimental (black, bottom traces) spectrum. The experimental spectrum (black, bottom) was measured with l = 18 cm, P ≈ 1.8 mbar, and nominal instrumental resolution 0.0015 cm−1. The calculated spectrum (red, top) was calculated using the molecular parameters in Table 6 (columns 4–6) and a Gaussian line width with Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc(FWHM) = 0.0015 cm−1. Decadic absorbance lg(I0/I) is shown. calc(FWHM) = 0.0015 cm−1. Decadic absorbance lg(I0/I) is shown. | ||
Initially, the spectroscopic constants of Watson's A-reduced effective Hamiltonian in the Ir representation for the ν12 state of c-C2H3DO were determined. Next, the transitions identified as belonging to the weaker ν13 band were assigned and fit separately (see Fig. 11). Then, these were added in a stepwise fashion into the analysis of the ν12 fundamental. The sextic parameters ϕJ, ϕKJ, ϕJK and ϕK of Watson's A reduced effective Hamiltonian were determined, and the Coriolis interaction between the ν12 and the ν13 state was estimated.
We first included only ξz in the fit, obtaining a value of 0.116 cm−1 for this parameter, compared to an ab initio estimate of ξz = 0.3. Fixing the parameter at this ab initio value gives an adequate but somewhat less good fit. We also carried out fits adjusting both ξz and exy, which improved the fit further, but still with limited physical significance. Given the relatively large uncertainties in the sextic parameters (ϕ, η) we also tried to fix these at their ground state values and adjusted only up to the quartic parameters. This, however, resulted in significantly less good representations of the experimental data. We thus consider the two options for sets of effective Hamiltonian parameters to be a reasonable compromise to best represent the experimental data. This improved the root mean square deviation to drms = 0.001164 cm−1. Nevertheless, it should be clear that the sextic parameters obtained in this way have large uncertainties and very limited physical significance, being “effective” parameters only (see also below). The transitions used in the fit are listed in the ESI† for this paper. Table 6 presents the parameters obtained for the excited vibrational states. The complete tables of the assigned lines can be found in the ESI.† It is important to note that these two fundamentals are not the only ones in this part of the infrared spectrum. As is seen in Table 1, the ν14 fundamental with a predicted band center around 817 cm−1 might also be interacting with ν13 and ν12: this band is significantly weaker and must be characterized to complete the analysis of the polyad spectrum in this region. Furthermore, the lowest fundamental, ν15, is also close, with possible further interactions. The parameters presented in Table 6 should thus be considered “effective” parameters including the influence of such interactions. The analysis of overlapping bands, as well as that of additional measurements of monodeuterated oxirane up to 3600 cm−1, is in progress and will be the subject of future publications.
The spectrum of c-C2H3DO in this region was simulated based on the parameters given in Table 6 (columns 4–6). Fig. 10 illustrates successive enlargements of the ν12 band in the P branch region. The extra transitions which cannot be reproduced by the simulation are associated with the undeuterated or doubly deuterated isotopomers c-C2H4O and c-C2H2D2O, or in some cases with dichloromethane, which were all present as impurities in the sample, without affecting the high-resolution analyses of the spectra.
 | ||
Fig. 11 Comparison of an extended section of the measured P-branch transitions (top trace, T = 295 K, l = 18 cm, P ≈ 1.8 mbar, nominal instrumental resolution 0.0015 cm−1) in the ν13 fundamental of c-C2H3DO with a spectrum calculated using the molecular parameters in Table 6 (columns 4–6) and a Gaussian line width with Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) calc(FWHM) = 0.0015 cm−1. The effective linewidth (full width at half maximum) Δ calc(FWHM) = 0.0015 cm−1. The effective linewidth (full width at half maximum) Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) FWHM ≈ 0.0025 cm−1, typically, for isolated lines in the spectrum. The assignments of the transitions are indicated in the figure. Decadic absorbance lg(I0/I) is shown. FWHM ≈ 0.0025 cm−1, typically, for isolated lines in the spectrum. The assignments of the transitions are indicated in the figure. Decadic absorbance lg(I0/I) is shown. | ||
6 Discussion and conclusions
High resolution spectroscopy provides one of the most powerful techniques to study the structure and dynamics of polyatomic molecules.76,77 It also allows us to identify structures in remote locations, from the Earth's atmosphere78 to interstellar space.79 Notably, for chiral structures there is so far little information available about their prevalence in the interstellar medium, and D1-oxirane is so far the only isotopically chiral molecule identified by astrophysical spectroscopy and, with the related methyl oxirane,80 one of so far overall two chiral structures identified in the interstellar medium. On the other hand, D1-oxirane can also be related to its achiral isomers with the relevant isotopomers of acetaldehyde (CH3CHO) vinyl alcohol (CH2CHOH) or methylhydroxycarbene (CH3COH), which are all interesting candidates for detection by astrophysical spectroscopy. In addition, detecting chiral compounds by planetary or interstellar spectroscopy opens a route towards detecting enantiomeric excess by means of high resolution vibrational circular dichroism spectra as proposed in ref. 22 as a possible signature of life (see also ref. 81–83). While this goes beyond current astrophysical detection, it provides further motivation for the future high-resolution study of such structures.22Building on our previous work on the GHz and THz far infrared rotational spectra of monodeutero-oxirane,14 we have obtained here a first analysis of high resolution rotation–vibration spectra of this molecule. This paves also the way for future astrophysical observations in the infrared region of the spectra which may become possible.18–21 The present analysis of the ν12 and ν13 fundamentals provides sufficiently accurate effective Hamiltonian parameters for the representation of the spectra including interpolation of data in the observed ranges of quantum numbers. At the same time, we have extended the boundaries of our accurate knowledge of the spectrum of the vibrational ground state, which can provide a benchmark for such a small to medium size molecule.
Future work in our currently ongoing investigations aims at extending the analysis to the lower frequency fundamentals ν14 and ν15, as well as further fundamentals extending into the mid to near infrared, and to further chiral isotopomers.15 Finally, fundamental studies of parity violation in chiral molecules will profit from the high resolution results of the present work.1–5 Also, monodeutero-oxirane is sufficiently small to serve as a benchmark molecule for theories relating spectra of chiral molecules to their quantum structure and dynamics by full-dimensional rotation–vibration calculations including even parity violation.56–60,84–88
Data availability
All relevant data are included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Schweizerischer Nationalfonds (including support initially under the Marie Heim-Vögtlin Program and grant no 200021-207787), ETH Zürich, an ERC Advanced Grant, COST MOLIM, COST COSY and the AGS (Alliance for Global Sustainability) is gratefully acknowledged, as well as help from and discussions with Carine Manca Tanner, Eduard Miloglyadov, Andreas Schneider, Georg Seyfang, Guido Grassi, Reto Ulrich, Daniel Zindel and Fabian Hobi, and Leon Becht, and in particular also continued support from Frédéric Merkt.References
- M. Quack, Angew. Chem., 1989, 101, 588 ( Angew. Chem., Int. Ed. Engl. , 1989 , 28 , 571 ) CrossRef CAS.
- R. Berger, G. Laubender, M. Quack, A. Sieben, J. Stohner and M. Willeke, Angew. Chem., 2005, 117, 3689 ( Angew. Chem., Int. Ed. , 2005 , 44 , 3623 ) CrossRef; see also A. Sieben, R. Berger, M. Quack and M. Willeke, Proc. 18th Coll. High Resol. Mol. Spectroscopy, Dijon, paper F4, 2003, p. 161 Search PubMed.
- M. Hippler, E. Miloglyadov, M. Quack and G. Seyfang, Mass and Isotope Selective Infrared Spectroscopy, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 2, pp. 1069–1118 Search PubMed.
- M. Quack, G. Seyfang and G. Wichmann, Chem. Sci., 2022, 13, 10598 RSC.
- M. Quack, Fundamental Symmetries and Symmetry Violations from High Resolution Spectroscopy, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 659–722 Search PubMed.
- M. Quack, Chem. Phys. Lett., 1986, 132, 147 CrossRef CAS.
- J. E. Dickens, W. M. Irvine, M. Ohishi, M. Ikeda, S. Ishikawa, A. Nummelin and A. Hjalmarson, Astrophys. J., 1997, 489, 753 CrossRef CAS.
- A. Nummelin, J. E. Dickens, P. Bergman, A. Hjalmarson, W. M. Irvine, M. Ikeda and M. Ohishi, Astron. Astrophys., 1998, 337, 275 CAS.
- M. Ikeda, M. Ohishi, A. Nummelin, J. E. Dickens, P. Bergman, A. Hjalmarson, W. M. Irvine and S. Ishikawa, Astrophys. J., 2001, 560, 792 CrossRef CAS.
- M. A. Requena-Torres, J. Martín-Pintado, S. Martín and M. R. Morris, Astrophys. J., 2008, 672, 352 CrossRef CAS.
- J. M. Lykke, A. Coutens, J. K. Jørgensen, M. H. D. van der Wiel, R. T. Garrod, H. S. P. Müller, P. Bjerkeli, T. L. Bourke, H. Calcutt, M. N. Drozdovskaya, C. Favre, E. C. Fayolle, S. K. Jacobsen, K. I. Öberg, M. V. Persson, E. F. van Dishoeck and S. F. Wampfler, Astron. Astrophys., 2017, 597, A53 CrossRef.
- L. S. Bernstein and D. K. Lynch, Astrophys. J., 2009, 704, 226 CrossRef CAS.
- S. Albert, K. Keppler Albert, P. Lerch and M. Quack, Faraday Discuss., 2011, 150, 71 RSC.
- S. Albert, Z. Chen, K. Keppler, P. Lerch, M. Quack, V. Schurig and O. Trapp, Phys. Chem. Chem. Phys., 2019, 21, 3669 RSC.
- Z. Chen, S. Albert, K. Keppler, M. Quack, V. Schurig and O. Trapp, Proc. 2021 Int. Symposium on Molecular Spectroscopy, Urbana, IL, USA, paper WJ01, 2021, p. 182.
- J. K. Jørgensen, M. H. D. van der Wiel, A. Coutens, J. M. Lykke, H. S. P. Müller, E. F. van Dishoeck, H. Calcutt, P. Bjerkeli, T. L. Bourke, M. N. Drozdovskaya, C. Favre, E. C. Fayolle, R. T. Garrod, S. K. Jacobsen, K. I. Öberg, M. V. Persson and S. F. Wampfler, Astron. Astrophys., 2016, 595, A117 CrossRef.
- H. S. P. Müller, J. K. Jørgensen, J.-C. Guillemin, F. Lewen and S. Schlemmer, Mon. Not. R. Astron. Soc., 2023, 518(1), 185 CrossRef.
- P. Jakobsen, P. Ferruit, C. Alves de Oliveira, S. Arribas, G. Bagnasco, R. Barho, T. L. Beck, S. Birkmann, T. Böker, A. J. Bunker, S. Charlot, P. de Jong, G. de Marchi, R. Ehrenwinkler, M. Falcolini, R. Fels, M. Franx, D. Franz, M. Funke, G. Giardino, X. Gnata, W. Holota, K. Honnen, P. L. Jensen, M. Jentsch, T. Johnson, D. Jollet, H. Karl, G. Kling, J. Köhler, M.-G. Kolm, N. Kumari, M. E. Lander, R. Lemke, M. López-Caniego, N. Lützgendorf, R. Maiolino, E. Manjavacas, A. Marston, M. Maschmann, R. Maurer, B. Messerschmidt, S. H. Moseley, P. Mosner, D. B. Mott, J. Muzerolle, N. Pirzkal, J.-F. Pittet, A. Plitzke, W. Posselt, B. Rapp, B. J. Rauscher, T. Rawle, H.-W. Rix, A. Rödel, P. Rumler, E. Sabbi, J.-C. Salvignol, T. Schmid, M. Sirianni, C. Smith, P. Strada, M. te Plate, J. Valenti, T. Wettemann, T. Wiehe, M. Wiesmayer, C. J. Willott, R. Wright, P. Zeidler and C. Zincke, Astron. Astrophys., 2022, 661, A80 CrossRef CAS.
- P. Ferruit, P. Jakobsen, G. Giardino, T. Rawle, C. Alves de Oliveira, S. Arribas, T. L. Beck, S. Birkmann, T. Böker, A. J. Bunker, S. Charlot, G. de Marchi, M. Franx, A. Henry, D. Karakla, S. A. Kassin, N. Kumari, M. López-Caniego, N. Lützgendorf, R. Maiolino, E. Manjavacas, A. Marston, S. H. Moseley, J. Muzerolle, N. Pirzkal, B. Rauscher, H.-W. Rix, E. Sabbi, M. Sirianni, M. te Plate, J. Valenti, C. J. Willott and P. Zeidler, Astron. Astrophys., 2022, 661, A81 CrossRef CAS.
- T. Böker, S. Arribas, N. Lützgendorf, C. Alves de Oliveira, T. L. Beck, S. Birkmann, A. J. Bunker, S. Charlot, G. de Marchi, P. Ferruit, G. Giardino, P. Jakobsen, N. Kumari, M. López-Caniego, R. Maiolino, E. Manjavacas, A. Marston, S. H. Moseley, J. Muzerolle, P. Ogle, N. Pirzkal, B. Rauscher, T. Rawle, H.-W. Rix, E. Sabbi, B. Sargent, M. Sirianni, M. te Plate, J. Valenti, C. J. Willott and P. Zeidler, Astron. Astrophys., 2022, 661, A82 CrossRef.
- S. M. Birkmann, P. Ferruit, G. Giardino, L. D. Nielsen, A. García Muñoz, S. Kendrew, B. J. Rauscher, T. L. Beck, C. Keyes, J. A. Valenti, P. Jakobsen, B. Dorner, C. Alves de Oliveira, S. Arribas, T. Böker, A. J. Bunker, S. Charlot, G. de Marchi, N. Kumari, M. López-Caniego, N. Lützgendorf, R. Maiolino, E. Manjavacas, A. Marston, S. H. Moseley, N. Pirzkal, C. Proffitt, T. Rawle, H.-W. Rix, M. te Plate, E. Sabbi, M. Sirianni, C. J. Willott and P. Zeidler, Astron. Astrophys., 2022, 661, A83 CrossRef CAS.
- M. Quack, Adv. Chem. Phys., 2014, 157, 249 Search PubMed.
- A. Bacmann, A. Faure and J. Berteaud, ACS Earth Space Chem., 2019, 3(6), 1000 CrossRef CAS.
- B. E. Turner and A. J. Apponi, Astrophys. J., 2001, 561, L207 CrossRef CAS.
- H. E. Matthews, P. Friber and W. M. Irvine, Astrophys. J., 1985, 290, 609 CrossRef CAS.
- P. Coll, J.-M. Bernard, R. Navarro-González and F. Raulin, Astrophys. J., 2003, 598(1), 700 CrossRef CAS.
- C. Puzzarini, A. Baiardi, J. Bloino, V. Barone, T. E. Murphy, H. D. Drew and A. Ali, Astrophys. J., 2017, 154, 82 Search PubMed.
- C. Puzzarini, M. Biczysko, J. Bloino and V. Barone, Astrophys. J., 2014, 785, 107 CrossRef PubMed.
- J.-M. Flaud, W. J. Lafferty, F. Kwabia Tchana, A. Perrin and X. Landsheere, J. Mol. Spectrosc., 2012, 271, 38 CrossRef CAS.
- C. Medcraft, C. D. Thompson, E. G. Robertson, D. R. T. Appadoo and D. McNaughton, Astrophys. J., 2012, 753, 1 CrossRef.
- H. Hollenstein, D. Luckhaus, J. Pochert, M. Quack and G. Seyfang, Angew. Chem., Int. Ed. Engl., 1997, 36, 140 CrossRef CAS.
- R. A. Nyquist and W. Putzig, Appl. Spectrosc., 1986, 40, 112 CrossRef CAS.
- T. Nakanaga, J. Chem. Phys., 1980, 73, 5451 CrossRef CAS.
- T. Nakanaga, J. Chem. Phys., 1981, 74, 5384 CrossRef CAS.
- D. K. Russell and R. Wesendrup, J. Mol. Spectrosc., 2003, 217(1), 59 CrossRef CAS.
- R. A. Creswell and R. H. Schwendeman, Chem. Phys. Lett., 1974, 27, 521 CrossRef CAS.
- C. Hirose, Astrophys. J., 1974, 189, L145 CrossRef CAS.
- C. H. Townes and A. Schawlow, Microwave Spectroscopy, Dover, New York, 1975 Search PubMed.
- L. Pan, S. Albert, K. V. L. N. Sastry, E. Herbst and F. C. De Lucia, Astrophys. J., 1998, 499, 517 CrossRef.
- F. Kwabia Tchana, J. M. Flaud, W. J. Lafferty and M. Ngom, Mol. Phys., 2014, 112, 1633 CrossRef CAS.
- M. Ngom, J.-M. Flaud, F. Kwabia-Tchana, W. J. Lafferty, X. Landsheere, A. Perrin and El. A. Ngom, Can. J. Phys., 2013, 91, 906 CrossRef CAS.
- W. J. Lafferty, J.-M. Flaud, F. Kwabia Tchana and J. M. Fernandez, Mol. Phys., 2013, 111, 1983 CrossRef CAS.
- C. Hirose, Bull. Chem. Soc. Jpn., 1974, 47(6), 1311 CrossRef CAS.
- H. S. P. Müller, J. K. Jørgensen, J.-C. Guillemin, F. Lewen and S. Schlemmer, J. Mol. Spectrosc., 2023, 394, 111777 CrossRef.
- M. Suter and M. Quack, Appl. Opt., 2015, 54, 4417 CrossRef CAS PubMed.
- S. Albert, K. Albert Keppler and M. Quack, Trends Opt. Photonics, 2003, 84, 177 Search PubMed; S. Albert, K. Keppler, V. Boudon, P. Lerch and M. Quack, J. Mol. Spectrosc., 2017, 337, 105 CrossRef CAS.
- S. Albert, K. Keppler and M. Quack, High Resolution Fourier Transform Infrared Spectroscopy, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 2, pp. 965–1019 Search PubMed.
- F. Kwabia Tchana, M. Ngom, A. Perrin, J.-M. Flaud, W. J. Lafferty, S. A. Ndiaye and El. A. Ngom, J. Mol. Spectrosc., 2013, 292, 1 CrossRef CAS.
- S. Albert, Z. Chen, Ph Lerch, K. Keppler, M. Quack, V. Schurig and O. Trapp, in Proceedings of the XXth Symposium on Atomic, Cluster and Surface Physics (SASP2016), Davos, Switzerland, 7–12 February, Innsbruck University Press, Innsbruck, 2016, ISBN 078-903122-04-08, 2016, pp. 161–164.
- S. Albert, Z. Chen, Ph Lerch, K. Keppler, M. Quack, V. Schurig and O. Trapp, 72nd International Symposium on Molecular Spectroscopy, Urbana, IL, USA, 17–21 June 2017, paper WA01 DOI:10.15278/isms.2017.WA01.
- K. K. Albert, S. Albert, M. Quack, J. Stohner, O. Trapp and V. Schurig, in Proceedings of the 19th Colloquium on High-Resolution Molecular Spectroscopy, Salamanca, Spain, 11–16 September 2005, Paper H15.
- S. Albert, K. Keppler, C. Manca Tanner, M. Quack, Z. Chen, J. Stohner, P. Lerch, V. Schurig and O. Trapp, in proceedings of the 26th Colloquium on High-Resolution Molecular Spectroscopy, Dijon, France, 26–30 August 2019.
- G. Guelachvili and K. Narahari Rao, Handbook of Infrared Standards, Academic Press, London, UK, 1986 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. M. A. Brett, J. G. Frey, R. Hinde, Y. Kuroda, R. Marquardt, F. Pavese, M. Quack, J. Stohner and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry, Abridged version, IUPAC & Royal Society of Chemistry, Cambridge, 4th edn, 2023 Search PubMed; E. R. Cohen, T. Cvitas, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry, 3rd Printing, IUPAC & Royal Society of Chemistry, Cambridge, 3rd edn, 3rd Printing, 2011 Search PubMed.
- M. Quack and J. Stohner, Chimia, 2005, 59, 530 CrossRef CAS.
- M. Quack, J. Stohner and M. Willeke, Annu. Rev. Phys. Chem., 2008, 59, 741 CrossRef CAS PubMed.
- M. Quack and J. Stohner, Z. Phys. Chem., 2000, 214, 675 Search PubMed; M. Quack and J. Stohner, Phys. Rev. Lett., 2000, 84, 3807 CrossRef CAS PubMed.
- M. Quack and J. Stohner, Chirality, 2001, 13, 745 CrossRef CAS PubMed.
- M. Quack and J. Stohner, J. Chem. Phys., 2003, 119, 11228 CrossRef CAS.
- J. Stohner, Int. J. Mass Spectrom., 2004, 233, 385 CrossRef CAS.
- J. K. G. Watson. in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier, Amsterdam, 1978, vol. 6, pp. 1–89 Search PubMed.
- S. Albert, K. Keppler Albert, H. Hollenstein, C. Manca Tanner and M. Quack, Fundamentals of Rotation–Vibration Spectra, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 117–173, LOOM4WANG was coded by Fabio Mariotti Search PubMed.
- D. Luckhaus and M. Quack, Mol. Phys., 1989, 68(3), 745 CrossRef CAS.
- F. Merkt and M. Quack, Molecular Quantum Mechanics and Molecular Spectra, Molecular Symmetry, and Interaction of Matter with Radiation, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 1–55 Search PubMed.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371 CrossRef CAS.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221 CrossRef CAS; C. M. Western and B. E. Billinghurst, Phys. Chem. Chem. Phys., 2019, 21, 13986 RSC; C. M. Western and B. E. Billinghurst, Phys. Chem. Chem. Phys., 2017, 19, 10222 RSC; C. M. Western, Introduction to Modeling High-Resolution Spectra, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1 Search PubMed.
- L. S. Rothman, I. E. Gordon, A. Barbe, D. Chris Benner, P. F. Bernath, M. Birk, V. Boudon, L. R. Brown, A. Campargue, J.-P. Champion, K. Chance, L. H. Coudert, V. Danaj, V. M. Devi, S. Fally, J.-M. Flaud, R. R. Gamache, A. Goldmann, D. Jacquemart, I. Kleiner, N. Lacome, W. J. Lafferty, J.-Y. Mandin, S. T. Massie, S. N. Mikhailenko, C. E. Miller, N. Moazzen-Ahmadi, O. V. Naumenko, A. V. Nikitin, J. Orphal, V. I. Perevalov, A. Perrin, A. Predoi-Cross, C. P. Rinsland, M. Rotger, M. Šimecková, M. A. H. Smith, K. Sung, S. A. Tashkun, J. Tennyson, R. A. Toth, A. C. Vandaele and J. Vander Auwera, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 533 CrossRef CAS.
- I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcisło, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Császár, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Müller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. Vander Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949 CrossRef CAS.
- A. Bauder, Fundamentals of Rotational Spectroscopy, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 2, pp. 57–116 Search PubMed.
- G. Wichmann, G. Seyfang and M. Quack, Mol. Phys., 2021, 119(17–18), e1959073 CrossRef.
- B. P. Winnewisser, J. Reinstädtler, K. M. T. Yamada and J. Behrend, J. Mol. Spectrosc., 1989, 136, 12 CrossRef CAS . LW5.11 code: Fred Stroh.
- S. Albert, M. Winnewisser and B. P. Winnewisser, Ber. Bunsenges. Phys. Chem., 1996, 100, 1876 CrossRef CAS.
- S. Albert, K. Albert Keppler and M. Quack, J. Mol. Struct., 2004, 695–696, 385 CAS.
- S. Albert, H. Hollenstein, M. Quack and M. Willeke, Mol. Phys., 2004, 102, 1671 CrossRef CAS.
- F. Merkt and M. Quack, Molecular Quantum Mechanics and Molecular Spectra, Molecular Symmetry, and Interaction of Matter with Radiation, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, ch. 1, vol. 1, pp. 1–55 Search PubMed.
- M. Quack, Bunsenmagazin, 2022, 24, 238 Search PubMed.
- J.-M. Flaud and J. Orphal, Spectroscopy of the Earth's Atmosphere, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 3, pp. 1971–1992 Search PubMed.
- L. M. Ziurys, Millimeter and Submillimeter Wave Spectroscopy and Astrophysical Applications, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 2, pp. 934–964 Search PubMed.
- Y. Ellinger, F. Pauzat, A. Markovits, A. Allaire and J.-C. Guillemin, Astron. Astrophys., 2020, 633, A49 CrossRef CAS.
- M. Quack, Angew. Chem., Int. Ed., 2002, 41, 4618 CrossRef CAS PubMed.
- R. Berger, M. Quack and J. Stohner, Angew. Chem., Int. Ed., 2001, 40, 1667 CrossRef CAS PubMed.
- M. Quack, Chem. Phys. Lett., 1986, 132(2), 147 CrossRef CAS.
- Y. Yamaguchi and H. F. Schaefer III, Analytic Derivative Methods in Molecular Electronic Structure Theory, A New Dimension to Quantum Chemistry and its Applications to Spectroscopy, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 325–362 Search PubMed.
- J. Tennyson, High Accuracy Rotation Vibration Calculations in Small Molecules, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 551–572 Search PubMed.
- T. Carrington, Using Iterative Methods to Compute Vibrational Spectra, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, 2011, vol. 1, pp. 573–586 Search PubMed.
- A. G. Császár, C. Fábri and T. Szidarovszky, Exact Numerical Methods for Stationary State Based Quantum Dynamics of Complex Polyatomic Molecules, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, 2021, ch. 2, pp. 43–78 Search PubMed.
- C. Fabri, R. Marquardt, A. G. Császár and M. Quack, J. Chem. Phys., 2019, 150, 01402 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00880h |
| This journal is © the Owner Societies 2025 |