Factors governing the protonation of Keggin-type polyoxometalates: influence of the core structure in clusters

Abstract

Atomic substitution is a promising approach for controlling structures and properties for developing clusters with desired responses. Although many possible coordination candidates could be deduced for substitution, not all can be prepared. Therefore, predicting the correlation between structures and physical properties is important prior to synthesis. In this study, regarding Keggin-type polyoxometalates (POMs) as a model cluster, the dominant factors affecting the protonation were investigated by atomic substitutions and geometry changes. The valence of Keggin-type POMs and the constituent elements of the cluster shell structure affect the charge and potential distribution, which change the protonation sites. Furthermore, the valence of Keggin-type POMs and the bond length between the core and shell structure determine the protonation energy. These factors also affect the HOMO–LUMO gap, which governs photochemical and redox reactions. These governing factors derived from actual parameters of the α-isomer of Keggin-type POMs enabled us to deduce the protonation energy of the β-isomer, which is more difficult to prepare and isolate than the α-isomer.

---

Introduction

Atomically precise nanoclusters such as polyoxometalates (POMs) are of great interest in various fields because of their characteristic structures, electronic states, and designable physicochemical properties.^1–4 Moreover, the properties of these clusters can be modified through partial atomic substitution in the framework and central parts and isomerisation.^5–7 The progress in synthetic procedures for nanoclusters including POMs enables us to control their conformations.^8–11 Nevertheless, the relationship between coordination and the properties of POMs has been deduced quantitatively only in a few cases.¹² POMs have been investigated for use in electronic devices, catalysts and sensors.^1,13–17 Protonation and deprotonation of POMs, which occur under acidic and basic conditions or in situ, are extremely important for their catalytic activities in many reactions, such as hydrogenation, dehydrogenation, oxygen reduction and hydrogen evolution,^18–20 and for model materials of molecular adsorption–desorption stimuli.^19–24 The redox behaviour of nanoclusters, as well as POMs with protonation and deprotonation, has been extensively investigated under various acidic and basic conditions.^25–29 Tuning protonation and deprotonation properties based on control of the coordination environment may broaden the range of POM applications.

This paper is the first report on the assessment of factors which govern the locations and energies of protonation of α- and β-isomers of Keggin-type POMs ([XM₁₂O₄₀]^z−: XM₁₂, X: heteroatom, B(III), Al(III), Ga(III), Si(IV), Ge(IV), P(V), As(V), and S(VI); M: addenda metal, Mo(VI) and W(VI)). These consist of a core structure XO₄ and a shell structure M₁₂O₃₆ (Fig. 1), which is similar to other nanoclusters (e.g., thiolate-protected Au₂₅ and Au₃₈ clusters are formed by core structures Au₁₃ and Au₂₃ with shell structures Au₁₂ and Au₁₅). Density functional theory (DFT) calculations demonstrated the estimation of the first protonation location and the first protonation energy by taking into consideration the type of addenda metal M, the bond length between the core and shell, and total charge z, respectively. The combination of valences and bond lengths of α-isomers, which are the most stable isomers that can be prepared, enabled us to predict the first protonation energies of β-isomers with high precision, indicating no need for isolation of β-isomers. Furthermore, these parameters can also allow us to speculate on HOMO–LUMO gaps (i.e., parameters corresponding to optical responses). These results provide universal descriptors for various physicochemical properties of Keggin-type POMs, which implies the importance of the core state of nanoclusters for their physicochemical properties.

Fig. 1 Polyhedral representation of the structure of (a) α- and (b) β-isomers of Keggin-type POMs ([XM₁₂O₄₀]^z−) with labelled oxygens and addenda metals. Red balls, the pink tetrahedron, and grey pyramid-shaped pentahedra are oxygen, the core structure of XO₄, and the fraction of MO₆ octahedra, respectively.

Experimental

Electronic structure calculations

We performed DFT calculations and conducted natural bond orbital (NBO) analysis using Gaussian16 revision C.01. The M06 functional was selected for exchange and correlation functionals.³⁰ The basis set comprised SDD^31,32 and cc-pVDZ^33–35 for the addenda metal M and other elements, respectively. Furthermore, SDD was used as the effective core potential (ECP) for the addenda metal M.^36–38 For comparison, Lanl2DZ was also used as a basis set and ECP.^33,39–41 The aprotic solvent, acetonitrile, was characterised using the PCM method^42–45 with ε = 36.64. The POMs separated by solvent were modelled without using the periodic boundary condition (see the .chk files of the ESI† for more details of the calculations).

For all models, geometry optimisation was performed without considering symmetry. Subsequently, vibrational frequencies were calculated to validate the local minima of structures and calculate Gibbs energies. All energies represent Gibbs energies at 298 K unless otherwise specified.

Protonation energies are given as:

E(H_ad) = E(HXM₁₂) − E(XM₁₂) (1)

where E(H_ad), E(HXM₁₂), and E(XM₁₂) respectively represent the energies of a proton, protonated XM₁₂, and bare XM₁₂. The energy of protonation, proton has no electron, is considered to be 0 and is not included in eqn (1).

Molecular electrostatic potential (MEP) surfaces, along with an electronic density isosurface (ρ = 10⁻³ e⁻ au⁻³), were visualised. To highlight differences between adsorption sites, the MEP values were changed in their total charge (−0.485 to −0.380 for divalent; −0.385 to −0.295 for trivalent; −0.285 to −0.210 for tetravalent; and −0.195 to −0.125 for pentavalent).

Computational models

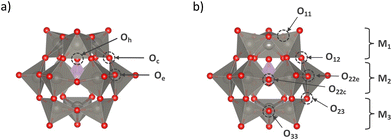
This study specifically addressed the α- and β-isomers of XM₁₂ with T_d and C_3v symmetry, respectively (Fig. 1). Bridged oxygen in the shell M₁₂O₃₆ structure was reported to be favourable for protonation.^46,47 In particular, non-equivalent bridged oxygen atoms, which were labelled based on symmetry, were identified as potential protonation sites. For α-XM₁₂, the corner-sharing oxygen between MO₆ octahedra, edge-sharing oxygen between MO₆ octahedra, and the oxygen in the central XO₄ tetrahedra were denoted as O_c, O_e, and O_h, respectively. Since three types of geometric arrangements of M were generated by π/3 rotation of an M₃O₁₃ unit in β-XM₁₂, respective Ms were represented with the indices as 1, 2, and 3 from the top to the bottom of the structure (Fig. 1(b)). The bridged oxygen was denoted as O_ij (i,j = 1,2,3) using the bonded M indices. Only O₂₂ needed to be denoted as O_22c and O_22e to identify corner-sharing or edge-sharing oxygen, respectively. Protons may strongly interact with the oxygen with the smallest E(H_ad) among all non-equivalent oxygen in each model. The O–H bond formed by protonation could slant from the plane of M–O–M. Therefore, we calculated such O–H bonds slanted to the right and left sides from the plane of M–O–M in advance to select the stable one as the protonated model. The .xyz files of the ESI† provide more details on the calculation models.

The bond valence sum⁴⁸ was used to convert bond lengths to empirical bond valences. According to the empirical equation in the report, bond lengths d (Å) were converted to bond valences s (−) using the following equation;

s = exp((d₀ − d)/0.37) (2)

where the d₀ values were 1.907 (Å) for Mo and 1.917 (Å) for W, respectively.

Results and discussion

Protonation sites

If nanoclusters work as catalysts, the protonation sites strongly affect the reactivity, such as product selectivity and yields. In addition, protonation sites are still unclear for α- and β-forms of the Keggin-type POMs although they were investigated with model compounds and limited types of POMs.^46,47,49 The first protonation sites of the Keggin-type POMs were explored by DFT calculations to elucidate the relationship between the type of addenda metal M and the total charge (z) of the POMs (Table S1†). Table 1 provides the most favoured protonation sites in [XM₁₂O₄₀]^z− (X = B, Al, Ga, Si, Ge, P, As, S; M = Mo, W). The protonation sites changed depending on z in the α-isomers: In the case of molybdenum POMs, the preferred protonation site changed when total charge z increased from 3 to 4 in the α-isomers, while there was no change in the β-isomers, which will be discussed in detail in subsequent sections. It is noted that the results obtained from calculations at the M06/cc-pVDZ and SDD levels, as employed in this study, reproduced the experimentally obtained protonation sites (specifically, O₁₂ at β-PW₁₂ and β-PMo₁₂).^50,51 However, calculations under a major condition (M06/Lanl2DZ level) failed to replicate these results (Table S2†). This disparity should come from the electron polarisation of oxygen atoms, which is an important factor for determining the protonation site. The calculation conditions in this study provided better concordance with the HOMO–LUMO gaps obtained from experiments than that reported in earlier works (Table S3†). This calculation setting can reflect both local (i.e., protonation sites) and global (i.e., the electronic structure of the entire cluster) features.

Table 1 Preferred protonation site

		α-isomer		β-isomer
X	z	M = Mo	M = W	M = Mo	M = W
B	5	Oe	Oe	O12	O22e
Al	5	Oe	Oe	O12	O22e
Ga	5	Oe	Oe	O12	O22e
Si	4	Oe	Oe	O12	O12
Ge	4	Oe	Oe	O12	O12
P	3	Oc	Oc	O12	O12
As	3	Oc	Oc	O12	O12
S	2	Oc	Oc	O12	O12

---

First protonation site of α-isomers

The dominance of the first protonation site was investigated based on the total charge (z) of α-isomers with high symmetry and low structural complexity. Fig. 2 shows the NBO charges for each bridged oxygen species of unprotonated α-XM₁₂ with bars representing the determined protonation sites at the bottom. The oxygen sites with smaller charges exhibit stronger coulombic attraction to protons. For α-GeW₁₂, the NBO charges of the two bridged oxygen sites were almost identical in a protonation energy difference of only 3.65 meV between O_e and O_c. Consequently, the NBO charge of the protonation sites is closely linked to the stability of the protonated structures.

Fig. 2 NBO charge on O_c and O_e without protonation in (a) α-XMo₁₂ and (b) α-XW. Red and blue plots represent NBO charge on O_c and O_e, respectively.

The charges of O_e gradually decreased with the increasing total charge (z) of POMs, while the charges of O_c increased. This difference of O_c and O_e in the charge trend could lie in the O–M bonding states: the O_c–M bonds are shorter than that of O_e–M in all of the POMs (Table S5†), which indicates that the O_c–M bond should induce higher covalency than the O_e–M bond. Under that assumption, the change of total charge (z), which originated from the replacement of heteroatoms (X), affects O–M bonding states, leading to excess electrons accumulating in the core structure of XO₄.⁵² The increase in electrons within the core structure may enhance the ionicity of O_e–M bonds (i.e., decreasing their covalency) and the covalency of O_c–M bonds, corresponding to a decrease in the charge of O_e and an increase in the charge of O_c, respectively. The charges of respective oxygen, O_e and O_c, in the reduced form of [PW₁₂O₄₀]³⁻ were calculated to investigate the effect of total charge on the charges of O_e and O_c (Fig. S1†). In the case of changing only the valence atom without changing the heteroatom, as excess electrons to reduce from [PW₁₂O₄₀]³⁻ are delocalised, both O_e and O_c charges decreased with an increase in the valence. Particularly, the decrease in the charge of O_e was more than that in O_c, which is similar to as shown in Fig. 2. This result indicates that excess electrons derived from the valence change cause an inversion of the order of the charge between O_c and O_e (i.e., change in the protonation site). Only α-BM₁₂ was different from the others in terms of the protonation site due to a characteristic electronic structure, related to the small size of the BO₄ core structure, where the HOMO consists of an orbital XO₄ core structure rather than a M₁₂O₃₆ shell structure.⁵²

First protonation sites of β-isomers

The factors influencing the manipulation of the first protonation sites were explored in β-isomers using both total charge and the addenda metal element M. NBO charges of O₁₂ and O_22e, corresponding to O_c and O_e in the α-isomers, respectively, as protonation sites in β-isomers were calculated, as shown in Fig. 3. The bars at the bottom of the figure indicate the protonation sites determined from protonation energies. A comparison of the charge amounts with protonation sites clarifies that bridged oxygen atoms with larger negative charges serve as protonation sites, except for β-BMo₁₂. The changes in the NBO charges of O₁₂ and O_22e are similar to those of O_c and O_e. However, the trend of the change in the charge of O_22e in β-XMo₁₂ was slightly different from those of β-XW₁₂ and α-XM₁₂ because of the pseudo-Jahn–Teller effect, which resulted in cluster distortion generated from more shrinkage of d orbitals in a Mo atom than a W atom.⁵² This effect enhances the covalency of bonds,^55,56 which results in a near plateau behaviour in Fig. 3(a) by offsetting charge decreases from the natural ionicity of the O_22e site and charge increases with the covalency. The pseudo-Jahn–Teller effect is particularly pronounced when the HOMO–LUMO gap of the system is narrow.⁵⁷ β-Isomers of Keggin-type POMs have a narrower HOMO–LUMO gap than α-isomers (Table S4†),^58,59 indicating that only the β-XMo₁₂ isomer exhibits the pseudo-Jahn–Teller effect. These results suggest that the difference in the change in charges is due to the O–M bond characteristics.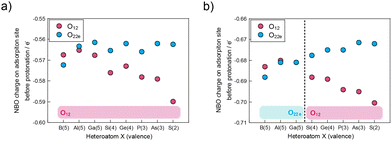

Fig. 3 NBO charge on O₁₂ and O_22e without protonation in (a) β-XMo₁₂ and (b) β-XW₁₂. Magenta and sky-blue plots represent NBO charge on O₁₂ and O_22e, respectively.

The preferential first protonation sites were explored considering both electronic effects and structural effects, to find the reasons why O₁₂ and O_22e were appropriate for protonation sites in β-isomers, considering both electronic effects and structural effects. The charge of each bridged oxygen was calculated with a proton to find electronic factors that determine the preferential protonation sites (Fig. 4). O_22e was the most appropriate site for gathering electrons by protonation. Regarding the proton, O_22e emerged as the most effective electron-donating site during protonation (Fig. S2†). These findings indicate that O_22e increases its own charges and donates electrons to the proton, which leads to forming a stable O–H bond as a covalent bond.

Fig. 4 Box plot of NBO charge change on the adsorption site by protonation in (a) β-XMo₁₂ and (b) β-XW₁₂. The upper and lower whiskers, respectively, represent the maximum and minimum values. Magenta, sky-blue, and grey boxes represent the change in NBO charge on O₁₂, O_22e, and other adsorption sites, respectively.

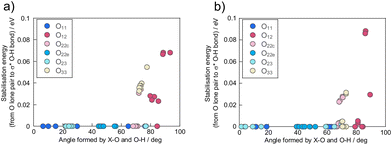
The conformational effects on the first protonation sites were investigated in terms of the angle formed by the heteroatom, protonated oxygen, and proton (X⋯O–H) to obtain box–whisker plots at each bridged oxygen (Fig. 5). Oxygen such as as O₁₂, O_22c and O₂₃, corresponding to O_c in the α-isomer form large angles of X⋯O–H, while oxygen such as as O₁₁, O_22e, O₃₃, corresponding to O_e in the α-isomer form small angles. Similarly, O_c in the α-isomers formed larger X⋯O–H angles than O_e (Fig. S3†). Isomerisation from α-isomers to β-isomers by a π/3 rotation of a M₃O₁₃ unit induces distortion in the region between M₁ and M₂ in the Keggin-type POMs,⁵⁰ contributing to O₁₂ displaying the largest X⋯O–H angle. The X⋯O–H angle near 0 degrees corresponds to the proton being adsorbed normally to the surface of the POM clusters, whereas the angle near 90 degrees corresponds to the proton being adsorbed tangentially to the surface of the POMs. The first proton protonated to O₁₂ approaches the surface of the Keggin-POMs closely. We deduced that the first proton adsorbed on O₁₂ was stabilised by some interactions with another oxygen, including hydrogen bonds.

Fig. 5 Box plot illustrating the relationship between the adsorption sites and protonation angles, angles between X–O and O–H in (a) β-XMo₁₂ and (b) β-XW₁₂. The upper and lower whiskers represent the maximum and minimum values. Points lying outside the whisker are regarded as outliers.

Hydrogen bond strength is associated with the stabilisation energy resulting from charge transfer from the lone pair of hydrogen-bonded oxygen to the σ* antibonding orbital in the hydroxy group, as determined by NBO analysis.⁶⁰ In the context of NBO analysis, the stabilisation energy arises from the hybridisation of a donor and acceptor level in NBO orbitals, employing the second-order perturbation theory (Fig. S4†). Because the orbital shapes of both donor and acceptor levels are strongly related to hydrogen bond formation, we investigated the relationship between protonation angles and the stabilisation energies from hydrogen bond formation (Fig. 6). The reddish and bluish colour plots respectively correspond to protonation sites derived from O_c and O_e. This relationship reflects that oxygen with large X⋯O–H angles forms a strong hydrogen bond, and the same correlations were also observed in α-isomers (Fig. S5†). However, the hydrogen bond alone is insufficient for a full explanation on the observed conformational effect, because its strength is one order of magnitude less than that of a typical hydrogen bond.

Fig. 6 Relationship between stabilisation energy and the protonation angles, angles between X–O and O–H in (a) β-XMo₁₂ and (b) β-XW₁₂. Reddish and bluish regions correspond to O_c derived and O_e derived bridge oxygen.

The spatial charge distribution arising from nuclei and electron structures within the system forms regions of cation-attractive and cation-repulsive forces in the vicinity of cluster surfaces. The MEP of β-PM₁₂ and the other POMs on the same electron density surface are shown in Fig. 7 and S6,† with the red and blue regions, corresponding to proton-attractive and proton-repulsive regions, respectively. In terms of the coulombic interaction with the bridged oxygen itself, the MEP indicates that preferential protonation occurs on O_22e rather than on O₁₂, in accordance with the site preference observed in the electronic effect. Additionally, considering the neighbour potentials, the red region near O₁₂ serves as a site for proton binding and stabilisation, making the protonation on O₁₂ preferred. The protons adsorbed to O₁₂ of all β-isomers verge toward this region (please refer to the .chk files in the ESI†). O₁₂ has the highest capacity to stabilise protons through coulombic interaction, primarily because O₁₂ exhibits strong negative potentials at the position where the verged proton is located (i.e., structural effect).

Fig. 7 MEP mappings in (a) β-PMo₁₂, (b) β-PW₁₂, and (c) the pristine model of β-PM₁₂. Reddish and bluish regions in MEP mappings represent proton-attractive and repulsive regions.

The electronic states of the site and spatial interaction with the target atom or molecule determine the adsorption site on a cluster.

Protonation energies

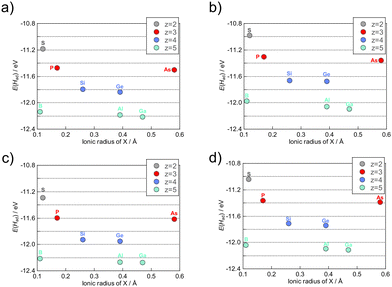
The acid–base characteristics of the cluster and consideration of the environment around the cluster, such as the solvents, are needed to consider the protonation energies of a cluster which are related to pK_a according to the equation: pK_a = −E(H_ad)/ln(10)RT, where R and T are the gas constant and temperature. Furthermore, understanding the trend and controlling factors of first protonation energies can be extended to the adsorption of other atoms or molecules. The factors of the protonation energies on Keggin-type POMs were investigated. The protonation energy of each XM₁₂ was used for a value of the most stable protonation site among the available protonation sites (Table S1†). These values were in general agreement with the experimental values (Table S6†). Since first protonation energies are continuous values, a quantitative prediction of these energies requires continuous values of the factors. Therefore, we examined the relationship between the ionic radii of the heteroatom and protonation energies, to confirm whether the first protonation energies depend on the ionic radii or the total charge of POMs (Fig. 8). The results suggest that protonation energies depend on the ionic radii and the total charge (z) of POMs, while addenda metals are not clearly shown to affect protonation energies since binary values are not enough quantitatively to evaluate the influence. Thus, quantitative effects of the addenda metals on the protonation energies were not covered in this paper. The β-XMo₁₂ isomer exhibited the lowest first protonation energies among α-XM₁₂ and β-XM₁₂, which is attributed to the higher covalency and harder basicity of O–M bonds, as discussed in the earlier section, in accordance with the Hard and Soft Acids and Base (HSAB) theory. As acidity increases with the T–O–T angle increasing in zeolites,⁶¹ the first protonation energies increased with the M–O–M angle increasing in the Keggin-type POMs (Fig. 7 and Table S5†).

Fig. 8 Relationship between the proton adsorption energy and the ionic radius of the heteroatom in (a) α-XMo₁₂, (b) α-XW₁₂, (c) β-XMo₁₂, and (d) β-XW₁₂. Plot colours correspond to the total charge of POMs’ z.

It is important to predict the chemical and physical properties of novel clusters prior to their synthesis. A promising strategy involves predicting such properties of cluster groups which are difficult to be prepared and isolated such as the β-isomer of Keggin-type POMs because of their instability,⁵⁹ using properties of cluster groups which can be easily prepared and isolated such as the α-isomer of Keggin-type POMs. The first protonation energy was predicted using the data obtained from the α-isomers. The redox potentials of the Keggin-type POMs were strongly related to bond valences between addenda metals and oxygen (O_h) bound to the heteroatoms determined empirically from the concept of the bond valence sum⁴⁸ and the total charge of POMs.¹² Regression analysis for the first protonation energy was carried out from bond valences and total charge considering the dependence of the first protonation energies on the ionic radii of heteroatoms and the total charge of XM₁₂. The equation of the bond valence sum (see eqn (2)) is related to the ionic radii of heteroatoms according to the change of the O_h position between M and X. Fig. 9 illustrates the results of the regression analysis for protonation energies by cluster total charge and bond valence. R² values of ≥0.997 were achieved for all addenda metal M and isomers, even without any information on the protonation sites of each POM. The first protonation energies of β-isomers could be obtained by regression from only those of α-isomers.

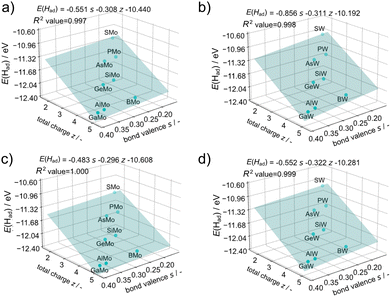Fig. 9 Protonation energy regression with the total charge of POMs’ z and the bond valence s in (a) α-XMo₁₂, (b) α-XW₁₂, (c) β-XMo₁₂, and (d) β-XW₁₂.

The bond valence sum concept originates from inorganic crystal studies. To assess its applicability to clusters, the bond valences obtained through DFT calculations were compared with those determined using the empirical equation (Fig. S7†). However, there was no correlation between them; they exhibit a good correlation except for X = B (Fig. S8†). The distinctive electronic structure of BM₁₂ and the different components of HOMO⁵³ may cause the difference between the DFT calculation and the empirical value. On the other hand, the regression with empirical values in Fig. 9 and S9† showed good correlation, even including BM₁₂, which suggests that the actual descriptor is not the bond valence but the bond length of O_h–M in the empirical equation. It is particularly interesting that no significant change was found in the size of the shell structure M₁₂O₃₆ with varying heteroatoms (X).⁵⁴ For that reason, the sum of bond lengths of X–O_h and O_h–M remained almost constant irrespective of X. Therefore, the first protonation energies could be governed by the X–O_h bond length and total charge of the core structure of XO₄. Because the shell structure of M₁₂O₃₆ (M = W⁶⁺ and Mo⁶⁺) has no valence in the fully oxidised form, protonation at the shell structure of M₁₂O₃₆ is governed by the properties of the core structure of XO₄.

Predicting other properties from factors governing the first protonation

The atom adsorption/desorption events, represented by the first protonation energies, can be predicted by the total charge of POMs and bond valence, which may predict the other events as well as redox potential.¹² To this end, HOMO–LUMO gaps, parameters corresponding to the optical response, were selected as a target property of POMs for regression (Fig. 10 and S10†). As described earlier, BM₁₂ exhibits a different HOMO structure, thus, the regression was conducted except for X = B. The HOMO–LUMO gap trend corresponds to an increase in band gaps with valence increases, driven by an increase in the LUMO level.⁵²Fig. 10 exhibits the total charge (z) of POMs and the bond valence (s) of α-isomers also governs the optical responses.

Fig. 10 Regression of the HOMO–LUMO gap with the total charge of POMs’ z and the bond valence s (a) in α-XMo₁₂, (b) in α-XW₁₂, (c) in β-XMo₁₂, and (d) in β-XW₁₂.

Additionally, these factors can also predict the NBO charges of XO₄ core structures (Fig. S11 and S12†), which implies that various events involving a cluster can be controlled by the manipulation of the core–shell interaction such as charge transfer through a change of these governing factors.

Conclusion

In Keggin-type POMs, the first protonated position was found to be governed by the addenda metal species and total charge. The addenda metal species M affected the charge of the adsorption site through the pseudo-Jahn–Teller effect and covalency of the M–O bond. In the β-isomers, two sites were found to be preferential protonation sites: O_22e, which is bound covalently to a proton, and O₁₂, which forms hydrogen bonds and interactions between the proton and special distributed potential.

The first protonation energy was found to be governed by the total charge and the O_h–M bond length. It is noted that the protonation energy of the β-isomers was predicted with high accuracy using the bond length of the α-isomers which can be obtained experimentally. Chemical and physical properties of the β-isomers, which are experimentally difficult to prepare and isolate, could be predicted from the parameters of the α-isomers.

These parameters have previously been demonstrated as factors governing the redox potential.¹² In this paper, we found that these parameters also act as controlling factors for the protonation energy and the HOMO–LUMO gap (optical response). This finding demonstrates the versatility of these parameters. This knowledge not only provides a way to control various physical properties of Keggin-type POMs, but can also contribute to the elucidation of the governing factors for the diverse events of other core–shell structured nanoclusters such as metal nanoclusters.^62–64 Indeed, many protons were coupled with POMs depending on the pH and reduction levels of POMs. If DFT calculations, similar to the present study, are conducted for POMs with more than one proton, multiple protonation sites could be clarified, which will be investigated in the future.

Conflicts of interest

There is no conflict to declare.

Acknowledgements

This work was partly achieved using the supercomputer system at the Information Initiative Center, Hokkaido University, Sapporo, Japan. This work was partly carried out at the Joint Research Center for Environmentally Conscious Technologies in Materials Science (Project No. 02304) at ZAIKEN, Waseda University. In addition, this study was supported by a Grant-in-aid for Scientific Research (No. 25410095) from the Ministry of Education, Culture, Sports, Science and Technology of Japan, the JSPS Core-to-Core Collaboration in Advanced Research Network, the International Network on Polyoxometalate Science for Advanced Functional Energy Materials and the Centre for Functional Nano Oxide at Hiroshima University, Takahashi Industrial and Economic Research Foundation (12-003-147), and Cabinet Office grant-in-aid, Evolution to Society 5.0 Agriculture Driven by IoP (Internet of Plants), Japan.

References

1. X. Kang, Y. Li, M. Zhu and R. Jun, Chem. Soc. Rev., 2020, 49, 6443–6514.
2. X. Kang and M. Zhu, Chem. Soc. Rev., 2019, 48, 2422–2457.
3. N. A. Gadjieva, A. M. Champsaur, M. L. Steigerwald, X. Roy and C. Nuckolls, Eur. J. Inorg. Chem., 2020, 14, 1245–1254.
4. W. W. Xu, X. C. Zheng and Y. Gao, Acc. Chem. Res., 2018, 51(11), 2739–2747.
5. T. Higaki, Q. Li, M. Zhou, S. Zhao, Y. Li, S. Li and R. Jin, Acc. Chem. Res., 2018, 51(11), 2764–2773.
6. T. Kawawaki, Y. Imai, D. Suzuki, S. Kato, I. Kobayashi, T. Suzuki, R. Kaneko, S. Hossain and Y. Negishi, Eur. J. Chem., 2020, 26(69), 16150–16193.
7. V. Singh, Priyanka, P. V. More, E. Hemmer, Y. K. Mishra and P. K. Khanna, Mater. Adv., 2021, 2, 1204–1228.
8. S. Wang, Q. Li, X. Kang and M. Zhu, Acc. Chem. Res., 2018, 51(11), 2784–2792.
9. S. Hossain, Y. Niihori, L. V. Nair, B. Kumar, W. Kurashige and Y. Negishi, Acc. Chem. Res., 2018, 51(12), 3114–3124.
10. X. Kang and M. Zhu, Coord. Chem. Rev., 2019, 394, 1–38.
11. E. Khatun and T. Pradeep, ACS Omega, 2021, 6(1), 1–16.
12. K. Nakajima, K. Eda and S. Himeno, Inorg. Chem., 2010, 49(11), 5212–5215.
13. D. Bain, S. Maity and A. Patra, Phys. Chem. Chem. Phys., 2019, 21, 5863–5881.
14. L. Chen, A. Black, W. J. Parak, C. Klinke and I. Chakraborty, Aggregate, 2022, 3(4), e132.
15. D.-D. Qin, Y. Tang, G. Ma, L. Qin, C.-L. Tao, X. Zhang and Z. Tang, Int. J. Hydrogen Energy, 2021, 46(51), 25771–25781.
16. T. Ueda, ChemElectroChem, 2018, 5, 823–838.
17. T. Ueda, Anal. Sci., 2021, 37, 107–118.
18. G. Sun and P. Sautet, Acc. Chem. Res., 2021, 54(20), 3841–3849.
19. H. Shun, S. Xiang, Z. Xu, C. Liu, X. Li, C. Sun, S. Lin, B. K. Keo and N. Zheng, Nano Res., 2020, 13, 1908–1911.
20. Q. Tang, G. Hu, V. Fung and D.-E. Jiang, Acc. Chem. Res., 2018, 51(11), 2793–2802.
21. C. Simms, A. Kondinski and T. N. P. Vogt, Eur. J. Inorg. Chem., 2020, 27, 2559–2572.
22. A. Patel and R. Sadasivan, Prog. Mater. Sci., 2021, 118, 100759.
23. R. Liu and C. Streb, Adv. Energy Mater., 2021, 11(25), 2101120.
24. E. Janusson, N. D. Kler, L. V. Nadal, D.-L. Long and L. Cronin, Chem. Commun., 2019, 55, 5797–5800.
25. W. Zhou, N. Ogiwara, Z. Weng, N. Tamai, C. Zhao, L.-K. Yan and S. Uchida, Chem. Commun., 2021, 57, 8893–8896.
26. L. Yang, J. Lei, J.-M. Fan, R.-M. Yuan, M.-S. Zheng, J.-J. Chen and Q.-F. Dong, Adv. Mater., 2021, 33(50), 2005019.
27. B. Fabre, C. Falaise and E. Cadot, ACS Catal., 2022, 12(19), 12055–12091.
28. S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115(11), 4893–4962.
29. B. Yu, B. Zou and C.-W. Hu, J. CO₂ Util., 2018, 26, 314–322.
30. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
31. T. H. Dunning Jr. and P. J. Hay, in Modern Theoretical Chemistry, ed. H. F. Schaefer III, Plenum, New York, 1977, vol. 3, 1–28.
32. L. V. Szentpály, P. Fuentealba, H. Preuss and H. Stoll, Chem. Phys. Lett., 1982, 93(6), 555–559.
33. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
34. D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358–1371.
35. E. R. Davidson, Chem. Phys. Lett., 1996, 260, 514–518.
36. A. Nicklass, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1995, 102, 8942–8952.
37. T. Leininger, A. Nicklass, H. Stoll, M. Dolg and P. Schwerdtfeger, J. Chem. Phys., 1996, 105, 1052–1059.
38. X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147.
39. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
40. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
41. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
42. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
43. S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245.
44. J. L. P. Ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127–1138.
45. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
46. W. Guan, L.-K. Yan, Z.-M. Su, E.-B. Wang and X.-H. Wang, Int. J. Quantum Chem., 2006, 106, 1860–1864.
47. X. López, C. Bo and J. M. Poblet, J. Am. Chem. Soc., 2002, 124, 12574–12582.
48. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
49. X. López, I. A. Weinstock, C. Bo, J. P. Sarasa and J. M. Poblet, Inorg. Chem., 2006, 45(16), 6467–6473.
50. T. Ueda, K. Kodani, H. Ota, M. Shiro, S.-X. Guo, J. F. Boas and A. M. Bond, Inorg. Chem., 2017, 56, 3990–4001.
51. T. Ueda and K. Isai, Anal. Sci., 2013, 29(4), 447–453.
52. X. López, J. J. Carbó, C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537–7571.
53. I.-M. Mbomekallé, X. López, J. M. Poblet, F. Sécheresse, B. Keita and L. Nadjo, Inorg. Chem., 2010, 49, 7001–7006.
54. F. Steffler, G. F. D. Lima and H. A. Duarte, J. Mol. Struct., 2020, 1213, 128159.
55. L. Yan, X. López, J. J. Carbó, R. Sniatynsky, D. C. Duncan and J. M. Poblet, J. Am. Chem. Soc., 2008, 130(26), 8223–8233.
56. I. B. Bersuker, Chem. Rev., 2013, 113, 1351–1390.
57. I. B. Bersuker, Chem. Rev., 2021, 121, 1463–1512.
58. X. López, J. M. Maestre, C. Bo and J. M. Poblet, J. Am. Chem. Soc., 2001, 123(39), 9571–9576.
59. X. López and J. M. Poblet, Inorg. Chem., 2004, 43, 6863–6865.
60. M. G. Siskos, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2015, 13, 8852–8868.
61. M. Boronat and A. Corma, Catal. Lett., 2015, 145, 162–172.
62. S. Yamazoe, S. Takano, W. Kurashige, T. Yokoyama, K. Nitta, Y. Negishi and T. Tsukuda, Nat. Commun., 2016, 7, 10414.
63. M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130(18), 5883–5885.
64. H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132(24), 8280–8281.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt00799a

---