On the brink of self-hydration: the water heptadecamer

Abstract

For pure, neutral, isolated molecular clusters, (H₂O)₁₇ marks the transition from structures with all water molecules on the cluster surface to water self-hydration, i.e., cluster structures around one central water molecule. Getting this right with water model potentials turns out to be challenging. Even the best water potentials currently available, which reproduce collective properties very well, still deliver contradicting results for (H₂O)₁₇, when different low-energy isomers from global structure optimizations are examined. Interestingly, ab initio quantum chemistry also struggles with the only seemingly simple question if (H₂O)₁₇ is all-surface or water-centered. Hence, although the long history of water potential development may be entering its final phase, it is not quite finished yet.

---

1 Introduction

For many decades, no water potential came close to capturing most or all macroscopic properties of water correctly.^1–4 Recently, however, several newly developed potentials have claimed this achievement, including the q-AQUA and q-AQUA-pol potentials^5–7 and the MB-pol potential,^8–13 with its most recent incarnation MB-pol (2023).¹⁴ See citations in these references and in recent reviews^3,4,15–17 for a comprehensive overview of the water potential landscape that is far too vast to be covered here.

In these studies, impressive agreement between experimental data and simulations employing q-AQUA(-pol) and MB-pol was shown, for many bulk-collective properties and for small clusters (H₂O)_n, n = 2, 3,…, 6. However, while the water hexamer has long been recognized as the smallest water cluster with a significant multitude of minimum-energy structures that differ qualitatively (prism, cage, book, etc.), it still is a very small cluster. As a general rule for atomic and molecular clusters, this automatically means that energy differences between the lowest-energy hexamer isomers are relatively large. In contrast, for larger clusters these low-lying energy differences quickly shrink towards zero.

In fact, it is well established that huge qualitative differences in global minimum-energy structures are fairly rare for (H₂O)_n up to n = 16, even if older water potentials are employed, including TIP4P¹⁸ or the TTMx-F series.^19–21 The simple reasons for this finding are the preference of water for cubes and pentagonal prisms, and the surprisingly numerous possibilities for building clusters (H₂O)_n for 8 ≤ n ≤ 16 from fused cubes and pentagonal prisms.

At the same time, for n ≤ 16 there essentially is no low-energy way to avoid having all water molecules on the cluster surface. In contrast, for n = 17 it is geometrically and energetically feasible for the first time to have one water molecule in the cluster center, with all other water molecules forming a first hydration shell around it.

The above has been pointed out already 20 years ago.²² Using global cluster structure optimization, it was demonstrated that the very different water models TIP4P and TTM2-F essentially agree on global minimum-energy structures for (H₂O)_n up to n ≤ 16 but then strongly diverge for n = 17 and n = 21. In particular, for these two sizes TIP4P features all-surface structures while TTM2-F favors molecule-centered isomers. Incidentally, the TTM2-F structures were later confirmed as energetically lower at the MP2/aug-cc-pVTZ level.²³ For (H₂O)₁₇, this result was later again confirmed²⁴ at the CCSD(T)/aug-cc-pVTZ level – but the calculations reported below cast some doubt on that. Incidentally, this latter study found a new (H₂O)₁₆ global minimum-energy candidate at this level, comprised of two fused pentagonal prisms, which turned out to be 2–4 kJ mol⁻¹ lower in energy than the previous best candidate consisting of three fused cubes. This again nicely illustrates the well-known preference for cubes and pentagonal prisms, and the surprising versatility of these as cluster building blocks.

As mentioned above, so far studies with q-AQUA, q-AQUA-pol and MB-pol2016/2023 either have not included clusters larger than (H₂O)₆ or have not examined (H₂O)₁₇ in detail.²⁵ Even the impressively comprehensive and detailed water model comparison by Herman and Xantheas¹⁷ focused only on one (water-centered) isomer for this cluster size. Hence, it is interesting to find out how these potentials fare for (H₂O)₁₇ when used in global cluster structure optimization, i.e., when the most important low-energy isomers of this cluster size are examined, which is the topic of this contribution.

2 Computational methods

To quickly and unbiasedly generate a large pool of global minimum-energy candidate structures for (H₂O)₁₇, we have used the original q-AQUA and MB-pol potential implementations, as well as the other water models mentioned below, as backends for energy calculations and local structure optimizations in our OGOLEM suite^26–28 for global structure optimization.

OGOLEM employs genetic/evolutionary algorithms (GA/EA) as non-deterministic global optimization method.^29–32 The power of this approach has been proven in numerous studies, ranging from abstract benchmarks³³ and real-life benchmarks^34–36 to real-world applications.^37,38 Special expertise for water clusters has been collected with various potentials, including NEMO,³⁹ TIP4P,^35,40–47 TTM2-F^48,49 and TTM3-F.^34,50,51

Original source codes for q-AQUA, q-AQUA-pol, MB-pol2016 and MB-pol2023 were obtained from their respective websites,^52–54 compiled, tested and interfaced with OGOLEM.

For (H₂O)₁₇ and each of the q-AQUA and MB-pol potentials, 10–20 global optimization runs of 25k steps were performed, collecting not only global minimum-energy candidates but also interesting low-energy local minima. In each case, the best global minimum-energy candidate was found repeatedly, in about 50% of the runs. Similar sets of global optimizations were also done for TIP3P, TIP4P, TIP4P/2005⁵⁵ and TTM3-F, all natively implemented in OGOLEM, and with the AMOEBA⁵⁶ and AMOEBA+^57,58 water potentials that were coupled to OGOLEM via its interface to TINKER.^59,60 Only a small but representative subset of all these globally optimized structures is presented here. Of course, structures found with one water potential were locally re-optimized with the other water potentials. As further complement of the spectrum of methods, also the semiempirical method GFN2-xTB^61,62 and the GFN-FF⁶³ force field derived from it were employed.

Similarly, these structures were also re-optimized locally at various density-functional theory (DFT) and ab initio theory levels of quantum chemistry. For these calculations, the Orca package⁶⁴ v5.0.4 was employed. For DFT, the range-separated hybrid functional ωB97X-V⁶⁵ and the double-hybrid functional B2PLYP^66,67 were used, with basis sets ranging from def2-TZVP to def2-QZVPPD⁶⁸ and without and with D4 dispersion correction.^69,70 This was complemented by wavefunction-based explicit correlation approaches, namely SCS-MP2⁷¹ and DLPNO-CCSD(T)⁷² with RIJCOSX,^73,74 both with fixed basis sets (from triple-zeta to quintuple-zeta) and with complete basis set extrapolation (CBS). Following Kjaergaard,⁷⁵ also f12 basis sets were used at the CCSD(T) level. To make contact to the large body of work on the water hexamer in the literature, results for these levels of theory for (H₂O)₆ are compiled in the ESI.†

Obviously, the levels of ab initio methods could be refined even further. As pointed out by Klopper et al. for the water dimer,⁷⁶ core–valence correlation leads to further small corrections. As indicated by Lane,⁷⁷ employing non-perturbative triples in CC-theory or including quadruples makes sense only if scalar-relativistic and diagonal-non-Born–Oppenheimer corrections are also calculated, which are not easily accessible in practice for systems as large as (H₂O)₁₇. However, these levels of refinement were not used in the ab initio data q-AQUA and MB-pol were trained on. Additionally, structure re-optimizations at the CCSD(T)-level arguably could be more important than all these corrections. For reasons of prohibitive computational costs, no local re-optimizations were done here at the CCSD(T) level; instead, only single-point calculations were done, using the structures locally re-optimized at the B2PLYP-D4/def2-TZVPPD level.

In summary, global cluster structure optimizations were performed with all water potentials, the pairwise-additive fixed-point-charge ones (TIP3P, TIP4P, TIP4P2005), the polarizable ones (TTM3-F, AMOEBA, AMOEBA+) and the machine-learning many-body models (q-AQUA and MB-pol). From the collected results of these global optimizations, a small but representative subset of structures was selected. These structures were then locally re-optimized with all water potentials and at all levels of DFT and ab initio theory, with the single exception of CCSD(T) (in several variants). For these CCSD(T) approaches, only single-point calculations were performed, for the structures locally optimized at the B2PLYP-D4/def2-TZVPPD level.

In all cases for which local optimizations were done, the cluster structures remained qualitatively the same, no conversion from one structure to any other one was observed. Nevertheless, as it is standard, accidental convergence of local optimizations to saddle points was excluded by frequency calculations. For all structures shown here, all frequencies were real (and positive or zero), not a single imaginary frequency was found. Hence, all these structures are true minima.

I am deliberately not including any zero-point vibrational energy (ZPVE) correction, since the focus here is on performance for bare potential energies. ZPVE can be included with any efficiency only in the harmonic approximation, which for differing hydrogen-bond patterns likely introduces errors much larger than the small potential energy differences shown in the results section below. In an alternative approach already in 1996, Liu et al.⁷⁸ have used a rigid-monomer water potential in fully anharmonic diffusion quantum Monte-Carlo calculations for the remaining nuclear degrees of freedom, showing for the hexamer that ZPVE corrections on the order of 5000 cm⁻¹ caused a reversal of the energy ordering of prism versus cage, from the prism being favored by 213 cm⁻¹ without ZPVE to the cage being favored by 62 cm⁻¹ with ZPVE. This hexamer finding was confirmed by the Bowman group in their q-AQUA paper,⁵ using a similar approach. With inclusion of intramolecular degrees of freedom and for the larger clusters under study here, this situation would be exacerbated even more towards small differences between large numbers, which is never favorable for accuracy. Finally, for water potentials fitted to experimental data one could argue that these indirectly contain ZPVE (which makes their comparisons below somewhat skewed). However, both q-AQUA-pol and MB-pol were fitted to ZPVE-free ab initio data, such that their comparisons on a ZPVE-free level should be more meaningful.

Many quantum-chemical cluster studies use counterpoise corrections of basis set superposition errors (BSSE). Despite the long history of this concept (and its correction), arguments persists to this day⁷⁹ that what is usually seen as BSSE is in large parts actually basis set imbalance, from which it follows that counterpoise corrections may or may not work. This nicely ties in with typical findings in the applied quantum-chemistry literature of the past 30 years: counterpoise corrections are sometimes found to be a necessary improvement, while at other times results without counterpoise correction are significantly better. In the current context, the ab initio data used for q-AQUA and MB-pol fitting do employ BSSE corrections while for example the study by Xantheas et al.²⁴ does not. Here, I am not employing BSSE corrections, for three reasons: (1) whether BSSE is based on basis set incompleteness artifacts or basis set imbalance, it has to disappear in the CBS limit, and be very small for large basis sets; both situations are targeted here. (2) As pointed out by Klopper et al.,⁷⁶ BSSE corrections should be complemented by structural fragment/monomer relaxations, leading to further and possibly larger corrections. (3) In this study, I am not trying to establish dissociation energies into monomers but instead compare different fully hydrogen-bonded cluster isomers of the same size, with not identical but very similar water–water neighborhoods. For such direct isomer comparisons, both the usual “ghost basis” prescription for the electronic part and the fragment/monomer relaxation becomes awkward or even impossible. Furthermore, artificially referring each isomer structure to a fully dissociated collection of water monomers, just for counterpoise and relaxation purposes, may actually induce additional errors, by having monomer sets with different ghost basis sets and geometries, and by compounding two different BSSE and geometry corrections (isomer1–monomers and isomer2–monomers), which may or may not lead to cancellation of BSSE/geometry correction errors.

As a practical note of caution, standard convergence thresholds and standard grids of Orca (and other quantum-chemistry packages) were not sufficient to provide a clear-cut energy ordering at the DFT/ab initio level. This was detected accidentally, when local geometry optimizations from slightly different starting structures at the double-hybrid DFT level ended up with an energy difference of 0.75 kJ mol⁻¹, although they should have been exactly identical and indeed seemed visually identical in molecular viewers (later re-examination showed small deviations of 0.01 Å in a few oxygen–oxygen distances and of 1° in a few angles and dihedrals between water molecules). Requesting tighter convergence thresholds and denser grids (in Orca: verytightSCF, verytightopt, defgrid3 and Stol 10⁻⁷) resulted in disappearance of the very tiny structure deviations just mentioned and in lowering the energy differences into a range of 0.0004–0.08 kJ mol⁻¹, which is small enough for the comparison scale presented in the Results section below. Note that this is an artifact of the DFT/ab initio energy scale (zero of energy at dissociation into isolated electrons and nuclei). Since the model potentials have their zero of energy at dissociation into isolated water molecules, their standard (and fairly loose) convergence thresholds suffice to produce an energy error bar on the order of <0.001 kJ mol⁻¹, well below the accuracy of the present comparison.

As a final side note, the CCSD(T) calculations revealed that the T1 diagnostic for all structures is in the range of 0.0086–0.0096. This is well below the threshold of 0.02 for multireference character, justifying the single-reference quantum-chemical treatments used here, as to be expected for these systems.

3 Results and discussion

The lowest-energy (H₂O)₁₇ structures emerging from the production calculations described above can be sorted into the four groups depicted in Fig. 1. “Prisms” is a stack of two pentagonal prisms, with a water dimer attached across a square side face. Similarly, “cubes” is a stack of three cubes, with a single water molecule added to an edge. “Twisted cubes” essentially consists of two non-aligned cubes joined by several bridging water molecules. All these structures have all water molecules at the cluster surface. Only in “w-centered” structures there is one inner water molecule, surrounded by a hydration shell consisting of four-, five- and six-membered water rings.

Fig. 1 The four main structural types of (H₂O)₁₇, with their one-letter abbreviations used below.

Incidentally, these essentially are the same four structural types as shown in Fig. 2 of ref. 24, although there the optimal hydrogen-bond patterns were not present in all cases. Given the small energy differences between these four structural types, different H-bond patterns may easily change their energy ordering. To illustrate this, while still keeping the number of structures presented sufficiently small to avoid confusion, a few different H-bond patterns and three actual but subtle changes of the water molecule frameworks will be added in the following. Specifically, four different H-bond patterns in the p-class are shown (p1 through p4), one minor but important structural change in the t-class (t1 and t2), three H-bond variations and one structural change in the w-class (w1 through w4), and one different water attachment location in the c-class (c1 and c2). All global minimum-energy candidates found in the global structure optimization runs are contained in this set. Atomic coordinates (xyz files) and depictions of all these structures can be found in the ESI.†

Fig. 2 summarizes the findings for the top-level ab initio/DFT approaches used here. For clarity, short abbreviations for the actual levels of theory are used: “e34” stands for CBS extrapolation of DLPNO-CCSD(T), using the Orca-implemented CBS extrapolation formulae and its parameters, employing the def2-TZVPP and def2-QZVPP bases. “ccsdt/f12” designates DLPNO-CCSD(T) with the cc-pVQZ-F12 basis set, with an augmented quintuple-zeta auxiliary basis set for the correlation calculation. “ccsdt/qz” is the isolated DLPNO-CCSD(T)/def2-QZVPP result of the above “e34” calculation. Note that the above three theory levels were performed as single-point calculations, for the structures locally optimized at the “b2plyp” level mentioned just below. The following three levels were all accompanied with local structure optimizations. “mp2” is short for SCS-MP2/def2-TZVPPD. “b2plyp” designates the double-hybrid B2PLYP-D4/def2-TZVPPD level. “wb97” stands for ωB97M-D4/def2-TZVPPD. RIJCOSX was used in all calculations. Note that for each individual level of theory, its best structure was chosen as “zero” for the comparison of relative energies. Tabulated numerical values for relative and absolute energies are provided in the ESI.†

Fig. 2 Ab initio/DFT results for the full set of 12 structures, representing the four structural types shown in Fig. 1. Abbreviations for theory levels are explained in the text.

To briefly summarize the contents of Fig. 2: either p1 or w1 are the best structures, in all cases. We have e34, ccsdt/qz and b2plyp favoring p1 over w1 (or t1), and ccsdt/f12, mp2 and wb97 favoring w1 over p1 (or w2). Note that ccsdt/f12 has w1 and p1 only 0.23 kJ mol⁻¹ apart. wb97 has them 2.3 kJ mol⁻¹ apart (with w2 in-between), but this clearly is the lowest ab initio/DFT level. Putting it somewhat differently, the best four structures are always taken from p1, p2, t1, w1, w2, and these span only 1–2 kJ mol⁻¹. As an aside, c1 is never among the first four entries (and c2 is worse still). Interestingly, all this means that these somewhat high-level but still mostly standard ab initio or DFT calculations can NOT decide if all-surface or water-centered is better for (H₂O)₁₇. Not even the CCSD(T) calculations can do that, since it is not necessarily obvious if e34 (predicting the all-surface structure p1) or ccsdt/f12 (favoring water-centered w1) should be considered as more reliable.

Obviously, the applied quantum-chemistry literature is full of examples drilling down such difficult cases to a final decision, by applying increasing levels of further sophistication. However, this is not my aim here. For the present purposes, it is sufficient to show that the global minimum-energy structure for (H₂O)₁₇ in general is not immediately clear with limited-effort ab initio/DFT approaches, and neither is the question all-surface versus water-centered. Whatever the final outcome may be, this clearly indicates that (H₂O)₁₇ is very close to the structural transition from all-surface to water-centered.

While the question all-surface versus water-centered is not really decidable from the data in Fig. 2, results at all theory levels agree upon energy ordering within each of the four groups (with the single exception of w3–w4). This will change in the results reported below.

In the following, results from the various water model potentials will be compared to the above ab initio/DFT results. For this, I am presenting similar plots as in Fig. 2, in which – for visual clarity – the ab initio/DFT results are not repeated individually but instead indiscriminately summarized by the overall areas their results span in this figure, irrespective of the individual levels of theory. Again, tabulated numerical values for all water model potentials can be found in the ESI.† The ESI,† also provides tabulated numerical comparison metrics between the data shown in Fig. 2–6.

The MB-pol2016 and MB-pol2023 results are shown in Fig. 3, in direct comparison to the ab initio/DFT results of Fig. 2, summarized by the shaded areas. As before, the zero of relative energies is given by the lowest energy for each level of theory or each model potential, respectively. The global minimum candidate for MB-pol2030 is p1, which can be interpreted as being in agreement with the quantum-chemistry results. MB-pol2016, however, features c1 as lowest-energy structure, in clear contrast to all levels of quantum-chemistry theory. This seems to be related to both MB-pol versions assigning energies to the c-class that are too low. Both MB-pol versions produce energies that are systematically too high for the class of water-centered structures, in contrast to the quantum-chemistry results that have all-surface and water-centered structures in very close competition. Furthermore, while the energy-ordering trends within all four classes are qualitatively correct, this fails for p4 for both MB-pol versions, and MB-pol2023 has w4 at an energy that is clearly too high. Nevertheless, compared to results shown below, the MB-pol results agree rather well with the quantum-chemistry results.

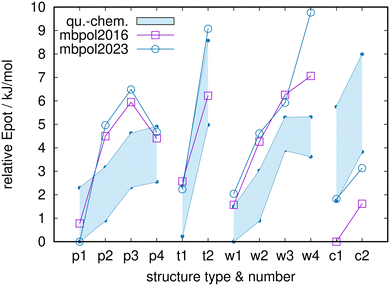Fig. 3 Relative potential energies for MB-pol2016 and MB-pol2023 for the full set of 12 structures, in direct comparison to the quantum-chemistry energies of Fig. 2 (shaded areas). Note the slightly changed span of the ordinate.

The results of q-AQUA and q-AQUA-pol for the twelve structures are displayed in Fig. 4. Water-centered w1 and all-surface t1 are the global minimum candidates for q-AQUA and q-AQUA-pol, respectively, mirroring the quantum-chemistry results pretty well. However, in contrast to the underestimation by MB-pol, the c-class has markedly too high energies here, overshooting the energy range of Fig. 2. Similarly, t2 is too high in q-AQUA, and both model potential variants significantly disadvantage w4. While q-AQUA-pol overall stays closer to the quantum-chemistry results, essentially on-par with the MB-pol2023 deviations, it does change the energy ordering in the p- and w-classes.

Fig. 4 Relative potential energies for q-AQUA and q-AQUA-pol for the full set of 12 structures, in direct comparison to the quantum-chemistry energies of Fig. 2 (shaded areas). Note the markedly extended span of the ordinate.

Fig. 5 compares the quantum-chemistry data to TTM3-F, a traditional but more recent and refined water model potential with smeared charges and polarizabilities, to the recent version AMOEBA+^57,58 of the polarizable AMOEBA water potential,⁵⁶ and to the old veteran TIP4P water model. Interestingly, both TTM3-F and AMOEBA+ agree in having the water-centered w1 as the global minimum candidate, but grossly disadvantage the whole p-class (all-surface), to the extent that the energy spans of the p- and w-classes (almost) do not even overlap, in stark contrast to the quantum-chemistry results. Compared to that, and regarding its intrinsic simplicity, TIP4P does surprisingly well. Another interesting point is that all three approaches invert the energy ordering in the t-class, and only AMOEBA+ gets the energy ordering in the c-class right. Further comparisons to TIP4P/2005 and AMOEBA2014 are shown in the ESI,† because the differences to TIP4P and AMOEBA+, respectively, are fairly small.

Fig. 5 Relative potential energies for TTM3-F, AMOEBA+ and TIP4P for the full set of 12 structures, in direct comparison to the quantum-chemistry energies of Fig. 2 (shaded areas). Note the somewhat extended span of the ordinate.

Finally, to put all this into proper perspective, Fig. 6 compares the quantum-chemistry data to the results of the water model TIP3P, of the semiempirics GFN2-xTB, and of the general force field GFN-FF. Although TIP3P still is heavily used in biochemical simulations, and despite getting w1 right as global minimum candidate, it performs significantly worse here than TIP4P (cf.Fig. 5). This mirrors the well-known bad behavior of TIP3P in collective properties, e.g., the phase diagram.^80–82 While one could argue that the phase diagram is not highly relevant to biochemical simulations at room temperature and standard pressure, energy-ordering of nearest-neighbor water molecules clearly is immediately relevant. I find it interesting that GFN-FF performs only somewhat worse than TIP3P, and that GFN2-xTB performs on par with the approaches shown in Fig. 5, despite the whole set of GFN methods not being designed for accuracy of relative energies.

Fig. 6 Relative potential energies for TIP3P, GFN2-xTB and GFN-FF for the full set of 12 structures, in direct comparison to the quantum-chemistry energies of Fig. 2 (shaded areas). Note the strongly extended span of the ordinate.

On the other hand, when disregarding the quantum-chemistry data areas in Fig. 6 and accepting that the model-potential energy differences are much larger than the quantum-chemistry energy differences (a frequent finding for molecular systems, nicely traced back to a lack of explicit many-body terms in pairwise additive potentials in ref. 17), the overall picture is not too bad, regarding that the p- and w-class are roughly isoenergetic. In this sense, all those biochemical simulations may not be so bad after all.

4 Conclusions

Clearly, there has been a lot of progress in water models, from TIP3P all the way to q-AQUA and MB-pol. If the latter would end up solidly in the quantum-chemistry data windows spanned here, one could declare this development finished, for this particular test. Apparently, however, we are almost but not quite there yet. Of course, this particular test on (H₂O)₁₇ only is a stand-in for larger sets of larger water clusters.

To some extent, one may question the point of this exercise, given that the quantum-chemistry data, at the level used here, cannot pin down the “actual” global minimum candidate for (H₂O)₁₇. Why should water model potentials be required to succeed with that? Indeed, this is not the actual lesson to be learned here. Rather, the lack of clarity in the “naked” ab initio results (even before ZPVE estimations blur the picture further) indicates that further big-data machine-learning efforts are warranted only after greater efforts have been made to make the ab initio reference data even more reliable. If this has been achieved, I hope that patterns of agreements and disagreements similar to those pointed out here in Fig. 3 and 4 may contribute to the next (and possibly final) step of water potential development.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author thanks Prof. F. Paesani for help regarding proper use of the MB-pol potential routines and Dr J. M. Dieterich for unwavering support, maintenance and development of the OGOLEM framework. Funding by the DFG (Deutsche Forschungsgemeinschaft), grant number Ha2498/16-2, is gratefully acknowledged.

References

1. B. Guillot, J. Mol. Liq., 2002, 101, 219–260.
2. C. Vega, J. L. F. Abascal, M. M. Conde and J. L. Aragones, Faraday Discuss., 2009, 141, 251–276.
3. E. Brini, C. J. Fennell, M. Fernandez-Serra, B. Hribar-Lee, M. Luksic and K. A. Dill, Chem. Rev., 2017, 117, 12385–12414.
4. A. V. Onufriev and S. Izadi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1347.
5. Q. Yu, C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. Lett., 2022, 13, 5068–5074.
6. C. Qu, Q. Yu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Chem. Theory Comput., 2023, 19, 3446–3459.
7. Q. Yu, C. Qu, P. L. Houston, A. Nandi, P. Pandey, R. Conte and J. M. Bowman, J. Phys. Chem. Lett., 2023, 14, 8077–8087.
8. V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395–5403.
9. V. Babin, G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2014, 10, 1599–1607.
10. G. R. Medders, V. Babin and F. Paesani, J. Chem. Theory Comput., 2014, 10, 2906–2910.
11. S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, J. Chem. Phys., 2016, 145, 194504.
12. F. Paesani, Acc. Chem. Res., 2016, 49, 1844–1851.
13. S. L. Bore and F. Paesani, Nat. Commun., 2023, 14, 3349.
14. X. Zhu, M. Riera, E. F. Bull-Vulpe and F. Paesani, J. Chem. Theory Comput., 2023, 19, 3551–3566.
15. G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Chem. Rev., 2016, 116, 7501–7528.
16. O. Demerdash, L.-P. Wang and T. Head-Gordon, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1355.
17. K. M. Herman and S. S. Xantheas, Phys. Chem. Chem. Phys., 2023, 25, 7120–7143.
18. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
19. C. J. Burnham and S. S. Xantheas, J. Chem. Phys., 2002, 116, 5115–5124.
20. G. S. Fanourgakis and S. S. Xantheas, J. Chem. Phys., 2008, 128, 074506.
21. C. J. Burnham, D. J. Anick, P. K. Mankoo and G. F. Reiter, J. Chem. Phys., 2008, 128, 154519.
22. B. Hartke, Phys. Chem. Chem. Phys., 2003, 5, 275–284.
23. A. Lagutschenkov, G. S. Fanourgakis, G. Niedner-Schatteburg and S. S. Xantheas, J. Chem. Phys., 2005, 122, 194310.
24. S. Yoo, E. Aprà, X. C. Zeng and S. S. Xantheas, J. Phys. Chem. Lett., 2010, 1, 3122–3127.
25. Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2011, 134, 094509.
26. J. M. Dieterich and B. Hartke, Mol. Phys., 2010, 108, 279.
27. OGOLEM framework for GA-based global optimization, https://www.ogolem.org/.
28. OGOLEM framework for GA-based global optimization of chemical problems, https://github.com/ogolem/ogolem.
29. B. Hartke, J. Phys. Chem., 1993, 97, 9973–9976.
30. B. Hartke, Angew. Chem., Int. Ed., 2002, 41, 1468–1487.
31. B. Hartke, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 879–887.
32. B. Hartke, Rev. Comput. Chem., 2022, 32, 1.
33. J. M. Dieterich and B. Hartke, Appl. Math., 2012, 3, 1552–1564.
34. J. M. Dieterich and B. Hartke, J. Comput. Chem., 2014, 35, 1618.
35. J. M. Dieterich and B. Hartke, Inorganics, 2017, 5, 64.
36. M. Dittner and B. Hartke, Comput. Theor. Chem., 2017, 1107, 7–13.
37. A. Freibert, J. M. Dieterich and B. Hartke, J. Comput. Chem., 2019, 40, 1978–1989.
38. C. Witt, M. Schmidt, C. Schröder, S. Schauermann and B. Hartke, J. Phys. Chem. C, 2021, 125, 26167–26179.
39. B. Hartke, M. Schütz and H.-J. Werner, Chem. Phys., 1998, 239, 561–572.
40. B. Hartke, Z. Phys. Chem., 2000, 214, 1251–1264.
41. B. Hartke, A. Charvat, M. Reich and B. Abel, J. Chem. Phys., 2002, 116, 3588–3600.
42. F. Schulz and B. Hartke, ChemPhysChem, 2002, 3, 98–106.
43. F. Schulz and B. Hartke, Phys. Chem. Chem. Phys., 2003, 5, 5021–5030.
44. F. Schulz and B. Hartke, Theor. Chem. Acc., 2005, 114, 357–379.
45. B. Hartke, Chem. Phys., 2008, 346, 286–294.
46. B. Hartke, J. Chem. Phys., 2009, 130, 024905.
47. Y. Li and B. Hartke, ChemPhysChem, 2013, 14, 2678–2686.
48. B. Hartke, Eur. Phys. J. D, 2003, 24, 57–60.
49. B. Bandow and B. Hartke, J. Phys. Chem. A, 2006, 110, 5809.
50. U. Buck, C. C. Pradzynski, T. Zeuch, J. M. Dieterich and B. Hartke, Phys. Chem. Chem. Phys., 2014, 16, 6859–6871.
51. J. M. Dieterich and B. Hartke, Phys. Chem. Chem. Phys., 2015, 17, 11958–11961.
52. q-AQUA github site, https://github.com/jmbowma/q-AQUA.
53. q-AQUA-pol github site, https://github.com/jmbowma/q-AQUA-pol.
54. MB-pol github site and google group, https://github.com/paesanilab/MBX, https://groups.google.com/g/mbx-users.
55. J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
56. M. L. Laury, L.-P. Wang, V. S. Pande, T. Head-Gordon and J. W. Ponder, J. Phys. Chem. B, 2015, 119, 9423–9437.
57. C. Liu, J.-P. Piquemal and P. Ren, J. Chem. Theory Comput., 2019, 15, 4122–4139.
58. C. Liu, J.-P. Piquemal and P. Ren, J. Phys. Chem. Lett., 2020, 11, 419–426.
59. J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, J. Chem. Theory Comput., 2018, 14, 5273–5289.
60. Tinker molecular modeling, https://dasher.wustl.edu/tinker/.
61. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
62. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e01493.
63. S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673.
64. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
65. N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
66. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
67. F. Neese, T. Schwabe and S. Grimme, J. Chem. Phys., 2007, 126, 124115.
68. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
69. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
70. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
71. S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102.
72. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101.
73. A. K. Dutta, F. Neese and R. Izsák, Mol. Phys., 2018, 116, 1428–1434.
74. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109.
75. J. R. Lane and H. G. Kjaergaard, J. Chem. Phys., 2009, 131, 034307.
76. W. Klopper, J. G. C. M. van Duijneveldt-van de Rijdt and F. B. van Duijneveldt, Phys. Chem. Chem. Phys., 2000, 2, 2227–2234.
77. J. R. Lane, J. Chem. Theory Comput., 2013, 9, 316–323.
78. K. Liu, M. G. Brown, C. Carter, R. J. Saykally, J. K. Gregory and D. C. Clary, Nature, 1996, 381, 501–503.
79. F. Jensen, J. Chem. Theory Comput., 2024, 20, 767–774.
80. J. L. F. Abascal and C. Vega, Phys. Rev. Lett., 2007, 98, 237801.
81. S. Blazquez and C. Vega, J. Chem. Phys., 2022, 156, 216101.
82. C. Vega and J. L. F. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688.

---

Footnote

† Electronic supplementary information (ESI) available: Cluster structures (figures and xyz-files) and tabulated energies. See DOI: https://doi.org/10.1039/d4cp00816b

---