Open Access Article
Open Access ArticleDesign of triple and quadruple phase boundaries and chemistries for environmental SO2 electrochemical sensing†
Moran
Balaish
 a and
Jennifer L. M.
Rupp
a and
Jennifer L. M.
Rupp
 *ab
*ab
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: jrupp@mit.edu
bDepartment of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
First published on 23rd June 2021
Abstract
Air pollution is a major environmental risk to the health of humans and vegetation, leading to increasing demand for real-time monitoring of toxins and harmful pollutants. Recently, the first type III electrochemical sensors tracking lethal concentrations of SO2 were developed based on a fast-conducting Li garnet Li7La3Zr2O12 (LLZO) solid electrolyte. Despite the successful proof-of-concept demonstration, the ideal sensing electrode issues concerning its preferred microstructure and chemistry remain unresolved as no catalysts are involved to ensure the low cost of such future devices. The challenging task to secure an efficient ionic, electronic, and gas pathways are needed for further sensor performance improvement. Here, the focus was placed on manipulating the electrochemical reaction zones from triple phase boundaries (TPBs) to quadrupole phase boundaries (QPBs) by merely changing the processing temperature of a Li2SO4–CaSO4 composite sensing electrode. The intended manipulation enforced the desired shift from TPB to QPB reaction zones and unlocked a larger effective surface area for the electrochemical reaction. The sensor operated at 480 °C with up to one-order-of-magnitude-lowered response time and up to a 75% decrease in the recovery time down to ∼5 min for the QPB-based configuration compared to the TPB-based one. This study demonstrates novel tools and strategies to favorably engineer sensing reaction zones through electrode processing techniques and enrich the functionality of the Li-garnet Li7La3Zr2O12 fast-conducting electrolyte for sensing applications beyond batteries.
1 Introduction
The highly reactive sulfur dioxide (SO2) gas negatively contributes to particle pollution, visibility (haze), health, and climate via its oxidation to sulfuric acid and reaction with other compounds in the atmosphere. The main sources of SO2 emissions are the combustion of sulfur-containing materials (e.g., coal and oil resources) at power plants and in the oil and gas industry,1 which are typically accompanied by the release of greenhouse gases into the atmosphere and acid rain. Additional sources of SO2 emissions include degassing volcanic sources and ore smelters. Exposure to SO2 and subsequent particulate matter (e.g., sulfates) can lead to severe health problems, including breathing difficulties, respiratory illnesses, and heart and lung diseases, and is life-threatening once concentrations above 100 ppm are reached. Although the air pollution issue is globalizing, recent trends in global SO2 emissions show that developing countries are the predominant world-wide emission contributors, with a share of 83%.2 Therefore, novel cost-effective, continuous, and real-time tracking technologies are urgently needed to further reduce SO2 emissions, especially in developing nations.Currently, commercial analytical tools based on infrared (IR) and ultraviolet (UV) optical technologies can accurately detect over a wide measuring range from zero up to 20–2000 ppm SO2 at high resolution (1 ppm to 1 ppb) and with a fast response of 10–60 s.3–5 Nonetheless, such instruments suffer from a large power demand and high cost, are rather bulky in size, and are not necessarily suited for real-time monitoring, which limit their active use-cases. In the quest for continuous monitoring of SO2 pollutants, portable and smaller-sized solid-state electrochemical sensors represent a promising alterative to UV and IR optical sensors.
Among the plethora of solid-state electrochemical sensors, the so-called potentiometric sensors operating under thermodynamic equilibrium are a promising technology based on the conversion of chemical quantities into electrical signals, namely an open-circuit voltage, according to the Nernst equation (see the schematic in Fig. 1). Owing to their simple structure and operating principles, potentiometric electrochemical sensors can track SO2 gases by coupling an auxiliary sensing electrode (SE) to an ion-conducting solid electrolyte and a reference electrode (RE) (Fig. 1). The most widely used solid-electrolyte material groups for monitoring SO2 are oxygen-ion (O2−) conductors such as yttria-stabilized zirconia6 and magnesia-stabilized zirconia,7 and Na+-ion conductors such as sodium beta-alumina8 or NASICON.9 Despite the proof-of-concept demonstration of their ability to fulfill the role as an electrolyte for these sensors, their rather low carrier mobility typically necessitates high operating temperatures beyond 500 °C to ensure sufficient ionic conductivity and a fast response and recovery time for the sensor. It has been shown that developments in solid-state batteries (SSBs)10 have been strongly connected to the new discoveries of novel solid-state electrolyte and electrode candidates,11,12 which have recently been slowly integrated in beyond-battery applications such as sensors and memristors.13–15
Very recently, a first proof-of-concept for a potentiometric type III SO2 sensor (where the auxiliary sensing electrode contains both the gaseous SO2 species and the Li+ mobile carrier of the solid electrolyte) based on a Li2SO4–CaSO4–LLZO composite sensing electrode and Li6.54La3.00Zr1.36Ta0.50O11.73 solid electrolyte was demonstrated, showing a close-to-theoretical sensitivity of 47.7 mV dec−1 at a remarkably low operating temperature of the sensor of 240 °C.13 This work demonstrated the ability to widen the range to track more gas pollutants from CO2 to SO2 with a similar sensor geometry.13,16 Nonetheless, the SO2 sensing performance was shown to be limited with a long response time on the order of ∼30–40 min, which was attributed to the sluggish kinetics at the sensing-electrode interfaces and the rather dense microstructure of the sensing electrode. As the sensing-electrode reaction primarily occurs at the ionic/electronic/gas junctions, it was evident that creating and making interconnected designs may be an interesting pathway for the future; however, this route has not yet been tackled.
Through this work, we target the existing issues to further improve the response and recovery time of Li-garnet-based SO2 sensors by defining and controlling the quadruple-phase-boundary (QPB) reaction zones of the sensing electrode microstructure. In general, the electrochemical sensing reaction occurs at the so-called triple-phase boundary (TPB), a junction between the sensing electrode/electrolyte/SO2 gas phase. In this case, the sensing electrode is typically processed as a dense ceramic entity on top of a dense electrolyte, and open triple points toward the gas phase are the effective reaction zones (see the schematic in Fig. 2). The performance of SO2 sensors relies on a composite electrode, such as a phase mixture of Li2SO4–CaSO4, to ensure a stable and fast electrochemical reaction. One may envision that instead of a dense composite sensor electrode, an auxiliary sensing structure incorporating porosity to foster interconnected reaction zones could be used, which would newly define a quadruple-phase boundary (QPB), where the electrochemical reaction takes place between the auxiliary phase of Li2SO4–CaSO4, the Au current collector, the LLZO electrolyte, and the gaseous phase of SO2 (see the schematic Fig. 3). The role of the auxiliary sensing electrode composition, microstructure, and interfacial reactions must be explored for QPB designs, and further attention regarding the optimum available surface area for the reaction is needed to ensure an adequate gas diffusion pathway and efficient adsorption/desorption processes. In that sense, we propose two configurations of the Li2SO4–CaSO4 sensing electrode (one dense and one porous structure) by merely changing the processing temperature to ensure a larger effective area for the reaction at the QPB and explore the sensing characteristics toward SO2.
2 Experimental
2.1 Synthesis of the LLZO solid electrolyte
The solid electrolyte Li6.5La3Zr1.5Ta0.5O12 (LLZO) was prepared via the solid-state reaction route detailed elsewhere.13 In short, stoichiometric amounts of La(OH)3 (Sigma Aldrich, 99.9%), ZrO2 (Sigma Aldrich, 99.9%), and Ta2O5 (Sigma Aldrich, 99.99%) and an excess amount of 50 wt% LiOH (Alfa Aesar, purity 99.8%) to compensate for the lithium evaporation during the high-temperature calcination of the powder were ball-milled in absolute isopropanol, dried, and calcined two times at 750 °C for 10 h at a heating rate of 5 °C min−1 under a constant flow of synthetic air. Finally, a weighed amount of the LLZO powder was pressed into a pellet using a die with a diameter of 12 mm and thickness of 1.5 mm in a uniaxial press (2.2 tons per cm2). The green pellets were sintered in a MgO crucible at 1100 °C for 5 h at heating/cooling rates of 10 °C min−1 under a constant flow of pure oxygen (50 sccm). The sintered LLZO pellets were dry-polished to ensure consistency among all the samples.2.2 Fabrication of the sensing electrode and sensor device
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to the different Li2SO4
2 to the different Li2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaSO4 powder mixtures and was crushed and homogenized using a mortar until a smooth paste was produced. The paste was brushed on a quarter of the solid electrolyte and heated at 750 °C for 2 h at a heating rate of 10 °C min−1 under a constant flow of pure oxygen. After the auxiliary (sensing) electrode preparation, gold paste (conductive epoxy GOLD paste, EMS) was brush-painted on the second quarter of the solid-electrolyte surface, serving as the reference electrode (RE). A thin layer of the gold paste was brushed on the auxiliary (sensing) electrode, serving as a current collector. Platinum wires (0.1 mm diameter, 99.995%, BeanTown Chemical) were connected to the auxiliary (sensing) and reference electrodes using the gold paste. The complete sensor construction was annealed at 300 °C for 4 h in an oxygen atmosphere to cure the gold paste. An adhesive sealant was applied on the reference electrode (898FS, Cotronics Corp.) and cured again at 300 °C for 2 h in an oxygen atmosphere.
CaSO4 powder mixtures and was crushed and homogenized using a mortar until a smooth paste was produced. The paste was brushed on a quarter of the solid electrolyte and heated at 750 °C for 2 h at a heating rate of 10 °C min−1 under a constant flow of pure oxygen. After the auxiliary (sensing) electrode preparation, gold paste (conductive epoxy GOLD paste, EMS) was brush-painted on the second quarter of the solid-electrolyte surface, serving as the reference electrode (RE). A thin layer of the gold paste was brushed on the auxiliary (sensing) electrode, serving as a current collector. Platinum wires (0.1 mm diameter, 99.995%, BeanTown Chemical) were connected to the auxiliary (sensing) and reference electrodes using the gold paste. The complete sensor construction was annealed at 300 °C for 4 h in an oxygen atmosphere to cure the gold paste. An adhesive sealant was applied on the reference electrode (898FS, Cotronics Corp.) and cured again at 300 °C for 2 h in an oxygen atmosphere.
2.3 Sensing system setup and electrochemical sensing measurements
The SO2 gas sensing experiments were conducted using a Linkam stage (HFS600E) with an internal volume of ∼50 cm3 equipped with a heating element in the temperature range of 25–600 °C. The experimental set-up has been detailed elsewhere.13 In short, two automated mass flow controllers (red-y, Vogtlin instruments, Switzerland) were used to balance between 50 ppm SO2 (in dry synthetic air) and dry synthetic air (21% volume O2 in N2) to achieve different concentrations of the analyzed gas, namely 0–10 ppm SO2 in 2.5 ppm steps, held for 1–2 h. The open-circuit voltage (OCV) was measured using a Keithley 2612B electrometer. The reference and auxiliary (sensing) electrodes were connected using Pt wires, which were glued to the electrodes with gold paste. The sensitivity of the sensor was evaluated through sensing experiments, where the OCV was measured as a function of SO2 concentration at a constant and calibrated temperature of either 240, 320, 400, or 480 °C at a heating/cooling rate of 10 °C min−1.2.4 Surface and bulk characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaSO4, namely 1
CaSO4, namely 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 4
2, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The measurement was conducted under synthetic air from room temperature to 900 °C, held for 5 min, and cooled back to room temperature at a ramp rate of 10 °C min−1 for both the heating and cooling steps.
1. The measurement was conducted under synthetic air from room temperature to 900 °C, held for 5 min, and cooled back to room temperature at a ramp rate of 10 °C min−1 for both the heating and cooling steps.
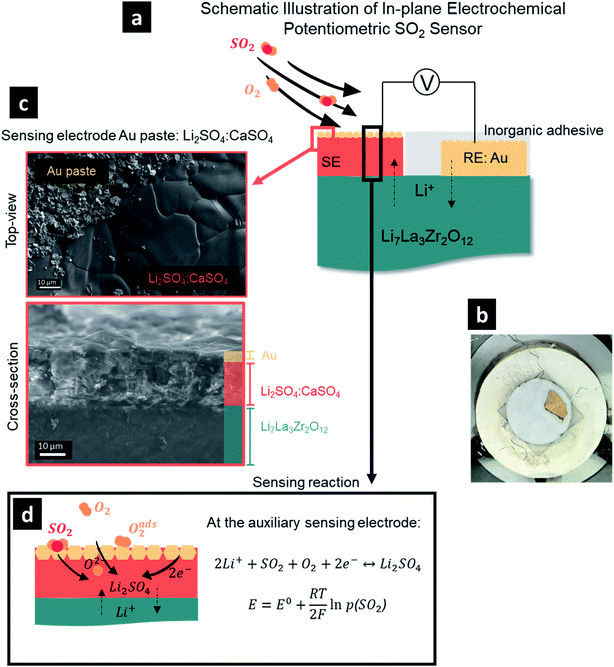
3 Results and discussion
3.1 Phase compatibility and synthesis protocol for a SO2 sensing electrode/Li-garnet electrolyte joint
As a first step, we had to define a processing protocol for the manufacture of a sensing electrode, where we could vary the pores and two-phase constituents via melting and firing on a pre-made sintered pellet. This was an important step, as it later defined the variability of the sensor electrode microstructures and bonding to LLZO and was critical for defining the QPBs and the tool to control the sensor performance for this interface. We designed and fabricated a sulfur dioxide sensor architecture in an in-plane geometry consisting of a Ta-doped Li7La3Zr2O12 (LLZO) pellet electrolyte with a sensing electrode and gold reference electrode forming a type III-electrochemical cell, Fig. 1a. For this, the gold reference electrode was brush-painted as a paste on top of the dense LLZO pellet and sealed with inorganic adhesive, serving as a protective layer for tight isolation from possible water vapor and SO2 gas in the atmosphere (Fig. 1b). One challenging aspect in the SO2 sensor design was to define the chemical composition of the sensing electrode, as it can largely determine the cell voltage and response of the sensor. It has been established that Li2SO4 can effectively serve as an auxiliary sensing electrode with a relatively fast response to SO2. However, sluggish recovery times necessitated two or multiple auxiliary phase components, with CaSO4,7 BaSO4,6 V2O5,17 or La2O2SO4–K2SO4 typically added to facilitate higher ionic conductivities and suppress interference attributed to the presence of humidity.18–21 For example, it was reported that by merely changing the chemical composition of the auxiliary sensing electrode from the single component Li2SO4 to multi-component Li2SO4–CaSO4–SiO2 at a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, a one-order-of-magnitude decrease in the average response (∼15 s) and recovery (∼8 min) rates to SO2 at 650 °C was observed when MgO-stabilized zirconia was used as the solid electrolyte.7 In the current study, the use of the Li-garnet solid electrolyte obviates the use of SiO2 to avoid the decomposition of the electrolyte through the formation of lithium silicate (Li2SixO2x+1) compounds, which resulted in our selection of a two-component auxiliary sensing electrode, i.e. Li2SO4–CaSO4. While creating the sensor, it was important to ensure good adhesion between the molten-salt-brushed and fired sensing electrode and the previously sintered pellet electrolyte. We identified an optimum 1
1, a one-order-of-magnitude decrease in the average response (∼15 s) and recovery (∼8 min) rates to SO2 at 650 °C was observed when MgO-stabilized zirconia was used as the solid electrolyte.7 In the current study, the use of the Li-garnet solid electrolyte obviates the use of SiO2 to avoid the decomposition of the electrolyte through the formation of lithium silicate (Li2SixO2x+1) compounds, which resulted in our selection of a two-component auxiliary sensing electrode, i.e. Li2SO4–CaSO4. While creating the sensor, it was important to ensure good adhesion between the molten-salt-brushed and fired sensing electrode and the previously sintered pellet electrolyte. We identified an optimum 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio of Li2SO4–CaSO4 (see ESI, Fig. S1,† for further mixtures) for firing at 750 °C to ensure improved adhesion between the dense sensing electrode and solid electrolyte (Fig. 1c).
1 mole ratio of Li2SO4–CaSO4 (see ESI, Fig. S1,† for further mixtures) for firing at 750 °C to ensure improved adhesion between the dense sensing electrode and solid electrolyte (Fig. 1c).
Collectively, the SO2 sensor was composed of the following electrochemical cell:
| Au|Li6.54La3.00Zr1.36Ta0.50O11.73|Li2SO4–CaSO4|Au, SO2, O2, |
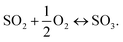 | (1) |
Thus, the overall reaction at the sensing electrode is
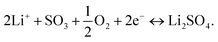 | (2) |
At the reference electrode, Li+ ions are expected to react mainly with oxygen (close reference configuration), possibly according to the following equation:
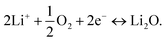 | (3) |
Under the equilibrium state, the emf of the sensor can be expressed according to the Nernst equation (Fig. 1d). Thus, under a fixed temperature and the partial pressure of O2 (p[O2]), the electromotive force, E, is determined by the partial pressure of SO2 (p[SO2]) and according to the Nernst equation:
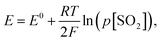 | (4) |
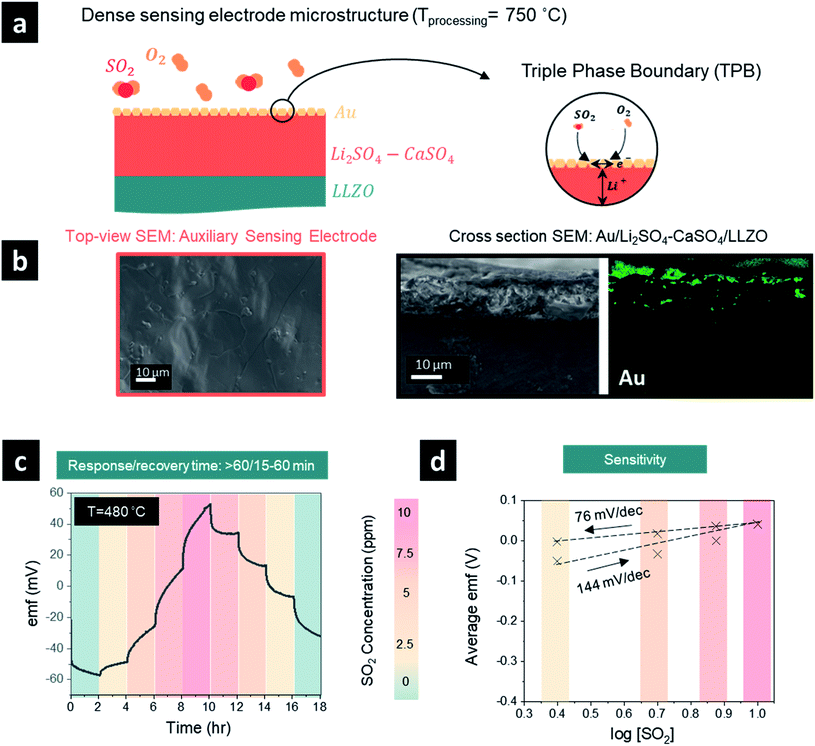
3.2 Sensing electrode microstructure and SO2 sensor voltage response
After elucidating the optimum protocol to design dense Li2SO4–CaSO4 sensing electrodes, we investigated the effect of having either a TPB (Fig. 2) or QPB (Fig. 3) for the electrochemical reaction sites, whereby first a dense structure and second a porous structure were achieved, respectively, by manipulating the sensing electrode firing temperatures from 750 °C (Fig. 2) to 600 °C (Fig. 2), respectively. In the following section, the full sensor design and testing are reported.With the material design and theoretical concept for SO2 sensing, we then targeted the SO2 sensor operation to investigate its performance characteristics employing a dense sensing electrode microstructure (Fig. 2a and b). We set the sensing protocol by modulating the SO2 concentration from 0 to 10 ppm and down to 0 ppm with 2.5 ppm step changes in dry synthetic air. The electromotive force (emf) values were recorded to define the SO2 concentration sensitivity in detection; the response and recovery times were also recorded. Note that these times were defined as the time required for the sensor to reach 90% of the steady final signal and for the sensor to return to 10% of the steady signal, respectively.
The emf response of the electrochemical cell to the SO2 concentration steps at 480 °C is depicted in Fig. 2c. During the concentration step change of SO2 from 0 to 10 ppm, the emf voltage response implies a difference in the chemical potentials of Li+ ions in the garnet LLZO solid electrolyte established at the interfaces with the sensing and reference electrodes, respectively. Moreover, the initial negative polarity in the presence of synthetic air or low SO2 concentrations indicates an accumulation of Li+ ions at the reference electrode and the depletion of Li+ ions at the sensing electrode. The transfer of Li+ ions is accompanied by the occurrence of reaction [2] from right to left at the sensing electrode interface and reaction [3] from left to right at the Au reference electrode. Increasing the SO2 concentration further induced the reverse transfer of Li+ ions from the reference electrode to the sensing electrode and the opposite occurrence of reactions [2] and [3].20 The average emf values and the logarithm of the SO2 gas concentration were fitted with the Nernst equation to evaluate the sensitivity of the sensor and were determined to be 144 (n = 1.3 e−) and 76 (n = 1.96 e−) mV dec−1 for the sensor response step of 0–10 ppm and a recovery step of 10–0 ppm (Fig. 1d). These values are similar to or higher than the theoretical sensitivity for a two-electron reaction of 74.64 mV dec−1. The differences between the theoretical and calculated sensitivity, especially in the response stage, imply more efficient desorption, compared to adsorption, of SO2 gas at the surface of the sensing electrode. It is evident that the recovery appears easier to achieve within ∼15–60 min depending on the SO2 concentration, whereas the response time was typically longer than >60 min (except in the case of 0–2.5 ppm, where t90% = 21 min). Although the emf in the recovery stage was stable, it did not return to the initial emf value, and we conclude that a longer period beyond >2 h may be required to ensure full recovery. The long response and recovery times may be attributed to the lack of a catalyst for fast SO2 oxidation and long processes of adsorption and desorption of SO2 in addition to the TPB-based sensing electrode dense design, which can significantly affect the sensing capabilities.
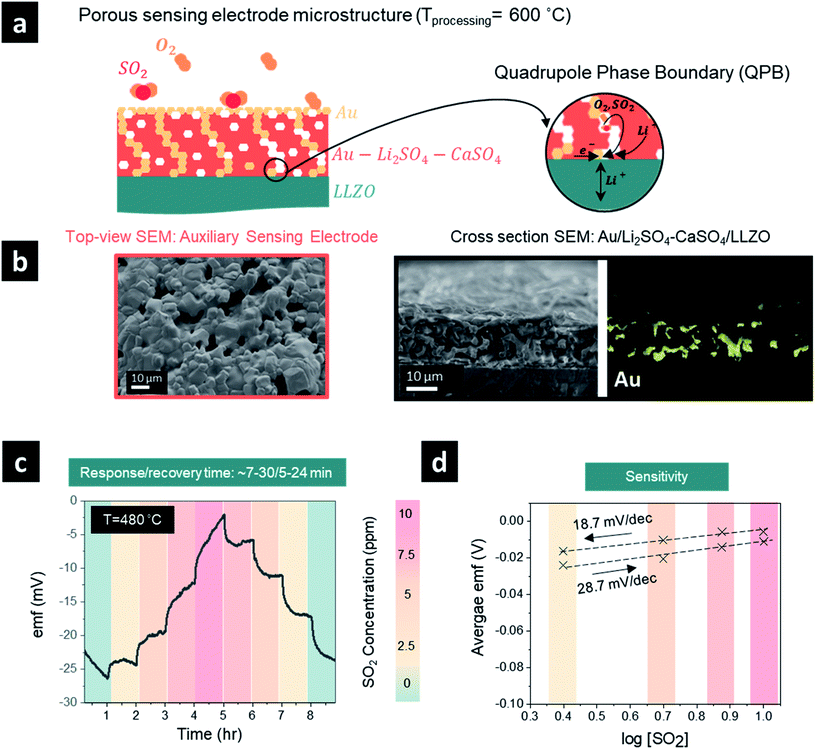
One promising strategy to shorten the response/recovery time is to introduce a porous auxiliary sensing electrode to facilitate faster adsorption and diffusion of sulfur dioxide through a “porous” sensing electrode structure (Fig. 3a and b). This strategy could increase the effective surface area for reaction and the number of sulfur dioxide molecules that participate in the electrochemical reaction. In general, the sensing reaction occurs at the QPB reactive sites in the case of a porous auxiliary sensing electrode (or at the TPB sites in the case of a dense electrode, Fig. 2a), where the electrochemical equilibrium requires a quadruple contact between the auxiliary phase of Li2SO4–CaSO4, the Au current collector, the LLZO electrolyte, and the gaseous phase of SO2 (Fig. 3a). To improve the distribution of Au particles and increase the density of QPB reaction sites throughout the sensing electrode, we designed in the next step a porous microstructure for the sensing electrode with an approximate pore diameter ranging from 5 to 10 μm by lowering the processing temperature of the sensing electrode from 750 to 600 °C (Fig. 3b). Turning to a porous sensing electrode structure, we analyzed the response and recovery times at 480 °C to 2.5 ppm SO2 in the concentration ranges of 0–10 ppm and 10–0 ppm (Fig. 3c). The graph shows a clear improvement in the response time of the porous sensing electrode compared with the dense electrode processed at two different temperatures. Here, the porous sensing electrodes reduced the response time from >∼60 min (dense) to ∼7–30 min (porous) and the recovery time from ∼15–60 min (dense) to ∼5–24 min (porous) depending on the selected SO2 concentration step within 0–10 ppm. The cross-sectional scanning electron microscopy (SEM) images and energy-dispersive X-ray spectroscopy (EDS) elemental mapping of the sensing electrode/solid electrolyte interface (Fig. 3b) revealed that the porous sensing electrode structure with an average thickness of ∼20 μm ensured homogeneous incorporation of the gold paste into the porous sensing electrode, creating multiple QPB contact points for the cermet structure, which account for the improvement in the response time after SO2 exposure (Fig. 3b). Although it is a common practice to mitigate the challenge of slow response times after gas exposure by incorporating gold nanoparticles into the composite sensing electrode to maintain better metallic conductivity and improve the phase boundary contact areas, this approach resulted in limited success in our case. Alternatively, our porous sensing electrode structure supported a continuous ion percolating network for Li2SO4 and LLZO phases and the electronic one for the gold particles accompanied by the infiltration of sulfur dioxide into the porous structure (Fig. 3b) and effectively increased the available surface area for the electrochemical reaction. Nonetheless, the fly in the ointment is that a porous structure with efficient QPBs may not only ensure a higher effective surface area for reaction and favorable diffusion of sulfur dioxide into the porous sensing electrode structure but may also induce additional degradation reactions between the solid electrolyte and sensing electrode. Indeed, once the average emf values and the logarithm of the SO2 gas concentration were fitted with the Nernst equation to evaluate the sensitivity (mV dec−1), the sensitivity was determined to be 28.7 mV dec−1 (n = 5.2 e−) and 18.7 mV dec−1 (n = 7.9 e−) for the sensor response step (0–10 ppm) and recovery step (10–0 ppm), respectively, significantly lower than the theoretical sensitivity of 74.64 mV dec−1 and the sensitivities determined for the dense sensing electrode (Fig. 3d). When the voltage does not approximately follow the Nernst law, the system is considered to be not in thermodynamic equilibrium. The higher electron number determined, compared to the theoretical one, may imply that additional degradation reactions are taking place and necessitate further investigation.
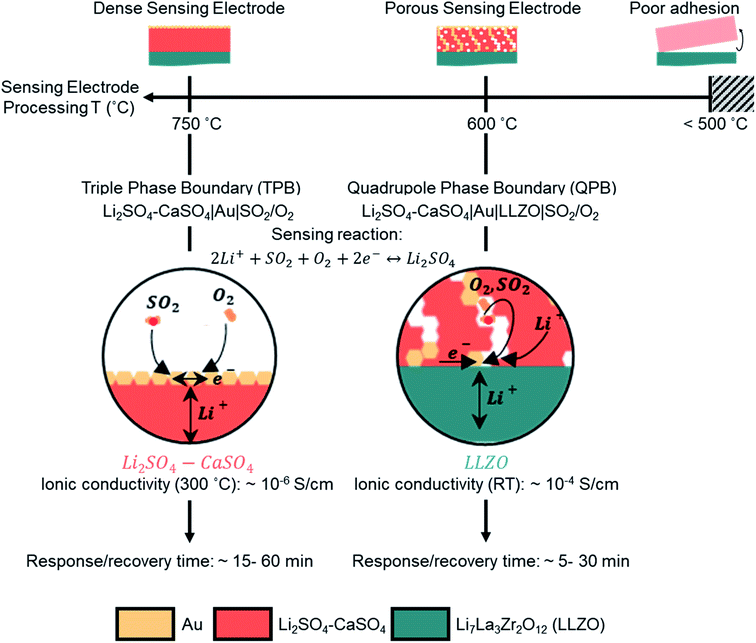
Our investigation revealed that by lowering the processing temperature of the Li2SO4–CaSO4 sensing electrode from 750 to 600 °C, the transition from a dense to a porous structure of the sensing electrode, i.e. from TPBs to QPBs, can be easily achieved (Fig. 4). The importance of transitioning to a porous QPB-based configuration is two-fold: (i) the formation of the porous electrode structure increases the surface area for the electrochemical sensing reaction to occur, which may facilitate faster gas adsorption/desorption processes and improve the response/recovery time and (ii) the Li+-ion diffusion pathways in the low-conducting Li2SO4–CaSO4 phase (∼10−6 S cm−1 at 300 °C) are shortened compared to the Li+-ion diffusion pathways through dense, several-micron-thick sensing electrodes. The low sensitivities observed for the porous sensing electrode microstructure imply that the voltage does not approximately follow the Nernst law and that the system is considered to not be in thermodynamic equilibrium. The higher electron number determined, compared to the theoretical one, may imply that additional degradation reactions are occurring and necessitate further investigation.
4 Conclusion
Successful design of an electrochemical potentiometric type III sensor requires thoughtful selection of materials and microstructures that balance ion–electron–gas exchange processes at thermodynamically stable materials and interfaces under a corrosive SO2 environment. In this work, we explored electrochemical sensing electrode designs concerning their ideal chemistry and ion–electronic pathways toward a Li-garnet, Li6.54La3.00Zr1.36Ta0.50O11.73, solid electrolyte for potentiometric type III SO2 sensors. Only very recently, a first proof-of-concept was demonstrated for the suitability of a well-known battery electrolyte for SO2 sensors; however, guidelines on how to design the electrode microstructure and chemistry toward fast ionic transfer have remained untouched. A main requirement for the functionality of this sensor is the assurance of fast transport kinetics in the ionic, electrical, and gas boundary zones. A challenging part of this electrochemical device is that multiple phases of ion conductors (Li2SO4–CaSO4) and electronic conductors (gold) must be used to ensure ionic–electronic pathways, while also allowing enough gas exchange with SO2 for adsorption and desorption. For this, we created model sensing electrode structures composed of Li2SO4–CaOS4 and defined as either dense or porous and tested the cells with a porous gold layer as the reference electrode. To succeed in defining the SO2 sensing electrode chemistry and phase and its stability toward the new LLZO electrolyte, we had to probe the phase compatibility and invent a synthesis protocol for the SO2 sensing electrode/electrolyte joint under the critical and society-relevant limit of 0–10 ppm SO2 at 480 °C. The focus was strategically placed on one of the major aspects, which affects the emf response according to the Nernstian behavior and the response/recovery time of the sensor, explicitly the microstructure of the auxiliary sensing electrode.We discovered that it is possible by ceramic design to ensure a larger effective area for the SO2 sensing reaction and two configurations were presented, dense and porous structures of the Li2SO4–CaSO4 sensing electrode, by merely lowering the processing temperature. The last manipulation enforced the desired shift from TPB to QPB reaction zones, as pores were formed and unlocked new effective electrochemical sensing zones with conductive Au channels. We identified that the QPB-based configuration resulted in up to a one-order-of-magnitude lowered response time and up to 75% decrease in the recovery time down to ∼5 min compared with the TPB-based configuration and was superior in performance. This work contributes to the first discussions in the field on how such catalyst-free sensor electrode designs could look like and provides the first performance characteristics and manufacturing guidelines. We conclude that the electrochemical concept of QPBs clearly shows potential and can be further extended considering other auxiliary phases for SO2 sensors or may be considered for other type III garnet-based sensors for future CO2, NO2, and H2S tracking as a strategy to design structure-to-performance for their sensing electrodes.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported in part by SENSE.nano under award number 2629303. M. B. acknowledges financial support from the US–Israel Fulbright Program, the Zuckerman Israeli Postdoctoral Scholar Program, and the MIT–Technion Postdoctoral Fellowship. J. L. M. R. thanks the Thomas Lord Foundation for financial support. This work made use of the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-1419807. This work was performed in part at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), supported by the National Science Foundation under NSF award no. 1541959. CNS is part of Harvard University.References
- S. Dahiya, A. Anhäuser, A. Farrow, H. Thieriot, A. Kumar and L. Myllyvirta, Ranking the World's Sulfur Dioxide (SO2) Hotspots: 2019-2020 A closer look at the colourless gas that is poisoning our air and health, 2020 Search PubMed.
- Q. Zhong, H. Shen, X. Yun, Y. Chen, Y. Chen, Y. Ren, H. Xu, G. Shen, W. Du, W. Du, J. Meng, W. Li, J. Ma and S. Tao, Environ. Sci. Technol., 2020, 54, 6508–6517 CrossRef CAS PubMed.
- L. Cubic Sensor and Instrument Co., Online Infrared Flue Gas Analyzer—Gasboard 3000, https://en.gassensor.com.cn/GasAnalyzer/info_itemid_291.html, accessed 20 January 2021 Search PubMed.
- Acoem-ECOTECH, The Serinus ® 50 sulfur dioxide (SO2) analyser, 2020 Search PubMed.
- Thermo Scientific, User Manual: 43iQ Sulfur Dioxide Analyzer, 2020 Search PubMed.
- Y. Yan, Y. Shimizu, N. Miura and N. Yamazoe, Chem. Lett., 1992, 21, 635–638 CrossRef.
- Y. Yan, Y. Shimizu, N. Miura and N. Yamazoe, Sens. Actuators, B, 1994, 20, 81–87 CrossRef CAS.
- R. Akila and K. T. Jacob, Sens. Actuators, 1989, 16, 311–323 CrossRef CAS.
- S.-D. Choi, W.-Y. Chung and D.-D. Lee, Sens. Actuators, B, 1996, 36, 263–266 CrossRef CAS.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Adv. Energy Mater., 2020, 2002689 Search PubMed.
- M. Balaish, J. C. Gonzalez-Rosillo, K. J. Kim, Y. Zhu, J. D. Hood and J. L. M. Rupp, Nat. Energy, 2021, 6, 227–239 CrossRef CAS.
- Y. Zhu, J. C. Gonzalez-Rosillo, M. Balaish, Z. D. Hood, K. J. Kim and J. L. M. Rupp, Nat. Rev. Mater., 2021, 6, 313–331 CrossRef CAS.
- M. Balaish and J. L. M. Rupp, Adv. Mater., 2021, 33(20), 2100314 CrossRef CAS PubMed.
- M. Struzik, I. Garbayo, R. Pfenninger and J. L. M. Rupp, Adv. Mater., 2018, 30, 1–10 CrossRef PubMed.
- J. C. Gonzalez-Rosillo, M. Balaish, Z. D. Hood, N. Nadkarni, D. Fraggedakis, K. J. Kim, K. M. Mullin, R. Pfenninger, M. Z. Bazant and J. L. M. Rupp, Adv. Mater., 2020, 32, 1907465 CrossRef CAS PubMed.
- M. Balaish, Z. D. Hood and J. L. M. Rupp, Gas sensor device containing Lithium garnet, US Pat., 63, 2021 Search PubMed.
- K. Chen, M. Zhang, H. Wang and H. Gu, Rev. Sci. Instrum., 2019, 90, 065001 CrossRef PubMed.
- G. Hötzel and W. Weppner, Sens. Actuators, 1987, 12, 449–453 CrossRef.
- A. Lundén, K. Schroeder and H. Ljungmark, Solid State Ionics, 1988, 28–30, 262–266 CrossRef.
- F. Ménil, B. O. Daddah, P. Tardy, H. Debéda and C. Lucat, Sens. Actuators, B, 2005, 107, 695–707 CrossRef.
- K. Singh and V. K. Deshpande, Solid State Ionics, 1984, 13, 157–164 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta02399c |
| This journal is © The Royal Society of Chemistry 2021 |