Excited-states of BODIPY–cyanines: ultimate TD-DFT challenges?

Abstract

We have investigated with first principle approaches the optical signatures of derivatives combining a BODIPY core and cyanine-like side chains. More precisely, we computed the 0–0 energies with a Time-Dependent Density Functional Theory (TD-DFT) procedure systematically including both vibrational and continuum solvent effects. However, despite its refinement, this protocol yields large deviations compared to experimental references. For this reason, we turned towards a mixed protocol where the potential energy surfaces of both the ground and the first electronically excited states are evaluated with TD-DFT whereas the vertical transition energies (both absorption and emission) are determined with the CIS(D)/SOS-CIS(D) approaches, that include a perturbative correction for the double excitations. The pros and cons of such a mixed method are discussed in the framework of these challenging dyes.

---

1 Introduction

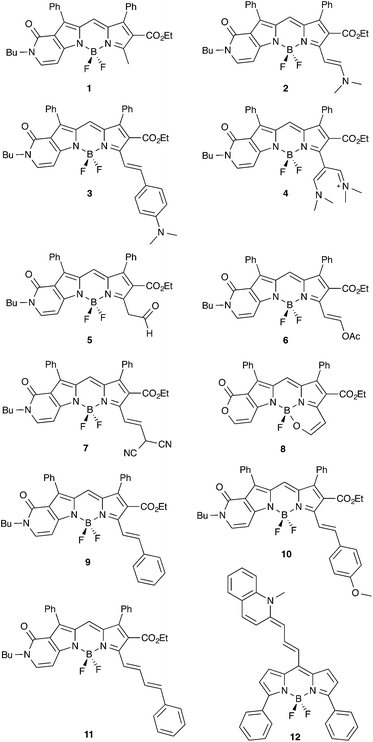
The accurate determination of the properties of electronically excited-states (ES) remains one of the important challenges faced by theoretical chemistry. One of the difficulties is that, contrary to ground-state (GS) properties that allow one to perform straightforward theory–experiment comparisons, it is often difficult to correlate theoretical and experimental data for ES. For the two simplest and most widely-available experimental results, namely absorption and emission spectra, well-grounded simulations require the calculation of band shapes and/or 0–0 energies,^1–7 two properties that necessitate the calculation of ES vibrations. This task, implying the access to second derivatives of the ES energy, dramatically restricts the number of methods that can be used for “real-life” molecules. Indeed, the most accurate theoretical approaches for ES, e.g., Complete Active Space with Second-order Perturbation Theory (CAS-PT2), Equation-Of-Motion Coupled-Cluster Single and Doubles (EOM-CCSD) and Multi-Reference Configuration Interaction (MR-CI), are in practice limited to vertical calculations (typically on a frozen GS geometry) but for trivial or very specific molecules. Therefore, in practice, one resorts to less refined methods, e.g., CAS-Self Consistent Field (CAS-SCF), Configuration Interaction Singles (CIS) and Time-Dependent Density Functional Theory (TD-DFT), as well as, to some extend second-order approximate CC (CC2), for exploring the potential energy surfaces and determining transition energies. Amongst these methods, TD-DFT clearly stands as the most popular approach for computing both 0–0 energies and band shapes and it has been widely used in dye chemistry during the last decade.⁸

In the present work, we investigate a series of boradipyrromethene–cyanine compounds that have been recently synthesized by Kovtun and coworkers (see Fig. 1).^9–15 These molecules are particularly appealing due to their near-infrared emission resulting from the addition of side streptocyanine-like chains to a central BODIPY core, that can itself be viewed as a constrained cyanine.^16–20 These dyes therefore combine two different cyanine-like chromogens to obtain the best of both worlds: chemical stability and large quantum yields with BODIPY and strongly redshifted wavelengths with streptocyanine. Clearly, determining the ES properties of Kovtun's chromophores is far from a piece-of-cake task for theoretical chemistry. Indeed, amongst the molecules that are particularly challenging for ES modeling, cyanine and their derivatives occupy a specific spot. For model cyanines, Send and coworkers performed a series of highly-refined wavefunction calculations, including Diffusion Monte-Carlo (DMC), third-order CC (exCC3) and CAS-PT2 and they obtained, for the chain containing nine carbon atoms, vertical transition energies of 2.62, 2.53 and 2.46 eV, respectively.²¹ Using these data as references, it can be shown that both CIS and TD-DFT are strongly off, by ca. 0.5 eV,^22–25 though CAS calculations do not reveal any significant multi-determinantal character for medium-sized cyanines.^21,22 The most convincing explanation given to the failure of TD-DFT is that it does not correctly describe the difference of dynamic electronic correlation between the two states.^25–27 In that framework, Grimme and Neese have shown that double hybrids that explicitly include contributions from the virtual orbitals indeed provide more accurate estimates than other exchange-correlation functionals but the errors remain quite large.²⁶ In fact the two “lighter” methods (in terms of computational cost) able to reproduce Send's reference results are on the one hand, Head-Gordon's CIS(D) method and its Scaled Opposite Spin counterpart, SOS-CIS(D) approach that add a perturbative correction for double excitations to the CIS result,^25,26,28 and the Bethe–Salpeter (BSE) self-consistent approach of Blase and coworkers.²⁹

Fig. 1 Compounds investigated in the present study.

All these results apparently indicate that we will be seriously handicapped for the molecules shown in Fig. 1: (i) the very accurate approaches, e.g., CAS-PT2 or exCC3, are obviously not computationally tractable; (ii) CIS(D) and BSE are only available for the computation of vertical transition energies and this does not permit direct comparisons with experiment; and (iii) TD-DFT and CIS allow the calculation of 0–0 energies, but they will probably be inaccurate. We thus propose herein to combine two approaches, namely CIS(D) and TD-DFT, and we assess such mixed scheme for Kovtun's dyes.

2 Methods

2.1 Protocol

As explained in the introduction the 0–0 energies are one of the properties that can be directly compared to experiment, and more precisely to the absorption-fluorescence crossing point (AFCP). We have recently designed a specific protocol to obtained these AFCP energies using two atomic basis sets (SBS: small atomic basis set and LBS: large atomic basis set) and accounting for solvent effects through the corrected Linear Response (cLR) approach, using both equilibrium (eq) and non-equilibrium (neq) limits (see next section).⁴ We briefly summarize the TD-DFT procedure below. The AFCP energies are determined as

E^AFCP_TD-DFT (cLR, neq) = E^0–0 (cLR, eq) + ΔE_neq/eq (cLR) (1)

where E^0–0 (cLR, eq) and ΔE_neq/eq (cLR) are defined as:

E^0–0 (cLR, eq) = E^adia (cLR, eq) + ΔE^adia_BS (LR, eq) + ΔE^ZPVE (LR, eq) (2)

In the first equation, E^adia (cLR, eq) is the adiabatic energy, that is the difference between ES and GS energies computed at their respective minima, whereas ΔE^adia_BS (LR, eq) is a correction for basis set effects,

ΔE^adia_BS (LR, eq) = E^adia_LBS (LR, eq) − E^adia_SBS (LR, eq) (4)

and ΔE^ZPVE (LR, eq), the difference of zero-point vibrational energy (ZPVE) between the two states. ΔE^abso_neq/eq (cLR) and ΔE^fluo_neq/eq (cLR) are correction terms for absorption and emission, respectively. They are simply the difference between non-equilibrium and equilibrium vertical absorption (emission) energies. The interest reader will find more details and justifications regarding this protocol in our two previous methodological contributions,^4,30 but we underline that the E^AFCP (cLR, neq) obtained in that way correspond to state-of-the-art TD-DFT estimates.

As the used CIS(D) implementation only allows vertical gas-phase calculations, and hence, no analytic optimization nor calculation of ZPVE energies are possible on the ES, we have used the DFT and TD-DFT geometries to determine a gas-phase CIS(D) adiabatic energy following the procedure defined previously,³¹

E^adia_CIS(D) (gas) = E^ES_CIS(D) (gas) − E^GS_MP2 (gas) (5)

Next, we have computed the same adiabatic energies with TD-DFT in gas-phase,

E^adia_TD-DFT (gas) = E^ES_TD-DFT (gas) − E^GS_DFT (gas) (6)

This allowed us to obtain a corrected CIS(D) value for the AFCP energies, using

E^AFCP_CIS(D) (cLR, neq) = E^AFCP_TD-DFT (cLR, neq) + E^adia_CIS(D) (gas) − E^adia_TD-DFT (gas) (7)

This blend value can be viewed as either a TD-DFT energy corrected for double excitation or a CIS(D) energy using TD-DFT for both structures and solvent effects. Similarly, CIS(D) absorption and fluorescence energies in condensed phase can be estimated as:

E^abso_CIS(D) (cLR, neq) = E^abso_TD-DFT (cLR, neq) + E^abso_CIS(D) (gas) − E^abso_TD-DFT (gas) (8)

E^fluo_CIS(D) (cLR, neq) = E^fluo_TD-DFT (cLR, neq) + E^fluo_CIS(D) (gas) − E^fluo_TD-DFT (gas) (9)

Of course the SOS-CIS(D) data are obtained through the same approach considering SOS-MP2 energies for the GS. We note that similar approaches combining TD-DFT for computing structures and vibrations and CIS(D) for excited-state energies have already appeared.^2,32

2.2 Computational details

All computations, but the SOS-CIS(D) simulations, have been performed with the Gaussian09 program package,³³ applying default thresholds except for a tighten self-consistent field convergence (10⁻⁸ to 10⁻¹⁰ a.u.) and an improved optimization threshold (10⁻⁵ a.u. on average forces). For each molecule, we have optimized the geometry of both the ground and the first excited states, as well as computed the vibrational spectra of both states. The same DFT integration grid (so-called fine or ultrafine) was used for all calculations on a given molecule. For all calculations, we have used the M06-2X exchange-correlation functional,³⁴ that has been shown to be an adequate choice for investigating excited-state energies and structures of many classes of molecules.^4,34–39 Interestingly, several previous benchmarks dedicated to model cyanine chains have already appeared.^{21,24–27,29,40} It turned out that all global and range-separated hybrids provide too large transition energies (see the Introduction) but one of the most successful functional is M06-2X that returns results reasonably close to DMC.²⁴ This was rationalized by showing that functionals of the M06 series tend to decrease the overlocalisation error common to most DFT approaches.²⁵ For fluoroborates, we have previously performed several TD-DFT benchmarks as well.^30,41–43 In the work specifically devoted to BODIPY,⁴¹ we showed that the linear determination coefficient (R²) obtained by comparing theoretical and experimental 0–0 energies for 35 derivatives attains 0.98 with M06-2X, the largest of the six tested approaches (B3LYP, PBE0, BMK, M06-2X, CAM-B3LYP and ωB97X-D, e.g., the R² is only 0.576 with B3LYP). Therefore, there is no need to perform further ”functional benchmark” for the systems treated here: M06-2X is clearly a reasonable choice. In a recent work, we have performed an extensive assessment of basis set effects for aza-BODIPY dyes.³⁰ We have found that the geometrical and vibrational parameters can be determined with a relatively compact atomic basis set, that is 6-31G(d) [SBS], whereas the adiabatic energies need to be corrected using a more extended basis set, namely 6-311+G(2d,p) [LBS]. The inclusion of environmental effects is crucial to estimate the electronic transition energies, and to fit experiments. Solvation effects (here dichloromethane) have been quantified using the Polarizable Continuum Model (PCM).⁴⁴ Here, we have applied the linear-response (LR) scheme^45,46 for geometry optimizations and calculations of the vibrational frequencies, whereas the total and transition energies have been tackled with the corrected LR approach.⁴⁷ Some test calculations have also been achieved with the state-specific (SS) model.⁴⁸ For all these PCM variations, two limits exist: the equilibrium (eq) and non-equilibrium (neq) schemes. In the neq limit, only the electrons of the solvent do adapt to the new electronic configuration of the solute (fast process). Clearly, the absorption and emission energies better correspond to a neq scheme. On the contrary, in the eq approach, the solvent has time to adapt to the new electronic configuration of the solute (slow process). This latter approach is the recommended approach to calculate excited-states geometries, vibrational signatures and consequently adiabatic energies. The gas phase TD-DFT and CIS(D) transition energies have been performed through “single-point” calculations on the GS and ES structures optimized with PCM, as these gas phase results are only used as corrections through differences, see eqn (7)–(9). The SOS-CIS(D) (and SOS-MP2) energies were determined with the Q-Chem package using the Resolution of the Identity (RI) scheme, with a double-ζ auxiliary basis set.⁴⁹

3 Results

3.1 Influence of the chemical model

As stated in the Introduction, both cyanine and BODIPY derivatives remain challenging for theoretical approaches, and only highly-correlated theories seem able to provide consistent answers. As these approaches are computationally demanding, one might wish to apply them on smaller (model) systems. For this reason, although we have considered full molecular structures in the following, we have decided to assess the impact of selecting simpler chemical models for 1 and 2. In x-a (x = 1 or 2), the side butyl and ethyl chains have been replaced by methyl groups, whereas in x-b, the top phenyl rings have been replaced by hydrogen atoms. x-c combine the two simplifications.

Key results are given in Table 1 and it is obvious that the reduction of the length of the side alkyl chain is not problematic (maximal variation of 0.010 eV). This result is in the line of available experimental data performed on the methyl and n-Bu derivatives, that present λ_max differing by only 2 nm.¹⁵ On the contrary, the phenyl rings are mandatory as they induce bathochromic shifts of ca. 0.2 eV. This result is consistent with the non-perpendicularity of these rings that present dihedral angles of ca. 43° (GS) and 39° (ES) with the central core and cannot be viewed as independent from the chromophore. In short, Table 1 demonstrates that all π-electrons of the system have to be considered to reach chemically meaningful results, which prevents the use of highly-correlated schemes.

Table 1 Absorption, fluorescence and adiabatic energies computed at the PCM(DCM)-M06-2X/6-31G(d) level for 1 and 2 and the corresponding simplified chemical models. All values are in eV

	E^abso (cLR, neq)	E^fluo (cLR, neq)	E^adia (cLR, eq)
1	2.580	2.355	2.472
1-a	2.590	2.363	2.479
1-b	2.765	2.582	2.673
1-c	2.753	2.593	2.685
2	2.369	2.109	2.225
2-a	2.370	2.107	2.226
2-b	2.475	2.283	2.379
2-c	2.480	2.273	2.385

---

3.2 Nature of the electronic transitions

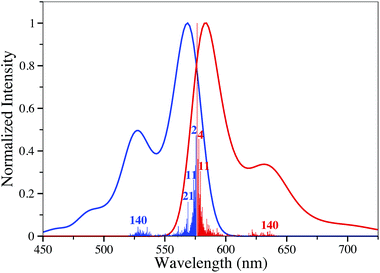
To analyze the nature of the electronic transitions, we have computed the differences of total electronic densities between the ES and GS, Δρ. Results obtained for four representative structures, namely 1, 3, 11 and 12 can be found in Fig. 2. It turns out that one can systematically recognize the alternance of regions loosing/gaining electron density in the BODIPY core, typical of cyanine transitions. In addition, in 3, the p-dimethylamino phenyl acts as a donor group (almost only in blue) which is unsurprising. For this dye, Le Bahers' charge-transfer model,^50,51 yields a distance of 3.06 Å between the barycenters of density depletion and gain, confirming the partial charge-transfer nature of the transition. In both 11 and 12, the addition of ethenyl segments increases the delocalization and hence the effective length of the cyanine, which qualitatively explains the bathochromic displacements. It is also noteworthy that for the three first dyes shown in Fig. 2, the top phenyl rings do not directly participate in the ES though they induce significant auxochromic effects (see above).

Fig. 2 Δρ computed for four representative dyes: 1 (top left), 3 (top right), 11 (bottom left) and 12 (bottom right). The blue (red) regions indicate decrease (increase) of electron density following photon absorption. The isocontour threshold was systematically set to 0.0004 a.u.

For 8, we have also performed vibrationally-resolved calculations of the absorption and emission band shapes using the FCclasses package.^6,51,52 The results are displayed in Fig. 3 and we notice that: (i) the computed absolute extinction coefficient is extremely large (log(ε) > 5); (ii) the absorption and emission are nearly mirror shaped but for the side peak; (iii) the emergence of a significant additional band at higher energy (for absorption). All these signatures are typical of a cyanine excited-state.^53,54 While the main bands imply vibronic couplings with low-frequency modes, the second maxima can in part be attributed to mode n° 140 (at 1597 cm⁻¹ for the ES), that implies CC stretching mainly localized in the two six-member ring located at the left and right sides of the BODIPY core.

Fig. 3 Computed stick and convoluted vibronic spectra for 8. Normalized intensities are presented.

3.3 Solvent effects

For both absorption and emission, we have compared the results obtained with gas-phase, LR, cLR and SS environmental models (Table 2). For fluorescence, neq LR values are ill-defined and have not been used. For absorption, solvent effects tend to decrease the transition energies (positive solvatochromism), compared to gas phase. Whilst this trend is expected, the magnitude of the effect is much larger with the simplest LR model (−0.155 eV on average for twelve dyes) than with the more refined cLR (−0.016 eV) and SS (−0.033 eV) schemes, the two latter often providing very close E^abso for the vast majority of dyes. For fluoroborate derivatives, a similar overshooting of solvatochromism with LR was reported previously.^42,43 For emission, both cLR and SS give small but non-negligible solvation corrections of −0.031 eV and −0.055 eV on average, respectively. In short, this study demonstrates that the LR approach is probably not suited for BODIPY–cyanine dyes, and we have continued with cLR in the following of this work.

Table 2 Vertical absorption and emission energies computed with TD-DFT using different continuum models in their non-equilibrium limit. All values are in eV and have been determined with SBS in dichloromethane systematically considering the PCM optimized structures

	E^abso				E^fluo
	Gas	LR	cLR	SS	Gas	cLR	SS
1	2.587	2.455	2.580	2.574	2.379	2.355	2.336
2	2.358	2.238	2.369	2.386	2.139	2.109	2.087
3	2.231	2.070	2.178	2.102	2.040	1.944	1.865
4	2.438	2.142	2.401	2.341	2.234	2.187	2.124
5	2.568	2.442	2.568	2.566	2.363	2.348	2.333
6	2.453	2.320	2.455	2.456	2.261	2.250	2.243
7	2.544	2.415	2.538	2.530	2.341	2.320	2.300
8	2.445	2.358	2.467	2.492	2.238	2.238	2.247
9	2.374	2.244	2.377	2.380	2.184	2.175	2.169
10	2.329	2.199	2.328	2.325	2.135	2.113	2.096
11	2.304	2.170	2.303	2.302	2.106	2.089	2.077
12	2.442	2.157	2.311	2.226	2.277	2.189	2.162

---

3.4 0–0 energies

Let us now turn towards the comparison of the AFCP energies for the series of compounds shown in Fig. 1. The main data are collected in Table 3. As stated in the Introduction, vertical transition energies do not correspond to experimental wavelength of maximal absorption/emission but we have nevertheless listed these data as such comparison remains common in the literature. We have therefore decided to report these data with the SBS to see if a quick simulation might be useful.

Table 3 Comparison between experimental and theoretical data for the dyes shown in Fig. 1. For the theoretical part, we give the vertical absorption and fluorescence energies and the AFCP energy obtained as described in the Methods section. Dichloromethane is modeled with the cLR-PCM (neq limit) model and the basis set corrections with the LBS are taken into account in the E^AFCP, but not for vertical absorption and emission energies. The experimental results are taken from literature (ref. 14 for 1–7, ref. 12 for 8, ref. 15 for 9–11 and ref. 10 for 12) and the absorption and emission data are obtained from the corresponding wavelength of maximal absorption/emission. All results are in eV. At the bottom of the Table, statistical analysis is given, excluding 7 (see text)

	TD-DFT			CIS(D)			SOS-CIS(D)			Experiment
	E^abso	E^fluo	E^AFCP	E^abso	E^fluo	E^AFCP	E^abso	E^abso	E^AFCP	E^abso	E^fluo	E^AFCP
1	2.580	2.355	2.377	2.486	2.308	2.259	2.182	1.980	1.983	2.109	2.006	2.057
2	2.369	2.109	2.175	2.256	2.027	2.019	2.003	1.687	1.753	1.905	1.764	1.834
3	2.178	1.944	2.000	2.150	1.928	1.901	1.869	1.598	1.639	1.736	1.442	1.589
4	2.401	2.187	2.210	2.332	2.142	2.111	2.054	1.824	1.845	2.043	1.946	1.994
5	2.568	2.348	2.363	2.474	2.297	2.254	2.168	1.969	1.976	2.094	1.962	2.028
6	2.455	2.250	2.259	2.378	2.218	2.156	2.071	1.882	1.885	2.003	1.931	1.967
7	2.528	2.320	2.345	2.451	2.277	2.237	2.148	1.949	1.963	2.066	1.977	2.022
8	2.467	2.238	2.287	2.372	2.177	2.151	2.098	1.836	1.873	2.036	1.943	1.990
9	2.377	2.175	2.192	2.326	2.171	2.105	2.025	1.837	1.839	1.931	1.864	1.898
10	2.328	2.113	2.149	2.284	2.129	2.063	1.989	1.774	1.801	1.890	1.807	1.849
11	2.303	2.089	2.117	2.280	2.114	2.039	1.996	1.796	1.805	1.879	1.815	1.847
12	2.311	2.189	2.183	2.149	1.990	1.943	1.951	1.725	1.712	1.746	1.664	1.705
MSE	0.451	0.350	0.323	0.374	0.305	0.204	0.094	−0.021	−0.059
MAE	0.451	0.350	0.323	0.374	0.305	0.204	0.094	0.062	0.069
R^2	0.852	0.718	0.772	0.928	0.837	0.910	0.908	0.819	0.909

---

For 5, there is a possible keto–enol equilibrium, but the free energies indicate that the aldehyde isomer should indeed be favored by 9.2 kcal mol⁻¹ (GS) and 6.4 kcal mol⁻¹ (ES), and only this tautomer was considered. Note that this result is fully consistent with the experimental NMR measurements performed in chloroform.¹⁴ For 7, a possible equilibrium between the canonical and unprotonated (with a negative charge on the dicyano arm) isomer has also been tested because experimentally, such form attains ca. 10% of the mix.¹⁴ We consistently found that the canonical isomer represented in Fig. 1 is more stable, but the calculations also revealed that the anionic compound presents significantly different transition energies (−0.278 eV for absorption and −0.379 eV for emission), so that the experimental data originates from the overlapping of individual spectra of two systems. This makes comparisons between measurements and theory rather unsteady. For this reason 7 was not included in our statistical analysis below.

Overall, the data listed in Table 3 indicate that CIS(D) values are closer from experimental data than their TD-DFT counterparts, and the improvements becomes much more significant with SOS-CIS(D), which is in the line of the results of ref. 31. It is also important to see if theory can estimate auxochromic shifts. The series 9 → 10 → 3 correspond to increasingly strong donor groups and hence larger CT. This yields successive experimental E^AFCP shifts of −0.092 eV and −0.309 eV, that are significantly underrated by TD-DFT (−0.043 eV and −0.149 eV, respectively) and CIS(D) nor SOS-CIS(D) do bring significant improvements: −0.042/−0.038 eV and −0.162/−0.168 eV, for CIS(D)/SOS-CIS(D), respectively. The extension of the π-delocalisation (9 → 11) induces a small shift of E^AFCP (−0.051 eV) that is reasonably reproduced by all approaches (TD-DFT: −0.075 eV, CIS(D): −0.066 eV and SOS-CIS(D): −0.034 eV).

Let us now turn towards the statistical analysis starting with the physically well-defined E^AFCP. We provide mean signed error (MSE), mean absolute error (MAE) and R² in Table 3. A comparison of the theoretical results obtained with the three approaches with experimental values of Kovtun and coworkers is provided in Fig. 4. It turns out that, consistently with the above analysis, TD-DFT provides a sound general evolution of the transition energies, but is not very effective at discriminating subtile chemical effects. On the contrary, including CIS(D) corrections yields a much more consistent evolution across the full panel of dyes (improved R²), though the systematic overshooting of experimental transition energies pertains. SOS-CIS(D) offers the best approach as it delivers smaller deviations, while conserving the large determination coefficient obtained with CIS(D). It is crystal clear from the statistical data listed at the bottom of Table 3 that the results obtained with eqn (7) considering SOS-CIS(D) are much more satisfying than the one obtained with TD-DFT alone: the average error is down to 0.069 eV (instead of 0.323 eV with TD-DFT), and the determination coefficient, R² is greatly improved (from 0.772 to 0.909): theory does not “explain” ca. 9% (with CIS(D) or SOS-CIS(D) corrections) of the experimental variance rather than ca. 23% (with pure TD-DFT). One can logically conclude that, despite the computational effort implied in such a mixed approach, it is probably worth for describing large compounds with ES of cyanine-like nature. For the remaining absolute errors as well as the too small slope of SOS-CIS(D) obtained in Fig. 4, it is not possible to determine, at this stage, if they come from the limitations of the SOS-CIS(D) model, from incomplete description of solvent effects (with PCM), from inaccuracies in the optimal GS and ES geometries (with TD-DFT), or from a blend of the three effects. If one wishes to go for the faster vertical approximation, then, as can be seen at the bottom of Table 3, the approach including [SOS-]CIS(D) correction helps providing both smaller deviations and larger R².

Fig. 4 Comparison between theoretical and experimental E^AFCP (in eV). TD-DFT and [SOS-]CIS(D) data correspond to eqn (1) and (7), respectively. The dotted lines correspond to the linear correlation line. The central diagonal line indicates a perfect theory–experiment match.

4 Conclusions and outlook

Using ab initio theoretical tools, we have investigated the optical spectra of twelve recently proposed large dyes including both a central BODIPY core and side group(s) enhancing the cyanine character of the first electronic transition. As expected, the results obtained with TD-DFT are far from fully satisfying. Indeed, even when including solvent effects with a refined model and accounting for ZPVE corrections, the average theory–experiment deviation attains 0.323 eV, and more importantly, the R² relating TD-DFT and experimental energies is poor (0.772) despite the chemical similarity of the molecules investigated. As we have shown that simplifying the chemical structure, so to allow the easier use of highly accurate wavefunction methods, would also imply large errors, we proposed a mixed approach in which the structures and solvent effects are modeled with TD-DFT and the transition energies are calculated with SOS-CIS(D). This mixed scheme allows not only to reduce the absolute average deviations by ca. 80%, but also vastly improves the R² (0.909), therefore paving the way towards theoretical design of new members of this challenging class of dyes.

We are currently investigating other structures with this mixed approach in order to determine if the improvements noted here pertain when one considers other molecules, including those for which TD-DFT is known to be a reasonably accurate approach.

Acknowledgements

D.J. is indebted to Siwar Chibani and Dr Adèle D. Laurent (Nantes) for fruitful discussions about the use of SOS-CIS(D) for large dyes. D.J. acknowledges the European Research Council (ERC) and the Région des Pays de la Loire for financial support in the framework of a Starting Grant (Marches – 278845) and a recrutement sur poste stratégique, respectively. This research used resources of the GENCI-CINES/IDRIS (Grant c2014085117), of the CCIPL (Centre de Calcul Intensif des Pays de Loire) and of a local Troy cluster.

References

1. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447.
2. L. Goerigk and S. Grimme, J. Chem. Phys., 2010, 132, 184103.
3. R. Send, M. Kühn and F. Furche, J. Chem. Theory Comput., 2011, 7, 2376–2386.
4. D. Jacquemin, A. Planchat, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2012, 8, 2359–2372.
5. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hattig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630.
6. F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, J. Chem. Theory Comput., 2013, 9, 2072–2082.
7. C. Fang, B. Oruganti and B. Durbeej, J. Phys. Chem. A, 2014, 118, 4157–4171.
8. A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356.
9. V. P. Yakubovskyi, M. P. Shandura and Y. P. Kovtun, Eur. J. Org. Chem., 2009, 3227–3243.
10. V. P. Yakubovskyi, M. P. Shandura and Y. P. Kovtun, Dyes Pigm., 2010, 87, 17–21.
11. M. P. Shandura, V. P. Yakubovskyi, A. O. Gerasov, O. D. Kachkovsky, Y. M. Poronik and Y. P. Kovtun, Eur. J. Org. Chem., 2012, 1825–1834.
12. M. P. Shandura, V. P. Yakubovskyi and Y. P. Kovtun, Org. Biomol. Chem., 2013, 11, 835–841.
13. M. P. Shandura, V. P. Yakubovskyi, Y. V. Zatsikha, O. D. Kachkovsky, Y. M. Poronik and Y. P. Kovtun, Dyes Pigm., 2013, 98, 113–118.
14. Y. V. Zatsikha, V. P. Yakubovskyi, M. P. Shandura and Y. P. Kovtun, RSC Adv., 2013, 3, 24193–24201.
15. Y. V. Zatsikha, V. P. Yakubovskyi, M. P. Shandura, I. Y. Dubey and Y. P. Kovtun, Tetrahedron, 2013, 69, 2233–2238.
16. A. D. Quartarolo, N. Russo and E. Sicilia, Chem.–Eur. J., 2006, 12, 6797–6803.
17. A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932.
18. G. Ulrich, R. Ziessel and A. Harriman, Angew. Chem., Int. Ed., 2008, 47, 1184–1201.
19. P. A. Bouit, K. Kamada, P. Feneyrou, G. Berginc, L. Toupet, O. Maury and C. Andraud, Adv. Mater., 2009, 21, 1151–1154.
20. M. E. Alberto, B. C. De Simone, G. Mazzone, A. D. Quartarolo and N. Russo, J. Chem. Theory Comput., 2014, 10, 4006–4013.
21. R. Send, O. Valsson and C. Filippi, J. Chem. Theory Comput., 2011, 7, 444–455.
22. M. Schreiber, V. Bub and M. P. Fülscher, Phys. Chem. Chem. Phys., 2001, 3, 3906–3912.
23. J. Fabian, Theor. Chem. Acc., 2001, 106, 199–217.
24. D. Jacquemin, Y. Zhao, R. Valero, C. Adamo, I. Ciofini and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 1255–1259.
25. B. Moore II and J. Autschbach, J. Chem. Theory Comput., 2013, 9, 4991–5003.
26. S. Grimme and F. Neese, J. Chem. Phys., 2007, 127, 154116.
27. H. Zhekova, M. Krykunov, J. Autschbach and T. Ziegler, J. Chem. Theory Comput., 2014, 10, 3299–3307.
28. M. Head-Gordon, D. Maurice and M. Oumi, Chem. Phys. Lett., 1995, 246, 114–121.
29. P. Boulanger, D. Jacquemin, I. Duchemin and X. Blase, J. Chem. Theory Comput., 2014, 10, 1212–1218.
30. S. Chibani, B. Le Guennic, A. Charaf-Eddin, O. Maury, C. Andraud and D. Jacquemin, J. Chem. Theory Comput., 2012, 8, 3303–3313.
31. S. Chibani, A. D. Laurent, B. Le Guennic and D. Jacquemin, J. Chem. Theory Comput., 2014 DOI:10.1021/ct00655k.
32. S. Grimme and E. I. Izgorodina, Chem. Phys., 2004, 305, 223–230.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
34. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
35. R. Li, J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 12697–12701.
36. M. Isegawa, R. Peverati and D. G. Truhlar, J. Chem. Phys., 2012, 137, 244104.
37. S. S. Leang, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2012, 136, 104101.
38. A. Charaf-Eddin, A. Planchat, B. Mennucci, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 2749–2760.
39. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
40. D. Jacquemin, E. A. Perpète, G. Scalmani, M. J. Frisch, R. Kobayashi and C. Adamo, J. Chem. Phys., 2007, 126, 144105.
41. S. Chibani, B. Le Guennic, A. Charaf-Eddin, A. D. Laurent and D. Jacquemin, Chem. Sci., 2013, 4, 1950–1963.
42. S. Chibani, A. Charaf-Eddin, B. Le Guennic and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 3127–3135.
43. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
44. M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717.
45. R. Cammi and B. Mennucci, J. Chem. Phys., 1999, 110, 9877–9886.
46. M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520.
47. R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103.
48. Y. Shao, L. Fusti-Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. Distasio Jr., R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191.
49. T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506.
50. D. Jacquemin, T. Le Bahers, C. Adamo and I. Ciofini, Phys. Chem. Chem. Phys., 2012, 14, 5383–5388.
51. F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509.
52. S. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 184102.
53. S. Pascal, A. Haefele, C. Monnereau, A. Charaf-Eddin, D. Jacquemin, B. Le Guennic, C. Andraud and O. Maury, J. Phys. Chem. A, 2014, 118, 4038–4047.
54. S. Chibani, A. Charaf-Eddin, B. Mennucci, B. Le Guennic and D. Jacquemin, J. Chem. Theory Comput., 2014, 10, 805–815.

---