Asymmetric transport of water molecules through a hydrophobic conical channel

Abstract

Unlike macroscale systems, symmetry breaking could lead to surprising results for nanoscale systems. Although great attention has been paid to the transport properties of water molecules through nanochannels in recent years, most of the existing studies are related to symmetric channels (e.g. cylindrical ones). Herein, we use molecular dynamics simulations to study the transport of water through a hydrophobic conical channel. Surprisingly, without any dynamic load, when the channel becomes more asymmetric (the wide radius increases) net water fluxes along the divergent direction are observed, which should be related to the thermal noise. To further explore the asymmetric properties of the conical channel, we then apply the pressure differences for the convergent and divergent directions, respectively. We find that the convergent flux is changed from smaller to larger than the divergent one with the increase of pressure. However, for the salt solution, the convergent flux is coupled to ions due to the blocking effect at low pressures; while the divergent flux is almost independent of ions. These results demonstrate some new physical insights of the ratchet effect of conical channels, and further a pressure controlled water rectification that could have deep implications for designing highly efficient nanoporous materials for sea water desalination.

---

Introduction

During the past decades considerable attention has been paid to the transport properties of water molecules through nanochannels, due to their relevance to biological activities^1,2 and potential industrial applications.³ Actually, not only our daily life but also life itself depends on the transport of water. Water molecules are selectively and efficiently transported in and out of cells through nanopores such as transmembrane proteins, aquaporins and so on.

Recent experimental^4,5 and theoretical^6,7 studies proved carbon nanotubes (CNTs) as fast water transporters, where the water flow rate exceeds the prediction of conventional nonslip hydrodynamic flow by several orders of magnitude. Hence, if such CNTs can be utilized in the sea water desalination or polluted water filtration, the energy required is expected to be reduced significantly. To some extent, the fast conduction of water inside CNTs is not only due to the CNT itself, such as its regular structure, its smooth interior surface and its hydrophobic nature, but also relevant to the strong interaction between water molecules and the resulting unique structures different from a bulk system.² Thus, the water flow enhancement strongly depends on the channel size.^8,9 Up to now, many experiments have confirmed the filling of narrow CNTs with water, e.g., transmission electron microscopy,¹⁰ nuclear magnetic resonance spectroscopy,¹¹ neutron diffraction,¹² density gradient centrifugation,¹³ as well as Raman spectroscopy for single-file water chains.¹⁴ Consequently, in view of their superiority as a water transporter, within the experimentally available materials, carbon nanotubes should be an ideal model of nanochannels for theoretical studies. Furthermore, the transport of water molecules through CNTs are also relevant to the design of novel nanofluidic devices, such as molecular sieves,¹⁵ novel desalination machines,¹⁶ fuel cells,¹⁷ drug delivery,¹⁸ biosensors,¹⁹ as well as nanometer water gates.^20,21

Although a large amount of studies on the water transport through nanochannels can be found, as far as we know, most of the existing reports both in experiment^4,5,10–14 and theory^{2,6–9,15,16,20,21} concern the uniform or symmetric cylinder channels. Little effort has been made for the transport properties of asymmetric channels. When the channel is asymmetric, e.g., for a conical channel, previous simulation work showed the ratchet motion of a simple liquid, i.e., a net mass transport can be achieved under a zero-average time-dependent drive.²² They ascribe the fascinating phenomenon to an entropic ratchet, where the longitudinal motion is driven by an external field, while the transversal motion is dominated by a symmetry breaking in geometrical confinement. As atoms can not be aware of the increasing space along the divergent direction, the divergent flux is always smaller than the convergent flux, leading to a diode effect. Actually, such a diode effect of conical channel has motivated considerable interest for experimental studies of the transport of individual molecules, particles, or cells.^23,24 Examples include ion current rectification,²⁵ electric-field controlled wetting and dewetting gates,^26,27 ion sieves,²⁸ as well as a potential biosensor.²⁹ Even without any external field, such as pressure and electric field, the diffusion ion currents are also asymmetric and dependent on the concentration gradient direction.³⁰ Thus, understanding the transport properties of conical channels is not only of great importance to pure scientific interest, but also crucial to the design of novel nanofluidic devices.

Model and simulation method

Herein, we use molecular dynamics (MD) simulations to study the transport of water molecules through a conical CNT. We consider both pure water and salt solution systems. Fig. 1 shows the snapshot of the simulation system, where a conical CNT with length of 4 nm, narrow radius of r = 0.4 nm, and wide radius of R = 1.1 nm, combined with two graphite sheets (5.08 × 5.08 nm²), is embedded in a periodic water box with 3136 molecules, representing an asymmetric water channel. Clearly, the narrow end can only accommodate single-file water, while the water structure at the wide end should be similar to that in bulk. To provide insight into the effects of conical slope, we also consider two additional channels with a size of only varying R to 0.8 nm and 1.4 nm, respectively. Technically, it is still difficult to fabricate conical CNTs in experiments and our model should represent the general hydrophobic channels that is different from the experimentally fabricated conical nanopore with a tip size of 1–2 nm.^28–30 In the present study, we first explore the water transport without any external driving force, where we vary the channel size (only R) and temperatures. Then, for R = 1.1 nm and T = 300 K, a pressure difference is applied either along the convergent (+z, +P) or the divergent (−z, −P) direction to drive water flow. Following the method proposed by Zhu et al.,³¹ we applied an additional acceleration to each water molecule to obtain the pressure difference between the two ends of the CNT channel. Note that all the waters in the system are assigned the acceleration rather than only the waters near the two channel ends. The pressure difference between the two membrane sides can be estimated as P = nf/A, where A is clearly the surface area of the membrane not a specific channel. In our present simulation, we count A as the area of graphene not the channel ends. Thus, the pressure difference here is a theoretical value and independent of the channel size and shape. We define the upflux/downflux as the total number of water molecules (or ions) per nanosecond conducted through the CNT from bottom/top (−z/+z) to top/bottom (+z/−z), respectively. The convergent/divergent flux is the difference between the upflux/downflux and downflux/upflux, respectively, while the flow is the sum of upflux and downflux.

Fig. 1 Snapshot of the simulation system. A conical nanotube with length of 4.0 nm, upper diameter of 0.8 nm, and bottom diameter of 2.2 nm, combined with two graphite sheets (5.08 × 5.08 nm²), is embedded in a periodic water box with 3136 molecules, representing an asymmetric water channel. A pressure difference is applied either along the convergent (+z, +P) or the divergent (−z, −P) direction to drive water flux.

All MD simulations were carried out at constant volume and temperature using the Nose–Hoover method for temperature coupling with Gromacs 3.3.1 simulation package.³² For most cases, the temperature is fixed to T = 300 K. The TIP3P water model was used.³³ Known carbon³⁴ and ion³⁵ parameters were used. The Lennard-Jones (LJ) potential cut-off was 1.2 nm. The particle-mesh Ewald method was used to treat the long-range electrostatic interactions (1.2 nm cut-off in real space).³⁶ Periodic conditions were applied in all directions. A time-step of 2 fs was used, and data were collected every 0.5 ps. The carbon nanotube combined with two graphite sheets were held fixed during the simulations. For each channel size, temperature or pressure, we conducted 130 ns MD runs, and the last 125 ns trajectory was used for data analysis.

Results and discussion

First, we consider the water transport without any dynamic load, i.e., a purely self-diffusion process. We present the water flow and flux as a function of the wide radius R in Fig. 2, where the narrow radius and channel length are fixed to 0.4 nm and 4.0 nm, respectively. For a comparison with cylinder CNT channels, we also give the water flow of CNTs with a radius of (r + R)/2 that can be regarded as the average of conical radius. For R = 0.8 nm, we find the water transport in both directions is almost symmetric, i.e., the water flux is almost zero (0.38 ns⁻¹ and can be considered as statistical fluctuation), similar to CNTs. Surprisingly, considerable net water flux is observed along the divergent direction for both R = 1.1 nm and 1.4 nm. It seems counterintuitive that a net flux can be generated without any dynamic load. This net flux should be induced by thermal noise, according to a recent theoretical analysis.³⁷ The correlation lengths of the thermal fluctuations become significantly long for nanoscale systems. This differs from macroscopic systems in which the thermal noises are usually treated as white noise. Different from macroscopic systems, we should put extra energy into the nanoscale system to hold the asymmetrical structure of the channel.

Fig. 2 The water flow and flux as a function of the wide end radius of conical channel, where the narrow end radius is fixed as r = 0.4 nm. The water flow for CNTs with different radius is also presented for comparison, where the CNT radius is the average of the two ends of conical channel [(r + R)/2]. The water flow is the average number of water molecules per nanosecond conducting through the channel; the water flux is the net water number conducting through in one channel direction, and here is along the divergent.

Furthermore, the water flow and flux for R = 1.1 and 1.4 nm are very close to each other, while the flow in CNTs increases almost linearly with radius increasing. This is not surprising, since the narrow end should be a bottleneck for water flow through the conical channel. It is believed that if R becomes infinity, there should be no water flux since the conical channel becomes a graphene with a nanopore. Thus, the water flux will have a maximum behavior with R increasing. But huge simulation system is required to consider larger R further, which is beyond our current computational ability. To further understand the energy variation of a water molecule moving through the conical channel, we show in Fig. 3 the free energy profiles as a function of the water position along the channel axis. The free energy here is counted according to the water density fluctuation.³⁸ Clearly, from bulk water to the conical channel, the free energy barrier is slightly larger than 1.5 k_BT at the narrow end, similar to previous study;³⁸ while for the wide end, the barrier increases from 0.25 k_BT to 0.5 k_BT as R decreases from 1.4 nm to 0.8 nm. Thus, the barrier difference between the two ends is around k_BT and water should favor the divergent direction. Nonetheless, in a very elaborate calculation, a low free energy of −5 kJ mol⁻¹ (−2k_BT) is found for the same narrow CNT based on the SPC/E water model.³⁹ They also showed different free energy profiles for different water models, especially for the narrow CNT, where positive values are found for the other two water models. Generally, when water enters narrow CNTs it will loss hydrogen bonds and the energy will be increased. The water will also gain some rotational entropy to compensate its energy increase, and someone found the compensation is equal to the energy increase for the TIP3P model.⁴⁰ Thus, the average free energy of a water molecule is the same as that in the bulk. In a word, it might be still a little difficult to definitely determine the free energy of confined water, since the value is small and comparable to k_BT. Our free energy profiles indicate that a k_BT is consumed to move a water molecule from the narrow end to the wide end. This is reasonable as the energy required here is from thermal noise.

Fig. 3 The free energy 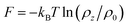as a function of the water position along the convergent direction. Here ρ₀ is the bulk water density, fixed as 1.0 g cm⁻³; ρ_z is the water density along the channel axis.

As the water flux is induced by thermal noise, it should be related to the system temperature. To further understand it, we show in Fig. S1(a) (in the ESI†) the water flow and flux as a function of temperature for R = 1.1 nm. The water flow increases almost linearly with the increase of temperature. This can be well understood as the kinetic energy of water is proportional to the temperature, and they can go through the channel fast at a high temperature. Interestingly, the water flux along the divergent direction also shows a linear increase with the temperature. This should confirm the relation between water flux and thermal noise. We also consider a typical salt solution of 1.77 M NaCl (100 NaCl pairs in our system) at T = 300 K, and we find similar net water flux along the divergent direction. It is noted that, naturally, a water molecule should try to find a position to maximize its hydrogen bond (H-bond) number. The average H-bond number of individual water as a function of its position along the channel convergent direction is presented in Fig. S1(b).† Here, two water molecules are hydrogen bonded when their inter-oxygen distance is less than 0.35 nm, and simultaneously the angle between the O–O axis and one of the O–H bonds is less than 30°. Slight fluctuations can be observed for different H-bond definitions,⁴¹ but should not affect any conclusion here. Clearly, inside the conical channel, the H-bond number decreases from 3.22 to 1.82 when a water molecule moves from the divergent to convergent end. Thus water molecules should favor the divergent direction much more. This result, to some extent, supports the net water flux along the divergent direction. We should point out again that such a conical channel is not a mechanical water pump that does not need any additional energy, as it should consume some external energy to keep the channel asymmetry in the nanoscale.³⁷

We further investigate the transport of water under the drive of pressure difference between the two channel ends. We consider both the convergent (+z, +P) and divergent (−z, −P) pressure (T = 300 K and R = 1.1 nm). The net water flux for both pure water and salt solution are shown in Fig. 4. For the pure water system, the convergent flux is smaller than the divergent one at low pressures. This can be well understood since the convergent flux exits without pressure. Under large pressures, the convergent flux becomes the larger one, similar to the cases with simple liquid²² and ions.^25,28–30 Actually, the rectification direction can be changed by the channel charge inversion.²⁸ Here, an important conclusion is that the rectification of such conical CNT for water can be tuned by pressures. The ratio of convergent flux to divergent flux for our studied pure water is increased from 0.49 to 1.62 with the increase of pressure, which is comparable to the simple liquid²² and experimental results of ion current rectification induced by concentration difference.³⁰

Fig. 4 Water flux and its ratio (+P/−P) as a function of the pressure difference for pure water (top) and salt solution (bottom) at R = 1.1 nm. +P: convergent pressure difference; −P: divergent pressure difference. The water flux is along the pressure direction.

It will be more interesting for the case of salt solution, also shown in Fig. 4. The overall asymmetric water flux in the convergent and divergent directions is similar to the pure water case, i.e., the convergent flux changes from the smaller one to larger one with the increase of pressure. However, the overlap point (ratio = 1.0) clearly shifts to higher pressure regions. As can be seen, the divergent flux is similar to the pure water case, while the convergent flux does not increase remarkably with the increase of pressure for P ≤ 181 MPa (denoted by the dotted line). This is because the ions near the convergent outlet greatly hinder the convergent flux, where a typical snapshot of a Na⁺–water cluster is shown in Fig. 5(a) inset. Clearly, this cluster will block the convergent outlet, and thus prevent the water transport. For P > 181 MPa, the convergent flux increases dramatically with the pressure. This is because at such large pressures, the ion–water cluster becomes unsteady, and the ion will be pulled out of the channel. These assumptions can be further confirmed by the ion flux, presented in Fig. 5(a), where the convergent ion flux becomes appreciable only for P > 181 MPa. The divergent ion flux is completely zero at our studied pressure range, which stems from large free energy barrier for an ion entering small channels.⁴² From thermal dynamic point of view, the free energy profiles for ions should be independent of its moving direction (either divergent or convergent), as it only has to do with the position along the channel. It can be expected that when ion moves along the convergent direction, its free energy barrier should become higher slowly, since the channel diameter becomes smaller continuously, thus ions do not have to overcome a sharp barrier at one time to move ahead. Beside, ions will be always inside the channel for long time even if they fail to get through the narrow end, i.e., they have more chance to be close to the narrow end. Under high pressures, the ion–water cluster become easy to be destroyed and thus ions can go through the narrow end. When ions are moving in the divergent direction under divergent pressure, ions will encounter a large barrier directly at the narrow channel end. Also, when they fail to enter the narrow end they should be not always close to the narrow end since they are in the bulk water. Thus, in the divergent direction no ion flux can be observed, similar to previous results.⁴²

Fig. 5 (a) Ion flux and (b) average ion occupancy as a function of the pressure difference for salt solution at R = 1.1 nm. The ion flux is along the pressure direction. The inset in (a) shows a typical cluster of an ion (Na⁺) around by water molecules near the convergent outlet of the channel.

The asymmetric ion flux in the convergent and divergent direction is probably related to the ion occupancy inside the channel. In Fig. 5(b) we further demonstrate the average ion occupancy as a function of the pressure differences. Remarkably, for the positive (convergent) pressure, the ion occupancy exhibits increasing, followed by a sudden drop and then increases with the increase of pressure. For P = 0 (not shown), 〈N〉 = 3.59 is smaller than that of P = 36.2 MPa. Actually, this occupancy behavior is coupled to the ion flux behavior in Fig. 5(a). For small pressures (P < 181 MPa), ion can not transport through the narrow end, thus more ions will be accumulated inside the channel with the pressure increasing. For P ≥ 181 MPa, ion can move across the narrow end, thus the occupancy is subjected to a sudden decrease; however, for further larger pressures, although the ion flux increases, more ion can be accumulated, suggested by the occupancy increase. Thus, there should be a competition between ion flux and accumulation. For negative (divergent) pressures, the ion occupancy decreases as a whole with the increase of pressure. This can be well understood, since under negative pressures, no ion can move across the narrow end, leading to no compensation. Consequently, with the increase of pressure more ions will move out of the channel with no compensation from the narrow end, and at the largest pressure the ion occupancy is close to zero. Note that ion can also move (against the pressure direction) into the channel through the wider end by thermal fluctuation, thus the ion occupancy should be always nonzero if the pressure is not extremely large, just as the case here. We also presented the evolution of ion occupancy as a function of simulation time in Fig. S2 (ESI†). For positive pressures, the occupancy will always fluctuate with time and no visible difference can be observed for different pressures. For negative pressures, the occupancy becomes less fluctuation with increasing values in zero.

Actually, the asymmetric ion conduction through conical channels has been observed by recent experiments.^25,28–30 Herein, the pressure of P = 181 MPa can be regarded as a threshold. These results should have deep implications for the sea water desalination when using conical channels. For P ≤ 181 MPa, we should use the divergent direction; while for P > 181 MPa, we may use the convergent direction to achieve high water flux if we do not mind the small ion flux. By the way, if we strictly define the threshold pressure as the minimum value to induce the convergent ion flux, the threshold value should be independent of salt solutions. This is because the threshold pressure is only responsible for the rupture of the ion–water cluster (see Fig. 5(a) inset); however, it is believed that at low salt solutions, the probability of ion blocking in the convergent outlet should be low, thus the convergent flux may be not affected remarkably, where the threshold pressure may not be obviously identified according to flux.

Conclusions

In summary, we have conducted molecular dynamics simulations to study the transport of water molecules through a hydrophobic conical channel. For the both the pure water and salt solution systems, we find net water flux along the divergent direction without any dynamic load when the channel achieves certain asymmetry (R = 1.1 nm or larger). A recent work indicates that short cut-off values for the Lennard-Jones (LJ) potential will lead to artifact water flux.⁴³ In Fig. S3 (in the ESI†), we show the water flow and flux as a function of the cut-off distance for R = 1.1 nm. The water flux only slightly decreases with fluctuation with the increase of cut-off. To make a further comparison, we conducted 55 ns MD runs in Lammps package (we do not run 130 ns as in Gromacs because Lammps is running several times slower).⁴⁴ The final 50 ns statistic results are also shown in Fig. S3.† The resulting flux is 14.4 ns⁻¹, comparable to 18.5 ns⁻¹ derived by using Gromacs. Thus, our qualitative conclusion should be independent of the cut-off scheme and simulation software. It is believed that the net flux should be induced by thermal noise, where its correlation time length is large for the nanoscale system.³⁷ The variation in hydrogen bond number also indicates that water favors the divergent direction. The divergent flux is larger than the convergent one under small pressures. While, under high pressures the convergent flux becomes the larger one. Similar results are also observed in the simple liquid²² and ion current rectification in recent experiments.^25,28–30 In particular, ions at the convergent outlet will strongly hinder the convergent water flux at small pressures, thereby the ion flux is close to zero; while at high pressures, ions will be pulled out, and thus the ion flux and water flux increase with pressures dramatically. In contrast, under the divergent pressures, ions in the outside of the divergent inlet can not affect the water flux remarkably. This is because the ion–water cluster should not always block the divergent inlet. These results demonstrate a pressure-tuned reversal rectification for water flux, and should have deep implications for the design of high efficient water channels and devices for water desalination.

Acknowledgements

This work is financially supported by the National Science Foundation of China (21204093, 21174154, 20874110) and Chinese Academy of Sciences (KJCX2-YW-H19). The allocated computer time at the Supercomputer Center of Chinese Academy of Sciences is gratefully acknowledged.

References

1. B. L. De Groot and H. Grubmuller, Science, 2001, 294, 2353–2537.
2. J. C. Rasaiah, S. Garde and G. Hummer, Annu. Rev. Phys. Chem., 2008, 59, 713–740.
3. M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717.
4. M. Majumder, N. Chopra, R. Andrews and B. Hinds, Nature, 2005, 438, 44.
5. J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037.
6. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190.
7. S. Joseph and N. R. Aluru, Nano Lett., 2008, 8, 452–458.
8. J. A. Thomas and A. J. H. McGaughey, Nano Lett., 2008, 8, 2788–2793.
9. J. A. Thomas and A. J. H. McGaughey, Phys. Rev. Lett., 2009, 102, 184502.
10. N. Naguib, H. Ye, Y. Gogotsi, A. G. Yazicioglu, C. M. Megaridis and M. Yoshimura, Nano Lett., 2004, 4, 2237–2243.
11. H. J. Wang, X. K. Xi, A. Kleinhammes and Y. Wu, Science, 2008, 322, 80–83.
12. A. I. Kolesnikov, J. M. Zanotti, C. K. Loong, P. Thiyagarajan, A. P. Moravsky, R. O. Loutfy and C. J. Burnham, Phys. Rev. Lett., 2004, 93, 035503.
13. S. Cambré and W. Wenseleers, Angew. Chem., Int. Ed., 2011, 50, 2764–2768.
14. S. Cambré, B. Schoeters, S. Luyckx, E. Goovaerts and W. Wenseleers, Phys. Rev. Lett., 2010, 104, 207401.
15. X. J. Gong, J. C. Li, K. Xu, J. F. Wang and H. Yang, J. Am. Chem. Soc., 2010, 132, 1873–1877.
16. A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180.
17. Q. Z. Yuan and Y. P. Zhao, J. Am. Chem. Soc., 2009, 131, 6374–6376.
18. A. A. Bhirde, V. Patel, J. Gavard, G. F. Zhang, A. A. Sousa, A. Masedunskas, R. D. Leapman, R. Weigert, J. S. Gutkind and J. F. Rusling, ACS Nano, 2009, 3, 307–316.
19. Y. S. Tu, P. Xiu, R. Z. Wan, J. Hu, R. H. Zhou and H. P. Fang, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18120–18124.
20. R. Z. Wan, J. Y. Li, H. J. Lu and H. P. Fang, J. Am. Chem. Soc., 2005, 127, 7166–7170.
21. J. Y. Li, X. J. Gong, H. J. Lu, D. Li, H. P. Fang and R. H. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3687–3692.
22. M. Chinappi, E. De Angelis, S. Melchionna, C. M. Casciola, S. Succi and R. Piva, Phys. Rev. Lett., 2006, 97, 144509.
23. W. J. Lan and H. S. White, ACS Nano, 2012, 6, 1757–1765.
24. Z. S. Siwy and S. Howorka, Chem. Soc. Rev., 2010, 39, 1115–1132.
25. W. J. Lan, D. A. Holden and H. S. White, J. Am. Chem. Soc., 2011, 133, 13300–13303.
26. M. R. Powell, L. Cleary, M. Davenport, K. J. Shea and Z. S. Siwy, Nat. Nanotechnol., 2011, 6, 798–802.
27. S. N. Smirnov, I. V. Vlassiouk and N. V. Lavrik, ACS Nano, 2011, 5, 7453–7461.
28. Y. He, D. Gillespie, D. Boda, I. Vlassiouk, R. S. Eisenberg and Z. S. Siwy, J. Am. Chem. Soc., 2009, 131, 5194–5202.
29. I. Vlassiouk, T. R. Kozel and Z. S. Siwy, J. Am. Chem. Soc., 2009, 131, 8211–8220.
30. Z. S. Siwy, I. D. Kosinska, A. Fulinski and C. R. Martin, Phys. Rev. Lett., 2005, 94, 048102.
31. F. Q. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2002, 83, 154–160.
32. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
33. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
34. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
35. R. M. Lynden-Bell and J. C. Rasaiah, J. Chem. Phys., 1996, 105, 9266–9280.
36. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
37. R. Z. Wan, J. Hu and H. P. Fang, Sci. China: Phys., Mech. Astron., 2012, 55, 751–756.
38. H. J. Lu, J. Y. Li, X. J. Gong, R. Z. Wan, L. Zeng and H. P. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 174115.
39. T. A. Pascala, W. A. Goddarda and Y. Jung, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11794–11798.
40. H. Kumar, B. Mukherjee, S. T. Lin, C. Dasgupta, A. K. Sood and P. K. Maiti, J. Chem. Phys., 2011, 134, 124105.
41. R. Kumar, J. R. Schmidt and J. L. Skinner, J. Chem. Phys., 2007, 126, 204107.
42. B. Corry, J. Phys. Chem. B, 2008, 112, 1427–1434.
43. D. J. Bonthuis, K. Falk, C. N. Kaplan, D. Horinek, A. N. Berker, L. Bocquet and R. R. Netz, Phys. Rev. Lett., 2010, 105, 209401.
44. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra07034h

‡ Present address: Department of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA.

---