Structural engineering of MXenes for enhanced magnesium ion diffusion: a computational study

Abstract

The unique layered structure and tunable surface terminations of MXenes play a critical role in Mg²⁺ storage and diffusion dynamics. This study systematically investigates the behavior of Mg²⁺ in Ti₃C₂O₂ and its nitrogen-doped derivatives through theoretical calculations. In Ti₃C₂O₂ monolayers, Mg²⁺ exhibits a high diffusion barrier of 0.81 eV due to strong electrostatic interactions. However, AA-stacking reduces this barrier to 0.32 eV by introducing staggered active sites. The instability caused by interlayer O–O repulsion is mitigated by modulating the N/O ratio (Ti₃C₂O_1.78N_0.22), resulting in a diffusion barrier of 0.27 eV. Transition metal substitution further optimizes performance, as exemplified by Nb₃C₂N₂, which achieves an ultralow barrier of 0.23 eV through weakened N–N covalency and enhanced metal-N interactions. Voltage analysis reveals that Nb₃C₂N₂ possesses dual functionality as both cathode (4.00 V) and anode (0.64 V), contrasting with the anode-specific behavior observed in Ti-based MXenes.

---

Introduction

With the rapid depletion of fossil fuels, sustainable energy storage solutions grow increasingly vital.¹ In the past few decades, rechargeable lithium-ion batteries (LIBs) have dominated portable electronics and energy storage systems through their high energy density and cycling stability.^2,3 However, natural scarcity and dendritic growth risks of LIBs^4–6 necessitate alternative solutions.⁷ Rechargeable magnesium ion batteries (MIBs) emerge as a promising alternative to LIB, offering high energy density and superior electrochemical stability.⁸ Mg is the fifth most abundant element in the Earth's crust,⁹ enabling substantial cost savings compared to Li. The melting temperature of Mg is measured at 923 K, much higher than that of Li (453.7 K), making MIBs the safer option for working at high temperatures like in aviation. Divalent Mg²⁺ delivers doubled volumetric capacity (3833 vs. 2046 mA h cm⁻³) and dendrite-free operation with low reduction potential (−2.37 vs. SHE), and is expected to achieve reversible deposition in multiple electrolytes.^8,10–12

However, Mg²⁺ (0.72 Å) has a similar ionic radius to Li⁺ (0.76 Å).¹³The large charge/radius ratio of Mg²⁺ leads to strong electrostatic interaction with the electrode framework, resulting in sluggish ion diffusion.^14,15 Previous research on MIB electrode materials mainly focused on the transition metal–oxygen/sulfide, polyanionic compounds, and other two-dimensional materials. In transition metal oxides/sulfides systems (e.g., α-V₂O₅,¹⁶ α-MoO₃,¹⁷ Ti₂S₃/TiS₂ (ref. 18)), strong Mg²⁺-framework electrostatic interactions induce structural transformations that elevate Mg²⁺ diffusion barriers to 0.9–1.30 eV. By contrast, Chevrel phases and polyanionic compounds exhibit reversible Mg²⁺ (de)intercalation with mitigated electrostatic interactions.¹⁹ But even for polyanionic materials with good ion mobility, their energy barrier in MIBs is usually higher than 0.6 eV, such as Mg_0.25FePO₄ (1.03 eV) and NaV₂O₂(PO₄)₂F (0.78 eV).²⁰ Moreover, for the olivine-type Mg_xMnSiS₄, the strong Mn–S covalent interaction weakens the electrostatic interactions between Mg²⁺ and the host material ions, thereby enhancing Mg²⁺ diffusion compared to its oxide counterpart Mg_xMnSiO₄. However, the diffusion barrier for Mg²⁺ in Mg_xMnSiS₄ remains as high as 0.76 eV.

Transition metals-based layered materials have stable structures and excellent electrical conductivity.²¹ More importantly, the layered space provides a broad diffusion channel for Mg²⁺. Thus, 2D materials possess a lower diffusion barrier than the above materials, such as Si₂BN (0.08–0.35 eV), TiSe₂ (0.88 eV), VSe₂ (0.346 eV) and VS₂ (0.593 eV).^22,23 As a layered material, MXenes have garnered significant attention in electrochemical energy storage due to their electrical conductivity, large specific surface area, and stable layered architecture for the guest ions.^16,24,25 Lukatskaya et al. showed that Ti₃C₂T_x can provide ample accommodation to accommodate cations, such as Li⁺, Na⁺, K⁺, NH₄⁺, Mg²⁺ and Al³⁺, which produce large volumetric capacitance.²⁶ Xie et al.¹⁵ confirm that MXene monolayer cation storage occurs in a comparatively low voltage window, which could be used as anodes for rechargeable batteries. Currently, about 40 MXenes have been synthesized experimentally and hundreds of new MXenes are simulated theoretically.^27–30 It is crucial for MIB to investigate and enhance the diffusion performance of Mg ions within MXene materials.^31,32 Moreover, traditional research on MXene batteries typically focuses on ion storage mechanisms under the default stacking configuration. In fact, the existence of different stacking types is an important feature of layered materials. The most typical example is the layered oxide cathode of potassium-ion batteries. Their different stacking structures can form different potassium-ion storage environments, such as edge-sharing octahedral (O3) or face-sharing prismatic (P2). O3-type materials have high structural stability and can effectively inhibit the migration of transition metals into the K layer, thereby reducing structural degradation during the cycling process. P2-type materials exhibit excellent rate performance due to their unique prismatic coordination environment, which provides shorter K ion migration paths and lower energy barriers. Obviously, stacking type has a significant impact on the storage and migration of ions.³³ However, research on the impact of stacking configurations on the MXene electrochemical properties and the corresponding modulation mechanisms is still lacking.

This work investigates the Mg²⁺ storage and diffusion mechanisms in MXene-based materials, emphasizing the interplay between structural configurations and electrochemical performance. Based on integrating stacking engineering, functional group modulation, and transition metal substitution strategies, we elucidate the fundamental principles governing Mg²⁺ behavior, such as mitigating electrostatic interactions, optimizing interlayer covalent bonding, and modulating electronic structures. These findings demonstrate that hierarchical structural design-stacking control, doping, and metal substitution-significantly enhances Mg²⁺ kinetics and stability, advancing high-performance MIB electrodes.

Method

All first-principles density functional theory (DFT) calculations are performed using the Vienna Ab initio Simulation Package (VASP)^34–37 based on Perdew–Burke–Ernzerhof's (PBE) generalized gradient approximation (GGA-PBE).^38,39 The plane wave truncation energy is set to 550 eV. The valence electron selection for pseudopotential elements is as follows: Mg-3s²3p⁰, O-2s²2p⁴, C-2s²2p², N-2s²2p³, Cl-3s²3p⁵, S-3s²3p⁴, F-2s²2p⁵, Ti-3d²4s², V-3d³4s², Zr-4d²5s², Nb-4d⁴5s¹. Considering the strong correlation system of transition metal D-orbital electrons, GGA + U method is adopted in the calculation, and the U values of Ti, Nb, V and Zr are set as 2.5 eV, 2.0 eV, 2.5 eV and 2.0 eV respectively, which are obtained from the reference of element U values given by Materials Studio software. Conjugate gradient method was used to optimize the lattice structure. The energy convergence standard was set to 10–6 eV per atom and the force convergence standard was set to 0.01 eV Å⁻¹. In addition, this work adopts the CI-NEB method^40–42 to simulate the diffusion performance of Mg²⁺ in single/multilayer M₃C₂T_x (M = Ti, V, Zr, Nb, T = O, N) in a 3 × 3 × 1 supercell model. Including the beginning and end positions before and after diffusion, a total of 7 insertion points are set, and the convergence standard is that the force of each insertion point is less than 0.03 eV Å⁻¹.

Results and discussion

Structure and properties of bulk phase Ti₃C₂O₂

The Ti₃C₂ structure is stacked by the Ti–C–Ti–C–Ti layer. In each layer, the atoms are arranged in hexagons. During the preparation of MXene, the –OH in the etched aqueous solution will spontaneously adsorb on the surface, forming –O terminated groups and water. Based on the type of molten salt and subsequent treatment conditions, other terminated groups, such as –Cl, –I, –Br, –S, –Se and –N could also be adsorbed on the surface of MXene layers. Among these function groups, previous theoretical studies mainly considered –O adsorbed in MXene electrode materials. Because divalent O²⁻ with a larger chemical activity has more affinity for the cation exposed framework. The adsorbed atoms inherit the hexagonal arrangement of the Ti–C–Ti–C–Ti layer, which distributes above the middle Ti atoms (Fig. 1).

Fig. 1 (a) The top and side views of the three Mg²⁺ adsorption sites, namely, H₁, H₂ and T site on monolayer Ti₃C₂O₂. (b) Binding energy and valence states of Mg²⁺ at H₁, H₂ and T sites.

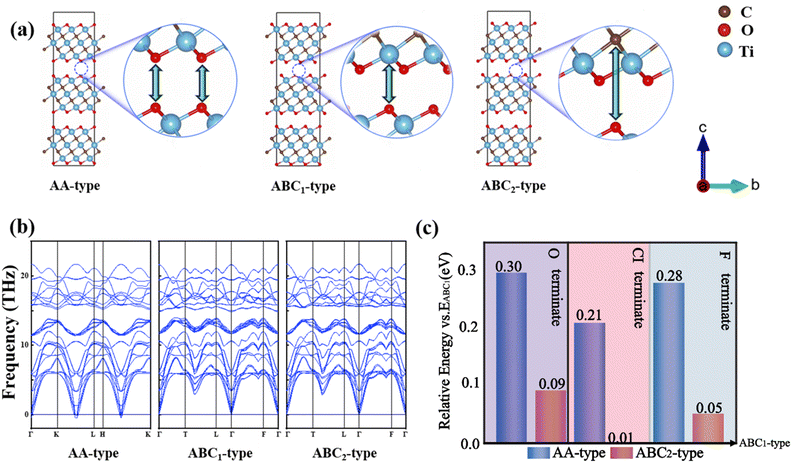
Generally, the synthesized MXene materials are bulk rather than monolayer. According to the relative position of adjacent layers, the Mxene structure has three possible stacking types, including AA (Table S1†), ABC₁ (Table S2†) and ABC₂ (Table S3†) types (Fig. 2a). For ABC₁ and ABC₂ types, terminal O is directly opposite to the outer Ti and C in the adjacent Ti₃C₂O₂ layer, respectively. The AA-stacking structure is characterized by the alignment of the terminal O groups of adjacent Ti₃C₂O₂ layers. According to the calculated phonon spectra, the phonon band for AA-stacking appears at −0.40 THz, which indicates a slight kinetic instability (Fig. 2b). By contrast, the phonon band structures without imaginary frequencies suggest that ABC₁ and ABC₂-stacking configurations are more likely to exist in nature. Moreover, our calculated relative energies show that the Ti₃C₂O₂ bulk with ABC₁-stacking is the most stable configuration (Fig. 2c). In comparison, the AA and ABC₂ types have relatively higher energy of 0.30 and 0.09 eV, respectively. Such relative stability of ABC₁-stacking is also applies consistently to the case of –Cl and –F terminate.

Fig. 2 (a) The side-views of the three stacked Ti₃C₂O₂, namely ABC₁ type, AA type and ABC₂ type. (b) The phonon band structures of AA-, ABC₁- and ABC₂-stacked configuration. (c) The relative energy of ABC₁- and ABC₂-type vs. the energy of AA-type for Ti₃C₂O₂, Ti₃C₂Cl₂ and Ti₃C₂F₂, respectively, in left to right order.

Adsorption of Mg²⁺ in Ti₃C₂O₂

Each surface of the Ti₃C₂O₂ layer has three possible Mg²⁺ active sites named H₁, H₂ and T, which are above the C, Ti and O atoms, respectively (Fig. 1a). H₁ and H₂ sites in two triangular hollow regions formed by three O and three Ti atoms, respectively. While the T site has only one coordinated O atom. To determine the most favorable Mg²⁺ active site, the Mg²⁺ binding energy E_b on the 2 × 2 × 1 Ti₃C₂O₂ monolayer was calculated through the following formula:

E_b = E_Ti3C2N2Mgx − E_Ti3C2N2 − xE_Mg (1)

where E_MgxTi3C2O2, E_Ti3C2O2 and E_Mg are the total energy of Ti₃C₂O₂Mg_x, Ti₃C₂O₂ and one atom of metal Mg. The calculation results show that the H₁ site exhibited a more negative E_b (−2.16 eV) than H₂ (−1.36 eV) site. While the Mg²⁺ on T site migrates to the adjacent H₁ site after structural optimization. In the case of fixed Mg²⁺ at a specific xy coordinate, the binding energy at the T site is only −0.68 eV. This indicates that a low coordination degree is not favorable for Mg²⁺ storage. According to the Bader charge analysis, the valence states of Mg²⁺ on H₁, H₂ and T site was +1.55, +1.41 and +0.84, respectively (Fig. 1b). Obviously, Mg²⁺ at the H₁ site is closer to its theoretical standard valence state, which is more conducive to its binding. When the Ti₃C₂O₂ layers are stacked to form the bulk, the Mg²⁺ active site is provided by both upper and lower Ti₃C₂O₂ layers. All possible adsorption sites of Mg²⁺ in the three 42 configurations are taken into account. For the AA-stacking type, the two Ti₃C₂O₂ layers form H₁, H₁₂ and T active sites for Mg²⁺, where the “H₁₂” site means the combination of the H₁ and H₂ sites from two adjacent Ti₃C₂O₂ layers, respectively. ABC₁-Ti₃C₂O₂ forms H₁, H₂ and H₁₂ sites. ABC₂-Ti₃C₂O₂ forms TH₁, H₁ and H₂ sites. For all these three stacking configurations, the H₁ site exhibited stronger binding energy than the other sites (Fig. 3), which is consistent with the Mg²⁺ adsorption behavior for Ti₃C₂O₂ monolayer. Among the three configurations, the H₁ site in AA-stacked structure exhibited the most negative adsorption energy, which indicated that the AA-stacking is more favorable adsorptive configuration for Mg²⁺. According to the optimized crystal, the lower the binding energy, the smaller the lattice parameter c. This suggests that the strong coulomb attraction between the O atoms and the adsorbed Mg²⁺ can mitigate volume expansion during ion storage. Moreover, it is evident that the structural energy difference between the ABC₁- and ABC₂-Ti₃C₂O₂ is very small (Fig. 2c and 4). Furthermore, during structural optimized, Mg²⁺ adsorbed ABC₂-Ti₃C₂O₂ will relax into ABC₁ type through the sliding of adjacent Ti₃C₂O₂ layers. Therefore, the ABC₂ configuration is improbable to form under practical conditions and will hence not be considered in subsequent studies.

Fig. 3 The binding energy of Mg²⁺ at each adsorption site of Ti₃C₂O₂ and the change trend of lattice parameter c.

Fig. 4 (a) Diffusion path of magnesium on single layer Ti₃C₂O₂ surface. (b) Diffusion paths of Mg²⁺ in AA type and (c) ABC₁ type Ti₃C₂O₂ structure, respectively. (d) Diffusion energy barrier of Mg²⁺ in AA type, ABC₁ type and single layer Ti₃C₂O₂.

Mg²⁺ diffuses in AA, ABC₁ and monolayer Ti₃C₂O₂

The rate performance of anode is determined by the kinetics of electronic and ionic diffusion. To further study the Mg²⁺ diffusion kinetic properties for the AA- and ABC₁-stacking structures, the Mg²⁺ diffusion barrier is evaluated in the 3 × 3 × 1 Ti₃C₂O₂ bulk/monolayer using the CI-NEB method. In each configuration, Mg²⁺ is simulated to migrate between two energetically favorable active sites (Fig. 4a). On Ti₃C₂O₂ monolayer, the diffusion of Mg²⁺ between two adjacent H₁ sites across H₂ site (described as H₁ → H₂ → H₁) has a relatively large barrier of 0.81 eV (Fig. 4d). Such a value is close to the Mg²⁺ barrier (0.72 eV) on the Ti₂NO₂ monolayer reported by Wang et al.²⁸ According to that work, the univalent Li⁺, Na⁺, K⁺ diffusion barriers are lower than 0.3 eV, which suggests that the pathway of Ti₂NO₂ monolayer is insufficient to provide an adequate coordination environment for the bivalent Mg²⁺.

In the AA-stacking Ti₃C₂O₂, the Mg²⁺ barrier is significantly improved to 0.32 eV. The optimized AA-stacking structure shows that the adjacent H₁₂ active sites provided by the upper and lower Ti₃C₂O₂ surfaces are opposite, which can be described as 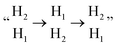(Fig. 4b). Notably, compared with the Ti₃C₂O₂ monolayer, Mg²⁺ can only move from through a single step, and can thereby transfer from one H₁ active site to another. It can be seen that the periodic migration path of Mg²⁺ has been shortened by almost half. Besides, according to the CI-NEB method, the ionic migration barrier is obtained by subtracting the energy of the stable state (SS) from that of the transition state (TS), i.e., E_barrier = E_TS − E_SS.⁴³ The contribution of metastable H₂ site in AA-Ti₃C₂O₂ increases the E_SS, alleviating energy changes during Mg²⁺ migration. In comparison, the Mg²⁺ diffusion channel in the ABC₁-Ti₃C₂O₂ can be described as (Fig. 4c). The stable active site composed of two stable H₁ sites lead to a low E_SS value. While the metastable H₂ and exceptionally unstable T site significantly increases the E_TS. Such substantial energy disparity between E_TS and E_SS lead to a large diffusion barrier of 2.01 eV for ABC₁-Ti₃C₂O₂. To further investigate the influencing factors of Mg²⁺ diffusion barrier, the Bader charge of Mg²⁺ in stable states (e_S) and transition states (e_T) as well as the charge difference (Δe = |e_s − e_T|) between them were calculated based on the CI-NEB image. The result showed that the Δe for AA and ABC₁ types are 0.005 and 0.206e, which are consistent with their barrier order of 0.32, and 2.01 eV, respectively. The Mg²⁺ channel in ABC₁-Ti₃C₂O₂ has large fluctuation on electron capture, which is also an important factors that cause the largest diffusion barrier.

Diffusion of Mg²⁺ in AA-Ti₃C₂T_x (T = O, N)

According to the above discussion, the adsorption and migration behavior of Mg²⁺ exhibits a pronounced preference for the AA-Ti₃C₂O₂. Regrettably, in layered stacking structures, the coulombic effect between layers significantly influence the stacking configuration. For the AA-Ti₃C₂O₂, the O–O electrostatic repulsion from the adjacent layers leads to a preference for staggered arrangement in Ti₃C₂O₂ bulk, thereby increasing the interlayer spacing and rendering the AA-Ti₃C₂O₂ unstable. One effective approach to mitigate electrostatic repulsion is to substitute bivalent O with monovalent halogens such as F or Cl. However, the introduction of F/Cl functional groups does reduce the energy difference between the AA- and ABC₁-Ti₃C₂O₂, yet the AA configuration remains relatively unstable (Fig. 2c). The remaining stacking control method is to utilize higher valence N as functional group, thereby converting electrostatic repulsion into covalent bonding through the addition of electrons.

Consequently, the O function group in AA, ABC₁ and ABC₂ configurations are replaced by N (Fig. 5a). The calculated relative energy revealed that the AA-type Ti₃C₂N₂ become the most stable configuration. Taking AA-Ti₃C₂N₂ as the reference structure, the relative energies of ABC₁ and ABC₂ are 6.82 eV and 7.89 eV, respectively (Fig. 5b). Such large values indicate that the introduction of interlayer N–N covalent bonding significantly enhances the stability of the AA-stacking configuration. In the AA-Ti₃C₂N₂ system, the diffusion energy barrier of Mg²⁺ calculated using the CI-NEB method is 1.07 eV, which is 0.94 eV lower than that in the stable ABC₁ configuration for Ti₃C₂O₂. Evidently, the electrostatic interaction between layers does not directly influence the migration of Mg²⁺. Instead, it indirectly facilitates a favorable migration environment for Mg²⁺ by inducing structural changes. Despite this reduction, the barrier of 1.07 eV still represents a poor diffusion performance. This can be attributed to the strong bonding between nitrogen atoms in adjacent Ti₃C₂N₂ layers, which results in reduced layer spacing and hinders the migration of Mg²⁺. Consequently, it is crucial to determine an appropriate N doping concentration to maintain optimal layer spacing while controlling the MXene stacking type.

Fig. 5 (a) AA-, ABC₁- and ABC₂-Ti₃C₂N₂ interlayer structure. (b) The relative energy of ABC₁- and ABC₂-Ti₃C₂N₂ with respect to AA-type. (c) The relative energies of AA and ABC₁ configurations with different N content. (d) Diffusion barrier comparison of Mg²⁺ in AA-stacking Ti₃C₂N₂ and Ti₃C₂N_1.78N_0.22 structures.

The calculation of the relative energies for AA and ABC₁ configurations with varying N contents reveals that when the N concentration reaches 11%, the stable phase MXene bulk transitions to the AA-stacking type, corresponding to the chemical formula Ti₃C₂O_1.78N_0.22 (Fig. 5c). For this configuration, the Mg²⁺ diffusion barrier is decreased to 0.27 eV, which is significantly lower by 0.8 eV compared to Ti₃C₂N₂ bulk. Notably, Mg²⁺ diffusion predominantly occurs near O functional groups rather than N functional groups (Fig. 5d). This can be attributed to the additional energy required for Mg²⁺ to overcome the interlayer N–N covalent bonds during diffusion, thereby increasing the migration energy barrier.

On the other hand, the strong interlayer N–N covalent bonding in the AA-Ti₃C₂N₂ structure is primarily responsible for the poor Mg diffusion kinetic property. Based on the such bonding situation, it can be proposed that enhancing the metal–N bond strength may weaken the interlayer N–N covalency, thereby improving ionic conductivity. In the periodic table, we have selected three transition metal elements, V, Zr and Nb, to substitute for Ti in AA-Ti₃C₂N₂. V (3d³4s²), Nb (4d⁴5s¹), and Zr (4d²5s²) each enhance N bonding through distinct mechanisms compared to Ti (3d²4s²). V and Nb provide additional valence electrons for covalent interactions, while Zr achieves stronger binding via reduced electronegativity-driven ionic attraction. After replacing Ti atoms in AA-stacking Ti₃C₂N₂ with V, Zr and Nb, the dynamical stability of these four conformations are checked through examining the phonon band structures (Fig. 6a–d), which indicated that they are dynamically stable configurations with no states associated with imaginary frequencies.

Fig. 6 Phonon spectra of (a) Nb₃C₂N₂, (b) Ti₃C₂N₂, (c) V₃C₂N₂ and (d) Zr₃C₂N₂. (e) Diffusion energy barrier of Mg²⁺ in AA-M₃C₂N₂ (M = Ti, V, Zr, Nb).

Diffusion of Mg²⁺ in AA-M₃C₂N₂ (M = Nb, V, Zr)

Subsequently, to analyze the diffusion behavior of Mg²⁺ in AA-M₃C₂N₂ (M = V, Zr and Nb), the Mg²⁺ migration pathways and corresponding energy barriers are investigated within 3 × 3 × 1 supercell. With a single Mg²⁺ intercalation into M₃C₂N₂, it was relaxed to the site after structure optimization and the corresponding the half of diffusion pathways were described as 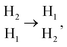which showed that Mg²⁺ diffusion behavior in M₃C₂N₂ bulks (including Ti₃C₂N₂) is consistent. The diffusion barriers of Mg²⁺ in V₃C₂N₂, Zr₃C₂N₂ and Nb₃C₂N₂ had decreased compared with in Ti₃C₂N₂ by 0.37 eV, 0.79 eV and 0.84 eV, respectively. Notably, Nb₃C₂N₂ exhibits the smallest barrier of 0.23 eV. This indicates that N–N covalent binding is weakened more effectively by replacing Ti with Nb than with V and Zr (Fig. 6e). Overall, the Nb₃C₂N₂ obtained by using the transition metal element Nb to replace Ti in AA-Ti₃C₂N₂ has the lowest energy barrier (Fig. S1†).

Theoretical voltage value of AA-stacking Nb₃C₂N₂

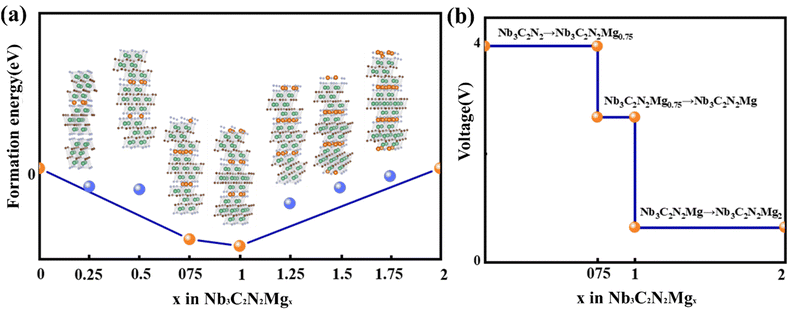
According to the above discussion, the favorite absorption site of Mg²⁺ is site. Based on this, the formation energy of Nb₃C₂N₂Mg_x (0 ≤ x ≤ 1) was calculated via the following equation to explore the thermodynamically stable Mg-containing phases,where E_Nb3C2N2Mgx, E_Nb3C2N2Mg2 and E_Nb3C2N2 are total energies for Nb₃C₂N₂Mg_x, Nb₃C₂N₂Mg₂ and Nb₃C₂N₂, correspondingly, x is the Mg²⁺ adsorption degrees in Nb₃C₂N₂Mg_x, including 0, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75 and 2 (Fig. 7a). Our result suggests that the thermodynamically stable configurations are Nb₃C₂N₂Mg_0.75, Nb₃C₂N₂Mg and Nb₃C₂N₂Mg₂, with their E_f points located at the bottom edge of the convex hull. Based on this, the open circuit voltage (OCV) of AA-stacking Nb₃C₂N₂ with different Mg²⁺ adsorption degrees is calculated from the following formula,where and are the total energies of Nb₃C₂N₂ with different Mg²⁺ adsorption degrees x₁ and x₂, E_Mg is the energy of a Mg atom in metal Mg, charge value n = 2 for Mg²⁺. Interestingly, the calculated voltages contain two distinct plateaus at 4.00 V and 0.64 V, corresponding to the ranges of x = 0–0.75 and x = 1–2, respectively (Fig. 7b). This results indicate that when a monolayer of Mg²⁺ is intercalated between the Nb₃C₂N₂ layers, the binding affinity of Mg²⁺ to the Nb₃C₂N₂ layers significantly decreases. Such a significant voltage difference indicates that the material can function as both the positive and negative electrode of the battery under varying ion concentrations. This behavior is analogous to that observed in Prussian blue materials used in potassium-ion batteries.⁴⁴ By contrast, the voltage platforms presented by Ti-based MXene belong to the anode range (Fig. S2†). From a voltage stability perspective, Ti₃C₂O₂Mg_x and Ti₃C₂O_1.78N_0.22Mg_x exhibit three short platforms decreasing in the concentration of 0 < x < 1. Although Ti₃C₂N₂ possesses two stable platforms, the voltage of 0.02 V is too low for electrode, which is easy to transform the Mg²⁺ intercalation mechanism into electroplating.

Fig. 7 (a) Formation energy and (b) theoretical voltage value of Nb₃C₂N₂Mg_x.

Conclusions

This study systematically investigates the Mg²⁺ storage and diffusion mechanisms in MXene materials, focusing on Ti₃C₂O₂ and its nitrogen-doped derivatives. The strong electrostatic interaction between divalent Mg²⁺ and electrode frameworks leads to high diffusion barriers (0.81 eV in monolayers), which are mitigated by optimizing MXene stacking configurations and functional group engineering. AA-stacking Ti₃C₂O₂ exhibits strong Mg²⁺ adsorption energy of −2.16 eV and low diffusion barrier of 0.32 eV due to staggered active sites shortening migration paths. However, its instability from interlayer O–O repulsion necessitates structural modifications. Replacing O with N transforms stable ABC₁-Ti₃C₂O₂ to AA-Ti₃C₂N₂ through enhanced interlayer N–N covalent bonding. However, excessive N doping increases the energy barrier (1.07 eV) due to decreased layer spacing. One effective approach is to control the N/O ratio, which balances interlayer spacing and covalent interactions, resulting in an energy barrier of 0.27 eV in the Ti₃C₂O_1.78N_0.22 structure. Another strategy involves substituting transition metals into the MXene framework to modulate interlayer bonding. Introducing transition metals (V, Zr, Nb) into Ti₃C₂N₂ weakens N–N covalency, with Nb₃C₂N₂ achieving an ultralow barrier of 0.23 eV. Nb₃C₂N₂ possesses dual voltage platforms (4.00 V and 0.64 V), enabling its dual role as cathode/anode, while Ti-based MXenes exhibit anode-specific behavior. These findings highlight that tailored MXene structures, through stacking control, nitrogen doping, and metal substitution, significantly enhance Mg²⁺ kinetics and stability, positioning them as promising high-performance electrodes for next-generation Mg-ion batteries.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Hebei Natural Science Foundation Youth Foundation (No. 606020324086), the Advanced Talents Incubation Program of the Hebei University (No. 521000981394), the Scientific Research and Innovation Team of Hebei University (Grant No. IT2023B03) and the High-Performance Computing Center of Hebei University.

References

1. Y. Shabeer, S. S. Madani, S. Panchal, M. Mousavi and M. Fowler, Different Metal–Air Batteries as Range Extenders for the Electric Vehicle Market: A Comparative Study, Batteries, 2025, 11(1), 35.
2. D. A. Kolosov and O. E. Glukhova, High-Capacity Ion Batteries Based on Ti2C MXene and Borophene First Principles Calculations, Inorganics, 2023, 11(3), 95.
3. X. Zhang, A. Wang, X. Liu and J. Luo, Dendrites in Lithium Metal Anodes: Suppression, Regulation, and Elimination, Acc. Chem. Res., 2019, 52(11), 3223–3232.
4. F. Sun, H. Liu, L. Ni and X. Wang, Growth Mechanisms of Li Dendrite and the Suppression Strategies, Chin. Sci. Bull., 2021, 66(9), 1046–1056.
5. X. Chen, B. Zhao, C. Yan and Q. Zhang, Review on Li Deposition in Working Batteries: From Nucleation to Early Growth, Adv. Mater., 2021, 33(8), 2004128.
6. Y.-G. Lee, S. Fujiki, C. Jung, N. Suzuki, N. Yashiro, R. Omoda, D.-S. Ko, T. Shiratsuchi, T. Sugimoto, S. Ryu, J. H. Ku, T. Watanabe, Y. Park, Y. Aihara, D. Im and I. T. Han, High-Energy Long-Cycling All-Solid-State Lithium Metal Batteries Enabled by Silver–Carbon Composite Anodes, Nat. Energy, 2020, 5(4), 299–308.
7. G. A. Shaikh, A. M. Satawara, S. K. Gupta and P. N. Gajjar, Unlocking the Potential of Mg-Ion Batteries: Cu2C MXene Anode with Ultrahigh Storage and Energy Density with Rapid Mg Diffusion, Chem. Eng. J., 2024, 498, 155368.
8. R. Dominko, J. Bitenc, R. Berthelot, M. Gauthier, G. Pagot and V. Di Noto, Magnesium Batteries: Current Picture and Missing Pieces of the Puzzle, J. Power Sources, 2020, 478, 229027.
9. Y. Du, Y. Chen, S. Tan, J. Chen, X. Huang, L. Cui, J. Long, Z. Wang, X. Yao, B. Shang, G. Huang, X. Zhou, L. Li, J. Wang and F. Pan, Strong Solvent Coordination Effect Inducing Gradient Solid-Electrolyte-Interphase Formation for Highly Efficient Mg Plating/Stripping, Energy Storage Mater., 2023, 62, 102939.
10. K. A. Papadopoulou, A. Chroneos and S.-R. G. Christopoulos, Mg-Ion Diffusion on the Surface of Ti3C2S2 MXene, J. Phys. Chem. Solids, 2022, 166, 110713.
11. B. Li, R. Masse, C. Liu, Y. Hu, W. Li, G. Zhang and G. Cao, Kinetic Surface Control for Improved Magnesium-Electrolyte Interfaces for Magnesium Ion Batteries, Energy Storage Mater., 2019, 22, 96–104.
12. M. Deng, L. Wang, B. Vaghefinazari, W. Xu, C. Feiler, S. V. Lamaka, D. Höche, M. L. Zheludkevich and D. Snihirova, High-Energy and Durable Aqueous Magnesium Batteries: Recent Advances and Perspectives, Energy Storage Mater., 2021, 43, 238–247.
13. J. Nai, Y. Han, S. Zhang, Y. Li, X. Chen, R. Wu, L. Wang and L. Jiang, Sulfite Activation by ZnO-Encapsulated Hydrogels for Degradation of Trimethylphenol, Nano Res., 2023, 16(10), 12345–12356.
14. M. Hammouri, M. Arsentev and A. Petrov, Ab Initio Studies of Ti2S3 as a New Cathode Material for Magnesium Secondary Batteries, Mater. Today Commun., 2019, 20, 100598.
15. Y. Xie, Y. Dall'Agnese, M. Naguib, Y. Gogotsi, M. W. Barsoum, H. L. Zhuang and P. R. C. Kent, Prediction and Characterization of MXene Nanosheet Anodes for Non-Lithium-Ion Batteries, ACS Nano, 2014, 8(9), 9606–9615.
16. R. Xiao, J. Xie, T. Luo, L. Huang, Y. Zhou, D. Yu, C. Chen and Y. Liu, Phase Transformation and Diffusion Kinetics of V₂ O₅ Electrode in Rechargeable Li and Mg Batteries: A First-Principle Study, J. Phys. Chem. C, 2018, 122(3), 1513–1521.
17. T. A. Barnes, L. F. Wan, P. R. C. Kent and D. Prendergast, Hybrid DFT Investigation of the Energetics of Mg Ion Diffusion in α-MoO₃, Phys. Chem. Chem. Phys., 2018, 20(38), 24877–24884.
18. D. S. Tchitchekova, A. Ponrouch, R. Verrelli, T. Broux, C. Frontera, A. Sorrentino, F. Bardé, N. Biskup, M. E. Arroyo-de Dompablo and M. R. Palacín, Electrochemical Intercalation of Calcium and Magnesium in TiS₂ : Fundamental Studies Related to Multivalent Battery Applications, Chem. Mater., 2018, 30(3), 847–856.
19. G. Li, Z. Yao and C. Li, In-Situ Multi-Scale Structural Engineering of Cathode and Electrolyte for High-Rate and Long-Life Mg Metal Batteries, J. Energy Chem., 2025, 105, 44–53.
20. J. Wang, S. Tan, G. Zhang, Y. Jiang, Y. Yin, F. Xiong, Q. Li, D. Huang, Q. Zhang, L. Gu, Q. An and L. Mai, Fast and Stable Mg2+ Intercalation in a High Voltage NaV2O2(PO4)2F/rGO Cathode Material for Magnesium-Ion Batteries, Sci. China Mater., 2020, 63(9), 1651–1662.
21. S. Li, Y. Sun, Y. Pang, S. Xia, T. Chen, H. Sun, S. Zheng and T. Yuan, Recent Developments of Layered Transition Metal Oxide Cathodes for Sodium-ion Batteries toward Desired High Performance, Asia-Pac. J. Chem. Eng., 2022, 17(4), e2762.
22. P. Panigrahi, S. B. Mishra, T. Hussain, B. R. K. Nanda and R. Ahuja, Density Functional Theory Studies of Si₂ BN Nanosheets as Anode Materials for Magnesium-Ion Batteries, ACS Appl. Nano Mater., 2020, 3(9), 9055–9063.
23. M. Mao, X. Ji, S. Hou, T. Gao, F. Wang, L. Chen, X. Fan, J. Chen, J. Ma and C. Wang, Tuning Anionic Chemistry To Improve Kinetics of Mg Intercalation, Chem. Mater., 2019, 31(9), 3183–3191.
24. Y. Zhang, Z. Yuan, L. Zhao, Y. Li, X. Qin, J. Li, W. Han and L. Wang, Review of Design Routines of MXene Materials for Magnesium-ion Energy Storage Device, Small, 2023, 19(34), 2301815.
25. B. Zhou, H. Shi, R. Cao, X. Zhang and Z. Jiang, Theoretical Study on the Initial Stage of a Magnesium Battery Based on a V₂ O₅ Cathode, Phys. Chem. Chem. Phys., 2014, 16(34), 18578–18585.
26. M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall'Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Cation Intercalation and High Volumetric Capacitance of Two-Dimensional Titanium Carbide, Science, 2013, 341(6153), 1502–1505.
27. M. Naguib, M. W. Barsoum and Y. Gogotsi, Ten Years of Progress in the Synthesis and Development of MXenes, Adv. Mater., 2021, 33(39), 2103393.
28. D. Wang, Y. Gao, Y. Liu, D. Jin, Y. Gogotsi, X. Meng, F. Du, G. Chen and Y. Wei, First-Principles Calculations of Ti₂ N and Ti₂ NT₂ (T = O, F, OH) Monolayers as Potential Anode Materials for Lithium-Ion Batteries and Beyond, J. Phys. Chem. C, 2017, 121(24), 13025–13034.
29. D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, Ti₃ C₂ MXene as a High Capacity Electrode Material for Metal (Li, Na, K, Ca) Ion Batteries, ACS Appl. Mater. Interfaces, 2014, 6(14), 11173–11179.
30. M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, New Two-Dimensional Niobium and Vanadium Carbides as Promising Materials for Li-Ion Batteries, J. Am. Chem. Soc., 2013, 135(43), 15966–15969.
31. Z. Zhang, Z. Sun, S. Sun, J. Liu, J. Jiang, W. Shang and Y. Wen, MXene Modified Anode of Magnesium Battery to Improve the Problems of Voltage Lag and Irreversibility, J. Alloys Compd., 2023, 960, 170609.
32. J. Zhu, R. Shi, Y. Liu, Y. Zhu, J. Zhang, X. Hu and L. Li, 3D Interwoven MXene Networks Fabricated by the Assistance of Bacterial Celluloses as High-Performance Cathode Material for Rechargeable Magnesium Battery, Appl. Surf. Sci., 2020, 528, 146985.
33. R. Rajagopalan, Y. Tang, X. Ji, C. Jia and H. Wang, Adv. Funct. Mater., 2020, 1909486.
34. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48(17), 13115–13118.
35. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186.
36. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
37. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775.
38. J. P. Perdew and W. Yue, Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33(12), 8800–8802.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
40. J. Luo, T. Fan, J. Zhang, P. Qiu, X. Shi and L. Chen, Automatic Identification of Slip Pathways in Ductile Inorganic Materials by Combining the Active Learning Strategy and NEB Method, npj Comput. Mater., 2025, 11(1), 41.
41. G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113(22), 9901–9904.
42. G. Henkelman and H. Jónsson, Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points, J. Chem. Phys., 2000, 113(22), 9978–9985.
43. C. Teng, Y. Wang and J. L. Bao, Physical Prior Mean Function-Driven Gaussian Processes Search for Minimum-Energy Reaction Paths with a Climbing-Image Nudged Elastic Band: A General Method for Gas-Phase, Interfacial, and Bulk-Phase Reactions, J. Chem. Theory Comput., 2024, 20(10), 4308–4324.
44. Q. Wang, J. Li, H. Jin, S. Xin and H. Gao, Prussian-blue Materials: Revealing New Opportunities for Rechargeable Batteries, Infomat, 2022, 4(6), e12311.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01985k

‡ Mingxiao Ma and Xiangyu Yao contributed equally to this work.

---