Open Access Article
Open Access ArticleExploring the oxidation behavior of undiluted and diluted iron particles for energy storage: Mössbauer spectroscopic analysis and kinetic modeling†
Jonas
Spielmann‡
a,
Daniel
Braig‡
b,
Antonia
Streck
a,
Tobias
Gustmann§
c,
Carola
Kuhn
d,
Felix
Reinauer
a,
Alexandr
Kurnosov
e,
Oliver
Leubner
f,
Vasily
Potapkin
a,
Christian
Hasse
 b,
Olaf
Deutschmann
b,
Olaf
Deutschmann
 df,
Bastian J. M.
Etzold
g,
Arne
Scholtissek
*b and
Ulrike I.
Kramm
df,
Bastian J. M.
Etzold
g,
Arne
Scholtissek
*b and
Ulrike I.
Kramm
 *a
*a
aTechnical University of Darmstadt, Department of Chemistry, Eduard-Zintl-Institute, Otto-Berndt-Str. 3, Germany. E-mail: Ulrike.kramm@tu-darmstadt.de
bTechnical University of Darmstadt, Department of Mechanical Engineering, Simulation of reactive Thermo-Fluid Systems, Otto-Berndt-Straße 2, 64287 Darmstadt, Germany. E-mail: scholtissek@stfs.tu-darmstadt.de
cLeibniz Institute for Solid State and Materials Research Dresden, 01069 Dresden, Germany
dInstitute for Chemical Technology and Polymer Chemistry, Karlsruhe Institute of Technology (KIT), Engesserstr. 20, Karlsruhe, 76131, Germany
eBayerisches Geoinstitut, University of Bayreuth, Bayreuth, Germany
fInstitute of Catalysis Research and Technology, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, Eggenstein-Leopoldshafen, 76344, Germany
gTechnical University of Darmstadt, Department of Chemistry, Ernst-Berl-Institute, Peter-Grünberg-Straße 8, Germany
First published on 10th April 2024
Abstract
Iron is an abundant and non-toxic element that holds great potential as energy carrier for large-scale and long-term energy storage. While from a general viewpoint iron oxidation is well-known, the detailed kinetics of oxidation for micrometer sized particles are missing, but required to enable large-scale utilization for energy production. In this work, iron particles are subjected to temperature-programmed oxidation. By dilution with boron nitride a sintering of the particles is prevented enabling to follow single particle effects. The mass fractions of iron and its oxides are determined for different oxidation times using Mössbauer spectroscopy. On the basis of the extracted phase compositions obtained at different times and temperatures (600–700 °C), it can be concluded that also for particles the oxidation follows a parabolic rate law. The parabolic rate constants are determined in this transition region. Knowledge of the particle size distribution and its consideration in modeling the oxidation kinetics of iron powder has proven to be crucial.
Introduction
In response to climate change, an increasing number of people agree on the replacement of all fossil energy resources by renewables. This represents a tremendous challenge, since more than 80% of the world wide primary energy supply still stems from fossil fuels.1Considering geographical and political implementations, renewable energies will not be equally accessible in all countries. While there are regions, such as many tropic regions, North Africa, or Australia, for which excess production of renewable energy is realizable and thus enables its export, other regions e.g., Central Europe or Eastern China will most likely remain partially dependent on (renewable) energy imports.2,3
In turn, the need for an energy carrier that allows long-term storage and long-distance transport in an efficient and sustainable way is required. These criteria can be met by choosing chemical energy carriers and devices, such as hydrogen, or metals as storage media or batteries.4–6 For storage and transportation, high volumetric energy densities are favored. In this context, metal fuels, and specifically iron, are of great interest.7–10
Considering iron as an energy carrier and tradeable commodity, energy storage will be realized by reducing iron oxide powders in countries with excess production of renewable energy. The resulting iron powder will then be transported to locations of energy demand, where it is burned to release the chemical energy. The oxidation behavior makes iron also suitable as heat source for e.g. steam turbines or retrofitting of existing coal-fired power plants.11,12 Existing infrastructure can thus be used and retrofitted for its implementation in the future energy network, making it also attractive from a socioeconomic viewpoint. Considering a complete oxidation and reduction circle with their local constrains, a first holistic process evaluations estimated round-trip efficiencies of 19–29%,8 being comparable to green H2, ammonia, or CH4.
To enable technological implementation, knowledge of iron oxidation and reduction kinetics are required. While the process of iron oxidation at elevated temperatures is well known for bulk materials from steel and iron making industry,13 only few studies deal with micron-sized iron particles.14–16
The oxidation of iron is exothermic and – as known from bulk materials – initially dependent on external mass transport of oxygen. The oxidation of iron can be classified into three temperature regimes: 1. Below 570 °C, 2. between 570–700 °C and 3. above 700 °C.17
This work focusses on the transition regime (570–700 °C): As soon as an initial surface oxide layer is formed, it acts as a barrier, hindering diffusion of oxygen to the metal surface.18 In consequence, the diffusion of iron ions to the outer oxide layers becomes rate limiting.19,20 Diffusion of oxygen through the outermost oxide layer further contributes to the oxidation. Induced by these constrains, layered structures of iron and its oxides are formed with increasing degree of oxidation from the center to the outmost layer:13,21,22 Iron in the core, wüstite (Fe1−xO), magnetite (Fe3O4) and hematite (α-Fe2O3) as the surface.21 Wüstite is only formed above 570 °C and increases the speed of oxidation since it poses less diffusion resistance to iron ions as compared to magnetite or hematite.18,20 Therefore, the formation of thicker layers is not favored specifically close to 570 °C.23,24
Under isothermal conditions oxidation starts with a fast step, in which the temperature and oxygen partial pressure at the surface are the main factors determining the kinetics of oxidation.18 With growing oxide layers the oxidation slows down until reaching a parabolic oxidation regime following Wagner's theory.25 For planar samples, ratios of oxide scale thicknesses are constant in the parabolic regime, only the overall degree of oxidation, e.g. total oxide scale thickness, is increasing with temperature and oxidation time. For temperatures above 700 °C, this thickness ratio always reaches ∼ 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for Fe1−xO: Fe3O4: α-Fe2O3, independent of temperature and oxygen partial pressure in the atmosphere.
1 for Fe1−xO: Fe3O4: α-Fe2O3, independent of temperature and oxygen partial pressure in the atmosphere.
To the best of our knowledge, in all studies concerning iron slab oxidation so far, iron remained in its metallic state in the center of the material, while full oxidation is desired when considering iron as a chemical energy carrier.26,27 When applying the findings obtained for slab oxidation to powders in the low micrometer range, the initial oxidation step will play a much more substantial role, being more relevant the smaller the particles are and the higher the oxidation temperature is.28,29 Values for rate constants are usually obtained in units of mass gain of oxide layer per surface area and time (kp), or in units of scale thickness per time (kx).13 Both options do not provide an obvious answer for how the reference data should be treated for a particle, when considering that the density of oxides is roughly 65 to 75% of that of iron and powders have a distinct particle size distribution.
So far, the analytical method of choice for oxidation studies of iron powders is thermogravimetric analysis.14–16,28,30,31 Korshunov14 compared the oxidation of particles with particle-number averaged sizes of 0.1 μm and 45 μm under isothermal conditions and for constant heating rates in air. During heating with 10 K min−1 the smaller particles reached full oxidation at 600 °C while the 45 μm sized particles reached full oxidation only at 1000 °C. The same trend was observed by other authors for different sized particles.16,30 Korshunov further probed isothermal oxidation at temperatures between 450–500 °C.14 The powder with larger particles revealed a parabolic dependence in mass gain and an average activation energy of Ea = 144 kJ mol−1, which is in accordance with slab oxidation data,32,33 indicating an overall similar oxidation behavior.
Thermogravimetric analysis was further combined with post-mortem X-ray diffraction to provide proof of the conclusions derived from temperature programmed oxidation (TPO) data.14,30 However, the derived kinetic parameter mostly refer to the overall oxidation process from Fe to Fe2O3. Additionally, it was mentioned that sintering of the iron powder occurred during TPO measurements of pure iron powder.14,16 While its influence was found to be neglectable for studies at T < 500 °C and small sample masses,28 its contribution to the oxidation behavior at higher reaction temperatures is obvious.
With this motivation, we explore the temperature and time dependent changes during the oxidation of iron for pure iron particles and after diluting them with boron nitride, to avoid sintering. Post-mortem Mössbauer spectroscopy is performed and complemented by TPO. For the optimized system, the isothermal oxidation is investigated in the temperature range 600–700 °C. It will be shown that dilution effectively hinders sintering of iron particles occurring due to local overheating13,16 of the pure particles already at low temperatures. Using this approach, the iron-related composition formed during the oxidation of single iron particles is to the best of our knowledge followed for the first time to disentangle the contribution of the individual steps in the oxidation to the overall process.
Experimental section
Chemicals
Iron powder (particle size distribution shown in Fig. 1) is purchased from Eckart TLS GmbH, Germany with a purity of 99.8%. The iron powder is kept in a desiccator under vacuum after delivery to limit the formation of an iron oxide passivation layer on the surface. Boron nitride powder is obtained from Sigma-Aldrich (98%, CAS-No: 10043-11-5, mean particle size of ∼1 μm). For gases, nitrogen (Linde, 99.995%) was used as inert gas during heating and compressed ambient air (houseline) for oxidation.Initial characterization of iron powder
The particle size distribution is measured with a Camsizer X2, Retsch Technology. SEM measurements are performed with a ZEISS EVO 10 with SmartSEM V6.03 software package. Optical images are obtained with a BRESSER Science ADL 601 P 40-600x microscope.Thermogravimetric measurements
Temperature programmed oxidation (TPO) experiments are per-formed on a STA 449 C/3/MFC/G Jupiter device from Netzsch, with a constant flow of synthetic air (air liquide, 20.5 vol% O2, alphagaz) of 50 mL min−1 and 20 ± 2 mg iron powder, either pure or as mixture (with addition of 30 wt% BN). The mass of the mixture is 29.3 ± 1.5 mg to keep the amount of iron within the intended interval of 20 ± 2 mg. For the BN decomposition measurement 8.9 mg are used. Experiments for pure iron are performed under constant heating rates of 1, 2, 5 and 10 K min−1. For the Fe–BN mixture and BN decomposition test, 10 K min−1 are used. Isothermal thermogravimetric experiments are performed with a Netzsch STA 409. The sample is heated in nitrogen atmosphere (200 mL min−1) to the desired temperature. Once the temperature was reached, the gas was automatically switched from N2 to synthetic air with a gas flux of 100 mL min−1.Preparation of oxidized samples
For oxidation, the iron powder samples are filled in corundum boats (VWR, incinerating dishes, rectangular, dimensions (l × w × h): 50 × 25 × 20 mm). The amount used in each experiment is 300 mg for the pure iron powder (except for the samples prepared at 100 °C, 200 °C and 300 °C for which 100 mg are used). For the BN-diluted samples, for each experiment approximately 190 mg of iron powder and 85 mg of BN are filled in an Eppendorf tube (Eppendorf AG, 1.5 mL) and mixed two times for 15 min with a Grant Instruments™ Multi-Vortexer V-32. After obtaining a homogeneous mixture (by color) 220 ± 10 mg of this powder (corresponding to 150 ± 7 mg of iron) are used in each oxidation experiment. The oxidation is carried out in a Carbolite HST 1200 tube furnace with external temperature control unit. Two variation series are investigated that are described in the following.57Fe Mössbauer spectroscopy
57Fe Mössbauer spectroscopy is performed at room temperature with a home-build setup composed of a velocity drive unit from Halder instruments, a proportional counter as detector, a preamplifier, an amplifier and a CMCA-500 (Wissel) for discrimination and data collection. The 57Co/Rh source had an initial activity of 100 mCi and is continuously kept at room temperature. The source is moved in triangular waveform, and a 25 μm α-iron foil is used as calibration standard. Fitting of the experimental data is performed with the MossA software package.34 Sample quantities are kept between the lower and higher limit of the ideal loading approximation as suggested by Long et al.35,36 The used sample holders are custom made and consists of a threaded body with two screw lids for top and bottom. Conversion of spectral absorption areas to composition is done using Lamb-Mössbauer-factors (LMF) found in literature.37–44 For FeO, the LMF is set to the value of Fe.45,46 The calculations are shown in the ESI† (P2–P11 and Tables S1–S9).Kinetic modeling
The iron microparticles are simulated utilizing a 0D state-of-the-art iron particle model, including curvature correction and a parabolic rate law for oxidation.47 The model is implemented in an in-house C++ code48 and numerically solved with CVODE from the Sundials suite.49 The parabolic rate constants are determined with ANSYS® optiSLang50 by minimization of the mean squared error between model prediction and experimental data for the species mass fractions. Temperature and oxygen concentration of the environment are prescribed in accordance with the experimental conditions.Results and discussion
Characterization of the initial state
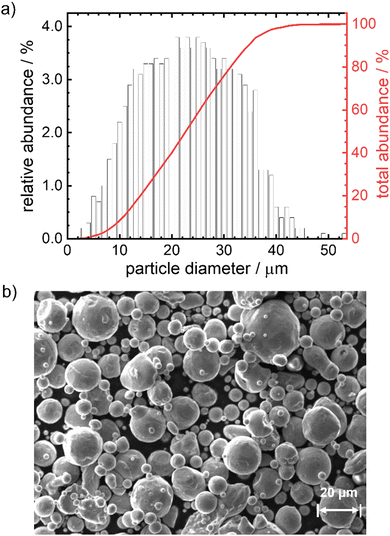
In Fig. 1 the particle size distribution (PSD) and a SEM image of the particles are given. The average size of the particles is 23 μm, 95% of the particles have a diameter <37 μm. The Sauter mean diameter d32 equals 18.6 μm. The SEM image indicates a smooth, satellite-free surface of the particles and overall pronounced spherical shape. According to the elemental analysis (Table S10, ESI†) the particles consist of 99.8 wt% iron with impurities of Mn, Cr, Si, Ni and C (decreasing quantities in the given order, maximum = 0.017 wt%, minimum = 0.007 wt%). Based on size and composition, these particles would be suitable for the anticipated reaction conditions and can therefore be used in the model experiments.12 As will be shown below, the outcome of the kinetic modeling significantly differs considering either a mean diameter or a PSD.Oxidation behavior of pure iron powder
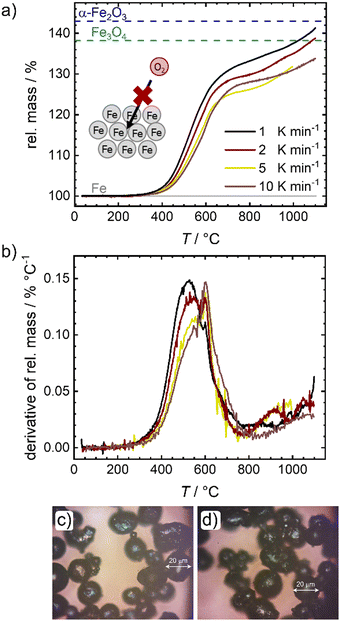
In a first step the oxidation of pure iron powder is followed by temperature programmed oxidation (TPO). Fig. 2 shows the relative masses (a) and their derivatives (DTG) (b) for four different heating ramps as a function of temperature. In Fig. 2(a), lines are added that represent the theoretically expected relative mass for a full conversion of metallic iron to magnetite (Fe3O4) and hematite (α-Fe2O3). In all cases, salient mass gain starts from temperatures of ca. 380 °C while the slope is sharpest for the lowest heating ramp. Above 600 °C, the slope changes significantly, and the oxidation and related mass gain, is slowed down. Fig. 2(b) further depicts this change in slope. Two peaks are distinguishable, with the first one showing an expected shift in its maximum14,30 from 530 °C (1 K min−1) to approx. 550 °C (10 K min−1), while the second maximum seems independent from the heating ramp and is located at 600 °C. It will later be shown that 600 °C seems to be a critical temperature for oxidation of the iron powder under study. A much smaller peak appears at ca. 900 °C. Even at 1100 °C none of the samples reaches the theoretical relative mass associated with a complete oxidation of iron to hematite, a maximum mass gain of 40% is reached for the lowest heating ramp.This observation is in line with previous reports that show for larger particles a full conversion at temperatures between 820–1100 °C, whereas for smaller particles a plateau associated with a mass gain of 38% was reached between 600–800 °C.14,16 Since the oxidation rate is known to increase with decreasing particle size (as indicated by the larger slope of mass gain), this observation; however, is counter intuitive. As stated in the following, we assume that an increase in effective particle dimension by sintering processes is the most likely explanation: After the first initial oxidation of the surface, diffusion of iron cations from the iron core through the oxide layers to the particle surface becomes rate limiting. An increase in particle dimensions will thus lead to longer diffusion paths, significantly slowing down the speed of average oxidation. Since previous reports also used pure iron powder, sintering should have been similarly present in their experiments,14,16,28 although only mentioned as a side note in explaining the data. The microscope images of the powder samples in Fig. 2(c) and (d) further support the role of sintering. Even at temperatures around 300 °C, when the oxidation process just starts, adhesion of the iron particles is clearly visible (Fig. 2(c)). In order to obtain the images shown in Fig. 2(c) and (d) the samples were ground in a mortar and could not be further separated. Due to strong sintering processes at temperatures >600 °C (Fig. S1e, ESI†), pulverizing samples for Mössbauer spectroscopy is not possible for the probed time of oxidation. An illustration of the oxidation procedure and the samples prior to grinding can be found in Fig. S1a, ESI.†
Mössbauer spectroscopy is used to determine the composition of the samples after oxidation in air and heated (1 K min−1) to the desired temperature. The spectra are shown in Fig. S2 (ESI†) and the sample compositions (metallic iron, magnetite and hematite are found) are given in Fig. S1f, ESI.† The findings agree with the oxide scale compositions for oxidation below 570 °C.13 As observed by TPO, also the Mössbauer spectra reveal that the oxidation starts between 300 °C and 400 °C. Up to 600 °C, varying amounts of magnetite and hematite are found in the samples, while the average oxidation state steadily increases to 2.1 at 600 °C.
In the following section, we will demonstrate that dilution is a secure solution to enable the study of single particle effects.
Oxidation behavior of BN-diluted system
To overcome the sintering of the pure iron samples, physically separating the particles by mixing the iron powder with an inert diluting agent is found to be successful. In catalysis SiC, SiO2 or Al2O3 are often used as supporting agent or dilutant for strong exothermal reactions.51–53 While in the given temperature regime, all three options are sufficiently inert, they reveal a strong attenuation of the 14.4 keV γ-radiation, hindering the envisioned Mössbauer spectroscopy. As an alternative, boron nitride (BN) is identified as solution in this work. Fig. 3(a) compares the calculated relative transmission of 14.4 keV radiation for different thicknesses of SiC, SiO2, Al2O3 and BN. The values are significantly higher for BN as compared to the other dilutants, hence mixing with BN is used to enable Mössbauer spectroscopy in a reasonable time frame.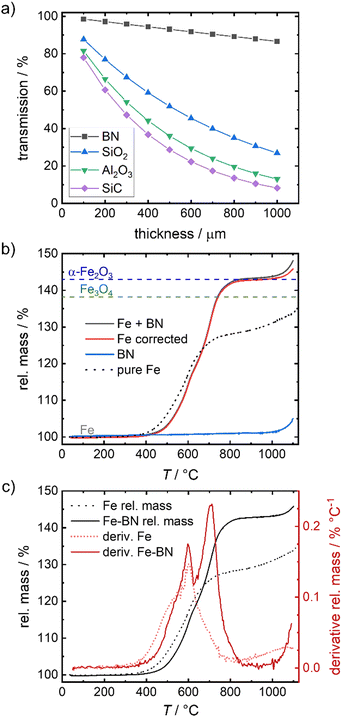 | ||
| Fig. 3 Relative transmission of γ-radiation of 14.4 keV through different thicknesses associated for different dilution agents54 (a), TGA of Fe mixed with BN (b) and related derivative (10 K min−1, air) (c) in comparison to the pure iron sample. In (b) Fe corrected corresponds to the rel. mass of Fe + BN mathematically corrected for the rel. mass of BN (in the given mass fractions). The dashed lines in (b) indicate the mass gain assigned to a full oxidation to Fe3O4 and α-Fe2O3. | ||
By default, a mass ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Fe
3 (Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BN) is selected as compromise of measurement economy (in terms of time) and sufficient particle separation. Photographs and microscope images of the diluted samples are shown in Fig. S3, ESI.†
BN) is selected as compromise of measurement economy (in terms of time) and sufficient particle separation. Photographs and microscope images of the diluted samples are shown in Fig. S3, ESI.†
To check the contribution of BN to the overall oxidation process, TPO measurements of the diluted system (Fe + BN) and pure BN are performed and compared to that of pure iron (Fig. 3(b)). BN remains inert up to 1000 °C which is far above the temperatures of interest in this work. As illustrated in Fig. 3(b), the relative mass associated with full conversion is reached at ca. 800 °C.
A chemical interference of BN with the oxidation process is deemed neglectable in the relevant temperature regime, as demonstrated by the mathematically corrected relative mass of iron. The obtained “Fe corrected” (red line) in Fig. 3(b) indicates that only above 1000 °C a reaction with BN cannot be excluded (otherwise the relative mass should have remained constant at a maximum of 143%).
Comparing the mass gain found for the diluted system with that obtained for the pure iron powder, a shift in oxidation onset to higher temperatures is visible by BN addition. It is known,13,14,55,56 that the oxidation of iron causes an overheating of the sample, that is stronger the smaller the particle size gets and the worse the heat transfer to the surroundings is. In consequence, oxidation of the pure iron sample occurs faster at lower temperatures for our samples. With increasing degree of sintering, the particle surface decreases, hindering the oxidation (compare illustration in Fig. 2(a)) so that it becomes mainly dependent on iron cation diffusion through the now increased effective size of the iron specimen, slowing down the oxidation process. In the diluted system, particle separation effectively hinders sintering, thus maintaining single particles and enabling close to single particle oxidation behavior. Fig. S3c (ESI†) reveals that at most linear particle composites result from oxidation of the diluted system up to 800 °C, while for pure iron powder, a solid, inseparable bulk is obtained under equal conditions (Fig. S1e, ESI†).
No significant external mass transport limitations occur during our TPO investigations of the diluted system with the given sample mass and oxidation conditions due to the rather slow oxidation rate. For the diluted system, the derivative of the relative mass in Fig. 3(c) reveals the typical two stage oxidation process known for iron powders during constant heating in air,14,30 with the peaks being located at 598 ± 2 °C and 707 ± 5 °C. For the pure iron powder, the second peak is missing. We do not assume that the overall process of oxidation has changed, but that at about 600 °C the sintering becomes dominant yielding a more solid and non-porous bulky particle.
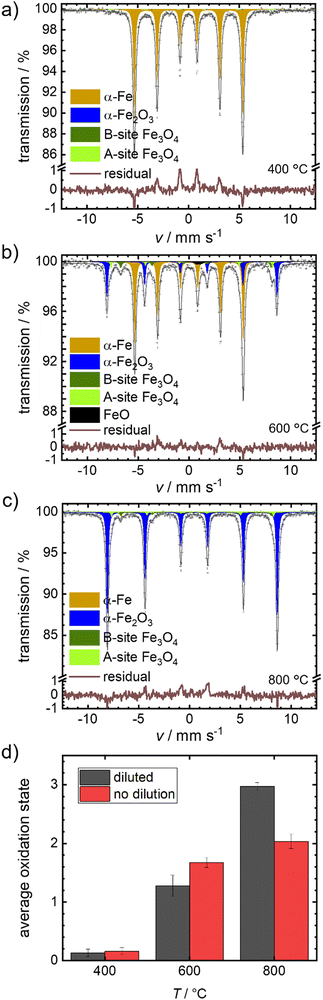
We selected the temperature interval between 570–700 °C, where full oxidation is possible but remains sufficiently slow to be followed by post-mortem Mössbauer spectroscopy. In Fig. 4(a)–(c), the obtained spectra after isothermal oxidation of Fe + BN for 30 min in air at 400 °C, 600 °C and 800 °C are shown. For reasons of comparison, experiments under equal conditions, but without dilution are performed; the resulting Mössbauer spectra are shown in Fig. S4 (ESI†).
Fig. 4(d) compares the average oxidation states of the mixed samples Fe + BN (diluted) vs. the pure iron powder. At 400 °C practically no oxidation is observed for both variations. At 600 °C, a mixture of oxides is obtained. The average oxidation state using the pure iron powder as precursor is higher, which is in line with the previous hypothesis: Overheating is more severe in case of pure iron, so that the actual temperature in the sample gets higher compared to the Fe + BN mixture, leading to a higher degree of oxidation. At 800 °C, an almost complete oxidation to hematite is found for the Fe + BN mixed sample, while without dilution the complete oxidation cannot be reached due to sintering.
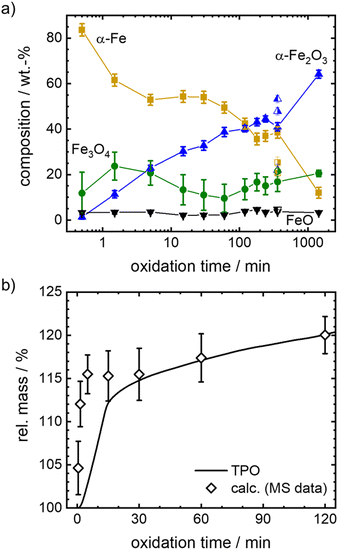
Since oxidation progresses with reasonable speed for the envisioned isothermal experiments, temperatures between 600–700 °C are selected to follow the oxidation kinetics. Mössbauer spectra are recorded after oxidative times between 0.5 to 1440 min in case of 600 °C, and between 20–360 min in case of higher temperatures, as described in detail in the experimental part. The fitted Mössbauer spectra are given in Fig. S5–S9 (ESI†). Based on the relative absorption areas of iron sites and the Lamb-Mössbauer factors (LMF), the mass fractions of the different iron species are determined and plotted as a function of time in Fig. 5(a) for the 600 °C series.
It is known that isothermal oxidation of iron starts with a kinetically limited fast initial oxidation stage, that then transitions to a bulk-diffusion-controlled oxidation, where the overall mass gain follows a parabolic rate law.13,18,25 Based on the trends in Fig. 5(a), it seems that after a rapid change in iron composition (<5 min), the process of oxidation is slowed down. At the start of the initial phase the major oxidation product is magnetite, that then gets further oxidized to hematite. For all dwell times a small fraction of wüstite is found. Overall, the amount of hematite increases fast.
To further elaborate on the accuracy of the experimental method, isothermal TPO at 600 °C is performed with the same mixture of iron and boron nitride. Since the oxidation process cannot be stopped in an infinitely small time interval during sample generation for Mössbauer spectroscopy, the obtained compositions for small dwell times will likely overestimate the process of oxidation. The difference is demonstrated in Fig. 5(b), by comparing the relative mass calculated from the sample compositions as obtained from Mössbauer spectroscopy to the relative mass directly measured during TPO. The overestimation of the mass gain during the initial oxidation phase (0 to 15 min) by the post-mortem MS samples reaches as high as 15%, while the agreement is very good for oxidation times of >30 min. Hence, since accurate sample compositions during the parabolic oxidation phase are accessible by this experimental approach, samples prepared at higher temperatures (633 °C, 666 °C and 700 °C) aim at oxidation times that are within this oxidation regime. The data is presented in Fig. 6. For the following kinetic analysis, only data from the parabolic oxidation regime is used.
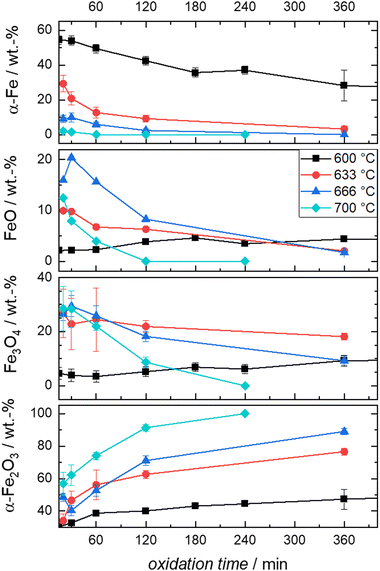 | ||
| Fig. 6 Compositions derived from post-mortem Mössbauer spectroscopy obtained from the oxidation of Fe + BN mixtures at the indicated times and temperatures. | ||
It is evident from Fig. 6 that the trends in mass fraction obtained during oxidation at 600 °C differ significantly from those at higher temperatures. As will be shown in the following, this also affects the kinetics of oxidation.
Kinetic analysis
For the kinetic model calibration, the scale model is used as a basis. In the following, it is shown how the quantitative information for the mass fractions obtained from Mössbauer spectroscopy allows developing a kinetic model for spherical particles adhering to the parabolic rate law. We will show that the outcome changes on whether using an average diameter or considering the overall particle size distribution (PSD) and justify that a PSD should always be included in the simulation of particle oxidation for accurate extraction of kinetic data. As depicted in Fig. 5, the measurements show a two-step process: a rapid initial oxidation, followed by a slower second phase, which can be described by the parabolic rate law (Wagner's theory). This theory has proven useful if the oxidation is limited by diffusion processes in the solid phase25,57 and we show further below how the oxidation behavior of planar iron scales and spherical particles are related. For the particles, it is assumed that iron and its oxides form a layered structure (from inside-out: Fe–FeO–Fe3O4–Fe2O3) similar to the structures identified for planar samples.13,21Based on Wagner's theory, Mi et al.58 proposed a model for the iron particle oxidation rate which depends on the oxide layer thicknesses. In this work, the oxidation kinetics are modeled by a curvature corrected parabolic rate law (eqn (4)).13,59,60 It is derived from eqn (1) and (2),
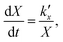 | (1) |
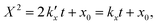 | (2) |
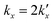 is the parabolic rate constant, and x0 is the initial oxide layer thickness. The parabolic rate constant is represented by an Arrhenius-type expression as follows in eqn (3)
is the parabolic rate constant, and x0 is the initial oxide layer thickness. The parabolic rate constant is represented by an Arrhenius-type expression as follows in eqn (3)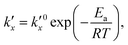 | (3) |
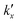 being the pre-exponential factor, Ea the activation energy, R the ideal gas constant, and T the temperature in K. The curvature corrected oxidation rate of an iron particle is then defined as:
being the pre-exponential factor, Ea the activation energy, R the ideal gas constant, and T the temperature in K. The curvature corrected oxidation rate of an iron particle is then defined as: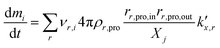 | (4) |
For planar samples, it has been reported that the transition from the initial fast oxidation phase to the slower second phase (following the parabolic rate law) occurs after 30 to 60 minutes for ∼600 °C and earlier for higher temperatures.21,61
This transition point, which defines the initial conditions for the model, is specified as 60 min for 600 °C, 30 min for 633 °C, and 20 min for both, 666 °C and 700 °C in the present work. To account for the different size-dependent initial oxidation states of the particles, it is assumed that during the initial rapid oxidation the thicknesses of the oxide layers grow at the same rate for each particle. This leads to different initializations for separate particle classes, since the smallest particles are already completely oxidized, while large particles still contain a large unreacted iron core. The initial oxidation state for 666 °C is visualized in Fig. 7. The overall oxidation state of the sample corresponds to the measurement at the transition point.
After defining the initial state, the model is used to calculate the oxidation evolution for all particle fractions of the PSD. To determine the kinetic parameters, 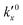 and Ea, for all reactions (six unknowns in total), the error between the model's prediction for the species mass fractions and the experimental results is minimized.
and Ea, for all reactions (six unknowns in total), the error between the model's prediction for the species mass fractions and the experimental results is minimized.
Two optimizations are performed: The first optimization includes all points recorded for the parabolic region from 600 °C to 700 °C and shows an overall good agreement with the experimental results. However, differences in the consumption speed of Fe remain (not shown here, see Table S11 and Fig. S11, ESI†). In accordance with reports in the literature,13,61 it is hypothesized that these discrepancies are due to the fact that 600 °C is close to the stability limit of FeO (570 °C)62 and this aspect is revisited later. Therefore, a second optimization is carried out separating the kinetic parameters for 600 °C and the temperature range of 633 °C to 700 °C. The following discussion is focused on the latter temperature range. For reference, the optimization results for 600 °C are reported in the ESI,† Fig. S12.
Fig. 8 shows the simulation results of the optimized model for the temperature range 633 °C to 700 °C. An excellent agreement between model and experimental data is obtained, including an accurate representation of the Fe consumption rate. Further, the evolution of the intermediates FeO and Fe3O4, as well as the product species Fe2O3, is accurately captured including correct trends with increasing temperature. The kinetic parameters obtained from the optimization are summarized in Table 1. It is noted that approximating the PSD with a monodisperse particle distribution with equivalent Sauter mean diameter showed inferior results, particularly with discrepancies for the trend at longer oxidation times (further details in Fig. S13, ESI†). The influence of the PSD can be readily understood from Fig. 7 which illustrates that with progressing oxidation, more and more smaller particles are completely oxidized and do not contribute further to the oxidation progress. The influence of the PSD for the other temperatures (600 °C, 666 °C and 700 °C) is given in Fig. S14–S16, ESI.†
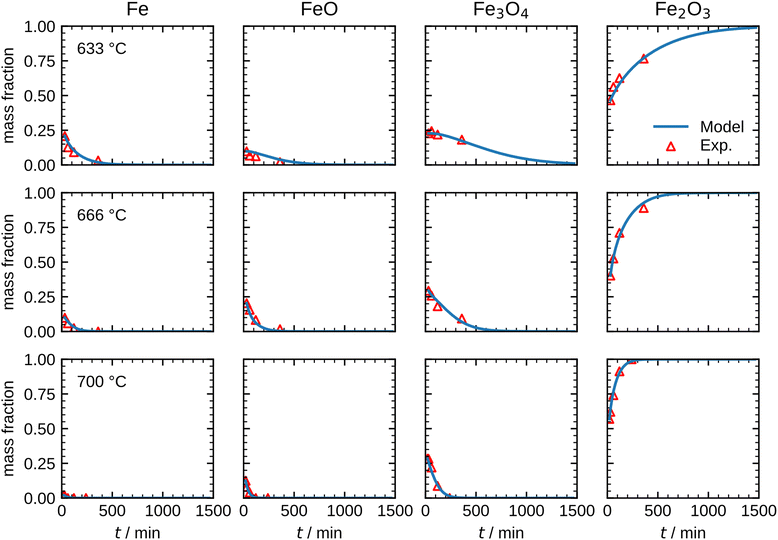 | ||
| Fig. 8 Comparison between the measurements and the optimized model results for the species mass fractions in the temperature range 633–700 °C. | ||
The results shown in Fig. 8 illustrate that the present model accurately describes the isothermal oxidation for the parabolic region of micron-sized spherical particles between 633 °C and 700 °C. We proceed relating the obtained kinetics to reference data from literature, which has mainly been focused on planar scales in the past.13,21,22,24,56 The oxidation rate of planar iron scales is usually quantified by the parabolic constant Kp (unit: g2 cm−4 s−1) which describes the total mass gain of the oxide layer per surface area. For a planar sample, Kp can be easily measured and is constant if unreacted iron is present. However, for a spherical particle and using the same definition, Kp depends on the oxide layer thicknesses due to curvature effects. The difference between the rate constant for planar scales and spherical particles is shown in Fig. 9versus time. As can be seen, the initial values for Kp are equal but with increasing oxide layer thicknesses and progressing oxidation, Kp decreases for the particle due to curvature effects. As previously stated, another effect that reduces the observed Kp for spherical particles is that smaller particles of the PSD are fully converted and do not further contribute to the oxidation rate, which in turn declines the values for the overall sample.
These influences do not permit a direct comparison of Kp from particle samples to planar scales or even to other particle samples with a different PSD. To compare the oxidation rates of spherical particles with the ones of planar scales from the literature, the extracted kinetics are used in a model for a planar sample, i.e. it considers the same reactions but does not include curvature correction and curvature effects. The comparison for the obtained Kp to literature data is shown in Fig. 10. For both fits (600 °C and 633–700 °C) the determined Kp are lower than the rates reported in the literature, but an analogous change in the slope for Kp around 600 °C is observed similar to the findings by Davies et al.24 and Schmahl et al.56,61 Notably, the composition of the oxide layer shows a larger proportion of the higher oxides, Fe2O3 and Fe3O4, than for the planar samples.22,23,56,61 The reason for this behavior remains a subject for future research. From the literature it is known that a more uniformly structured outer oxide layer leads to slower overall oxidation rate and a change in the composition of the oxide layer.19,63 Furthermore, the growing oxide layers have a lower density than iron, such that sheer stresses arise in the outer oxide layers during their growth, reportedly leading to defects.13,63 It is hypothesized here, that these stresses are reduced for spherical particles since the sphericity naturally offers more space for oxide layer growth in the outward direction which supposedly results in a more uniform oxide layer with less defects. This hypothesis would also explain the comparably lower oxidation rates for spherical particles originating from more coherent Fe3O4 and Fe2O3 oxide layers. This hypothesis cannot be conclusively verified with the experimental methodologies reported here, but it seems a likely explanation and represents a promising starting point for future research.
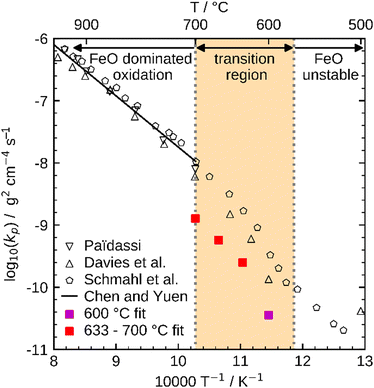 | ||
| Fig. 10 Comparison of Kp determined with the present kinetics to reference values from the literature (Paidassi,21,22 Davies et al.,24 Schmahl et al.,56,61 and Chen and Yuen13). | ||
In summary, the present model accurately describes the isothermal oxidation of iron microparticles in the parabolic region between 633 °C and 700 °C considering the PSD. The determined kinetic parameters are lower for these particles compared to reference values of planar samples reported in literature. Further investigations are required to better understand the differences between spherical particles and planar scales as well as the initial fast oxidation phase, which is necessary for a full description of the oxidation behavior of iron microparticles.
Conclusion
In this work the isothermal oxidation of micrometer-sized iron particles is followed by post-mortem Mössbauer spectroscopy and assisted by TPO. Sintering is demonstrated to significantly influence particle oxidation behavior. Separating particles physically by an inert dilution agent mitigates this issue and thus allows to extract data that is close to single particle oxidation behavior. Following the isothermal oxidation in the temperature interval of 600–700 °C, kinetic parameters for the second reaction phase are determined. The particle size distribution of the iron powder is identified as an essential variable for accurately describing the oxidation kinetics. Overall, the present study demonstrates that novel insights obtained from post-mortem Mössbauer spectroscopy for the evolution of iron oxidation of spherical particles are well-suited for model development and validation. Future work will consider experiments in a wider temperature range and explore modeling approaches for the initial oxidation phase, for which many different models have been proposed and discussed, but a definite solution is still missing.13Author contributions
U. I. K. conceptualized the study, J. S., A. S., T. G., C. K., F. R., A. K., J. G., O. L. V. P., O. D. and B. J. M. E. contributed to the experimental data and formal analysis of the results. D. B. and A. Sch. performed the simulation experiments that were discussed with C. H. J. S., D. B., A. Sch. and U. I. K. wrote the original manuscript draft. All authors contributed to the reviewing and editing of the manuscript and have given their approval for its submission.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the LOEWE cluster project CleanCircles funded by the Hessian Ministry of Arts and Science. U. I. K. and V. P. further like to thank the Federal Ministry of Education and Research via project 05K19RD1.Notes and references
- IEA, World Energy Outlook 2021 – Analysis – IEA, https://www.iea.org/reports/world-energy-outlook-2021, (accessed July 20, 2023).
- B. Johansson, Energy, 2013, 61, 598–605 CrossRef.
- X. Xu, H. H. Chen, Y. Feng and J. Tang, J. Renewable Sustainable Energy, 2018, 10 Search PubMed.
- O. Z. Sharaf and M. F. Orhan, Renewable Sustainable Energy Rev., 2014, 32, 810–853 CrossRef CAS.
- J. M. Bergthorson, Renewable Sustainable Energy Rev., 2018, 68, 169–196 Search PubMed.
- P. Alotto, M. Guarnieri and F. Moro, Renew. Sustain. Energy Rev., 2014, 29, 325–335 CrossRef CAS.
- P. Debiagi, R. C. Rocha, A. Scholtissek, J. Janicka and C. Hasse, Renewable Sustainable Energy Rev., 2022, 165, 112579 CrossRef CAS.
- J. Neumann, R. C. Da Rocha, P. Debiagi, A. Scholtissek, F. Dammel, P. Stephan and C. Hasse, Appl. Energy. Combust. Sci, 2023, 14, 100128 Search PubMed.
- M. Baumann, L. Barelli and S. Passerini, Adv. Energy Mater., 2020, 10, 2001002 CrossRef CAS.
- J. M. Bergthorson, S. Goroshin, M. J. Soo, P. Julien, J. Palecka, D. L. Frost and D. J. Jarvis, Appl. Energy, 2015, 160, 368–382 CrossRef CAS.
- M. Fedoryk, B. Stelzner, S. Harth and D. Trimis, Appl. Energy Combust. Sci., 2023, 13, 100111 Search PubMed.
- J. Janicka, P. Debiagi, A. Scholtissek, A. Dreizler, B. Epple, R. Pawellek, A. Maltsev and C. Hasse, Appl. Energy, 2023, 339, 120950 CrossRef CAS.
- R. Y. Chen, Oxid. Met., 2003, 59, 433–468 CrossRef CAS.
- A. V. Korshunov, Russ. J. Phys. Chem. B, 2012, 6, 368–375 CrossRef CAS.
- S. Rebeyrat, J. Grosseau-Poussard, J. Dinhut and P. Renault, Thin Solid Films, 2000, 379, 139–146 CrossRef CAS.
- A. G. Zhygotsky, J. Therm. Anal. Calorim., 2000, 62, 575–578 CrossRef CAS.
- P. Kofstad, High Temperature Corrosion, Elsevier Applied Science, London, 1988 Search PubMed.
- A. G. Goursat and W. W. Smeltzer, High-Temperature Materials Coatings and Surface Interactions: Freund Publishing House, Israel, 1980 Search PubMed.
- N. Bertrand, C. Desgranges, D. Poquillon, M. C. Lafont and D. Monceau, Oxid. Met., 2010, 73, 139–162 CrossRef CAS.
- L. Himmel, R. F. Mehl and C. E. Birchenall, JOM, 1953, 5, 827–843 CrossRef CAS.
- J. Païdassi, Acta Metall., 1958, 6, 184–194 CrossRef.
- J. Païdassi, Acta Metall., 1958, 6, 219–221 CrossRef.
- J. Païdassi, Acta Metall., 1958, 6, 184–194 CrossRef.
- M. H. Davies, M. T. Simnad and C. E. Birchenall, JOM, 1951, 3, 889–896 CrossRef CAS.
- C. Wagner, Z. Phys. Chem., 1933, 21B, 25–41 CrossRef.
- C. Kuhn, A. Düll, P. Rohlfs, S. Tischer, M. Börnhorst and O. Deutschmann, Appl. Energy Combust. Sci., 2022, 12, 100096 Search PubMed.
- J. Janicka, P. Debiagi, A. Scholtissek, A. Dreizler, B. Epple, R. Pawellek, A. Maltsev and C. Hasse, Appl. Energy, 2023, 120950 CrossRef CAS.
- D. Wen, P. Song, K. Zhang and J. Qian, J. Chem. Technol. Biotechnol., 2011, 86, 375–380 CrossRef CAS.
- E. M. Hunt and M. L. Pantoya, J. Appl. Phys., 2005, 98 Search PubMed.
- E. N. Lysenko, A. P. Surzhikov, S. P. Zhuravkov, V. A. Vlasov, A. V. Pustovalov and N. A. Yavorovsky, J. Therm. Anal. Calorim., 2014, 115, 1447–1452 CrossRef CAS.
- E. N. Lysenko, A. P. Surzhikov, E. V. Nikolaev, V. A. Vlasov and S. P. Zhuravkov, J. Therm. Anal. Calorim., 2018, 134, 307–312 CrossRef CAS.
- L. Del Campo, R. B. Pérez-Sáez and M. J. Tello, Corros. Sci., 2008, 50, 194–199 CrossRef CAS.
- R. J. Hussey and M. Cohen, Corros. Sci., 1971, 11, 699–711 CrossRef CAS.
- C. Prescher, C. McCammon and L. Dubrovinsky, J. Appl. Crystallogr., 2012, 45, 329–331 CrossRef CAS.
- G. J. Long, T. E. Cranshaw and G. Longworth, Möss. Eff. Ref. Data J., 1983, 6, 42–49 Search PubMed.
- F. Grandjean and G. J. Long, Chem. Mater., 2021, 33, 3878–3904 CrossRef CAS.
- W. Sturhahn, T. S. Toellner, E. E. Alp, X. Zhang, M. Ando, Y. Yoda, S. Kikuta, M. Seto, C. W. Kimball and B. Dabrowski, Phys. Rev. Lett., 1995, 74, 3832–3835 CrossRef CAS PubMed.
- A. I. Chumakov, R. Rüffer, A. Q. R. Baron, H. Grünsteudel and H. F. Grünsteudel, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R9596–R9599 CrossRef CAS PubMed.
- T. S. Toellner, M. Y. Hu, W. Sturhahn, K. Quast and E. E. Alp, Appl. Phys. Lett., 1997, 71, 2112–2114 CrossRef CAS.
- E. de Grave and A. van Alboom, Phys. Chem. Miner., 1991, 18, 337–342 CrossRef CAS.
- S. J. Oh, D. C. Cook and H. E. Townsend, Hyperfine Interact., 1998, 112, 59–66 CrossRef CAS.
- V. Procházka, P. Novák, A. Stejskal, M. Dudka and V. Vrba, Phys. Lett. A, 2022, 442, 128195 CrossRef.
- W. Meisel and G. Kreysa, Z. Anorg. Allg. Chem., 1973, 395, 31–36 CrossRef.
- R. M. Persoons, E. de Grave and R. E. Vandenberghe, Hyperfine Interact., 1990, 54, 655–660 CrossRef CAS.
- L. Aldon and J.-C. Jumas, Solid State Sci., 2012, 14, 354–361 CrossRef CAS.
- D. A. Channing and M. J. Graham, Corros. Sci., 1972, 12, 271–289 CrossRef CAS.
- J. Mich, D. Braig, T. Gustmann, C. Hasse and A. Scholtissek, Combust. Flame, 2023, 256, 112949 CrossRef CAS.
- ULF - Universal Laminar Flame Solver, Contribution (Poster) by A. Zschutschke, D. Messig, A. Scholtissek, C. Hasse, https://figshare.com/articles/poster/ULF_code_pdf/5119855/2, (accessed July 20, 2023).
- A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, ACM Trans. Math. Softw., 2005, 31, 363–396 CrossRef.
- Ansys|Engineering Simulation Software, https://www.ansys.com/, (accessed July 20, 2023).
- M. Liao, Y. Chen, Z. Cheng, C. Wang, X. Luo, E. Bu, Z. Jiang, B. Liang, R. Shu and Q. Song, Appl. Energy, 2019, 252, 113435 CrossRef CAS.
- E. M. Petersen, R. G. Rao, B. C. Vance and J.-P. Tessonnier, Appl. Catal., B, 2021, 286, 119904 CrossRef CAS.
- Y. Xu, X. Du, J. Li, P. Wang, J. Zhu, F. Ge, J. Zhou, M. Song and W. Zhu, J. Fuel Chem. Technol., 2019, 47, 199–208 CrossRef CAS.
- Compute X-ray Absorption – Online Tool by Argonne Advanced Photon Source, https://11bm.xray.aps.anl.gov/absorb/absorb.php?mode=calc&spectrumtype=Energy&spectrum=14.4&formula=SiC&radius=0.05&densitytype=RHO&density=3.21&submit=Compute, (accessed July 20, 2023).
- D. Caplan, J. Electrochem. Soc., 1960, 107, 359 CrossRef.
- N. G. Schmahl, H. Baumann and H. Schenck, Arch. Eisenhuettenwes., 1956, 27, 707–713 CAS.
- A. Atkinson, Rev. Mod. Phys., 1985, 57, 437–470 CrossRef CAS.
- X. Mi, A. Fujinawa and J. M. Bergthorson, Combust. Flame, 2022, 240, 112011 CrossRef CAS.
- A. T. Fromhold, J. Phys. Chem. Solids, 1988, 49, 1159–1166 CrossRef CAS.
- G. Tammann, Z. Anorg. Allg. Chem., 1920, 111, 78–89 CrossRef.
- N. G. Schmahl, H. Baumann and H. Schenck, Steel Res. Int., 1958, 29, 83–88 CrossRef CAS.
- H. Wriedt, J. Pet. Eng., 1991, 12, 170–200 CAS.
- D. Caplan and M. Cohen, Corros. Sci., 1966, 6, 321–335 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03484d |
| ‡ Joint first authorship. |
| § Present affiliation: OSCAR PLT GmbH, Hamburger Ring 11, Klipphausen/Germany. |
| This journal is © the Owner Societies 2024 |