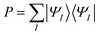Multi-state pair-density functional theory†
Jie J.
Bao‡
 ,
Chen
Zhou‡
,
Chen
Zhou‡
 ,
Zoltan
Varga
,
Zoltan
Varga
 ,
Siriluk
Kanchanakungwankul
,
Siriluk
Kanchanakungwankul
 ,
Laura
Gagliardi
,
Laura
Gagliardi
 * and
Donald G.
Truhlar
* and
Donald G.
Truhlar
 *
*
Department of Chemistry, Chemical Theory Center, and Minnesota Supercomputing Institute, University of Minnesota, 207 Pleasant Street SE, Minneapolis, MN 55455-0431, USA. E-mail: gagliard@umn.edu; truhlar@umn.edu
First published on 7th May 2020
Abstract
Multi-configuration pair-density functional theory (MC-PDFT) has previously been applied successfully to carry out ground-state and excited-state calculations. However, because they include no interaction between electronic states, MC-PDFT calculations in which each state’s PDFT energy is calculated separately can give an unphysical double crossing of potential energy surfaces (PESs) in a region near a conical intersection. We have recently proposed state-interaction pair-density functional theory (SI-PDFT) to treat nearly degenerate states by creating a set of intermediate states with state interaction; although this method is successful, it is inconvenient because two SCF calculations and two sets of orbitals are required and because it puts the ground state on an unequal footing with the excited states. Here we propose two new methods, called extended-multi-state-PDFT (XMS-PDFT) and variational-multi-state-PDFT (VMS-PDFT), that generate the intermediate states in a balanced way with a single set of orbitals. The former uses the intermediate states proposed by Granovsky for extended multi-configuration quasi-degenerate perturbation theory (XMC-QDPT); the latter obtains the intermediate states by maximizing the sum of the MC-PDFT energies for the intermediate states. We also propose a Fourier series expansion to make the variational optimizations of the VMS-PDFT method convenient, and we implement this method (FMS-PDFT) both for conventional configuration-interaction solvers and for density-matrix-renormalization-group solvers. The new methods are tested for eight systems, exhibiting avoided crossings among two to six states. The FMS-PDFT method is successful for all cases for which it has been tested (all cases in this paper except O3 for which it was not tested), and XMS-PDFT is successful for all eight cases except the mixed-valence case. Since both XMS-PDFT and VMS-PDFT are less expensive than XMS-CASPT2, they will allow well-correlated calculations on much larger systems for which perturbation theory is unaffordable.
1. Introduction
Kohn–Sham density functional theory (KS-DFT)1 has been successful in treating many chemical problems, but it is less accurate for treating inherently multi-configurational electronic states – which are called strongly correlated states – than for treating states well represented by a single Slater determinant – which are called weakly correlated.2 Strong correlation usually arises from near degeneracy of two or more states, and excited electronic states are usually strongly correlated, and often they strongly interact with other states. Thus, the accurate treatment of strongly correlated states is necessary for spectroscopy and photochemistry.3,4 Furthermore, the accurate treatment of strongly correlated sets of states is also required to properly describe magnetic effects.5,6Although KS-DFT has lower accuracy for strongly correlated states than for weakly correlated ones, for large molecules it is much less expensive than wave function theory (WFT) methods of comparable accuracy. We have proposed multi-configuration pair-density functional theory (MC-PDFT) as a method that builds on a multi-configurational self-consistent-field (MCSCF) reference wave function and is more innately suitable for strongly correlated systems than KS-DFT; MC-PDFT also has the advantage of being computationally less expensive compared with WFT methods in terms of computer time and memory with comparably accurate treatments of correlation energy.7,8 We refer the reader to a recent review article9 that compares PDFT to other ways to combine wave function methods and density functional methods for excited-state calculations.
When states are nearly degenerate and have the same symmetry, they interact strongly with each other, and they should be treated by a method that gives the correct topography4 of adiabatic potential energy surfaces (PESs) at conical intersections; such methods are called multi-state (MS) methods. For example, in WFT, multireference Møller–Plesset perturbation theory10 is a state-specific method because it calculates the final approximation of the energy of each state separately, whereas multi-configuration quasi-degenerate perturbation theory (MC-QDPT)11 and extended MC-QDPT (XMC-QDPT)12 are multi-state methods because the final energies are eigenvalues of the same matrix (hence they interact through the off-diagonal elements of that matrix). Similarly, complete active space perturbation theory (CASPT2)13 is a state-specific method, and multi-state CASPT2 (MS-CASPT2)14 and extended MS-CASPT2 (XMS-CASPT2)15 are multi-state methods.
The original MC-PDFT is a state-specific method. We recently proposed state-interaction PDFT (SI-PDFT) as a multi-state generalization;16 SI-PDFT yields the correct topography of adiabatic PESs for conical intersections and it has been applied successfully to several problems;16–18 but it is inconvenient because two MCSCF calculations and two sets of orbitals are required, and it puts the ground state on an unequal footing with the excited states, which is sometimes undesirable (for example, for treating magnetic states). In the present paper we present two new multi-state methods that eliminate these drawbacks of SI-PDFT. One is called extended-multi-state-PDFT (XMS-PDFT) because it uses the intermediate basis proposed by Granovsky12 for XMC-QDPT, and the other is called variational-multi-state-PDFT (VMS-PDFT) because it obtains an intermediate basis by variationally maximizing the sum of MC-PDFT energies for the intermediate states. We approximate the VMS-PDFT method by using a Fourier series expansion; this method for VMS-PDFT is called the Fourier-multi-state-PDFT (FMS-PDFT) method.
A key aspect of all the above-mentioned MS methods is that they determine a model space spanned by the states to be treated as strongly interacting. Similar to XMC-QDPT or XMS-CASPT2, XMS-PDFT and VMS-PDFT build up a model space that spans the N lowest-energy states optimized in a state-averaged CASSCF (SA-CASSCF) calculation. (Generalizations to incomplete active spaces and smaller model spaces are straightforward but are not considered here.) The model space states are called the intermediate basis and are obtained by unitary transformation from the SA-CASSCF states.
Section 2 explains the two new methods and the Fourier-based approximation of VMS-PDFT. Section 3 specifies the computational details for several test systems, including those that were previously studied by SI-PDFT. Section 4 presents applications of the new methods to these test systems and evaluates their performances. Section 5 provides the concluding remarks.
2. Theory
2.1 MC-PDFT
The MC-PDFT method may be based on single-state CASSCF (SS-CASSCF) calculations or on SA-CASSCF calculations. In the present article we consider the latter type of calculation, in which case one starts with a reference wave function obtained by performing an SA-CASSCF calculation and given by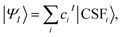 | (1) |
| EMC-PDFTI = Te + Velec + Eot(ρI,ΠI), | (2) |
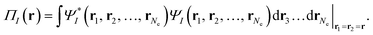 | (3) |
Eqn (2) applies to MC-PDFT calculations starting with either SS-CASSCF or SA-CASSCF. We note that it does not separate the energy into an uncorrelated component, a static correlation component, and a dynamic correlation component. Because the original MC-PDFT method computes the state energies independently, it is a state-specific method in the sense that the final energy of each state is computed separately, even if one starts with SA-CASSCF kinetic energies, densities, and on-top densities.
2.2 Multi-state MC-PDFT
To obtain the correct topography of PESs at conical intersections, we have proposed the SI-PDFT method16 as an MS extension of MC-PDFT. In SI-PDFT, we generate a set of intermediate states with the reference SA-CASSCF states and an auxiliary state from a state-specific ground-state CASSCF calculation. The ground intermediate state is obtained by projecting the SS-CASSCF state into the space spanned by the SA-CASSCF states, and the other intermediate states are obtained by performing Schmidt orthogonalization of the excited states obtained by the SA-CASSCF calculation to the ground intermediate state. Then one constructs an effective Hamiltonian in the intermediate state basis and diagonalizes it to get the SI-PDFT energy for each state. This treats the ground and excited states unequally. Moreover, using different orbital sets (i.e., using both the orbitals from the SS-CASSCF calculation and those from the SA-CASSCF calculation) is inconvenient. To avoid these problems, we next propose two new multi-state MC-PDFT methods that use only one set of orbitals.In general, the intermediate states are obtained by a unitary transformation:
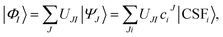 | (4) |
We construct an effective Hamiltonian in the intermediate-state basis with diagonal elements defined as
| HeffII = EMC-PDFTI, | (5) |
| HeffIJ = 〈ΦI|H|ΦJ〉 | (6) |
Following the above scheme, we next introduce two strategies (XMS-PDFT and VMS-PDFT) to generate the matrix U, yielding UX and UV, respectively.
2.3 XMS-PDFT
The intermediate basis in XMS-PDFT diagonalizes the effective Hamiltonian suggested by Granovsky for XMC-QDPT in ref. 12, where he stressed that “the effective Hamiltonian should be a function of the subspace spanned by the selected CI vectors, rather than a function of any particular choice of basis in this subspace” and that “the computed energies must be uniquely defined, continuous and smooth functions of the molecular geometry and any other external parameters, with possible exceptions at the manifolds of their accidental degeneracy such as conical intersections”. The XMS-CASPT2 method also uses this intermediate basis. We use the XMS-CASPT2 procedure15 to explain this, and the explanation starts by recalling the procedure for MS-CASPT2.In MS-CASPT2, the unperturbed Hamiltonian is defined as
| H0 = PFP + QFQ, | (7) |
is the projection operator onto the SA-CASSCF state space and
| Q = 1 − P |
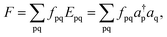 | (8) |
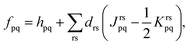 | (9) |
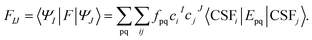 | (10) |
The state-space Fock matrix defined in eqn (10) is not necessarily diagonal, because the reference wave functions (i.e., the SA-CASSCF wave functions) are the eigenstates of the Hamiltonian operator, not necessarily the eigenstates of the state-space Fock operator or the zeroth-order Hamiltonian.
The MS-CAPST2 method neglects the off-diagonal elements of the state-space Fock matrix, but following the prescription used in the XMS-CASPT2 method, the XMS-PDFT method diagonalizes the state-space Fock matrix by a transformation matrix UX:
(UX)†FUX = ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) . . | (11) |
The UX matrix determined this way then yields the intermediate states defined by
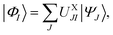 | (12) |
(UX)†HUX = ![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) , , | (13) |
![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) is the Hamiltonian matrix in the basis of the intermediate states.
is the Hamiltonian matrix in the basis of the intermediate states.
After the intermediate states are obtained, XMS-PDFT defines an effective Hamiltonian in the intermediate basis such that the diagonal element HeffII is the MC-PDFT energy of intermediate state ΦI, and the off-diagonal element HeffIJ is ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) IJ. The XMS-PDFT energies (EXMS-PDFTI) and eigenvectors are obtained by diagonalizing the effective Hamiltonian matrix.
IJ. The XMS-PDFT energies (EXMS-PDFTI) and eigenvectors are obtained by diagonalizing the effective Hamiltonian matrix.
We notice that the off-diagonal elements in the state-space Fock matrix are zero for states with different symmetries. This suggests that the XMS-PDFT method is identical to MC-PDFT if all states in the model space belong to different irreps (similarly, XMS-CASPT2 is identical to MS-CASPT2 or even single-state CASPT2 for such a case). This is not a problem, but we have found that the off-diagonal elements in the state-space Fock matrix are almost zero for many geometries in some mixed-valence19 systems (see Fig. S3,† where sections and figures with the prefix S are in the ESI†) even when the states have the same symmetry, and we will see that XMS-PDFT does not always give good results for such systems. Next we present the VMS-PDFT method which does not have this problem (but it is more expensive).
2.4 VMS-PDFT
The trace of the effective Hamiltonian defined above is given by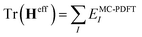 | (14) |
Although the kinetic energy component in an MC-PDFT energy (i.e. the first term of eqn (2)) is unitarily invariant, the classical electrostatic energy and the on-top energy are not, and therefore the trace in eqn (14) depends on the transformation matrix U. In VMS-PDFT, the transformation matrix UV that yields the intermediate basis is chosen so that this trace is maximized. Just as in XMS-PDFT, but using the new intermediate basis, VMS-PDFT then evaluates the energies by diagonalizing an effective Hamiltonian defined such that the diagonal elements are MC-PDFT energies in the intermediate basis and the off-diagonal elements are computed by standard wave function theory in the intermediate basis.
The motivation for using a transformation that maximizes the sum of on-top energies for intermediate states is a physical one, namely that the diagonalization of the effective Hamiltonian can be interpreted as adding extra correlation to the energies of intermediate states, so this correlation energy should not already be present in the diagonal elements.
At present, we do not have an analytic procedure to find the transformation matrix UV that completely maximizes eqn (14). Instead, we propose here a numerical way to approximate the maximization in a practical and smooth way by fitting eqn (14) to a Fourier series. We call this implementation the FMS-PDFT method.
We first present FMS-PDFT for a two-state calculation. The unitary transformation between two states (ΨI,ΨJ) can be parameterized as
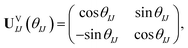 | (15) |
| (ΨI,ΨJ)UVIJ(θIJ) = (ΦI,ΦJ). | (16) |
Now consider applying 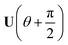 to the two states; this yields
to the two states; this yields
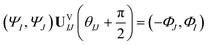 | (17) |
Comparing eqn (16) and (17) shows that UVIJ(θIJ) and 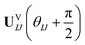 generate the same two states but with different ordering, and thus they give the same trace of the effective Hamiltonian matrix. This means that the trace of the effective Hamiltonian matrix has a period of
generate the same two states but with different ordering, and thus they give the same trace of the effective Hamiltonian matrix. This means that the trace of the effective Hamiltonian matrix has a period of 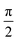 , and therefore the Fourier expansion of the effective Hamiltonian can be written as
, and therefore the Fourier expansion of the effective Hamiltonian can be written as
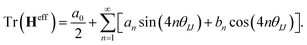 | (18) |
We keep only the terms with n = 1 in the sum on the right hand side of eqn (18); then the equation can be parameterized as
Tr(Heff) = A + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(4θIJ) + C sin(4θIJ) + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4θIJ), cos(4θIJ), | (19) |
For FMS-PDFT calculations with N states (where N is greater than 2), we write UV as a product of transformation matrices
| UV = U12U23…UI(I+1)…U(N−1)N, | (20) |
| Φ(I) = Φ(I−1)UI(I+1), | (21) |
Notice that neither do we include all the N(N − 1)/2 transformation matrices UIJ (I < J) nor do we transform the states iteratively to reach the absolute maximum trace. Since strong couplings mostly occur between adjacent states, it is a reasonable and economical practice to only consider the (N − 1) unitary transformations UI(I+1) as presented above. Furthermore, we will see below that the results are already good with a single pass as in eqn (20). Furthermore, stopping with a single pass gives smoother results than one would obtain if one used a convergence criterion that led to different numbers of iterations at different geometries.
The FMS-PDFT method is also implemented for wave functions optimized with the density matrix renormalization group20–25 (DMRG) approach; the combination of state-specific PDFT and DMRG was introduced previously26,27 and is here extended to an MS treatment. The FMS-PDFT/DMRG method is an extension of the FMS-PDFT method described above except that it is based on an SA-DMRG28 calculation instead of an SA-CASSCF starting point, and this requires a change in implementation since the DMRG wave function is not explicitly expanded in a CSF basis. Therefore we do not obtain intermediate states with eqn (4); instead, the MC-PDFT energies for intermediate states are calculated with the transformed one-body and two-body density matrices,
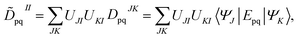 | (22) |
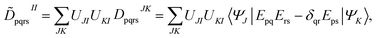 | (23) |
![[D with combining tilde]](https://www.rsc.org/images/entities/b_char_0044_0303.gif) II and
II and ![[d with combining tilde]](https://www.rsc.org/images/entities/b_char_0064_0303.gif) II are one-body and two-body density matrices for the intermediate state I.
II are one-body and two-body density matrices for the intermediate state I.
3. Computational details
The calculations are performed in OpenMolcas v18.09, tag 548-g19e2926-dirty,29 with codes modified to perform XMS-PDFT and FMS-PDFT calculations. The DMRG calculations are performed with the QCMaquis software suite25,30–32 in OpenMolcas v18.11, tag 17-g792ff65-dirty, which is modified to perform FMS-PDFT/DMRG calculations.In XMS-CAPST2 calculations, an ionization-potential-electron-affinity (IPEA) shift33 of 0.25 a.u. is used. In the FMS-PDFT/DMRG calculations for phenol, we used the same active space as we used for regular FMS-PDFT calculations. The bond dimension (M) is set to 500. In the PDFT calculations, we used the translated PBE (tPBE) on-top functional.
Table 1 presents the wave function symmetry, basis set, number of averaged states, number of active electrons, and identities of active MOs for each system studied. The internal coordinates that are scanned for each system are shown in Table 2. The geometries are available in Section S1.†
| System | Sym | Basis set | N states | n | Active MOs |
|---|---|---|---|---|---|
| LiF | C 1 | jun-cc-pVQZ34,35 | 2 | 8 | 2pz of F, 2s of Li |
| LiH | C 2v | aug-cc-pVQZ34 | 4 | 2 | 2s, 2pz, 3s, 3pz of Li, 1s of H |
| HNCO | C 1 | cc-pVDZ34 | 2 | 16 | Valence shell (2s and 2p of C, N, and O atoms and 1s of H atom) |
| CH3NH2 | C 1 | 6-31++G(d,p)36,37 | 2 | 6 | 2σ, 1σ*, 2pz, 3s, and 3pz of N |
| C6H5OH | C 1 | jul-cc-pVDZ34,35 | 2 or 3 | 12 | 3π, 3π*, σOH, 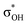 , σCO, , σCO, 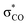 and pz of O and pz of O |
| O + O2 (3A′) | C s | cc-pVTZ34 | 6 | 12 | 9 2p orbitals |
| O3 (3A′) | C s | cc-pVTZ34 | 6 | 12 | 9 2p orbitals |
| Spiro | C 2v | 6-31G(d)38 | 2 | 11 | See ref. 17 |
| System | Internal coordinates scanned |
|---|---|
| LiF | r(LiF) = [1.0–9.0] Å |
| LiH | r(LiH) = [1.0–12.0] Å |
| HNCO | r(NC) = [1.25–3.00] Å and τ(HNCO) = [180–130]° |
| CH3NH2 | r(NH) = [0.8–3.6] Å and τ(H6–C4–N1–H3) = 0, 90, 95, or 100° |
| C6H5OH | r(OH) = [0.5–3.0 ] Å and τ(C–C–O–H) = 1 or 10° |
| O + O2 (3A′) | r(O1O3) = [1.0–2.5] Å |
| O3 (3A′) | α(O2O1O3) = [60–180]° |
| Spiro | See Section 4.8 |
For the HNCO calculations with bond length r(NC) = 2.0–2.5 Å and torsion angle τ(HNCO) = 150° (discussed in Section 4.3), we carried out the VMS-PDFT calculations using a numerical maximization procedure instead of the Fourier series algorithm because the 3-point fitting in FMS-PDFT fails for that limited region due to the trace of the effective Hamiltonian changing slowly with respect to the rotation angle, so that keeping only the terms with n = 1 in the sum on the right hand side of eqn (18) is inadequate. In all other cases the Fourier series method proved adequate.
4. Results and discussion
4.1 Lithium fluoride (LiF)
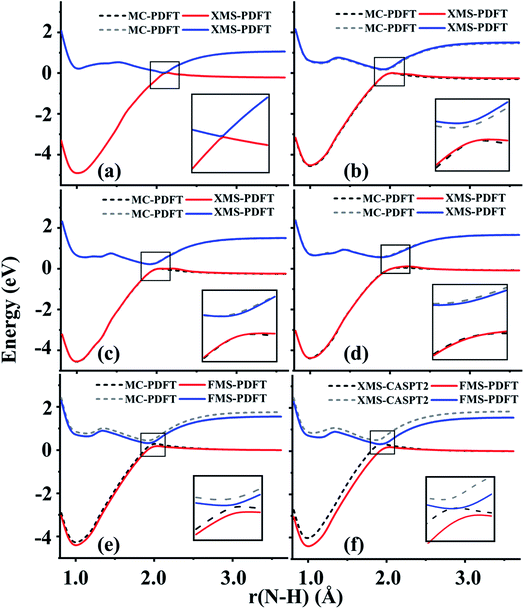
Lithium fluoride has an avoided crossing of the ground state and first excited state that has been widely studied.39–46 The ground state at the equilibrium distance is ionic, corresponding to the (2pz,F)2(2sLi)0 configuration. The ground state has A1 symmetry in the C2v group. This state interacts with another A1 state that corresponds to two neutral ground-state atoms, namely (2pz,F)1(2sLi)1. The accurate value of the distance of the avoided crossing is about 7.4 Å.39 However, theoretical calculations usually underestimate the distance by 1.0 Å, with an exception being the calculation in ref. 41.The MC-PDFT method gives an unphysical double crossing between 4 Å and 6 Å, associated with a “dip” of the energy curve, as shown in Fig. 1(a) and (c). The XMS-PDFT and FMS-PDFT methods, however, remove the incorrect double crossing and also recover the expected shape of the avoided crossing at a larger distance. Additionally, the two new multi-state PDFT methods preserve the correct asymptotic character of the two states, and they work well for the whole potential energy curve.
Fig. 1(b) and (d) show that the XMS-PDFT and FMS-PDFT results agree with XMS-CASPT2 for the overall shapes of the two curves. The minimum separation of the two curves is 0.18 eV at 5.97 Å by XMS-PDFT, 0.15 eV at 5.92 Å by FMS-PDFT, and 0.11 eV at 6.11 Å by XMS-CASPT2. The bond lengths with the minimum energy separation obtained by the two methods are significantly shorter than 7.4 Å because the calculations underestimate the electron affinity of F, which is a very hard47 problem.
To check the fitting accuracy of FMS-PDFT, we compare the trace of the effective Hamiltonian matrix obtained by 3-point fitting to that obtained by non-fitted calculations. In Table 3, we list the rotation angles for various Li–F bond lengths and the corresponding trace of the effective Hamiltonian obtained by calculations with and without fitting. The mean unsigned error (MUE) of the trace in the fitted calculation is less than 3 meV, which is much less than the intrinsic error in the method and is adequate for most applications.
| R Li–F (Å) | Rotation angle (deg) | ΔE (eV) |
|---|---|---|
| 0.8 | 26.34 | −0.0016 |
| 1.6 | 5.06 | 0.0078 |
| 2.4 | 15.72 | 0.0008 |
| 3.2 | 28.66 | −0.0026 |
| 4.0 | 38.46 | −0.0015 |
| 4.8 | 13.00 | −0.0102 |
| 5.6 | 4.10 | 0.0033 |
| 6.4 | 1.37 | 0.0020 |
| 7.2 | 0.42 | 0.0007 |
| 8.0 | 0.07 | 0.0001 |
| 10.0 | 0.14 | −0.0003 |
| MUE | 0.0028 |
4.2 Lithium hydride (LiH)
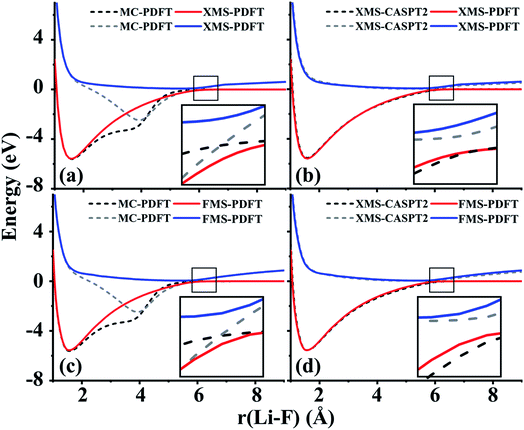
The ground state of lithium hydride is an ionic state near the equilibrium geometry, but this state interacts with three covalent states, corresponding to (2sLi)1(1sH)1, (2spz,Li)1(1sH)1, and (3sLi)1(1sH)1 configurations, as the Li–H bond dissociates. All four states have A1 symmetry in the C2v point group.Despite the complexity of the ionic state of LiH crossing with at least three other states as shown in Fig. 2, a similar pattern to LiF is still found for the third and fourth states of LiH beyond 10 Å. The zoomed-in regions in Fig. 2(a) and (c) show that the MC-PDFT curves for the third and fourth states still have a dip and a double crossing, while XMS-PDFT and FMS-PDFT recover the avoided crossing of the two states and also remove the dip.
The first (red) and second (blue) states calculated by XMS-PDFT and FMS-PDFT agree very well with those calculated by XMS-CASPT2. The minimum energy separation between the third and fourth states is 0.10 eV at 10.66 Å by XMS-PDFT, 0.08 eV at 11.63 Å by FMS-PDFT, and 0.07 eV at 11.28 Å by XMS-CASPT2. The shapes of the XMS-CASPT2 curves match much better with XMS-PDFT and FMS-PDFT than with MC-PDFT, especially for the energy minima of the excited states.
The potential energy curves of XMS-CASPT2 and FMS-PDFT overlap very well, demonstrating the superiority of physically motivated FMS-PDFT, and also showing that applying only (N −1) rotations to an N-state calculation without iteration is sufficient for FMS-PDFT. Note that there is a bump around 3 Å for the FMS-PDFT potential energy curve. A similar but more indistinct bump can also be found on the XMS-PDFT potential energy curve. The bumps are a result of the interaction of the 4th state and the next higher one, which is not included in the calculation. This is a problem not just with the methods presented here but with the potential curves calculated by any method based on SA-CASSCF; the highest included state usually has an avoided crossing with the first unincluded state, and this causes some nonsmoothness in the potential curves.
4.3 Isocyanic acid (HNCO)
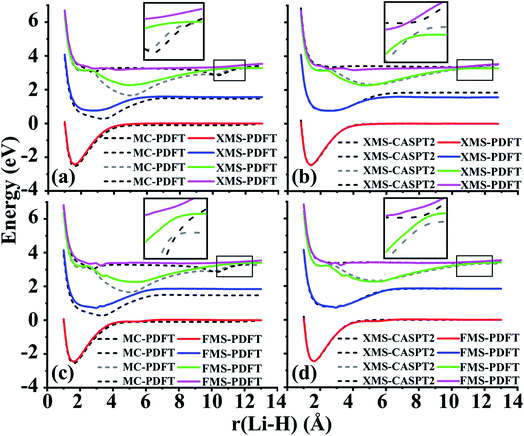
We next turn to avoided-crossing regions in polyatomics, and we remind the reader that avoided crossings along a polyatomic path are a signal that one is close to a conical intersection.48For planar HNCO, the first two singlet states have A′ and A′′ symmetry in the Cs point group. Along the dissociation path of the NC bond, these two states cross each other. However, if the molecule becomes nonplanar, the crossing becomes avoided (since their coupling becomes symmetry-allowed), and the states switch character as they pass the locally avoided crossing. Based on previous work in our group,49 we fixed two bond lengths, r(HN) = 1.0584 Å (2.0a0) and r(CO) = 1.1906 Å (2.5a0), and two bond angles, α(HNC) = 110°, and β(NCO) = 100° and then varied the r(NC) bond length from 1.25 to 3.00 Å and the τ(HNCO) torsion angle from 180 to 130°. We present the curves when the torsion angle is 150° and 175° in Fig. 3 and the curves at other torsion angles are shown in Fig. S1.†
Fig. 3 shows that the shapes of the potential curves predicted by XMS-PDFT are similar to those obtained with XMS-CASPT2, although XMS-PDFT predicts a slightly wider energy separation (about 0.17–0.22 eV) of the two states in the region of the equilibrium well and around the region of the energy barrier close to the planar geometry. Fig. S1† shows that further from the planar geometry, with the τ(HNCO) torsion angle less than 140°, the wider energy separation of XMS-PDFT still holds for the region of the energy barrier, but in the region of the equilibrium well the energy separation of XMS-PDFT becomes slightly narrower than that of XMS-CASPT2. Despite these minor differences between the curves of the two methods, both methods are successful in showing the avoided crossing. Close to the equilibrium geometry, XMS-PDFT places the avoided crossing at an N–C distance about 0.1 Å shorter than that of XMS-CASPT2. Since the two states obtained with XMS-PDFT have a slightly wider separation, the avoidance of the two states is more obvious than the avoidance with XMS-CASPT2. Further from the planar geometry, the crossing point of the two states moves to a shorter N–C distance, and we find that the two states still avoid each other smoothly.
A torsion angle of 150° is chosen to test the performance of the FMS-PDFT method. A similar avoided crossing around 1.7 Å is observed for both FMS-PDFT and XMS-CASPT2. Although the separation of the two states in the region of 2.0–2.5 Å is still wider for VMS-PDFT compared with XMS-CASPT2, VMS-PDFT is shown to be well-behaved, even though we used a combination of FMS-PDFT and numerical VMS-PDFT in this case, as discussed in Section 3.
4.4 Methylamine (CH3NH2)
The potential energy surfaces, dynamics, and spectroscopy of CH3NH2 have been widely studied both experimentally and theoretically.18,50–63 Due to the involvement of the conical intersection region in the photodissociation of methylamine, computational methods should be chosen carefully to correctly describe the strong couplings between the electronic states. The ground and first excited singlet states were studied along four N–H bond dissociation potential energy curves with XMS-PDFT and FMS-PDFT. These four paths correspond to the N–H bond fissions with conformations shown in Fig. 1 in ref. 18; these conformations are denoted by eclipsed-H3, staggered, 95° and 100°, respectively. FMS-PDFT was tested only for the staggered conformation, but MC-PDFT and XMS-PDFT were tested for all four.The calculated potential energy curves along the four paths are plotted in Fig. 4. The potential energy curves calculated by both new methods show correct topographies for avoided crossings near the conical intersection seam, both globally and in the zoomed-in regions. However, the distance at which the minimum energy separation occurs is predicted to be shorter by MC-PDFT and XMS-PDFT than by XMS-CASPT2. The N–H bond distances at the minimum energy separation and the corresponding energy separations are listed in Table 4. For all four paths, the PDFT bond distances at the avoided crossing are about 0.056 Å longer than those predicted by XMS-CASPT2. However, Table 4 also shows that the minimum energy separations all agree within 0.08 eV.
| Method | R N–H (Å) | Energy separations (eV) |
|---|---|---|
| Eclipsed-H3 | ||
| XMS-CASPT2 | 2.01 | 0.007 |
| MC-PDFT | 2.07 | 0.010 |
| XMS-PDFT | 2.07 | 0.010 |
| Staggered | ||
| XMS-CASPT2 | 1.91 | 0.20 |
| MC-PDFT | 1.97 | 0.18 |
| XMS-PDFT | 1.97 | 0.23 |
| FMS-PDFT | 1.97 | 0.18 |
| 95° | ||
| XMS-CASPT2 | 1.92 | 0.33 |
| MC-PDFT | 1.98 | 0.30 |
| XMS-PDFT | 1.98 | 0.28 |
| 100° | ||
| XMS-CASPT2 | 1.95 | 0.73 |
| MC-PDFT | 2.00 | 0.68 |
| XMS-PDFT | 2.02 | 0.65 |
Although MC-PDFT does not diagonalize an effective Hamiltonian matrix in the last step, we note that MC-PDFT still gives correct topographies of PESs for the tested four paths of methylamine. Generally speaking, though, MC-PDFT cannot be trusted for regions near conical intersections.
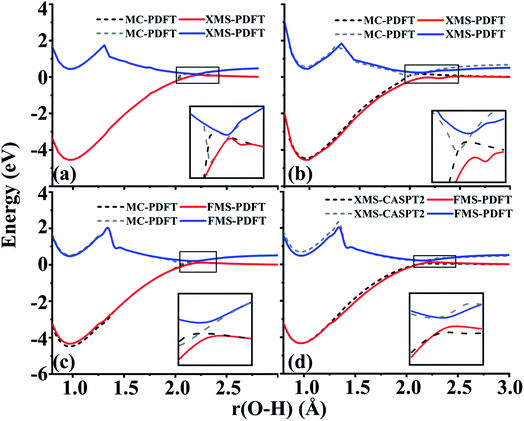
4.5 Phenol (C6H5OH)
The O–H bond dissociation in phenol has been well studied in the past and it can be used as a model system for testing whether a method gives a proper description of potential energy curves for photodissociation. We tested MC-PDFT, XMS-PDFT, FMS-PDFT, and FMS-PDFT/DMRG for the O–H dissociation in phenol with an H–O–C–C dihedral angle of 1° (nearly planar) or 10°.Fig. 5 shows that the MC-PDFT potential energy curves are qualitatively wrong at both angles, with a double crossing when the dihedral angle is 1° and a lack of avoidance at 10°. The XMS-PDFT method successfully produces avoided crossings near 2.2 Å for both torsion angles with minimum energy separations of 0.04 and 0.28 eV for 1° and 10°, respectively. The corresponding O–H distances are 2.21 and 2.15 Å.
In regions that are far away from the avoided crossings for each dihedral angle, the XMS-PDFT curves agree very well with the MC-PDFT ones. However, we noticed that for this molecule XMS-PDFT presents a noticeable “bump” after the avoided crossing. This is apparently because the geometry dependence of the off-diagonal elements of the effective Hamiltonian matrix is not consistent enough with the geometry dependence of the diagonal elements. However, the bumps are no greater than 0.07 eV, corresponding to 1.6 kcal mol−1, which is usually accurate enough for treating electronically excited states.
The FMS-PDFT method is tested for O–H dissociation with the H–O–C–C dihedral angle at 10°. Fig. 5(c) shows that FMS-PDFT also succeeds in removing the unphysical double crossing of MC-PDFT. Similar to the issue discussed in regard to the LiH test, the bump near 1.3 Å for both states again results from an interaction between the highest included state and the lowest unincluded state. This analysis is confirmed by Fig. 6, which shows that including the third state in the model space replaces the bump with an avoided crossing. However, a new bump now occurs near 1.5 Å due to the interaction between the third and the uninvolved fourth states. The bump could be removed by involving more states in the SA-CASSCF calculation, but a bump due to the interaction between the highest involved state in the SA-CASSCF calculation and higher states not included in the SA calculation is inevitable (although occasionally one is lucky enough that this only occurs at such a high energy as to be insignificant for practical purposes). This is another case that shows it is sufficient in FMS-PDFT to consider only (N − 1) rotations between adjacent states in an N-state calculation.
Because DMRG can be used to extend CASSCF to large systems with large active spaces, we also implemented and tested FMS-PDFT based on DMRG. This test involves two-state treatment of the phenol molecule with the H–O–C–C dihedral angle at 10°. To verify the accuracy of the DMRG implementation, the active space used in FMS-PDFT/DMRG is the same as that used in FMS-PDFT. Table 5 provides the differences between FMS-PDFT/DMRG and FMS-PDFT for the rotation angles of two reference states and for the energies of the two states for a range of O–H distances. The rotation angles for generating the intermediate basis are different by no more than 0.001°, while the energies for the two states agree within 0.04 meV. The motivation for using DMRG is to study much larger active spaces with MC-PDFT (with state-specific MC-PDFT/DMRG we previously studied 30 active electrons in 30 active orbitals26 and 34 active electrons in 35 active orbitals27), but the comparison presented here is to show that DMRG agrees well with a conventional solver when the conventional solver is affordable. The good agreement shows that the FMS-PDFT/DMRG method is a promising method for studying the PESs and dynamics of large systems.
| R O–H (Å) | Δθ (deg) | ΔE1 (meV) | ΔE2 (meV) |
|---|---|---|---|
| 0.8 | −0.0004 | 0.007 | 0.026 |
| 1.0 | 0.0005 | −0.002 | −0.012 |
| 1.2 | 0.0001 | 0.008 | 0.007 |
| 1.4 | −0.0003 | −0.040 | −0.021 |
| 1.6 | 0.0001 | 0.016 | −0.007 |
| 1.8 | 0.0004 | 0.008 | −0.005 |
| 2.0 | 0.0000 | 0.017 | −0.005 |
| 2.2 | −0.0004 | 0.022 | 0.031 |
| 2.4 | 0.0000 | −0.007 | 0.013 |
| 2.6 | 0.0007 | −0.004 | 0.005 |
| 2.8 | 0.0000 | 0.004 | −0.006 |
| 3.0 | 0.0001 | −0.014 | 0.003 |
| 3.2 | 0.0000 | −0.006 | 0.010 |
4.6 Oxygen atom plus oxygen molecule collision in triplet state (O + O2)
Two example cuts of the six lowest energy triplet A′ potential energy curves of the O3 system were calculated. Since the three atoms are always in a plane, Cs point group symmetry can be applied for this system. For the separated O2 + O case, the ground energy level corresponds to the combination of an O2(3Σg−) molecule and an O(3P) atom. If only spatial degeneracy is considered, this ground energy level has three-fold degeneracy and two of the degenerate states belong to the A′ irrep. The first excited energy level for the separated atom and diatom corresponds to O2(1Δg) plus O(3P); this energy level has six-fold spatial degeneracy, and three of these six states belong to the A′ irrep. Finally, the second excited energy level of the separated system corresponds to O2(1Σg+) plus an O(3P) atom; this level has threefold spatial degeneracy, and one of these three states belongs to the A′ irrep. Altogether, this makes six 3A′ states that are considered here (the six 3A′′ states and the singlet and quintet states are not considered here).The first example considered corresponds to an O2 + O collision with the atom, labeled O3, impinging on the O1 end of the O1O2 diatom. The r(O1O2) distance is 1.208 Å, and the bond angle of the three O atoms is close to linear, α(O2O1O3) = 175°. These two geometric parameters were fixed, and the r(O1O3) distance was scanned from 1.0 to 2.5 Å. Fig. 7 shows that there are several avoided crossings as O3 approaches and that the potential curves obtained by XMS-PDFT calculations agree well with those obtained by XMS-CASPT2.
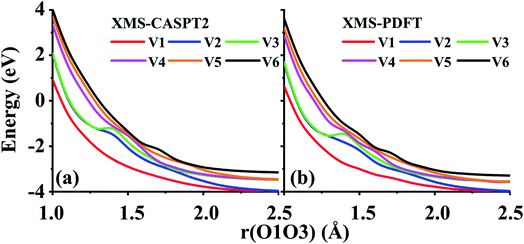 | ||
| Fig. 7 Six potential energy curves of triplet O + O2 collisions calculated by (a) XMS-CASPT2 and (b) XMS-PDFT. | ||
Examination of the configuration interaction coefficients shows that at large r(O1O3), states with configurations corresponding to curves V2 (blue) and V4 (purple) leave the six-state model space when r(O1O3) is decreased to ∼2.5 Å, and two new states arrive. For r(O1O3) < 1.4 Å, these two new states correspond to curves V2 (blue) and V3 (green). It is very encouraging that XMS-PDFT agrees well with XMS-CASPT2 even for this rugged landscape with multiple avoided crossings.
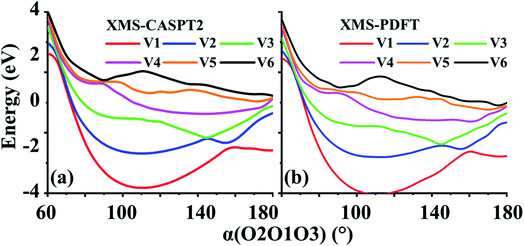
4.7 Triplet ozone (O3)
In the second example, r(O1O2) is again 1.208 Å, and r(O1O3) is fixed at 1.4 Å. The scanning parameter is the bond angle, α(O2O1O3), varying from 60 to 180°; see Fig. 8. This example, like the previous one, also contains several avoided crossings. However, due to the shapes of the curves, it is easier to follow the changes. The avoided crossings clearly show how the ground electronic state (corresponding to curve V1) at 180° correlates to a higher energy state as the bond angle decreases. The avoided crossing of curves V1 and V2 is at ∼160°, that of V2 and V3 is at ∼145°, that of curves V3 and V4 is at ∼115°, that of curves V4 and V5 is at ∼90°, and that of curves V5 and V6 is at ∼85°.Again, the characteristics of the XMS-PDFT calculations are in strikingly good agreement with those of XMS-CASPT2. There are, however, some minor differences, chief among which is that close to 180°, the XMS-PDFT curves are slightly more rugged than the XMS-CASPT2 curves.
4.8 Spiro cation
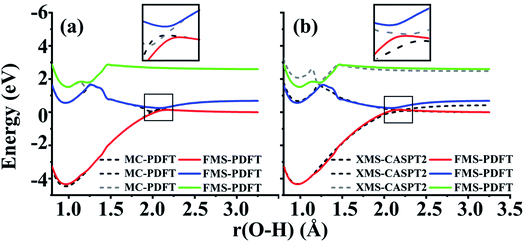
In this section, we test the 2,2′,6,6′-tetrahydro-4H,4′H-5,5′-spirobi[cyclopenta[c]pyrrole] molecule, which is simply called the spiro cation in this paper. The structure of the spiro cation is shown in Fig. 1 in ref. 17. The spiro cation can be viewed as a mixed-valence compound19 that is composed of two organic subsystems (one on the left, one on the right) with a hole due to the removal of an electron to make the cation. The hole is partly localized on either the left or the right subsystem, which results in their geometries being slightly different from one another. We denote the geometry when the hole is mainly on the left as geometry A, and that where the hole is mainly on the right as geometry B. Then, as in ref. 17, we define a reaction path from geometry A to geometry B by using the linear synchronous transit method64 as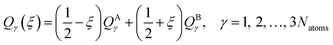 | (24) |
For this very difficult test case, the XMS-PDFT curves resemble the MC-PDFT curves, and the XMS-CASPT2 curves resemble the MS-CASPT2 curves, which is the expected result when the intermediate basis is the same as the CASSCF basis (zero rotation angle). The XMS-CASPT2, MC-PDFT, and FMS-PDFT potential energy curves along the path of eqn (24) are plotted in Fig. 9. It can be seen that XMS-CASPT2 and FMS-PDFT both give good results with local minima for the ground state when ξ = ±0.35 and a local maximum and avoided crossing in the ground state when ξ = 0. However, MC-PDFT and XMS-PDFT do not show local minima for the ground state near ξ = ±0.35 or ±0.5, and they show an unphysical dip when ξ = 0. The great improvement of FMS-PDFT compared with MC-PDFT again shows the value of FMS-PDFT.
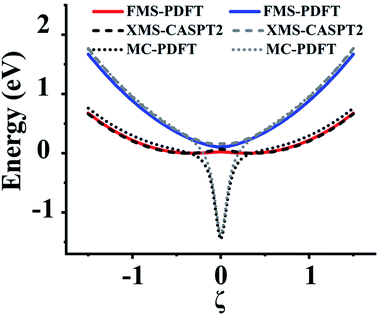 | ||
| Fig. 9 Potential energy curves of the two lowest states of the spiro cation calculated by FMS-PDFT, XMS-CASPT2, and MC-PDFT. | ||
Section S3 in the ESI† shows some other mixed-valence cases where XMS-PDFT fails to give the correct topography of PESs.
5. Conclusions
A general scheme for multi-state MC-PDFT is proposed in this paper. In this scheme, the CASSCF reference states are rotated to a set of intermediate states via a unitary transformation, and an effective Hamiltonian matrix in the intermediate-state basis is constructed using the MC-PDFT method for the diagonal elements and wave function theory for the off-diagonal ones. Two practical methods, XMS-PDFT and VMS-PDFT, for the unitary transformations are proposed in this paper, and they are tested on eight systems exhibiting avoided crossings of two to six states. The XMS-PDFT method uses the transformation proposed by Granovsky for XMC-QDPT; VMS-PDFT chooses the transformation that maximizes the trace of the effective Hamiltonian. We implemented the VMS-PDFT method using a convenient Fourier series expansion, and the resulting method is called FMS-PDFT. Tests are performed on systems with avoided crossings to compare the two new multi-state methods, XMS-PDFT and VMS-PDFT (mainly in the FMS-PDFT version), to state-specific MC-PDFT and the more expensive multi-state method, XMS-CASPT2. We find that FMS-PDFT, like our earlier but less convenient SI-PDFT, gives reasonable potential energy curves for all test cases examined, and it shows great improvement over MC-PDFT. Similarly, XMS-PDFT gives good results for all systems except the mixed-valence spiro cation. Since XMS-PDFT is less expensive than VMS-PDFT and since it usually gives good results, we expect that both VMS-PDFT and XMS-PDFT will be useful for future work. We also implemented the FMS-PDFT method based on DMRG wave functions as a proposed strategy for calculations with large active spaces. The two new multi-state methods proposed here are preferred to the previous SI-PDFT because they treat the ground state and excited states on an equal footing and they require only a single SA-CASSCF calculation and a single set of orbitals.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation under grant CHE-1746186. The work of Zoltan Varga was supported by the Air Force Office of Scientific Research by grant FA9550-19-1-0219.References
- W. Kohn, A. D. Becke and R. G. Parr, Density functional theory of electronic structure, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- H. S. Yu, S. L. Li and D. G. Truhlar, Perspective: Kohn–Sham density functional theory descending a staircase, J. Chem. Phys., 2016, 145, 130901 CrossRef.
- W. Domcke, H. Köppel and L. S. Cederbaum, Spectroscopic effects of conical intersections of molecular potential energy surfaces, Mol. Phys., 1981, 43, 851–875 CrossRef CAS.
- A. W. Jasper, B. K. Kendrick, C. A. Mead and D. G. Truhlar, Non-Born–Oppenheimer Chemistry: Potential Surfaces, Couplings, and Dynamics, in Modern Trends in Chemical Reaction Dynamics: Experiment and Theory (Part 1), ed. X. Yang and K. Liu, World Scientific, Singapore, 2004, pp. 329–391 Search PubMed.
- R. Maurice, P. Verma, J. M. Zadrozny, S. Luo, J. Borycz, J. R. Long, D. G. Truhlar and L. Gagliardi, Single-ion magnetic anisotropy and isotropic magnetic couplings in the metal–organic framework Fe2(dobdc), Inorg. Chem., 2013, 52, 9379–9389 CrossRef CAS.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, A theoretical analysis of chemical bonding, vibronic coupling, and magnetic anisotropy in linear iron(II) complexes with single-molecule magnet behavior, Chem. Sci., 2013, 4, 139–156 RSC.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, Multiconfiguration pair-density functional theory, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Multiconfiguration pair-density functional theory: a new way to treat strongly correlated systems, Acc. Chem. Res., 2017, 50, 66–73 CrossRef CAS.
- S. Ghosh, P. Verma, C. J. Cramer, L. Gagliardi and D. G. Truhlar, Combining wave function methods with density functional theory for excited states, Chem. Rev., 2018, 118, 7249–7292 CrossRef CAS.
- K. Hirao, Multireference Møller–Plesset method, Chem. Phys. Lett., 1992, 190, 374–380 CrossRef CAS.
- H. Nakano, Quasidegenerate perturbation theory with multiconfigurational self-consistent-field reference functions, J. Chem. Phys., 1993, 99, 7983–7992 CrossRef CAS.
- A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: the new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134, 214113 CrossRef.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Second-order perturbation theory with a CASSCF reference function, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, Communication: extended multi-state complete active space second-order perturbation theory: energy and nuclear gradients, J. Chem. Phys., 2011, 135, 081106 CrossRef.
- A. M. Sand, C. E. Hoyer, D. G. Truhlar and L. Gagliardi, State-interaction pair-density functional theory, J. Chem. Phys., 2018, 149, 024106 CrossRef.
- S. S. Dong, K. B. Huang, L. Gagliardi and D. G. Truhlar, State-interaction pair-density functional theory can accurately describe a spiro mixed valence compound, J. Phys. Chem. A, 2019, 123, 2100–2106 CrossRef CAS.
- C. Zhou, L. Gagliardi and D. G. Truhlar, State-interaction pair density functional theory for locally avoided crossings of potential energy surfaces in methylamine, Phys. Chem. Chem. Phys., 2019, 21, 13486–13493 RSC.
- M. B. Robin and P. Day, Mixed Valence Chemistry: A Survey and Classification, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1968, vol. 10, pp. 247–422 Search PubMed.
- S. R. White, Density matrix formulation for quantum renormalization groups, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef.
- S. R. White, Density-matrix algorithms for quantum renormalization groups, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345–10356 CrossRef CAS.
- K. H. Marti and M. Reiher, The density matrix renormalization group algorithm in quantum chemistry, Z. Phys. Chem., 2010, 224, 583–599 CrossRef CAS.
- Y. Kurashige and T. Yanai, Second-order perturbation theory with a density matrix renormalization group self-consistent field reference function: theory and application to the study of chromium dimer, J. Chem. Phys., 2011, 135, 094104 CrossRef.
- R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, The ab-initio density matrix renormalization group in practice, J. Chem. Phys., 2015, 142, 034102 CrossRef.
- S. Knecht, E. D. Hedegård, S. Keller, A. Kovyrshin, Y. Ma, A. Muolo, C. J. Stein and M. Reiher, New approaches for ab initio calculations of molecules with strong electron correlation, Chimia, 2016, 70, 244–251 CrossRef CAS.
- P. Sharma, V. Bernales, S. Knecht, D. G. Truhlar and L. Gagliardi, Density matrix renormalization group pair-density functional theory (DMRG-PDFT): singlet–triplet gaps in polyacenes and polyacetylenes, Chem. Sci., 2019, 10, 1716–1723 RSC.
- C. Zhou, L. Gagliardi and D. G. Truhlar, Multiconfiguration pair-density functional theory for iron porphyrin with CAS, RAS, and DMRG active spaces, J. Phys. Chem. A, 2019, 123, 3389–3394 CrossRef CAS.
- S. Wouters, W. Poelmans, P. W. Ayers and D. Van Neck, CheMPS2: A free open-source spin-adapted implementation of the density matrix renormalization group for ab initio quantum chemistry, Comput. Phys. Commun., 2014, 185, 1501–1514 CrossRef CAS.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From source code to insight, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef.
- S. Keller, M. Dolfi, M. Troyer and M. Reiher, An efficient matrix product operator representation of the quantum chemical Hamiltonian, J. Chem. Phys., 2015, 143, 244118 CrossRef.
- S. Keller and M. Reiher, Spin-adapted matrix product states and operators, J. Chem. Phys., 2016, 144, 134101 CrossRef.
- Y. Ma, S. Knecht, S. Keller and M. Reiher, Second-order self-consistent-field density-matrix renormalization group, J. Chem. Theory Comput., 2017, 13, 2533–2549 CrossRef CAS.
- G. Ghigo, B. O. Roos and P.-Å. Malmqvist, A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2), Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, Perspectives on basis sets beautiful: seasonal plantings of diffuse basis functions, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS.
- D. Feller, The role of databases in support of computational chemistry calculations, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis set exchange: a community database for computational sciences, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- L. R. Kahn, P. J. Hay and I. Shavitt, Theoretical study of curve crossing: ab initio calculations on the four lowest 1Σ+ states of LiF, J. Chem. Phys., 1974, 61, 3530–3546 CrossRef CAS.
- B. J. Botter, J. A. Kooter and J. J. C. Mulder, Ab-initio calculations of the covalent–ionic curve crossing in LiF, Chem. Phys. Lett., 1975, 33, 532–534 CrossRef CAS.
- H. J. Werner and W. Meyer, MCSCF study of the avoided curve crossing of the two lowest 1Σ+ states of LiF, J. Chem. Phys., 1981, 74, 5802–5807 CrossRef CAS.
- J. P. Finley and H. A. Witek, Diagrammatic complete active space perturbation theory: calculations on benzene, N2, and LiF, J. Chem. Phys., 2000, 112, 3958–3963 CrossRef CAS.
- J. Meller, J.-P. Malrieu and J.-L. Heully, Size-consistent multireference configuration interaction method through the dressing of the norm of determinants, Mol. Phys., 2003, 101, 2029–2041 CrossRef CAS.
- Ö. Legeza, J. Röder and B. A. Hess, QC-DMRG study of the ionic–neutral curve crossing of LiF, Mol. Phys., 2003, 101, 2019–2028 CrossRef.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, A simple approximate perturbation approach to quasi-degenerate systems, Theor. Chem. Acc., 2006, 116, 434–439 Search PubMed.
- M. Hanrath, Multi-reference coupled-cluster study of the ionic–neutral curve crossing LiF, Mol. Phys., 2008, 106, 1949–1957 CrossRef CAS.
- F. Sasaki and M. Yoshimine, Configuration-interaction study of atoms. II. Electron affinities of B, C, N, O, and F, Phys. Rev. A: At., Mol., Opt. Phys., 1974, 9, 26–34 CrossRef.
- D. G. Truhlar and C. A. Mead, Relative likelihood of encountering conical intersections and avoided intersections on the potential energy surfaces of polyatomic molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 32501 CrossRef.
- H. Nakamura and D. G. Truhlar, Extension of the fourfold way for calculation of global diabatic potential energy surfaces of complex, multiarrangement, non-Born–Oppenheimer systems: application to HNCO(S0,S1), J. Chem. Phys., 2003, 118, 6816–6829 CrossRef CAS.
- J. V. Michael and W. A. Noyes, The photochemistry of methylamine, J. Am. Chem. Soc., 1963, 85, 1228–1233 CrossRef CAS.
- E. Kassab, J. Gleghorn and E. Evleth, Theoretical aspects of the photochemistry of methanol, methylamine, and related materials, J. Am. Chem. Soc., 1983, 105, 1746–1753 CrossRef CAS.
- G. Waschewsky, D. Kitchen, P. Browning and L. Butler, Competing bond fission and molecular elimination channels in the photodissociation of CH3NH2 at 222 nm, J. Phys. Chem., 1995, 99, 2635–2645 CrossRef CAS.
- C. L. Reed, M. Kono and M. N. R. Ashfold, Near-UV photolysis of methylamine studied by H-atom photofragment translational spectroscopy, J. Chem. Soc., Faraday Trans., 1996, 92, 4897–4904 RSC.
- K. M. Dunn and K. Morokuma, Ab initio study of the photochemical dissociation of methylamine, J. Phys. Chem., 1996, 100, 123–129 CrossRef CAS.
- S. J. Baek, K.-W. Choi, Y. S. Choi and S. K. Kim, Spectroscopy and dynamics of methylamine. I. Rotational and vibrational structures of CH3NH2 and CH3ND2 in à states, J. Chem. Phys., 2003, 118, 11026–11039 CrossRef CAS.
- M. H. Park, K.-W. Choi, S. Choi, S. K. Kim and Y. S. Choi, Vibrational structures of methylamine isotopomers in the predissociative à states: CH3NHD, CD3NH2, CD3NHD, and CD3ND2, J. Chem. Phys., 2006, 125, 084311 CrossRef.
- D.-S. Ahn, J. Lee, J.-M. Choi, K.-S. Lee, S. J. Baek, K. Lee, K.-K. Baeck and S. K. Kim, State-selective predissociation dynamics of methylamines: The vibronic and H/D effects on the conical intersection dynamics, J. Chem. Phys., 2008, 128, 224305 CrossRef.
- C. Levi, R. Kosloff, Y. Zeiri and I. Bar, Time-dependent quantum wave-packet description of H and D atom tunneling in N–H and N–D photodissociation of methylamine and methylamine-d2, J. Chem. Phys., 2009, 131, 064302 CrossRef.
- R. Marom, C. Levi, T. Weiss, S. Rosenwaks, Y. Zeiri, R. Kosloff and I. Bar, Quantum tunneling of hydrogen atom in dissociation of photoexcited methylamine, J. Phys. Chem. A, 2010, 114, 9623–9627 CrossRef CAS.
- D.-S. Ahn, J. Lee, Y. C. Park, Y. S. Lee and S. K. Kim, Nuclear motion captured by the slow electron velocity imaging technique in the tunnelling predissociation of the S1 methylamine, J. Chem. Phys., 2012, 136, 024306 CrossRef.
- J. O. Thomas, K. E. Lower and C. Murray, Observation of NH X3Σ– as a primary product of methylamine photodissociation: Evidence of roaming-mediated intersystem crossing?, J. Phys. Chem. Lett., 2012, 3, 1341–1345 CrossRef CAS.
- H. Xiao, S. Maeda and K. Morokuma, Theoretical study on the photodissociation of methylamine involving S1, T1, and S0 states, J. Phys. Chem. A, 2013, 117, 5757–5764 CrossRef CAS.
- M. Epshtein, Y. Yifrach, A. Portnov and I. Bar, Control of nonadiabatic passage through a conical intersection by a dynamic resonance, J. Phys. Chem. Lett., 2016, 7, 1717–1724 CrossRef CAS.
- T. A. Halgren and W. N. Lipscomb, The synchronous-transit method for determining reaction pathways and locating molecular transition states, Chem. Phys. Lett., 1977, 49, 225–232 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: It contains geometries, HNCO potential curves, systems where XMS-PDFT fails, and absolute energies in hartrees. See DOI: 10.1039/d0fd00037j |
| ‡ These two authors contributed equally to this paper. |
| This journal is © The Royal Society of Chemistry 2020 |