Open Access Article
Open Access ArticleOrganic electrode materials with solid-state battery technology
Juho
Heiska
 ,
Mikko
Nisula
,
Mikko
Nisula
 and
Maarit
Karppinen
and
Maarit
Karppinen
 *
*
Department of Chemistry and Materials Science, Aalto University, 00076 Aalto, Finland. E-mail: maarit.karppinen@aalto.fi
First published on 25th July 2019
Abstract
The quest for next-generation sustainable (resource-wise, safe and eco-friendly), high performance (light-weight and energy/power dense) and cost-efficient rechargeable energy storage devices has been catalyzing the research on new battery chemistries. In this research rush, organic electrode materials have ticked many of the wish-list boxes, but there are also a few obstacles to overcome, the two major ones being their intrinsically poor electronic conductivity and instantaneous dissolution into liquid electrolytes. In this critical review, we first provide the readers with a brief account of the various organic material families considered for electrode materials, with their particular benefits and problems. Then, using some basic concepts borrowed from the field of organic electronics we aim to gain a deeper insight into the conductivity of organics in electrochemical systems – an issue little discussed so far. To address the solubility issue we discuss – with some illustrative examples – the benefits and challenges possibly emerging by combining the organic electrodes with a solid electrolyte instead of the conventional liquid electrolyte. As one of the highlights we discuss thin-film microbatteries fabricated using the atomic/molecular layer deposition (ALD/MLD) technique, where ultrathin layers of the LiPON electrolyte are combined with lithium quinone and terephthalate electrodes. Such a thin-film configuration is intriguing in the sense that it does not contain any additives, thus serving as an ideal model system for fundamental studies.
1 Introduction
Secondary batteries are already everyday commodities in a diverse range of applications. Portable electronics, in particular, rely on secondary batteries but there is a strong aspiration to integrate these batteries to stationary applications as well.1 In this rush in developing new battery technologies for the expanding market, one single new battery chemistry may not turn out to be the winner in terms of all the demands such as the high energy density, cyclability, sustainability, safety, and low cost.2–4 Therefore, numerous different technologies and strategies have been actively promoted to move beyond the current state-of-the-art Li-ion batteries (LIBs); these include but are not limited to alternative electrode materials, alternative metal chemistries (Na, Mg, etc.), as well as Li–air, Li–S, Li–organic, redox-flow and solid-electrolyte batteries, the main aims being to improve the energy density, answer to the sustainability issues, and decrease the cost per kW h−1. All of these technologies still have room for major breakthroughs, and in some cases, even the fundamental understanding is yet limited.Batteries based on organic electrode materials have been considered as one of the most sustainable alternatives as they are composed of abundant and light-weight elements, which also puts their price tag lower than in the case of inorganic materials.5 Processing of inorganic materials is a very energy-intensive process, and for example cobalt – one of the constituent elements in current electrodes – is classified as a critical raw material. Organic materials, on the other hand, could be thermally recycled, since the precursors can be newly derived from the biomass.2 The actual electrochemical performance of the organics is not inferior either. Their gravimetric capacity is high thanks to the light elements, and they can be charged and discharged at a very high rate. The organics are also non-ion-specific, which means that the progress made with the Li+-ion battery chemistry would benefit the Na+-ion battery chemistry, and vice versa; even Mg2+ works in a similar fashion with the organics.6,7
For the last decade there has been a steady increase in publications related to organic electrodes in battery applications, see Fig. 1. The scope of different organic molecules is enormous, being evident from the numerous comprehensive reviews summarizing the different organic compounds and their electrochemical performances.4,8–21 The different approaches to improve electrochemical performance, such as introducing heteroatoms, functional groups, or polymerization effects, have been discussed in detail as well. While organics offer clear advantages, they at the same time suffer from issues such as low electronic conductivity and low redox stability.12,16 Most critically, the high solubility of the organic electrode materials in conventional liquid electrolytes and the capacity decay caused by it form a major challenge that needs to be addressed to pave the way for the future commercialization.
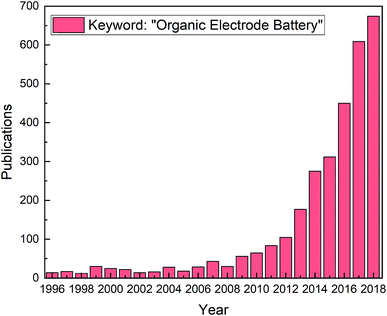 | ||
| Fig. 1 Publications from 1996 to 2018 with the keyword “organic electrode battery”; data acquired from Web of Science. | ||
The recent progress in the solid-state electrolyte technology has provided possible answers to the safety and stability problems present in conventional liquid electrolyte systems. The hype around the most promising solid electrolyte systems has been extensive creating positive expectations towards better cycle life and enhanced volumetric and gravimetric energy densities realized by minimizing the dead weight (e.g. separators) in the battery packing; an additional advantage would be the ease of miniaturization.22–24 However, in spite of the massive progress in developing new solid electrolyte materials with ionic conductivity values even exceeding those of traditional liquid electrolytes,25 these materials still suffer from low redox stability towards oxidation or reduction depending on the material.
Applying solid electrolytes to organic electrodes is not a truly new concept;26 however, it has not been extensively elaborated yet. The topic thus warrants increasing attention, in particular owing to the rapidly growing variety of new solid electrolyte materials. The most obvious benefit of combining the organic electrode materials with a solid electrolyte is the possibility to fully circumvent the solubility issue of the organics in conventional liquid electrolytes. However, an equally important benefit of this combination is that many promising solid electrolyte materials that suffer from stability issues when combined with the state-of-the-art inorganic electrode materials could be readily used with organic electrodes due to their narrower operational voltage window and beneficial mechanical properties.
In this focused review, one of the main goals is to discuss the mutual advantages provided and the challenges met by using the organic electrode materials in the combination with solid electrolytes. We start by providing a brief general introduction to the already extensive family of organic electrode materials using selected representative organic materials and material groups as examples to identify the main challenges and possibilities in the field. The major problem of the organic electrodes, that is, their poor electronic conductivity, is often bypassed in literature just by acknowledging the inconvenience. Conversely, in the related field of organic semiconductors, the topic has been much more extensively studied. Here we aim to bring some of the knowledge and basic principles from organic semiconductors to the field of the organic batteries. Finally, we will propose the emerging atomic/molecular layer deposition (ALD/MLD) thin-film technique not only as a vital future fabrication technology for such all-solid-state microbatteries but also as a useful platform for investigating the underlining interface interactions.
2 Redox reaction types of organics
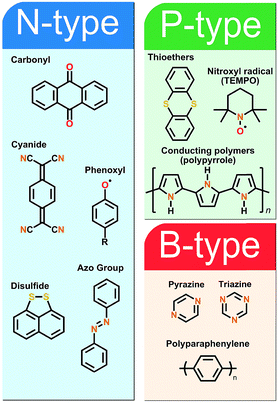
The fundamental requirement for an active secondary battery electrode material is its capability to undergo reversible redox reactions. The present state-of-the-art inorganic positive electrode materials such as Lix(Co,Ni,Mn)O2 rely on the valence state changes of the transition metal constituent upon the Li-ion intercalation, e.g. between Co3+ and Co4+ in Lix(Co,Ni,Mn)O2,27 while the electrochemical activity of the negative electrode graphite arises from its π-bonds being able to accept electrons.28 In the case of the organic electrode materials, the electrochemical activity derives from the charge state of their electroactive bonds, functional groups or moieties typically connected to a conjugated backbone structure to promote the electron transport and charge stabilization.8Organic electrode materials are commonly grouped based on the role they perform in the redox reaction: P-type materials contribute to the redox reaction by donating electrons, N-type materials by accepting electrons, while B-type materials may be either oxidized (P-type reaction) or reduced (N-type reaction) depending on the applied voltage. Among the classical redox active organics, nitrogen radicals, amines and thioethers are usually of the P-type, carbonyls, quinoxalines, phenazines, cyanides, azo compounds, and disulfides of the N-type, and hydrocarbons and conjugated nitrogen systems can be classified as B-type materials. Representative example molecules of each type are presented in Fig. 2.
An N-type organic molecule undergoes an insertion-type redox reaction:
| Organic(N) + xLi+ + xe− ⇌ Li+–organic(N)−. |
Upon reduction, an anion is formed when the molecule accepts an electron to its lowest unoccupied molecular orbital (LUMO). This extra negative charge is then typically stored in the conjugated backbone of the organic moiety and balanced by the cation, e.g. Li+. Usually, this reaction occurs during the discharge when the N-type material is applied as a positive electrode in an electrochemical cell. Some of the N-type organics have relatively low redox potentials and can be therefore also applied as a negative electrode.29,30 The charge-balancing ion with the N-type organics is not limited to lithium. This is a significantly different behavior compared to the often ion-size-sensitive inorganic electrode materials and is a highly beneficial feature for the organic electrode materials. For the N-type organics, relevant examples are known where the cation is a proton,31 Na+,15 K+,32 and Mg2+.7 However, the kinetics of the heavier metal ions are slower than for the light Li-ion.
The P-type organics usually possess higher redox potentials compared to the N-type materials, as expected since the electrons of P-type compounds are removed from the HOMO (highest occupied molecular orbital) or SOMO (single occupied molecular orbital). The charge balancing species in the P-type organics is the negative counter ion from the electrolyte rather than the positive metal ion as is the case with the N-type materials. Hence, for the P-type organic electrode materials, the metal ion is not playing the key role; this is why these batteries are often called dual-ion batteries.33 During charging the P-type material is oxidized at the positive electrode yielding cations. The nonaqueous electrolyte (e.g. Li+PF6−) salt plays an important role as it provides both the negative counter-ions (PF6−) for the positive electrode and the positive Li-ions for the negative electrode (Li metal). Opposite reactions occur during the discharge and the electrolyte regenerates.
Charging (electrolyte provides Li+ and PF6−):
Positive electrode:
| Organic(P) + PF6− → organic(P)+PF6− + e− |
Negative electrode:
| Li+ + e− → Li |
The B-type materials function according to the principles described above such that the N-type mechanism works at the lower potentials and the P-type mechanism at the higher potentials. Here it is important to distinguish the truly B-type materials with separate N- and P-type reactions from the few N-type organics which can undergo reversible redox reactions at different organic moieties within the same molecule. A prototype example of the truly B-type organic material is polyparaphenylene (PPP). A battery based on PPP at both electrodes undergoes N-type reactions at the negative electrode (∼0.2 V) where Li+ is stored to the benzene backbone with delocalized negative charge and P-type reactions at the positive electrode (∼4.1 V) where PPP is oxidized and negative anion from the electrolyte functions as a charge balancing species (Fig. 3). Accordingly, it could be utilized as an all-organic battery of an average redox voltage of 3 V.34 On the other hand, tetralithium salt of 2,5-dihydroxy terephthalate is an example of organics undergoing two different N-type reactions: one on carboxyl at ∼0.8 V and another on quinone at ∼2.6 V, resulting in a symmetrical cell with an operation potential of 1.8 V (Fig. 3).35
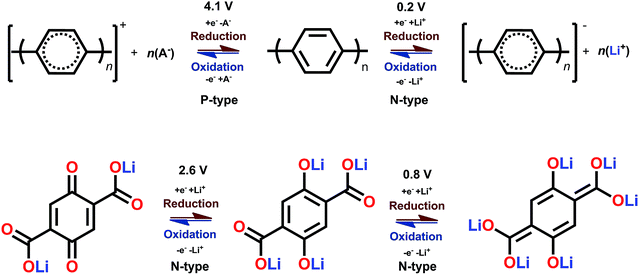 | ||
| Fig. 3 Examples of a truly B-type bipolar battery (polyparaphenylene) and an N-type ambipolar battery (tetralithium salt of 2,5-dihydroxy terephthalate).34,35 | ||
3 Electroactive organic moieties
The variety of plausible organic electrode materials with a wide range of organic backbones and functional groups is immense. Here our goal is – rather than summarize the extensive literature4,8–21 – to discuss the basic electrochemical behaviors of different functional groups with illustrative examples. In particular, the most evident challenges of each material class are underlined, since the problems faced are usually similar within the same electroactive group. The electrochemical performances of these materials are most commonly evaluated on the basis of cyclic voltammetry and galvanostatic cycling tests; for the basics of these characterization methods in the context of organic battery, see e.g.ref. 20.3.1 Carbonyl group
Organics based on the carbonyl group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) have been widely studied as promising electrode materials for actual energy storage applications because of their many desirable characteristics, such as high theoretical capacity and fast reaction kinetics.16 The number of feasible carbonyl compounds is enormous, as previously well documented in an extensive review.8 Carbonyl compounds are in general N-type materials since upon reduction electron is added to the C
O) have been widely studied as promising electrode materials for actual energy storage applications because of their many desirable characteristics, such as high theoretical capacity and fast reaction kinetics.16 The number of feasible carbonyl compounds is enormous, as previously well documented in an extensive review.8 Carbonyl compounds are in general N-type materials since upon reduction electron is added to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group LUMO resulting in a negative anion (Fig. 4) which is then balanced by a cation provided by the electrolyte.
O group LUMO resulting in a negative anion (Fig. 4) which is then balanced by a cation provided by the electrolyte.
 | ||
| Fig. 4 Redox scheme of the carbonyl group: R is a stabilizing species, often connected to a larger conjugated system.8 | ||
Carbonyls cover a wide potential area where the redox reactions can take place, ranging even from 0.5 to 3.0 V. The major criterion determining the redox potential is whether the organic moiety gains (high potential) or loses (lower potential) aromaticity. Hence, carbonyl compounds that lose aromaticity upon lithiation are excellent anode candidates, while those gaining conjugation or additional aromaticity could be considered as cathode materials. Moreover, the size of the aromatic core affects the reduction voltage; the more aromatic the molecule is after the lithiation the higher is the discharge potential, when the aromaticity is determined by calculating the amount of Clar sextets.36 However, it should be noted that the position of the carbonyl may also have a drastic effect on the resultant voltage. The roles of aromaticity and carbonyl-group position in determining the reduction voltage have been discussed in detail in ref. 37 and 38.
Prime examples of different types of carbonyl compounds are dilithium terephthalate29 and anthraquinone.39 Both of them undergo reversible redox reactions on their carbonyl groups but in drastically different potential areas. The low potential of dilithium terephthalate arises from loss of its aromaticity, though still retaining the conjugation, and the electron donating nature of the – OLi unit directly connected to the carboxylate carbon. The electron donating effect is explained later on. Conversely, the anthraquinone gains an additional benzene ring, as demonstrated in Fig. 5.
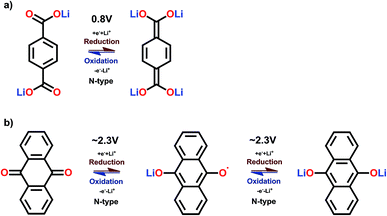 | ||
| Fig. 5 Redox schemes of (a) dilithium terephthalate, and (b) anthraquinone.29,39 | ||
Many of the carbonyl compounds exhibit a relatively flat charge/discharge plateau, even though in reality many of them undergo an intermediate process involving a radical formation, see the case of anthraquinone in Fig. 5. This intermediate state is observable in cyclic voltammetry if anthraquinone is dissolved in a liquid.40 The actual redox reaction is very fast in carbonyls, and some of them have been reported to work at temperatures as low as −70 °C.41 The energy density of carbonyl compounds typically depend on the number of stabilizing groups in the molecular structure such that for the small carbonyls the theoretical gravimetric capacity is appreciably high, e.g. 496 mA h g−1 for p-benzoquinone; here the tradeoff is the stability though. For the larger polymer structures with multiple aromatic rings, the gravimetric capacity may drop far below 100 mA h g−1, but the larger aromatic backbone often results in better cycling stability. Moreover, if the aromatic core is not adequate compared to the number of carbonyl groups, part of the carbonyls will simply remain inactive.42
The redox voltage can be tailored through so-called substitution or functionalization processes, where for example a carbon atom is substituted by e.g. nitrogen with more electrons, or a hydrogen atom is replaced with a functional group that shows either electron donating or electron withdrawing character. These modifications tend to directly alter the HOMO and/or LUMO energies and thereby the redox voltage, as these orbitals are involved in the relevant redox reactions. They can also cause charge reorganizations or structural modifications in addition to the creation of the empty or filled states, often observed as changes in the shape of the charge discharge curve.13,43,44
The solubility of the high energy density quinones in the common liquid electrolytes is one of the most serious problems they face in practice. To solve this problem many different approaches such as polymerization, salt formation, and anchoring has been investigated, as discussed in previous reviews.8,17,18 Another enormous problem is the low electronic conductivity of these materials in the bulk form. It is important to understand that electrical conductivity within the organic molecule is usually very high and not the limiting factor, but the challenge is the conductivity between the molecules and the composite electrode. Electronic conductivity is essentially controlled by the π-orbital overlap along the conjugated structure.45 Therefore anchoring the organic electrodes along the surface of carbon fibers or nanotubes is a promising technique to improve the electrical conductivity. The general electron conductivity of organics is discussed in more details in Chapter 4.
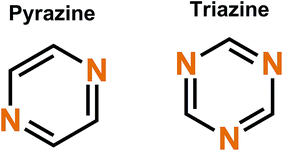
3.2 Conjugated nitrogen
Nitrogen-based aromatic systems such as pyrazines46 and triazines47 (Fig. 6) have started to gain increasing attention in recent years and a review solely focused on them is still lacking. These systems can be either N-, P- or B-type depending on the stabilizing aromatic backbone and the voltage applied.The phenazine molecule consisting of two benzene rings connected to the pyrazine can undergo normal N-type insertion at moderate potentials. During the lithiation, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond is broken and a new N–Li bond is formed, leading to the loss of aromaticity. Both nitrogen atoms are electroactive and the redox reaction is reversible (Fig. 7). The solvent used in the electrolyte solution may have a huge effect on the electrochemical performance and might even act as a steric hindrance for the redox reactions.48 Interestingly, once the phenazine nitrogen atoms are substituted the redox behavior changes to the P-type (Fig. 7).49 In the N,N′-substituted phenazine nitrogen is oxidized during charging to a positive cation forming one double and one single bond to the carbon atoms next to it while retaining the single bond to the N-substituent. The positive charge is stabilized by increased conjugation and the anion provided by the electrolyte. As usual with P-type compounds, this reaction occurs in relatively high potentials (>3 V vs. Li+/Li) and is very fast. However, as with all dual-ion battery concepts, the counter-ion has a huge effect on the electrochemical performance and the number of groups participating in the redox reactions.
N bond is broken and a new N–Li bond is formed, leading to the loss of aromaticity. Both nitrogen atoms are electroactive and the redox reaction is reversible (Fig. 7). The solvent used in the electrolyte solution may have a huge effect on the electrochemical performance and might even act as a steric hindrance for the redox reactions.48 Interestingly, once the phenazine nitrogen atoms are substituted the redox behavior changes to the P-type (Fig. 7).49 In the N,N′-substituted phenazine nitrogen is oxidized during charging to a positive cation forming one double and one single bond to the carbon atoms next to it while retaining the single bond to the N-substituent. The positive charge is stabilized by increased conjugation and the anion provided by the electrolyte. As usual with P-type compounds, this reaction occurs in relatively high potentials (>3 V vs. Li+/Li) and is very fast. However, as with all dual-ion battery concepts, the counter-ion has a huge effect on the electrochemical performance and the number of groups participating in the redox reactions.
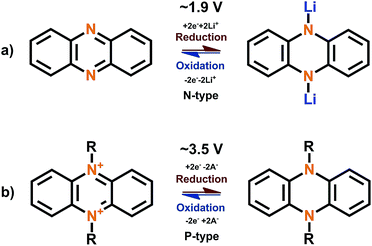 | ||
| Fig. 7 Redox schemes for (a) phenazine of N-type and (b) N,N′-substituted phenazine of P-type.48,50 | ||
Triazine rings are usually polymerized together with different linkers such as benzene, forming huge polymer structures. These triazine polymers work in a similar fashion as phenazine since both N- and P-type redox schemes have been reported,47,51 but they are intrinsical of the B-type and with a very smooth transition between the N- and P-types where the open circuit voltage of the cell lies between the P- to N-type transition point. The N- and P-type mechanisms work by stabilizing the extra negative charge or extra positive charge to the aromatic triazine ring, with a metal ion or negative ion from the electrolyte working as a charge balancing species, respectively (Fig. 8).
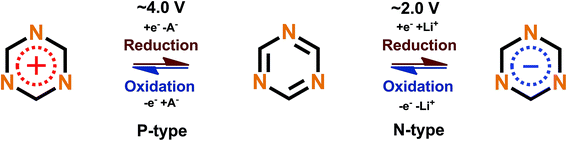 | ||
| Fig. 8 Redox scheme of triazine proposed by Sakaushi et al.51 | ||
To be able to utilize triazine to its maximum theoretical capacity a very broad voltage range has to be used, which is not favorable for an electrode material, since the output voltage of the battery would decrease over time when it is discharged. In addition, the N-type redox reactions in triazine and phenazine occur in a potential range (1–2 V) which is relatively hard to utilize in practice since it is not high enough for cathodes and is too high for anodes. On the other hand, the advantage of this potential range is that the formation of the solid electrolyte interphase (SEI) is largely suppressed.52 The efficient way to utilize these materials is only limited to the P-type reaction since it occurs at a relatively high potential with a high rate capability.
The main challenge with the aromatic nitrogen compounds is their super-high solubility in the liquid electrolytes, being even more prominent than with the carbonyls. Moreover, not only the N-type reaction occurs in a voltage area that is not practical, but also the voltage profile shows undesirable sloping behavior (typical for polymers).52
3.3 Cyanide group
The early reports on the cyanide group based Li-ion battery cathode materials are already from 1984.53 The first molecule reported, i.e. 7,7,8,8-tetracyanoquinodimethane (TCNQ), was also highlighted and extensively studied as an organic metal TTF–TCNQ.54 The TCNQ molecule undergoes an N-type lithium insertion reaction forming TCNQ− and TCNQ2−, stabilized by lithium ions (Fig. 9). The two reaction steps of TCNQ can be clearly seen in a liquid cell. If the cell is brought to lower potentials (<1 V vs. Li+/Li) it is also possible that an irreversible reaction occurs and LiCN is formed.53 The Li+ insertion potential into the cyanide group is among the highest of N-type compounds, which makes this material highly promising.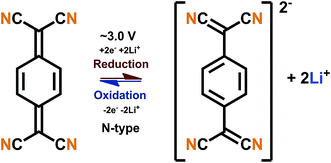 | ||
| Fig. 9 Schematic of the redox mechanism of TCNQ.55 | ||
Another way of utilizing the cyanide is to connect the group directly to the aromatic ring. This approach may, however, be less interesting since the redox reactions occur in the 1–2 V range, and also stability issues have been reported.56 Cycling in a liquid cell reveals the most apparent problem with the cyanide group. The liquid cell shows much lower initial capacity compared to the solid-state cell since the dissolution of the compound in the electrolyte is high.55 Some effort has been made to anchor the molecule, but further efforts are needed to fully solve the dissolution issue.57 Currently, the cyanide-based organics are most feasible when being applied with solid-state electrolytes due to the N-type behavior and high redox voltage. However, reversibility of the electrochemical reaction has to be confirmed.
3.4 Azo group
The discovery of electroactivity of the azo group in the context of a rechargeable battery is relatively recent.58 The underlining redox reaction is of the N-type where the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond breaks, taking up two lithium or sodium ions (Fig. 10); this is the unique feature of the azo group since usually only one cation can be bound by a single functional group.
N double bond breaks, taking up two lithium or sodium ions (Fig. 10); this is the unique feature of the azo group since usually only one cation can be bound by a single functional group.
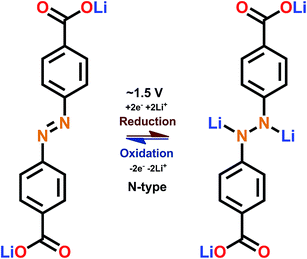 | ||
| Fig. 10 Schematic of the redox reaction with the azo-group.59 | ||
The redox potential of the azo group between two benzene rings is just below 2 V vs. Li+/Li; this intermediate redox potential value means that it is hard to utilize the azo group in actual batteries since the potential is too high for an optimal anode material and too low for an optimal cathode material. In addition, the dissolution problem is also present. The situation can be improved by combining the azo groups with electron donating carboxylate groups which could reduce the dissolution and lower the redox potential to be on par with lithium titanate (1.5 V). Also, nitrogen present in the organic molecule is a true double-edged sword, as nitrogen in general enhances the interaction with lithium ions increasing the rate capability but also it is prone to be irreversibly reduced (e.g. LiCN) and it takes actively part in the solid electrolyte interphase.59
3.5 Schiff bases
Schiff bases are based on a sequence of R1–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–R2, where R1 and R2 are typically selected to be aromatic groups for the electrochemical applications. The synthesis of polymers based on the Schiff motif is an environmentally friendly process since it simply consists of a reaction between aldehydes and amines and produces only water as the byproduct. The N-type two-electron redox reaction with Schiff bases takes place below 1 V vs. Li+/Li, which indicates towards their potential use as a negative electrode material in batteries. In one of the reported systems, the Schiff base was polymerized to repeat the electrochemically active unit of –N
CH–R2, where R1 and R2 are typically selected to be aromatic groups for the electrochemical applications. The synthesis of polymers based on the Schiff motif is an environmentally friendly process since it simply consists of a reaction between aldehydes and amines and produces only water as the byproduct. The N-type two-electron redox reaction with Schiff bases takes place below 1 V vs. Li+/Li, which indicates towards their potential use as a negative electrode material in batteries. In one of the reported systems, the Schiff base was polymerized to repeat the electrochemically active unit of –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Ar–CH
CH–Ar–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–; it should be noted that the inverse unit of –CH
N–; it should be noted that the inverse unit of –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–Ar–N
N–Ar–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– is not electrochemically active since the aniline is coplanar with the chain, even though it is electrochemically conductive and improves the stabilization within the chain.60,61 The specific reaction mechanism in the case of the Schiff bases is not completely clear and would require more extensive studies. So far the research focus has been mainly on incorporating the optimal amount of electroactive groups on to the polymer chain. An interesting fact is that with these materials the C
CH– is not electrochemically active since the aniline is coplanar with the chain, even though it is electrochemically conductive and improves the stabilization within the chain.60,61 The specific reaction mechanism in the case of the Schiff bases is not completely clear and would require more extensive studies. So far the research focus has been mainly on incorporating the optimal amount of electroactive groups on to the polymer chain. An interesting fact is that with these materials the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond seems to stay intact during lithiation, as confirmed with FTIR. A valid explanation for the two-electron mechanism could be: formation of a radical anion in the first redox reaction between the azo and carbo radical (which includes dimerization), then followed by the second redox reaction yielding the anion.61
N bond seems to stay intact during lithiation, as confirmed with FTIR. A valid explanation for the two-electron mechanism could be: formation of a radical anion in the first redox reaction between the azo and carbo radical (which includes dimerization), then followed by the second redox reaction yielding the anion.61
As with all polymers, sloping voltage profiles are seen for the polymeric form of Schiff bases; however, since the electroactive group is well identified it is straightforward to incorporate an optimal amount of these groups to minimize the non-electroactive units.61 Moreover, the rate capability of these compounds is only moderate.
3.6 Disulfide group
The report of the redox behavior of disulfides goes back to 1989.62 The redox mechanism is simple N-type breakage of the R1–S–S–R2 bond to form two R1,2–S− Li+ groups. The S–S bond is electroactive by its own and does not require any stabilizing functional groups. In principle, the disulfides are very attractive since their gravimetric capacities are particularly high. However, the peak separation seen in cyclic voltammetry between the anodic and cathodic peaks is often large, even up to 2 V, which is a clear indication of really poor reaction kinetics. The major problem is the recombination of the S–S bond since it is completely broken upon the lithiation such that the two sulfur atoms are separated. During the first cycle, the reduction peak in cyclic voltammetry is often relatively sharp and well defined. The oxidation peak often shows humps, is wide, and expresses poor kinetics. The peak separation can be decreased by molecularly locking the sulfur atoms in place (Fig. 11).62,63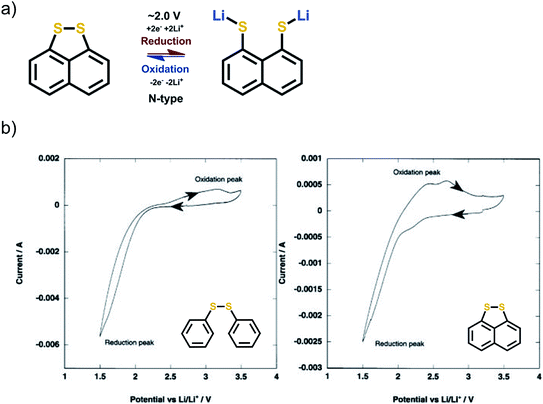 | ||
| Fig. 11 (a) Reaction mechanism of disulfide compounds, and (b) cyclic voltammetry of two structurally related disulfides. The increase in peak separation is evident when the disulfide groups are not bound together by other means. Reproduced with permission from J. Electrochem. Soc. 2003 volume 150, issue 1, A128–A132. Copyright 2003, The Electrochemical Society.63 | ||
Another challenge arises from the fact that the thiolate ion formed during reduction is highly soluble in common liquid electrolytes, which makes these materials hard to be utilized in conventional wet cells. The disulfide systems so far studied have often utilized a pseudo-solid or gel electrolyte to alleviate the dissolution. Due to the aforementioned issues, the interest in disulfides has greatly declined. Furthermore, using sulfur as a dopant in Na-ion carboxylates has remained a highly prospective approach for N-type batteries.64
3.7 Thioethers
Thioethers are P-type materials of the R1–S–R2 formulae where R1 and R2 are conjugated stabilizing units. The redox reaction proceeds such that the sulfur atom gives out electrons and becomes positively charged during charging, and the positive charge is then balanced by a negative ion from the electrolyte, as expected for a P-type reaction. Thianthrene is a good example of thioethers for which the loss of electrons is compensated by an increase in conjugation (Fig. 12).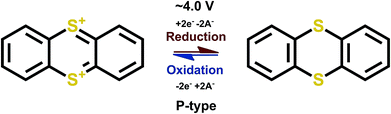 | ||
| Fig. 12 Redox scheme of thianthrene.65,66 | ||
The redox potential of thianthrene of ∼4.0 V vs. Li+/Li, is among the highest potential values achieved for the organic electrode materials, with a theoretical capacity of 194 mA h g−1 for a one-electron process. In addition, the redox kinetics are fast and the over-potential is manageable, which makes this material really promising. Moreover, assuming a reversible second electron transfer the theoretical capacity would be 388 mA h g−1, which is very high among the P-type organics. In practice, utilizing the second electron reaction is troublesome and would require ultra-dry conditions; accordingly, there are no reports to confirm the feasibility of the two-electron reaction scheme. In addition, only reports with polymerized thianthrene exist due to the rapid dissolution of the material which then lowers the actual theoretical capacity to ∼100 mA h g−1 (depending on the polymerization group). Furthermore, the coulombic efficiency is not 100%, which raises the question if the electrochemical process is truly reversible.65 Later on, much better cyclability of the compound was reported, therefore the preparation, electrolyte and/or the choice of polymer skeleton is important and should be carefully evaluated.67
3.8 Radicals
Organic compounds with an unpaired electron are called radicals. The unpaired electron facilitates the super-high reactivity of the radicals, rendering some of the radicals unusable due to self-dimerization. Nevertheless, stable radicals such as nitroxyl and phenoxyl offer simple and ultra-fast redox reactions; these stable radicals do not undergo self-dimerization thanks to the unfavorable thermodynamics, radical being sterically hindered, or the electronic resonance provided by the adjacent groups.68 By far the most studied radical is 2,2,6,6-tetramethyl-4-piperidinyl-N-oxyl (TEMPO). The TEMPO radical is a B-type material but the N-type reaction is rarely utilized due to its poor stability and reversibility; hence we may consider TEMPO as P-type material.69 However, it is important to note here that the N-type reaction is impractical only with some of the nitroxyl radicals such as TEMPO, and e.g. phenoxyl radicals work only with N-type mechanism70 while some nitroxyl radicals show stable ambipolar complexes.71 The redox schemes for the nitroxyl and phenoxyl radicals and TEMPO are shown in Fig. 13.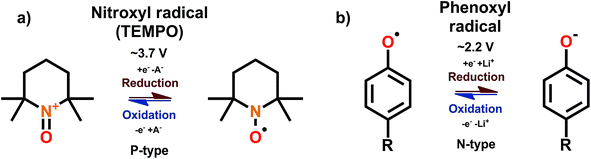 | ||
| Fig. 13 Redox schemes for (a) nitroxyl radical TEMPO, and (b) phenoxyl radicals.68,70 | ||
The observed redox voltage is ∼3.7 V with a theoretical capacity of ∼100 mA h g−1 depending on the polymerizing unit. The peak separation is also usually below 100 mV indicating fast kinetics,72 and with proper preparation of the active material the cells can be discharged in 1 minute with only a minimal capacity loss.73 Discarding the dissolution, the radical itself is indeed stable in traditional electrolyte solutions for at least a year. Due to low theoretical capacity and volumetric energy density, the radical-based batteries are not true candidates for applications such as mobile phones and laptops. Still, the super-fast kinetics is what makes the radical batteries attractive for some more specialized applications such as emergency backup for computers or RFID tags, since they hold charge better than supercapacitors and still can be rapidly discharged.74 These materials could in principle fill the gap between high energy LIBs and high power double layer capacitors, being thus the material group among the organics that is closest to commercialization.
3.9 Hydrocarbons
Hydrocarbons, which can be as simple as graphite, polyethylene or polyphenylene, are fully bipolar materials with N-type insertion mechanism below 2 V and P-type mechanism over 3 V vs. Li+/Li. However, getting both the redox reaction types to work reversibly is not an easy task and requires careful planning of the electrolyte's composition.75 Polyparaphenylene (PPP) is one of the compounds which can reversibly utilize both N-type and P-type reactions, see Fig. 3.34 The N-type reactions usually show excellent cyclic capabilities with capacities reaching almost the theoretical ones. The P-type mechanism is often more problematic. The electron is removed from the π-conjugated system during oxidation and to stabilize this loss 3–5 aromatic rings are needed, depending on the degree of conjugation in the carbon skeleton.76 This causes the observed capacities to be low, in the best case scenario ca. 100 mA h g−1; however, when taking into account also the mass of the counterion, the reality is often ca. 50 mA h g−1. In addition, the intercalation of the huge anion into the structure may cause some stress to the lattice, thus inducing amorphization and sloping voltage profiles.33 These P-type materials are not necessarily the best in terms of capacity, but the fact that they allow the use of the same material as both anode and cathode in dual-ion cells is an intriguing concept since it makes the manufacturing of the cells straightforward.3.10 Polymers
A polymer as it is used here is a term for various redox-active centers which are polymerized together either with a conjugated or non-conjugated backbone. Therefore, polymers do not possess any specific redox mechanism but inherit the redox mechanism of the given redox active unit. In previous sections, it was already discussed that polymerization is often the main tool of decreasing the solubility of the compound.The polymer can be either conjugated or non-conjugated. Conducting polymers like polypyrrole are a perfect example of the former type (Fig. 14). Conducting polymers were actually originally investigated for the use in the secondary batteries pre-dating the conventional LIBs.77 The conjugated backbone of these polymers has high electronic conductivity owing to the overlapping π-orbitals connecting the redox centers electrically. During (dis)charging the redox centers interact with each other causing the cell voltage to slope since the chemical potential is continuously changing due to the intercalation of ions. An additional drawback limiting their applicability is that typically less than 50% of the expected “one charge balancing species per redox active unit” is achieved.20
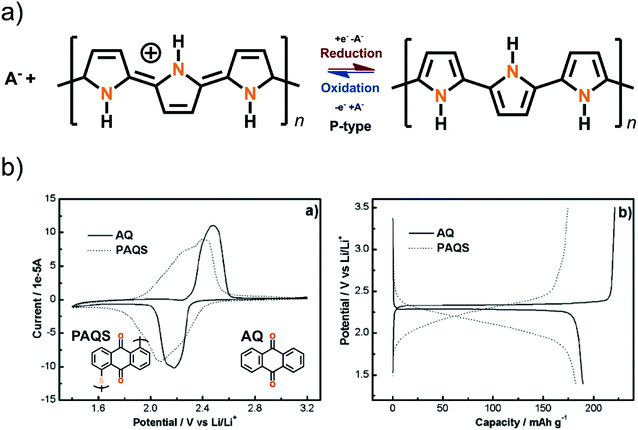 | ||
| Fig. 14 (a) Schematic of the structure of the redox mechanism of polypyrrole usually reaching doping levels of three monomers per one negative counterion. In (b) the performance of AQ before and after polymerization.19,35 | ||
Polymers with a non-conjugated backbone do not suffer from the aforementioned issues, at least not to the same extent. Creating an insulating backbone can be as simple as connecting two redox active moieties together with sulfur bridges. For example, AQ, which was discussed in more detail in the section about carbonyls, can be polymerized to form thioether bonds to adjacent molecules. When comparing the cyclic voltammetry and the cycling results of monomer AQ and polymerized form, it is still apparent that polymerization causes some negative effects on the performance of the material. In the CV, the peaks become wider and not as well defined and the flat plateau during (dis)charging shows slight sloping behavior. In addition, the average discharge voltage decreases, and polarization increases (Fig. 14). This is the cost of increased cyclic performance.39 Thus, even if the polymer is just there to give durability and to suppress the dissolution (cycling efficiency), it still causes minor effects on the other aspects of electrochemical performance.
4 Electron transport in organic electrode materials
Electron transport mechanisms in organic materials is a heavily studied subject in the fields of organic electronics and organic semiconductors. Unfortunately, this knowledge is poorly carried over to the field of organic battery electrodes. Here we aim to discuss some of this accumulated knowledge on the electron transport mechanisms in the context of organic electrode materials.There are several issues and apparent differences between the organic semiconductors and organic electrode materials which make the discussion difficult. Firstly, the basic understanding of the conduction mechanisms is yet to be improved in particular when it comes to the transition from the band-like conductivity to the polaron hopping conductivity. Secondly and possibly most distinctively, in organic semiconductors, we often consider electron–hole pairs while in the case of organic electrode materials an electric field and considerably heavier positive charge carriers, i.e. Li+ ions, are involved. It is still evident that similar conduction pathways are utilized in both cases, e.g. π–π stacking within the layers.78,79 Therefore, we may adopt important concepts such as the reorganization energy and electronic coupling and the effects of different π–π stackings from the semiconductor field to be considered in the context of the organic electrodes as well.80 The third critical issue that has been extensively studied in the two related fields – but rather separately – is the interfaces and energy level alignment between π-conjugated organic films and the metals. This is an important aspect since the metal–organic transfer occurs each time when an organic moiety receives or releases an electron to the outer circuit in a battery. We must emphasize that taking a direct analog to the organic semiconductors is an adventurous simplification for an electrochemical cell. Nevertheless, we believe that the knowledge from the semiconductor side (for the in-depth reviews, see ref. 80–86) could provide us with useful guidelines for the better understanding and more mature design of organic electrode materials.
4.1 Transport models
The electron transport in organic semiconductors is classically divided into two extreme regimes, the band conduction regime and the hopping conduction regime. In the band-like conduction regime, the carrier wave function is delocalized over many molecules and causes minimal strain on the lattice, while in the hopping regime the charge is localized to a single molecule where the extra charge causes local distortions,85 see Fig. 15.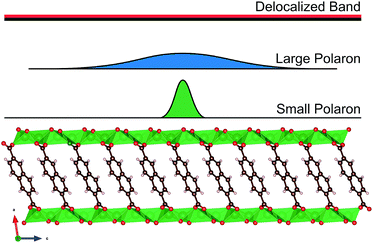 | ||
| Fig. 15 Charge carrier (de)localization in the band (delocalized) and hopping (polaron-type) conduction regimes.83 | ||
When two molecules are brought together in close proximity, their HOMO and LUMO orbitals split and the hole and electron conduction bands are formed, respectively.80 These bands are very narrow compared to the conduction bands in inorganic semiconductors, which means that they are easily disturbed by impurities or thermal vibrations.84 Such disturbances create dynamical disorder in the lattice and are the reason for the low carrier mobility. This is why band-like conductivity is observed only with specific organic moieties at room temperature.82 For the organic electrode materials, the hopping mechanism is much more probable than the band conduction mechanism.
For organic semiconductors, the hopping phenomena are commonly explained on the basis of the Marcus theory.81 This theory has its own weaknesses and has also been criticized in particular in the context of the high-mobility organic semiconductors.82 Nevertheless, it is the only theory that has been applied to organic electrode materials so far,78,79 and was found useful to gain insight of the conduction of e.g. LiFePO4.87,88 We believe that the parameters of Marcus theory will help to understand the underlying issues even if the theory would not perfectly describe the system. In Marcus theory, hopping is seen as a chemical reaction between two adjacent molecules. According to the Marcus rate equation,81
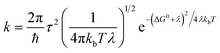 | (1) |
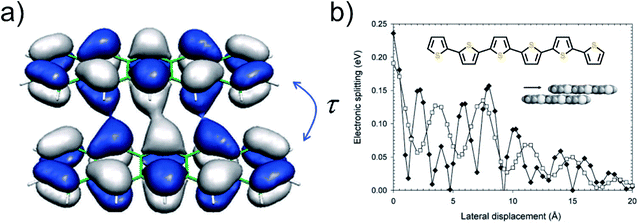 | ||
| Fig. 16 (a) Coupling of the HOMOs of two pentacene molecules,85 and (b) HOMO and LUMO splitting oscillation with respect to shift from cofacial coordination in sexithiophene molecule.86 To note is that this is a specific behavior of sexithiophene; other molecules will show a different kind of oscillation depending on the symmetry. Adapted with permission from Chem. Rev., 2004, 104, 4971–5004. Copyright 2004 American Chemical Society. | ||
The reorganization energy can be visualized from Fig. 17 where the electron coupling is presented as an overlap of two adiabatic potential energy surfaces along the reaction coordinate. In this illustration the electronic coupling, λ, is seen as the energy required for the vertical transition between the two potential energy curves. The intramolecular reorganization energy is a sum of the reorganization energies at the two sites. The two energies are typically nearly identical in value and therefore for simplicity often only the sum, 2|τ| is considered.90
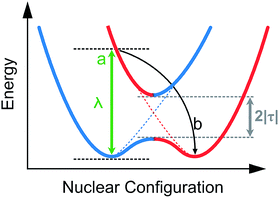 | ||
| Fig. 17 Potential energy surface sketches of adiabatic (solid) and diabatic (dashed) electron transfer between two neighboring sites, where (a): simultaneous oxidation and reduction on neighboring sites with frozen geometry (b): relaxation.85,86 | ||
Undeniably, there is an interconnection between the electronic geometric structure in conjugated organic moieties, and a strong correlation between the hole mobility and the intramolecular reorganization energy has been reported.86,91 Hutchison et al.92 studied systematically the effects of different heteroatoms, substituents, and chain length on the reorganization energy, and found that the number of monomer units had the largest impact; with an increasing number of monomer units, the reorganization energy first increases and then saturates to a value that depends on the monomer used. The torsional effect also had a significant impact, which in turn breaks the π-delocalization by alternating the dihedral angle of the C–C bonds. This means that sterically hindered structures commonly display larger reorganization energy values. Most importantly, to minimize the reorganization energy the changes in crystallographic lattice itself need to be as small as possible.92 For the organic electrode materials, this is not a simple task since the required diminished impact on the crystal lattice would be most straightforwardly achieved by increasing the conjugated area (e.g. the number of benzene rings) but only on the expense of the gravimetric capacity.
4.2 Engineering of molecular crystals
Molecular crystal engineering is a very old concept; the ultimate goal of making the crystal by design for a specific purpose is attempted by modifying the chemical structure by elemental (i.e. metal constituent) or functional group substitutions, which cause an effect on the chemical bonding and surroundings.93 The same approach would naturally be valid to improve the π–π stacking of the adjacent molecules. There are three main ways to affect the π–π stacking: (i) optimization of the molecular stacking, (ii) introduction of steric hindrance, and (iii) functionalization of the carbon skeleton.94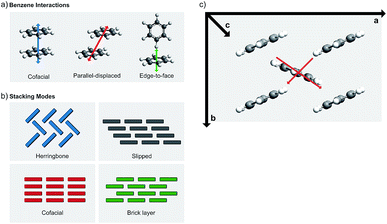 | ||
| Fig. 18 Schematic illustrations for (a) different interaction geometries between benzene molecules, (b) different stacking geometries derived from the possible interactions,94 and (c) conduction pathways in oligoacenes with herringbone stacking (modified from ref. 86). | ||
Among the different stacking types, the herringbone stacking is rather common. At the first glance, one might think that it would not enable electrical conductivity; this is however not necessarily true as a significant degree of HOMO and LUMO splitting occurs in many oligoacene compounds (multiple benzene rings) not only in the slipped stacked column but also through the middle herringbone column, see Fig. 18(c).80 Some herringbone structures experience orbital splitting along the a and b axes and through the herringbone layer, but the oligoacenes mostly show splitting through the axis a and the herringbone layer. Typically, only minuscule splitting is seen along the c axis (out of plane). This means that most of the herringbone-type materials conduct only in the ab plane so that the conductivity is two-dimensional.80
In the cofacial stacking, the molecules simply form columns along the π–π stacking. The slipped and brick stackings are both variations of the cofacial stacking. In the slipped stacking, each layer is slipped by a set amount, while in the brick stacking the slip alternates between n configurations every n:th layer. Even though the herringbone packed materials transport carriers well, according to reports the most favorable packing for achieving the fast transport is the cofacial brick stacking, where each molecule interacts with four other molecules.95–97 In order to stabilize the cofacial brick-type stacking it is important to note that the C–H-π interaction causing the materials to adopt the herringbone stacking is rather strong; and to overcome it, strong edge–edge interactions have to be designed.97
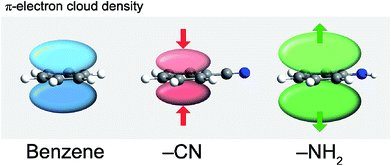 | ||
| Fig. 19 Changes in the π-electron cloud density caused by different functional groups: electron withdrawing CN and electron donating NH2 (in comparison to H in nonsubstituted benzene).98 | ||
The polarization of the carbon skeleton may be achieved also by replacing one or more carbon atoms in the benzene ring with a (typically) more electronegative heteroatom, e.g. nitrogen or sulfur. This induces non-uniformity in the electron delocalization such that the negative charge is shifted towards the more electronegative heteroatom. Addition of electronegative heteroatoms to the conjugated carbon skeleton has been shown to decrease the band gap by decreasing/increasing the LUMO/HOMO energy, respectively.99 Heteroatoms can also influence the packing mode of the crystal.94
For organic electrodes, functionalization has been commonly applied to modify the LUMO energy and thereby the redox voltage of the compound. Hence, most rationally one might design a scheme based on an optimal electron-withdrawing group to enhance the redox voltage (lower LUMO), which could at the same time enhance the interactions between adjacent benzene rings. Moreover, it is well known that the best electron conductivity characteristics are achieved for electron deficient materials.100 In reality, this scheme may be more complicated due to the introduction of positive ions. Many important organic electrode materials adopt the herringbone arrangement where the distances between benzene rings are likely to be locked due to metal–oxygen layers.
4.3 Organic–metal interface
As already discussed, organics rarely form electronic bands but their properties are rather reminiscent of a single molecule or polymer. This further means that in the battery configuration electron transfer from the metallic current collector or from electron conducting media is to a single molecule or chain only. In a microbattery, this interface is much more important than in a conventional battery where there is a conductive carbon matrix present in the cell design. The work function is an important parameter when discussing the underlining metal–organics interfaces. In solid-state physics, the work function is defined (in the unit of eV) as the energy required to bring an electron from the vacuum level (reference point) to the Fermi level of a solid. In electrochemical applications, the concept is otherwise the same but the energy is given in volts and the reference point varies in respect to the counter electrode; here the standard hydrogen electrode is set by definition to 0 V (∼4.4 eV in absolute scale). In an electrochemical system the potential energy of electrons changes upon probing the system with different voltages or by applying current that would alter the potential (and work function) according to Ohm's law.101The interface formed is very sensitive to the chosen metal and organic molecule. Also, the way the interface was prepared and the resultant bonding scheme may affect the behavior of the interface. The possible interface phenomena include the surface polarization (depending on the electron density of the organics), charge transfer (causing rearrangements), surface reactions, and formation of various interface states.101 There are no exact models available to precisely predict how the interface of different metal–organic pairs would behave. The distinct difference between the fields of organic electronics and organics in batteries is that in batteries the interface is bi-directional, i.e. electrons flow from metal to organics and vice versa during charging and discharging. In addition, the metal surface is always oxidized which makes the interface even less ideal. The integer charge-transfer model is often used to describe the situation. The metal-to-organics electron transfer occurs if the work function of the metal (current collector) is larger than the work function of the neutral organic molecule and in inverse when the work function of the current collector is smaller than the work function of the reduced form (i.e. lithiated) of the organic molecule.102 Upon reduction, the organic moiety forms a polaron and undergoes significant changes in geometric and electronic structure. This effect can shift the Fermi level in the reacted molecule and is observed as overpotential in the actual cell.103 The resultant barrier can be in tens of eV depending on the molecule, but not so much affected by the metal.104 The Fermi level can also shift with the degree of lithiation if the molecules are interconnected as observed in polymers, causing the sloping voltage profiles. Analogously, a flat voltage plateau is observed if there are no significant changes in the Fermi level. In reality, the situation is much more complex involving integer charge transfer states located within the band gap and Fermi level pinning; in-depth discussion on the topic is found e.g. in the review by Braun et al.102
Precht et al.103 studied tetracyanoquinodimethane (TCNQ) by photoemission spectroscopy to explain its metal–organic interface behavior upon lithiation/delithiation. Both the charged and discharged forms of TCNQ have a very similar work function resulting in the observed flat voltage plateau. However, the integer charge transfer occurs only if there is no spontaneous charge transfer between the current collector and the molecule. Spontaneous charge transfer occurs if the work function of the metal lies outside of the HOMO–LUMO gap. In this case, a dipole layer is formed and the electronic conduction resistance might be anisotropic which could lead to different resistance depending on whether the electron is moved from the organics to the metal or vice versa.
4.4 Notable examples
The conduction phenomena of the organic electrode materials are most commonly investigated by comparing the Nyquist plots of similar materials in a series or the effects caused by cycling,20,105 without much discussion provided. Ogihara et al.78,79 studied both theoretically and experimentally conductivity mechanisms of dilithium-4,4′-biphenyl dicarboxylate (Bph(COOLi)2) and dilithium-2,6-naphthalene dicarboxylate (Naph(COO)Li2). These studies continued their previous works where they reported improvements in the electrochemical performance of Naph(COO)Li2 when the material was annealed at high temperatures to densify the packing of aromatic naphthalene rings thus improving the π-conjugation.106 Calculations showed that the pristine Naph(COO)Li2 exhibits anisotropic conduction in the π-stacking of naphthalene while the lithiated Naph(COO)Li2 also shows conductivity through the herringbone layer. The same observation was confirmed from the Nyquist plot, where pristine Naph(COO)Li2 displayed only ionic conductivity, while the lithiated sample exhibited both ionic and electronic conductivity (Fig. 20). This was a direct proof of a switchable electronic conductivity depending on the lithiation state of the material. Lithiated Naph(COO)Li2 also loses its electronic conductivity upon heating to 200 °C due to the disappearance of the crystal structure responsible for the hopping, increase in separation of naphthalene rings, and formation of an insulating Li-containing layer. Interestingly, this behavior could be utilized as a safety switch in case of thermal runaway in batteries.79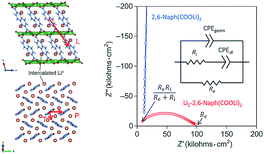 | ||
| Fig. 20 Electronic conduction pathways observed in lithiated samples of Naph(COO)Li2. The hopping path for the pristine sample is only along direction P, while lithiated sample also shows conductivity along the direction T. In the Nyquist plot the lithiated sample shows a clear half circle, which is attributed to a mixed ion and electronic conductivity, while pristine sample only shows ionic conductivity.79 | ||
In their follow up study the same research group focused on a very similar material Bph(COOLi)2REF. This material also contains two benzene rings, with the difference that the rings are connected through a single C–C bond. This makes the structure much more flexible and causes the material to undergo stepwise electron transfer, first to form a radical biphenyl unit followed by the reduction of both phenyls. This is also seen in charge/discharge curves where two plateaus are observed. The flexibility of the structure allows the material to twist around the C–C bond and accommodate lithium in various positions. In addition, the lithiation causes the crystal structure to shrink, which decreases the distances between neighboring organic moieties increasing their interaction. Next, the electron hopping mobilities were calculated for Li2Bph(COOLi)2 and Li2Naph(COO)Li2 using Marcus theory. The reorganization energy was found to be by 0.3 eV smaller for Bph(COOLi)2 than for Naph(COO)Li2 which also resulted in a 23-fold increase in the total drift mobility of hopping. The largest differences arose from the hopping through the herringbone layer (direction T in Fig. 20), which is the quickest conduction pathway in the crystal. This is a prime example of how small modifications to the organic moiety can make a huge difference in the electronic conductivity and thereby the electrochemical performance of the material. The examples discussed above moreover manifested the fact that the general guidelines and principles applied in organic semiconductor research are also applicable to organic batteries once the proper precautions are taken into account, as the organic battery systems are often much more complex and less ideal than the organic semiconductors.
5 Solid electrolytes for organic batteries
The largest problem with the organic electrode materials in a conventional wet-cell configuration is without a doubt their solubility in all the commonly used liquid electrolytes. An all-solid-state cell would naturally circumvent this problem completely. A handful of reports exists where organic electrodes are combined with a solid electrolyte with greatly enhanced cyclic performance.55,107–115 In this chapter, the two main types and the biggest problems of solid-state electrolytes are briefly accounted followed by a discussion of how the organic materials could fit together with these electrolytes.5.1 Solid electrolyte types
Solid-state batteries are currently of great interest in the research community since they can in practice increase the energy density of the cells by removing the need for the separator and would allow the use of lithium anode since the dendrite formation is suppressed. Solid electrolytes would also increase the safety of the cell since the largest safety hazard in LIBs is the electrolyte reacting with air.116 The current solid electrolyte materials can be divided into two main categories (with few sub-groups in each case): (i) salt-in-solid solvent electrolytes, and (ii) inorganic ceramic conductors; a comprehensive review on the topic is found in ref. 23.The salt-in-solid solvent electrolytes are flexible solid materials with decent conductivity and stability, especially with metallic lithium. The solid solvent or so-called plastic crystal electrolyte can be a polymer117 or other organic solid with a high polarity such as succinonitrile.118 Polymer electrolytes are traditionally based on poly(ethylene oxide) (PEO) with lithium salt solvated into the polymer. Another option is to also add solvent to form a polymer gel to increase conductivity. Both of the approaches have been applied with organic electrodes.112,119 To truly tackle the dissolution problem only the completely solid approaches are attractive since even if the gel-polymer electrolyte does improve the cycling stability it does not completely evade the dissolution issue.119 A common way is to prepare SiO2 particle ionic liquid quasi-solid on top of the PEO membrane, which is a very effective way to suppress dissolution.114 Polymers; however, often suffer from low stability towards oxidation and possess limited thermal stability, which limits the variety of suitable cathode materials. The ion selectivity, ion transference number, and conductivity are also not as high as with the state-of-the-art inorganic solid electrolytes.120
Inorganic solid electrolytes, such as LIPON, Li3N, sulfide, (anti)perovskite, garnet-type, and NASICON-type compounds, are positive ion conductors with a rigid structure. The movement of ions is based on point defects in the lattice. The different types of solid electrolytes each come with their own benefits and drawbacks, as extensively discussed in ref. 120 and 121. Some have very high ionic conductivity which is on par with liquid electrolytes and even stability up to 9 V vs. Li, but they are not stable in ambient atmosphere. Others are very stable, but their conductivity should be improved. Since these materials are so rigid and hard, ensuring good contact at the electrode–electrolyte interface is the largest challenge. In addition, large volume changes during lithiation at the electrodes only makes this problem more difficult to solve.
5.2 Limitations
Solid state electrolytes are often cited as a highly promising technology in the context of high voltage cathode materials and a metallic lithium anode. In practice, developing such ideas to the commercial level cells will be a huge engineering challenge. Only a few solid electrolytes such as LIPON possess simultaneously high reductive and oxidation stability; moreover, the ionic conductivity of these materials is not fast enough for bulk scale applications, making them truly applicable only in microbatteries.122 Concerning the metallic lithium anode, the biggest issue is the formation of dendrites upon plating. Solid electrolytes were believed to largely suppress the dendrite formation, which is indeed the case if the density or the shear modulus of the solid electrolyte is higher than that of lithium metal. However, it has been already demonstrated that if the solid electrolyte is not perfect single crystal lithium starts to propagate through existing pinholes widening the cracks thus creating heterogenous metal zones which may induce electrical short-circuiting and lithium which is rendered useless.116 In addition, a high capacity negative electrode materials often suffer from high volumetric expansion, which in the worst case causes delamination of the interfaces and loss of contact. To overcome these obstacles, many different approaches have been proposed, such as coating the active materials123 or additional material design solutions to accompany the large volumetric expansion. These precautions lead to decreased energy density in the full cell constructions. These issues have raised the question if adaption of lithium anode should only be the end goal since materials with high redox stability, fast conductivity, and with physical properties that could suppress the dendrite formation are hard to realize. By studying the interphase evolution during cycling with known stable materials one should be able to gather important information on how the ionic transport fundamentally functions over the interfaces and how the performance could be improved. Nevertheless, just the immediate benefits of replacing the liquid electrolyte by a solid one, i.e. the improve the safety of the batteries by a large margin and the far lower packing and thermal management requirements, are strong arguments for the fast adaptation of solid electrolytes.124,125The cathode side is not problem-free either. The lattice mismatch often observed between the solid electrolytes and cathode materials gives rise to high grain-boundary resistance. In some cases, even an SEI may form consisting of decomposition products like Co3O4 (from LiCoO2). In addition, conventional cathode materials also suffer from changes upon lithiation although these changes are usually smaller compared to those with graphite or other conversion electrode materials. These problems can be solved with a thin inter-diffusion or buffer layer, which aids with chemical stability and still conducts Li-ions. Common buffer layers utilized are NbO3, Li2ZrO3, and LiCO3 depending on the material combination chosen for the solid electrolyte and the cathode. Applying the buffer layer most likely requires a completely separate process step which makes the manufacturing process more expensive. Many vapor deposition methods could work here, but the atomic layer deposition (ALD) technique has a crucial benefit over other methods since it can produce thin yet pinhole-free layers, which are absolutely necessary for the application.116,125–127
Kerman et al.116 introduced a simple fishbone diagram to highlight different failure covering aspects in solid-state battery cells (Fig. 21). The aspects which require material innovation are mainly related to the interfaces and compositional tuning of the electrolyte. Therefore, it is crucial to test which kind of electrode materials would show good activity with solid electrolytes. As already mentioned several times, the mutual suitability of organic materials and solid electrolytes has not yet been thoroughly addressed; in the next section, the reported organic materials investigated in combination with a solid electrolyte are reviewed.
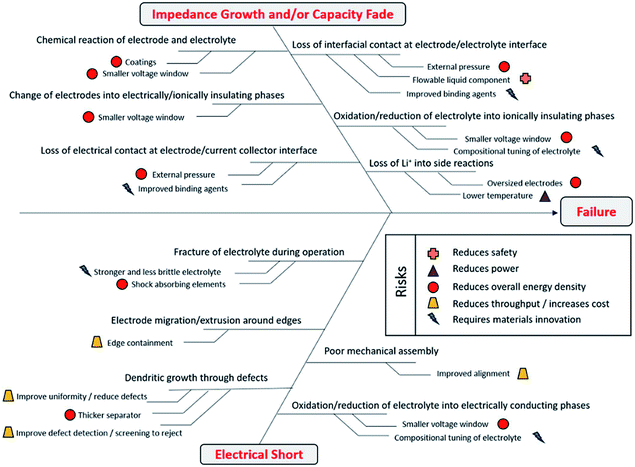 | ||
| Fig. 21 Different aspects causing failures in solid-state Li-ion battery cells.116 | ||
5.3 Organics with solid-state electrolyte
Applying solid electrolytes with N-type materials is relatively straightforward and a handful of reports already exist where polymer or glass type solid electrolytes are used with N-type organics.55,107–115 This approach also allows the use of lithium anode, which solves the problem of N-type organic materials being in a non-lithiated state. The P-type organics are much harder to combine with a solid electrolyte. Ideally, the cell should be designed as Li|solid-electrolyte|P-type organic material, to gain the benefit from the high redox potentials of P-type materials and the Li metal anode. However, since the P-type compounds require the negative anion from the electrolyte, the traditional ceramic and glass based solid electrolytes (such as LIPON128) are out of the question since they mainly only conduct positive ions. On the other hand, solid polymer electrolytes are feasible, since in them similar lithium salt (LiClO4) is dissolved in the polymer or another solid solvent.23 For example, a fully organic Na-ion battery with N-type negative and P-type positive electrode was constructed with solid succinonitrile electrolyte.107 Another approach would be to ditch out lithium and move to another battery chemistries such as fluorine.129 In such cells, fluoride anions are shuttled across the electrolyte instead of the Li+ ions. In principle, a P-type material could work either as a positive or a negative electrode, depending on the choice of the metal or metal fluoride on the respective electrode. Only one patent could be found where a P-type organic material is used in a fluorine battery.130 In this patent, an fluorine-doped polyaniline anode is described which is used with ionic liquid based electrolyte; the results seemed promising but the analysis was very limited. Therefore, it is still an open question if fluoride is capable to function as a charge balancing species for P-type organics especially in a solid-state environment and how a battery like this would perform.
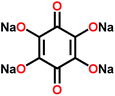
Chi et al.111 first reported the use of a sulfide-based solid electrolyte, Na3PS4, with organic electrodes. Sulfide electrolytes are promising in terms of ion conductivity; however, the stability range is not very wide, i.e. only up to 2.7 V vs. Na+/Na. For the organic electrode, the organic salt Na4C6O6 (usable both as an anode and a cathode) was chosen as it's working potential is relatively high but yet within the stability range of the electrolyte (Fig. 22). The ionic conductivity of the reduced species (S, P2S5, and PS3n−) was found to be low, making the limit strict. Cells with Na4C6O6 cathode and SnNa anode offered very good performance for a sodium battery, but the high rate capability remained yet to be achieved since the capacity decay was around 57% just from increasing C-rate from 0.1 to 0.5. Owing to the ambipolar nature of Na4C6O6 also full cells where it functioned as both the positive and negative electrode could be tested. The cells showed relatively stable cycling after a large initial drop. Accordingly, the 1st charge–discharge curve was found to be completely different from the following cycles, indicating the formation of an SEI-like layer or some other irreversible reaction. In addition, SEM images revealed slight cracking of the cathode after cycling probably due to volume changes upon sodiation. Nevertheless, these results for a prototype cell could be considered highly promising.111
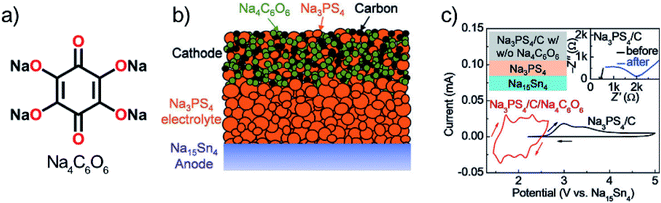 | ||
| Fig. 22 (a) Structure of ambipolar organic electrode Na4C6O6, (b) cell design tested, and (c) observed working potential and decomposition at the slightly higher potential. Reproduced from ref. 111 Copyright © 2018 by John Wiley Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. | ||
Similarly to the aforementioned example, also the lithium-based Li3PS4 solid electrolyte has been tested in combination with organic electrode materials.115 The chosen electrode was an azobenzene-type compound with a carboxylate group at the end, which can create strong ionic bonds with the solid electrolyte stabilizing the structure without affecting the electrochemical activity of the azo-group. This was confirmed by Raman, FTIR, XPS, and DFT calculations. The stability window of the solid electrolyte was found to be narrow, i.e. 1.71–2.31 V, in all-solid-state LIBs and therefore the azo-groups redox reactions lie outside of this range, which is seen in very low coulombic efficiency during the 1st cycle. The coulombic efficiency of 100% was reached during long-term cycling (Fig. 23). Contrary to the sodium-based analog, the reduction products did not annihilate the cell's performance probably due to the very strong ionic bonds or due to a formation of a very stable SEI-like layer. The ionic bond also solves the issues with volumetric expansion during lithiation maintaining the good connection between the electrode and electrolyte even during the cycling. All these factors make this cell configuration considerably more feasible than with a liquid electrolyte.115
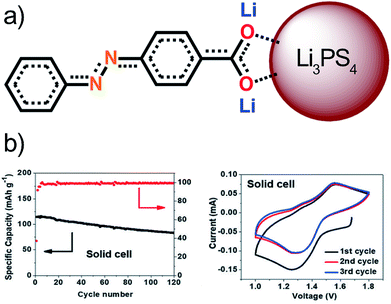 | ||
| Fig. 23 (a) Interaction between the organic electrode and the solid electrolyte particle forming an ionic bond. (b) Performance of the solid cell. Reproduced from ref. 115 Copyright © 2018 by John Wiley Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. | ||
The most common way so far has been to combine organic electrodes with a solid polymer electrolyte with some kind of filler material (e.g. SiO2 or ceramic solid electrolyte) to increase the RT conductivity. Published works along this line have reported good compatibility between the solid polymer electrolyte and the organic electrode, for all the different organic moieties investigated.108,110,112,113 This does not come as a huge surprise since the materials are intrinsically similar. Normally the cathodic stability of polymers is problematic, but since the organic cathode works at a relatively low potential, no problems were encountered and the performance was systematically improved when compared to similar systems with a liquid electrolyte. Li et al.112 compared the interfacial resistances and reported an increase by over one order of magnitude for their liquid electrolyte cell while for the one with the solid electrolyte the resistance stayed relatively constant, which indicates very good cycling properties for the solid electrolyte. Wei et al.110 demonstrated nearly identical reaction kinetics values for their liquid and solid electrolyte organic-electrode cells after the solid electrolyte was well optimized. Thus, the solid polymer electrolytes seem to be of considerable promise in solving many of the issues related to the organic electrodes. The major challenges arise from the optimization of the electrolyte composition to enhance conductivity and stability.
Efforts have also been made to utilize polar organic molecule solids to dissolve the lithium salt to create very similar solid electrolytes as with the above described solid polymer electrolytes. Conductivity maybe even better, but such cells typically suffer from the smaller electrochemical window.107 Nevertheless, by carefully choosing the organic electrode materials (negative electrode poly(anthraquinonyl sulfide) and positive electrode aniline-nitroaniline) Zhu et al.107 were able to fabricate fully organic cells with N- and P-type compounds. The high-rate performance of the cells was superior in comparison to liquid electrolyte based cells, while the cells simultaneously showed decent capacity and an operating voltage of 2.4 V.
An effective approach is to carefully design every interface in the cell. Typically at least one quasi-solid component is utilized to achieve the high ionic conductivity, but then a PEO membrane is applied to suppress the dissolution of the organic cathode, as illustrated in Fig. 24. The composite electrolyte could be e.g. quasi-solidified ionic liquid on SiO2 particles with the high ionic conductivity of the order of 1 mS cm−1.131 Promising results have been reported for cyano55 and quinone114 based organic electrodes.
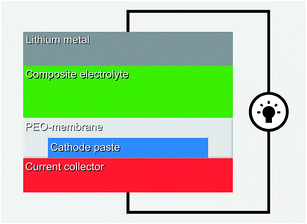 | ||
| Fig. 24 Schematic of the quasi-solid system utilizing PEO membrane.114 | ||
Comparing the electrochemical performance of solid electrolyte and liquid electrolyte is not always straightforward. The main benefit of combining the organic electrode materials with a solid electrolyte is the suppressed dissolution and therefore usually the better capacity retention upon cycling. The solid electrolyte may naturally have other benefits as well, e.g. with cell design and longer lifetime, which are not often directly seen or quantified in the traditional electrochemical testing. In addition, since the research field of solid electrolytes is in its infancy yet, little effort has been made so far in optimizing the systems for e.g. interfaces or composition. If similar cells with the same electrode composition are investigated, the rate capability is usually lower in the case of the solid cell due to the lower ionic conduction of the solid electrolyte. Nevertheless, we gathered in Table 1 basic electrochemical performance data for some representative organic-electrode/solid-electrolyte systems in comparison with similar systems with a liquid electrolyte.
| Formula or name and ref. | Structure | Electrode composition in electrolyte | Cell voltage (V) vs. reference | Cycling: initial capacity (mA h g−1), retention, cycles, rate capability: currents used, retention | Notes |
|---|---|---|---|---|---|
Na4C6O6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
|
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, solid electrolyte, carbon in Na3PS4 1 active, solid electrolyte, carbon in Na3PS4 |
2.6–1.5 Na+/Na | 164, 76%, 100 cycles, 0.1C → 0.5C, 57% | Solid electrolyte at 60 °C |
Na4C6O6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.78 0.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, binder, carbon in 1 M NaClO4 in PC 1 active, binder, carbon in 1 M NaClO4 in PC |
1.5–0.4 Na+/Na | 125, 45%, 15 cycles | Low coulombic efficiency | |
| PTCDA108 |
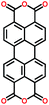
|
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 active, binder, carbon in PPCB-SPE 2 active, binder, carbon in PPCB-SPE |
3.5–1.5 V K+/K | 113, 84%, 40 cycles, 10 mA g−1 → 100 mA g−1, 67% | Solid electrolyte at room temperature (RT) |
| PTCDA132 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 active, binder, carbon in 0.5 M KPF6 in EC 2 active, binder, carbon in 0.5 M KPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC DEC |
3.5–1.5 K+/K | 131, 69%, 200 cycles, 10 mA g−1 → 100 mA g−1, 70% | ||
| PCTB110 |
|
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 active, binder, carbon in PEO–LiClO4–Li0.3La0.566TiO3 3 active, binder, carbon in PEO–LiClO4–Li0.3La0.566TiO3 |
3.2–1.6 Li+/Li | 104, 98%, 100 cycles | Solid electrolyte at 70 °C |
| PCTB133 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 active, binder, carbon in 1 M LiPF6 DEC 3 active, binder, carbon in 1 M LiPF6 DEC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC EC |
3.2–1.6 Li+/Li | 110, 63%, 100 cycles, 30 mA g−1 → 300 mA g−1, 58% | ||
| AQ112 |
|
3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 active, carbon, LiTFSI, PEG in PEO-γ-LiAlO2 3 active, carbon, LiTFSI, PEG in PEO-γ-LiAlO2 |
3.5–1.5 Li+/Li | 183, 50%, 50 cycles, 0.1C → 1C, 50% | Solid electrolyte at 35 °C |
| AQ112 | 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 active, carbon, LiTFSI, PEG in 1 M LiTFSI/DOL + DME 3 active, carbon, LiTFSI, PEG in 1 M LiTFSI/DOL + DME |
3.5–1.5 Li+/Li | 197, 28%, 20 cycles | ||
| Pillar[5]quinone113 |
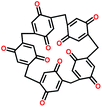
|
5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 active, carbon, CNT, graphene, solid electrolyte, binder in PMA/PEG–LiClO4–SiO2 composite 0.5 active, carbon, CNT, graphene, solid electrolyte, binder in PMA/PEG–LiClO4–SiO2 composite |
3.25–1.75 Li+/Li | 418, 95%, 50 cycles, 0.3C → 1C, 50% | Solid electrolyte at RT |
| Pillar[5]quinone113 | 6.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 active, carbon, CNT, graphene, binder in 1 M LiPF6 EC 0.5 active, carbon, CNT, graphene, binder in 1 M LiPF6 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC DMC |
3.25–1.75 Li+/Li | 409, 55%, 3 cycles | ||
| THBQ114 |
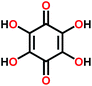
|
4.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.69 2.69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 active, carbon, binder in quasi-solid electrolyte 0.6 active, carbon, binder in quasi-solid electrolyte |
3.75–1.5 Li+/Li | 290, 86%, 10 cycles | Solid electrolyte at RT |
| THBQ114 | 4.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.69 2.69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 active, carbon, binder in 1 M LiClO4 in EC 0.6 active, carbon, binder in 1 M LiClO4 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC DEC |
3.75–1.5 Li+/Li | 170, 23%, 10 cycles | ||
| TCNQ55 |
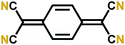
|
4.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.566 active, carbon, binder in RTIL composite quasi solid electrolyte 0.566 active, carbon, binder in RTIL composite quasi solid electrolyte |
4.0–2.1 Li+/Li | 216, 78%, 100 cycles | Solid electrolyte at RT |
| TCNQ55 | 4.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.566 active, carbon, binder in 1 M LiClO4 in EC 0.566 active, carbon, binder in 1 M LiClO4 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC DEC |
4.0–2.1 Li+/Li | 215, 13%, 5 cycles | ||
| PBALS115 |

|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, solid electrolyte, carbon in LPS 1 active, solid electrolyte, carbon in LPS |
3.0–1.0 Li+/Li | 120, 69%, 120 cycles, 10 mA g−1 → 80 mA g−1, 63% | |
| PBALS115 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, carbon, binder in 1 M LiPF6 in EC 1 active, carbon, binder in 1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC DEC |
3.0–1.0 Li+/Li | 75, 16%, 20 cycles | ||
| PTO134 |
|
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, PEO–NaClO4, carbon, binder in Na beta-alumina 1 active, PEO–NaClO4, carbon, binder in Na beta-alumina |
3.0–1.25 Na+/Na | 362, 80%, 50 cycles, 0.1C → 0.5C, 44% | Solid electrolyte at 60 °C |
| PTO134 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 active, carbon, binder in 1 M NaClO4 in diglyme 1 active, carbon, binder in 1 M NaClO4 in diglyme |
3.0–1.25 Na+/Na | 380, 9%, 20 cycles |
Recently we developed another essentially new fabrication approach enabling the integration of the glass-type solid electrolyte LiPON with quinones.30,109,128 All active layers were deposited utilizing the strongly emerging atomic/molecular layer deposition (ALD/MLD) thin film technique.135 This technique is superior for the deposition of ultrathin pinhole-free thin films of metal–organic hybrid materials with atomic/molecular level accuracy. Most importantly, the ALD/MLD technique allows in situ fabrication of thin films of Li-benzoquinone in its lithiated state – a material not readily accessible by any other technique. The performance of the quinone/LiPON stack was evaluated vs. electrodeposited lithium, vaporized germanium, and ALD/MLD-grown organic lithium terephthalate anode. The cyclic performance with metallic anode was not optimal, due to the degradation of the negative current collector and poor performance of the metallic anode. Cycling performance of the cells increased substantially when lithium terephthalate was used as the anode, which confirmed that the poor performance of the cells was due to the negative electrode. Significantly, for the ALD/MLD fabricated thin-film cells with ultrathin Li-benzoquinone and LiPON layers, ultrahigh redox reaction rates were realized; the charge/discharge times as short as ∼0.25 s (plus energy/power densities of ∼100 mW h cm−3 and ∼500 W cm−3) are excellent considering that the full cell setup was far from optimized yet. We believe that this scheme could be a step towards the dream to merge the high energy density of batteries with the high power density of supercapacitors.109 This work also verified the compatibility of LiPON with organic electrode materials since only a small parasitic reaction was observed during initial cycles.109 We have also demonstrated that ALD-grown LiPON is highly compatible with lithium terephthalate anode, improving its cyclic and high rate performance and suppressing the formation of SEI.30
What is clearly lacking so far are the reports on the application of ceramic electrolytes such as perovskites, lanthanide oxides, and garnets in organic cells. This is understandable though since organics would not particularly benefit from the specific advantages of ceramic electrolytes such as their mechanical stiffness and stability in an electrochemical environment. Ceramic electrolytes would be better than the liquid electrolytes in suppressing dendrite growth; however, the active layers should be appreciably thin in order to break-even in energy density.120,126 Thinner layers in general demand more from the manufacturing process. Nevertheless, deposition of even ultrathin layers of ceramic electrolytes on top of organic electrodes is possible with advanced gas-phase thin-film deposition techniques such as ALD, cf. the growth of LiPON films.30 Actually, stiff but still thin surface coating might be one of the most efficient solutions for suppressing the dissolution of organic electrode materials.
5.4 Mutual benefits
From the examples discussed in the previous sections, it is clear that a solid electrolyte is a highly beneficial – if not mandatory – condition for solving the crucial dissolution issue of organic electrodes. Furthermore, even a thin solid-electrolyte coating would improve the performance of organic electrode materials in liquid electrolytes.30,136–138 In addition, the benefits go hand in hand. The lower working potential of organic electrodes considerably widens the variety of usable solid electrolytes. This is particularly good news since the fast conducting solid electrolytes commonly suffer from stability issues.120 Moreover, the gravimetric power density of the cell is not compromised since the intrinsically low working potential is compensated by the large gravimetric capacity. For example, organic positive electrode materials can reach capacities up to 350–500 mA h g−1 with an average potential of 2.2 to 2.8 V vs. Li+/Li. This can result in specific energy density values up to 960–1100 W h kg−1. These values are on par with those of the high voltage inorganic cathode materials.76Interface issues such as the chemical interactions and mutual compatibilities between the different components are crucially important for the solid-state battery function.125 So far the reformability of the interfaces between organic electrodes and solid electrolytes has not gained much attention. This is understandable since most of the works have focused on the softer solid electrolytes. Reformability is inversely related to the material's elastic modulus.125 Hence, organics with their intrinsically low elastic modulus should be – in comparison with the ceramics – superior in reformability.139 Then, with the clever tuning of the organic moieties strong ionic bonds can possibly be formed between the organic electrode and the solid electrolyte, to ensure the strong and flexible contact.115 In addition, the volumetric expansion of the organics is a parameter that is controlled by proper design of the crystal structure and carbon skeleton. For example, the volume change for lithium terephthalate (negative electrode material) is ∼6%,140 but only 0.33% for dilithium-2,6-naphthalene with two benzene rings instead of one in the carbon skeleton.141 It should be emphasized that both of these values are smaller than the volume change of graphite, i.e. 13.2%.142 Unfortunately, the smaller volume changes for the materials with the larger carbon skeletons often come with the expense of the lower gravimetric capacity.76
In thin-film form, additional benefits can be anticipated, as only active materials are present which neglects most of the compatibility issues. In addition, the poor conductivity of organics is of less problematic in the case of thin electrode layers. Among the thin-film deposition techniques, ALD has been widely seen as an elegant tool for interface engineering123 and for fabrication of high-quality thin films of the active materials, in particular, solid electrolytes.143 Most excitingly, the recent advances in the combined ALD/MLD technique have widened the repertoire of electrode materials from inorganic materials to cover also many organic electrode materials.135,144–148 Thin films of the organic electrode and inorganic solid-electrolyte materials deposited from gaseous precursors on top of each other is in principle the simplest form of a microbattery,109,149 and – potentially – by moving from planar to three-dimensional substrates high footprint capacity can be achieved.150 In addition, since the ALD/MLD fabricated thin-film microbattery can be made without any additives it forms the simplest system where the interactions of the layers could in principle be studied in an electrochemical half-cell. This unique possibility has not yet truly challenged, though, leaving exciting possibilities to foreseen future.30,109
6. Conclusions and outlook
Altogether, the abundance and structural diversity of various organic backbones and functionalities promises that these materials will be playing a role in energy storage applications in the future. In our short summary of the current material variety, we divided the organics according to their active functional group; this provided the premises to discuss the underlying chemistries in organic electrode materials. With illustrative examples, we then aimed to identify the particular benefits and major shortcomings of each group. The solubility in liquid electrolytes and the poor electronic conductivity are the common problems among the organic electrode materials.Here we approached the conductivity issues in organic batteries from a viewpoint of organic semiconductors – learning from the related field where the conduction phenomena have been traditionally most thoroughly studied. This is an obviously daring interpretation as in semiconductors the intrinsic system is very different from the organic batteries. Nevertheless, the same basic principles also govern the latter. This approach gave us two important parameters to optimize: reorganization energy and electronic coupling, which have a strong correlation on the electronic conductivity of organic materials. The general goal is to minimize the reorganization energy by minimizing the expansion or shrinking of the crystallographic lattice upon lithiation. This could be achieved by maximizing the conjugated area or by clever modifications which add flexibility to the structure. Both of these approaches usually come at the expense of gravimetric capacity. There is a vast amount of possibilities to add flexibility to the structure, such as dispersing two benzenes with different bridges or by adding various functional groups. The second parameter is the electronic coupling, which should be maximized to improve the electronic conductivity. Many of the organic electrode materials adopt the herringbone stacking, which is not the most favorable. In an ideal case, by introducing bulky substituents or functional groups the arrangement can be modified and therefore the electronic conductivity is improved. The functionalization has been a hot topic in the organic battery community, but the focus has been mainly on comparing the electrochemical performance and the changes in potential due to inductive effects. The electrochemical performance can be easily misleading since the experimental conditions vary from article to article. It would therefore be vital to understand the underlying reasons why the functionalization causes modifications to the electrochemical performance and what other effects it can cause, such as the poorer electronic coupling between adjacent molecules.
Combining the organic electrode materials with solid state electrolytes not only solves the dissolution issue of organics but also enables the use of a wider variety of solid electrolyte materials, which are not compatible with high voltage cathode materials. The organics are also malleable and the volumetric changes can be controlled, which are preferable properties for the solid–solid electrode–electrolyte interfaces to ensure good contact during battery cycling. The interface rarely is ideal and chemically stable, which contributes to the capacity decay. Therefore for the future, it is vital to study the interactions between organic electrode materials and solid electrolytes.
A thin-film microbattery where the components are deposited from gaseous precursors is the simplest system (without any additives), where organic electrodes and solid electrolytes and their interactions could be directly studied. This benefits both of the fields of research simultaneously since even a thin electrolyte coating could solve some of the performance issues of the organic electrodes. Among the plausible deposition methods, ALD is widely recognized as the most sophisticated tool for controlling the interfaces. Owing to the recent advancements, many organic electrode materials (even in lithiated state) and solid electrolytes can be deposited with ALD/MLD and ALD, respectively. In addition, it is foreseen that with high probability some kind of (ALD) coating will be required to intercorporate the solid electrolytes with the solid electrode to aid with lattice mismatch, poor contact, or space-charging. Hybrid coatings consisting of metals and organics can play an important role in this due to their soft, malleable, and insulating nature, while still being able to conduct Li-ions. Also, when the basis of the solid–solid interface system is well understood, it is easier to add components and move on to more complex systems and to pinpoint what might cause any of the problems. Logically, this development also allows the fabrication of thin-film batteries solely using the ALD/MLD technique, which is known to yield highly conformal coatings on practically any kind of complex surface. The feasibility of this approach was recently shown by us for the quinone-LiPON-terephthalate battery. Developing and combining distinct ALD/MLD processes is a key asset for studying the interactions and ultimately to fabricate 3D thin-film battery architectures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Advanced Grant Agreement (No. 339478) and under the European Union's Horizon 2020 Research and Innovation Programme ERC Proof-of-Concept Grant Agreement (No. 780041), and also from the Academy of Finland (No. 296299, 303452).Notes and references
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- H. Chen, M. Armand, G. Demailly, F. Dolhem, P. Poizot and J. M. Tarascon, ChemSusChem, 2008, 1, 348–355 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2014, 7, 19–29 CrossRef PubMed.
- V. Dieterich, J. D. Milshtein, J. L. Barton, T. J. Carney, R. M. Darling and F. R. Brushett, Transl. Mater. Res., 2018, 5, 034001 CrossRef.
- I. A. Rodríguez-Pérez, Y. Yuan, C. Bommier, X. Wang, L. Ma, D. P. Leonard, M. M. Lerner, R. G. Carter, T. Wu, P. A. Greaney, J. Lu and X. Ji, J. Am. Chem. Soc., 2017, 139, 13031–13037 CrossRef PubMed.
- J. Bitenc, K. Pirnat, T. Bančič, M. Gaberšček, B. Genorio, A. Randon-Vitanova and R. Dominko, ChemSusChem, 2015, 8, 4128–4132 CrossRef CAS PubMed.
- B. Häupler, A. Wild and U. S. Schubert, Adv. Energy Mater., 2015, 5, 1402034 CrossRef.
- G. Xu, P. Nie, H. Dou, B. Ding, L. Li and X. Zhang, Mater. Today, 2017, 20, 191–209 CrossRef CAS.
- Q. Zhao, Y. Lu and J. Chen, Adv. Energy Mater., 2017, 7, 1601792 CrossRef.
- M. Miroshnikov, K. P. Divya, G. Babu, A. Meiyazhagan, L. M. Reddy Arava, P. M. Ajayan, G. John, L. Mohana, R. Arava, P. M. Ajayan and G. John, J. Mater. Chem. A, 2016, 4, 12370–12386 RSC.
- Y. Zhang, J. Wang and S. N. Riduan, J. Mater. Chem. A, 2016, 4, 14902–14914 RSC.
- S. Lee, G. Kwon, K. Ku, K. Yoon, S.-K. Jung, H.-D. Lim and K. Kang, Adv. Mater., 2018, 30, 1704682 CrossRef PubMed.
- Q. Zhao, C. Guo, Y. Lu, L. Liu, J. Liang and J. Chen, Ind. Eng. Chem. Res., 2016, 55, 5795–5804 CrossRef CAS.
- V.-A. Oltean, S. Renault, M. Valvo and D. Brandell, Materials, 2016, 9, 1–27 CrossRef PubMed.
- Z. Song and H. Zhou, Energy Environ. Sci., 2013, 6, 2280–2301 RSC.
- T. B. Schon, B. T. McAllister, P.-F. Li and D. S. Seferos, Chem. Soc. Rev., 2016, 45, 6345–6404 RSC.
- Y. Liang, Z. Tao and J. Chen, Adv. Energy Mater., 2012, 2, 742–769 CrossRef CAS.
- C. Zhang, C. Lu, F. Zhang, F. Qiu, X. Zhuang and X. Feng, J. Energy Chem., 2018, 27, 86–98 CrossRef.
- S. Muench, A. Wild, C. Friebe, B. Häupler, T. Janoschka and U. S. Schubert, Chem. Rev., 2016, 116, 9438–9484 CrossRef CAS PubMed.
- Y. Xu, M. Zhou and Y. Lei, Mater. Today, 2018, 21, 60–78 CrossRef CAS.
- Y.-S. Hu, Nat. Energy, 2016, 1, 16042 CrossRef CAS.
- J. W. Fergus, J. Power Sources, 2010, 195, 4554–4569 CrossRef CAS.
- K. Takada, Acta Mater., 2013, 61, 759–770 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 1–7 Search PubMed.
- M. Liu, J. Electrochem. Soc., 1991, 138, 1896 CrossRef CAS.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- J. Xu, Y. Dou, Z. Wei, J. Ma, Y. Deng, Y. Li, H. Liu and S. Dou, Adv. Sci., 2017, 4, 1700146 CrossRef PubMed.
- M. Armand, S. Grugeon, H. Vezin, S. Laruelle, P. Ribière, P. Poizot and J.-M. Tarascon, Nat. Mater., 2009, 8, 120–125 CrossRef CAS PubMed.
- M. Nisula and M. Karppinen, Nano Lett., 2016, 16, 1276–1281 CrossRef CAS PubMed.
- R. Emanuelsson, M. Sterby, M. Strømme and M. Sjödin, J. Am. Chem. Soc., 2017, 139, 4828–4834 CrossRef CAS PubMed.
- Q. Xue, D. Li, Y. Huang, X. Zhang, Y. Ye, E. Fan, L. Li, F. Wu and R. Chen, J. Mater. Chem. A, 2018, 6, 12559–12564 RSC.
- I. A. Rodríguez-Pérez, Z. Jian, P. K. Waldenmaier, J. W. Palmisano, R. S. Chandrabose, X. Wang, M. M. Lerner, R. G. Carter and X. Ji, ACS Energy Lett., 2016, 1, 719–723 CrossRef.
- L. M. Zhu, A. W. Lei, Y. L. Cao, X. P. Ai and H. X. Yang, Chem. Commun., 2013, 49, 567–569 RSC.
- S. Wang, L. Wang, K. Zhang, Z. Zhu, Z. Tao and J. Chen, Nano Lett., 2013, 13, 4404–4409 CrossRef CAS PubMed.
- M. Solà, Front. Chem., 2013, 1, 4–11 Search PubMed.
- L. Miao, L. Liu, Z. Shang, Y. Li, Y. Lu, F. Cheng and J. Chen, Phys. Chem. Chem. Phys., 2018, 20, 13478–13484 RSC.
- D. Wu, Z. Xie, Z. Zhou, P. Shen and Z. Chen, J. Mater. Chem. A, 2015, 3, 19137–19143 RSC.
- Z. Song, H. Zhan and Y. Zhou, Chem. Commun., 2009, 448–450 RSC.
- W. Wang, W. Xu, L. Cosimbescu, D. Choi, L. Li and Z. Yang, Chem. Commun., 2012, 48, 6669 RSC.
- X. Dong, Z. Guo, Z. Guo, Y. Wang and Y. Xia, Joule, 2018, 2, 902–913 CrossRef CAS.
- Q. Zou, W. Wang, A. Wang, Z. Yu and K. Yuan, Mater. Lett., 2014, 117, 290–293 CrossRef CAS.
- Y. Liang, P. Zhang, S. Yang, Z. Tao and J. Chen, Adv. Energy Mater., 2013, 3, 600–605 CrossRef CAS.
- J. Lüder, F. Legrain, Y. Chen and S. Manzhos, MRS Commun., 2017, 7, 523–540 CrossRef.
- D. M. Carlton, D. K. McCarthy and R. H. Genz, J. Phys. Chem., 1964, 68, 2661–2665 CrossRef CAS.
- C. Peng, G.-H. Ning, J. Su, G. Zhong, W. Tang, B. Tian, C. Su, D. Yu, L. Zu, J. Yang, M.-F. Ng, Y.-S. Hu, Y. Yang, M. Armand and K. P. Loh, Nat. Energy, 2017, 2, 17074 CrossRef CAS.
- K. Sakaushi, E. Hosono, G. Nickerl, T. Gemming, H. Zhou, S. Kaskel and J. Eckert, Nat. Commun., 2013, 4, 1485 CrossRef PubMed.
- B. Tian, Z. Ding, G.-H. Ning, W. Tang, C. Peng, B. Liu, J. Su, C. Su and K. P. Loh, Chem. Commun., 2017, 53, 2914–2917 RSC.
- G. Dai, X. Wang, Y. Qian, Z. Niu, X. Zhu, J. Ye, Y. Zhao and X. Zhang, Energy Storage Materials, 2019, 16, 236–242 CrossRef.
- M. Lee, J. Hong, B. Lee, K. Ku, S. Lee, C. B. Park and K. Kang, Green Chem., 2017, 19, 2980–2985 RSC.
- K. Sakaushi, G. Nickerl, F. M. Wisser, D. Nishio-Hamane, E. Hosono, H. Zhou, S. Kaskel and J. Eckert, Angew. Chem., Int. Ed., 2012, 51, 7850–7854 CrossRef CAS PubMed.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon, 2016, 105, 52–76 CrossRef CAS.
- S. Tobishima, J. Electrochem. Soc., 1984, 131, 57 CrossRef CAS.
- K. P. Goetz, D. Vermeulen, M. E. Payne, C. Kloc, L. E. McNeil and O. D. Jurchescu, J. Mater. Chem. C, 2014, 2, 3065–3076 RSC.
- Y. Hanyu and I. Honma, Sci. Rep., 2012, 2, 453 CrossRef PubMed.
- Q. Deng, S.-J. He, J. Pei, C. Fan, C. Li, B. Cao, Z.-H. Lu and J. Li, Electrochem. Commun., 2017, 75, 29–32 CrossRef CAS.
- Y. Wang, C. Fang, Y. Huang, Q. Liu, R. Zhao, X. Ding and Y. Huang, RSC Adv., 2018, 8, 24900–24905 RSC.
- C. Luo, X. Ji, S. Hou, N. Eidson, X. Fan, Y. Liang, T. Deng, J. Jiang and C. Wang, Adv. Mater., 2018, 30, 1706498 CrossRef PubMed.
- C. Luo, O. Borodin, X. Ji, S. Hou, K. J. Gaskell, X. Fan, J. Chen, T. Deng, R. Wang, J. Jiang and C. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2004–2009 CrossRef CAS PubMed.
- E. Castillo-Martínez, J. Carretero-González and M. Armand, Angew. Chem., Int. Ed., 2014, 53, 5341–5345 CrossRef PubMed.
- M. López-Herraiz, E. Castillo-Martínez, J. Carretero-González, J. Carrasco, T. Rojo and M. Armand, Energy Environ. Sci., 2015, 8, 3233–3241 RSC.
- M. Liu, J. Electrochem. Soc., 1989, 136, 2570 CrossRef CAS.
- T. Inamasu, D. Yoshitoku, Y. Sumi-otorii, H. Tani and N. Ono, J. Electrochem. Soc., 2003, 150, A128 CrossRef CAS.
- H. Zhao, J. Wang, Y. Zheng, J. Li, X. Han, G. He and Y. Du, Angew. Chem., Int. Ed., 2017, 56, 15334–15338 CrossRef CAS PubMed.
- M. E. Speer, M. Kolek, J. J. Jassoy, J. Heine, M. Winter, P. M. Bieker and B. Esser, Chem. Commun., 2015, 51, 15261–15264 RSC.
- T. P. Vaid, M. E. Easton and R. D. Rogers, Synth. Met., 2017, 231, 44–50 CrossRef CAS.
- A. Wild, M. Strumpf, B. Häupler, M. D. Hager and U. S. Schubert, Adv. Energy Mater., 2017, 7, 1601415 CrossRef.
- K.-A. Hansen and J. P. Blinco, Polym. Chem., 2018, 9, 1479–1516 RSC.
- C. Friebe and U. S. Schubert, Top. Curr. Chem., 2017, 375, 19 CrossRef PubMed.
- T. Jähnert, B. Häupler, T. Janoschka, M. D. Hager and U. S. Schubert, Macromol. Rapid Commun., 2014, 35, 882–887 CrossRef PubMed.
- T. Sukegawa, A. Kai, K. Oyaizu and H. Nishide, Macromolecules, 2013, 46, 1361–1367 CrossRef CAS.
- K. Nakahara, S. Iwasa, M. Satoh, Y. Morioka, J. Iriyama, M. Suguro and E. Hasegawa, Chem. Phys. Lett., 2002, 359, 351–354 CrossRef CAS.
- K. Nakahara, J. Iriyama, S. Iwasa, M. Suguro, M. Satoh and E. J. Cairns, J. Power Sources, 2007, 165, 870–873 CrossRef CAS.
- K. Nakahara, K. Oyaizu and H. Nishide, Chem. Lett., 2011, 40, 222–227 CrossRef CAS.
- C. Y. Chan, P.-K. Lee, Z. Xu and D. Y. Yu, Electrochim. Acta, 2018, 263, 34–39 CrossRef CAS.
- Y. Liang and Y. Yao, Joule, 2018, 2, 1690–1706 CrossRef CAS.
- A. Mohammadi, J. Electrochem. Soc., 1986, 133, 947 CrossRef CAS.
- Y. Ozawa, N. Ogihara, M. Hasegawa, O. Hiruta, N. Ohba and Y. Kishida, Commun. Chem., 2018, 1, 65 CrossRef.
- N. Ogihara, N. Ohba and Y. Kishida, Sci. Adv., 2017, 3, e1603103 CrossRef PubMed.
- J. L. Bredas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- F. Ortmann, F. Bechstedt and K. Hannewald, Phys. Status Solidi A, 2011, 248, 511–525 CrossRef CAS.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347 RSC.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- M. Z. Bazant, Acc. Chem. Res., 2013, 46, 1144–1160 CrossRef CAS PubMed.
- P. Bai and M. Z. Bazant, Nat. Commun., 2014, 5, 3585 CrossRef PubMed.
- K. Hannewald and P. A. Bobbert, Phys. Rev. B, 2004, 69, 075212 CrossRef.
- N. E. Gruhn, D. A. da Silva Filho, T. G. Bill, M. Malagoli, V. Coropceanu, A. Kahn and J.-L. Brédas, J. Am. Chem. Soc., 2002, 124, 7918–7919 CrossRef CAS PubMed.
- B. C. Lin, C. P. Cheng and Z. P. M. Lao, J. Phys. Chem. A, 2003, 107, 5241–5251 CrossRef CAS.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350 CrossRef CAS PubMed.
- D. Braga, Chem. Commun., 2003, 2751 RSC.
- Z.-F. Yao, J.-Y. Wang and J. Pei, Cryst. Growth Des., 2018, 18, 7–15 CrossRef CAS.
- S. Ando, R. Murakami, J. Nishida, H. Tada, Y. Inoue, S. Tokito and Y. Yamashita, J. Am. Chem. Soc., 2005, 127, 14996–14997 CrossRef CAS PubMed.
- O. Ostroverkhova, D. G. Cooke, F. A. Hegmann, R. R. Tykwinski, S. R. Parkin and J. E. Anthony, Appl. Phys. Lett., 2006, 89, 192113 CrossRef.
- F. Frausto, Z. C. Smith, T. E. Haas and S. W. Thomas III, Chem. Commun., 2015, 51, 8825–8828 RSC.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- J. Casado, M. Moreno Oliva, M. C. Ruiz Delgado, R. Ponce Ortiz, J. Joaquín Quirante, J. T. López Navarrete, K. Takimiya and T. Otsubo, J. Phys. Chem. A, 2006, 110, 7422–7430 CrossRef CAS PubMed.
- J. E. Anthony, A. Facchetti, M. Heeney, S. R. Marder and X. Zhan, Adv. Mater., 2010, 22, 3876–3892 CrossRef CAS PubMed.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- R. Precht, R. Hausbrand and W. Jaegermann, Phys. Chem. Chem. Phys., 2015, 17, 6588–6596 RSC.
- M. Bokdam, D. Çakır, G. Brocks, D. Akr and G. Brocks, Appl. Phys. Lett., 2011, 98, 113303 CrossRef.
- G. Liu, S. Xun, N. Vukmirovic, X. Song, P. Olalde-Velasco, H. Zheng, V. S. Battaglia, L. Wang and W. Yang, Adv. Mater., 2011, 23, 4679–4683 CrossRef CAS PubMed.
- T. Yasuda and N. Ogihara, Chem. Commun., 2014, 50, 11565–11567 RSC.
- X. Zhu, R. Zhao, W. Deng, X. Ai, H. Yang and Y. Cao, Electrochim. Acta, 2015, 178, 55–59 CrossRef CAS.
- H. Fei, Y. Liu, Y. An, X. Xu, G. Zeng, Y. Tian, L. Ci, B. Xi, S. Xiong and J. Feng, J. Power Sources, 2018, 399, 294–298 CrossRef CAS.
- M. Nisula and M. Karppinen, J. Mater. Chem. A, 2018, 6, 7027–7033 RSC.
- W. Wei, L. Li, L. Zhang, J. Hong and G. He, Electrochem. Commun., 2018, 90, 21–25 CrossRef CAS.
- X. Chi, Y. Liang, F. Hao, Y. Zhang, J. Whiteley, H. Dong, P. Hu, S. Lee and Y. Yao, Angew. Chem., Int. Ed., 2018, 57, 2630–2634 CrossRef CAS PubMed.
- W. Li, L. Chen, Y. Sun, C. Wang, Y. Wang and Y. Xia, Solid State Ionics, 2017, 300, 114–119 CrossRef CAS.
- Z. Zhu, M. Hong, D. Guo, J. Shi, Z. Tao and J. Chen, J. Am. Chem. Soc., 2014, 136, 16461–16464 CrossRef CAS PubMed.
- Y. Hanyu, Y. Ganbe and I. Honma, J. Power Sources, 2013, 221, 186–190 CrossRef CAS.
- C. Luo, X. Ji, J. Chen, K. J. Gaskell, X. He, Y. Liang, J. Jiang and C. Wang, Angew. Chem., Int. Ed., 2018, 57, 8567–8571 CrossRef CAS PubMed.
- K. Kerman, A. Luntz, V. Viswanathan, Y.-M. Chiang and Z. Chen, J. Electrochem. Soc., 2017, 164, A1731–A1744 CrossRef CAS.
- J. Mindemark, B. Sun, E. Törmä and D. Brandell, J. Power Sources, 2015, 298, 166–170 CrossRef CAS.
- N. U. Taib and N. H. Idris, J. Membr. Sci., 2014, 468, 149–154 CrossRef CAS.
- Y. Zhang, Y. An, S. Dong, J. Jiang, H. Dou and X. Zhang, J. Phys. Chem. C, 2018, 122, 22294–22300 CrossRef CAS.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef CAS.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS.
- J. Liu and X. Sun, Nanotechnology, 2015, 26, 24001 CrossRef CAS PubMed.
- X. Yu and A. Manthiram, Energy Environ. Sci., 2018, 11, 527–543 RSC.
- B. Wu, S. Wang, W. J. Evans, D. Z. Deng, J. Yang and J. Xiao, J. Mater. Chem. A, 2016, 4, 15266–15280 RSC.
- F. Hao, F. Han, Y. Liang, C. Wang and Y. Yao, MRS Bull., 2018, 43, 775–781 CrossRef CAS.
- J. Haruyama, K. Sodeyama, L. Han, K. Takada and Y. Tateyama, Chem. Mater., 2014, 26, 4248–4255 CrossRef CAS.
- M. Nisula, Y. Shindo, H. Koga and M. Karppinen, Chem. Mater., 2015, 27, 6987–6993 CrossRef CAS.
- F. Gschwind, G. Rodriguez-Garcia, D. J. S. Sandbeck, A. Gross, M. Weil, M. Fichtner and N. Hö Rmann, J. Fluorine Chem., 2016, 182, 76–90 CrossRef CAS.
- I. Darolles, C. M. Weiss, M. M. Alam, A. Tiruvannamalai and S. C. Simon, US9166249B2, 2011.
- A. Unemoto, Y. Iwai, S. Mitani, S.-W. Baek, S. Ito, T. Tomai, J. Kawamura and I. Honma, Solid State Ionics, 2011, 201, 11–20 CrossRef CAS.
- Y. Chen, W. Luo, M. Carter, L. Zhou, J. Dai, K. Fu, S. Lacey, T. Li, J. Wan, X. Han, Y. Bao and L. Hu, Nano Energy, 2015, 18, 205–211 CrossRef CAS.
- W. Wei, L. Li, L. Zhang, J. Hong and G. He, Mater. Lett., 2018, 213, 126–130 CrossRef CAS.
- X. Chi, F. Hao, J. Zhang, X. Wu, Y. Zhang, S. Gheytani, Z. Wen and Y. Yao, Nano Energy, 2019, 62, 718–724 CrossRef CAS.
- P. Sundberg and M. Karppinen, Beilstein J. Nanotechnol., 2014, 5, 1104–1136 CrossRef PubMed.
- Y. S. Jung, A. S. Cavanagh, L. A. Riley, S.-H. Kang, A. C. Dillon, M. D. Groner, S. M. George and S.-H. Lee, Adv. Mater., 2010, 22, 2172–2176 CrossRef CAS.
- L. Zhao, J. Zhao, Y. S. Hu, H. Li, Z. Zhou, M. Armand and L. Chen, Adv. Energy Mater., 2012, 2, 962–965 CrossRef CAS.
- C. Luo, J. Wang, X. Fan, Y. Zhu, F. Han, L. Suo and C. Wang, Nano Energy, 2015, 13, 537–545 CrossRef CAS.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059 RSC.
- Y. Y. Zhang, Y. Y. Sun, S. X. Du, H.-J. Gao and S. B. Zhang, Appl. Phys. Lett., 2012, 100, 1–4 Search PubMed.
- N. Ogihara, T. Yasuda, Y. Kishida, T. Ohsuna, K. Miyamoto and N. Ohba, Angew. Chem., Int. Ed., 2014, 53, 11467–11472 CrossRef CAS PubMed.
- S. Schweidler, L. de Biasi, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2018, 122, 8829–8835 CrossRef CAS.
- L. Ma, R. B. Nuwayhid, T. Wu, Y. Lei, K. Amine and J. Lu, Adv. Mater. Interfaces, 2016, 3, 1600564 CrossRef.
- J. Penttinen, M. Nisula and M. Karppinen, Chem.–Eur. J., 2017, 23, 18225–18231 CrossRef CAS PubMed.
- A. Tanskanen and M. Karppinen, Sci. Rep., 2018, 8, 8976 CrossRef CAS PubMed.
- A. Khayyami and M. Karppinen, Chem. Mater., 2018, 30, 5904–5911 CrossRef CAS PubMed.
- K. B. Klepper, O. Nilsen and H. Fjellvåg, Dalton Trans., 2010, 39, 11628 RSC.
- K. B. Lausund, V. Petrovic and O. Nilsen, Dalton Trans., 2017, 46, 16983–16992 RSC.
- A. J. Pearse, T. E. Schmitt, E. J. Fuller, F. El-Gabaly, C.-F. Lin, K. Gerasopoulos, A. C. Kozen, A. A. Talin, G. Rubloff and K. E. Gregorczyk, Chem. Mater., 2017, 29, 3740–3753 CrossRef CAS.
- S. Moitzheim, J. E. Balder, R. Ritasalo, S. Ek, P. Poodt, S. Unnikrishnan, S. De Gendt and P. M. Vereecken, ACS Appl. Energy Mater., 2019, 2, 1774–1783 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |