Open Access Article
Open Access ArticleLiquid-phase exfoliation of graphite into graphene nanosheets in a hydrocavitating ‘lab-on-a-chip’
Xiaoyu
Qiu
a,
Vincent
Bouchiat
b,
Damien
Colombet
a and
Frederic
Ayela
 *a
*a
aLaboratoire des Ecoulements Geophysiques et Industriels, Univ. Grenoble Alpes, CNRS, 38000 Grenoble, France. E-mail: frederic.ayela@legi.cnrs.fr
bInstitut Néel, CNRS, 25 Avenue des Martyrs, 38000 Grenoble, France. E-mail: vincent.bouchiat@neel.cnrs.fr
First published on 24th January 2019
Abstract
Hydrodynamic cavitation ‘on a chip’ has been used to achieve liquid-phase exfoliation of natural graphite to get graphene. We have taken advantage of the small size of such a ‘lab-on-a-chip’ (LOC) with low input-power consumption, to produce afterwards few layers of graphene nanosheets in a surfactant suspension. Characterization of the processed material has been performed by TGA analysis, SEM, TEM, AFM and Raman measurements. Observations have demonstrated the presence of monolayers and few layers of graphene with a lateral size around 300 nm, exfoliated from a graphite powder suspension flowing through the microsystem.
1. Introduction
Since the first report of its production in 2004,1 graphene has been attracting a lot of interest in the nanomaterials area.2 Enormous efforts have been attempted to achieve all the powerful applications made possible by its excellent properties, for example in areas ranging from printed electronics, conductive coatings, to polymer-based composite fillers.3 Industrial-scale production of graphene at low cost is therefore becoming critically important. Liquid-phase exfoliation, which is a versatile technique, has proved to produce large quantities of defect-free nanosheets of graphene.4,5 This technique is funded either on sonication,6–11 or on liquid single-phase high-shear rate flow,12–16 as well as hydrodynamic cavitation.17–20 Moreover, liquid phase exfoliation can be performed with aqueous solutions, thus being a so-called green process. Among all these methods, sonication has been widely employed because of its simplicity of implementation. But the inhomogeneity of the acoustic field and the limited amount of solution that can be processed are serious limiting factors for the use of sonication as an industrial method. Furthermore, the use of more advanced hydrodynamic techniques such as cavitation and high-shear mixing, which are up-scalable and more homogeneous processes, are presented by only a few researchers.12–18,20–23 The formation of microjets and the high-shear rate induced in the flow are both thought to be responsible for the particle exfoliation in hydrodynamic cavitation.13–19 Although graphite flakes are linked by the weak van der Waals interaction, authors attempt to apply high pressure input13,18,19 (>20 MPa) to macroscopic set-up, in order to get high-shear rates together with cavitating flows. Recently, a mixed approach, funded on both sonication and microfluidization of graphite, has been proposed.24,25 The respective role hold by the collapsing bubbles and by the turbulent shear rate in the exfoliation process is not clearly understood. Knowing whether or not high input pressures are required to perform liquid-phase exfoliation is still an open question.Performing liquid-phase exfoliation under moderate pressure drops (i.e. below 10 bars) means that the required hydraulic power, which is the product of the pressure drop by the flow rate, would be low. That could offer an exciting opening for any further industrial development of what would provide a low-energy and green process. A question arises then, about the ability to reach high-shear rates and/or cavitating flows together with a low-pressure input. Lab-on-a-chip (LOC) technology may offer a wonderful opportunity to achieve that challenge, because hydrodynamic cavitation ‘on-a-chip’ inside a microchannel has been demonstrated in the past.26,27 The small sizes of a microchannel make possible an integration of the set-up in clean rooms or in any other devoted environment. Furthermore a lot of microchannels may be machined in a parallel array onto a single wafer, so the flow rate of the liquid under test may be consequent. Within the scope of fundamental studies, LOC allow to scrutinize easily different sorts of flow regimes (laminar, turbulent, single-liquid phase or cavitating flows) with high-shear rates. The ultimate size reduction is limited by the size of the initial pristine graphite particles, which must not clog the channel. In this paper, we have employed a low input-pressure cavitating lab-on-a-chip to exfoliate surfactant stabilized graphene from natural graphite powder. The bubbles collapse and the high shear rates are believed to exfoliate therefore graphitic particles. Atomic force microscopy (AFM), Raman spectroscopy and Transmission electron microscopy (TEM) show that a large number of monolayers of graphene are present in the processed solution.
2. Experimental methods
2.1. Experimental set up and exfoliation process
The graphite powder used in the experiments presented here was purchased from Sigma-Aldrich (production number 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2863, <20 μm) and used without further treatment. The graphite powder was dispersed in 400 mL of deionized water at a solid concentration of 50 g L−1, the suspension was stabilized by Sodium Cholate (SC, Sigma C1254-25g) surfactant at a concentration of 1 g L−1 (that initial suspension is referenced as A0). The choice of the ratio 1
2863, <20 μm) and used without further treatment. The graphite powder was dispersed in 400 mL of deionized water at a solid concentration of 50 g L−1, the suspension was stabilized by Sodium Cholate (SC, Sigma C1254-25g) surfactant at a concentration of 1 g L−1 (that initial suspension is referenced as A0). The choice of the ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 between sodium cholate and graphite concentrations was motivated by former studies devoted to the optimisation of surfactant concentration.8
50 between sodium cholate and graphite concentrations was motivated by former studies devoted to the optimisation of surfactant concentration.8
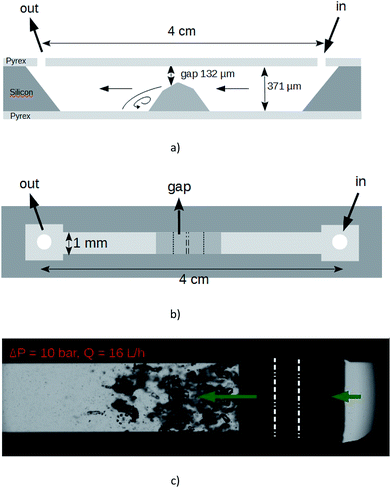
The suspension was furthermore exfoliated through a lab-on-a-chip (LOC). The device, which is micromachined on a silicon wafer, integrates one straight channel several millimeters long with a localized microstep at the middle length giving way to a gap of height 132 μm in the microchannel whose total height and width are 371 μm and 1 mm respectively.28 The machined silicon part is anodically bonded between two flat Pyrex caps. The profile of the Pyrex–silicon–Pyrex microfluidic device under test is shown in Fig. 1. The hydraulic connections and the fluid delivery have been described elsewhere.28 With that device under test, cavitation occurs above a pressure drop Pin − Pout ≈ 7 bars. In our experiments, the applied pressure drop was 10 bars, corresponding to a flow rate of 16 L h−1. An illustration of the cavitating microflow with pure deionized water is shown in Fig. 1(c). Note that the forthcoming presence of graphitic microparticles will not affect the hydraulic characteristics of the flow. During the experiments with the particles in the liquid solutions, the average particle velocity was 14 m s−1 inside the main channel and 33 m s−1 through the gap. An electronic control system has been developed to ensure a steady flow supply with a back and forth motion of the fluid between input and output tanks. The symmetry of the channel made possible the inception of cavitation whatever the direction of the fluid was. The onset of cavitation is the consequence of the increase of the dynamical pressure above a critical level, in the gap above the microstep. Bubbles collapse downstream where the average velocity of the fluid falls back to its initial value. As the channel is 4 cm long, each particle resides a time lapse below 2.8 ms inside the microchannel at each pass. But it is uneasy to define the exact length of time during which each particle is really submitted to bubbles collapse, as the collapse occurs downstream the step and in a recirculating area. We state that an useful duration of the process for each particle should be of a few seconds. So, for each experiment, the graphite solution was submitted to ≈2000 passes. After each experiment, a sample of the processed solution (referenced as A1) was selected in order to be subjected to a liquid cascade centrifugation.29
The sample was firstly centrifuged at 2 krpm (563 g) for 1 h. Then, the supernatant (named A1-1) was centrifuged at 3 krpm (1267 g) for 1 h. The resulting supernatant (referenced as A1-2) and the resulting dark sediment (referenced as A1-3) were collected. Samples A1-2 were used only for thermal gravimetry analysis (TGA) and UV Vis spectroscopy. Further characterization was performed on samples A1-3. That two steps centrifuge process, where it is the sediment resulting from an initial supernatant volume which is analyzed, allows fading away large unexfoliated particles and small particles. By considering the relationship between spherical particles and centrifugation acceleration, the two acceleration rates selected here let expect the selection of spherical particles with diameter D such as 100 nm < D < 200 nm.18 By considering also the centrifugal velocity of thin plates, which is different from that of spherical particles, we estimate that most of the produced nanosheets, if any, should be present in the solution A1-3.
2.2. Characterization methods
The suspensions were firstly visualized by Scanning Electron Microscopy (Leo 1530) before and after the process. The resulting concentration of exfoliated nanosheets was measured by thermal gravimetry analysis (TGA) (DSC-TGA3+, Mettler-Toledo). Then, UV-Vis absorption spectroscopy (Hitachi UH5300) has lead to the determination of the extinction coefficient α obeying the Beer lambert law A = αCGl, where A is the absorbance measured at 660 nm, l the length passed by the light (1 cm) and CG the solid concentration. The profile of the particles isolated by the centrifugation process was furthermore investigated, by using transmission electron microscopy (TEM, Philips-FEI microscope operating at an accelerating voltage of 200 kV and equipped with a TVIPS TemCam F216 camera). In order to determine the number of layers per flakes and the presence of monolayers, measurements by Atomic Force Microscopy (Veeco NS V apparatus) have been realized. Furthermore, Raman spectra were acquired using a WITec alpha 500 Raman microscope, with a 532 nm laser excitation wavelength and a 600 g mm−1 grating.3. Results
3.1. SEM observations
Fig. 2(a) shows that the pristine graphite powder (batch A0) consists of polydispersed flakes with a lateral size below 50 μm, and a thickness below 10 μm, according to the data supplied by the furnisher. In comparison, the SEM observation of the suspension issued from the batch A1, after the 2016 passes, has demonstrated that the process had a significant mechanical impact on the graphite particles; the average size of the particles is much smaller and they look like more homogenous, with a lateral size below 10 μm and with now a thickness of a few micrometers (Fig. 2(b)). As a matter of fact, the homogeneous phase of the A1 solution remains over longer timeframes than the original one A0, for which a total settling occurs after typically four days. Moreover, the suspension obtained after centrifugation (batch A1-3, Fig. 2(c)) showed as expected only a large number of small flakes with a lateral size below <1 μm and a thickness much smaller than what was mainly observed in the batch A1. Such concentrated flakes were never present in the unprocessed solutions which were submitted to the same centrifugation steps. It is obvious that the process inside the microchannel has resulted in exfoliation and fragmentation of the pristine particles. We note that the clear border in SEM image may result from charges accumulation onto electrically insulating surfactant.3.2. TGA analysis and UV Vis spectroscopy
TGA measurements were performed on A1-2 and A1-3 samples (supernatant and sediment extracted from the sample A1-1 after the second centrifugation). As expected, the solid concentration CG,3 measured in samples A1-3 is higher than the solid concentration CG,2 measured in samples A1-2. The measured values correspond to a solid concentration CG,1 in the supernatant A1-1 obeying 1.32 g L−1 < CG,1 < 1.50 g L−1, whereas the solid concentration in the sediment A1-3 can reach CG,3 ≈ 10 g L−1. These solid concentrations measured by TGA analysis are in agreement with the absorbances A measured on samples A1-i (i = 1, 2, 3) at several levels of dilution. We find an experimental coefficient of extinction α = 1816 ± 182 L g−1 m−1. As the particle population or surfactant concentration present in a solution submitted to a liquid phase exfoliation process would influence the absorbance, various values of α have been published in the literature.6,8,9,12,13,18,30,31 In graphene\SC\water systems, the published values of that coefficient are α = 3778 L g−1 m−1 (ref. 12) (50 g L−1 initial graphite with 5 g L−1 SC) or α = 1458 L g−1 m−1 (ref. 31) and α = 6600 L g−1 m−1 (ref. 8) (5 g L−1 initial graphite with 0.1 g L−1 SC). Our experimental value of α is in the range of magnitude of these published data.3.3. TEM observations
In order to minimize aggregation of the flakes during the deposition of a droplet onto the grid, the suspension A1-3 was diluted 25 times (A1-3-25×) before analysis. A drop of the dispersion A1-3-25× was deposited onto a carbon grid. An example of TEM images is shown in Fig. 3(a). There are several small particles in the dispersion, and a statistic analysis of the dimensions of 100 isolated particles has demonstrated that their mean lateral sizes were around 200–400 nm (Fig. 3(b)). | ||
| Fig. 3 (a) TEM images of graphene flakes (sample A1-3 diluted 25×); (b) histogram analysis of the lateral dimensions of 100 isolated particles extracted from TEM images similar to that of (a). | ||
3.4. AFM profiles
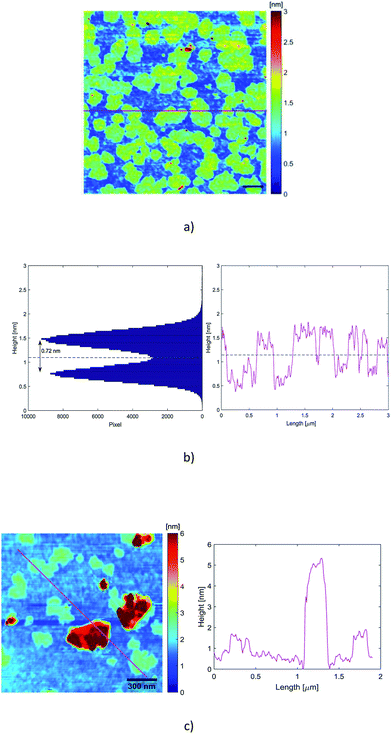
In our experiments, the suitable dispersion exhibiting minor aggregation of the flakes was obtained when the dispersion A1-3 was diluted 125 times with deionized water (A1-3-125×). Therefore, a 10 μL drop of that dispersion was drop-casted on a preheated (120 °C) Si/SiO2 substrate (0.5 cm × 0.5 cm, 300 nm thick oxide). After deposition, the wafer was rinsed in a beaker of 10 mL deionized water and a beaker of 10 mL isopropanol in order to remove exceeding surfactant as much as possible. For our AFM images, scanning parameters were adapted on each measurement. Image sizes ranged from 0.5 to 5 μm, with 1024 samples per line and 256 lines per image. Each line was scanned at a frequency of 0.5 Hz. Only regions without evident aggregated particles were scrutinized.Fig. 4 displays mappings, height profiles and histogram analysis of homogeneous sets of nanosheets. As we can see from the height profiles, the top and bottom areas exhibit some roughness of similar level. That means that the surfactant has not been completely removed from the substrate and that it is also encompassing the nanosheets, contributing to the total measured height of the nanoparticles. An exact height analysis must take into account both the presence on the substrate of residual surfactant without any embedded particle inside, and the presence of graphene nanosheets embedded in the surfactant.
The average thickness of the residual surfactant free from nanosheets has been determined from the analysis of the height profiles recorded by the scan. The thickness of the residual surfactant has been found to be 0.32 nm ± 0.10 nm. The histogram analysis in Fig. 4(b) exhibits two peaks corresponding on the one hand to the residual surfactant covering the ground level and on the other hand to the top of the embedded nanosheets. The average height of the residual surfactant displayed by the histogram in Fig. 4 (0.75 nm ± 0.10 nm) does not match the average measured thickness obtained from the scans, because the origin of the height axis has been fixed by the deepest point of the scan. So, a slight tilt of the substrate behind the horizontal position is likely to shift regularly and to broaden the two peaks of the histogram.
The histogram and the height profiles indicate that the average distance between the flakes and the substrate is 0.72 nm ± 0.20 nm (Fig. 4(b)). That distance integrates the thickness of the surfactant embedding the spreaded nanosheets. So, these values are consistent with the presence of single layer graphene. There are also some relatively thick particles, as displayed in Fig. 4(c) where the profile looks like one of a few layers nanosheet.
3.5. Raman spectroscopy
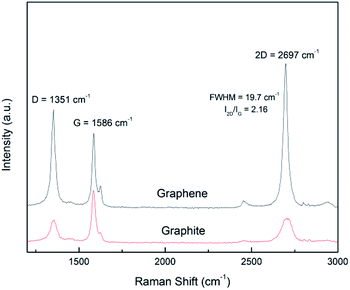
Raman spectroscopy is a versatile tool for scrutinizing the quality of graphene nanosheets. Three bands are commonly recorded:32 D peak (∼1350 cm−1), G peak (∼1580 cm−1) and 2D peak (∼2700 cm−1). In comparison to graphite, a graphene monolayer will exhibit a 2D peak shifted down to a lower wavenumber, with a full width at half maximum (FWHM) below 25 cm−1 and with a intensity greater than the one of the G peak.32 Moreover, it has been noticed that a FWHM greater than 65 cm−1 corresponds to more than 5 stacked layers in the flake.33 The ratio of the intensities ID/IG is inversely related to the average length between two structural defaults.34 However, for small sized particles as nanosheets containing edges which act as defects, this ratio is an alternative path to get the lateral average size 〈L〉 of the particles.7,12 It has been proposed35 that ID/IG = ID/IG powder + k/〈L (μm)〉 with 0.17 < k < 0.26.In Fig. 5 are displayed the spectra recorded from a pristine graphite particle (red) and from a processed flake (black) respectively. Three characteristic features of the presence of graphene are present: the increase of the ratio of the amplitudes of the 2D and G peaks (I2D/IG > 2), the sharpening of the full width at half maximum (FWHM) of the 2D peak and its shift to a lower wavenumber. Regarding the increase of the ratio ID/IG and considering it is related to the lateral size of the nanosheets, the application of the former relationship with 0.17 < k < 0.26 leads to 210 nm < 〈L〉 < 320 nm. That is in perfect agreement with the histogram recorded from the TEM observations and displayed in Fig. 3(b).
4. Discussion
The liquid phase exfoliation, inside a LOC, of 20 μm graphitic particles, obeying the process presented here (pressure driven flow with ΔP = 10 bars, two phase cavitating flow, 2000 passes, initial solid concentration 50 g L−1 with 1 g L−1 of surfactant) has been performed five times and has given repeatable results. Various physical parameters are involved in the liquid phase exfoliation of graphene by hydrodynamic cavitation: pressure drop, duration of the process, solid and surfactant concentrations, type of cavitation. The experiments presented here were devoted to demonstrate the possibility to exfoliate graphene with a low power hydraulic microdevice, and ΔP = 10 bars was the upper fixed limit. The parameters that have been scrutinized were the duration of the process (i.e. the number of passes through the device) for an initial 50 g L−1 graphite solution, and the initial graphite solid concentration for a duration of the process of ≈5.6 seconds. We have noted a slight decrease of the final nanosheets concentration above 2500 passes. That is explained by a possible damage of the surfactant submitted to both cavitation and shearing, as a damaged surfactant cannot prevent from van der Waals bonding of nanosheets anymore. The solid concentration of the graphite particles has proven to be a key parameter. Supplementary experiments have been performed at ΔP = 10 bars but with a solid concentration of 10 g L−1 together with 0.2 g L−1 of sodium cholate surfactant. The average absorbances of the corresponding centrifugated solutions A-1 were around A ≈ 2 corresponding to a nanosheet concentration of 0.11 g L−1. For a cavitating flow of fixed intensity, increasing the initial pristine graphite concentration has non-linearly increased the final concentration of graphene nanosheets. We believe that mechanical interactions between micron-sized particles may enhance the exfoliation process. A loading of 50 g L−1 of graphite particles corresponds to a volumetric concentration of 2.3%. Considering that the particles have a spherical shape of diameter 20 μm, it can be shown that the average distance between two neighbouring particles is ≈40 μm. That distance raises up to 80 μm when considering a solid concentration of 10 g L−1. Mechanical interactions between graphite particles, enhanced by cavitation, are thus likely to promote graphene yields.5. Conclusions
The 0.4 liter of a 50 g L−1 pristine graphite suspension has been processed through a cavitating microchannel around 2000 times with a pressure drop of 10 bars and a flow rate of 16 L h−1. It corresponds to a hydraulic power and to a relative energetic consumption of ≈ 5W and 2 MJ L−1 respectively.We have demonstrated that such a low-power microfluidic system is able to produce, by hydrodynamic cavitation ‘on-a-chip’, relatively large quantities of homogeneous small flakes down to graphene monolayers. The experiments presented here, which obey a green process, were performed five times and gave repeatable results. We got a yield of production of graphenic nanosheets that is 2.5 g for an energy cost of 1 kW h. Various physical parameters are involved in the liquid phase exfoliation of graphene by hydrodynamic cavitation: pressure drop, duration of the process, solid and surfactant concentrations, type of cavitation. In this paper, we have focused on an operation at a fixed moderate pressure drop inside a designed microchannel. Our results indicate that long duration but low power processes are likely to produce relatively high quantity and high quality nanosheets, enhanced by an adequate initial solid concentration of the pristine graphite. As a very low input power is required for this system, an attractive industrial and green production of graphene becomes possible, by imagining an array of parallel cavitating microreactors. Further experiments will have to be performed, to browse the different flow regimes that can be studied with a given set of reactors, such as single-phase laminar or turbulent liquid flow. The ability to study these different flow regimes with microsystems is one of the added values of a LOC. This unique advantage would give us more fundamental informations about the respective contribution of shear rate, bubble collapse, and particles interactions to the exfoliation process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by a financial support from the C.N.R.S. (Projets Exploratoires Premier Soutien, INSIS). The teams of the Nanofab platform and of the Electron Microscopy Platform of the Néel Institute are greatly acknowledged for technical support and having granted access to SEM, AFM, TEM and Raman equipment. Special thanks to B. Fernandez (SEM micrographs). The TEM images were recorded by Dr J.-L. Putaux (CERMAV) and the authors thank the NanoBio-ICMG Platform (FR 2607, Grenoble, France), for granting access to the electron microscopy facility. TGA analyses have been performed by Dr A. Fernandez-Martinez within the analytical chemistry platform of ISTerre (OSUG – France). The AFM images were recorded with the help of S. Le Denmat. The Raman spectrum was recorded with the help of R. Othmen and W. Liu. We thank Dr J.-L. Putaux, C. Lancelon-Pin (CERMAV) and J.-M. Barnoud (LEGI) for their help and for useful discussions.Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS
.
- C. E. E. Rao, A. E. Sood, K. E. Subrahmanyam and A. Govindaraj, Angew. Chem., Int. Ed., 2009, 48(42), 7752–7777 CrossRef CAS
.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS
.
- M. Yi and Z. Shen, J. Mater. Chem. A, 2015, 3, 11700–11715 RSC
.
- Y. Wei and Z. Sun, Curr. Opin. Colloid Interface Sci., 2015, 20, 311–321 CrossRef CAS
.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun’ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS PubMed
.
- U. Khan, A. O'Neill, M. Lotya, S. De and J. N. Coleman, Small, 2010, 6, 864–871 CrossRef CAS
.
- M. Lotya, P. J. King, U. Khan, S. De and J. N. Coleman, ACS Nano, 2010, 4, 3155–3162 CrossRef CAS
.
- M. Buzaglo, M. Shtein, S. Kober, R. Lovrincic, A. Vilan and O. Regev O, Phys. Chem. Chem. Phys., 2013, 15, 4428 RSC
.
- J. Shen,
et al.
, Nano Lett., 2015, 15, 5449–5454 CrossRef CAS
.
- A. Ciesielski and P. Samori, Chem. Soc. Rev., 2014, 43, 381–398 RSC
.
- K. R. Paton,
et al.
, Nat. Mater., 2014, 13, 624–630 CrossRef CAS
.
- Y. Arao, Y. Mizuno, K. Araki and M. Kubouchi, Carbon, 2016, 102, 330–338 CrossRef CAS
.
- X. Chen, J. F. Dobson and C. L. Raston, Chem. Commun., 2012, 48, 3703–3705 RSC
.
- J. Shang, F. Xue and E. Ding, Chem. Commun., 2015, 51, 15811–15814 RSC
.
- P. G. Karagiannidis,
et al.
, ACS Nano, 2017, 11, 2742–2755 CrossRef CAS
.
- L. Liu, Z. Shen, M. Yi, X. Zhang and S. Ma, RSC Adv., 2014, 4, 36464–36470 RSC
.
- T. J. Nacken, C. Damm, J. Walter, A. Ruger and W. Peukert, RSC Adv., 2015, 5, 57328–57338 RSC
.
- M. Yi, Z. Shen, W. Zhang, J. Zhu, L. Liu, S. Liang, X. Zhang and S. Ma, Nanoscale, 2013, 5, 10660–10667 RSC
.
- Z. Shen, J. Li, M. Yi, X. Zhang and S. Ma, Nanotechnology, 2011, 22, 365306 CrossRef
.
- M. Yi, J. Li, Z. Shen, X. Zhang and S. Ma, Appl. Phys. Lett., 2011, 99, 123112 CrossRef
.
- S. Liang, Y. Min, Z. Shen, L. Liu, X. Zhang and S. Ma, RSC Adv., 2014, 4, 16127–16131 RSC
.
- M. Yi and Z. Shen, Carbon, 2014, 78, 622–626 CrossRef CAS
.
- W. Liu, V. A. Tanna, B. M. Yavitt, C. Dimitrakopoulos and H. H. Winter, ACS Appl. Mater. Interfaces, 2015, 7, 27027 CrossRef CAS
.
- Y. Z. Wang, T. Chen, X. F. Gao, H. H. Liu and X. X. Zhang, Mater. Express, 2017, 7, 491–499 CrossRef CAS
.
- M. Medrano, P. J. Zermatten, C. Pellone, J. P. Franc and F. Ayela, Phys. Fluids, 2011, 23, 127103 CrossRef
.
- M. Medrano, C. Pellone, P. J. Zermatten and F. Ayela, Phys. Fluids, 2012, 24, 047101 CrossRef
.
- X. Qiu, W. Cherief, D. Colombet and F. Ayela, J. Micromech. Microeng., 2017, 27, 047001 CrossRef
.
- C. Backes,
et al.
, ACS Nano, 2016, 10, 1589–1601 CrossRef CAS PubMed
.
- M. Lotya,
et al.
, J. Am. Chem. Soc., 2009, 131, 3611–3620 CrossRef CAS
.
- S. Wang, M. Yi and Z. Shen, RSC Adv., 2016, 6, 56705–56710 RSC
.
- A. C. Ferrari,
et al.
, Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS
.
- D. Graf, F. Molitor, K. Ensslin, C. Stampfer, A. Jungen, C. Hierold and L. Wirtz, Nano Lett., 2007, 7, 238–242 CrossRef CAS PubMed
.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126–1130 CrossRef CAS
.
- U. Khan, A. O'Neill, H. Porwal, P. May, K. Nawaz and J. N. Coleman, Carbon, 2012, 50, 470–475 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2019 |