Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measuring the relative concentration of particle populations using differential centrifugal sedimentation†
Alexander G.
Shard
 a,
Katia
Sparnacci
a,
Katia
Sparnacci
 b,
Aneta
Sikora‡
a,
Louise
Wright
a,
Dorota
Bartczak
b,
Aneta
Sikora‡
a,
Louise
Wright
a,
Dorota
Bartczak
 c,
Heidi
Goenaga-Infante
c and
Caterina
Minelli
c,
Heidi
Goenaga-Infante
c and
Caterina
Minelli
 *a
*a
aNational Physical Laboratory, Hampton Road, Teddington, Middlesex TW11 0LW, UK. E-mail: caterina.minelli@npl.co.uk; Fax: +44 (0)20 8943 6453; Tel: +44 (0)20 8943 6689
bUniversità del Piemonte Orientale “A. Avogadro”, Viale T. Michel 11, I-15121 Alessandria, Italy
cLGC Limited, Queens Road, Teddington, Middlesex TW11 0LY, UK
First published on 30th May 2018
Abstract
The factors that affect the accuracy and precision of differential centrifugal sedimentation (DCS) for the analysis of nanoparticle concentration are described. Particles are separated by their sedimentation rate and detected using light absorption. In principle, the relative concentration of particles in different populations can be found, but the uncertainty in such measurements is unclear. We show that the most appropriate measurement of particle concentration using this technique is the mass concentration, rather than the number concentration. The relative mass concentration of two discrete populations can be measured with reasonable precision, usually without resorting to complicated data analysis. We provide practical approaches to find the relative mass concentrations for two cases: spherical particles of different materials and agglomerated particles of the same material. For spherical particles made of different materials, naïve analysis of the results can provide relative mass concentrations that are many orders of magnitude in error. Correction factors can be calculated that reduce the error to less than 50%. In the case of agglomerated particles we show that errors of less than 20% are possible and demonstrate, in the case of gold particles, that a combination of UV-visible spectroscopy and DCS enable practical values of mass and number based particle concentrations to be obtained.
Introduction
The unique advantages of nanoparticles can only be realised with sufficient specification of shape, size, concentration, aggregation state and surface chemistry. It is critically important that dispersity in these parameters is understood and controlled. The measurement of absolute concentration is particularly important because this parameter is important to ensure repeatability in processing, performance and, in biological settings, dose. Relative concentrations within a particle population directly impact the measurement of average particle size and agglomeration. Therefore, analytical methods which are capable of measuring both the absolute1 and the relative concentrations of particles within discrete populations require particular attention and development. Such measurements are used to establish the size distribution of particles, where the distribution can be thought of as a combination of many discrete populations. Whilst many analytical methods provide a representation of the size distribution of nanoparticles, it is unclear whether they are accurate due to material, size and shape dependent biases.2–6Many commonly employed methods are able to provide accurate measurements under the ideal conditions of perfect sphericity, homogeneous composition and monodispersity, but struggle to produce meaningful results if these conditions are not met. For example, the ability to distinguish two populations of different spherical diameters from a monodisperse population of rod-like particles is a particular issue for a number of routine population-based approaches. Another rather common problem in the preparation of particles for biological and sensing applications is the aggregation of particles during processing steps.7
One of the most appropriate strategies to overcome this analytical problem is to separate the particles prior to detection and analysis for example, using field-flow fractionation8 or analytical ultracentrifugation9 with a variety of detection or measurement methods. One of the critical issues is the translation of the detection signal into a useful measure of relative concentration.
If the particle separation process provides highly resolved particle populations and the sample is sufficiently understood then the detection method can be rather simple. In the case of differential centrifugal sedimentation (DCS), the typical relative resolution in particle diameter is 5% which, in the case of well controlled particles, is more than sufficient to separate distinct populations of particles. The detection method is usually based upon light attenuation which, provided the refractive indices of the particle components and fluid are known, along with the shape and internal structure of the particles, provides sufficient information to measure the relative concentration of particles in different populations. Whilst the requirement for detailed understanding of the optical properties of the particles seems overwhelming, in many cases these can be reasonably approximated without incurring significant error. Here, we show that the absolute measurement of particle concentration could be rather inaccurate with DCS, but the measurement of relative concentrations between different populations are quite reasonable. If the particle populations are different shapes and sizes of the same material then, usually, the accuracy in the relative mass concentration of the populations can be within 20%.
Theory
In a DCS experiment, the instrument records the intensity of light at a given wavelength transmitted through a liquid medium as a function of time. Here, we consider a particle population with low dispersity (<10%) in size and shape such that useful mean values can be found for parameters such as diameter and extinction cross sections.The time scale is converted into a particle diameter, D, based upon various densities, viscosities and instrumental parameters that are either measured or assumed. The intensity scale is converted into a total mass per diameter step, M/ΔD, scale using eqn (1), which is justified in the ESI S.1.†
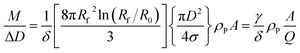 | (1) |
The total mass of a monodisperse particle population is obtained by integrating the mass scale over its diameter range in the data. By equating ΔD with the infinitesimal dD, eqn (1) can be integrated to provide eqn (2):
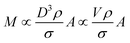 | (2) |
Eqn (2) is valid if the particle density and extinction cross sections are known. In principle, to correct the measured mass Mm into the true mass, M, a conversion factor is required, this is defined in eqn (3), and is also given in ESI S.2.†
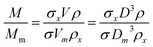 | (3) |
If two particle populations are present in the data, it is possible to determine the relative mass or number concentration by adapting eqn (3). The two populations are designated ‘A’ and ‘B’ and their relative mass in the sample w = (MA/MB) can be found from their measured relative mass Mm in a single experiment. The relationship is expressed in eqn (4).
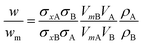 | (4) |
Different materials
We consider a simple case of two monodisperse populations of spherical particles made of different materials and the data analysed using the properties of particle A. Mixtures of different nanomaterials have been used to generate novel functionality,10–12 and the measurement of relative concentration in the mixture is therefore important. In this case, σxA = σA and VmA = VA. If the Mie cross sections are σ(nf, n, k, D) then, provided these can be calculated, eqn (4) becomes eqn (5), which may be used to convert the measured relative fraction into the actual mass fraction.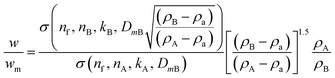 | (5) |
Dimeric particles
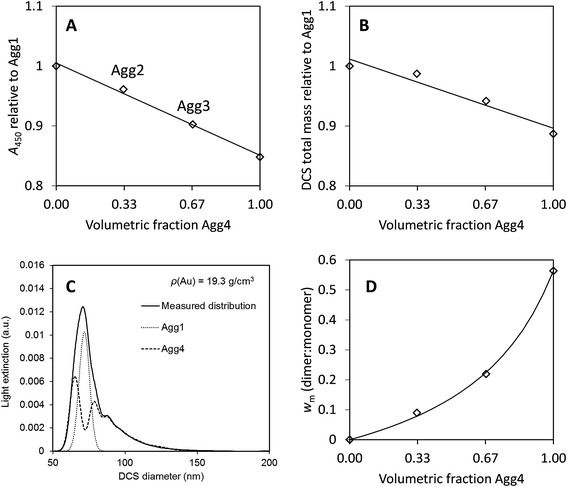
It is commonly observed in DCS that nominally monodisperse particles contain some level of aggregation, evident as distinct populations at defined diameters larger than the primary population. Here we focus upon the relative concentration of dimeric particles (i.e. two particles stuck together), and call this population A. If the primary particle population, B, is spherical and the density and refractive index are known then eqn (4) simplifies to eqn (6).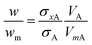 | (6) |
As described in ESI S.2,† the shape of the particle changes the frictional force by a factor, χ, known as the dynamic shape factor, which is generally greater than 1. For DCS this results in VA = χ1.5VmA. The measured diameter is different to the equivalent volumetric diameter by a factor 1/χ0.5. In DCS, dimers are typically observed at DmA = 1.20(±0.01)DmB implying χ ≈ 1.10(±0.02).
These dimeric particles can have a profound effect on nanoparticle size measurements because, in the Rayleigh limit, they have a fourfold higher scattering cross section than primary particles and their apparent size in techniques such as dynamic light scattering (DLS) and particle tracking analysis (PTA) is approximately a factor χ larger than the volume-equivalent diameter, i.e. an apparent diameter ∼1.4 times larger than the primary population.
The value of σxA can be calculated using Mie theory from the apparent diameter of the dimers, DmA. It is not straightforward to obtain σA. However, it is possible using, for example, the superposition T-Matrix method13 as shown shortly. Certain limiting cases can be established without such methods.
For non-plasmonic particles in the Rayleigh limit (much less than 50 nm diameter) the orientation-averaged extinction cross section is rather independent of particle shape and σ is proportional to Vy, where y = 1 for particles which absorb light and y = 2 for particles that scatter light.8 Therefore, in this limit, w = χ1.5(1−y)wm and the measured mass fraction for particles which absorb light, since (1 − y) = 0 and w = wm, is accurate. For particles which only scatter light, the measured mass fraction of dimers to monomers should be multiplied by χ−1.5 = 0.87 to obtain the correct value, i.e. in the data, the relative mass concentration of the dimer population is overestimated by ∼15%. Note that if this relative mass concentration were converted into a relative number concentration using the measured volume ratio, VB/VmA = 0.58, rather than the actual volume ratio, VB/VA = 0.5, the relative number concentration of dimers to monomers would be overestimated by ∼15% for absorbing particles and ∼30% for scattering particles.
For non-plasmonic particles with strong absorbance that are much larger than the wavelength of light, the extinction cross section is proportional to the average area of the particle projected onto a plane. The orientation-averaged projected area of a dimeric particle is 1.165 times larger than its volume-equivalent sphere and eqn (6) becomes w = (χ0.5/1.165) = 0.90wm. In this limit, the relative dimer mass fraction is overestimated by ∼11%.
These analyses suggest that the simplest method of reporting the DCS fractional concentrations of different populations of the same type of nanomaterial is as the mass fraction. In the limits analysed above, the error in using this approach is <20%. Conversion to a relative number concentration requires caution because of general uncertainties in diameter resulting from the unknown shape factor, χ.
To confirm the general applicability of this approach outside the limiting cases described above, accurate extinction cross sections for dimeric particles were calculated using the T-Matrix approach for randomly oriented dimers.13 Fortran code available from a NASA website [http://www.giss.nasa.gov/staff/mmischenko/t_matrix.html] was translated into MATLAB and eqn (6) evaluated for particles with a range of refractive indexes, n, extinction coefficients, k, and primary particle diameters, DB. The MATLAB script is provided in ESI S6.† The wavelength of light was selected to be 405 nm, consistent with some DCS instruments, and the refractive index of the fluid, nf, was assumed to be 1.34 at this wavelength and typical fluid composition. These choices are not important for the general conclusions. The T-Matrix results were assessed for convergence and numerical stability by changing the number of expansion functions and confirming that there was a negligible change in the resulting cross sections. The effect of particle separation in the dimer was assessed by performing the calculations at 1 nm, 2 nm and 5 nm separations. For the particles considered here this separation distance has a small, <2%, effect. However for plasmonic particles (typically, n < 0.5 and k > 1) it is, as may be anticipated,14 a very serious issue.
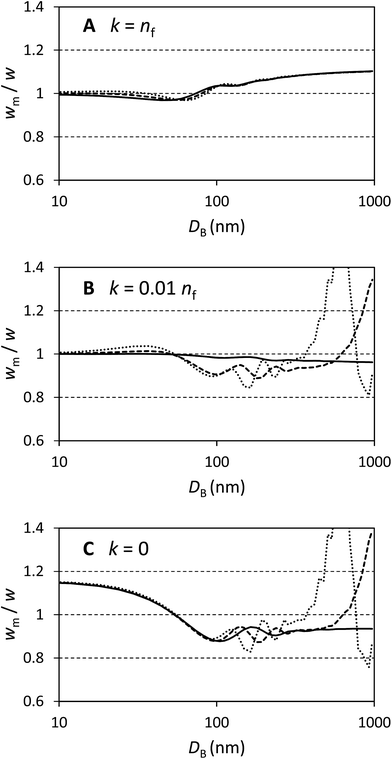
In Fig. 1 selected results are shown for particles with n/nf = 1.05, 1.25 and 1.45 (n = 1.41, 1.68 and 1.94 respectively) and k/nf = 0, 0.01 and 1 representing scattering particles, weakly absorbing particles and strongly absorbing particles. The plots are over the range DB = 10 nm to 1000 nm and show wm/w, i.e. the factor by which the directly measured relative mass concentration of population A to population B is different to the theoretical relative mass concentration.
Fig. 1A shows that this method works well for absorbing particles, with an error of less than 10% and limiting values of wm/w = 1 at small sizes and wm/w = 1.11 at large sizes, as expected. There is some structure in the curves which depends upon the particle refractive index, but this is a rather small (<5%) effect.
Fig. 1C shows that the method works less well for transparent particles. Here the detailed structure of the scattered intensity causes very large errors in some cases. At small sizes wm/w = 1.15 as expected and with DB < 100 nm the bias is nearly identical for all particles considered. In this region the curves are closely described by wm/w = 1 + 0.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(πDB/110). For particles which have refractive indexes close to that of the medium, the error remains less than 20% over a wide range of diameters. For the particles with n = 1.68 the error exceeds 20% at DB = 850 nm and for n = 1.94 the error exceeds 20% at DB = 500 nm. Therefore, for transparent particles with both a large size and refractive index, relative mass concentrations are highly inaccurate.
cos(πDB/110). For particles which have refractive indexes close to that of the medium, the error remains less than 20% over a wide range of diameters. For the particles with n = 1.68 the error exceeds 20% at DB = 850 nm and for n = 1.94 the error exceeds 20% at DB = 500 nm. Therefore, for transparent particles with both a large size and refractive index, relative mass concentrations are highly inaccurate.
Fig. 1B represents weakly absorbing particles. It is clear that these represent a case intermediate between the extremes shown in the other two panels. Scattering cross sections are small at low values of DB and, in this regime, even weak absorption has a strong effect. At large values of DB the scattering cross section for particles dominates and, especially for particles with a high value of n, the values of wm/w are similar to those in panel Fig. 1C. This extends a previous study of weakly absorbing particles with a small refractive index difference to the medium.15 In that work it was also shown that, for large particles, the error in using volume equivalent sphere scattering cross sections for dimeric particles can be of the order of 10% to 20% and, additionally, that the error increased with the number of particles in the aggregate.
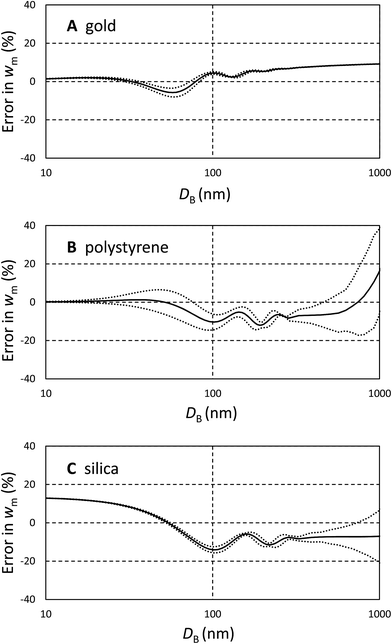
It is important to understand these errors in the context of other contributions to uncertainty encapsulated in eqn (3). Because the volume ratio, VA/VB = 2, is known, the dynamic shape factor, χ, is known to within 2%, and the assumed density cancels, the important source of uncertainty is the extinction cross section, σ. Errors in the input parameters to the Mie calculations may, or may not, be important in determining w. One potential source of error is the uncertainty in particle size, possibly resulting from incorrect particle or fluid densities. This error becomes increasingly significant as the density of the particle approaches that of the fluid. The other sources of error are the assumed optical constants for the particles and fluids.
Since these errors relate only to the assumed values of σ, they may be analysed using Mie calculations to find (δσ/δD) and (δσ/δn) using small changes to D and n. To estimate the uncertainty we propagate the resulting values of σ through eqn (3) for both types of particle and establish the change in wm, (δwm/δD) and (δwm/δn). To estimate the uncertainties due to these factors, the change in wm, Δwm, for a finite change in D, ΔD, is taken to be Δwm = (δwm/δD)ΔD, and similarly for changes in n. We use a 5% error in both n and D and combine the resulting fractional changes in wm in quadrature to provide a description of the potential magnitude of these sources of error in comparison with the bias calculated above.
The magnitude of these estimated errors are shown in Fig. 2 plotted as dotted lines around the bias. As may be anticipated from Fig. 1A, for strongly absorbing particles such as gold the dominant error is the bias due to shape effects. The errors in diameter and refractive index tend to cancel. We note here that if longer wavelengths (>480 nm) are used to analyse gold, plasmonic effects cause the scattered intensity and absorption to be strongly dependent upon shape and the wavelength of light.14,16 These prohibit an easy form of quantitative analysis. For polystyrene and silica, errors in diameter and refractive index are more significant, and increase with the refractive index of the particle. So, for polystyrene it is questionable whether a correction for the bias induced by shape is justifiable. However, for silica it is clear that this is still the dominant effect. We note that, for these particles, the error due to refractive index is the dominant effect and is typically 5 times that of a similar relative error in diameter. If an error in diameter arises from an incorrect density difference then, because diameter scales with the square root of density difference, it is clear that even a 10% error in density will usually result in less than 1% error in relative mass concentration. However, it is important to note that here we consider two populations separated in size by only 20% and the errors will be more significant when the populations have a greater size difference.
Materials and methods
Gold nanoparticles with nominal size of 80 nm and 100 nm were purchased from BBI International (Cardiff, UK). The particle manufacturer declared a size of the particles of 78.8 nm and 98.0 nm respectively, as measured by Transmission Electron Microscopy (TEM), and a concentration of 1.1 × 1010 NPs per mL and 5.6 × 109 NPs per mL respectively.Polystyrene nanoparticles of nominal size 300 nm were synthesized by emulsion polymerization of styrene using sodium dodecyl sulphate (SDS) as surfactant. The polymerization reactions were carried out in a 1 L five-neck reactor equipped with a condenser, a mechanical stirrer, a thermometer and inlets for nitrogen and styrene. 500 mL of ultrapure water eventually containing 0.3 g SDS were introduced into the reactor at room temperature with a stirring rate of 300 rpm, then 50 mL of styrene was added dropwise. The mixture was purged with nitrogen, and nitrogen was fluxed during the entire polymerization procedure. The reactor was heated to 80 °C, then a potassium persulfate aqueous solution (5.0 mL, 0.74 mmol) was added, and the mixture was reacted for 24 h. The obtained latex was purified from surfactant and unreacted monomer by repeated dialyses against ultrapure water (cellulose membrane, molecular weight cut-off 12 kDa). The particle concentration was determined gravimetrically. In detail, five aliquots of 1.00 mL of nanoparticle suspension were placed in pre-weighed aluminum dishes and dried in a vacuum oven at 80 °C for 24 hours, then weighed to quantify the residual. The solid content is the average of the five measurement and the relative standard deviation is ∼3%.
Silica nanoparticles of nominal size 100 nm were provided by Anthoine Thill, CEA. The number concentration was measured by particle tracking analysis (PTA) using an NS500 instrument (Malvern Panalytical, UK) equipped with a 405 nm laser and EMCCD camera. Particles were individually tracked and counted using the manufacturer's software NTA3.2. The estimated uncertainty in the particle number concentration is ∼10%. The particle concentrations were in good agreement with inductively coupled plasma mass spectrometry (ICPMS) measurements based upon the total silicon content of the particles.
Samples with mixed populations of particles were produced by mixing the original particles samples to obtain the nominal concentrations indicated in Table 1. The nominal concentrations for gold are known to ∼20% accuracy from UV-vis measurements17 and those of the PS particles are estimated gravimetrically.
| Sample | Component A | Component B | Nominal [A] (NPs per mL) | Nominal [B] (NPs per mL) |
|---|---|---|---|---|
| Mix 1 | 100 nm Au NPs | 100 nm SiO2 NPs | 4 × 109 | 1 × 1012 |
| Mix 2 | 300 nm PS NPs | 100 nm SiO2 NPs | 4 × 108 | 1 × 1012 |
The aggregation of the gold particles of nominal size 80 nm was induced by using a surface biotin-streptavidin strategy. One batch of the particles, batch 1, was incubated in a 28.5 μM solution of 2,5,8,11,14,17,20-heptaoxadocosane-22-thiol (mPEG-thiol, Mw 356.5, Polypure, Oslo, Norway) in 1 mM 3-[4-(2-hydroxyethyl)-1-piperazinyl]propanesulfonic acid (EPPS, Sigma). Another batch of the particles, batch 2, was incubated in a 1 mM EPPS containing 22.8 μM mPEG-thiol and 6.42 μM biotinPEG-thiol (Mw 788.0, Polypure, Oslo, Norway). The particle batches were incubated for 2 hours under gentle shaking. The excess thiols were removed via centrifugation. 4 cycles of 1 hour centrifugation of the samples at 500 rcf were followed by gentle removal of the supernatant and redispersion of the particles in fresh 1 mM EPPS buffer at pH 7.8. The two batches of particles were analysed by DCS and the distributions are shown in S4 of the ESI.† Batch 1 particles remain unagglomerated and a low level of aggregation is observed for the batch 2 particles.
Batch 2 was subsequently incubated in Neutralised Chimeric Avidin (NCAvd, Mw 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324) to induce further agglomeration of the particles. The NCAvd was based on a previously described thermostable avidin form,18 which was developed by applying charge-neutralized mutations.19,20 The production and characterization of the NCAvd are detailed elsewhere.21,22 For the agglomeration to take place, the particles were centrifuged for 1 hour at 500 rcf in presence of 0.87 μM NCAvd. After centrifugation, the sample was gently shaken to disperse the particles.
324) to induce further agglomeration of the particles. The NCAvd was based on a previously described thermostable avidin form,18 which was developed by applying charge-neutralized mutations.19,20 The production and characterization of the NCAvd are detailed elsewhere.21,22 For the agglomeration to take place, the particles were centrifuged for 1 hour at 500 rcf in presence of 0.87 μM NCAvd. After centrifugation, the sample was gently shaken to disperse the particles.
Four samples exhibiting increasing level of aggregation were produced by mixing the two batches of particles in EPPS buffer in different ratios according to Table 2. The final volume of the particles was the same as the initial volume of the unmodified particles. The total particle concentration is therefore expected to be close to the nominal particle concentration of 1.10 × 1010 NPs per mL, although the centrifugation steps for the removal of excess PEG molecules may have caused some loss of particles. The excess NCAvd was left in solution.
| Sample name | Batch 1 (nominal) | Batch 2 (nominal) | Batch 1 (measured) | Batch 2 (measured) | [C]NCAvd |
|---|---|---|---|---|---|
| Agg1 | 100% | — | 100% | 0% | — |
| Agg2 | 67% | 33% | 64% | 36% | 0.14 μM |
| Agg3 | 33% | 67% | 34% | 66% | 0.29 μM |
| Agg4 | — | 100% | 0% | 100% | 0.44 μM |
DCS
DCS was performed using a CPS 24000 disc centrifuge (CPS Instruments Inc., Stuart, Florida, USA) equipped with an LED laser emitting light with wavelength between 385 nm and 425 nm and with spectral intensity peak at 405 nm. The instrument was operated at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm with a typical 14.4 mL 8% to 24% (w/w) sucrose gradient of in water (average gradient density ρf = 1.064 g cm−3) if not otherwise stated. This was generated by injections of decreasing sucrose concentration, followed by a final addition of 0.5 mL dodecane as an evaporation barrier. A period of 30 min was allowed prior to measurement acquisition to facilitate thermal equilibrium. A calibration of the instrument was performed before each sample injection by using polyvinyl chloride (PVC) calibration particles with nominal size of 237 nm and density 1.385 g cm−3 provided by the instrument manufacturer. The uncertainty of these values was independently measured to be 5% and 3.5% respectively for a confidence level of 95%.23 The injected sample volume was measured by weighing the syringe containing the sample before and after each injection and assuming a density of the sample solution of 1 g cm−3. Table 3 summarises the values of materials density, refractive index and absorptions used for the data analysis.
000 rpm with a typical 14.4 mL 8% to 24% (w/w) sucrose gradient of in water (average gradient density ρf = 1.064 g cm−3) if not otherwise stated. This was generated by injections of decreasing sucrose concentration, followed by a final addition of 0.5 mL dodecane as an evaporation barrier. A period of 30 min was allowed prior to measurement acquisition to facilitate thermal equilibrium. A calibration of the instrument was performed before each sample injection by using polyvinyl chloride (PVC) calibration particles with nominal size of 237 nm and density 1.385 g cm−3 provided by the instrument manufacturer. The uncertainty of these values was independently measured to be 5% and 3.5% respectively for a confidence level of 95%.23 The injected sample volume was measured by weighing the syringe containing the sample before and after each injection and assuming a density of the sample solution of 1 g cm−3. Table 3 summarises the values of materials density, refractive index and absorptions used for the data analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mix and the second for the PS
SiO2 mix and the second for the PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SiO2 mix
SiO2 mix
| Materials | Density ρ (g cm−3) | Refractive index n (405 nm) | Absorption k (405 nm) |
|---|---|---|---|
| Gold (Au) | 19.3 | 1.62 | 1.95 |
| Polystyrene (PS) | 1.052 | 1.594 | 0.02 |
| Silica (SiO2) | 1.91 | 1.457 | 0 |
| Fluid | 1.064, 1.018 | 1.357, 1.340 | 0 |
UV-visible spectra
UV-visible spectra were acquired in triplicate using quartz cuvettes using a LAMBDA 850 spectrophotometer (Perkin Elmer Inc., MA, USA). Samples were analysed over the wavelength range 250 nm to 800 nm.DLS
DLS was used to measure the hydrodynamic radius of the particles and particle agglomerates. These were obtained in triplicate on a Zetasizer Nano ZS 3600 (Malvern Instruments Ltd., Malvern, UK) equipped with a max. 4 mW He–Ne laser, emitting at 633 nm. The measurements were performed in disposable capillary cuvettes (DTS1070, Malvern Instruments Ltd., UK) at 23 °C and preceded by a 3 min equilibration time. The scattered-light intensity-weighted size distributions were expressed in terms of their Z-average (Z-ave) calculated by the instrument software by applying the cumulant method.Results
Samples with mixed populations
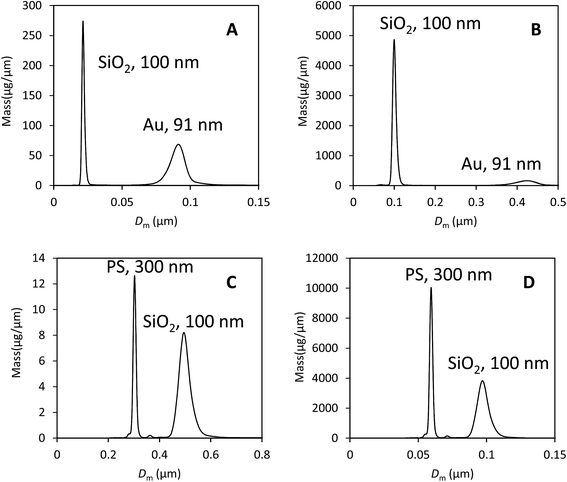
We illustrate that our approach to the analysis of samples containing different materials is justifiable using data from two binary mixtures of particles. These data are shown in Fig. 3 and comprise, in the first case, a mixture of gold (Au) and silica (SiO2) particles of approximately equal diameter.In Fig. 3A the data have been analysed using the material properties of gold and in Fig. 3B with those of silica. The second sample is a mixture of polystyrene (PS) and silica particles. In Fig. 3C the data have been analysed using the material properties of PS and in Fig. 3D with those of silica. The various material properties used in this analysis are provided in Table 3. In both cases there is a clear separation of the two populations and the particles have the correct size when their densities are used in the analysis. The results of the analysis of both data sets using, in each case, the two different particle properties are provided in Table 4.
| Particle A, B | Mixture | |||||||
|---|---|---|---|---|---|---|---|---|
| SiO2 and Au | SiO2 and PS | |||||||
| Au | SiO2 | SiO 2 | Au | PS | SiO2 | SiO 2 | PS | |
| D A , DmB (nm) | 91 | 22 | 100 | 420 | 300 | 500 | 97 | 59 |
| M A , MmB (μg) | 1.0 | 0.66 | 54 | 11 | 0.18 | 0.43 | 39 | 28 |
| σ A , σxB (nm2) |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 000 000
|
280 | 48 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 000 000
|
340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
42 | 3.5 |
Here, the measured diameter, mass and calculated extinction cross section for particle type ‘A’ is provided and highlighted in bold. The results of selecting the other type of particle as type ‘A’ are shown in the next column. Because these particles are close to spherical and the optical properties known, we can expect that data analysis using the correct parameters (i.e. particle ‘A’) will yield a precise measurement of the injected mass. However, we note that the measured DCS mass is lower than the expected mass of injected particles for silica (100 μg), PS (0.6 μg) and Au (3.0 μg). The measured values are a factor of 2 or 3 lower than expected, showing reasonable consistency in error despite the large difference in particle densities and optical properties. Also in Table 4 are the incorrect measured diameters, masses and calculated cross sections for particle type ‘B’.
There are two methods of obtaining the true mass fraction, w, of the different populations. Having analysed the data using two different material parameters, the ratio of the measured injected masses, MA, is the most directly useful in a practical context. Alternatively, in each individual experiment, the value of wm can be converted into w using eqn (5). These should give similar values, but are not expected to be identical because the size dispersity of the particle populations has not been accounted for in the second method. In Table 5 the methods are compared and show a reasonable accord in the mass fraction values, w. Comparison of these to the values obtained for wm clearly show that the error can exceed two orders of magnitude if the material densities and optical properties are incorrect. In comparison, the precision in both the modal diameter and wm in DCS is better than 1% in repeat measurements. This is illustrated in S3 of the ESI.†
SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au Au |
w |
| Nominal | 33 |
M
A (SiO2 analysis)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MA (Au analysis) MA (Au analysis) |
54 |
SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS PS |
w |
| Nominal | 170 |
M
A (SiO2 analysis)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MA (PS analysis) MA (PS analysis) |
220 |
The method of reanalysing the data for each material is to be preferred, but the correction provided in eqn (5) can be useful if, for example, the raw data are not accessible.
Samples with agglomerated populations
By applying a binding strategy based on the strong affinity of biotin to Avidin we succeeded in producing a set of samples with a defined and stable level of agglomeration. This is shown in S5 of the ESI,† where the high resolution light extinction-based size distributions of the samples measured by DCS are shown as well as DLS data results and UV-visible spectra. As described in S5, standard methods of interpreting the data from UV-visible and DLS data show that the agglomerated nature of samples cannot easily be identified.The Agg1 sample demonstrates a monomodal DCS peak, enabling the concentration of this sample to be measured with ∼20% accuracy directly from the UV-vis data as 7.3 × 109 NPs per mL. This is approximately two thirds of the starting concentration, implying a significant loss of particles in the preparation procedure. For 80 nm diameter particles, this number concentration translates to 38 μg mL−1 of gold, which may be compared to the integrated DCS value of 15 μg mL−1. The disparity is significant, and similar to that noted above in the mixed samples. It may be thought, in this case, to arise from the presence of the surface coating on the gold particles which, in DCS, reduces the density, increasing the sedimentation time and causing the diameter of the particle to be underestimated24 as 71 nm. However, in this case, the extinction cross section of gold is approximately proportional to the volume and eqn (2) indicates that the total mass of gold should be unchanged. The effect of a coating on the gold also increases the local refractive index around the gold and this will lead to a change in extinction cross section of particles. We note, however, that this will affect both the UV-vis and the DCS results in a similar fashion. Inspection of eqn (1) demonstrates that the DCS value has high uncertainty due to a number of instrumental details (such as detector position) and experimental factors (such as the viscosity gradient) that may bias the results. There may also be other losses during the injection procedure. Therefore the UV-vis results are thought to be more accurate in this case. However, on the basis of the results from mixed particles, it seems reasonable to assume that the relative concentrations found by DCS are representative of the sample.
The concentration of the most agglomerated sample, Agg4, may be analysed in a similar fashion. Although the particle size is not well defined, the value of the UV-visible absorbance at 450 nm, A450, will be approximately proportional to the mass concentration of gold in the sample. Similarly, the total mass of gold may be obtained directly from the DCS analysis and the relative value to the Agg1 sample compared. Here it is assumed that the bias in the DCS results is consistent for all samples. In Fig. 4A and B we compare both of these methods to the values obtained for the monomodal Agg1 sample and the mixed samples.
 | ||
| Fig. 4 Results from agglomerated samples. (A) UV-vis absorbance at 450 nm, A450, normalised to the monomodal sample, Agg1. (B) Total mass of particles from DCS normalised to the monomodal sample, Agg1. (C) Fit to DCS data for sample Agg3, using descriptions of Agg1 and Agg4 data. (D) Relative mass of dimers to monomers from DCS, wm. Lines are fits to the data, in (A) and (B) they are linear, for Deqn (7) is used with a = 3.1. | ||
In Fig. 4A the value of A450 is divided by that of the sample Agg1. If the two particle populations do not interact we expect this absorbance to be linear with, φ, the volume fraction of Agg4 in the mixture. Here, there is excellent precision and this result suggests that the relative concentration of gold in Agg4 is 85% ± 2% of that in Agg1. A similar analysis of DCS data shown in Fig. 4B provides a similar result with lower precision, 89% ± 4%. In both cases, there is some additional uncertainty associated with the concentration of higher agglomerates because their extinction cross sections are unknown.
A further method of analysing the DCS data enables the relative concentration of monomeric particles in the two samples to be assessed. Essentially, we use the Agg1 particles as an internal calibrant in the Agg2 and Agg3 mixtures to find the concentration of the Agg4 sample.
We demonstrate in the ESI, S5,† that the DCS data for Agg4 can be closely matched by a fit describing different aggregated populations. A summary of the relative mass and number concentrations of populations of particles in Agg4 is provided in Table 6. The equivalent volume diameters, DVeq, for each population are based upon an estimate of the primary particle diameter of 85 nm, which takes account of the TEM core diameter (79 nm) plus the additional coatings. We note that the monodisperse Agg1 sample, which has a thin PEG coating, has a DLS diameter of 81 nm and the NCAvd molecule is ∼4 nm in size,22 but is unlikely to completely coat the particles, therefore 85 nm is a reasonable value for the primary particle diameter. The relative diameters in DCS enables measurement of the dynamic shape factor, χ, with reasonable certainty up to the tetramer, beyond this the populations are no longer distinct and therefore the fit is uncertain.
| Population | Primary | Dimer | Trimer | Tetramer | Pentamer | 6+-mer |
|---|---|---|---|---|---|---|
| D Veq (nm), estimated | 85 | 107 | 123 | 135 | 145 | 154+ |
| χ, observed | 1 | 1.10 | 1.16 | 1.18 | (1.17) | — |
| Fractional mass (%) | 39 | 22 | 15 | 7 | 7 | 10 |
| Fractional number (%) | 65 | 19 | 8 | 3 | 2 | <3 |
In these fits to the DCS data the primary particle and doublet peaks are sufficiently resolved to measure wm (dimer:monomer) for this sample. Analysis of the data using a variety of different input densities to account for the effect of the coating reveals that these have a negligible effect on the result and we find wm = 0.56 ± 0.01, where the dominant error arises from the quality of the fit.
For samples Agg2 and Agg3, the data can be described by a linear combination of the Agg1 and Agg4 results, as shown in Fig. 4C. These fits provide the measured results given in Table 2, which confirm the Agg1:Agg4 volumetric composition of the samples. Note here that the particle size is incorrect, but the relative mass of gold detected in each population should not be affected by this, as described previously. From the fits, the mass of gold found for the Agg1 population can be added to the monomer population in the Agg4 fit and the value of wm found for each sample. The results are shown in Fig. 4D.
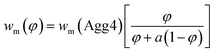 | (7) |
The value of wm can be described by eqn (7), where φ is the volume fraction of Agg4 mixed solution and a is the mass ratio of primary particles in the Agg1 suspension to that in the Agg4 suspension. By fitting the data in Fig. 4D, we find a = 3.1 ± 0.1. Because the mass of gold in the two primary particles are equal, and the UV-vis number concentration for Agg1 is accurate, the number concentration of primary particles in Agg4 is found to be 2.4 × 109 NPs per mL. The dominant error in this result is the ∼20% error in the Agg1 number concentration from the UV-vis spectrum. Using the mass distribution in DCS, this permits measurement of the relative concentration of gold in Agg4 to that in Agg1, and we find a value of 84% ± 2%, which is consistent with the UV-vis estimate.
From Table 6, it is possible to provide two important particle number concentrations for Agg4: The number concentration of primary particles is found from the relative mass fractions as 6.2 × 109 NPs per mL and the number concentration of discrete particles (counting clusters as single particles) as 3.7 × 109 NPs per mL. The former would be relevant to methods which have difficulty distinguishing aggregates, such as SAXS, and the latter would be relevant to techniques such as single particle ICPMS, particle tracking analysis and resistive pulse sensing which count agglomerated particles as single entities.
The average particle size can also be estimated, with the number-weighted average size being 97 nm and the mass-weighted average size as 110 nm. We note that the DLS Z-average size of Agg4 is 121 nm. Therefore, if the definition of a nanomaterial is that the average particle size should be less than 100 nm, this sample would be classified as a nanomaterial by some methods, but not by others.
Conclusion
In this paper we describe the factors that affect the accuracy of DCS photosedimentation for measuring the concentration of particles. We demonstrate that the accurate measurement of particle mass concentrations is feasible, but requires substantial knowledge of the instrumental and experimental details as well as the physical properties of the particles. We find that, in cases where there is a reliable independent measurement of particle concentration, that the DCS measurement underestimates the mass concentration by a factor of 2 or 3. The origin of this discrepancy requires further investigation. By assuming that this error remains constant during a single experiment regardless of particle type, we show that the measurement of relative mass concentrations of different particle populations is feasible with reasonable accuracy. For particle populations of different types, it is possible to correct the data to provide a reasonable estimate of the relative mass concentrations and show, using example mixtures, that these estimates are consistent to within a factor of 2. This compares to order of magnitude errors without such corrections.For different particle populations of the same type of material, we demonstrate that the relative mass concentrations are reliable. For particles that are weakly aggregated the relative mass concentrations of the dimeric population compared to the monomeric population have a typical error of less than 20% over a wide range of particle size. Furthermore, this measurement is insensitive to small (∼5%) errors in the assumed refractive indexes and densities of the particles. This analysis is demonstrated on an agglomerated gold sample, where calibration using a non-agglomerated internal reference enables an accurate measurement of the particle number concentration, both in terms of primary particle number and the number of discrete particles.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge support from the European Metrology Programme for Innovation and Research (EMPIR) as part of the InNanoPart 14IND12 project. The EMPIR initiative is co-funded by the European Union's Horizon 2020 research and innovation programme and by the EMPIR participating states. Silica particles were kindly supplied by Antoine Thill (CEA Saclay, Gif Sur Yvette, France). Neutralised Chimeric Avidin was kindly supplied by Vesa Hytönen, University of Tampere, Finland. AGS, CM and LW also acknowledge the Metrology for Advanced Coatings and Formulated Products theme of the UK Department of Business, Energy and Industrial Strategy.References
- J. Shang and X. Gao, Nanoparticle Counting: Towards Accurate Determination of the Molar Concentration, Chem. Soc. Rev., 2014, 43, 7267–7278 RSC.
- J. A. Gallego-Urrea, J. Tuoriniemi, T. Pallander and M. Hassellöv, Measurements of Nanoparticle Number Concentrations and Size Distributions in Contrasting Aquatic Environments Using Nanoparticle Tracking Analysis, Environ. Chem., 2010, 7, 67–81 CrossRef.
- C. M. Hoo, N. Starostin, P. West and M. L. Mecartney, A Comparison of Atomic Force Microscopy (Afm) and Dynamic Light Scattering (Dls) Methods to Characterize Nanoparticle Size Distributions, J. Nanopart. Res., 2008, 10, 89–96 CrossRef.
- R. D. Boyd, S. K. Pichaimuthu and A. Cuenat, New Approach to Inter-Technique Comparisons for Nanoparticle Size Measurements; Using Atomic Force Microscopy, Nanoparticle Tracking Analysis and Dynamic Light Scattering, Colloids Surf., A, 2011, 387, 35–42 CrossRef.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, E. P. Gray, C. P. Higgins and J. F. Ranville, Single Particle Inductively Coupled Plasma-Mass Spectrometry: A Performance Evaluation and Method Comparison in the Determination of Nanoparticle Size, Environ. Sci. Technol., 2012, 46, 12272–12280 CrossRef PubMed.
- W. Anderson, D. Kozak, V. A. Coleman, Å. K. Jämting and M. A. Trau, Comparative Study of Submicron Particle Sizing Platforms: Accuracy, Precision and Resolution Analysis of Polydisperse Particle Size Distributions, J. Colloid Interface Sci., 2013, 405, 322–330 CrossRef PubMed.
- J. Cheng, B. A. Teply, I. Sherifi, J. Sung, G. Luther, F. X. Gu, E. Levy-Nissenbaum, A. F. Radovic-Moreno, R. Langer and O. C. Farokhzad, Formulation of Functionalized Plga–Peg Nanoparticles for in Vivo Targeted Drug Delivery, Biomaterials, 2007, 28, 869–876 CrossRef PubMed.
- D.-H. Tsai, T. J. Cho, F. W. DelRio, J. Taurozzi, M. R. Zachariah and V. A. Hackley, Hydrodynamic Fractionation of Finite Size Gold Nanoparticle Clusters, J. Am. Chem. Soc., 2011, 133, 8884–8887 CrossRef PubMed.
- J. M. Zook, V. Rastogi, R. I. MacCuspie, A. M. Keene and J. Fagan, Measuring Agglomerate Size Distribution and Dependence of Localized Surface Plasmon Resonance Absorbance on Gold Nanoparticle Agglomerate Size Using Analytical Ultracentrifugation, ACS Nano, 2011, 5, 8070–8079 CrossRef PubMed.
- S. L. Westcott, S. J. Oldenburg, T. R. Lee and N. J. Halas, Formation and Adsorption of Clusters of Gold Nanoparticles onto Functionalized Silica Nanoparticle Surfaces, Langmuir, 1998, 14, 5396–5401 CrossRef.
- S. L. Westcott, S. J. Oldenburg, T. R. Lee and N. J. Halas, Construction of Simple Gold Nanoparticle Aggregates with Controlled Plasmon–Plasmon Interactions, Chem. Phys. Lett., 1999, 300, 651–655 CrossRef.
- N. Liu, B. S. Prall and V. I. Klimov, Hybrid Gold/Silica/Nanocrystal-Quantum-Dot Superstructures: Synthesis and Analysis of Semiconductor–Metal Interactions, J. Am. Chem. Soc., 2006, 128, 15362–15363 CrossRef PubMed.
- M. I. Mishchenko and D. W. Mackowski, Light Scattering by Randomly Oriented Bispheres, Opt. Lett., 1994, 19, 1604–1606 CrossRef PubMed.
- I. Romero, J. Aizpurua, G. W. Bryant and F. J. G. De Abajo, Plasmons in Nearly Touching Metallic Nanoparticles: Singular Response in the Limit of Touching Dimers, Opt. Express, 2006, 14, 9988–9999 CrossRef PubMed.
- R.-L. Heng, K. C. Sy and L. Pilon, Absorption and Scattering by Bispheres, Quadspheres, and Circular Rings of Spheres and Their Equivalent Coated Spheres, J. Opt. Soc. Am. A, 2015, 32, 46–60 CrossRef PubMed.
- N. G. Khlebtsov, Determination of Size and Concentration of Gold Nanoparticles from Extinction Spectra, Anal. Chem., 2008, 80, 6620–6625 CrossRef PubMed.
- W. Haiss, N. T. Thanh, J. Aveyard and D. G. Fernig, Determination of Size and Concentration of Gold Nanoparticles from Uv-vis Spectra, Anal. Chem., 2007, 79, 4215–4221 CrossRef PubMed.
- V. P. Hytönen, J. A. E. Määttä, T. K. M. Nyholm, O. Livnah, Y. Eisenberg-Domovich, D. Hyre, H. R. Nordlund, J. Hörhä, E. A. Niskanen, T. Paldanius, T. Kulomaa, E. J. Porkka, P. S. Stayton, O. H. Laitinen and M. S. Kulomaa, Design and Construction of Highly Stable, Protease-Resistant Chimeric Avidins, J. Biol. Chem., 2005, 280, 10228–10233 CrossRef PubMed.
- V. P. Hytönen, J. A. E. Määttä, H. Kidron, K. K. Halling, J. Hörhä, T. Kulomaa, T. K. M. Nyholm, M. S. Johnson, T. A. Salminen, M. S. Kulomaa and T. T. Airenne, Avidin Related Protein 2 Shows Unique Structural and Functional Features among the Avidin Protein Family, BMC Biotechnol., 2005, 5, 28 CrossRef PubMed.
- V. P. Hytönen, T. K. M. Nyholm, O. T. Pentikäinen, J. Vaarno, E. J. Porkka, H. R. Nordlund, M. S. Johnson, J. P. Slotte, O. H. Laitinen and M. S. Kulomaa, Chicken Avidin-Related Protein 4/5 Shows Superior Thermal Stability When Compared with Avidin While Retaining High Affinity to Biotin, J. Biol. Chem., 2004, 279, 9337–9343 CrossRef PubMed.
- B. Taskinen, D. Zauner, S. I. Lehtonen, M. Koskinen, C. Thomson, N. Kähkönen, S. Kukkurainen, J. A. E. Määttä, T. O. Ihalainen, M. S. Kulomaa, H. J. Gruber and V. P. Hytönen, Switchavidin: Reversible Biotin–Avidin–Biotin Bridges with High Affinity and Specificity, Bioconjugate Chem., 2014, 25, 2233–2243 CrossRef PubMed.
- S. Ray, R. T. Steven, F. M. Green, F. Hook, B. Taskinen, V. P. Hytonen and A. G. Shard, Neutralized Chimeric Avidin Binding at a Reference Biosensor Surface, Langmuir, 2015, 31, 1921–1930 CrossRef PubMed.
- V. Kestens, V. A. Coleman, P.-J. De Temmerman, C. Minelli, H. Woehlecke and G. Roebben, Improved Metrological Traceability of Particle Size Values Measured with Line-Start Incremental Centrifugal Liquid Sedimentation, Langmuir, 2017, 33, 8213–8224 CrossRef PubMed.
- N. C. Bell, C. Minelli and A. G. Shard, Quantitation of Igg Protein Adsorption to Gold Nanoparticles Using Particle Size Measurement, Anal. Methods, 2013, 5, 4591–4601 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ay00491a |
| ‡ Current address: Polpharma SA Pharmaceutical Works, 83-200 Starogard Gdański, Poland. |
| This journal is © The Royal Society of Chemistry 2018 |