Open Access Article
Open Access ArticleThe conformational space of the neurotransmitter serotonin: how the rotation of a hydroxyl group changes all†
Martin
Wilke
a,
Christian
Brand
ab,
Josefin
Wilke
a and
Michael
Schmitt
*a
aHeinrich-Heine-Universität, Institut für Physikalische Chemie I, D-40225 Düsseldorf, Germany. E-mail: mschmitt@hhu.de; Fax: +49 211 8112179; Tel: +49 0211 8112100
bFaculty of Physics, University of Vienna, VCQ, QuNaBioS, Boltzmanngasse 5, A-1090 Vienna, Austria
First published on 26th April 2016
Abstract
The 5-hydroxytryptamine receptors (5HTn) are optimized for 5-hydrotryptamine molecules, resulting in a significantly enhanced psychoactive response compared with the 4-, 6-, 7-isomers. This is despite their relatively similar energetic stabilities, excited state lifetimes and emission characteristics. In this work we investigate the conformational space of serotonin (5-hydroxytryptamine) using a combination of rotationally resolved electronic spectroscopy and ab initio calculations. The geometries of the four most abundant conformers are assigned from their molecular parameters in the electronic ground and excited state. We find a conformer-dependent competition between two polar groups trying to establish a hydrogen bond with the same H-atom in the most stable conformer of serotonin. The result explains some remarkable deviations with respect to the conformational space of the closely related neurotransmitter tryptamine. Based on the comparison to other 5-substituted indoles we propose to generalize this finding to explain the conformational preferences of indole-based neurotransmitters.
1 Introduction
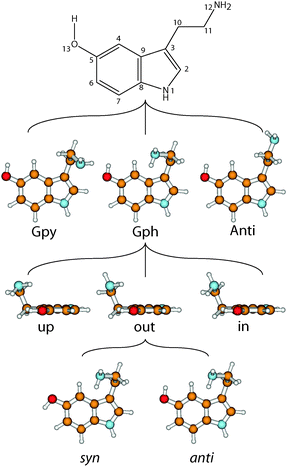
The neurotransmitter and hormone serotonin is a derivative of the aromatic amino acid tryptophan. It is the natural ligand which activates the 5-hydroxytryptamine (5-HT) receptors which are mostly G protein coupled receptors.1,2 The omnipresence of these receptors in the body leads to a multitude of different effects.3 Serotonin modulates neural activity, neuropsychological processes and has vascular effects (both vasoconstriction and vasodilation). Furthermore, it has cardiac functions and affects the respiratory system, the endocrine system and metabolism, as well as the gastrointestinal system.4 A deeper understanding of the interaction of neurotransmitters with their specific receptors requires a better knowledge of the influences which shape their conformational space.A suitable nomenclature for the conformational space of serotonin is depicted in Fig. 1.5 For all experimentally observed conformers, the ethyl amino side chain is perpendicular to the aromatic plane which results in three possible conformations of the NH2 group: gauche to the pyrrole ring (Gpy), gauche position to the phenyl moiety (Gph) or pointing away from the chromophore (Anti). For both gauche conformations the lone pair (LP) of the NH2 group can point up, out, or in. The in conformers, however, are much higher in energy and will be neglected in this study. For the Anti conformers the LP can point up or to either one of the rings: phenyl (ph) or pyrrole (py). Finally, the orientation of the OH-group is denoted with anti when it is anti-parallel to the NH bond of the pyrrole ring, or syn- for the other option. In the end a set of 14 possible conformers exists which is shown in the online ESI.†
An experimental investigation of the conformational space of the protonated form was performed by Lagutschenkov et al.6 Both the bare5 and the singly hydrated neutral serotonin7 were studied with vibrational resolution in the group of Zwier. They found eight conformers which they divided into a group of five transitions labeled as A to E, blue-shifted by around 200 cm−1 from the second group of three transitions labeled as F to H.5 The lowest energy conformation was stated to be the Gpy(out)/anti conformer like in the closely related neurotransmitter tryptamine which essentially is serotonin without the hydroxyl group. Later, this assignment was corrected by Cabezas et al.8 who established the Gph(out)/anti conformer to be the global minimum based on rotational spectroscopy. This is in agreement with theoretical predictions from Srivastava and Singh9 who performed a comprehensive computational study on serotonin at various levels of theory. Also Van Mourik and Emson investigated the conformational space of serotonin and tryptamine theoretically.10
Apart from the conformational analysis the study of LeGreve et al. pointed to some intriguing irregularities in the vibronic spectrum of serotonin.5 The energetic gap between the syn- and the anti-conformer with respect to the hydroxyl group is relatively constant at 230 cm−1, close to the respective value for 5-hydroxindole.11,12 However, for the Gph(out) conformers the energetic gap is increased by 30 cm−1. This is very surprising as the only difference is a rotation about a single OH-bond by 180°. Furthermore, the nitrogen atom of the ethyl amino side chain is 510 pm away from the oxygen atom of this group, making a direct interaction unlikely. So far, this effect has been tentatively explained in the literature by electronic5,9 or dipole–dipole interactions.6,7 Additionally, the most stable conformer of serotonin does not coincide with the energetically lowest one of tryptamine. Thus, the question arises which kind of mechanism leads to this remarkable stabilization and irregularity for the Gph(out)/anti conformer of serotonin.
In the present contribution, we use a combination of rotationally resolved electronic spectroscopy and high-level quantum mechanical calculations to investigate the conformational space of serotonin and compare it to that of tryptamine. Tryptamine itself has been studied at rotational13 and vibronic resolution14 as well as at partial15,16 and full17–19 rovibronic resolution. Seven different conformers were identified and assigned based on their rotational constants and vibrational spectra. Based on the comparison of the existing data on serotonin derivatives,20–22 we propose the formation of intramolecular hydrogen bonds to be responsible for the conformational preference for many indole-based neurotransmitter. The results give new and important insights into the stabilization mechanisms of this complex class of molecules.
2 Techniques
2.1 Experimental procedures
Serotonin (≥97%) was purchased from Wako and used without further purification. The experimental set-up for the rotationally resolved laser induced fluorescence spectroscopy is described in detail elsewhere.23 In brief, the laser system consists of a single frequency ring dye laser (Sirah Matisse DS) operated with Rhodamine 6G and Kiton Red, pumped with 8 W of the 514 nm line of an Ar+-ion laser (Coherent, Sabre 15 DBW). The dye laser output was coupled into an external folded ring cavity (Spectra Physics Wavetrain) for second harmonic generation. The resulting output power was constant at about 15 mW during the experiment. The molecular beam was formed by co-expanding serotonin, heated to 210 °C, and 250 mbar of argon through a 200 μm nozzle into the vacuum chamber. The molecular beam machine consists of three differentially pumped vacuum chambers that are linearly connected by skimmers (1 mm and 3 mm, respectively) in order to reduce the Doppler width. The resulting resolution is 18 MHz (FWHM) in this set-up. In the third chamber, 360 mm downstream of the nozzle, the molecular beam crosses the laser beam at a right angle. The imaging optics set-up consists of a concave mirror and two plano-convex lenses to focus the resulting fluorescence onto a photomultiplier tube, which is mounted perpendicularly to the plane defined by the laser and molecular beam. The signal output was then discriminated and digitized by a photon counter and transmitted to a PC for data recording and processing. The relative frequency was determined with a quasi confocal Fabry–Perot interferometer. The absolute frequency was obtained by comparing the recorded spectrum to the tabulated lines in the iodine absorption spectrum.243 Computational methods
3.1 Quantum chemical calculations
Structure optimizations were performed employing Dunning's correlation consistent polarized valence triple zeta (cc-pVTZ) basis set from the Turbomole library.25,26 The equilibrium geometries of the electronic ground and the lowest excited singlet states were optimized using the approximate coupled cluster singles and doubles model (CC2) employing the resolution-of-the-identity approximation (RI).27–29 Vibrational frequencies and zero-point corrections to the adiabatic excitation energies have been obtained from numerical second derivatives using the NumForce script30 implemented in the TURBOMOLE program suite.31 Second-order perturbation theory (MP2) optimizations were performed with the 6-311++G(d,p) basis set using the GAUSSIAN 09 program package.32 For the MP2 optimized geometries a Natural Bond Orbital (NBO) analysis33 has been performed.3.2 Fits of the rovibronic spectra using evolutionary algorithms
The search algorithm employed for the fit of the rotationally resolved electronic spectra is an evolutionary strategy (ES) adapting normal mutations via a covariance matrix adaptation (CMA) mechanism. This (CMA-ES) algorithm was developed by Ostermeier and Hansen34,35 and is designed especially for optimization on rugged search landscapes that are additionally complicated due to noise, local minima and/or sharp bends. It belongs to a group of global optimizers that were inspired by natural evolution. For a detailed description of these evolutionary strategies refer to ref. 36–39.4 Results and discussion
4.1 Computational results
The assignment of the experimental spectra and identification of the respective structures is based on high level ab initio calculations. Table 1 shows the calculated molecular properties of the lowest 14 conformers of serotonin obtained from CC2/cc-pVTZ calculations. As the rotational constants are mainly determined by the orientation of the NH2 group, we can sort the conformers into three families (Gpy, Gph and Anti). However, inside a family the rotational constants are quite similar and an assignment solely based on their absolute values is difficult.| Conformer | A′′/MHz | B′′/MHz | C′′/MHz | A′/MHz | B′/MHz | C′/MHz | θ/° | ϕ/° |
|---|---|---|---|---|---|---|---|---|
| Gpy(out)/anti | 1294.3 | 578.1 | 440.8 | 1295.8 | 574.6 | 438.8 | +27 | 76 |
| Gpy(out)/syn | 1288.8 | 580.9 | 441.8 | 1300.1 | 574.0 | 438.8 | +35 | 75 |
| Gpy(up)/anti | 1276.5 | 580.1 | 441.3 | 1293.4 | 570.9 | 437.1 | +26 | 76 |
| Gpy(up)/syn | 1275.5 | 581.1 | 441.6 | 1303.1 | 568.3 | 436.2 | +34 | 75 |
| Gph(out)/anti | 1164.4 | 663.9 | 445.0 | 1167.7 | 657.9 | 453.1 | +23 | 78 |
| Gph(out)/syn | 1165.0 | 662.1 | 454.8 | 1172.9 | 654.4 | 452.9 | +31 | 76 |
| Gph(up)/anti | 1184.0 | 640.5 | 454.2 | 1177.9 | 640.2 | 452.8 | +24 | 76 |
| Gph(up)/syn | 1179.3 | 644.3 | 455.4 | 1176.8 | 643.0 | 454.1 | +33 | 75 |
| Anti(ph)/anti | 1178.3 | 562.1 | 394.3 | 1171.9 | 563.5 | 395.1 | +12 | 80 |
| Anti(ph)/syn | 1175.1 | 562.7 | 394.4 | 1177.7 | 561.3 | 394.7 | +20 | 80 |
| Anti(py)/anti | 1183.4 | 556.5 | 392.4 | 1180.7 | 557.3 | 393.0 | +13 | 80 |
| Anti(py)/syn | 1177.3 | 560.3 | 393.5 | 1179.9 | 558.8 | 393.7 | +21 | 80 |
| Anti(up)/anti | 1177.7 | 557.3 | 392.6 | 1175.9 | 558.0 | 393.4 | +13 | 80 |
| Anti(up)/syn | 1175.2 | 559.2 | 393.4 | 1178.9 | 557.5 | 393.8 | +21 | 79 |
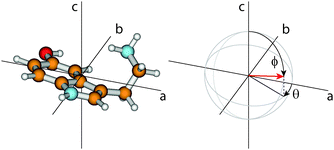
The orientation of the transition dipole moment (TDM) given by its angles θ with the inertial a-axis and ϕ with the c-axis (cf.Fig. 2), provides additional information to distinguish the conformers. The respective values for all 14 conformers are also listed in Table 1. While ϕ is quite similar for all conformers and no systematic differences can be observed, the changes of θ are a reliable measure to distinguish between syn- and anti-conformers: For the anti-conformers θ is always smaller by 8° than those of the respective syn counterparts.
In the case of tryptamine it has been shown that the most stable ground state conformer is Gpy(out) followed by Gpy(up) and Gph(out).40–42 Also for serotonin the Gpy(out)/anti conformer is the most stable ground state conformer according to density functional theory (DFT).5,9 Using functionals including dispersion interaction9 or changing to perturbation theory5,9 results in a change of the relative energy order, in agreement with the experimental findings from Cabezas et al.8 who found the Gph(out)/anti conformation to be the most stable one. The relative ground state energies of the seven most stable tryptamine conformers43 are compared to those of the 14 serotonin conformers9 in Table 2.
| Tryptamine | Serotonin | ||||
|---|---|---|---|---|---|
| MP2/6-311++G(d,p)43 | MP2/6-311++G(d,p)9 | CC2/cc-pVTZ | |||
| anti-5OH | syn-5OH | anti-5OH | syn-5OH | ||
| Gpy(out) | 0.0 | 8.4 | 122.8 | 155.6 | 270.4 |
| Gpy(up) | 125.6 | 93.7 | 243.4 | 158.1 | 285.1 |
| Gph(out) | 136.4 | 0.0 | 375.3 | 0.0 | 330.5 |
| Gph(up) | 304.3 | 352.9 | 482.3 | 252.9 | 351.5 |
| Anti(py) | 482.3 | 524.3 | 629.6 | 710.4 | 790.8 |
| Anti(ph) | 475.0 | 460.6 | 695.7 | 622.9 | 804.1 |
| Anti(up) | 499.8 | 527.4 | 656.2 | 626.4 | 747.4 |
4.2 High resolution electronic spectra of the serotonin conformers
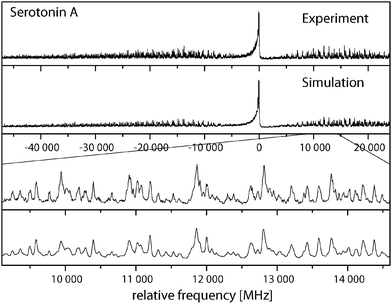
Fig. 3 shows the rotationally resolved spectrum of the electronic origin of the most intensive band in the laser induced fluorescence (LIF) spectrum recorded by LeGreve et al.,5 denoted as serotonin A. It is accompanied by a simulation using the best parameters from a fit, given in Table 3. The spectra and simulations of the other conformers (B, C, and F) are given in the online ESI.† For all four conformers a similar redshift of around 13 cm−1 in the origin frequencies can be observed in comparison to the low-resolution values.5 The band type of all conformers is mainly ab hybrid as can be inferred from the values of θ and ϕ in Table 3. Excited state lifetimes range from 5 to 9 ns for conformers A to C and are larger than 12 ns for F.| A | Gpy(out)/anti | B | Gpy(up)/anti | C | Gph(out)/anti | F | Gpy(out)/syn | |
|---|---|---|---|---|---|---|---|---|
| A′′/MHz | 1286.50(1) | 1294.3 | 1267.28(1) | 1276.5 | 1163.12(1) | 1164.4 | 1281.86(1) | 1288.8 |
| B′′/MHz | 571.74(1) | 578.1 | 574.75(1) | 580.1 | 650.60(1) | 663.9 | 573.92(1) | 580.9 |
| C′′/MHz | 435.63(1) | 440.8 | 436.11(1) | 441.3 | 450.06(1) | 455.0 | 436.39(1) | 441.8 |
| ΔI′′/amu Å2 | −116.66 | −118.15 | −119.27 | −121.74 | −88.37 | −84.65 | −116.75 | −118.40 |
| A′/MHz | 1286.82(1) | 1295.8 | 1269.06(1) | 1293.4 | 1164.19(1) | 1167.7 | 1287.31(1) | 1300.1 |
| B′/MHz | 567.46(1) | 574.6 | 570.14(1) | 570.9 | 644.10(1) | 657.9 | 567.85(1) | 574.0 |
| C′/MHz | 433.20(1) | 438.8 | 433.89(1) | 437.1 | 447.13(1) | 453.1 | 433.59(1) | 438.8 |
| ΔI′/amu Å2 | −116.71 | −117.74 | −119.87 | −119.57 | −88.45 | −85.58 | −116.99 | −117.45 |
| ΔA/MHz | +0.32(1) | +1.5 | +1.78(1) | +16.9 | +1.07 | +3.3 | +5.45 | +11.3 |
| ΔB/MHz | −4.28(1) | −3.5 | −4.61(1) | −9.2 | −6.50 | −6.0 | −6.07 | −6.9 |
| ΔC/MHz | −2.43(1) | −2.0 | −2.22(1) | −4.2 | −2.93 | −1.9 | −2.80 | −3.0 |
| θ/° | ±38.83 | +27 | ±44.84 | +26 | ±34.60 | +23 | ±46.52 | +35 |
| ϕ/° | 69.65 | 76 | 70.53 | 76 | 73.93 | 78 | 65.29 | 75 |
| ν 0/cm−1 | 32571.60 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 029 029 |
32535.23 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007 007 |
32532.30 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 023 |
32341.26 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 653 |
| τ/ns | 6 | — | 5 | — | 9 | — | >12 | — |
The experimental parameters (rotational constants of the electronic ground (A′′, B′′, C′′) and excited state (A′, B′, C′), the inertial defect of both states (ΔI), the center frequencies of the respective bands (ν0) and the orientation of the TDM) of the four conformers are given in Table 3 and are compared to the results of the ab initio calculations. The assignments will be discussed in the next section.
4.3 Conformational assignments
For an assignment of the rovibronic bands to certain conformers we take a closer look at the rotational constants that are obtained from the analysis of the four spectra. Comparing the rotational constants of the A, B and F band with the calculated constants in Table 1, it is evident that they all belong to a gauche pyrrole conformation. For band C an assignment to the gauche phenyl family can be made. However, within each family, the differences of the rotational constants are not large enough to make an unequivocal assignment.LeGreve et al.5 assigned the group of transitions F–H to the syn-conformers based on the origin shifts in 5-hydroxyindole (5OHI). If we follow this argumentation, bands A and B are members of the Gpy/anti family while band F belongs to the Gpy/syn family. The shift of the electronic origins between band A and F amounts to 230.34 cm−1, which is very close to the shift of the respective syn- and anti-conformers in 5OHI (230.91 cm−1).12 Regarding the rotational constants, a difference of +4.64 MHz in the A′′, −2.18 MHz in the B′′ and −0.76 MHz in the C′′ constant is observed experimentally between band A and F. For the anti- and syn-conformers of Gpy(out) (Gpy(up)) a change of +5.5 (+1.0) MHz in the A′′, −2.8 (−1.0) MHZ in the B′′ and −1.0 (−0.3) MHz in the C′′ constant is calculated from the ab initio optimized geometries. Hence, we assign the band A to Gpy(out)/anti and the band F to the respective syn-conformer. A confirmation of this assignment is given by the orientations of the transition dipole moments for the different conformers. It was mentioned that the CC2/cc-pVTZ calculations predict an increase of 8° in the angle θ when we go from a anti to a syn-conformation. A shift by the same amount can be observed between the experimentally determined angles of serotonin A and F. An additional affirmation can be extracted from the excited state lifetimes. In 5OHI it increases from 7.5 to 10 ns when going from the anti- to the syn-conformer.12 In the same manner the excited state lifetime increases from serotonin A (6 ns) to serotonin F (>12 ns).
For band B we know that it belongs to the Gpy/anti family which has three members. Gpy(out)/anti is already assigned to band A and Gpy(in)/anti is excluded by its high energy. Thus, the only possible assignment for band B is to the Gpy(up)/anti conformer. This is supported by the differences between the experimental rotational constants of the B conformer and the ab initio calculated Gpy(up)/anti rotational constants (ΔA = +9.2 MHz, ΔB = +5.3 MHz, ΔC = +5.2 MHz) which are very similar to the respective differences of the A conformer (ΔA = +7.8 MHz, ΔB = +6.4 MHz, ΔC = +5.2 MHz). A comparable deviation between theory and experiment can be expected for members of the same family. For the syn-conformers the deviations are higher, supporting the assignment that the grouping into syn- and anti-conformers is correct.
In Table 4 the least squares of the differences of the rotational constants of the A, B, and C conformers with the respective calculated values of anti-conformers of Gpy(out) and (up) and Gph(out) and (up) are determined. The A band shows the lowest χ2 value and thus the best agreement with Gpy(out)/anti. The B band has its best least square with Gpy(up)/anti and the C band shows the best agreement with Gph(out)/anti.
| Conformer | Gpy(out)/anti | Gpy(up)/anti | Gph(out)/anti | Gph(up)/anti |
|---|---|---|---|---|
| A | 504 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 561![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 892 892 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121 121 |
| B | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801 801 |
1541 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 832![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 778 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739 739![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 439 439 |
| C | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258 258![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 435 435 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777 |
An independent argument for this assignment arises from the comparison of the experimental ground state rotational constants in Table 3 with those from microwave spectroscopy.8 Cabezas et al. identified three conformers on the basis of the nuclear quadrupole constants as Gpy(out)/anti, Gpy(up)/anti and Gph(out)/anti. Since the rotational constants show an excellent agreement with our ground state values, the aforementioned assignment is confirmed unambiguously.
4.4 Energetic differences and comparison to tryptamine
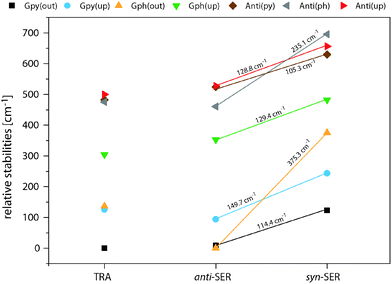
Fig. 4 compares the relative energies of the 14 most stable conformers of serotonin, derived from CC2/cc-pVTZ calculations. It is evident that the anti(OH)-conformers are always more stable in the electronic ground state and less stable in the electronically excited state. Furthermore, the energy difference between the syn- and anti-conformers is comparable within each electronic state if we exclude both Gph(out) conformers. In the electronic ground state the mean energetic difference amounts to 121 ± 31 cm−1 and the corresponding value for the excited state is 264 ± 43 cm−1. The values are comparable to those of 5-hydroxyindole indicating that the energetic difference in both states is mostly unaffected by the addition of an ethyl amino side chain.12 For the Gph(out) conformers, however, the energetic gap in the S0 state increases to 330 cm−1 while it is reduced to 81 cm−1 in the S1 state. Thus, the conformation of the OH group either (i) stabilizes the anti-conformer in both electronic states by 200 cm−1 with respect to the syn-conformer or (ii) destabilizes the syn-conformer in both states by the same energy difference or (iii) does a mixture of both.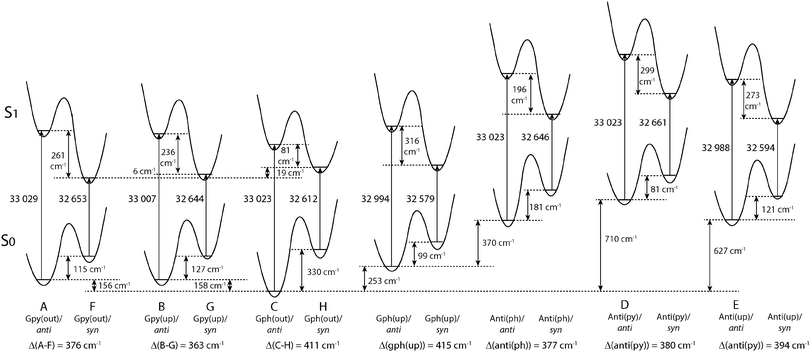 | ||
| Fig. 4 Relative energies of the 14 most stable conformers of serotonin according to the CC2/cc-pVTZ calculations. All energies are zero-point corrected and given in cm−1. The letters refer to the designation of LeGreve et al.5 | ||
In order to answer this question we compare the conformational spaces of serotonin and tryptamine on the same level of theory, as shown in Fig. 5. The respective relative energies are given in Table 2. Most of the conformers follow a common trend. The relative energy of a conformer is comparable in tryptamine and the respective anti(OH)-conformation. Rotating the OH-bond to the syn-conformation increases the relative energy by around 120 cm−1. Two conformers do not follow this trend: Anti(ph) and Gph(out). Judging from the distance between the NH2 group and the chromophore this points to a long-range effect between the OH and the NH2 group for Anti(ph). However, the most pronounced effect is observed for Gph(out) where the anti-conformation is stabilized significantly while the syn-conformer is destabilized by a comparable energy.
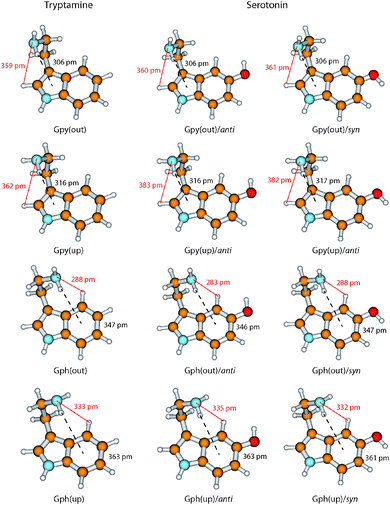
In Fig. 6 we take a detailed look at the structures of the Gpy and Gph conformers of tryptamine and serotonin. In tryptamine the energetic ordering can be explained by the π–H distances which are increasing in the same way as the conformers are shifting towards higher energies. This confirms the explanation of a hydrogen bond formation between the amino hydrogen and the pyrrole (Gpy) or phenyl (Gph) π cloud as given by Carney et al.14 Addition of the hydroxyl group changes these distances only slightly, so that another effect must be responsible for the modulation of the excitation energy of the Gph(out) conformers.
A possible candidate for the additional stabilization is the interaction of the amino LP and an adjacent hydrogen atom at the indole chromophore (H2 at C2 for the Gpy conformers and H4 at C4 for the Gph conformers, cf.Fig. 1). For the Gpy(up) and Gph(up) conformers of serotonin this can be excluded since the amino LP points away from the hydrogen atom. Also for Gpy(out) no effect is expected, because the distances do not change in comparison to tryptamine. For Gph(out)/anti, however, the amino LP is oriented towards the hydrogen atom H4 and the distance shortens from 288 pm to 283 pm by the addition of an hydroxyl group in anti orientation. In the case of the respective syn-conformer the LP of both the oxygen and the nitrogen atom are oriented towards H4. Hence, a competition of these LP to form a hydrogen bond or an electrostatic repulsion of both lone pairs seems to be a likely explanation for the destabilization of the syn-conformer and an increase of the amino LP hydrogen distance.
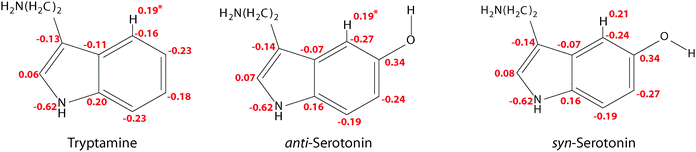
In this context one might ask why the additional stabilization through a hydrogen bond between the amino LP and H4 does not happen for the Gph(out) conformer in tryptamine. The answer for this can be given based on the natural charges in the indole chromophore as shown in Fig. 7.
In the pyrrole ring no or small changes between the natural charges of the tryptamine and serotonin conformers can be observed. This is different for the phenyl ring. Here, a pronounced increase in the electron density at C4 and C6 occurs, while C7 and especially C5 become more positive. The main difference between the syn- and anti-conformers of serotonin is the charge distribution at the carbon atoms C4 and C6: the electron density depends on the orientation of the lone pair and is either −0.24 or −0.27. When the lone pair is pointing towards the respective atom, the negative charge is decreased. This trend is in agreement with the results from Srivastava and Singh9 and Oeltermann et al.12
We propose that the increase of electron density at the C4 atom increases the polarity of the CH-bond which activates it for hydrogen bond formation. In tryptamine this activation is not possible. In turn, we assign the leading contribution of the stabilization of the Gph(out)/anti conformer to an intramolecular hydrogen-bond between the amino nitrogen LP and H4-atom at the phenyl ring. In general, a red shift of the C4–H4 stretch frequency due to a hyper-conjugative interaction between the lone pair of the nitrogen and the anti-bonding CH orbital is expected. The calculations, however, predict a blueshift of around 12 cm−1 between the CH vibrations of Gph(out)/anti and the other anti-conformers with Gpy, Gph and Anti conformation.9 It can be explained by the concept of “improper” hydrogen bonds.44 Following the argumentation of Joseph and Jemmis45 hydrogen bonds can be decomposed into long-range and short-range interactions. In the former, the electron density of hydrogen bond acceptor leads to a polarization of the covalent bond. The resulting increase in the electrostatic interaction between C and H leads to a shortened bond length and in a blueshift of the stretch vibration. When the acceptor comes closer the hyperconjugative interaction leads in most cases to the familiar redshift. Mo et al. have computed the change in CH bond length for the system F3C–H⋯NH3 which may provide a guideline for the discussed interaction.46 They found that for donor–acceptor distances larger than 210–240 pm the CH bond length is decreased. As in the present case the distance for the hydrogen bond is around 280 pm it is likely that the electrostatic interaction is dominating, leading to the predicted blueshift.
In case of the Gph(out)/syn-conformer we postulate a destabilization mechanism which arises from an intramolecular competition between the amino nitrogen and oxygen lone pair for the hydrogen bond with the H4-atom. This is backed by the computed C4–H4 stretch frequencies for the Gph(out)/syn and the other syn-conformers with Gpy, Gph and Anti conformation which show a similar blue shift of around 9 cm−1,9 close to our MP2 values.
A closely related system is mexamine (5-methoxytryptamine). The exchange of the hydroxyl group by an methoxy group leads to a decrease in the total number of observed conformers.20 Like in serotonin, also for 5-methoxytryptamine theoretical calculations predict the Gph(out)/anti as lowest energy conformer in the ground state. Additionally, the calculated energy gap between syn and anti increases for the Gph(out) by 200 cm−1 which is in good agreement with the values presented here for serotonin. Hence, the same effect is expected to be responsible for the shape of the mexamine conformational space as well. The same trend was observed for 5-methoxy N-acetyl tryptophan methyl amide, where only one conformer is observed in the IR-UV holeburn spectrum.22 This is assigned to a structure in which one of the LP of an oxygen atom is pointing towards H4. Also for the 5-methoxy substituted N-acetyltryptamine (melatonin)21 the anti-conformers are selectively stabilized. For the two most abundant conformers a hydrogen bond is formed between H4 and the N-acetylamino side chain: either with the LP of the oxygen or the nitrogen atom. Thus, the stabilization of anti-conformers via oxygen atoms connected to position 5 in the indole chromophore seems to be a general effect in these class of neurotransmitters.
5 Conclusions
Four conformers of serotonin were analyzed and assigned to the Gpy(out)/anti (band A), Gpy(up)/anti (band B), Gph(out)/anti (band C) and Gpy(out)/syn (band F) structures on the basis of the rotational constants and other molecular parameters from rotationally resolved electronic spectra. The orientation of the hydroxyl group is deduced from a characteristic difference in the TDM orientation by 8°. Moreover, the excited state lifetime is an additional molecular property that shows significant changes depending on the hydroxyl group orientation. Our results confirm the assignment made by LeGreve et al. based on vibrationally resolved spectroscopy.5 The addition of a hydroxyl group at position 5 to tryptamine in Gph(out) confirmation leads to a stabilization of the respective anti(OH)- and destabilization of the syn-conformer in the ground state. As a consequence Gph(out)/anti becomes the most stable conformer of serotonin, while for tryptamine this is Gpy(out). The energetic ordering in tryptamine is based on the H–π interaction between the amino hydrogen and the indole chromophore. For the Gph(out) conformers of serotonin an additional hydrogen bond between the LP of the amino group and the H4 atom at the indole chromophore is formed. This additional hydrogen bond selectively stabilizes the respective anti-conformer. For the syn-conformer a destabilization occurs due to a intramolecular competition between the O⋯H4 and N⋯H4 hydrogen bonds.Since the anti-conformers are always more stable in the ground state and the syn-conformers in the excited state (cf.Fig. 4) a stabilization of Gph(out)/anti and a destabilization of Gph(out)/syn leads to an increase of the syn–anti gap in the ground state and a decrease in the excited state. This might be the reason for the larger experimental difference in the excitation energies between both Gph(out) conformers.
The present results illustrate that even substituents which do not interact directly can communicate via competitive interactions and have a large influence on the shape of the conformational space. We could show that for various 5-substituted tryptamines (5-hydroxytryptamine, 5-methoxytryptamine, N-acetyl-5-methoxytryptamine, 5-methoxy N-acetyl tryptophan methyl amide) the hydrogen bond between the flexible side chain and H4 is a central motif which governs the most stable structure that can be experimentally observed.
Acknowledgements
Financial support of the Deutsche Forschungsgemeinschaft via grant SCHM1043 12-1 is gratefully acknowledged. Christian Brand acknowledges financial support from the Alexander von Humboldt foundation through a Feodor-Lynen fellowship. We thank the Universitätsrechenzentrum Köln for granted computing time and Olivia Oeltermann for assistance with the experiments.References
- D. E. Nichols and C. D. Nichols, Chem. Rev., 2008, 106, 1614–1641 CrossRef PubMed.
- D. Hoyer, D. E. Clarke, J. R. Fozard, P. R. Hartig, G. R. Martin, E. J. Mylecharane, P. R. Saxena and P. P. A. Humphrey, Pharmacol. Rev., 1994, 46, 157–203 CAS.
- F. Boess and I. Martin, Neuropharmacology, 1994, 33, 275–317 CrossRef CAS PubMed.
- M. Berger, J. A. Gray and B. L. Roth, Annu. Rev. Med., 2009, 102, 355–366 CrossRef PubMed.
- T. A. LeGreve, E. E. Baquero and T. S. Zwier, J. Am. Chem. Soc., 2007, 129, 4028–4038 CrossRef CAS PubMed.
- A. Lagutschenkov, J. Langer, G. Berden, J. Oomens and O. Dopfer, J. Phys. Chem. A, 2010, 114, 13268–13276 CrossRef CAS PubMed.
- T. A. LeGreve, W. H. James III and T. S. Zwier, J. Phys. Chem. A, 2009, 113, 399–410 CrossRef CAS PubMed.
- C. Cabezas, M. Varela, I. Peña, J. C. López and J. L. Alonso, Phys. Chem. Chem. Phys., 2012, 14, 13618–13623 RSC.
- S. K. Srivastava and V. B. Singh, RSC Adv., 2015, 5, 28141–28157 RSC.
- T. van Mourik and L. E. V. Emson, Phys. Chem. Chem. Phys., 2002, 4, 5863–5871 RSC.
- S. Arnold and M. Sulkes, Chem. Phys. Lett., 1992, 200, 125–129 CrossRef CAS.
- O. Oeltermann, C. Brand, M. Wilke and M. Schmitt, J. Phys. Chem. A, 2012, 116, 7873–7879 CrossRef CAS PubMed.
- W. Caminati, Phys. Chem. Chem. Phys., 2004, 6, 2806–2809 RSC.
- J. R. Carney and T. S. Zwier, J. Phys. Chem. A, 2000, 104, 8677 CrossRef CAS.
- L. A. Philips and D. H. Levy, J. Chem. Phys., 1988, 89, 85–90 CrossRef CAS.
- Y. R. Wu and D. H. Levy, J. Chem. Phys., 1989, 91, 5278–5284 CrossRef CAS.
- T. Nguyen, T. Korter and D. Pratt, Mol. Phys., 2005, 103, 1603–1613 CrossRef CAS.
- M. Schmitt, M. Böhm, C. Ratzer, C. Vu, I. Kalkman and W. L. Meerts, J. Am. Chem. Soc., 2005, 127, 10356–10364 CrossRef CAS PubMed.
- M. Böhm, R. Brause, C. Jacoby and M. Schmitt, J. Phys. Chem. A, 2009, 113, 448–455 CrossRef PubMed.
- T. B. C. Vu, I. Kalkman, W. L. Meerts, C. Brand, Y. N. Svartsov, S. Wiedemann, R. Weinkauf and M. Schmitt, Phys. Chem. Chem. Phys., 2009, 11, 2433–2440 RSC.
- J. T. Yi, C. Brand, M. Wollenhaupt, D. W. Pratt, W. L. Meerts and M. Schmitt, J. Mol. Spectrosc., 2011, 268, 115–122 CrossRef CAS.
- B. C. Dian, G. M. Florio, J. R. Clarkson, A. Longarte and T. S. Zwier, J. Chem. Phys., 2004, 120, 9033–9046 CrossRef CAS PubMed.
- M. Schmitt, J. Küpper, D. Spangenberg and A. Westphal, Chem. Phys., 2000, 254, 349–361 CrossRef CAS.
-
S. Gerstenkorn and P. Luc, Atlas du spectre d'absorption de la molécule d'iode 14
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–20
800–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, CNRS, Paris, 1986 Search PubMed.
000 cm−1, CNRS, Paris, 1986 Search PubMed. - R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- J. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951 CrossRef.
- C. Hättig, J. Chem. Phys., 2002, 118, 7751–7761 CrossRef.
- P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518 CrossRef CAS.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. Ostermeier, A. Gawelczyk and N. Hansen, in Step-Size Adaptation Based on Non-Local Use of Selection Information, ed. Y. Davidor, H.-P. Schwefel and R. Männer, Springer, 1994, pp. 189–198 Search PubMed.
- N. Hansen and A. Ostermeier, Evolutionary Computation, 2001, 9, 159–195 CrossRef CAS PubMed.
- W. L. Meerts, M. Schmitt and G. Groenenboom, Can. J. Chem., 2004, 82, 804–819 CrossRef CAS.
- W. L. Meerts and M. Schmitt, Phys. Scr., 2005, 73, C47–C52 CrossRef.
- W. L. Meerts and M. Schmitt, Int. Rev. Phys. Chem., 2006, 25, 353–406 CrossRef CAS.
- M. Schmitt and W. L. Meerts, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley and Sons, 2011 Search PubMed.
- Y. K. Sturdy and D. C. Clary, Phys. Chem. Chem. Phys., 2007, 9, 2065–2074 RSC.
- M. Schmitt, R. Brause, C. Marian, S. Salzmann and W. L. Meerts, J. Chem. Phys., 2006, 125, 124309 CrossRef PubMed.
- J. R. Clarkson, B. C. Dian, L. Moriggi, A. DeFusco, V. McCarthy, K. D. Jordan and T. S. Zwier, J. Chem. Phys., 2005, 122, 214311 CrossRef PubMed.
- N. Mayorkas, A. Bernat, S. Izbitski and I. Bar, J. Chem. Phys., 2013, 138, 124312 CrossRef PubMed.
- P. Hobza, V. Špirko, H. L. Selzle and E. W. Schlag, J. Phys. Chem. A, 1998, 102, 2501–2504 CrossRef CAS.
- J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632 CrossRef CAS PubMed.
- Y. Mo, C. Wang, L. Guan, B. Braïda, P. C. Hiberty and W. Wu, Chem. – Eur. J., 2014, 20, 8444–8452 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02130a |
| This journal is © the Owner Societies 2016 |