Testing the limits of NMR crystallography: the case of caffeine–citric acid hydrate

Abstract

The crystal structure of a new 1 : 2 caffeine–citric acid hydrate cocrystal is presented. The caffeine molecules are disordered over two positions, with the nature of the disorder confirmed to be static by ¹³C solid-state NMR. NMR linewidths in statically disordered systems reflect the distribution of local chemical environments, and this study investigates whether the disorder contribution to ¹³C linewidths can be predicted computationally. The limits of NMR crystallography calculations using density functional theory are tested by investigating how geometry optimisation conditions affect calculated NMR parameters. Careful optimisation is shown to reduce differences between ¹³C constants of symmetry-related sites to about 0.1 ppm. This is just sufficient to observe a correlation between calculated and experimental linewidths, and also show that systematic errors associated with geometry optimisation do not compromise other applications of “NMR crystallography”. In addition, the unit cell enthalpies calculated after careful optimisations provide insight into why the disordered structure is adopted.

---

Introduction

Bragg diffraction provides information on the average periodic structure of crystalline materials. This mean structure, however, does not fully describe structures containing disorder, and so complementary techniques are required to provide a more complete picture. NMR is one of the most powerful tools for probing disorder in materials. Static disorder results in line-broadenings, reflecting the distribution of local environments, but it is difficult to interpret such line-broadenings quantitatively given the indirect nature of the link between structure and chemical shifts. The development of “NMR crystallography”^1–3 has been driven by the development of density functional theory (DFT)-based computational codes that allow NMR chemical shifts to be calculated for real systems with useful accuracy.⁴ It is not obvious, however, that DFT calculations are sufficiently accurate to reproduce NMR linewidths due to disorder, which are typically only a few ppm for ¹³C NMR.

Molecular solids involving caffeine are frequently observed to involve disorder due to the nearly symmetrical structure of the caffeine molecule. This is exemplified by the two forms of anhydrous caffeine. The β form crystallises in C2/c and has two and a half independent molecules in the asymmetric unit; one fully ordered and the others exhibiting different orientational disorder over two positions. This challenging structure was determined using single crystal X-ray diffraction data in combination with high field ¹³C solid-state NMR (SSNMR).⁵ Above its glass transition, the α form is a rotator phase of high symmetry (space group is R3̄c) with the caffeine molecules orientationally disordered on their lattice sites. This disorder is at least partially frozen out below the glass transition, and so the ¹³C lineshapes of both α and β forms at room temperature are significantly broadened compared to caffeine hydrate, in which the caffeine molecules are ordered.^6,7 Caffeine disorder has also been observed in several caffeine-containing cocrystals,^8–10 though the nature of the disorder has yet to be determined.

For ¹³C shifts calculated via the gauge-including-projector-augmented-wave (GIPAW) approach,¹¹ experimental chemical shifts and calculated shieldings are generally found to agree within about 2 ppm.⁴ Similar levels of agreement have been observed using alternative approaches to calculating ¹³C shifts in solids.^12,13 The fact that different correlations are obtained between experimental shifts and calculated shieldings for different types of carbon^12–14 implies, however, that a significant fraction of this uncertainty is systematic. In the case of sites with the same chemical environment (including the limit of symmetry-related sites), the systematic “uncertainties” should be much lower, and are likely to be dominated by incomplete optimisation of the geometry, which is a pre-requisite for obtaining good correlations between experimental and calculated parameters. Here we assess whether these uncertainties can be reduced to the point such that ¹³C linewidths can be predicted for disordered systems, using a previously unreported hydrated cocrystal between caffeine and citric acid (1 : 2) as a model system.

Experimental

Synthesis

1 : 2 caffeine–citric acid hydrate (CCA) was produced by neat grinding of caffeine and citric acid monohydrate in a 1 : 2 molar ratio in a mortar and pestle at an ambient temperature of 20 °C. This grinding product was used for all NMR experiments. Liquid assisted grinding, with a few drops of water added prior to grinding, also yielded the CCA cocrystal, while neat grinding at an ambient temperature of ∼30 °C yielded a mixture of the 1 : 1 anhydrous cocrystal¹⁵ (KIGKER in the CSD) and citric acid. Single crystals of CCA were grown by slow cooling of the neat grinding product dissolved in nitromethane. The solution was cooled to room temperature over several hours, the resulting precipitate filtered off (found to be the previously reported 1 : 1 cocrystal¹⁵) and the solution left in the fridge for 3 weeks, after which clear block crystals of 1 : 2 CCA were obtained. Attempts to crystallise bulk quantities of the 1 : 2 CCA failed due to the propensity of the 1 : 1 cocrystal to precipitate out before CCA crystals could grow. The grinding product was stable on storage in air at ambient temperature over 9 months, although degradation was observed under the conditions of the NMR experiment after a period of several hours via the appearance of weak anhydrous cocrystal and citric acid peaks (without noticeable broadening of the cocrystal hydrate peaks). No degradation peaks are visible in the ¹³C spectrum acquired for the much shorter periods used below.

Crystallography

Single-crystal X-ray diffraction data was collected on an Xcalibur, Sapphire3, Gemini ultra diffractometer using graphite-monochromated Mo Kα radiation. The raw data were collected using the CrysAlisPro (Agilent Technologies) software. Structure solution and refinement was carried out using SHELXS-87³⁸ and ShelXL2014³⁹ within Olex2.⁴⁰ All of the non-hydrogen atoms were refined anisotropically. A mixed hydrogen atom treatment was used: hydrogen atoms attached to carbon were placed geometrically and refined using a riding model, while those attached to oxygen and involved in hydrogen bonding were located in the difference map and refined freely. Examination of the raw data frames showed no evidence of diffuse scattering. Crystal structure and refinement data are given in Table 1. Crystallographic data have been deposited with the Cambridge Crystallographic Data Centre, CCDC deposit number 1471476.

Table 1 Crystal data and structure refinement for CCA

Empirical formula	C20H30N4O18
Formula weight/g mol^−1	614.48
Temperature/K	120(2)
Crystal system	Monoclinic
Space group	C2/c
a/Å	16.7407(6)
b/Å	9.5561(3)
c/Å	16.5918(6)
β/°	90.525(3)
Volume/Å^3	2654.17(16)
Z	4
ρ calc/g cm^−3	1.538
μ/mm^−1	0.137
F(000)	1288.0
Crystal size/mm^3	0.44 × 0.29 × 0.14
Radiation	Mo Kα (λ = 0.71073 Å)
2Θ range for data collection/°	5.478 to 61.266
Index ranges	−23 ≤ h ≤ 23, −13 ≤ k ≤ 13, −23 ≤ l ≤ 23
Reflections collected	13 722
R int	0.0531
Data/restraints/parameters	3787/1/240
Goodness-of-fit on F^2	1.050
Final R indexes [I ≥ 2σ (I)]	R 1 = 0.0457, wR2 = 0.1000
Final R indexes [all data]	R 1 = 0.0630, wR2 = 0.1108
Largest diff. peak/hole/e Å^−3	0.38/−0.30

---

Solid-state NMR spectroscopy

Solid-state NMR experiments were performed on the grinding product using a Bruker Avance III HD spectrometer operating at 125.7 MHz for ¹³C with a 5 mm (rotor o.d.) HX magic-angle spinning (MAS) probe. Variable-amplitude cross-polarization was used with contact times of 1–2 ms, at 8 kHz MAS with recycle delays of 10–30 s. SPINAL64 heteronuclear decoupling was applied with 50 kHz ¹H nutation rate, and the spectra referenced by setting the carbonyl resonance of replacement sample of α-glycine to 176.5 ppm. ¹³C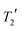 measurements used a ¹³C π pulse duration of 10 μs. Seven τ increments were acquired from 1–16 ms in increments of 1.25 ms (equal to 10τ_r where τ_r is the rotor period) with only 48 transients per increment in order to minimise sample degradation under MAS conditions.

Computational methods

Unless otherwise stated, first-principles calculations were performed using CASTEP v8.0.¹⁶ As discussed below, the disordered crystal structure was resolved into two ordered structures denoted 1111 and 2222, see Fig. 1. Using the Avogadro molecular editor,¹⁷ individual caffeine molecules in the 1111 structure were flipped 180° about the caffeine pseudo-rotation axis to create a further 14 simulated-disorder structures consisting of different combinations of caffeine orientation. These form symmetry-related pairs, e.g. the 1111 and 2222 pair, which is denoted 1111 for concision. Configuration ensemble methods using larger supercells could be used, as has been previously applied to crystal structure prediction of β-caffeine,^18,19 but these would be excessively computationally demanding for first-principles calculations.

Fig. 1 (i) A schematic of CCA solved in the C2/c space group with ellipsoids viewed at the 50% probability level. The dashed line indicates the rotation axis between the two disordered orientations. i = 1 − x, +y, 3/2 − z. (ii) The labelling for a single orientation of the caffeine molecule as used for assignment of NMR spectra. (iii) The theoretical unit cell of 1111, with the citric acid/water framework in black and caffeine molecules labelled such that the ABCD order reflects the order of the 1111 labels, i.e. flipping molecule C results in the structure 1121. Hydrogen atoms are omitted for clarity.

All calculations used the Perdew–Burke–Ernzerhorf functional, and either Vanderbilt ultrasoft pseudopotentials (USP)²⁰ or the on-the-fly-generated ultrasoft pseudopotentials (OTFG). The centre of mass was fixed and a cut-off energy of either 400 eV or 700 eV was used, which is above the fine cut-off of 340 eV for the hardest element (oxygen). Integrals were taken over the Brillouin zone using a Monkhorst–Pack grid with a minimum k-point sample spacing of 0.1 Å⁻¹, corresponding to one k-point. Geometry optimisations were carried out using the Broyden–Fletcher–Goldfarb–Shanno scheme²¹ using the different conditions given in Table 2.

Table 2 Conditions used in the different optimisation methods

Name^a	Cut-off energy/eV	dEelectronic/10^−5 eV	dEgeometry/10^−5 eV	|F|max/10^−2 eV per atom	Mean ΔE between pairs/eV
a Codes used: D – dispersion correction applied, O – on-the-fly-generated pseudopotentials used, W – convergence window increased from 2 to 10, C – unit cell optimised. b |F|max converged to within 0.1 × 10^−2 eV per atom but did not reach the 0.01 × 10^−2 eV per atom tolerance.
[1]	400	1	2	5	0.036
[2]	700	0.1	0.2	1	0.009
[2-D]	700	0.1	0.2	1	0.012
[3]	700	0.001	0.002	0.01^b	0.005
[3-D]	700	0.001	0.002	0.01^b	0.004
[3-DO]	700	0.001	0.002	0.01^b	0.002
[3-DW]	700	0.001	0.002	0.01^b	0.004
[3-DC]	700	0.001	0.002	0.01^b	0.005

---

All 288 atomic positions were optimised with the unit cell parameters fixed, except in case [3-DC] where the unit cell parameters were allowed to relax. dE_electronic is the threshold (energy per atom) for convergence of the electronic self-consistent field minimisation in each geometry optimisation step, while dE_geometry is the corresponding convergence threshold between successive geometry optimisation steps. The latter parameter cannot be meaningfully tightened beyond the former. |F|_max is the convergence parameter on the maximum atomic force, while the convergence window sets the number of successive iterations within which both the energy and force tolerances are achieved for the optimisation to be considered converged. The dispersion correction used here is the Tkatchenko–Scheffler (TS) scheme,²² which has been shown to return reliable distance and unit cell parameters in molecular crystals.^23,24 No finite basis correction was applied in the variable unit cell calculations.

Since the initial structures were obtained by manual manipulation of the atomic co-ordinates, an initial crude geometry optimisation (using CASTEP v6.0) was used to provide reasonable starting points for the subsequent tight optimisations (all performed in CASTEP v8.0). Table S1 in the ESI† gives additional information on the time taken and the number of successive iterations required to complete the geometry optimisations.

NMR calculations used OTFG pseudopotentials and cut-off energy of 700 eV in all cases. The k-point sample spacing was 0.05 Å⁻¹ (12 k-points) with an offset of (0.25, 0.25, 0.25) in fractional co-ordinates. Simulated disorder spectra were calculated using the MagresPython²⁵ library to read in the CASTEP outputs and pNMRsim²⁶ to create the spectra.

Results

Crystallography

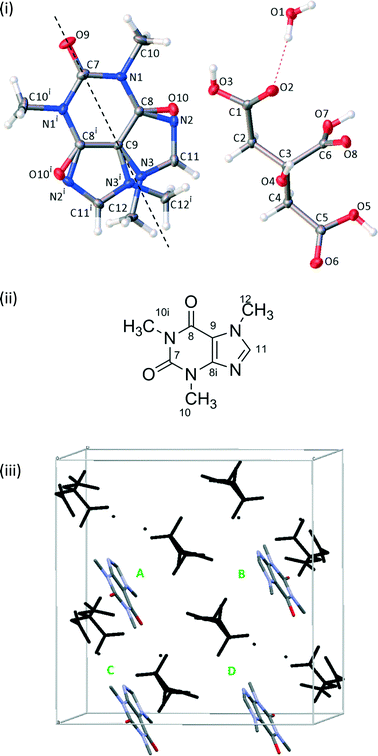
Single crystals were solved in the monoclinic space group C2/c. The asymmetric unit contains half a caffeine molecule, one citric acid molecule and one water molecule. The caffeine molecule is refined as disordered over two positions across a 2-fold rotation axis with occupancies necessarily fixed at 50 : 50, see Fig. 1. Some crystals from different batches were found to refine better in Cc rather than C2/c as the occupancy of the disordered caffeine appeared to be ∼73 : 27, which differs significantly from 50 : 50 required in C2/c. The crystal structure presented here was also refined in Cc and the disorder ratio refined to ∼50 : 50. Variable temperature measurements found the same structure at both 120 K and 295 K, suggesting that the disorder is static. The crystal packing around the planar caffeine molecule and intermolecular hydrogen bonding interactions are likely to make any rotation difficult. The extensive hydrogen bonding between the citric acid and water molecules and between citric acid and caffeine molecules creates a 3-dimensional structure, as documented in Table 3.

Table 3 Hydrogen bonding in CCA

D–H⋯A	d D–H/Å	d H⋯A/Å	d D⋯A/Å	D–H–A/°
^1 1 − x, 1 − y, 1 − z; ^2 ½ − x, ½ − y, 1 − z; ^3 ½ − x, ½ + y, ½ − z; ^4x, −1 + y, z; ^5x, 1 + y, z.
O4–H4⋯O9^1	0.82(2)	2.13(2)	2.885(1)	154(2)
O7–H7⋯O10^2	0.92(3)	1.63(3)	2.550(8)	175(2)
O7–H7⋯N2^2	0.92(3)	1.82(3)	2.735(9)	171(2)
O1–H1A⋯O8^3	0.87(2)	1.93(2)	2.787(2)	166(2)
O1–H1B⋯O2	0.87(2)	1.95(2)	2.795(2)	167(2)
O5–H5⋯O1^4	0.91(1)	1.69(1)	2.591(2)	169(3)
O3–H3⋯O6^5	0.83(2)	1.93(2)	2.708(2)	157(2)

---

Solid-state NMR spectroscopy

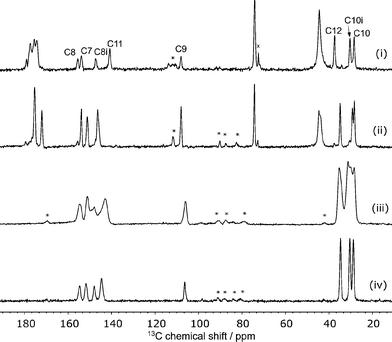
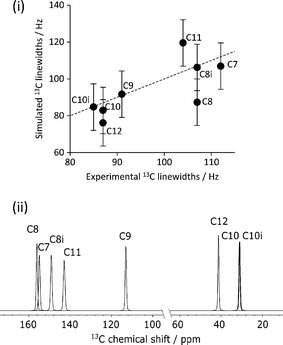
The ¹³C spectrum of the raw grinding product, Fig. 2, shows the presence of excess citric acid. Interestingly, the chemical shifts of these peaks correspond to those of anhydrous citric acid²⁷ rather than the monohydrate starting material. These peaks do not overlap with the caffeine peaks of interest and so no purification was attempted.

Fig. 2 ¹³C CP spectra of (i) CCA, (ii) the anhydrous 1 : 1 cocrystal, (iii) β-caffeine and (iv) caffeine hydrate at 8 kHz MAS. Peaks marked with ‘x’ are excess anhydrous citric acid and ‘*’ are spinning sidebands.

The disorder of the caffeine over the 2-fold rotation axis in C2/c means that the pairs of carbons C8/C8i and C10/C10i are crystallographically indistinguishable and share the same label, see Fig. 1(ii). They are, however, chemically distinct and are distinguished in the ¹³C NMR spectrum. No changes were observed in variable-temperature ¹³C SSNMR experiments between 22 °C and 70 °C conducted at a low magic-angle spinning rate of 3 kHz to highlight any effect of dynamics on spinning sideband patterns. Additionally, no peaks were visible in spectra acquired with short (1–5 s) recycle delays, confirming that the caffeine disorder is static rather dynamic.

The caffeine linewidths are slightly broader than the ordered caffeine hydrate, but sharper than those of the highly disordered anhydrous β-caffeine, see Fig. 2. The quantitative prediction of NMR linewidths is complicated by magnetic susceptibility effects. While magic-angle spinning is effective at removing the effects of local variations of the bulk magnetic susceptibility, χ, the anisotropy of the bulk magnetic susceptibility (ABMS) tensor is not fully averaged, resulting in a uniform but orientation-dependent shift of the NMR frequencies.^28–30 Quantitative calculation of this effect on the linewidths of polycrystalline samples is non-trivial,³⁰ but we have previously shown that the parameter |4πΔχ|, where Δχ is the anisotropy of the magnetic susceptibly tensor, provides a useful metric for the line broadening due to ABMS.³¹ This factor, calculated from the CASTEP-calculated susceptibility tensor, is 1.1 ppm for CCA compared to 2.0 ppm for the 1 : 1 cocrystal.¹⁵ Since the linewidths for CCA are 0.09 ppm broader on average than those for the 1 : 1 co-crystal, this implies that broader lines for CCA are indeed associated with static disorder. The linewidths due to the static disorder is small, however, and their computational prediction is a challenging test of NMR crystallography protocols.

Geometry optimisation

It is well established that geometry optimisation of hydrogen positions obtained from XRD structures is necessary prior to calculation of NMR chemical shifts. As this optimisation is iterative and involves convergence criteria, there will be some systematic uncertainties introduced into subsequent calculations. These uncertainties have not previously been investigated, but may be significant for the prediction of NMR linewidths.

The current system is an ideal test case, since the 16 simulated-disorder models form 8 symmetry-related pairs of structures whose NMR parameters should be identical in the limit of perfect geometry optimisation. After the initial crude optimisation, however, there is no discernible pattern to the calculated lattice energies, see Fig. S1 in the ESI,† and tighter convergence of the structures is required.

Fig. 3 shows that the final energies of the 16 structures depend on the parameters of the final geometry optimisation step. Tightening the energy tolerances by one order of magnitude compared to the default, [2] and [2-D], results in the 1111 pair (yellow) converging to approximately 0.03 eV higher in energy than the other structures. Other matching pairs emerge as the convergence criteria are further tightened, [3], [3-D] and [3-DO].

Fig. 3 Final energies of each structure following different optimisations. Symmetry-related pairs discussed in the main text are coloured/shaded for clarity.

A slightly different pattern of energies is observed when the unit cell parameters are allowed to vary, [3-DC]; the 1212 pair (blue) converge to lower energy rather than the 1122 pair (green). This correlates with a larger percentage change in the α and γ unit cell angles for 1212 compared to the other simulated pairs, see Fig. S2 in the ESI.† In the material, however, the unit cells are those of the average unit cell, and so the optimisations in which the unit cell parameters are constrained to those of the mean unit cell from XRD are more physically meaningful.

Including dispersion correction systematically lowers all the energies, but does not change the relative energetic ordering. Using OTFG pseudopotentials with dispersion correction also results in the same pattern of energies, although the energy gaps between pairs (see Table 2) and different sets (see Fig. 3) are noticeably smaller. Increasing the convergence window so that the convergence criteria need to be matched over 10 iterations, [3-DW], does not improve the convergence of the final energies of symmetry-related pairs. Instead, none of the calculations converge with respect to the energy due to the over-tight termination conditions. This set of optimisations is not discussed further.

The degree of convergence between symmetry-related pairs can also be tested using the root-mean-square difference (RMSD) between the positions of the non-H atoms. As might be expected, these show the same trends, Fig. S3,† as observed in Fig. 3. The pseudo-rotation axis shown in Fig. 1 is not precisely retained following geometry optimisation, see Fig. 4, but these deviations are within the boundaries of the thermal ellipsoids i.e. the optimised structures are indistinguishable from the original crystal structure within the experimental uncertainties.

Fig. 4 Overlays of the caffeine molecules in symmetry-related pair 1111 (i) before and (ii) after geometry optimisation using [3-DO] optimisation parameters. View is along the crystallographic c axis.

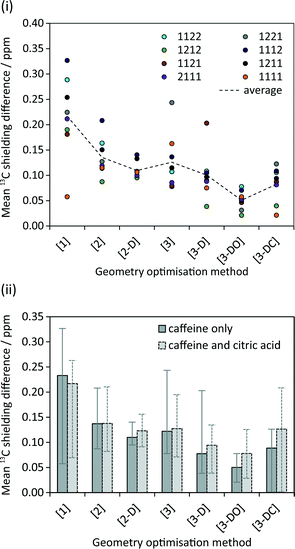
Calculated NMR parameters

The calculated NMR parameters for matching sites in the symmetry-related structure pairs should also be identical in the limit of perfect geometry optimisation. As seen in Fig. 5(i), no pattern was observed between the calculated ¹³C shielding values of the eight symmetry-related pairs; for example, no particular symmetry-related pair showed consistently higher or lower average differences in shielding. Hence Fig. 5(ii) simply plots the overall average difference between the calculated isotropic shieldings of related carbon sites. Even with the relatively crude initial optimisation, [1], the mean differences are about an order of magnitude smaller than the typical “uncertainties” on DFT-calculated shifts relative to experiment. The difference is further reduced, to about 0.1 ppm, on tightening the convergence criteria. Ignoring the crude optimisation, the average difference is consistently smaller when considering just caffeine sites. This may reflect the rigid nature of the caffeine molecule, which should reduce the complexity of the optimisation surface compared to the more flexible citric acid molecules.

Fig. 5 (i) Mean difference in calculated isotropic ¹³C shielding between related caffeine carbon sites in the given symmetry-related pairs following different geometry optimisations. (ii) Average of these differences over all pairs. The “caffeine only” dataset corresponds to the dotted line in (i), with the “error bars” indicating the maximum and minimum values in (i).

Optimisations including dispersion correction consistently lower the mean ¹³C shielding difference. The pattern in Fig. 5(ii) generally reflects the energy differences in Fig. 3; the smallest differences in energy between symmetry-related pairs are seen for [3-D] and [3-DO] and similarly these optimisations result in the lowest mean ¹³C shielding differences. The fewer iterations needed for convergence of the optimisations with dispersion correction (cf. Table S1†) may reflect a smoother energy landscape for geometry optimisation, but further work would be required to confirm this speculation.

Fig. 6 examines the relationship between the geometry optimisation and agreement with experimental chemical shifts. The calculated ¹³C shieldings of all simulated-disorder structures were averaged for each carbon site and then referenced using δ_calc = mσ_calc + c, where m and c are determined by linear regression of the average calculated ¹³C shieldings against the experimental ¹³C chemical shifts. Due to the overlap of the citric acid resonances with those of excess citric acid only the caffeine carbon atoms were considered. Given that the effects of imperfect geometry optimisation are of the order of 0.1 ppm, it is unsurprising that there is no observable correlation between the geometry optimisation protocol and the quality of agreement with experimental chemical shifts. [3-DO] shows a significantly larger mean difference compared to the optimisations using the USP pseudopotentials. This is consistent with the systematic limitations of DFT being the major source of disagreement with experiment.^13,14,32 Including dispersion correction has no significant effect, in keeping with previous observations of only marginal improvement in the agreement of ¹⁵N shifts.³³

Fig. 6 Root mean squares differences between experimental ¹³C caffeine shifts and average calculated shieldings after referencing as described in the text.

The mean difference between the shieldings of chemically related ¹³C sites caused by geometry optimisation conditions is significant in the simulation of CCA linewidths, see Fig. 7(i). A full description of the linewidth simulation method is given in the ESI† but, in brief, the ¹³C linewidths were simulated by summing the spectra of the 16 simulated-disorder structures from the [3-DO] geometry optimisation yielding a single simulated-disorder spectrum, Fig. 7(ii). The homogeneous linewidth³⁴ of each site is taken as 1/π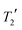 with a Lorentzian lineshape, where the 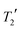values are measured from spin-echo experiments, see Table S2.† The inhomogeneous linewidth (incorporating quadrupolar broadening contributions from adjacent ¹⁴N nuclei and ABMS effects) is taken from the inhomogeneous linewidths measured on the ordered 1 : 1 cocrystal and is modelled with a Gaussian lineshape, see Table S3.† There is a reasonable correlation between calculated and experimental linewidths (R² = 0.54), but the uncertainties associated with geometry optimisation clearly limit the quality of the correlation (the uncertainties in the experimental linewidths are less than a few Hz) i.e. within the size of the symbols used.

Fig. 7 (i) Experimental vs. simulated ¹³C caffeine linewidths of CCA derived from the simulated spectra of individual ¹³C sites summed over the 16 simulated-disorder structures optimised using the [3-DO] method, (ii). “Error bars” indicate the uncertainty associated with geometry optimisation of 0.1 ppm. Shifts referenced using δ_calc = −σ_calc + σ_ref, where σ_ref is 174 ppm. The dashed line corresponds to y = x.

Discussion and conclusions

This study has shown that uncertainties associated with incomplete geometry optimisation are non-negligible. These can be reduced to about 0.1 ppm for ¹³C isotropic shieldings by judicious tightening of the convergence criteria, at the expense of significantly lengthened calculation times (about 2–3 times longer). These uncertainties are about an order of magnitude smaller than the root-mean-square deviations between calculated and experimental shifts, confirming that geometry optimisation is not a limiting factor, say, for assignment of chemically distinct sites. However, these results suggest that it is possible to investigate much more subtle differences in shifts for sites in the same local bonding environment. For example, changes in ¹³C shifts of different hydration states of sildenafil citrate well below the 2 ppm “limit” have recently been observed to be computationally predictable.³⁵

In the case of caffeine citric acid hydrate, the uncertainties associated with geometry optimisation are significant compared to the limited line-broadening associated with the disorder. In other systems, however, such as β-caffeine, the effects of disorder on the NMR spectrum are much stronger and should be computable. The approach described may be particularly valuable where 2D NMR is being used to probe the correlation between shifts in disordered systems.³⁴

Tight control of the geometry optimisation is also essential when trying to compare lattice energies, since the uncertainties are of a similar magnitude to the differences in lattice energies of polymorphic forms.³⁶ Although the absolute energies of the systems are highly dependent on the optimisation protocol and DFT parameters, the relative energies of the symmetry-related pairs converge well as the optimisation criteria are tightened, giving some confidence that the lattice energies between the different (but chemically very similar) disordered structures can be meaningfully compared, cf.Fig. 3. Although the pair of structures based on the 1212 configuration, S₁₂₁₂, are calculated to be about 2.5 kJ mol⁻¹ lower in energy per unit cell than a disordered structure, S_disord, based on an equally weighted random distribution of configurations, there is an “entropic” bias towards the disordered structure (which has 16 configurations compared to 2). Very crudely, the “Boltzmann ratio” for S_disord/S₁₂₁₂, is about 3 at ambient temperature (k_BT = 2.5 kJ mol⁻¹). Similar energetic arguments have recently been used to understand the presence of disorder in some, but not all, solvates of droperidol,³⁷ and the presence of disorder in β-caffeine but not isocaffeine.¹⁹ Although crystallisation is a complex phenomenon, largely controlled by kinetic factors, kinetics are also likely to favour the less ordered structure. Hence the first-principles calculations provide insight into why this system adopts a disordered rather than an ordered structure.

Acknowledgements

H. E. K. is supported by an EPSRC Doctoral Training Grant studentship. The authors thank Prof. Branton Campbell and Dr Ivana Radosavljevic Evans for helpful discussions, and Dr Jonathan Yates for comments on a draft version. This work also benefitted from discussions within the context of the EPSRC-funded collaborative computational project for NMR crystallography (CCPNC). H. E. M. is grateful to the University of Durham for financial support.

References

1. R. K. Harris, R. E. Wasylishen and M. J. Duer, NMR Crystallography, John Wiley & Sons Ltd, West Sussex, UK, 2009.
2. L. Mafra, Solid State Nucl. Magn. Reson., 2015, 65, 1.
3. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186.
4. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733.
5. G. D. Enright, V. V. Terskikh, D. H. Brouwer and J. A. Ripmeester, Cryst. Growth Des., 2007, 7, 1406.
6. H. G. M. Edwards, E. Lawson, M. deMatas, L. Shields and P. York, J. Chem. Soc., Perkin Trans. 2, 1997, 10, 1985.
7. D. J. Sutor, Acta Crystallogr., 1958, 11, 453.
8. D.-K. Bučar, R. F. Henry, X. Lou, R. W. Duerst, T. B. Borchardt, L. R. MacGillivray and G. G. Zhang, Mol. Pharmaceutics, 2007, 4, 339.
9. D.-K. Bučar, R. F. Henry, X. Lou, R. W. Duerst, L. R. MacGillivray and G. G. Z. Zhang, Cryst. Growth Des., 2009, 9, 1932.
10. N. Schultheiss, M. Roe and S. X. M. Boerrigter, CrystEngComm, 2011, 13, 611.
11. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
12. S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Phys., 2014, 141, 164121.
13. J. D. Hartman, S. Monaco, B. Schatschneider and G. J. Beran, J. Chem. Phys., 2015, 143, 102809.
14. S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Theory Comput., 2015, 11, 5229.
15. S. Karki, T. Friscic, W. Jones and W. D. Motherwell, Mol. Pharmaceutics, 2007, 4, 347.
16. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
17. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
18. R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201.
19. M. Habgood, Cryst. Growth Des., 2011, 11, 3600.
20. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
21. B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233.
22. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
23. J. Binns, M. R. Healy, S. Parsons and C. A. Morrison, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 259.
24. J. van de Streek and M. A. Neumann, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 544.
25. S. Sturniolo, T. F. G. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson, 2016 DOI:10.1016/j.ssnmr.2016.05.004.
26. P. Hodgkinson, pNMRsim: a general simulation program for large problems in solid-state NMR, 2013, https://www.dur.ac.uk/paul.hodgkinson/pNMRsim, Last accessed 2016-07-27.
27. J. W. Fischer, L. H. Merwin and R. A. Nissan, Appl. Spectrosc., 1995, 49, 120.
28. D. L. Vanderhart, W. L. Earl and A. N. Garroway, J. Magn. Reson., 1981, 44, 361.
29. A. N. Garroway, D. L. VanderHart and W. L. Earl, Philos. Trans. R. Soc., A, 1981, 299, 609.
30. M. Alla and E. Lippmaa, Chem. Phys. Lett., 1982, 87, 30.
31. A. J. Robbins, W. T. Ng, D. Jochym, T. W. Keal, S. J. Clark, D. J. Tozer and P. Hodgkinson, Phys. Chem. Chem. Phys., 2007, 9, 2389.
32. R. Laskowski, P. Blaha and F. Tran, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87.
33. N. Mercadal, S. P. Day, A. Jarmyn, M. B. Pitak, S. J. Coles, C. Wilson, G. J. Rees, J. V. Hanna and J. D. Wallis, CrystEngComm, 2014, 16, 8363.
34. S. Cadars, A. Lesage, C. J. Pickard, P. Sautet and L. Emsley, J. Phys. Chem. A, 2009, 113, 902.
35. A. Abraham, D. C. Apperley, S. J. Byard, A. J. Ilott, A. J. Robbins, V. Zorin, R. K. Harris and P. Hodgkinson, CrystEngComm, 2016, 18, 1054.
36. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154.
37. A. Bērziņš and P. Hodgkinson, Solid State Nucl. Magn. Reson., 2015, 65, 12.
38. G. M. Sheldrick, Acta Crystallogr., Sect. A, 2008, 64, 112–122.
39. G. M. Sheldrick, Acta Crystallogr., Sect. C, 2015, 71, 3–8.
40. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.

---

Footnote

† Electronic supplementary information (ESI) available: Including details of the optimisation calculations, correlation plots between the energies and atom displacements of the simulated disorder structures and details of the ¹³C NMR linewidth simulation method. CCDC 1471476. Original research data can be accessed through DOI: 10.15128/r1np193917h. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce01453d

---