Open Access Article
Open Access ArticleAn in vivo study of electrical charge distribution on the bacterial cell wall by atomic force microscopy in vibrating force mode†
Christian
Marlière
*a and
Samia
Dhahri
b
aInstitut des Sciences Moléculaires d'Orsay, ISMO, University Paris-Sud, CNRS, Orsay, France. E-mail: christian.marliere@u-psud.fr; Tel: (+33) 169 157 511
bUniversity of Carthage, High Institute of Environmental Science and Technology of Borj Cedria, Ben Arous, Tunisia
First published on 13th April 2015
Abstract
We report an in vivo electromechanical atomic force microscopy (AFM) study of charge distribution on the cell wall of Gram+ Rhodococcus wratislaviensis bacteria, naturally adherent to a glass substrate, under physiological conditions. The method presented in this paper relies on a detailed study of AFM approach/retract curves giving the variation of the interaction force versus distance between the tip and the sample. In addition to classical height and mechanical (as stiffness) data, mapping of local electrical properties, such as bacterial surface charge, was proved to be feasible at a spatial resolution better than a few tens of nanometers. This innovative method relies on the measurement of the cantilever's surface stress through its deflection far from (>10 nm) the repulsive contact zone: the variations of surface stress come from the modification of electrical surface charge of the cantilever (as in classical electrocapillary measurements) likely stemming from its charging during contact of both the tip and the sample electrical double layers. This method offers an important improvement in local electrical and electrochemical measurements at the solid/liquid interface, particularly in high-molarity electrolytes when compared to techniques focused on the direct use of electrostatic force. It thus opens a new way to directly investigate in situ biological electrical surface processes involved in numerous practical applications and fundamental problems such as bacterial adhesion, biofilm formation, microbial fuel cells, etc.
Introduction
Solid/liquid interfaces may be subject to bacterial adhesion and biofilm formation. If the microbial consortia are pathogenic these surfaces will be a starting point for nosocomial and food borne infections. It is well known that bacterial adhesion on inert surfaces is mainly steered by non-covalent molecular interactions with long-range interactions such as van der Waals, electrostatic (mainly resulting from the overlapping of electrical double layers) or short-range ones such as Lewis acid–base and hydration interactions.1 However gaining knowledge of the basic processes governing bacterial adhesion to abiotic surfaces still remains an important task. Electrostatic interactions are one of the key factors as the bacterial cell surface is known to carry a net negative charge under most physiological conditions.2 The problem is intricate, as bacterial surfaces are chemically and structurally heterogeneous.3 As an example, the bacterial membrane contains pore-forming integral membrane proteins constituting channels of conduction for charged particles. Ions, typically, will thus flow through the cellular membrane, provided that a driving force exists for ionic movement such as, for instance, an electrochemical gradient.4 Studies of these local electrophysiological properties of bacteria have been mainly performed by the patch-clamp technique. For it, a small patch of membrane containing one or a few channels (several tenths of nanometers in diameter) needs to be isolated and placed at the tip of a micropipette (tip opening ∼1 μm), filled with an ionic solution. The conditioning of the membrane's sample for patch-clamp experiments resorts to aggressive techniques such as lysozyme digestion, a mandatory step for the completion of the needed spheroplasts. Thanks to this technique, important results on gating kinetics and ion permeability of membrane channels sensitive to osmotic pressure have been obtained.5,6However little is known about the electrical properties of the bacterial cell surface at the nanometer level and under low perturbative conditions, as valuable methods for investigating local surface charge or potential distribution are still missing, especially in aqueous solutions with high ionic strength. Atomic force microscopy (AFM) may be a valuable choice for local investigation of dielectric properties in physiological environments as nanometric spatial resolution is easily reached and AFM can be used in various electrical or electrochemical modes. Significant progress has been made with AFM operating in liquid environments when focusing on topographic7–9 or mechanical10 aspects. In ambient and vacuum environments, the electrostatic properties of surfaces can be easily mapped by Kelvin probe force microscopy.11 The presence of mobile ions in the liquid environment complicates the implementation of such techniques so that it was mainly applied to non-polar liquids (i.e. containing a few mobile ions)12 or low-molarity electrolytes (<10 mM).13,14 The presence of mobile ions and bias voltage applied between the tip and the sample led to induced charge dynamics, ion diffusion and a capacitive coupling between them depending on the electrochemical properties of the solution (ionic strength, etc.).15 In search of a quantitative imaging of local dielectric properties in electrolyte solutions with nanoscale spatial resolution, most of the studies have been done by applying high frequency voltages16 between the cantilever and the sample. By working at frequencies greater than the dielectric relaxation frequency of the medium (in the MHz range for 1 mM KCl17) and by scanning the probe at distances much larger than the Debye length (typically 10 nm in 1 mM monovalent electrolytes), spatially resolved mapping of the dielectric properties of patterned samples is feasible.18 Working at a high frequency is an efficient way to actuate the cantilever solely by electrostatic force and not by surface stress forces that contribute significantly to the cantilever vibration in the low frequency regime.17,19 Derived methods based on a similar concept were used to characterize samples with charged domains in liquid media at low ionic strength.13,14,20 As the voltage varies at time scales much lower than the typical time related to bulk diffusion of ions (a few microseconds for a distance of 100 nm21) these techniques avoid the formation of the electrical double layer (EDL) and hence hinder its use for the study of the EDL itself and consequently of the underlying surface repartition of charges on the sample.
In this paper we present a new experimental method for the investigation of local electrical surface charges. It is based on the original combination of two complementary physical processes already largely documented in the literature.
The first one is based on the study of the electrical double layer (EDL) by the use of immersion and emersion of a metallic electrode. From a pioneering idea of Kenrick,22 this method was used to study different properties of the EDL: potential of zero charge,23,24 ion absorption25etc. It was shown that the electrode can be removed from an electrolyte to air26 or vacuum25 as well. It was shown that the electric double layer is then intact, provided that there is no faradic current at the used voltage. It was thus proved that both the charge on the electrode and the potential across the emerging double layer remain fixed as this electrode is removed.27 The proposed model25 was based on the hypothesis that the “unzipping” of the EDL during the electrode's emersion takes place just outside the outer Helmholtz plane as defined in classical theory of EDL.28,29 Probing the EDL by a metallic probe was recently revisited at the nanometer scale by Yoon et al.30
The second physical process involved in the therein presented method is based on the so-called electrocapillary equation (numbered 13.1.31 in ref. 28), relating changes in (i) the surface (or interfacial) tension, (ii) the electrode potential, (iii) its surface charge density, (iv) the electrolytic solution composition (by means of the electrochemical potentials) and finally (v) relative surface excess of ions. This equation theoretically stemmed from the thermodynamic development of the Gibbs adsorption isotherm. It permitted the interpretation of surface tension measurements at mercury–electrolyte interfaces in the dropping mercury electrode (DME) method and consequently a substantial improvement in knowledge of EDL structure. An elegant way of measuring, at a sub-micrometric scale, the surface tension is to study variations of the surface stress of AFM cantilevers as these two quantities are linked thanks to the Shuttleworth equation.31 Variations in the surface stress indeed cause the bending of the AFM cantilever the amplitude of which can be measured thanks to the reflection of the laser beam as currently used in AFM experiments.32 Several authors took advantage of that concept to measure adsorbate-induced surface stress changes in a vacuum,33 electrocapillary-like curves of noble metals,34 changes of the surface stress of silicon nitride upon varying the pH,35 binding of proteins in aqueous electrolyte36 or pH-induced protein conformation changes.37 As the variation of electrical properties (charge, potential) of the thin plate generates changes in the surface tension28,38via the electrocapillary equation, we decided to investigate local electrical properties of substrates of biological interest by AFM in an approach/retract mode at high frequency (≈ 0.1 kHz). These experiments were performed in aqueous liquid phase with a “high” (≈ 0.15 M) ionic force (Debye length, λD, in the range of tenths of nanometers), i.e. under physiological conditions. The approach/retract movement of the AFM tip at every pixel could be split in two main segments: the first one corresponds to a zone of “high” distance from the substrate (it means larger than several λD) where the electrical state of the cantilever's EDL is constant and a second one where the two EDL are in contact. In this last one the AFM tip's EDL reaches a new state of equilibrium leading to a change in surface stress: this is detected by the change of flexion of the cantilever as measured by the “force” signal far away (≫λD) from the substrate.
We studied living bacteria under their standard physiological conditions and naturally adherent (i.e. without any forced immobilization) to the glass substrate. We proved that, provided the adequate choice of experimental parameters (mainly time constants), imaging of local bacterial surface density of charge in its steady state is feasible at a spatial resolution better than a few tens of nanometers. Furthermore, a dynamic effect of electrical charging was detected both by the new electro-mechanical method we present in this paper and by direct current measurement. This last effect was tentatively attributed to the detection of ionic current stemming from bacterial membrane pores.
Material and methods
Bacterial preparation
This study was done with Rhodococcus wratislaviensis (Rhodo. w.) bacterial strain known for its ability to degrade hydrocarbon compounds in aqueous effluents. This strain is registered at the Collection Nationale de Cultures de Microorganismes (CNCM), Paris, France under number CNCM I-4088 and was provided to us by IFPEN. Stock cultures were kept frozen at −80 °C in 20% glycerol (v/v). The culture medium used was a vitamin-supplemented mineral medium (MM). This medium contained KH2PO4, 1.40 g l−1; K2HPO4, 1.70 g l−1; MgSO4·7H2O, 0.5 g l−1; NH4NO3, 1.5 g l−1; CaCl2·2H2O, 0.04 g l−1. A vitamin solution and an oligo-element solution were added as previously described.39,40 The pH of this medium is equal to 6.9.40 After inoculation (10%), the adequate carbon source (in the present case toluene) was added, and the cultures were incubated at 30 °C with constant agitation. Cultures were grown in flasks closed with a cap equipped with an internal Teflon septum to avoid any loss of substrate either by volatilization or by adsorption. The headspace volume was sufficient to prevent any O2 limitation during growth. Growth was followed by measuring the optical density at a wavelength of 660 nm. Bacteria were transplanted in fresh medium once a week. 500 μL of this culture medium was pipetted when the strain was in its exponential growth phase and introduced into the AFM liquid cell. It must be emphasized that we proved10 that bacteria studied under these conditions are alive.AFM sample preparation
The samples we used for the AFM experiments were borosilicate glass substrates recovered by an indium-tin-oxide (ITO) layer (purchased from Neyco, Paris, France). These samples were then cleaned by sonication in a diluted solution of detergent (pH around 9) for 15 minutes before being carefully rinsed with high purity water (Milli-Q). Drying was done below the flux of a pure inert gas.The sample preparation method was derived from that extensively described in ref. 10. To summarize: the bacterial suspension in its culture medium was gently vortexed during three minutes. Forty microliters (μL) were then deposited and remained on the glass slide during 10 min. Excess solution was thereafter removed and the substrate was further left under ambient atmosphere (22 °C and around 60% of relative humidity) till the dehydration front started moving throughout the sample (around 5 minutes). The sample was then rinsed twice with the culture medium under gentle conditions before being placed at the bottom of the liquid cell, ECCell® from JPK.41 Finally 500 μL of the MM medium were promptly poured into the liquid cell. The final bacterial surface concentration on the glass substrate for the AFM experiments was around 2 × 105 units per mm2, as checked by optical microscopy. No spontaneous detachment of bacteria from the sample towards the planktonic phase was evidenced by optical or AFM microscopy. This method was proved10 to be very efficient for AFM imaging of alive bacteria under their genuine physiological conditions. No aggressive external immobilization protocol, neither chemical nor mechanical, was needed: Rhodo. w. self-immobilized on the ITO/glass substrate. Under identical conditions gliding movements of cyanobacteria were studied in real time by the AFM tip,10 directly proving its minute level of disturbances and of course its non-lethal characteristics. These Rhodo. w. bacteria, in the initial stage of biofilm forming, are then studied by AFM under their genuine physiological conditions. As no chemical templates for immobilization (such as gelatin, polylysine etc.) are used, the bacterial membrane is not recovered by any polymeric exogenic compounds: the present electrical measurements are directly related to phenomena inherent to the bacterial membrane eventually through a self-secreted extra polymeric substance (EPS).
AFM data acquisition
Atomic force microscopy studies were carried out using a Nanowizard III (JPK Instruments AG, Berlin, Germany) and its electrochemical cell (ECCell® from JPK41). The AFM head is working on a commercial inverted microscope (Axio Observer.Z1, Carl Zeiss, Göttingen, Germany). This combined AFM/optical microscope was placed on an isolation vibration table. All the experiments were performed with Rhodo. w. in their liquid culture medium at a temperature of 24.0 ± 0.2 °C. It must be emphasized that special care was taken regarding thermal stability in order to minimize temperature fluctuation: particularly the experimental setup was placed in a temperature-controlled room located in the basement floor to minimize both building vibrations and thermal drift. As detailed in the Results section, residual thermal drift was measured and corrected as it was found to be linear with time.AFM measurements were performed using a fast-speed approach/retract mode (Quantitative Imaging® (QI) mode). At each pixel of the image, a complete force–distance curve, at a defined constant velocity, is acquired. In all the presented results, the pixel-by-pixel extend/retract curves were recorded at a constant speed of 125 μm s−1 on a total extension of 600 nm (data were stored for the first 500 nm from the substrate during both approach and retract movements of the cantilever). Thus the cantilever oscillating frequency is close to 85 Hz. Two hundred points were acquired during each approach or retract curves. Typical images were obtained on the basis of a surface scanning with 64 by 64 or 128 by 128 pixels. We used standard beam AFM probes (PPP-CONTPt, Nanosensors, Neuchatel, Switzerland) with a nominal value of stiffness around 0.30 N m−1. Their values were precisely measured by thermal noise.42 The sensitivity of detection of the vertical deflection thanks to the photodiode system was measured during the approach to a clean glass substrate. The typical tip height is about 15 microns. These commercial cantilevers are coated by a 25 nm thick double layer of chromium and platinum–iridium alloy on both sides. The maximum applied force was set at 6 nN. No major changes in the quality of AFM data as presented here were observed with time. No contamination of the apex of the tip was detectable during experiments. Each AFM image is scanned line by line, starting from the bottom of the image to its top. For each of these lines pixels are successively scanned from the left side to the right one.
All the presented height AFM images and approach/retract curves are raw data (without any post-treatment such as flattening, filtering, smoothing, etc.). Mathematical treatments, such as calculation of the so-called Basic_Line Force signal (BL_Force; see below) or stiffness data, were done by custom Matlab (from MathWorks, Natick, USA) programs. The stiffness data were calculated from the slope of the approach (i.e. extend) curves (force versus scanner elongation) at the point of maximum force as averaged on a distance interval of 10 nm. Other numerical treatments of AFM data were done using OriginPro software (from OriginLab Corporation, Northampton, USA).
Electrical/electro-mechanical measurements
The presented AFM experiments were performed in JPK's electrochemical cell equipped with three electrodes. The first one, the working electrode (WE), was the Pt-covered AFM cantilever; the counter-electrode (CE) is the ITO/glass plate. The third electrode is a platinum wire (0.6 mm in diameter) with a ring shape: its distance to the AFM tip (and consequently to the CE) is equal to ≈8 mm; its diameter is equal to 15 μm (see Fig. 1a for a schematic). This was the reference electrode (REF) from which the electrical potentials were measured. It must be emphasized that we preferred not to use the classical Ag/AgCl or calomel quasi reference electrodes in order to avoid any contamination of the culture medium by silver or mercury species: thus we get rid of any anti-bacterial effects and modification from the genuine ionic composition of the aqueous medium. Calibration of this Pt pseudo-reference electrode was done using aqueous solution of potassium ferrocyanide (E0 = +360 mV vs. Norma Hydrogen Electrode – NHE)28: in this paper potentials (VPt) will be given versus our Pt pseudo-electrode (Vvs. NHE = VPt + 95 mV).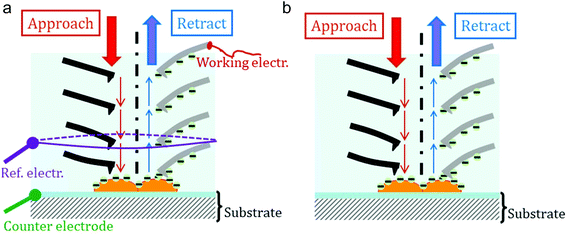 | ||
| Fig. 1 Schematics of the experimental set-up: (a) in the case of measurements of both the δFBL signal and the direct electric current; (b) in the case of the lone measurement of the δFBL signal. | ||
The electrical connection to the AFM tip/cantilever system was made as follows. The silicon platelet holding the cantilever was stuck on the JPK glass block holder by a two-component glue (purchased from JPK Instruments AG, Berlin, Germany), insoluble in water and culture medium. A polyester-imide insulated copper wire (purchased from Goodfellow, London, England), 100 microns in diameter and 11 cm in length, was stripped at both ends (along a few millimeters) with optical sand-paper to ensure electrical contacts with the potentiostat's cables (see below). This wire was then glued in the vicinity of the cantilever holder with the same product as that used for its fixation. One of the copper wire ends was then approached to the Pt-covered silicon platelet and fixed on it by depositing a droplet of a conductive epoxy glue (Epoxy Technology, USA) followed by curing at 110 °C during 1 hour. Next, a drop of nail polish was poured on the electrical contact and the silicon cantilever holder and allowed to dry at 40 °C during one hour to electrically isolate the tip/cantilever complex from ionic solution. Thus the electric connection is made on the cantilever's side holding the tip. Electrodes were connected to a potentiostat (Modulab, Solarton analytical, AMETEK Advanced Measurement Technology, USA). For the current measurements an integration period of 150 ms was chosen. Synchronization between time evolution of AFM data and electrical measurements from the potentiostat was carried out through short voltage pulses (10 mV amplitude) applied to the electrochemical cell.
Results
Approach/retract curves
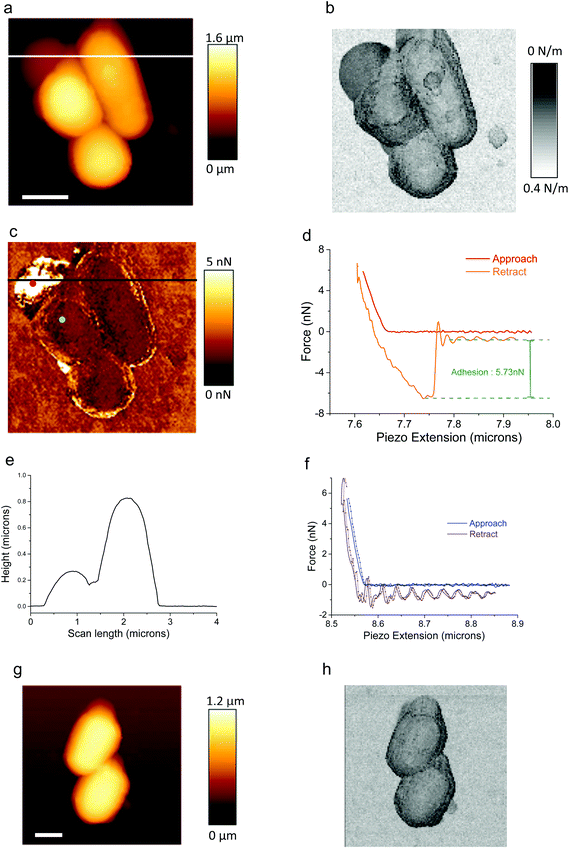
A typical AFM height image of Rhodo. w. is shown in Fig. 2a where three associated bacteria are visible. The corresponding stiffness image is shown in Fig. 2b. The typical height of those bacteria is in the range of 1 μm. At the top-left corner of Fig. 2a, a bump is visible. Its height is around 300 nm as deduced from the profile (Fig. 2e) along the white line in Fig. 2a. This bump corresponds to a zone of high adhesion as seen in Fig. 2c. Adhesion forces are there in the range of 5–6 nN as seen in one particular retract curve (Fig. 2d, orange curve) as measured at the red dot in Fig. 2c. As explained in detail in ref. 10, this high adhesion zone corresponds to the presence of a polymeric substance likely secreted by the bacterium itself: this ensures its self-adhesion on the ITO/glass substrate. It must be noted that, in this particular medium (MM medium) with a high ionic strength (0.15 M) no jump-to-contact is observed in the approach curve (Fig. 2d, red curve), nor attractive long-distance interaction as expected when working in high salinity media as electrostatic forces are shielded.43 Typical approach/retract curves from the region of low adhesion zone (around 96% of the whole image) – see Fig. 2c, blue dot – are plotted in Fig. 2f: these curves are displayed for two adjacent pixels (full and dotted lines; these two pixels are at a distance of 31 nm and the time interval between them is 12 ms). Approach curves (in blue) reveal only two zones: the “long distance” zone (what we will call the “basis line”, shortly named as BL) where the force is constant at an accuracy of 15 pN (see below) and the repulsive regime up to the set-up force at which retract of the cantilever begins. For the retract curve the repulsive regime is followed again by an almost constant force regime with superimposed oscillations: they are due to free oscillations of the cantilever as it abruptly goes off the adhesive contact. As seen in Fig. 2d and f, a shift along the force axis between approach and retract curves is clearly evidenced. This is explained by hydrodynamic drag forces (viscous forces) due to the movement of the cantilever through the liquid medium. We indeed checked that this drag force, as characterized by the difference between extend and retract curves, (i) varies linearly with the pulling speed of the cantilever, (ii) has a constant value whatever the pixel's number, (iii) is proportional to the effective area of the cantilever (we checked it with various cantilevers as PPP-CONTPt, Nanosensors, Neuchatel, Switzerland and CSC37, MikroMasch, Wetzlar, Germany) and (iv) the measured values for this hydrodynamic drag force are in the same range of values as those reported in the literature.44 Due to that hydrodynamic effect, all retract curves are thus shifted from their corresponding approach curve, along the force axis, by the same quantity for the constant conditions we imposed for AFM imaging. This fact combined with the lack of quasi-free oscillations in extend curves far away from the repulsive regime justifies why only the approach curves were analyzed.Definition of the so-called “basis-line force” (BL_force) signal
As already mentioned, the value of the interaction force between the AFM tip and the substrate, during the approach phase, is constant for distances higher than those corresponding to the repulsive regime. Its mean value is called the BL_Force signal and will be denoted as FBL. Its exact determination is explained in detail in ESI† and Fig. SI01. The standard deviation for FBL was proved to be lower than or equal to 15 pN for all pixels of all AFM data presented in this paper and quantifies the accuracy of the so-called BL_Force measurement. The laser beam reflected by the AFM cantilever was aligned with the center of the four-quadrant photodiode at the beginning of each experimental session (corresponding to every studied set of bacteria) and thus the FBL signal is equal to zero at this time t = 0. As shortly explained in the Introduction part, the variation of FBL is sensitive to the variation of curvature of the cantilever as caused by changes, for example, in the electrical state of the cantilever and its ionic environment as will be detailed below.Two classes of electrical status for AFM experiments
AFM experiments we will now discuss were performed under two different electrical conditions: The first one was done when no voltage was applied to the sample, nor current measurement was performed: we called this regime the “Open Circuit” (O.C.). The typical example we studied is that of a consortium of three bacteria we have already shortly described (Fig. 2a–f). The second one was for AFM experiments where the voltage was kept constant and equal to 0 mV versus the reference electrode and the intensity of the current was measured using the ammeter/potentiostat simultaneously with AFM acquisition. One typical example is that reported for the case of a consortium of two bacteria as shown in Fig. 2f and g. It must be emphasized that the standard way of plotting AFM data by commercial software to obtain height images rubs out any effect of possible variations of what we called BL_Force effects as data are shifted to a constant level of “BL_Force”. We also verified that AFM data – in height, stiffness and adhesion modes – are independent of the electrical status we worked with, consequently proving that no perturbation in (i) AFM acquisition and imaging and (ii) in bacterial metabolism is engendered, at least at first order.In order to check the electrochemical status in our experiments, we performed cyclic voltammogram in a narrow window of potentials. One example is shown in Fig. SI02.† It must be pointed out that such similar curves were measured whatever the point of observation (above or beside the bacteria) either with the AFM cantilever oscillating in QI mode or static at a constant distance (500 μm) from the substrate. No difference was observed when the digitization rate was changed. The main conclusion is that we do not observe any faradic current for this range of voltages: only a quasi-linear behavior is observed. As explained in ref. 28 its slope (estimated from Fig. S102† to be 1.5 MΩ−1) corresponds to an equivalent resistance between CE and REF electrodes. This resistance is due to two series connected resistances: one due to the contact resistance between the conductive electrodes and solution and the other to the own conduction of the aqueous medium. This last one can be estimated to be 1.1 kΩ (conductivity of culture medium equal to 14 mS cm−1). The first one is mainly due to polymeric substances constituting the bacterial membrane and extra-cellular substances partly involved in self-adhesion on the substrate.
Results in the so-called “fast” regime
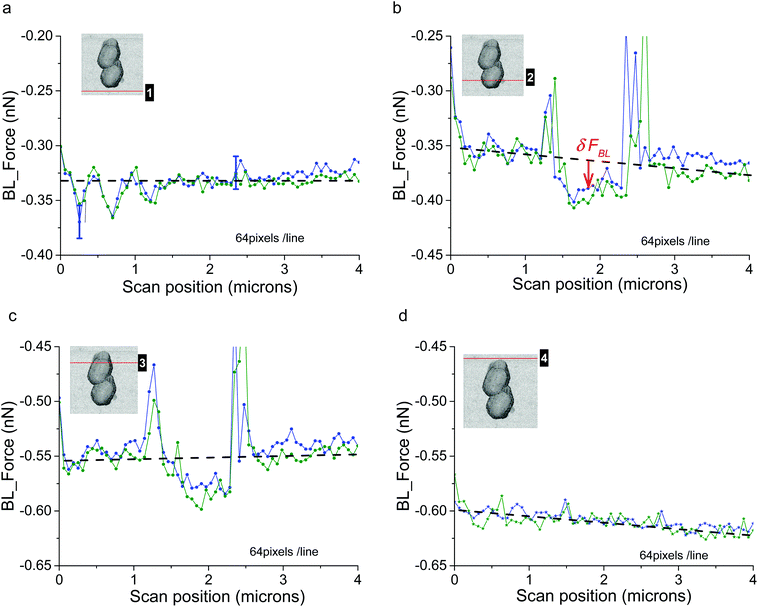
The first case we will present is that of a constant voltage (0 mV) relative to the REF electrode. It is illustrated with the consortium of two bacteria (Fig. 2g and h). As detailed above, FBL was measured during the AFM scanning of this bacterial consortium. Raw variations of FBL along the fast axis (horizontal in the shown AFM images) are plotted in Fig. 3 at four locations as indicated by the red lines in the simultaneously acquired stiffness image (see inserts in gray levels): the positions numbered 1 (4 respectively) in Fig. 3a (3d resp.) correspond to the bare substrate. The positions numbered 2 and 3 (see Fig. 3b and c) are related to scan lines upon bacteria. The green and blue curves correspond to two adjacent (successive) fast scan lines. Out of the bacteria (Fig. 3a and d) these green and blue curves are superimposed at an accuracy of 15 pN, the estimated error for FBL. These experimental data are slightly dispersed along a linear fit of FBL (dashed black lines) for the whole scan line. On the opposite, Fig. 3b and c reveal an important original feature: a lower FBL signal is measured for pixels upon the bacterial complex when compared to the linear approximation as calculated from both sides of the scan line out of bacteria. The mean value of that slope when averaged on all scan lines as acquired during the whole set of experiments on a bacterial consortium (see for instance Fig. SI04†) is equal to ≈−7 ± 1 pN μm−1 corresponding to a rate in time space of around −10 ± 2 pN s−1. This is attributed to an un-compensated thermal drift as will be seen in more detail in the following. It must be noted that the signals of high intensity at the edges of the bacteria are related to a computing effect as explained in more detail in ESI† (see the caption of Fig. SI01). To further explain this new feature, the lower FBL signal upon bacteria, we define the δFBL signal, as calculated, at each pixel, by the difference between values of the FBL signal and of the corresponding linear fit (black dashed line in Fig. 3), as taken at each pixel (see Fig. 3b). That δFBL signal is plotted in Fig. 4. A net variation of the δFBL signal is clearly visible upon bacteria as is shown in Fig. 4a (three bacteria consortium) and 4c (two bacteria). For the complex of two bacteria as studied at 0 mV relative to the REF electrode, the mean value of δFBL over the bacteria is equal to δFBL = −40 ± 12 pN. Such a behavior was equally observed in a quite different electrical state. The three bacteria consortium was studied while no voltage was applied and no current measurement was performed. However similar features in the δFBL signal were detected (Fig. 4c). The amplitude of this signal is similar to that measured in the case of constant voltage (0 mV): δFBL = −50 ± 15 pN. Furthermore we checked that this δFBL signal is not directly linked to a spurious AFM effect where local variations of height would induce parasitic variations of δFBL. We indeed plot in Fig. 4b the δFBL signal corresponding to that in Fig. 4a for only points higher than 100 nm above the substrate's level: we can see that the thick exopolymeric substance with high adhesion properties (see Fig. 2c) gives no δFBL signal (δFBL ≈ 0), which is quite different from that detected over bacteria (∼−50 pN). The same kind of observation was made in the case of two bacteria (see Fig. 4d).It is worth noting that this observation of a negative δFBL signal above the bacteria was observed whatever the AFM scanning conditions: this is detailed in ESI† Fig. SI03. Upon bacteria, δFBL signal is almost constant even if heterogeneities are visible in Fig. 4: they will be addressed below. Typical time of variation of the δFBL signal between zero level on the substrate and that on bacteria is in the range of 30 ms. This is shorter than the characteristic time of the second phenomenon we will discuss in the next paragraph. Thus this first effect will be called “fast effect”.
Results in the so-called “slow” regime
In this sub-section the evolution of the raw BL_Force signal versus time is detailed. When FBL(t) is plotted for a complete sequence of successive AFM data acquisitions (Fig. SI04†) a continuous linear drift is clearly observed whatever the scanning conditions. It is attributed to an un-compensated thermal drift. Its mean that the slope equals −8 ± 2 pN s−1 in the case of a constant voltage (two bacteria; see Fig. SI04b†) and is very close to the value obtained from study in Fig. 3. In another set of experiments where no electrical measurement was done (in the case of the consortium of three bacteria) this slope is equal to −1.5 pN s−1. In the following this thermal drift was systematically removed from the raw BL_Force signal: as for data in Fig. 4 (and SI03†) we will now plot δFBL signals. In order to get rid of the previously described fast effect, a smoothening of δFBL signal was systematically done: it corresponds to a temporal filter with a time constant of 150 ms, equivalent to a scanning time of twelve successive pixels. As mentioned in the Material and methods section, the analogic time constant for current measurements was set at a similar value (150 ms).In the case of AFM study at constant voltage (0 mV), time variations of height (raw data), δFBL (smoothened as described above) and current intensity signals are plotted in Fig. 5a–c. As height data are not temporally filtered the saw teeth corresponding to the AFM fast axis scan are clearly visible. The envelope of these height data gives the rough shape of bacteria and allows us to situate the point of AFM scanning in the time diagram we will now describe in more detail: as an example the numbered markers correspond to the four scanning lines studied in Fig. 3a–d: on the glass substrate before scanning the bacteria, on the bottom bacterium and then the top bacterium and finally the glass substrate after the AFM scanning of bacteria. We will now show that a supplementary signal can be measured with both δFBL signal and current intensity, provided that the AFM scan speed is below a characteristics time. Indeed for AFM data (in the case of two bacteria) taken at a digitization rate of 64 pixels per line (Fig. 5a and b) we observe that both δFBL and intensity signals are constant, at the accuracy of our measurements, during the whole AFM scanning. This was observed independently of surface scan size, (5 μm)2 for Fig. 5a and (4 μm)2 for Fig. 5b. Surprisingly, when the digitization rate reaches 128 pixels (Fig. 5c, scan size: (4 μm)2) it is worth noting that both signals are no more constant. These two signals noticeably increase in a very similar way. We found that a total variation of δFBL signal, Δ(δFBL) (as defined in Fig. 5c), is of the order of 400 pN while current intensity increases by roughly 20 nA starting for a constant level of 172 ± 2 nA before bacteria scanning. This last value corresponds to current intensity as measured at 0 V during voltage cycling (see voltammogram in Fig. SI02†). This new effect will be called a “slow” effect as it is clearly evidenced by applying a high-pass time filter, the cut-off time of which is about 150 ms (integration time for current measurement and temporal smoothening for δFBL signal as well). The fast effect described above is thus not observable in the data presented in Fig. 5 as its characteristic time (30 ms) is lower than the applied time filtering.
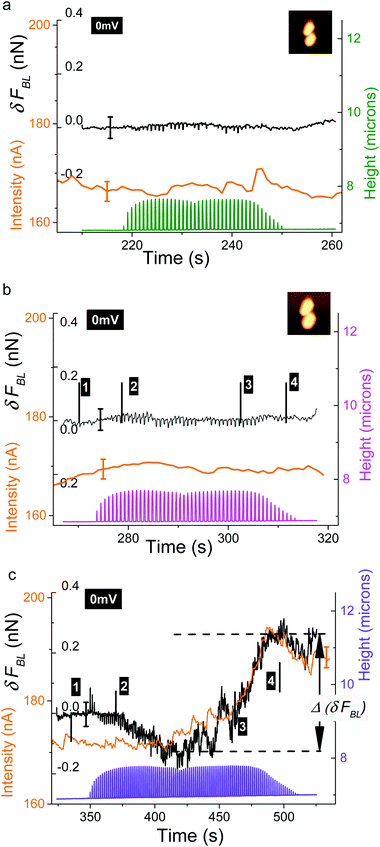 | ||
| Fig. 5 Variations of the δFBL signal (black lines), current intensity (orange curves) and height (the same color code as in Fig. SI04a, b†) signals versus time for three AFM scanning conditions: (a) scanned area (5 μm)2; digitization rate (64 pixels); (b) scanned area (4 μm)2; digitization rate (64 pixels)2; (c) scanned area (4 μm)2; digitization rate (128 pixels)2. The potential was kept constant and equal to 0 mV versus the pseudo-reference electrode. Spatial variations of δFBL along horizontal scan lines starting at times noted by numbered markers in (b) and (c) are shown in Fig. 3 and SI06† respectively. | ||
Remarkably we observed that this slow effect is observable by the lone measurement of the δFBL signal. Indeed when working in the so-called open circuit (O.C.) configuration, identical observations (see Fig. SI05†) to these detailed above can be made. The slow effect is again revealed only for the 128 pixels per line digitization rate (Fig. SI05b†) and not at 64 pixels per line (Fig. SI05a†). This slow effect is characterized (Fig. SI05b†) by the same type of variation of δFBLversus time within the same range of magnitude, Δ(δFBL) ≈ 400 pN, when the AFM tip scans the bacterial consortium.
When no time filtering is applied the fast effect is observed as superimposed on the slow effect (see Fig. 4). In order to figure out in a better manner what is occurring during that AFM scan at a digitization rate of 128 pixels per line, the only condition when the slow effect is evidenced under our experimental conditions, we performed a similar treatment to that shown in Fig. 3. Detailed comments are available in ESI† (see also Fig. SI06).
The previously described experiments were performed with alive bacteria in their physiological medium. We also studied these R. wratisl. bacteria after they were starved to death: they were put in the electro-chemical cell filled with a pure NaCl solution (0.15 M) – i.e. without any nutriment – during a minimum of 5 hours before AFM imaging. Under these conditions, neither slow nor fast effects on δFBL signal were observed whatever the digitization rate (Fig. SI07†). It must be noted too that the related voltammogram, taken under identical conditions to those described in the Material and methods section, is quite similar to that shown for alive bacteria (Fig. SI02†).
From the simultaneous observation of this so-called slow effect on both BL_Force signal and current intensity the following remarks can be made:
(i) the observed signals in FBL (or δFBL) are not due to artifacts due to signal processing and computing of AFM data as it is observed by two independent measurements, one based on direct measurement of the electric current, and the other by the detection of a mechanical effect (the flexion of the AFM cantilever);
(ii) as shown in Fig. 5c, in the case of the slow effect, variation of δFBL signal is associated with the appearance of an over-current when compared to the base current stemming from the equivalent circuit of the electrochemical cell (as explained in more detail in the Material and methods section; see also Fig. SI02†). The δFBL signal is shown to be proportional to this over-current as clearly shown in Fig. 5c. Thus the physical origin of variations of the δFBL signal is very likely due to the change of state of electrical charging of the cantilever electrode, generating a current detectable by the ammeter when the electric circuit constituted by the ionic solution, conductive electrodes and wires is closed.
(iii) in the frame of this hypothesis it is possible to write that:
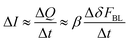 | (1) |
We thus suggest that the BL_Force signal is related to the electric charging of the AFM tip/cantilever complex when contacting bacteria. We will develop this hypothesis and argue in this direction in the next section. The consequences on local measurements of electrophysiological properties of bacteria will then be presented.
Discussion
AFM is a powerful way to image in real space various substrates in various media with a sub-nanometric resolution. This method basically relies on the measurement of the small deflections of a microcantilever. That deflection is mainly due to two factors: the first one is the presence of an interaction (a force in the pico- or nano-newton ranges) between the apex of the tip and the underlying sample. The second one comes from the variation of the difference of the surface stress between the two main surfaces of the cantilever. This second effect may come from specific adhesion on one side of the cantilever37 or have a pure electrical origin as detailed below. Various kinds of interactions, such as electrostatic, van der Waals, magnetic, etc. with different distance dependencies, contribute to the total force between the probing tip and the sample. The electrostatic force between two electrodes (the tip/cantilever system and the sample) can be expressed17 as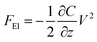 | (2) |
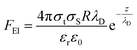 | (3) |
The second origin for a modification of the flexion of the cantilever is, as said above, surface stress effects. Surface stress at the interface between the two phases, A and B, ΓAB, is related to surface tension (surface free energy), γAB, by the Shuttleworth relation,31
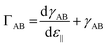 | (4) |
This is no longer the case when one of the phases is elastic. As shown in ref. 51, compressibility of the interfacial region, through the Poisson ratio near the interface, determines the difference between surface stress and surface energy. However we will suppose in the following, as frequently done,52 that the following equation
| ΓSL ∼ γSL | (5) |
One way to change surface stress is to vary the electrical potential of the solid or, more generally, the electrical state of the interface between a solid electrode and the surrounding ionic liquid (aqueous in the present case). By thermodynamical considerations28,38 it is possible to derive the so-called electrocapillary equation:38
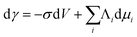 | (6) |
In case of no variation of these chemical potentials, eqn (6) leads to Lippmann's equation:
| dγ = −σdV | (7) |
The property of varying surface stress by changes in the electric state of the solid/liquid interface was already drawn on with asymmetric AFM cantilevers19,52,53 (a metallic layer on one side), standard commercial levers coated on both sides17 and highly doped silicon cantilevers.53 One important point revealed by papers by Umeda et al.17,19 is that the cantilever behavior is dominated by surface-stress effects when the frequency of the excitation signal is much lower than a characteristics frequency fc_SS.17
In our case (ionic force of 0.15 M and an AFM tip and bacterium heights around a few microns,) fc_SS is close to 35 kHz. That value is thus much higher than the typical frequency relevant for the experiments described in this paper: fV = 83 Hz for the forced oscillations related to the approach/retract curves. Thus surface stress effects are dominant. Furthermore the fact that the magnitude of the surface stress only depends on the difference in the surface properties of both surfaces (tip side and backside) of the cantilever – and not on the distance between the cantilever and the counter electrode as with electrostatic force – well explains our observation of a tip–sample interaction force constant during the most of each approach curve. This feature further proves that the experimental results we described above are related to the surface stress effect.
As mentioned in the Material and methods section, the electrical connection with the cantilever is directly made on its side holding the AFM tip, the electro-active part of the cantilever. So an increase in stress of this surface due to a change of surface electrical properties of the AFM cantilever will be detected by photodiodes as a more attractive force and thus causes a decrease of the δFBL signal. The relationship between the (absolute) value of δFBL signal and the surface stress can be deduced from Stoney's equation.54,55 We chose a Young's modulus and a Poisson's ratio of 150 GPa and 0.3 respectively, typical values for standard silicon cantilevers.37 The length, width and thickness of the cantilever have been taken to be 450 μm, 50 μm and 2 μm respectively. Surface stress and δFBL variations are then related through ΔΓ (in mN m−1) = −1.5 ± 0.5 × 10−3Δ(δFBL) (in pN). Thus the module of variation of surface stress for the fast effect (|Δ(δFBL)| ≈ 40 pN) is in the range of 56 μN m−1.
As mentioned earlier we hypothesize that the variation of δFBL signal is related to an uptake of electric charges by the AFM tip when contacting the bacteria. We will show now that this hypothesis is fully compatible in sign and magnitude with data currently available about electric charge surface density for standard bacteria. In the case of the experiments (Fig. 4c–d and SI03a–c†) performed at a constant potential, 0 mV versus our REF electrode(i.e. Vvs. NHE = +95 mV), this potential is higher than the potential of zero charge, VPZC. Raiteri et al.52 indeed found negative values for VPZC for the AFM cantilevers, similarly to ours, they used: between −500 mV/NHE for a gold electrode in 0.1 M KCl and slightly below 0 V for a Pt electrode in NaClO4/HClO2 solution. It means that,28 in experiments presented in this paper, there is thus a net positive surface charge on the cantilever. When referring to the fast effect (Fig. 4 and SI03†) we observe a decrease in δFBL signal upon bacteria. According to preceding remarks, this corresponds to a decrease of the σV|VPZC term in Lippmann's equation (eqn (7)). As voltage may be considered constant, this is related to an uptake of negative charge by the AFM tip when upon the bacteria. From Δ(δFBL) variation (∼−40 pN upon bacteria for the fast effect, see Fig. 3 and 4) a rough estimation of the uptake charge can be proposed. We suppose that the charge uptake occurs when the two double layers are in contact; it means mainly during the repulsive phase of the approach/retract curves (Fig. 2d and f). This lasts τ ≈ 0.5 ms as deduced from extend/retract curves. During that time lapse, ions are supposed to stem from an interfacial area corresponding to a surface limited by diffusion, ∼Dτ ≅ 2 μm2, and to charge the surface of the cantilever (area L![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , with L = 450 μm and
, with L = 450 μm and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 50 μm). By using Stoney54,55 and Lippmann's equations successively we obtain a rough value of σbact ∼ −0.5 C m−2 for bacterial surface density. For this surface density determination we supposed that the electric potential is of the order of magnitude of the standard electrode potential in aqueous solution for platinum at 25 °C, ∼1 V versus NHE.56 The value for surface charge we obtained from δFBL signal, σbact ∼ −0.5 C m−2, does satisfactorily agree with values from the literature for Gram positive bacteria at neutral pH: for instance, Bulard et al.57 found around σbact ∼ −0.4 C m−2 for Lactococcus lactis in NaCl at 1.5 mM; Poortinga et al.2 measured for several Gram-positive bacteria, including Rhodococci, surface charges ranging from −0.2 C m−2 to −0.5 C m−2 in 1 mM KNO3. It must be emphasized that our estimation of surface charge was done in situ with alive bacteria in their physiological medium (150 mM). We put the stress on the fact that this σbact ∼ −0.5 C m−2 value we assessed does not depend on AFM surface scan size, the number of pixels per line or the electric type of measurement (constant potential or open circuit). As visible in Fig. 4 and SI03,† the distribution of the charges over the bacteria is rather uniform. Some surface heterogeneity is however visible: this feature will be detailed below. It must be emphasized that during this fast effect the δFBL signal and, in the frame of our hypothesis, the charge of cantilever, reaches a constant value as soon as the AFM tip is over the bacteria and then keeps a constant charge all over the surface of the bacteria. This observation may explain why no extra current will flow through the ammeter as seen in Fig. 5a and b. On the opposite, during the so-called slow effect, a continuous increase of δFBL signal is observed corresponding to a total net change of approximately |Δ(δFBL)| ≈ 400 pN (Fig. 5c and SI05b†), ten times higher than that detected for the fast effect. From that we can estimate the variation of the total charge |ΔQ| ≈ 1.35 × 10−11 C. From that, it could tentatively be given an estimation for related current intensity flowing through the system and the ammeter. Indeed similarly to arguments invoked above for the fast effect this charge increase might be considered to occur during an equivalent contact time between both double layers of τ ≈ 0.5 ms. This would lead to a net intensity current of roughly 30 nA, a value of the same order of magnitude as that observed experimentally, ∼20 nA (Fig. 5c). These remarks contribute to strengthening the hypothesis we made of an uptake of electric charge thanks to intermittent contact between both electric double layers, one from the underneath substrate and the other from the AFM tip/cantilever complex and its indirect measurement thanks to an electro-mechanical effect based on the variation of flexion of the cantilever through the electrocapillary effect.
= 50 μm). By using Stoney54,55 and Lippmann's equations successively we obtain a rough value of σbact ∼ −0.5 C m−2 for bacterial surface density. For this surface density determination we supposed that the electric potential is of the order of magnitude of the standard electrode potential in aqueous solution for platinum at 25 °C, ∼1 V versus NHE.56 The value for surface charge we obtained from δFBL signal, σbact ∼ −0.5 C m−2, does satisfactorily agree with values from the literature for Gram positive bacteria at neutral pH: for instance, Bulard et al.57 found around σbact ∼ −0.4 C m−2 for Lactococcus lactis in NaCl at 1.5 mM; Poortinga et al.2 measured for several Gram-positive bacteria, including Rhodococci, surface charges ranging from −0.2 C m−2 to −0.5 C m−2 in 1 mM KNO3. It must be emphasized that our estimation of surface charge was done in situ with alive bacteria in their physiological medium (150 mM). We put the stress on the fact that this σbact ∼ −0.5 C m−2 value we assessed does not depend on AFM surface scan size, the number of pixels per line or the electric type of measurement (constant potential or open circuit). As visible in Fig. 4 and SI03,† the distribution of the charges over the bacteria is rather uniform. Some surface heterogeneity is however visible: this feature will be detailed below. It must be emphasized that during this fast effect the δFBL signal and, in the frame of our hypothesis, the charge of cantilever, reaches a constant value as soon as the AFM tip is over the bacteria and then keeps a constant charge all over the surface of the bacteria. This observation may explain why no extra current will flow through the ammeter as seen in Fig. 5a and b. On the opposite, during the so-called slow effect, a continuous increase of δFBL signal is observed corresponding to a total net change of approximately |Δ(δFBL)| ≈ 400 pN (Fig. 5c and SI05b†), ten times higher than that detected for the fast effect. From that we can estimate the variation of the total charge |ΔQ| ≈ 1.35 × 10−11 C. From that, it could tentatively be given an estimation for related current intensity flowing through the system and the ammeter. Indeed similarly to arguments invoked above for the fast effect this charge increase might be considered to occur during an equivalent contact time between both double layers of τ ≈ 0.5 ms. This would lead to a net intensity current of roughly 30 nA, a value of the same order of magnitude as that observed experimentally, ∼20 nA (Fig. 5c). These remarks contribute to strengthening the hypothesis we made of an uptake of electric charge thanks to intermittent contact between both electric double layers, one from the underneath substrate and the other from the AFM tip/cantilever complex and its indirect measurement thanks to an electro-mechanical effect based on the variation of flexion of the cantilever through the electrocapillary effect.
We propose the following mechanism to tentatively explain the process of uptake of electric charges by the AFM tip when approaching the sample's surface. From studies done with the electrode plunging and emerging from an aqueous electrolyte27,29,58 it was shown that the electrochemical double layer can be retained intact on an electrode surface as the electrode is emersed25 to air or vacuum as well. It was indeed proved that both the charge on the electrode and the potential across the emerging double layer remain fixed as this electrode is removed.27 The model25 that was proposed is based on the hypothesis that the “unzipping” of the EDL during the electrode's emersion takes place just outside the outer Helmholtz plane as defined in classical theory of EDL.28,29 Furthermore it was detailed that immersion/emersion cycles of the electrode can be repeated many times without perturbation at any potential not dominated by Faradaic currents, on either side of the p.z.c.27
Let us come back to the so-called slow effect. We will now suggest a mechanism, related to bacterial metabolism, as a hypothetic explanation for the only detection of the slow effect in the case of a high digitalization rate (Fig. 5c and SI05b†). It is well known that ion channels are widespread in prokaryotic membranes.59,60 Some of these ionic channels can present mechanosensitive properties.61 Numerous studies based on electrophysiological experiments have indeed shown that different types of mechanosensitive channels are present through the cytoplasmic membrane of bacteria. These channels (MscL, MscS, and MscM in Escherichia coli cells,62 MscCG in Corynebacterium glutamicum,5Vibrio cholerae6etc) can release intracellular molecules and ions to reduce osmotic pressure when the cells are challenged with osmotic stresses. Typical channel surface densities are typically in the range of 10 channels per micrometer-square.5,6 Furthermore, depending on the activated channel, the time constant of the opening of mechanosensitive channels is in the range of a few 10–100 ms.5 From that, we can deduce that this effect might be detected in our experiment if the following condition is satisfied: the duration for electric contact between the tip and the substrate has to be at least in the range of 10–100 ms (time of opening for one ionic channel) for a scanned surface of 0.1 μm2 (minimum area to be scanned to statistically find one ionic channel). As already mentioned, the electric contact between the tip and the substrate occurs when both double layers are in interaction thus in the repulsive phase. This interaction time is equal to ∼0.5 ms per pixel. From that, we deduce that the time spent by the tip in electric contact is ∼15 ms in the case of digitization rate of 64 pixels and ∼50 ms in the case of 128 pixels for an investigated bacterial surface area of 0.1 μm2 (AFM images of (4 μm)2). Our experiments showed that there is a time threshold between these two limiting experimental cases (64p and 128p) we can place at a few tens of milliseconds. This threshold is compatible with data from patch-clamp measurements that measured an opening time of ionic channels around 10–100 ms as mentioned above. We are thus confident in the fact that the slow effect could be related to the detection of ionic current stemming from the opening of channels at the bacterial membrane.
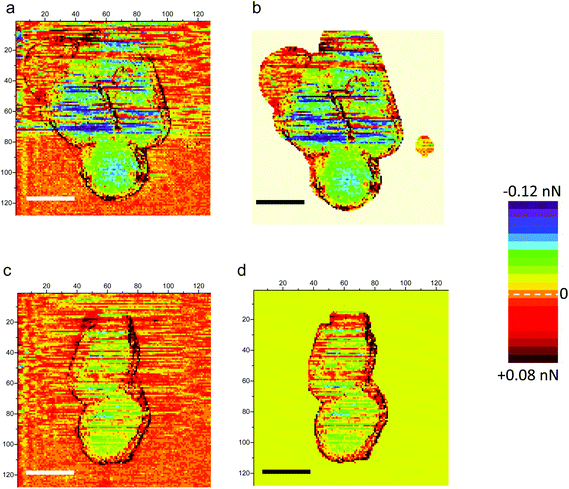
As seen in Fig. 6, heterogeneities in surface charge distribution are present. The stiffness image related to the height image in Fig. 2a is plotted in Fig. 6a: zones of bacteria with a slightly lower stiffness are visible. We will focus our attention on the circular zone situated on the right bacterium as shown by the white or black circle in Fig. 6a (stiffness data) or 6b (δFBL signal). This heterogeneous zone is better evidenced on height profiles (Fig. 6c and d, green curves), stiffness curves (Fig. 6c, black curves) and δFBL profile (blue curves in Fig. 6d). Profiles right across the protuberance (full line in Fig. 6a) and slightly above it (dashed line in Fig. 6a) are plotted in Fig. 6c and d: the thick (thin respectively) lines are for the section across (resp. above) the protuberance. This one protuberance is located between the two dotted-dashed black lines (Fig. 6c and d). It is evidenced that the protuberance corresponds to a zone with a lower stiffness and a slight increase in δFBL. This corresponds, according to former remarks, to a local charge less negative than in the main part of bacteria. This might be interpreted as a localized lack of teichoic acid leading to a decrease of electrical negative charge in relation to a lower stiffness of the bacterial membrane.63 This explanation can be advanced as we verified (see the Results section) that roughness and electro-mechanical effects are uncorrelated. The stress has to be put on the fact that these last observations are valid whatever the AFM digitization rate. Thus these measurements might reveal that the study of δFBL led to important information about the permanent state of charge of the bacterial membrane. Furthermore this proves that BL_Force signal can provide information on local charge distribution at a spatial resolution better than a few tens of nanometers.
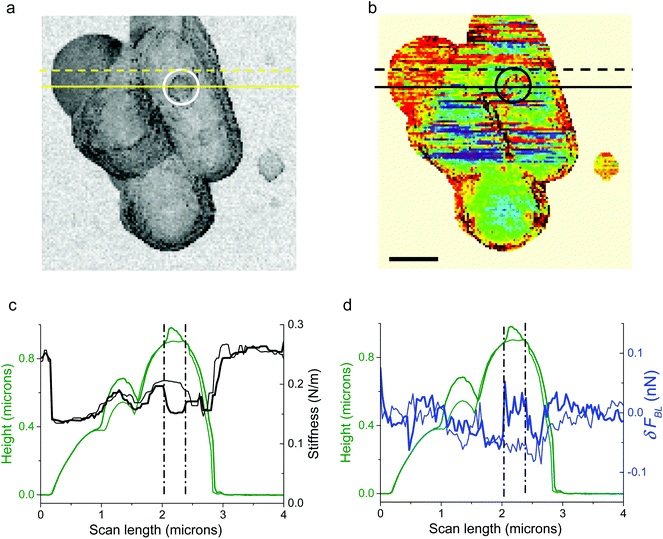 | ||
| Fig. 6 AFM stiffness and δFBL images of a bacterial consortium of Fig. 2a are plotted in (a) (see also Fig. 2b) and (b) (see also Fig. 4b) respectively. The zone circled by a white line in the stiffness image – and by a black one for δFBL data – is studied in more detail in profiles plotted in (c, d): the profiles in the thick line are taken along the yellow full line in (a); it characterizes the heterogeneous white-circled zone visible in (a). This heterogeneous zone is located by the two dot-dash lines in (c, d). In (c, d), height profiles are plotted in green, stiffness in black and δFBL in blue lines. The profiles in thin lines (c, d) are plotted along the dashed yellow line in (a) and are characteristic of points outside of the white-circled zone. It is thus shown that surface charge heterogeneity is linked with bacterium morphology. | ||
It is worth noting that the experimental set-up was chosen in order to be able to correlate the evolution of δFBL signal with that obtained from a direct measurement of electric current under well controlled electrochemical conditions. For that purpose a conductive substrate (ITO on glass) was used. We thus observed that δFBL variation under the, what we called, open-circuit conditions was similar to that we measured with the cantilever in a well characterized electric state (at a null potential versus our reference). This shows that the electrical state spontaneously reached by the cantilever before AFM experiments (self-potential as it is often called) corresponds to a potential near that of the experiment with direct electric current measurement (0 mV versus the reference electrode we used). We thus proved that local measurement of surface charge – and its variation with time (due to the opening of ionic channels as hypothesized here) – does not need the use of the ammeter as we showed that it can be realized by only the measurement of the δFBL signal. In that last case a conductive substrate is not needed.
From preceding remarks, it can be anticipated too that disjoined polarization of both cantilever and a conductive substrate – via a bi-potentiostat – is likely feasible: interesting studies about effects of polarization on physiology of bacteria are thus possible.
In the experiments presented here, the applied potential (when electric circuitry was used) and the self-potential (in the opposite case) were higher than the potential of zero charge. The same kind of results can be obtained for potentials lower than VPZC: indeed in the experiment described in this paper, according to Lippmann's equation (eqn (6)) a decrease of δFBL is related to an uptake of negative charge whatever the relative potential of working potential versus VPZC provided that the resulting potential due to the charging does not change in relative position versus VPZC (as the electrocapillary curve is maximum at VPZC).
It must be mentioned that typical times for extend and retract ramps of the cantilever have to be chosen in a narrow window: larger than that related to reach the charging equilibrium between the two facing double layers (estimated to be of the order of ≈10 μs) and lower than those related to relaxation processes. As mentioned in the paper by Raiteri et al.52 where kinetic measurements were performed, these latter processes may be related to (i) a first effect with an intermediate time constant of the order of a few tens of milliseconds and hypothetically attributed to a residual electrochemical effect and (ii) a slower component (around a few tenths of seconds) tentatively related to a “diffusion controlled process”. As mentioned above, in our experiments, a new charging equilibrium is reached every ∼15 ms at every ramping down of the cantilever, therefore minimizing the role of these relaxation processes with longer time scales. Further studies to study in detail these time effects are under way.
Conclusion
We reported an in vivo electromechanical AFM study of charge distribution on the cell wall of Gram+ Rhodococcus wratislaviensis bacteria, naturally adherent to a glass substrate, under physiological conditions. The new method presented in this paper relies on a detailed study of AFM approach/retract curves giving the variation of the interaction force versus distance between the tip and the sample. In addition to classical height and mechanical (as stiffness) data, mapping of local electrical properties, such as bacterial surface charge, was proved to be feasible at a spatial resolution better than a few tens of nanometers. This was done by studying the constant level of the cantilever's bending far away (>10 nm) from the contact zone between the AFM tip and the sample during the approach of the tip to the sample, the so-called BL_Force signal. The resulting deflection of the cantilever, due to surface stress variations, comes, as in classical electrocapillary experiments, from the variation of its surface charge density. The electrical charging is supposed to occur during the contact of the two electrical double layers the typical thickness of which is below 1 nm as these AFM experiments are performed in a high ionic strength liquid medium (0.15 M). Estimation of electrical surface charge was done and proved to be compatible with results from standard macroscopic electrophoretic mobility measurements. Furthermore, an additional electrical signal detected by both the deflection of the AFM cantilever and simultaneous direct current measurements was detected at low scanning rates. It was tentatively attributed to the detection of the current stemming from ionic channels the opening of which might be triggered by local mechanical overpressure generated by AFM contact. More work is now needed in order to better understand the mechanisms for local charging of the cantilever.This method offers an important improvement in local electrical and electrochemical measurements at the solid/liquid interface, particularly in high-molarity electrolytes when compared to techniques focused on the direct use of electrostatic force. The experimental results presented in this paper tend indeed to prove that the careful study of the BL_Force signal is an elegant way of performing patch-clamp-like experiments on alive bacteria in their physiological medium without the need for an indirect method such as the preparation of giant spheroplasts by lysozyme digestion of the native bacteria. The counterpart is the temporal restriction to variations of electromechanical signal slower than a few tens of milliseconds. However it could be overcome soon as further studies aimed to progress in this direction are under way. The method we detailed here thus opens a new way to directly investigate “in vivo” biological electrical surface processes involved in numerous practical applications and fundamental problems such as bacterial adhesion, biofilm formation, microbial fuel cells, etc.
Acknowledgements
This work was supported by Agence Nationale de la Recherche, Paris, France within the framework of the ECOTECH programme “BIOPHY”. The authors are grateful to IFP Energies Nouvelles, Rueil-Malmaison, France (Dr Françoise Fayolle-Guichard and Yves Benoit) for the free disposal of Rhodococcus wratislaviensis, IFP 2016 strain, through Dr Fabienne Battaglia, Marie-Christine Dictor, Jean-Christophe Gourry and Caroline Michel, BRGM, Orléans, France. This work was launched at the Geosciences Montpellier laboratory thanks to the support of Dr S. Lallemand, J.-L. Bodinier and P. Pezard. S.D. acknowledges support from Région Languedoc-Roussillon, France.References
- Y. H. An and R. J. Friedman, J. Biomed. Mater. Res., 1998, 43, 338–348 CrossRef CAS PubMed.
- A. T. Poortinga, R. Bos, W. Norde and H. J. Busscher, Surf. Sci. Rep., 2002, 47, 1–32 CrossRef CAS.
- E. M. Sonnenfeld, T. J. Beveridge and R. J. Doyle, Can. J. Microbiol., 1985, 31, 875–877 CrossRef CAS PubMed.
- A. H. Delcour, Annu. Rev. Microbiol., 2013, 67, 179–197 CrossRef CAS PubMed.
- Y. Nakayama, K. Yoshimura and H. Iida, Biophys. J., 2013, 105, 1366–1375 CrossRef CAS PubMed.
- I. Rowe, M. Elahi, A. Huq and S. Sukharev, J. Gen. Physiol., 2013, 142, 75–85 CrossRef CAS PubMed.
- S. Dhahri, M. Ramonda and C. Marlière, PLoS One, 2013, 8, e61663 CAS.
- B. W. Hoogenboom, H. J. Hug, Y. Pellmont, S. Martin, P. L. T. M. Frederix, D. Fotiadis and A. Engel, Appl. Phys. Lett., 2006, 88, 193109 CrossRef.
- M. Pfreundschuh, D. Alsteens, M. Hilbert, M. O. Steinmetz and D. J. Müller, Nano Lett., 2014, 14, 2957–2964 CrossRef CAS PubMed.
- M. Pfreundschuh, U. Hensen and D. J. Müller, Nano Lett., 2013, 13, 5585–5593 CrossRef CAS PubMed.
- M. Nonnenmacher, M. P. O'Boyle and H. K. Wickramasinghe, Appl. Phys. Lett., 1991, 58, 2921–2923 CrossRef.
- A. L. Domanski, E. Sengupta, K. Bley, M. B. Untch, S. A. L. Weber, K. Landfester, C. K. Weiss, H.-J. Butt and R. Berger, Langmuir, 2012, 28, 13892–13899 CrossRef CAS PubMed.
- N. Kobayashi, H. Asakawa and T. Fukuma, Rev. Sci. Instrum., 2010, 81, 123705 CrossRef PubMed.
- N. Kobayashi, H. Asakawa and T. Fukuma, J. Appl. Phys., 2011, 110, 044315 CrossRef.
- Intermolecular and Surface Forces, ed. J. N. Israelachvili, Academic Press, San Diego, 3rd edn, 2011, p. iii Search PubMed.
- T. L. Sounart, H. V. Panchawagh and R. L. Mahajan, Appl. Phys. Lett., 2010, 96, 203505 CrossRef.
- K. Umeda, K. Kobayashi, N. Oyabu, Y. Hirata, K. Matsushige and H. Yamada, J. Appl. Phys., 2013, 113, 154311 CrossRef.
- G. Gramse, M. A. Edwards, L. Fumagalli and G. Gomila, Appl. Phys. Lett., 2012, 101, 213108 CrossRef.
- K. Umeda, N. Oyabu, K. Kobayashi, Y. Hirata, K. Matsushige and H. Yamada, Appl. Phys. Express, 2010, 3, 065205 CrossRef.
- D. J. Marchand, E. Hsiao and S. H. Kim, Langmuir, 2013, 29, 6762–6769 CrossRef CAS PubMed.
- L. Collins, S. Jesse, J. I. Kilpatrick, A. Tselev, O. Varenyk, M. B. Okatan, S. A. L. Weber, A. Kumar, N. Balke, S. V. Kalinin and B. J. Rodriguez, Nat. Commun., 2014, 5, 3871 CAS.
- B. Kenrick, Z. Phys. Chem., 1896, 19, 229 Search PubMed.
- B. Jakuszewski and H. Scholl, Electrochim. Acta, 1972, 17, 1105–1111 CrossRef CAS.
- J. Jakuszewski, M. Przasnyski, H. Scholl and A. Siekowska, Electrochim. Acta, 1975, 20, 119–123 CrossRef.
- W. N. Hansen, Surf. Sci., 1980, 101, 109–122 CrossRef CAS.
- D. M. Kolb and W. N. Hansen, Surf. Sci., 1979, 79, 205–211 CrossRef CAS.
- W. N. Hansen, C. L. Wang and T. W. Humpherys, J. Electroanal. Chem. Interfacial Electrochem., 1978, 93, 87–98 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, ed. A. J. Bard and L. R. Faulkner, Wiley, New York, 2nd edn, 2001, New York: Wiley, c1980 Search PubMed.
- W. N. Hansen, J. Electroanal. Chem. Interfacial Electrochem., 1983, 150, 133–140 CrossRef CAS.
- Y.-H. Yoon, D.-H. Woo, T. Shin, T. D. Chung and H. Kang, J. Phys. Chem. C, 2011, 115, 17384–17391 CAS.
- R. Shuttleworth, Proc. Phys. Soc. Sect. A, 1950, 63, 444 CrossRef.
- R. Raiteri, H.-J. Butt and M. Grattarola, Electrochim. Acta, 2000, 46, 157–163 CrossRef CAS.
- D. Sander, U. Linke and H. Ibach, Surf. Sci., 1992, 272, 318–325 CrossRef CAS.
- H. Ibach, C. E. Bach, M. Giesen and A. Grossmann, Surf. Sci., 1997, 375, 107–119 CrossRef CAS.
- H.-J. Butt, J. Colloid Interface Sci., 1996, 180, 251–260 CrossRef CAS.
- R. Raiteri, M. Grattarola, H.-J. Butt and P. Skládal, Sens. Actuators, B, 2001, 79, 115–126 CrossRef CAS.
- G. Thakur, K. Jiang, D. Lee, K. Prashanthi, S. Kim and T. Thundat, Langmuir, 2014, 30, 2109–2116 CrossRef CAS PubMed.
- D. M. Mohilner and N. Hackerman, Electrochim. Acta, 1966, 11, 1669–1684 CrossRef CAS.
- F. Fayolle, G. Hernandez, F. L. Roux and J.-P. Vandecasteele, Biotechnol. Lett., 1998, 20, 283–286 CrossRef CAS.
- P. Piveteau, F. Fayolle, J. P. Vandecasteele and F. Monot, Appl. Microbiol. Biotechnol., 2001, 55, 369–373 CrossRef CAS PubMed.
- JPK Instruments, Nanowizard 3.
- R. Levy and M. Maaloum, Nanotechnology, 2002, 13, 33–37 CrossRef.
- D. J. Muller, D. Fotiadis, S. Scheuring, S. A. Muller and A. Engel, Biophys. J., 1999, 76, 1101–1111 CrossRef CAS PubMed.
- H. Janovjak, J. Struckmeier and D. J. Müller, Eur. Biophys. J., 2005, 34, 91–96 CrossRef CAS PubMed.
- M. Guggisberg, M. Bammerlin, C. Loppacher, O. Pfeiffer, A. Abdurixit, V. Barwich, R. Bennewitz, A. Baratoff, E. Meyer and H.-J. Güntherodt, Phys. Rev. B, 2000, 61, 11151–11155 CrossRef CAS.
- L. Fumagalli, G. Ferrari, M. Sampietro, I. Casuso, E. Martínez, J. Samitier and G. Gomila, Nanotechnology, 2006, 17, 4581 CrossRef CAS PubMed.
- G. Gouy, J. Phys. Radium, 1910, 9, 457 Search PubMed.
- G. Gouy, Compt. Rend., 1910, 149, 654 Search PubMed.
- D. L. Chapman, Philos. Mag., 1913, 25, 475 CrossRef.
- O. Stern, Z. Elektrochem., 1924, 30, 508 CAS.
- J. H. Weijs, J. H. Snoeijer and B. Andreotti, Phys. Rev. E, 2014, 89, 042408 CrossRef.
- R. Raiteri and H.-J. Butt, J. Phys. Chem., 1995, 99, 15728–15732 CrossRef CAS.
- K. Umeda, K. Kobayashi, K. Matsushige and H. Yamada, Appl. Phys. Lett., 2012, 101, 123112 CrossRef.
- G. G. Stoney, Proc. R. Soc. London, Ser. A, 1909, 82, 172–175 CrossRef CAS.
- J. E. Sader and L. White, J. Appl. Phys., 1993, 74, 1–9 CrossRef CAS.
- A. J. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, CRC Press, New York, 1st edn, 1985 Search PubMed.
- E. Bulard, M.-P. Fontaine-Aupart, H. Dubost, W. Zheng, M.-N. Bellon-Fontaine, J.-M. Herry and B. Bourguignon, Langmuir, 2012, 28, 17001–17010 CrossRef CAS PubMed.
- W. N. Hansen, C. L. Wang and T. W. Humphryes, J. Electroanal. Chem. Interfacial Electrochem., 1978, 90, 137–141 CrossRef CAS.
- D. Ren, B. Navarro, H. Xu, L. Yue, Q. Shi and D. E. Clapham, Science, 2001, 294, 2372–2375 CrossRef CAS PubMed.
- B. Martinac, Y. Saimi and C. Kung, Physiol. Rev., 2008, 88, 1449–1490 CrossRef CAS PubMed.
- B. Martinac, M. Buechner, A. H. Delcour, J. Adler and C. Kung, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 2297–2301 CrossRef CAS.
- N. Levina, S. Totemeyer, N. R. Stokes, P. Louis, M. A. Jones and I. R. Booth, EMBO J., 1999, 18, 1730–1737 CrossRef CAS PubMed.
- E. M. Sonnenfeld, T. J. Beveridge, A. L. Koch and R. J. Doyle, J. Bacteriol., 1985, 163, 1167–1171 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr00968e |
| This journal is © The Royal Society of Chemistry 2015 |