Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Parameter-free continuous drift–diffusion models of amorphous organic semiconductors
Pascal
Kordt
*a,
Sven
Stodtmann
b,
Alexander
Badinski
b,
Mustapha
Al Helwi
cd,
Christian
Lennartz
b and
Denis
Andrienko
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: kordt@mpip-mainz.mpg.de; denis.andrienko@mpip-mainz.mpg.de
bBASF SE, Scientific Computing Group, 67056 Ludwigshafen, Germany
cBASF SE, GVE/M-B009, 67056 Ludwigshafen, Germany
dIHF Institut, Technische Universität Braunschweig, Braunschweig, Germany
First published on 3rd August 2015
Abstract
Continuous drift–diffusion models are routinely used to optimize organic semiconducting devices. Material properties are incorporated into these models via dependencies of diffusion constants, mobilities, and injection barriers on temperature, charge density, and external field. The respective expressions are often provided by the generic Gaussian disorder models, parametrized on experimental data. We show that this approach is limited by the fixed range of applicability of analytic expressions as well as approximations inherent to lattice models. To overcome these limitations we propose a scheme which first tabulates simulation results performed on small-scale off-lattice models, corrects for finite size effects, and then uses the tabulated mobility values to solve the drift–diffusion equations. The scheme is tested on DPBIC, a state of the art hole conductor for organic light emitting diodes. We find a good agreement between simulated and experimentally measured current–voltage characteristics for different film thicknesses and temperatures.
1 Introduction
Macroscopic and mesoscopic properties of organic semiconductors, such as charge carrier mobility or the width of the density of states, are often extracted by fitting the solution of the drift–diffusion equation1–5 to the experimentally measured current–voltage (I–V) characteristics. The mobility and diffusion constant of charge carriers, which enter these equations, depend on charge carrier density, ρ, electric field, F, and temperature, T.6,7 For one-dimensional transport and specific rate expressions these dependencies can be obtained analytically.8,9 In three dimensions, semi-empirical analytic expressions based on fits to lattice models have been obtained.6,7,10–12 The extended Gaussian disorder model (EGDM),6 for example, provides a parametrization of the mobility, μ(ρ,F,T), for uncorrelated, Gaussian-distributed site energies, while the extended correlated disorder model (ECDM)11 additionally accounts for spatial site energy correlations due to long-range charge–dipole interactions.The aforementioned approach has become a standard tool for analyzing experimental data.13 It has, however, several issues: (i) Gaussian disorder models are parametrized only for materials with moderate energetic disorder, σ < 0.15 eV at room temperature, while many amorphous materials have a higher σ. (ii) The spatial correlation of site energies in the ECDM is material-independent and has an (approximate) 1/r decay, where r is the intermolecular distance, but recent studies show that this decay may be different.14 (iii) Due to the non-Gaussian shape of the density of states,15 the energetic disorder and the lattice constant are different from those provided by microscopic calculations,14 thus making them merely fitting parameters without a comprehensive link between macroscopic properties and the chemical composition of the material.
In this paper we propose an approach which does not have these limitations. In a nutshell, the mobility dependence on charge density, field, and temperature is first tabulated by combining quantum mechanical, classical atomistic and coarse-grained stochastic models for charge transfer and transport. These tables, corrected for finite-size effects, are then used to solve the drift–diffusion equations.
To illustrate the advantages of the method, we compare it to the ECDM and the Mott–Gurney model16 as well as to experimental measurements performed on amorphous layers of Tris[(3-phenyl-1H-benzimidazol-1-yl-2(3H)-ylidene)-1,2-phenylene]Ir (DPBIC), a hole-conducting material used in organic light emitting diodes (OLEDs)17 and organic photovoltaic cells (OPVs).18
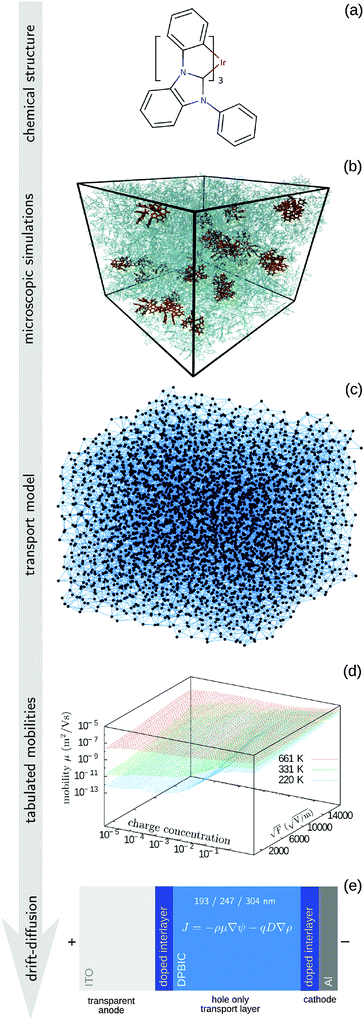
The paper is organized as follows. In the Methods section we describe the coarse-grained, off-lattice transport model, the procedure used to tabulate the charge carrier mobility, the algorithm used to solve drift–diffusion equations, and the parametrization of the extended correlated Gaussian disorder model. The entire workflow is summarized in Fig. 1. We also recapitulate the main results of the Mott–Gurney model and provide details of experimental measurements. The I–V curves, electrostatic potential, and charge density profiles are then compared in Section 3, where we also validate the transferability of the method by studying different layer thicknesses and temperatures. A short summary concludes the paper.
2 Methods
2.1 Tabulated mobility
To tabulate charge carrier mobility as a function of temperature, field, and charge density, we first simulate amorphous morphologies of N = 4000 molecules using molecular dynamics simulations in the NPT ensemble with a Berendsen barostat and thermostat.19 The simulation box is equilibrated at 700 K for 1 ns, which is well above the glass transition temperature, and then quenched to 300 K during 1.3 ns. The force-field is tailored for the DPBIC molecule as described elsewhere20 by performing potential energy scans using density functional theory (DFT) calculations with the B3LYP functional and the 6-311g(d,p) basis set. The Gaussian package21 was used for all energy calculations.The charge transport network is then generated as follows. A list of links is constructed from all molecules with adjacent conjugated segments closer than 0.7 nm. For each link a charge transfer rate is calculated using Marcus theory, i.e., in the high-temperature limit of the non-adiabatic charge transfer theory,22
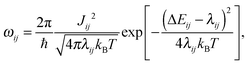 | (1) |
Electronic couplings Jij are evaluated for each dimer by using the dimer projection method,23 the PBE functional and the def2-TZVP basis set. These calculations were performed using the TURBOMOLE package.24 Note that the values of electronic couplings can deviate by up to 50%, depending on the functional and the basis set size.25,26 This deviation is, however, systematic and will result in a constant prefactor for the mobility, i.e., we do not expect any changes in functional dependencies on the external field, charge density, or temperature.
The hole reorganization energy,27λij = 0.068 eV, was evaluated in the gas phase using the B3LYP functional and 6-311g(d,p) basis set. Site energy differences, ΔEij = Ei − Ej were evaluated using a perturbative scheme28 with the molecular environment modeled by a polarizable force-field, parametrized specifically for these calculations. In this approach, the site energy Ei = Einti + Eeli + Epoli + qF·ri is the sum of the gas phase ionization potential, Einti = 5.87 eV, an electrostatic part, Eeli, an induction contribution, Epoli, and the contribution due to an external electric field, qF·ri. The mean value of these energies gives an ionization potential of EIP = 5.28 eV.
The electrostatic contribution was evaluated using the Ewald summation technique29,30 adapted for charged, semi-periodic systems31,32 and distributed multipole expansions.33,34 Note that using an interaction cutoff would yield a shifted energetic landscape with an underestimated spatial correlation of energies.35
The induction contribution, Epoli, was calculated self-consistently using the Thole model36,37 with a 3 nm interaction range. Note that the set of Thole polarizabilities were scaled in order to match the volume of the polarizability ellipsoid calculated using the B3LYP functional and 6-311g(d,p) basis set. This step is required to account for larger polarizabilities of conjugated, as compared to biological, molecules.
The resulting charge transport network is used to parametrize the coarse-grained model, by matching characteristic morphological and transport properties of the system, such as the radial distribution function of molecular positions, the list of neighboring molecules, the site energy distribution and spatial correlation, and the distance-dependent distribution of transfer integrals.14,38 The coarse-grained model allows to study larger systems, here of 4 × 104 and 4 × 105 sites, which are required to perform simulations at low charge carrier densities, in our case from 0.025 down to 10−5 carriers per site.
Charge transport is modeled using the kinetic Monte Carlo (KMC) algorithm. Note that charge carriers interact only via the exclusion principle, i.e., a double occupation of a molecule is forbidden. Charge mobility is evaluated by averaging the carrier velocity along the field, μ = 〈v〉·F/F2. KMC simulations are repeated for eight different temperature values, from 220 K to 992 K, and twelve field values, in the range of 2.5–30 × 107 V m−1.
To avoid finite size effects, an extrapolation procedure39,40 is used for small charge carrier densities. The mobility is simulated at a range of higher temperatures, where mobilities are non-dispersive and hence system-size independent. The extrapolation to lower temperatures is performed by parametrizing the analytic mobility versus temperature dependence available for one-dimensional systems8 or, alternatively, using the box-size scaling relation.39
The tabulated mobility is finally interpolated and smoothed by the scattered data interpolation method using radial base functions,41 which can treat many-dimensional, unstructured data.
2.2 Drift–diffusion modeling
Macroscopic dynamics of electrons/holes (n/p) is modeled using one-dimensional drift diffusion equations| Jn/p = ±ρn/pμn/p ∇ψ − Dn/p ∇ρn/p, | (2) |
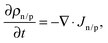 | (3) |
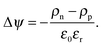 | (4) |
Since charge carriers occupy energetic levels according to Fermi–Dirac statistics, the carrier density is related to the quasi-Fermi level, η, as
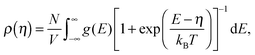 | (5) |
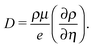 | (6) |
Eqn (2)–(6) are solved using an iterative scheme, until a self-consistent solution for electrostatic potential, ψ, density, ρ, and current, I, is found.43 First the equations are rescaled to ensure numerical stability, which is necessary since carrier density and electrostatic potential vary by several orders of magnitude. Then they are discretized according to a scheme proposed by Scharfetter and Gummel,44 linearized,45 and solved by using the Gummel iteration method,46 adapted to organic semiconductors at finite carrier density. This method is less sensitive to the initial value than a Newton algorithm and thus is the method of choice despite its slower convergence47 in terms of iteration steps. The tabulated mobility values, μ(F,ρ,T), computed in Section 2.1, are used while solving eqn (2)–(6).
We use Dirichlet boundary conditions for the electrostatic potential, ψ, by setting the potential difference at the boundaries to ψeff = Vapp − Vint, where Vapp is the applied potential and Vint the built-in potential, defined as the difference of the materials' work functions. For ITO and Aluminum we use experimental values: the work function of ITO is reported to lie in the range from 4.15 eV to 5.3 eV,48–51 and for Aluminum from 4.06 eV to 4.26 eV.52 Here we assume average values of 4.73 eV for ITO and 4.16 eV for Aluminum. In combination with the calculated DPBIC solid-state ionization potential (IP) of 5.28 eV, which is the mean value of the site energies, Ei, that are calculated as described before, this yields injection barriers of ΔEITO = 0.55 eV and ΔEAl = 1.12 eV.
The charge density at the electrodes is fixed to the density resulting from inserting ΔEITO/Al into eqn (5). To model the doped interlayers (see Section 2.5) within a five nanometer range from both electrodes, an additional charge concentration of 3 × 10−4 carriers per site, estimated from previous calculation53 is added in these regions when solving the Poisson eqn (4), leading to high hole densities in the doped regions even without space-charge limited effects.
2.3 Lattice model
To test the validity of lattice models, we have also parametrized the extended correlated disorder model (ECDM)11 by fitting the simulation results to the ECDM expression for mobility. The fit was performed for charge densities, ρ, in the range of 8.7–140 × 1023 m−3, including an extrapolated, non-dispersive zero-density mobility,40 and electric fields in the range of 3–9 × 107 V m−1. For the extrapolation temperatures from 1200 K to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K, giving non-dispersive transport in the small system, were used. All simulations were performed at 300 K.
000 K, giving non-dispersive transport in the small system, were used. All simulations were performed at 300 K.
The fit to the ECDM model yields a lattice constant of a = 0.44 nm, an energetic disorder of σ = 0.211 eV, and a zero-field zero-density mobility of μ0(300 K) = 1.8 × 10−13 m2 V−1 s−1.20 These values serve mainly for providing a fitting and extrapolation function as they differ from the values observed in microscopic simulations (a = 1.06 nm, σ = 0.176 eV, μ0(300 K) = 3.4 × 10−12 m2 V−1 s−1).
2.4 Mott–gurney model
The Mott–Gurney, or trap-free insulator model,16 predicts a current density of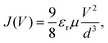 | (7) |
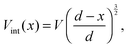 | (8) |
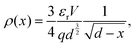 | (9) |
2.5 Experimental measurements
I–V curves were measured for three film thicknesses: 203 nm, 257 nm and 314 nm, including two interlayers of DPBIC doped with molybdenum trioxide (MoO3) of 5 nm thickness on both sides of the DPBIC film. These serve to enhance the injection efficiency, which has been taken into account in our model by the previously mentioned additional charge in these regions. The hole-conducting DPBIC layer was sandwiched between a 140 nm indium tin oxide (ITO) anode and a 100 nm aluminum cathode. To control the temperature, the samples are placed into the oil reservoir of a cryostat, which allows for a variation between 220 K and 330 K. The voltage was varied between 0 V and 20 V.All films were fabricated by vacuum thermal evaporation of DPBIC on a glass substrate, patterned with the ITO layer. Thicknesses were determined by optical ellipsometry after a simultaneous deposition of the same amount of DPBIC on a silicon wafer.
3 Validation
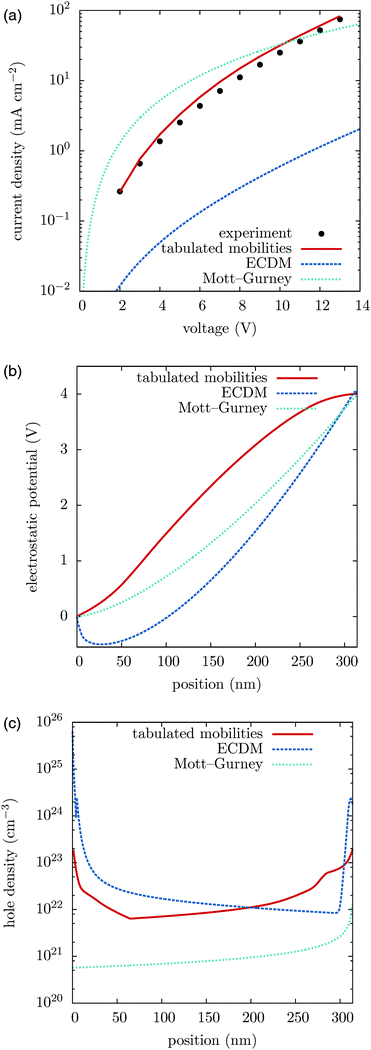
We first compare the current–voltage characteristics, the electrostatic potential and the hole density profiles calculated using tabulated and ECDM mobilities, which are shown in Fig. 2, together with the experimentally measured current–voltage characteristics. One can see that the experimentally measured current–voltage characteristics are well reproduced using the tabulated mobilities. The ECDM underestimates the current by an order of magnitude and there is a clear mismatch of the slope, as it can be seen in Fig. 2(a). It also predicts a negative electrostatic force at the beginning of the slab, Fig. 2(b), and a very steep charge accumulation at the injecting anode, Fig. 2(c). The disagreement is due to the high energetic disorder obtained from the fit, σ = 0.211 eV, which is outside the range used to parametrize the ECDM expression. In addition, the ECDM does not reproduce the spatial correlation of site energies well. Finally, the Mott–Gurney model does not reproduce experimental results even qualitatively: it neither takes into account doped layers nor field- or density-dependence of the mobility.To illustrate the transferability of the proposed method we also compare current–voltage characteristics for different temperatures and different film thicknesses. Fig. 3 shows that for high temperatures the agreement between theory and experiment is excellent. At 233 K deviations are significant and can be attributed to the breakdown of the drift–diffusion description, since at low temperature and large energetic disorder charge transport becomes dispersive, showing anomalous diffusion.53 Its description using equilibrium distributions, mobility and diffusion constant cannot be justified in this situation. Moreover, Marcus theory only applies to sufficiently high temperatures. The crossover temperature below which Miller–Abrahams rates54 become a more appropriate description has been estimated to be about 250 K.55
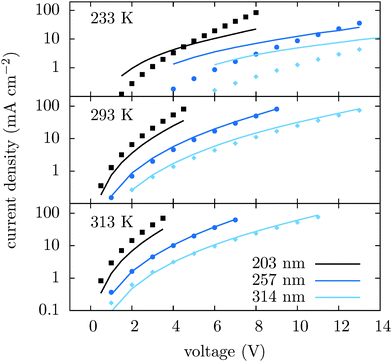 | ||
| Fig. 3 Current–voltage characteristics for different temperatures and slab thicknesses simulated using tabulated mobilities (lines) and measured (symbols). | ||
4 Conclusions
To conclude, we have proposed a parametrization scheme for drift–diffusion equations which is based on evaluation of charge transfer rates, simulation of charge transport in a coarse-grained charge transport network, and tabulation of charge carrier mobility as a function of field, charge density and temperature. The method is rather general, in part because it is not limited to functional dependencies build into the ECDM and EGDM models and, therefore, allows to treat systems with large energetic disorder and material-specific spatial site energy correlation functions.Using this scheme, we have simulated I–V characteristics of a single-layer device, and found them to be in a good agreement with the experimentally measured I–V curves, whereas significant deviations have been observed for the ECDM and Mott–Gurney models.
Acknowledgements
This project has received funding from the “NMP-20-2014 – Widening materials models” program (project MOSTOPHOS) under grant agreement No. 646259. The work was also partially supported by Deutsche Forschungsgemeinschaft (DFG) under the Priority Program “Elementary Processes of Organic Photovoltaics” (SPP 1355), BMBF grant MESOMERIE (FKZ 13N10723) and MEDOS (FKZ 03EK3503B), and DFG program IRTG 1404. We are grateful to Carl Poelking, Anton Melnyk, Paul Blom, Kurt Kremer, and Aoife Fogarty for a critical reading of the manuscript.References
- E. Knapp, R. Häusermann, H. U. Schwarzenbach and B. Ruhstaller, J. Appl. Phys., 2010, 108, 054504 CrossRef PubMed.
- J. J. M. van der Holst, M. A. Uijttewaal, B. Ramachandhran, R. Coehoorn, P. A. Bobbert, G. A. de Wijs and R. A. de Groot, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085203 CrossRef.
- J. J. M. van der Holst, F. W. A. van Oost, R. Coehoorn and P. A. Bobbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 085206 CrossRef.
- Y. Xu, T. Minari, K. Tsukagoshi, R. Gwoziecki, R. Coppard, M. Benwadih, J. Chroboczek, F. Balestra and G. Ghibaudo, J. Appl. Phys., 2011, 110, 014510 CrossRef PubMed.
- J. J. Brondijk, F. Maddalena, K. Asadi, H. J. van Leijen, M. Heeney, P. W. M. Blom and D. M. de Leeuw, Phys. Status Solidi B, 2012, 249, 138–141 CrossRef CAS PubMed.
- W. F. Pasveer, J. Cottaar, C. Tanase, R. Coehoorn, P. A. Bobbert, P. W. M. Blom, D. M. de Leeuw and M. A. J. Michels, Phys. Rev. Lett., 2005, 94, 206601 CrossRef CAS.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef PubMed.
- K. Seki and M. Tachiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 014305 CrossRef.
- H. Cordes, S. D. Baranovskii, K. Kohary, P. Thomas, S. Yamasaki, F. Hensel and J.-H. Wendorff, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094201 CrossRef.
- S. V. Novikov, D. H. Dunlap, V. M. Kenkre, P. E. Parris and A. V. Vannikov, Phys. Rev. Lett., 1998, 81, 4472–4475 CrossRef CAS.
- M. Bouhassoune, S. L. M. v. Mensfoort, P. A. Bobbert and R. Coehoorn, Org. Electron., 2009, 10, 437–445 CrossRef CAS PubMed.
- O. Rubel, S. D. Baranovskii, P. Thomas and S. Yamasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 014206 CrossRef.
- M. Kuik, G.-J. A. H. Wetzelaer, H. T. Nicolai, N. I. Craciun, D. M. De Leeuw and P. W. M. Blom, Adv. Mater., 2014, 26, 512–531 CrossRef CAS PubMed.
- P. Kordt, O. Stenzel, B. Baumeier, V. Schmidt and D. Andrienko, J. Chem. Theory Comput., 2014, 10, 2508–2513 CrossRef CAS.
- F. May, B. Baumeier, C. Lennartz and D. Andrienko, Phys. Rev. Lett., 2012, 109, 136401 CrossRef.
- N. F. Mott and R. W. Gurney, Electronic Processes in Ionic Crystals, Clarendon Press, Oxford, 2nd edn, 1948 Search PubMed.
- A. Hunze, C.-S. Chiu and R. Krause, US Pat., US8441187 B2, 2013 Search PubMed.
- N. G. Pschirer, F. Eickemeyer, J. Schoeneboom, J. H. Hwang, M. Karlsson and I. Bruder, US Pat., US20100282309 A1, 2010 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS PubMed.
- P. Kordt, J. J. M. van der Holst, M. Al Helwi, W. Kowalsky, F. May, A. Badinski, C. Lennartz and D. Andrienko, Adv. Funct. Mater., 2015, 25, 1955–1971 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01 Search PubMed.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- TURBOMOLE V6.3 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmhbH, 1989–2007, Turbomole GmbH, since 2007.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105 CrossRef PubMed.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2015, 142, 129905 CrossRef PubMed.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- A. J. Stone, The Theory of intermolecular forces, Clarendon Press, Oxford, 1997 Search PubMed.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef PubMed.
- E. R. Smith, Proc. R. Soc. London, Ser. A, 1981, 375, 475–505 CrossRef CAS.
- C. Poelking, M. Tietze, C. Elschner, S. Olthof, D. Hertel, B. Baumeier, F. Würthner, K. Meerholz, K. Leo and D. Andrienko, Nat. Mater., 2014, 14, 434–439 CrossRef PubMed.
- C. Poelking and D. Andrienko, J. Am. Chem. Soc., 2015, 6320–6326 CrossRef CAS PubMed.
- A. J. Stone and M. Alderton, Mol. Phys., 1985, 56, 1047–1064 CrossRef CAS PubMed.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef CAS.
- C. Poelking and D. Andrienko, J. Chem. Theory Comput., 2015 Search PubMed , submitted.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- B. Baumeier, O. Stenzel, C. Poelking, D. Andrienko and V. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 184202 CrossRef.
- P. Kordt, T. Speck and D. Andrienko, Phys. Rev. B: Condens. Matter Mater. Phys., 2015 Search PubMed , submitted.
- A. Lukyanov and D. Andrienko, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 193202 CrossRef.
- M. S. Floater and A. Iske, J. Comput. Appl. Math., 1996, 73, 65–78 CrossRef.
- Y. Roichman and N. Tessler, Appl. Phys. Lett., 2002, 80, 1948–1950 CrossRef CAS PubMed.
- S. Stodtmann, R. M. Lee, C. K. F. Weiler and A. Badinski, J. Appl. Phys., 2012, 112, 114909 CrossRef PubMed.
- D. Scharfetter and H. Gummel, IEEE Trans. Electron Devices, 1969, 16, 64–77 CrossRef.
- R. Courant and D. Hilbert, Methods of Mathematical Physics, Wiley-VCH Verlag GmbH, 1989, pp. 164–274 Search PubMed.
- H. Gummel, IEEE Trans. Electron Devices, 1964, 11, 455–465 CrossRef.
- E. Knapp and B. Ruhstaller, Opt. Quantum Electron., 2011, 42, 667–677 CrossRef CAS.
- W.-K. Oh, S. Q. Hussain, Y.-J. Lee, Y. Lee, S. Ahn and J. Yi, Mater. Res. Bull., 2012, 47, 3032–3035 CrossRef CAS PubMed.
- R. Schlaf, H. Murata and Z. H. Kafafi, J. Electron Spectrosc. Relat. Phenom., 2001, 120, 149–154 CrossRef CAS.
- G. M. Wu, H. H. Lin and H. C. Lu, Vacuum, 2008, 82, 1371–1374 CrossRef CAS PubMed.
- C. H. Kim, C. D. Bae, K. H. Ryu, B. K. Lee and H. J. Shin, Solid State Phenom., 2007, 124–126, 607–610 CrossRef CAS.
- D. R. Lide, CRC Handbook of Chemistry and Physics, 79th ed.: A Ready-Reference Book of Chemical and Physical Data, Crc Press, Auflage, 79th edn, 1998 Search PubMed.
- S. Stodtmann, PhD thesis, Ruprecht-Karls-Universität, Heidelberg, 2015.
- A. Miller and E. Abrahams, Phys. Rev., 1960, 120, 745–755 CrossRef CAS.
- S. T. Hoffmann, S. Athanasopoulos, D. Beljonne, H. Bässler and A. Köhler, J. Phys. Chem. C, 2012, 116, 16371–16383 CAS.
| This journal is © the Owner Societies 2015 |