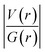DOI:
10.1039/D5CE00838G
(Paper)
CrystEngComm, 2026, Advance Article
Investigation of noncovalent interactions in organofluorine compounds with C–F bonds in different electronic environments†
Received
29th August 2025
, Accepted 8th December 2025
First published on 16th December 2025
Abstract
We have synthesized a series of fluorine substituted 2-methylpropanamide compounds including a pair of polymorphs with the fluorine substitution at the aromatic ring and methyl carbon to investigate the relevance of weak non-covalent interactions in the solid-state. The compounds are structurally characterized using the single crystal X-ray diffraction technique and their supramolecular behaviours are explored methodically regarding the contribution of strong hydrogen bonds like N–H⋯O, acting in conjunction with C–H⋯O, and the ancillary support of weak C–H⋯F interaction. PIXEL calculations allowed for the estimation of the different intermolecular interaction energies of the derived dimers and the overall lattice energies of the different crystalline solids. It is observed that the molecular motifs consisting of C(sp2)–H⋯F–C(sp2) interaction are more stable in comparison to other C–H⋯F interactions. QTAIM analysis further supports these interactions via a topological analysis of the electron density distribution at the bond critical point. A detailed experimental and computational evaluation has been carried out to evaluate the effect of the environment surrounding the carbon atom, i.e. the role of hybridization of the carbon atom, connected to the acceptor fluorine atom and the donor hydrogen atom as well.
Introduction
The contribution of organic fluorine in the formation of weak interactions and the reinforcement of the molecular crystal has been an important topic of discussion over the past few years.1 There is a substantial body of literature in which the significance of intermolecular interactions involving organic fluorine and their exclusive involvement in controlling the crystal structures are well-explored through different computational and experimental approaches.2–4 The role of strong and conventional hydrogen bonds in controlling the crystal architecture has been reliable5 but the independent existence of these weak interactions involving organic fluorine, instead of strong hydrogen bonds, is still under consideration.6–8 From previous studies, among all these weak interactions, the important contribution of C–H⋯F interaction in the stabilization has been recognized despite the presence of strong hydrogen bonds.9 However, the hybridization of the carbon atom attached to the fluorine and the hydrogen atoms has a subtle impact on the stability of the bond, the participation of the fluorine atom in the formation of different stable motifs and the robustness of these motifs in the systematic exploration of supramolecular assemblies.10,11 In this context, the C–H⋯F interaction can be classified into four categories: C(sp3)–H⋯F–C(sp3), C(sp3)–H⋯F–C(sp2), C(sp2)–H⋯F–C(sp3), and C(sp2)–H⋯F–C(sp2). The greater the s-character of the carbon atom attached to hydrogen, the greater the acidic nature of the participating hydrogen atom, thus resulting in higher stability of the hydrogen bond formed.12,13
The majority investigations in the past involved the presence of a fluorine atom connected to aromatic ring carbon atom (sp2 hybridized).11,14,15 Lately, the capability of a fluorine atom attached to an sp3 hybridized carbon atom has been investigated in the generation of different structural motifs and their effect on crystal packing in a series of isomeric trifluoromethyl-substituted benzanilides.16 The charge density analysis reveals the intrinsic polarization of the electron density on the fluorine atom in the trifluoromethyl group.17 Another study, performed in a series of substituted benzanilides, consisting of both fluorine and trifluoromethyl group, unveils that C(sp2)–H⋯F–C(sp2) hydrogen bonds constitute the highest stabilized molecular motifs in comparison to C(sp2)–H⋯F–C(sp3) interactions.18 Furthermore, in a recent study, the electronic environment of the donor hydrogen and acceptor fluorine atoms has been varied in a series of fluorine substituted propanamide compounds, and consequently their influence in the molecular motifs and crystal packing has been comprehensively studied by analysing X-ray data.19 However, the study indicates that the interaction energy is relatively higher for C(sp2)–H⋯F–C(sp2) interactions, and variations in the interaction energies, i.e. the local stabilization energies, and the charge densities are noticed while considering C(sp3)–H⋯F–C(sp3), C(sp3)–H⋯F–C(sp2), and C(sp2)–H⋯F–C(sp3) interactions.
Contemplating the results of previous studies, a comprehensive study has been aimed to analyse the supporting role of weak C–H⋯F interactions in regulating crystalline solids, considering different electronic environments around the donor hydrogen and the acceptor fluorine atom. For this purpose, a series of propanamide compounds has been synthesized, where fluorine is substituted at the ortho, meta, and para positions of the aromatic ring (sp2 hybridization), and at a methyl carbon (sp3 hybridization). The current study has four objectives. Firstly, the compounds are synthesized and crystallized, and the molecular structures are determined by single crystal X-ray diffraction. Secondly, the salient features of the crystal packing incorporating strong and weak intermolecular interactions have been explored thoroughly. Next, the PIXELC method has been utilized to derive the molecular motifs consisting of weak C–H⋯F interactions in the presence of strong hydrogen bonds, and their interaction energies are evaluated. Furthermore, analysis of the topological parameters at the bond critical points has been performed to showcase the nature of these interactions. Moreover, an attempt is made to perceive the trend that unveils the influence of the hybridization of carbon in the formation of favourable C–H⋯F interactions.
Experimental section
Synthesis and crystallization of compounds 1, 2, and 3
The fluoro-substituted organic acid (1.50 mmol, 0.14 mL) (Scheme 1) was placed in a 25 mL round-bottom flask and dissolved in 4 mL dichloromethane (DCM). Two drops of DMF were added under a N2 atmosphere and the flask was cooled in an ice bath. Oxalyl chloride (1.80 mmol, 0.15 mL) was then added dropwise at the same temperature (0 °C). The resulting reaction mixture was stirred at room temperature for 8 h. After complete consumption of the starting material, as monitored by thin layer chromatography (TLC), the solvent and excess oxalyl chloride were removed under reduced pressure in an inert atmosphere. The yellow-coloured liquid (the corresponding acid chloride) was obtained, which was used in the next step without further purification.
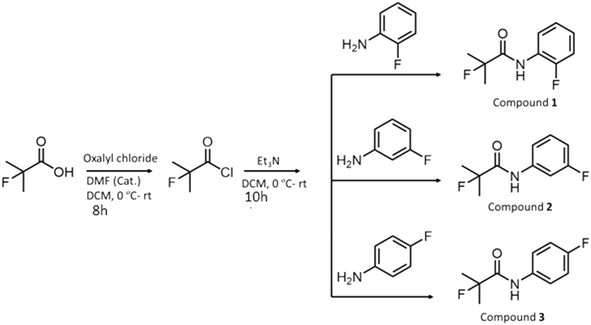 |
| | Scheme 1 Chemical scheme depicting the synthetic procedure for the obtained compounds. | |
Subsequently, the obtained acid chloride (1.50 mmol, 0.14 mL) was dissolved in 4 mL of DCM under a N2 atmosphere at 0 °C. Triethylamine (9.00 mmol, 1.2 mL) and the corresponding fluoro-substituted aniline (1.50 mmol, 0.14 mL) were added to the solution at the same temperature. The reaction mixture was stirred at room temperature for 10 h. Upon completion of the reaction, as monitored by TLC, the reaction mixture was quenched with water and 5% HCl and extracted with DCM (50 mL × 3). The organic layer was collected and dried over anhydrous sodium sulphate, and the solvent was then evaporated under reduced pressure. The resulting crude compound was purified by column chromatography (with a solvent mixture of ethyl acetate and hexane as the eluent) to obtain compounds 1, 2 and 3 as white solids in 54%, 50% and 51% yields, respectively.
The compounds were dissolved in different organic solvents, namely ethyl acetate/hexane, dichloromethane (DCM)/hexane, ethanol, toluene, CDCl3, acetone and benzene. In most cases, aggregates were obtained. The crystals obtained via slow evaporation of solvents at both ambient (24–28 °C) and low temperatures (4 °C) were examined under an optical microscope and further screened for collection of the X-ray diffraction data. The solvent system, from which the final crystals utilized for diffraction measurement were obtained, is shown in Table 1.
Table 1 Crystal and refinement data of compounds 1, 2, 3-form-I and 3-form-II
| Sample code |
1 |
2 |
3-Form-I |
3-Form-II |
| Formula |
C10H11F2NO |
C10H11F2NO |
2(C10H11F2NO) |
C10H11F2NO |
| Formula weight |
199.20 |
199.20 |
398.39 |
199.20 |
| Temperature (K) |
105(2) |
103(2) |
102(2) |
94(2) |
| Wavelength (Å) |
0.71073 |
0.71073 |
0.71073 |
0.71073 |
| Solvent |
DCM and hexane (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
DCM |
Toluene |
DCM and hexane (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
| CCDC number |
2483272 |
2483273 |
2483274 |
2483275 |
| Crystal system |
Orthorhombic |
Orthorhombic |
Monoclinic |
Triclinic |
| Space group |
P212121 |
Pca21 |
P21/n |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a (Å) |
5.1128(8) |
12.0624(7) |
9.5100(11) |
5.1799(14) |
| b (Å) |
6.7751(11) |
9.4612(6) |
11.0959(13) |
9.618(3) |
| c (Å) |
27.331(5) |
8.6588(4) |
19.198(2) |
10.442(3) |
| α (°) |
90 |
90 |
90 |
81.822(9) |
| β (°) |
90 |
90 |
102.991(4) |
80.772(9) |
| γ (°) |
90 |
90 |
90 |
74.442(9) |
| V (Å3) |
946.8(3) |
988.18(10) |
1974.0(4) |
491.9(2) |
| Z |
4 |
4 |
4 |
2 |
| Density (g cm−3) |
1.398 |
1.339 |
1.341 |
1.345 |
| μ (mm−1) |
0.117 |
0.112 |
0.112 |
0.113 |
| F(000) |
416 |
416 |
832 |
208 |
| θ (min, max) |
3.098, 30.133 |
2.736, 30.036 |
2.177, 29.130 |
2.210, 30.357 |
| Treatment of hydrogen atoms |
Mixed |
Mixed |
Constrained |
Constrained |
| hmin,max, kmin,max, lmin,max |
(−7, 5), (−9, 9), (−38, 37) |
(−16, 16), (−13, 13), (−9, 12) |
(−13, 11), (−15, 15), (−26, 23) |
(−7, 7), (−13, 13), (−14, 14) |
| No. of total ref. |
9776 |
8140 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 866 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 517 |
| No. of unique/obs ref. |
2790/2274 |
2362/2058 |
5283/3423 |
2947/1714 |
| No. of parameters |
133 |
133 |
257 |
165 |
| Rall, Robs |
0.0580, 0.0394 |
0.0519, 0.0408 |
0.0917, 0.0477 |
0.1221, 0.0548 |
| wR2all, wR2obs |
0.0844, 0.0786 |
0.1039, 0.0989 |
0.1156, 0.0998 |
0.1400, 0.1181 |
| Δρmin,max (e Å−3) |
−0.194, 0.271 |
−0.264, 0.413 |
−0.246, 0.329 |
−0.253, 0.285 |
| G. O. F. |
1.036 |
1.044 |
1.030 |
1.047 |
Nuclear magnetic resonance (NMR) spectroscopy. 1H NMR spectra were obtained on a Bruker Avance Neo 500 MHz spectrometer for all compounds using CDCl3 and DMSO-d6 as solvents. The spectral analysis is provided in Fig. S1–S3.
Liquid chromatography-mass spectrometry (LC-MS). The experiments were performed with a Bruker micrOTOF-Q II mass spectrometer. There was a good correlation observed between the calculated mass and experimental mass for all the compounds (Fig. S4).
Molecular structure determination by single crystal X-ray diffraction. All compounds are structurally characterized by single crystal X-ray diffraction using a Bruker APEX-II CCD single crystal diffractometer equipped with a graphite monochromator (MoKα radiation (λ = 0.71073 Å)) controlled by APEX2.20 The data collection were performed at 105(2) K, 103(2) K, 102(2) K and 94(2) K for 1, 2, 3-form-I and 3-form-II, respectively. Data were corrected for Lorentz and polarization effects using SAINT.21 The absorption correction was done using the multi-scan method using SADABS-2014/2.22 The structures are solved by direct methods using SHELXT 2014/5 (ref. 23) and refined by the full-matrix least-squares method using the SHELXL-2016/6 program.24 All non-hydrogen atoms are refined anisotropically, and all hydrogen atoms bound to carbon atoms are placed in the calculated positions where thermal parameters are refined isotropically with Ueq = 1.2–1.5Ueq(C). The hydrogen atoms attached to nitrogen atoms are located from the difference Fourier map and refined isotropically with Ueq = 1.2Ueq(N). All structural geometrical parameters are derived using PLATON.25 The geometrical parameters related to hydrogen bonds are analysed from the .lst file in the PARST program.26 The 4-fluorophenyl ring in 3-form-II is disordered in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Only one conformer is considered for further discussion. Details of the X-ray measurements and crystal parameters of all the compounds are given in Table 1. The weak intermolecular interactions are considered based on the following criteria: the sum of the vdW's radii + 0.2 Å and directionality ≥110° and are further validated via QTAIM calculations.
1 ratio. Only one conformer is considered for further discussion. Details of the X-ray measurements and crystal parameters of all the compounds are given in Table 1. The weak intermolecular interactions are considered based on the following criteria: the sum of the vdW's radii + 0.2 Å and directionality ≥110° and are further validated via QTAIM calculations.
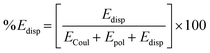
Theoretical calculations. The lattice energies for all four compounds are calculated using the PIXELC method in the CLP module.27 The interaction energies estimated for molecular pairs are partitioned in four types of energy terms: coulombic (Ecoul), polarization (Epol), dispersion (Edisp), and repulsion (Erep).28,29 For this purpose, the wave function related to the electron density of the molecules is obtained by DFT theory at the B3LYP/6311++G(d,p) basis set using Gaussian16 (ref. 30) considering H atoms at their neutron distances. The percentage contribution of electrostatic and dispersion energy towards total stabilization is calculated as:| |
 | (1) |
| | |
%Eelec = 100 − %Edisp
| (2) |
Molecular Hirshfeld surfaces31,32 generated through CrystalExplorer21.5 (ref. 33) are mapped over the normalised contact distance (dnorm), shape index and curvedness surfaces. The existence of red, white and blue dots on the dnorm surface indicates shorter contacts, contacts around vdW separation and longer contacts, respectively. The percentage contribution of each possible contact is represented by decomposed 2D fingerprint plots34–37 composed by de (the distance from the point to the nearest nucleus external to the surface) and di distances (the distance from the point to the nearest nucleus internal to the surface). Moreover, the lattice energy38 of all compounds is computed using CrystalExplorer21.5 through an accurate method B3LYP/6–31G(d,p) given in section S1 (Table S3).Consequently, the molecular pairs comprising of C–H⋯F interactions are taken into consideration to characterize the interactions through the “quantum theory of atoms in molecules” (QTAIM)39 using AIMAll software.40 This analysis includes the topological parameters such as electron charge density (ρ(r)), the Laplacian of electron charge density (∇2(ρ(r), local potential energy density (V(r)), kinetic energy density (G(r)), and total energy density (H(r)). The interaction energy (Eint) is calculated by the method proposed by Espinosa41 using the local potential energy density (V(r)) as Eint = −313.754 × V(r) (in kcal mol−1).42
Results and discussion
Analysis of the molecular structure and crystal packing of compounds 1, 2, and 3-form-I & II
Crystal packing and molecular pairs in 1 [2-fluoro-N-(2-fluorophenyl)-2-methylpropanamide]. Compound 1 crystallizes in the orthorhombic non-centrosymmetric space group P212121 with Z = 4. The asymmetric unit contains two fluorine atoms where one is connected to C8(sp3) and the other is substituted at the ortho-position of the benzene ring (Fig. 1a). Some selected torsion angles, bond lengths, and bond angles are mentioned in Table 2, S1 and S2, respectively. The crystal structure of 1 is stabilized through strong hydrogen bonds like N–H⋯O along with the presence of weak C–H⋯O and C–H⋯F hydrogen bonds and further supported by weak C–H⋯π interactions. Firstly, the N–H⋯O interaction supported by C–H⋯O and C–H⋯F interactions, involving H9B, H10B and F2, constitute the most stabilized motif I (I.E. = −37.5 kJ mol−1), which assists the molecules to form a molecular chain along the a-axis through translational symmetry (x − 1, y, z). These chains are connected via motif IV (I.E. = −8.4 kJ mol−1) where H10C is oriented towards the centroid (Cg1) of the π-ring (Fig. 2f), with a hydrogen to centroid distance (H⋯Cg1) of 2.75 Å (Fig. 2a). It is observed that the inclusion of strong hydrogen bonds in motif I (Fig. 2c) result in significant electrostatic (67%) contributions. Moreover, motif IV is also electrostatic in nature with the contribution of 59% towards the total interaction energy (Table 3). In another substructure, the C–H⋯O interaction assists the molecules to form a dimer (motif II, I.E. = −10.3 kJ mol−1). These dimers are connected to each other (red blocks in Fig. 2b) to form an infinite chain along the b-axis with the utilization of C–H⋯F interactions, involving H9C and F2 (motif V, I.E. = −7.1 kJ mol−1). Consequently, long infinite chains are connected in an anti-parallel manner, through another C–H⋯F interaction (green blocks in Fig. 2b), including H3 and F1 (motif III, I.E. = −9.9 kJ mol−1), and generating a two-dimensional supramolecular structure in the bc-plane. The partitioning of the energy contribution reveals that motif III, consisting of C(sp2)–H⋯F–C(sp2) interactions (Fig. 2e), has equal contribution from both electrostatic and dispersion energies (50%) whereas motif V, incorporating C(sp3)–H⋯F–C(sp3) interactions (Fig. 2g), is dispersive in nature (59%). Moreover, motif II (including C–H⋯O) and motif VI (including C–H⋯π/Cg) are both stabilized by dispersion energies, with the contribution being 61% and 69%, respectively (Fig. 2d and h).
 |
| | Fig. 1 ORTEP of compounds (a) 1, (b) 2, (c) 3-form-I, and (d) 3-form-II (compound 3 that exists as form-I and form-II) with the thermal ellipsoid of 30% probability. | |
Table 2 Selected torsion angles (°)
| Compounds |
1 |
2 |
3-Form-I |
3-Form-II |
| C6–C1–N1–C7 |
131.9(2) |
156.9(2) |
131.5(2) |
134.1(2) |
| C16–C11–N2–C17 |
— |
— |
−154.6(2) |
— |
| C1–N1–C7–C8 |
−174.2(2) |
−178.7(2) |
−177.9(2) |
−176.7(2) |
| C11–N2–C17–C18 |
— |
— |
176.6(2) |
— |
| N1–C7–C8–C9 |
−130.8(2) |
−109.2(2) |
−115.6(2) |
−118.5(2) |
| N2–C17–C18–C19 |
— |
— |
−115.4(2) |
— |
| N1–C7–C8–C10 |
103.5(2) |
125.7(2) |
117.5(2) |
115.7(2) |
| N2–C17–C18–C20 |
— |
— |
118.9(2) |
— |
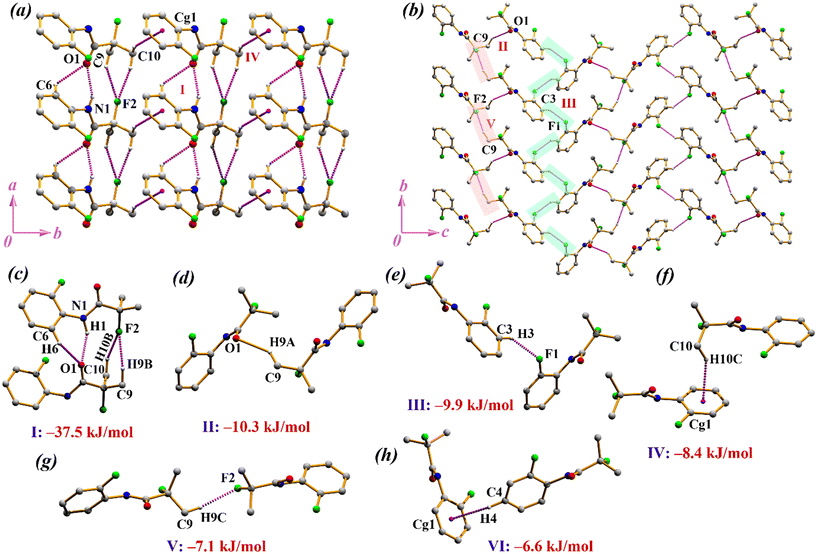 |
| | Fig. 2 (a and b) Crystal packing of 1. (c–h) Molecular pairs extracted from PIXEL calculation along with their interaction energies in 1. | |
Table 3 Interaction energies (kJ mol−1) of the molecular pairs/motifs of compounds 1, 2, 3-form-I and 3-form-II. The distances are neutron normalized
| Motifs |
Symmetry code |
Cg⋯Cg |
ECoul |
EPol |
EDisp |
ERep |
Etot |
Involved interactionsa |
Geometry (Å/°) D⋯A, H⋯A, ∠D–H⋯A |
| 1 |
| I |
(x − 1, y, z) |
5.113 |
−48.9 |
−15.2 |
−31.2 |
57.8 |
−37.5 |
C6–H6⋯O1 |
3.223(2), 2.48, 125 |
| N1–H1⋯O1 |
2.976(2), 2.05, 148 |
| C10–H10B⋯F2 |
3.343(2), 2.36, 150 |
| C9–H9B⋯F2 |
3.465(2), 2.57, 140 |
| II |
(x − 1/2, −y + 1/2, −z + 1) |
6.747 |
−6.7 |
−3.3 |
−15.5 |
15.3 |
−10.3 |
C9–H9A⋯O1 |
3.505(2), 2.55, 147 |
| III |
(−x, y + 1/2, −z + 1/2) |
8.646 |
−7.7 |
−2.1 |
−9.8 |
9.7 |
−9.9 |
C3–H3⋯F1 |
3.190(2), 2.35, 134 |
| IV |
(x, y − 1, z) |
6.775 |
−8.1 |
−3.4 |
−16.3 |
19.5 |
−8.4 |
C10–H10C⋯Cg1 |
3.707(2), 2.75, 146 |
| V |
(x + 1/2, −y + 3/2, −z + 1) |
9.434 |
−5.9 |
−2.0 |
−11.5 |
12.3 |
−7.1 |
C9–H9C⋯F2 |
3.500(2), 2.51, 152 |
| VI |
(−x + 1, y − 1/2, −z + 1/2) |
8.466 |
−3.9 |
−2.0 |
−12.9 |
12.2 |
−6.6 |
C4–H4⋯Cg1 |
3.834(2), 2.85, 150 |
| 2 |
| I |
(−x + 1/2, y, z + 1/2) |
4.356 |
−46.9 |
−16.0 |
−34.8 |
66.0 |
−31.7 |
N1–H1⋯O1 |
2.953(2), 1.96, 162 |
| C6–H6⋯O1 |
3.255(3), 2.48, 128 |
| II |
(x − 1/2, −y + 2, z) |
7.789 |
−9.8 |
−4.1 |
−19.4 |
20.4 |
−12.9 |
C4–H4⋯O1 |
3.396(3), 2.47, 144 |
| III |
(−x, −y + 1, z − 1/2) |
8.374 |
−9.7 |
−2.8 |
−10.3 |
11.3 |
−11.5 |
C10–H10C⋯O1 |
3.561(3), 2.51, 166 |
| C10–H10A⋯F2 |
3.773(3), 2.72, 166 |
| IV |
(−x + 1/2, y − 1, z + 1/2) |
10.416 |
−2.8 |
−1.0 |
−5.7 |
5.8 |
−3.7 |
C9–H9A⋯F1 |
3.284(3), 2.58, 122 |
| 3-Form-I |
| I (AB) |
(x − 1/2, −y + 1/2, z − 1/2) |
5.172 |
−46.2 |
−14.5 |
−28.9 |
55.4 |
−34.3 |
N1–H1⋯O2 |
2.871(2), 1.95, 148 |
| C19–H19C⋯F2 |
3.558(2), 2.62, 145 |
| C20–H20A⋯F2 |
3.524(2), 2.57, 147 |
| II (AB) |
(x, y, z) |
4.803 |
−34.6 |
−12.0 |
−25.5 |
37.9 |
−34.2 |
N2–H2⋯O1 |
2.992(1), 2.05, 151 |
| C2–H2⋯F4 |
3.813(2), 2.75, 167 |
| III (AA) |
(−x + 3/2, y − 1/2, −z + 1/2) |
7.392 |
−21.4 |
−7.8 |
−15.2 |
27.4 |
−17.1 |
C10–H10A⋯F1 |
3.929(2), 2.90, 160 |
| C3–H3⋯O1 |
3.244(2), 2.20, 161 |
| IV (AB) |
(−x + 3/2, y − 1/2, −z + 1/2) |
5.417 |
−12.5 |
−4.2 |
−23.6 |
24.2 |
−16.1 |
C9–H9B⋯O2 |
3.733(2), 2.70, 159 |
| C20–H20B⋯O1 |
3.797(2), 2.75, 163 |
| V (BB) |
(−x + 2, −y, −z + 1) |
6.449 |
−4.5 |
−3.2 |
−20.6 |
15.4 |
−12.8 |
H12⋯H12 |
2.32 |
| VI (AB) |
(−x + 1/2, y + 1/2, −z + 1/2) |
11.937 |
−12.7 |
−2.3 |
−8.1 |
10.5 |
−12.6 |
C5–H5⋯F3 |
3.437(2), 2.43, 155 |
| C15–H15⋯F1 |
3.444(2), 2.39, 165 |
| VII (AA) |
(−x + 2, −y, −z) |
9.156 |
−12.7 |
−2.7 |
−12.3 |
15.2 |
−12.5 |
C10–H10C⋯F2 |
3.474(2), 2.41, 170 |
| VIII (AB) |
(−x + 3/2, y + 1/2, −z + 1/2) |
5.846 |
−14.8 |
−5.3 |
−30.6 |
39.8 |
−10.9 |
C10–H10B⋯F3 |
3.616(2), 2.56, 167 |
| Cg1⋯Cg2 |
4.197(2) |
| C19–H19B⋯F1 |
3.544(2), 2.47, 171 |
| IX (AB) |
(x − 1, y, z) |
9.627 |
−5.5 |
−1.3 |
−7.6 |
7.9 |
−6.6 |
C20–H20C⋯F1 |
3.591(2), 2.65, 145 |
| C19–H19A⋯F1 |
3.567(2), 2.62, 146 |
| X (AA) |
(−x + 1, −y, −z) |
6.312 |
0.0 |
−2.4 |
−12.4 |
8.6 |
−6.2 |
H9B⋯H6 |
2.32 |
| 3-Form-II |
| Cg1 is the centroid of the π-ring (C1–C6) in 1 and 3-form-I and Cg2 is the centroid of the π-ring (C11–C16) in 3-form-I. |
| I |
(x − 1, y, z) |
5.180 |
−63.7 |
−21.7 |
−42.8 |
99.7 |
−28.5 |
C6–H6⋯O1 |
3.177(4), 2.42, 126 |
| N1–H1⋯O1 |
2.954(2), 2.02, 150 |
| C10–H10B⋯F2 |
3.502(2), 2.57, 144 |
| C9–H9B⋯F2 |
3.458(3), 2.50, 148 |
| II |
(−x + 1, −y + 1, −z) |
5.307 |
−12.8 |
−4.0 |
−23.1 |
22.7 |
−17.1 |
C9–H9A⋯O1 |
3.783(3), 2.73, 165 |
| III |
(−x, −y + 1, −z + 1) |
5.731 |
−8.9 |
−2.8 |
−22.7 |
19.5 |
−15.0 |
C10–H10C⋯F1 |
3.546(2), 2.48, 167 |
| IV |
(−x, −y, −z + 1) |
11.908 |
−13.9 |
−2.6 |
−8.9 |
11.7 |
−13.7 |
C5–H5⋯F1 |
3.418(5), 2.39, 160 |
| V |
(−x, −y + 2, −z) |
9.299 |
−9.7 |
−2.4 |
−11.6 |
13.2 |
−10.6 |
C10–H10A⋯F2 |
3.566(2), 2.49, 175 |
Crystal packing and molecular pairs in 2 [2-fluoro-N-(3-flurorophenyl)-2-methylpropanamide]. Compound 2 crystallizes in the orthorhombic non-centrosymmetric space group Pca21 with Z = 4. The asymmetric unit contains one moiety whose benzene ring is substituted with fluorine at the meta-position (Fig. 1b). In the solid-state, the crystal structure is stabilized through N–H⋯O, C–H⋯O, and C–H⋯F hydrogen bonds. First, the molecules are connected to each other by N–H⋯O and C–H⋯O interactions to form a one-dimensional chain along the c-axis (motif I, I.E. = −31.7 kJ mol−1) generated through the c-glide symmetry (−x + 1/2, y, z + 1/2). Again, similar molecular chains are connected through C–H⋯O interactions (motif II, I.E. = −12.9 kJ mol−1) with the aid of an a-glide plane perpendicular to the crystallographic b-axis (Fig. 3a). Subsequently, the parallel molecular chains are further connected through C–H⋯O supported by C–H⋯F interactions (motif III, I.E. = −11.5 kJ mol−1), resulting in a two-dimensional supramolecular arrangement (Fig. 3a). It is noted that motif I (Fig. 3b), comprising N–H⋯O and C–H⋯O, is supported with an additional F⋯O short contact (2.991(1) Å) and this motif is majorly stabilized by contribution from electrostatics (64%). Although motif II includes short C–H⋯O interactions, it shows dispersive nature with 58% contribution (Fig. 3c). Interestingly, motif III containing C(sp3)–H⋯F–C(sp3) and C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions (Fig. 3d) possesses 55% electrostatic energy contribution in the total energy, whereas motif IV stabilized by C(sp3)–H⋯F–C(sp2) interactions is dispersive in nature with 60% contribution (Fig. 3e).
C interactions (Fig. 3d) possesses 55% electrostatic energy contribution in the total energy, whereas motif IV stabilized by C(sp3)–H⋯F–C(sp2) interactions is dispersive in nature with 60% contribution (Fig. 3e).
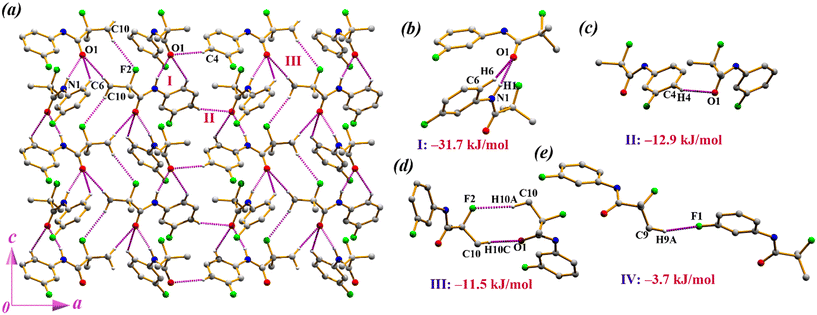 |
| | Fig. 3 (a) Supramolecular self-assembly in 2. (b–e) All favourable molecular pairs extracted from PIXEL calculation along with their interaction energies in 2. | |
Crystal packing and molecular pairs in 3-form-I [2-fluoro-N-(4-fluorophenyl)-2-methylpropanamide]. Compound 3 exhibits structural polymorphism [3-form-I & 3-form-II] (Fig. 1c and d) where the asymmetric units of I and II contain two molecular moieties and one molecular moiety, respectively, with the substitution of the fluorine atom at the para-position in the benzene ring. 3-Form-I crystallizes in the monoclinic centrosymmetric space group P21/n with Z = 8 and Z′ = 2, and 3-form-II crystallizes in the triclinic centrosymmetric space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z = 2 and Z′ = 1.
with Z = 2 and Z′ = 1.In 3-form-I, different crystal packings have been observed incorporating N–H⋯O along with C–H⋯O, C–H⋯F and π–π interactions. In the first substructure depicted in Fig. 4a, moieties A and B together form an infinite molecular chain incorporating N–H⋯O and C–H⋯F interactions, involving H2, H19C, H20B, F2 and F4 (motif I, I.E. = −34.3 kJ mol−1 and motif II, I.E. = −34.2 kJ mol−1). The molecular chain propagates along the c-axis with the symmetry (x − 1/2, −y + 1/2, z − 1/2). The chains are further connected to each other through C–H⋯F interactions involving H19A, H20C and F1 (motif IX, I.E. = −6.6 kJ mol−1), resulting in a two-dimensional supramolecular self-assembly in the ac-plane. Due to the presence of strong hydrogen bond N–H⋯O, motifs I & II (Fig. 5a and b) are electrostatic in nature (68% & 65% respectively), whereas motif IX exhibits dispersive nature (53%) consisting of C(sp3)–H⋯F–C(sp2) interactions (Fig. 5i) with H⋯F distances of 2.65 and 2.62 Å. In Fig. 4b, C–H⋯O and C–H⋯F interactions, involving H10A and F1 in motif III (I.E. = −17.1 kJ mol−1), form a zigzig molecular chain and these chains are further connected via a centrosymmetric dimeric ring (motif VII, I.E. = −12.5 kJ mol−1) consisting of a short C–H⋯F interaction (dH⋯F = 2.41 Å), thus forming a two-dimensional supramolecular arrangement. In this case, motifs III & VII are both electrostatic in nature (66% and 56%, respectively) (Fig. 5c and g). However, motif IV (I.E. = −16.1 kJ mol−1) stabilized through C–H⋯O interactions is connected to each other via C–H⋯F interactions (motif VI, I.E. = −12.6 kJ mol−1 and motif VIII, I.E. = −10.9 kJ mol−1), forming a two-dimensional supramolecular network (Fig. 4c). Motif IV is dispersive in nature (59%) (Fig. 5d), whereas motif VI consisting of short C(sp2)–H⋯F–C(sp2) interactions (dH⋯F = 2.43 Å and 2.39 Å) is stabilized by electrostatic energy (65%) (Fig. 5f). Moreover, motif VIII includes a π–π interaction (Cg1–Cg2) with a centroid separation of 4.197(2) Å along with the C(sp3)–H⋯F–C(sp2) interactions (Fig. 5h), having a higher dispersion energy (60%) contribution. Lastly, motif V (I.E. = −12.8 kJ mol−1) and motif X (I.E. = −6.2 kJ mol−1) are stabilized by H⋯H short contacts (Fig. 5e and j) and these are dispersive in nature with contributions of 73% and 84%, respectively.
 |
| | Fig. 4 (a–c) Supramolecular self-assemblies in 3-form-I. The carbon atoms are deep grey in moiety A and turquoise blue in moiety B. | |
 |
| | Fig. 5 (a–j) Molecular pairs in 3-form-I extracted from PIXEL calculation along with their interaction energies. The carbon atoms are deep grey in moiety A and turquoise blue in moiety B. | |
Crystal packing and molecular pairs in 3-form-II [2-fluoro-N-(4-fluorophenyl)-2-methylpropanamide]. In 3-form-II, the molecules are arranged in the solid-state through N–H⋯O, C–H⋯O and C–H⋯F interactions. Firstly, N–H⋯O in association with C–H⋯O and C–H⋯F interactions, involving H9B, H10B and F2, forms an infinite molecular chain (motif I, I.E. = −28.5 kJ mol−1) involving the translational symmetry (x − 1, y, z). Next, two such chains are connected to each other via a centrosymmetric dimeric ring stabilized by C–H⋯F interactions (motif IV, I.E. = −13.7 kJ mol−1) and generated through the inversion symmetry (−x, −y, −z + 1), resulting in another infinite molecular chain. These molecular chains are further connected to each other (Fig. 6a) via a centrosymmetric dimeric ring containing C–H⋯F interactions (motif V, I.E. = −10.6 kJ mol−1) (Fig. 6g). It is observed that motif I (Fig. 6c), containing strong N–H⋯O hydrogen bonds, is electrostatic in nature (67%). Importantly, motif IV (Fig. 6f) exhibits electrostatic nature (65%) involving short C(sp2)–H⋯F–C(sp2) interactions (dH⋯F = 2.39 Å) whereas, motif V, consisting of C(sp3)–H⋯F–C(sp3) interactions (dH⋯F = 2.49 Å), also shows electrostatic nature with less contribution (51%) compared to IV. In another substructure, the alternative association of C–H⋯O (motif II, I.E. = −17.1 kJ mol−1) and C–H⋯F interactions (motif III, I.E. = −15.0 kJ mol−1) helps the molecules to assemble in an infinite molecular chain generated by the symmetries (−x + 1, −y + 1, −z) and (−x, −y + 1, −z + 1), respectively. These parallel chains are connected to each other via motif V, resulting in a two-dimensional supramolecular assembly in the bc-plane (Fig. 6b). However, motif II comprising C–H⋯O and motif III comprising C(sp3)–H⋯F–C(sp2) interactions contribute more to the dispersion energy (58% and 66%, respectively) in comparison to other motifs (Fig. 6d and e).
 |
| | Fig. 6 (a and b) Supramolecular packing in 3-form-II. (c–g) Molecular pairs extracted from PIXEL calculation along with their interaction energies in 3-form-II. | |
Lattice energy. The total lattice energies for 1, 2, 3-form-I and 3-form-II are also calculated from PIXEL calculation depicted in Table 4. The highest coulombic energy is possessed by 3-form-II (−89.9 kJ mol−1) and the lowest by 2 (−71.7 kJ mol−1). A cell dipole contribution of −3.1 kJ mol−1 appears in 2 due to the association with a polar space group. The contribution of dispersion energy is the highest for 2 (52%). Moreover, the total lattice energy is occupied by 1 with a value of −87.8 kJ mol−1.
Table 4 Lattice energy (kJ mol−1) for 1, 2, 3-form-I and 3-form-II
| Compounds |
ECoul |
EPol |
EDisp |
ERep |
Ecd |
ETot |
| 1 |
−83.8 |
−27.2 |
−109.5 |
132.7 |
0.0 |
−87.8 |
| 2 |
−71.7 |
−24.8 |
−103.0 |
125.2 |
−3.1 |
−77.4 |
| 3-Form-I |
−79.1 |
−26.4 |
−100.7 |
123.3 |
0.0 |
−82.8 |
| 3-Form-II |
−89.9 |
−30.1 |
−106.6 |
152.6 |
0.0 |
−74.0 |
Hirshfeld surface analysis. The Hirshfeld surface analysis has been carried out for all compounds to characterize the intermolecular interactions controlling the crystal structures and the favourable molecular dimers. The Hirshfeld surfaces are mapped over dnorm, shape index and curvedness (Fig. S5), where the feasible hydrogen bonds are visualized as bright-red spots on the dnorm surface and π–π interactions are visible as red-blue triangles on the shape index and flat region on the curvedness surface. The intense bright red spots indicate the presence of N–H⋯O interactions in all compounds. The less bright-red spots on the surface near fluorine atoms are characterized as contributors to the weak hydrogen bonds. As 3-form-I contains π–π interactions in the packing, a red-blue triangle and a flat region are evidenced on the shape index and curvedness, respectively (Fig. S5c).Additionally, 2D fingerprint plots (Fig. 7) of all compounds are studied to quantify the percentage contribution of each probable contact occurring in the crystal structures. All the decomposed fingerprint plots are depicted in Fig. S6–S9. The significant contribution of F⋯H/H⋯F contacts is observed in all compounds and their contribution ranges from 20.8% to 25.2%, which denotes more contribution than O⋯H/H⋯O contacts ranging from 9.4% to 11.5%. In 1, C–H⋯π is evidenced from the wings appearing in the decomposed fingerprint plot for C⋯H/H⋯C contacts. In 2 and 3-form-I, the contributions of F⋯O/O⋯F contacts are also observed with contributions of 0.8% and 0.3%, respectively. The highest contribution for C⋯F/F⋯C contacts is 6.1% in 2 amongst all the compounds. Similarly, as the most favourable centrosymmetric dimers incorporating C–H⋯F interactions have been found in 3-form-I (A & B) and II, the highest contribution for F⋯H/H⋯F contacts has been availed by the polymorphs with contributions of 25.2%, 24.3%, and 23.3%. Moreover, 3-form-I (A & B) and II reveal the existence of F⋯F contacts with contributions of 0.2%, 1.4%, and 1.3%, respectively, whereas there are no such contacts found in compounds 1 and 2. The percentage contribution of the contacts in all compounds is shown in a bar graph (Fig. 8).
 |
| | Fig. 7 2D fingerprint plots for all contacts observed in all compounds. | |
 |
| | Fig. 8 Percentage contributions of various contacts to the Hirshfeld surface area in all four compounds. | |
Analysis from quantum theory of atoms in molecules. Topological analysis based on the electron density distribution has been performed for C–H⋯F interactions observed in these compounds. The existence of (3, −1) bond critical points (BCPs) and associated bond paths characterizes these contacts at their crystal geometry. The results are tabulated in Table 5 for C–H⋯F interactions only, and the topological parameters of other interactions in the selected motifs are listed in Table S4. It is of interest to study the order of the strength of C–H⋯F bonds in terms of the hybridization of the carbon atom attached to hydrogen and the fluorine atoms. We have categorized these interactions into four classes in terms of the hybridization of the carbon atom, i.e., C(sp3)–H⋯F–C(sp3), C(sp2)–H⋯F–C(sp3), C(sp3)–H⋯F–C(sp2), and C(sp2)–H⋯F–C(sp2). A total of seven motifs featuring C(sp3)–H⋯F–C(sp3) interactions (Fig. 9a, c, d, f, j, m and p) have been observed in which the hydrogen atom bonded to an sp3-hybridized carbon acts as a donor to the fluorine atom, which is also attached to an sp3 hybridized carbon. The electron density at the bond critical point (BCP) varies from 0.0297 to 0.0622 e Å−3 corresponding to the bond dissociation energy ranging from 3.5578 to 8.4336 kJ mol−1. The highest electron density at the BCP of C(sp3)–H⋯F–C(sp3) interactions is exhibited by motif I in 1 (Fig. 9a). The corresponding Laplacian of charge density (∇2(ρ)) ranges from 0.4056 to 0.8377 e Å−5.
Table 5 Analysis of topological parameters of intermolecular C–H⋯F interactions in compounds 1, 2, and 3-form-I & II
| Compound |
Motif |
ρ(r) (e Å−3) |
∇2(ρ) (e Å−5) |
V(r) (a.u.) |
G(r) (a.u.) |
H(r) (a.u.) |
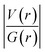
|
De (kJ mol−1) |
| C(sp3)−H⋯F−C(sp3) |
| 1 |
I (C) |
0.0622 |
0.8377 |
−0.0064 |
0.0075 |
0.0011 |
0.8533 |
8.4336 |
| (D) |
0.0412 |
0.5673 |
−0.0041 |
0.0050 |
0.0009 |
0.8200 |
5.4029 |
| V (F) |
0.0500 |
0.6421 |
−0.0049 |
0.0058 |
0.0009 |
0.8448 |
6.4575 |
| 2 |
III (G) |
0.0297 |
0.4056 |
−0.0027 |
0.0035 |
0.0008 |
0.7714 |
3.5578 |
| 3-Form-I |
I (K) |
0.0399 |
0.5480 |
−0.0040 |
0.0048 |
0.0008 |
0.8333 |
5.2710 |
| (L) |
0.0358 |
0.4973 |
−0.0035 |
0.0043 |
0.0008 |
0.8140 |
4.6120 |
| VII (S) |
0.0608 |
0.7677 |
−0.0060 |
0.0070 |
0.0010 |
0.8571 |
7.9065 |
| 3-Form-II |
I (Z1) |
0.0460 |
0.6301 |
−0.0046 |
0.0056 |
0.0010 |
0.8214 |
6.0619 |
| (Z2) |
0.0399 |
0.5552 |
−0.0040 |
0.0049 |
0.0009 |
0.8163 |
5.2710 |
| V (Z5) |
0.0514 |
0.6445 |
−0.0049 |
0.0058 |
0.0009 |
0.8448 |
6.4571 |
| C(sp2)−H⋯F−C(sp3) |
| 3-Form-I |
II (N) |
0.0277 |
0.3790 |
−0.0025 |
0.0032 |
0.0007 |
0.7813 |
3.2945 |
| C(sp3)−H⋯F−C(sp2) |
| 2 |
IV (I) |
0.0453 |
0.6276 |
−0.0046 |
0.0055 |
0.0009 |
0.8364 |
6.0619 |
| 3-Form-I |
III (O) |
0.0203 |
0.2945 |
−0.0018 |
0.0024 |
0.0006 |
0.7500 |
2.3722 |
| VIII (T) |
0.0514 |
0.6494 |
−0.0050 |
0.0058 |
0.0008 |
0.8621 |
6.5890 |
| (V) |
0.0426 |
0.5504 |
−0.0041 |
0.0049 |
0.0008 |
0.8367 |
5.4029 |
| IX (W) |
0.0331 |
0.4659 |
−0.0033 |
0.0041 |
0.0008 |
0.8049 |
4.3487 |
| (X) |
0.0399 |
0.5287 |
−0.0039 |
0.0047 |
0.0008 |
0.8298 |
5.1391 |
| 3-Form-II |
III (Z3) |
0.0507 |
0.6397 |
−0.0049 |
0.0058 |
0.0009 |
0.8448 |
6.4571 |
| C(sp2)−H⋯F−C(sp2) |
| 1 |
III (E) |
0.0608 |
1.3639 |
−0.0067 |
0.0104 |
0.0037 |
0.6442 |
8.8292 |
| 3-Form-I |
VI (Q) |
0.0541 |
0.7097 |
−0.0053 |
0.0063 |
0.0010 |
0.8413 |
6.9842 |
| (R) |
0.0575 |
0.7556 |
−0.0056 |
0.0067 |
0.0011 |
0.8358 |
7.3794 |
| 3-Form-II |
IV (Z4) |
0.0575 |
0.7749 |
−0.0058 |
0.0069 |
0.0011 |
0.8406 |
7.6432 |
 |
| | Fig. 9 Distribution of bond critical points (BCP) and bond paths of intermolecular interactions in the molecular pairs involving C–H⋯F interactions in (a–c) 1, (d and e) 2, (f–l) 3-form-I, and (m–p) 3-form-II, respectively. | |
Next, C(sp2)–H⋯F–C(sp3) interactions are present in motif II of 3-form-I only (Fig. 9g). The electron density at the BCP of C2–H2⋯F4 interactions (motif II in 3-form-I) has a value of 0.0277 e Å−3, while the corresponding Laplacian and dissociation energy values are 0.3790 e Å−5 and 3.2945 kJ mol−1, respectively. These values are considerably lower in magnitude compared to those of the above-mentioned C(sp3)–H⋯F–C(sp3) interactions.
Subsequently, the focus is on the other two classes of C–H⋯F interactions (C(sp3)–H⋯F–C(sp2) and C(sp2)–H⋯F–C(sp2)) involving the fluorine atom attached to the sp2 carbon atom of the aryl ring. To analyse the topological parameters for C(sp3)–H⋯F–C(sp2) interactions, five motifs have been considered (Fig. 9e, h, k, l and n). The electron density at the BCP ranges from a minimum of 0.0203 e Å−3 (C10–H10A⋯F1 in 3-form-I, Fig. 9h) to a maximum of 0.0514 e Å−3 (C19–H19B⋯F1 in 3-form-I, Fig. 9k). These interactions reveal the corresponding Laplacian of electron density in the range of 0.2945 to 0.6494 e Å−5 and dissociation energy between 2.3722 kJ mol−1 and 6.5890 kJ mol−1.
Lastly, there are only three motifs which are stabilized by C(sp2)–H⋯F–C(sp2) interactions (Fig. 9b, i and o). The electron density lies in a comparatively elevated range of 0.0541 e Å−3 (C15–H15⋯F1 in 3-form-I, Fig. 9i) to 0.0608 e Å−3 (C3–H3⋯F1 in 1, Fig. 9b) corresponding to stronger interactions than those of other three classes. The dissociation energy values, ranging from 6.9842 kJ mol−1 to 8.8292 kJ mol−1, also suggest a relatively strong bond strength. Moreover, the Laplacian of electron density has the highest value of 1.3639 e Å−5 and the lowest value of 0.7097 e Å−5.
A comparison of all the topological parameters and their detailed analysis suggest that the presence of C(sp3)−H⋯F−C(sp3) and C(sp2)−H⋯F−C(sp2) interactions acquire higher stabilization in comparison to the C(sp3)−H⋯F−C(sp2) and C(sp2)−H⋯F−C(sp3) interactions. Similar observations have also been made in the previous study done by Panini et al.10 Moreover, the range of the ρ value, the positive value of the Laplacian of ρ[∇2(ρ) > 0] and 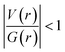 at BCPs confirm the bonding nature of these hydrogen bonds and establish them to be closed shell interactions. Furthermore, the variation of the electron density at the BCP and the Laplacian of electron density with the bond path length of H⋯F contacts is shown (Fig. S10).
at BCPs confirm the bonding nature of these hydrogen bonds and establish them to be closed shell interactions. Furthermore, the variation of the electron density at the BCP and the Laplacian of electron density with the bond path length of H⋯F contacts is shown (Fig. S10).
Conclusions
The present investigation depicts the role of weak C–H⋯F interactions in addition to strong H-bonds. The pertinent contribution of organic fluorine attached to two different hybridized carbon atoms (sp3/sp2) has been analysed in terms of their reoccurrence in structural motifs in the presence of strong hydrogen bonds. The intermolecular interactions co-exist in the crystal packing and play the role of secondary interactions in the formation of different supramolecular structures. The combined contribution of different interactions towards the formation of different supramolecular motifs was quantified from PIXEL. Topological parameters characterized via the QTAIM method establish that individual interactions that constitute these supramolecular motifs are closed-shell interactions. Henceforth, it would be of interest to study the impact of the hybridization of carbon atoms (sp3/sp2) with a greater number of fluorine atoms on the aryl framework towards the overall stabilization of the crystal structures. Future studies will be directed towards such investigations.
Conflicts of interest
The authors declare no conflict of interest.
Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ce00838g.
CCDC 2483272–2483275 contain the supplementary crystallographic data for this paper.43a–d
Acknowledgements
PD gratefully acknowledges the Department of Science and Technology (Govt. of India) for DST-Inspire fellowship (DST/INSPIRE Fellowship/2019/IF190666). The authors thank IISER Bhopal for research facilities and infrastructure.
References
- D. Chopra and T. N. Guru Row, Role of organic fluorine in crystal engineering, CrystEngComm, 2011, 13, 2175–2186 RSC.
- M. Inoue, Y. Sumii and N. Shibata, Contribution of Organofluorine Compounds to Pharmaceuticals, ACS Omega, 2020, 5, 10633–10640 CrossRef CAS PubMed.
- P. Panini and D. Chopra, Experimental and Theoretical Characterization of Short H-Bonds with Organic Fluorine in Molecular Crystals, Cryst. Growth Des., 2014, 14(7), 3155–3168 CrossRef CAS.
- H. J. Schneider, Hydrogen bonds with fluorine. Studies in solution, in gas phase and by computations, conflicting conclusions from crystallographic analyses, Chem. Sci., 2012, 3, 1381–1394 Search PubMed.
- G. R. Desiraju, A Bond by Any Other Name, Angew. Chem., Int. Ed., 2011, 50, 52–59 CrossRef CAS PubMed.
- C. Dalvit, C. Invernizzi and A. Vulpetti, Fluorine as a Hydrogen-Bond Acceptor: Experimental Evidence and Computational Calculations, Chem. – Eur. J., 2014, 20, 11058–11068 Search PubMed.
- M. R. Sarkar and D. Chopra, Evolution in the Understanding of Noncovalent Interactions Involving Fluorine: From Inception to Maturity to Properties, Cryst. Growth Des., 2024, 24, 8674–8687 Search PubMed.
- L. Singla, H. R. Yadav and A. R. Choudhury, Structural and Computational Analysis of Organic Fluorine-Mediated Interactions in Controlling the Crystal Packing of Tetrafluorinated Secondary Amides in the Presence of Weak C–H···O=C Hydrogen Bonds, Cryst. Growth Des., 2022, 22, 1604–1622 Search PubMed.
- P. Das, G. B. D. Rao, S. Bhandary, K. Mandal, S. K. Seth and D. Chopra, Quantitative Investigation into the Role of Intermolecular Interactions in Crystalline Fluorinated Triazoles, Cryst. Growth Des., 2024, 24, 703–721 CrossRef CAS.
- P. Panini, R. G. Gonnade and D. Chopra, Experimental and computational analysis of supramolecular motifs involving Csp2(aromatic)–F and CF3 groups in organic solids, New J. Chem., 2016, 40, 4981–5001 Search PubMed.
- P. Panini and D. Chopra, Experimental and computational insights into the nature of weak intermolecular interactions in trifluoromethyl-substituted isomeric crystalline N-methyl-N-phenylbenzamides, New J. Chem., 2015, 39, 8720–8738 RSC.
- C. R. Pitts, M. A. Siegler and T. Lectka, Intermolecular Aliphatic C–F···H–C Interaction in the Presence of “Stronger” Hydrogen Bond Acceptors: Crystallographic, Computational, and IR Studies, J. Org. Chem., 2017, 82, 3996–4000 Search PubMed.
- D. Dey and D. Chopra, Evaluation of the Role of Isostructurality in Fluorinated Phenyl Benzoates, Cryst. Growth Des., 2017, 17, 5117–5128 CrossRef CAS.
- D. Dey, S. K. Seth, T. P. Mohan and D. Chopra, Quantitative analysis of intermolecular interactions in crystalline substituted triazoles, J. Mol. Struct., 2023, 1273, 134380 CrossRef CAS.
- A. Hasija and D. Chopra, Concomitant dimorphism in diphenyl (3, 4–difluorophenyl) phosphoramidates, Acta Crystallogr., Sect. A: Found. Adv., 2017, 73, C782–C782 Search PubMed.
- A. Hasija, R. Bhowal and D. Chopra, Quantitative investigation of weak intermolecular interactions of –F and –CF3 substituted in situ cryocrystallized benzaldehydes, Cryst. Growth Des., 2020, 20, 7921–7933 CrossRef CAS.
- P. Panini and D. Chopra, Role of intermolecular interactions involving organic fluorine in trifluoromethylated benzanilides, CrystEngComm, 2014, 14, 1972–1989 Search PubMed.
- P. Panini and D. Chopra, Quantitative insights into energy contributions of intermolecular interactions in fluorine and trifluoromethyl substituted isomeric N-phenylacetamides and N-methylbenzamides, CrystEngComm, 2013, 15, 3711–3733 Search PubMed.
- P. Dey, R. Bhowal, S. K. Seth and D. Chopra, Understanding the Nature and Energetics of C–H···F Interactions in Crystalline Propanamides, Cryst. Growth Des., 2025, 25, 4263–4282 CrossRef CAS.
- Bruker, APEX2, Bruker AXS Inc., Madison, Winconsin, USA, 2012 Search PubMed.
- SAINT and SADABS, Bruker AXS Inc., Madison, Wisconsin, USA, 2008 Search PubMed.
- G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- L. J. Farrugia, WinGX and ORTEP for windows: an update, J. Appl. Crystallogr., 2012, 45, 8 Search PubMed.
- A. I. Spek, Single-crystal structure validation with the program PLATON, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- M. Nardelli, PARST95-an update to PARST: a system of Fortran routines for calculating molecular structure parameters from the results of crystal structure analyses, J. Appl. Crystallogr., 1995, 28, 659 Search PubMed.
- A. Gavezzotti, Efficient computer modelling of organic materials. The atom–atom, Coulomb–London–Pauli (AA–CLP) model for intermolecular electrostatic–polarization, dispersion and repulsion energies, New J. Chem., 2011, 35, 1360 Search PubMed.
- A. Gavezzoti, Calculation of intermolecular interaction energies by direct numerical integration over electron densities. 1. Electrostatic and polarization energies in molecular crystals, J. Phys. Chem. B, 2002, 106, 4145–4154 CrossRef.
- A. Gavezzoti, Calculation of intermolecular interaction energies by direct numerical integration over electron densities. 2. An improved polarization model and the evaluation of dispersion and repulsion energies, J. Phys. Chem. B, 2003, 107, 2344–2353 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- M. A. Spackman and J. J. McKinnon, Fingerprinting intermolecular interactions in molecular crystals, CrystEngComm, 2002, 4, 378–392 RSC.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces, Chem. Commun., 2007, 3214–3816 Search PubMed.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolf, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, Crystal Explorer: a program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystal, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Novel tools for visualizing and exploring intermolecular interactions in molecular crystals, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed.
- A. L. Rohl, M. Moret, W. Kaminsky, K. Claborn, J. J. Mckinnon and B. Kahr, Hirshfeld surfaces identify inadequacies in computations of intermolecular interactions in crystals: pentamorphic 1,8–dihydroxyanthraquinone, Cryst. Growth Des., 2008, 8, 4517–4525 CrossRef CAS.
- P. Das, S. Islam and S. K. Seth, Structural elucidation and interpretation of 2D–3D supramolecular assemblies featuring lone-pair⋯π interaction in two Cu(II)–PDA complexes: experimental and computational assessment, J. Mol. Struct., 2024, 1308, 138088 Search PubMed.
- N. Abad, P. Das, J. T. Mague, A. Y. A. Alzahrani, E. M. Essassi, S. K. Seth and Y. Ramli, Exploring the solid-state structural aspects of novel hybrid quinoxaline based isoxazole compound: Inputs from experimental and computational studies, J. Mol. Struct., 2025, 1324, 140963 Search PubMed.
- S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures, J. Chem. Theory Comput., 2018, 14, 1614–1623 Search PubMed.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 Search PubMed.
- T. A. Keith, AIMAll (Version 13.05.06), TK Gristmill Software, Overland Park KS, USA, 2013 Search PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- C. Lepetit and M. L. Kahn, QTAIM and ELF topological analyses of zinc-amido complexes, Res. Chem. Intermed., 2021, 47, 377–395 CrossRef CAS.
-
(a) CCDC 2483272: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc1kp;
(b) CCDC 2483273: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc1lq;
(c) CCDC 2483274: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc1mr;
(d) CCDC 2483275: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc1ns.
Footnote |
| † Dedicated to Professor Resnati, celebrating a career in fluorine and noncovalent chemistry on the occasion of his 70th birthday. |
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b,
Dona Mathewb,
Arnab Duttab,
Kanu Priya Dhabhaib,
Saikat Kumar Seth
b,
Dona Mathewb,
Arnab Duttab,
Kanu Priya Dhabhaib,
Saikat Kumar Seth *a and
Deepak Chopra
*a and
Deepak Chopra *b
*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)
1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)
1)![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866
866![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517
517![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Only one conformer is considered for further discussion. Details of the X-ray measurements and crystal parameters of all the compounds are given in Table 1. The weak intermolecular interactions are considered based on the following criteria: the sum of the vdW's radii + 0.2 Å and directionality ≥110° and are further validated via QTAIM calculations.
1 ratio. Only one conformer is considered for further discussion. Details of the X-ray measurements and crystal parameters of all the compounds are given in Table 1. The weak intermolecular interactions are considered based on the following criteria: the sum of the vdW's radii + 0.2 Å and directionality ≥110° and are further validated via QTAIM calculations.


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions (Fig. 3d) possesses 55% electrostatic energy contribution in the total energy, whereas motif IV stabilized by C(sp3)–H⋯F–C(sp2) interactions is dispersive in nature with 60% contribution (Fig. 3e).
C interactions (Fig. 3d) possesses 55% electrostatic energy contribution in the total energy, whereas motif IV stabilized by C(sp3)–H⋯F–C(sp2) interactions is dispersive in nature with 60% contribution (Fig. 3e).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z = 2 and Z′ = 1.
with Z = 2 and Z′ = 1.
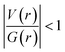 at BCPs confirm the bonding nature of these hydrogen bonds and establish them to be closed shell interactions. Furthermore, the variation of the electron density at the BCP and the Laplacian of electron density with the bond path length of H⋯F contacts is shown (Fig. S10).
at BCPs confirm the bonding nature of these hydrogen bonds and establish them to be closed shell interactions. Furthermore, the variation of the electron density at the BCP and the Laplacian of electron density with the bond path length of H⋯F contacts is shown (Fig. S10).