Phage probes couple to DNA relaxation dynamics to reveal universal behavior across scales and regimes

Abstract

Microrheology has become an indispensable tool for measuring the dynamics of macromolecular systems. Yet, its ability to characterize polymer dynamics across spatiotemporal scales, which vary among polymers and concentration regimes, is limited by the selection of probe morphologies and sizes. Here, we introduce semiflexible M13 phage as a powerful microrheological probe able to circumvent these constraints to robustly capture the dynamics of polymeric solutions across decades of concentrations, sizes, and ionic conditions. We show that phage mobility directly couples to the relaxation dynamics of DNA solutions spanning from semidilute to entangled regimes with ionic strengths varying by four orders of magnitude. Phage mobility metrics across a broad range of timescales collapse onto universal master curves that are unexpectedly insensitive to ionic strength and exhibit robust crossovers from semidilute to entangled regime scaling, not captured by current theoretical models. Our results open the door to the use of phage probes to elucidate the complex dynamics of systems exhibiting a spectrum of thermal and active relaxation processes.

---

Introduction

The mechanical properties of biopolymers dictate diverse biological functions, from the formation of condensates¹ to the mechanics of the cytoskeleton² to DNA replication and transcription.³ Microrheology^4–6 has become an indispensable tool for measuring the rheology of biological polymer systems⁷ because of the much smaller sample volumes required as compared to bulk rheology techniques, as well as the ability to probe local heterogeneities^8,9 that are ubiquitous in these systems. In a typical microrheology experiment, the mechanical properties of a system are extracted from the thermal (passive) or driven motion of a probe particle using the generalized Stokes–Einstein relation (GSER),^4,6 which assumes that the medium is a homogeneous continuum. Satisfying this assumption, however, is rarely trivial in biopolymer systems, which typically have a range of length scales above and below which the system dynamics are expected to differ.

Coupling of the motion of microrheological probes to the system dynamics, therefore, depends strongly on the length scales characterizing the medium. In dilute and semidilute polymer solutions, these length scales include the radius of gyration R_g and correlation length or mesh size ξ. In entangled solutions, more typical of the conditions encountered in biological systems (e.g., chromosomal DNA, mucus, cytoskeleton, extracellular matrix), the dominant length scales predicted by the reptation model include the diameter d_T of the nominal tube confining the transverse fluctuations of each polymer, and the polymer length between entanglements l_e with the surrounding chains that form the confining tube. In its simplest implementation, microrheology experiments use spherical probe particles with diameters that are greater than all of these length scales to satisfy the continuum assumption necessary for the GSER.⁶ This criterion is necessary but often not sufficient for probing the continuum limit in biopolymer systems.¹⁰ Moreover, characterizing the mechanics of biopolymer fluids across a broad range of polymer concentrations renders selecting the probe size non-trivial, because not only do the intrinsic length scales depend on polymer concentration but the dominant length scale changes from one regime to the other. Finally, the ratio of the probe size to the characteristic length scale of the system, which changes with concentration for a single probe size, is often a determining factor used for interpreting microrheological properties.^11–13

In contrast to spheres, anisotropic probes such as oblates, rods, and filaments have at least two intrinsic length scales, and thereby offer the opportunity to probe the mechanics of complex fluids across different length scales.¹⁴ For example, rods diffuse faster than spheres of similar hydrodynamic radius in polymer solutions,¹⁵ melts,¹⁶ and hydrogels,¹⁷ confirming that they couple differently to the relaxation dynamics of the surrounding polymer matrix. For probes of modest anisotropy (aspect ratios AR = L/d ≈ 10, where L and d are respectively the contour length and diameter of the probe), the macroscopic moduli of entangled polymer solutions can be determined using rotational diffusion microrheology performed on particle-tracking^18,19 or scattering²⁰ data. However, this approach relies on the coupling of rotational and translational motion, which breaks down for systems that exhibit dynamic arrest such as concentrated and entangled polymer solutions and gels. This decoupling limits the ability to determine viscoelastic moduli from rotational diffusion.²¹ Moreover, like conventional microrheology, the rotational diffusion framework requires the probe length scales to be greater than the solution mesh size.

Probes of higher aspect ratio (AR > 10) exhibit more diverse mechanisms for transport through polymer solutions owing to their semiflexibility, which allows for bending, reptation, constraint release, and contour length fluctuations.^22–25 The relative importance of these relaxation mechanisms depends largely on the degree of confinement of the probe, determined by the intrinsic length scales of the system, e.g., the tube diameter and entanglement length. For example, the transverse bending modes of semiflexible carbon nanotubes have been shown to probe the macroscopic rheology of concentrated polymer solutions.^14,26 However, these studies have largely focused on highly entangled systems in which the contribution of bending modes to the dynamics is amplified due to the extreme confinement of the nanotubes. The ability of high-aspect-ratio semiflexible probes to detect rheological properties of semidilute and marginally entangled systems, however, remains unclear.

Regardless of the probe geometry, another important consideration in microrheology experiments is the interaction between the probe and surrounding polymers. Accurate interpretation of microrheological data relies on the assumption that the probe and polymers only interact via steric interactions without adsorption or repulsion. This requirement often necessitates passivating microsphere probes with neutral polymers such as bovine serum albumin (BSA) or polyethylene glycol (PEG). Carbon nanotubes also need to be treated with a surfactant or wrapped with DNA oligos to reduce their hydrophobicity.^14,26,27

Bacteriophage particles are attractive alternatives to these synthetic probes that circumvent many of the issues described above. M13 Bacteriophage, or phage, are short (length ∼1 μm, width ∼10 nm) anisotropic viruses, without a distinct geometrical head or tail structure common to other types of phage; their persistence length is comparable to their length, such that they behave as semiflexible filaments.²⁸ They are uniform in shape and size and are selected by evolution for low non-specific binding,²⁹ so are naturally well-suited for use as microrheology probes. Their high degree of monodispersity, simple coupling to photostable dyes, natively non-interacting surface chemistry, and commercial availability further render phage particles facile and versatile probes. Previous studies of phage diffusion in semidilute solutions of the synthetic polyelectrolyte poly(styrene sulfonate) (PSS)³⁰ demonstrated that phage transport provides rich information about the local structure and mechanics of unentangled polyelectrolyte solutions. However, the applicability of these initial findings to different concentration regimes, solvent conditions, and polymer properties, which all contribute to the distinct intrinsic length and time scales of polymeric solutions, remains unknown.

Here, we demonstrate the use of phage particles as powerful microrheology probes that strongly couple to the relaxation dynamics of the surrounding medium across the dilute, semidilute, and entangled regimes. We use DNA as our model system and investigate the effect of polymer concentration and ionic strength on the dynamics of solutions that span two decades in polymer concentration, encompassing the elusive crossover regime from semidilute to entangled regimes, as well as four decades in salt concentration. We establish that phage particles can accurately capture the diversity of relaxation dynamics of DNA solutions across this broad parameter space.

Our motivation for using DNA solutions stems from the decades of work showing that DNA is a model system for testing concepts in polymer physics^31–37 due to its uniform dispersity and relative thinness compared to synthetic polymers. Specifically, its Kuhn length (l_b ≃ 100 nm) is ∼50 × larger than its width (w ≃ 2 nm), whereas synthetic polymers generally have more isotropic monomers (i.e., b ∼ w). This anisotropy leads to a much larger ratio of excluded volume (EV) to occupied volume (OV), given by EV/OV ≈ b²w/bw² ≈ b/w for athermal solvents.^38,39 This distinction allows DNA solutions with volume fractions as low as 1% to be highly entangled, whereas synthetic polymers often must be in the melt phase to have a similar degree of entanglements. Thus, DNA uniquely enables access to the elusive and poorly understood crossover regions that connect dilute to semidilute to entangled regimes. However, the polyelectrolyte nature of DNA, with charge density −5.9e nm⁻¹ that is comparable to that of synthetic polyelectrolytes (e.g., −6.5e nm⁻¹ for PSS), complicates the ability to use DNA to test predictions for neutral polymers from, e.g., the reptation model. To address this issue, it is common practice to supplement standard DNA buffers with 10 mM NaCl, which has been shown to effectively screen the negative backbone of the DNA and render its behavior similar to that of a neutral polymer with an effective diameter set by the screening length scale.^40,41 As the salt concentration is lowered below 10 mM NaCl, the persistence length l_p = l_b/2 has been shown to increase dramatically,^42–44 which is expected to lead to an increase in the radius of gyration via the scaling relation R_g ∼ L^νl_p^1−ν, where L is the contour length and ν is the Flory exponent that ranges from 1/3 to ∼3/5 depending on the solvent quality. At the same time, previous studies reported only a modest decrease in the dilute limit R_g of DNA as salt concentration was lowered from 10 mM to 2 mM NaCl.⁴⁵ Despite numerous theoretical and experimental investigations on the topic, the effect of ionic strength on DNA persistence length and coil size remains controversial.^41–43

Using the phage probe microrheology platform, we discover that DNA dynamics are surprisingly robust to variations in ionic conditions across all polymer concentration regimes, which arises from the insensitivity of the DNA coil size to varying ionic strength. Specifically, the normalized phage diffusion coefficients along with those of individual DNA molecules collapse onto a single master curve as a function of DNA concentration for all ionic strengths, with no rescaling or assumptions. Importantly, our findings are counter to expectations based on previous studies that have reported an increase in persistence length with decreasing ionic strength over the ionic strengths we investigate.^41,43,44 The power-law scaling describing this universal behavior is indicative of neutral flexible polymers in good solvent conditions, and is distinct from results and predictions for spherical particles and rigid rods. Moreover, the length and time scales that govern the scaling relations align remarkably well with predicted values for the DNA tube diameter and radius of gyration in the entangled and semidilute regimes, with clear crossover behavior between the two regimes. By scaling the DNA concentration by the size-dependent overlap concentration, we show that solutions of ∼20-fold longer DNA molecules collapse onto the same universal curves, further demonstrating that the phage dynamics are controlled by the characteristic length scales of the DNA solutions and accurately report the relaxation dynamics of polymeric solutions across orders of magnitude in governing spatiotemporal scales. We expect our results to open the door to the use of biological phage particles as facile and versatile microrheological probes to access and elucidate the complex dynamics of polymeric systems that exhibit a diversity of thermal and active relaxation processes, including, e.g., intensely investigated cytoskeleton-based active matter, bio-synthetic composites, biomolecular condensates, and topological polymer blends. Our results also have important implications for the rapidly growing field of designer DNA-based soft materials.

Results

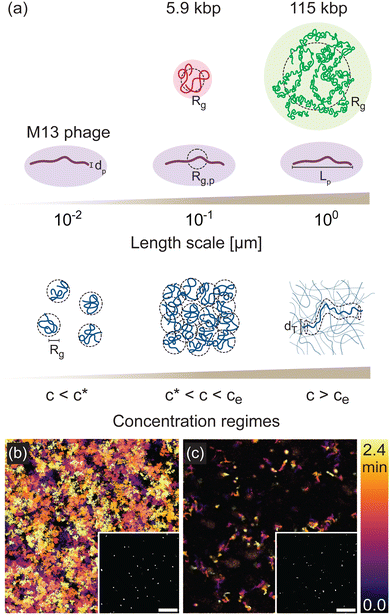
To demonstrate the multiscale rheological measurements afforded by phage, and the ability to parse distinct contributions to relaxation dynamics in systems of widely varying spatiotemporal scales, we track the motion of M13 phage suspended in solutions of DNA of two sizes, 5.9 kilobasepair (kbp) and 115 kbp. M13 phage have contour length L_p ≃ 900 nm, diameter d_p ≃ 10 nm, and radius of gyration R_g,p ≃ 160 nm. The phage radius of gyration is comparable to the radius of gyration of the 5.9 kbp DNA (R_g ≃ 180 nm) and the phage length is comparable to the radius of gyration of the 115 kbp DNA (R_g ≃ 960 nm) (Fig. 1(a)). By varying the DNA concentration from c ≃ 200 μg mL⁻¹ to 12 mg mL⁻¹ we capture the dynamics from below the overlap concentration c* to above the nominal entanglement concentration c_e, accessing the dilute, semidilute, and entangled regimes. These variations in concentration also enable characteristic lengths of the DNA solutions, such as the radius of gyration R_g and tube diameter d_T, to be systematically tuned across a broad range that is bounded below and above by the phage diameter d_p and length L_p, ensuring accurate measurements across a wide range of relative length scales of probe and polymer.

Fig. 1 Phage as a model system for investigating polymer dynamics. (a) Schematic of length scales and concentration regimes in systems of M13 phage (purple) embedded in solutions of 5.9 kilobasepair (kbp) (red) and 115 kbp (green) DNA at concentrations that span from dilute (c < c*) to semidilute (c* < c < c_e) to entangled (c > c_e). Dashed circles denote the radius of gyration R_g of each construct. The governing length scales in each concentration regime, including R_g and the reptation tube diameter d_T, are shown. (b) and (c) Temporal color maps, which colorize the features in each 84 μm × 84 μm frame (examples shown in insets) according to the time t at which the frame is captured, as indicated by the color scale (t = 0 [black] to t = 2.4 min [orange]), depict fast and slow motion of phage in 5.9 kbp DNA solutions with concentrations (b) c = 1 mg mL⁻¹ and (c) c = 12 mg mL⁻¹, respectively. Insets are fluorescence micrographs of fluorescently labeled M13 phage in the corresponding DNA solution. The scale bars are 20 μm.

To determine phage mobility, we image fluorescently-labeled phage embedded at trace concentrations in the DNA solutions (Fig. 1(b) and (c) insets) and track their center-of-mass trajectories over time (Fig. 1(b) and (c)). The temporal color maps in Fig. 1(b) and (c) clearly depict the slowing of phage motion with increasing DNA concentration. At low concentration (Fig. 1(b)), there are more and longer trajectories than are seen for higher concentration (Fig. 1(c)), demonstrating that phage can easily enter and leave the field-of-view and move further distances in the same time frame.

Phage transport in DNA solutions is insensitive to ionic strength

From the center-of-mass trajectories, we determine the mean-squared displacements (MSDs) 〈Δx²〉 of the phage as a function of lag time Δt for DNA solutions of varying concentrations that span from dilute (c < c*) to semidilute unentangled (c* < c < c_e) to entangled (c > c_e), maintaining fixed ionic strength (Fig. 2(a)). The MSDs generally increase in magnitude with decreasing DNA concentration, as expected given the decreased density of steric hindrances to phage motion and consistent with the visual depiction in Fig. 1(b) and (c). For all DNA concentrations, phage particles exhibit normal Brownian diffusion (dashed lines), i.e., 〈Δx²〉 ∼ Δt^α with α = 1, above a critical lag time τ_c. This crossover time for the onset of diffusive (α = 1) scaling depends on DNA concentration, which we discuss in later sections.

Fig. 2 Dynamics of phage in DNA solutions depend on DNA concentration but are insensitive to ionic strength. Mean-squared displacement 〈Δx²〉 as a function of lag time Δt for phage in solutions of 5.9 kbp DNA of (a) various DNA concentrations (listed in mg mL⁻¹) at I = 10⁻³ mM, and (b) various ionic strengths (listed in legend) at a fixed DNA concentration of c = 4.5 mg mL⁻¹. Dashed lines represent linear scaling 〈Δx²〉 ∼ Δt indicative of normal diffusion. Arrows indicate the crossover time τ_c at which MSDs appear to transition from subdiffusive to diffusive behavior.

We next examine the impact of increasing ionic strength on phage mobility. Because DNA is a polyelectrolyte with a charge density of −5.9e nm⁻¹, theoretical models predict that l_p and thus R_g should decrease with increasing ionic strength, as discussed in the Introduction.^41,44,46 We thus expected that increasing the ionic strength would increase phage mobility due to the reduction in overlap and entanglements of surrounding DNA at a given concentration. Surprisingly, we find that phage MSDs measured in DNA solutions with ionic strengths that span four decades (I = 1 μM to 10 mM NaCl) while maintaining good solvent conditions,^40,47 are indistinguishable and collapse onto a single master curve (Fig. 2(b)). This insensitivity is particularly surprising because the range of salt concentrations we examine (I≤ 10 mM) resides in the region over which the most dramatic impact of salt on l_p is observed.^42–44 It is also at odds with the significant effect reported for phage diffusivity in solutions of synthetic PSS, with similar R_g (∼192 nm) and charge density (−6.5e nm⁻¹) to that of the 5.9 kbp DNA we examine here.³⁰

Phage diffusion exhibits flexible polymer scaling behavior that mirrors DNA dynamics

To understand the counterintuitive robustness of phage mobility to variations in ionic strength, coupled with the strong dependence on DNA concentration, we examine the phage diffusion coefficients D in the long Δt limit, where α = 1, as a function of DNA concentration for all ionic conditions. The concentration dependence of D/D₀, where D₀ is the phage diffusivity in the absence of DNA, collapses to a single master curve for all ionic conditions and concentrations, showing once again the insensitivity to ionic strength (Fig. 3(a)). Moreover, the data exhibit power-law scaling D ∼ c^−b, with two distinct scaling exponents for concentrations below and above c_c ≃ 3 mg mL⁻¹, respectively. The low-concentration scaling exponent aligns with the Rouse model prediction b ≃ 0.5 for semidilute solutions of unentangled flexible polymers, while the high concentration scaling follows the reptation model prediction b ≃ 1.75 for solutions of entangled flexible polymers.^48,49

Fig. 3 Long-time diffusion of phage particles uniquely couple to DNA relaxation dynamics. (a) Phage diffusivity D, normalized by the corresponding diffusivity in the absence of DNA D₀, as a function of DNA concentration c for I = 10⁻³ (blue closed circles), 10⁰ (red closed diamonds), and 10¹ (orange closed right-pointing triangles). Open grey symbols are diffusion coefficients for 5.9 kbp DNA molecules reproduced from ref. 47 (semidilute) and measured in this study (entangled) for various DNA concentrations and buffer conditions: I = 10⁻³ mM (circles), TE (I ≈ 10¹) (up-pointing triangles), and TE10 (I ≈ 20) (down-pointing triangles). Inset: Data in (a) shown as D/D₀ × (c/c*)^0.5 as a function of c/c*. (b) Concentration dependence of D/D₀ of spherical particles of various diameters (listed in legend) embedded in the same DNA solutions examined in (a) with ionic strengths listed. (c) Phage diffusivity D (data shown in (a)) normalized by Broersma's prediction for a rigid rod D_Br.^50–52 Dashed, solid, and dotted lines represent scalings for dilute, semidilute, and entangled regimes, respectively. Shaded regions indicate the range of reported DNA entanglement concentrations c_e.

These scaling relations are also in agreement with the scaling of diffusion coefficients of tracer DNA embedded in solutions both below and above the reported critical entanglement concentration.⁴⁷ To more closely compare diffusion coefficients of phage and DNA in the same 5.9 kbp DNA solutions, we include in Fig. 3(a) the 5.9 kbp data from ref. 47, which span the semidilute regime, and DNA diffusion coefficients measured here for two higher concentrations that lie within the entangled regime. Indeed, we observe excellent quantitative agreement between the diffusion coefficients of phage and DNA across both regimes. Moreover, the data shown from ref. 47 were measured in aqueous solutions of TE10 buffer with I ≈ 20 mM, whereas our phage experiments are carried out in deionized water with various NaCl concentrations (I ≈ 10⁻³ mM to 10 mM). The close correspondence between these data suggests that both ionic strength and buffer conditions have surprisingly minimal impact on DNA mobility. To confirm this conjecture, we also perform DNA diffusion measurements for solutions suspended in TE (no added salt, I ≈ 10 mM) and deionized water (I ≈ 10⁻³ mM), which show that the diffusivity is statistically indistinguishable across buffer and ionic conditions. These comparisons are strong evidence that phage directly couple to the DNA relaxation dynamics.

The excellent and quantitative agreement between the diffusion of phage and DNA in similar solutions is surprising given the semiflexible nature of phage compared to flexible DNA. Moreover, the observed scaling relations agree with predictions for neutral flexible polymers rather than polyelectrolytes, in which the predicted scalings depend on the ionic strength of the solution. While this agreement may be expected for the highest salt concentration of I = 10 mM NaCl, which is in the limit of saturating charge screening,^40,47 the extension of this agreement down to 1 μM is counter to expectations. The insensitivity of the scaling to ionic strength and the agreement with neutral polymer predictions together suggest that DNA may be much more weakly dependent on ionic conditions than predicted and as compared to synthetic polyelectrolytes of similar charge density.³⁰

For both phage and DNA, the transition from the semidilute regime (in which the diffusion coefficients scale as c^−0.5) to the entangled regime (c^−1.75) is obvious as shown by rescaling D/D₀ by (c/c*)^0.5 (see inset to Fig. 3(a)). The crossover concentration at which entanglement dynamics emerge occurs at c_c ≈ 3 mg mL⁻¹≈ 10c*, which is at the high end of the range of entanglement concentrations c_e ≈ (4–10)c* reported for DNA.^31,47,53

Deviations from colloid and rigid rod diffusion reflect unique coupling to DNA dynamics

Importantly, this coupling of phage mobility to the dynamics of the DNA is not seen for diffusion measurements of spherical particles with diameters both above and below R_g and R_g,p, which exhibit strikingly different concentration dependence compared to phage scaling. Spheres of diameter 0.6 μm and 1 μm (>R_g) display two power-law regimes, similar to phage, but with much larger scaling exponents of b ≃ 1.3 and b ≃ 3.9 in the low and high concentration regimes (Fig. 3(b)). Considering the Stokes relation D ∼ η⁻¹, the measured scalings align with predictions for the viscosity scaling with concentration η ∼ c^b for the Rouse model b ≃ 1.3⁵⁴ and reptation model b ≃ 3.9 for neutral flexible polymers in good solvent conditions.⁵⁵ To determine whether smaller particles (<R_g) are able to couple to the DNA relaxations, we also examine D/D₀ for 0.1 μm diameter particles. The scaling exponent of D/D₀ in the low concentration regime is less than 1.3 but greater than the value of 0.5 predicted for Rouse dynamics, indicating that the small spherical probes are unable to accurately detect bulk viscosity but are similarly unable to capture DNA relaxation dynamics. These results indicate that spherical particles of large enough size probe the continuum limit behavior of the solutions, described by bulk viscosity, but are unable to couple to the polymer relaxation dynamics regardless of their size relative to the intrinsic length scales of the system. By contrast, phage particles appear to strongly couple to the relaxation dynamics of the DNA in the solutions, providing a richer picture of the physics of the system.

While the scaling of diffusion with concentration is markedly different for spheres compared to phage particles, the insensitivity to ionic conditions is maintained. Namely, D/D₀ for spheres in DNA solutions at all ionic strengths I collapse to a single master curve. This finding, as well as the scalings agreeing with predictions for the bulk viscosity of solutions of neutral flexible polymers, corroborate the lack of polyelectrolyte characteristics that DNA solutions manifest. Two notable takeaways from these results are: (1) phage appear to uniquely couple to the dynamics of the DNA solution in ways not recapitulated with simple spherical probes; and (2) the dynamics of semidilute and entangled DNA are surprisingly robust to varying ionic conditions in the range of ionic strengths where dependence is expected to be strongest.⁴⁶

The difference between diffusion of phage and spherical probes may be expected given that phage are more closely modeled as rigid or semiflexible rods rather than spheres, so we may expect the scaling of diffusion with concentration to more closely align with predictions for rod-like particles. To investigate this possibility, we compare D to the predicted diffusion coefficient for rigid rods as described by the Broersma (Br) model.^50–52 This model predicts that rod diffusivity is inversely proportional to the bulk solution viscosity η following D_Br= (k_BT/3πηL)[δ − 1/2(γ_‖ + γ_⊥)], where k_BT is the thermal energy and L is the rod length. The parameter δ accounts for the contribution from the finite rod length, while γ_‖ and γ_⊥ correct for anisotropic drag based on the geometry of rod as described in the Supplementary Materials. In our analysis, D_Br is calculated at each concentration using the bulk viscosity η determined from the large spherical probe diffusion measurements via the Stokes–Einstein equation D = k_BT/6πηR, where R is the radius of the sphere. For minimally overlapping conditions (c ≤ 0.25 mg mL⁻¹), the normalized diffusivity is D/D_Br ≈ 1 (Fig. 3(c)), indicating that phage diffusion is dictated by the solution viscosity, consistent with a previously reported value D_fd = 1.04 D_Br for the fd virus,⁵⁶ a filamentous bacteriophage similar to M13 in dimensions and properties, commonly used in studies of rod-like particle dynamics. As DNA concentration increases, however, D becomes increasingly larger than D_Br, and D/D_Br exhibits power-law scaling D/D_Br ∼ c^β with β ≃ 0.8 and β ≃ 2.15 for concentrations above and below ∼c_e, respectively. To understand the power-law scaling of D/D_Br, we note that D_Br ∼ η⁻¹. From our spherical probe results, we have established that η ∼ c^1.3 for c < c_e and η ∼ c^3.9 for c > c_e. Combining these scaling relations with phage diffusivity scaling D ∼ c^−0.5 and D ∼ c^−1.75 from Fig. 3(a), we obtain D/D_Br ∼ D × η ∼ c^0.8 and D/D_Br ∼ c^2.15 for c < c_e and c > c_e, respectively, which is exactly what we observe in Fig. 3(c) for all ionic conditions. This deviation from D_Br suggests that, while the combined scaling of D and D_Br aligns with experimental data, the phage diffusion is not solely dependent on the bulk viscosity of the DNA solution, as would be the case if D followed D_Br precisely, but is also strongly influenced by the relaxation dynamics of the polymer matrix.¹²

This behavior also aligns with results from mode coupling theory (MCT), which predicts that the particle diffusivity in polymer solutions is not only dictated by the bulk viscosity but also by non-hydrodynamic force contributions that are associated with particle-polymer coupling and structural relaxations.^30,57 These contributions become increasingly important as the polymer concentration is increased.^57,58 Thus, the increase in D/D_Br with concentration further supports the physical picture that phage dynamics are strongly coupled to the dynamics of the surrounding DNA. Further, MCT also predicts that the non-hydrodynamic contributions to diffusivity become more important as the ratio of polymer size to probe size increases.⁵⁷ We hypothesize that these contributions are more important for phage than for spherical particles because the polymer length scales greatly exceed the phage diameter.

Phage dynamics are sensitive to DNA coil size

We have conjectured that the insensitivity of phage dynamics to varying ionic conditions arises because the DNA coils do not swell or compact appreciably with decreasing or increasing ionic strength I, at odds with expectations for polyelectrolyte solutions.^30,59 An alternative explanation is that the phage dynamics are insensitive to changes in DNA coil size that arise from varying I. However, if we assume reported dependences of R_g of DNA on I⁵⁹ and scale the concentration by c*(R_g(I)), we observe no data collapse (ESI,† Fig. S1). To further investigate the effect of DNA coil size on the dynamics of phage particles, we measure phage diffusion in solutions of 115 kbp DNA at similar ionic conditions and concentrations as the 5.9 kbp DNA. This ∼20 × longer DNA has a ∼5 × larger radius of gyration R_g ≃ 960 nm, which is comparable to the length of the phage (L_p ≃ 900 nm). We find that D/D₀ for 115 kbp DNA is lower than for the 5.9 kbp case for all concentrations (Fig. 4(a)). This reduction becomes more pronounced with increasing polymer concentration, indicating that the phage dynamics are indeed sensitive to changes in DNA coil size. Specifically, for semidilute and entangled polymer solutions, D is predicted to scale as D ∼ L^−0.5 and D ∼ L⁻², respectively.⁶⁰ Thus, if the phage were coupled to the DNA dynamics then we expect D/D₀ in 115 kbp solutions to be lower than for 5.9 kbp solutions, and this difference should become larger in the entangled regime, exactly as we see in Fig. 4(a).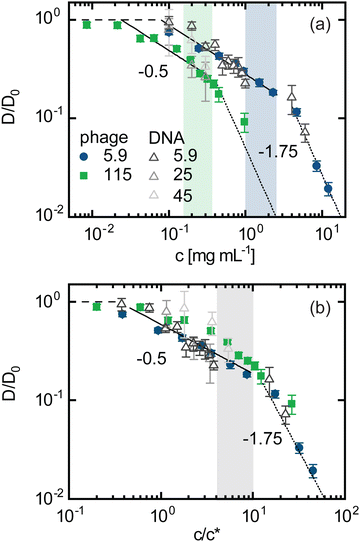

Fig. 4 Phage dynamics depend on DNA size following ideal neutral polymer coil statistics. Normalized diffusion coefficients for phage probes (closed symbols) and DNA (open triangles) as a function of (a) DNA concentration c and (b) c scaled by the overlap concentration c* in solutions of DNA of lengths (kbp): 5.9 (blue circles, dark grey triangles), 25 (grey triangles), 45 (light grey triangles), 115 (green squares). Phage data shown is for I = 10⁻³ mM, whereas DNA data is for TE10 (I ≈ 20 mM). DNA data for c ≲ 1 mg mL⁻¹ is from ref. 47. Dotted lines represent Rouse and reptation model scaling predictions, respectively, for neutral flexible polymers. Shaded regions indicate the range of expected DNA entanglement concentrations c_e.

Despite the lower values of D/D₀ for the longer DNA, the scaling with concentration is remarkably similar to that of the shorter DNA, with both exhibiting scalings indicative of Rouse (b ≃ 0.5) and reptation (b ≃ 1.75) dynamics below and above a critical concentration, respectively.⁶¹ The critical crossover concentration c_c is lower for the larger DNA, as we may expect if the crossover is dictated by the critical entanglement concentration c_e, represented as the green and blue shaded regions in Fig. 4(a). We also show data from ref.47 for the diffusion of 25 kbp and 45 kbp DNA in their respective solutions, suspended in TE10, which fall between the phage data for 115 kbp and 5.9 kbp DNA, further demonstrating the effect of coil size on the diffusivity of both phage and DNA.

To determine if the differences shown in Fig. 4(a) arise solely from the DNA size, we scale the concentration by the corresponding overlap concentration c*, which scales as LR_g⁻³∼R_g⁻¹, assuming ideal coil statistics expected in the semidilute overlapping regime.^47,62 Upon this rescaling, the phage data for both DNA lengths and the DNA diffusion data for three different DNA lengths⁴⁷ approximately collapse to a single curve with a crossover between b ≃ 0.5 and b ≃ 1.75 scaling occurring near ∼c_e (Fig. 4(b)). This collapse demonstrates that the degree of polymer overlap, which is set by both DNA size and concentration, does, in fact, dictate the phage dynamics, corroborating the physical picture that the DNA coil size and thus c/c* do not appreciably change with ionic conditions over the range I = 10⁻³–10¹ mM. This result is counterintuitive considering the expectation that in this regime the negative charge of the DNA backbone is not substantially screened by counterions. We note that the data for the larger DNA (≳ 25 kbp) exhibits slightly more curvature in the nominal semidilute unentangled regime (below c_e) compared to the shorter constructs (Fig. 4(b)), which may be due to the reported extended crossover regime near c* over which excluded volume interactions are increasingly screened.⁶³ Because EV effects are more substantial for longer chains, we expect this extended crossover to more strongly affect the longer DNA, in line with our observations.

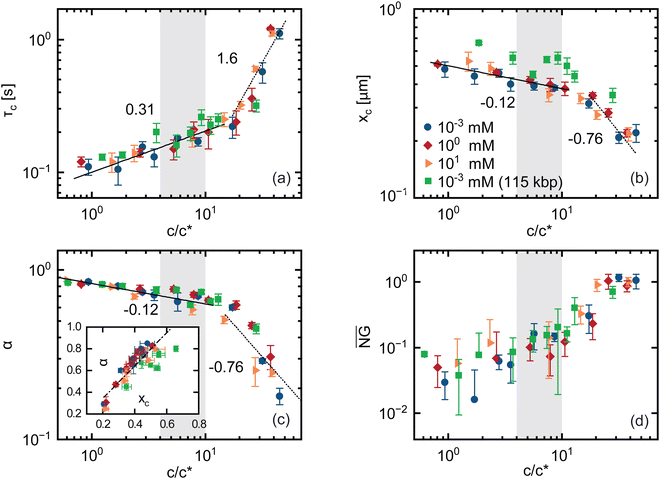
Phage exhibit concentration-dependent subdiffusive dynamics governed by the intrinsic length scales of DNA solutions

The previous sections focused on the long lag-time behavior, where phage exhibit normal diffusion (α = 1), with a concentration dependence that appears to be dictated by the diffusivity of the DNA solutions. The mean-square displacements in Fig. 2, however, show that below a critical lag time τ_c phage particles exhibit subdiffusive dynamics (α < 1), indicative of strongly confined and heterogeneous transport. The extent to which α deviates from 1 and the timescale over which subdiffusion occurs (i.e., τ_c) both appear to increase substantially with increasing DNA concentration, while remaining insensitive to ionic strength (Fig. 2(a) and 5(c)). To quantify the concentration dependence of these features of the data, we evaluate the power-law scalings of MSD/Δt versus Δt (Fig. S3, ESI†) in the short-time (Δt < τ_c) and long-time (Δt > τ_c) regimes in which the scaling exponents are approximately constant. For normal diffusion MSD/Δt is independent of Δt, whereas subdiffusion manifests as negative power-law scaling (i.e., α − 1). We identify τ_c as the time at which the power-law fit lines for these two regimes intersect, and determine α from the fit of the short time (Δt < τ_c) data.

Fig. 5 Intrinsic DNA length scales dictate the subdiffusive dynamics of phage. (a) Crossover time τ_c, (b) crossover length x_c, (c) anomalous exponent α, and (d) time-averaged non-Gaussian parameter as a function of scaled concentration c/c* of 5.9 kbp and 115 kbp DNA for various ionic strengths listed in the legend in (b). Solid and dashed lines in (a)–(c) represent scaling relations predicted by Rouse and reptation models, respectively: (a) τ_R ∼ c^0.31 and τ_D ∼ c^1.6, (b), (c) R₀ ∼ c^−0.12 and d_T ∼ c^−0.76. Inset in (c) shows the anomalous exponent α as a function of crossover length x_c, with the dashed-dotted line representing linear scaling. Shaded regions indicate the range of expected DNA entanglement concentrations c_e.

Similar to the long-time diffusion coefficient (Fig. 3(a)), the anomalous exponent α displays two distinct regimes of concentration dependence for all ionic strengths and both DNA sizes. The rate of decrease of α with increasing c is greater at higher DNA concentrations (Fig. 5(c)). Similarly, the crossover time τ_c displays two regimes, with power-law dependence on DNA concentration τ_c ∼ c^x with different x values above and below ∼c_c (Fig. 5(a)). Below c_c, x aligns well with the predicted concentration scaling for the Rouse time for flexible polymers in good solvent conditions τ_R ∼ c^0.31, where τ_R is the longest relaxation timescale for overlapping unentangled polymers.⁶⁴ Above c_c, the scaling becomes steeper and more closely aligns with the predicted scaling for the disengagement time for flexible polymers in good solvent conditions τ_D ∼ c^1.6, which sets the longest relaxation time for entangled polymers.⁴⁹ Importantly, both exponents correspond to predictions for flexible neutral polymers in good solvent conditions, consistent with the scalings observed for long-time phage dynamics, but not necessarily intuitive given the semiflexible nature of phage and the expected polyelectrolyte nature of DNA. We also note that the crossover between the two scaling regimes is less well-defined for 115 kbp DNA compared to shorter DNA (Fig. 5(a)), which may be due to the extended dilute-semidilute crossover behavior that we discuss above.⁶³

To further connect the phage behavior to that of the DNA, we compare our measured τ_c values with predicted values for τ_R and τ_D for the 5.9 kbp DNA solution. Using the prediction for the Rouse time in semidilute solutions in good solvent conditions, τ_R ≃ τ_R1(c/c*)^0.31 where τ_R1 ≃ 2NR_g²/π²D₀, we compute τ_R ≃ 100 ms for c ≃ c*, which increases to τ_R ≃ 163 ms at c ≃ 5c*. These values are in remarkable agreement with the corresponding values of τ_c≃ 110 ms and τ_c≃ 160 ms measured at ∼ c* and ∼ 5c*, respectively (Fig. 5(a)).

For concentrations above c_e we expect the disengagement time to dictate the relaxation dynamics of the DNA, so τ_c should more closely align with τ_D rather than τ_R if the phage is truly coupling to the DNA dynamics. To determine τ_D for different concentrations c > c_c, we use the predicted expression τ_D ≃ 3Zτ_R, where Z ≃ (c/c_e)^1.3 is the entanglement density.^31,47,61 Taking c_e ≈ c_c, we compute values of τ_D ≃ 1.3 s for c ≃ 3.2 mg mL⁻¹ ≃ c_e and τ_D ≃ 3.5 s for c ≃ 9 mg mL⁻¹ ≃ 2.8c_e. The corresponding τ_c values at these concentrations are ∼360 ms and ∼740 ms, as shown in Fig. 5(a), which are both ∼ 4-fold lower than their predicted τ_D value. However, for entangled polymers with a modest number of entanglements, i.e., Z < 10, as is the case for most of the concentration range we examine, contour length fluctuations (CLF) are predicted to substantially speed up the disengagement process, thereby lowering τ_D, according to the predicted expression

where X is a constant of order unity.⁶¹ This relation yields τ_D,CLF values that match τ_c for c_c and 2.8c_c considering an X value of ∼ 0.5, close to unity, for both concentrations. This notable agreement between τ_D,CLF and τ_c suggests that contour length fluctuations indeed play an important role in the relaxation of entangled DNA, as previously reported,⁶⁵ and that phage particles are sensitive to this higher order relaxation mechanism that alters the classical disengagement time.

To independently verify the predicted relaxation timescales, we perform bulk rheology measurements on the 5.9 kbp DNA solutions at concentrations corresponding to ∼5c* and ∼34c* (Fig. S2, ESI†). The frequency-dependent elastic and viscous moduli G′(ω) and G′′(ω) show clear crossovers at frequencies ω_c from a low-frequency terminal flow regime to viscoelastic behavior, with the higher concentration data exhibiting a clear elastic plateau indicative of entanglements, in agreement with our phage data. From ω_c we determine the longest relaxation time of the solutions via τ ≃ 2π/ω_c, yielding τ ≃ 150 ms and τ ≃ 900 ms for the ∼5c* and ∼34c* solutions, respectively. These values are in close agreement with τ_c ≃ 160 ms and τ_c ≃ 750 ms measured in our phage experiments (Fig. 5(a)), as well as the predicted values of τ_R ≃ 163 ms and τ_D,CLF ≃ 740 ms for the 5c* and 34c* solutions, respectively.

The excellent agreement between τ_c and the governing relaxation timescales of the DNA solutions corroborate that phage dynamics are strongly coupled to the DNA solution in the short time subdiffusive regime as well as the long time diffusive regime. To further connect short-time phage dynamics to characteristics of the DNA solution, we evaluate the length scale x_c at which the crossover from subdiffusive transport to normal diffusion occurs, which we define as x_c ≃ 〈Δx(Δt = τ_c)²〉^1/2. For unentangled polymers, the characteristic correlation length scale is typically taken to be the polymer coil size , which sets the length scale over which polymer motion becomes decorrelated from its starting point, and is predicted to scale with concentration as R₀ ≃ c^−0.12 in good solvent conditions. Below R₀, non-continuum heterogeneities and chain connectivity lead to anomalous diffusion.¹⁰ For entangled polymers, the relevant length scale that controls confinement and continuum-limit behavior is the tube diameter d_T, which is predicted to scale with concentration as d_T ∼ c^−0.76.⁶⁴ These scaling relations closely align with the scaling of x_c with concentration below and above c_c, respectively (Fig. 5(b)). This agreement is further validation that the universal crossover between scaling regimes that we observe for all of our metrics is indicative of the crossover from semidilute unentangled behavior to the entanglement regime.

To quantitatively verify the connection between x_c and governing length scales of the DNA solutions, we compare predicted values for R₀ and d_T in the low and high concentration limits to our measured x_c values. We compute R₀ ≃ 650 nm from the known dilute limit R_g value, which is comparable to x_c ≃ 510 nm measured at the lowest concentration (∼0.8c*). To determine d_T we estimate from our rheology measurements a plateau modulus G⁰ ≃ 10 Pa at c≃ 34c*, from which we compute the polymer length between entanglements l_e and the corresponding tube diameter d_T ≈ (l_kl_e)^1/2via the predicted expression G₀ ≃ (cN_A/M_w)(k_BTL/l_e) where M_w is the polymer molecular weight. These relations yield d_T ≃ 224 nm for c ≃ 34c* which is in notable agreement with x_c ≃ 210 nm measured at the same concentration (Fig. 5(b)).

Interestingly, the subdiffusive exponent α appears to follow similar scaling with concentration as x_c in both semidilute and entangled regimes (Fig. 5(c)). Indeed, α scales approximately linearly with x_c (Fig. 5(c) inset), demonstrating that the phage diffusion is controlled by the structural properties of the surrounding matrix of DNA chains. This linkage further indicates that the length scale over which the phage motion becomes decorrelated from its initial position, reflected by x_c, and the degree to which its motion is constrained beyond normal diffusion, indicated by α, are coupled, suggesting that it is the degree of confinement that dictates subdiffusive behavior.

The robust coupling between the short-time diffusive behavior of phage and predicted scalings and values for Rouse and reptation dynamics of DNA, below and above c_c, is consistent with the two-regime scaling behavior and crossover concentration we observe for the long-time diffusivity (Fig. 3(a)). This universal agreement provides unequivocal evidence of the strong coupling of phage dynamics to the relaxation of the surrounding DNA solution, and demonstrates that this coupling persists across decades of length and timescales (ESI,† Fig. S5). Table 1 summarizes our experimental scaling relations as well as predicted scaling laws for neutral polymers and polyelectrolytes in semidilute and entangled regimes.

Table 1 Scaling predictions for neutral polymers in good solvent, polyelectrolytes at no salt, and microrheology in semidilute and entangled regimes. The errors for microrheology data represent the uncertainties obtained by fitting data across all salt concentrations

	Neutral in good solvent		Polyelectrolytes (no salt)		Microrheology
	Semidilute	Entangled	Semidilute	Entangled	Semidilute	Entangled
Values marked with * represent data from spherical probes rather than phage.
Polymer size	R ∼ c^−0.12	d T ∼ c^−0.76	R ∼ c^−0.25	d T ∼ c^−0.5	R∼c^−0.12±0.01	d T ∼ c^−0.65±0.05
Relaxation time	τ chain ∼ c^0.31	τ rep ∼ c^1.6	τ chain ∼ c^−0.5	τ rep ∼ c^0	∼c^0.28±0.01	∼c^1.71±0.07
Polymer viscosity	∼c^1.3	∼c^3.9	∼c^0.5	∼c^1.5	∼c^1.24±0.01 *	∼c^3.84±0.03*
Diffusion coefficient	∼c^−0.54	∼c^−1.75	∼c^0	∼c^−0.5	∼c^−0.55±0.01	∼c^−1.79±0.04

---

Anomalous subdiffusion is often an indicator of non-Gaussian and/or non-ergodic transport, which has been shown to arise from structural heterogeneity,^66,67 hopping between transient cages,^68,69 anisotropic hydrodynamic interactions,^30,70,71 or viscoelasticity of the matrix.^72–74 To determine the extent to which these mechanisms play a role in the short-time anomalous subdiffusion, we evaluate the time-averaged non-Gaussian parameter and ergodicity breaking parameter (EB) (see ESI† for details). We find that is close to zero for c < c_c, which is expected for normal diffusion. However, for c > c_c, exhibits signatures of anomalous transport, monotonically increasing with concentration until reaching a concentration-independent plateau value of for c ≳ 3c_c (Fig. 5(d)). Likewise, EB at long times (Δt ≳ τ_c) adheres to Brownian expectations, increasing linearly with lag time, but deviates from this ergodic behavior at short times (Δt ≲ τ_c) (Fig. S6, ESI†), in line with the transition from normal diffusion to anomalous subdiffusion that we observe at τ_c (Fig. 2).

Closer inspection of the probability distribution of displacements (PDD) shows that phage exhibit non-Gaussian PDDs at short lag times but revert to Gaussian PDDs at longer lag times (Fig. S7, ESI†), similar to the behavior of EB. The extended tails of the PDDs, which become more pronounced with increasing confinement, suggest contributions from caging and hopping dynamics and/or differences in the extent of coupling of the dynamics of the anisotropic phage to those of the DNA as they move along or normal to their main axis. Moreover, our bulk rheology experiments confirm the increased viscoelasticity of DNA solutions, evidenced by a pronounced frequency-independent plateau modulus G⁰ (Fig. S2, ESI†). Thus, our experiments and analysis collectively indicate that the short-time anomalous diffusion of the phage particles is intricately linked with transient non-Gaussian and non-ergodic dynamics as well as the concentration-dependent viscoelasticity of the medium. Notably, the crossover time for the onset of these transient phenomena aligns closely with the time at which phage dynamics transition to diffusive behavior, underscoring a strong correlation between the microscopic mechanisms of motion and the mesoscopic observation of diffusion.

Discussion

We have introduced and comprehensively validated the use of phage particles as microrheological probes capable of coupling to the relaxation dynamics of the surrounding medium over decades of lengths and timescales and across multiple regimes of behavior. Specifically, we measured the transport of M13 phage particles in solutions of overlapping and entangled DNA chains of varying concentrations, ionic conditions and sizes, spanning multiple decades of these parameters to capture dynamics in the nominal semidilute unentangled and entangled regimes as well as the crossover region that connects them. We show that the dynamics of phage in DNA solutions are remarkably coupled to the dynamics of the DNA in both unentangled and entangled regimes, an effect not observed with simple spherical probe particles or expected for rigid rod probes. This robust coupling provides a powerful tool for microrheological investigations that are not limited to Stokes–Einstein approximations, including polymeric systems that span multiple regimes and spatiotemporal scales.

Using this approach, we discover that the dynamics of semidilute and entangled DNA molecules, captured by the diffusive behavior of the phage particles, are surprisingly robust to changing ionic conditions. The DNA molecules behave as neutral polymers, at odds with conventional thought, across four decades of salt concentration and two decades of DNA concentration. We reveal a universal collapse of the data across all ionic strengths and DNA concentrations, with no rescaling necessary, for numerous metrics including mean-squared displacements, diffusion coefficients and anomalous scaling exponents. We further show that scaling of the dynamics with concentration for solutions of ∼20-fold longer DNA also collapse to the same master curve when the concentration is rescaled by the overlap concentration, which is set by the coil size. These observations collectively demonstrate that the phage dynamics are sensitive probes of the dynamics of the surrounding DNA chains that are governed by the degree of polymer overlap and entanglements, which are distinctly insensitive to ionic strength.

To shed light on this insensitivity, we first note that the effect of ionic strength on the flexibility and conformation of DNA remains a topic of debate.⁷⁵ The presence of counterions screens the negatively charged backbone of the DNA in solution, which is expected to decrease its persistence length and effective diameter. While empirical results and theories mostly agree that the effect of monovalent ions saturates above I ≈ 20 mM, reaching a minimum value of l_p ≃ 40 nm, the effects of electrostatics on l_p at lower ionic strengths, such as those we examine here, remain controversial.^{41,43,44,75–78} Importantly, most of these studies model DNA as a wormlike chain, which is accurate for DNA below ∼20l_p (≃1 μm) where the semiflexible nature of the chain cannot be ignored. Larger DNA, by contrast, follow predictions that more closely align with the freely-jointed chain model with self-avoidance.^31,32,40,53 Moreover, previous studies have also reported effective diameters of d_I ≃ 15–24 nm for DNA in the presence of 10 mM NaCl, which increases to ∼ 30–56 nm at 1 mM NaCl.⁴¹ Different theoretical models and experiments, however, provide different d_I values and functional dependences on I.^41,78 Beyond these conflicting reports, there is also a lack of consensus regarding how varying l_p and d_I values alter the DNA coil size.^79,80 For example, prior tracking measurements of tracer 115 kbp DNA showed only a 4% increase in coil size at 2 mM NaCl compared to 10 mM, which is substantially lower than the ∼20% increase predicted from the scaling l_p ∼ I^−0.3 and the freely jointed chain model expression R₀ ≃ (2Ll_p)^1/2.^44,45 Similarly, our results provide strong evidence that monovalent salt has little influence on the coil size of DNA of sufficient length (⪅38l_p) for I ≤ 10 mM, at odds with predictions for polyelectrolytes as well as results for synthetic polymers of similar charge density.³⁰

We also reveal universal crossover behavior, apparent in numerous independent metrics, from dynamics that align with predictions for semidilute unentangled polymers to those that follow reptation model predictions. This crossover behavior is not predicted by current theoretical models that lack the ability to span different regimes to describe the functional form of the crossover. There is also a dearth of experimental data spanning this crossover regime due to the limited number of synthetic polymer systems capable of accessing both regimes in solution. DNA is an exception to this rule: it can form a high number of entanglements at very low volume fractions (<1%) while also maintaining an ample semidilute unentangled regime (c* < c < c_e). Capturing dynamics across this broad range requires probes with multiple intrinsic length scales that can couple to the different concentration-dependent length scales of the system, a non-trivial requirement that we have demonstrated here using M13 phage.

Our work opens the door to the use of phage particles as sensitive microrheological probes to measure the dynamics of a wide range of macromolecular systems with different intrinsic spatiotemporal scales. This approach will prove particularly invaluable to understanding complex heterogeneous systems that have a spectrum of relevant lengths and timescales, such as blends, composites, and crowded systems, as well as active matter and out-of-equilibrium systems. More generally, we expect phage to be broadly applicable for studying biological and polymeric systems that are generally neutral or negatively charged in solution. Key considerations for their use are ensuring that the ionic strength, pH, and other environmental conditions of the system do not cause aggregation or adsorption of the phage to the surrounding material. We also anticipate that the intriguing results we present will spark new theoretical endeavors to describe the crossover behavior between semidilute and entangled polymer regimes, and understand the distinct insensitivity to ionic strength that semidilute and concentrated solutions of DNA exhibit.

Materials and methods

DNA synthesis and characterization

Double-stranded DNA, of lengths 5.9 kilobasepairs (kbp) and 115 kbp, are prepared via replication of pYES2 plasmid constructs and k16 BAC constructs in Escherichia coli followed by extraction, purification, and concentrating as described previously.^47,81,82 Briefly, to replicate DNA, Escherichia coli cultures containing the plasmid or BAC clone are grown from frozen glycerol stocks. To extract the DNA, cells are lysed via treatment with an alkaline solution. The extracted DNA is then renatured via treatment with an acidic detergent, precipitated in isopropanol, washed with 70% ethanol, and resuspended in nanopure deionized water (DI). To convert DNA to linear topology, 5.9 kbp and 115 kbp constructs are treated with restriction endonucleases BamHI-HF (New England BioLabs) and M1UI-HF (New England BioLabs), respectively, which cut the circular DNA constructs at a single site. To purify the DNA, the solutions are treated with RNase A (to remove contaminating RNA) followed by phenol–chloroform extraction and dialysis (to remove proteins). Purity is assessed using UV absorbance and gel electrophoresis.⁸¹ The purified DNA solutions are concentrated via rotary vacuum concentration to achieve final concentrations of c = 12.6 mg mL⁻¹ for the 5.9 kbp DNA and c = 2.4 mg mL⁻¹ for the 115 kbp DNA, as determined via gel electrophoresis and band intensity analysis, employing Life Technologies E-Gel Imager and Gel Quant Express software. DNA is stored at 4 °C for up to 6 months.

The radius of gyration R_g of the linear 5.9 kbp and 115 kbp constructs were previously determined to be, respectively, R_g ≃ 180 nm and R_g ≃ 960 nm by measuring the diffusion coefficients at infinite dilution and using the Stokes–Einstein relation and relationships between the hydrodynamic radius and radius of gyration.^40,81 The corresponding overlap concentrations c* = M_w/(4/3)πR_g³N_A where M_w is the polymer molecular weight and N_A is Avogadro's number, are c* ≃ 266 μg mL⁻¹ and c*≃ 35 μg mL⁻¹.

Phage particles

Filamentous M13 phage were purchased from Guild Biosciences. M13 has a contour length of L_p= 880–950 nm and its persistence length is reported to be 1250 < l_p < 2000 nm.^83–85 The resulting contour to persistence length ratio of 0.44 < L_p/l_p < 0.72 identifies M13 as a semiflexible rod. Alexa Fluor 555 N-hydroxysuccinimide (NHS) ester (Thermo Fisher Scientific; peak excitation and emission at 488 and 532 nm, respectively) was used to fluorescently label the phage.^30,71 Labeled phage carry a weak negative charge, ranging from −22 ± 2 mV at 10⁻³ mM to −11 ± 1 mV at 100 mM NaCl solutions, respectively.³⁰ This negative charge minimizes non-specific interactions with DNA, ensuring that their motion reflects the intrinsic rheological properties of the system rather than probe-specific interactions.

Sample preparation

Glass vials were cleaned by soaking in a concentrated solution of potassium hydroxide in isopropanol overnight. The vials were then rinsed multiple times with Millipore water and dried in an oven. 5.9 and 116 kbp DNA solutions at various concentrations and ionic strengths I were prepared by dilution from stock solutions. Millipore DI water was used to prepare near salt-free solutions with an approximate ionic strength of I = 10⁻³ mM, resulting from DNA counterions and dissociated water ions.^86,87 DNA solutions with ionic strengths of 10⁰ and 10¹ mM were prepared using sodium chloride (NaCl) buffer solutions. Prior studies found that the addition of monovalent ions at low concentrations does not significantly influence the pH of the solutions.⁴⁴ The DNA samples were placed on a horizontal mixer at 10 rpm overnight until completely homogenized and were stored at 4 °C for later use. Phage at a volume fraction of ∼4 × 10⁻⁴ were added to the DNA solutions prior to imaging.

Fluorescence imaging

Air-tight capillary chambers for imaging were fabricated using 10 × 10 mm² coverslips attached to a 46 × 60 mm² glass microscope slide (Epredia; no. 1 Thickness). The DNA solutions were centrifuged at 2000 rpm for 30 s prior to injection to ensure bubble-free solutions. Approximately 15 μL of the sample solution was pipetted into the chamber and sealed with UV-curable epoxy (Norland Products). A TCS SP8 confocal mounted on an inverted DMi8 microscope equipped with a 63× (N.A. 1.4) oil immersion objective (Leica Microsystems) was used to image the phage in DNA solutions. For each sample, four series of at least 2500 images at different locations in the x−y plane were collected at 28 frames per second (36 ms exposure time). To avoid surface effects, the images were captured in the bulk solution at least 20 μm away from the surface of the microscope slide.

Particle tracking

Particle trajectories over time were obtained using particle tracking algorithms.⁸⁸ Phage are imaged as diffraction-limited spots because their size is smaller than the optical resolution, allowing only the calculation of the translational diffusivity. From the trajectories, we calculated the one-dimensional ensemble averaged mean-squared displacement (MSD) 〈Δx²〉 = 〈(x(t + Δt) − x(t))²〉, where x(t) is the x-position of the particle's center of mass at time t, Δt is the lag time, and 〈…〉 denotes an average over time. Each MSD data point was obtained by averaging over at least 5 × 10³ time steps. The long-time diffusion coefficient D was determined from a fit to 〈Δx²〉 = 2DΔt^α at large lag-times where α = 1, indicating normal diffusion. At shorter lag times, α < 1 indicates subdiffusive motion. To characterize the deviation of particle distributions from Gaussian behavior, we calculated the non-Gaussian parameter NG = [〈Δx⁴〉/3 〈Δx²〉²] − 1. To demonstrate that the 1D MSDs accurately capture the 3D Brownian motion of the phage particles, we perform principal component analysis and evaluate particle displacements along the major and minor axes of motion (Fig. S8, ESI†). We find that the distributions of particle displacements along each axis are indistinguishable from one another and the anisotropy of displacements is similar for spheres and phage (Fig. S8, ESI†).

DNA diffusion measurements

To measure the diffusivity of DNA, we labeled 5.9 kbp DNA with covalent dye Mirus-488 (Mirus Bio) at a dye : basepair ratio 1 : 5 using the Mirus Label IT Nucleic Acid Labeling Kit (Mirus Bio) following manufacturer protocols. We added 2 μg mL⁻¹ of fluorescently-labeled DNA to the same DNA solutions using the same sample preparation methods as used in phage diffusion experiments. We performed measurements in DNA solutions suspended in Millipore DI water (I = 10⁻³ mM), TE (10 mM Tris–HCl (pH 8), 1 mM EDTA, I = 10 mM), and TE10 (TE buffer supplemented with 10 mM NaCl, I = 20 mM). We imaged fluorescently-labeled DNA embedded in each solution with an Olympus IX73 epifluorescence microscope with an X-Cite LED light source, 488-nm emission and 535-nm detection filter cube, and a 60×, 1.2NA objective (Olympus). We captured time series of images of 1440 × 1920 pixels (87.3 μm × 116 μm) at a frame rate of 10 fps for 10 s using a Hamamatsu Orca-Flash 2.8. Diffusion coefficients were determined from MSDs using similar particle-tracking algorithms as described above and in ref. 89. Each data point shown is an average over 3 samples and >10 videos per sample with error bars representing one standard deviation.

Data availability

Data are available upon reasonable request from the corresponding author (JCC).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JCC thanks the National Science Foundation (CBET-2004652, CBET-2113769) and Welch Foundation (E-1869) for support. RMRA thanks the Air Force Office of Scientific Research (FA9550-21-1-0361) and National Institutes of Health (2R15GM123420-02) for support. CC thanks the National Science Foundation (CHE-2050846) for support. All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.†

References

1. W. Pönisch, T. C. Michaels and C. A. Weber, Biophys. J., 2023, 122, 197–214.
2. A. F. Pegoraro, P. Janmey and D. A. Weitz, Cold Spring Harbor Perspect. Biol., 2017, 9, a022038.
3. J. R. Lange and B. Fabry, Exp. Cell Res., 2013, 319, 2418–2423.
4. T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282.
5. F. C. MacKintosh and C. F. Schmidt, Curr. Opin. Colloid Interface Sci., 1999, 4, 300–307.
6. T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438.
7. D. Weihs, T. G. Mason and M. A. Teitell, Biophys. J., 2006, 91, 4296–4305.
8. M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud’homme, M. Beck and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061506.
9. S. N. Ricketts, J. L. Ross and R. M. Robertson-Anderson, Biophys. J., 2018, 115, 1055–1067.
10. C. D. Chapman, K. Lee, D. Henze, D. E. Smith and R. M. Robertson-Anderson, Macromolecules, 2014, 47, 1181–1186.
11. T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250–1253.
12. L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853–7863.
13. P. Nath, R. Mangal, F. Köhle, S. Choudhury, S. Narayanan, U. Wiesner and L. A. Archer, Langmuir, 2018, 34, 241–249.
14. K. Nishi, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 2021, 127, 158001.
15. K. L. Lee, L. C. Hubbard, S. Hern, I. Yildiz, M. Gratzl and N. F. Steinmetz, Biomater. Sci., 2013, 1, 581–588.
16. J. Choi, M. Cargnello, C. B. Murray, N. Clarke, K. I. Winey and R. J. Composto, ACS Macro Lett., 2015, 4, 952–956.
17. K. A. Rose, N. Gogotsi, J. H. Galarraga, J. A. Burdick, C. B. Murray, D. Lee and R. J. Composto, Macromolecules, 2022, 55, 8514–8523.
18. Z. Cheng and T. Mason, Phys. Rev. Lett., 2003, 90, 018304.
19. M. Molaei, E. Atefi and J. C. Crocker, Phys. Rev. Lett., 2018, 120, 118002.
20. E. Andablo-Reyes, P. Díaz-Leyva and J. L. Arauz-Lara, Phys. Rev. Lett., 2005, 94, 106001.
21. C. Gutiérrez-Sosa, A. Merino-González, R. Sánchez, A. Kozina and P. Díaz-Leyva, Macromolecules, 2018, 51, 9203–9212.
22. P.-G. de Gennes, J. Chem. Phys., 1971, 55, 572–579.
23. M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1789–1801.
24. T. Odijk, Macromolecules, 1983, 16, 1340–1344.
25. G. H. Koenderink, M. Atakhorrami, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 2006, 96, 138307.
26. N. Fakhri, F. C. MacKintosh, B. Lounis, L. Cognet and M. Pasquali, Science, 2010, 330, 1804–1807.
27. N. Fakhri, A. D. Wessel, C. Willms, M. Pasquali, D. R. Klopfenstein, F. C. MacKintosh and C. F. Schmidt, Science, 2014, 344, 1031–1035.
28. B. K. Kay, J. Winter and J. McCafferty, Phage Display of Peptides and Proteins: A Laboratory Manual, Elsevier, 1996.
29. J. Kim, R. Poling-Skutvik, J. R. Trabuco, K. Kourentzi, R. C. Willson and J. C. Conrad, Analyst, 2017, 142, 55–64.
30. F. Safi Samghabadi, A. H. Slim, M. W. Smith, M. Chabi and J. C. Conrad, Macromolecules, 2022, 55, 10694–10702.
31. S. Banik, D. Kong, M. J. San Francisco and G. B. McKenna, Macromolecules, 2021, 54, 8632–8654.
32. K. Regan, S. Ricketts and R. Robertson-Anderson, Polymers, 2016, 8, 336.
33. T. T. Perkins, D. E. Smith and S. Chu, Science, 1994, 264, 819–822.
34. D. R. Tree, A. Muralidhar, P. S. Doyle and K. D. Dorfman, Macromolecules, 2013, 46, 8369–8382.
35. R. M. Robertson and D. E. Smith, Macromolecules, 2007, 40, 8737–8741.
36. E. S. G. Shaqfeh, J. Non-Newtonian Fluid Mech., 2005, 130, 1–28.
37. Y. Zhou and C. M. Schroeder, Phys. Rev. Lett., 2018, 120, 267801.
38. C. M. Schroeder, J. Rheol., 2018, 62, 371–403.
39. K.-W. Hsiao, C. Sasmal, J. Ravi Prakash and C. M. Schroeder, J. Rheol., 2017, 61, 151–167.
40. R. M. Robertson, S. Laib and D. E. Smith, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7310–7314.
41. N. M. Toan and C. Micheletti, J. Phys.: Condens. Matter, 2006, 18, S269.
42. J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770.
43. C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190.
44. S. Guilbaud, L. Salomé, N. Destainville, M. Manghi and C. Tardin, Phys. Rev. Lett., 2019, 122, 028102.
45. W. M. Mardoum, S. M. Gorczyca, K. E. Regan, T.-C. Wu and R. M. Robertson-Anderson, Front. Phys., 2018, 6, 53.
46. R. H. Colby, Rheol. Acta, 2010, 49, 425–442.
47. R. M. Robertson and D. E. Smith, Macromolecules, 2007, 40, 3373–3377.
48. P.-G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979.
49. M. Doi, Introduction to Polymer Physics, Oxford University Press, 1996.
50. S. Broersma, J. Chem. Phys., 1960, 32, 1626–1631.
51. S. Broersma, J. Chem. Phys., 1960, 32, 1632–1635.
52. S. Broersma, J. Chem. Phys., 1981, 74, 6989–6990.
53. S. Pan, D. Ahirwal, D. A. Nguyen, T. Sridhar, P. Sunthar and J. R. Prakash, Macromolecules, 2014, 47, 7548–7560.
54. M. Rubinstein, Phys. Rev. Lett., 1986, 57, 3023–3026.
55. R. H. Colby and M. Rubinstein, Macromolecules, 1990, 23, 2753–2757.
56. T. Maeda and S. Fujime, Macromolecules, 1985, 18, 2430–2437.
57. S. Egorov, J. Chem. Phys., 2011, 134, 084903.
58. R. Chen, R. Poling-Skutvik, M. P. Howard, A. Nikoubashman, S. A. Egorov, J. C. Conrad and J. C. Palmer, Soft Matter, 2019, 15, 1260–1268.
59. L. M. Bravo-Anaya, M. Rinaudo and F. A. S. Martínez, Polymers, 2016, 8, 51.
60. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986.
61. M. Doi, W. W. Graessley, E. Helfand and D. S. Pearson, Macromolecules, 1987, 20, 1900–1906.
62. P. E. Rouse, et al. , J. Chem. Phys., 1953, 21, 1272.
63. A. Jain, B. Dünweg and J. R. Prakash, Phys. Rev. Lett., 2012, 109, 088302.
64. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, New York, 2003.
65. P. Khanal, K. R. Peddireddy, J. Marfai, R. McGorty and R. M. Robertson-Anderson, J. Rheol., 2022, 66, 699–715.
66. W. He, H. Song, Y. Su, L. Geng, B. J. Ackerson, H. Peng and P. Tong, Nat. Commun., 2016, 7, 11701.
67. A. H. Slim, R. Poling-Skutvik and J. C. Conrad, Langmuir, 2020, 36, 9153–9159.
68. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631.
69. C. Xue, X. Shi, Y. Tian, X. Zheng and G. Hu, Nano Lett., 2020, 20, 3895–3904.
70. Y. Han, A. M. Alsayed, M. Nobili, J. Zhang, T. C. Lubensky and A. G. Yodh, Science, 2006, 314, 626–630.
71. M. Smith, R. Poling-Skutvik, A. H. Slim, R. C. Willson and J. C. Conrad, Macromolecules, 2021, 54, 4557–4563.
72. B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164.
73. D. Ernst, J. Köhler and M. Weiss, Phys. Chem. Chem. Phys., 2014, 16, 7686–7691.
74. C. Xue, X. Zheng, K. Chen, Y. Tian and G. Hu, J. Phys. Chem. Lett., 2016, 7, 514–519.
75. J. P. Peters and L. J. Maher, Q. Rev. Biophys., 2010, 43, 23–63.
76. C.-C. Hsieh, A. Balducci and P. S. Doyle, Nano Lett., 2008, 8, 1683–1688.
77. A. Brunet, C. Tardin, L. Salomé, P. Rousseau, N. Destainville and M. Manghi, Biophys. J., 2016, 110, 403a.
78. G. S. Manning, Biophys. J., 2006, 91, 3607–3616.
79. J. R. C. van der Maarel, Introduction to Biopolymer Physics, World Scientific, 2008.
80. S. Pan, D. At Nguyen, T. Sridhar, P. Sunthar and J. Ravi Prakash, J. Rheol., 2014, 58, 339–368.
81. S. Laib, R. M. Robertson and D. E. Smith, Macromolecules, 2006, 39, 4115–4119.
82. D. Michieletto, P. Neill, S. Weir, D. Evans, N. Crist, V. A. Martinez and R. M. Robertson-Anderson, Nat. Commun., 2022, 13, 4389.
83. J. Newman, H. L. Swinney and L. A. Day, J. Mol. Biol., 1977, 116, 593–603.
84. L. Song, U.-S. Kim, J. Wilcoxon and J. M. Schurr, Biopolymers, 1991, 31, 547–567.
85. A. S. Khalil, J. M. Ferrer, R. R. Brau, S. T. Kottmann, C. J. Noren, M. J. Lang and A. M. Belcher, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4892–4897.
86. J. Cohen, Z. Priel and Y. Rabin, J. Chem. Phys., 1988, 88, 7111–7116.
87. C. G. Lopez and W. Richtering, J. Phys. Chem. B, 2019, 123, 5626–5634.
88. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
89. J. Garamella, K. Regan, G. Aguirre, R. J. McGorty and R. M. Robertson-Anderson, Soft Matter, 2020, 16, 6344–6353.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01150c

---