Fulleride superconductivity tuned by elastic strain due to cation compositional disorder

Abstract

Dynamical fluctuations of the elastic strain in strongly correlated systems are known to affect the onset of metal-to-insulator or superconducting transitions. Here we report their effect on the properties of a family of bandwidth-controlled alkali-intercalated fullerene superconductors. We introduce elastic strain through static local structural disorder in a systematic and controllable way in the fcc-structured K_xCs_3−xC₆₀ (with potassium content, 0.22 ≤ x_K ≤ 2) series of compositions by utilizing the difference in size between the K⁺ and Cs⁺ co-dopants. The occurrence of the crossover from the Mott–Jahn–Teller insulating (MJTI) state into the strongly correlated Jahn–Teller metal (JTM) on cooling is evidenced for the compositions with x_K < 1.28 by both synchrotron X-ray powder diffraction (SXRPD) – anomalous reduction of the unit cell volume – and ¹³³Cs NMR spectroscopy – sudden suppression in the ¹³³Cs spin-lattice relaxation rates. The emerging superconducting state with a maximum critical temperature, T_c = 30.9 K shows a characteristic dome-like dependence on the unit-cell volume or equivalently, on the ratio between the on-site Coulomb repulsion, U, and the bandwidth, W. However, compared to the parent Cs₃C₆₀ composition in which cation disorder effects are completely absent, the maximum T_c is lower by ∼12%. The reduction in T_c displays a linear dependence on the variance of the tetrahedral-site cation size, σ_T², thus establishing a clear link between structural-disorder–induced attenuation of critical elastic strain fluctuations and the electronic ground state.

---

1 Introduction

Superconductors in which the electronically active units are molecules rather than atoms typically incorporate π-electron open-shell units. Among the members of the family of molecular superconductors, the trivalent alkali fullerides, A₃C₆₀ (A = alkali metal) are best-in-class representatives exhibiting the highest superconducting transition temperature, T_c (at 38 K under applied pressure)¹ and with their zero-resistance state surviving to extremely high magnetic fields (H_c2 > 90 T).² Very importantly, it has been also established that electron correlations play a dominant role in the superconducting pairing mechanism, thereby rendering these materials members of the family of unconventional high-T_c superconductors.^3–7

All studies reported so far attest that the transitions between the various electronic states of the A₃C₆₀ fullerides are achieved principally via altering the interfullerene separation, which modifies the size of the bandwidth, W, and therefore tunes the ratio (U/W), where U is the on-site Coulomb repulsion.⁸ For molecular systems like the A₃C₆₀ fullerides, U is on the order of 1 eV and varies little across the various compositions.^5–7 The parent hyperexpanded compound Cs₃C₆₀, in which (U/W) is maximal, is a magnetic insulator at ambient pressure and crystallizes as either the A15-structured (primitive cubic phase comprising orientationally ordered C₆₀³⁻ units) or the fcc-structured (face-centred cubic phase comprising merohedrally disordered C₆₀³⁻ units) polymorph.^3,4 Application of physical pressure to both polymorphs suppresses the magnetic state leading to a Mott-insulator-to-metal transition as the interfullerene separation is reduced, W increases, and (U/W) shifts below a critical value. Upon cooling, superconductivity emerges from the metallic state with a dome-shaped dependence of T_c with volume, V, occupied per C₆₀³⁻ anion.^1,3,4,8–10 The maximum T_c is somewhat higher for the A15 Cs₃C₆₀ phase at 38 K compared to the value measured for the fcc Cs₃C₆₀ phase (35 K).

However, while the A15 structure is encountered only at the high-packing densities of the parent Cs₃C₆₀ phase, the fcc-structured A₃C₆₀ phases are stable over a broad range of packing densities, and therefore (U/W) ratios. As a result, application of physical and/or chemical pressure to the most expanded fcc-structured Cs₃C₆₀ phase has allowed the exploration of the electronic phase diagram of the fullerides in great detail.^11–18 Firstly, as the orbital overlap of neighbouring C₆₀³⁻ anions increases upon pressurisation, the MJTI state is destroyed. The metallic state, which emerges from the insulator is unconventional and is characterized by fluctuating microscopically heterogeneous co-existence of both localized Jahn–Teller-active and itinerant electrons (JTM). Further pressurization, leads to the gradual disappearance of localised Jahn–Teller features and the evolution of the unconventional JTM to a conventional Fermi liquid. At the same time, the s-wave superconducting state evolves from an unconventional correlated superconductor in the strong-coupling limit to a weak-coupling BCS-like superconductor. Notably, the JTM is the parent state of the unconventional fulleride superconductor with the highest T_c encountered at the crossover between JTM and Fermi liquid behaviour.¹¹

Manipulation of the fcc-structured Cs₃C₆₀ phase by chemical pressure was successfully achieved by altering the cation occupation of the tetrahedral (T) interstitial sites, which are smaller (r_T = 1.12 Å) than the ionic size of the heavier alkali dopants (K⁺, Rb⁺, and Cs⁺). As a result, fulleride packing density can be sensitively controlled by the occupation of the tetrahedral sites as the proportions of isovalent K⁺, Rb⁺, and Cs⁺ ions vary. Increased amounts of the smaller size ions lead to lattice contraction, increased values of W, and smaller values of (U/W).¹¹ On the other hand, the occupancy of the octahedral (O) sites by different alkali ions plays a minor role as the hole size (r_O = 2.06 Å) is larger than the ionic radius of all alkali ions. The detailed investigation of the chemical pressure effect across the fcc-structured members of the Rb_xCs_3−xC₆₀ (0.35 ≤ x ≤ 2) series revealed the existence of an electronic phase diagram entirely comparable to that established upon physical pressurization of the parent Cs₃C₆₀ phase.¹¹ This is consistent with the dominant role of the intermolecular overlaps in controlling the magnetic and metallic/superconducting states of the materials.^3,4 Notably, however, these studies revealed a small but significant (∼5%) reduction of the maximum T_c, which appears smaller (33.2 K) in the chemically pressurized analogues when compared to physically pressurized Cs₃C₆₀ (35.1 K). This T_c reduction is evident at all packing densities, V despite the expected identical values of the bandwidth, W and the corresponding (U/W) ratios.

This observation necessitates a revisit of the role of the alkali ions in determining the superconducting properties of the fulleride phases. In particular, there is a well-defined difference in the occupation of the tetrahedral interstices in the Rb_xCs_3−xC₆₀ (0 ≤ x ≤ 3) phase field: when x = 0, 2, and 3, the tetrahedral holes are occupied by either Cs⁺ or Rb⁺ alone, while for all other values of x, they are occupied by a disordered mixture of Rb⁺ and Cs⁺ cations. Such disorder of cation occupation of available structural cavities and the associated cooperative fluctuations of the elastic strain generated have been shown before to influence sensitively a variety of electronic responses¹⁹ including metal-insulator and superconducting transitions in strongly correlated transition metal oxide phases such as the magnetoresistive manganites²⁰ and the high-T_c cuprates,²¹ respectively.

This raises the issue whether the generic nature of such elastic interactions is also relevant to the electronic properties of fulleride superconductors and could be responsible for the small, but significant, suppression in the magnitude of their T_c encountered when cation disorder is present. Here, we undertake a systematic study of the structural and electronic properties of the series of fcc-structured K_xCs_3−xC₆₀ (with nominal content, 0.12 ≤ x ≤ 2) fullerides at both ambient and elevated pressures. Due to the increased difference in size between the K⁺ and Cs⁺ constituent ions, we are able to enhance further the ionic size effects, culminating in even larger suppression (on the order of 12%) of the values of T_c observed in the absence of disorder at the same fulleride packing density. The high quality of the experimental data allowed us to establish quantitatively the effects of cation disorder and the associated cooperative elastic interactions on T_c.

2 Materials and methods

2.1 Synthesis and characterisation

Polycrystalline K_xCs_3−xC₆₀ (nominal K content, 0.12 ≤ x ≤ 2) compounds were synthesized by high-temperature reactions of stoichiometric quantities of sublimed C₆₀ and phase-pure K₆C₆₀ and Cs₆C₆₀ precursors (Fig. S1†). The exact experimental protocol is detailed in the ESI.† As small amounts of reactants are employed in these preparations, the use of free-flowing A₆C₆₀ (A = K, Cs) powders instead of K and Cs metals allows better stoichiometry control of the target compositions. Due to the extreme air- and moisture-sensitivity, all sample manipulations were carried out in an Ar-filled glove box. Laboratory X-ray powder diffraction (Bruker D8 Advance, Debye–Scherrer geometry, CuK_α1 radiation, λ = 1.54056 Å) was used to monitor the quality of all intermediate and the final polycrystalline products. Samples were obtained as free-flowing black-coloured powders.

2.2 Structural measurements at ambient and elevated pressures

High-resolution synchrotron X-ray powder diffraction (SXRPD) measurements of the samples at ambient pressure were performed using a helium-flow cryostat between 10 and 300 K with the multidetector diffractometer on beamline ID31 and ID22 (λ ∼ in the range 0.35 to 0.4 Å) at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. Data for the x = 1 sample were obtained between 112 and 300 K with the diffractometer on beamline BL44B2 (λ = 0.81887 Å) at SPring-8, Japan.²² Pressure-dependent high-resolution SXRPD data (λ ∼ 0.41 Å) were collected at 7 K for samples of nominal composition K_xCs_3−xC₆₀ (x = 0.25, 0.75, 1) at pressures between 0.2 and 10 GPa on beamline BL10XU, SPring-8, Japan. Data analysis of the SXRPD profiles at both ambient and elevated pressures was performed with the GSAS suite of Rietveld analysis programs.²³

2.3 Magnetic measurements at ambient and elevated pressures

Ambient-pressure magnetic measurements were carried out with a Quantum Design SQUID MPMS magnetometer on ∼20–25 mg powder samples loaded in thin-walled quartz ampoules and sealed under a He gas partial pressure (∼300 mbar). The magnetization, M, of all samples was measured at an applied field of either 10 or 20 Oe between 1.8 and 40 K under both zero-field-cooled (ZFC) and field-cooled (FC) protocols. Temperature-dependent magnetic susceptibility, χ, data were also collected at 3 and 5 T under FC protocols between 1.8 and 300 K. High-pressure magnetization measurements at 20 Oe under ZFC protocols were carried out under applied pressures of up to 10.3 kbar with an easyLab Technologies piston-cylinder high-pressure cell (Mcell 10). High-purity Sn was used as an in situ manometer with Daphne mineral oil as the pressure transmitting medium.

2.4 NMR spectroscopy

¹³³Cs (spin I = 7/2) and ³⁹K NMR (spin I = 3/2) spectra and spin-lattice relaxation, T₁, times were measured for K_xCs_3−xC₆₀ [nominal content, x = 0.35, 0.5, 2; refined content, x_K = 0.53, 0.64, 2 (vide infra)] powders at a magnetic field of 9.39 T. Samples were sealed into Pyrex glass tubes under a low-pressure He atmosphere. Measurements were conducted between 4 and 420 K in a liquid He flow cryostat with a temperature stability better than ±0.1 K over the entire temperature range. As a ¹³³Cs NMR reference, a CsNO₃ standard was used with a corresponding reference frequency, ν_ref(¹³³Cs) = 52.4609 MHz. In the ¹³³Cs NMR experiments, a solid-echo pulse sequence (β)–τ–(β)–τ-echo was used with a pulse length, τ(β) = 4 μs, an interpulse delay, τ = 50 μs and appropriate phase cycling. The same pulse sequence was also used to detect the ³⁹K NMR signal (KCl standard, ν_ref(³⁹K) = 18.6633 MHz) but with a larger pulse width of 14 μs and an interpulse delay, τ of 200 μs. For spin-lattice relaxation measurements, the inversion recovery technique was applied in both cases.

As the K_xCs_3−xC₆₀ phase assemblages might contain Cs₄C₆₀ and/or CsC₆₀ impurity phases (vide infra), we employed a similar strategy as in our earlier work on overexpanded Cs₃C₆₀ samples^3,4 in order to relatively enhance the ¹³³Cs NMR signal arising from the fcc phases. The symmetry of the Cs⁺ sites of the Cs₄C₆₀ phase is lower than axial (point group C_2v), leading to broadening of the respective NMR spectral lines by quadrupole interactions. As a result, such lineshape broadening together with the low phase concentration, and the experimental pulse-length optimization for the fcc Cs₃C₆₀ phase suppress the Cs₄C₆₀ contribution to the NMR signal amplitude.^3,4 In addition, the ¹³³Cs NMR signal of the CsC₆₀ impurity is shifted by ∼800 ppm relative to the reference and is thus well separated from the main O- and T-site signals. Indeed, while the ¹³³Cs NMR signal of the CsC₆₀ impurity is detected in Cs₃C₆₀ samples,^3,4 it is too low in intensity to be observed in the K_xCs_3−xC₆₀ series (Fig. S2†).

3 Results

3.1 Structural evolution of K_xCs_3−xC₆₀ at ambient and elevated pressures

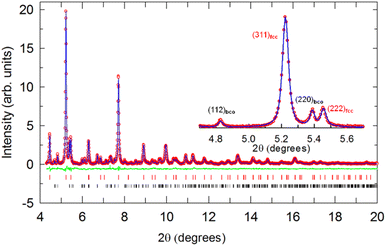
A series of eight K_xCs_3−xC₆₀ samples with nominal x varying between 0.12 and 2 were synthesized. Inspection of their high-resolution SXRPD profiles (Fig. S3†) collected at ambient temperature reveals in all cases the formation of cubic fulleride phases with fcc symmetry (Fig. 1a) and with an increasing lattice size, a as the content of the smaller K⁺ cation, x decreases. At the same time, the purity of the samples degrades with increasing Cs⁺ content – decreasing x – as the fractions of co-existing Cs₄C₆₀ and CsC₆₀ phases grow at the expense of that of the fcc-structured phases. As established before, both fcc Cs₃C₆₀ (ref. 4) and the expanded fcc fullerides Rb_xCs_3−xC₆₀ (ref. 11) are not accessible in phase-pure form due to the competing disproportionation reaction into CsC₆₀ and Cs₄C₆₀ – driven by the size mismatch between the large Cs⁺ and Rb⁺ cations and the small tetrahedral fcc interstitial sites – that leads to the isolation of three-phase assemblages. Rietveld analysis of the SXRPD data was undertaken by employing the established merohedrally disordered fulleride model (space group Fm3̄m) for the fcc-structured components.

Fig. 1 (a) Crystal structure of fcc fullerides (space group Fm3̄m) with stoichiometry A₃C₆₀ (A is an alkali metal cation; blue spheres depict cations residing in tetrahedral (T) and red in octahedral (O) interstices, respectively). The C₆₀³⁻ units are merohedrally disordered; here only one of the two possible orientations is depicted at each lattice position. (b) ³⁹K NMR spectra measured for K_3−xCs_xC₆₀ (refined x_K = 0.53, 0.64, 2, 3) powders at 300 K. The T and O peaks are labelled in blue and red colour, respectively. The spectrum of K_3−xCs_xC₆₀ (x = 3) is been reproduced from ref. 24.

An important issue which arises from the different size of the octahedral (r_O = 2.06 Å) and tetrahedral (r_T = 1.12 Å) cavities in the fcc unit cell relates to their possible preferred occupation by the larger Cs⁺ (r_Cs⁺ = 1.67 Å) and smaller K⁺ (r_K⁺ = 1.38 Å) ions, respectively. This can be addressed experimentally by an element-specific experimental technique such as NMR spectroscopy. Fig. 1b shows the ³⁹K NMR spectra for the K_xCs_3−xC₆₀ series (with refined x_K varying between 0.53 and 3) at ambient temperature. For disorder-free K₃C₆₀ (x = 3), sharp peaks of both O- and T-lattice-sites can be clearly recognized.²⁴ On the other hand, the O-site peak is completely suppressed for K₂CsC₆₀ (x_K = 2), implying preferential occupation of the O site by the larger Cs⁺ ion with K⁺ residing in the T cavities. This trend persists as x becomes smaller, albeit with the observation of a significantly broadened T-site ³⁹K NMR peak (Fig. S4†). This is the signature of increased cation disorder due to the random distribution of the differently sized K⁺ and Cs⁺ cations amongst the T-sites of the fcc lattice (vide infra).

Rietveld analysis of the ambient-temperature data (Fig. 2, S5–S11 and Table S1†) was therefore undertaken by incorporating the information from NMR spectroscopy – K⁺ ions were only included in the T sites while, for x < 2, Cs⁺ ions were allowed to occupy both T and O sites. Across the K_xCs_3−xC₆₀ series, we find that the lattice constants of the cubic phases with fcc symmetry decrease monotonically as the K content increases. At the same time, the refined stoichiometry of the fcc phase in each sample and the composition of the phase assemblage were determined. The refined stoichiometries differ from the nominal ones, except for the x = 2 sample, with the refined K-content, x_K being consistently higher than the nominal value. At the same time, the refined fcc phase fractions increase from 31.5(2)% (the remaining comprising Cs₄C₆₀ and CsC₆₀) for the most expanded phase, x_K = 0.22(1) to 94.05(1)% for x_K = 1.626(4) and 100% for x_K = 1.996(6). The results are summarized in Tables S2–S9.† Fig. S12† shows that the fcc lattice parameter, a varies linearly with the refined K content, x_K across the K_xCs_3−xC₆₀ series in agreement with Vegard's law and confirming the random distribution of the K⁺ and Cs⁺ alkali ions amongst the lattice T-sites. Notably the slope da/dx_K = −0.234(3) Å is significantly larger than that determined for the Rb_xCs_3−xC₆₀ analogues (da/dx_Rb = −0.150(4) Å (ref. 11)), as expected by the smaller ionic size of K⁺ than that of the Rb⁺ intercalant.

Fig. 2 Rietveld refinement of the synchrotron XRPD data collected at 300 K for fcc-structured K_xCs_3−xC₆₀ with refined K-content, x_K = 0.87(1) (λ = 0.39984 Å). Red circles, blue lines and green lines represent the observed, calculated and difference profiles, respectively. Ticks mark the reflection positions of the fcc (85.18(7)%, red) and the body-centred-orthorhombic (bco) Cs₄C₆₀ (14.8(1)%, black) phases. Inset: expanded view in the range 4.7° to 5.7° with reflections labelled by their hkl Miller indices.

The temperature dependence of the fcc crystal structures of the members of the K_xCs_3−xC₆₀ series with x_K = 0.35, 0.64, 0.87, and 1.28, as studied by SXRPD, shows that the cubic structure is robust and survives to the lowest temperature of the present experiments. In particular, the thermal behaviour of the unit cell volume of the K_xCs_3−xC₆₀ composition with a high K-content, x_K = 1.28 mimics that of the parent Cs₃C₆₀ (ref. 4) showing a smooth lattice contraction on cooling that can be accounted for with a Debye–Grüneisen model (see the corresponding text in the ESI† for details of the Debye–Grüneisen analysis).²⁵ On the other hand, the contraction of the unit cell volume of the compositions with x_K = 0.35, 0.64, and 0.87 with decreasing temperature is not smooth and exhibits an anomalous reduction, ΔV from the value derived from the Debye–Grüneisen fits below a characteristic temperature, T′ ∼ 97, 170, and 220 K, respectively (Fig. 3 and Table S10†). The normalised volume changes, ΔV/V_T′ range between 0.2 and 0.4% (inset Fig. 3). Rietveld refinements (Fig. S13–S16, Tables S4–S6 and S8†) establish the isosymmetric nature of the structure across the observed anomalies in the lattice metrics. In a similar fashion to the V(T) response of the Rb_xCs_3−xC₆₀ (0.25 ≤ x ≤ 1.5) analogues,^11,14T′ shifts to higher temperatures and the anomalous behaviour extends over a larger temperature range as the lattice contracts with increasing K content, x_K.

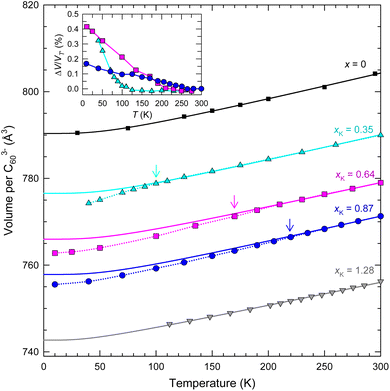Fig. 3 Temperature evolution of volume, V, occupied per C₆₀³⁻ anion for fcc-structured K_xCs_3−xC₆₀ samples with x_K = 0.35, 0.64, 0.87 and 1.28 and for Cs₃C₆₀.⁴ The arrows mark the onset temperatures of the change in lattice response, denoted T′, where present. The solid lines through the data are Debye–Grüneisen fits²⁵ for T > T′ (or over all T for x = 0 and x_K = 1.28) (Table S10†). The dotted lines through the data at T < T′ are guides to the eye. Inset: temperature dependence of the normalised volume change, ΔV/V_T′ for x_K = 0.35, 0.64 and 0.87 – ΔV is the difference in volume between that predicted by the Debye–Grüneisen fits and that derived experimentally. The errors in V per C₆₀³⁻ from Rietveld analysis are smaller than the size of the data points.

The pressure dependence of the low-temperature crystal structures of the three K_xCs_3−xC₆₀ samples with x_K = 0.35, 0.87 and 1.28 was also followed by SXRPD to 10 GPa at 7 K. Rietveld analysis of the diffraction profiles confirms the robustness of the fcc structure under the high-pressure conditions too (Fig. S17–S19 and Tables S11–S13†). Fits of the non-linear pressure dependence of the 7 K unit cell volume to the semi-empirical second-order Murnaghan equation-of-state (EoS)²⁶ for each composition (Fig. S20†) allow us to extract the values of the zero-pressure isothermal bulk moduli, K₀ (∼18–19 GPa) and their pressure derivatives, These, and the resulting low-temperature volume compressibilities, κ (∼0.05 GPa⁻¹) are comparable to those derived before for fcc-structured Cs₃C₆₀ (ref. 4) and the Rb_xCs_3−xC₆₀ analogues¹¹ (Table S14†).

3.2 Electronic properties of K_xCs_3−xC₆₀ at ambient and elevated pressures

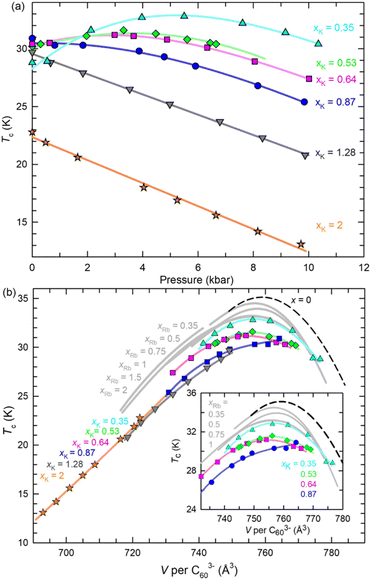
The superconducting properties of the K_xCs_3−xC₆₀ samples (x_K content in the range between 0.22 and 2) at ambient pressure were investigated by low-field magnetization measurements. Bulk superconductivity is observed with T_c initially increasing from 26.5 K in overexpanded K_0.22Cs_2.78C₆₀ (shielding fraction 16%) to 30.9 K in optimally expanded K_0.87Cs_2.13C₆₀ (40%) and then decreasing to 22.8 K in underexpanded K₂CsC₆₀ (52%) (Fig. 4a, b and S21†). The variation of T_c with K content in fcc K_xCs_3−xC₆₀ mimics the T_c(V) behaviour of fcc Cs₃C₆₀ (ref. 4) and the T_c(V) and T_c(x) behaviour of isostructural Rb_xCs_3−xC₆₀,¹¹ displaying well-defined dome shape (Fig. 4c). At large unit cell volumes – i.e. at low co-doping levels of K⁺ or Rb⁺ – there is little change in T_c at fixed lattice sizes between the K_xCs_3−xC₆₀ and Rb_xCs_3−xC₆₀ systems. However, at small unit cell volumes as the amount of the K⁺ or Rb⁺ co-dopants in the tetrahedral interstices increases, T_c is markedly suppressed in the K_xCs_3−xC₆₀ family relative to those in Rb_xCs_3−xC₆₀ (maximum T_c at 33.2 K) and pressurized Cs₃C₆₀ (maximum T_c at 35.1 K).

Fig. 4 Temperature dependence of the ZFC magnetisation, M, of the K_xCs_3−xC₆₀ samples divided by the applied magnetic field. (a) Samples with K-content, 0.22 ≤ x_K ≤ 0.87. (b) Samples with K-content, 1.28 ≤ x_K ≤ 2. The insets show expanded regions of the respective M(T) data near the superconducting T_c. (c) Variation of ambient pressure superconducting T_c with volume, V occupied per C₆₀³⁻ anion at T = T_c for K_xCs_3−xC₆₀ (0.22 ≤ x_K ≤ 2) and for Rb_xCs_3−xC₆₀ (0.22(1) ≤ x_Rb ≤ 2)^11,14 together with that for fcc Cs₃C₆₀ under pressure.⁴ Volumes per C₆₀³⁻ for K_xCs_3−xC₆₀ at T_c are estimated by extrapolation of the unit cell volumes determined from low-temperature structural data. The inset shows the dependence of T_c on x_K (red squares) and x_Rb (blue circles). All solid lines through the data points are guides-to-the-eye.

The superconducting properties of the materials were also investigated by magnetization measurements, M(T) as a function of both chemical and physical pressure (to ∼10.3 kbar) (Fig. S22†). For the most expanded sample studied, K_0.35Cs_2.65C₆₀, T_c increases with increasing pressure with an initial pressure coefficient, (dT_c/dP)_P=0 = +1.5(2) K kbar⁻¹. As x_K increases, the rate of change rapidly decreases, approaching zero for the K_0.87Cs_2.13C₆₀ composition, which shows the highest T_c at ambient pressure. (dT_c/dP)_P=0 then becomes negative upon further chemical pressurization (−0.88(1) K kbar⁻¹ for K_1.28Cs_1.72C₆₀, −0.99(3) K kbar⁻¹ for K₂CsC₆₀). Further increase in pressure leads to superconductivity domes for the 0.35 ≤ x_K ≤ 0.87 compositions while T_c of the 1.28 ≤ x_K ≤ 2 compositions decreases smoothly (Fig. 5a). The variation of the superconducting T_c of K_xCs_3−xC₆₀ (0.35 ≤ x ≤ 2) with unit cell volume, V, at low temperature extracted using the T_c(P) data together with 7 K V(P) data (Fig. S20†) is shown in Fig. 5b – the T_c(V) domes show maxima in the vicinity of 760 ų per C₆₀³⁻ in a comparable fashion to the behaviour of pressurized fcc-structured Cs₃C₆₀ and Rb_xCs_3−xC₆₀.

Fig. 5 (a) Variation of the superconducting critical temperature, T_c with pressure for fcc-structured K_xCs_3−xC₆₀ (0.35 ≤ x_K ≤ 2). Solid lines through data points are guides to the eye except those for x_K = 1.28 and 2 that represent linear fits to the data. (b) Variation of T_c with volume, V, occupied per C₆₀³⁻ anion at low temperature for fcc-structured K_xCs_3−xC₆₀ (0.35 ≤ x ≤ 2), Rb_xCs_3−xC₆₀ (0.35 ≤ x ≤ 2) (grey solid lines) and Cs₃C₆₀ (dashed black line). Solid lines through x_K data points are guides-to-the-eye. The inset shows an expanded view of dome-shaped T_c (V) data.

Paramagnetic susceptibility measurements, χ(T), as a function of temperature at ambient pressure in the normal state have proven before^3,4,11 to be an excellent probe of the electronic properties of fullerides, sensitively tracking the insulator-to-metal crossover associated with the lattice anomalies evident in diffraction for selected compositions (vide supra). However, χ(T) data for the present K_xCs_3−xC₆₀ phase assemblages at small x_K suffer from also incorporating significant impurity-phase contributions to the measured susceptibility. As a result, well-defined cusps on cooling that provide evidence for insulator-to-metal crossover are hard to ascertain – there is only some weak evidence of maxima in χ(T) at ∼68 and 97 K for K_0.22Cs_2.78C₆₀ and K_0.35Cs_2.65C₆₀, respectively (Fig. S23†). The χ(T) data for moderately expanded compositions with x_K = 0.53 and 0.64 no longer display any cusps but they do not exhibit a temperature-independent Pauli susceptibility term either. Such a term, which is consistent with a metallic ground state from which superconductivity emerges on cooling, appears to be present for underexpanded compositions with x_K = 1.28 and 2.

Given the ambiguities associated with the χ(T) datasets due to the multiphase nature of the samples, we used the local-probe NMR technique to follow the temperature evolution of the electronic properties of the K_0.64Cs_2.36C₆₀ composition. The ¹³³Cs spin-lattice relaxation rate divided by temperature, 1/¹³³T₁T, which measures the imaginary part of the dynamic electron spin susceptibility, provides a sensitive insight into the electronic degrees of freedom as they develop across the insulator-to-metal crossover.^3,4,11 On cooling from high temperatures, 1/¹³³T₁T for both O- and T-sites of K_0.64Cs_2.36C₆₀ slightly increases with decreasing temperature (see Fig. S24† and the corresponding text in the ESI† for details of the spectral and ¹³³Cs relaxation rate analysis) showing qualitatively comparable behaviour to that previously observed in RbCs₂C₆₀ and in Mott-insulating low-spin (S = ½) Cs₃C₆₀ (ref. 4, 11 and 14) (Fig. 6). Consistent with the structural results, 1/¹³³T₁T of K_0.64Cs_2.36C₆₀ begins to decrease below T' ∼ 170 K, as expected for a crossover to a Jahn–Teller metal¹¹ and in close similarity with the behaviour of RbCs₂C₆₀. Above T′, the 1/¹³³T₁T datasets for the two samples with comparable unit-cell volumes show different dependences with increasing temperature with the difference increasing as we move away from the insulator-to-metal crossover line. This implies the existence of another control parameter, namely interstitial site disorder (vide infra), which further controls the local electronic properties.

Fig. 6 Temperature dependence of the ¹³³Cs spin-lattice relaxation rates divided by temperature, 1/¹³³T₁T for K_0.64Cs_2.36C₆₀ (solid symbols) and for similarly expanded RbCs₂C₆₀ (open symbols) from ref. 11. In both cases, squares and circles mark the data for T- and O-sites, respectively. The dotted lines mark the temperature, T′ at which maxima in 1/¹³³T₁T are observed and the onset of superconductivity at T_c in the NMR magnetic field of 9.39 T.

Below T_c = 27 K (the value of the critical temperature in the NMR magnetic field of 9.39 T), 1/¹³³T₁T of K_0.64Cs_2.36C₆₀ is suddenly suppressed indicating the opening of a superconducting gap, Δ, while at the same time, no Hebel–Slichter coherence peak is observed. The spin-lattice relaxation rate adopts a thermally activated dependence 1/¹³³T₁ ∝ exp[−Δ₀/k_BT], in agreement with an isotropic s-wave superconducting gap (Fig. S25†). The semilog plot allows us to extract an estimate of the superconducting gap, Δ₀. The normalized gap value, 2Δ₀/k_BT_c ∼ 5 is significantly enhanced relative to that of a weakly coupled BCS superconductor (2Δ₀/k_BT_c = 3.52) in a similar fashion to the behaviour of the overexpanded members of the Rb_xCs_3−xC₆₀ family.¹¹

4 Discussion

The electronic phase diagram of selected fcc-structured A₃C₆₀ fullerides was mapped out in the past both by the application of physical pressure to the highly expanded MJTI Cs₃C₆₀ phase^4,13 and of chemical pressure in the series of Rb_xCs_3−xC₆₀ (0 ≤ x ≤ 2) compositions in which Cs⁺ is quasi-continuously replaced by the smaller Rb⁺ cation.^11,14,27 The K_xCs_3−xC₆₀ (0 ≤ x ≤ 2) phases investigated here are direct analogues of their antecedents in the Rb_xCs_3−xC₆₀ (0 ≤ x ≤ 2) series with the smaller K⁺ ion being now employed as a direct substituent of Cs⁺. The fcc unit cell size decreases again linearly with increasing content of the smaller K⁺ ion (Fig. S12†), thereby permitting the exploration of the electronic properties of the K_xCs_3−xC₆₀ (0 ≤ x ≤ 2) fullerides across a broad region of the phase diagram from underexpanded to overexpanded via optimally expanded compositions. The existence of a superconductivity dome and the presence of a crossover of the normal metallic state from a correlated JT metal to a Fermi liquid, as the packing density of the fulleride units decreases are essentially identical observations to those established before for the fcc Rb_xCs_3−xC₆₀ compounds.^11,14 However, a noticeable difference in behaviour of the K_xCs_3−xC₆₀ (0 ≤ x ≤ 2) compositions, as evidenced in Fig. 4c and 5b, is the presence of a significant suppression of the superconducting transition temperature, T_c when compared with the values measured in both Rb_xCs_3−xC₆₀ and pressurised Cs₃C₆₀ at the same packing densities, V/C₆₀³⁻.

In order to understand the origin of the suppression of T_c in the K_xCs_3−xC₆₀ series, we first examine the variation of the packing density, V/C₆₀³⁻ with the average radius of the ions occupying the tetrahedral sites, 〈r_A,_T〉 (A = K, Rb, Cs). Fig. S26† shows that the identity of the ions themselves is important in determining the packing density. As the amount of the K⁺ or Rb⁺ co-intercalants into the tetrahedral sites of the Cs₃C₆₀ structure increases by partially replacing the larger Cs⁺ ions, the packing density smoothly decreases. However, the rate of decrease is distinctly different between the K_xCs_3−xC₆₀ (dV/d〈r_A,T〉 = 250(3) Ų) and the Rb_xCs_3−xC₆₀ (dV/d〈r_A,_T〉 = 306(9) Ų) series. This leads to an increasing deviation between their corresponding V/C₆₀³⁻vs. 〈r_A,_T〉 lines at the same average ionic size for large co-intercalant content (Fig. S26†). It is an indication of the potential importance of disorder in the tetrahedral sites – that arises from the difference in size mismatch between the intercalants, namely (r_Cs⁺ − r_K⁺) > (r_Cs⁺ − r_Rb⁺) – on the structural and electronic properties of the materials.

The degree of cation disorder may be quantified by the magnitude of the statistical variance, σ_T² in the distribution of the T-site ionic radii, namely σ_T² = ∑x_A,Tr_A,T² − 〈r_A,_T〉². The inset in Fig. S26† shows the variation in cation disorder with the average cation radius, 〈r_A,T〉 of the tetrahedral sites for both K_xCs_3−xC₆₀ and Rb_xCs_3−xC₆₀. The magnitude of σ_T² gradually increases as we replace Cs⁺ with K⁺ or Rb⁺ ions at the T-sites of fcc-structured Cs₃C₆₀. In both cases, it reaches a maximum value and then decreases, producing a dome-shaped scaling of cation size variance with 〈r_A,_T〉. The degree of cation disorder is significantly larger in the case of the K⁺ co-intercalant for the K_xCs_3−xC₆₀ series whereas it is absent in the parent Cs₃C₆₀ and A₂CsC₆₀ (A = K, Rb) phases for which σ_T² = 0.

The static local structural disorder quantified by σ_T² is directly associated with the elastic strain whose fluctuations affect critical temperatures. Returning to Fig. 5b, which displays the values of superconducting T_c for fcc Cs₃C₆₀ under pressure together with those for Rb_xCs_3−xC₆₀ and K_xCs_3−xC₆₀ at ambient pressure vs. the packing density of the fulleride units, it is apparent that there are three distinct domes peaking roughly at comparable values of V/C₆₀³⁻ but displaced vertically – one for each family. The highest value of the measured T_cs at each V is encountered for pressurized Cs₃C₆₀, followed by that for Rb_xCs_3−xC₆₀, and then by that for K_xCs_3−xC₆₀. For instance, (T_c)_max for the K_xCs_3−xC₆₀ (x_K = 0.87, V = 757.9 ų) composition at ambient pressure at the top of the dome is 30.9 K. For the same lattice size of the fulleride salts, T_c increases first to 33.2 K at ambient pressure for the Rb_xCs_3−xC₆₀ family and then to 35.1 K for pressurized Cs₃C₆₀, an overall increase of 4.2 K. This trend is associated with a decrease in the value of the T-site cation size variance, σ_T² from 0.021 Ų (in the K-substituted series) to 0.005 Ų (in the Rb-substituted series) to 0 Ų (in pressurized Cs₃C₆₀). Fig. 7 displays the variation of the T_c suppression, ΔT_c = T_c(Cs₃C₆₀) − T_c(K_xCs_3−xC₆₀, P = 1 atm) with σ_T² and with packing density, V/C₆₀³⁻ as an implicit parameter for compositions lying at the maximum and on the overexpanded side of the superconductivity dome. ΔT_c varies linearly with σ_T² with a slope of dΔT_c/dσ_T² = 210(4) K Å⁻², thus demonstrating a clear link between T-site disorder of the electronically inactive alkali ions and suppression of T_c.

Fig. 7 Dependence of the suppression of the ambient-pressure superconducting T_c of the K_xCs_3−xC₆₀ (0.22 ≤ x_K ≤ 0.87) compounds relative to that of the pressurized binary analogue, Cs₃C₆₀ at the same C₆₀ packing density on the tetrahedral-site cation size variance. The solid red line is a linear fit to the data.

Such effects have attracted considerable interest before in other classes of strongly correlated materials, namely perovskite transition-metal oxides. For instance, it was demonstrated that the metal-to-insulator transition temperature in colossal magnetoresistive manganites, (RE_1−xAE_x)MnO₃ responds sensitively to changes in lattice strain associated with the variation in ionic size mismatch of the electronically inactive rare earth (RE) and alkaline earth (AE) supporting cations.^20,28 In a similar fashion, the superconducting T_c in high-temperature cuprate superconductors, (RE_1−xAE_x)₂CuO₄ decreases linearly with increasing disorder of the supporting cation site arising from differences in size between the rare earth and alkaline earth cations.^21,29 Similar observations of the importance of ionic size disorder effects in controlling the onset of phase transitions have been also made for nickelates,³⁰ titanates,³¹ and ferroelectrics.³² Theoretically the large effect of ionic size disorder on Mott-like phase transitions has been understood in terms of dynamic fluctuations of the resulting elastic strain as demonstrated in statistical mechanical models, which incorporate cooperative lattice distortions coupled explicitly to the electronic degrees of freedom.¹⁹ Thus it appears that comparable strong elastic interactions are also relevant in strongly correlated molecular systems such as the fcc-structured alkali fullerides, Here the onset of superconductivity is shown to be tunable not only by purely electronic effects associated with the fulleride sublattice – as quantified by the (U/W) ratio – but also by elastic strain effects – as quantified by the variance in the distribution of the radii of the supporting A and A′ cations residing in the T-sites of the fcc structure.

5 Conclusions

In conclusion, we have investigated in detail the structural and electronic properties of the series of fcc-structured K_xCs_3−xC₆₀ fullerides (0.22 ≤ x_K ≤ 2) by means of SXRPD, NMR spectroscopy, and SQUID magnetometry at both ambient and elevated pressures. High-resolution synchrotron XRPD shows that there are no structural phase transitions occurring for any of the compositions studied at all temperatures and pressures investigated. Insulator-to-metal crossovers are encountered on cooling at ambient pressure, evident by both a lattice size decrease without an accompanying crystal symmetry change and a maximum in the 1/¹³³T₁T vs. T¹³³Cs NMR spin lattice relaxation data. Composition-dependent T_c measurements at both ambient and elevated pressures reproduce dome-shaped responses to changes in the fulleride packing density.

At the same time, the results permit the extension of the electronic phase diagram of the fcc-structured A₃C₆₀ fullerides to compositions with significantly increased chemical disorder, as quantified by the statistical variance, σ_T² in the distribution of tetrahedral-site ionic radii. We establish a very sensitive dependence of T_c on the lattice strains associated with the cation size variance at the same packing density, V/C₆₀³⁻ – the suppression of T_c from its value in the absence of disorder varies linearly with lattice strains at a rate of 210(4) K Å⁻².

Data availability

All the necessary data to support the findings of this study can be found within the main text and ESI.†

Author contributions

Synthesis, H. E. O. and R. H. C.; synchrotron X-ray diffraction—data collection and analysis, H. E. O., R. H. C., Y. T., K. K., and K. P.; high-pressure synchrotron X-ray diffraction—data collection and analysis, H. E. O., R. H. C., Y. T., Y. O., and K. P.; NMR spectroscopy, P. J. and D. A.; conceptualization and overall conclusions, D. A., Y. K., and K. P.; project supervision, K. P.; writing—review and editing, D. A. and K. P. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the ESRF and SPring-8 for access to synchrotron X-ray facilities. This work was financially supported by Grants-in-Aid for Scientific Research (JSPS KAKENHI Grant Numbers JP21H01907 and JP22K18693), the Japan Atomic Energy Agency (JAEA) (REIMEI Research Program) and the Slovenian Research Agency (Grant Numbers P1-0125 and J1-3007). The experiments at SPring-8 were performed under Proposals No. 2013A1194 and 2017A1363.

Notes and references

1. A. Y. Ganin, Y. Takabayashi, Y. Z. Khimyak, S. Margadonna, A. Tamai, M. J. Rosseinsky and K. Prassides, Nat. Mater., 2008, 7, 367–371.
2. Y. Kasahara, Y. Takeuchi, R. H. Zadik, Y. Takabayashi, R. H. Colman, R. D. McDonald, M. J. Rosseinsky, K. Prassides and Y. Iwasa, Nat. Commun., 2017, 8, 14467.
3. Y. Takabayashi, A. Y. Ganin, P. Jeglic, D. Arcon, T. Takano, Y. Iwasa, Y. Ohishi, M. Takata, N. Takeshita, K. Prassides and M. J. Rosseinsky, Science, 2009, 323, 1585–1590.
4. A. Y. Ganin, Y. Takabayashi, P. Jeglič, D. Arčon, A. Potočnik, P. J. Baker, Y. Ohishi, M. T. McDonald, M. D. Tzirakis, A. McLennan, G. R. Darling, M. Takata, M. J. Rosseinsky and K. Prassides, Nature, 2010, 466, 221–227.
5. M. Capone, M. Fabrizio, C. Castellani and E. Tosatti, Rev. Mod. Phys., 2009, 81, 943–958.
6. Y. Nomura, S. Sakai, M. Capone and R. Arita, Sci. Adv., 2015, 1, e1500568.
7. S. Hoshino and P. Werner, Phys. Rev. Lett., 2017, 118, 177002.
8. Y. Takabayashi and K. Prassides, Philos. Trans. R. Soc., A, 2016, 374, 20150320.
9. H. Alloul, P. Wzietek, T. Mito, D. Pontiroli, M. Aramini, M. Riccò, J. P. Itie and E. Elkaim, Phys. Rev. Lett., 2017, 118, 237601.
10. Y. Ihara, H. Alloul, P. Wzietek, D. Pontiroli, M. Mazzani and M. Ricco, Phys. Rev. Lett., 2010, 104, 256402.
11. R. H. Zadik, Y. Takabayashi, G. Klupp, R. H. Colman, A. Y. Ganin, A. Potocnik, P. Jeglic, D. Arcon, P. Matus, K. Kamaras, Y. Kasahara, Y. Iwasa, A. N. Fitch, Y. Ohishi, G. Garbarino, K. Kato, M. J. Rosseinsky and K. Prassides, Sci. Adv., 2015, 1, e1500059.
12. Y. Takabayashi and K. Prassides, Struct. Bonding, 2016, 172, 119–138.
13. R. H. Zadik, Y. Takabayashi, R. H. Colman, G. Garbarino and K. Prassides, Mater. Chem. Front., 2018, 2, 993–998.
14. M. Menelaou, Y. Takabayashi, H. E. Okur, R. H. Zadik and K. Prassides, Int. J. Mod. Phys. B, 2018, 32, 1840020.
15. G. Klupp, P. Matus, K. Kamarás, A. Y. Ganin, A. McLennan, M. J. Rosseinsky, Y. Takabayashi, M. T. McDonald and K. Prassides, Nat. Commun., 2012, 3, 912.
16. P. Wzietek, T. Mito, H. Alloul, D. Pontiroli, M. Aramini and M. Ricco, Phys. Rev. Lett., 2014, 112, 066401.
17. A. Potočnik, A. Krajnc, P. Jeglič, Y. Takabayashi, A. Y. Ganin, K. Prassides, M. J. Rosseinsky and D. Arčon, Sci. Rep., 2014, 4, 4265.
18. A. Potocnik, A. Y. Ganin, Y. Takabayashi, M. T. McDonald, I. Heinmaa, P. Jeglic, R. Stern, M. J. Rosseinsky, K. Prassides and D. Arcon, Chem. Sci., 2014, 5, 3008–3017.
19. G. G. Guzman-Verri, R. T. Brierley and P. B. Littlewood, Nature, 2019, 576, 429–432.
20. L. M. Rodriguez-Martinez and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R15622–R15625.
21. J. P. Attfield, A. L. Kharlanov and J. A. McAllister, Nature, 1998, 394, 157–159.
22. K. Kato and H. Tanaka, Adv. Phys.: X, 2016, 1, 55–80.
23. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS) Report LAUR 86-748, Los Alamos National Laboratory, 2004.
24. Y. Yoshinari, H. Alloul, V. Brouet, G. Kriza, K. Holczer and L. Forro, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 6155–6166.
25. F. Sayetat, P. Fertey and M. Kessler, J. Appl. Crystallogr., 1998, 31, 121–127.
26. F. D. Murnaghan, Am. J. Math., 1937, 59, 235–260.
27. H. E. Okur and K. Prassides, J. Phys. Chem. Solids, 2019, 131, 44–49.
28. Y. L. Wang, M. F. Liu, R. Liu, Y. L. Xie, X. Li, Z. B. Yan and J.-M. Liu, Sci. Rep., 2016, 6, 27840.
29. J. A. McAllister and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 014514.
30. S. Catalano, M. Gibert, J. Fowlie, J. Iniguez, J.-M. Triscone and J. Kreisel, Rep. Prog. Phys., 2018, 81, 046501.
31. T. Katsufuji, Y. Taguchi and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 10145–10153.
32. P. V. Balachandran, S. R. Broderick and K. Rajan, Proc. R. Soc. A, 2011, 467, 2271–2290.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details of the experimental methods; tables of the refined parameters of the Rietveld analysis results of the synchrotron X-ray diffraction data at ambient and elevated pressures (Tables S1–S14); figures of the Rietveld fits of the diffraction data, of additional NMR spectral information, and of magnetic susceptibility data (Fig. S1–S26). See DOI: https://doi.org/10.1039/d4sc03399j

---