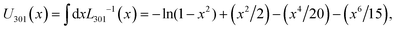Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mesoscale modelling of polymer-mediated adhesion: application to tack tests†
Aristotelis P.
Sgouros
 *ab,
Stefan
Knippenberg
c,
Anthony
Bocahut
d,
Phillip M.
Rauscher
e,
Ben
Sikora
e,
Stefano
Caputo
f,
Hee-Sung
Choi
g,
Vincent
Finsy
h,
Maxime
Guillaume
*ab,
Stefan
Knippenberg
c,
Anthony
Bocahut
d,
Phillip M.
Rauscher
e,
Ben
Sikora
e,
Stefano
Caputo
f,
Hee-Sung
Choi
g,
Vincent
Finsy
h,
Maxime
Guillaume
 c and
Doros N.
Theodorou
c and
Doros N.
Theodorou
 *a
*a
aSchool of Chemical Engineering, National Technical University of Athens, 9 Heroon Polytechniou Street, Zografou Campus, GR-15780 Athens, Greece. E-mail: doros@central.ntua.gr; Fax: +30 210 772 3112; Tel: +30 210 772 3157
bTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, Vass. Constantinou 48, GR-11635 Athens, Greece. E-mail: asgouros@eie.gr; Tel: +30 210 727 3807
cBattery Modeling and Simulation, Syensqo SA, 98, Rue de la Fusée, B-1130 Brussels, Belgium
dPolymer Physics, Specialty Polymers, Syensqo SA, Saint-Fons, Auvergne-Rhône-Alpes, France
ePolymer Physics, Specialty Polymers, Syensqo SA, Alpharetta, GA, USA
fBattery Modeling and Simulation, Specialty Polymers, Syensqo SA, Viale Lombardia 20, 20021, Bollate (MI), Italy
gBattery Modeling and Simulation, EWHA, Syensqo SA, Seoul, South Korea
hSolid State Battery Applicability Laboratory, Syensqo SA, 98 rue de la fusée, B-1120 Brussels, Belgium
First published on 11th March 2025
Abstract
We develop a generic computational methodology to understand and predict adhesion between polymers and solid substrates. The motion of coarse-grained polymer segments is tracked via a hybrid particle-field mesoscopic simulation method (BD/kMC) combining Brownian dynamics (BD) and kinetic Monte Carlo (kMC) for the entanglement dynamics as described by the slip-spring model. The method addresses entangled polymer films capped between solid surfaces under both quiescent and nonequilibrium conditions. The latter entail imposing constant rate extension along the aperiodic (normal) direction, while keeping the lateral dimensions constant. Experimentally relevant length scales and elongation rates can be addressed thanks to the coarse-graining inherent in the approach. These simulations are representative of “tack” tests, employed routinely for assessing the performance of soft adhesive materials. The performance of each interface is characterized by the stress–strain curves, yield stress, and toughness. The failure mechanism is determined upon analyzing the evolution of the stress–strain curve and the morphology of the fractured interfaces. The simulations are conducted over a broad parameter space by varying the rate of elongation, the rate constants for attachment/detachment of polymer segments to/from the surface, and the activation length. The latter describes the coupling with the pulling forces exerted on the particles at the interface by the rest of the polymer. Setting the activation length to zero is suitable for describing strong adhesives or highly compressible materials (foams). Under these conditions, toughness is maximized and increases significantly with elongation rate, sometimes leading to chain fracture. With increasing activation length the toughness of the interface decreases and detachment becomes more efficient at higher elongation rates since the increased stress accelerates the detachment process. In all cases considered here, toughness increases monotonically with adhesion. Furthermore, the yield stress increases consistently with increasing elongation rate due to the inability of the polymer to relax the imposed stress.
Design, System, ApplicationDesigning adhesives with tailor-made properties for specific applications constitutes a complex challenge involving chemistry, physical chemistry, and mechanics. We develop a mesoscopic computational strategy for quantifying the adhesion of long polymer chains on solid surfaces, with relaxation times spanning the millisecond to second time regime. The short-time dynamics of the coarse-grained moieties evolves with Brownian dynamics. The entanglement dynamics of the polymer chains is described with the Slip-Spring model. Computational specimens are subjected to constant rate elongation experiments, mimicking the setup of experimental tack tests. The performance of the interfaces is quantified by the evolution of stress-strain curves, toughness, and the morphology of the fractured surface. Toughness depends on a complex interplay of elongation rate, attachment/detachment rate constants, and the coupling of the pulling force with the rate constants. High elongation rates lead to increased yield stress, enhanced toughness, and pronounced fibrillation/cavitation, especially for strongly adhering polymers. In addition, the polymer chains detach more efficiently (at lower strains) with increasing elongation rate, especially as the coupling between the detachment rate and the pulling force improves. Our computational strategy is versatile, generic and can be applied to a range of industrial polymers and solid surfaces. |
1. Introduction
The optimal design of adhesives and adhesive joints for specific materials is a very challenging problem involving chemistry, physical chemistry, and mechanics.1–6 Apart from chemical bonding and physical interactions at the adhesive/substrate interface, the topography of the substrate surface and the elastic, viscoelastic, and ultimate properties of adhesive and substrate play a significant role. Tackiness is the characteristic property of pressure-sensitive adhesives (PSA) enabling them to adhere to surfaces upon simple contact, without requiring heat or chemical reactions.5 In other words, low contact pressure and short contact time are sufficient for bond formation with sufficient adhesive strength, referred to as ‘tack’ (ref. 4 cited in ref. 7). The higher the work of detachment per unit area the higher the tackiness of the PSA.7Tack experiments are employed routinely for the characterization of the adhesive properties and toughness of polymer/solid interfaces.5,8–11 A weight, with a flat or spherical tip, is brought into contact with the adhesive film and kept in contact for a given time. Subsequently, the weight is lifted at a steady rate, thus subjecting the interface to tensile deformation. By normalizing9 the recorded force and displacement throughout the course of the experiment one can obtain the tensile stress (σ) as a function of the engineering strain (ε). Accompanying the tack experiments with real-time in situ optical observations allows determining the failure mechanism and the form of the fractured interface.8 The mode of failure depends on interplay between the cohesive interaction of the polymer and the adhesive strength of the polymer/solid interface. Good adhesion promotes cohesive failure and rough end surfaces with bridging fibrils (fibrillation). Weak adhesion, on the other hand, favors adhesive failure; i.e., the polymer detaches completely from the solid surface. The pulling rate (or debonding rate)5 affects significantly the fracture mechanism as well; in general, fast (slow) pulling rates promote adhesive (cohesive) failure.5,9
Modeling adhesion has been dominated by continuum fracture mechanics analyses and numerical simulations (e.g., by the finite element method), using criteria based on the local stress state to describe crack propagation.12,13 Atomistic molecular dynamics simulations have been invoked to understand crack propagation and cohesive failure in two-dimensional materials such as graphene,14 brittle solids such as NaCl,15 a silica crystal (α-cristobalite) and a nanoporous, highly crosslinked polymer (saccharose-based heat-activated carbon).16 The latter study is particularly thorough in that it compares loading curves from molecular dynamics against the corresponding continuum mechanics predictions. It clearly shows that linear fracture mechanics works well in the case of the silica crystal, a brittle solid, but fails for the porous polymer, where the process zone is an order of magnitude larger. The introduction of a cohesive zone to describe plastic deformation past the crack tip in the continuum analysis reconciles the continuum description with the atomistic molecular dynamics.16
Failure at bi-material interfaces has been simulated with atomistic molecular dynamics for various systems. An interface between asphalt and crystalline silica was subjected to tension normal to the interface by Xu and Wang17 under elongation rates on the order of 109 s−1; it was shown that fast/slow pulling rates promote adhesive/cohesive failure in accordance with experimental tack tests.5,9 An effort to simulate pulling, peeling, and sliding in polyimide/silica glass systems using steered molecular dynamics and model systems of finite (nanoscopic) size was presented by Min et al.18 The molecular dynamics simulations of Gersappe and Robbins19 demonstrated that failure occurs in the region with the lowest initial yield stress and cannot be solely predicted by equilibrium interfacial free energies. As a result, failure can arise either at the polymer/solid interface (adhesive) or within the polymer film (cohesive).
In a very recent set of atomistic nonequilibrium molecular dynamics simulations, Kallivokas et al.20 predicted the conditions of local failure for graphene/epoxy interfaces subjected to shear stress over a range of temperatures, using periodic computational specimens. They found that failure times exhibited an extended Boltzmann–Arrhenius–Zhurkov dependence on stress and temperature. They also determined how the activation energy and activation volume governing the kinetics of failure changed upon introduction of defects or polar functional groups on the graphite surface. A similar study was conducted on carbon nanotube/epoxy interfaces.21
In general, atomistic molecular dynamics simulations of adhesion are limited by the high elongation rates and the small model system sizes they employ. When polymeric adhesives are present, atomistic simulations are typically confined to short chain lengths. Results are strongly rate dependent and cannot capture the extended plastic deformation zones associated with crack propagation in real polymeric materials.
Mesoscopic simulations offer the opportunity to address larger length and time scales. An important early work was that of Stevens.22 He undertook molecular dynamics simulations of interfacial fracture between highly cross-linked polymer networks, intended to mimic epoxy resins, and a solid surface, using a Kremer–Grest bead and spring model for the chains. Some of the wall particles were assumed to bond to polymer beads by breakable bonds; they were arranged in regular patches on the surface. The surface fraction occupied by these patches was varied systematically and its impact on the stress–strain curve and failure mode was examined. More recently, mesoscopic molecular dynamics of cohesive-adhesive failure of melts with Kremer–Grest chains slightly above the entanglement molar mass sandwiched between two “chemically heterogeneous” surfaces have been presented by Baggioli et al.23 The model surfaces consisted of strongly and weakly adsorbing sites in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion, but were characterized by different degrees of segregation of these sites. When strongly and weakly adsorbing sites were randomly interspersed on the surface, the surface behaved as a homogeneous one and adhesion was strong. As the distribution of strongly (and weakly) adsorbing sites became more “patchy”, characterized by larger length scales, adhesion weakened. In addition, Baljon et al.24 demonstrated that adhesive energy increases with prolonged contact duration between the polymeric material and the surface due to the redistribution of the polymer segments across the surface.
1 proportion, but were characterized by different degrees of segregation of these sites. When strongly and weakly adsorbing sites were randomly interspersed on the surface, the surface behaved as a homogeneous one and adhesion was strong. As the distribution of strongly (and weakly) adsorbing sites became more “patchy”, characterized by larger length scales, adhesion weakened. In addition, Baljon et al.24 demonstrated that adhesive energy increases with prolonged contact duration between the polymeric material and the surface due to the redistribution of the polymer segments across the surface.
A set of mesoscopic entanglement network-based simulations explored adhesion between polypropylene and polyamide 6 in the presence of polypropylene chains terminally grafted to the polyamide surface.25 It was determined that there is an optimal areal density of grafted chains, for which the fracture energy is maximized and which can play a role when barrier properties or penetration issues are regarded for light elements.26
The effect of varying the crosslinking density has been investigated by Jin et al.27 and Solar et al.11 In the absence of crosslinks the interface fails cohesively, whereas increasing the crosslinking degree enhances the tendency for adhesive failure. The performance of the interface was maximized for intermediate crosslinking degrees; at high degrees of crosslinking, even though the plateau stress increased, the sample became more brittle and failed at lower strains. The shape of the stress–strain curve at small strains was not affected by the crosslink density.
Subjecting highly entangled polymer chains to shear28,29 and extensional30,31 flows can result in bimodal chain end-to-end distance distributions under specific conditions. When specimens are subjected to extensional flow, they can undergo a flow-induced phase separation, resulting in the formation of distinct domains: one dominated by coiled macromolecules and another by significantly stretched, chain-like structures.30,31
A recent work by some of the authors32 proposed a multiscale simulation strategy for investigating and predicting interfacial structure and dynamics at entangled molten polymer/solid interfaces over a wide range of time and length scales, using polyethylene/graphite as an example. At the mesoscopic level, Brownian dynamics was used to follow the motion of beads in three-dimensional space while, in parallel, kinetic Monte Carlo simulation tracked slippage across entanglements, generation and loss of entanglements at chain ends, and adsorption/desorption events of coarse-grained segments on the solid substrate. The multi-chain slip-spring model was employed to represent entanglements,33–45 imposing constraints on the lateral motion of chains relative to their contour. The slip-spring model, a tube theory-based model, has demonstrated remarkable success in reproducing the experimental viscoelastic properties of polymers.29,34,46–52 The mesoscopic polyethylene/graphite model, extending the engine for mesoscopic simulations of polymer networks (EMSiPoN)29,34,53 to interfaces, was parameterized entirely on the basis of atomistic molecular dynamics simulations of shorter-chain melts at the same interface.32,54 The residence time of chains in the adsorbed state and their relaxation time under equilibrium conditions were determined as functions of molar mass, in good agreement with experiments.
The performance of the mesoscopic model has been tested extensively over a wide range of system geometries (e.g., bulk conditions,29,34 free films55 and polymer-solid32 interfaces), chain architectures,51–53 and flow conditions.29,52 The variation of the viscoelastic properties with increasing chain molecular weight conforms with scaling theories and data from atomistic simulations and experiments.29,56–58 Under high shear rate deformations, the model reproduces the startup stress overshoot observed in both simulations59,60 and experiments.61,62 Furthermore, it exhibits shear viscosities that scale with Weissenberg number similarly to those observed in slip-link simulations63 and experiments.62,64 The transition of chain end-to-end distance distributions from unimodal to broad bimodal,29 indicative of chain extension followed by rapid retraction, aligns with observations from detailed atomistic simulations.28
Single-chain slip-link65–67 and slip-spring33,43 models describe accurately the long-time dynamics and relaxation phenomena in highly entangled polymers. Despite being computationally efficient,67 single-chain models exhibit limitations, such as neglecting the spatial correlations between chains, the spatial inhomogeneities at the interfaces, and other effects.40,43 On the contrary, multi-chain slip-link45 and slip-spring29,34,38–40,63 models incorporate three-dimensional correlations. Being more detailed, multi-chain models can be connected more readily to atomistic calculations, and applied straightforwardly to a variety of situations, including free polymer surfaces,55 branched polymers,68 nanocomposites,32etc. According to Masubuchi and Uneyama,69 the chain conformations, diffusion and relaxation modulus are compatible among multichain slip-link and slip-spring models; there are, however, significant discrepancies in inter-chain cross-correlations within the relaxation modulus. A key advantage of slip-spring models over slip-link models is their foundation in a well-defined free-energy description, which facilitates the incorporation of interchain interactions.43
In this work we develop a mesoscopic simulation framework to model the constant-rate elongation of polymer films confined between adhesive solid surfaces. Throughout the simulation the lateral dimensions of the system are kept constant. The aforementioned setup is similar to the configuration employed in experimental tack tests.5 A step-by-step procedure is provided for parameterizing the mesoscopic model in a bottom-up or top-down fashion based on observables from atomistic simulations or experiments, respectively. For demonstration purposes, we parameterize the mesoscopic model using a minimal set of data representative of a noncrystallizable fluoropolymer. The response of the stress–strain curves and the corresponding failure mode are explored across a broad parameter space in terms of varying the attachment/detachment rate constants, the elongation rate and the coupling of the interfacial kinetics with the pulling force exerted by the polymer segments within the polymer film.
The article is structured as follows: methodological details are provided in section 2. In particular, section 2.1 develops the mesoscopic model for adhesive surfaces, section 2.2 provides a bottom-up parameterization framework for mapping the atomistic observables to the mesoscopic model, and section 2.3 illustrates the equilibration protocol preceding the tack tests. Section 3 discusses the findings from the tack test simulations. Section 3.1 illustrates the setup of tack simulations. Section 3.2 discusses results from the model with constant-rate interfacial kinetics. Section 3.3 introduces the effect of coupling the attachment/detachment rates with the pulling forces exerted by the polymer within the film. Finally, section 4 concludes the manuscript.
2. Methods
2.1 Mesoscopic model
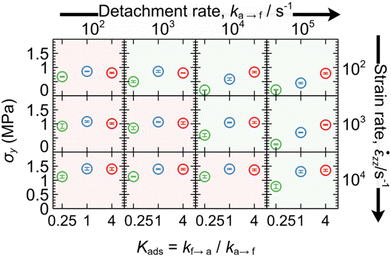
Each bead describes a polymer subchain of several Kuhn segments. Neighboring beads in the same chain are connected with entropic springs (hereafter referred to as strands) modelling the entropic elasticity of the chains, as shown in Fig. 1. Different chains can be connected with permanent (crosslinks)53 or temporary springs; the latter will be referred to as “slip-springs” (SS) and mimic the effect of chain entanglement.The beads can be attached to/detached from a solid surface subject to the transition rates:
 | (1) |
 | (2) |
 is the transition rate in the absence of normal force coupling. The transitions take place within an interfacial domain of thickness Ld. The attached beads are fixed in relation to the nearest solid surface for as long as they reside in the attached state.
is the transition rate in the absence of normal force coupling. The transitions take place within an interfacial domain of thickness Ld. The attached beads are fixed in relation to the nearest solid surface for as long as they reside in the attached state.
The thermodynamics is described by a Helmholtz free energy functional of the form:29,32
| A({rij}, {ρ(r)}, T) = Ab({rij}, T) + ASS({rij}, T) + Aexnb({ρ(r)}, T) + Awall{rij}. | (3) |
and
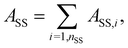 | (4) |
 | (5) |
being Kröger's approximation of the inverse Langevin function,29,70λstrand/SS the slope of the force at small extensions, and x = ri/rmax,strand/SS the extension ratio, where rmax,strand/SS and ri are the maximum extension and length of the strand/SS, respectively. A breaking criterion was incorporated to simulate chain scission, triggered when a strand's length exceeded its contour length, Lcontour,strand; see section 2.2.3.
A
exnb is the contribution from the nonbonded interactions,
 | (6) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = ρ/ρ*,
= ρ/ρ*, ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) = P/P*,
= P/P*, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = T/T*, and rSL = P*Mbead/(ρ*RT*), with ρ*, P* and T* being the characteristic mass density, pressure and temperature of the equation of state, and Mbead the molar mass of the bead. The rightmost term in eqn (6) multiplied by P* corresponds to the ideal gas contribution; P*
= T/T*, and rSL = P*Mbead/(ρ*RT*), with ρ*, P* and T* being the characteristic mass density, pressure and temperature of the equation of state, and Mbead the molar mass of the bead. The rightmost term in eqn (6) multiplied by P* corresponds to the ideal gas contribution; P*![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif)
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) /rSL = nbeadkBT, with
/rSL = nbeadkBT, with| nbead = ρ/mbead, |
The spatial discretization of the domain is realized via a kernel-based discretization scheme,72 where the local bead density (nbead,i = ρi/mbead,i) is assigned to individual particles through a weighting kernel with finite support, rc:72
 | (7) |
 | (8) |
Finally, Awall is the contribution from the polymer-wall interactions:
| Awall = Nawa + Nfwf | (9) |
wa − wf = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Kads) ln(Kads) | (10) |
| Kads = kf→a/ka→f | (11) |
The concentration of the attached (Ca) and detached (Cf = 1 − Ca) beads at the interface is dictated by the microscopic reversibility condition, Caka→f = Cfkf→a, or equivalently, by the equilibrium constant for attachment,
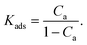 | (12) |
Although wa and wf do not affect the forces (and consequently, the dynamics), they contribute indirectly to the adhesion tension of the interface. Supposing that the solid surface is incompressible, the adhesion tension can be defined as the difference between the surface free energy of the solid substrate (γsv) and the interfacial energy (γsf):74
| γadh ≡ (γsv − γsf). | (13) |
 | (14) |
The mesoscopic particles execute Langevin dynamics in the high friction limit, subject to the stochastic equation of motion:29,32
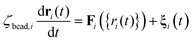 | (15) |
The dynamics of the slip-springs are dictated by a microscopically reversible kinetic Monte Carlo scheme (hopping scheme)29,34 for non-constant number of slip-springs (ensemble is grand-canonical with respect to the slip-springs) subject to an activity zactiv = eμ/kBT, where μ is the corresponding SS chemical potential. The hopping probability of a slip-spring end to an adjacent bead along the chain on which it lies is calculated according to the following equation:34
 | (16) |
| Pform,i = vhopzactivncands,iΔtkMC | (17) |
2.2 Bottom-up parameterization framework
We have developed a parameterization framework for mapping the mesoscopic model to observables from atomistic simulations and/or experimental measurements. As a case study, we will parameterize the mesoscopic model based on the minimal data set illustrated in Tables 1–3.| M mon (Da) | 50 |
| l c–c (Å) | 1.54 |
| θ c–c–c (°) | 112 |
| N mon/chain | M chain (kDa) | R ete 2 [Å] | N mon/chain D (1012 m2 s−1) |
|---|---|---|---|
| 50 | 2.5 | 619 | 24.863 |
| 100 | 5 | 1395 | 45.972 |
| 150 | 7.5 | 2113 | 44.264 |
| 200 | 10 | 2843 | 44.798 |
| M chain (kDa) | P (bar) | T (K) | ρ (kg m−3) |
|---|---|---|---|
| 10 | 1 | 300 | 1500 |
| 10 | 100 | 300 | 1545 |
| 10 | 200 | 300 | 1557 |
| 7.5 | 1 | 300 | 1499 |
| 7.5 | 1 | 400 | 1425 |
| 7.5 | 1 | 500 | 1328 |
In particular, Table 1 displays the molar mass of the effective monomer Mmon (average molar mass per backbone carbon bond), the bond length lc–c between successive backbone carbon atoms and the bond angle θc–c–c formed by triplets of backbone carbon atoms. Table 2 depicts indicative structural (mean squared end-to-end distance) and dynamical properties (diffusion coefficient) of the polymer across the Rouse regime. Table 3 illustrates the volumetric properties of the reference polymer as a function of molar mass, temperature and pressure. The dataset of the reference sample is indicative of a noncrystallizable fluoropolymer and was obtained via atomistic simulations. Table 4 presents key quantities extracted from the dataset in Tables 1–3.
| Quantity | Value | Equation | Description |
|---|---|---|---|
| C ∞ | 6 | 23 | Flory's characteristic ratio |
| b k (Å) | 11.15 | 24 | Kuhn length |
| M e (kDa) | 22.56 | 20 | Molar mass between entanglements |
| a tube (Å) | 79.33 | 30 | Tube diameter |
| ζ mon (10−12 kg s−1) | 92.13 | 29 | Monomeric friction coefficient |
| ρ 300 K (kg m−3) | 1504.1 | 6 | Mass density (limit Mchain → ∞) |
| κ ex,300 K (MPa−1) | 0.00585 | 22 | Excess isothermal compressibility |
The mesoscopic model can be parameterized via a six-step procedure which has as follows:
1. Coarse graining
2. Volumetric properties
3. Conformational statistics
4. Bead dynamics
5. Slip-spring kinetics
6. Kernel optimization
For the convenience of the reader, the parameters of the mesoscopic model are illustrated in Table 5. The following sections provide a detailed description of each step.
| Scheme | Quantity | Value | Description |
|---|---|---|---|
| Coarse-graining | N mon/bead | 160 | Monomers per bead |
| M bead (kDa) | 8 | Bead molar mass | |
| Strand | λ strand (kcal mol−1 Å−2) | 0.0031 | Strand stiffness |
| r max,strand (Å) | 204.27 | Strand maximum extension | |
| x tol,strand | 0.99 | Strand extension tolerance | |
| Slip-spring | λ ss (kcal mol−1 Å−2) | 0.0004 | Slip-spring stiffness |
| r max,SS (Å) | 119 | Slip-spring maximum extension | |
| x tol,SS | 0.99 | Slip-spring extension tolerance | |
| Kinetic Monte Carlo | r attempt (Å) | 117.8 | Slip-spring formation radius |
| v hop (s−1) | 65.21 | Hop pre-exponential factor | |
| z activ | 0.002235365 | Slip-spring activity | |
| EOS | ρ* (kg m−3) | 1559.83 | EoS characteristic density |
| P* (MPa) | 20.3 | EoS characteristic pressure | |
| T* (K) | 759.86 | EoS characteristic temperature | |
| Kernel | r c (Å) | 50 | Kernel support |
| C W | 0.953 | Kernel weighting factor | |
| C ζ | 0.900 | Kernel friction factor | |
| Brownian dynamics | ζ bead (10−9 kg s−1) | 14.74 | Bead friction coefficient |
| Δtcrit (ns) | 58 | Maximum time step |
| Mbead < Me | (18) |
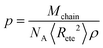 | (19) |
| Me = NAnt2ρp3 | (20) |
The packing length of the longest chain considered in Table 2 is p = 3.89 Å at 300 K, resulting in Me = 22.56 kDa. The bead mass was set to Mbead = 8 kDa per bead, roughly three times smaller than Me. This corresponds to Nmon/bead = Mbead/Mmon = 160 monomers per bead.
 | (21) |
| κex−1 = nbead(∂Pex/∂nbead)|T | (22) |
 | ||
| Fig. 2 (a) Density versus pressure, temperature and chain molar mass from the reference sample (solid, Table 3), and the equation of state (diagonal pattern) with the optimized EoS parameters listed in Table 5. (b) Evolution of the merit function (eqn (21)) during the course of the optimization starting with the initial set of parameters, (ρ*,P*,T)init = (1692.77 kg m−3, 43.6 MPa, 769.81 K). | ||
 | (23) |
A useful quantity for the mapping atomistic segments to the mesoscopic level, is the Kuhn length (bk):81
 | (24) |
 | (25) |
| 〈Rete, strand2〉 = Nk/beadbk2 | (26) |
| Lcontour,strand = Nk/beadbk | (27) |
The bonded terms of the free energy were parameterized based on the conformational statistics of Table 2. For clarity, the variation of the end-to-end vector with molar mass of the reference system is illustrated in Fig. 3. Flory's characteristic ratio was estimated as C∞ = 6 for the largest chain considered here (eqn (23)). The corresponding Kuhn length equals bk = 11.15 Å (eqn (24)) and the number of Kuhn segments per bead is Nk/bead = 18.33 (eqn (25)). Modelling finitely extensible strands, as in eqn (5), necessitates defining both their maximum extension (rmax,strand) and stiffness (λstrand). The former was set equal to the contour length of the strand, rmax,strand = Lcontour,strand = 204.27 Å (eqn (27)). The maximum extension tolerance was set to xtol,strand = 0.99. The stiffness was optimized to λstrand = 0.0031 kJ mol−1 Å−2) upon matching the second moment of the strand length distribution with eqn (26), 〈rstrand2〉 ∼ 〈Rete,strand2〉, using Brent's optimization algorithm.79 As shown in Fig. 3, the mesoscopic model faithfully reproduces the conformations of the reference dataset and the corresponding random walk model, eqn (26).
 | (28) |
 | (29) |
Fig. 4 illustrates the self-diffusion coefficient scaled by the number of monomers for each chain in Table 2. The friction coefficient was estimated viaeqn (29) across the plateau region in Fig. 4 to ζmon = 92.13 × 10−12 kg s−1. As shown in Fig. 4, the mesoscopic model reproduces the short-time dynamics from the reference system and the corresponding Rouse model (eqn (29)). It is noted that the model exhibits limitations in accurately capturing short-time dynamics, particularly those associated with segmental motions of the polymer chains. This shortcoming is evident in the limited accuracy of predictions for G′ and G′′ at high frequencies.34
 | ||
| Fig. 4 Self-diffusion coefficient scaled by the number of monomers per chain of the reference polymer from Table 2 (circles), the mesoscopic model (squares) and the Rouse model, eqn (29) (dashed line). The mesoscopic simulations were conducted using the parameters in Table 5 without slip-springs (since Mchain < Me). | ||
The tube diameter can be estimated from Me based on eqn (30):83
 | (30) |
The number of slip-springs per bead can be estimated based on the number of entangled strands per chain:
 | (31) |
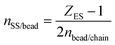 | (32) |
The preexponential factor vhop is a chain-length-independent quantity dictating the hopping frequency. An upper bound can be obtained by the following equation:34
 | (33) |
Simulations in the grand-canonical ensemble require inputting the slip-spring activity which can be estimated as follows:29
 ∼ 60 beads. We introduce the following reference units of length, σr = [mbead/ρ300 K]1/3 = 2.067 × 10−9 m; mass, mr = mbead = 1.328 × 10−23 kg; energy, εr = kBT = 4.14 × 10−21 J; and time,
∼ 60 beads. We introduce the following reference units of length, σr = [mbead/ρ300 K]1/3 = 2.067 × 10−9 m; mass, mr = mbead = 1.328 × 10−23 kg; energy, εr = kBT = 4.14 × 10−21 J; and time, 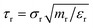 = 1.17063 × 10−10 s. According to ref. 72, an upper bound for the (reduced) time step can be obtained from the empirical formula, Δ
= 1.17063 × 10−10 s. According to ref. 72, an upper bound for the (reduced) time step can be obtained from the empirical formula, Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) crit ∼ (1/6)
crit ∼ (1/6)![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) c2.4
c2.4![[small zeta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e126.gif)
![[small kappa, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1e8.gif) ex,T=300 K = 495; or, in real units, Δtcrit ∼ 58 ns. The compensating factors for the weighting kernel (w′ → CWw, eqn (8)) and friction (
ex,T=300 K = 495; or, in real units, Δtcrit ∼ 58 ns. The compensating factors for the weighting kernel (w′ → CWw, eqn (8)) and friction ( eqn (28)) were determined from a bulk simulation with 800 beads at 300 K as CW = ρCW=1/ρEoS = 0.953 and Cζ = DCζ=1/DEinstein = 0.900, where DEinstein = kBT/(Nmon/beadζbead). For additional details the reader is referred to section 3.2 in ref. 72.
eqn (28)) were determined from a bulk simulation with 800 beads at 300 K as CW = ρCW=1/ρEoS = 0.953 and Cζ = DCζ=1/DEinstein = 0.900, where DEinstein = kBT/(Nmon/beadζbead). For additional details the reader is referred to section 3.2 in ref. 72.
Even though successful parameterization of the kernel scheme can restore the desired volumetric properties, the scheme exhibits limitations in accurately capturing structural features at short length scales. As demonstrated in ref. 72, the radial distribution function softens at small interparticle distances, and this effect intensifies with increasing coarsening. The range over which errors in representing structural features are introduced is commensurate with the characteristic length scale of the density discretization scheme.
2.3 Equilibration protocol
An initial configuration with 400 chains, each one with molecular weight 120 kDa (15 beads per chain) was generated with the EMSiPoN code29,34,85 at T = 300 K and ρ = 1500 kg m−3 subject to the constraint that the polymer be confined between the solid surfaces along the z-axis. The connectivity of the strands and slip-springs was described with the fixed image convention.86 The generation was realized with a Monte Carlo scheme which conducts reverse sampling from the probability distribution dictated by the free energy of the strands (eqn (5)); for details see section S2.3 in ref. 87.A common criterion for minimizing finite-size effects is a box dimension-to-chain radius of gyration ratio of approximately four. In our simulations, the box dimension along each direction was set to ∼37.6 nm; roughly five times larger than the chain radius of gyration (∼7.5 nm); test simulations with lateral dimensions of 3.5 and 7 times the chain's Rg produced very similar results.
Fig. 5 illustrates the evolution of box size, normal pressure and number of slip-springs during the stages of the equilibration protocol. Initially, a sample of noninteracting chains (deactivated nonbonded interactions) was simulated in the NVT ensemble in order to efficiently relax their conformations. Next, the nonbonded interactions were activated and the sample was simulated in the NVT ensemble and subsequently in the NLxLyσzzT ensemble to relax the normal stress. The simulation continued with the grand canonical slip-spring scheme activated subject to the activity listed in Table 5 until the number of slip-springs fluctuated about a plateau value. A hopping frequency 100 times higher than the standard value in Table 5 was used in this step to accelerate slip-spring dispersion. Note that the final slip-spring distribution is a thermodynamic property, independent of the hopping frequency (see Appendix B in ref. 29). Also note that the equilibrium number of slip-springs of the capped polymer is lower than that of a bulk counterpart of the system with the same temperature and number of chains (dashed line in Fig. 5c), because the number of entanglements is lower at the polymer/solid interfaces.32,36,37
After thoroughly equilibrating the sample, the surface attachment/detachment scheme was activated subject to the prescribed transition rates (ka→f, kf→a) and activation lengths (la→f, lf→a) until the populations of attached/detached beads converged. The resulting concentration depends strictly on Kads = kf→a/ka→f and not on the individual values of kf→a and ka→f. This is demonstrated in Fig. 6a which depicts the evolution of the concentration of adsorbed beads (Ca) for various values of Kads = kf→a/ka→f and ka→f. At long times, Ca plateaus to the concentration dictated by Kads in eqn (12), regardless of the magnitude of ka→f. Decreasing ka→f results in the same concentration, albeit equilibrium is achieved in longer times. According to Fig. 6b, the total bead population close to the interfacial region increases slightly with Kads, because the effective polymer/surface interactions become more attractive. The increase in density near the solid surface depends on the strength of the attractive interactions from the solid surface relative to the compressibility of the polymer.88,89
 | ||
| Fig. 6 Evolution of the (a) concentration of adsorbed beads (Ca) and (b) population of adsorbed and free beads within an interfacial domain with thickness rads = 19.42 Å, following the relaxation protocol described in Fig. 5. Several cases are examined here where (Kads, ka→f/s−1) = (1/4, 106), (1, 106), (4, 106), (1, 105) and (1, 104) corresponding to green, light blue, red, blue and dark blue colours, respectively. The dashed lines in (a) illustrate the prediction of the concentration from eqn (12); Ca ∼ Kads/(1 + Kads). | ||
The mesoscopic representations were visualized with the open source Visual Molecular Dynamics (VMD, v1.9.4)90 package and the Photopea Photo Editor (last accessed 15/12/2024).91 The graphs were prepared using the Veusz package (v.3.6.2).92
3. Results
3.1 Principles of tack tests
Tack tests were simulated by elongating the simulation domain along the z-direction at a constant elongation rate according to eqn (34):Lz(t) = Lz,0(1 + ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zzt). zzt). | (34) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, with εmax being the maximum engineering strain.
zz, with εmax being the maximum engineering strain.
Unless otherwise stated, the time step was set to Δt = min(Δtcrit/2, ka→f−1, kf→a−1). By default, the maximum value was set to half the critical time step (Δtcrit = 59 ns) predicted by the analysis in section 2.2.6.72 However, in cases with fast interfacial kinetics, Δt was decreased to the lowest value of the inverse detachment or attachment rate constant to accurately capture attachment and detachment events.
Fig. 7a displays the evolution of the normal stress during the course of the tack test. Fig. 7b illustrates snapshots at strain increments of 0.2. During the initial phase, the stress increases at a rate commensurate with the elastic modulus of the material. This continues until the stress reaches a maximum value, at which point the material can no longer sustain higher loads. Thereafter, stress decreases progressively and cavities expand toward the center of the film until the eventual failure of the interface, either cohesive or adhesive.
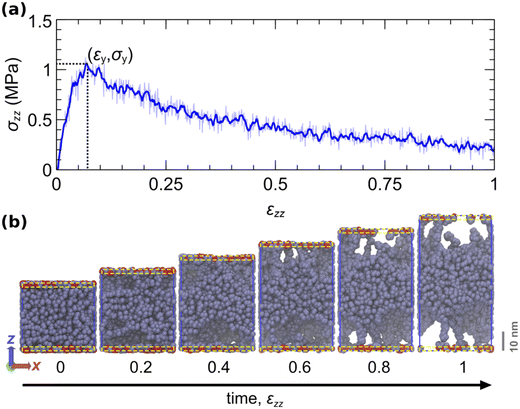 | ||
Fig. 7 Illustration of an indicative tack test simulation. (a) Stress–strain curve of the tack test. The thin blue curve indicates the instantaneous stress. The thick line depicts the smoothed stress–strain curve with a Savitzky–Golay filter79,93 over a window Δε = 0.012. The dotted lines indicate the point where the stress becomes maximum. (b) Snapshots of the simulated trajectory at strain increments of 0.2. The system comprises 400 chains, each with a molecular weight of 120 kDa. The periodic x and y box dimensions remain constant. The aperiodic z-dimension of the box is elongated at a steady rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 103 s−1. Beads within an interfacial region of thickness ∼19.42 Å near each surface (yellow dashed rectangles) can reversibly attach and detach with rates ka→f = kf→a = 104 s−1 (Kads = 1). Here, the activation lengths are set to zero (no force coupling). Attached/detached beads are displayed with red/gray colour. The simulations are conducted with the parameters listed in Table 5. zz = 103 s−1. Beads within an interfacial region of thickness ∼19.42 Å near each surface (yellow dashed rectangles) can reversibly attach and detach with rates ka→f = kf→a = 104 s−1 (Kads = 1). Here, the activation lengths are set to zero (no force coupling). Attached/detached beads are displayed with red/gray colour. The simulations are conducted with the parameters listed in Table 5. | ||
3.2 Constant-rate interfacial kinetics
A series of tack tests have been realized, spanning a broad parameter range in terms of varying elongation rate![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, detachment rate constant ka→f, and equilibrium constant for adsorption Kads, as shown in Table 6. The elongation rate spans three orders of magnitude and ranges from 102 s−1 to 104 s−1. The desorption rate constant spans four orders of magnitude, ranging between 102 s−1 to 105 s−1. For reference, the desorption rate constant of the weakly adsorbing PE/graphite interface32 is ∼1.73 × 107 s−1. The adsorption equilibrium constant has been set to 1/4, 1 and 4, values indicative of weak, moderate and good adhesion, respectively. The thickness of the interfacial region was set to the radius of gyration corresponding to the mesoscopic beads,
zz, detachment rate constant ka→f, and equilibrium constant for adsorption Kads, as shown in Table 6. The elongation rate spans three orders of magnitude and ranges from 102 s−1 to 104 s−1. The desorption rate constant spans four orders of magnitude, ranging between 102 s−1 to 105 s−1. For reference, the desorption rate constant of the weakly adsorbing PE/graphite interface32 is ∼1.73 × 107 s−1. The adsorption equilibrium constant has been set to 1/4, 1 and 4, values indicative of weak, moderate and good adhesion, respectively. The thickness of the interfacial region was set to the radius of gyration corresponding to the mesoscopic beads,  . The activation lengths in eqn (1) and (2) will be set to zero for the time being (lf→a = la→f = 0); therefore, attachment/detachment rates remain constant throughout the simulation;
. The activation lengths in eqn (1) and (2) will be set to zero for the time being (lf→a = la→f = 0); therefore, attachment/detachment rates remain constant throughout the simulation;  and
and 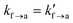 in eqn (1) and (2). This assumption is relevant in situations where strong bonds are formed between the polymer and the solid surface; e.g., detachment of strong adhesives. Given that the energy barriers are significantly high, the effect of the activation length term in eqn (1) and (2) becomes minimal. The maximum engineering strain will be set to εmax = 1 which is large enough for the cavitation/fibrillation processes to kick in and the damage of the polymer/solid interface to be considered irreversible. This contraint on the maximum strain will be relaxed in the next section. For each combination of parameters we conducted three individual experiments starting with a different configuration. A total of 108 simulated tack tests have been conducted serially, taking a total of ∼20 days on a Intel(R) Xeon(R) Silver 4314 CPU@2.40GHz processor with 16 physical cores.
in eqn (1) and (2). This assumption is relevant in situations where strong bonds are formed between the polymer and the solid surface; e.g., detachment of strong adhesives. Given that the energy barriers are significantly high, the effect of the activation length term in eqn (1) and (2) becomes minimal. The maximum engineering strain will be set to εmax = 1 which is large enough for the cavitation/fibrillation processes to kick in and the damage of the polymer/solid interface to be considered irreversible. This contraint on the maximum strain will be relaxed in the next section. For each combination of parameters we conducted three individual experiments starting with a different configuration. A total of 108 simulated tack tests have been conducted serially, taking a total of ∼20 days on a Intel(R) Xeon(R) Silver 4314 CPU@2.40GHz processor with 16 physical cores.
| Quantity | Value | Description |
|---|---|---|
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz
(s–1)
zz
(s–1) |
102–104 | Elongation rate |
| k a→f (s–1) | 102–105 | Detachment rate |
| K ads = kf→a/ka→f | 0.25, 1, 4 | Equilibrium adsorption constant |
| r ads = Rg,bead (Å) | 19.42 | Interfacial thickness |
| l f→a = la→f | 0 | Activation lengths |
Fig. 8 illustrates the stress–strain curves from the tack tests in dependence of the elongation rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz (increasing from top-to-bottom), detachment rate ka→f (increasing from left-to-right) and equilibrium constant for adsorption Kads (green < blue < red). The corresponding snapshots for Kads = 1/4, 1 and 4 are illustrated in Fig. 9, 10 and 11, respectively.
zz (increasing from top-to-bottom), detachment rate ka→f (increasing from left-to-right) and equilibrium constant for adsorption Kads (green < blue < red). The corresponding snapshots for Kads = 1/4, 1 and 4 are illustrated in Fig. 9, 10 and 11, respectively.
 | ||
Fig. 8 Stress–strain curves in dependence of the detachment rate ka→f (increasing from left to right), elongation rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz (increasing from top to bottom) and adsorption constant Kads = kf→a/ka→f = 1/4 (green), 1 (blue) and 4 (red). Scenarios where zz (increasing from top to bottom) and adsorption constant Kads = kf→a/ka→f = 1/4 (green), 1 (blue) and 4 (red). Scenarios where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz is smaller than (larger than or equal to) ka→f are indicated with green (red) shades. The stress has been smoothed with a Savitzky–Golay filter79,93 over a window Δε = 0.012. zz is smaller than (larger than or equal to) ka→f are indicated with green (red) shades. The stress has been smoothed with a Savitzky–Golay filter79,93 over a window Δε = 0.012. | ||
 | ||
| Fig. 10 Same as Fig. 9 but for Kads = 1. | ||
 | ||
| Fig. 11 Same as Fig. 9, for Kads = 4. | ||
In situations where the strain-rate is slower than the detachment rate constant (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz < ka→f) the interface has adequate time to respond to the deformation and relax the imposed tensile stress. Such conditions promote fast detachment in general, albeit the effect is sensitive to the equilibrium adsorption constant. To elaborate, for the smallest equilibrium adsorption constant considered here (Kads = 1/4), we find a consistent behavior where failure is strictly adhesive across this regime; e.g., panels with green shade in Fig. 8 and 9. For intermediate values (Kads = 1) the polymer detaches fully at ε = 1, with two exceptions; (
zz < ka→f) the interface has adequate time to respond to the deformation and relax the imposed tensile stress. Such conditions promote fast detachment in general, albeit the effect is sensitive to the equilibrium adsorption constant. To elaborate, for the smallest equilibrium adsorption constant considered here (Kads = 1/4), we find a consistent behavior where failure is strictly adhesive across this regime; e.g., panels with green shade in Fig. 8 and 9. For intermediate values (Kads = 1) the polymer detaches fully at ε = 1, with two exceptions; (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, ka→f) = (102, 103) and (103, 104) s−1 in Fig. 10. However, for Kads = 4, no instances of complete polymer detachment from the surface were observed at ε = 1 within the parameter range investigated here; see mesoscopic configurations in Fig. 11.
zz, ka→f) = (102, 103) and (103, 104) s−1 in Fig. 10. However, for Kads = 4, no instances of complete polymer detachment from the surface were observed at ε = 1 within the parameter range investigated here; see mesoscopic configurations in Fig. 11.
Scenarios where the elongation rate is faster than the detachment rate constant, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz ≥ ka→f (red-shaded plots in Fig. 8), promote partial detachment, in general, because mesoscopic segments do not have adequate time to respond to the deformation. For Kads = 1, the adhesion between the polymer and the surface is already quite strong; therefore, further increasing Kads does not significantly affect the system's response. Interestingly, when the timescale separation between deformation and detachment rate is large (
zz ≥ ka→f (red-shaded plots in Fig. 8), promote partial detachment, in general, because mesoscopic segments do not have adequate time to respond to the deformation. For Kads = 1, the adhesion between the polymer and the surface is already quite strong; therefore, further increasing Kads does not significantly affect the system's response. Interestingly, when the timescale separation between deformation and detachment rate is large (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz ≫ ka→f) the system's response becomes insensitive to the latter. For example, note that the two leftmost panels in the last row of Fig. 8 are practically identical; the same applies in Fig. 9–11 as well. This occurs because the detachment rate becomes negligible in relation to the elongation rate and thus only the initial concentration of adsorbed segments (dictated by Kads) affects the system's response.
zz ≫ ka→f) the system's response becomes insensitive to the latter. For example, note that the two leftmost panels in the last row of Fig. 8 are practically identical; the same applies in Fig. 9–11 as well. This occurs because the detachment rate becomes negligible in relation to the elongation rate and thus only the initial concentration of adsorbed segments (dictated by Kads) affects the system's response.
According to our simulations, the general trend is that strongly adsorbing surfaces (high Kads) result in slow detachment (cohesive failure is promoted), whereas weakly adsorbing ones (low Kads) in fast detachment (promotion of adhesive failure). According to ref. 23 and 27, increasing the crosslink density (which in turn, improves the cohesion of the polymer network) enhances the tendency for adhesive failure, and vice versa. It appears that the failure mechanism is a strong function of the ratio between strength of the polymer–polymer (cohesion) and surface-polymer (adhesion) interactions. Supposing that the adhesion of the polymer to the solid is much stronger than the cohesive interactions, the sample is expected to fail cohesively. On the other hand, a weakly adsorbing surface is expected to fail adhesively.
According to experimental tack tests,5,9 the roughness and fibrillation degree at the fractured material surface depend strongly on the imposed elongation rate. Low deformation rates result in sparse distributions of thick fibers and large cavities. High deformation rates, on the other hand, result in dense distributions of thin fibers.
The mesoscopic model yields a similar behavior:
• At slow elongation rates we observe thick and sparse fibers forming bridges between the edges of the simulation box. This response is illustrated clearly in the top row of Fig. 9–11 for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 102 s−1 with red shades (partial detachment).
zz = 102 s−1 with red shades (partial detachment).
• At moderate rates (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 103 s−1), we observe denser distributions of thinner fibers, as shown in the second row of Fig. 9–11.
zz = 103 s−1), we observe denser distributions of thinner fibers, as shown in the second row of Fig. 9–11.
• At the highest rates considered here (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 104 s−1), the rate of elongation of the box boundaries (and the velocity of the adsorbed beads) becomes commensurate with the relaxation rate on the strand level (∼ζbead/mbead). This rapid elongation induces a shock, where strands lack sufficient time to respond, leading to the formation of a low density region between the adsorbed layer and the bulk polymer. This region is populated by highly ordered strands and is indicative of extreme fibrillation conditions.
zz = 104 s−1), the rate of elongation of the box boundaries (and the velocity of the adsorbed beads) becomes commensurate with the relaxation rate on the strand level (∼ζbead/mbead). This rapid elongation induces a shock, where strands lack sufficient time to respond, leading to the formation of a low density region between the adsorbed layer and the bulk polymer. This region is populated by highly ordered strands and is indicative of extreme fibrillation conditions.
Overall, we observe a trend toward smaller cavities/denser distributions of thinner fibers as the elongation rate increases and a progressive orientation of the polymer chains5,94 along the pulling direction. Similar fibril-like nanomorphologies and cavitation tendencies have been reported in relevant simulation studies.11,22,23,27
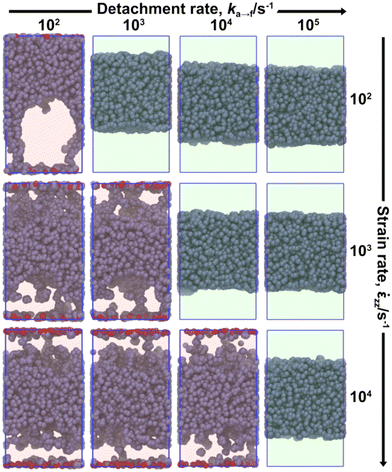
Fig. 12 illustrates the yield tensile stress (σy) at the end of the reversible portion (also see Fig. 7a) of the stress–strain curve, averaged over three individual tack tests performed for each scenario considered in Table 6. The yield stress is an increasing function of the elongation rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, e.g., inspect Fig. 12 from top to bottom. This happens because the polymer cannot relax the imposed stress efficiently under fast elongation rates. This response conforms with reports from experimental tack tests5,9 and relevant atomistic17,18 and mesoscopic23 simulations. In addition, the maximum stress reported from experimental tack tests5 is in the order of 0.1–1 MPa; in good quantitative agreement with our findings. Kads indicates higher adsorption rates and enhanced concentration of adsorbed beads (see eqn (12)), therefore increased adhesion. In situations where
zz, e.g., inspect Fig. 12 from top to bottom. This happens because the polymer cannot relax the imposed stress efficiently under fast elongation rates. This response conforms with reports from experimental tack tests5,9 and relevant atomistic17,18 and mesoscopic23 simulations. In addition, the maximum stress reported from experimental tack tests5 is in the order of 0.1–1 MPa; in good quantitative agreement with our findings. Kads indicates higher adsorption rates and enhanced concentration of adsorbed beads (see eqn (12)), therefore increased adhesion. In situations where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz ≥ ka→f (red background in Fig. 12) σy increases from Kads = 1/4 to 1. Further increasing Kads does not increase stress, indicating that above a threshold value the concentration of the adsorbed beads at the interface is high enough and cavitation is realized slightly further towards the bulk phase.
zz ≥ ka→f (red background in Fig. 12) σy increases from Kads = 1/4 to 1. Further increasing Kads does not increase stress, indicating that above a threshold value the concentration of the adsorbed beads at the interface is high enough and cavitation is realized slightly further towards the bulk phase.
In cases where ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz < ka→f, σy increases monotonically in most cases (panels with green background in Fig. 12). In cases with pronounced timescale separation ka→f ≪
zz < ka→f, σy increases monotonically in most cases (panels with green background in Fig. 12). In cases with pronounced timescale separation ka→f ≪ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, the maximum stress is practically insensitive to detachment rate. For instance, the panels (
zz, the maximum stress is practically insensitive to detachment rate. For instance, the panels (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz/s−1, ka→f/s−1) = (104, 102), (104, 103), (104, 104) are identical with each other in Fig. 12.
zz/s−1, ka→f/s−1) = (104, 102), (104, 103), (104, 104) are identical with each other in Fig. 12.
The evolution of stress during a tack test is directly related to the strength of the cohesive interactions within the polymer. If adhesion to the surface is significant, the larger the elastic modulus of the polymer, the higher the resistance to deformation (i.e., the induced stress).5,9 This effect is demonstrated in Fig. 13 which compares the stress–strain curves for samples with increasing bulk modulus, or conversely, decreasing compressibility. The red curve shows the case where we consider the default parameters in Table 5, whereas the blue and green curves illustrate cases where the compressibility has been decreased by 10 and 100 times, respectively. It is evident that decreasing compressibility results in steeper stress increase at low strains and higher yield stress. In addition, the samples become more brittle with decreasing compressibility, as the location of yield stress moves toward zero.
 | ||
Fig. 13 Stress–strain curve from a tack experiment with ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = ka→f = 103 s−1 and Kads = 1. Red curve illustrates a case using the default parameters in Table 1. Blue/green curve illustrates the impact of decreasing compressibility by a factor of 10/100 upon multiplying the characteristic pressure P* by 10/100, respectively. zz = ka→f = 103 s−1 and Kads = 1. Red curve illustrates a case using the default parameters in Table 1. Blue/green curve illustrates the impact of decreasing compressibility by a factor of 10/100 upon multiplying the characteristic pressure P* by 10/100, respectively. | ||
3.3 Effect of pulling force
The present section relaxes the assumption incorporated in the previous section and considers the effect of coupling the normal forces exerted on the beads to the interfacial kinetics. The coupling is tuned by the activation lengths in eqn (1) and (2). The higher the activation length, the higher the coupling with the pulling forces. As a result, beads near the interface that experience pulling forces toward the bulk region are more likely to detach, and less likely to attach to the interface. On the contrary, beads that experience forces toward the solid surface will attach more frequently and detach at a slower pace. According to Transition State Theory, the activation length is commensurate with the distance between the coordinate of the current state (attached/detached) and the coordinate at the free energy barrier beyond which a transition in state occurs (detached/attached). A recent model for the fracture of polymer chains95 demonstrated that, even though this approach correctly estimates the order of magnitude of the activation length, it can underestimate it by a factor 38–60%.To simplify our analysis we will consider the extreme scenarios shown Table 6. Specifically, we will address weakly (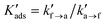 = 1/4) and strongly (
= 1/4) and strongly (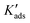 = 4) adsorbing interfaces exhibiting either slow (
= 4) adsorbing interfaces exhibiting either slow ( = 102 s−1) or fast (
= 102 s−1) or fast ( = 105 s−1) kinetics. Note that
= 105 s−1) kinetics. Note that  denotes the normal force-independent factor of the transition rate, which increases with decreasing transition barriers Ei→j, as indicated in eqn (1) and (2). Several values for the activation length will be considered here, with a maximum value set to Rg,bead = 19.42 Å. We will consider the faster elongation rates in Table 6 (
denotes the normal force-independent factor of the transition rate, which increases with decreasing transition barriers Ei→j, as indicated in eqn (1) and (2). Several values for the activation length will be considered here, with a maximum value set to Rg,bead = 19.42 Å. We will consider the faster elongation rates in Table 6 (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 103 s−1 and 104 s−1) in order to access very large deformations. The time step is set to 29 ns for the case
zz = 103 s−1 and 104 s−1) in order to access very large deformations. The time step is set to 29 ns for the case ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 103 s−1, and 2.9 ns for the case
zz = 103 s−1, and 2.9 ns for the case ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 104 s−1 and the normal forces are averaged for 2000 time steps in each case. In doing so, the normal forces are averaged within the same number of steps and “strain window”, Δε = 2000
zz = 104 s−1 and the normal forces are averaged for 2000 time steps in each case. In doing so, the normal forces are averaged within the same number of steps and “strain window”, Δε = 2000![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zzdt = 0.058. For each scenario, two simulations were performed, each initialized with a different initial condition. A total of 32 simulated tack tests have been conducted serially, taking a total of ∼10 days on a Intel(R) Xeon(R) Silver 4314 CPU@2.40GHz processor with 16 physical cores.
zzdt = 0.058. For each scenario, two simulations were performed, each initialized with a different initial condition. A total of 32 simulated tack tests have been conducted serially, taking a total of ∼10 days on a Intel(R) Xeon(R) Silver 4314 CPU@2.40GHz processor with 16 physical cores.
Fig. 14a illustrates the stress–strain curves of weakly (Kads = 1/4) and strongly (Kads = 4) adsorbing interfaces as a function of the activation length at various elongation rates. The detachment rate has been set to  = 102 s−1 indicative of slow interfacial kinetics (high transition barriers).
= 102 s−1 indicative of slow interfacial kinetics (high transition barriers).
In situations where la→f = 0 (leftmost panels of Fig. 14a), there is delayed failure at higher elongation strains and significantly increased stress. Interestingly, for the fastest elongation rate, ∼1% of chains fractured during the course of the simulation, indicating a tendency for partial cohesive failure. The stress is maximized in this case and reaches ca. 4 MPa. This behavior is expected, since the detachment rate is two orders of magnitude lower than the elongation rate; therefore, the segments cannot respond efficiently to the rapidly imposed deformation. This is also illustrated by Fig. 15 which illustrates the evolution of a system with Kads = 4 and la→f = 0 for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 103 s−1 and
zz = 103 s−1 and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz = 104 s−1 (see panels (a) and (b), respectively).
zz = 104 s−1 (see panels (a) and (b), respectively).
 | ||
Fig. 15 Evolution of the configurations for [la→f/Å, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz/s−1] equal to (a) [0, 103], (b) [0, 104], (c) [9.71, 103] and (d) [9.71, 104]. In all cases, zz/s−1] equal to (a) [0, 103], (b) [0, 104], (c) [9.71, 103] and (d) [9.71, 104]. In all cases,  = 4 and = 4 and  = 102 s−1. = 102 s−1. | ||
With increasing activation length the polymer detaches from the solid surface at much lower strains. The effect is very pronounced in the weakly adsorbing interface where Kads = 1/4. In addition, the trend observed in the previous case (la→f = 0) reverses and detachment is realized at lower strains with increasing elongation rate. E.g., compare panels (c) and (d) of Fig. 15. This response is in accordance with theoretical17 and experimental5,9 observations.
The reversible portion of the stress–strain curve preceding the yield strain (ca. 0.06) does not depend on the value of the activation length. That is to say, the low strain portion in Fig. 14a is practically the same from left to right. Finally, the maximum value of the stress is an increasing function of the elongation rate for all cases considered in Fig. 14a.
Fig. 16a depicts the same quantities as in Fig. 14a but for interfaces with fast detachment kinetics ( = 105 s−1), indicative of low transition barriers. Because detachment rate is much faster than deformation rate, failure occurs prematurely at significantly lower elongation strains. With increasing activation length detachment is facilitated, though the enhancement is less pronounced than in cases with slow interfacial kinetics. Failure is always adhesive for this detachment rate.
= 105 s−1), indicative of low transition barriers. Because detachment rate is much faster than deformation rate, failure occurs prematurely at significantly lower elongation strains. With increasing activation length detachment is facilitated, though the enhancement is less pronounced than in cases with slow interfacial kinetics. Failure is always adhesive for this detachment rate.
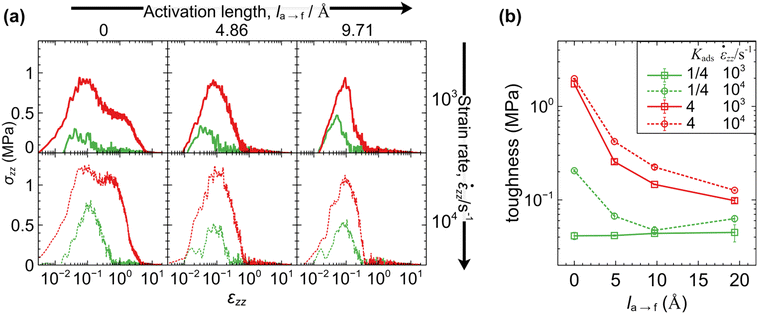 | ||
Fig. 16 As in Fig. 14 for  = 105 s−1. In all cases, the samples exhibit cohesive failure, and no chain rupture events are observed. = 105 s−1. In all cases, the samples exhibit cohesive failure, and no chain rupture events are observed. | ||
The toughness of the interfaces can be quantified by the integral of the stress–strain curve:
 | (35) |
4. Concluding remarks
The present work develops a generic mesoscopic model, capable of addressing high molar mass amorphous polymers above their glass temperature capped between two solid surfaces, under quiescent and nonequilibrium conditions. The latter are imposed by subjecting the samples to constant rate elongation across the aperiodic (normal) direction, as in the so-called tack tests. A detailed six-stage parameterization framework is established for deriving essential parameters of the mesoscopic model, including the optimization of the equation of state coefficients, the mesoscopic force fields, and chain dynamics in the Rouse and entangled regimes. The framework is generic and applicable to polymers of arbitrary architecture and chemical constitution. The parameterization can be performed either in a bottom-up or a top-down fashion, based on input from atomistic simulations or experimental data, respectively.As a case study, we apply the parameterization framework based on a minimal data set from an indicative noncrystallizable fluoropolymer. The agreement of the volumetric properties, conformational statistics and dynamics between the mesoscopic model and the atomistic reference data set is excellent.
We present results from simulated tack experiments conducted over a wide parameter space, including: the rate of elongation ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz, detachment rate constant ka→f, activation lengths of the attachment/detachment transitions (la→f, lf→a), and the adsorption equilibrium constant Kads = kf→a/ka→f. The resulting failure mechanism depends on a complex interplay between these parameters. The attachment/detachment rate constants dictate the frequency at which the polymer chains attach/detach from the surface. The magnitudes of the activation lengths tune the coupling of the attachment/detachment rates with the normal forces exerted on the mesoscopic beads at the interface. The adsorption equilibrium constant is a thermodynamic property and determines the adhesive strength of the interface. The performance of each interface was characterized by stress–strain curves from which yield strain and toughness were extracted.
zz, detachment rate constant ka→f, activation lengths of the attachment/detachment transitions (la→f, lf→a), and the adsorption equilibrium constant Kads = kf→a/ka→f. The resulting failure mechanism depends on a complex interplay between these parameters. The attachment/detachment rate constants dictate the frequency at which the polymer chains attach/detach from the surface. The magnitudes of the activation lengths tune the coupling of the attachment/detachment rates with the normal forces exerted on the mesoscopic beads at the interface. The adsorption equilibrium constant is a thermodynamic property and determines the adhesive strength of the interface. The performance of each interface was characterized by stress–strain curves from which yield strain and toughness were extracted.
We begin the recapitulation of our findings with situations where the activation length is negligible in relation to the transition energy barriers or, alternatively, the normal forces generated by the polymer at the interface are weak. This scheme is suitable for modeling the detachment of strong adhesives and also highly compressible materials (such as foams) that generate weak normal forces.
When the detachment rate is faster than the elongation rate (ka→f > ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz), the interface can respond efficiently and relax the imposed stress. Weakly adsorbing interfaces (Kads = 1/4) promote cavitation very close to the surface, enabling easy detachment of the polymer at short times. The corresponding toughness becomes minimal in these cases. With increasing Kads, the toughness increases slightly.
zz), the interface can respond efficiently and relax the imposed stress. Weakly adsorbing interfaces (Kads = 1/4) promote cavitation very close to the surface, enabling easy detachment of the polymer at short times. The corresponding toughness becomes minimal in these cases. With increasing Kads, the toughness increases slightly.
In situations where the elongation rate is faster than the detachment rate (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz > ka→f), pronounced fibrillation tendencies are observed. Interestingly, when the timescale separation is very large (
zz > ka→f), pronounced fibrillation tendencies are observed. Interestingly, when the timescale separation is very large (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz ≫ ka→f), the magnitude of the detachment rate becomes irrelevant and the outcome depends strictly on the initial concentration of attached beads, dictated by the equilibrium adsorption constant. The toughness of the interface is maximized under these conditions and becomes a strongly increasing function of elongation rate.
zz ≫ ka→f), the magnitude of the detachment rate becomes irrelevant and the outcome depends strictly on the initial concentration of attached beads, dictated by the equilibrium adsorption constant. The toughness of the interface is maximized under these conditions and becomes a strongly increasing function of elongation rate.
We now turn our attention to situations with finite activation lengths. Note that the effect of force coupling becomes more pronounced as the transition barriers decrease (low Ei→j in eqn (1) and (2)) and also when modelling incompressible materials. Contrary to the previous case, the polymer detaches more efficiently (at lower strains) with increasing elongation rate, because the attached beads are pulled more strongly toward the polymer film with increasing strain. Indeed, when the normal force coupling is very strong (la→f ≫ Ea→f/〈Fz〉) toughness decreases considerably, since the polymer detaches from the surface very readily, even for the smallest ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) zz/ka→f ratio considered here. This response conforms with the picture from experimental tack tests.5,9
zz/ka→f ratio considered here. This response conforms with the picture from experimental tack tests.5,9
We note a consistent trend where toughness is a strictly increasing function of Kads. In addition, regardless of the activation length, the yield stress increases monotonically with elongation rate due to the inability of the interface to efficiently relax the imposed stress. At high elongation rates the polymer becomes stiff, leading to the formation of dense distributions of thinner fibers. At low elongation rates, on the other hand, the polymer can relax the imposed stress efficiently and the behavior becomes more ductile, leading to the formation of large cavities—in other words thick and sparse fibers, forming bridges between the edges of the simulation box. Furthermore, the yield stress exhibits an inverse relationship with compressibility. Low compressibility is indicative of stiffer samples that resist deformation and yield at increased stress under load.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
A. P. Sgouros thanks Syensqo S.A., Bollate, Italy, for financial support. The authors would like to congratulate Prof. J. J. de Pablo on his birthday and wish him many fruitful years in science to come. S. K. and S. C. are grateful to Prof. Theodorou and Dr. Sgouros for their productive stay at NTUA in January 2023.References
- A. J. Kinloch, Adhesion and adhesives: science and technology, Springer Science& Business Media, 2012 Search PubMed.
- R. A. Pethrick, Proc. Inst. Mech. Eng., Part L, 2015, 229, 349–379 CAS.
- H. R. Gualberto, F. do Carmo Amorim and H. R. M. Costa, J. Braz. Soc. Mech. Sci. Eng., 2021, 43, 389 CrossRef.
- D. Son, V. Liimatainen and M. Sitti, Small, 2021, 17, 2102867 CrossRef CAS PubMed.
- C. Creton and P. Fabre, in Adhesion Science and Engineering, ed. D. A. Dillard, A. V. Pocius and M. Chaudhury, Elsevier Science B.V., 2002, pp. 535–575 Search PubMed.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 46601 CrossRef PubMed.
- A. Zosel, Colloid Polym. Sci., 1985, 263, 541–553 CrossRef CAS.
- A. Zosel, J. Adhes., 1989, 30, 135–149 CrossRef CAS.
- H. Lakrout, P. Sergot and C. Creton, J. Adhes., 1999, 69, 307–359 CrossRef CAS.
- A. Chiche, P. Pareige and C. Creton, C. R. Acad. Sci., Ser. IV:Phys., Astrophys., 2000, 1, 1197–1204 CrossRef CAS.
- M. Solar, Z. Qin and M. J. Buehler, J. Mater. Res., 2014, 29, 1077–1085 CrossRef CAS.
- T.-P. Fries and M. Baydoun, Int. J. Numer. Methods Eng., 2012, 89, 1527–1558 CrossRef.
- P.-A. Guidault, O. Allix, L. Champaney and C. Cornuault, Comput. Meth. Appl. Mech. Eng., 2008, 197, 381–399 CrossRef.
- Z. Zhang, X. Wang and J. D. Lee, J. Appl. Phys., 2014, 115, 114314 CrossRef.
- S.-H. Cheng and C. T. Sun, J. Nanomechanics Micromech., 2014, 4, 1–8 Search PubMed.
- L. Brochard, G. Hantal, H. Laubie, F. J. Ulm and R. J. M. Pellenq, Int. J. Fract., 2015, 194, 149–167 CrossRef.
- G. Xu and H. Wang, Constr. Build. Mater., 2016, 121, 246–254 CrossRef.
- K. Min, A. R. Rammohan, H. S. Lee, J. Shin, S. H. Lee, S. Goyal, H. Park, J. C. Mauro, R. Stewart, V. Botu, H. Kim and E. Cho, Sci. Rep., 2017, 7, 1–11 CrossRef PubMed.
- D. Gersappe and M. O. Robbins, Europhys. Lett., 1999, 48, 150–155 CrossRef CAS.
- S. V. Kallivokas, A. P. Sgouros and D. N. Theodorou, Phys. Rev. E, 2020, 102, 30501 CrossRef CAS PubMed.
- I. Delasoudas, S. V. Kallivokas and V. Kostopoulos, Polymer, 2024, 296, 126830 CrossRef CAS.
- M. J. Stevens, Macromolecules, 2001, 34, 2710–2718 CrossRef CAS.
- A. Baggioli, M. Casalegno, A. David, M. Pasquini and G. Raos, Macromolecules, 2021, 54, 195–202 CrossRef CAS.
- A. R. C. Baljon, J. Vorselaars and T. J. Depuy, Macromolecules, 2004, 37, 5800–5806 CrossRef CAS.
- A. F. Terzis, D. N. Theodorou and A. Stroeks, Macromolecules, 2002, 35, 508–521 CrossRef CAS.
- E. Voyiatzis and A. Stroeks, J. Phys. Chem. B, 2022, 126, 6102–6111 CrossRef CAS PubMed.
- K. Jin, D. López Barreiro, F. J. Martin-Martinez, Z. Qin, M. Hamm, C. W. Paul and M. J. Buehler, Polymer, 2018, 154, 164–171 CrossRef CAS.
- M. H. Nafar Sefiddashti, B. J. Edwards and B. Khomami, J. Rheol., 2015, 59, 119–153 CrossRef CAS.
- A. P. Sgouros, G. Megariotis and D. N. Theodorou, Macromolecules, 2017, 50, 4524–4541 CrossRef CAS.
- M. H. Nafar Sefiddashti, B. J. Edwards, B. Khomami and E. S. G. Shaqfeh, J. Chem. Phys., 2021, 154, 204907 CrossRef CAS PubMed.
- M. H. Nafar Sefiddashti, B. J. Edwards and B. Khomami, Phys. Rev. Lett., 2018, 121, 247802 CrossRef PubMed.
- A. P. Sgouros, G. G. Vogiatzis, G. Megariotis, C. Tzoumanekas and D. N. Theodorou, Macromolecules, 2019, 52, 7503–7523 CrossRef CAS.
- A. E. Likhtman, Macromolecules, 2005, 38, 6128–6139 CrossRef CAS.
- G. G. Vogiatzis, G. Megariotis and D. N. Theodorou, Macromolecules, 2017, 50, 3004–3029 CrossRef CAS.
- T. Uneyama and Y. Masubuchi, J. Chem. Phys., 2011, 135, 184904 CrossRef PubMed.
- A. Ramírez-Hernández, B. L. Peters, M. Andreev, J. D. Schieber and J. J. de Pablo, J. Chem. Phys., 2015, 143, 243147 CrossRef PubMed.
- J. Kirk, Z. Wang and P. Ilg, J. Chem. Phys., 2019, 150, 094906 CrossRef PubMed.
- M. Langeloth, Y. Masubuchi, M. C. Böhm and F. Müller-plathe, J. Chem. Phys., 2013, 138, 104907 CrossRef PubMed.
- T. Uneyama and Y. Masubuchi, J. Chem. Phys., 2012, 137, 154902 CrossRef PubMed.
- V. C. Chappa, D. C. Morse, A. Zippelius and M. Müller, Phys. Rev. Lett., 2012, 109, 148302 CrossRef PubMed.
- A. Ramírez-Hernández, B. L. Peters, L. Schneider, M. Andreev, J. D. Schieber, M. Müller and J. J. de Pablo, J. Chem. Phys., 2017, 146, 014903 CrossRef PubMed.
- A. Ramírez-Hernández, F. A. Detcheverry, B. L. Peters, V. C. Chappa, K. S. Schweizer, M. Müller and J. J. de Pablo, Macromolecules, 2013, 46, 6287–6299 CrossRef.
- Y. Masubuchi, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 11–33 CrossRef CAS PubMed.
- Y. Masubuchi, J. Chem. Phys., 2015, 143, 224905 CrossRef PubMed.
- Y. Masubuchi, J. I. Takimoto, K. Koyama, G. Ianniruberto, G. Marrucci and F. Greco, J. Chem. Phys., 2001, 115, 4387–4394 CrossRef CAS.
- S. F. Edwards, Proc. Phys. Soc., 1967, 92, 9–16 CrossRef CAS.
- P. G. de Gennes, J. Chem. Phys., 1971, 55, 572 CrossRef.
- M. Doi, J. Polym. Sci., Polym. Phys. Ed., 1983, 21, 667–684 CrossRef CAS.
- S. T. Milner and T. C. B. McLeish, Phys. Rev. Lett., 1998, 81, 725–728 CrossRef CAS.
- A. E. Likhtman and T. C. B. McLeish, Macromolecules, 2002, 35, 6332–6343 CrossRef CAS.
- N. Evangelou, G. Megariotis, A. P. Sgouros, G. G. Vogiatzis, N. A. Romanos and D. N. Theodorou, AIP Conf. Proc., 2021, 2343, 130008 CrossRef CAS.
- A. P. Philippas, A. P. Sgouros, G. Megariotis and D. N. Theodorou, AIP Conf. Proc., 2021, 2343, 130003 CrossRef CAS.
- G. Megariotis, G. G. Vogiatzis, A. P. Sgouros and D. N. Theodorou, Polymers, 2018, 10, 1156 CrossRef PubMed.
- A. P. Sgouros, G. G. Vogiatzis, G. Kritikos, A. Boziki, A. Nikolakopoulou, D. Liveris and D. N. Theodorou, Macromolecules, 2017, 50, 8827–8844 CrossRef CAS.
- A. P. Sgouros, A. T. Lakkas, G. Megariotis and D. N. Theodorou, Macromolecules, 2018, 51, 9798–9815 CrossRef CAS.
- V. A. Harmandaris, V. G. Mavrantzas, D. N. Theodorou, M. Kröger, J. Ramírez, H. C. Öttinger and D. Vlassopoulos, Macromolecules, 2003, 36, 1376–1387 CrossRef CAS.
- M. Ansari, A. Alabbas, S. G. Hatzikiriakos and E. Mitsoulis, Int. Polym. Process., 2010, 25, 287–296 CrossRef CAS.
- Y. Masubuchi, Y. Doi and T. Uneyama, J. Phys. Chem. B, 2022, 126, 2930–2941 CrossRef CAS PubMed.
- P. Ilg and M. Kröger, J. Rheol., 2011, 55, 69 CrossRef CAS.
- P. S. Stephanou, I. C. Tsimouri and V. G. Mavrantzas, Macromolecules, 2016, 49, 3161–3173 CrossRef CAS.
- T. Schweizer, J. van Meerveld and H. C. Öttinger, J. Rheol., 2004, 48, 1345 CrossRef CAS.
- S.-Q. Wang, Nonlinear polymer rheology: macroscopic phenomenology and molecular foundation, John Wiley & Sons, 2018 Search PubMed.
- A. Ramírez Hernández, M. Müller and J. J. de Pablo, Soft Matter, 2013, 9, 2030–2036 RSC.
- D. Nichetti and I. Manas-Zloczower, J. Rheol., 1998, 42, 951–969 CrossRef CAS.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1802–1817 CAS.
- C. C. Hua and J. D. Schieber, J. Chem. Phys., 1998, 109, 10018–10027 CAS.
- J. D. Schieber and M. Andreev, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 367–381 CrossRef CAS PubMed.
- Y. Masubuchi, Macromolecules, 2018, 51, 10184–10193 CrossRef CAS.
- Y. Masubuchi and T. Uneyama, Soft Matter, 2018, 14, 5986–5994 RSC.
- M. Kröger, J. Nonnewton. Fluid Mech., 2015, 223, 77–87 CrossRef.
- I. C. I. C. Sanchez and R. H. R. H. Lacombe, Macromolecules, 1978, 11, 1145–1156 CrossRef CAS.
- A. P. Sgouros and D. N. Theodorou, J. Phys. Chem. B, 2024, 128, 6907–6921 CrossRef CAS PubMed.
- L. B. Lucy, Astron. J., 1977, 82, 1013–1024 CrossRef.
- K. F. Mansfield and D. N. Theodorou, Macromolecules, 1991, 24, 4295–4309 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1949, 17, 338–343 CrossRef CAS.
- J. T. Padding and W. J. Briels, J. Chem. Phys., 2001, 114, 8685–8693 CrossRef CAS.
- L. J. Fetters, D. J. Lohse and R. H. Colby, Phys. Prop. Polym. Handb., 2006, 445–452 Search PubMed.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 Search PubMed.
- P. Virtanen, R. Gommers, T. E. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, Nat. Methods, 2020, 17, 261–272 CAS.
- D. N. Theodorou, in Computer Simulations of Surfaces and Interfaces, ed. B. Dünweg, D. P. Landau and A. I. Milchev, 2003, NATO Science Series, pp. 329–419 Search PubMed.
- D. N. Theodorou, in Polymers at Surfaces and Interfaces, ed. B. Dünweg, D. P. Landau and A. I. Milchev, 2003, NATO Science Series, pp. 329–419 Search PubMed.
- V. A. Harmandaris, V. G. Mavrantzas and D. N. Theodorou, Macromolecules, 1998, 31, 7934–7943 CrossRef CAS.
- Y. H. Lin, Macromolecules, 1987, 20, 3080–3083 CrossRef CAS.
- Y. Masubuchi, G. Ianniruberto, F. Greco and G. Marrucci, J. Chem. Phys., 2003, 119, 6925–6930 CrossRef CAS.
- G. Megariotis, G. G. Vogiatzis, L. Schneider, M. Müller and D. N. Theodorou, J. Phys.: Conf. Ser., 2016, 738, 012063 CrossRef.
- A. P. Sgouros and D. N. Theodorou, Computation, 2023, 11, 106 Search PubMed.
- A. P. Sgouros, S. Knippenberg, M. Guillaume and D. N. Theodorou, Soft Matter, 2021, 17, 10873–10890 RSC.
- A. P. Sgouros, C. J. Revelas, A. T. Lakkas and D. N. Theodorou, J. Phys. Chem. B, 2022, 126, 7454–7474 CrossRef CAS PubMed.
- C. J. Revelas, A. P. Sgouros, A. T. Lakkas and D. N. Theodorou, Computation, 2021, 9, 57 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 Search PubMed.
- I. Kuckir, https://www.photopea.com/.
- J. Sanders, Veusz-3.6.2, https://veusz.github.io/ Search PubMed.
- A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- R. J. Good and R. K. Gupta, J. Adhes., 1988, 26, 13–36 CrossRef CAS.
- D. N. Theodorou, J. Chem. Phys., 2024, 161, 184905 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4me00199k |
| This journal is © The Royal Society of Chemistry 2025 |