Quantum chemical studies of the reaction mechanisms of enzymatic CO2 conversion
Baoyan
Liu
 abc,
Beibei
Lin
abc,
Hao
Su
abc,
Beibei
Lin
abc,
Hao
Su
 *ac and
Xiang
Sheng
*ac and
Xiang
Sheng
 *ac
*ac
aKey Laboratory of Engineering Biology for Low-Carbon Manufacturing, Tianjin Institute of Industrial Biotechnology, Chinese Academy of Sciences, Tianjin 300308, P. R. China. E-mail: suhao@tib.cas.cn; shengx@tib.cas.cn
bHaihe Laboratory of Synthetic Biology, Tianjin 300308, P. R. China
cNational Center of Technology Innovation for Synthetic Biology, Tianjin 300308, P. R. China
First published on 23rd September 2024
Abstract
Enzymatic capture and conversion of carbon dioxide (CO2) into value-added chemicals are of great interest in the field of biocatalysis and have a positive impact on climate change. The quantum chemical methods, recognized as valuable tools for studying reaction mechanisms, have been widely employed in investigating the reaction mechanisms of the enzymes involved in CO2 utilization. In this perspective, we review the mechanistic studies of representative enzymes that are either currently used or have the potential for converting CO2, utilizing the quantum chemical cluster approach and the quantum mechanical/molecular mechanical (QM/MM) method. We begin by summarizing current trends in enzymatic CO2 conversion, followed by a brief description of the computational details of quantum chemical methods. Then, a series of representative examples of the computational modeling of biocatalytic CO2 conversion are presented, including the reduction of CO2 to C1 species (carbon monoxide and formate), and the fixation of CO2 to form aliphatic and aromatic carboxylic acids. The microscopic views of reaction mechanisms obtained from these studies are helpful in guiding the rational design of current enzymes and the discovery of novel enzymes with enhanced performance in converting CO2. Additionally, they provide key information for the de novo design of new-to-nature enzymes. To conclude, we present a perspective on the potential combination of machine learning with quantum description in the study of enzymatic conversion of CO2.
1. Introduction
As a trace gas in Earth's atmosphere, the concentration of CO2 has risen by more than 50% from pre-industrial levels of 280 parts per million (ppm) to 423.65 ppm as of April 2024,1 largely due to anthropogenic excess emissions. Atmospheric CO2 levels have been consistently increasing on an annual average, according to data measured by NOAA’S Global Monitoring Laboratory.2 This persistent rise has made CO2 capture and utilization an urgent global challenge and a booming area of research. Enzymatic CO2 conversion, involved in both primary and secondary metabolic pathways, is considered a green and sustainable option.3–7 Natural CO2 fixation pathways include the CBB cycle, the reductive glycine pathway, the Wood–Ljungdahl pathway, the reverse TCA cycle, the 3HP/4HB cycle, the 3HP bicycle, and the dicarboxylate/4-hydroxybutyrate cycle. Modifying these natural pathways or de novo designing new synthetic pathways provides efficient solutions for CO2 capture and utilization. Examples include ASAP,8 CETCH,9,10 HOPAC,11 rGPS-MCG,12 POAP,13 and GED.14The central carbon atom in CO2 is in its highest oxidation state, rendering its formation energetically favored. Therefore, the utilization of CO2 requires the provision of electrons or energy to pull it from the ‘bottom of the potential energy well’.15 Some enzymes have evolved to rely on cofactors, such as NADPH and NADH, which can transfer a hydride ion, thereby donating two electrons along with energy.14,16–18 Others utilize electron transfer agents known as ferredoxins, which are capable of producing a reduction potential of around −500 mV when the ferredoxin pool is 95% reduced.19,20 Another strategy involves using the direct energy from the hydrolysis of ATP.21,22 Additionally, certain enzymes coordinate CO2 binding with bivalent metal ions in the active site, thereby activating it.23,24 Furthermore, enzymes such as RuBisCO25 and phosphoenolpyruvate carboxylase (PEPC)26 utilize their high-energy substrates, which are ribulose-1,5-bisphosphate (RuBP) and phosphoenolpyruvate (PEP), respectively, to drive their respective reactions.
Enzymatic CO2 conversion consists of mainly two types of reactions: the reduction of CO2 to carbon monoxide or formate by dehydrogenases,27,28 and the carboxylation, which introduces an additional carbon atom to a substrate, utilizing CO2 as the carbon source.23,24 The carboxylation mechanism generally comprises two key steps: the generation of an enol or enolate nucleophile, and the nucleophilic attack of the enol (or enolate) on the carbon of CO2 to form a C–C bond.3 However, it is important to note that certain enzymes, such as prenylated FMN-dependent ferulic acid decarboxylases29 and thiamin pyrophosphate (TPP)-dependent ferredoxin oxidoreductase,30,31 follow different pathways. Understanding the reaction mechanisms of enzymatic CO2 conversion is crucial for developing new strategies for CO2 capture and utilization.
Quantum chemical (QC) methods have become essential tools for studying different aspects of enzymatic reactions, including substrate specificity, reaction mechanism and various selectivities.32–39 While biocatalytic CO2 conversion follows some common rules, each reaction exhibits unique features due to the differences in substrates and enzyme properties. In-depth quantum chemical illustrations of enzymatic CO2 reduction and carboxylation can elucidate specific reaction steps and identify key factors that shift the equilibrium toward the energetically less favorable direction. Moreover, these depictions can provide critical information for the enzyme design of new catalysts with enhanced efficiency or tailored properties, thereby improving their potentials in industrial applications.
In this perspective, we present the utilization of quantum chemical calculations, specifically through the cluster approach and the hybrid quantum mechanical/molecular mechanical (QM/MM) method, in investigating the reaction mechanisms of enzymatic CO2 conversion. The technical aspects of the two methods are first briefly discussed. Then, we illustrate case studies of enzymatic transformation of CO2 into various compounds, including C1 species, aliphatic acids, and aromatic carboxylic acids. Furthermore, we highlight the promising integration of machine learning with quantum chemical techniques, which represents a significant advancement that could open up new possibilities for accelerating the discovery and optimization of CO2-converting enzymes with enhanced catalytic performance.
2. Methodology
2.1 Quantum chemical cluster approach
The quantum chemical cluster approach, also known as the all-QM approach, has been extensively applied to elucidate various aspects of enzyme catalysis.34–37 It allows a direct comparison of energy profiles for all possible reaction pathways, which is invaluable in identifying the most favorable substrate binding mode to the enzyme, as well as in elucidating the most plausible reaction mechanism that the enzyme may adopt. Moreover, the cluster approach has recently been expanded to model various selectivities of enzymatic reactions, and to provide insights into the pivotal roles of metal in the metal-dependent enzymes. Some of these studies identified the roles of key residues in catalysis, which are crucial for enzyme engineering and rational design.The basic idea of the cluster approach is to focus on a small, chemically relevant portion of the enzyme's active site, along with its proximate surroundings. The entire model is treated using the quantum mechanical method. Historically, it has been demonstrated that even a small active site model consisting of less than 100 atoms can effectively elucidate the reaction mechanism. Nowadays, a cluster model can contain more than 400 atoms, including substrates, organic cofactors, metal ions, and neighboring residues that constitute the active site. This expansion enhances the ability of the cluster approach to model selectivities and strategically design mutants. However, it is suggested that one should begin mechanistic investigations with a relatively small model, then gradually increase the model size to detect multiple minima errors and gain chemical insights into different functional groups. To accurately simulate the enzyme systems, a selection of atoms at the periphery of the model are fixed to mimic the steric influence of the actual binding pocket, and an implicit homogeneous polarizable solvation medium, generally with a dielectric constant ε = 4, is used to provide an approximate description of solvation effect.
Among all the quantum chemical methods, density functional theory (DFT), particularly the B3LYP hybrid functional, which balances speed and accuracy well, has been broadly used. When describing dispersion interactions, one can add an empirical dispersion correction to the B3LYP calculations, for example, Grimme's D3 dispersion correction. Alternatively, the Minnesota M06 suite, which includes weak interactions in its training set, can also be used. Geometries are often optimized using the 6-31G(d,p) basis set, while single-point energies are typically calculated with a larger basis set, such as 6-311++G(2d,2p). For metals, the SDD40 pseudopotential basis set is commonly employed. It is important to note that different theoretical methods may be adopted depending on the specific requirements of each study. For a detailed methodology, readers are referred to the original paper.
The entropy effect is usually not considered in the cluster approach, because the constraints at the periphery of the model render the entropy calculation inaccurate and the entropy effect is deemed to contribute very little to the barriers. However, when it comes to reactions involving the gas molecule entering or exiting an enzyme pocket, the translational entropy of the gas molecule is suggested to be factored into the calculations. Alternatively, harmonic confining potentials can be introduced to the computational model to achieve unconstrained geometry relaxations.41,42
2.2 Quantum mechanical/molecular mechanical (QM/MM) method
The quantum mechanical/molecular mechanical (QM/MM) method is a robust computational method designed to investigate complex systems with high efficiency.38,39 It combines accuracy with speed by calculating the key region using a high level of QM theory, similar to the QC cluster approach discussed above, and its environment with a low-cost level of QM theory or a classical molecular mechanics (MM) simulation. This dual-level strategy allows for a comprehensive analysis of reaction mechanisms and other properties within complex biological systems.Depending on the way of dealing with the interface between the two types of systems, there are subtractive and additive schemes to calculate the overall potential energy by QM/MM method. In these methods, the real catalytic system is artificially divided into two parts, and the overall energy is composed of particle interactions within the quantum mechanical (QM) region, the atomic interactions within the molecular mechanical (MM) region, and the interactions between QM and MM particles. In the subtractive scheme, the potential energy of the total system is calculated by summing the MM-level energy of the whole system and the QM-level energy of the isolated QM system, then subtracting the MM energy of the QM system. In the additive schemes, which are considered more accurate, the potential energy of the total system is calculated as the sum of QM region energy terms, classical MM region energy terms, and QM/MM boundary energy terms.
As the QM/MM method provides an approximation of the potential energies of embedded quantum-chemical systems in a larger molecular environment, the proper treatment of the interaction between the QM and MM regions is important for the accuracy of the method. The QM/MM coupling boundary is composed of both non-bonded and bonded parts. For the non-bonded part, van der Waals interactions and electrostatic interactions demand careful consideration. The latter can be calculated using one of three methods: mechanical embedding, electronic embedding, or polarized embedding. For the covalently bonded part, it is necessary to saturate the dangling bond of the QM system to prevent the appearance of bond cleavage. To this end, and also to mitigate the potential over-polarization, three schemes have been developed: link-atom schemes, boundary atom schemes and localized-orbital schemes. In practice, link-atom schemes are more commonly used than the others because of its simplicity and robustness.
In the QM/MM calculations on enzymatic reactions, numerous minima and transition states are expected to be identified due to the extensive configuration space of studied large molecules. Therefore, multiple snapshots from classical MD simulations should be chosen as starting structures for the mechanistic investigation to ensure that the most plausible pathway is obtained. Alternatively, one can employ the computationally demanding QM/MM molecular dynamics calculations to fulfill the requirement for thorough sampling of the configuration space.
In the following section, we will present examples that demonstrate how quantum chemical computational research can aid in elucidating the reaction mechanism of CO2-converting enzymes and provide relevant information. The discussed enzymes are those catalyzing the reduction of CO2 to form C1 compounds (Section 3.1), and the carboxylation to generate aliphatic acids (Section 3.2) and aromatic acids (Section 3.2). This perspective paper ends with an outlook on the promising integration of machine learning with quantum chemical techniques, highlighting their potential application in CO2 fixation.
3. Emerging practices in application
Quantum chemical calculations allow us to investigate mechanistic proposals involving the enzyme–substrate complex, intermediates, transition states, and the enzyme–product complex. By assessing the calculated energies, we can evaluate the feasibility of these proposals. In the following sections, case studies of the reaction mechanisms of CO2 conversion into various compounds, including C1 species, aliphatic acids, and aromatic carboxylic acids, are presented. For the reduction of CO2 to C1 species, the discussed enzymes are the molybdenum-containing formate dehydrogenase (Mo-FDH), the Ni, Fe-containing carbon monoxide dehydrogenase (CODH), and the artificial human carbonic anhydrase (hCAII). In the section on the fixation of CO2 to form aliphatic acids, the ribulose 1,5-bisphosphate carboxylase (RuBisCO), the crotonyl-CoA carboxylases/reductase (CCR), the biotin-dependent pyruvate carboxylase (PC) and two ThDP-dependant enzymes are discussed. For the carboxylation to generate aromatic carboxylic acids, the prFMN-dependent UbiD family and the (de)carboxylases from the amidohydrolase superfamily are presented. All the enzymes and their catalytic reactions illustrated in this paper are listed in Table 1.| Enzyme | Reaction schemea |
|---|---|
| a Reactions of decarboxylases with carboxylation activity are depicted in the carboxylation direction. | |
| Molybdenum-containing formate dehydrogenase (Mo-FDH) |

|
| Ni,Fe-containing carbon monoxide dehydrogenase (CODH) |

|
| Artificial human carbonic anhydrase (hCAII) |

|
| Ribulose 1,5-bisphosphate carboxylase/oxygenase (RuBisCO) |

|
| Crotonyl-CoA carboxylases/reductases (CCR) |

|
| Pyruvate carboxylase (PC) |

|
| Pyruvate decarboxylase (PDC) |
|
| Pyruvate dehydrogenase (PDHc) E1 subunit |

|
| Ferulic acid decarboxylase (AnFdc1) |

|
| 3,4-Dihydroxybenzoic acid decarboxylases (AroY) |

|
| Pyrrole-2-carboxylic acid decarboxylase (HudA) |

|
| Decarboxylases from amidohydrolase superfamily (AHS) |

|
3.1 Reduction of carbon dioxide to C1 compounds
The active sites of Mo-FDHs are highly conserved, and their reaction mechanisms have been extensively studied using both quantum calculations and laboratory experiments.44–47 In a mechanistic study by Dong et al., previously proposed mechanisms were evaluated employing combined QM/MM and large-scale QM calculations.46 It was suggested that the CO2 or formate molecule binds in the second coordination sphere of molybdenum, rather than binding directly to the metal, and the CO2 reduction involves a hydride transfer via the sulfido group, yielding Mo6+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S from Mo4+–SH (Fig. 1a).46 However, the full energy diagram was not reported in this study.
S from Mo4+–SH (Fig. 1a).46 However, the full energy diagram was not reported in this study.
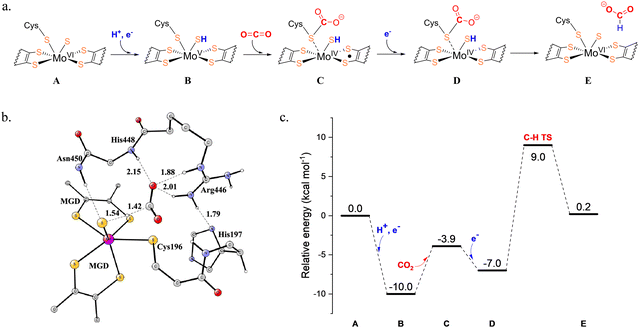 | ||
| Fig. 1 (a) Proposed mechanism of the molybdenum-containing formate dehydrogenase (Mo-FDH) for CO2 reduction. (b) The optimized transition state for the hydride transfer to CO2 and (c) the calculated energy profile of CO2 reduction. Reprinted with permission from ref. 47, Copyright 2022 American Chemical Society and CC-BY 4.0. | ||
Siegbahn conducted a thorough theoretical study of the CO2/formate interconversion catalyzed by Mo-FDH using the quantum chemical cluster approach.47 In the starting point of the reduction direction before the binding of CO2, the electronic structure of Mo(VI) was confirmed to be in the closed-shell singlet state. A (H+, e−) couple was then added before the CO2 was bound, and the localized spin on Mo indicated a Mo(V) state. Subsequently, CO2 bound to the sulfur of Cys196. This led to the spin on Mo being delocalized over the ligands, indicating a Mo(IV) state. Then, an electron was added and therefore a closed-shell Mo(IV) was obtained. During this step, the structure of the Mo complex hardly changed, while the spin distribution changed significantly. Finally, the calculations showed that the hydride transfer to CO2 involves a proton from sulfide ligand and two electrons from Mo(IV) (Fig. 1b), giving the formate product and Mo(VI). Additionally, it was proposed that the barrier for the reduction of CO2 is 19.0 kcal mol−1, calculated from the resting state after the addition of the (H+, e−) couple to the hydride-transfer transition state (Fig. 1c). The added electron turns out to stabilize the binding of CO2. The overall reduction reaction energy is +0.2 kcal mol−1, which aligns well with the experimental result, indicating that this process is barrierless at a −0.4 V redox potential.43 For the oxidation direction, the rate-limiting barrier is 16.9 kcal mol−1, calculated from the resting point after CO2 has left, followed by the release of (H+, e−), up to the hydride-transfer transition state. This study considered the entire oxidation cycle, rather than focusing solely on the chemical steps as in the previous study, thereby offering a more comprehensive view of CO2 reduction catalyzed by Mo-FDH.
 | ||
| Scheme 1 Reaction mechanism of Ni, Fe-containing carbon monoxide dehydrogenase (CODH). Adapted with permission from ref. 49, Copyright 2019 American Chemical Society. | ||
The binding and release of CO2 by CODH have also been investigated using quantum mechanics calculations.51 All possible spin-coupling schemes for three reduced C-cluster states were investigated using a small model, and the states with low energies were finally used for a large model. The calculations of the CO2 binding and release processes revealed that these two steps highly depend on the protonation state of His93, and the oxidation state of the asymmetrical [Ni–Fe–S] cluster. In detail, CO2 binds to the dielectronic reduction state of C-cluster when His93 is doubly protonated, and is released when His93 is singly protonated and the C-cluster is in an oxidized state.
Possible reaction mechanisms of hCAII-catalyzed conversion of CO2 to HCOOH were proposed and evaluated.54 The simulations using a cluster model of 50 atoms demonstrated that the initial step of the catalytic cycle, namely the activation of H2 by Rh(I), occurs without an energy barrier. Subsequently, CO2, acting as a Lewis base, coordinates to Rh(III) through one oxygen atom, then inserts into the Rh(III)–H bond, finally giving rise to the 1d species. For the subsequent formation of formic acid, both reductive elimination and σ-bond metathesis mechanisms were considered, with the latter being preferred according to the calculated energies (Fig. 2a). The release of formic acid and the restoration of the catalytic cycle were also examined. It was found that the energy barrier for the release of the product is 12.8 kcal mol−1 (6b–6d, Fig. 2b), which is the rate-determining step of the overall reaction.
 | ||
| Fig. 2 (a) Proposed mechanistic scheme for the reduction of CO2 by [Rh(hCAII)]. (b) Energy profiles for the proposed mechanisms. Adopted with permission of John Wiley & Sons – Books from ref. 55; permission conveyed through Copyright Clearance Center, Inc. | ||
In a later study, the role of explicit water molecules in the catalysis was examined using the ONIOM QM/QM′ (B3LYP/PM6) method, defining a high-level layer QM region and a low-level layer QM′ region.55 The energy profile obtained from the QM/QM′ simulations follows the same trend as the one from the QM cluster calculations (Fig. 2b). Consistent with the previous cluster calculations, the catalytic process was shown to follow the σ-bond metathesis mechanism, and the rate-limiting step is the release of formic acid. An interesting finding was that for the product release the energy barrier from the QM/QM′ investigation, obtained without the presence of water in the active site, increased to 21.0 kcal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1, compared to 12.8 kcal
mol−1, compared to 12.8 kcal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1 (TS6c–6d) obtained from the cluster approach without including explicit water in the model (Fig. 2b). However, when considering the presence of two water molecules in the active pocket, which decreased the reaction distances and increased the Lewis base character of CO2, the activation barrier for the rate-limiting step sharply reduced to 11.7 kcal mol−1. These results clearly revealed the important role of the water molecules in the reaction.
mol−1 (TS6c–6d) obtained from the cluster approach without including explicit water in the model (Fig. 2b). However, when considering the presence of two water molecules in the active pocket, which decreased the reaction distances and increased the Lewis base character of CO2, the activation barrier for the rate-limiting step sharply reduced to 11.7 kcal mol−1. These results clearly revealed the important role of the water molecules in the reaction.
The mechanistic studies on Rh-substituted hCAII using QM cluster and QM/QM′ methods predicted the ability of this new artificial enzyme in catalyzing the hydrogenation of CO2 to formate. However, it has been shown that rhodium can non-specifically bind to histidine residues on the surface of hCAII, thereby limiting its practical application.52,53 Nevertheless, combining metal catalysts with enzymes, instead of utilizing cofactors like NADH to hydrogenate the substrates, is a promising way to create artificial enzymes that complement nature's toolkit.
3.2 Fixation of carbon dioxide to form aliphatic acids
In 1998, Cleland et al. described the overall reaction catalyzed by RuBisCO as involving the enolization of the ribulose 1,5-bisphosphate (RuBP), the addition of CO2 and H2O, the C2–C3 carbon–carbon cleavage, and the stereospecific protonation of atom C2 to form 3-P-glyceric acid (3-PGA).56 Subsequently, quantum chemical calculations have been carried out for separate reaction steps to reveal the mechanistic details. Proton wires, following the classical Grotthuss proton-shuttle mechanism, were proposed to facilitate the rapid transportation of protons involved in the rate-limiting catalytic steps.57,58
Since the previously reported energy barriers for the step of the initial enolate formation vary significantly across different studies, Douglas-Gallardo et al. employed QM/MM molecular dynamics simulation in combination with an advanced projector-embedding method to calculate the minimum free-energy path and gained accurate protonation states of catalytic residues.59 The energies of proton transfer from the C3 hydroxyl group to His294 or carbamylated Lys201 (Kcx201) were evaluated. It was found that the proton transfer to Kcx201 has a lower free-energy barrier and is thus the preferred pathway (Scheme 2).
 | ||
| Scheme 2 Reaction mechanism of RuBisCO: the enolization of RuBP, the carboxylation and hydration steps, the scission of C2–C3, and the stereospecific protonation of C2.58–60 | ||
The activation barrier of the following carboxylation step was calculated to be 4.7 kcal mol−1, indicating that this elementary step is not rate-limiting. Meanwhile, the reaction energy of this process is −12.2 kcal mol−1, consistent with the experimental results that the carboxylation is irreversible.61
Large-scale quantum chemical calculations were carried out to specifically evaluate four possible pathways for the direction of water molecule addition during the hydration reaction step.60 The calculations suggested that the water molecule approaches C3 from the opposite side of the added CO2 and is deprotonated by Kcx201 (Scheme 2). The subsequent C2–C3 bond scission and C2 stereospecific protonation were proposed to be assisted by the protonation of the C2 carboxylate group and the phosphate group with the Kcx201 and His294 residues being the potential proton sources.57
The conserved lysine (Lys175) was believed to provide the necessary proton in stereospecific protonation of C2.56,57 To investigate the feasibility of this assumption, Cummins et al. used DFT(B3LYP) and ab initio molecular dynamics simulations with umbrella sampling to determine the mechanisms of the C2–C3 bond scission and the stereospecific protonation.62 It was concluded that the Lys175 is not the direct proton donor to C2 during the product formation according to the free energy change. Instead, a proton from the P1 phosphate of RuBP is plausibly transported via a water molecule to C2, following the Grotthuss mechanism (Scheme 2).
According to these calculations, the RuBisCO carboxylation process starts with the abstraction of a proton from the carbon C3 of ribulose-1,5-bisphosphate (RuBP) by the carbamylated Lys201, forming an enolate intermediate. Then, this intermediate undergoes a proton rearrangement, and subsequently performs a nucleophilic attack on CO2, adding CO2 to its C2 atom to form 2-carboxy-3-keto-D-arabinitol-1,5-bisphosphate (CKABP). The reaction further proceeds with the hydration of CKABP and the C2–C3 bond cleavage concurrent with C2 stereospecific protonation, ultimately producing two molecules of 3-phospho-D-glyceric acid (3-PGA) (Scheme 2). These mechanistic insights can be helpful in investigating the catalytic limitation on the reactivity of RuBisCO, whose rate constants are much lower than those of classical central metabolic enzymes.
The catalytic reaction of CCR follows the general mechanism of ECR enzymes. This process involves a hydride transfer from NADPH to the β-carbon of crotonyl-CoA, forming an enolate intermediate. The enolate then undergoes a nucleophilic attack on CO2 to form (2S)-ethylmalonyl-CoA. Stoffel et al. revealed the function of four amino acids that contribute significantly to the high efficiency of the carboxylation activity of CCR through a combination of QM/MM approach and experimental assays.63 It was demonstrated that Asn81 is crucial for positioning the CO2 molecule correctly through its carboxamide NH2 interacting with CO2. His365 and Glu171 jointly coordinate an ordered water molecule, forming a water network that helps control the positioning of CO2. Meanwhile, Phe170 shields the active site from water, preventing the enolate from being protonated into the reduction side product butyryl-CoA.
Interestingly, a C2-ene adduct was experimentally detected in CCR reaction in the absence of CO2.66,67 Similar adduct has also been experimentally characterized in mammalian fatty acid synthase, which was then computationally confirmed.68 To reveal the role of this adduct intermediate in the catalysis, Recabarren et al. have evaluated two possible reaction pathways for CCR, including a direct mechanism and a C2 mechanism (Scheme 3).69 Instead of directly transferring a hydride from N4 of NADPH to the Cβ of the substrate, forming an enolate that reacts with CO2 in the direct mechanism, the C2 mechanism involves a Michael addition between the C2 of NADPH and the Cα of the substrate to form a C2-ene adduct. This adduct is followed by subsequent carboxylation (Scheme 3). According to the calculated free energy landscapes, this adduct can react with CO2 with a similar activation barrier to the direct reaction pathway. It was thus proposed that the formation of the C2-ene adduct is a strategy employed by this enzyme to store enolate intermediate when CO2 is absent from the active site. It becomes reactive when CO2 is available, thereby improving CO2-fixing efficiency. This adduct also acts as a stable intermediate to avoid the reduction side reaction.
 | ||
| Scheme 3 Reaction mechanism of crotonyl-CoA carboxylases/reductases: direct mechanism (a) and C2 mechanism (b). Adapted with permission from ref. 69, Copyright 2023 American Chemical Society. | ||
In conclusion, factors that determine the high efficiency of CO2 fixation by CCR may include: the unidirectional formation of the enolate; key residues that control the position of CO2 being attacked; suppression of competing (re)protonation reactions by shielding the active pocket from water; and the formation of a C2-ene adduct, which restores the enolate intermediate and prevents side reduction reactions.
Yoshizawa et al. investigated the plausible reaction mechanisms accomplished in the BC domain using quantum calculations.72 According to the detailed analysis of potential energy surfaces, a two-step reaction mechanism was proposed (Scheme 4). Initially, bicarbonate is phosphorylated by attacking on the γ-phosphate group of ATP to form a short-lived carboxy-phosphate (CP) intermediate. During this process, the Mg2+ ion promotes the formation of CP by alleviating the electrostatic repulsion between bicarbonate and ATP. In the second step, CP serves as a general acid–base catalyst, facilitating the enolization of biotin and subsequently generating a bent CO2 to react with enolic biotin. This step can be interpreted as the nucleophilic attack by the ureido nitrogen of biotin on the carboxyl group of CP to form carboxybiotin. The rate-limiting step is the formation of CP in the first step.
 | ||
| Scheme 4 Reaction mechanism of the biotin carboxylation in the BC domain of pyruvate carboxylase.72 | ||
Sheng et al. conducted a successive study on the catalytic mechanism of the CT domain in pyruvate carboxylase from Staphylococcus aureus,73,74 exploring how posttranslational modifications (PTMs) affect enzyme activity. At first, the elementary steps in the catalytic cycle occurring within the CT domain were investigated.73 Four steps were proposed, including the decarboxylation of carboxybiotin to generate an enol–biotin intermediate and a free CO2 molecule, the proton transfer from T908 to enol–biotin, the proton transfer from pyruvate to T908, and the nucleophilic attack by enol-pyruvate at the generated CO2 (Scheme 5). Subsequently, Sheng et al. investigated the roles of the carboxylated lysine and a water molecule coordinated to Zn2+ in the catalysis.74 While following the same reaction mechanism, the new model, which includes the entire modified lysine and a water molecule in the QM region of QM/MM calculations, showed significantly lower energy barriers of all the elementary steps compared to the previous calculations, which was based on a model without the inclusion of the carboxylate group on the modified lysine and the water molecule. In particular, the energy barrier of the overall reaction using the new model is approximately 14 kcal mol−1, which is much lower than that in the previous study. The Zn-coordinated water molecule was explained to enhance the stabilization of the transition state during the carboxylation of enol-pyruvate. Meanwhile, the modified lysine was proposed to facilitate the reaction by positioning and orienting the substrate and cofactor in a proper position during the catalysis, and also by regulating the charge of zinc cation.
 | ||
| Scheme 5 Reaction mechanism of the pyruvate carboxylation in the CT domain of pyruvate carboxylase.73 | ||
 | ||
| Scheme 6 Decarboxylation mechanism of pyruvate decarboxylase from Zymomonas mobilis (ZmPDC).78 | ||
Using density functional theory calculations, Wang et al. investigated the reaction mechanism of ScPDC.79 According to the calculations, a proton relay among Glu51 (equivalent to Glu50 in Scheme 6), N1′ and the 4′-amino group of ThDP facilitates the deprotonation of C2, forming the ylide intermediate. This process also affects the basicity of the 4′-amino group, which deprotonates the α-hydroxyl of HEThDP, thereby accelerating the release of acetaldehyde. Glu477 and Asp28 facilitate the decarboxylation of LThDP by forming strong hydrogen bonds with its carboxylate group, making the reaction endothermic. Subsequently, a proton is transferred from His115 via Asp28 to the α-carbanion in a concerted manner to form HEThDP. However, the cluster model used in this study was small, and the roles of other key active site residues were not discussed.
A QM/MM theoretical study of PDC from Zymomonas mobilis (ZmPDC) was carried out to determine the protonation states and the roles of active site catalytic residues.78 Three models with varying protonation states of the key active site residues were considered for different mechanisms. In the most plausible mechanism, the ionizable residues in the active site, including Asp27, Glu50, His113, His114 and Glu473, were proposed to be in their protonated states. Asp27 was suggested to provide a proton to the HEThDP carbanion/enamine intermediate, differing from the proposed mechanism of ScPDC discussed above.79 His113 and His114 interact with the substrate and intermediates during the reaction process. According to the energy profile, the LThDP and HEThDP intermediates have lower energies than all the other intermediates, including the enzyme–substrate and enzyme–product complexes. This is consistent with the experimentally observed accumulation of these two compounds.80 The decarboxylation of this enzyme was calculated to be the rate-determining step.
These calculations have confirmed the protonation sates of the ionizable residues in the active site of PDC, and also the roles of these residues in the catalysis.
The quantum chemical studies on the PDHc E1 subunit provided support to the reaction mechanism discussed above. In the mechanistic study on the PDHc E1 from Escherichia coli using the cluster approach,81 the roles of several active site residues were confirmed. In particular, Glu571 and Glu522 play essential roles in ThDP ylide formation, pyruvate addition, acetaldehyde release, and the positioning of the carboxyl of pyruvate, while His640 and a water molecule are involved in a concerted proton transfer processes to protonate the enamine.
In a subsequent study, also using the cluster approach, Sheng and Liu investigated four possible pathways for the PDHc E1 from Bacillus stearothermophilus. In these pathways, the 4′-amino of the ylide, His271 (a residue not considered in the study on the PDHc E1 from E. coli discussed above), and His128 (equivalent to His640 in the PDHc E1 from E. coli) were proposed to act as the general acid/base in various combinations in the processes of decarboxylation and reductive acylation.82 It was found that the most favorable pathway involved the 4′-amino group of the ylide and protonated His128 acting as acid/base groups, with His271 deprotonated (Scheme 7). The C–C bond cleavage that releases CO2 was calculated to be the rate-limiting step.
 | ||
| Scheme 7 The reaction mechanism of PDHc E1 subunit. Adapted with permission from ref. 82, Copyright 2013 American Chemical Society. | ||
The computational studies on PDC and PDHc E1 showed that the decarboxylation reactions follow a similar mechanism. However, the energetics, protonation states, and roles of active site residues can vary between different enzymes. This highlights the importance of calculating the entire mechanisms in detail and the corresponding energy profiles to gain accurate insights into the reaction.
3.3 Fixation of carbon dioxide to form aromatic acids
A 1,3-dipolar cycloaddition mechanism was first proposed for the UbiD enzymes on the basis of the study of the ferulic acid decarboxylase (Fdc1) from Aspergillus niger.83 Given the azomethine ylide character of prFMN and the alkene dipolarophiles of α,β-unsaturated carbonyl group, the 1,3-cycloaddition reaction was suggested to occur between the co-factor and the substrate. This leads to the formation of the [3+2] covalent substrate–prFMN pyrrolidine adduct, which involves the substrate Cα binding to the C1′ of prFMN and the substrate Cβ binding to the C4α of prFMN concurrently. The reaction proceeds with decarboxylation coupled with the breaking of the Cβ−C4α bond, the protonation of phenylpyruvate adduct by E282, the formation of the second cycloadduct species, and then the cycloelimination to form final styrene product (Scheme 8).
 | ||
| Scheme 8 Proposed 1,3-cycloaddition mechanism for ferulic acid decarboxylase (Fdc1).83 | ||
The decarboxylation mechanism of Fdc1 was investigated by using both the cluster approach84 and the QM/MM method.85 According to the calculations, the Fdc1 reaction indeed follows the 1,3-cycloaddition mechanism and Glu282 was confirmed to play important role in catalysis being as a general acid group. In the former study, using α-methylcinnamic acid as the representative substrate, the decomposition of the second pyrrolidine intermediate was calculated to be the rate-limiting step.84 While in the latter one, the calculations showed that for the decarboxylation of cinnamic acid the protonation step is rate-limiting.85
Quantum chemical cluster calculations revealed a distinct reaction mechanism from 1,3-cycloaddition for 3,4-dihydroxybenzoic acid decarboxylases (AroY), which also belongs to the UbiD enzyme family.86 The reversible reaction of aromatic catechol substrates was suggested to initiate by a nucleophilic attack of the substrate Cα to the C1′ of prFMN. Instead of forming 1,3-dipolar cycloaddition intermediate, a quinoid binding to the cofactor adduct via a single covalent bond is formed (Scheme 9). The overall barrier of the reaction is 19.9 kcal mol−1, according to the calculated energy profile. Moreover, the calculations confirmed that a cycloadduct intermediate is unlikely to form in the case of AroY, as the energy of such an intermediate is as high as 37 kcal mol−1. Interestingly, by using also the cluster approach, a similar intermediate was later found in the cinnamic acid cycloaddition by Fdc1.29 However, such intermediates were not located in the reaction of phenylpropiolic or crotonic acid by Fdc1.
 | ||
| Scheme 9 Proposed nucleophilic attack mechanism for 3,4-dihydroxybenzoic acid decarboxylases (AroY).86 | ||
Theoretical analysis of UbiD enzyme pyrrole-2-carboxylic acid decarboxylase (HudA),87 a virulence attenuation factor from Pseudomonas aeruginosa, suggests a nucleophilic attack of C1′ at the pyrrole C2 position of heteroaromatic substrates. It follows the electrophilic aromatic substitution mechanism, with a Wheland-type intermediate formed. A recent mechanistic study of HudA and two other prFMN-dependent decarboxylases (HmfF and lnD) using heteroaromatic substrates suggested that the decarboxylation adopts a nucleophilic attack mechanism while the carboxylation follows a 1,3-dipolar cycloaddition mechanism.88 For the carboxylation of furoic acid, pyrrole, and indole, it was proposed that they favor the formation of a 1,3-dipolar cycloadduct in the initial step because of the lack of a carboxyl group on one side. The “absent” carboxyl group was proposed to hinder electron donation to the cofactor, making it unfavourable to form the Wheland-type intermediate.
Decarboxylation mechanisms of five members of this family have been theoretically investigated, which mainly consist of two key steps: the protonation of the carbon of the substrate and the cleavage of the C–C bond.89 In combination with crystallographic study, the substrates were confirmed to bind to the metals in a bidentate mode. Upon the binding, the hydroxyl groups lose their protons. The initial reaction products of the enzymatic decarboxylation were confirmed to be CO2 rather than the bicarbonate proposed in previous studies,94 because a high-energy hydrated carboxylate intermediate is involved in the reaction pathway to form bicarbonate.
Among these decarboxylases being investigated, the rate-limiting steps are not the same for each one (Table 2). The proton transfer is the rate-limiting step for LigW,89 γ-RSD,90 2,3-DHBD91 and SDC,92 while the C–C bond cleavage is rate-limiting for IDCase.93 Initially, the divalent metal ion dependency of the AHS superfamily was believed to be Zn2+.94–96 However, according to the five research studies carried out using quantum chemical calculations in combination with experimental validation (Table 2), 2,3-DHBD is active with both Mn2+ and Mg2+,91 LigW,89 IDCase93 and γ-RSD90 prefer to depend on Mn2+, while SDC is Mg2+-dependent.92
These calculations on AHS decarboxylases show that the quantum chemical modeling is a powerful tool in investigating reaction mechanism, and can also be used in clarifying the metal identity and other properties of the enzymes.
4. Perspective
Our perspective closes with a viewpoint on the potential of combining machine learning (ML) and quantum descriptions in investigating enzymatic CO2 conversion.CO2-converting enzymes generally catalyze at rather low kcat values, ranging from 10 s−1 (average for RubisCO)97 to 100 s−1 (ECRs).9,98 Therefore, there is an urgent need to enhance the performance of existing carbon-fixation enzymes or to design new-to-nature CO2-converting enzymes. Recently, ML has shown significant promise in accelerating enzyme engineering. This is due to substantial improvements in protein representations and deep learning models, which can incorporate numerous parameters as needed.
Using data obtained from quantum chemistry calculations to train ML models is an efficient way to predict the electronic properties of reactants and the thermodynamic properties of reactions, thereby to predict the reactivity and selectivity of CO2 conversion reactions. ML has successfully been applied to study the chemisorption, binding, activation, and hydrogenation of CO2, in combination with quantum chemical computations in chemical systems.99–102 For example, Zheng et al. reported quantum-informed machine-learning force fields (QMLFFs) that can predict the binding free energy landscape of CO2 chemisorption in Mg-MOF-74.99 Chen et al. developed neural network (NN) ML models based on DFT calculations to discover catalysts capable of circumventing the scaling relation for CO2 reduction reactions.103 Zhu et al. proposed ML models based on DFT calculations to predict the free energy changes along the reaction pathway and the product probability for methanol, methane and formaldehyde in CO2 reduction reaction catalyzed by metal-zeolites.104
With the ability to analyze and learn from large size of data, ML methods can dramatically expand the applicability range of conventional QM-based simulations to biological systems. We believe that combining quantum descriptions with machine learning can be valuable in addressing the reaction mechanisms of specific CO2-converting enzymes and can contribute to the discovery of novel enzyme activities, the rational design of enzymes, or the improvement of efficiency in biocatalytic CO2 conversion.
Author contributions
Baoyan Liu: investigation, writing – original draft, visualization; Beibei Lin: visualization; Hao Su: visualization, writing – original draft; Xiang Sheng: conceptualization, supervision, visualization, writing – review & editing.Data availability
No primary research results, software or code have been included and no new data were generated or analyzed as part of this perspective.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the Strategic Priority Research Program of the Chinese Academy of Sciences (XDC0120200), the Innovation Fund of Haihe Laboratory of Synthetic Biology (22HHSWSS00020) and the CAS Project for Young Scientists in Basic Research (YSBR-072) are acknowledged.References
- X. Lan, P. Tans and K. W. Thoning, Trends in globally-averaged CO2 determined from NOAA Global Monitoring Laboratory measurements, Version 2024-04 DOI:10.15138/9N0H-ZH07.
- A. R. Jacobson, K. N. Schuldt, P. Tans, A. Andrews, J. B. Miller, T. Oda, J. B. Abshire, K. Aikin, S. Aoki, B. Baier, J. Bartyzel, A. Beyersdorf and T. Biermann, CarbonTracker CT, 2022, https://carbontracker.noaa.gov.
- S. Bierbaumer, M. Nattermann, L. Schulz, R. Zschoche, T. J. Erb, C. K. Winkler, M. Tinzl and S. M. Glueck, Enzymatic conversion of CO2: from natural to artificial utilization, Chem. Rev., 2023, 123, 5702–5754 CrossRef CAS PubMed.
- Y. Fan, J. Feng, M. Yang, X. Tan, H. Fan, M. Guo, B. Wang and S. Xue, CO2(aq) concentration–dependent CO2 fixation via carboxylation by decarboxylase, Green Chem., 2021, 23, 4403–4409 RSC.
- A. Gulzar, A. Gulzar, M. B. Ansari, F. He, S. Gai and P. Yang, Carbon dioxide utilization: a paradigm shift with CO2 economy, Chem. Eng. J. Adv., 2020, 3, 100013 CrossRef CAS.
- I. Bernhardsgrütter, G. M. Stoffel, T. E. Miller and T. J. Erb, CO2-converting enzymes for sustainable biotechnology: from mechanisms to application, Curr. Opin. Biotechnol, 2021, 67, 80–87 CrossRef PubMed.
- G. A. Aleku, G. W. Roberts, G. R. Titchiner and D. Leys, Synthetic Enzyme-Catalyzed CO2 Fixation Reactions, ChemSusChem, 2021, 14, 1781–1804 CrossRef CAS PubMed.
- T. Cai, H. Sun, J. Qiao, L. Zhu, F. Zhang, J. Zhang, Z. Tang, X. Wei, J. Yang, Q. Yuan, W. Wang, X. Yang, H. Chu, Q. Wang, C. You, H. Ma, Y. Sun, Y. Li, C. Li, H. Jiang, Q. Wang and Y. Ma, Cell-free chemoenzymatic starch synthesis from carbon dioxide, Science, 2021, 373, 1523–1527 CrossRef CAS PubMed.
- T. Schwander, L. S. von Borzyskowski, S. Burgener, N. S. Cortina and T. J. Erb, A synthetic pathway for the fixation of carbon dioxide in vitro, Science, 2016, 354, 900–904 CrossRef CAS PubMed.
- T. E. Miller, T. Beneyton, T. Schwander, C. Diehl, M. Girault, R. McLean, T. Chotel, P. Claus, N. S. Cortina, J.-C. Baret and T. J. Erb, Light-powered CO2 fixation in a chloroplast mimic with natural and synthetic parts, Science, 2020, 368, 649–654 CrossRef CAS PubMed.
- R. McLean, T. Schwander, C. Diehl, N. S. Cortina, N. Paczia, J. Zarzycki and T. J. Erb, Exploring alternative pathways for the in vitro establishment of the HOPAC cycle for synthetic CO2 fixation, Sci. Adv., 2023, 16, eadh4299 CrossRef PubMed.
- S. Luo, P. P. Lin, L.-Y. Nieh, G.-B. Liao, P.-W. Tang, C. Chen and J. C. Liao, A cell-free self-replenishing CO2-fixing system, Nat. Catal., 2022, 5, 154–162 CrossRef CAS.
- L. Xiao, G. Liu, F. Gong, H. Zhu, Y. Zhang, Z. Cai and Y. Li, A Minimized Synthetic Carbon Fixation Cycle, ACS Catal., 2022, 12, 799–808 CrossRef CAS.
- A. Satanowski, B. Dronsella, E. Noor, B. Vögeli, H. He, P. Wichmann, T. J. Erb, S. N. Lindner and A. Bar-Even, Awakening a latent carbon fixation cycle in Escherichia coli, Nat. Commun., 2020, 11, 5812 CrossRef CAS PubMed.
- M. Aresta, E. Quaranta, R. Liberio, C. Dileo and I. Tommasi, Enzymatic synthesis of 4-OH-benzoic acid from phenol and CO2: the first example of a biotechnological application of a Carboxylase enzyme, Tetrahedron, 1998, 54, 8841–8846 CrossRef CAS.
- I. Bernhardsgrütter, K. Schell, D. M. Peter, F. Borjian, D. A. Saez, E. Vöhringer-Martinez and T. J. Erb, Awakening the Sleeping Carboxylase Function of Enzymes: Engineering the Natural CO2-Binding Potential of Reductases, J. Am. Chem. Soc., 2019, 141, 9778–9782 CrossRef PubMed.
- I. Sánchez-Andrea, I. A. Guedes, B. Hornung, S. Boeren, C. E. Lawson, D. Z. Sousa, A. Bar-Even, N. J. Claassens and A. J. M. Stams, The reductive glycine pathway allows autotrophic growth of Desulfovibrio desulfuricans, Nat. Commun., 2020, 11, 5090 CrossRef PubMed.
- T. Kanao, M. Kawamura, T. Fukui, H. Atomi and T. Imanaka, Characterization of isocitrate dehydrogenase from the green sulfur bacterium Chlorobium limicola, Eur. J. Biochem., 2002, 269, 1926–1931 CrossRef CAS PubMed.
- S. G. Huwiler, C. Löffler, S. E. L. Anselmann, H.-J. Stärk, M. von Bergen and J. Flechsler, R. Rachel and M. Boll, One-megadalton metalloenzyme complex in Geobacter metallireducens involved in benzene ring reduction beyond the biological redox window, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2259–2264 CrossRef CAS PubMed.
- A. Witt, R. Pozzi, S. Diesch, O. Hädicke and H. Grammel, New light on ancient enzymes – in vitro CO2 Fixation by Pyruvate Synthase of Desulfovibrio africanus and Sulfolobus acidocaldarius, FEBS J., 2019, 286, 4494–4508 CrossRef CAS PubMed.
- P. Wongkittichote, N. Ah Mew and K. A. Chapman, Propionyl-CoA carboxylase – A review, Mol. Genet. Metab., 2017, 122, 145–152 CrossRef CAS PubMed.
- M. Scheffen, D. G. Marchal, T. Beneyton, S. K. Schuller, M. Klose, C. Diehl, J. Lehmann, P. Pfister, M. Carrillo, H. He, S. Aslan, N. S. Cortina, P. Claus, D. Bollschweiler, J.-C. Baret, J. M. Schuller, J. Zarzycki, A. Bar-Even and T. J. Erb, A new-to-nature carboxylation module to improve natural and synthetic CO2 fixation, Nat. Catal., 2021, 4, 105–115 CrossRef CAS.
- X. Sheng and F. Himo, Mechanisms of metal-dependent non-redox decarboxylases from quantum chemical calculations, Comput. Struct. Biotechnol. J., 2021, 19, 3176–3186 CrossRef CAS PubMed.
- S. E. Payer, K. Faber and S. M. Glueck, Non-oxidative enzymatic (de) carboxylation of (hetero) aromatics and acrylic acid derivatives, Adv. Synth. Catal., 2019, 361, 2402–2420 CrossRef CAS PubMed.
- G. Tcherkez, The mechanism of Rubisco-catalysed oxygenation, Plant, Cell Environ., 2016, 39, 983–997 CrossRef CAS PubMed.
- Y. Kai, H. Matsumura and K. Izui, Phosphoenolpyruvate carboxylase: three-dimensional structure and molecular mechanisms, Arch. Biochem. Biophys., 2002, 414, 170–179 CrossRef.
- M. Can, F. A. Armstrong and S. W. Ragsdale, Structure, function, and mechanism of the nickel metalloenzymes, CO dehydrogenase, and acetyl-CoA synthase, Chem. Rev., 2014, 114, 4149–4174 CrossRef CAS PubMed.
- T. Wagner, U. Ermler and S. Shima, The methanogenic CO2 reducing-and-fixing enzyme is bifunctional and contains 46 [4Fe–4S] clusters, Science, 2016, 354, 114–117 CrossRef CAS.
- S. S. Bailey, K. A. P. Payne, A. Saaret, S. A. Marshall, I. Gostimskaya, I. Kosov, K. Fisher, S. Hay and D. Leys, Enzymatic control of cycloadduct conformation ensures reversible 1,3-dipolar cycloaddition in a prFMN-dependent decarboxylase, Nat. Chem., 2019, 11, 1049–1057 CrossRef CAS PubMed.
- S. Menon and S. W. Ragsdale, Mechanism of the Clostridium thermoaceticum pyruvate: ferredoxin oxidoreductase: evidence for the common catalytic intermediacy of the hydroxyethylthiamine pyropyrosphate radical, Biochemistry, 1997, 36, 8484–8494 CrossRef CAS PubMed.
- C. Furdui and S. W. Ragsdale, The roles of coenzyme A in the pyruvate: ferredoxin oxidoreductase reaction mechanism: rate enhancement of electron transfer from a radical intermediate to an iron–sulfur cluster, Biochemistry, 2002, 41, 9921–9937 CrossRef CAS PubMed.
- D. R. Salahub, Multiscale molecular modelling: from electronic structure to dynamics of nanosystems and beyond, Phys. Chem. Chem. Phys., 2022, 24, 9051–9081 RSC.
- W.-J. Wei, H.-X. Qian, W.-J. Wang and R.-Z. Liao, Computational Understanding of the Selectivities in Metalloenzymes, Front. Chem., 2018, 6, 638 CrossRef CAS.
- X. Sheng and F. Himo, The quantum chemical cluster approach in biocatalysis, Acc. Chem. Res., 2023, 56, 938–947 CrossRef CAS.
- P. E. M. Siegbahn, A quantum chemical approach for the mechanisms of redox-active metalloenzymes, RSC Adv., 2021, 11, 3495–3508 RSC.
- X. Sheng, M. Kazemi, F. Planas and F. Himo, Modeling enzymatic enantioselectivity using quantum chemical methodology, ACS Catal., 2020, 10, 6430–6449 CrossRef CAS.
- F. Himo, Recent trends in quantum chemical modeling of enzymatic reactions, J. Am. Chem. Soc., 2017, 139, 6780–6786 CrossRef CAS PubMed.
- M. G. Quesne, T. Borowski and S. P. de Visser, Quantum Mechanics/Molecular Mechanics Modeling of Enzymatic Processes: Caveats and Breakthroughs, Chem. – Eur. J., 2016, 22, 2562–2581 CrossRef CAS PubMed.
- S. F. Sousa, A. J. M. Ribeiro, R. P. P. Neves, N. F. Brás, N. M. F. S. A. Cerqueira, P. A. Fernandes and M. J. Ramos, Application of Quantum Mechanics/Molecular Mechanics Methods in the Study of Enzymatic Reaction Mechanisms, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1281 Search PubMed.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Energy-adjusted ab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- S. Dasgupta and J. M. Herbert, Using atomic confining potentials for geometry optimization and vibrational frequency calculations in quantum-chemical models of enzyme active sites, J. Phys. Chem. B, 2020, 124, 1137–1147 CrossRef CAS PubMed.
- P. E. Bowling, S. Dasgupta and J. M. Herbert, Eliminating imaginary vibrational frequencies in quantum-chemical cluster models of enzymatic active sites, J. Chem. Inf. Model., 2024, 64, 3912–3922 CrossRef CAS PubMed.
- A. Bassegoda, C. Madden, D. W. Wakerley, E. Reisner and J. Hirst, Reversible Interconversion of CO2 and Formate by a Molybdenum-Containing Formate Dehydrogenase, J. Am. Chem. Soc., 2014, 136, 15473–15476 CrossRef CAS PubMed.
- L. B. Maia, L. Fonseca, I. Moura and J. J. G. Moura, Reduction of Carbon Dioxide by a Molybdenum-Containing Formate Dehydrogenase: A Kinetic and Mechanistic Study, J. Am. Chem. Soc., 2016, 138, 8834–8846 CrossRef CAS PubMed.
- N. M. F. S. A. Cerqueira, P. J. Gonzalez, P. A. Fernandes, J. J. G. Moura and M. J. Ramos, Periplasmic Nitrate Reductase and Formate Dehydrogenase: Similar Molecular Architectures with Very Different Enzymatic Activities, Acc. Chem. Res., 2015, 48, 2875–2884 CrossRef CAS PubMed.
- G. Dong and U. Ryde, Reaction mechanism of formate dehydrogenase studied by computational methods, JBIC, J. Biol. Inorg. Chem., 2018, 23, 1243–1254 CrossRef CAS PubMed.
- P. E. M. Siegbahn, Energetics for CO2 Reduction by Molybdenum-Containing Formate Dehydrogenase, J. Phys. Chem. B, 2022, 126, 1728–1733 CrossRef CAS PubMed.
- S. W. Ragsdale and M. Kumar, Nickel-containing carbon monoxide dehydrogenase/acetyl-CoA synthase, Chem. Rev., 1996, 96, 2515–2540 CrossRef CAS PubMed.
- R.-Z. Liao and P. E. M. Siegbahn, Energetics for the Mechanism of Nickel-Containing Carbon Monoxide Dehydrogenase, Inorg. Chem., 2019, 58, 7931–7938 CrossRef CAS PubMed.
- J.-H. Jeoung and H. Dobbek, Carbon Dioxide Activation at the Ni,Fe-Cluster of Anaerobic Carbon Monoxide Dehydrogenase, Science, 2007, 318, 1461–1464 CrossRef CAS PubMed.
- R. Breglia, F. Arrigoni, M. Sensi, C. Greco, P. Fantucci, L. De Gioia and M. Bruschi, First-Principles Calculations on Ni,Fe-Containing Carbon Monoxide Dehydrogenases Reveal Key Stereoelectronic Features for Binding and Release of CO2 to/from the C-Cluster, Inorg. Chem., 2021, 60, 387–402 CrossRef CAS PubMed.
- Q. Jing, K. Okrasa and R. J. Kazlauskas, Stereoselective hydrogenation of olefins using rhodium-substituted carbonic Anhydrase—A new reductase, Chem. – Eur. J., 2009, 15, 1370–1376 CrossRef CAS PubMed.
- Q. Jing and R. J. Kazlauskas, Regioselective hydroformylation of styrene using rhodium-substituted carbonic anhydrase, ChemCatChem, 2010, 2, 953–957 CrossRef CAS.
- P. Piazzetta, T. Marino, N. Russo and D. R. Salahub, Direct Hydrogenation of Carbon Dioxide by an Artificial Reductase Obtained by Substituting Rhodium for Zinc in the Carbonic Anhydrase Catalytic Center. A Mechanistic Study, ACS Catal., 2015, 5, 5397–5409 CrossRef CAS.
- P. Piazzetta, T. Marino, N. Russo and D. R. Salahub, Explicit Water Molecules Play a Key Role in the Mechanism of Rhodium-Substituted Human Carbonic Anhydrase, ChemCatChem, 2017, 9, 1047–1053 CrossRef CAS.
- W. W. Cleland, T. J. Andrews, S. Gutteridge, F. C. Hartman and G. H. Lorimer, Mechanism of Rubisco: the carbamate as general base, Chem. Rev., 1998, 98, 549–562 CrossRef CAS PubMed.
- T. C. Taylor and I. Andersson, Structure of a product complex of spinach ribulose-1,5-bisphosphate carboxylase/oxygenase, Biochemistry, 1997, 36, 4041–4046 CrossRef CAS PubMed.
- P. L. Cummins and J. E. Gready, Kohn–Sham Density Functional Calculations Reveal Proton Wires in the Enolization and Carboxylase Reactions Catalyzed by Rubisco, J. Phys. Chem. B, 2020, 124, 3015–3026 CrossRef CAS PubMed.
- O. A. Douglas-Gallardo, J. A. Murillo-López, J. Oller, A. J. Mulholland and E. Vöhringer-Martinez, Carbon Dioxide Fixation in RuBisCO is Protonation-State-Dependent and Irreversible, ACS Catal., 2022, 12, 9418–9429 CrossRef CAS.
- P. L. Cummins, B. Kannappan and J. E. Gready, Revised mechanism of carboxylation of ribulose-1,5-biphosphate by rubisco from large scale quantum chemical calculations, J. Comput. Chem., 2018, 39, 1656–1665 CrossRef CAS PubMed.
- G. H. Lorimer, T. Andrews, J. Pierce and J. Schloss, 2-carboxy-3-keto-D-arabinitol 1, 5-bisphosphate, the six-carbon intermediate of the ribulose bisphosphate carboxylase reaction, Philos. Trans. R. Soc., B, 1986, 313, 397–407 CAS.
- P. L. Cummins, B. Kannappan and J. E. Gready, Ab Initio Molecular Dynamics Simulation and Energetics of the Ribulose-1,5-biphosphate Carboxylation Reaction Catalyzed by Rubisco: Toward Elucidating the Stereospecific Protonation Mechanism, J. Phys. Chem. B, 2019, 123, 2679–2686 CrossRef CAS PubMed.
- G. M. M. Stoffel, D. A. Saez, H. DeMirci, B. Vögeli, Y. Rao, J. Zarzycki, Y. Yoshikuni, S. Wakatsuki, E. Vöhringer-Martinez and T. J. Erb, Four amino acids define the CO2 binding pocket of enoyl-CoA carboxylases/reductases, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13964–13969 CrossRef CAS PubMed.
- D. M. Peter, L. Schada von Borzyskowski, P. Kiefer, P. Christen, J. A. Vorholt and T. J. Erb, Screening and engineering the synthetic potential of carboxylating reductases from central metabolism and polyketide biosynthesis, Angew. Chem., Int. Ed., 2015, 54, 13457–13461 CrossRef CAS PubMed.
- T. J. Erb, I. A. Berg, V. Brecht, M. Müller, G. Fuchs and B. E. Alber, Synthesis of C5-dicarboxylic acids from C2-units involving crotonyl-CoA carboxylase/reductase: the ethylmalonyl-CoA pathway, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 10631–10636 CrossRef CAS PubMed.
- R. G. Rosenthal, M.-O. Ebert, P. Kiefer, D. M. Peter, J. A. Vorholt and T. J. Erb, Direct evidence for a covalent ene adduct intermediate in NAD (P) H-dependent enzymes, Nat. Chem. Biol., 2014, 10, 50–55 CrossRef CAS PubMed.
- R. G. Rosenthal, B. Vögeli, N. Quade, G. Capitani, P. Kiefer, J. A. Vorholt, M.-O. Ebert and T. J. Erb, The use of ene adducts to study and engineer enoyl-thioester reductases, Nat. Chem. Biol., 2015, 11, 398–400 CrossRef CAS PubMed.
- F. E. Medina, M. J. Ramos and P. A. Fernandes, Complexities of the Reaction Mechanisms of CC Double Bond Reduction in Mammalian Fatty Acid Synthase Studied with Quantum Mechanics/Molecular Mechanics Calculations, ACS Catal., 2019, 9, 11404–11412 CrossRef CAS.
- R. Recabarren, M. Tinzl, D. A. Saez, A. Gomez, T. J. Erb and E. Vöhringer-Martinez, Covalent Adduct Formation as a Strategy for Efficient CO2 Fixation in Crotonyl-CoA Carboxylases/Reductases, ACS Catal., 2023, 13, 6230–6241 CrossRef CAS.
- P. V. Attwood and J. C. Wallace, Chemical and catalytic mechanisms of carboxyl transfer reactions in biotin-dependent enzymes, Acc. Chem. Res., 2002, 35, 113–120 CrossRef CAS PubMed.
- A. L. Menefee and T. N. Zeczycki, Nearly 50 years in the making: defining the catalytic mechanism of the multifunctional enzyme, pyruvate carboxylase, FEBS J., 2014, 281, 1333–1354 CrossRef CAS PubMed.
- Y. Ito, H. Kondo, Y. Shiota and K. Yoshizawa, Theoretical Analysis of the Reaction Mechanism of Biotin Carboxylase, J. Chem. Theory Comput., 2008, 4, 366–374 CrossRef CAS PubMed.
- X. Sheng and Y. Liu, QM/MM study of the reaction mechanism of the carboxyl transferase domain of pyruvate carboxylase from Staphylococcus aureus, Biochemistry, 2014, 53, 4455–4466 CrossRef CAS PubMed.
- X. Sheng, Q. Hou and Y. Liu, Computational evidence for the importance of lysine carboxylation in the reaction catalyzed by carboxyl transferase domain of pyruvate carboxylase: a QM/MM study, Theor. Chem. Acc., 2019, 138, 17 Search PubMed.
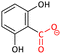
- M. Miyazaki, M. Shibue, K. Ogino, H. Nakamura and H. Maeda, Enzymatic synthesis of pyruvic acid from acetaldehyde and carbon dioxide, Chem. Commun., 2001, 1800–1801 RSC.
- R. A. W. Frank, F. J. Leeper and B. F. Luisi, Structure, mechanism and catalytic duality of thiamine-dependent enzymes, Cell. Mol. Life Sci., 2007, 64, 892–905 CrossRef CAS PubMed.
- S. Prajapati, F. R. von Pappenheim and K. Tittmann, Frontiers in the enzymology of thiamin diphosphate-dependent enzymes, Curr. Opin. Struct. Biol., 2022, 76, 102441 CrossRef CAS PubMed.
- Q. Hou, J. Gao, Y. Liu and C. Liu, A QM/MM study on the catalytic mechanism of pyruvate decarboxylase, Theor. Chem. Acc., 2012, 131, 1–9 Search PubMed.
- J. Wang, H. Dong, S. Li and H. He, Theoretical study toward understanding the catalytic mechanism of pyruvate decarboxylase, J. Phys. Chem. B, 2005, 109, 18664–18672 CrossRef CAS PubMed.
- D. Meyer, P. Neumann, C. Parthier, R. Friedemann, N. Nemeria, F. Jordan and K. Tittmann, Double Duty for a Conserved Glutamate in Pyruvate Decarboxylase: Evidence of the Participation in Stereoelectronically Controlled Decarboxylation and in Protonation of the Nascent Carbanion/Enamine Intermediate, Biochemistry, 2010, 49, 8197–8212 CrossRef CAS PubMed.
- J. Wang and S. Li, Theoretical study toward understanding the catalytic mechanism of pyruvate dehydrogenase multienzyme complex E1 component, J. Theor. Comput. Chem., 2006, 5, 447–459 CrossRef CAS.
- X. Sheng and Y. Liu, Theoretical study of the catalytic mechanism of E1 subunit of pyruvate dehydrogenase multienzyme complex from Bacillus stearothermophilus, Biochemistry, 2013, 52, 8079–8093 CrossRef CAS PubMed.
- K. A. Payne, M. D. White, K. Fisher, B. Khara, S. S. Bailey, D. Parker, N. J. Rattray, D. K. Trivedi, R. Goodacre, R. Beveridge, P. Barran, S. E. Rigby, N. S. Scrutton, S. Hay and D. Leys, New cofactor supports α,β-unsaturated acid decarboxylation via 1,3-dipolar cycloaddition, Nature, 2015, 522, 497–501 CrossRef CAS PubMed.
- C.-L. Lan and S.-L. Chen, The Decarboxylation of α,β-Unsaturated Acid Catalyzed by Prenylated FMN-Dependent Ferulic Acid Decarboxylase and the Enzyme Inhibition, J. Org. Chem., 2016, 81, 9289–9295 CrossRef CAS PubMed.
- G. Tian and Y. Liu, Mechanistic insights into the catalytic reaction of ferulic acid decarboxylase from Aspergillus niger: a QM/MM study, Phys. Chem. Chem. Phys., 2017, 19, 7733–7742 RSC.
- S. E. Payer, S. A. Marshall, N. Bärland, X. Sheng, T. Reiter, A. Dordic, G. Steinkellner, C. Wuensch, S. Kaltwasser, K. Fisher, S. E. J. Rigby, P. Macheroux, J. Vonck, K. Gruber, K. Faber, F. Himo, D. Leys, T. Pavkov-Keller and S. M. Glueck, Regioselective para-Carboxylation of catechols with a prenylated flavin dependent decarboxylase, Angew. Chem., Int. Ed., 2017, 56, 13893–13897 CrossRef CAS PubMed.
- K. A. P. Payne, S. A. Marshall, K. Fisher, S. E. J. Rigby, M. J. Cliff, R. Spiess, D. M. Cannas, I. Larrosa, S. Hay and D. Leys, Structure and Mechanism of Pseudomonas aeruginosa PA0254/HudA, a prFMN-Dependent Pyrrole-2-carboxylic Acid Decarboxylase Linked to Virulence, ACS Catal., 2021, 11, 2865–2878 CrossRef CAS PubMed.
- K. Wen, Y. Tao, W. Jiang, L. Jiang, J. Zhu and Q. Li, (De)carboxylation mechanisms of heteroaromatic substrates catalyzed by prenylated FMN-dependent UbiD decarboxylases: an in silico study, Int. J. Biol. Macromol., 2024, 260, 129294 CrossRef CAS PubMed.
- X. Sheng, W. Zhu, J. Huddleston, D. F. Xiang, F. M. Raushel, N. G. J. Richards and F. Himo, A Combined Experimental-Theoretical Study of the LigW-Catalyzed Decarboxylation of 5-Carboxyvanillate in the Metabolic Pathway for Lignin Degradation, ACS Catal., 2017, 7, 4968–4974 CrossRef CAS.
- X. Sheng, Y. Patskovsky, A. Vladimirova, J. B. Bonanno, S. C. Almo, F. Himo and F. M. Raushel, Mechanism and Structure of γ-Resorcylate Decarboxylase, Biochemistry, 2018, 57, 3167–3175 CrossRef CAS PubMed.
- G. Hofer, X. Sheng, S. Braeuer, S. E. Payer, K. Plasch, W. Goessler, K. Faber, W. Keller, F. Himo and S. M. Glueck, Metal Ion Promiscuity and Structure of 2,3-Dihydroxybenzoic Acid Decarboxylase of Aspergillus oryzae, ChemBioChem, 2020, 22, 652–656 CrossRef PubMed.
- F. Chen, Y. Zhao, C. Zhang, W. Wang, J. Gao, Q. Li, H. Qin, Y. Dai, W. Liu, F. Liu, H. Su and X. Sheng, A combined Computational–Experimental study on the substrate binding and reaction mechanism of salicylic acid decarboxylase, Catalyst, 2022, 12, 1577 CrossRef CAS.
- X. Sheng, K. Plasch, S. E. Payer, C. Ertl, G. Hofer, W. Keller, S. Braeuer, W. Goessler, S. M. Glueck, F. Himo and K. Faber, Reaction mechanism and substrate specificity of iso-orotate decarboxylase: a combined theoretical and experimental study, Front. Chem., 2018, 6, 608 CrossRef CAS PubMed.
- R. Kluger, Decarboxylation, CO2 and the Reversion Problem, Acc. Chem. Res., 2015, 48(11), 2843–2849 CrossRef CAS PubMed.
- S. Xu, W. Li, J. Zhu, R. Wang, Z. Li, G.-L. Xu and J. Ding, Crystal structures of isoorotate decarboxylases reveal a novel catalytic mechanism of 5-carboxyl-uracil decarboxylation and shed light on the search for DNA decarboxylase, Cell Res., 2013, 23, 1296–1309 CrossRef CAS PubMed.
- M. Song, X. Zhang, W. Liu, J. Feng, Y. Cui, P. Yao, M. Wang, R.-T. Guo, Q. Wu and D. Zhu, 2,3-Dihydroxybenzoic acid decarboxylase from fusarium oxysporum: crystal structures and substrate recognition mechanism, ChemBioChem, 2020, 21, 2950–2956 CrossRef CAS PubMed.
- A. Bar-Even, E. Noor, Y. Savir, W. Liebermeister, D. Davidi, D. S. Tawfik and R. Milo, The Moderately Efficient Enzyme: Evolutionary and Physicochemical Trends Shaping Enzyme Parameters, Biochemistry, 2011, 50, 4402–4410 CrossRef CAS PubMed.
- C. A. Cotton, C. Edlich-Muth and A. Bar-Even, Reinforcing carbon fixation: CO2 reduction replacing and supporting carboxylation, Curr. Opin. Biotechnol, 2018, 49, 49–56 CrossRef CAS PubMed.
- B. Zheng, F. L. Oliveira, R. Neumann Barros Ferreira, M. Steiner, H. Hamann, G. X. Gu and B. Luan, Quantum informed machine-learning potentials for molecular dynamics simulations of CO2's chemisorption and diffusion in Mg-MOF-74, ACS Nano, 2023, 17, 5579–5587 CrossRef CAS PubMed.
- B. M. Abraham, O. Piqué, M. A. Khan, F. Viñes, F. Illas and J. K. Singh, Machine learning-driven discovery of key descriptors for CO2 activation over two-dimensional transition metal carbides and nitrides, ACS Appl. Mater. Interfaces, 2023, 15(25), 30117–30126 CrossRef CAS PubMed.
- R. Mathur, M. C. Muniz, S. Yue, R. Car and A. Z. Panagiotopoulos, First-principles-based machine learning models for phase behavior and transport properties of CO2, J. Phys. Chem. B, 2023, 127, 4562–4569 CrossRef CAS PubMed.
- O. A. Ojelade, CO2 hydrogenation to gasoline and aromatics: mechanistic and predictive insights from DFT, DRIFTS and machine learning, ChemPlusChem, 2023, 88, e202300301 CrossRef CAS PubMed.
- Z. W. Chen, Z. Gariepy, L. Chen, X. Yao, A. Anand, S.-J. Liu, C. G. Tetsassi Feugmo, I. Tamblyn and C. V. Singh, Machine-learning-driven high-entropy alloy catalyst discovery to circumvent the scaling relation for CO2 reduction reaction, ACS Catal., 2022, 12, 14864–14871 CrossRef CAS.
- Q. Zhu, Y. Gu, X. Liang, X. Wang and J. Ma, A Machine Learning Model to Predict CO2 Reduction Reactivity and Products Transferred from Metal-Zeolites, ACS Catal., 2022, 12, 12336–12348 CrossRef CAS.
| This journal is © the Owner Societies 2024 |