Radiative heat transfer at the nanoscale: experimental trends and challenges
Christophe
Lucchesi
a,
Rodolphe
Vaillon
 b and
Pierre-Olivier
Chapuis
b and
Pierre-Olivier
Chapuis
 *a
*a
aUniv Lyon, CNRS, INSA-Lyon, Université Claude Bernard Lyon 1, CETHIL UMR5008, F-69621 Villeurbanne, France. E-mail: christophe.lucchesi@insa-lyon.fr; olivier.chapuis@insa-lyon.fr
bIES, Univ Montpellier, CNRS, Montpellier, France. E-mail: rodolphe.vaillon@ies.univ-montp2.fr
First published on 18th January 2021
Abstract
Energy transport theories are being revisited at the nanoscale, as macroscopic laws known for a century are broken at dimensions smaller than those associated with energy carriers. For thermal radiation, where the typical dimension is provided by Wien's wavelength, Planck's law and associated concepts describing surface-to-surface radiative transfer have to be replaced by a full electromagnetic framework capturing near-field radiative heat transfer (photon tunnelling between close bodies), interference effects and sub-wavelength thermal emission (emitting body of small size). It is only during the last decade that nanotechnology has allowed for many experimental verifications – with a recent boom – of the large increase of radiative heat transfer at the nanoscale. In this minireview, we highlight the parameter space that has been investigated until now, showing that it is limited in terms of inter-body distance, temperature and object size, and provide clues about possible thermal-energy harvesting, sensing and management applications. We also provide an outlook on open topics, underlining some difficulties in applying single-wavelength approaches to broadband thermal emitters while acknowledging the promise of thermal nanophotonics and observing that molecular/chemical viewpoints have been hardly addressed.
Context: revisiting thermal radiation energy transport and conversion at the nanoscale
The current energy challenge, which requires saving energy or energy harvesting in order to limit greenhouse gas emissions, requires a fresh eye on many thermodynamic concepts. They date back to the XIXth century, when the laws of thermodynamics were established by famous names such as Carnot, Boltzmann, and many others. Heat transfer has been studied more accurately since that time. While heat conduction and convection are usually well understood (in particular because they are described by local partial differential equations), radiative heat transfer, i.e. the transfer of heat by photons, is often tackled in simplified ways. It is generally addressed either by considering surface-to-surface thermal radiation or radiation in semi-transparent/participating media. The first way considers thermal radiation only as a surface property, omitting the fact that photon emission takes place in some matter volume. The second way, which is solved with the radiative transfer equation, is more complex as non-local interactions must be considered (volumes located very far from each other interact all the time). In both cases the wave nature of thermal radiation is largely neglected. Among the neglected phenomena, interference effects are of course to be mentioned, but other types of wave effects, such as tunnelling, are also out of the framework. Unfortunately, this is possible only at sizes much larger than the contributing wavelengths and therefore incorrect at the nanoscale. In the last twenty years, a huge community dealing with nanophotonics, i.e. the engineering of matter to provide particular properties for routing light and enhancing absorption/emission at particular wavelengths, has expanded. At the crossroad of these fields, i.e. energy management and nanophotonics, nanoscale thermal radiation effects are being studied and have the potential for many novel applications. In this context, this minireview aims at summarizing the types of configurations already tested experimentally and pointing to advances expected for applications of nanoscale radiative heat transfer in the near future, therefore complementing previous general reviews.1–3 Thermal management, energy conversion and spectroscopy are among the key application fields.Thermal radiation at the nanoscale: key principles
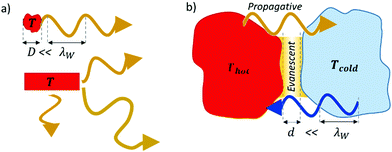
The physics of thermal radiation is as follows: in matter, partially-charged particles, atoms or ions move, therefore generating electromagnetic waves which carry energy away. At equilibrium, such an energy loss is compensated by the local absorption of a similar amount of energy, which is possible due to the work of external electromagnetic fields on these partial charges. Since electromagnetic waves are screened when they travel in an absorbing medium, it can often be considered that only a skin layer at the boundaries of a body contributes to the associated radiative heat transfer, and hence the ensuing surface-to-surface theory. At the nanoscale, such a condition is not easy to meet, and one could think that using the volume theory instead could be sufficient. An issue is that a macroscopic theory cannot be applied when the considered sizes go down to thermal radiation wavelengths, which lie in the micrometric range in general (recall that Wien's wavelength is given by λWT = 2890 μm K, where T is temperature). For bodies of micrometric to sub-micrometric sizes, one has to consider sub-wavelength thermal emission (see Fig. 1(a)), and the emissivity concept associated with the surface theory breaks down (the simplest finite object, i.e. the sphere, has been addressed theoretically,4–6 while various types of experimental evidence7,8 has been provided, where the shape of the bodies also plays a role). In addition, the distance between bodies exchanging thermal radiation can also be sub-wavelength, when the bodies are interacting in their near field. This leads to near-field radiative heat transfer (see Fig. 1(b)) (note that both sub-λ and near-field effects can happen at the same time). While the first type of effect has only been studied since very recently (see an outlook9), there is now a body of work for the second type, which was predicted a long time ago, in the frame of spatial (low temperature induces large near-field dimensions)†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and Casimir-related (fluctuational electrodynamics)11 applications (see reviews12,13). In particular, theory allows computing semi-analytically the energy exchange between shapes such as flat materials including multilayers,14 cylinders,15 cones,16 spheres17–19 including nanoparticles20–22 involving ellipsoidal23,24 shapes and nanoparticle arrays, and gratings. Numerical methods have been developed in the last 5–10 years, allowing one in principle to compute exactly radiative heat transfer between arbitrary shapes25–27 provided one does not run up against the computing capability limits (some shapes can be numerically very demanding). For smoothly-curved and close surfaces, the proximity (Derjaguin) approximation,28–31 which assimilates facing bodies as a sum of locally-planar and parallel surfaces, can be applied more easily. All these studies have shown that the impact of the shape on near-field radiative heat transfer is strong. Finding the maximal radiative flux that can be transferred in the near field and ways to reach it is now an active field of research.32–34 Finally, controlling thermal radiation properties by an external means is another active field of research. This can lead for instance to switches or logic-related devices (see initial proposals for rectifiers and transistors35,36). Such devices can be fully-thermal (this may require some heat input by another phenomenon than thermal radiation, for instance heat conduction) and based on phase change materials (VO2 was used in experiments around room temperature37–41), or based on phenomena modifying optical properties, such as magnetic fields,42 strain, etc. These devices could be useful in the medium to long term for thermal management in housing, in order to spare energy losses, or for computation (logics) with heat.43
10 and Casimir-related (fluctuational electrodynamics)11 applications (see reviews12,13). In particular, theory allows computing semi-analytically the energy exchange between shapes such as flat materials including multilayers,14 cylinders,15 cones,16 spheres17–19 including nanoparticles20–22 involving ellipsoidal23,24 shapes and nanoparticle arrays, and gratings. Numerical methods have been developed in the last 5–10 years, allowing one in principle to compute exactly radiative heat transfer between arbitrary shapes25–27 provided one does not run up against the computing capability limits (some shapes can be numerically very demanding). For smoothly-curved and close surfaces, the proximity (Derjaguin) approximation,28–31 which assimilates facing bodies as a sum of locally-planar and parallel surfaces, can be applied more easily. All these studies have shown that the impact of the shape on near-field radiative heat transfer is strong. Finding the maximal radiative flux that can be transferred in the near field and ways to reach it is now an active field of research.32–34 Finally, controlling thermal radiation properties by an external means is another active field of research. This can lead for instance to switches or logic-related devices (see initial proposals for rectifiers and transistors35,36). Such devices can be fully-thermal (this may require some heat input by another phenomenon than thermal radiation, for instance heat conduction) and based on phase change materials (VO2 was used in experiments around room temperature37–41), or based on phenomena modifying optical properties, such as magnetic fields,42 strain, etc. These devices could be useful in the medium to long term for thermal management in housing, in order to spare energy losses, or for computation (logics) with heat.43
Trends in experimental demonstrations
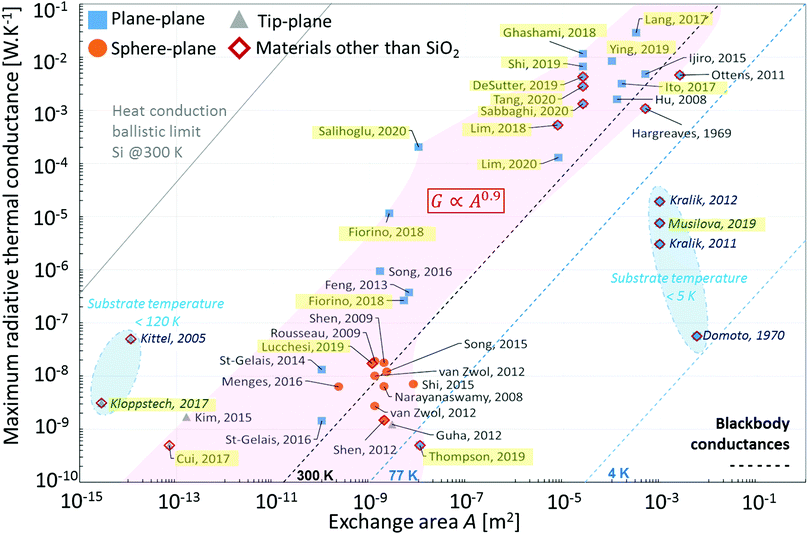
It is interesting to observe that the parameter space investigated experimentally so far is limited. The three key variables, temperature, power density and size, allow classifying the experiments performed up to now. First, one can observe that the vast majority of experiments were performed with the body of lowest temperature at around 300 K (exceptions in italics in Fig. 2). Fig. 2 shows that only three types of geometries (plane–plane, microsphere–plane, and nanotip–plane) have been tested, associated each with a certain (projected) area of near-field radiative exchange. Large experiments are easier at low temperature, but up to ∼cm2 room-temperature devices have been demonstrated in recent years, involving piezo-actuators, interferometric devices and capacitors. There seems to be a limit in the temperature difference ΔT reached so far, maybe due to the difficulty in managing large temperature variations in the surrounding elements in the setups. Note a recent experiment44 for near-field thermophotovoltaic conversion could apparently test a larger ΔT, but did not systematically investigate the temperature dependence. On the other hand, keeping microscale objects at higher temperature is easier, as illustrated by the microscale experiments. Finally, small temperature differences cannot be resolved by experiments with a small exchange area, which highlights the challenge of detecting low fluxes at the picowatt scale and below. The analysis of the transferred power is given in Fig. 3, where the thermal conductance (power per unit temperature) is represented vs. the exchange area. To provide ideas of reference thermal conductances, diagonal lines indicate the blackbody emissive power per kelvin (4σT3) at various typical temperatures (4, 77, and 300 K) and a natural conductance associated with heat conduction at room temperature (ballistic conductance 〈cv〉/4, which corresponds to the maximum heat transfer by conduction in a solid, where 〈cv〉 is the integral of the product of modal heat capacity and velocity). The figure shows that the maximal conductance detected in the near field indeed correlates approximately linearly with the area, and it can also be observed that near-field increases of two orders of magnitude at best over the far-field value have been demonstrated in many cases. Experiments with weak emitters such as metals can exhibit maximal conductances well below the blackbody limit (see e.g. the sub-120 K blue zone on the right). In almost all cases, the near-field radiative conductances are far below the conductive ones. Only experiments with scanning tunnelling microscopes (STM) lead to huge maximal thermal conductances just before electrical contact. Surprisingly, a large share of the experiments were conducted only with SiO2 (known, in contrast to metals, for its high near-field contribution due to phonon polaritons and for coherence inducing narrow-band energy confinement45), which leaves the door open for studies of many other materials as will be discussed below.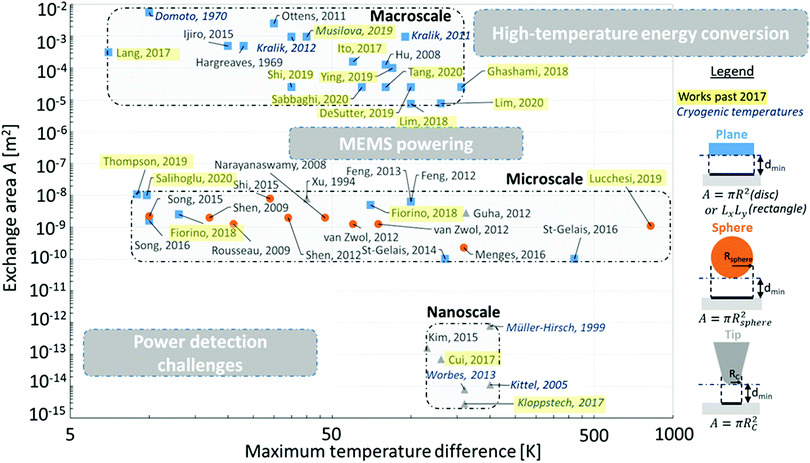 | ||
| Fig. 2 Classification of the experiments involving near-field radiative heat transfer according to the exchange area and temperature difference. | ||
Applications enabled by the current state-of-the-art
The power exchanged depends clearly on the size, and it is interesting to note that the three classes of experiments identified in Fig. 2 can be associated with various applications. Large-area experiments46–58 address in particular the requirements for near-field thermophotovoltaic (TPV) conversion,44,59–62 where infrared (IR) energy emitted by a hot body is converted into electrical energy by a dedicated IR photovoltaic cell.63 High-temperature thermal sources are expected to be used for energy harvesting. One possibility is first to concentrate solar light in order to heat up an emitter, in what is called solar TPV,64 and then benefit from the near-field increase to improve the device performances.65 Near-field thermal radiation effects also play a critical role in thermionic devices,66 alone or in combination with TPV conversion.67,68 Either used for generating electricity or refrigerating,69 the so-called near-field radiative thermoelectric energy converters70 are all promising applications. However, scaling up laboratory proof of concept system sizes71 must chiefly address the challenge of building nanoscale gaps between macroscale planes with sufficiently large temperature differences, for example by using thermally low-conducting but mechanically stable spacers up to high temperature. Spacers made of polystyrene beads,48,51 pillars in SU-8 photoresist56 or silica,49 or suspended devices72,73 were used, leading to fixed distances for many current large-area experiments. Currently the best gaps are of the order of a few tens of nanometers for these experiments, with a recent claim of having reached the sub-10 nm region74 with piezoelectric alignment. Extremely flat samples (roughness less than 1 nm) are required, which is possible thanks to silicon technology, without any surface bowing. The rapid deployment of autonomous devices and the associated Internet of Things (IoT) call also for miniaturized autonomous electrical sources. Harvesting small amounts of power from the environment could be performed by near-field TPV devices with smaller surface imprints, as shown by the micrometric experiments19,37,39,40,72,73,75–86 reaching progressively the microwatt level with power densities close to 1 W cm−2.62 However, the temperature differences required so far are still larger than the few-kelvin difference common situation widely encountered under real conditions. ΔTs of 10–100 K may be observed in self-heating micro-electromechanical systems (MEMS), where such devices could be helpful. Thermal management of electronics, which can require the local cooling of hot spots of Integrated Circuits (ICs), is probably also a natural field of application. Note also that micrometric-to-millimetric bolometers based on suspended membranes collecting radiation could be powered with similar devices (note the thickness-dependence of the emissivity of such membranes87,88). Small-area experiments,89–94 essentially tip-based ones aiming at spatial investigation in the xy plane, are currently limited to large temperature differences due to the lack of sensitivity and call for other types of methods for detecting flux exchanges beyond the pW K−1 thermal conductance level around room temperature. Current methods involve devices based on the Seebeck effect (conversion of a temperature difference into a voltage by means of a thermocouple made of Au and Ni,89 Pt90,91,93 or Cr92,94),95 on the temperature dependence of the electrical conductivity (resistive thermometry),39,62 and on bimaterial deflection involving an inhomogeneous temperature field in a cantilever.82–84,86,96 At low temperature other thermometries are possible, for instance based on superconducting junctions.97 Bimaterial deflection is in principle the most sensitive method (temperature variations down to 10−5 K−1 can be measured), but has been less popular recently, probably because it does not allow one to easily scan in contact. Gold-coated SiN cantilevers were used for these experiments. Usually the tip is at a higher temperature than the sample, simply heated with the laser spot of the AFM, which limits the maximum achievable temperature. Higher temperature can be reached with self-heated resistive cantilevers.62 The thermal sensitivity is especially important for spectroscopy, as only part of the power is located in a limited spectral range. Current near-field thermal spectroscopy is based on scattering the near-field energy to the far field, where it can be analysed.98–102 Lock-in tip oscillation techniques may be needed as the spectral power is weak. However, the better sensitivity of IR photovoltaic cells/photodetectors60,62 could lead to nanoscale thermal spectroscopic devices that would avoid the use of bulky Fourier-transform IR spectroscopes. Hyperspectral near-field thermal radiation imaging with such set-ups seems attractive. Current tip-based imaging devices without spectroscopes are based on flux measurements and were shown to be sensitive to monolayers on surfaces,91,103 while scattering techniques allow for detecting at different depths depending on the wavelength.98 Finally, another fascinating field of study is the transition between thermal radiation and heat conduction, which could be investigated in the last nanometres before contact with AFM-based instruments92 or even below with STM-based ones.90,93,94 Note that non-local optics (permittivity with spatial dispersion ε(ω,k)) is expected to play a role at such gaps.104,105For many of the applications the key is to find a trade-off between the tailoring of the radiative spectrum and the need for large power transfer. While the radiative transfer can be constrained to one or more narrow bands (at a single wavelength maximal transfer of radiation between two bodies can be achieved, as the optical transmission coefficient can reach unity), for instance due to polariton resonance(s), this can lead to reducing the exchanged power to a minute value. The Bose–Einstein distribution associated with thermal photons unfortunately limits in principle the spectral power exchanged between bodies; however, approaching the bodies in the near field and benefitting from the coupling between optical resonances allows one to tunnel heat and increase the exchanged power. The complex electromagnetic field pattern showing up when more than two bodies are present was shown to allow increasing heat transfer.80
Outlook related to thermal nanophotonics
Many of the experiments conducted so far involve at least one flat surface, while nanophotonics has been expanding for twenty years in various directions, in particular for focusing energy (see ref. 106 for a review on the interest for far-field devices). There are avenues for spatially-resolved near-field thermal radiation devices, which would benefit from the knowledge gained in photonics. Here we discuss briefly a few existing or possible ideas, related to metamaterials, 2D materials, nanoparticles/single objects, and scanning probes, which may deserve original experimental investigations. The main parameters with which one would like to play are the spectrum, the polarization distribution, the flux amplitude, the distance dependence (z) and the position dependence (xy) of the flux. They may of course be entangled. Note that few studies91,96,103,107 have probed the near-field thermal radiation of laterally nano/micro-architectured materials so far.Metamaterials can cloak or focus energy, but they often work in a narrow band and it is not straightforward to translate the monochromatic results for a broadband spectrum. Photonic crystals allow one to tailor the far-field spectrum and modify also the spectrum in the near-field with spectral gaps and resonant modes.57Hyperbolic materials possess dispersion relations leading to enhanced heat transfer.96 Fabry–Pérot like metal–insulator flat materials54 can be included in this category. In addition, routing energy by means of surface polaritons has been predicted:108 near-field transfer can be a way to excite and/or absorb them.109Metasurfaces110,111 allow shaping wavefronts could be useful in this respect; however, broadband transfer may be difficult to achieve in practice. Manipulating the heat flow at sub-wavelength sizes in the xy plane is appealing for the purpose of very large-scale integration (VLSI) of IR sensors, which are now constrained by the far-field diffraction limit associated with their wavelength: arrays of concentrating near-field devices operating at different wavelengths can be thought up.
2D materials controlled electrically such as gated graphene57,85,112,113 or other single-atom thick materials like boron nitride, black phosphorus and transition-metal dichalcogenides (TMDC) appear interesting in order to control polaritons and therefore the intensity and spectrum of near-field radiative heat transfer. They can be combined with metamaterials such as hyperbolic materials (especially flat ones) as was shown in numerous theoretical proposals.
It is intriguing that applications of near-field radiative heat transfer with nanoparticles or single objects (e.g. nanoscale pads) standing on substrates have been difficult to envision until now, which is probably due to the low power they can transfer. However, their spectra are different from similar large-particle counterparts, and spectroscopic applications with intense fields are certainly possible.114Arrays of nanoparticles109 can lead to photonic crystal properties, useful for tailoring emissive properties. The magneto-optical response of particles was shown to allow the flux to circulate in preferential paths (rotations).42
Such configurations could be probed by scanning-probe tips sensitive to magnetic fields, such as U-shaped or MFM-based ones, in order to perform local characterization of the thermal fields, in particular polarisation effects. Taking advantage of local field enhancement by resonances on the sample surface is a way to increase the signal. This is reminiscent of molecular spectroscopy performed at a single wavelength, which could also be performed thermally in principle. We note that, while the interaction between nanoparticles was treated analytically20 and the atom/surface radiative exchange was studied in the frame of Bose–Einstein condensates,115 the radiative heat exchange between molecules and other bodies has not been treated extensively until now. Since single-molecule spectroscopy is a popular topic,116 there should be progress in this direction in the coming years.
Conclusions and prospects
The goal of this minireview has been to summarize the experimental efforts performed until now in the field of nanoscale radiative heat transfer. The analysis highlights various avenues, both for applications and fundamental science, which involve nanostructuring. In particular, it sheds light on the persisting challenge of building larger temperature differences (>700 K) between macroscale areas separated by nanoscale gaps in energy conversion devices, or at the opposite end on the need for improved thermal (sub-1 K) and transverse spatial resolution (sub-10 nm). It has also been shown that spectroscopic techniques avoiding scattering to the far field are proper alternative options. Many photonic techniques could be used for these purposes; however, the strong entanglement between the spectrum, the polarization distribution, the flux amplitude, the distance dependence (z) and the position dependence (xy) of the flux is not easy to deal with and will require advanced engineering methods. At the crossroad of nanophotonics, optoelectronics, MEMS engineering, scanning probe microscopy and energy, nanoscale radiative heat transfer is now expected to spread among many applicative fields, including energy conversion, thermal management, or material analysis by means of imaging and spectroscopy techniques.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge discussions with many colleagues over the years, and critical reading by O. Merchiers. The authors acknowledge support from French ANR project DEMO-NFR-TPV (ANR-16-CE05-0013), EU project EFINED (H2020-FETOPEN-1-2016-2017/766853), local projects IdexLyon Labex IMUST (ANR-10-LABX-0064) ATTSEM and ElanERC Thermonano (ANR-16-IDEX-005/ELAN-004).Notes and references
- J. C. Cuevas and F. J. García-Vidal, ACS Photonics, 2018, 5(10), 3896–3915 CrossRef CAS.
- B. Song, A. Fiorino, E. Meyhofer and P. Reddy, AIP Adv., 2015, 5, 53503 CrossRef.
- K. Park and Z. Zhang, Front. Heat Mass Transfer, 2013, 4, 013001 CrossRef.
- G. W. Kattawar and M. Eisner, Appl. Opt., 1970, 9, 2685 CrossRef CAS.
- M. Krüger, G. Bimonte, T. Emig and M. Kardar, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115423 CrossRef.
- K. L. Nguyen, O. Merchiers and P.-O. Chapuis, Appl. Phys. Lett., 2018, 112, 111906 CrossRef.
- D. Thompson, L. Zhu, R. Mittapally, S. Sadat, Z. Xing, P. McArdle, M. M. Qazilbash, P. Reddy and E. Meyhofer, Nature, 2018, 561, 216 CrossRef CAS.
- S. Shin, M. Elzouka, R. Prasher and R. Chen, Nat. Commun., 2019, 10, 1377 CrossRef.
- J. C. Cuevas, Nat. Commun., 2019, 10, 3342 CrossRef.
- E. G. Cravalho, C. L. Tien and R. P. Caren, J. Heat Transfer, 1967, 89, 351 CrossRef.
- D. Polder and M. Van Hove, Phys. Rev. B: Solid State, 1971, 4, 3303 CrossRef.
- K. Joulain, J.-P. Mulet, F. Marquier, R. Carminati and J.-J. Greffet, Surf. Sci. Rep., 2005, 57, 59 CrossRef CAS.
- A. I. Volokitin and B. N. J. Persson, Rev. Mod. Phys., 2007, 79, 1291 CrossRef CAS.
- M. Francoeur, M. Pinar Mengüç and R. Vaillon, J. Quant. Spectrosc. Radiat. Transfer, 2009, 110, 2002 CrossRef CAS.
- V. A. Golyk, M. Krüger and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 046603 CrossRef.
- A. P. McCauley, M. T. H. Reid, M. Krüger and S. G. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165104 CrossRef.
- A. Narayanaswamy and G. Chen, Appl. Phys. Lett., 2003, 82, 3544 CrossRef CAS.
- K. Sasihithlu and A. Narayanaswamy, Opt. Express, 2014, 22, 14473 CrossRef.
- B. Guha, C. Otey, C. B. Poitras, S. Fan and M. Lipson, Nano Lett., 2012, 12, 4546 CrossRef CAS.
- G. Domingues, S. Volz, K. Joulain and J. J. Greffet, Phys. Rev. Lett., 2005, 94, 085901 CrossRef.
- P. O. Chapuis, M. Laroche, S. Volz and J. J. Greffet, Appl. Phys. Lett., 2008, 92, 201906 CrossRef.
- A. Manjavacas and F. J. de Abajo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 75466 CrossRef.
- S.-A. Biehs, O. Huth, F. Rüting and M. Holthaus, J. Appl. Phys., 2010, 108, 14312 CrossRef.
- R. Incardone, T. Emig and M. Krüger, EPL, 2014, 106, 41001 CrossRef.
- M. T. H. Reid and S. G. Johnson, IEEE Trans. Antennas Propag., 2015, 63, 3588 Search PubMed.
- A. G. Polimeridis, M. T. H. Reid, W. Jin, S. G. Johnson, J. K. White and A. W. Rodriguez, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 134202 CrossRef.
- S. Edalatpour and M. Francoeur, J. Quant. Spectrosc. Radiat. Transfer, 2014, 133, 364 CrossRef CAS.
- K. Sasihithlu and A. Narayanaswamy, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 161406 CrossRef.
- C. Otey and S. Fan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245431 CrossRef.
- V. A. Golyk, M. Krüger, A. P. McCauley and M. Kardar, EPL, 2013, 101, 34002 CrossRef CAS.
- K. L. Nguyen, O. Merchiers and P. O. Chapuis, J. Quant. Spectrosc. Radiat. Transfer, 2017, 202, 154 CrossRef CAS.
- S. A. Biehs, M. Tschikin and P. Ben-Abdallah, Phys. Rev. Lett., 2012, 109, 104301 CrossRef.
- S. Molesky, P. S. Venkataram, W. Jin and A. W. Rodriguez, Phys. Rev. B, 2020, 101, 35408 CrossRef CAS.
- P. S. Venkataram, S. Molesky, W. Jin and A. W. Rodriguez, Phys. Rev. Lett., 2020, 124, 13904 CrossRef CAS.
- C. R. Otey, W. T. Lau and S. Fan, Phys. Rev. Lett., 2010, 104, 154301 CrossRef.
- P. Ben-Abdallah and S. A. Biehs, Phys. Rev. Lett., 2014, 112, 044301 CrossRef.
- P. J. van Zwol, L. Ranno and J. Chevrier, Phys. Rev. Lett., 2012, 108, 234301 CrossRef CAS.
- K. Ito, K. Nishikawa, H. Iizuka and H. Toshiyoshi, Appl. Phys. Lett., 2014, 105, 253503 CrossRef.
- F. Menges, M. Dittberner, L. Novotny, D. Passarello, S. S. P. Parkin, M. Spieser, H. Riel and B. Gotsmann, Appl. Phys. Lett., 2016, 108, 171904 CrossRef.
- A. Fiorino, D. Thompson, L. Zhu, R. Mittapally, S.-A. Biehs, O. Bezencenet, N. El-Bondry, S. Bansropun, P. Ben-Abdallah, E. Meyhofer and P. Reddy, ACS Nano, 2018, 12, 5774 CrossRef CAS.
- K. Ito, K. Nishikawa, A. Miura, H. Toshiyoshi and H. Iizuka, Nano Lett., 2017, 17, 4347 CrossRef CAS.
- A. Ott, R. Messina, P. Ben-Abdallah and S.-A. Biehs, J. Photonics Energy, 2019, 9, 1 Search PubMed.
- P. Ben-Abdallah and S. A. Biehs, Z. Naturforsch., A: Phys. Sci., 2017, 72, 151 CAS.
- T. Inoue, T. Koyama, D. D. Kang, K. Ikeda, T. Asano and S. Noda, Nano Lett., 2019, 19, 3948 CrossRef CAS.
- A. Babuty, K. Joulain, P. O. Chapuis, J. J. Greffet and Y. De Wilde, Phys. Rev. Lett., 2013, 110, 146103 CrossRef.
- C. M. Hargreaves, Phys. Lett. A, 1969, 30, 491 CrossRef.
- G. A. Domoto, R. F. Boehm and C. L. Tien, J. Heat Transfer, 1970, 92, 412 CrossRef CAS.
- P. Sabbaghi, L. Long, X. Ying, L. Lambert, S. Taylor, C. Messner and L. Wang, J. Appl. Phys., 2020, 128, 025305 CrossRef CAS.
- L. Tang, J. DeSutter and M. Francoeur, ACS Photonics, 2020, 7, 1304 CrossRef CAS.
- S. Lang, G. Sharma, S. Molesky, P. U. Kränzien, T. Jalas, Z. Jacob, A. Y. Petrov and M. Eich, Sci. Rep., 2017, 7, 13916 CrossRef CAS.
- L. Hu, A. Narayanaswamy, X. Chen and G. Chen, Appl. Phys. Lett., 2008, 92, 133106 CrossRef.
- R. S. Ottens, V. Quetschke, S. Wise, A. A. Alemi, R. Lundock, G. Mueller, D. H. Reitze, D. B. Tanner and B. F. Whiting, Phys. Rev. Lett., 2011, 107, 014301 CrossRef CAS.
- T. Kralik, P. Hanzelka, V. Musilova, A. Srnka and M. Zobac, Rev. Sci. Instrum., 2011, 82, 55106 CrossRef CAS.
- M. Lim, J. Song, S. S. Lee and B. J. Lee, Nat. Commun., 2018, 9, 4302 CrossRef.
- M. Ghashami, H. Geng, T. Kim, N. Iacopino, S. K. Cho and K. Park, Phys. Rev. Lett., 2018, 120, 175901 CrossRef CAS.
- X. Ying, P. Sabbaghi, N. Sluder and L. Wang, ACS Photonics, 2019, 7, 190 CrossRef.
- K. Shi, Y. Sun, Z. Chen, N. He, F. Bao, J. Evans and S. He, Nano Lett., 2019, 19, 8082 CrossRef CAS.
- M. Lim, J. Song, S. S. Lee, J. Lee and B. J. Lee, Phys. Rev. Appl., 2020, 14, 14070 CrossRef CAS.
- S. Basu, Z. M. Zhang and C. J. Fu, Int. J. Energy Res., 2009, 33, 1203 CrossRef CAS.
- A. Fiorino, L. Zhu, D. Thompson, R. Mittapally, P. Reddy and E. Meyhofer, Nat. Nanotechnol., 2018, 13, 806 CrossRef CAS.
- G. R. Bhatt, B. Zhao, S. Roberts, I. Datta, A. Mohanty, T. Lin, J.-M. Hartmann, R. St-Gelais, S. Fan and M. Lipson, Nat. Commun., 2020, 11, 2545 CrossRef CAS.
- C. Lucchesi, D. Cakiroglu, J.-P. Perez, T. Taliercio, E. Tournié, P.-O. Chapuis and R. Vaillon, 2019, ArXiv 1912.09394.
- S. Basu, Y.-B. Chen and Z. M. Zhang, Int. J. Energy Res., 2007, 31, 689 CrossRef CAS.
- A. Lenert, D. M. Bierman, Y. Nam, W. R. Chan, I. Celanović, M. Soljačić and E. N. Wang, Nat. Nanotechnol., 2014, 9, 126 CrossRef CAS.
- M. Elzouka and S. Ndao, Sol. Energy, 2017, 141, 323 CrossRef CAS.
- A. Datas, Appl. Phys. Lett., 2016, 108, 143503 CrossRef.
- A. Datas and R. Vaillon, Nano Energy, 2019, 61, 10 CrossRef CAS.
- A. Datas and R. Vaillon, Appl. Phys. Lett., 2019, 114, 133501 CrossRef.
- L. Zhu, A. Fiorino, D. Thompson, R. Mittapally, E. Meyhofer and P. Reddy, Nature, 2019, 566, 239 CrossRef CAS.
- E. Tervo, E. Bagherisereshki and Z. Zhang, Front. Energy, 2018, 12, 5 CrossRef.
- M. P. Bernardi, D. Milovich and M. Francoeur, Nat. Commun., 2016, 7, 12900 CrossRef CAS.
- C. Feng, Z. Tang, J. Yu and C. Sun, Sensors, 2013, 13, 1998 CrossRef CAS.
- C. Feng, Z.-A. Tang and J. Yu, Chin. Phys. Lett., 2012, 29, 38502 CrossRef.
- H. Salihoglu, W. Nam, L. Traverso, M. Segovia, P. K. Venuthurumilli, W. Liu, Y. Wei, W. Li and X. Xu, Nano Lett., 2020, 20, 6091 CrossRef CAS.
- R. St-Gelais, B. Guha, L. Zhu, S. Fan and M. Lipson, Nano Lett., 2014, 14, 6971 CrossRef CAS.
- B. Song, Y. Ganjeh, S. Sadat, D. Thompson, A. Fiorino, V. Fernández-Hurtado, J. Feist, F. J. Garcia-Vidal, J. C. Cuevas, P. Reddy and E. Meyhofer, Nat. Nanotechnol., 2015, 10, 253 CrossRef CAS.
- B. Song, D. Thompson, A. Fiorino, Y. Ganjeh, P. Reddy and E. Meyhofer, Nat. Nanotechnol., 2016, 11, 509 CrossRef CAS.
- R. St-Gelais, L. Zhu, S. Fan and M. Lipson, Nat. Nanotechnol., 2016, 11, 515 CrossRef CAS.
- A. Fiorino, D. Thompson, L. Zhu, B. Song, P. Reddy and E. Meyhofer, Nano Lett., 2018, 18, 3711 CrossRef CAS.
- D. Thompson, L. Zhu, E. Meyhofer and P. Reddy, Nat. Nanotechnol., 2020, 15, 99 CrossRef CAS.
- J.-B. Xu, K. Läuger, R. Möller, K. Dransfeld and I. H. Wilson, J. Appl. Phys., 1994, 76, 7209 CrossRef CAS.
- A. Narayanaswamy, S. Shen and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115303 CrossRef.
- E. Rousseau, A. Siria, G. Jourdan, S. Volz, F. Comin, J. Chevrier and J. J. Greffet, Nat. Photonics, 2009, 3, 514 CrossRef CAS.
- S. Shen, A. Narayanaswamy and G. Chen, Nano Lett., 2009, 9, 2909 CrossRef CAS.
- P. J. van Zwol, S. Thiele, C. Berger, W. A. de Heer and J. Chevrier, Phys. Rev. Lett., 2012, 109, 264301 CrossRef CAS.
- S. Shen, A. Mavrokefalos, P. Sambegoro and G. Chen, Appl. Phys. Lett., 2012, 100, 233114 CrossRef.
- S. Edalatpour and M. Francoeur, J. Quant. Spectrosc. Radiat. Transfer, 2013, 118, 75 CrossRef CAS.
- P. J. van Zwol, D. F. Vles, W. P. Voorthuijzen, M. Péter, H. Vermeulen, W. J. van der Zande, J. M. Sturm, R. W. E. van de Kruijs and F. Bijkerk, J. Appl. Phys., 2015, 118, 213107 CrossRef.
- W. Müller-Hirsch, A. Kraft, M. T. Hirsch, J. Parisi and A. Kittel, J. Vac. Sci. Technol., A, 1999, 17, 1205 CrossRef.
- A. Kittel, W. Müller-Hirsch, J. Parisi, S. A. Biehs, D. Reddig and M. Holthaus, Phys. Rev. Lett., 2005, 95, 224301 CrossRef.
- L. Worbes, D. Hellmann and A. Kittel, Phys. Rev. Lett., 2013, 110, 134302 CrossRef.
- K. Kim, B. Song, V. Fernández-Hurtado, W. Lee, W. Jeong, L. Cui, D. Thompson, J. Feist, M. T. H. Reid, F. J. García-Vidal, J. C. Cuevas, E. Meyhofer and P. Reddy, Nature, 2015, 528, 387 CrossRef CAS.
- K. Kloppstech, N. Könne, S. A. Biehs, A. W. Rodriguez, L. Worbes, D. Hellmann and A. Kittel, Nat. Commun., 2017, 8, 14475 CrossRef CAS.
- L. Cui, W. Jeong, V. Fernández-Hurtado, J. Feist, F. J. García-Vidal, J. C. Cuevas, E. Meyhofer and P. Reddy, Nat. Commun., 2017, 8, 14479 CrossRef CAS.
- K. Kim, W. Jeong, W. Lee and P. Reddy, ACS Nano, 2012, 6, 4248 CrossRef CAS.
- J. Shi, B. Liu, P. Li, L. Y. Ng and S. Shen, Nano Lett., 2015, 15, 1217 CrossRef CAS.
- F. Giazotto, T. T. Heikkilä, A. Luukanen, A. M. Savin and J. P. Pekola, Rev. Mod. Phys., 2006, 78, 217 CrossRef CAS.
- Y. De Wilde, F. Formanek, R. Carminati, B. Gralak, P.-A. Lemoine, K. Joulain, J.-P. Mulet, Y. Chen and J.-J. Greffet, Nature, 2006, 444, 740 CrossRef CAS.
- A. C. Jones and M. B. Raschke, Nano Lett., 2012, 12, 1475 CrossRef CAS.
- Y. Kajihara, K. Kosaka and S. Komiyama, Rev. Sci. Instrum., 2010, 81, 033706 CrossRef.
- F. Huth, M. Schnell, J. Wittborn, N. Ocelic and R. Hillenbrand, Nat. Mater., 2011, 10, 352 CrossRef CAS.
- Q. Weng, S. Komiyama, L. Yang, Z. An, P. Chen, S.-A. Biehs, Y. Kajihara and W. Lu, Science, 2018, 360, 775 CrossRef CAS.
- A. Kittel, U. F. Wischnath, J. Welker, O. Huth, F. Rüting and S.-A. Biehs, Appl. Phys. Lett., 2008, 93, 193109 CrossRef.
- P. O. Chapuis, S. Volz, C. Henkel, K. Joulain and J. J. Greffet, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035431 CrossRef.
- F. Singer, Y. Ezzahri and K. Joulain, J. Quant. Spectrosc. Radiat. Transfer, 2015, 154, 55 CrossRef CAS.
- W. Li and S. Fan, Opt. Express, 2018, 26, 15995 CrossRef CAS.
- T. Ijiro and N. Yamada, Appl. Phys. Lett., 2015, 106, 23103 CrossRef.
- D.-Z. A. Chen, A. Narayanaswamy and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155435 CrossRef.
- E. J. Tervo, O. S. Adewuyi, J. S. Hammonds and B. A. Cola, Mater. Horiz., 2016, 3, 434 RSC.
- X. Liu and Z. Zhang, ACS Photonics, 2015, 2, 1320 CrossRef CAS.
- O. Quevedo-Teruel, H. Chen, A. Díaz-Rubio, G. Gok, A. Grbic, G. Minatti, E. Martini, S. Maci, G. V. Eleftheriades, M. Chen, N. I. Zheludev, N. Papasimakis, S. Choudhury, Z. A. Kudyshev, S. Saha, H. Reddy, A. Boltasseva, V. M. Shalaev, A. V. Kildishev, D. Sievenpiper, C. Caloz, A. Alù, Q. He, L. Zhou, G. Valerio, E. Rajo-Iglesias, Z. Sipus, F. Mesa, R. Rodríguez-Berral, F. Medina, V. Asadchy, S. Tretyakov and C. Craeye, J. Opt., 2019, 21, 73002 CrossRef.
- J. Yang, W. Du, Y. Su, Y. Fu, S. Gong, S. He and Y. Ma, Nat. Commun., 2018, 9, 4033 CrossRef.
- N. H. Thomas, M. C. Sherrott, J. Broulliet, H. A. Atwater and A. J. Minnich, Nano Lett., 2019, 19, 3898 CrossRef CAS.
- A. I. Volokitin and B. N. J. Persson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 45417 CrossRef.
- C. Henkel and M. Wilkens, Europhys. Lett., 1999, 47, 414 CrossRef CAS.
- W. E. Moerner, Y. Shechtman and Q. Wang, Faraday Discuss., 2015, 184, 9 RSC.
Footnote |
| † Note an incomplete treatment of evanescent waves at the time. |
| This journal is © The Royal Society of Chemistry 2021 |