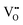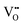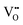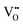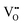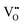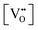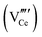Design strategies for ceria nanomaterials: untangling key mechanistic concepts†
Yuwen
Xu
 *,
Sajjad S.
Mofarah
*,
Sajjad S.
Mofarah
 ,
Rashid
Mehmood
,
Rashid
Mehmood
 ,
Claudio
Cazorla
,
Claudio
Cazorla
 ,
Pramod
Koshy
,
Pramod
Koshy
 and
Charles C.
Sorrell
and
Charles C.
Sorrell
 *
*
School of Materials Science and Engineering, UNSW Sydney, Australia. E-mail: yuwen.xu@unswalumni.com; C.Sorrell@unsw.edu.au
First published on 28th September 2020
Abstract
The morphologies of ceria nanocrystals play an essential role in determining their redox and catalytic performances in many applications, yet the effects of synthesis variables on the formation of ceria nanoparticles of different morphologies and their related growth mechanisms have not been systematised. The design of these morphologies is underpinned by a range of fundamental parameters, including crystallography, optical mineralogy, the stabilities of exposed crystallographic planes, CeO2−x stoichiometry, phase equilibria, thermodynamics, defect equilibria, and the crystal growth mechanisms. These features are formalised and the key analytical methods used for analysing defects, particularly the critical oxygen vacancies, are surveyed, with the aim of providing a source of design parameters for the synthesis of nanocrystals, specifically CeO2−x. However, the most important aspect in the design of CeO2−x nanocrystals is an understanding of the roles of the main variables used for synthesis. While there is a substantial body of data on CeO2−x morphologies fabricated using low cerium concentrations ([Ce]) under different experimental conditions, the present work fully maps the effects of the relevant variables on the resultant CeO2−x morphologies in terms of the commonly used raw materials [Ce] (and [NO3−] in Ce(NO3)3·6H2O) as feedstock, [NaOH] as precipitating agent, temperature, and time (as well as the complementary vapour pressure). Through the combination of consideration of the published literature and the generation of key experimental data to fill in the gaps, a complete mechanistic description of the development of the main CeO2−x morphologies is illustrated. Further, the mechanisms of the conversion of nanochains into the two variants of nanorods, square and hexagonal, have been elucidated through crystallographic reasoning. Other key conclusions for the crystal growth process are the critical roles of (1) the formation of Ce(OH)4 crystallite nanochains as the precursors of nanorods and (2) the disassembly of the nanorods into Ce(OH)4 crystallites and NO3−-assisted reassembly into nanocubes (and nanospheres) as an unrecognised intermediate stage of crystal growth.
Introduction
Ceria (CeO2) is a wide band gap semiconductor of considerable importance through its multifarious uses in catalysis,1–4 photocatalysis,5,6 energy storage,7 energy conversion,2,8,9 gas sensing,3 and health.10 Most of these applications depend on the oxygen storage capacity of what effectively is CeO2−x.12 It also has therapeutic prospects in biomedicine,11–13 cancer treatments,12 and neurodegenerative disorder treatments13 owing to its controllable and pH-dependent Ce4+ ↔ Ce3+ redox switching capability.14 The oxygen storage and redox capacities of CeO2−x are largely dependent on the type and concentrations of defects, particularly oxygen vacancies, which depend on the particle morphologies and associated exposed crystallographic surfaces.14–17More specifically, CeO2−x has been emerging as a significant functional material, including as catalysts for automotive catalytic convertors (three-way catalysts), steam reforming, water-gas shift reaction, hydrocarbon reforming, dehalogenation, and hydrogenation; as catalyst support; in fuel cells (as electrolyte in solid oxide fuel cells and oxygen permeation membrane in polymer exchange membrane fuel cells); as electrochromic films; as sensors for O2, NO, and hydrocarbons; and as ultraviolet absorbents.18–20 Conventionally, it is well known as a glass polishing compound and, more recently, it has been used in both biomedicine as a redox catalyst for cell therapies and in environmental chemistry as a photocatalyst for water and air purification.
Ce metal is present at an average concentration of 66.5 ppm in the earth's crust, making it the 25th most abundant of the 94 naturally occurring elements in the earth's crust and the most abundant of the 15 elements known as rare earths, lanthanides, or 4f.21 Ce metal was identified first by Jöns Jacob Berzelius and Wilhelm Hisinger in Stockholm in 1803 and was named after the recently discovered asteroid Ceres.22 Its first technical application was as a minority element in ThO2-CeO2 mantles for gaslighting in the 1890s.23
The most stable oxide of Ce is CeO2, which is unique among the rare earths as Ce is the only such element to exhibit a stable 4+ valence.23 CeO2 is known as ceria, cerium dioxide, ceric oxide, or its mineral name cerianite. However, since the most stable valence for all other lanthanides (Ln) is 3+, then Ce2O3 (cerium sesquioxide, dicerium trioxide, or cerous oxide) is a second highly stable oxide. CeO2 is produced commercially by beneficiation from bastnäsite (a lanthanide fluoride carbonate rock) and monazite (a lanthanide thorium phosphate mineral).
According to the Web of Science database, the first 20th Century technical paper on CeO2, which was on CeO2–ThO2 catalysts, was published in 1928.24 The total number of papers published between the second paper on CeO2 in 1950 (ZrO2–CeO2 phase equilibria) and 1979 was only 29; these papers included the first consideration of CeO2 in solid oxide fuel cells in 1966.25
However, continued interest in CeO2 as an electrolyte for this application led to an increase in the number of publications on CeO2 to ∼8 per year until 1987, at which point the annual publication numbers reached double-digit, as shown in Fig. 1. Since then, the publication rate has increased significantly, reaching a plateau of 1537 publications in 2017 and remaining nearly constant until today (the projection of 1500 publications for 2020 is based on the current publication rate).
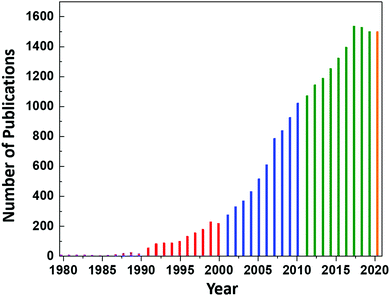 | ||
| Fig. 1 Annual number of publications according to the search word ceria databased by the Web of Science. | ||
CeO2 crystallography
The crystal structure of CeO2, drawn to scale according to the eightfold (VIII) coordinated Ce and fourfold (IV) coordinated O radii (the crystal radii are to be used in solids) by Shannon26 and using the equivalent positions,27 is shown in Fig. 2. The corresponding crystallographic data for CeO2 are summarised in Table 1.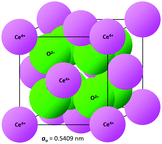 | ||
| Fig. 2 CeO2 crystal structure drawn to scale (CeVIII4+ = 0.111 nm, OIV2− = 0.124 nm26). | ||
| Category | Details | Information |
|---|---|---|
| Crystal system27 | Cubic | |
| Prototype structure27 | CaF2 (fluorite) | |
| Space group27 | International tables | No. 225 |
| Hermann–Mauguin notation |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m or F4/m m or F4/m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/m 2/m |
|
| Schoenflies notation | O 5h | |
| Hall notation | −F 4 2 3 | |
| Point group |
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
| Pearson symbol | cF12 | |
| Strukturbericht designation | C1 | |
| Wyckoff sequence | 225,ca | |
| Ions per unit cell | 12 | |
| Equivalent positions27 | ||
|---|---|---|
| Cerium sublattice | Oxygen sublattice | |
| Corners | Faces | Corners |
| 0, 0, 0 | 1/4, 1/4, 1/4 | |
| 1/4, 3/4, 1/4 | ||
| 0, 1/2, 1/2 | 1/4, 1/4, 3/4 | |
| 1/2, 0, 1/2 | 1/4, 3/4, 3/4 | |
| 1/2, 1/2, 0 | 3/4, 1/4, 1/4 | |
| 3/4, 3/4, 1/4 | ||
| 3/4, 1/4, 3/4 | ||
| 3/4, 3/4, 3/4 | ||
| Void type | Diameter (nm) | Radius (nm) |
|---|---|---|
| Central interstice | 0.220 | 0.110 |
| Ce sublattice face | 0.319 | 0.160 |
| O sublattice face | 0.135 | 0.067 |
The void sizes of the central interstice and the sublattices through which dopants and impurities must pass in order to be dissolved have been calculated because these illustrate the considerable capacity for interstitial solid solubility as two of three of these voids are larger than the ionic radii of the nearly all cations.26
CeO2 surface stabilities
Although optical mineralogy is useful in describing exposed crystallographic planes, an important complementary approach to materials design is first principles computational methods, typically based on density functional theory (DFT). The stabilities of the different exposed crystallographic planes in CeO2 can be determined reliably, largely as a result of the ability to solve the relevant quantum mechanical equations without having to make significant approximations of the electronic interactions.28Uncertainties arising from energy band considerations present various challenges to DFT simulations, so several strategies to deal efficiently with the electronic exchange energy and electronic correlations have been developed.29–32 As a result, a range of DFT approaches has been applied, the most commonly used of which are (1) local density approximation (LDA),28,33 (2) generalised gradient approximation (GGA),28,33,34 (3) Becke 3-parameter Lee–Yang–Parr hybrid functional (B3LYP),33 and (4) Heyd–Scuseria–Ernzerhof range-separated hybrid functional (HSE).32 The commonly used LDA and GGA approaches often incorporate a Hubbard-like U term into the relevant quantum Hamiltonian (e.g., LDA+U and GGA+U) in order to compensate for self-interaction errors.30 For stoichiometric CeO2 and nonstoichiometric CeO2−x, the electronic structure is dominated by the Ce 4f electronic band at the bottom of the conduction band (CB) and the O 2p orbitals at the top of the valence band (VB). The hybridisation of these and other states is assessed by projecting the partial density of states (pDOS) for atomic orbital contributions.34 This assessment allows the determination of the band gap (Eg) (ESI,† Fig. S1).
Another important capability of DFT is the examination of surfaces as semi-infinite slabs of typically 10–20 atomic layers thickness.35 This approach can be designed to incorporate different crystallographic orientations, plane polarities, plane ionic terminations, and surface oxygen vacancies. These variables can be introduced and then used to determine, inter alia, surface formation energies and adsorption energies. Fig. 3 shows ball-and-stick models of several low-index CeO2 slabs used to simulate CeO2 surfaces using DFT. An important outcome of these simulations is the capability of contrasting the stabilities of the different crystallographic planes through the surface formation energies. Table 2 contrasts the stability rankings of the principal low-index planes determined using different approaches, including an early study of molecular mechanics (MM) performed with classical interatomic potentials (IP).36
CeO2−x stoichiometry
It is well known that CeO2−x is a nonstoichiometric compound owing to the presence of what effectively are intrinsic oxygen vacancies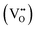 .37–39 As each
.37–39 As each 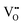 is charge compensated by two Ce4+ → Ce3+ reduction reactions, then an accurate definition of the form of the stoichiometry of CeO2−x is:
is charge compensated by two Ce4+ → Ce3+ reduction reactions, then an accurate definition of the form of the stoichiometry of CeO2−x is:where □ is an oxygen vacancy. This stoichiometry variability is largely responsible for the disagreements in the literature concerning data that are fundamental to CeO2−x, including the lattice parameter (ao), true density (ρTrue), and optical indirect band gap (Eg). These uncertainties are clarified in Fig. 4 by showing the extent of oxygen deficiency (x) as a function of temperature and oxygen partial pressure of Bulfin et al.40 and by using the linear composite data of Schwab et al.41 for the effects of temperature and oxygen deficiency on the lattice parameter of CeO2−x. The latter data have been used to calculate the true density as a function of these two variables. Further, the optical indirect band gap as a function of oxygen deficiency and concentration of oxygen vacancies
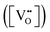 has been determined in the present work (ESI,† Fig. S1) by density functional theory (DFT) simulations based on further refinement of earlier work by the authors.42 The range of Eg values spans stoichiometric CeO2 to CeO1.5, the latter of which represents the maximal theoretical level of
has been determined in the present work (ESI,† Fig. S1) by density functional theory (DFT) simulations based on further refinement of earlier work by the authors.42 The range of Eg values spans stoichiometric CeO2 to CeO1.5, the latter of which represents the maximal theoretical level of 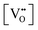 of 25%. The equations for these relations are as follows:
of 25%. The equations for these relations are as follows:| ao = 0.5409 + (6.2708 × 10−6)T |
| ao = 0.5409 + (4.5800 × 10−2)x |
| ρTrue = 7224.6 − (2.4875 × 10−1)T |
| ρTrue = 7224.6 − (1.2860 × 103)x |
| Eg = 3.0 − (3.2 × 10−2) |
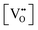
| Eg = 3.0 − (1.6)x |
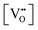 = oxygen vacancy concentration in %.
= oxygen vacancy concentration in %.
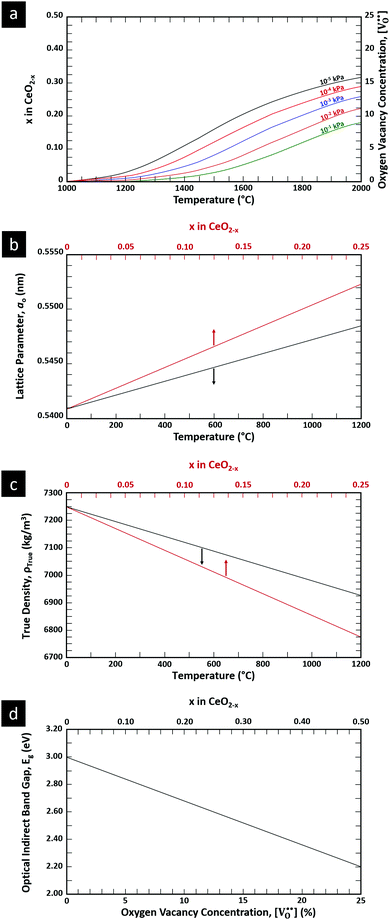 | ||
| Fig. 4 (a) Effect of temperature on oxygen deficiency,40 (b) effect of temperature and oxygen deficiency on lattice parameter,41 (c) effect of temperature and oxygen deficiency on true density (authors’ unpublished work), (d) effect of oxygen nonstoichiometry on optical indirect band gap of CeO2−x (authors’ unpublished work). | ||
Ce–O phase equilibria
The condensed oxide phase equilibria in their entirety are shown in Fig. 5. While these data are based principally on the summary of Okamoto,43 they have been modified to formalise the five low-stability phases of the suboxide series CenO2n−4, where n = 18–22 in integers. The stoichiometries of these phases as reported (Ce9O16, Ce19O34, Ce5O9, Ce31O56, Ce11O20) scale nearly perfectly to a sequence (Ce18O32, Ce19O34, Ce20O36, Ce21O38, Ce22O40) that is almost certainly an analogue of a similar series of the nonstoichiometric phases in the Ti–O system. These Magnéli phases44 are a homologous series of suboxide compositions of the stoichiometry TinO2n−1, where n = 4–10 in integers. They are based on the same TiO2 crystal structures but differentiated by crystallographic shear in which planar defects are introduced as a function of oxygen deficiency.45,46 The phase diagram draws attention to a number of potential materials design trajectories for functional materials: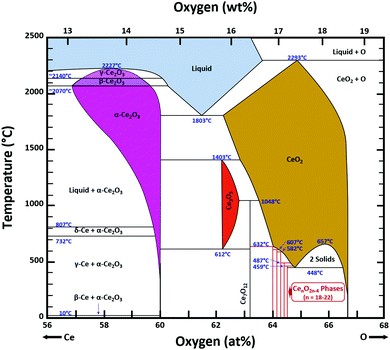 | ||
| Fig. 5 Ce–O condensed phase diagram based largely on the summary of Okamoto;43 analogue CenO2n−4 suboxide series inferred. | ||
• CeO2 exhibits solid-state immiscibility at 448–657 °C. These compositions would be likely to generate high concentrations of interfaces, which could serve as sites for 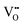 formation and active sites for catalysis.
formation and active sites for catalysis.
• The oxygen deficiency in CeO2−x increases with increasing temperature, reaching a maximum of CeO1.65 or Ce0.304+Ce0.703+O1.652−□0.35 (62.25 at% oxygen; Ce0.3775O0.6225, x = 0.35; 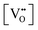 = 17.5%) at 1803 °C. The use of high temperatures in reducing atmospheres would be likely to increase the
= 17.5%) at 1803 °C. The use of high temperatures in reducing atmospheres would be likely to increase the 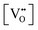 .
.
• Ce2O3 has not been investigated to any great degree. Its extent of oxygen deficiency also suggests that it may offer properties that can be engineered similarly to those of CeO2−x.
• Ce3O5 does not appear to have been investigated at all. Although its temperature range of stability is limited by eutectoid decomposition at 612 °C and peritectoid decomposition at 1403 °C, it probably can be quenched to room temperature. Its homogeneity range also suggests that it may exhibit interesting properties as a function of stoichiometry variation.
• The CenO2n−4 suboxide phases of the inferred analogue of the Magnéli phase series also do not appear to have been investigated. In common with the Magnéli phases, these may exhibit applications as thermoelectrics,46 conducting oxides,47 charge storage devices,48 antiferromagnets,49 and lubricants.50
Finally, the composition of maximal 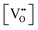 sometimes is referred to as Ce2O3. While this is correct stoichiometrically, the phase diagram demonstrates that this is a misnomer as this phase is a compound distinctly different from CeO2. Consequently, the correct designation for CeO2−x of maximal
sometimes is referred to as Ce2O3. While this is correct stoichiometrically, the phase diagram demonstrates that this is a misnomer as this phase is a compound distinctly different from CeO2. Consequently, the correct designation for CeO2−x of maximal 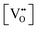 is CeO1.5.
is CeO1.5.
Ce–O thermodynamics
The thermodynamic database for the system Ce–O is incomplete. The standard database is that of FactSage 7.3 (ThermFact Inc. & GTT-Technologies, Montreal, Canada), which includes data for CeO2, Ce2O3, Ce3O5 (as Ce18O31), and Ce7O12 (as Ce6O11). Owing to the absence of data for the Ce2O2n−4 suboxides, these data have been calculated using the database and software of HSC Chemistry 6.0 (Metso Outotec, Helsinki, Finland). The standard-state data are given in Table 3.The Gibbs free energies as a function of temperature are shown graphically in Fig. 6; the stability diagram as a function of temperature and oxygen partial pressure (pO2), calculated using the FactSage 7.3 database,76 also is given. The equations for the Gibbs free energies of the four principal oxides are as follows:
| CeO2 → −1031.95 + (0.2051·ΔT) |
| Ce2O3 → −857.65 + (0.1370·ΔT) |
| Ce3O5 → −947.41 + (0.1708·ΔT) |
| Ce7O12 → −981.62 + (0.1828·ΔT) |
| Ce18O32 → −934.47 + (0.1700·ΔT) |
| Ce19O34 → −935.21 + (0.1712·ΔT) |
| Ce20O36 → −937.71 + (0.1720·ΔT) |
| Ce21O38 → −939.09 + (0.1728·ΔT) |
| Ce22O40 → −940.35 + (0.1735·ΔT) |
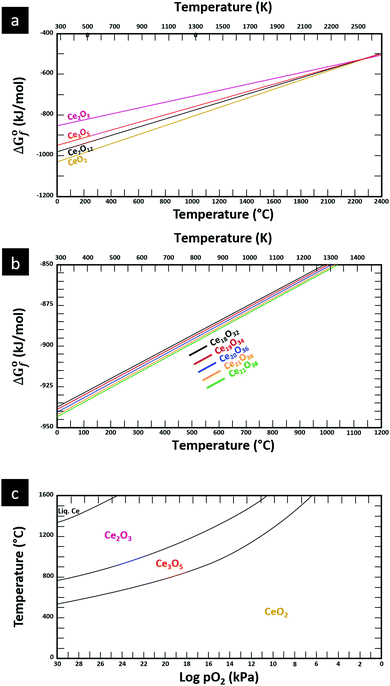 | ||
| Fig. 6 Thermodynamic data for the system Ce–O: (a) Gibbs free energies for principal oxides based on FactSage 7.3 data, (b) Gibbs free energies for Ce2O2n−4 suboxide series calculated using HSC Chemistry 6.0 data (authors’ unpublished work), (c) stability diagram calculated on basis of FactSage 7.3 data.76 | ||
Ce–O defect equilibria
The synthesis and characterisation of functional materials, such as CeO2−x, are synonymous with point defect engineering. The role of point defects is critical to the performance of these oxides and similar materials and their characterisation is critical to the interpretation of their performance.However, the defect chemistries of most semiconducting oxides have been reported at high temperatures (≥500 °C) as these are required owing to thermodynamic limitations, which restrict the concentrations and mobilities of charge carriers typically required for the manifestation of the effects as well as detection.51 In contrast, most reports of the synthesis of CeO2−x typically detail procedures based on precipitation and hydrothermal synthesis, which have been done at considerably lower temperatures (≤200 °C). However, in the case of CeO2−x, the ready Ce4+ ↔ Ce3+ redox switching, even at room temperature under the influence of pH change,6,14 demonstrates that at least some point defects in CeO2−x (viz., surface defects) are mobile at low temperatures.
Defect equilibria in oxides generally are expressed in terms of Kröger–Vink notation.52 However, a full description of the possible types of defect equilibria using this formalism does not appear to have been presented. Table 4 gives the full range of defect equilibria associated with the five main causation factors:
• Intrinsic: for pure CeO2−x
• Extrinsic: for doped CeO2−x
• Intervalence charge transfer: for doped and codoped CeO2−x
• Multivalence charge transfer: for codoped CeO2−x
• Colour centres: for pure and doped CeO2−x
Since CeO2−x is expressed as 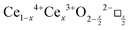 and Ce4+ → Ce3+ reduction is viewed as being ionically charge compensated by
and Ce4+ → Ce3+ reduction is viewed as being ionically charge compensated by 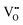 formation, then this point defect is critical to the synthesis and properties of CeO2−x. The
formation, then this point defect is critical to the synthesis and properties of CeO2−x. The 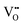 formation energy is highly positive and can be varied in the range 1.20–2.25 eV, depending on the crystallite size and exposed facets.53,54 The most commonly investigated methods of defect formation involve intrinsic or extrinsic considerations. Intrinsic
formation energy is highly positive and can be varied in the range 1.20–2.25 eV, depending on the crystallite size and exposed facets.53,54 The most commonly investigated methods of defect formation involve intrinsic or extrinsic considerations. Intrinsic 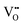 typically are generated by heating in vacuum or under reducing atmospheres and extrinsic
typically are generated by heating in vacuum or under reducing atmospheres and extrinsic 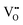 generally are induced by acceptor doping (p-type) with transition or rare earth metals. However, there are other methods by which these and other defects can be introduced:
generally are induced by acceptor doping (p-type) with transition or rare earth metals. However, there are other methods by which these and other defects can be introduced:
• Electrochemical defect generation by proton-assisted 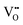 creation (PAOVC) is a novel approach to form high concentrations of volumetric
creation (PAOVC) is a novel approach to form high concentrations of volumetric 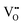 , where the integration of protons (H˙) in an aqueous solution can lower significantly the energy (electrical potential) required for the formation of
, where the integration of protons (H˙) in an aqueous solution can lower significantly the energy (electrical potential) required for the formation of 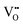 .42,55
.42,55
• Intervalence charge transfer (IVCT), involving electron exchange between dopant and matrix ions or between codopant ions, and multivalence charge transfer (MVCT), involving electron exchange between multiple-dopant ions and matrix ions, both without defect formation otherwise, represent underappreciated means of explaining valence changes.56–69
• Three types of colour centres (F0, F+, F++) have been suggested by modelling70 and validated experimentally for pure CeO2−x.71 While, the latter were generated at room temperature, high-energy irradiation often is required to create the Schottky pairs that are involved in the generation of such F-centres.72 Doped CeO2−x exhibits similar behaviour although this generally is attributed to an F-centre exchange (FCE) coupling mechanism involving magnetic dopant ions and 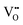 .73–75 These mechanisms also often are ignored sources of defects.
.73–75 These mechanisms also often are ignored sources of defects.
It is only in recent years that the instrumentation for the direct detection and quantitative analysis of these point defects has become widely available. Table 5 summarises these types of instrumentation and the data that can be generated with their use. The table is linked to a series of resultant images published largely by the authors of the present work (ESI,† Fig. S6–S11).
CeO2 crystal growth mechanisms
The conventional perception of the crystal growth process under conditions of the generally used methods of precipitation and hydrothermal synthesis is that nanoparticles grow in two stages:126 During processing, nucleation occurs in the precursor solution followed by subsequent growth of the resultant nuclei. Both of these stages can be controlled by varying the synthesis conditions to obtain nanoparticles of different morphologies, sizes, and degrees of crystallinity. The most commonly used experimental variables that determine these characteristics include the cerium concentration [Ce], usually from Ce(NO3)3·6H2O as solute; sodium hydroxide concentration [NaOH] as precipitating agent; reaction temperature (T), invariably ≤200 °C; and reaction time (t), commonly ≤24 h. Since the first reports of the hydrothermal growth of CeO2,77–79 most studies have used the preceding conditions for synthesis, although alternative Ce salts as solutes,15,78,80–93 and different precipitating agents78,84–101 to generate these and alternative morphologies, including nanotubes,80,82,94 nanoplates,95 nanosheets,96 nanorod flowers,97 nanoneedles,98 and solid and hollow nanospheres,85,99–101 have been used.Table 6 comprehensively surveys hydrothermal synthesis data for nanoceria morphologies, with variables [Ce] (viz., [Ce(NO3)3·6H2O]), [NaOH], T, and t. Since sixteen of the previous eighteen studies used low [Ce] (≤0.60 M) and limited [NaOH] (≤22.5 M), the present work supplements these studies by using high [Ce] (2.00 M) and an extended range of high [NaOH] (7.0–35.0 M) concentrations. All of these studies involved the sole use of Ce(NO3)3·6H2O and NaOH; no other salts were present.
| [Ce] (M) | [NaOH] (M) | Ageing time | Temp. (°C) | Morphology | Note | Ref. |
|---|---|---|---|---|---|---|
| (A) By precipitation over 2 h without reported ageing. (B) By precipitation over 2 h followed by ageing for 24 h at 25 °C. (C) Nanopolyhedra described as nanooctahedra. (D) Wu et al.119 Ce(NO3)3·6H2O + NaOH gave nanorods and nanocubes but Ce(NO3)3·6H2O + Na3PO4·12H2O gave nanooctahedra; Liu et al.120 Ce(NO3)3·6H2O + NaOH gave nanorods and nanocubes but Ce(NO3)3·6H2O + CH3COONH4 gave nanoctahedra. (E) Ce(NO3)3·6H2O + NaOH gave nanocubes but CeCl3·7H2O gave nanorods. (F) Term nanoparticles used but TEM images show nanooctahedra. (G) Hexagonal → square nanorod conversion mechanism proposed. (H) Uncertainty about cross sectional shape of rods since (111) facets indicated hexagonal rods but HAADF imaging suggested rectangular cross section. (I) Two variants: Both chains and hexagonal rods oriented in growth direction [110] or [211]. (J) By precipitation over 10–30 min followed by 24 h ageing at 25 °C. (K) Suggested mechanism (Scheme 1 in ref. 108) indicates that the nanoparticles were the decomposition product of nanotubes or nanowires. (L) Morphology of nanotubes not specified. (M) Nanowires stated to form by deposition on nanotube ends. (N) Hexagonal nanorods assumed on basis of use of high [Ce]. | ||||||
| 0.0016 | 0.11 | — | 25 | Truncated octahedra | A | Kamimura et al.114 |
| 0.0052 | 0.38 | Truncated octahedra | ||||
| 0.0259 | 1.88 | Truncated octahedra | ||||
| 0.01 | 0.15 | 24 h | 25 | Simple octahedra + truncated octahedra | B | Liu et al.107 |
| 0.03 | 0.03 | 24 h | 180 | Simple octahedra + truncated octahedral | — | Lin et al.115 |
| 0.08 | Truncated octahedra | |||||
| 0.10 | Truncated octahedra | |||||
| 0.13 | Truncated octahedra | |||||
| 0.33 | Truncated octahedra | |||||
| 0.10 | 0.10 | Truncated octahedra | ||||
| 0.05 | 0.01 | 24 h | 100, 180 | Truncated octahedra | C | Mai et al.104 |
| 1.00, 3.00 | 100 | Truncated octahedra + square rods | ||||
| 6.00, 9.00 | 100 | Square rods | — | |||
| 6.00 | 140 | Square rods + cubes | ||||
| 180 | Cubes | |||||
| 0.10 | 1.00 | 10 h | 100–150 | Truncated octahedra + square rods | — | Torrente-Murciano et al.17 |
| 2.00–10.0 | 150 | Square rods | ||||
| 4.00–10.0 | <100 | Truncated octahedra | ||||
| <5.00 | 180 | Truncated octahedra + square rods + cubes | ||||
| 10.0–15.0 | 70 | Square rods | ||||
| 15.0 | 180 | Cubes | ||||
| 0.13 | 0.45 | 24 h | 90 | Truncated octahedra | — | Lykaki et al.118 |
| 2.75 | Truncated octahedra + square rods | |||||
| 0.45 | 180 | Cubes | ||||
| 0.35 | 0.01 | — | 25 | Simple Octahedra + truncated octahedra | B | Zhou et al.105 |
| 2.00 | 10 h | 100 | Square rods | — | ||
| 0.40 | 6.90 | 7 h | 100 | Hexagonal rods | — | Guo and Zhou117 |
| 15 h | Hexagonal rods | |||||
| 24 h | Hexagonal rods | |||||
| 48 h | Hexagonal rods | |||||
| 0.40 | 6.90 | 24 h | 100 | Square rods | — | Li et al.118 |
| 0.40 | 6.90 | 24 h | 100 | Square rods | D | Wu et al.,119 Liu et al.120 |
| 180 | Cubes | |||||
| 0.40 | 7.20 | 24 h | 180 | Cubes | E | Wu et al.15 |
| 0.45 | <10.0 | 24 h | <70 | Truncated octahedra | — | Mehmood et al.12 |
| 10.0 | 100–150 | Square rods | ||||
| 5.00–20.0 | 180-200 | Cubes | ||||
| 0.45 | 10.0 | 24 h | 180 | Cubes | — | Bhatta et al.121 |
| 0.45–0.60 | <5.00 | 24 h | <100 | Simple octahedra | F | Sakthivel et al.16,111 |
| 5.00–22.5 | 50–150 | Hexagonal rods | G | |||
| 150–200 | Cubes | — | ||||
| 0.50 | 15.0 | 24 h | 100 | Hexagonal rods | H | Agarwal et al.110 |
| 180 | Cubes | |||||
| 2.00 | 0.80 | 12 min | 100 | Truncated octahedra chains | I | Du et al.106 |
| 2.00 | Truncated octahedra chains | |||||
| >5.00 | Hexagonal rods | |||||
| 2.00 | 14.0 | 40 days | 5 | Hexagonal rods | — | Present work |
| 30 min | 50–200 | Hexagonal rods | ||||
| 1–2 h | 50–100 | Hexagonal rods | ||||
| 1 h | 150–200 | Hexagonal rods + cubes | ||||
| 2 h | 150 | Hexagonal rods + cubes | ||||
| 2 h | 200 | Cubes | ||||
| 7.00 | 2 h | 200 | Hexagonal rods + cubes | |||
| 14.0 | Cubes | |||||
| 7.00–35.0 | 24 h | 25 | Hexagonal rods | J | ||
| 100–150 | Hexagonal rods + cubes | — | ||||
| 150–200 | Cubes | |||||
| 3.20 | 14.0 | — | 25 | Particles | B, K | Pan et al.108 |
| 72 h | 100 | Tubes | L | |||
| 24 h | 110 | Wires | M | |||
| 120 | Truncated octahedra | — | ||||
| 140 | Truncated octahedra + cubes | |||||
| 160 | Cubes | |||||
| 2 h | 180 | Truncated octahedra + hexagonal rods + cubes | N | |||
| 24 h | Cubes | — | ||||
Autoclave pressure
Although four variables have been specified, the use of hydrothermal syntheses introduces a fifth, which is vapour pressure (P). While, in the autoclave, this degree of freedom is fixed by the T and [NaOH] and so P is not considered, it remains an unknown. Fig. 7 completes the experimental picture by showing the internal autoclave vapour pressure at the ranges of T and [NaOH] regularly used. These data were interpolated from the Othmer diagram for NaOH aqueous solutions.102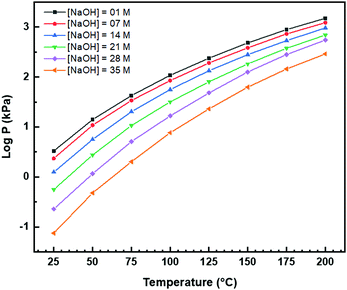 | ||
| Fig. 7 Autoclave vapour pressure (P) at different [NaOH] and T determined from Othmer diagram for NaOH aqueous solutions.102 | ||
Other considerations
A final issue is the potential for the effects of the use of other salts as the sources of Ce, such as CeCl3·7H2O, and other precipitating agents, such as NH4OH. Such species may play important roles in altering or directing the development of different morphologies. However, as stated, Table 6 reports data only for the use of Ce(NO3)3·6H2O and NaOH as raw materials.The range of CeO2 morphologies often is uncertain owing to difficulties in imaging ultrafine grains, agglomeration, irregular shape outlines, and nonisometric facet outlines.103 These challenges have resulted in reports of morphologies described as nanopolyhedra104 and nanoparticles,16 where these appear to be ultrafine simple octahedra or truncated octahedra. Further, there may be up to three variants of nanorods, one square105 and possibly two hexagonal.106 Unusually, these nanorods do not exhibit true prismatic cross sections as the optical mineralogy forms include pinacoids and rhombic prisms, often of similar dimensions, although the nanorods appear to exhibit identical growth directions.105–107 In some cases, these nanorods have been reported to consist of Ce(OH)3 while wet, oxidising to CeO2 upon drying.15,16,80,104,108
The studies by Du et al.106 and Nabavi et al.109 are important because these are the only works to demonstrate the formation of metastable nanochains of individual crystallites of truncated nanooctahedra during heating at 100 °C106 or at room temperature.109 These are precursors that self-assemble and coalesce into square and hexagonal nanorods. However, two growth directions for hexagonal nanorods have been suggested, these being the commonly observed [110]16,106,108,110,111 and the less commonly observed [211].106,111
Despite many studies using hydrothermal synthesis to generate different nanoceria morphologies, the summary of Table 6 shows that many uncertainties remain. Although several proposals concerning possible growth mechanisms have been conjectured,15,16,106,112,113 these remain poorly understood owing to insufficient data for mechanistic validation.
Supplementary experimentation
Electron microscopy
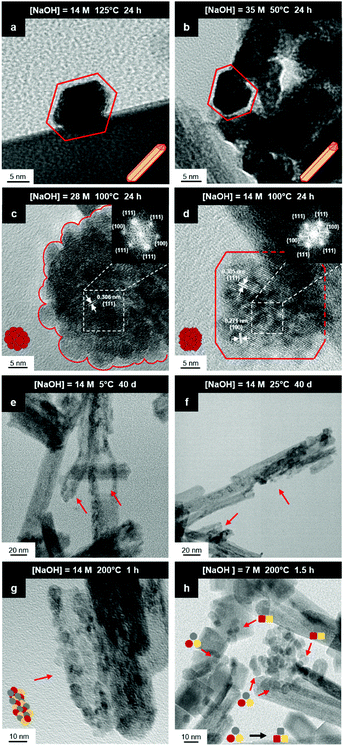
Fig. 8(a) and (b) show two of the variants of the hexagonal nanorod cross sections, which confirm the nature of the hexagonal nanorods as nonprismatic (ESI,† Fig. S2). These are consistent with the two equilibrium shapes predicted by Wulff constructions considered previously.122–124 TEM analyses reveal that the prism cross sections are bounded by four {111} facets and two {100} facets; each of the c axis terminations consists of pyramids containing four {111} facets (other two unknown); the growth directions are 〈110〉, as observed previously.16,106,108,110,111The presence of ∼100 nm nanospheres was observed occasionally under the synthesis conditions of T = 75–125 °C and [NaOH] = 14.0–35.0 M. In agreement with others,96,125 these were found to be single-crystal. Fig. 8(c) reveals the mechanism by which this singular morphology (spheroids) develops, which is by the self-assembly, intergrowth, and coalescence of self-assembled precursor crystallites. The resultant single-crystal nanospheres were established at sizes in the range ∼20–50 nm diameter, with the larger size's being predominant. The same mechanism appears to apply to {111}-truncated nanocubes (cuboids) as shown in Fig. 8(d), which coalesce and form truncated nanocubes (ESI,† Fig. S3(a) and (b)). Further, simple cuboids also form by this mechanism (ESI,† Fig. S3(c) and (d)). The cuboids were of variable size (commonly ∼20–30 nm but as large as 165 nm when coalesced) but they were less common than the nanospheres.
Assuming that the fast Fourier transformation (FFT) patterns (Fig. 8(c) and (d)) indicate exposed facets of the crystallites, then the spheroids are likely to be octahedron-like, comprised of multiple crystallites with mutual {111} interfaces, and the cuboids are likely to be cube-like, comprised of multiple crystallites with mutual {100} interfaces. The outlines of the latter morphology are indistinct but the detection of multiple examples of these confirms that they are consistent forms (ESI,† Fig. S3(c) and (d), ESI†).
The principal differences between these formation conditions are that the spheroids|nanospheres formed at lower temperatures (75–125 °C) and higher [NaOH] (14.0–35.0 M) than the cuboids|truncated nanocubes, which formed at higher temperature 100–125 °C and lower [NaOH] (14.0–21.0 M). However, established truncated nanocubes of sizes much smaller (∼4–5 nm) than observed for the cuboids were observed commonly. Since such a size differential was not observed for the nanospheres, then there may be a size effect for the formation of cuboids according to T and t effects, although the data do not rule out this possibility for the spheroids as well. These morphological effects are interpreted in terms of thermal vibrations, where low intensities would facilitate self-assembly, intergrowth, and coalescence, thus allowing the formation of the larger spheroids and established nanospheres while the greater disturbance from high intensities would limit formation to the smaller forms of cuboids and established truncated nanocubes (but possibly nanospheres as well).
The species subject to thermal vibrations, which intergrow, self-assemble, and coalesce to establish the final established forms, are crystallites that are generated by the disassembly of the nanorods, as shown in Fig. 8(e) and (f). This process is shown more clearly in Fig. 8(g) and (h). These four images demonstrate that the hexagonal nanorods are destabilised and deteriorate under the conditions of both low temperature (5 °C)|long time (40 days) and high temperature (200 °C)|short time (1.5 h).
Crystal growth
In conventional crystal growth by precipitation, it is assumed that each individual nucleus acts as a potential source of epitaxial growth.126 In contrast, the present work suggests an interposing four- or five-stage process of some difference:(1) Disassembly by destabilisation and deterioration
(2) Resultant establishment of independent crystallites
(3) Possible adsorptive alteration of the crystallite morphology
(4) Crystallite self-assembly
(5) Crystallite coalescence into established grain
This process effectively introduces an unrecognised intermediate stage of crystal growth between those of nucleation and grain establishment. For Stage 3, high temperatures favour NO3− anion selective adsorption15 and alteration of octahedral spheroidal crystallites (decagons) into cuboidal crystallites (squares) and nanocube establishment. When the temperature is insufficient to activate NO3− anion selective adsorption on {100}, retention of octahedral spheroidal crystallites and nanosphere establishment occur, precluding Stage 3. The observed morphologies of the nanosphere and nanocube variants are shown in Fig. 9; the truncations on the nanocubes are too small to image at these magnifications (ESI,† Fig. S3(a) and (b)).
 | ||
| Fig. 9 TEM images: (a) sphere (circled) (b) intergrowths, (c) multicubes, (d) cubes with adsorbed smaller CeO2 nanocubes (authors’ unpublished work). | ||
Ce(OH)3 nanorods
Zhou et al.80 suggested a solution-reprecipitation process for the conversion of what were assumed to be Ce(OH)3 nanorods in 15% H2O2 at room temperature to CeO2 nanotubes. Wu et al.15 and Mai et al.104 used X-ray diffraction (XRD) to identify hexagonal Ce(OH)3 nanorods hydrothermally synthesised from CeCl3·7H2O and NaOH and from Ce(NO3)3·6H2O and NaOH, respectively. Both studies15,104 reported a Ce(OH)3 → CeO2 nanorod conversion upon oxidation. Wu et al.15 reported the conversion of nanorods to nanocubes by NO3− adsorption on {100}. Ji et al.127 noted the importance of the anions in solution to the CeO2 morphology formed, although they considered the anions in terms of oxidation rather than selective adsorption.Sakthivel et al.16 reported the fabrication of what were assumed to be Ce(OH)3 hexagonal nanorods, although these were considered to be metastable, converting to nanocubes at higher temperatures, both morphologies of which converted to CeO2 upon drying. Pan et al.107 reported the synthesis of what were assumed to be Ce(OH)3 nanorods, which oxidised under hydrothermal conditions to CeO2. They proposed a conversion mechanism for nanowires of mixed Ce4+/Ce3+ valences into apparently stable equiaxed nanoparticles of ∼15 nm size, with conversion of these into nanocubes at higher temperatures. This mechanism is problematic in that it contradicts the three published morphology maps,12,16,17 which show that increasing temperatures result in a stepwise conversion as follows:
Nanooctahedra → Nanorods → Nanocubes
These three reports12,16,17 did not provide supporting microscopy evidence for the suggested mechanisms.
Nanochains
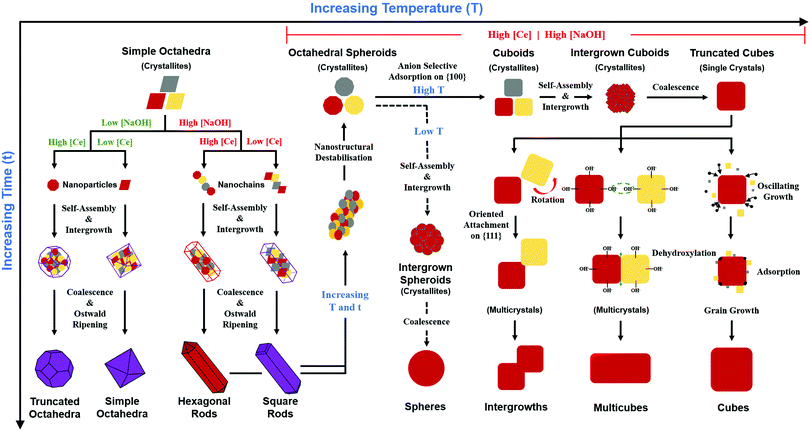
A key point of these mechanisms is the nature of the crystallites, which are illustrated in Fig. 10 as rhomboids (simple octahedra), octahedra ({100} truncated octahedra), and decagons ({110} and {100} truncated octahedra). As will be explained subsequently, these crystallites consist of Ce(OH)4 precipitates. The roles of the simple octahedral and truncated octahedral crystallites are critical to the formation of nanochains (at 100 °C (ESI,† Fig. S4106) or at room temperature),109 which act as precursors to the square and hexagonal nanorods, respectively. The proposed nanochain-to-nanorod conversion mechanisms are illustrated in Fig. 11. A summary of the reports of the resultant crystallographies of the two types of nanorods is given in Table 7. | ||
| Fig. 11 Proposed mechanisms for conversion of nanochains into square and hexagonal nanorods (hydroxyl bonding is shown as a simplification of the probable anionic ligand bonding). | ||
| Square CeO2 nanorods | ||||
|---|---|---|---|---|
| Growth directions | Tetragonal prism | Note | Ref. | |
| Pinacoid A | Pinacoid B | |||
| (A) True tetragonal prism, where both pinacoids are crystallographically equivalent to form a true prism in cubic symmetry (a1, a2, a3). (B) Specified planes not crystallographically possible pairs. (C) True hexagonal prism, where rhombic prism and pinacoid are crystallographically equivalent to form a true prism in hexagonal symmetry (a1, a2, a3, c). (D) Growth directions not crystallographically consistent with hexagonal prism planes (although 〈211〉 can be normal to {111}). | ||||
| [001] | (100) | (010) | A | — |
| 〈110〉 | {110} | {100} | — | Mehmood et al.12 |
| Wu et al.15 | ||||
| Sakthivel et al.16 | ||||
| Torrente-Murciano et al.17 | ||||
| Mai et al.104 | ||||
| Zhou et al.105 | ||||
| Lykaki et al.116 | ||||
| Li et al.118 | ||||
| {111} | {100} | B | Wu et al.119 | |
| Wang et al.131 | ||||
| — | — | — | Liu et al.120 | |
| Hexagonal CeO2 nanorods | ||||
|---|---|---|---|---|
| Growth directions | Hexagonal prism | Note | Ref. | |
| Rhombic prism | Pinacoid | |||
| [001] | {110} | {100} | C | — |
| 〈110〉 | {111} | {100} | — | Sakthivel et al.16 |
| Du et al.106 | ||||
| Sakthivel et al.111 | ||||
| Guo and Zhou117 | ||||
| Present Work | ||||
| {111} | {111} | B | Agarwal et al.110 | |
| — | — | — | Pan et al.108 | |
| 〈211〉 | {111} | — | D | Du et al.106 |
| Sakthivel et al.111 | ||||
The conversion of the Ce(OH)4 precipitates into nanochains and then square or hexagonal nanorods through the development of different crystallographic planes can be interpreted in consideration of the data given in Table 2, which show that the order of stability of the relevant planes is {100} < {110} < {111}, as also will be discussed subsequently.
Square nanorods
For the nanochains of simple octahedra of Ce(OH)4, the uniquely present {111} planes undergo face-to-face adsorption through anionic ligand bonding, which subsequently condenses. As these are the only planes available, then their mutual adsorption is the only option. The driving force for this adsorption is surface energy reduction by partial annihilation of two planes, resulting in the formation of a zigzag nanostructure, which has been observed before for simple octahedra.128–130 Decreasing surface area (and attendant surface energy) is a similar driving force for the octahedra to form {110} and {100} truncations on the outer surfaces. Subsequently, coalescence of the octahedra and Ostwald ripening result in the formation of a square nanorod with the commonly observed tetragonal prism consisting of single {110} and {100} pinacoids and the consistently observed 〈110〉 growth directions.12,15–17,104,105,116,118–120,131Hexagonal nanorods
In the case of the nanochains of truncated octahedra of Ce(OH)4, the less stable planes are {100},33,34,36 which are polar, unlike nonpolar {111}.132,133 The low stability and presence of the dipole for the former of these two oxygen-terminated (and hence negatively charged) planes134–137 explain the preferential adsorption of the anionic ligand on the {100} planes; this epitaxial attachment has been observed before.138 So face-to-face adsorption occurs by the preceding processes but with annihilation of {100} planes, again resulting in a zigzag nanostructure, which is required for 〈110〉 growth directions. The surface area decreases through growth of the outer {111} and remaining {100} planes, followed by coalescence and Ostwald ripening to establish a single crystal with a hexagonal prism consisting of a {111} rhombic prism and a {100} pinacoid, again with 〈110〉 growth directions. This mechanism is supported by the observation by Du et al.106 (Table 6) of the alteration of nanochains of truncated octahedra to hexagonal nanorods with increased [NaOH].The starting point for the assessment of the growth mechanisms for square nanorods and hexagonal nanorods is the 〈110〉 growth directions for both types. This is a key observation because both growth mechanisms must meet this criterion. For simple octahedra, only {111} planes are available and so only the zigzag nanostructure would result in 〈110〉 growth. In the case of the truncated nanorods, if the commonly observed {100} truncations were aligned linearly, this corner-to-corner growth would not result in 〈110〉 growth. However, while {110} octahedral truncations are less commonly observed, they quality as being suitable for 〈110〉 edge-to-edge growth. However, this is considered unlikely for the two reasons that (1) Table 2 shows that {110} planes are more stable than {100} planes, so annihilation of the latter is more probable and (2) {110} truncations are not observed commonly but hexagonal nanorods are.
Oxygen vacancies
It is well known that play a key role in the properties of CeO2−x.6,14,142–144Table 4 confirms that there are many possible mechanisms by which
play a key role in the properties of CeO2−x.6,14,142–144Table 4 confirms that there are many possible mechanisms by which 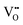 can form, although the previous text explains that undoped CeO2−x exhibits intrinsic
can form, although the previous text explains that undoped CeO2−x exhibits intrinsic 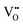 that are charge compensated by Ce4+ → Ce3+ reduction. However,
that are charge compensated by Ce4+ → Ce3+ reduction. However, 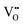 also appear to play a role in CeO2−x surfaces. This is indicated in the inset red cubes in Fig. 9(b), which show {111} planes with corner-to-corner joining. This is counter-intuitive as Table 2 shows that these planes are the most stable and therefore unlikely to annihilate in the presence of the less-stable {100} planes. The reason for the observation of this preferred joining is the additional surface energy provided by the roughness of the {111} truncations. This roughness develops owing to the lower stabilities of the {110} and {100} planes, which convert to subfacets of the more stable {111} planes under the destabilising influence of
also appear to play a role in CeO2−x surfaces. This is indicated in the inset red cubes in Fig. 9(b), which show {111} planes with corner-to-corner joining. This is counter-intuitive as Table 2 shows that these planes are the most stable and therefore unlikely to annihilate in the presence of the less-stable {100} planes. The reason for the observation of this preferred joining is the additional surface energy provided by the roughness of the {111} truncations. This roughness develops owing to the lower stabilities of the {110} and {100} planes, which convert to subfacets of the more stable {111} planes under the destabilising influence of 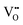 .121,145
.121,145
Principal variables
The schematic of Fig. 10 formalises the effects of the four main processing variables [Ce] (thus fixing [NO3−]), [NaOH], temperature (thus fixing P), and time (ESI,† Fig. S5); Fig. 10 shows the different physicochemical mechanisms; and it combines the variables and mechanisms to explain the generation of the observed different morphologies and their variants. However, this schematic applies only to the commonly used raw materials Ce(NO3)3·6H2O and NaOH; other morphological outcomes have been reported for the use of alternative, less commonly used, Ce salts as solutes (Table 8) and precipitating agents (Table 9).| Anionic ligand | Morphology observed | Crystallographic data | Note | Ref. |
|---|---|---|---|---|
| (A) Cl−/NO3− ratio: 3/1 = nanowires + nanoparticles; 1/1 = rounded or cubic nanoparticles + nanowires; 1/3 = nanoparticles. (B) Precipitating agents NaOH + formaldehyde (CH2O). (C) Gelation synthesis. (D–J) Hydrothermal syntheses with precipitating agents: (D) Na3PO4·6H2O, (E) urea (CO(NH2)2), (F) ethanol, (G) H2O2, (H) ethylenediamine (C2H4(NH2)2), (I) ammonium acetate (CH3COONH4), (J) oleyamine (C18H35NH2). | ||||
| Hydrothermal synthesis using NaOH precipitating agent | ||||
| Cl− | Nanorods | [110] growth | — | Wu et al.15 |
| {110} & {100} faces | ||||
| Nanowires | (111) faces | — | Fu et al.81 | |
| Nanotubes | [100] growth | — | Tang et al.82 | |
| Nanoparticles | — | — | Kannan and Sundrarajanya139 | |
| Cl− + NO3− | Nanocubes | — | — | Wu et al.15 |
| Br− | Nanorods | — | — | Wu et al.15 |
| BrO3− | Nanoparticles | — | — | Wu et al.15 |
| I− | Nanorods | — | — | Wu et al.15 |
| SO42− | Nanooctahedra | — | — | Wu et al.24 |
| Nanorods | — | — | Wu et al.15 | |
| Nanotubes | Polycrystalline | — | Zhou et al.80 | |
| Hydrothermal synthesis using NH4OH precipitating agent | ||||
| Cl− | Nanowires | {111} faces | — | Wang et al.84 |
| Nanorods | [110] growth | — | Vantomme et al.86 | |
| Cl− + NO3− | Various | — | A | Wang et al.84 |
| SO42− | Nanoparticles | — | — | Hirano and Kato78 |
| CH3COO− | Nanowires | Polycrystalline | — | Sun et al.87 |
| Other synthesis methods and precipitating agents | ||||
| NO3− | Nanobelts | Polycrystalline | B | Rao et al.140 |
| Cl− | Nanooctahedra | — | C | Laberty-Robert et al.88 |
| Nanorods | [211] growth | D | Ji et al.89 | |
| {111} & {100} faces | ||||
| Nanowires | Polycrystalline | E | Yan et al.91 | |
| Nanospheres | Crystalline | F | Zarinkamar et al.141 | |
| Cl− + NH2− | Hollow Nanospheres | Polycrystalline | E + G | Yang et al.85 |
| Nanorods | — | H | Sun et al.90 | |
| SO42− | Rounded Nanoparticles | Polycrystalline | E | Hirano and Inagaki92 |
| CH3COO− | Nanooctahedra | — | I | Liu et al.120 |
| Nanorods | 〈100〉 growth | J | Lin et al.93 | |
| Precipitating agent | Morphology observed | Crystallographic data | Note | Ref. |
|---|---|---|---|---|
| (A) Decomposition of urea considered to be a source of NH3 gas bubbles to facilitate hollow nanosphere formation. (B) Na3PO4·6H2O considered to be a mineraliser; crystallographic data for nanorods; nanocubes not illustrated but stated to form at pH > 10. | ||||
| H2O2 | Nanoneedles | [100] growth | — | Tang et al.98 |
| H2O2 + urea | Hollow nanospheres | Polycrystalline | A | Zhang et al.100 |
| Urea | Nanorods | [110] growth | Tang et al.146 | |
| {111} & {100} faces | ||||
| Nanocubes | {111} truncations | |||
| NH4OH | Nanooctahedra | — | — | Han et al.93 |
| Nanowires | {111} faces | |||
| Nanotubes | {111} faces | |||
| Nanooctahedra | — | — | Wang et al.101 | |
| Na3PO4·6H2O | Nanooctahedra | [100] growth | B | Yan et al.147 |
| Nanorods | {100} faces | |||
| Nanocubes | ||||
| Nanooctahedra | — | — | Yu et al.97 | |
| Nanorods | [100] growth | |||
| Na3PO4·12H2O | Nanooctahedra | — | — | Liu et al.,148 Wang et al.131 |
| Organic acids | Solid nanospheres | Polycrystalline | — | Wang and Kobiro99 |
Crystallography and optical mineralogy
The data for the square nanorods are completely consistent (Table 7), revealing 〈110〉 growth directions and a tetragonal prism consisting of {110} and {100} pinacoids, thereby resulting in what actually is a rectangular cross section. Apparently, the only investigation reporting the tetragonal bipyramid is that by Mehmood et al.,12 who identified (111} planes. Fig. 11 shows that the proposed growth mechanism indicates that this is as expected, as are the complementary {100} planes, each of which forms a dome.The data for the hexagonal nanorods generally are consistent (Table 7). Although the most commonly observed crystallographic relation reveals 〈110〉 growth directions,16,106,108,110,111 there are two reports of 〈211〉 growth directions.106,111 However, both studies report 〈211〉 growth directions as being parallel to {111} planes, which is not crystallographically possible. Apart from these two reports, the hexagonal prism actually consists of a {111} rhombic prism and one {100} pinacoid.16,106,108,111 There also is a single report of a hexagonal prism consisting of {111} planes110 but this is not crystallographically possible. The nature of the hexagonal prism can be considered in terms of the internal angles between the planes:
| {111} − {100} Angle = 125.26° |
| {111} − {111} Angle = 109.47° |
It is clear that these planes cannot form a true hexagonal prism as this requires a single internal angle of 120°. These angular relations are supported by the sums of the six angles:
| True Hexagonal Prism: 6(120.00°) = 720.00° |
| Actual Hexagonal Prism: 4(125.26°) + 2(109.47°) = 719.98° |
There are few comments concerning the hexagonal dipyramid terminating the hexagonal prism. The present work indicates that this consists of a {111} rhombic prism and one of the eight possible ±(122) pinacoids. The {111} planes have been confirmed by others,109,110 who observed {111} facets on the ends of nanorods. As there do not appear to be any reports of a terminating {110} pedion or pinacoid normal to the family of principal 〈110〉 axes, then the hexagonal dipyramid must converge to a point, which requires all six of the planes to exhibit the same angle with the hexagonal prism planes. As the {111} − {111} angle is 109.47° and the only other possible plane with this angle is {100} − {122}, then the latter identifies the unknown pinacoid, as shown in grey in Fig. 11. However, this pinacoid cannot include the full family of {122} planes as the alternative ±(211) and ±(212) variants exhibit different angles, which confirms the unique pinacoid orientation (of the three possibilities). The formation of this pinacoid is supported by the high stability of the (122} plane shown in Table 2, which generally is second only to that of the {111} planes.
Anionic ligand
Other investigators have observed more limited morphological outcomes when the nanoparticles were synthesised using different Ce salts. A survey of these reports is given in Table 8. The importance of the anionic ligand, particularly NO3−, to the morphological development was recognised as long ago as 1996 by Hirano and Kato78 and more recently has been reviewed by Zhang et al.149 The hydroxyl bonding shown in Fig. 11 is a probable simplification of the actual ligand bonding in that the orientation relations that are established between the octahedral crystallites of the nanochains may be controlled by monodentate, bidentate, or mixed-ligand bonding with NO3−. In effect, the nature of the anionic ligands may be one of the factors determining the orientations of the nanochains, which in turn determine the crystallographic relations of the nanorods. It also is likely that (with the exceptions of the use of Na3PO4·6H2O100 and urea (CO(NH2)2)128 as precipitating agents), the formation of nanocubes is dependent on the selective adsorption of NO3− on the crystallites that form from the destabilisation and deterioration of the nanorods, as shown in Fig. 10.Precipitating agent
The role the precipitating agent has not been examined probably because NaOH is used so commonly, as shown in Tables 6 and 8. Although Table 8 canvasses the use of other precipitating agents, salts other than Ce(NO3)3·6H2O also have been used. Table 9 summarises reports on the use of this salt but with different precipitating agents. During the precipitation of a hydroxide (viz., Ce(OH)4), the cation of the precipitating agent (viz., Na+vs. NH4+) would not be expected to play a direct chemical role in morphological development. However, alternative anions, such as NH2− (from urea,85,91,92 ethylenediamine,90 or oleyamine,93Table 8) and PO43− (from Na3PO4·6H2O,95,100Table 9), would be expected to have an influence.Summary of variables
In summary, there are seven general variables that determine the morphological development of CeO2 during precipitation and hydrothermal synthesis (where the types of anion and precipitating agent are fixed in the present work and where T and [NaOH] fix the autoclave pressure (P)102):• Concentration of parent Ce in soluble salt
• Type of anionic ligand of Ce salt
• Concentration of anionic ligand
• Type of precipitating agent
• Concentration of precipitating agent
• Temperature
• Time
Pourbaix diagram
According to the modified Ce4+/3+–H2O Pourbaix diagram, which was prepared for the Ce4+/3+–Na+–NO3−–H2O system, shown in Fig. 12, the blue predominance region is for the crystallites that comprise the nanochains, which begin as precipitates of Ce(OH)4 amorphous species (pt) and then convert readily to hydroxylated (s) and hydrated crystalline species (s) during aging, ultimately drying rapidly under oxidising conditions in the sequence:| Ce(OH)4(pt) → Ce(OH)4(s) → CeO2·2H2O(s) → CeO2(s) |
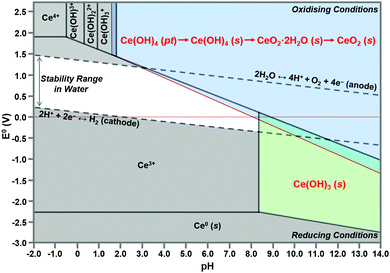 | ||
| Fig. 12 Modified Pourbaix diagram for Ce4+ and Ce3+ soluble species (predominance region for Ce(OH)4 (pt) based on DFT calculation of its free energy; other predominance regions based on previous work76,150 (pt = amorphous precipitate, s = crystalline solid). | ||
The formation of solid Ce(OH)4 is supported by earlier versions of this diagram.76,150 These diagrams also show the formation of solid Ce(OH)3 according to the green predominance region, so Ce(OH)3 could be present as a minor phase at intermediate pH values (∼7–11). The specific locations and extents of these predominance regions are unique to each individual chemical system, which explains the possible observation of Ce(OH)3 nanorods.15,16,80,104,108 Since Ce(OH)3 is considered to oxidise readily to CeO2,15,16,80,104,108 this supports by analogy the sequence Ce(OH)4(pt) → CeO2(s). Differentiation between Ce(OH)4 and Ce(OH)3 is complicated by the relatively easy redox switching between the two Ce valence states.12,103,104,151 Since the crystal structure of Ce(OH)4 has been reported to be identical to that of cubic CeO2,152,153 but that of Ce(OH)3 has been reported to be hexagonal,16,104 it is possible that these crystal structures reflect the cross sections of the respective nanorods. However, since the present work indicates that cubic Ce(OH)4 can generate both square and hexagonal nanorods, then the only implication is that Ce(OH)3 may be a precursor to hexagonal nanorods.
In conclusion, the preparation of alternative Pourbaix diagrams for different anionic ligands and precipitating agents can illustrate the effects of different chemical species on the sizes and locations of the Ce(OH)4 and Ce(OH)3 predominance regions (in the stability range in water), thereby predicting the potential for the formation of solid Ce(OH)4 or Ce(OH)3 and the required pH conditions.
Fig. 10 also shows the role of the destabilisation of the nanorods (considered to be metastable16) by increasing T and/or t). Fig. 8 shows that, unlike the crystallites that comprise the nanochains,106,110 the crystallites that are liberated by this destabilisation are more rounded and so they exhibit a greater extent of truncation to expose both {110} and (100} planes. These rounded crystallites are subject to subsequent NO3− anion selective adsorption on the {100} planes,15 which facilitates their conversion to cuboidal crystallites that undergo self-assembly, intergrowth, and coalescence into nanocubes. The subsequent growth mechanisms that generate the nanocube variants have been considered by others as well.15,16,104,113
Speciation diagrams
The construction of speciation diagrams is an essential preliminary stage to the construction of Pourbaix diagrams.154,155 Speciation diagrams provide information on the conditions for nonfaradaic chemical reactions of Ce ions, in the absence of oxidation reactions, to form solid Ce(OH)4 (Fig. 13(a) or Ce(OH)3 (Fig. 13(b)). They also define the pH range at which solids will form as well as their concentrations. At a basic level, these diagrams differentiate the aqueous equilibria according to the Ce valence of the precursor salt used for synthesis. In contrast, Pourbaix diagrams include all metal valences and hence incorporate redox reactions. However, Pourbaix diagrams generally consider only the predominant metal-based species of the system while speciation diagrams include all species of the system. The diagrams calculated in the present work are distinctive because they are the first to include data for Ce(OH)4(pt), the Gibbs free energy of which was calculated using DFT.42 Both speciation diagrams indicate that the concentrations of the anionic ligand NO3− are in excess at all pH values. This demonstrates that, for these systems, the concentration of the anionic ligand does not represent a variable that influences the morphological development. In contrast, the solubility curves for NaOH demonstrate that both the type and concentration of this precipitating agent are variables that do have an impact on the morphological development.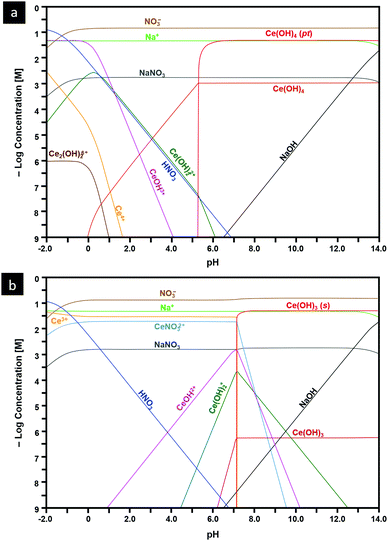 | ||
| Fig. 13 Speciation diagrams calculated at [Ce4+] and [Ce3+] = 50 mM, [NO3−] = 150 mM, [Na+] = 50 mM for: (a) system Ce4+–H2O and (b) Ce3+–H2O (pt = amorphous precipitate, s = crystalline solid). | ||
Conclusions
The present work provides an introductory but extensive summary of the fundamental parameters that underpin the design of nanoparticulate morphologies:• Crystallography
• Optical mineralogy
• Surface plane stabilities
• Stoichiometry
• Phase equilibria
• Thermodynamics
• Defect equilibria
• Crystal growth mechanisms
When these parameters are known and can be controlled and utilised, the designer of nanomaterials, such as CeO2−x, can leverage these to synthesise nanocrystals whose properties have been engineered strategically.
The present work also reports a comprehensive survey of the effects of the key experimental variables [Ce] (and, by association, [NO3−]), [NaOH], T (and, by association, P), and t on the morphologies of nanoceria formed during precipitation and hydrothermal synthesis as determined in published reports and the present supplementary experimentation. These data have generated a comprehensive schematic that describes the roles of these variables on the resultant morphologies and the associated mechanisms by which the morphologies are generated, where the variables associated with the types of anionic ligand (NO3−) and precipitating agent (NaOH) are fixed.
The present work also clarifies the importance of the formation of nanochains, which are precursors to both square and hexagonal nanorods. The respective mechanisms for the conversion of the nanochains into nanorods have been elucidated crystallographically and reflect a four-stage process of the following:
(1) Anionic ligand bonding between:
– {111} − {111} planes for simple octahedra|square nanorods → zigzag nanochains
– {100} − {100} planes for truncated octahedra|hexagonal nanorods → zigzag nanochains
In the case of truncated octahedra, preferential adsorption of the anionic ligand on the {100} planes to form zigzag nanochains occurs owing to the low stability and polarity of these crystallographic planes.
(2) Condensation and anionic ligand decomposition to establish epitaxy and consolidate the zigzag morphology
(3) Self-assembly and intergrowth to establish pinacoids that form the prism and dipyramid faces
(4) Coalescence and Ostwald ripening to recrystallise single-crystal nanorods
The formation of nanorods is critical to the potential to form nanocubes because the former are precursors to the latter. This conversion process takes place in four or five stages (where Stage 3 may or may not occur), depending on the effects of the anionic ligand on the ultimate morphology:
(1) Disassembly of the nanorods by destabilisation and deterioration
(2) Establishment of rounded crystallites (octahedral spheroids)
(3) NO3− selective adsorption or nonadsorption:
– High T: NO3− selective adsorption – resultant cube formation
– Low T: nonadsorption – resultant sphere formation
(4) Crystallite self-assembly (cuboids and spheroids)
(5) Crystallite coalescence into established grains
This process effectively includes an unrecognised intermediate stage of crystal growth between those of nucleation and grain establishment.
The apparent uncertainties and contradictions about the crystallographies of the square and hexagonal nanorods have been resolved. These morphologies are not true prismatic nanorods as they do not exhibit true fourfold tetragonal and sixfold hexagonal axial symmetries.
The roles of the anionic ligands have been clarified as well. It is likely that the type and hence the bonding of the anionic ligand are critical to the formation of the nanochains and subsequently their conversion to nanorods. Also, attention has been drawn to the role of NO3−, in contrast with other anions, in selective adsorption on {100} in facilitating the conversion of the Ce(OH)4 crystallites, which form upon the destabilisation and deterioration of the nanorods, into nanocubes. Alternatively, when the temperature is too low for the activation of NO3− anion selective adsorption on {100}, nanospheres are formed by the process of self-assembly, intergrowth, coalescence, and Ostwald ripening.
A new Ce4+/3+–H2O Pourbaix diagram has been prepared for the predominant Ce-based phases that form in the Ce4+/3+–Na+–NO3−–H2O system. It is distinctive in that it illustrates the importance of the precipitation of amorphous Ce(OH)4, which supports the conclusion that the crystallites that form nanochains and convert to square and hexagonal nanorods originate in Ce(OH)4 crystallites. Other more indicative Pourbaix diagrams for this and alternative systems provide the basis to assess the potential for crystallite and nanoparticle formation as well as the pH ranges suitable to these ends.
Matching new speciation diagrams for the Ce4+–Na+–NO3−–H2O and Ce3+–Na+–NO3−–H2O systems also have been prepared. These are the first such diagrams to include the critical data for the amorphous Ce(OH)4 precipitate, which converts readily to the crystalline analogue. Such diagrams of other chemical systems provide the basis for assessing the pH ranges suitable for the exsolution of the Ce(OH)4 and Ce(OH)3 crystallites, which provide the building blocks for the range of morphologies that can form during precipitation and hydrothermal synthesis. Such diagrams are particularly relevant when they indicate the formation of Ce(OH)3(s), which is the basis for a possible CeO2 nanorod formation pathway not considered in the present work. These diagrams also provide guidance for the selection of precursor salts of different valences, which represent another option open to the researcher seeking to engineer CeO2−x of specific morphologies. Thus, these diagrams are relevant to the identification of alternative systems that can be used for the synthesis of the range of morphologies open to CeO2−x.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge financial support from the Australian Research Council (ARC), Grant No. DP170104130, and the characterisation facilities provided by the Australian Microscopy & Microanalysis Research Facilities (AMMRF) node at UNSW Sydney.References
- J. Kašpar, P. Fornasiero and M. Graziani, Catal. Today, 1999, 50, 285–298 CrossRef.
- D. Ding, X. Li, S. Y. Lai, K. Gerdes and M. Liu, Energy Environ. Sci., 2014, 7, 552–575 RSC.
- N. Izu, W. Shin, N. Murayama and S. Kanzaki, Sens. Actuators, B, 2002, 87, 95–98 CrossRef CAS.
- S. S. Mofarah, E. Adabifiroozjaei, Y. Wang, R. Pardehkhorram, Y. Yao, M. H. N. Assadi, R. Mehmood, W.-F. Chen, C. Tsounis, J. Scott, S. Lim, R. F. Webster, V. Zhong, Y. Xu, P. Koshy and C. C. Sorrell, J. Mater. Chem. A, 2020, 8, 4753–4763 RSC.
- S. S. Mofarah, E. Adabifiroozjaei, R. Pardehkhorram, M. H. N. Assadi, M. Hinterstein, Y. Yao, X. Liu, M. B. Ghasemian, K. Kalantar-Zadeh, R. Mehmood, C. Cazorla, R. Shahmiri, G. Bahmanrokh, S. Bhattacharyya, M. C. Spadaro, J. Arbiol, S. Lim, Y. Xu, H. Arandiyan, J. Scott, P. Koshy and C. C. Sorrell, Adv. Mater., 2019, 31, 1905288 CrossRef.
- R. Mehmood, S. S. Mofarah, W.-F. Chen, P. Koshy and C. C. Sorrell, Inorg. Chem., 2019, 58, 6016–6027 CrossRef CAS.
- A. Younis, D. Chu and S. Li, J. Mater. Chem. A, 2015, 3, 13970–13977 RSC.
- A. Corma, P. Atienzar, H. Garcia and J.-Y. Chane-Ching, Nat. Mater., 2004, 3, 394–397 CrossRef CAS.
- A. Primo, T. Marino, A. Corma, R. Molinari and H. Garcia, J. Am. Chem. Soc., 2011, 133, 6930–6933 CrossRef CAS.
- R. Si, Y.-W. Zhang, L.-P. You and C.-H. Yan, Angew. Chem., Int. Ed., 2005, 117, 3320–3324 CrossRef ; Angew. Chem., Int. Ed., 2005, 44, 3256–3260.
- I. Celardo, J. Z. Pedersen, E. Traversa and L. Ghibelli, Nanoscale, 2011, 3, 1411–1420 RSC.
- R. Mehmood, X. Wang, P. Koshy, J.-L. Yang and C. C. Sorrell, CrystEngComm, 2018, 20, 1536–1545 RSC.
- A. Estevez and J. S. Erlichman, Nanomedicine, 2014, 9, 1437–1440 CrossRef CAS.
- R. Mehmood, N. Ariotti, J.-L. Yang, P. Koshy and C. C. Sorrell, ACS Biomater. Sci. Eng., 2018, 4, 1064–1072 CrossRef CAS.
- Q. Wu, F. Zhang, P. Xiao and H. Tao, J. Phys. Chem. C, 2008, 112, 17076–17080 CrossRef CAS.
- T. Sakthivel, S. Das, A. Kumar, D. Reid, A. Gupta, D. Sayle and S. Seal, ChemPlusChem, 2013, 78, 1446–1455 CrossRef CAS.
- L. Torrente-Murciano, A. Gilbank, B. Puertolas, T. Garcia, B. Solsona and D. Chadwick, Appl. Catal., B, 2013, 132, 116–122 CrossRef.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS.
- C. Sun, H. Li and L. Chen, Energy Environ. Sci., 2012, 5, 8475–8505 RSC.
- A. Trovarelli, Catal. Rev., 1996, 38, 439–520 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, Taylor & Francis, Boca Raton, FL, 95st edn, 2014, pp. 14–19 Search PubMed.
- J. Wisniak, Chem. Educator, 2000, 5, 343–350 CrossRef CAS.
- B. T. Kilbourn, Kirk-Othmer Encyclopedia of Chemical Technology, Wiley-Interscience, New York, 5th edn, 2004, vol. 5, pp. 670–692 Search PubMed.
- A. B. Goggs, J. Chem. Soc., 1928, 2667–2669 RSC.
- T. Takahashi, K. Ito and H. Iwahara, Denki Kagaku, 1966, 34, 205–209 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- R. W. G. Wyckoff, Crystal Structures, Wiley-Interscience, New York, 2nd edn, 1963, vol. I, pp. 239–244 Search PubMed.
- C. Cazorla and J. Boronat, Rev. Mod. Phys., 2017, 89, 035003 CrossRef.
- Y. Zhang and W. Yang, J. Chem. Phys., 1998, 109, 2604–2608 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089–10094 CrossRef CAS.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- M. M. Branda, R. M. Ferullo, M. Causà and F. Illas, J. Phys. Chem. C, 2011, 115, 3716–3721 CrossRef CAS.
- Y. Jiang, J. B. Adams and M. van Shilfgaarde, J. Chem. Phys., 2005, 123, 064701 CrossRef.
- C. Noguera, Surf. Rev. Lett., 2001, 8, 121–167 CrossRef CAS.
- J. C. Conesa, Surf. Sci., 1995, 339, 337–352 CrossRef CAS.
- I. Riess, H. Janczikowski and J. Nölting, J. Appl. Phys., 1987, 61, 4931–4933 CrossRef CAS.
- M. Hillert and B. Jansson, J. Am. Ceram. Soc., 1986, 69, 732–734 CrossRef CAS.
- H. L. Tuller and A. S. Nowick, J. Electrochem. Soc., 1979, 126, 209–217 CrossRef CAS.
- B. Bulfin, A. J. Lowe, K. A. Keogh, B. E. Murphy, O. Lübben, S. A. Krasnikov and I. V. Shvets, J. Phys. Chem. C, 2013, 117, 24129–24137 CrossRef CAS.
- R. G. Schwab, R. A. Steiner, G. Mages and H.-J. Beie, Thin Solid Films, 1992, 207, 288–293 CrossRef CAS.
- S. S. Mofarah, E. Adabifiroozjaei, Y. Yao, P. Koshy, S. Lim, R. Webster, X. Liu, R. K. Nekouei, C. Cazorla, Z. Liu, Y. Wang, N. Lambropoulos and C. C. Sorrell, Nat. Commun., 2019, 10, 2594 CrossRef.
- H. Okamoto, J. Phase Equil. Diff., 2008, 29, 545–547 CrossRef CAS.
- S. Andersson, B. Collén, U. Kuylenstierna and A. Magnéli, Acta Chem. Scand., 1957, 11, 1641–1652 CrossRef CAS.
- F. Wang, R. Shi, Y. Lei, Z. Lei, R. Jiang, D. Wang, Z. Liu and J. Sun, CrystEngComm, 2019, 21, 524–534 RSC.
- S. Harada, K. Tanaka and H. Inui, J. Appl. Phys., 2010, 108, 083703 CrossRef.
- A. F. Arif, R. Balgis, T. Ogi, F. Iskandar, A. Konoshita, K. Nakamura and K. Okuyama, Sci. Rep., 2017, 7, 3646 CrossRef.
- A. C. M. Padilha, H. Raebiger, A. R. Rocha and G. M. Dalpian, Sci. Rep., 2016, 6, 28871 CrossRef CAS.
- I. Slipukhina and M. Ležaić, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155133 CrossRef.
- M. N. Gordos, Tribol. Lett., 2000, 8, 65–78 CrossRef.
- J. E. Wertz, in Mass Transport in Oxides, ed. J. B. Wachtman Jr. and A. D. Franklin, National Bureau of Standards, Washington, D.C., 1968, pp. 11–23 Search PubMed.
- F. A. Kröger and H. J. Vink, in Solid State Physics, ed. F. Seitz and D. Turnbull, Elsevier, City, 1956, vol. 3, pp. 307–435 Search PubMed.
- A. Migani, G. N. Vayssilov, S. T. Bromley, F. Illas and K. M. Neyman, Chem. Commun., 2010, 46, 5936–5938 RSC.
- H.-F. Wang, H.-Y. Li, X.-Q. Gong, Y.-L. Guo, G.-Z. Lu and P. Hu, Phys. Chem. Chem. Phys., 2012, 14, 16521–16535 RSC.
- T. Close, G. Tulsyan, C. A. Diaz, S. J. Weinstein and C. Richter, Nat. Nanotechnol., 2015, 10, 418–422 CrossRef CAS.
- G. Bahmanrokh, C. Cazorla, S. S. Mofarah, R. Shahmiri, Y. Yao, I. Ismail, W.-F. Chen, P. Koshy and C. C. Sorrell, Nanoscale, 2020, 12, 4916–4934 RSC.
- V. Kumar, W.-F. Chen, X. Zhang, Y. Jiang, P. Koshy and C. C. Sorrell, Ceram. Int., 2019, 45, 22085–22094 CrossRef CAS.
- Z. Liu, W.-F. Chen, X. Zhang, J. Zhang, P. Koshy and C. C. Sorrell, J. Phys. Chem. C, 2019, 123, 11781–11790 CrossRef CAS.
- Y. Jiang, W.-F. Chen, P. Koshy and C. C. Sorrell, J. Mater. Sci., 2019, 54, 5266–5279 CrossRef CAS.
- D. Mittal, W.-F. Chen, P. Koshy, H.-K. Chen, I. Kabir, Y. Jiang, Z. Liu and C. C. Sorrell, SN Appl. Sci., 2019, 1, 234 CrossRef.
- Y. Cui, W.-F. Chen, A. Bastide, X. Zhang, P. Koshy and C. C. Sorrell, J. Phys. Chem. Solids, 2019, 126, 314–321 CrossRef CAS.
- W.-F. Chen, S. S. Mofarah, D. A. H. Hanaor, P. Koshy, H.-K. Chen, Y. Jiang and C. C. Sorrell, Inorg. Chem., 2018, 57, 7279–7289 CrossRef CAS.
- W.-F. Chen, H. Chen, P. Koshy, A. Nakaruk and C. C. Sorrell, Mater. Chem. Phys., 2018, 205, 334–346 CrossRef CAS.
- H. Ren, J. Wang, H. Ma, F. Cao, Y. Jiang, P. Koshy and C. C. Sorrell, New J. Chem., 2018, 42, 19685–19691 RSC.
- W.-F. Chen, P. Koshy, L. Adler and C. C. Sorrell, J. Austral. Ceram. Soc., 2017, 53, 569–576 CrossRef CAS.
- L. Chung, W.-F. Chen, P. Koshy and C. C. Sorrell, Mater. Chem. Phys., 2017, 197, 236–239 CrossRef CAS.
- W.-F. Chen, P. Koshy, Y. Huang, E. Adabifiroozjaei, Y. Yao and C. C. Sorrell, Int. J. Hydrogen Energy, 2016, 41, 19025–19056 CrossRef CAS.
- H. Ren, P. Koshy, F. Cao and C. C. Sorrell, Inorg. Chem., 2016, 55, 8071–8081 CrossRef CAS.
- W.-F. Chen, P. Koshy and C. C. Sorrell, Int. J. Hydrogen Energy, 2015, 40, 16215–16229 CrossRef CAS.
- L. R. Shah, B. Ali, H. Zhu, W. G. Wang, Y. Q. Song, H. W. Zhang, S. I. Shah and J. Q. Xiao, J. Phys.: Condens. Matter, 2009, 21, 486004 CrossRef.
- S. Aškrabić, Z. D. Dohčević-Mitrović, V. D. Araújo, G. Ionita, M. M. de Lima Jr. and A. Cantarero, J. Phys. D: Appl. Phys., 2013, 46, 495306 CrossRef.
- J.-M. Costantini, G. Lelong, M. Guillaumet, W. J. Weber, S. Takaki and K. Yasuda, J. Phys.: Condens. Matter, 2016, 28, 325001 CrossRef.
- S. Soni, S. Kumar, R. S. Meena, V. S. Vats and S. Dalela, AIP Conf. Proc., 2015, 1665, 130029 CrossRef.
- Q.-Y. Wen, H.-W. Zhang, Y.-Q. Song, Q.-H. Yang, H. Zhu and J. Q. Xiao, J. Phys.: Condens. Matter, 2007, 19, 246205 CrossRef.
- S.-Y. Chen, C.-H. Tsai, M.-Z. Huang, D.-C. Yan, T.-W. Huang, A. Gloter, C.-L. Chen, H.-J. Lin, C.-T. Chen and C.-L. Dong, J. Phys. Chem. C, 2012, 116, 8707–8713 CrossRef CAS.
- D. Channei, S. Phanichphant, A. Nakaruk, S. S. Mofarah, P. Koshy and C. C. Sorrell, Catalysts, 2017, 7, 45 CrossRef.
- E. Tani, M. Yoshimura and S. Sōmiya, J. Mater. Sci. Lett., 1982, 1, 461–462 CrossRef CAS.
- M. Hirano and E. Kato, J. Am. Ceram. Soc., 1996, 79, 777–780 CrossRef CAS.
- G.-S. Li, S.-H. Feng and L.-P. Li, J. Solid State Chem., 1996, 126, 74–79 CrossRef CAS.
- K. Zhou, Z. Yang and S. Yang, Chem. Mater., 2007, 19, 1215–1217 CrossRef CAS.
- X. Q. Fu, C. Wang, H. C. Yu, Y. G. Wang and T. H. Wang, Nanotechnology, 2007, 18, 145503 CrossRef.
- C. Tang, Y. Bando, B. Liu and D. Golberg, Adv. Mater., 2005, 17, 3005–3009 CrossRef CAS.
- N.-C. Wu, E.-W. Shi, Y.-Q. Zheng and W.-J. Li, J. Am. Ceram. Soc., 2002, 85, 2462–2468 CrossRef CAS.
- W. Wang, J. Y. Howe, Y. A. Li, X. F. Qiu, D. C. Joy, M. P. Paranthaman, M. J. Doktycz and B. H. Gu, J. Mater. Chem., 2010, 20, 7776–7781 RSC.
- Z. Yang, J. Wei, H. Yang, K. Liu, H. Liang and Y. Yang, Eur. J. Inorg. Chem., 2010, 3354–3359 CrossRef CAS.
- A. Vantomme, Z.-Y. Yuan, G. Du and B.-L. Su, Langmuir, 2005, 21, 1132–1135 CrossRef CAS.
- C. Sun, H. Li, Z. X. Wang, L. Chen and X. Huang, Chem. Lett., 2004, 33, 662–663 CrossRef CAS.
- C. Laberty-Robert, J. W. Long, E. M. Lucas, K. A. Pettigrew, R. M. Stroud, M. S. Doescher and D. R. Rolison, Chem. Mater., 2006, 18, 50–58 CrossRef CAS.
- Z. Ji, X. Wang, H. Zhang, S. Lin, H. Meng, B. Sun, S. George, T. Xia, A. E. Nel and J. I. Zink, ACS Nano, 2012, 6, 5366–5380 CrossRef CAS.
- C. Sun, H. Li, H. Zhang, Z. Wang and L. Chen, Nanotechnology, 2005, 16, 1454–1463 CrossRef CAS.
- L. Yan, X. Xing, R. Yu, J. Deng, J. Chen and G. Liu, Phys. B, 2007, 390, 59–64 CrossRef CAS.
- M. Hirano and M. Inagaki, J. Mater. Chem., 2000, 10, 473–477 RSC.
- H.-L. Lin, C.-Y. Wu and R.-K. Chiang, J. Colloid Interface Sci., 2010, 341, 12–17 CrossRef CAS.
- W.-Q. Han, L. Wu and Y. Zhu, J. Am. Chem. Soc., 2005, 127, 12814–12815 CrossRef CAS.
- H.-L. Lin, C.-Y. Wu and R.-K. Chiang, J. Colloid Interface Sci., 2010, 341, 12–17 CrossRef CAS.
- T. Yu, B. Lim and Y. Xia, Angew. Chem., Int. Ed., 2010, 122, 4586–4589 CrossRef ; Angew. Chem. Int. Ed., 2010, 49, 4484-4487.
- R. Yu, L. Yan, P. Zheng, J. Chen and X. Xing, J. Phys. Chem. C, 2008, 112, 19896–19900 CrossRef CAS.
- B. Tang, L. Zhuo, J. Ge, G. Wang, Z. Shi and J. Niu, Chem. Commun., 2005, 3565–3567 RSC.
- P. Wang and K. Kobiro, Pure Appl. Chem., 2014, 86, 785–800 CAS.
- Y. Zhang, T. Cheng, Q. Hu, Z. Fang and K. Han, J. Mater. Res., 2007, 22, 1472–1478 CrossRef CAS.
- W. Wang, J. Y. Howe, Y. Li, X. Qiu, D. C. Joy, M. P. Paranthaman, M. J. Doktycz and B. Gu, J. Mater. Chem., 2010, 20, 7776–7781 RSC.
- Anonymous, Solid – Liquid Equilibrium (SLE) and Vapour – Liquid Equilibrium (VLE) of Aqueous NaOH (M. Conde Engineering, Zurich, Switzerland, June 2014).
- A. Trovarelli and J. Llorca, ACS Catal., 2017, 7, 4716–4735 CrossRef CAS.
- H.-X. Mai, L.-D. Sun, Y.-W. Zhang, R. Si, W. Feng, H.-P. Zhang, H.-C. Liu and C.-H. Yan, J. Phys. Chem. B, 2005, 109, 24380–24385 CrossRef CAS.
- K. Zhou, X. Wang, X. M. Sun, Q. Peng and Y. Li, J. Catal., 2005, 229, 206–212 CrossRef CAS.
- N. Du, H. Zhang, B.-D. Chen, X.-Y. Ma and D.-R. Yang, J. Phys. Chem. C, 2007, 111, 12677–12680 CrossRef CAS.
- Z. Liu, X.-J. Li, M. Mayyas, P. Koshy, J. N. Hart and C. C. Sorrell, CrystEngComm, 2017, 19, 4766–4776 RSC.
- C. Pan, D. Zhang, L. Shi and J. Fang, Eur. J. Inorg. Chem., 2008, 2429–2436 CrossRef CAS.
- M. Nabavi, O. Spalla and B. Cabane, J. Colloid Interface Sci., 1993, 160, 459–471 CrossRef CAS.
- L. Agarwal, B. Lefferts, D. Mojet, E. D. Ligthart, D. Hensen, W. Mitchell, B. Erasmus, E. Anderson, J. Olivier, J. Neethling and A. Datye, ChemSusChem, 2013, 6, 1898–1906 CrossRef.
- T. S. Sakthivel, D. L. Reid, U. M. Bhatta, G. Möbus, D. C. Sayle and S. Seal, Nanoscale, 2015, 7, 5169–5177 RSC.
- Q. Yuan, H.-H. Duan, L.-L. Li, L.-D. Sun, Y.-W. Zhang and C.-H. Yan, J. Colloid Interface Sci., 2009, 335, 151–167 CrossRef CAS.
- S.-W. Yang and L. Gao, J. Am. Chem. Soc., 2006, 128, 9330–9331 CrossRef CAS.
- Y. Kamimura, M. Shimomura and A. Endo, J. Colloid Interface Sci., 2014, 436, 52–62 CrossRef CAS.
- M. Lin, Z. Y. Fu, H. R. Tan, J. P. Y. Tan, S. C. Ng and E. Teo, Cryst. Growth Des., 2012, 12, 3296–3303 CrossRef CAS.
- M. Lykaki, E. Pachatouridou, E. Iliopoulou, S. A. C. Carabineiro and M. Konsolakis, RSC Adv., 2017, 7, 6160–6169 RSC.
- X. Guo and R. Zhou, J. Power Sources, 2017, 361, 39–53 CrossRef CAS.
- J. Li, Z.-Y. Zhang, Z.-M. Tian, X.-M. Zhou, Z.-P. Zheng, Y.-Y. Ma and Y.-Q. Qu, J. Mater. Chem. A, 2014, 2, 16459–16466 RSC.
- Z.-L. Wu, M.-J. Li, J. Howe, H. M. Meyer and S. H. Overbury, Langmuir, 2010, 26, 16595–16606 CrossRef CAS.
- Y.-J. Liu, Z.-F. Li, H.-B. Xu and Y.-Y. Han, Catal. Commun., 2016, 76, 1–6 CrossRef CAS.
- U. M. Bhatta, D. Reid, T. Sakthivel, T. X. T. Sayle, D. Sayle, M. Molinari, S. C. Parker, I. M. Ross, S. Seal and G. Möbus, J. Phys. Chem. C, 2013, 117, 24561–24569 CrossRef CAS.
- C. Lei, A. Rockett and I. M. Robertson, J. Appl. Phys., 2006, 100, 073518 CrossRef.
- K. H. Hansen, T. Worren, S. Stempel, E. Lægsgaard, M. Bäumer, H.-J. Freund, F. Besenbacher and I. Stensgaard, Phys. Rev. Lett., 1999, 83, 4120–4123 CrossRef CAS.
- J. E. Prieto and I. Markov, Europhys. Lett., 2014, 108, 46007 CrossRef.
- X.-D. Feng, D. C. Sayle, Z.-L. Wang, M. S. Paras, B. Santora, A. C. Sutorik, T. X. T. Sayle, Y. Yang, Y. Ding, X.-D. Wang and Y.-S. Her, Science, 2006, 312, 1504–1508 CrossRef CAS.
- J. W. Mullin, Crystallization, Butterworth-Heinemann, London, 3rd edn, 1997, pp. 172–260 Search PubMed.
- Z. Ji, X. Wang, H. Zhang, S. Lin, H. Meng, B. Sun, S. George, T. Xia, A. E. Nel and J. I. Zink, ACS Nano, 2012, 6, 5366–5380 CrossRef CAS.
- D.-S. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. D. Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS.
- V. K. Ivanov, P. P. Fedorov, A. Y. Baranchikov and V. V. Osiko, Russ. Chem. Rev., 2014, 83, 1204–1222 CrossRef CAS.
- J. Zhang, F. Huang and Z. Lin, Nanoscale, 2010, 2, 18–34 RSC.
- S. Wang, L. Zhao, W. Wang, Y. Zhao, G. Zhang, X. Ma and J. Gong, Nanoscale, 2013, 5, 5582–5588 RSC.
- G. Spezzati, A. D. Benavidez, A. T. DeLaRiva, Y. Su, J. P. Hofmann, S. Asahina, E. J. Olivier, J. H. Neething, J. T. Miller, A. K. Datye and E. J. M. Hensen, Appl. Catal., B, 2019, 243, 36–46 CrossRef CAS.
- A. Röckert, J. Kullgren, P. Broqvist, S. Alwan and K. Hermansson, J. Chem. Phys., 2020, 152, 104709 CrossRef.
- M. Nolan, S. C. Parker and G. W. Watson, Surf. Sci., 2005, 595, 223–232 CrossRef CAS.
- Y. Pan, N. Nilius, C. Stiehler, H.-J. Freund, J. Goniakowski and C. Noguera, Interfaces, 2014, 1, 1400404 Search PubMed.
- J. Huang, Y. Yu, J. Zhu and R. Yu, Sci. China Mater., 2017, 60, 903–908 CrossRef CAS.
- Y. Lin, Z. Wu, J. Wen, K. Ding, X. Yang, K. R. Poeppelmeier and L. D. Marks, Nano Lett., 2015, 15, 5375–5381 CrossRef CAS.
- M. S. A. Asghar, B. J. Inkson and G. Möbus, J. Mater. Sci., 2020, 55, 2815–2825 CrossRef CAS.
- S. K. Kannan and M. Sundrarajan, Int. J. Nanosci., 2014, 13, 1450018 CrossRef CAS.
- R. Rao, M. Yang, Q. Ling, Q. Zhang, H. Liu, A. Zhang and W. Chen, Microporous Mesoporous Mater., 2013, 169, 81–87 CrossRef CAS.
- M. Zarinkamar, M. Farahmandjou and T. P. Firoozabadi, Ceram. Proc. Res., 2016, 17, 166–169 Search PubMed.
- R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. M. Rupp, Chem. Soc. Rev., 2020, 49, 554–592 RSC.
- C. Sun, H. Li and L. Chen, Energy Environ. Sci., 2012, 5, 8475–8505 RSC.
- A. Trovarelli, Catal. Rev., 1996, 38, 439–520 CrossRef CAS.
- Y. Lin, Z. Wu, J. Wen, K. R. Poeppelmeier and L. D. Marks, Nano Lett., 2013, 14, 191–196 CrossRef.
- W.-X. Tang and P.-X. Gao, MRS Commun., 2016, 6, 311–329 CrossRef CAS.
- L. Yan, R. Yu, J. Chen and X. Xing, Cryst. Growth Des., 2008, 8, 1474–1477 CrossRef CAS.
- B. Liu, M. Yao, B. Liu, Z. Li, R. Liu, Q. Li, D. Li, B. Zou, T. Cui and G. Zou, J. Phys. Chem. C, 2011, 115, 4546–4551 CrossRef CAS.
- D. Zhang, X. Du, L. Shi and R. Gao, Dalton Trans., 2012, 41, 14455–14475 RSC.
- S. A. Hayes, P. Yu, T. J. O’Keefe, M. J. O’Keefe and J. O. Stoffer, J. Electrochem. Soc., 2002, 149, 623–630 CrossRef.
- T. V. Plakhova, A. Y. Romanchuk, S. N. Yakunin, T. Dumas, S. Demir, S. Wang, S. G. Minasian, D. K. Shuh, T. Tyliszczak, A. A. Shiryaev, A. V. Egorov, V. K. Ivanov and S. N. Kalmykov, J. Phys. Chem. C, 2016, 120, 22615–22626 CrossRef CAS.
- P. Abellan, T. H. Moser, I. T. Lucas, J. W. Grate, J. E. Evans and N. D. Browning, RSC Adv., 2017, 7, 3831–3837 RSC.
- A. A. Ansari and A. Kaushik, J. Semicond., 2010, 31, 033001 CrossRef.
- S. Fränzle, B. Markert and S. Wünschmann, Introduction to Environmental Engineering, Wiley-VCH, Weinheim, Germany, 2012, pp. 212–225 Search PubMed.
- E. D. Verink, Jr., in Uhlig's Corrosion Handbook, ed. R. W. Revie, John Wiley, New York, 3rd edn, 2011, pp. 93–101 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh00654h |
| This journal is © The Royal Society of Chemistry 2021 |






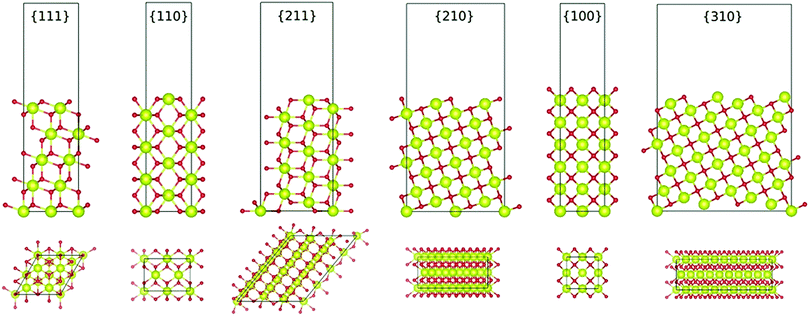
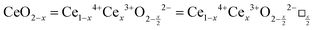
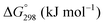
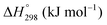
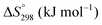
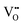
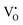
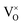
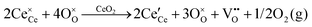
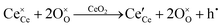
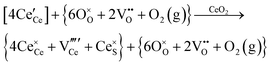
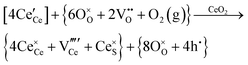
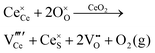
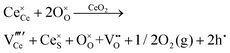
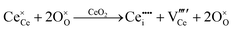
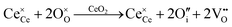

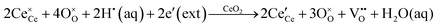
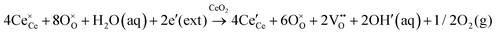

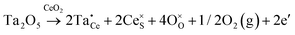
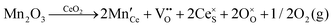
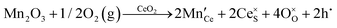
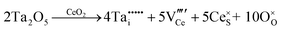
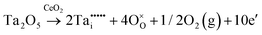
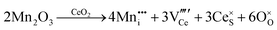
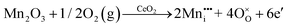
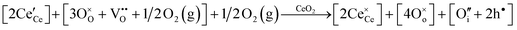



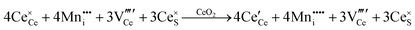
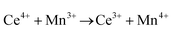
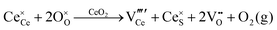
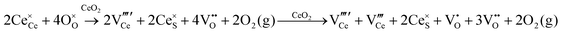
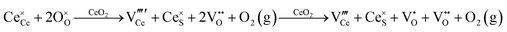
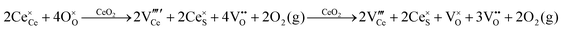
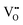
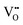
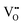
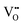
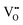
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: