Towards stable biologics: understanding co-excipient effects on hydrophobic interactions and solvent network integrity†
Jonathan W. P.
Zajac
 ae,
Praveen
Muralikrishnan
be,
Caryn L.
Heldt
ae,
Praveen
Muralikrishnan
be,
Caryn L.
Heldt
 c,
Sarah L.
Perry
c,
Sarah L.
Perry
 d and
Sapna
Sarupria
d and
Sapna
Sarupria
 *ae
*ae
aDepartment of Chemistry, University of Minnesota, Minneapolis, MN 55455, USA. E-mail: sarupria@umn.edu
bDepartment of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
cDepartment of Chemical Engineering, Michigan Technological University, Houghton, MI 49931, USA
dDepartment of Chemical Engineering, University of Massachusetts Amherst, MA 01003, USA
eChemical Theory Center, University of Minnesota, Minneapolis, MN 55455, USA
First published on 4th March 2025
Abstract
The formulation of biologics for increased shelf life stability is a complex task that depends on the chemical composition of both the active ingredient and any excipients in solution. A large number of unique excipients are typically required to stabilize biologics. However, it is not well-known how these excipient combinations influence biologics stability. To examine these formulations at the molecular level, we performed molecular dynamics simulations of arginine – a widely used excipient with unique properties – in solution both alone and with equimolar concentrations of lysine or glutamate. We studied the effects of these mixtures on a hydrophobic polymer model to isolate excipient mechanisms on hydrophobic interactions relevant in both protein folding and aggregation, crucial phenomena in biologics stability. We observed that arginine is the most effective single excipient in stabilizing hydrophobic polymer folding, and its effectiveness is augmented by lysine or glutamate addition. We decomposed the free energy of polymer folding/unfolding to identify that the key source of arginine–lysine and arginine–glutamate synergy is a reduction in destabilizing polymer–excipient interactions. We additionally applied principles from network theory to characterize the local solvent network embedding the hydrophobic polymer. Through this approach, we found arginine supports a more highly connected and stable local solvent network than in water, lysine, or glutamate solutions. These network properties are preserved when lysine or glutamate are added to arginine solutions. Taken together, our results highlight important molecular features in excipient solutions that establish the foundation for rational formulation design.
Design, System, ApplicationAddition of excipient molecules to biological formulations is an effective strategy for improving the shelf life of biologics. Multiple unique excipients are typically required for a single formulation, however, the combinatorial effects of these excipients are rarely understood. In this work, we utilize molecular dynamics simulations of a hydrophobic polymer to resolve the effects of binary excipient formulations on a key aspect of biologics stability–hydrophobic interactions. A better understanding of co-excipient effects on this fundamental aspect of stability will lead to more efficient excipient selection during the formulation design process, saving both time and cost. |
1 Introduction
Biologics are complex pharmaceutical products that often contain proteins.1,2 The physicochemical stability of proteins—relevant in the shelf life of biologics—involves physical stability related to protein unfolding and aggregation, as well as chemical stability (e.g., oxidation).3–15 The most common strategy to increase stability involves lowering the storage temperature16–20 and/or adding excipient molecules.21–27Excipients are typically small molecules such as amino acids or sugars. Excipient selection in the development of biologics is a high-throughput and empirical process.28–30 Excipients are deployed in combinations of four or more unique molecules, on average.27 This vast design space and a limited understanding of the combinatorial effects results in a time-consuming trial-and-error selection of compatible excipients, bottlenecking formulation development.31 By some estimates, the development of novel excipients takes a long time frame of ∼12 years, costing ∼$35m in that span.17,32,33 Understanding the molecular details of excipient mechanisms will aid in predicting optimal excipient selections for novel formulations, reducing both the time and cost associated with this stage of biologics production.
To gain molecular insights into excipient mechanisms, a reasonable strategy building toward predictive abilities would be to understand the effects of excipients on the key interactions (e.g., hydrophobic, electrostatic, hydrogen bonding, etc.) that govern protein stability. Decoupling and studying the effects of excipients on specific interactions is non-trivial in wet-lab experiments. On the other hand, molecular dynamics (MD) simulations provide an excellent avenue to achieve this. We use a hydrophobic polymer that serves as a model for protein folding/unfolding34–40 to probe the effect of excipients on hydrophobic interactions. Hydrophobic interactions are the driving and dominant interactions that govern protein folding and aggregation.6,41–48 Thus, studies of hydrophobic interactions provide critical insight into the underlying mechanisms driving excipient behavior. For example, the denaturant urea weakens hydrophobic interactions,35,38,49–54 while the stabilizing osmolyte trimethylamine N-oxide (TMAO) negligibly affects or strengthens these effects.55–61
As a starting point towards establishing excipient design rules, we turned our attention to a widely used excipient, arginine (Arg). Arg is a versatile excipient with a wide range of reported effects on protein stability. Arg is frequently used in protein and vaccine storage, purification techniques, and as an aggregation reducer.22,62–66 However, in some contexts, Arg has been found to denature proteins,67–69 accelerate aggregation,70–72 and inactivate viruses.40,73,74 In situations where Arg is denaturing, addition of charged co-excipients has been observed to reverse the denaturing properties of Arg.68 In a separate context where Arg was found to be stabilizing, synergy was observed between Arg and glutamate (Glu) in the solubilization of model proteins.75 Recently, we proposed that the multi-faceted effects of Arg arise from its positioning at the edge of a mechanistic flip between indirect- and direct-dominated mechanisms on hydrophobic interactions.40 Due to its placement at this edge, we aimed to understand whether subtle changes in formulation composition alters the stabilizing properties of Arg. To this end, we investigated hydrophobic polymer folding in solutions of lysine (Lys), Glu, and Arg, as well as equimolar formulations of Arg/Lys, Arg/Glu, and Lys/Glu. We discovered that adding Lys or Glu to Arg/water solutions enhances hydrophobic polymer stability, underscoring the importance of co-excipient selection in protein folding and stability.
2 Methods
2.1 System setup and molecular dynamics simulations
To probe the effects of Arg, Lys, Glu, and binary excipient mixtures on hydrophobic interactions, we performed MD simulations of a hydrophobic polymer in excipient solutions at various concentrations. Replica exchange umbrella sampling (REUS)76 simulations were utilized to calculate the potential of mean force (PMF) of hydrophobic polymer folding in different excipient solutions. The hydrophobic polymer was modeled as a linear coarse-grained chain with 26 monomers. Each monomer is represented as a bead with Lennard-Jones parameters σ = 0.373 nm and ε = 0.5856 kJ mol−1.55 The polymer–water ε parameter was modified to achieve an approximately even distribution of folded and unfolded polymer states in pure water.40 Box dimensions were defined such that 1.5 nm of space separated the fully elongated polymer from the nearest box edge. All systems were solvated with roughly 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TIP4P/2005 water molecules.77 The salt forms of all excipients (Arg+/Cl−, Lys+/Cl−, Glu−/Na+) under study were added to the simulation box until the desired concentration was reached (Table S1†). The CHARMM22 force field was used to describe excipient molecules and ions.78,79 With this protocol, we generated systems comprised of 0.25 M, 0.5 M, and 1.0 M Arg/water, Lys/water, Glu/water, Arg/Lys, Arg/Glu, and Lys/Glu. In binary excipient solutions, equimolar concentrations were used, with the total concentration kept constant.
000 TIP4P/2005 water molecules.77 The salt forms of all excipients (Arg+/Cl−, Lys+/Cl−, Glu−/Na+) under study were added to the simulation box until the desired concentration was reached (Table S1†). The CHARMM22 force field was used to describe excipient molecules and ions.78,79 With this protocol, we generated systems comprised of 0.25 M, 0.5 M, and 1.0 M Arg/water, Lys/water, Glu/water, Arg/Lys, Arg/Glu, and Lys/Glu. In binary excipient solutions, equimolar concentrations were used, with the total concentration kept constant.
All systems were energy minimized using the steepest descent algorithm. 1 ns NVT equilibration simulations were carried out at 300 K, followed by 1 ns NPT equilibration simulations at 300 K and 1 atm. During equilibration, temperature was controlled according to the V-rescale thermostat,80 while pressure was controlled via the Berendsen barostat.81 Following equilibration, NPT production runs were completed using the Nosé–Hoover thermostat (τT = 5 ps)82 and Parrinello–Rahman barostat (τP = 25 ps).83 Production runs were 20 ns long for excipient/water systems, and between 50–250 ns per window for excipient/polymer/water REUS simulations (Table S1†). Convergence was assessed by comparing PMFs as a function of simulation time and noting the point at which PMFs from three replicate simulations converged (Fig. S1†). The particle mesh Ewald (PME) algorithm was used for electrostatic interactions (cutoff = 1 nm). A reciprocal grid of 42 × 42 × 42 cells was used with 4th order B-spline interpolation. A single cutoff point of 1 nm was used for van der Waals interactions. The neighbor search was performed every 10 steps. Lorentz–Berthelot mixing rules84,85 were used to calculate nonbonded interactions between different atom types. All simulations were run in GROMACS 2021.4.86
2.2 Replica exchange umbrella sampling (REUS)
REUS76 simulations were performed to sample the hydrophobic polymer conformational landscape in excipient solutions. REUS simulations were done using GROMACS 2021.4 (ref. 86) with the PLUMED 2.8.0 (ref. 87 and 88) patch applied. The radius of gyration (Rg) of the hydrophobic polymer was used as a reaction coordinate, placing 12 umbrella potential centers evenly between Rg = 0.3 nm and Rg = 0.9 nm. A force constant of K = 5000 kJ mol−1 nm−2 was used in all windows, with the exception of the window centered at Rg = 0.45 nm, which used K = 1000 kJ mol−1 nm−2.40The potential of mean force (PMF) of polymer folding/unfolding was calculated as W(Rg) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(P(Rg)). Biased probability distributions were reweighted according to the weighted histogram analysis method (WHAM).89 The free energy of polymer unfolding (ΔGu) was calculated according to:
ln(P(Rg)). Biased probability distributions were reweighted according to the weighted histogram analysis method (WHAM).89 The free energy of polymer unfolding (ΔGu) was calculated according to:
 | (1) |
 . ΔGu reflects the difference in free energy of the unfolded state relative to the folded state (i.e., ΔGu = Gunfolded − Gfolded).
. ΔGu reflects the difference in free energy of the unfolded state relative to the folded state (i.e., ΔGu = Gunfolded − Gfolded).
We decomposed the PMF into individual components to further investigate the role of arginine in polymer folding. Following the methods outlined by several others,40,90–93 the PMF was separated into intrapolymer degrees of freedom in vacuum, Wvac, and a solvent contribution, Wsolv as:
| W(Rg) = Wvac(Rg) + Wsolv(Rg) | (2) |
| Wsolv(Rg) = Wcav(Rg) + Eps(Rg) | (3) |
| Eps(Rg) = Epw(Rg) + Epa(Rg) + Epc(Rg) | (4) |
2.3 Preferential interaction coefficients
Distribution of water and excipient molecules with respect to any solute can be quantified via the preferential interaction coefficient, ΓPA.100–102 This parameter is calculated in simulations using the two-domain formula:103–105 | (5) |
Wyman–Tanford theory relates any equilibrium process and preferential interaction as:106–108
 | (6) |
2.4 Arginine clustering
Several studies have identified the importance of Arg clustering in the multi-faceted effects of the excipient.74,112–118 As a free molecule, Arg forms self-associated clusters via three primary interactions: (i) backbone–backbone (COO−–NH3+), (ii) backbone–sidechain (Gdm+–COO−), and (iii) sidechain–sidechain (Gdm+–Gdm+). To quantify the extent of Arg cluster formation, we applied the following geometric criteria for the interactions defined above between pairs of molecules i and j, where i ≠ j: (i) at least one COO− oxygen from i within 2.0 Å of an NH3+ hydrogen from j, (ii) at least one COO− oxygen from i within 2.0 Å of a Gdm+ hydrogen from j, and (iii) at least one Gdm+ carbon from i within 4.0 Å of a Gdm+ carbon from j.For binary excipient solutions, criteria (i) and (ii) may be met via the sidechains of Glu and Lys, which introduce additional COO− and NH3+ groups into the system, respectively. Criterion (iii) may only be achieved via two interacting Arg molecules. For every excipient molecule i in solution, we iteratively searched over every other excipient molecule j. Molecules found to match the criteria outlined above were used to construct individual graphs, gi, with a central node positioned on molecule i and edges connecting i to all interacting residues j. NetworkX119 was used to merge any individual graphs with shared edges into clusters. The largest cluster size is reported as the maximum value of elements within any of the ci constructed clusters.
To characterize excipient clusters according to interaction types, we computed an interaction efficiency metric, η, according to:
| η = (nk/Nk) × 100 | (7) |
2.5 Network analysis
Several techniques from network theory were applied to quantify the solvent structure of the local polymer domain. Graphs, G(t), were constructed for a configuration at time t using NetworkX.119 Nodes were defined as any solvent molecule (which includes either water or excipient) center-of-mass within 0.7 nm of the hydrophobic polymer. An edge was constructed between nodes if a pair of heavy atoms i and j, belonging to solvent molecules I and J, were within 0.35 nm of each other. Network analysis was performed on configurations taken every 100 ps from the REUS trajectories.We used the Wasserman and Faust improved formula to calculate closeness centrality for all nodes in the graph:120,121
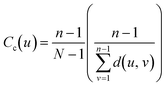 | (8) |
 | (9) |
We measured graph stability by computing a fragmentation threshold, f. In this approach, we began with all complete graphs G(t) for which the number of independent graphs was equal to 1. Iteratively, we randomly removed individual nodes and any associated edges from the graph. At each step, the number of disconnected graphs was computed, and the point at which this value changed from 1 to 2 was recorded as the fragmentation threshold. This point is equivalent to the critical point at which a lattice reaches catastrophic failure, resulting in its collapse.124 In practice, we report this value as the fraction of nodes removed, f = u/U, where u is the number removed and U is the total number of nodes in the graph. Because the fragmentation threshold will be sensitive to the sequence through which nodes are removed, we performed 100 iterations of our random node removal algorithm per configuration, and report the average value of f.
In addition to the stochastic node removal algorithm described above, we explored the effect of removing only nodes that are continuously connected to one another. For example, following removal of node s, the options for sequential node removal are only neighboring nodes t(s). We refer to this approach as continuously connected node removal, which can be thought of as identifying more optimal pathways for solvent network fragmentation.
2.6 Hydration shell dynamics
The rotational dynamics of water was measured by computing the characteristic reorientation time of the water dipole vector, μ.118,125,126 This dipole was taken as the vector connecting the oxygen atom and the center of the two hydrogen atoms of a water molecule. The time evolution of this vector was monitored by computing the time correlation function: | (10) |
Unbiased MD simulations were performed for water dynamics analyses. Configurations from the folded and unfolded ensemble obtained from the REUS simulations were clustered using HDBSCAN127 (Fig. S2 and S3†). Representative configurations corresponding to the highest cluster membership probability were then used to start the unbiased simulations. The unbiased simulations were performed for 300 ps in the NPT ensemble and configurations were stored every 0.1 ps.
3 Results and discussion
The goal of this study is to elucidate the mechanisms underpinning the stabilization of biological formulations by amino acids. To this end, we examined the effects of single excipient solutions of the amino acids Arg, Lys, Glu, and their binary mixtures on the stability of a model hydrophobic polymer.3.1 High concentrations of excipients favor folding of a hydrophobic polymer
The free energy of hydrophobic polymer unfolding in excipient solutions is reported in Fig. 1. At 0.25 M concentration, hydrophobic polymer folding is favored in Arg/water solutions (ΔGu > 0), while unfolding is favored in Lys/water and Glu/water solutions (ΔGu < 0). At 0.5 M and 1.0 M concentrations, Arg/water, Lys/water, and Glu/water solutions favor hydrophobic polymer folding. At all concentrations, Arg is the most effective single excipient in stabilizing the folded hydrophobic polymer state. Lys is the next most effective excipient, while Glu is the least effective.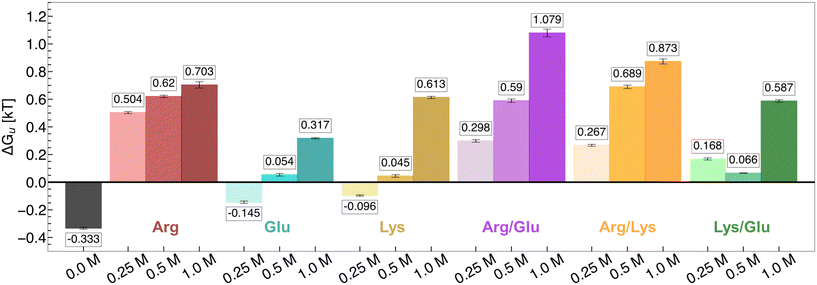 | ||
| Fig. 1 Free energy of hydrophobic polymer unfolding in Arg, Glu, Lys, Arg/Glu, Arg/Lys, and Lys/Glu solutions. Increasing excipient concentration is denoted by increased shading (light to dark; left to right). Mean values are reported from three replicate REUS simulations. Error bars were estimated via error propagation (see ESI† for details). | ||
Among binary excipient mixtures, both Arg/Glu and Arg/Lys stabilized the folded polymer state, with stability increasing with concentration (Fig. 1). Our results indicate that 1.0 M Arg/Lys and Arg/Glu mixtures are synergistic relative to their single excipient solutions, as the free energy of polymer unfolding in these solutions is less favorable than in any single excipient solution. In Lys/Glu mixtures, hydrophobic polymer folding is favored at 0.25 M, whereas the unfolded polymer is favored in Lys/water and Glu/water solutions at this concentration. Hence, we identify Lys/Glu mixtures to be synergistic at 0.25 M, although at higher concentrations this synergy is not observed.
3.2 Thermodynamic components of hydrophobic polymer folding in excipient solutions
To explore the thermodynamic origins of the excipient effects on hydrophobic polymer folding, we decomposed the PMF into components as discussed in eqn (4). Fig. 2 shows the change in each component upon unfolding in an excipient solution relative to that observed in water. The first Δ arises from the difference between folded and unfolded states (e.g., ΔE = 〈Eu〉 − 〈Ef〉), and the second Δ arises from the difference between the excipient solution (ΔEexc) and water (ΔEwat) (e.g., ΔΔE = ΔEexc − ΔEwat). In all cases, we found ΔΔGvac ≈ 0, as Wvac does not depend on the solvent. Additionally, the change in polymer–counterion interaction energy, ΔΔEc, was observed to be near 0 in all cases. Hence, these terms were omitted from Fig. 2 for clarity.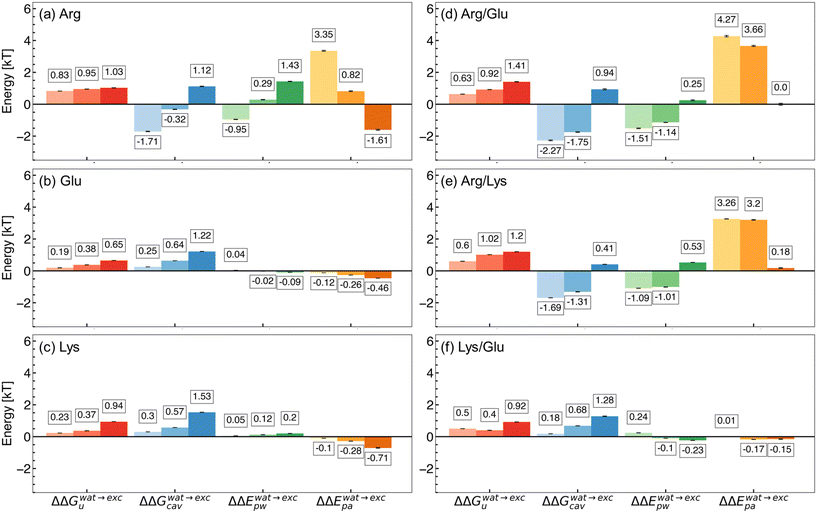 | ||
| Fig. 2 Contributions to the free energy of hydrophobic polymer unfolding in excipient solutions relative to water. (a) Arg/water, (b) Glu/water, (c) Lys/water, (d) Arg/Glu, (e) Arg/Lys, and (f) Lys/Glu solutions. Changes in free energy of unfolding (ΔΔΔGu), cavitation contribution (ΔΔGcav), polymer–water interactions (ΔΔEpw), and polymer–amino acid interactions (ΔΔEpa) are shown. Increasing additive concentration is denoted by increased shading (light to dark; left to right). Mean values are reported from three replicate REUS simulations. Error bars were estimated via error propagation (see ESI† for details). | ||
In Arg/water solutions and at low concentrations, direct polymer–Arg interactions favor folding, while at high concentrations, the cavity component and polymer–water interactions drive folded state stability.40 For Glu/water (Fig. 2b) and Lys/water (Fig. 2c) solutions, polymer folding is favored with increasing concentration. This is driven primarily by a favorable cavity component, while polymer–Glu and polymer–Lys interactions oppose folding. The polymer–water component is negligible in Lys/water and Glu/water solutions.
For binary mixtures, Arg/Glu (Fig. 2d) and Arg/Lys (Fig. 2e), direct polymer–amino acid interactions favor polymer folding at 0.25 M and 0.5 M, while at 1.0 M, this contribution is negligible. In contrast, the cavity component and polymer–water interactions favor polymer unfolding at 0.25 M and 0.5 M, while these components favor polymer folding at 1.0 M. In the case of Lys/Glu (Fig. 2f) solutions, stabilization of the folded polymer is almost fully determined by the cavity component. A monotonic increase in this component is observed with increasing Lys/Glu concentration, while polymer–water and polymer–amino acid interactions are negligible.
3.3 Excipient synergy is driven by changes in direct interactions
To quantify the extent of synergy (and non-ideality) in binary excipient mixtures, we computed the excess unfolding free energy (ΔGexcessu) as:| ΔGexcessu = ΔGmixu − ΔGidealu | (11) |
 | ||
| Fig. 3 Excipient synergy observed in 0.25 M, 0.50 M, and 1.0 M (a) Arg/Glu, (b) Arg/Lys, and (c) Lys/Glu solutions. Changes in overall free energy of unfolding (ΔGexcessu), direct interactions (ΔGexcessdir), and indirect interactions (ΔGexcessind) and polymer are shown. Increasing additive concentration is denoted by increased shading (light to dark; left to right). Mean values are reported from three replicate REUS simulations. Error bars were estimated via error propagation (see ESI† for details). | ||
In all binary excipient solutions, we observe favorable changes (ΔGexcessu > 0) in the free energy of polymer unfolding, relative to single excipient solutions. In Arg/Glu (Fig. 3a) and Arg/Lys (Fig. 3b) solutions, this increased folding state favorability is associated with a favorable change in direct polymer–amino acid interactions. At the same time, folded state stability is opposed by unfavorable indirect components, relative to in single excipient solutions. The same observations are made for Lys/Glu (Fig. 3c), albeit to a lesser extent. Interestingly, a different optimal concentration (with maximal ΔGexcessu) is observed for each pair of excipients – 1.0 M for Arg/Glu, 0.5 M for Arg/Lys, and 0.25 M for Lys/Glu.
The manifestation of the observed synergy describes a mechanism for improving the effectiveness of Arg-containing solutions. We observe that, while Arg is effective in stabilizing hydrophobic polymer folding, attractive polymer–Arg interactions drive unfolding at 1.0 M concentration. In the presence of Lys or Glu, this opposition to folding is eliminated. Hence, co-excipient addition is a suitable strategy to alter excipient effects on hydrophobic polymer folding.
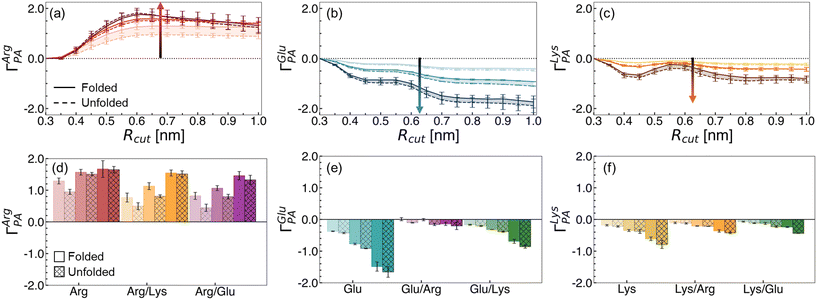
Co-excipient synergy results from a re-balancing of polymer–water–excipient interactions. This balance is captured by the preferential interaction coefficient, ΓPA. ΓPA > 0 indicates relative accumulation of an excipient (and a corresponding depletion of water) in the local polymer domain, while ΓPA < 0 indicates relative depletion (and corresponding preferential hydration). In Fig. 4, we report ΓPA for the excipient solutions in this study. We find Arg preferentially interacts with the hydrophobic polymer (Fig. 4a), while Glu (Fig. 4b) and Lys (Fig. 4c) are preferentially excluded. These trends increase with concentration.
We explored the change in excipient distribution by considering ΓPA of an excipient when in a single excipient versus binary excipient solution. In Fig. 4d–f, we show ensemble averaged ΓPA values using an Rcut value of 0.7 nm. This value is selected as a cutoff distance because, beyond this distance, no significant changes in ΓPA are observed for the excipients (Fig. S5†). From this perspective, the preferential accumulation of Arg near the polymer is reduced in Arg/Lys or Arg/Glu solutions, relative to in Arg/water solutions (Fig. 4d). We have previously highlighted that, at 1.0 M Arg concentration, direct polymer–Arg interactions drive unfolding.40 Hence, we hypothesize that a reduction in polymer–Arg interactions upon Lys or Glu incorporation in the solution results in net stabilization of the folded hydrophobic polymer.
Alongside the changes in Arg distribution, the relative accumulation of Lys or Glu is increased in Arg/Lys and Arg/Glu solutions, relative to in single excipient solutions (Fig. 4e and f). Overall, these findings imply a mutual recruitment of excipient A into the preferred domain of excipient B in binary excipient solutions.
The change in ΓPA observed in binary excipient solutions describes, in part, the effects observed in Fig. 3. In Arg/Glu and Arg/Lys solutions, there is a depletion in ΓArgPA relative to in Arg/water, resulting in a net reduction of polymer–amino acid interactions. Correspondingly, a favorable change in the direct component, ΔGexcessu, arises in Arg/Glu and Arg/Lys solutions, conferring increased stabilization of hydrophobic polymer folding.
3.4 Stabilizing co-excipients preserve the network effects of Arg
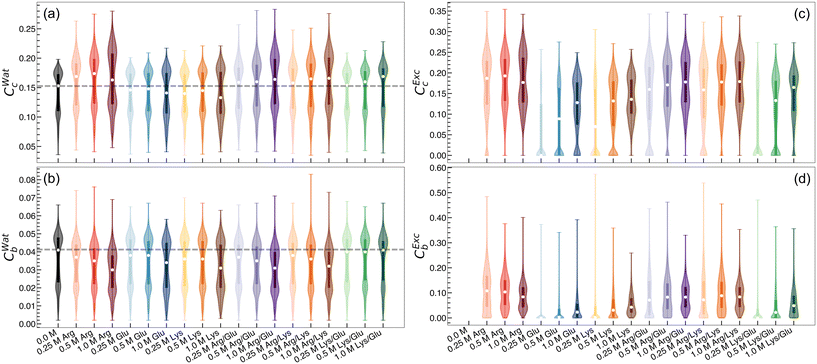
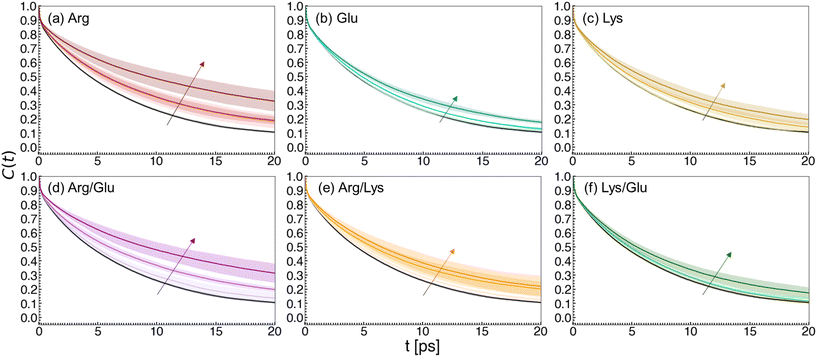
Networks of excipient–water interactions embedding the hydrophobic polymer were analyzed using principles of network theory. In this approach, we treat the center-of-mass of all excipient and water molecules within 0.7 nm of any polymer bead as nodes. A 0.7 nm cutoff was selected because, beyond this distance, the ratio of excipient to water molecules remained approximately constant. Edges are constructed between nodes where any pair of heavy atoms are located within 0.4 nm of one another (Fig. 5). To quantify the flow of molecular interactions within the solvent network, we measured closeness centrality,120,121Cc, and betweenness centrality,121–123Cb. Closeness centrality can be regarded as a measure of how long it takes to spread information from node u to all other nodes sequentially. Correspondingly, this quantity is a measure of how close a node is to the center of the network. Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes. In other words, this quantity measures the propensity for a node to act as a “hub” of information propagation. For both measurements, we resolve centrality from all water or excipient nodes.Distributions of centrality measurements obtained from folded state configurations are shown in Fig. 6. Distributions from unfolded configurations result in qualitatively similar trends to folded configurations (Fig. S5 and S6†), and hence were omitted from Fig. 6, for clarity. In Arg/water solutions, we observe an increase in water closeness centrality (CWatc) (Fig. 6a) and a decrease in water betweenness centrality (CWatb) (Fig. 6b). The increase in CWatc indicates shorter distances from water nodes to all other nodes – in other words, in Arg/water solutions, connectivity is increased among water molecules. This observation supports previous attempts to describe excipient effects via a network-based approach, which found that proteins in solution with stabilizing excipients have more compact interaction networks relative to those in the presence of denaturants.128
The decrease in CWatb suggests water molecules do not act as key transmitters within the local solvent network. Correspondingly, relatively high excipient betweenness (CExcb) distributions are observed for Arg/water solutions (Fig. 6d). This conveys that Arg molecules integrate well into the local polymer environment, acting as central hubs for information transfer in the local solvent structure. Elsewhere, it has been reported that stabilizing osmolytes have similarly high betweenness centrality values.129 Taken together, this indicates that having a well-connected local solvent environment promotes excipient-driven stability of biologics.
Network analysis reveals several key differences between Lys/water and Glu/water solutions relative to Arg/water solutions. In Lys/water and Glu/water, both CWatc and CWatb are found to decrease, or at least result in negligible changes relative to polymer–water systems. This suggests that water molecules become less connected within the local solvent environment network (Fig. 6a), while also becoming less essential hubs for information propagation (Fig. 6b). In contrast to Arg/water solutions, CExcc and CExcb are both relatively low, implying that Lys and Glu do not integrate into the local solvent environment as well as Arg (Fig. 6c and d). These results are consistent with our preferential interaction coefficient analysis, with the additional takeaway that connectivity among water molecules is reduced in Lys/water and Glu/water solutions.
Overall, we observe strongly connected networks in Arg/water solutions, and networks with poor connectivity in Lys/water and Glu/water solutions, relative to Arg solutions. In binary excipient solutions containing Arg (Arg/Lys and Arg/Glu), we observe an overall preservation of the strong connectivity identified in Arg solutions alone. Specifically, CWatc is found to increase in Arg/Lys and Arg/Glu solutions relative to polymer/water systems, reflecting increased connectivity among water molecules (Fig. 6a). Similar to Arg/water solutions, CWatb is observed to decrease with a concomitant increase in CExcb, reflecting favorable integration of excipient molecules into the local polymer environment in Arg/Lys and Arg/Glu solutions (Fig. 6b and d). Finally, CExcc is consistently higher in Arg/Lys and Arg/Glu solutions relative to Lys/water and Glu/water, marking an increase in local excipient connectivity in these binary excipient solutions (Fig. 6c). In general, the Lys/Glu binary excipient solution reflects network properties similar to Lys/water or Glu/water solutions.
We hypothesize that solutions with stronger connectivity in the solvent environment local to the hydrophobic polymer may confer greater stability to the network itself. To assess this, we compute a fragmentation metric, f, which measures the average number of nodes that must be removed from a fully-connected graph of the local solvent environment to form disconnected graphs. This metric corresponds to the point where it becomes impossible to transfer information throughout the entire local solvent environment. Our approach is inspired by percolation theory, and has been used elsewhere to measure the stability of large biomolecular assemblies, including viral capsids.130,131 To our knowledge, this is the first time such an approach has been used to measure the network stability of a local solvent environment.
To better quantify differences in fragmentation distributions, we computed the Earth mover's distance (EMD)132 as a measure of distribution dissimilarity, where higher EMD values indicate less overlap between two distributions. On average, local polymer environments are more resistant to fragmentation in Arg/water, Arg/Lys, and Arg/Glu solutions (Fig. 7a and S8a†), as indicated by increasing f distributions and relatively large EMD values. For all solutions, f values are higher in the local environments of folded polymer states, relative to unfolded polymer states (Fig. S8b†). However, this appears to be a general trend, as the differences between folded state and unfolded state graph stability do not depend on solution identity (Fig. 7b). We also observed qualitatively similar trends between stochastic node removal and continuously connected node removal (Fig. S8c†). Intuitively, we could consider the pathways that lead to fragmentation with the least number of nodes removed as the optimal pathways for local solvent network fragmentation. All f distributions are observed to decrease following continuously connected node removal, which indicates that continuous fragmentation results in faster disruption of the solvent network. We also noticed that the difference between folded and unfolded state f values (Δf = ffold − funfold) decreased when changing from stochastic to continuously connected node removal (ΔΔf = fcontinuous − fstochastic) (Fig. S8d†). For Glu, Lys, Arg/Glu, Arg/Lys, and Lys/Glu, this ΔΔf value increases with concentration, which we interpret as an indication that random node removal results in a fragmentation pathway further from the optimum in a given excipient solution. For these solutions, this deviation from optimal fragmentation increases with concentration. The inverse appears to be true for Arg—as more Arg is added, the difference between a randomly generated fragmentation pathway and the optimal fragmentation pathway becomes smaller. We may interpret this as Arg naturally forming more fragmentation–prone pathways within the local solvent network. Addition of Lys or Glu to Arg solutions, then, appears to reduce the probability of observing these fragmentation–prone configurations.
3.5 Explaining co-excipient synergy
Overall, we have uncovered that Arg/water solutions stabilize hydrophobic polymer folding to a greater extent than Lys/water, Glu/water, or Lys/Glu solutions. Addition of Lys or Glu to Arg/water solutions gives rise to synergistic effects, as the resulting Arg/Lys and Arg/Glu solutions are the most effective stabilizing solutions in this study. These synergies are associated with stabilizing indirect effects at high concentrations and a dramatic reduction in destabilizing direct interactions. Correspondingly, the solvent distribution, as characterized by preferential interaction coefficient analysis, reflects a reduction in Arg accumulation in the local hydrophobic polymer domain with addition of Lys or Glu.Network analysis implies that Arg integrates well into the local polymer environment, increases connectivity among water molecules, and increases the stability of the solvent network embedding the hydrophobic polymer. Importantly, these key network properties persist for Arg/water solutions to a greater extent than in Lys/water and Glu/water solutions. Moreover, the addition of Lys or Glu to Arg/water solution preserves the network properties of Arg/water alone, which may be a key aspect giving rise to the observed synergy among these excipients.
Based on these observations, we hypothesize that the addition of Lys or Glu to Arg/water solutions results in the formation of the same stable, highly connected local polymer environment as in solutions containing only Arg, while simultaneously reducing the penalty associated with direct polymer–Arg interactions. To better understand the unique roles played by Lys or Glu in this observed synergy, additional analyses were carried out.
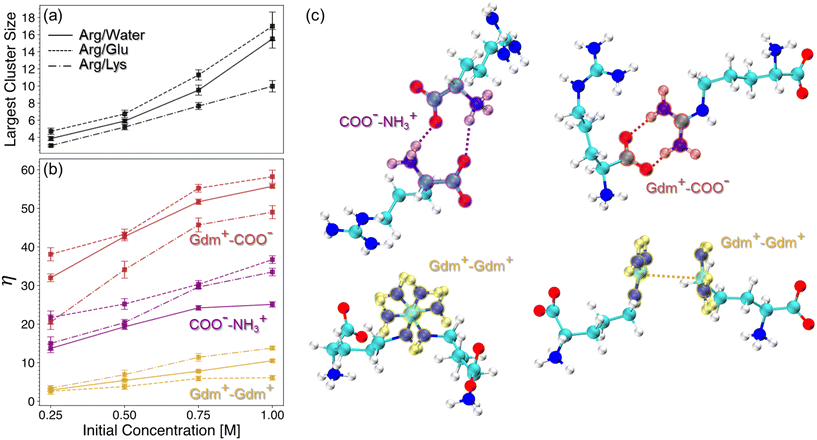
Overall, the extent of cluster formation, as measured by the average largest cluster size, is greater in Arg/water and Arg/Glu solutions than in Arg/Lys (Fig. 8a). We attribute this finding to favorable electrostatic interactions between Arg and Glu, as well as the unique properties of the Gdm+ sidechain of Arg that enable favorable like-charge interactions.114,133–136 The presence of cluster formation in all Arg-containing solutions is primarily driven by Gdm+–COO− interactions (Fig. 8b and c), a finding consistent with previous work detailing the importance of Arg “head-to-tail” stacking.114 Interestingly, while excipient clustering is reduced overall in Arg/Lys solutions relative to Arg/water, the extent of Gdm+–Gdm+ pairing among Arg molecules is increased.
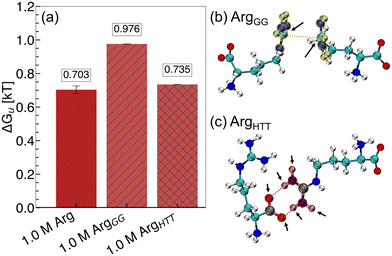
To probe the importance of these interactions relevant to excipient clustering, we performed two additional REUS simulations of hydrophobic polymer folding with modified Arg–Arg interaction parameters (Fig. 9). To simulate increased Gdm+–Gdm+ pairing among Arg molecules (ArgGG), we scaled the interaction strength between Gdm+ carbon atoms by 150% (Fig. 9b). Similarly, to simulate increased Gdm+–COO− head-to-tail pairing among Arg molecules (ArgHTT), the interaction strength between COO− oxygen atoms and Gdm+ hydrogen atoms was scaled by 150% (Fig. 9c). From these simulations, the free energy of polymer unfolding in ArgGG solution becomes significantly less favorable relative to unmodified Arg solutions, while ArgHTT results in only a small increase in folded state stability (Fig. 9a).
These results demonstrate the importance of the Gdm+ sidechain of Arg in hydrophobic polymer unfolding. Gdm+ is a known protein denaturant and has been shown to drive unfolding of an elongated hydrophobic polymer at high concentrations.91 We have shown previously that direct interactions between the Gdm+ sidechain of Arg and the hydrophobic polymer favors polymer folding at lower concentrations and are destabilizing at high concentrations.40 Overall, our mechanistic explanation for Arg/Lys synergy involves a Lys-mediated increase in Gdm+–Gdm+ “stickiness” among Arg molecules. Upon addition of Lys, the increase in Gdm+–Gdm+ pairing among Arg molecules gives rise to the favorable change in ΔΔEpa observed in Arg/Lys solutions. This is achieved by limiting the number of Gdm+ interaction sites available to interact with the polymer, resulting in a relative depletion of Arg from the local polymer domain.
We computed water reorientation dynamics in the local hydrophobic polymer domain for our excipient solutions (Fig. 10). The characteristic reorientation time for each solution was computed by fitting water dipole correlation functions to an exponential decay (Fig. S8†). With increasing excipient concentration, the reorientation time (τ) of local water molecules was observed to increase, indicating a slowing of water dynamics (Table 1). This effect is most pronounced in Arg/water and Arg/Glu solutions.
| Concentration (M) | Arg/water | Lys/water | Glu/water | Arg/Glu | Arg/Lys | Lys/Glu |
|---|---|---|---|---|---|---|
| 0.0 M | 6.54 (0.02) | — | — | — | — | — |
| 0.25 M | 8.52 (1.2) | 6.46 (0.1) | 6.49 (0.1) | 7.07 (0.5) | 7.24 (0.1) | 6.9 (0.1) |
| 0.5 M | 8.64 (0.4) | 7.85 (0.5) | 7.17 (0.1) | 8.86 (0.4) | 8.56 (1.4) | 7.17 (0.3) |
| 1.0 M | 12.6 (1.0) | 9.29 (1.4) | 8.4 (0.4) | 12.37 (0.8) | 8.81 (0.9) | 8.48 (0.6) |
Similar reductions in hydration shell dynamics have been associated with an increase in melting temperature of proteins. A recent study has proposed that stabilizing osmolytes slow down the dynamics of water, while denaturants accelerate water dynamics, inducing a pseudo-temperature change experienced by the protein.137 Other studies have highlighted that some stabilizing excipients increase hydrogen bond relaxation time among water molecules and reduce rotational, translational, and tumbling motions of water.126,138–142
We hypothesize that the key consequence associated with this phenomenon is the formation of a rigid solvent network embedding the hydrophobic polymer in Arg/water and Arg/Glu solutions. In the case of Arg/Glu, Glu may provide an advantage relative to Arg/water alone due to a reduction of Gdm+ sidechain accumulation in the local polymer domain, as reflected by ΓPA. This results in the favorable change in ΔΔEpa, similar to Arg/Lys, while retaining the reduced water dynamics and stable local network associated with Arg solutions.
4 Conclusions
Excipient incorporation is a time-consuming and costly endeavor in the development of stable biologics. Excipients with high sensitivity to the solution environment, such as arginine, cause an additional layer of complexity to this step. In some cases, addition of co-excipients to formulations that include Arg has resulted in reversals68 or synergistic75 effects. Recently, we demonstrated that the peculiar placement of Arg at the edge of a mechanistic flip between indirect- and direct-dominated effects on hydrophobic interactions may be a key feature that allows tuning of the effect of Arg on stability.40 Our findings here show that, not only is Arg a more effective stabilizer of hydrophobic interactions than its Lys or Glu counterparts, but the addition of these less effective excipients augments the effectiveness of Arg solution stability. For simplicity, we limited the scope of our solutions to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole fractions of excipients in our binary mixtures. However, we acknowledge that there may be a limited range of mole fractions where excipient effects arise or even improve. Investigating the effect of varying the mole fractions of the binary components would be an appropriate direction for future studies.
1 mole fractions of excipients in our binary mixtures. However, we acknowledge that there may be a limited range of mole fractions where excipient effects arise or even improve. Investigating the effect of varying the mole fractions of the binary components would be an appropriate direction for future studies.
We observed that the primary mechanism associated with Arg/Glu and Arg/Lys synergy is a substantial reduction in direct polymer–excipient interactions that oppose polymer folding at high Arg concentration. Through preferential interaction coefficient analysis, we further identified that Lys and Glu are both effective at reducing the relative accumulation of Arg molecules in the local polymer domain, providing a molecular explanation for the favorable change in ΔΔEpa.
Analysis of the solvent network embedding the hydrophobic polymer provides an explanation for how excipients alter the local solvent environment. We found that Arg increases connectivity among water molecules, integrates favorably into the local environment, and increases the stability of the network by delaying the onset of simulated graph fragmentation. These features are more pronounced in Arg solutions than in Lys, Glu, or Lys/Glu solutions. Importantly, we identified these same features in Arg/Lys and Arg/Glu solutions, indicating that stabilizing co-excipients preserve the network effects of Arg.
Finally, we established two hypotheses for Arg/Lys and Arg/Glu synergy. In the case of Arg/Lys, there is an increase in Gdm+–Gdm+ pairing among Arg molecules, reducing the number of available Gdm+ sidechains that drive polymer unfolding at high concentrations. From simulations of increased Gdm+–Gdm+ interaction strength between Arg molecules, we found this change to be sufficient for stabilizing polymer folding. In the case of Arg/Glu, we did not find increased Gdm+–COO− pairing in solution was sufficient to drive co-excipient synergy. However, we observed a reduction in the dynamics of water molecules local to the hydrophobic polymer in these solutions. Similar reductions in local water dynamics have been linked to increased melting temperature of proteins in the presence of stabilizing osmolytes.126,138–142
In this study, we demonstrated that changes in excipient composition alter hydrophobic interactions, the dominant force associated with several biologically-important processes including protein folding and self-assembly. As it pertains to formulations, this is an important factor in preventing protein denaturation and aggregation. Due to its placement on the edge of a mechanistic flip, formulations containing Arg as an excipient may be improved by shifting the balance of direct- and indirect-mediated effects. To this end, we increased the relative stability of hydrophobic polymer folding by reducing destabilizing direct effects via co-excipient addition of either Lys or Glu. Overall, these results highlight the investigation of molecular-level insights of excipient mechanisms as an important endeavor in the rational design of stable biologics. In future studies, the hydrophobic polymer model can be built upon by studying systems with added complexity such as polyelectrolytes, block copolymers, and miniproteins.
Data availability
Data for this article, including simulation parameter files and analysis scripts, are available at https://github.com/SAMPEL-Group/Hydrophobic-Polymer-Binary-Excipients.Author contributions
JWPZ: investigation – computational, validation, formal analysis, visualization, writing – original draft, writing – review and editing; PM: investigation – computational, validation, writing – review and editing; CLH: conceptualization, funding acquisition, resources, writing – review and editing; SLP: conceptualization, funding acquisition, resources, writing – review and editing; SS: conceptualization, methodology, validation, supervision, project administration, funding acquisition, resources, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the National Science Foundation under DMREF Grant No. 2118788, 2118693, and 2118638. Computational resources were provided by the Minnesota Supercomputing Institute at the University of Minnesota – Twin Cities.References
- M. A. Strassburg, Am. J. Infect. Control, 1982, 10, 53–59 CrossRef CAS PubMed.
- W.-W. Zhang, L. Li, D. Li, J. Liu, X. Li, W. Li, X. Xu, M. J. Zhang, L. A. Chandler, H. Lin, A. Hu, W. Xu and D. M.-K. Lam, Hum. Gene Ther., 2018, 29, 160–179 CrossRef CAS PubMed.
- P. L. Privalov, Crit. Rev. Biochem. Mol. Biol., 1990, 25, 281–306 CrossRef CAS PubMed.
- K. Heremans, Annu. Rev. Biophys. Bioeng., 1982, 11, 1–21 CrossRef CAS PubMed.
- S. Sarupria, T. Ghosh, A. E. García and S. Garde, Proteins: Struct., Funct., Bioinf., 2010, 78(7), 1641–1651 CrossRef CAS PubMed.
- W. Kauzmann, Advances in Protein Chemistry, Elsevier, 1959, vol. 14, pp. 1–63 Search PubMed.
- H. S. Frank and M. W. Evans, J. Chem. Phys., 1945, 13, 507–532 CrossRef CAS.
- L. K. Christensen, C. R. Trav. Lab. Carlsberg, Ser. Chim., 1952, 28, 37–69 CAS.
- G. Hummer, S. Garde, A. E. García, M. E. Paulaitis and L. R. Pratt, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1552–1555 CrossRef CAS PubMed.
- T. Ghosh, A. E. García and S. Garde, J. Am. Chem. Soc., 2001, 123, 10997–11003 CrossRef CAS PubMed.
- Y. Le Basle, P. Chennell, N. Tokhadze, A. Astier and V. Sautou, J. Pharm. Sci., 2020, 109, 169–190 CrossRef CAS PubMed.
- J.-R. Authelin, M. A. Rodrigues, S. Tchessalov, S. K. Singh, T. McCoy, S. Wang and E. Shalaev, J. Pharm. Sci., 2020, 109, 44–61 CrossRef CAS PubMed.
- D. J. A. Crommelin, A. Hawe and W. Jiskoot, Formulation of Biologics Including Biopharmaceutical Considerations, Springer International Publishing, Cham, 2024, pp. 95–117 Search PubMed.
- B. R. Clarkson, A. Schön and E. Freire, Drug Discovery Today, 2016, 21, 342–347 CrossRef CAS PubMed.
- A. Mazzeo and P. Carpenter, Handbook of Stability Testing in Pharmaceutical Development, Springer New York, New York, NY, 2009, pp. 353–369 Search PubMed.
- C. M. Hanson, A. M. George, A. Sawadogo and B. Schreiber, Vaccine, 2017, 35, 2127–2133 CrossRef PubMed.
- Y. B. Yu, K. T. Briggs, M. B. Taraban, R. G. Brinson and J. P. Marino, Pharm. Res., 2021, 38, 3–7 CrossRef CAS PubMed.
- D. J. Crommelin, T. J. Anchordoquy, D. B. Volkin, W. Jiskoot and E. Mastrobattista, J. Pharm. Sci., 2021, 110, 997–1001 CrossRef CAS PubMed.
- A. Thielmann, M.-T. Puth and B. Weltermann, PLoS One, 2019, 14, e0225764 CrossRef CAS PubMed.
- A. Thielmann, M.-T. Puth and B. Weltermann, Vaccine, 2020, 38, 7551–7557 CrossRef PubMed.
- T. J. Kamerzell, R. Esfandiary, S. B. Joshi, C. R. Middaugh and D. B. Volkin, Adv. Drug Delivery Rev., 2011, 63, 1118–1159 CrossRef CAS PubMed.
- T. Arakawa, K. Tsumoto, Y. Kita, B. Chang and D. Ejima, Amino Acids, 2007, 33, 587–605 CrossRef CAS PubMed.
- A. Bongioanni, M. S. Bueno, B. A. Mezzano, M. R. Longhi and C. Garnero, Int. J. Pharm., 2022, 613, 121375 CrossRef CAS PubMed.
- S. H. Jeong, Arch. Pharmacal Res., 2012, 35, 1871–1886 CrossRef CAS PubMed.
- W. Wang, Int. J. Pharm., 2005, 289, 1–30 CrossRef CAS PubMed.
- S. Y. Patro, E. Freund and B. S. Chang, Biotechnology Annual Review, Elsevier, 2002, vol. 8, pp. 55–84 Search PubMed.
- Y. Ionova and L. Wilson, PLoS One, 2020, 15, e0235076 CrossRef CAS PubMed.
- M. A. Capelle, R. Gurny and T. Arvinte, Eur. J. Pharm. Biopharm., 2007, 65, 131–148 CrossRef CAS PubMed.
- M. Zidar, G. Posnjak, I. Muševič, M. Ravnik and D. Kuzman, Pharm. Res., 2020, 37, 27 CrossRef CAS PubMed.
- S. J. Shire, Curr. Opin. Biotechnol., 2009, 20, 708–714 CrossRef CAS PubMed.
- V. S. Dave, S. D. Saoji, N. A. Raut and R. V. Haware, J. Pharm. Sci., 2015, 104, 906–915 CrossRef CAS PubMed.
- Y. B. Yu, M. B. Taraban, K. T. Briggs, R. G. Brinson and J. P. Marino, Pharm. Res., 2021, 38, 2179–2184 CrossRef CAS PubMed.
- D. P. Elder, M. Kuentz and R. Holm, Eur. J. Pharm. Sci., 2016, 87, 88–99 CrossRef CAS PubMed.
- P. R. ten Wolde and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6539–6543 CrossRef CAS PubMed.
- R. Zangi, R. Zhou and B. J. Berne, J. Am. Chem. Soc., 2009, 131, 1535–1541 CrossRef CAS PubMed.
- D. Nayar and N. F. A. van der Vegt, J. Phys. Chem. B, 2018, 122, 3587–3595 CrossRef CAS PubMed.
- J. Mondal, G. Stirnemann and B. J. Berne, J. Phys. Chem. B, 2013, 117, 8723–8732 CrossRef CAS PubMed.
- M. V. Athawale, S. Sarupria and S. Garde, J. Phys. Chem. B, 2008, 112, 5661–5670 CrossRef CAS PubMed.
- S. N. Jamadagni, R. Godawat and S. Garde, Langmuir, 2009, 25, 13092–13099 CrossRef CAS PubMed.
- J. W. P. Zajac, P. Muralikrishnan, I. Tohidian, X. Zeng, C. L. Heldt, S. L. Perry and S. Sarupria, arXiv, 2024, preprint, arXiv:2403.11305 [cond-mat], DOI:10.48550/arXiv.2403.11305.
- C. Tanford, J. Am. Chem. Soc., 1962, 84, 4240–4247 CrossRef CAS.
- C. Tanford, Science, 1978, 200, 1012–1018 CrossRef CAS PubMed.
- K. A. Dill, Biochemistry, 1990, 29, 7133–7155 CrossRef CAS PubMed.
- H. J. Savage, C. J. Elliott, C. M. Freeman and J. L. Finney, J. Chem. Soc., Faraday Trans., 1993, 89, 2609 RSC.
- G. Hummer, S. Garde, A. Garcia and L. Pratt, Chem. Phys., 2000, 258, 349–370 CrossRef CAS.
- L. R. Pratt and A. Pohorille, Chem. Rev., 2002, 102, 2671–2692 CrossRef CAS PubMed.
- A. Ben-Naim, Hydrophobic interactions, Plenum Press, New York, 2005 Search PubMed.
- D. Chandler, Nature, 2005, 437, 640–647 CrossRef CAS PubMed.
- A. Wallqvist, D. G. Covell and D. Thirumalai, J. Am. Chem. Soc., 1998, 120, 427–428 CrossRef CAS.
- M. Ikeguchi, S. Nakamura and K. Shimizu, J. Am. Chem. Soc., 2001, 123, 677–682 CrossRef CAS PubMed.
- T. Ghosh, A. Kalra and S. Garde, J. Phys. Chem. B, 2005, 109, 642–651 CrossRef CAS PubMed.
- N. F. A. Van Der Vegt, M.-E. Lee, D. Trzesniak and W. F. Van Gunsteren, J. Phys. Chem. B, 2006, 110, 12852–12855 CrossRef CAS PubMed.
- M.-E. Lee and N. F. A. Van Der Vegt, J. Am. Chem. Soc., 2006, 128, 4948–4949 CrossRef CAS PubMed.
- T. A. Shpiruk and M. Khajehpour, Phys. Chem. Chem. Phys., 2013, 15, 213–222 RSC.
- M. V. Athawale, J. S. Dordick and S. Garde, Biophys. J., 2005, 89, 858–866 CrossRef CAS PubMed.
- S. Paul and G. N. Patey, J. Phys. Chem. B, 2008, 112, 11106–11111 CrossRef CAS PubMed.
- R. D. Macdonald and M. Khajehpour, Biophys. Chem., 2013, 184, 101–107 CrossRef CAS PubMed.
- P. Ganguly, N. F. A. Van Der Vegt and J.-E. Shea, J. Phys. Chem. Lett., 2016, 7, 3052–3059 CrossRef CAS PubMed.
- Z. Su, G. Ravindhran and C. L. Dias, J. Phys. Chem. B, 2018, 122, 5557–5566 CrossRef CAS PubMed.
- A. Folberth, S. Bharadwaj and N. F. A. Van Der Vegt, Phys. Chem. Chem. Phys., 2022, 24, 2080–2087 RSC.
- P. Ganguly, D. Bubák, J. Polák, P. Fagan, M. Dračínská, N. F. A. Van Der Vegt, J. Heyda and J.-E. Shea, J. Phys. Chem. Lett., 2022, 13, 7980–7986 CrossRef CAS PubMed.
- K. Tsumoto, M. Umetsu, I. Kumagai, D. Ejima, J. Philo and T. Arakawa, Biotechnol. Prog., 2004, 20, 1301–1308 CrossRef CAS PubMed.
- K. Tsumoto, D. Ejima, Y. Kita and T. Arakawa, Protein Pept. Lett., 2005, 12, 613–619 CrossRef CAS PubMed.
- P. Stärtzel, J. Pharm. Sci., 2018, 107, 960–967 CrossRef PubMed.
- J. Hamborsky, A. Kroger and C. Wolfe, Epidemiology and prevention of vaccine-preventable diseases, Centers for Disease Control and Prevention, Atlanta, GA, 13th edn, 2015 Search PubMed.
- M. J. Mistilis, J. C. Joyce, E. S. Esser, I. Skountzou, R. W. Compans, A. S. Bommarius and M. R. Prausnitz, Drug Delivery Transl. Res., 2017, 7, 195–205 CrossRef CAS PubMed.
- Q. Xie, T. Guo, J. Lu and H.-M. Zhou, Int. J. Biochem. Cell Biol., 2004, 36, 296–306 CrossRef CAS PubMed.
- B. Anumalla and N. P. Prabhu, Appl. Biochem. Biotechnol., 2019, 189, 541–555 CrossRef CAS PubMed.
- T. Arakawa and N. K. Maluf, Int. J. Biol. Macromol., 2018, 107, 1692–1696 CrossRef CAS PubMed.
- E. Smirnova, I. Safenkova, B. Stein-Margolina, V. Shubin and B. Gurvits, Amino Acids, 2013, 45, 845–855 CrossRef CAS PubMed.
- D. Shah, A. R. Shaikh, X. Peng and R. Rajagopalan, Biotechnol. Prog., 2011, 27, 513–520 CrossRef CAS PubMed.
- T. B. Eronina, N. A. Chebotareva, N. N. Sluchanko, V. V. Mikhaylova, V. F. Makeeva, S. G. Roman, S. Y. Kleymenov and B. I. Kurganov, Int. J. Biol. Macromol., 2014, 68, 225–232 CrossRef CAS PubMed.
- C. Meingast and C. L. Heldt, Biotechnol. Prog., 2020, 36, e2931 CrossRef CAS PubMed.
- C. L. Meingast, P. U. Joshi, D. G. Turpeinen, X. Xu, M. Holstein, H. Feroz, S. Ranjan, S. Ghose, Z. J. Li and C. L. Heldt, Biotechnol. J., 2021, 16, 2000342 CrossRef CAS PubMed.
- D. Shukla and B. L. Trout, J. Phys. Chem. B, 2011, 115, 11831–11839 CrossRef CAS PubMed.
- Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, year CrossRef.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. Berendsen, J. P. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, Compt. Rendus, 1898, 126, 1703–1855 Search PubMed.
- E. Lindahl, M. J. Abraham, B. Hess and D. van der Spoel, Gromacs 2021.4 source code, 2021, https://zenodo.org/record/5636567 Search PubMed.
- T. P. Consortium, Nat. Methods, 2019, 16, 670–673 CrossRef PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- F. Zhu and G. Hummer, J. Comput. Chem., 2011, 33, 453–465 CrossRef PubMed.
- M. V. Athawale, G. Goel, T. Ghosh, T. M. Truskett and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 733–738 CrossRef CAS PubMed.
- R. Godawat, S. N. Jamadagni and S. Garde, J. Phys. Chem. B, 2010, 114, 2246–2254 CrossRef CAS PubMed.
- N. F. A. van der Vegt and D. Nayar, J. Phys. Chem. B, 2017, 121, 9986–9998 CrossRef CAS PubMed.
- S. Dasetty and S. Sarupria, J. Phys. Chem. B, 2021, 125, 2644–2657 CrossRef CAS PubMed.
- L. R. Pratt and D. Chandler, J. Chem. Phys., 1977, 67, 3683–3704 CrossRef CAS.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- P. R. T. Wolde, J. Phys.: Condens. Matter, 2002, 14, 9445–9460 CrossRef.
- D. M. Huang and D. Chandler, J. Phys. Chem. B, 2002, 106, 2047–2053 CrossRef CAS.
- S. Garde, A. E. Garcia, L. R. Pratt and G. Hummer, Biophys. Chem., 1999, 78, 21–32 CrossRef CAS PubMed.
- D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638 CrossRef CAS PubMed.
- G. Scatchard, J. Am. Chem. Soc., 1946, 68, 2315–2319 CrossRef CAS PubMed.
- E. F. Casassa and H. Eisenberg, Adv. Protein Chem., 1964, 19, 287–395 CrossRef CAS PubMed.
- J. A. Schellman, Biopolymers, 1987, 26, 549–559 CrossRef CAS PubMed.
- H. Inoue and S. N. Timasheff, Biopolymers, 1972, 11, 737–743 CrossRef CAS PubMed.
- M. Record and C. Anderson, Biophys. J., 1995, 68, 786–794 CrossRef CAS PubMed.
- D. Shukla, C. Shinde and B. L. Trout, J. Phys. Chem. B, 2009, 113, 12546–12554 CrossRef CAS PubMed.
- J. Wyman, Advances in Protein Chemistry, Elsevier, 1964, vol. 19, pp. 223–286 Search PubMed.
- S. N. Timasheff, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 9721–9726 CrossRef CAS PubMed.
- D. Shukla, C. P. Schneider and B. L. Trout, Adv. Drug Delivery Rev., 2011, 63, 1074–1085 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- J. Mondal, D. Halverson, I. T. S. Li, G. Stirnemann, G. C. Walker and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9270–9275 CrossRef CAS PubMed.
- M. Mukherjee and J. Mondal, J. Phys. Chem. B, 2020, 124, 6565–6574 CrossRef CAS PubMed.
- U. Das, G. Hariprasad, A. S. Ethayathulla, P. Manral, T. K. Das, S. Pasha, A. Mann, M. Ganguli, A. K. Verma, R. Bhat, S. K. Chandrayan, S. Ahmed, S. Sharma, P. Kaur, T. P. Singh and A. Srinivasan, PLoS One, 2007, 2, e1176 CrossRef PubMed.
- C. P. Schneider and B. L. Trout, J. Phys. Chem. B, 2009, 113, 2050–2058 CrossRef CAS PubMed.
- D. Shukla and B. L. Trout, J. Phys. Chem. B, 2010, 114, 13426–13438 CrossRef CAS PubMed.
- C. P. Schneider, D. Shukla and B. L. Trout, J. Phys. Chem. B, 2011, 115, 7447–7458 CrossRef CAS PubMed.
- V. Vagenende, A. X. Han, M. Mueller and B. L. Trout, ACS Chem. Biol., 2013, 8, 416–422 CrossRef CAS PubMed.
- S. Santra, S. Dhurua and M. Jana, J. Chem. Phys., 2021, 154, 084901 CrossRef CAS PubMed.
- S. Santra and M. Jana, J. Phys. Chem. B, 2022, 126, 1462–1476 CrossRef CAS PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, Exploring network structure, dynamics, and function using NetworkX, in Proceedings of the 7th Python in Science Conference (SciPy2008), 2008, pp. 11–15 Search PubMed.
- S. Wasserman and K. Faust, Social Network Analysis: Methods and Applications, Cambridge University Press, 1st edn, 1994 Search PubMed.
- L. C. Freeman, Soc. Netw., 1978, 1, 215–239 CrossRef.
- U. Brandes, J. Math. Sociol., 2001, 25, 163–177 CrossRef.
- U. Brandes, Soc. Netw., 2008, 30, 136–145 CrossRef.
- K. Schrenk, M. Hilário, V. Sidoravicius, N. Araújo, H. Herrmann, M. Thielmann and A. Teixeira, Phys. Rev. Lett., 2016, 116, 055701 CrossRef CAS PubMed.
- H. Liu, S. Xiang, H. Zhu and L. Li, Molecules, 2021, 26, 5403 CrossRef CAS PubMed.
- A. Diaz and V. Ramakrishnan, Comput. Biol. Chem., 2023, 105, 107883 CrossRef CAS PubMed.
- L. McInnes, J. Healy and S. Astels, J. Open Source Softw., 2017, 2, 205 CrossRef.
- M. Miotto, N. Warner, G. Ruocco, G. G. Tartaglia, O. A. Scherman and E. Milanetti, arXiv, 2023, preprint, arXiv:2305.05038v1 [q-bio.BM], DOI:10.48550/arXiv.2305.05038.
- S. Sundar, A. A. Sandilya and M. H. Priya, J. Chem. Inf. Model., 2021, 61, 3927–3944 CrossRef CAS PubMed.
- N. E. Brunk, L. S. Lee, J. A. Glazier, W. Butske and A. Zlotnick, Phys. Biol., 2018, 15, 056005 CrossRef PubMed.
- N. E. Brunk and R. Twarock, ACS Nano, 2021, 15, 12988–12995 CrossRef CAS PubMed.
- Y. Rubner and C. Tomasi, The Earth Mover's Distance, Springer US, Boston, MA, 2001, pp. 13–28 Search PubMed.
- P. Gund, J. Chem. Educ., 1972, 49, 100 CrossRef CAS.
- P. E. Mason, G. W. Neilson, C. E. Dempsey, A. C. Barnes and J. M. Cruickshank, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 4557–4561 CrossRef CAS PubMed.
- O. Shih, A. H. England, G. C. Dallinger, J. W. Smith, K. C. Duffey, R. C. Cohen, D. Prendergast and R. J. Saykally, J. Chem. Phys., 2013, 139, 035104 CrossRef PubMed.
- M. Vazdar, J. Heyda, P. E. Mason, G. Tesei, C. Allolio, M. Lund and P. Jungwirth, Acc. Chem. Res., 2018, 51, 1455–1464 CrossRef CAS PubMed.
- M. Hishida, R. Anjum, T. Anada, D. Murakami and M. Tanaka, J. Phys. Chem. B, 2022, 126, 2466–2475 CrossRef CAS PubMed.
- G. S. Jas, E. C. Rentchler, A. M. Słowicka, J. R. Hermansen, C. K. Johnson, C. R. Middaugh and K. Kuczera, J. Phys. Chem. B, 2016, 120, 3089–3099 CrossRef CAS PubMed.
- G. Saladino, M. Marenchino, S. Pieraccini, R. Campos-Olivas, M. Sironi and F. L. Gervasio, J. Chem. Theory Comput., 2011, 7, 3846–3852 CrossRef CAS PubMed.
- I. Jahan and S. M. Nayeem, RSC Adv., 2020, 10, 27598–27614 RSC.
- J. Zeman, C. Holm and J. Smiatek, J. Chem. Eng. Data, 2020, 65, 1197–1210 CrossRef CAS.
- R. Gazi, S. Maity and M. Jana, ACS Omega, 2023, 8, 2832–2843 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation details, error estimations, and additional analysis. See DOI: https://doi.org/10.1039/d4me00201f |
| This journal is © The Royal Society of Chemistry 2025 |