Open Access Article
Open Access ArticleProbing the charged state of layered positive electrodes in sodium-ion batteries: reaction pathways, stability and opportunities
Jennifer H.
Stansby
 ab,
Neeraj
Sharma
ab,
Neeraj
Sharma
 a and
Damian
Goonetilleke
a and
Damian
Goonetilleke
 *c
*c
aSchool of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia
bAustralian Nuclear Science and Technology Organisation, Locked Bag 2001, Kirrawee DC, NSW 2232, Australia
cBattery and Electrochemistry Laboratory, Institute of Nanotechnology, Karlsruhe Institute for Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: damian.goonetilleke@kit.edu
First published on 19th November 2020
Abstract
Sodium-ion batteries have received significant interest as a cheaper alternative to lithium-ion batteries and could be more viable for use in large scale energy storage systems. However, similarly to lithium-ion batteries, their performance remains limited by the positive electrode materials. Layered transition metal oxides, with chemical formula NaxMO2, have been extensively investigated and appear to show the most promise. However, the inability to reversibly extract large amounts of sodium ions from these layered structures, by charging to high voltages, has limited the useful capacity and cycle life of these materials. To address this, numerous studies have attempted to resolve the structural and chemical changes that take place in positive electrode materials upon cycling. This is particularly important at and near the charged state, which is where the materials' structures are highly sodium deficient. Following a brief introduction into the status of sodium-ion battery positive electrodes, this work focuses on the development of knowledge and understanding into the structure of layered oxides at the charged state by highlighting cutting edge characterisation techniques that have been utilised. Finally, a perspective on future development is provided to direct further structural characterisation research which will enable the rational design of new and improved energy storage materials.
1. Introduction and nomenclature
Commercialisation of the lithium-ion battery has revolutionised the world. These batteries offer high energy density and reliable cycling performance which has enabled the development of a variety of portable electronic devices which are critical for the functioning of modern society. Further advances in battery technology have the potential to help address the global energy crisis and mitigate climate change.1 To achieve a sustainable yet high quality of life, our consumption of fossil fuels must be replaced by energy from renewable sources such as solar, wind and waves. Due to the scarcity of resources used to produce lithium-ion batteries, coupled with growing demand for their utilisation in electric vehicles, alternative battery technologies are required for large scale energy storage applications.2–4When considering large scale stationary energy storage, emphasis is placed on cost, accessibility and abundance of resources, in addition to the battery lifetime and hence electrode-level structural stability.5–7 As such, sodium-ion batteries, which can behave similarly to lithium-ion batteries, are a promising candidate.8 Sodium is uniformly distributed across the earth and is the fourth most abundant element, which presents an opportunity to significantly reduce the cost of positive electrode materials. Layered oxides, Prussian blue analogues and polyanionic materials have been prominently reported as potential positive electrodes for sodium-ion batteries.9–11 Due to their high specific capacity and in many cases facile synthesis, layered oxides (NaMO2, M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Li, and a mixture of multiple of these elements) are currently dominating the field of research.12,13 Through incorporation of multiple elements (electrochemically active and/or electrochemically inactive) on the M site significant improvements to the structural stability and hence reversible capacity have been made. Additionally, the voltage cut off and/or capacity limit can be tuned to minimise undesirable structural changes during cycling; the potential and capacity limit will likely be the same when charging at a slower current rate, whereas at higher current rates the voltage cut off is likely to be accessed before reaching the capacity limit yielding a lower capacity. This capacity in turn effects the amount of Na reversibly extracted upon charging and thus the charge compensation mechanism. Therefore, it is important to report the voltage, capacity, and current rate alongside structural data.14
The structure of layered oxides consists of repeating sheets of edge-sharing MO6 octahedra, which can (de-)intercalate alkali metal ions in between these layers. Differences in the relative orientation of adjacent metal oxide layers and hence stacking order gives rise to several unique crystal structures, for example, P2 (…ABBA…), O2 (…ABAC…), O3 (…ABCABC…) and P3 (…ABBCCA…), see Fig. 1. The two main groups of sodium layered oxides are classified based upon the sodium co-ordination environment, P-type (trigonal prismatic) or O-type (octahedral). Unique phases are also labelled with a number which represents repeated MO6 layers within the unit cell. Finally, a prime symbol is used to indicate a monoclinic distortion.15 Upon synthesis, the total sodium content has a significant influence on the phase that forms. For NaxMO2, the P2 phase typically forms when x ≈ 0.7, the O3 phase when 0.7 ≤ x ≤ 1 and the P3 phase when x ≈ 0.5. Due to the varying thermodynamic stabilities of each phase, the synthesis temperature can also be used to control the polymorph that forms. For example, O3 and P3 phases typically form at lower temperatures than P2-type phases.16 The phase has important implications on electrochemical performance. For example, the P2 phase has a low diffusion barrier enabling faster diffusion kinetics. Whereas the O3 phase normally displays a higher capacity on the initial charge due to the higher Na content.17
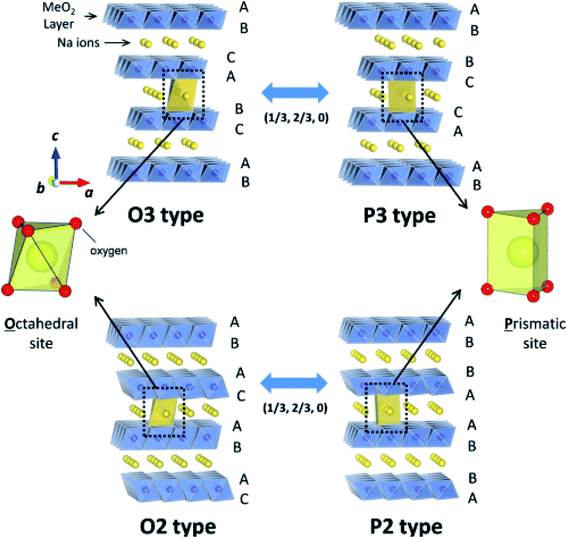 | ||
| Fig. 1 Schematic illustration of the prominent crystal structures adopted by sodium layered oxides (NaMO2), namely O3-type, P3-type, O2 type and P2-type according to the notation developed by Delmas et al.15 The O and P-type structures are related via gliding of the transition metal slabs (MO2) as depicted by the arrows. Reproduced with permission from ref. 18. Copyright 2014 American Chemical Society. | ||
The structural evolution of electrode materials during cycling provides valuable information about battery failure mechanisms. Upon charging, Na removal destabilises the structure resulting in rearrangement or layer gliding and in some cases phase transformation. For example, a P2 → O2 transition results in a change in the Na co-ordination environment from trigonal prismatic to octahedral.19 As Na ions present a larger ionic radii than Li ions, larger volume changes often take place during cycling resulting in more complex structural evolution. As such, the performance of many primary layered materials (NaxMO2, where M is a single transition metal element), which were initially studied, are plagued by undesired, irreversible phase transitions and hence unacceptable capacity fade upon cycling.20 Researchers have made significant progress in finding materials with minimal structural changes during operation, particularly through different doping regimes. In this review, pertinent examples of primary, secondary, tertiary and quaternary layered oxide systems (NaxMO2, M is one, two, three or four different elements respectively) are presented. As the charged state is the most interesting from a structural viewpoint and the most common point of failure, (and arguably the most difficult to probe) this review focuses on the charged state structure of layered oxides and the associated techniques that have been used to probe the charged state.
2. Stability of layered oxide positive electrodes during cycling
The energy density which can be achieved from a sodium-ion cell (or any type of secondary battery) is given by the product of the specific capacity and the working voltage of the cell. The sodium content in the positive electrode decreases as the cell is charged to higher voltages, and hence in order to achieve high energy densities, a host material should be able to reversibly intercalate a large fraction of its sodium content. The ionic radius of Na (1.02 Å) compared to Li (0.76 Å) means that almost all first-row transition metal elements can form a layered NaxMO2 structure, and exhibit redox activity. In contrast, only Co and Ni can form primary layered LixMO2 compounds.21 However, the different redox activity of these elements gives rise to complex phase transformations during cycling, particularly at the charged state. Irreversible phase transformations lead to rapid capacity fade and therefore ideally should be avoided. Gliding of the MO2 slabs may lead to P → O or O → P transitions which may be accompanied by large changes in the lattice parameters.20 The conversion between P-type and O-type stacking is thought to adversely affect the battery performance with regard to energy efficiency, rate capability and cycle stability.21 As such, the design and synthesis of novel layered transition metal oxides with high structural stability at the charged state, and minimal structural changes/rearrangements during cycling, could present a route towards more stable sodium-ion battery systems with higher energy densities.2.1 Phase transitions at the charged state
The emergence of in situ characterisation techniques has enabled the identification of phase transitions and complex vacancy ordering mechanisms which take place at low sodium concentrations. In situ X-ray diffraction (XRD) has manifested as a particularly powerful tool for studying the structure–function relationships in layered oxide positive electrode materials. As such, irreversible phase transitions at the charged state have been identified as a major contributor to capacity fade. The various polymorphs of NaxMO2 undergo unique electrochemically driven phase transitions, with varying effects on battery performance. The characteristic behaviours of the different polymorphs are detailed below.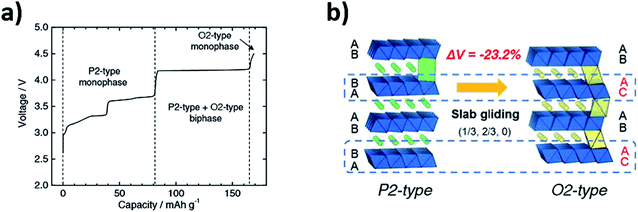 | ||
| Fig. 2 (a) Voltage profile of P2-Na2/3Ni1/3Mn2/3O2vs. Na/Na+ highlighting the formation of the O2-type phase. (b) Schematic illustration for the reversible P2–O2 phase transformation which takes place via gliding of the MO2 layers. Reproduced from ref. 24 under a CC BY 4.0 licence. | ||
The greater stability of the O2-type structure at high voltages/low Na content (cf. P2-type) has since been demonstrated by computational calculations.22 The phase transformations upon cycling were characterised via synchrotron XRD and confirmed using first principle calculations. Similarly, the mobility of sodium ions in the starting P2-type Na2/3Ni1/3Mn2/3O2 structure was determined both experimentally and theoretically by the galvanostatic intermittent titration technique (GITT) and Nudged Elastic Band (NEB) calculations respectively.22 Both techniques revealed that the mobility of sodium ions in the P2 structure is faster than lithium ions in the analogous O3 structure, within the 1/3 < x < 2/3 concentration region, demonstrating that these materials can deliver comparable performance to conventional positive electrode materials used in lithium-ion batteries. Significant shrinkage of the lattice parameters accompanies the P2–O2 transition. Consequently, the large volume change has detrimental effects on the electronic conduction path and may also give rise to voltage hysteresis, leading to poor battery performance.26 To achieve improved cyclability and capacity retention, it has been proposed that gliding of the transition metal layers should be avoided.27 The undesirable P2–O2 phase transition may be avoided by decreasing the voltage cut-off thereby limiting the amount of Na that is extracted from the structure. Cycling P2-Na2/3Ni1/3Mn2/3O2 within the voltage range of 2.0–4.1 V leads to significantly improved capacity retention of 95% after 50 cycles, in comparison to a retention of 64% after 10 cycles when cycled between 2.0–4.5 V.22 Alternatively, at the cost of capacity, changing the composition of P2-Na2/3Ni1/3Mn2/3O2 with dopants such as Cu, Zn or Mg enables the P2–O2 transition to be mitigated, as discussed in greater depth in Section 4.28–30
While doping may evade the P2–O2 phase transition, the P2–OP4 phase transition can instead be promoted. The OP4 phase is characterised by alternating stacking of octahedral (O2) and trigonal prismatic (P2) layers along the c axis. Consequently, the sodium ion vacancies are suggested to be located in the O-type layers, while the sodium ions remain in the P-type layers and can be considered as an intermediate, intergrowth phase between the P2 and O2 end members.31 Since the extent to which the transition metal layers glide upon extraction of sodium ions is minimised, the P2–OP4 phase transformation is more reversible (cf. P2–O2) and therefore leads to an improvement in the battery performance.32
The OP4-type phase was first reported for the P2-Na0.67Fe0.5Mn0.5O2 material, upon charging above 4.1 V. It was found to transition into a less crystalline phase with OP4-type stacking (Fig. 3).33 Below 3.8 V Yabuuchi et al. proposed that sodium ions are uniformly extracted from all layers, whereas above 3.8 V, sodium ions are selectively extracted resulting in the P2–OP4 phase transition. Similarly, the P2-Na2/3Fe2/3Mn1/3O2 composition was also found to transform into the OP4 phase when charged above 4.0 V.34 By increasing the Mn content to yield P2-Na2/3Fe0.6Mn0.4O2, the P2–OP4 phase transition can be avoided.35 However, for the endmember (P2-Na0.67MnO2) in which the MO2 layer is fully occupied by Mn, the onset of the P2–OP4 was found to occur around 3.5 V, corresponding to a plateau in the voltage profile. Interestingly, the detrimental effect of the P2–OP4 transition, namely larger polarization and greater capacity fade, was found to be more prominent in the quenched P2-Na0.67MnO2 sample compared to the analogous slow-cooled material, thereby demonstrating sensitivity of these materials to synthesis conditions.36
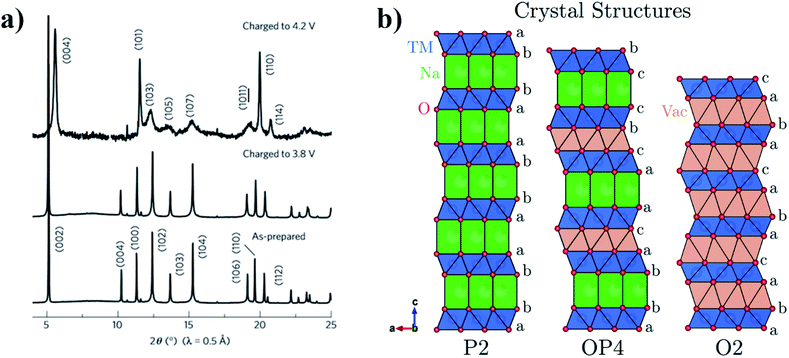 | ||
| Fig. 3 (a) XRD patterns showing the formation of the OP4-type phase when P2-NaxFe1/2Mn1/2O2 is charged to 4.2 V. (b) Projections of the P2, OP4 and O2 type crystal structures perpendicular to the stacking axis, highlighting the different stacking sequences. Reproduced from ref. 37 under a CC BY 3.0 licence. | ||
Removal of sodium ions upon charging gives rise to the formation of O-type stacking faults within the P2 structure. Consequently, the long-range order in layered oxide materials is modified or lost. In an XRD pattern, the loss of long-range order manifests as weaker, more diffuse peaks, as observed by Pang et al. upon extraction of sodium ions from P2-Na0.67Fe0.5Mn0.5O2. Direct observation of the structural evolution via operando synchrotron XRD showed that the P2–OP4 transition proceeds via a solid-solution-like two-phase reaction.38 This solid-solution-like phase, associated with highly broadened XRD peaks, has since been termed the “Z phase”.39
The “Z phase” can be thought of as a continuously changing intergrowth structure which may evolve from the initial P2-type structure to the O2-type structure, going through the ordered OP4 intermediate, see Fig. 4.40 Upon charging, sodium ions which reside in between the MO2 layers are removed from the layered oxide structure leading to an increase in O–O repulsion. The repulsion between the oxygen layers continues to destabilise the layered structure until gliding of the MO2 layers results in the formation of octahedral Na sites, which may be considered as O-type stacking faults.41 When the proportion of O-type stacking faults in a material reaches close to 50%, the ordered OP4 phase can form and on further charging more O-type stacking faults may form until eventually the pure O2 structure is formed.
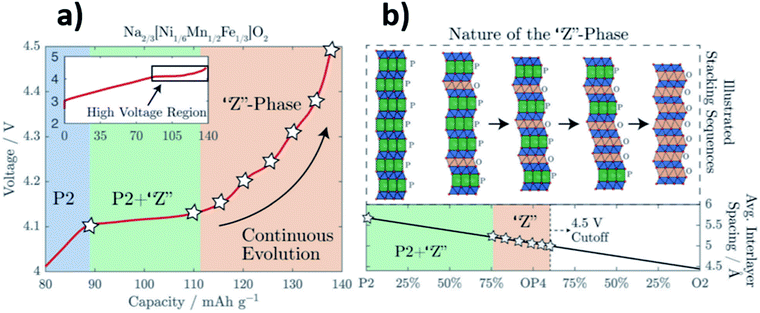 | ||
| Fig. 4 (a) Voltage profile of Na2/3[Ni1/6Mn1/2Fe1/3]O2 highlighting the regions in which the “Z” phase forms. (b) Schematic illustration depicting the “Z” phase as a continuously changing intergrowth structure between P2 and O2. Reproduced from ref. 40 under a CC BY 3.0 licence. | ||
Overall, the structural damage from gliding of layers is less severe and more reversible for the P2–OP4 phase transition when compared with the P2–O2 transition. However, there is still a large and undesirable reduction in volume associated with the P2–OP4 transition and even with a transition to the “Z” phase.42 Significant improvements in the long-term electrochemical performance of layered oxide positive electrode materials have been reported when phase transitions at high potentials are avoided.43
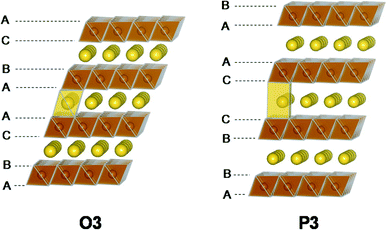 | ||
| Fig. 5 Illustrations of the O3-type and P3-type structures. The two structures are related to each other via layer gliding. Reproduced with permission from ref. 46. Copyright 2015 American Chemical Society. | ||
NaVO2, NaFeO2, Na2/3Fe2/3Mn1/3O2 and Na0.66Mg0.34Ti0.66O2 are a few exceptions of O3-type positive electrode materials that do not display the O3–P3 phase transformation upon charging.46–49 Alternatively, the O3–O′3 monoclinic distortion of the original rhombohedral phase is observed for NaVO2 and NaFeO2, giving rise to poor rate capability in comparison to materials that display the O3–P3 transition.46,47 For Na2/3Fe2/3Mn1/3O2 and Na0.66Mg0.34Ti0.66O2, a stable single-phase reaction mechanism is observed throughout the initial charge/discharge cycle.48,49
More complex structural evolution for O3-type positive electrodes has also been reported. For example, the quaternary O3-Na[Mn0.25Fe0.25Co0.25Ni0.25]O2 positive electrode material undergoes the O3–P3–O3′–O3′′ sequence of phase transitions upon extraction of sodium ions, when cycled between 1.9–4.3 V at C/10.50 Kubota et al. synthesised a solid solution of NaFeO2–NaCoO2 and found that upon charging up to 4.0 V, the O3-NaFe0.5Co0.5O2 composition transforms into a P3-type phase via a biphasic reaction, and subsequently transforms to the monoclinic P′3 type phase which was found to be coupled with sodium ion/vacancy ordering. Finally, as the composition approaches Na0.3Fe0.5Co0.5O2, an O3′ type phase evolves, yielding an O3–P3–P′3–O3′ sequence of phase transitions, see Fig. 6.51
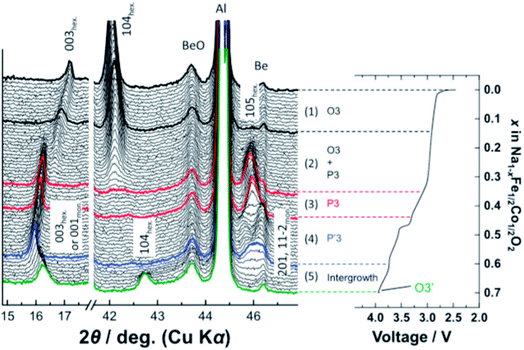 | ||
| Fig. 6 In operando XRD data of O3-NaFe1/2Co1/2O2 which displays an O3–P3–P′3–O3′ sequence of phase transitions upon extraction of sodium ions. Reproduced with permission from ref. 51. | ||
The insertion and extraction of sodium ions from the O3-NaNi1/3Mn1/3Co1/3O2 composition was also found to be associated with several phase transitions. Upon charging, the structure was found to evolve through the O3–O1–P3–P1 sequence; significant changes in the c lattice parameter were detected whereas the a lattice parameter remained almost unchanged.52 Starting with the monoclinic NaNiO2 positive electrode material, new transient phases were discovered through investigations into the structural evolution. During charging, multiple phase transitions corresponding to the sequence: O′3–O′′′′3–P′3–P′′3–P′′′3–O′′3–O′′′3 were identified.53 The occurrence of so many structural transitions has since been associated with poor rate capability in layered oxide positive electrode materials.21 In particular, the large volume changes and thermodynamic instability of the high voltage O3′′ phase has been associated with inferior cycling and rate performance for the Ni-rich O3-Na[NixFeyMn1−x−y]O2 (x = 0.6, 0.7 and 0.8) series.54
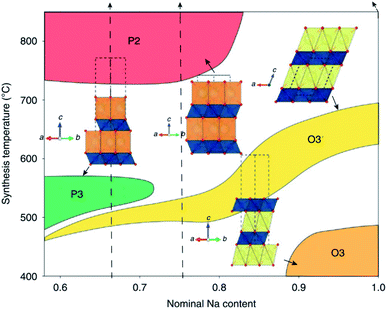 | ||
| Fig. 7 Schematic illustration depicting the synthetic accessibility of NaxCoO2 polytypes. Reproduced with permission from ref. 16. | ||
A unique feature of the P3-type layered oxides such as NayCo1−2xNixMnxO2 (x = 1/2, 1/3) is their ability to reversibly intercalate both Na and Li ions.56 P3-Na0.67Ni1/2Mn1/2O2 can reversibly intercalate both Na and Li ions whereas the similar P2-Na0.67Ni1/3Mn2/3O2 composition does not display any reversible lithium intercalation. Desodiation of P3-Na0.67Ni1/2Mn1/2O2 in Na cells to form Na0.3Ni1/2Mn1/2O2 around 4.0 V instigates a monoclinic distortion accompanied by a large interlayer expansion. However, upon further desodiation, charging up to 4.5 V, the monoclinic distortion disappears. In contrast, the P2-Na0.67Ni1/3Mn2/3O2 system retains the P2-type structure up to 4.0 V but displays the deleterious P2–O2 transition when charged to 4.5 V.57
Lithium intercalation into a sodium containing lattice has also been explored for the P3-NaxCo1/3Ni1/3Mn1/3O2 (0.38 ≤ x ≤ 0.75) system.58 During cycling, the initial P3-type structure was found to transform into the O3-type structure, where both lithium and sodium ions coexist in the alkaline layers. Counterintuitively, a higher reversible capacity and improved cycling stability was found for sodium rich oxides (0.75 ≥ x ≥ 0.67), compared to the equivalent sodium poor oxide (0.38 ≥ x ≥ 0.5), suggesting reversible intercalation of both lithium and sodium following the initial discharge cycle. Cycling in sodium cells was not tested, likely due to the dominance of P2 and O3-type phases for sodium-ion batteries. In a comparison between analogous P2 and P3-NaxCr0.63Ti0.37O2 compositions, Guo et al. found that the P2 phase displays better rate capability and cycling stability compared to the P3 phase, which can in part be explained by the lower Na diffusion barrier predicted by density functional theory (DFT) calculations for the P2 phase.59
2.2 Gliding of transition metal layers
As demonstrated above, interlayer gliding is widespread among NaxMO2 layered positive electrode materials and clearly plays a pivotal role in determining the structural stability near the charged state. To gain an atomistic understanding into the glide driven P- to O-type transitions, Arcelus et al. performed DFT calculations on the NaxVO2 system.60 The calculations showed that the energy barrier for gliding increases nearly linearly with increasing Na content and that the gliding process is mainly governed by electrostatic interactions. At low Na concentrations, the O-type structure becomes more thermodynamically stable, while at higher Na concentrations, the presence of Na in octahedral sites which share both edges and faces with neighbouring VO6 octahedra, as opposed to trigonal prismatic sites which only share either edges or faces, destabilises the structure. A special case is observed at x = 0.5, characterised by the presence of two energy barriers in the calculated energy pathways for layer gliding, where reordering of the sodium ions appears to be a prerequisite to the gliding process. The authors also found that during a P to O transformation each individual sodium ion is swept into a distorted co-ordination environment by the moving transition metal layers. Depending on whether the Na ions originate from edge-sharing or face-sharing prismatic sites, they are either forced into a distorted square pyramidal, which presents a much higher energy barrier, or tetrahedral site, respectively. Due to the high energy barrier, sodium ions may diffuse to adjacent edge-sharing sites prior to gliding, as observed for the NaxVO2 (x = 0.5) case. Moreover, the gliding can be mitigated by the presence of sufficient sodium ions occupying face-sharing sites which can be achieved at high Na concentrations (x ≥ 0.5), in keeping with the enhanced structural stability reported for the high Na-content P2-type Na45/54Li4/54Ni16/54Mn34/54O2 material, or via the introduction of electrochemically inactive elements to facilitate sodium ion/vacancy disorder.60,61 Further computational and experimental studies on more complex transition metal layered oxide materials (containing multiple transition metals and/or Jahn Teller active transition metals) are welcomed to provide a deeper understanding into glide-driven processes at the charged state.The wide variety of stacking sequences in NaxMO2 systems enables many complex phase transformations to take during sodium (de)intercalation. These phase transitions, associated with interlayer gliding to avoid oxygen–oxygen contacts, are unfavourable for battery performance and so the design of novel NaxMO2 layered materials should focus on suppressing gliding of the transition metal layers during cycling. Even reversible transformations are not desirable because they can have negative impacts on capacity retention by inducing stacking faults and lattice volume changes which can give rise to shear lattice strain.62 A comprehensive review into the adverse effect of interlayer gliding on the electrochemical performance of sodium layered transition metal oxides can be found in ref. 21.
2.3 Transition metal migration
In addition to lateral movement of the transition metal layer, vertical migration of transition metal ions into the adjacent alkali layer may also take place upon charging. The structural stability of layered oxide materials at the charged state can be strongly correlated to migration of transition metals into the sodium layer, which is therefore a critical performance limiting factor. In particular, irreversible transition metal migration upon extraction of sodium ions may contribute towards poor thermal stability, fast capacity fading and voltage decay.63 Due to the similar ionic radii of Li+ and the transition metal ions, cation migration behaviour is particularly prevalent in Li-based positive electrode materials.64–66 Despite the larger ionic radius of sodium ions, migration of transition metal ions upon charging has also been proposed for sodium-based positive electrode materials, primarily occurring in O3-type layered oxides such as O3-NaTiO2, O3-NaVO2, O3-NaCrO2 and O3-NaFeO2.47,67–69Migration of transition metal ions from the MO2 layer into the interlayer spacing in which sodium ions reside was first proposed in 1983 for the NaxTiO2 system to explain the occurrence of irreversible structural modifications at high voltages.67 A strong decrease in interslab distance and concomitant loss of cycling reversibility upon increasing the upper voltage limit was also observed for NaxVO2 and NaxCrO2 suggesting that migration of vanadium and chromium ions may take place in a similar manner.47,68 A follow up study by Bo et al. revealed that up to a composition of Na0.4CrO2 no Cr migration could be detected. However, upon further extraction of Na, formation of a rock salt structure via an intermediate phase that contains Cr in both the Na and transition layer takes place.20
The high abundance and low cost of Fe makes Fe containing electrodes appealing for sodium battery applications. However, akin to the compositions mentioned above, the reversibility of Fe-rich materials can, in some cases, be limited by the migration of Fe into the sodium layer. This idea was first proposed by Yabuuchi et al. for O3-Na1−xFeO2 (x > 0.5) and later supported by Li et al. via high resolution transmission electron microscopy (HRTEM) as well as Silvan et al. who tracked the migration of Fe with electrochemical impedance spectroscopy (EIS), operando XRD and the potentiostatic intermittent titration technique (PITT).69–71 The O3-NaFeO2 material exhibited migration of Fe into the sodium layer when charged beyond 40% of its theoretical capacity, and when charged above 4.0 V the migration became irreversible, as depicted in Fig. 8. The migration was found to shrink the interlayer distance, in contrast to the expansion observed as sodium is extracted from the majority of layered positive electrodes, due to O–O repulsion. This limited the available capacity likely by blocking sodium ion diffusion, highlighting that transition metal migration can be a significant source of performance degradation at high voltages. Of note was the finding that a proportion of the transition metal migration could be reversible with electrochemical cycling, acting to both stabilise the structure and deliver capacity. This suggests that transition metal migration can be optimised to preserve structure and deliver optimal capacity.
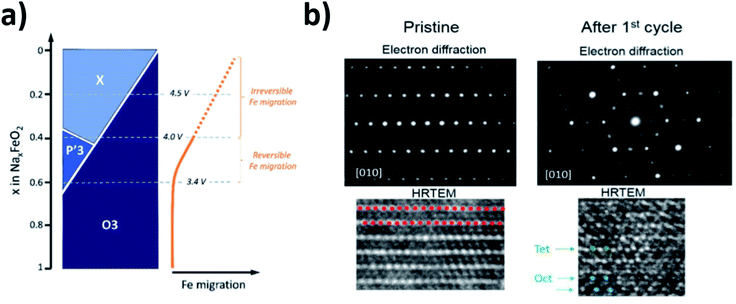 | ||
| Fig. 8 (a) Schematic illustration of the phase evolution and Fe migration upon extraction of Na for NaxFeO2. Reproduced with permission from ref. 74. (b) Electron diffraction and HRTEM images of NaxFeO2 after 1 cycle between 2.0 and 4.5 V at a rate of C/10. Red dots represent the transition metal layer, green dots represent Fe migrated to tetrahedral sites and blue dots represent Fe migrated to octahedral sites. Reproduced with permission from ref. 70. Copyright 2016 American Chemical Society. | ||
The irreversible migration of transition metal ions has also been shown to inhibit structural transitions during cycling. For example, migration of transition metal ions into the Na layer of O3-Na0.8Ni0.3Co0.3Ti0.6O2 during the initial charge cycle was found to inhibit the reversibility of the O3–P3 phase transformation, thus leading to rapid capacity fade upon subsequent cycling.72 Furthermore, transition metal cations located on tetrahedral sites in the alkali metal layer are thought to block the diffusion of sodium ions, giving rising to poor rate performance.73 However, if the reversibility of the cation migration is regulated, these drawbacks can be mitigated. In fact, transition metal migration in P2-Na0.67[Mn0.66Fe0.2Cu0.14]O2 was found to coincide with anionic redox activity, which allows additional capacity to be extracted from a battery.27
Through utilisation of X-ray pair distribution function (PDF) analysis, Talaie et al. showed that reversible migration of Fe in P2-Na0.67−zFe0.5Mn0.5O2 takes place at high potentials.43 Migration of the transition metal ions into a tetrahedral co-ordination within the Na layer perturbs the long-range order. As such PDF analysis, a technique that can be used to probe semi crystalline phases with short range order, was employed to confirm the reversible migration of the transition metals. More migration was found to take place upon extracting Na from the Fe-rich NaxFe0.5Mn0.5O2 material in comparison to NaxFe0.2Mn0.65Ni0.15O2. DFT calculations performed by Li et al. show that the energy barrier for Fe migration reduces as the Fe content in Fe rich transition metal oxides increases. Furthermore, they reported Fe migration to be fully suppressed in compositions that contain less than ≈30% Fe in addition to quaternary (NaxMM′M′′M′′′O2) compositions.70
Utilising high-angle annular dark field (HAADF) scanning transmission electron microscopy (STEM), direct observation of reversible transition metal migration in the O3-Na0.8Co0.4Ti0.6O2 positive electrode material has been reported.63 The HAADF-STEM images, shown in Fig. 9, enabled direct visualisation of the structure on an atomic scale; upon charging significant presence of transition metal ions in the sodium layers can be seen. The observations were supported by operando XRD which show a decrease in the c lattice parameter deep into charging, attributed to the larger positive charge of the transition metal ion (cf. Na+) residing in the sodium layer, thereby reducing electrostatic repulsion between oxygen atoms. Furthermore, electron density maps of the difference between observed and calculated XRD patterns revealed presence of electron density for the transition metal ions in the sodium layer. A schematic plot of the reversible transition metal migration process, along with the phase transitions, upon charging for O3-Na0.8Co0.4Ti0.6O2 is shown in Fig. 10.
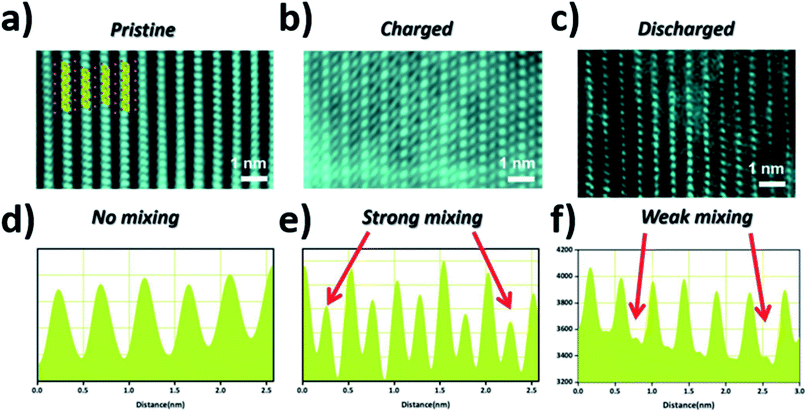 | ||
| Fig. 9 STEM images of the (a) pristine (b) charged (c) discharged electrodes viewed along the [010] direction and (d–f) their corresponding line profiles where the red arrows highlight the intensities corresponding to transition metal migration from the transition metal layers to the sodium layers. Reproduced with permission from ref. 63. | ||
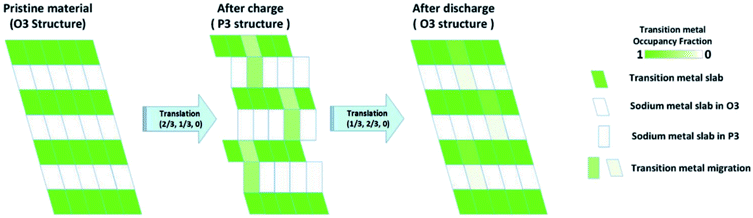 | ||
| Fig. 10 Schematic plot of the reversible transition metal migration upon cycling for O3-Na0.8Co0.4Ti0.6O2. Reproduced with permission from ref. 63. | ||
Inevitably, a number of works have since associated c lattice contraction close to the charged state with transition metal migration. While transition metal migration can be expected to induce a contraction in the interlayer distance, shrinkage of the c lattice parameter upon extraction of sodium ions has also been related to ordering of the sodium ion vacancies and phase transitions.71,75,76 However, rationalising these alternative explanations is somewhat more challenging. As such, uncertainties regarding the role of transition metal migration in phase transformations, such as formation of the “Z phase” from an initial P2-type structure, still remain. Therefore, advanced techniques such as HAADF-STEM, PDF or Mössbauer spectroscopy that enable the direct observation of transition metal migration should ideally be utilised to confirm its occurrence and overall mechanism.
There are two possible sites available in the O3-type structure for transition metal migration into the alkali metal layer: octahedral or tetrahedral sites.68 Since the energy difference between the tetrahedral and octahedral Na sites in the NaCrO2 material is small, ≈40 meV, Kubota et al. proposed that both sites may be almost evenly occupied by Cr ions.68 For the Na0.8Co0.4Ti0.6O2 system, Zhang et al. used Fourier difference maps to locate migrated transition metal ions within the sodium layer.77 The maps suggest that the migrated ions are situated on the octahedral interstitial sites directly in line with the oxygen atoms and are not pinned directly below the vacancy in the transition metal layer.
To identify the preferential site for Fe migration in NaFeO2 Silván et al. performed simulations to model the migration of Fe to Na octahedral sites or Na tetrahedral sites in different proportions.71 By comparing these results with operando XRD pattern evolution it was possible to identify that the Fe in NaFeO2 preferentially migrates to the tetrahedral sites. This suggests that tetrahedral sites in the Na layer need to be available for transition metal migration to occur. The preferential migration to the tetrahedral site in the Na layer has also been reported by Li et al. on the NaFeO2 system,78 as well as Talaie et al. on the P2-Na2/3[Mn1/2Fe1/2]O2 composition (upon transformation to an O2-type structure at high voltages).43 Due to the absence of tetrahedral sites within the Na layer in P-type structures, this would imply that transition metal migration is inhibited in P-type phases, or it is only observed when there is sufficient local O-type ordering (considering the gliding of planes described in Sections 2.1 and 2.2).
To gain a greater understanding of which transition metal ions preferentially migrate into the Na layer during electrochemical cycling, Chen et al. used atomic resolution scanning tunnel electron microscopy in combination with energy dispersive X-ray spectrometry (STEM-EDS) elemental mapping to study the quaternary NaNi0.3Co0.12Mn0.12Fe0.4O2 composition.79 They found that Fe migrates into both tetrahedral and octahedral sites within the Na layer, as depicted in Fig. 11. In contrast, Ni was found to predominantly migrate to the octahedral sites while Mn and Co mostly remained in the transition metal layers. Similarly, Guo et al. found that upon charging Na0.8Ni0.3Co0.1Ti0.6O2 some Ni atoms do reside in the Na layers whereas Ti and Co atoms mainly reside in the transition metal layer.72 The strong electrostatic interactions (attraction with the oxygen layers, leading to a decrease in the interlayer spacing, and repulsion with the approaching sodium ions) induced by the migrated transition metal ions is thought to have a detrimental impact on the reinsertion of sodium ions.79
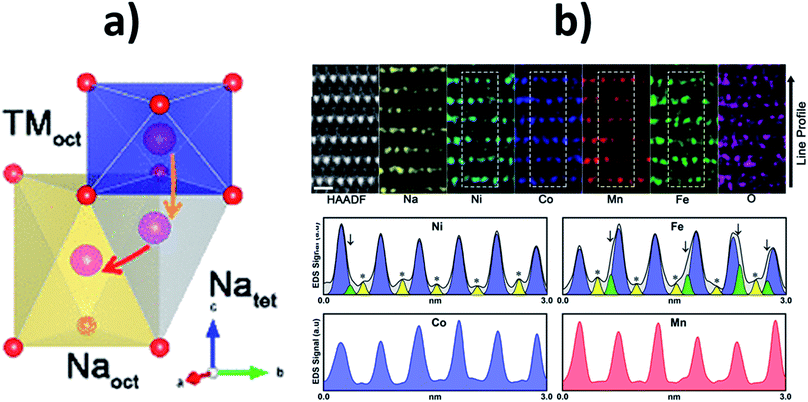 | ||
| Fig. 11 (a) Schematic of the transition metal migration pathway in an O3-type material showing the available Na tetrahedral and Na octahedral sites. (b) Atomic resolution STEM-HAADF image and EDS elemental mapping of the NaNi0.3Co0.12Mn0.12Fe0.4O2 material after 50 cycle shown along the [100] axis together with EDS mapping line profiles of Ni, Fe, Co and Mn. Yellow peaks marked with asterisks indicate transition metal octahedra in the Na layer and green peaks marked with arrows indicate transition metal tetrahedral in the Na layer. Reproduced with permission from ref. 79. Copyright 2020 American Chemical Society. | ||
Using DFT simulations, Zhang et al. went on to show that the energy penalty for migration of a transition metal ion is influenced by its neighbouring transition metal ions.80 More specifically, they showed that the shortened Fe–O bond length with neighbouring Cu (due to the large electronegativity of Cu) can significantly enhance the energy penalty, effectively preventing the Fe migration into the Na layer. Oxidation of Fe3+ to produce Jahn–Teller active Fe4+ ions accompanied by ligand to metal charge transfer (LMCT) from O orbitals to Fe orbitals thereby weakening the bonding to neighbouring atoms has also been suggested to facilitate migration of Fe into the Na layer.27,78 To support this idea, Li et al. performed DFT calculations on NaMO2 (M = Mn, Co, Ni, Fe) systems to show that when Fe is forced to be in the low spin, Jahn–Teller inactive spin state, the energy barrier for migration significantly increases to values as high as those in non-Fe containing systems.70
In lithium-rich layered oxides, transition metal migration has been identified as a critical factor in triggering anion redox, allowing extra capacity to be extracted upon charging.66 Furthermore, transition metal migration in the Li(Li0.2Ni0.4Mn0.4)O2 system was found to be reversible but asymmetric; upon deintercalation, transition metal migration into the alkali metal layer is followed by random hopping (displacement) and subsequently upon intercalation, the transition metal ions do not follow precisely the reverse pathway, thus inhibiting or influencing lithium diffusion. Similar mechanistic insights regarding transition metal migration and the (de)intercalation mechanism close to the charged state in sodium-based systems would help to facilitate the development of sodium-ion battery positive electrodes with improved electrochemical performance.
In summary, irreversible transition metal migration upon charging sodium layered oxides should be avoided to achieve an improved electrochemical performance. Reversible transition metal migration on the other hand may help to stabilise the charged state structure of sodium layered oxides and deliver additional capacity, alongside anionic redox activity.
2.4 Anionic redox activity
Operation of batteries at high voltages may also enable the redox activity of anions in layered oxide materials, such as O, to be accessed through anionic redox reactions (ARR). ARR active materials allow for extra capacity to be extracted from positive electrodes by utilising the charge on oxygen atoms.81 This behaviour has been documented in several metal oxide systems for lithium-ion batteries, for example Li[Li0.2Ni0.2Mn0.6]O2 among others,82–86 and a detailed explanation into the science underlying anion redox chemistry can be found in ref. 87. ARR activity has also been observed in various layered positive electrode materials for sodium-ion batteries, including Na-rich materials,88,89 as well as P2-type and O3-type materials.90,91 A recent review article regarding the mechanism of anionic redox specifically in sodium layered oxides together with a table summarising the pertinent sodium-based materials that have been reported to display anionic redox activity can be found in ref. 92.In both Na and Li based transition metal oxide systems, there are two distinct mechanisms associated with oxygen redox activity. In their simplest form, these are reversible anionic redox between oxo- (O2−) and peroxo-like (O2)n− species and irreversible anionic redox during which O2 gas is released.93 High metal to oxygen covalency has been identified to play a critical role in stabilising the highly reactive intermediate (O2)n− species, thereby enabling reversible ARR.86 The metastable (O2)n− species may also be stabilised by reorganisation of the oxygen network (the reductive coupling mechanism) or localisation via the generation of localised electron holes on the oxygen atoms.94 If the (O2)n− species cannot be stabilised through metal–oxygen interactions, they may react with the electrolyte, or break free from the adjacent transition metal ion, resulting in the complete oxidation of O2− to elemental oxygen and release of O2 gas, characteristic of irreversible ARR.95 While, oxygen redox activity may be concomitant with migration of transition-metal ions, House et al., showed that, vacancies in the transition metal layer are not required to trigger loss of oxygen.27,96 In summary, the goal is to develop materials that display fully reversible redox activity i.e. no loss of O2 gas during the process.
The difference in ionic radii and electronegativities between sodium and lithium ions means that the knowledge and understanding of anionic redox in lithium-ion batteries cannot necessarily be directly transposed to sodium-based systems. For example, the Li2MnO3 system displays a high capacity of up to 200 mA h g−1 with a long plateau in the voltage profile around 4.5 V, characteristic of anion redox activity. However, likely due to the mismatch in size between Mn4+ (0.53 Å) and Na+ (1.02 Å), the Na counterpart Na2MnO3 is yet to be synthesised.97 Additionally, in contrast to the Li series, formation of O2n− species via anionic redox processes for Na2Ru1−ySnyO2 (y > 0.5) is followed by the irreversible loss of O2.98
Existing investigations into anion redox activity in positive electrodes for lithium-ion batteries provide a good foundation for exploration of ARR in sodium-ion batteries. Considering the high capacity and redox activity reported for Li-rich layered materials such as Li1.2Nb0.5Mn0.5O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 and Li4Mn2O5,100 Perez et al. investigated the possibility of exploiting anionic redox participation in the Na-rich layered material Na2IrO3; simultaneous cationic and anionic redox processes were found to take place at potentials as low as 2.7 V vs. Na/Na+.101 Furthermore, no cationic migration or release of O2 took place upon cycling. Similar redox reactions have been reported in other Na-rich layered oxides including Na3RuO4,89 Na2SeO3,102 Na2Mn3O6.85,103 Na2Mn3O7,104 and Na1.2Mn0.4Ir0.4O2.105
99 and Li4Mn2O5,100 Perez et al. investigated the possibility of exploiting anionic redox participation in the Na-rich layered material Na2IrO3; simultaneous cationic and anionic redox processes were found to take place at potentials as low as 2.7 V vs. Na/Na+.101 Furthermore, no cationic migration or release of O2 took place upon cycling. Similar redox reactions have been reported in other Na-rich layered oxides including Na3RuO4,89 Na2SeO3,102 Na2Mn3O6.85,103 Na2Mn3O7,104 and Na1.2Mn0.4Ir0.4O2.105
Inspired by the prominent Li2MnO3 system, in which Mn has an oxidation state of 4+, the P2-Na0.6Li0.2Mn0.8O2 composition was investigated, where the Mn atoms also adopt a 4+ oxidation state. De la Llave et al. proposed, based upon electrochemical data and DFT calculations, that anion redox processes contribute to the capacity at high voltages.97 In alignment with these observations, Maitra et al. used P2-Na2/3[Mg0.28Mn0.72]O2 as an example to further demonstrate that excess alkali metal ions are not required to activate oxygen redox activity.106 Moreover, they proposed that removal of alkali metal ions from both the alkali ion and transition metal layers of alkali rich layered oxides such as Li[Li0.2Ni0.13Co0.13Mn0.54]O2 leads to under co-ordinated oxygen and non-bonded, electron deficient O 2p states which promotes the release of O2. Since the oxygen in P2-Na2/3[Mg0.28Mn0.72]O2 is always co-ordinated to at least three cations no oxygen loss, was observed experimentally, in line with the theory. Overall, the work highlights that suppressing oxygen loss is imperative if the ARR is to be practically used in battery applications.
P2-Na2/3Mn1−yZnyO2 (0 < y < 0.23)107 and P2-Na0.78Li0.25Mn0.75O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96 are additional examples of Na-deficient compositions that display ARR without loss of oxygen upon charging up to 4.5 V. Alike the Mg counterpart, their anionic redox activity is thought to arise from presence of O 2p nonbonding orbitals, created by substituting Mn for elements that form bonds with oxygen which are more ionic in character.107 When charged up to 5 V loss of oxygen can be detected from P2-Na0.78Li0.25Mn0.75O2. At such high voltages, Li+ may be removed from the structure. Consequently, oxygen becomes co-ordinated to less than 3 cations and is lost from the structure.96 In contrast, the low mobility of Mg2+ in P2-Na2/3[Mg0.28Mn0.72]O2 means that at least three cations co-ordinate to oxygen (2 × Mn4+ and 1 × Mg2+), even at the surface, and so the oxygen does not become under bonded, hence mitigating oxygen loss.
96 are additional examples of Na-deficient compositions that display ARR without loss of oxygen upon charging up to 4.5 V. Alike the Mg counterpart, their anionic redox activity is thought to arise from presence of O 2p nonbonding orbitals, created by substituting Mn for elements that form bonds with oxygen which are more ionic in character.107 When charged up to 5 V loss of oxygen can be detected from P2-Na0.78Li0.25Mn0.75O2. At such high voltages, Li+ may be removed from the structure. Consequently, oxygen becomes co-ordinated to less than 3 cations and is lost from the structure.96 In contrast, the low mobility of Mg2+ in P2-Na2/3[Mg0.28Mn0.72]O2 means that at least three cations co-ordinate to oxygen (2 × Mn4+ and 1 × Mg2+), even at the surface, and so the oxygen does not become under bonded, hence mitigating oxygen loss.
Taking advantage of the high operating voltage of Ni containing positive electrodes and the oxygen redox activity displayed by Na2/3[Zn0.3Mn0.7]O2,108 Konarov et al. designed and synthesised the Na2/3[(Zn0.5Ni0.5)0.3Mn0.7]O2 electrode.109 Through utilising the Ni2+/4+ and O2−/O− redox pairs, Na2/3[(Zn0.5Ni0.5)0.3Mn0.7]O2 is an exemplar high voltage anionic-based positive electrode material for use in sodium-ion batteries.110
More recently, increasing the covalency of the TM–O bond has been shown to be effective in suppressing oxygen release, hence improving electrochemical performance.86 The TM–O distance and TM–O bonding energy have also been identified as important factors in determining the activity and reversibility of the oxygen redox reaction. For example, Kong et al. showed that the shortening of TM–O bonds and enhanced TM–O bonding energy through synergic Cu/Mg co-doping improves the oxygen redox reversibility.111
Participation of oxygen anions in the charge compensation mechanism has also been explored in the transition metal deficient P2-Na0.78Ni0.23Mn0.69O2 and sodium deficient O3-Na0.6Li0.2Fe0.4Ru0.4O2.26,82 At high voltages, a plateau region associated with oxygen redox reaction was found to account for the 60 mA h g−1 of capacity in excess of the theoretical capacity of Na0.78Ni0.23Mn0.69O2, as highlighted in Fig. 12a. Moreover, electron energy loss spectroscopy (EELS) data showed the ARR behaviour to be concurrent with the particle-level formation of a surface to bulk transition metal oxidation state gradient as well as structural transformations at the surface of the cycled particles. Similar to Na0.78Ni0.23Mn0.69O2, a gradient in the valence state of Ni ions from the bulk to the surface was observed for the charged electrode, which coincided with a change in intensity of the O K-edge peak, as shown by Fig. 12b. The ARR activity in P2-Na2/3Ni1/3Mn2/3O2 accounts for the observed capacity of 228 mA h g−1 which is much higher than the theoretical value of 172 mA h g−1 based on cationic redox.112
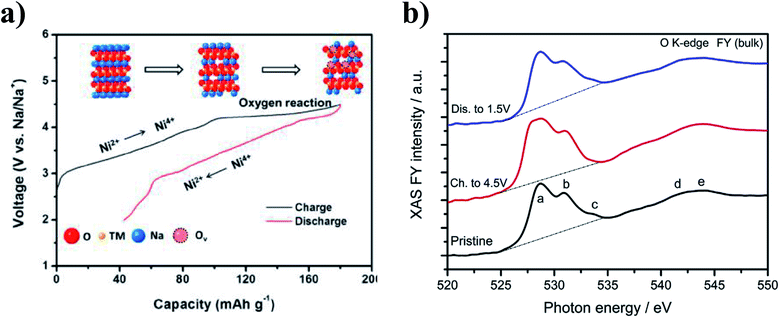 | ||
| Fig. 12 (a) Observed voltage profile for P2-Na0.78Ni0.23Mn0.69O2, highlighting the charge compensation mechanisms involved. Reproduced with permission from ref. 113. Copyright 2017 American Chemical Society. (b) O K-edge XAS data collected from the pristine P2-Na2/3Ni1/3Mn2/3O2 material, and after extraction at the charged and discharged states during the first electrochemical cycle. Reproduced with permission from ref. 112. | ||
Through comparison of X-ray photoelectron spectroscopy (XPS), operando Raman spectroscopy and electrochemical data, Jia et al. found that compared to the sodium deficient O3-Na0.6Li0.2Fe0.4Ru0.4O2, reversible anionic redox activity is more easily triggered in the P2-Na0.6Li0.35Fe0.1Ru0.55O2 material when charged up to 4.0 V, enabling the P2-type material to deliver a larger capacity.82 Furthermore, when the two similar materials were charged beyond 4.3 V, only the O3-type structure displayed evidence of irreversible oxygen evolution and superoxide species which is in keeping with the more stable cycling performance reported for P2-Na0.6Li0.35Fe0.1Ru0.55O2 in comparison to the O3-type material.
Reversibility of oxygen redox at high rates was first reported in P2-Na0.6[Mg0.2Mn0.6Co0.2]O2.110 DFT calculations suggest that the overlapping Co 3d and O 2p orbitals as well as the reduced bandgap of ≈ 0.61 eV (cf. ≈ 2.65 eV for the analogous Co free composition) upon incorporation of Co facilitates facile electron transfer, enabling long term oxygen redox reversibility. Transition metal (Ni) 3d–O 2p hybridization has also been reported to play an important role in stabilizing the anion redox activity of P3-Na0.67Ni0.2Mn0.8O2, which displays oxygen redox activity when charged to 4.4 V.114
The utilisation of the anion redox reaction has been associated with increased structural stability of layered oxide materials upon cycling. This is thought to be due to a reduced coulombic repulsion achieved via anion redox. Upon deintercalation, the negative charge carried by oxygen decreases with the oxidation of oxygen, minimizing the repulsions between the two oxygen layers between the empty or low concentration Na layers. As shown by Fig. 13, smaller variations in the interslab distance may take place upon cycling P2 materials that undergo ARR compared to those that do no display oxygen redox activity.115 Utilization of ARR in Mn-rich materials, such as P2-Na0.72[Li0.24Mn0.76]O2, could be particularly beneficial as distortions associated with Jahn–Teller active Mn3+ can be mitigated if Mn retains an oxidation state of 4+.
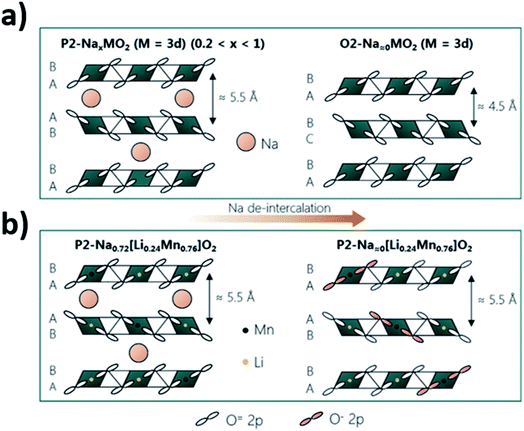 | ||
| Fig. 13 Comparison of the structural changes that may take place upon extraction of sodium ions from (a) P2-type layered oxides that do not display oxygen redox activity and (b) the P2-Na0.72[Li0.24Mn0.76]O2 phase for which oxygen oxidation (highlighted in pink) partakes in the charge compensation mechanism. Reproduced with permission from ref. 115. | ||
The additional capacity that can be accessed by triggering anion redox activity may be associated with some of unfavourable side effects such as irreversible cation migration, lower sodium ion diffusion and the release of O2 gas, resulting in accelerated capacity and voltage decay upon cycling.101 Although limiting the voltage cut-off can be an effective method to mitigate unwanted phase transformations, it also means that all the additional capacity from ARR is not accessed. Through incorporation of small amounts of electrochemically inactive elements such as Li, these structural transitions can be delayed to higher voltages.26 Overall, if the deleterious release of O2 gas and irreversible phase transformations can be avoided while accessing the high voltage ARR of oxygen, a significant improvement in capacity can be achieved. A synergistic optimisation of sodium extraction, reversible oxygen redox and reversible transition metal migration could help to minimise lattice-based structural distortions at high voltage and therefore better stability and energy density from these electrodes.
3. Improving the structural stability of layered oxides at the charged state
3.1 Chemistry and composition
In layered oxide materials, when sodium ions occupy sites between the MO6 layers, their electrons enter the available d orbitals of the transition metals in the host lattice. The mobility of the sodium ions and electrons, and the electrochemical potential of the electrode, is hence heavily dependent on the valance state, ionic radius, electronegativity and local environment of the cations (M) in the host lattice.116,117 While most studies have focused on improvements to specific capacity, it is also important to understand and consider the electrochemical potential of the material during cycling, the influence of electrode chemistry on ionic and electronic conductivity, the reversibility of intercalation reactions, and the structural stability of the positive electrode material. In reality, these factors will have a more profound effect on the applicability of new materials in devices which require high energy densities and reliable cycling performance at variable current densities.In the layered oxide structure, which contains sheets of edge sharing MO6 octahedra, the redox activity of the central, coordinated atom strongly influences the stability of the material during (de-)intercalation from the adjacent sodium layers. The layered structure is stabilised by the large difference in ionic radii between Na and M, and thus various metals can be incorporated into the structure to influence the electronic state.118 Initially unary compositions, containing a single element in the transition metal layer, such as NaCoO2, NaNiO2, or NaMnO2 were reported.119 Early investigations of unary compounds were limited to lower working voltages due to the unavailability of electrolytes resistant to oxidation by transition metals such as Cr, Co or Ni.67,120 Additionally, these compounds tend to deliver relatively low specific capacities as the upper cut-off voltage must be limited due to structural instabilities at low Na contents. NaTiO2 suffers from poor reversibility below x ≈ 0.7, as the trivalent state of Ti is unstable.67 More recent studies suggest a capacity of 152 mA h g−1 can be achieved, accompanied by a reversible O3–O′3 transition.121 NiNiO2 can reversibly intercalate up to x ≈ 0.5, however extracting further capacity by increasing the cut-off voltage leads to significant reductions in coulombic efficiency due to transitions to an electrochemically inactive phase.122 A cut-off voltage of 3.75 V limits the first cycle capacity to ≈120 mA h g−1, in comparison to a capacity exceeding 180 mA h g−1 when cycled to 4.5 V.123 NaCrO2 can similarly reversibly intercalate about half of its sodium content, however the process is accompanied by structural transitions, O3–O′3–P′3.120 Given the success of its Li-containing analogue, several polymorphs of NaCoO2 have been reported.124–126 Compared to LiCoO2, all types of NaCoO2 exhibit several plateaus in their electrochemical profiles as the material transitions between structures with different sodium ion/vacancy ordering and varying Na+–Co3+/4+ (low-spin, high-spin) interactions.126 Among the unary compounds, NaMnO2 delivers a relatively high capacity of 190 mA h g−1 in both the O3-type and P2-type form.127,128 Mn can achieve several valence states, however the high-spin Mn3+ state is unstable and induces distortion of the MnO6 octahedra due to the Jahn–Teller effect.129 Finally, O3-NaFeO2, with Fe favoured for its abundance and environmental inertness, can reversibly cycle to 3.5 V, but the narrow working voltage range limits the reversible capacity of just 80 mA h g−1.69 Further extraction of sodium results in the migration of Fe3+ into tetrahedral sites which can impede the diffusion of sodium ions on subsequent cycles.46,78
Each of these unary compounds clearly exhibits unique electrochemical behaviour despite structural similarity. By combining solid-solutions of elements with varying redox behaviours, interesting co-operative effects can result in improved electrochemical performance. Binary combinations of the above elements, such as Nax[MnyFe1−y]O2, Nax[MnyMg1−y]O2, or Nax[NiyMn1−y]O2, have been reported which offer increased working voltages and reversible capacities.33,130–132 Incorporation of further elements has led to more complex compositions, including ternary and quaternary or quinary compositions containing several elements.133–137 These more complex compositions have been synthesised in an attempt to smooth the electrochemical profile and suppress irreversible phase transitions at the charged state. For example, the combination of Co, Mn and Ti has been reported by Wang et al., in the ternary P2-Na0.66Co0.22Mn0.44Ti0.34O2 material. The material utilises the Co2+/3+ redox couple to raise the average oxidation state of Mn and suppress the structural instability caused by Jahn–Teller distortion of Mn3+, thereby achieving a reasonable reversible capacity of 120 mA h g−1.138 The oxidation state of Ti4+ is retained during cycling to further enhance structural stability at the charged state, up to 4.3 V. The combination of Mn with Fe and Ni has been suggested to enable additional reversible capacity when charging beyond 4 V. In studies of O3-type NaNi1/3Fe1/3Mn1/3O2, it was found that both the Ni2+/4+ and Fe3+/4+ redox couples contribute to capacity below 4 V, however the Fe redox couple remains dominant above 4 V.139 Despite stabilization of the Mn4+ state during cycling, Fe migration into the Na layer remains an issue at high voltages. High voltage stability has been observed in P2-NaxCo2/3Mn2/9Ni1/9O2, delivering a reversible capacity of 140 mA h g−1 at a charged state cut-off voltage of 4.5 V.140 Further characterization of the charged state behaviour revealed that the Mn retains a 4+ oxidation state up to 4.5 V. Charge compensation is instead achieved by oxidation of both the Co and Ni ions to a 4+ oxidation state, accompanied by anionic redox activity from oxygen atoms as depicted in Fig. 14.141In situ XRD further confirmed that the P2 structure is preserved over the entire voltage range. These examples highlight the cooperative ability of several elements to compensate for structural instability and deliver higher reversible capacities at higher working voltages.
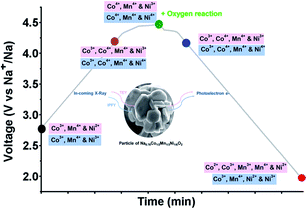 | ||
| Fig. 14 Oxidation states of Ni, Mn and Co observed during cycling of the ternary NaxCo2/3Mn2/9Ni1/9O2 positive electrode material, determined using X-ray absorption spectroscopy (XAS) and resonant inelastic X-ray scattering (RIXS). Reproduced from ref. 141 under a CC BY 4.0 licence. | ||
In contrast to the above-mentioned examples which exploit uniform doping, recently Wang et al. proposed non-uniform doping to be a more effective strategy for enhancing the charged state stability of layered positive electrode materials.142 A range of Mn-rich layered oxides including P2-Na0.67Ni0.23Mn0.67Cu0.1O2, P2-Na0.67Ni0.33Mn0.57Ti0.1O2, P2-Na0.67Ni0.23Mn0.67Zn0.1O2, P2-Na0.67Ni0.23Mn0.67Mg0.1O2, were investigated. Detailed imaging and energy dispersive X-ray spectroscopy (EDS) mapping showed that dopant segregation, leading to the non-uniform distribution of dopants, takes place in the Zn and Mg containing samples, which display superior capacity retentions of 85% and 82% compared to 69%, 55% and 31% for the Ti-doped, Cu-doped and undoped samples respectively, when cycled at a rate of C/10 between 2.0–4.5 V for 100 cycles. Atomic resolution STEM-HAADF imaging evidenced the presence of Zn dopants in the sodium layer after 50 cycles at C/10 between 2.0–4.5 V, which may further contribute towards the enhanced mechanical properties and cycling stability of the Zn-doped material. Overall, the work highlights the importance of considering the role and evolution of electrochemically inactive dopant ions both when synthesized and during cycling which opens new avenues for designing layered oxides with enhanced stability at high voltages.
3.2 Mixed phase materials
Combining multiple elements together in a single layered oxide material is widely accepted as an effective method for improving structural stability and hence battery performance of layered oxide materials. An alternative approach that has yet to be widely explored is the integration of multiple phases into a single material. Intergrowth materials, containing multiple polymorphs of the layered oxide structure, were first reported in studies of manganese oxide materials for use in lithium-ion batteries.143–145 Each layered oxide polymorph (P2/O3/P3) has their respective advantages and disadvantages. The P2-type polymorph typically displays high rate performance, but the sodium deficient nature of this framework also leads to comparatively low specific capacities. In contrast, the O3-type polymorph generally forms for sodium rich compositions, giving rise to higher capacities. However, the Na diffusion pathway between adjacent octahedral sites takes place via edge sharing tetrahedral sites, which contributes towards the higher energy barrier for diffusion of sodium ions and therefore poor rate performance. Finally, the P3 phase can be prepared at lower temperatures and may exhibit high reversible capacities but usually suffers from severe capacity fade owing to poor structural stability.146Through integrating more than one phase into a single material, it is possible to enhance the electrochemical performance of sodium layered oxide positive electrode materials. In many cases, biphasic and multiphasic materials have been reported to perform better than the corresponding single phase. However, it may also add further complexity in the possible reaction pathways near the charged state and the ability to probe them using analytical techniques; all of the above mentioned phase transitions for the individual phases are possible in addition to new pathways due to the proximity of different phases e.g. stabilisation and ion transfer.147 A table of known biphasic and multiphasic layered oxide materials along with their respective electrochemical performances can be found in ref. 148.
Another effective way to induce the intergrowth of mixed phase materials is through incorporation of Li. Investigations into P2/O3-Na0.67Mn0.55Ni0.25Ti0.2−xLixO2 (x = 0, 0.1, 0.2) indicate that both the O3 content and rate capability increases with Li substitution.151 Li was found to reside on the transition metal sites of the major P2 phase as well as alkali metal sites of the O3 phase. Using P2-Na0.5Fe0.5Mn0.5O2 as the parent material, Veerasubramani et al. investigated the criteria for synthesising biphasic positive electrodes via Li substitution.152 They found that when more than 10% Li is incorporated into the material, the O3 phase dominates as the main phase over the P2 structure. Having tested a range of compositions, they identified P2-rich Na0.5(Li0.1Fe0.45Mn0.45)O2 to be the best performing material. In line with these results, Bianchini et al. synthesised a P2-rich composite from earth abundant precursors with the formula P2/O3-Na0.67Li0.18Mn0.8Fe0.2O2 and found that the biphasic material displays an improved electrochemical performance relative to the Li-containing, single phase P2-Na0.85Li0.17Mn0.64Ni0.21O2 material.153 As such, it was proposed that the presence of a small amount of O3 phase may help to inhibit gliding of the main phase at high voltages.
Similarly, Guo et al. introduced Li into a P2-type phase to form a P2/O3 biphasic material with the formula Na0.66Li0.18Mn0.71Ni0.21Co0.08O2, and suggested that the larger c axis in the P2 component of the biphasic material relative to the pure P2 phase is beneficial for sodium diffusion.154 In contrast, the O3-rich P2/O3-Na0.7Li0.3Ni0.5Mn0.5O2 material synthesised via incorporation of Li into O3-NaNi0.5Mn0.5O2 was found to display the O3–P3 phase transformation during cycling (Fig. 15), limiting the electrochemical performance and demonstrating that the relative ratio of P2 and O3 phases is a critical factor in determining the materials structural stability at the charged state. As demonstrated by the synthesis of NaxLi0.18Mn0.66Co0.17Ni0.17O2+δ (x = 0.54, 0.66, 0.78 and 0.90) the addition of lithium may also induce the formation of P2/O′3 hybrid compositions, where O′3 represents a Li2MnO3-type phase (space group C2/m).155 Increasing the sodium content was reported to influence the surface morphology, leading to the growth of (102) and (104) facets and changing the side surface finish from ‘smooth’ to ‘ravine-like’. The most favourable morphology, comprising smooth surfaces with exposed 102 and 104 facets, was reported for the x = 0.66 composition, which retained a capacity of 186 mA h g−1 after 60 cycles.
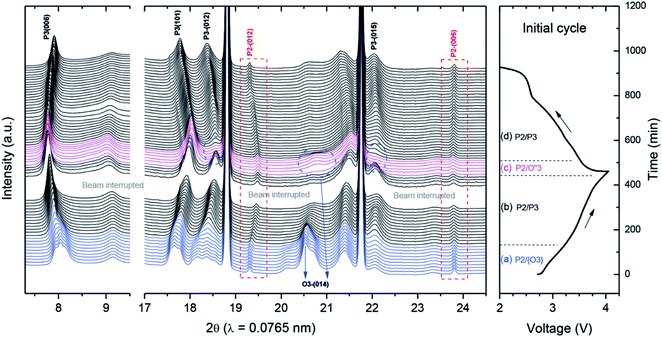 | ||
| Fig. 15 In situ synchrotron XRD of P2/O3-Na0.7Li0.3Ni0.5Mn0.5O2 during initial charge–discharge. While the P2 phase is retained, multiple phase transformations take place for the O3 component of the material. Reproduced with permission from ref. 158. | ||
Realising the importance of Co- and Ni-free materials for sodium-ion batteries, Yang et al. synthesised the biphasic P2 (34%)/O3 (60%) Na0.8Li0.2Fe0.2Mn0.6O2 material, containing a minor phase with C2/m symmetry.156 To investigate behaviour at high voltage, the material was cycled over a wide window of 2.0–4.6 V, which delivered an initial reversible capacity of 174 mA h g−1 and a capacity retention of 82% over 100 cycles at C/10. The capacity contribution was found to be dominated by the Fe3+/4+ redox couple, along with contributions from oxygen at high voltages and some reduction of Mn4+ to Mn3+ during discharge. Upon charging, several consecutive phase transitions (O → P → O) as well as a general loss in long-range order were identified using X-ray powder diffraction. Nonetheless, the biphasic nature of the material was preserved throughout cycling. The capacity vs. voltage curves exhibited a decrease in the average voltage over the first 20 cycles, which was attributed to some form of restructuring/ordering in the structure, such as migration of Fe or Li from the octahedral site to the sodium site in the material. 6/7Li solid-state NMR experiments confirmed the migration of Li from transition metal to alkali metal layers within the first cycle; subsequently the distribution of Li remained constant and hence it was suggested that lithium could act as a stabilizer.
Applying the principles discussed in Section 3.1, further improvements to P2/O3 biphasic materials can be made by tailoring the transition metal site occupancy as demonstrated by Hu et al. who compared the electrochemical performance of the Ti-free P2/O3-Na0.8Li0.27Mn0.73O2 composition with P2/O3-Na0.8Li0.27Mn0.68Ti0.05O2, prepared by Ti-substitution into the Mn site.157 The improved performance was attributed to mitigation of the Mn3+/Mn4+ redox couple, enhanced stability of the oxygen redox activity and retention of Li ions within the structure during cycling.
Overall, promising electrochemical performances have been reported for both P2-rich and O3-rich P2/O3 biphasic materials. The key parameters to consider here remain, the location and spread of the transition metals and dopants across the two phases, the nature of the material, i.e., an intergrowth of structures or mixture of individual particles, the ratio of the P2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O3 phases, phase evolution and electrochemical activity of each phase, and the influence the secondary or minor phase has on the stability of the primary phase near the charged state.
O3 phases, phase evolution and electrochemical activity of each phase, and the influence the secondary or minor phase has on the stability of the primary phase near the charged state.
Alternatively, substitution of electrochemically inactive elements such as Zn may induce the formation of a hybrid material. A core shell structure with the P3 phase located on the surface encompassing the core P2 phase was identified for the Na0.78Cu0.27Zn0.06Mn0.67O2 material using high-angle annular dark-field imaging (HAADF) and annular bright field (ABT) imaging techniques.161 Based on scanning transmission electron microscopy electron energy loss spectroscopy (STEM-EELS), Cu redox was found to take place in both the P2 and P3 phase, whereas Mn redox activity could only be detected in the P2 phase. The core shell material was found to inhibit formation of any highly disordered phases at high voltages, giving rise to good rate performance and cyclability.
In a study on NaxNi1/3Co1/3Mn1/3O2, Xu et al. make comparisons between single-phase, biphasic, and triphasic layered materials with comparable compositions.164 In terms of capacity and rate capability, the triphasic P2/O1/O3 material showed the best performance followed by the biphasic P2/O3 material and then the pure P2 phase. Operando XRD showed that the triphasic material can inhibit the irreversible P2–O2 transition at high voltages while improving the reversibility of structural transformations in the minor O1 and O3 phases. In contrast, the biphasic material displays an irreversible O3–P3 transition upon cycling and the single P2 phase material transitions to the “Z phase” during high voltage charging as seen in Fig. 16.
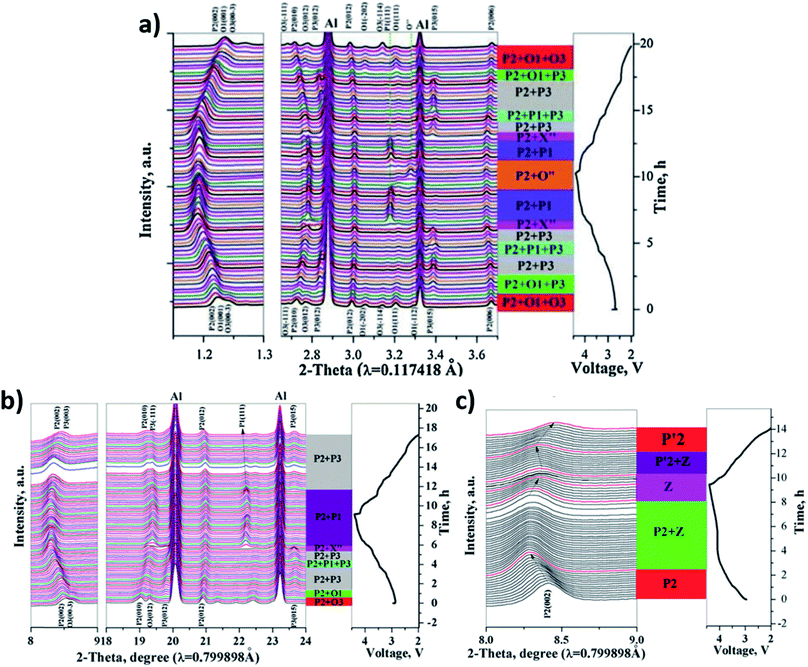 | ||
| Fig. 16 In operando XRD data for (a) P2/O1/O3 (b) P2/O3 (c) P2-NaxNi1/3Co1/3Mn1/3O2 cycling between 2.0–4.4 V at 0.1C together with their phase evolution. Reproduced from ref. 164 with permission from The Royal Society of Chemistry. | ||
Using high resolution XRD, Lee et al. identified the presence of four Na dominated phases (P2, O3, O′3, P3) and one Li dominated phase (O3) in the Li substituted sample, Na0.7Li0.3Ni0.5Mn0.5O2.158 However, various local environments were identified in the 7Li NMR suggesting that the Li may also reside in the Na phases. The presence of multiple phases, induced by incorporation of Li, was shown to improve the electrochemical performance. In situ XRD shows amalgamation of the Na-rich O3, O′3 and P3 phases into a single P3 phase and some irreversible extraction of Li from the O3 phase on the first charge. No phase transitions for the P2 phase were observed throughout, while the new P3 phase transitioned to an O3 phase at the charged state.
An improved performance in terms of capacity and average voltage was found for the O3 layered/spinel composite Na0.87Li0.25Ni0.4Fe0.2Mn0.4O2+δ electrode.166 The voltage profile of the composite material shows a reversible high voltage plateau while this plateau is irreversible in the spinel free material, suggesting that addition of the spinel phase contributed towards the enhanced structural and electrochemical stability, especially at high voltages, the mechanism of which is yet to be explored. Improved rate capability on the other hand could be ascribed to the improved charge transport kinetics due to direct connection between the 3D channels in the spinel phase and 2D channels in the layered phase modifying the diffusion pathway.166 A highly reversible transition at high voltages was also reported for the layered-tunnel intergrowth structure with the composition Na0.6MnO2.167 The highly reversible P2/tunnel to OP4/tunnel phase transition was detected using in situ XRD upon cycling the composite up to 4.3 V. Taking this further and combining P2, P3 and spinel structures to form the Na0.5[Ni0.2Co0.15Mn0.65]O2 nanocomposite, Hou et al. were able to synthesise a particularly stable composition for which no phase transitions were detected via ex situ XRD when cycled between 1.5 and 4.0 V vs. Na/Na+.168
3.3 Electrolytes
Layered oxide positive electrode materials are generally tested in Na half-cells against a Na metal counter electrode. The observed performance of positive electrode materials can be significantly influenced by the choice of electrolyte, application of surface coatings and inclusion of binders because they contribute toward the formation of a surface layer.174 The choice of electrolyte is particularly pertinent when considering the charged state of the positive electrode material because typically, the charged state cut off voltage for a cell is limited by the voltage window within which the electrolyte remains stable.The electrochemical stability of an electrolyte is determined by the salt anion onset potentials for oxidation or reduction. ClO4− and PF6− are known to be stable up to 4.5 V vs. Na/Na+ which, in combination with their good chemical stability, and low cost makes them suitable components in sodium-ion batteries.177 Despite being suitable candidates, they do present some limitations: ClO4− is a strong oxidant, meaning it is primarily of academic interest, while PF6− has safety issues at elevated temperatures and is particularly moisture sensitive.175 Alternative Na counter ions that have been reported such as BF4−, CF3SO3− (Tf) and [N(CF3SO2)2]− (TFSI) display more significant drawbacks. BF4− and Tf have stronger interactions with Na+ which reduces the availability of charge carriers, reducing the ionic conductivity, while TFSI (and Tf) are corrosive to the Al current collector. Consequently, NaClO4 and NaPF6 remain the Na salts of choice for organic liquid electrolytes, and so the structural stability of positive electrode materials beyond 4.5 V is incidental.178,179
3.4 Surface coatings
An alternative method to modifying the solid electrolyte interface (SEI) of layered materials, and potentially enhancing their performance, is by applying a surface coating. Coatings reduce atmospheric and electrochemical corrosion at the interface, thereby improving the structural and electrochemical stability and in some cases the electronic and ionic conductivity.189 Minimising structural transformations that take place at the charged state is therefore important in order to preserve the coating throughout cycling. Upon exposure to air, layered oxides easily absorb water leading to the formation of an electrically insulating layer at the surface composed of NaOH and/or NaCO3.190,191 As such the surface modifications documented for lithium-ion battery electrodes are not all necessarily applicable to sodium-ion battery materials.192 Due to the sensitivity of layered transition metal oxides to air, they should ideally be handled in a glovebox during electrode fabrication and cell preparation. It is also possible for coatings to influence the anion redox activity of high voltage positive electrode materials. There are several studies that have focused on limiting the evolution of O2 from Li-based transition metal oxides via application of a surface coating.193–196 However, the interplay between coatings and anion redox reactions in Na layered oxides is relatively unexplored and the mechanism is not well understood.197,198In addition to Al2O3, other metal oxide coatings have been investigated as surface coatings for sodium positive electrode materials. Kaliyappan et al. performed a comparative study on Al2O3, ZrO2 and TiO2 as surface coatings for P2-Na0.66(Mn0.54Co0.13Ni0.13)O2.205 The oxide surface coatings were found to improve the cycle stability of the positive electrode material when cycled up to a high voltage of 4.5 V. The greatest improvement was reported for Al2O3 which was attributed to its high band gap energy (9.00 eV) relative to ZrO2 (5.80 eV) and TiO2 (3.18 eV) meaning the Al2O3 surface coating remains redox-inactive throughout cycling.206 However, the greatest improvement in rate performance was observed for the ZrO2-coated material due to the its high fracture toughness.
A number of benefits of MgO coating have been reported including the suppression of side reactions between the cathode and electrolyte, including dissolution of transition metal ions into the electrolyte, and stabilisation of the CEI layer, all of which contribute towards the layered oxide structural stability.207 For instance, the capacity retention of Na0.67Mn0.5Fe0.5O2 after 100 cycles when cycled at 1C increased from 20% to 72% upon application of an MgO coating.208 Moreover, an MgO coating has been shown to mitigate undesirable high voltage phase transformations and reduce the interfacial resistance during high potential cycling for P2-Na0.5Ni0.33Mn0.67O2, P2-Na0.67Mn0.5Fe0.5O2 and O3-Na[Ni0.5Mn0.5]O2, the mechanism of which is still not fully understood.207–209 Similarly, Na2Ti3O7 has been shown to be effective in suppressing high voltage P2–O2 phase transitions in P2-Na2/3Ni1/3Mn2/3O2. In the process of increasing the coating content of Na2Ti3O7, the a lattice parameter and unit cell volume was found to increase and therefore, in view of larger ionic radius of Ti4+ (0.605 Å) compared with Mn4+ (0.53 Å) it was tentatively proposed that Ti4+ had been incorporated into the structure, which suppresses the sodium ion/vacancy ordering and the P2–O2 phase transition during cycling.210,211
By coating a layered oxide material with a second, related layered oxide material it is also possible to instigate doping. Zhang et al. demonstrated a facile method to surface coat and dope P2-Na0.7MnO2 in a single step process using P2-Na0.7Ni0.33Mn0.67O2.212 During the process, Ni is doped into the bulk material. The resulting material displays enhanced capacity retention of 68.9% over 100 cycles, compared to 20.7% for the unmodified P2-Na0.7MnO2 material, without sacrificing the initial discharge capacity. Conversely, through Ti enrichment to generate the O3-NaMn0.8Ti0.1Ni0.1O2 composition, the material was found to form an all-titanium protective layer. Guo et al. showed that the resultant spinel-like titanium oxide coating improved the structural and electrochemical stability relative to the Ti-free equivalent. The coating prevents contact between manganese and the external environment, thereby suppressing dissolution of Mn at the electrode/electrolyte interface as well as degradation of the positive electrode material upon cycling.189 The synergy of Ti4+ doping and TiO2 coating has also been reported for the O3-NaMn0.33Fe0.33Ni0.33O2 composition.213 The TiO2 layer mitigates side reactions at the surface, while Ti4+ doping enlarges the interslab spacing, facilitating sodium ion diffusion.
The above examples demonstrate that optimizing the particle surface composition and morphology of positive electrode materials is critical for improving the electrode–electrolyte interface and thus enhancing the materials cycling performance. Moreover, surface coatings have been shown to improve the stability of layered oxides in high voltage regions which facilitates the extraction of sodium ions and therefore the attainable capacity. Although limiting the cut-off voltage enables detrimental, high voltage phase transitions to be avoided, it decreases the reversible capacity and energy density of the battery. Although surface coatings are a promising means to improving the high voltage structural stability of layered oxide positive electrode materials without compromising the maximum cell voltage, the mechanism by which the coatings acts remain elusive to probe and likely require the combined analysis of both surface and bulk in situ techniques.
3.5 Sodium compensation additives
While sodium-ion half-cells are suitable for laboratory-scale material characterization, it is important to acknowledge that the behaviour of electrode materials in half-cells does not translate directly into full cells. When cycled against a hard carbon anode material, the formation of the SEI at the anode–electrolyte interface results in the irreversible consumption of sodium ions from the positive electrode material.218 The irreversible consumption of sodium ions can pose a significant problem for P2-type layered oxide structures which are inherently sodium deficient. On top of methods discussed earlier, such as electrolyte optimization (Section 3.3) and surface modifications (Section 3.4), the addition of sacrificial sodiation reagents to the anode and/or cathode material, such as sodium powder,214 NaN3,219 Na3P,220 Na2NiO2,221 Na2C4O4,218 Na2CO3,222 or NaNO2,223 has been reported to compensate for the sodium deficiency and significantly improve the performance of sodium ion full cells. For example, Guo et al. showed that the capacity retention in a full cell based on a hard carbon negative electrode and a P2-Na2/3Ni1/3Mn1/3Ti1/3O2 positive electrode can be increased from 63% to 85% after 200 cycles at 0.2C with a voltage window of 2.0–4.3 V by the addition of Na2C2O4.218 Exactly how these additives alter the charged state behaviour of layered oxide positive electrode materials remains an interesting avenue for future studies to explore.4. Techniques for probing the charged state
The studies discussed above have highlighted that a variety of useful information can be gained using various complimentary analytical techniques. During cycling, batteries present a complex system in which both chemical and physical changes are taking place simultaneously, such as structural expansion/contraction, phase transitions, and side reactions which may result in gas evolution or parasitic capacity loss. Improving understanding of the behaviour of the positive electrode material at high voltages could provide a route to improving the energy density and cycle life of sodium-ion batteries. Recent advances in both instrumentation and methodology continue to push the boundaries of materials characterisation, while better accessibility has enabled routine, comprehensive evaluation of potential positive electrode materials for sodium-ion batteries.224–226In situ studies have generated great interest as they allow for these changes to be correlated directly to the electrochemical state of the battery. In situ or operando characterisation is favoured for its ability to study the active materials under operating conditions. Typically, these studies require the use of modified cells or specially designed cells which allow for the materials of interest to probed. When modifying or designing cells, care must be taken to ensure that alterations do not have an adverse effect on the electrochemical behaviour of the system. For example, modified coin cells for in situ X-ray scattering studies have shown different electrochemical performance to identical cells prepared in unmodified casings.227 These considerations are of particular importance when attempting to resolve complex electrochemical processes which occur at the charged state, where the electrochemical system is not at equilibrium. For example, phenomena such as phase separation or reaction inhomogeneities may be kinetically driven, and can hence only be observed using operando studies. Contemporary characterisation techniques enable a wealth of complimentary information to be gathered, at various dimensions and scales, focusing on localised regions or bulk samples, and with varying time resolution. The charged state behaviour of positive electrodes may be illustrated via bulk phenomena such as structural changes or diffusion mechanisms. However, subtle inhomogeneities in sodium distribution within the electrode or transport mechanisms may be masked in these measurements. Use of other techniques, such as PDF analysis, to probe the local environment are particularly important when attempting to elucidate the subtle transition metal migration pathways and ARR. It should be noted that the challenges with low concentrations of elements and environments, e.g. small amounts of vacancies, small phase fractions, small percentage of transition metal migration, all make data analysis significantly challenging. These are compounded at the charged state where multiple pathways are possible. Meanwhile, ex situ analysis of electrode materials can also provide complimentary information and offers compatibility with a greater variety of characterisation techniques. For ex situ studies, electrode materials may be extracted from cells which have been charged to high voltages, but care is required to ensure that measurement results are not perturbed by contamination while handling the sample between battery cycling and characterisation, or relaxation effects.
4.1 Analysis of cycling data
Electrochemical characterisation techniques can provide a wealth of insight into the chemical behaviour of electrode materials at various states of charge (or levels of sodiation). The voltage vs. capacity profile observed during charge and discharge of batteries and can be used to elucidate a variety of information beyond the capacities delivered by the electrode materials. Characteristic features in the voltage profile can provide indications about the electrochemical reactions taking place in the electrode materials, such as kinetics, phase transitions and or reveal unfavourable side reactions which may contribute to capacity fade.228,229 For example, steps in the profile may be indicative of phase transitions. Furthermore, the relative change in shape and features of the voltage profile over successive cycles can indicate which electrochemical features contribute to capacity loss or impedance growth.230 A shift in the potential at which the features are observed may also be observed as the applied current is varied, which can be indicative of electrode polarisation.116,231 More recently, the application of statistical analysis and machine learning to voltage capacity profiles has also highlighted the potential for them to be a useful prognostic indicator to predict cycle life and cell failures.232The measured cell voltage is defined by the difference in sodium electrochemical potential between the two electrodes, and in the case of half-cells typically reported in literature, this means the potential is measured vs. sodium metal. The measured voltage varies with the sodium content in the electrode. Further inferences about the sodium intercalation mechanism in host materials can be drawn from the voltage (V) vs. capacity (Q) profile by derivation of the data. Two derivatives can be used to produce differential capacity (dQ/dV vs. V) or differential voltage (dV/dQ vs. Q) curves. Peaks in dQ/dV curves provide information about phase equilibria, while peaks in dV/dQ curves provide information about phase transitions.229 Some studies correlate these peaks to changes in oxidation state or phase transitions.25,29,233 However, this is typically implied using data from complementary techniques such as XPS, XANES or in situ XRD. More literally, dQ/dV curves describe the incremental capacity delivered by a device measured as a function of applied voltage. An example of a dQ/dV curve and the corresponding measured Q vs. V curve for the P2-Na2/3Co1/2Ti1/2O2vs. Na/Na+ half-cell is shown in Fig. 17. The peaks in these curves indicate the potentials at which the majority of the capacity is delivered by the battery. The position, height and shape of peaks in the differential curves can therefore be indicative of changes in electrochemical processes over time. For example, the width of peaks may provide information about the inhomogeneity of processes occurring in the electrode material. In summary, differential voltage analysis makes features in the V vs. Q data clearer and allows for possible quantification of the electrochemical processes taking place, which can particularly be useful to decipher the complex behaviours of positive electrode materials at high voltages.234
 | ||
| Fig. 17 Differential capacity (dQ/dV) vs. potential (V) of P2-Na2/3Co1/2Ti1/2O2, cycled vs. Na/Na+ in an electrochemical half-cell. Reproduced with permission from ref. 240. | ||
Other electrochemical techniques such as electrochemical impedance spectroscopy (EIS) or potentiostatic/galvanostatic intermittent titration techniques (PITT/GITT) can provide insight into the bulk conductivity of the electrode material. In both of these techniques, extracting meaningful information can be difficult due to impedance contributions from the various cell components. Three-electrode cell configurations have been demonstrated as a way to deconvolute the different impedance components in EIS measurements.235 PITT or GITT measurements can be conducted as part of conventional electrochemical testing, by using current pulses and open-circuit sequences to measure the resulting overpotential and its decay. However, as these measurements are applied to the entire cell, variations in the electrode's resistance must be decoupled from other sources of resistance such as the electrolyte, electronic contact resistance, or charge transfer resistance.236,237 Repeated cycling to high voltages may further increase the cell resistance, typically due to electrolyte decomposition.238 Furthermore, the occurrence of phase transitions creates additional challenges for interpreting PITT or GITT measurements when investigating the performance of positive electrode materials at the charged state.239
4.2 Structural characterisation using scattering studies
Scattering techniques, such as powder X-ray diffraction (XRD) or neutron powder diffraction (NPD) can be used to reveal structural information of electrode materials before, after or during cycling, including identifying phase transitions, lattice expansion and contraction or even atomic scale information about site occupancies or the movement of elements within the structure. X-ray radiation and neutron radiation differ in the way they interact with the sample, with X-rays scattering from electron density of atoms, while neutrons scatter from the nuclei of atoms in the sample.241,242 Hence compared to X-rays, neutrons tend to scatter more strongly from certain lighter elements in the presence of heavier elements, which can be useful for detecting sodium distributions in the electrode materials.243 The use of in situ diffraction to study structural changes in real-time has been well documented and used to study a variety of different functional materials.244 These techniques are especially useful for energy storage materials as they allow for the electrochemical state of the cell to be controlled and directly correlated to the structural changes taking place.245–250 During electrochemical cycling, the electrode materials are not under equilibrium conditions, allowing dynamic structural changes which can occur at high levels of de-sodiation to be captured.30,63 The structural evolution of positive electrode materials for sodium-ion batteries during high voltage cycling has been investigated using in situ scattering in several studies.35,41,164,251–256 Typically, quantification of diffraction data can be undertaken using peak fitting or Rietveld refinement to fit structural models to the Bragg reflections in the diffraction data.242 More recently, PDF analysis of scattering data has become more accessible to researchers, thanks to developments in instrumentation, software and expertise.257 This method of analysis takes advantage of the entire diffraction pattern, both Bragg scattering and underlying diffuse scattering, to extract information about short-range ordering using information contained in the broad, less well-defined features of the diffraction pattern.242 PDF analysis of diffraction data collected from energy storage materials has been reported in a number of studies.258–261 A particularly relevant example was presented by Talaie et al., who studied the effect of Ni substitution on the layered P2-Na2/3−z[Mn1/2Fe1/2]O2 system using a combination of operando XRD and PDF analysis.43 The PDF profiles presented in this study are shown in Fig. 18. These functions are generated by applying a Fourier transform to the diffraction data, yielding a spectra with characteristic peaks which can be assigned to various interatomic distances in the structure.242 By producing fits for the PDF data, the authors were able to model the structure of the z ≈ 0.5 material, and find evidence for the migration of transition metal ions into tetrahedral sites at high potential. Despite significant electrode polarization, the migration was found to be completely reversible in this P2-type system. | ||
| Fig. 18 Example of PDF data for (a) P2-Na0.67Fe0.5Mn0.5O2 and (b) Na0.14Fe0.5Mn0.5O2. PDF analysis can provide information about the inter-atomic bond lengths in the structure. In this example M–O and M–M distances are highlighted in blue and yellow respectively; second neighbour in-plane M–O and M–M distances are highlighted in lavender, and characteristic interlayer M–M distances are highlighted in green. Reproduced with permission from ref. 43 under a CC BY 4.0 licence. | ||
4.3 X-ray absorption spectroscopy
X-ray absorption spectroscopy (XAS) is an X-ray scattering technique in which the absorption coefficient of the sample is measured as a function of the wavelength of the incident radiation. XAS offers good elemental selectivity and chemical sensitivity, and can be used to probe the local chemical environment of elements of interest within the sample, thereby providing information about changes in oxidation state as well as corresponding atomic co-ordination.262 The absorption spectrum is typically considered in two major regions, the near edge region which covers from a few eV below the absorption edge to 50 eV above the edge, and the far from edge region which covers from 50 eV above the absorption edge and beyond. The analysis of these two regions is considered independently and are referred to as X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine-structure (EXAFS) respectively.263 XANES data is relatively straightforward to analyse and can be used to provide qualitative and quantitative data about the oxidation states of elements of interest, site symmetries and the strength of covalent bonding within the structure. The interpretation of EXAFS data can be quite involved, but fitting results can be used to reveal information about site co-ordination, bond lengths, and identify neighbouring elements. Soft XAS, where the energy range of the X-ray source is <1 keV, is sufficient for the analysis of low-Z elements and also the L-edges of 3d transition metal elements which are commonly present in layered positive electrode materials. Both ex situ and in situ studies have been carried out on sodium-ion battery systems.264 Recently, Wang et al. studied a P2-type layered material with composition Na2/3Zn1/4Mn3/4O2 in which the unfavourable P2–O2 transition is suppressed, which significantly improves the cycling stability and rate capability of the NaxMnO2 system.265In situ XRD confirmed that the transitions were suppressed during cycling to 4.5 V. The authors coupled this with in situ XAS studies to investigate the influence of Zn-doping on the electronic structure of the material. In situ XAS data, see Fig. 19, collected at the Mn K-edge exhibited a smaller energy shift in the Zn-substituted material compared to the pristine material, suggesting the redox activity of Zn allows the Mn to maintain a higher oxidation state during cycling. This in turn avoids the Jahn–Teller distortion associated with the reduction of Mn4+ to Mn3+, thereby suppressing the P2–O2 transition. | ||
| Fig. 19 X-ray absorption spectra collected at various states of charge from the Na2/3Zn1/4Mn3/4O2 electrode at the Mn K-edge. (a–c) Show XANES data and (d–f) show the Fourier transformed EXAFS during the first charge, first discharge, and second charge processes, respectively. Reproduced with permission from ref. 265. | ||
4.4 Mössbauer spectroscopy
Mössbauer spectroscopy is an isotope specific technique, sensitive to elements that have low lying excited states as well as a long-lived excited state, that provides information about the local environment of a nucleus. It is based on the phenomenon discovered by Rudolf Mössbauer in 1957 that the absorption and emission of gamma rays by nuclei bound in a solid takes place with minimal loss of energy from recoil of the nuclei.266 To record a Mössbauer spectrum, the sample is irradiated by an oscillating radiative source and absorption of gamma-rays are recorded as a function of oscillating velocity, see Fig. 20. When the energy of the gamma-rays matches the energy of a nuclear transition in the element under investigation, the radiation is absorbed giving rise to a peak in the spectrum. To this end, the sample must be sufficiently thin to allow for the penetration of gamma-rays.267 Since the energy levels of the absorbing nuclei is dependent on its environment, the technique can be used to provide information about the oxidation state of specific atoms.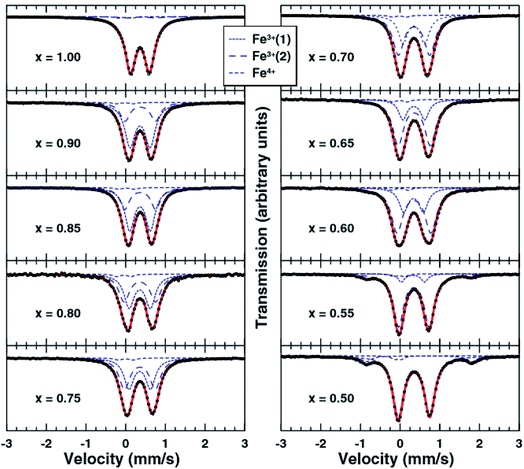 | ||
| Fig. 20 57Fe Mössbauer spectra of NaxFexMn1−xO2. The dashed lines represent the fitting components which sum together to yield the solid lines. The data are represented by black circles. Reproduced with permission from ref. 271. | ||
Unlike in lithium-ion batteries and sodium super ion conductor (NASICON) iron phosphate-based materials, reversibility of the Fe3+/4+ redox couple has been shown in a variety of sodium layered oxide materials.268 In the context of sodium-ion batteries, 57Fe Mössbauer spectroscopy is employed to probe the valence state of Fe at various states of charge/discharge. For example, Yabuuchi et al. used the technique to show that the Fe3+ present in P2-Nax[Fe1/2Mn1/2]O2, made from earth-abundant elements, is electrochemically active based on the Fe3+/4+ redox couple.33 For P2-Na2/3Mn1/3Fe1/3Co1/3O2, simultaneous oxidation of Co3+ and Fe3+ was found to take place upon charging up to 4.1 V.269 At the cut-off voltage of 4.1 V, approximately 40% of Fe present in the sample was found to be in the 4+ oxidation state. Given the low voltage hysteresis observed, it was suggested that the use of Co in combination with Fe may stabilize the oxidation of Fe3+ to Fe4+.
Due to their effect on neighbouring Fe3+ ions, 57Fe Mössbauer spectra can also be used to detect Na vacancies. Upon extraction of sodium ions from O3-NaxFexTi1−xO2 (x ≥ 0.75), Thorne et al. were able to identify several Na vacancies located near Fe3+ sites.270 Moreover, the concurrent oxidation of Fe3+ to Fe4+, accompanied by significant structural distortion, was proposed to be a major source of hysteresis and capacity fade. Analogous to the electrochemical behaviour of the O3-NaxFexMn1−xO2 (x > 0.65) system, the Mössbauer spectra showed that the cyclability can be improved by restricting the upper voltage so that the Fe3+/4+ redox couple is not utilized.271 Alternatively, inactivity of the Fe3+/4+ redox couple can be achieved by careful choice of composition. For instance, Mössbauer spectroscopy showed that the Fe3+/4+ redox reaction is not active up to 4.3 V in P2-Na2/3Mn0.8Fe0.1Ti0.1O2.75
While studying the changes in Fe oxidation states of O3-NaFeO2 electrodes during cycling via ex situ Mössbauer spectroscopy, Lee et al. noticed the instability of Fe4+ in a battery environment.46 During open circuit storage of the desodiated electrode, more than 20% of the Fe4+ species that had been generated upon charging spontaneously reduced back to Fe3+. Noting that Fe4+ is not stable outside electrochemical cells and therefore ex situ investigations may not provide accurate results, a limited number of in situ Mössbauer studies characterising the reversible oxidation of Fe3+ to Fe4+ have been published on Li-based electrochemical systems.272,273 To the best of our knowledge there are no reports of in situ Mössbauer studies on sodium-ion battery systems.
4.5 Nuclear magnetic resonance spectroscopy
Nuclear magnetic resonance (NMR) spectroscopy measures the magnetic field around atomic nuclei in order to provide information about the local environment of particular atoms. The technique is based on the principle that nuclei are electrically charged and certain nuclei have a spin which causes them to act as a magnet. In most molecular spectroscopy techniques, the excitation of molecules or electrons to higher states is measured. In the case of NMR spectroscopy an external magnetic field must be applied to the sample in order to generate two different energy levels.274 When an external magnetic field is applied to the sample, a radio frequency emission can be used to excite the nucleus to a higher spin state. The energy transfer required for this excitation process is dependent on the effective magnetic field at the nucleus. This field is dependent on the electron shielding around the nucleus, which is in turn dependant on the chemical environment or co-ordination of the atom, and thus information about the nucleus' local environment may derived from the spectra. For solid-phase media, such as battery electrodes, solid-state NMR (SS-NMR) of particular nuclei, such as 6Li, 7Li or 23Na, can be used to study the lithium or sodium storage mechanism.275 Several studies have successfully used SS-NMR to study the atomic environments and lattice dynamics (including the diffusion of ions) in various sodium-ion battery materials.276–279Recently, Yang et al. investigated the effect of lithium and iron co-doping in the layered NaxMO2 system by characterising P2-Na0.66Li0.18Fe0.12Mn0.7O2.278 Using 7Li NMR studies, the authors were able to identify three different local environments of lithium within the material's structure, see Fig. 21. The resonances at ≈1600 ppm and ≈1450 ppm were attributed to lithium nuclei in an ordered honeycomb arrangement within the transition metal layers, and the resonance at ≈750 ppm was attributed to lithium in the sodium layer. NMR quantification showed that at the charged state a significant amount of lithium had migrated from the transition metal layers into the sodium layers, 17% to 80%. After discharging to 1.5 V, the fraction of lithium in the transition metal layer decreased to 39% and appears to reach an equilibrium value around ≈21% after 50 cycles. Complementary in situ XRD data showed that the unfavourable P2–O2 transition was avoided during cycling of this material, enabling good capacity retention during cycling to 4.5 V. The migration of lithium between the sodium and transition metal layers appears to help stabilise the P2 structure even at high levels of de-sodiation at the charged state.
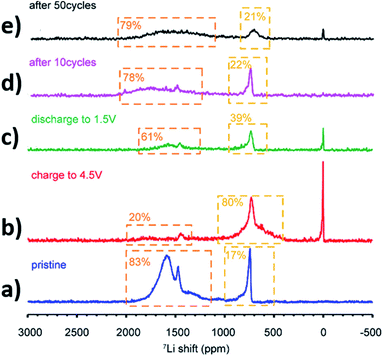 | ||
| Fig. 21 7Li NMR spectra of Na0.66Li0.18Fe0.12Mn0.7O2 electrode samples at various states of charge: (a) pristine powder (blue), (b) after initial charge to 4.5 V (red), (c) after first discharge to 1.5 V (olive), (d) after 10 cycles (violet), and (e) after 50 cycles (black). Reproduced with permission from ref. 278. | ||
4.6 Electron paramagnetic resonance spectroscopy
As opposed to the utilisation of the inherent spin of the atomic nuclei to perform NMR experiments, electron paramagnetic resonance (EPR) spectroscopy utilises the spin of electrons in paramagnetic materials. While information about Na–O–M interactions between the distinct layers can be obtained by NMR spectroscopy, EPR spectroscopy probes paramagnetic ions within the MO2 layer directly. The data obtained provides information about the oxidation state of transition metal ions and their relation to the local structure of sodium nuclei, which complements the information about the sodium environment that can be obtained via23Na NMR spectroscopy.56EPR has been used to show that the charge compensation of P3-NayCo1/3Ni1/3Mn1/3O2 (0.38 < y ≤ 0.75) upon extraction of sodium ions is achieved by selective oxidation of Ni2+ to Ni3+ and Ni4+, while the Co and Mn ions retain their valance states of +3 and +4 respectively, see Fig. 22.58 It was also found that a Mn oxidation state of +4 is maintained for the P3-NayNi1/2Mn1/2O2 (0.5 ≤ y < 0.75) composition, thereby minimising phase transitions induced by Jahn–Teller distortion of Mn3+.280
 | ||
| Fig. 22 EPR spectra of (a) P3-Na2/3Co1/3Ni1/3Mn1/3O2 (b) P3-Na1/2Ni1/2Mn1/2O2 (c) P2-Na2/3Ni1/3Mn2/3O2. Information about the transition metal oxidation states can be extracted by fitting Hamiltonian parameters the spectra. Reproduced with permission from ref. 56. | ||
4.7 Microscopy
A variety of microscopy techniques are available for studying materials at the microscale and nanoscale such as optical, electron, X-ray and scanning probe microscopy. Compared to other characterisation techniques discussed, which typically characterise the bulk electrode material or specific regions, microscopy can resolve materials' details at the particle level. For batteries in particular, these techniques can be used to derive information about particle size distributions, morphology, packing density, or porosity, and also monitor for signs of strain or stress such as particle cracking, electrode contact or degradation of interfacial layers.281In their study of the P2-type Na2/3Ni1/3Mn2/3O2 system, Wang et al. were able to identify a correlation between the P2–O2 phase transition, observed when the cell was charged to 4.2 V, and the generation of a high density of intragranular cracks using a combination of complementary techniques including SEM and TEM.233 This correlation explains the significant decay in performance after repeated cycling to high cut-off voltages. The transition generates unfavourable stress/strain at the P2/O2 phase boundary which was identified as the preferential site of crack initialisation. Similar observations of particle cracking have been observed in several lithium-ion battery systems, where performance degradation has also been attributed to the exposure of new surfaces to the electrolyte causing electrode surface decomposition and electrolyte consumption.285–288
A number of in situ electron microscopy studies have also been used to study the dynamic processes occurring in working batteries which have been summarised in some informative review articles.289,290
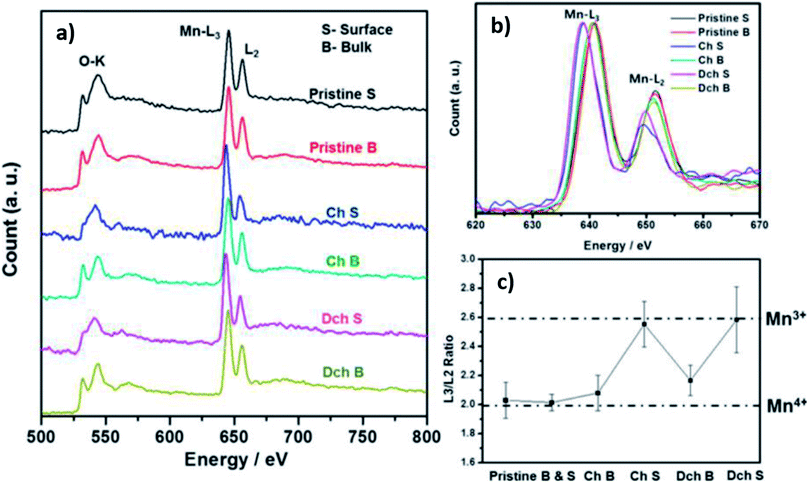 | ||
| Fig. 23 EELS spectra measured at the surface (S) and in the bulk (B) of NaxNi0.23Mn0.69O2 corresponding to (a) the O K-edge and Mn L-edge (b) Mn L-edge only (c) the Mn L3/L2 ratio, which is inversely proportional to the Mn charge state. Reproduced with permission from ref. 26. Copyright 2017 American Chemical Society. | ||
Using the combined STEM-EELS technique, Li et al. observed the presence of Mn charge ordering in Na5/8MnO2. Alongside findings that there exists a superstructure, the cooperative Jahn Teller effect was found to be linked with sodium ion/vacancy ordering. Overall, the work emphasises the important role that structural details play in determining electronic behaviour of a material.129 Participation of oxygen anions in the initial charge compensation mechanism of P2-Na0.78Ni0.23Mn0.69O2 has also been explored using EELS and XAS.26 In the electrochemically cycled particles, a difference in the electronic structure of the bulk and surface was found, whereby transition metal ions are in a lower valence state relative to the bulk. Moreover, loss of the O K-edge pre-peak at the surface signifies oxygen activity upon charging, see Fig. 23. It was therefore proposed that the charge compensation mechanism during the first cycle involves oxygen redox activity, resulting in a surface to bulk transition metal gradient.
Using a combination of operando XRD and TXM-XANES, Xie et al. studied the high voltage structural evolution of O3-Na[Ni1/3Fe1/3Mn1/3]O2.293 The TXM-XANES mapping was able to complement the structural evolution observed in the XRD data to reveal the distribution of phases in the solid-solution which forms during (de-)sodiation. The mapping revealed non-uniform distribution of mixed-phase zones, with compositions spanning a range varying between two thermodynamic phases, NaNi1/3Fe1/3Mn1/3O2 and Ni1/3Fe1/3Mn1/3O2, essentially providing a visualisation of the reaction front during the (de-)sodiation.
4.8 Computational studies
The use of computational simulation studies to assist with the atomic-scale prediction of a material's structure, reaction pathways, and ion mobility has played a vital role in the characterisation of layered positive electrode materials.296 Computational studies are complimentary to experimental studies; computational results can be used to determine appropriate experimental parameters, while experimental results can help to inform simulation input parameters for improved accuracy of computational models.For the study of solid-state materials, two main classes of computation modelling are typically used: interatomic potential-minimisation methods, which may use static lattice or molecular dynamics models, and electronic structure methods, which may employ density functional theory (DFT), for example. Several in-depth reviews have discussed how these techniques have been employed to study a variety of energy storage and energy generation materials. In particular, the versatility of computational studies in revealing atomic scale structures, processes and parameters which contribute to the behaviour of functional materials is considered.296–299
Sodium layered oxides exhibit numerous stable polymorphs and vacancy ordering arrangements at various levels of (de-)sodiation.125 By using the free energies determined from first principles calculations, the equilibrium voltages between the various stable structures can be determined, and this subsequently allows for the voltage profile of these materials to be constructed as a function of sodium concentration.299 Several studies have used the simulated voltage profile in tandem with experimental observations to identify the intermediate phases which form during cycling.300 This is of particular interest for studying the high voltage behaviour of sodium layered oxide materials where complex vacancy ordering mechanisms arise to compensate for the sodium deficient structure. For example, Toumar et al. used DFT calculations to generate theoretical electrochemical voltages curves for various O3-type layered oxides.301Fig. 24 shows an example of the computed voltage curve for O3-type NaxCrO2, along with the predicted ground-state vacancy orderings. Voltage curves were also calculated for other NaxMO2 systems, where M = Ti, V, Mn, Fe, Co, and Ni. The authors were able to identify 18 orderings which appear as ground states in one or more of the seven systems which were studied. In another study, Bai et al. also made use of DFT calculations to investigate the anionic redox activity of the P2-Na2/3Mn7/9Zn2/9O2 system at high voltages.107
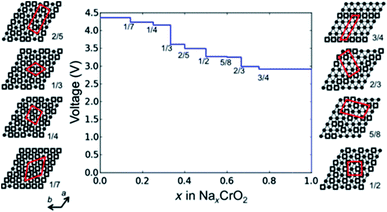 | ||
| Fig. 24 Computed O3-lattice voltage curve with illustrations of the predicted ground-state sodium ion/vacancy orderings for NaxCrO2 at various states of charge. Reproduced with permission from ref. 301. | ||
5. Summary and outlook
Layered oxides with the chemical formula NaxMO2 are a promising class of positive electrode material for application in rechargeable sodium-ion batteries. However, their performance is often limited by structural instability at the charged state, as a result of the host lattice being sodium deficient. This structrual instability gives rise to various structural phenomena as the lattice rearranges to accommodate the vacancies, such as phase transitions, migration of transition metals into the sodium layer and charge balancing via reduction of anions. If exploited appropriately, the reversible migration of atoms between the transition metal layer and alkali metal layer upon charging can stabilise the structure enabling more sodium and hence capacity to be extracted; the same outcome could be achieved through utilization of the oxygen redox reaction without loss of O2; or optimising the phase transitions to remain reversible. Continual advancement in knowledge regarding transition metal migration, phase transitions and the oxygen redox reaction in sodium layered oxides are essential to their development.As summarized in this review, there are several options for improving the structural stability of layered oxides at the charged state. Tuning the chemical composition is the method that has been most widely explored to date. Research in this space highlights the cooperative ability of several elements to compensate for structural instability and optimise reactions at high voltage. While there are still opportunities to fine tune the chemical composition of sodium layered oxides, investigations into alternative modifications such as composite materials, which exploit the assets of multiple-phase materials, or optimization of the cathode electrode interface could be more rewarding. Developing electrolytes and understanding the interaction between solid-state electrolytes and sodium layeredoxides could deliver viable solutions for long term, safe and reliable cycling.
To gain a mechanistic and structural understanding of layered materials on the atomic scale, cutting edge characterisation techniques are required. The wide range of complementary techniques available today has enabled numerous prospective sodium layered oxide materials to be scrutinised. While ex situ techniques may be more accessible, the development of in situ techniques has and will continue to facilitate the acquisition of more accurate information, correlated directly to device performance. Furthermore, the high resolution and intensity offered at synchrotron facilities will be key for characterising battery materials, probing both their long-range and short-range ordering. The knowledge and understanding gained from both existing and state-of-the-art techniques will be imperative for the continual development of next generation battery materials for large scale storage of renewable energy.
Conflicts of interest
The authors declare there are no conflicts of interest to address.Acknowledgements
J. S. and D. G. contributed equally to this work. J. S. acknowledges the support of UNSW/ANSTO for the PhD scholarship. N. S. would like to thank the Australian Research Council (ARC) for financial support provided via grants DP200100959 and FT200100707. The authors acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.References
- D. Lindley, Nature, 2010, 463, 18 CrossRef CAS
.
- B. Nykvist and M. Nilsson, Nat. Clim. Change, 2015, 5, 329–332 CrossRef
.
- G. L. Soloveichik, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 503–527 CrossRef CAS
.
- M. M. Thackeray, C. Wolverton and E. D. Isaacs, Energy Environ. Sci., 2012, 5, 7854–7863 RSC
.
- D. Kamath, R. Arsenault, H. C. Kim and A. Anctil, Environ. Sci. Technol., 2020, 54, 6878–6887 CrossRef CAS
.
- H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338 RSC
.
- A. Poullikkas, Renewable Sustainable Energy Rev., 2013, 27, 778–788 CrossRef
.
- H. S. Hirsh, Y. X. Li, D. H. S. Tan, M. H. Zhang, E. Y. Zhao and Y. S. Meng, Adv. Energy Mater., 2020, 10(32), 2001274 CrossRef CAS
.
- J. Barker, M. Saidi and J. Swoyer, Electrochem. Solid-State Lett., 2003, 6, A1–A4 CrossRef CAS
.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, Angew. Chem., Int. Ed., 2015, 54, 3431–3448 CrossRef CAS
.
- Y. Lu, L. Wang, J. Cheng and J. B. Goodenough, Chem. Commun., 2012, 48, 6544–6546 RSC
.
- M. H. Han, E. Gonzalo, G. Singh and T. Rojo, Energy Environ. Sci., 2015, 8, 81–102 RSC
.
- C. Delmas, Adv. Energy Mater., 2018, 1703137, DOI:10.1002/aenm.201703137
.
- N. Sharma, N. Tapia-Ruiz, G. Singh, A. R. Armstrong, J. C. Pramudita, H. E. A. Brand, J. Billaud, P. G. Bruce and T. Rojo, Chem. Mater., 2015, 27, 6976–6986 CrossRef CAS
.
- C. Delmas, C. Fouassier and P. Hagenmuller, Phys. B+C, 1980, 99, 81–85 CrossRef CAS
.
- M. Bianchini, J. Wang, R. J. Clement, B. Ouyang, P. Xiao, D. Kitchaev, T. Shi, Y. Zhang, Y. Wang, H. Kim, M. Zhang, J. Bai, F. Wang, W. Sun and G. Ceder, Nat. Mater., 2020, 19, 1088–1095 CrossRef CAS
.
- D. Zhou, W. Huang, X. Lv and F. Zhao, J. Power Sources, 2019, 421, 147–155 CrossRef CAS
.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS
.
- P. Hou, F. Li, Y. Wang, J. Yin and X. Xu, J. Mater. Chem. A, 2019, 7, 4705–4713 RSC
.
- S.-H. Bo, X. Li, A. J. Toumar and G. Ceder, Chem. Mater., 2016, 28, 1419–1429 CrossRef CAS
.
- Y. Sun, S. Guo and H. Zhou, Energy Environ. Sci., 2019, 12, 825–840 RSC
.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304 RSC
.
- R. J. Clément, P. G. Bruce and C. P. Grey, J. Electrochem. Soc., 2015, 162, A2589 CrossRef
.
- K. Kubota and S. Komaba, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS
.
- Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A1225–A1229 CrossRef CAS
.
- C. Ma, J. Alvarado, J. Xu, R. J. Clément, M. Kodur, W. Tong, C. P. Grey and Y. S. Meng, J. Am. Chem. Soc., 2017, 139, 4835–4845 CrossRef CAS
.
- E. Talaie, S. Y. Kim, N. Chen and L. F. Nazar, Chem. Mater., 2017, 29, 6684–6697 CrossRef CAS
.
- L. Zheng, J. Li and M. N. Obrovac, Chem. Mater., 2017, 29, 1623–1631 CrossRef CAS
.
- X. Wu, J. Guo, D. Wang, G. Zhong, M. J. McDonald and Y. Yang, J. Power Sources, 2015, 281, 18–26 CrossRef CAS
.
- P. F. Wang, Y. You, Y. X. Yin, Y. S. Wang, L. J. Wan, L. Gu and Y. G. Guo, Angew. Chem., Int. Ed., 2016, 55, 7445–7449 CrossRef CAS
.
- G. Singh, J. M. López del Amo, M. Galceran, S. Pérez-Villar and T. Rojo, J. Mater. Chem. A, 2015, 3, 6954–6961 RSC
.
- A. Gutierrez, W. M. Dose, O. Borkiewicz, F. Guo, M. Avdeev, S. Kim, T. T. Fister, Y. Ren, J. Bareño and C. S. Johnson, J. Phys. Chem. C, 2018, 122, 23251–23260 CrossRef CAS
.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef CAS
.
- N. Sharma, M. H. Han, J. C. Pramudita, E. Gonzalo, H. E. A. Brand, T. Rojo, V. K. Peterson, T. Rojo, X. Huang, Z. Ogumi, A. Wattiaux and C. Delmas, J. Mater. Chem. A, 2015, 3, 21023–21038 RSC
.
- W. M. Dose, N. Sharma, J. C. Pramudita, J. A. Kimpton, E. Gonzalo, M. H. Han and T. Rojo, Chem. Mater., 2016, 28, 6342–6354 CrossRef CAS
.
- J. Billaud, G. Singh, A. R. Armstrong, E. Gonzalo, V. Roddatis, M. Armand, T. Rojo and P. G. Bruce, Energy Environ. Sci., 2014, 7, 1387–1391 RSC
.
- J. W. Somerville, A. Sobkowiak, N. Tapia-Ruiz, J. Billaud, J. G. Lozano, R. A. House, L. C. Gallington, T. Ericsson, L. Häggström, M. R. Roberts, U. Maitra and P. G. Bruce, Energy Environ. Sci., 2019, 12, 2223–2232 RSC
.
- W. K. Pang, S. Kalluri, V. K. Peterson, N. Sharma, J. Kimpton, B. Johannessen, H. K. Liu, S. X. Dou and Z. Guo, Chem. Mater., 2015, 27, 3150–3158 CrossRef CAS
.
- L. Liu, X. Li, S.-H. Bo, Y. Wang, H. Chen, N. Twu, D. Wu and G. Ceder, Adv. Energy Mater., 2015, 5, 1500944 CrossRef
.
- J. W. Somerville, A. Sobkowiak, N. Tapia-Ruiz, J. Billaud, J. G. Lozano, R. A. House, L. C. Gallington, T. Ericsson, L. Häggström, M. R. Roberts, U. Maitra and P. G. Bruce, Energy Environ. Sci., 2019, 12, 2223–2232 RSC
.
- B. Mortemard de Boisse, D. Carlier, M. Guignard, L. Bourgeois and C. Delmas, Inorg. Chem., 2014, 53, 11197–11205 CrossRef CAS
.
- W. Zhao, Y. Tsuchiya and N. Yabuuchi, Small Methods, 2019, 3(4), 1800032 CrossRef CAS
.
- E. Talaie, V. Duffort, H. L. Smith, B. Fultz and L. F. Nazar, Energy Environ. Sci., 2015, 8, 2512–2523 RSC
.
- S. Komaba, T. Nakayama, A. Ogata, M. Shimizu, C. Takei, S. Takada, A. Hokura and I. Nakai, ECS Trans., 2009, 16, 43–55 CrossRef CAS
.
- P. F. Wang, Y. You, Y. X. Yin and Y. G. Guo, Adv. Mater., 2018, 8, 1701912 Search PubMed
.
- E. Lee, D. E. Brown, E. E. Alp, Y. Ren, J. Lu, J.-J. Woo and C. S. Johnson, Chem. Mater., 2015, 27, 6755–6764 CrossRef CAS
.
- C. Didier, M. Guignard, C. Denage, O. Szajwaj, S. Ito, I. Saadoune, J. Darriet and C. Delmas, Electrochem. Solid-State Lett., 2011, 14(5), A75 CrossRef CAS
.
- E. Gonzalo, M. H. Han, J. M. López del Amo, B. Acebedo, M. Casas-Cabanas and T. Rojo, J. Mater. Chem. A, 2014, 2, 18523–18530 RSC
.
- C. Zhao, M. Avdeev, L. Chen and Y. S. Hu, Angew. Chem., Int. Ed., 2018, 57, 7056–7060 CrossRef CAS
.
- X. Li, D. Wu, Y.-N. Zhou, L. Liu, X.-Q. Yang and G. Ceder, Electrochem. Commun., 2014, 49, 51–54 CrossRef CAS
.
- K. Kubota, T. Asari, H. Yoshida, N. Yaabuuchi, H. Shiiba, M. Nakayama and S. Komaba, Adv. Funct. Mater., 2016, 26, 6047–6059 CrossRef CAS
.
- M. Sathiya, K. Hemalatha, K. Ramesha, J. M. Tarascon and A. S. Prakash, Chem. Mater., 2012, 24, 1846–1853 CrossRef CAS
.
- M. H. Han, E. Gonzalo, M. Casas-Cabanas and T. Rojo, J. Power Sources, 2014, 258, 266–271 CrossRef CAS
.
- F. Ding, C. Zhao, D. Zhou, Q. Meng, D. Xiao, Q. Zhang, Y. Niu, Y. Li, X. Rong, Y. Lu, L. Chen and Y.-S. Hu, Energy Storage Mater., 2020, 30, 420–430 CrossRef
.
- Y. Wang, X. Wang, X. Li, R. Yu, M. Chen, K. Tang and X. Zhang, Chem. Eng. J., 2019, 360, 139–147 CrossRef CAS
.
- M. Kalapsazova, S. Ivanova, R. Kukeva, S. Simova, S. Wegner, E. Zhecheva and R. Stoyanova, Phys. Chem. Chem. Phys., 2017, 19, 27065–27073 RSC
.
- M. Kalapsazova, G. F. Ortiz, J. L. Tirado, O. Dolotko, E. Zhecheva, D. Nihtianova, L. Mihaylov and R. Stoyanova, ChemPlusChem, 2015, 80, 1642–1656 CrossRef CAS
.
- S. Ivanova, E. Zhecheva, R. Kukeva, G. Tyuliev, D. Nihtianova, L. Mihailov and R. Stoyanova, J. Phys. Chem. C, 2016, 120, 3654–3668 CrossRef CAS
.
- S. Guo, Y. Sun, J. Yi, K. Zhu, P. Liu, Y. Zhu, G.-z. Zhu, M. Chen, M. Ishida and H. Zhou, NPG Asia Mater., 2016, 8, e266 CrossRef CAS
.
- O. Arcelus and J. Carrasco, ACS Appl. Mater. Interfaces, 2019, 11, 12562–12569 CrossRef CAS
.
- C. Zhao, Z. Yao, Q. Wang, H. Li, J. Wang, M. Liu, S. Ganapathy, Y. Lu, J. Cabana, B. Li, X. Bai, A. Aspuru-Guzik, M. Wagemaker, L. Chen and Y. S. Hu, J. Am. Chem. Soc., 2020, 142, 5742–5750 CrossRef CAS
.
- M. D. Radin, J. Alvarado, Y. S. Meng and A. Van der Ven, Nano Lett., 2017, 17, 7789–7795 CrossRef CAS
.
- X. Zhang, S. Guo, P. Liu, Q. Li, S. Xu, Y. Liu, K. Jiang, P. He, M. Chen, P. Wang and H. Zhou, Adv. Energy Mater., 2019, 1900189, DOI:10.1002/aenm.201900189
.
- H. Yu, Y. Qian, M. Otani, D. Tang, S. Guo, Y. Zhu and H. Zhou, Energy Environ. Sci., 2014, 7(3), 1068–1078 RSC
.
- W. Liu, P. Oh, X. Liu, M. J. Lee, W. Cho, S. Chae, Y. Kim and J. Cho, Angew. Chem., Int. Ed., 2015, 54, 4440–4457 CrossRef CAS
.
- K. Ku, B. Kim, S. K. Jung, Y. Gong, D. Eum, G. Yoon, K. Y. Park, J. Hong, S. P. Cho, D. H. Kim and H. Kim, Energy Environ. Sci., 2020, 13(4), 1269–1278 RSC
.
- A. Maazaz, C. Delmas and P. Hagenmuller, J. Inclusion Phenom., 1983, 1, 45–51 CrossRef CAS
.
- K. Kubota, I. Ikeuchi, T. Nakayama, C. Takei, N. Yabuuchi, H. Shiiba, M. Nakayama and S. Komaba, J. Phys. Chem. C, 2014, 119, 166–175 CrossRef
.
- N. Yabuuchi, H. Yoshida and S. Komaba, Electrochemistry, 2012, 80, 716–719 CrossRef CAS
.
- X. Li, Y. Wang, D. Wu, L. Liu, S.-H. Bo and G. Ceder, Chem. Mater., 2016, 28, 6575–6583 CrossRef CAS
.
- B. Silván, E. Gonzalo, L. Djuandhi, N. Sharma, F. Fauth and D. Saurel, J. Mater. Chem. A, 2018, 6, 15132–15146 RSC
.
- S. Guo, Y. Sun, P. Liu, J. Yi, P. He, X. Zhang, Y. Zhu, R. Senga, K. Suenaga, M. Chen and H. Zhou, Sci. Bull., 2018, 63, 376–384 CrossRef CAS
.
- M. Wagemaker, Sci. Bull., 2018, 63, 529–530 CrossRef CAS
.
- B. Silván, E. Gonzalo, L. Djuandhi, N. Sharma, F. Fauth and D. Saurel, J. Mater. Chem. A, 2018, 6, 15132–15146 RSC
.
- M. H. Han, E. Gonzalo, N. Sharma, J. M. López Del Amo, M. Armand, M. Avdeev, J. J. Saiz Garitaonandia and T. Rojo, Chem. Mater., 2016, 28, 106–116 CrossRef CAS
.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC
.
- X. Zhang, S. Guo, P. Liu, Q. Li, S. Xu, Y. Liu, K. Jiang, P. He, M. Chen, P. Wang and H. Zhou, Adv. Energy Mater., 2019, 9, 1900189–1900196 CrossRef
.
- Y. Li, Y. Gao, X. Wang, X. Shen, Q. Kong, R. Yu, G. Lu, Z. Wang and L. Chen, Nano Energy, 2018, 47, 519–526 CrossRef CAS
.
- C. Chen, Z. Ding, Z. Han, C. Liang, X. Lan, P. Wang, P. Gao and W. Wei, J. Phys. Chem. Lett., 2020, 11, 5464–5470 CrossRef CAS
.
- Y. N. Zhang, S. Kim, G. Y. Feng, Y. Wang, L. Liu, G. Ceder and X. Li, J. Electrochem. Soc., 2018, 165, A1184–A1192 CrossRef CAS
.
- A. Grimaud, W. T. Hong, Y. Shao-Horn and J. M. Tarascon, Nat. Mater., 2016, 15, 121 CrossRef CAS
.
- M. Jia, Y. Qiao, X. Li, F. Qiu, X. Cao, P. He and H. Zhou, ACS Appl. Mater. Interfaces, 2020, 12, 851–857 CrossRef CAS
.
- W. Jiang, C. Yin, Y. Xia, B. Qiu, H. Guo, H. Cui, F. Hu and Z. Liu, ACS Appl. Mater. Interfaces, 2019, 11(15), 14023–14034 CrossRef CAS
.
- K. Luo, M. R. Roberts, N. Guerrini, N. Tapia-Ruiz, R. Hao, F. Massel, D. M. Pickup, S. Ramos, Y.-S. Liu and J. Guo, J. Am. Chem. Soc., 2016, 138, 11211–11218 CrossRef CAS
.
- C. Zhao, Q. Wang, Y. Lu, Y.-S. Hu, B. Li and L. Chen, J. Phys. D: Appl. Phys., 2017, 50, 183001 CrossRef
.
- Y. Zhang, M. Wu, J. Ma, G. Wei, Y. Ling, R. Zhang and Y. Huang, ACS Cent. Sci., 2020, 6, 232–240 CrossRef CAS
.
- G. Assat and J.-M. Tarascon, Nat. Energy, 2018, 3, 373–386 CrossRef CAS
.
- B. Su, H. Liang, J. Liu, J. Wu, N. Sharma, Q. Gu, B. Johannessen and D. Y. W. Yu, Chem. Commun., 2020, 56, 8245–8248 RSC
.
- Y. Qiao, S. Guo, K. Zhu, P. Liu, X. Li, K. Jiang, C.-J. Sun, M. Chen and H. Zhou, Energy Environ. Sci., 2018, 11, 299–305 RSC
.
- X. Bai, M. Sathiya, B. Mendoza-Sánchez, A. Iadecola, J. Vergnet, R. Dedryvère, M. Saubanère, A. M. Abakumov, P. Rozier and J. M. Tarascon, Adv. Energy Mater., 2018, 8, 1802379 CrossRef
.
- M. Jia, Y. Qiao, X. Li, F. Qiu, X. Cao, P. He and H. Zhou, ACS Appl. Mater. Interfaces, 2019, 12(1), 851–857 CrossRef
.
- C. Li, F. Geng, B. Hu and B. Hu, Mater. Today Energy, 2020, 17, 100474 CrossRef
.
- M. Saubanère, E. McCalla, J. M. Tarascon and M. L. Doublet, Energy Environ. Sci., 2016, 9, 984–991 RSC
.
- C. Zhao, Q. Wang, Y. Lu, Y.-S. Hu, B. Li and L. Chen, J. Phys. D: Appl. Phys., 2017, 50(18), 183001 CrossRef
.
- A. R. Armstrong, M. Holzapfel, P. Novák, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, J. Am. Chem. Soc., 2006, 128, 8694–8698 CrossRef CAS
.
- R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Roberts and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300 CrossRef
.
- E. de la Llave, E. Talaie, E. Levi, P. K. Nayak, M. Dixit, P. T. Rao, P. Hartmann, F. Chesneau, D. T. Major, M. Greenstein, D. Aurbach and L. F. Nazar, Chem. Mater., 2016, 28, 9064–9076 CrossRef CAS
.
- P. Rozier, M. Sathiya, A.-R. Paulraj, D. Foix, T. Desaunay, P.-L. Taberna, P. Simon and J.-M. Tarascon, Electrochem. Commun., 2015, 53, 29–32 CrossRef CAS
.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki and T. Inamasu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655 CrossRef CAS
.
- M. Freire, N. V. Kosova, C. Jordy, D. Chateigner, O. Lebedev, A. Maignan and V. Pralong, Nat. Mater., 2016, 15, 173–177 CrossRef CAS
.
- A. J. Perez, D. Batuk, M. Saubanère, G. Rousse, D. Foix, E. McCalla, E. J. Berg, R. Dugas, K. H. W. van den Bos, M.-L. Doublet, D. Gonbeau, A. M. Abakumov, G. Van Tendeloo and J.-M. Tarascon, Chem. Mater., 2016, 28, 8278–8288 CrossRef CAS
.
- B. Su, J. Zhang, M. Fujita, W. Zhou, P. H.-L. Sit and Y. Denis, J. Electrochem. Soc., 2019, 166, A5075–A5080 CrossRef CAS
.
- Q. Wang, W. Yang, F. Kang and B. Li, Energy Storage Mater., 2018, 14, 361–366 CrossRef
.
- B. Mortemard de Boisse, S.-I. Nishimura, E. Watanabe, L. Lander, A. Tsuchimoto, J. Kikkawa, E. Kobayashi, D. Asakura, M. Okubo and A. Yamada, Adv. Energy Mater., 2018, 8(20), 1800409 CrossRef
.
- X. Zhang, Y. Qiao, S. Guo, K. Jiang, S. Xu, H. Xu, P. Wang, P. He and H. Zhou, Adv. Mater., 2019, 31, e1807770 CrossRef
.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Perez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS
.
- X. Bai, M. Sathiya, B. Mendoza-Sánchez, A. Iadecola, J. Vergnet, R. Dedryvère, M. Saubanère, A. M. Abakumov, P. Rozier and J.-M. Tarascon, Adv. Energy Mater., 2018, 8, 1802379 CrossRef
.
- A. Konarov, J. H. Jo, J. U. Choi, Z. Bakenov, H. Yashiro, J. Kim and S.-T. Myung, Nano Energy, 2019, 59, 197–206 CrossRef CAS
.
- A. Konarov, H. J. Kim, J. H. Jo, N. Voronina, Y. Lee, Z. Bakenov, J. Kim and S. T. Myung, Adv. Energy Mater., 2020, 2001111, DOI:10.1002/aenm.202001111
.
- H. J. Kim, A. Konarov, J. H. Jo, J. U. Choi, K. Ihm, H. K. Lee, J. Kim and S. T. Myung, Adv. Energy Mater., 2019, 9, 1901181 CrossRef
.
- W. Kong, R. Gao, Q. Li, W. Yang, J. Yang, L. Sun and X. Liu, J. Mater. Chem. A, 2019, 7, 9099–9109 RSC
.
- T. Risthaus, D. Zhou, X. Cao, X. He, B. Qiu, J. Wang, L. Zhang, Z. Liu, E. Paillard, G. Schumacher, M. Winter and J. Li, J. Power Sources, 2018, 395, 16–24 CrossRef CAS
.
- C. Ma, J. Alvarado, J. Xu, R. l. J. Clément, M. Kodur, W. Tong, C. P. Grey and Y. S. Meng, J. Am. Chem. Soc., 2017, 139, 4835–4845 CrossRef CAS
.
- E. J. Kim, L. A. Ma, L. C. Duda, D. M. Pickup, A. V. Chadwick, R. Younesi, J. T. S. Irvine and A. R. Armstrong, ACS Appl. Energy Mater., 2019, 3, 184–191 CrossRef
.
- X. Rong, E. Hu, Y. Lu, F. Meng, C. Zhao, X. Wang, Q. Zhang, X. Yu, L. Gu, Y.-S. Hu, H. Li, X. Huang, X.-Q. Yang, C. Delmas and L. Chen, Joule, 2019, 3, 503–517 CrossRef CAS
.
- C. Liu, Z. G. Neale and G. Cao, Mater. Today, 2016, 19, 109–123 CrossRef CAS
.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 RSC
.
- Y. Nanba, T. Iwao, B. M. D. Boisse, W. Zhao, E. Hosono, D. Asakura, H. Niwa, H. Kiuchi, J. Miyawaki, Y. Harada and M. Okubo, Chem. Mater., 2016, 28(4), 1058–1065 CrossRef CAS
.
- H. Su, S. Jaffer and H. Yu, Energy Storage Mater., 2016, 5, 116–131 CrossRef
.
- X. Xia and J. R. Dahn, Electrochem. Solid-State Lett., 2012, 15, A1 CrossRef CAS
.
- D. Wu, X. Li, B. Xu, N. Twu, L. Liu and G. Ceder, Energy Environ. Sci., 2015, 8, 195–202 RSC
.
- P. Vassilaras, X. Ma, X. Li and G. Ceder, J. Electrochem. Soc., 2012, 160, A207–A211 CrossRef
.
- L. Wang, J. Wang, X. Zhang, Y. Ren, P. Zuo, G. Yin and J. Wang, Nano Energy, 2017, 34, 215–223 CrossRef CAS
.
- C. Delmas, J.-J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3, 165–169 CrossRef
.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80 CrossRef CAS
.
- L. W. Shacklette, J. Electrochem. Soc., 1988, 135, 2669 CrossRef CAS
.
- X. Ma, H. Chen and G. Ceder, J. Electrochem. Soc., 2011, 158, A1307 CrossRef CAS
.
- J. Billaud, R. J. Clement, A. R. Armstrong, J. Canales-Vazquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243–17248 CrossRef CAS
.
- X. Li, X. Ma, D. Su, L. Liu, R. Chisnell, S. P. Ong, H. Chen, A. Toumar, J. C. Idrobo, Y. Lei, J. Bai, F. Wang, J. W. Lynn, Y. S. Lee and G. Ceder, Nat. Mater., 2014, 13, 586–592 CrossRef CAS
.
- N. Yabuuchi and S. Komaba, Sci. Technol. Adv. Mater., 2014, 15, 043501 CrossRef
.
- T. Or, K. Kaliyappan, Z. Bai and Z. Chen, ChemElectroChem, 2020, 7, 3284–3290 CrossRef CAS
.
- Y. Huang, Z. Yan, W. Luo, Z. Hu, G. Liu, L. Zhang, X. Yang, M. Ou, W. Liu, L. Huang, H. Lin, C.-T. Chen, J. Luo, S. Li, J. Han, S. Chou and Y. Huang, Energy Storage Mater., 2020, 29, 182–189 CrossRef
.
- J. L. Yue, W. W. Yin, M. H. Cao, S. Zulipiya, Y. N. Zhou and Z. W. Fu, Chem. Commun., 2015, 51, 15712–15715 RSC
.
- C. Zhao, F. Ding, Y. Lu, L. Chen and Y.-S. Hu, Angew. Chem., Int. Ed., 2020, 59, 264–269 CrossRef CAS
.
- J. H. Stansby, W. M. Dose, N. Sharma, J. A. Kimpton, J. M. López del Amo, E. Gonzalo and T. Rojo, Electrochim. Acta, 2020, 135978, DOI:10.1016/j.electacta.2020.135978
.
- D. Yuan, X. Hu, J. Qian, F. Pei, F. Wu, R. Mao, X. Ai, H. Yang and Y. Cao, Electrochim. Acta, 2014, 116, 300–305 CrossRef CAS
.
- H. Yoshida, N. Yabuuchi, K. Kubota, I. Ikeuchi, A. Garsuch, M. Schulz-Dobrick and S. Komaba, Chem. Commun., 2014, 50, 3677–3680 RSC
.
- Q. C. Wang, E. Hu, Y. Pan, N. Xiao, F. Hong, Z. W. Fu, X. J. Wu, S. M. Bak, X. Q. Yang and Y. N. Zhou, Adv. Sci., 2017, 4, 1700219 CrossRef
.
- M. Jeong, H. Lee, J. Yoon and W.-S. Yoon, J. Power Sources, 2019, 439, 227064 CrossRef CAS
.
- S. Doubaji, M. Valvo, I. Saadoune, M. Dahbi and K. Edström, J. Power Sources, 2014, 266, 275–281 CrossRef CAS
.
- C. Hakim, N. Sabi, M. Dahbi, D. Brandell, K. Edström, L. C. Duda, I. Saadoune and R. Younesi, Commun. Chem., 2020, 3, 1–9 CrossRef
.
- K. Wang, P. Yan, Z. Wang, J. Fu, Z. Zhang, X. Ke and M. Sui, J. Mater. Chem. A, 2020, 8, 16690–16697 RSC
.
- T. A. Eriksson, Y. J. Lee, J. Hollingsworth, J. A. Reimer, E. J. Cairns, X.-f. Zhang and M. M. Doeff, Chem. Mater., 2003, 15, 4456–4463 CrossRef CAS
.
- S. Patoux, M. Dollé and M. M. Doeff, Chem. Mater., 2005, 17, 1044–1054 CrossRef CAS
.
- M. Dollé, S. Patoux and M. M. Doeff, Chem. Mater., 2005, 17, 1036–1043 CrossRef
.
- Q. Huang, S. Xu, L. Xiao, P. He, J. Liu, Y. Yang, P. Wang, B. Huang and W. Wei, Inorg. Chem., 2018, 57, 15584–15591 CrossRef CAS
.
- Y. P. Deng, Z. G. Wu, R. Liang, Y. Jiang, D. Luo, A. Yu and Z. Chen, Adv. Funct. Mater., 2019, 29(19), 1808522 CrossRef
.
- Y. Xiao, N. M. Abbasi, Y. F. Zhu, S. Li, S. J. Tan, W. Ling, L. Peng, T. Yang, L. Wang, X. D. Guo, Y. X. Yin, H. Zhang and Y. G. Guo, Adv. Funct. Mater., 2020, 2001334, DOI:10.1002/adfm.202001334
.
- X. Qi, L. Liu, N. Song, F. Gao, K. Yang, Y. Lu, H. Yang, Y. S. Hu, Z. H. Cheng and L. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 40215–40223 CrossRef CAS
.
- J. Chen, L. Li, L. Wu, Q. Yao, H. Yang, Z. Liu, L. Xia, Z. Chen, J. Duan and S. Zhong, J. Power Sources, 2018, 406, 110–117 CrossRef CAS
.
- Z.-Y. Li, J. Zhang, R. Gao, H. Zhang, L. Zheng, Z. Hu and X. Liu, J. Phys. Chem. C, 2016, 120, 9007–9016 CrossRef CAS
.
- G. K. Veerasubramani, Y. Subramanian, M.-S. Park, B. Senthilkumar, A. Eftekhari, S. J. Kim and D.-W. Kim, Electrochim. Acta, 2019, 296, 1027–1034 CrossRef CAS
.
- M. Bianchini, E. Gonzalo, N. E. Drewett, N. Ortiz-Vitoriano, J. M. López del Amo, F. J. Bonilla, B. Acebedo and T. Rojo, J. Mater. Chem. A, 2018, 6, 3552–3559 RSC
.
- S. Guo, P. Liu, H. Yu, Y. Zhu, M. Chen, M. Ishida and H. Zhou, Angew. Chem., Int. Ed., 2015, 54, 5894–5899 CrossRef CAS
.
- Q. Huang, P. He, L. Xiao, Y. Feng, J. Liu, Y. Yang, B. Huang, X. Cui, P. Wang and W. Wei, ACS Appl. Mater. Interfaces, 2020, 12, 2191–2198 CrossRef CAS
.
- L. Yang, J. M. L. Amo, Z. Shadike, S. M. Bak, F. Bonilla, M. Galceran, P. K. Nayak, J. R. Buchheim, X. Q. Yang, T. Rojo and P. Adelhelm, Adv. Funct. Mater., 2020, 2003364, DOI:10.1002/adfm.202003364
.
- B. Hu, F. Geng, C. Zhao, B. Doumert, J. Trebosc, O. Lafon, C. Li, M. Shen and B. Hu, ACS Appl. Mater. Interfaces, 2020, 12(37), 41485–41494, DOI:10.1021/acsami.0c11427
.
- E. Lee, J. Lu, Y. Ren, X. Luo, X. Zhang, J. Wen, D. Miller, A. DeWahl, S. Hackney, B. Key, D. Kim, M. D. Slater and C. S. Johnson, Adv. Energy Mater., 2014, 4, 1400458 CrossRef
.
- L. G. Chagas, D. Buchholz, C. Vaalma, L. Wu and S. Passerini, J. Mater. Chem. A, 2014, 2, 20263–20270 RSC
.
- X. Chen, X. Zhou, M. Hu, J. Liang, D. Wu, J. Wei and Z. Zhou, J. Mater. Chem. A, 2015, 3, 20708–20714 RSC
.
- Z. Yan, L. Tang, Y. Huang, W. Hua, Y. Wang, R. Liu, Q. Gu, S. Indris, S. L. Chou, Y. Huang, M. Wu and S. X. Dou, Angew. Chem., Int. Ed., 2019, 58, 1412–1416 CrossRef CAS
.
- Q. Huang, J. Liu, S. Xu, P. Wang, D. G. Ivey, B. Huang and W. Wei, Chem. Mater., 2018, 30, 4728–4737 CrossRef CAS
.
- M. Keller, D. Buchholz and S. Passerini, Adv. Energy Mater., 2016, 6, 1501555–1501566 CrossRef
.
- G.-L. Xu, R. Amine, Y.-F. Xu, J. Liu, J. Gim, T. Ma, Y. Ren, C.-J. Sun, Y. Liu, X. Zhang, S. M. Heald, A. Solhy, I. Saadoune, W. L. Mattis, S.-G. Sun, Z. Chen and K. Amine, Energy Environ. Sci., 2017, 10, 1677–1693 RSC
.
- J. Zheng, P. Yan, W. H. Kan, C. Wang and A. Manthiram, J. Electrochem. Soc., 2016, 163, A584–A591 CrossRef CAS
.
- C. Deng, P. Skinner, Y. Liu, M. Sun, W. Tong, C. Ma, M. L. Lau, R. Hunt, P. Barnes, J. Xu and H. Xiong, Chem. Mater., 2018, 30, 8145–8154 CrossRef CAS
.
- Y. Xiao, P.-F. Wang, Y.-X. Yin, Y.-F. Zhu, X. Yang, X.-D. Zhang, Y. Wang, X.-D. Guo, B.-H. Zhong and Y.-G. Guo, Adv. Energy Mater., 2018, 8, 1800492 CrossRef
.
- P. Hou, J. Yin, X. Lu, J. Li, Y. Zhao and X. Xu, Nanoscale, 2018, 10, 6671–6677 RSC
.
- J. Y. Hwang, S. M. Oh, S. T. Myung, K. Y. Chung, I. Belharouak and Y. K. Sun, Nat. Commun., 2015, 6, 6865 CrossRef CAS
.
- Y. K. Sun, S. T. Myung, M. H. Kim, J. Prakash and K. Amine, J. Am. Chem. Soc., 2005, 127, 13411–13418 CrossRef CAS
.
- S. Bao, S.-h. Luo, Z.-y. Wang, S.-x. Yan, Q. Wang and J.-y. Li, J. Power Sources, 2018, 396, 404–411 CrossRef CAS
.
- J. Ren, R. Dang, Y. Yang, K. Wu, Y. Lee, Z. Hu, X. Xiao and M. Wang, Energy Technol., 2020, 8, 1901504 CrossRef CAS
.
- C. Chen, Z. Han, S. Chen, S. Qi, X. Lan, C. Zhang, L. Chen, P. Wang and W. Wei, ACS Appl. Mater. Interfaces, 2020, 12, 7144–7152 CrossRef CAS
.
- G. G. Eshetu, G. A. Elia, M. Armand, M. Forsyth, S. Komaba, T. Rojo and S. Passerini, Adv. Energy Mater., 2020, 10, 2000093 CrossRef CAS
.
- A. Ponrouch, D. Monti, A. Boschin, B. Steen, P. Johansson and M. R. Palacín, J. Mater. Chem. A, 2015, 3, 22–42 RSC
.
- S. Komaba, T. Ishikawa, N. Yabuuchi, W. Murata, A. Ito and Y. Ohsawa, ACS Appl. Mater. Interfaces, 2011, 3, 4165–4168 CrossRef CAS
.
- A. Bhide, J. Hofmann, A. K. Durr, J. Janek and P. Adelhelm, Phys. Chem. Chem. Phys., 2014, 16, 1987–1998 RSC
.
- C.-H. Wang, Y.-W. Yeh, N. Wongittharom, Y.-C. Wang, C.-J. Tseng, S.-W. Lee, W.-S. Chang and J.-K. Chang, J. Power Sources, 2015, 274, 1016–1023 CrossRef CAS
.
- G. G. Eshetu, S. Grugeon, H. Kim, S. Jeong, L. Wu, G. Gachot, S. Laruelle, M. Armand and S. Passerini, ChemSusChem, 2016, 9, 462–471 CrossRef CAS
.
-
P. B. Balbuena, Electrolyte materials - Issues and challenges, in AIP Conference Proceedings, American Institute of Physics, June 2014, vol. 1597, ch. 1, pp. 82–97 Search PubMed
.
- L. G. Chagas, D. Buchholz, L. Wu, B. Vortmann and S. Passerini, J. Power Sources, 2014, 247, 377–383 CrossRef CAS
.
- J.-J. Kim, K. Yoon, I. Park and K. Kang, Small Methods, 2017, 1, 1700219 CrossRef
.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100 CrossRef
.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef
.
- T. Wei, Y. Gong, X. Zhao and K. Huang, Adv. Funct. Mater., 2014, 24, 5380–5384 CrossRef CAS
.
- L. Liu, X. Qi, Q. Ma, X. Rong, Y. S. Hu, Z. Zhou, H. Li, X. Huang and L. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 32631–32636 CrossRef CAS
.
- E. Quartarone and P. Mustarelli, Chem. Soc. Rev., 2011, 40, 2525–2540 RSC
.
- J. B. Goodenough and P. Singh, J. Electrochem. Soc., 2015, 162, A2387–A2392 CrossRef CAS
.
- S. Guo, Q. Li, P. Liu, M. Chen and H. Zhou, Nat. Commun., 2017, 8, 135 CrossRef
.
- M. H. Han, N. Sharma, E. Gonzalo, J. C. Pramudita, H. E. A. Brand, J. M. López del Amo and T. Rojo, J. Mater. Chem. A, 2016, 4, 18963–18975 RSC
.
- H. L. Andersen, E. A. Cheung, M. Avdeev, H. E. Maynard-Casely, D. P. Abraham and N. Sharma, J. Power Sources, 2020, 470, 228370 CrossRef CAS
.
- J.-Y. Hwang, S.-T. Myung, J. U. Choi, C. S. Yoon, H. Yashiro and Y.-K. Sun, J. Mater. Chem. A, 2017, 5, 23671–23680 RSC
.
- F. Wu, X. Zhang, T. Zhao, L. Li, M. Xie and R. Chen, ACS Appl. Mater. Interfaces, 2015, 7, 3773–3781 CrossRef CAS
.
- J. Liu and A. Manthiram, J. Mater. Chem., 2010, 20, 3961 RSC
.
- J. Zheng, M. Gu, J. Xiao, B. J. Polzin, P. Yan, X. Chen, C. Wang and J.-G. Zhang, Chem. Mater., 2014, 26, 6320–6327 CrossRef CAS
.
- S. J. Shi, J. P. Tu, Y. Y. Tang, X. Y. Liu, Y. Q. Zhang, X. L. Wang and C. D. Gu, Electrochim. Acta, 2013, 88, 671–679 CrossRef CAS
.
- Y. Wang, K. Tang, X. Li, R. Yu, X. Zhang, Y. Huang, G. Chen, S. Jamil, S. Cao, X. Xie, Z. Luo and X. Wang, Chem. Eng. J., 2019, 372, 1066–1076 CrossRef CAS
.
- J. H. Jo, J. U. Choi, A. Konarov, H. Yashiro, S. Yuan, L. Shi, Y.-K. Sun and S.-T. Myung, Adv. Funct. Mater., 2018, 28, 1705968 CrossRef
.
- J.-J. Ding, Y.-N. Zhou, Q. Sun and Z.-W. Fu, Electrochem. Commun., 2012, 22, 85–88 CrossRef CAS
.
- Y. Liu, X. Fang, A. Zhang, C. Shen, Q. Liu, H. A. Enaya and C. Zhou, Nano Energy, 2016, 27, 27–34 CrossRef CAS
.
- J. Alvarado, C. Ma, S. Wang, K. Nguyen, M. Kodur and Y. S. Meng, ACS Appl. Mater. Interfaces, 2017, 9, 26518–26530 CrossRef CAS
.
- H. V. Ramasamy, P. N. Didwal, S. Sinha, V. Aravindan, J. Heo, C. J. Park and Y. S. Lee, J. Colloid Interface Sci., 2020, 564, 467–477 CrossRef CAS
.
- K. Kaliyappan, J. Liu, A. Lushington, R. Li and X. Sun, ChemSusChem, 2015, 8, 2537–2543 CrossRef CAS
.
- J.-H. Park, K. Park, R.-H. Kim, D.-J. Yun, S.-Y. Park, D. Han, S.-S. Lee and J.-H. Park, J. Mater. Chem. A, 2015, 3, 10730–10737 RSC
.
- K. Kaliyappan, J. Liu, B. Xiao, A. Lushington, R. Li, T.-K. Sham and X. Sun, Adv. Funct. Mater., 2017, 27, 1701870 CrossRef
.
- H.-M. Cheng, F.-M. Wang, J. P. Chu, R. Santhanam, J. Rick and S.-C. Lo, J. Phys. Chem. C, 2012, 116, 7629–7637 CrossRef CAS
.
- H. V. Ramasamy, K. Kaliyappan, R. Thangavel, V. Aravindan, K. Kang, D. U. Kim, Y. Park, X. Sun and Y.-S. Lee, J. Mater. Chem. A, 2017, 5, 8408–8415 RSC
.
- W. Kong, H. Wang, L. Sun, C. Su and X. Liu, Appl. Surf. Sci., 2019, 497, 143814 CrossRef CAS
.
- J.-Y. Hwang, T.-Y. Yu and Y.-K. Sun, J. Mater. Chem. A, 2018, 6, 16854–16862 RSC
.
- R. Dang, M. Chen, Q. Li, K. Wu, Y. L. Lee, Z. Hu and X. Xiao, ACS Appl. Mater. Interfaces, 2019, 11, 856–864 CrossRef CAS
.
- Y. Zhang, Y. Pei, W. Liu, S. Zhang, J. Xie, J. Xia, S. Nie, L. Liu and X. Wang, Chem. Eng. J., 2020, 382, 122697 CrossRef CAS
.
- J. Zhang and D. Y. W. Yu, J. Power Sources, 2018, 391, 106–112 CrossRef CAS
.
- Y. Yu, W. Kong, Q. Li, D. Ning, G. Schuck, G. Schumacher, C. Su and X. Liu, ACS Appl. Energy Mater., 2020, 3, 933–942 CrossRef CAS
.
- K. Tang, Y. Huang, X. Xie, S. Cao, L. Liu, M. Liu, Y. Huang, B. Chang, Z. Luo and X. Wang, Chem. Eng. J., 2020, 384, 123234 CrossRef CAS
.
- K. W. Nam, S. Kim, E. Yang, Y. Jung, E. Levi, D. Aurbach and J. W. Choi, Chem. Mater., 2015, 27, 3721–3725 CrossRef CAS
.
- D. Lu, Z. Yao, Y. Zhong, X. Wang, X. Xia, C. Gu, J. Wu and J. Tu, ACS Appl. Mater. Interfaces, 2019, 11, 15630–15637 CrossRef CAS
.
- J. Xia, W. Wu, K. Fang and X. Wu, Carbon, 2020, 157, 693–702 CrossRef CAS
.
- Y. B. Niu, Y. J. Guo, Y. X. Yin, S. Y. Zhang, T. Wang, P. Wang, S. Xin and Y. G. Guo, Adv. Mater., 2020, 32, e2001419 CrossRef
.
- J. Martinez De Ilarduya, L. Otaegui, J. M. López del Amo, M. Armand and G. Singh, J. Power Sources, 2017, 337, 197–203 CrossRef CAS
.
- B. Zhang, R. Dugas, G. Rousse, P. Rozier, A. M. Abakumov and J. M. Tarascon, Nat. Commun., 2016, 7, 10308 CrossRef CAS
.
- K. Park, B.-C. Yu and J. B. Goodenough, Chem. Mater., 2015, 27, 6682–6688 CrossRef CAS
.
- M. Sathiya, J. Thomas, D. Batuk, V. Pimenta, R. Gopalan and J.-M. Tarascon, Chem. Mater., 2017, 29, 5948–5956 CrossRef CAS
.
- C.-H. Jo, J. U. Choi, H. Yashiro and S.-T. Myung, J. Mater. Chem. A, 2019, 7, 3903–3909 RSC
.
- C. Grey and J. Tarascon, Nat. Mater., 2017, 16, 45 CrossRef
.
- P. Harks, F. Mulder and P. Notten, J. Power Sources, 2015, 288, 92–105 CrossRef CAS
.
- J. Yang, S. Muhammad, M. R. Jo, H. Kim, K. Song, D. A. Agyeman, Y. I. Kim, W. S. Yoon and Y. M. Kang, Chem. Soc. Rev., 2016, 45(20), 5717–5770 RSC
.
- C. Tan, S. R. Daemi, O. O. Taiwo, T. M. Heenan, D. J. Brett and P. R. Shearing, Materials, 2018, 11, 2157 CrossRef
.
- H. Kato, Y. Kobayashi and H. Miyashiro, J. Power Sources, 2018, 398, 49–54 CrossRef CAS
.
- I. Bloom, A. N. Jansen, D. P. Abraham, J. Knuth, S. A. Jones, V. S. Battaglia and G. L. Henriksen, J. Power Sources, 2005, 139, 295–303 CrossRef CAS
.
- M. Lewerenz, A. Marongiu, A. Warnecke and D. U. Sauer, J. Power Sources, 2017, 368, 57–67 CrossRef CAS
.
- D. Goonetilleke, T. Faulkner, V. K. Peterson and N. Sharma, J. Power Sources, 2018, 394, 1–8 CrossRef CAS
.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring and D. Fraggedakis, Nat. Energy, 2019, 4, 383–391 CrossRef
.
- K. Wang, P. Yan and M. Sui, Nano Energy, 2018, 54, 148–155 CrossRef CAS
.
- H. M. Dahn, A. Smith, J. Burns, D. Stevens and J. Dahn, J. Electrochem. Soc., 2012, 159, A1405–A1409 CrossRef CAS
.
- L. A. Middlemiss, A. J. R. Rennie, R. Sayers and A. R. West, Energy Rep., 2020, 6, 232–241 CrossRef
.
- G. Yan, S. Mariyappan, G. Rousse, Q. Jacquet, M. Deschamps, R. David, B. Mirvaux, J. W. Freeland and J. M. Tarascon, Nat. Commun., 2019, 10, 585 CrossRef CAS
.
- J. Li, X. Xiao, F. Yang, M. W. Verbrugge and Y.-T. Cheng, J. Phys. Chem. C, 2011, 116, 1472–1478 CrossRef
.
- K. J. Nelson, G. L. d'Eon, A. T. B. Wright, L. Ma, J. Xia and J. R. Dahn, J. Electrochem. Soc., 2015, 162, A1046–A1054 CrossRef CAS
.
- Y. Zhu and C. Wang, J. Phys. Chem. C, 2010, 114, 2830–2841 CrossRef CAS
.
- N. Sabi, S. Doubaji, K. Hashimoto, S. Komaba, K. Amine, A. Solhy, B. Manoun, E. Bilal and I. Saadoune, J. Power Sources, 2017, 342, 998–1005 CrossRef CAS
.
-
R. E. Dinnebier and S. J. Billinge, Powder diffraction: theory and practice, Royal Society of Chemistry, 2008 Search PubMed
.
-
T. Egami and S. J. Billinge, Underneath the Bragg peaks: structural analysis of complex materials, Newnes, 2012 Search PubMed
.
-
E. H. Kisi and C. J. Howard, Applications of neutron powder diffraction, Oxford University Press, 2012 Search PubMed
.
- V. K. Peterson and C. M. Papadakis, IUCrJ, 2015, 2, 292–304 CrossRef CAS
.
- M. Morcrette, Y. Chabre, G. Vaughan, G. Amatucci, J. B. Leriche, S. Patoux, C. Masquelier and J. M. Tarascon, Electrochim. Acta, 2002, 47, 3137–3149 CrossRef CAS
.
- X. L. Wang, K. An, L. Cai, Z. Feng, S. E. Nagler, C. Daniel, K. J. Rhodes, A. D. Stoica, H. D. Skorpenske, C. Liang, W. Zhang, J. Kim, Y. Qi and S. J. Harris, Sci. Rep., 2012, 2, 747 CrossRef
.
- N. Sharma, W. K. Pang, Z. Guo and V. K. Peterson, ChemSusChem, 2015, 8, 2826–2853 CrossRef CAS
.
- P. Shearing, Y. Wu, S. J. Harris and N. Brandon, Interface, 2011, 20, 43 CAS
.
- A. Senyshyn, M. J. Mühlbauer, O. Dolotko, M. Hofmann, T. Pirling and H. Ehrenberg, J. Power Sources, 2014, 245, 678–683 CrossRef CAS
.
- S.-M. Bak, Z. Shadike, R. Lin, X. Yu and X.-Q. Yang, NPG Asia Mater., 2018, 10(7), 563–580 CrossRef
.
- T.-Y. Chen, B. Han, C.-W. Hu, Y.-f. Su, Y.-X. Zhou, H.-Y. Chen, P.-I. Pan, C.-M. Wu, A. Hu and J.-J. Kai, J. Phys. Chem. C, 2018, 122(24), 12623–12632 CrossRef CAS
.
- W. M. Dose, N. Sharma, J. C. Pramudita, M. Avdeev, E. Gonzalo and T. Rojo, Chem. Mater., 2018, 30, 7503–7510 CrossRef CAS
.
- D. Goonetilleke, S. Wang, E. Gonzalo, M. Galcerán, D. Saurel, S. J. Day, F. Fauth, T. Rojo and N. Sharma, J. Mater. Chem. A, 2019, 7, 12115–12125 RSC
.
- S. Kjeldgaard, S. Birgisson, A. G. Kielland and B. B. Iversen, J. Appl. Crystallogr., 2018, 51(5), 1304–1310 CrossRef CAS
.
- B. Mortemard de Boisse, J. H. Cheng, D. Carlier, M. Guignard, C. J. Pan, S. Bordère, D. Filimonov, C. Drathen, E. Suard, B. J. Hwang, A. Wattiaux and C. Delmas, J. Mater. Chem. A, 2015, 3, 10976–10989 RSC
.
- N. Tapia-Ruiz, W. M. Dose, N. Sharma, H. Chen, J. Heath, J. W. Somerville, U. Maitra, M. S. Islam and P. G. Bruce, Energy & Environmental Science, 2018, 11, 1470–1479 Search PubMed
.
- X. Qiu, J. W. Thompson and S. J. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS
.
- P. K. Allan, J. M. Griffin, A. Darwiche, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, A. J. Morris, P. J. Chupas, L. Monconduit and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 2352–2365 CrossRef CAS
.
- K. W. Chapman, MRS Bull., 2016, 41, 231–240 CrossRef
.
- J. Sottmann, M. Di Michiel, H. Fjellvåg, L. Malavasi, S. Margadonna, P. Vajeeston, G. B. M. Vaughan and D. S. Wragg, Angew. Chem., Int. Ed., 2017, 56, 11385–11389 CrossRef CAS
.
- K. M. Wiaderek, O. J. Borkiewicz, E. Castillo-Martínez, R. Robert, N. Pereira, G. G. Amatucci, C. P. Grey, P. J. Chupas and K. W. Chapman, J. Am. Chem. Soc., 2013, 135, 4070–4078 CrossRef CAS
.
- J. Yano and V. K. Yachandra, Photosynth. Res., 2009, 102, 241 CrossRef CAS
.
- F. de Groot, Chem. Rev., 2001, 101, 1779–1808 CrossRef CAS
.
- M. Chen, S.-L. Chou and S.-X. Dou, Batteries Supercaps, 2019, 2, 842–851 CrossRef
.
- Y. Wang, L. Wang, H. Zhu, J. Chu, Y. Fang, L. Wu, L. Huang, Y. Ren, C.-J. Sun, Q. Liu, X. Ai, H. Yang and Y. Cao, Adv. Funct. Mater., 2020, 30, 1910327 CrossRef CAS
.
- R. L. Mössbauer, Z. Phys., 1958, 151, 124–143 CrossRef
.
-
P. Gütlich, R. Link and A. Trautwein, Mössbauer Spectroscopy and Transition Metal Chemistry, Springer, Berlin Heidelberg, 2013 Search PubMed
.
- R. Rajagopalan, B. Chen, Z. Zhang, X. L. Wu, Y. Du, Y. Huang, B. Li, Y. Zong, J. Wang, G. H. Nam, M. Sindoro, S. X. Dou, H. K. Liu and H. Zhang, Adv. Mater., 2017, 29(12), 1605694 CrossRef
.
- J. S. Thorne, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2014, 161, A2232–A2236 CrossRef CAS
.
- J. S. Thorne, S. Chowdhury, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2014, 161, A1801–A1805 CrossRef
.
- J. S. Thorne, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2013, 160, A361–A367 CrossRef CAS
.
- E. McCalla, M. T. Sougrati, G. Rousse, E. J. Berg, A. Abakumov, N. Recham, K. Ramesha, M. Sathiya, R. Dominko, G. Van Tendeloo, P. Novak and J. M. Tarascon, J. Am. Chem. Soc., 2015, 137, 4804–4814 CrossRef CAS
.
- C. Drager, F. Sigel, R. Witte, R. Kruk, L. Pfaffmann, S. Mangold, V. Mereacre, M. Knapp, H. Ehrenberg and S. Indris, Phys. Chem. Chem. Phys., 2018, 21, 89–95 RSC
.
-
B. Diehl, in NMR Spectroscopy in Pharmaceutical Analysis, Elsevier, 2008, pp. 1–41 Search PubMed
.
- O. Pecher, J. Carretero-Gonzalez, K. J. Griffith and C. P. Grey, Chem. Mater., 2017, 29(1), 213–242 CrossRef CAS
.
- D. L. Smiley, D. Carlier and G. R. Goward, Solid State
Nucl. Magn. Reson., 2019, 103, 1–8 CrossRef CAS
.
- M. Miroshnikov, K. Kato, G. Babu, N. Kumar, K. Mahankali, E. Hohenstein, H. Wang, S. Satapathy, K. P. Divya, H. Asare, L. M. R. Arava, P. M. Ajayan and G. John, ACS Appl. Energy Mater., 2019, 2, 8596–8604 CrossRef CAS
.
- L. Yang, X. Li, J. Liu, S. Xiong, X. Ma, P. Liu, J. Bai, W. Xu, Y. Tang, Y.-Y. Hu, M. Liu and H. Chen, J. Am. Chem. Soc., 2019, 141, 6680–6689 CrossRef CAS
.
- R. J. Clément, J. Xu, D. S. Middlemiss, J. Alvarado, C. Ma, Y. S. Meng and C. P. Grey, J. Mater. Chem. A, 2017, 5, 4129–4143 RSC
.
- M. Kalapsazova, R. Stoyanova, E. Zhecheva, G. Tyuliev and D. Nihtianova, J. Mater. Chem. A, 2014, 2, 19383–19395 RSC
.
- J. Wu, M. Fenech, R. F. Webster, R. D. Tilley and N. Sharma, Sustainable Energy Fuels, 2019, 3, 1623–1646 RSC
.
-
R. F. Egerton, Physical principles of electron microscopy, Springer, 2005 Search PubMed
.
- Y. Wang, D. Dang, D. Li, J. Hu, X. Zhan and Y.-T. Cheng, J. Power Sources, 2019, 438, 226938 CrossRef CAS
.
- J. Li, A. R. Cameron, H. Li, S. Glazier, D. Xiong, M. Chatzidakis, J. Allen, G. Botton and J. Dahn, J. Electrochem. Soc., 2017, 164, A1534–A1544 CrossRef CAS
.
- P. Barai and P. P. Mukherjee, J. Electrochem. Soc., 2013, 160, A955–A967 CrossRef CAS
.
- F. P. McGrogan, S. R. Bishop, Y.-M. Chiang and K. J. Van Vliet, J. Electrochem. Soc., 2017, 164, A3709 CrossRef CAS
.
- Y. Zhang, C. Zhao and Z. Guo, Int. J. Mech. Sci., 2019, 155, 178–186 CrossRef
.
- R. Ruess, S. Schweidler, H. Hemmelmann, G. Conforto, A. Bielefeld, D. A. Weber, J. Sann, M. T. Elm and J. Janek, J. Electrochem. Soc., 2020, 167, 100532 CrossRef CAS
.
- J. Wu, M. Fenech, R. F. Webster, R. D. Tilley and N. Sharma, Sustainable Energy Fuels, 2019, 3(7), 1623–1646 RSC
.
- Y. Yuan, K. Amine, J. Lu and R. Shahbazian-Yassar, Nat. Commun., 2017, 8, 1–14 CrossRef
.
- A. L. D. Kilcoyne, T. Tyliszczak, W. F. Steele, S. Fakra, P. Hitchcock, K. Franck, E. Anderson, B. Harteneck, E. G. Rightor, G. E. Mitchell and A. P. Hitchcock, J. Synchrotron Radiat., 2003, 10(2), 125–136 CrossRef CAS
.
- M. Wolf, B. M. May and J. Cabana, Chem. Mater., 2017, 29, 3347–3362 CrossRef CAS
.
- Y. Xie, H. Wang, G. Xu, J. Wang, H. Sheng, Z. Chen, Y. Ren, C.-J. Sun, J. Wen, J. Wang, D. J. Miller, J. Lu, K. Amine and Z.-F. Ma, Adv. Energy Mater., 2016, 6(24), 1601306 CrossRef
.
- S. M. Salapaka and M. V. Salapaka, IEEE Contr. Syst. Mag., 2008, 28(2), 65–83 Search PubMed
.
- R. Kempaiah, G. Vasudevamurthy and A. Subramanian, Nano Energy, 2019, 65, 103925 CrossRef CAS
.
- M. S. Islam and C. A. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC
.
- C. R. A. Catlow, Z. X. Guo, M. Miskufova, S. A. Shevlin, A. G. H. Smith, A. A. Sokol, A. Walsh, D. J. Wilson and S. M. Woodley, Philos. Trans. R. Soc., A, 2010, 368, 3379–3456 CrossRef CAS
.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS
.
- Q. Bai, L. Yang, H. Chen and Y. Mo, Adv. Energy Mater., 2018, 1702998, DOI:10.1002/aenm.201702998
.
- W. Song, X. Cao, Z. Wu, J. Chen, Y. Zhu, H. Hou, Q. Lan and X. Ji, Langmuir, 2014, 30, 12438–12446 CrossRef CAS
.
- A. J. Toumar, S. P. Ong, W. D. Richards, S. Dacek and G. Ceder, Phys. Rev. Appl., 2015, 4, 064002 CrossRef
.
| This journal is © The Royal Society of Chemistry 2020 |