Cross-linker control of vitrimer flow

Abstract

Vitrimers are a class of covalent adaptable networks (CANs) that undergo topology reconfiguration via associative exchange reactions, enabling reprocessing at elevated temperatures. Here, we show that cross-linker reactivity represents an additional design parameter to tune stress relaxation rates in vitrimers. Guided by calculated activation barriers, we prepared a series of cross-linkers with varying reactivity for the conjugate addition—elimination of thiols in a PDMS vitrimer. Surprisingly, despite a wide range of stress relaxation rates, we observe that the flow activation energy of the bulk material is independent of the cross-linker structure. Superposition of storage and loss moduli from frequency sweeps can be performed for different cross-linkers, indicating the same exchange mechanism. We show that we can mix different cross-linkers in a single material in order to further modulate the stress relaxation behavior.

---

Introduction

The incorporation of reversible linkages within polymer chains or junctions creates dynamic networks that can achieve desirable characteristics such as self-healing, recyclability, and stimuli-responsivity.^1–8 Specifically, covalent adaptable networks (CANs) possess covalent bonds that can exchange under a stimulus, most often heat, allowing the network architecture to rearrange. When the covalent bond exchange is activated, the network can dissipate applied stress (i.e., stress relaxation). In the most well studied class of CANs, bond exchange occurs through dissociative mechanisms,^9–13 meaning that the cross-link must be broken before a new cross-link can form. Detailed structure–property studies of the sterics and electronics of the exchanging cross-links in dissociative CANs have enabled precise tuning of network mechanics as a function of temperature.^11,14

A more recently reported class of CANs that exchange by associative mechanisms, known as vitrimers,^15–18 retain a cross-linked structure during swelling and heating, but can still be remolded and repaired.⁵ Overall cross-link density is conserved since bond breakage only occurs after another covalent bond has been formed; these materials are expected to maintain a constant rubbery plateau modulus during topological rearrangement.² A wide array of associative dynamic covalent chemistries have been employed in vitrimers, including transesterification,^19–21 olefin metathesis,^22,23 dioxaborolane exchange,^24–26 silyl ether exchange,²⁷ and several others.^28–37 Surprisingly, despite the number of reactions studied, there are no systematic studies that examine the effect of the cross-linker structure on vitrimer properties. In this paper, we show that small structural modifications to cross-links in a vitrimer can offer control over stress relaxation over a wide range, without affecting the stiffness or flow activation energy of the materials.

Strategies to control the rate of vitrimer flow primarily rely on the effect of catalysts^38,39 and cross-link density,^31,40–42 with isolated examples examining macromolecular architecture⁴³ and strand flexibility.⁴⁴ In a pioneering study, Leibler and co-workers demonstrated that changing the catalyst type and concentration affects flow activation energies for ester-based vitrimers.⁴⁵ Bates and co-workers later identified a surprising inverse relationship between the pKa of Brønsted acid catalysts and flow activation energy.⁴⁶

Catalysts can suffer from leaching and deactivation, motivating our interest in catalyst-free exchange reactions for vitrimers. We previously demonstrated that the conjugate addition–elimination of thiols to a Meldrum's acid-derived acceptor⁴⁷ in a PDMS vitrimer enables at least ten reprocessing cycles without loss of properties (Scheme 1).⁴⁸ Here, we synthesize a series of conjugate acceptor cross-linkers and compare their reactivity in vitrimers. Key differences in reactivity can be rationalized based on calculated transition states. We obtain vitrimers exhibiting a wide range of stress relaxation times, spanning over 4 orders of magnitude, with nearly identical stiffnesses. We can superimpose frequency sweeps for three distinct cross-linkers with a horizontal shift factor, suggesting that relaxation occurs through a common mechanism. Finally, we can further tune the stress relaxation profiles by mixing cross-linkers with different reactivities into single networks. This study revealed two new cross-linkers that enable significantly faster stress relaxation compared to the original Meldrum's acid-derived acceptor.

Scheme 1 Mechanism of the conjugate addition–elimination exchange reactions in the elastomeric PDMS vitrimer studied here.

Experimental

Gel formation

Polydimethylsiloxane (PDMS) grafted with 13–17% propylthiol groups was obtained from Gelest (SMS-142, Molecular weight 3000–4000). Crosslinkers were added to the mixture in either 1.25 or 2 mol% relative to the siloxane repeat units. The mixture was heated to either 100 °C (CY crosslinker), 120 °C (MA, BA, IND, CN), or 150 °C (DP) for 12–16 hours. For the CN samples, xylenes (∼50 wt%) were used to solubilize the cross-linker in the PDMS and was later removed by evaporation in a vacuum oven at 150 °C for 24 hours. All samples were reprocessed once prior to testing using a hot press at 140–150 °C at a pressure of 10 tonnes for 15–30 minutes to ensure homogeneous samples. The sample thickness was kept constant at 1 mm by using 1 mm spacers during the reprocessing. For the mixed gel samples, 1 mol% of each crosslinker was mixed in the PDMS solution. The samples were heated at 120 °C overnight and reprocessed similarly.

Rheology

The viscoelastic properties of the networks were studied using a strain-controlled Anton Paar rheometer (MCR302). Measurements ranged between 100 and 150 °C for all studies. Parallel plate geometry with a diameter of 8 mm was used. The gap size was kept around 1 mm for all the samples. Frequency sweep measurements were performed using dynamic oscillatory measurements at a constant strain of 3%. It is important to note that all measurements took place in the linear viscoelastic regime as determined by amplitude sweeps. Stress relaxation measurements were performed at temperatures between 100 and 150 °C at 3% or 7% strain unless otherwise noted (all within the linear viscoelastic regime).

Cross-linker synthesis

All reactions were performed under nitrogen or argon with dry DMF which was obtained via passing degassed solvents through activated alumina columns. Chemicals were obtained from MilliporeSigma, TCI Chemicals, Alfa Aesar, and Oakwood. In addition to the original Meldrum's acid-based cross-linker (MA) and a commercial malonitrile derivative (CN), four cross-linkers were synthesized by base-assisted nucleophilic addition of the 1,3-dicarbonyl compound to CS₂, followed by methylation (Fig. 1a). These cross-linkers are named based on the dicarbonyl structures: cyclohexanedione (CY), barbituric acid (BA), indanedione (IND), and diphenylpropanedione (DP) (Fig. 1b). For additional synthesis details, see ESI.†

Fig. 1 (a) General synthesis for cross-linkers used in the study. (b) Structures of different cross-linkers used in the study.

Results and discussion

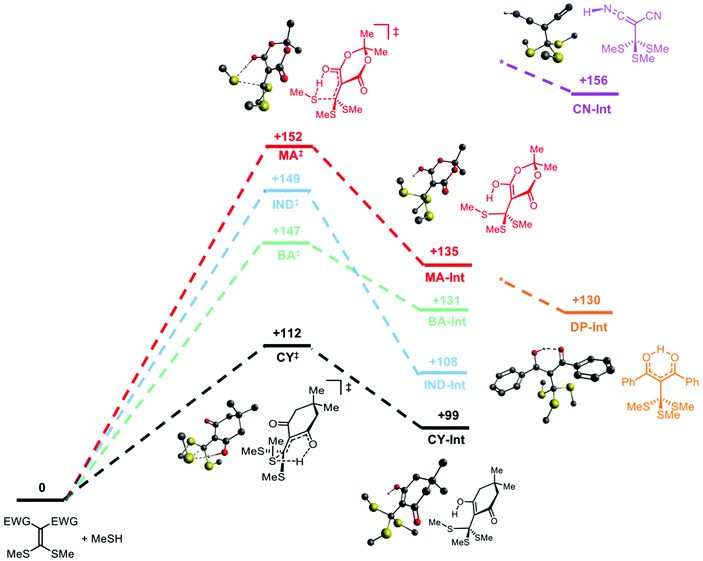
To predict differences in exchange rates between the different cross-linkers, we performed DFT calculations (B3LYP/def-TZVP gas phase). The initial conjugate addition step is rate limiting, so transition states for this step were calculated and minimized. The temperature used for the calculations was 135 °C. For the cyclic cross-linkers (MA, IND, BA, CY), closed, six-membered transition states were located (Fig. 2 and S16†). In normal reaction media, mobile solvent molecules or additives can aid the addition of thiols to Michael acceptors by acting as proton transfer agents.⁴⁷ However, in the nonpolar environment of the PDMS matrix, in which our polymer network is formed, it is reasonable to invoke the participation of an internal base (i.e., the carbonyl of the cross-linker) to mediate proton transfer from the thiol in a closed transition state. The lowest activation barrier belongs to CY (+112 kJ mol⁻¹), followed by BA, IND and MA, which have similar calculated ΔG^‡ values to each other (Fig. 2).

Fig. 2 Calculated transition states and intermediate energies (in kJ mol⁻¹) for the cross-linkers (energies are not drawn to scale). Representative optimized cyclic transition state and intermediates for the conjugate addition of methanethiol to MA and CY, and intermediates for CN and DP, are shown. H atoms on CH₃ groups are omitted for clarity. *No cyclic transition states were located for DP and CN.

Tetrahedral intermediates for the acyclic cross-linkers DP and CN orient the proton away from the thiols, and correspondingly, no closed transition states were located. The N_sp lone pairs on each nitrile of CN point away from the site of nucleophilic attack. The bond rotations required in DP to accommodate a cyclic transition state would likely result in unfavourable steric interactions (Fig. S15–S17†). Thus, the acyclic cross-linkers lack an internal base to accelerate the exchange process.

To compare the effect of cross-linker structure in vitrimers, stress relaxation experiments were performed using shear rheology (Fig. 3a; for additional details, see ESI†). The vitrimer networks are named based on the cross-linker used (e.g., CY-Net). The rate of the relaxation process can be characterized with respect to a characteristic relaxation time constant, τ*. Assuming Maxwell behaviour, τ* is defined as the time needed for the relaxation modulus to decrease to 1/e of its initial value. The τ* values for this series of cross-linkers span 4 orders of magnitude, following the trend CY < BA < IND ∼ MA ≪ CN ∼ DP (Fig. 3b). This trend is consistent with the calculated ΔG^‡ values, suggesting that the stress relaxation in these materials is directly correlated to the exchange kinetics. The wide range in stress relaxation rates was accompanied by modest differences in stiffness. The rubbery plateau moduli of these networks at 150 °C were determined by frequency sweeps between 100 and 1 rad s⁻¹ and were found to be similar for all cross-linkers, ranging between 100 and 130 kPa (Fig. 3b). The similarity of the plateau moduli and gel fraction studies (Table S10†) suggest that cross-link density is not affected by the structure of the cross-linker, consistent with an associative mechanism.

Fig. 3 Mechanical properties of the networks. (a) Representative normalized stress relaxation profiles at 150 °C. (b) Calculated τ* values for the different cross-linked vitrimers (bar graph, left axis) and their rubbery plateau moduli at the same temperature (circle symbols, right axis). Error bars are based on student's t distribution. The τ* values were calculated using 1/e of the relaxation modulus for the cyclic cross-linkers and by extrapolating a stretched exponential function for the acyclic cross-linkers (see ESI for more detail†). (c) Arrhenius plots for stress relaxation of networks derived from the cyclic cross-linkers. (d) Calculated flow activation energies for the networks. Error bars are based on the error analysis of the fitted slopes.

The flow activation energy (E_a) is determined by measuring τ* as a function of temperature based on the Arrhenius relationship (eqn (1)):

where R is the ideal gas constant, T is the temperature, and τ₀ is a pre-exponential factor.

Surprisingly, the flow activation energies calculated for the different cyclic cross-linkers were within experimental error, with their averages ranging between 60 and 68 kJ mol⁻¹ (Fig. 3c and 3d). While this result differs from the calculated ΔG^‡ values, for multistep reactions, Eyring ΔG^‡ values are not equivalent to Arrhenius activation energies (E_a). Instead, the difference in relaxation times is driven by the pre-exponential factor, τ₀, represented by the change in y-intercept (Table S11†). τ₀ has been defined as the relaxation time at infinite temperature, but the physical underpinnings of this value in vitrimers are not well understood.⁵ For the acyclic cross-linkers, the experimentally accessible temperature range was too narrow for an accurate Arrhenius analysis.

Activation energy values represent the temperature sensitivity of a process, and not the absolute kinetics. Rational strategies to tune the flow activation energy, E_a, and the pre-exponential factor, τ₀, are necessary to guide optimization of vitrimer properties. For example, to minimize creep at service temperatures but enable flow at elevated temperatures without decomposition, high E_a is desirable.²⁸ In ester and vinylogous urethane vitrimers, catalysts modulate relaxation times by changing both E_a and τ₀.^27,28,43 Our results show that the absolute rate of stress relaxation can be modulated without affecting the temperature dependence by changing the structure of the cross-linker. It should be noted, however, that the flow activation of the polymer can differ from the small molecule activation energies.^5,49

Some vitrimer systems exhibit a change in exchange mechanism as a function of temperature or additives.^50,51 We sought to confirm that changing the structure of the cross-linker in the vitrimer did not influence the mechanism of exchange. Typically, time–temperature superpositions (TTS) of frequency sweeps are used in polymer rheology to determine if the relaxation processes scale as a function of temperature. In order to determine if the relaxation processes in our vitrimers scale as a function of cross-linker reactivity, a time–cross-linker superposition (TCLS) was constructed at 150 °C (3% strain, 0.01–100 rad s⁻¹) for representative cross-linkers (Fig. 4). This type of analysis has been performed by researchers in dissociative systems where the shift factor of the superposition can relate to the kinetics or activation energy of cross-linker dissociation.^6,7 The networks in this study contained 1.25 mol% of the cross-linker, which allowed access to the terminal regime. We were able to superimpose the CY-Net and BA-Net storage (G′) and loss (G′′) moduli curves onto the reference IND-Net data using only horizontal shift factors. This superposition suggests that the mechanism of stress relaxation is indeed identical for the cyclic cross-linkers; the only difference between samples is how fast or slow the collective relaxation process is.

Fig. 4 Time—cross-linker superposition for both the storage (G′) and loss (G′′) moduli of networks with three different cross-linkers (IND, BA, and CY). IND was used as the reference.

The horizontal shift factors (α_T) were calculated from the crossover frequencies (ω_c), which are inversely related to the characteristic stress relaxation times τ* for an ideal Maxwell material (eqn (2)).

Furthermore, a vertical shift factor was not required, and the rubbery plateau moduli of the samples with 1.25 mol% cross-linker ranged between 8 and 11 kPa, again demonstrating that an associative exchange mechanism can decouple stiffness and stress relaxation.

For dissociative reversible networks, mixing cross-linkers with the same exchange mechanism but different relaxation rates modulates stress relaxation profiles.^15,52,53 While Dichtel,⁵⁴ Chen,⁵⁵ and Guo⁵⁶ have mixed associative and dissociative cross-links in a single network, we are interested in the effect of mixing mechanistically similar, kinetically distinct associative cross-links. We formulated three separate samples based on binary mixtures of cross-linkers (1 mol% each): CY/MA-Net, BA/MA-Net, and BA/DP-Net. Stress relaxation measurements were carried at 140 °C (Fig. 5). As expected based on the stress relaxation of the single cross-linker networks, the stress relaxation times follow the trend CY/MA-Net < BA/MA-Net < BA/DP-Net. Each stress relaxation profile is intermediate to those of its individual cross-linker counterparts (Fig. 5a through c).

Fig. 5 Normalized stress relaxation data for (a) CY-Net, CY/MA-Net, and MA-Net; (b) BA-Net, BA/MA-Net, and MA-Net; (c) BA-Net, BA/DP-Net, and DP-Net at 140 °C.

The shape of the normalized stress relaxation curves for the mixed systems indicate additional complexity. Surprisingly, the BA/MA-Net relaxation data could be fitted to an ideal Maxwell model with an activation energy similar to that of the individual cross-linkers (Fig. S13 and S14†), whereas CY/MA-Net and BA/DP-Net relaxation deviated from ideal Maxwell behaviour, suggesting that multiple relaxation modes are operative (Fig. S11 and S12†). We conclude that the presence of either a singular or multiple relaxation modes depends on the relative relaxation times for each individual cross-linker. If the relaxation times for the individual cross-linkers are within an order of magnitude, the mixed cross-linker system exhibits a single intermediate relaxation mode. When the individual relaxation rates differ by several orders of magnitude, we observe several distinct relaxation modes. This relaxation behaviour is more varied than what has been observed in dissociative systems: mixed boronic ester cross-links resulted in single unimodal Maxwell distributions,⁵² and mixed metal–ligand¹⁵ and protein–protein cross-links⁵³ showed a distinct relaxation mode for each component. The relevance of the Maxwell model to vitrimers is under investigation in our lab.

Conclusions

Decoupling spatial and temporal structure is a fundamental challenge in soft materials. Here, we show that the associative exchange reactions used in vitrimers enable synthetic control over stress relaxation independent of stiffness. The rate of stress relaxation in PDMS vitrimers was shown to be dependent on the structure and reactivity of the electrophilic cross-linker, while maintaining the same exchange mechanism and cross-link density. Thus, we can tune the stress relaxation profile of the network by several orders of magnitude with only small perturbations to the stiffness. The flow behavior may be further modulated by mixing cross-linkers with distinct rates. Our results suggest that in vitrimers with a common exchange mechanism, changing the structure of the exchange partner can dramatically alter the stress relaxation rate without altering the flow activation energy. This result is contrasted to the effect of catalysts, which generally accelerate flow in vitrimers by lowering the flow activation energy. These insights will enable rational optimization of vitrimers to strike the balance between limiting creep and accelerating repair.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the NSF Center for the Chemistry of Molecularly Optimized Networks (NSF CHE-1832256) and a 3M Non-Tenured Faculty Award for funding. This work made use of the Integrated Molecular Structure Education and Research Center at Northwestern, which has received support from the NIH (S10-OD021786-01). Rheological measurements were performed at the Materials Characterization and Imaging Facility which receives support from the MRSEC Program (NSF DMR-1720139) of the Materials Research Center at Northwestern University. The authors additionally thank Dr Scott Danielson, Prof. Michael Rubinstein, and Prof. Stephen Craig (Duke University) for helpful discussion as well as Mukund Kabra for help executing Python code, and Dr John Nardini for help with error analysis.

References

1. J. M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160.
2. C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161–7173.
3. Y. Jin, C. Yu, R. J. Denman and W. Zhang, Chem. Soc. Rev., 2013, 42, 6634–6654.
4. W. Zou, J. Dong, Y. Luo, Q. Zhao and T. Xie, Adv. Mater., 2017, 29, 1606100.
5. G. M. Scheutz, J. J. Lessard, M. B. Sims and B. S. Sumerlin, J. Am. Chem. Soc., 2019, 141, 16181–16196.
6. W. C. Yount, D. M. Loveless and S. L. Craig, J. Am. Chem. Soc., 2005, 127, 14488–14496.
7. E. A. Appel, R. A. Förster, A. Koutsioubas, C. Toprakcioglu and O. A. Scherman, Angew. Chem., Int. Ed., 2014, 53, 10038–10043.
8. Y.-C. Yu, P. Berndt, M. Tirrell and G. B. Fields, J. Am. Chem. Soc., 1996, 118, 12515–12520.
9. D. D. McKinnon, D. W. Domaille, J. N. Cha and K. S. Anseth, Adv. Mater., 2014, 26, 865–872.
10. V. Yesilyurt, M. J. Webber, E. A. Appel, C. Godwin, R. Langer and D. G. Anderson, Adv. Mater., 2016, 28, 86–91.
11. N. van Herck, D. Maes, K. Unal, M. Guerre, J. M. Winne and F. E. du Prez, Angew. Chem., 2020, 59, 3609–3617.
12. P. Chakma, Z. A. Digby, M. P. Shulman, L. R. Kuhn, C. N. Morley, J. L. Sparks and D. Konkolewicz, ACS Macro Lett., 2019, 8, 95–100.
13. P. Chakma, C. N. Morley, J. L. Sparks and D. Konkolewicz, Macromolecules, 2020, 53, 1233–1244.
14. L. Zhang and S. J. Rowan, Macromolecules, 2017, 50, 5051–5060.
15. S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216.
16. T. F. Scott, A. D. Schneider, W. D. Cook and C. N. Bowman, Science, 2005, 308, 1615–1617.
17. D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968.
18. W. Denissen, J. M. Winne and F. E. du Prez, Chem. Sci., 2016, 7, 30–38.
19. J. P. Brutman, P. A. Delgado and M. A. Hillmyer, ACS Macro Lett., 2014, 3, 607–610.
20. Y. Zhou, J. G. P. Goossens, S. van den Bergen, R. P. Sijbesma and J. P. A. Heuts, Macromol. Rapid Commun., 2018, 39, 1800356.
21. X. Niu, F. Wang, X. Li, R. Zhang, Q. Wu and P. Sun, Ind. Eng. Chem. Res., 2019, 58, 5698–5706.
22. Y.-X. Lu, F. Tournilhac, L. Leibler and Z. Guan, J. Am. Chem. Soc., 2012, 134, 8424–8427.
23. H. Liu, A. Z. Nelson, Y. Ren, K. Yang, R. H. Ewoldt and J. S. Moore, ACS Macro Lett., 2018, 7, 933–937.
24. M. Röttger, T. Domenech, R. van der Weegen, A. Breuillac, R. Nicolaÿ and L. Leibler, Science, 2017, 356, 62–65.
25. A. Breuillac, A. Kassalias and R. Nicolaÿ, Macromolecules, 2019, 52, 7102–7113.
26. F. Caffy and R. Nicolaÿ, Polym. Chem., 2019, 10, 3107–3115.
27. Y. Nishimura, J. Chung, H. Muradyan and Z. Guan, J. Am. Chem. Soc., 2017, 139, 14881–14884.
28. W. Denissen, M. Droesbeke, R. Nicola, L. Leibler, J. M. Winne and F. E. du Prez, Nat. Commun., 2017, 8, 4857.
29. W. Denissen, G. Rivero, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. du Prez, Adv. Funct. Mater., 2015, 25, 2451–2457.
30. D. J. Fortman, J. P. Brutman, C. J. Cramer, M. A. Hillmyer and W. R. Dichtel, J. Am. Chem. Soc., 2015, 137, 14019–14022.
31. R. L. Snyder, D. J. Fortman, G. X. de Hoe, M. A. Hillmyer and W. R. Dichtel, Macromolecules, 2018, 51, 389–397.
32. C. He, S. Shi, D. Wang, B. A. Helms and T. P. Russell, J. Am. Chem. Soc., 2019, 141, 13753–13757.
33. H. Geng, Y. Wang, Q. Yu, S. Gu, Y. Zhou, W. Xu, X. Zhang and D. Ye, ACS Sustainable Chem. Eng., 2018, 6, 15463–15470.
34. T. Stukenbroeker, W. Wang, J. M. Winne, F. E. du Prez, R. Nicolaÿ and L. Leibler, Polym. Chem., 2017, 8, 6590–6593.
35. Z. Ma, Y. Wang, J. Zhu, J. Yu and Z. Hu, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1790–1799.
36. J. Tellers, R. Pinalli, M. Soliman, J. Vachon and E. Dalcanale, Polym. Chem., 2019, 10, 5534–5542.
37. D. J. Fortman, J. P. Brutman, M. A. Hillmyer and W. R. Dichtel, J. Appl. Polym. Sci., 2017, 134, 44984.
38. T. E. Brown, B. J. Carberry, B. T. Worrell, O. Y. Dudaryeva, M. K. McBride, C. N. Bowman and K. S. Anseth, Biomaterials, 2018, 178, 496–503.
39. B. T. Worrell, S. Mavila, C. Wang, T. M. Kontour, C. H. Lim, M. K. McBride, C. B. Musgrave, R. Shoemaker and C. N. Bowman, Polym. Chem., 2018, 9, 4523–4534.
40. S. Zhao and M. M. Abu-Omar, Macromolecules, 2019, 52, 3646–3654.
41. J. P. Brutman, D. J. Fortman, G. X. de Hoe, W. R. Dichtel and M. A. Hillmyer, J. Phys. Chem. B, 2019, 123, 1432–1441.
42. M. Hayashi and R. Yano, Macromolecules, 2020, 53, 182–189.
43. C. Taplan, M. Guerre, J. M. Winne and F. E. du Prez, Mater. Horiz., 2020, 7, 104–110.
44. C. He, P. R. Christensen, T. J. Seguin, E. A. Dailing, B. M. Wood, R. K. Walde, K. A. Persson, T. P. Russell and B. A. Helms, Angew. Chem., 2020, 59, 735–739.
45. M. Capelot, M. M. Unterlass, F. Tournilhac and L. Leibler, ACS Macro Lett., 2012, 1, 789–792.
46. J. L. Self, N. D. Dolinski, M. S. Zayas, J. Read de Alaniz and C. M. Bates, ACS Macro Lett., 2018, 7, 817–821.
47. K. L. Diehl, I. v. Kolesnichenko, S. A. Robotham, J. L. Bachman, Y. Zhong, J. S. Brodbelt and E. v. Anslyn, Nat. Chem., 2016, 8, 968–973.
48. J. S. A. Ishibashi and J. A. Kalow, ACS Macro Lett., 2018, 7, 482–486.
49. A. Jourdain, R. Asbai, O. Anaya, M. M. Chehimi, E. Drockenmuller and D. Montarnal, Macromolecules, 2020, 53, 1884–1900.
50. M. Guerre, C. Taplan, R. Nicolaÿ, J. M. Winne and F. E. du Prez, J. Am. Chem. Soc., 2018, 140, 13272–13284.
51. B. B. Jing and C. M. Evans, J. Am. Chem. Soc., 2019, 141, 18932–18937.
52. V. Yesilyurt, A. M. Ayoob, E. A. Appel, J. T. Borenstein, R. Langer and D. G. Anderson, Adv. Mater., 2017, 29, 1605947.
53. L. J. Dooling and D. A. Tirrell, ACS Cent. Sci., 2016, 2, 812–819.
54. D. J. Fortman, R. L. Snyder, D. T. Sheppard and W. R. Dichtel, ACS Macro Lett., 2018, 7, 1226–1231.
55. M. Chen, L. Zhou, Y. Wu, X. Zhao and Y. Zhang, ACS Macro Lett., 2019, 8, 255–260.
56. Y. Chen, Z. Tang, Y. Liu, S. Wu and B. Guo, Macromolecules, 2019, 52, 3805–3812.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0py00233j

---