DOI:
10.1039/C9MH01899A
(Review Article)
Mater. Horiz., 2020,
7, 1279-1296
Erbium complexes as pioneers for implementing linear light-upconversion in molecules
Received
26th November 2019
, Accepted 20th January 2020
First published on 20th January 2020
Abstract
Since the non-linear optical (NLO) response of matter to incident excitation light does not require long-lived intermediate excited states working as relays, the conversion of low-energy photons into high energy light beams using second-harmonic generation (second-order NLO process) or two-photon absorption (third-order NLO process) can be implemented either in low-phonon macroscopic solids or in molecules containing high-energy vibrations. However, harnessing the very weak non-linear absorption coefficients requires (very) intense excitation sources, typically lasers, for getting reasonable emitted intensities. In contrast, the piling of successive near-infrared photons to get visible emission using linear optics, i.e. upconversion, is much more efficient, but it depends on the existence of intermediate excited states possessing long residence lifetimes. Therefore, upconversion usually occurs in low-phonon ionic solids or nanoparticles doped with pertinent activators. The recent recognition that trivalent erbium coordination complexes possessing high-frequency oscillators may act as dual visible/near-infrared activators, which implies the existence of at least one long-lived intermediate excited state in these complexes, paved the way for the implementation of the first upconversion processes within isolated molecules. Beyond a justification for using trivalent lanthanides, and especially erbium, for the manipulation of the energy of photons in molecules using linear optics, this tutorial review summarizes the current level of developments in the field of molecular-based upconversion and discusses some forthcoming challenges.

Bahman Golesorkhi
| Bahman Golesorkhi received his BSc from Shiraz University, Iran, in 2011 and MSc from Sharif University of Technology, Iran, in 2013. He then moved to the University of Geneva, Switzerland, and got his PhD in Chemistry in 2019 under the supervision of Prof. C. Piguet. The main research line of his doctoral research focused on the design of erbium activators for lanthanide-based light upconversion, but coupled with high-energy oscillators in coordination complexes. |

Homayoun Nozary
| Homayoun Nozary obtained his PhD degree in 2001 in the field of luminescent lanthanide complexes with liquid crystalline properties (lanthanidomesogens) under the supervision of Prof. C. Piguet from the University of Geneva. After postdoctoral periods in the field of mass spectrometry, he moved to Canada in 2005 to work as an R&D researcher in Photochimie St-Jean Inc. In 2007, he joined the Department of Inorganic Chemistry of the University of Geneva as a senior scientist. |

Alexandre Fürstenberg
| Alexandre Fürstenberg obtained his doctoral degree in the field of ultrafast spectroscopy with E. Vauthey from the University of Geneva in 2007 and was awarded the PhD Prize of the European Photochemistry Association in 2008. After moving into single-molecule spectroscopy and imaging working with W. E. Moerner at Stanford University, he started his independent research thanks to an Ambizione fellowship of the Swiss National Science Foundation. He is now a group leader at the University of Geneva jointly between the Departments of Inorganic and Analytical Chemistry and of Physical Chemistry. His research focuses on quantitative fluorescence spectroscopy and microscopy tools. |

Claude Piguet
| Claude Piguet earned his PhD degree in 1989 in coordination chemistry (A. F. Williams). After postdoctoral periods in supramolecular chemistry (J.-M. Lehn) and lanthanide chemistry (J.-C. G. Bünzli), he started research projects in the field of lanthanide supramolecular chemistry. He received the Werner Medal (1995) and was appointed as a full professor of inorganic chemistry at the University of Geneva (1999, successor to C. K. Jørgensen). He has co-authored more than 200 scientific contributions (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 citations, h-factor = 59). In 2009, he was awarded the Lecoq de Boisbaudran Senior Award from the European Rare Earth Society. 000 citations, h-factor = 59). In 2009, he was awarded the Lecoq de Boisbaudran Senior Award from the European Rare Earth Society. |
Manipulating the energy of photons in molecules: from organic chromophores (p-block) to transition metal complexes (d-block and f-block)
The year 2019 will probably remain well-known in chemistry for the celebration of 150 years of the original proposal by Mendeleev of the periodic table of the elements,1 a monument which became a strong support to the edification of the atomic theory at the beginning of the 20th century.2,3 With this in mind, the modern and logical left-step representation of the periodic table (Fig. 1) highlights a remarkable dichotomy existing in chemistry when optical properties are foreseen because the molecular structures built with s-block and p-block elements (right part) usually possess closed-shell electronic structures, while those containing d-block and f-block elements (left part) are characterized by open-shell configurations.
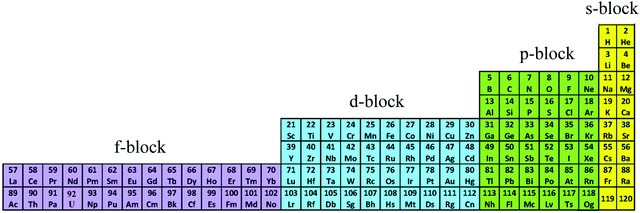 |
| | Fig. 1 Left-step representation of the periodic table of the elements. | |
Since light absorption and light emission in matter require the rearrangement/redistribution of electrons during the transitions between ground and excited states, these different electronic structures result in completely different optical properties. For closed-shell systems built with s-block and p-block atoms, which represent the major part of organic (bio)molecules, each delocalized bonding orbital is occupied by a pair of electrons with opposite spins as illustrated in the famous aromatic benzene molecule (Fig. 2a). The ground level thus corresponds to a single microstate characterized by the totally symmetric 1A1g label (D6h point group, Fig. 2b). Any non-negligible interaction between benzene molecules and incident light beams thus implies the promotion of at least one electron from a bonding (a2u or e1g) orbital into another antibonding (e1u or b2g) orbital.4 There is a limited number of possibilities for this process obeying the spin rule (ΔStot = 0) and the resulting accessible singlet excited states form a compact series of levels located at high energy (Fig. 2b). The ensuing irregular spacing of the electronic levels is characterized by a large energy gap between the ground state and the first excited state, the latter being rather close to the additional excited states located at higher energy (in the UV domain for benzene, Fig. 2b).
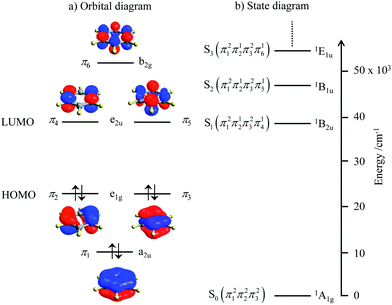 |
| | Fig. 2 (a) Electronic structure of the π-electrons in benzene and (b) associated energy diagram showing the ground level and the first singlet excited states responsible for the UV absorption spectrum. | |
Further thorough considerations of (i) intersystem crossing processes which allow the partial feeding of lower-energy triplet excited states, (ii) additional non-bonding orbitals provided by the replacement of some carbon atoms with electron-rich heteroatoms (N, O, S) and (iii) potential extension of the size of the delocalized aromatic systems may contribute to a significant reduction of the energy gap between the first excited state and the ground state in organic molecules. Nonetheless, the potential usefulness of closed-shell p-block chromophores for manipulating the energy of any interacting photons remains very limited in comparison to open-shell d-block or f-block systems which, as will be explained below, possess many more accessible, energetically more equally distributed, and longer-lived electronic energy levels. Moreover, the strong implication of bonding electrons in both optical transitions and vibrational modes in closed-shell systems produces broad absorption and emission bands (linewidth in the 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range), which prevent very selective color programming and optical addressing. Finally, the promotion of bonding electrons into anti-bonding orbitals alters the stability of the whole molecular edifices, which results in non-negligible optical bleaching through photochemical reactions occurring from reactive excited states upon exposure to light.
000 cm−1 range), which prevent very selective color programming and optical addressing. Finally, the promotion of bonding electrons into anti-bonding orbitals alters the stability of the whole molecular edifices, which results in non-negligible optical bleaching through photochemical reactions occurring from reactive excited states upon exposure to light.
The situation changes for molecules containing photophysically-active d-block or f-block centres, usually referred to as ‘complexes’ in coordination chemistry. In such molecular complexes, inter-electronic repulsions operating within the stable open-shell metal-based electronic structures provide one ground state and several excited energy levels without any need for promoting one electron from the d-orbitals or f-orbitals into empty orbitals of higher energy. Application of the Russell–Saunders coupling scheme for modeling electron–electron repulsion in open-shell d-block free ions provides one (d1 or d9) to sixteen (d5) atomic terms, which are spread over the complete UV-visible range (Fig. 3).5 Because of this higher number of accessible energy levels in the optical domain, the open-shell d-block ions offer larger perspectives than organic closed-shell p-block molecules for tuning light-absorption and light-emission properties. However, the valence d-block electrons are still implied in chemical bonding and the resulting mixing of metal-based orbitals with ligand-based orbitals in d-block complexes produces considerable ligand-field effects (Δ = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and vibronic coupling. The resulting intrashell spin-allowed d–d transitions appear as broad bands covering the UV-visible range and only a few spin–flip transitions, cleared from ligand-field effects, may display some thin absorption/emission features.6
000 cm−1) and vibronic coupling. The resulting intrashell spin-allowed d–d transitions appear as broad bands covering the UV-visible range and only a few spin–flip transitions, cleared from ligand-field effects, may display some thin absorption/emission features.6
 |
| | Fig. 3 Energy diagram of the atomic terms computed for the free ions’ dn configurations assuming B = 1000 cm−1 and C/B = 4.7 for the Racah parameters (the diagrams for d10−n are the same as those for dn).5 | |
The 4fn (n = 1–14) open-shell trivalent cations, Ln3+, offer even wider perspectives for manipulating the energy of interacting photons since (i) the 4f valence electrons are essentially not involved in chemical bonding, which removes disadvantageous broadband absorptions and emissions produced by vibronic coupling, (ii) electronic repulsion produces one atomic term for 4f1 and 4f13, but up to 119 atomic terms for the f7 configuration (compared with a maximum of 16 terms for a d5 configuration) and (iii) the spin–orbit coupling constants are large enough (700 ≤ ζ ≤ 3300 cm−1) for inducing non-negligible splitting of the 2S+1L atomic terms into numerous 2S+1LJ spectroscopic levels covering the entire electromagnetic spectrum from the near-infrared to the X-ray domain (Fig. 4).7 The total number of spectroscopic levels amounts to 2 for Ce3+(4f1) and Yb3+(4f13), but reaches the considerable number of 327 for Gd3+(4f7), without taking into account any inter-shell 4fn−15d1 configurations.8 Last, but not least, the crystal field induced by the bound donor atoms in lanthanide complexes results in minor and predictable (usually 100–400 cm−1, maximum 800–1000 cm−1) splitting of the degenerated 2J + 1 spectroscopic levels.
 |
| | Fig. 4 Energy diagram from the near-infrared to the UV range showing the 2S+1LJ spectroscopic levels of the trivalent lanthanides corresponding to the open-shell 4fn (n = 1–13) electronic configurations. Adapted from ref. 7. | |
Consequently, the rich energy diagram depicted in Fig. 4 for free ions also holds for molecular assemblies and can be used in coordination chemistry with only minor modifications. It is therefore easy to conclude that complexes of open-shell 4fn trivalent lanthanides, with their scale of regularly spaced excited levels, are ideally suited for manipulating the energy of photons with linear optics as long as radiative and non-radiative transitions between the different levels can be rationally controlled.
The toolkit for handling light-conversion in molecules
According to Fermi's ‘Golden Rule’ summarized in eqn (1), the probability per unit time Pab that an electronic transition will occur between two electronic states |a〉 (wavefunction φa) and |b〉 (wavefunction φb) is proportional to the square of the transition dipole moment |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 (Ĥp is the sum of the electric dipole and magnetic dipole perturbation operators) and to the Dirac delta function
ba|2 = 〈φb|Ĥp|φa〉2 (Ĥp is the sum of the electric dipole and magnetic dipole perturbation operators) and to the Dirac delta function 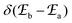 which ensures that the transition occurs with energy conservation.9
which ensures that the transition occurs with energy conservation.9| | 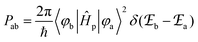 | (1) |
With this definition in hand, Einstein derived some quantitative coefficients measuring the probabilities of light absorption Bab (eqn (2)), of stimulated light emission Bba (eqn (2)) and of spontaneous light emission Aba (eqn (3)) when electronic transitions occur between the two states.10| | 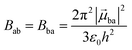 | (2) |
| | 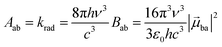 | (3) |
Introducing the pertinent atomic wavefunctions φa and φb into the expression of the transition dipole moment |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 led to the well-known selection rules controlling electronic transitions induced by electromagnetic waves. Firstly, the electronic transitions are only allowed when (i) the total spin does not change (spin rule ΔStot = 0) and (ii) the parity of the two incriminated wavefunctions should be inverted (Δl = ±1, 3…) for an electric dipole transition and conserved (Δl = ±0, 2…) for a magnetic dipole transition. Consequently, the intra-shell d ↔ d and f ↔ f transitions are electric-dipole forbidden, but magnetic-dipole allowed. Since the magnetic dipole transitions are three to four orders less intense than their electric dipole counterparts, this results in that intra-shell d ↔ d and f ↔ f are always weak, but they can be enhanced via some specific programming of the transition dipoles |
ba|2 = 〈φb|Ĥp|φa〉2 led to the well-known selection rules controlling electronic transitions induced by electromagnetic waves. Firstly, the electronic transitions are only allowed when (i) the total spin does not change (spin rule ΔStot = 0) and (ii) the parity of the two incriminated wavefunctions should be inverted (Δl = ±1, 3…) for an electric dipole transition and conserved (Δl = ±0, 2…) for a magnetic dipole transition. Consequently, the intra-shell d ↔ d and f ↔ f transitions are electric-dipole forbidden, but magnetic-dipole allowed. Since the magnetic dipole transitions are three to four orders less intense than their electric dipole counterparts, this results in that intra-shell d ↔ d and f ↔ f are always weak, but they can be enhanced via some specific programming of the transition dipoles |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2, for instance by removing the symmetry operator responsible for the parity of the wavefunctions and/or by increasing the energy gaps between the two incriminated levels for maximizing ν = (Eb − Ea)/h in eqn (3). However, transitions between electronic states are not induced by only electromagnetic radiation and non-radiative relaxation processes exist, among which dissipation of energy through vibrational processes plays a crucial role. The temperature-dependent rate constant kvibT for the quenching of a single excited level is described by eqn (4) with the assumption that the deactivating phonons/vibrations involved have all the same energy ħω (n is the number of phonons required to bridge the energy gap ΔE and kvibT=0 is the spontaneous rate at 0 K).11Eqn (4) implies that the phonon-assisted non-radiative quenching essentially depends on the energy gap ΔE between the emissive state and the highest sublevel of its ground, or receiving, multiplet. The smaller this gap, the easier is its closing by non-radiative deactivation processes, for instance through vibrations of high energy such as O–H, N–H, or C–H.
ba|2, for instance by removing the symmetry operator responsible for the parity of the wavefunctions and/or by increasing the energy gaps between the two incriminated levels for maximizing ν = (Eb − Ea)/h in eqn (3). However, transitions between electronic states are not induced by only electromagnetic radiation and non-radiative relaxation processes exist, among which dissipation of energy through vibrational processes plays a crucial role. The temperature-dependent rate constant kvibT for the quenching of a single excited level is described by eqn (4) with the assumption that the deactivating phonons/vibrations involved have all the same energy ħω (n is the number of phonons required to bridge the energy gap ΔE and kvibT=0 is the spontaneous rate at 0 K).11Eqn (4) implies that the phonon-assisted non-radiative quenching essentially depends on the energy gap ΔE between the emissive state and the highest sublevel of its ground, or receiving, multiplet. The smaller this gap, the easier is its closing by non-radiative deactivation processes, for instance through vibrations of high energy such as O–H, N–H, or C–H.| | 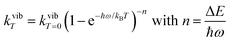 | (4) |
With this toolkit in hand, the light-downshifting process, which is defined as the conversion of one photon of high energy into one photon of lower energy, can be summarized with a three-level system as illustrated in Fig. 5a.
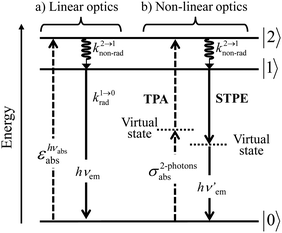 |
| | Fig. 5 Three-level diagram pertinent to closed-shell systems showing (a) a light-downshifting process using linear optics and (b) two-photon absorption (TPA) and spontaneous two-photon emission (STPE) processes using non-linear optics (NLO). | |
The initial light absorption promotes molecules from the |0〉 ground state into the |2〉 excited level. Its efficiency depends on the molar extinction coefficient εabs pertinent to the Lambert–Beer law, which is related to the square of the transition dipole moment |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 through the oscillator strength f (eqn (5), 9n/(n2 + 2)2 is the local electric field correction factor with the refractive index of the medium n,
ba|2 = 〈φb|Ĥp|φa〉2 through the oscillator strength f (eqn (5), 9n/(n2 + 2)2 is the local electric field correction factor with the refractive index of the medium n, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) is the transition wavenumber in cm−1 for εabs in L mol−1 cm−1).12
is the transition wavenumber in cm−1 for εabs in L mol−1 cm−1).12
| | 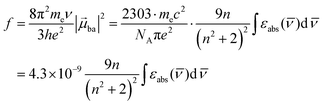 | (5) |
When the associated luminescence transition terminates onto the ground level, the radiative rate constant can be extracted from the oscillator strength with the help of simplified
eqn (6) (
c is the light velocity in vacuum,
n is the refractive index of the medium,
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
is the barycenter of the transition wavenumber,
NA is the Avogadro constant,
gGS is the degeneracy of the ground state, and
gES is the degeneracy of the excited state).
12c| | 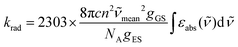 | (6) |
The maximization of
εabs, and consequently of
krad, requires the operation of an allowed electric dipole transition such as the π* ← π transitions found in polyaromatic compounds. Once the excited level |2〉 is occupied, relaxation may occur along two different pathways: (i) radiatively (
krad) according to
eqn (3) and/or (ii) non-radiatively (
knon-rad) according to
eqn (4). Since the energy gap (
hν2→1) is small between excited levels |2〉 and |1〉,
eqn (3) predicts that
k2→1rad will be small. On the contrary, the plethora of high-energy vibrations which are at disposal in closed-shell polyaromatic molecules, combined with large vibrational overlap integrals (Franck–Condon factor) due to the small energy gap, result in fast non-radiative relaxation processes so that
k2→1non-rad ≫
k2→1rad and the excitation energy is efficiently funneled onto the lowest excited state |1〉 without light-emission. The latter excited state becomes the unique emissive level delivering a single photon at energy
hνem (
Fig. 5a) because its large energy gap with respect to the ground state now ensures
k1→0rad ≫
k1→0non-rad, a prediction often experimentally observed and referred to as Kasha's rule.
13 Altogether, a photon of high-energy
hvabs is absorbed and transformed into an emitted photon of lower-energy
hvem with concomitant heat dissipation (
Fig. 5a), a linear optical process known as light-downshifting for which the maximum quantum yield is 100%.
14 The possibilities of light-downshifting are largely amplified when the absorption and emission processes are performed by separate entities. The centre responsible for the absorption of light, known as the sensitizer S, is optimized for the efficient collection of photons of high energies, while the activator A,
i.e. the centre responsible for photon emission, is fitted with a maximum number of radiative emitting levels spread over the whole electromagnetic spectrum. Putting these two partners into a single molecule, in which an efficient S → A energy transfer operates, produces efficient light-downshifting according to a mechanism called the
antenna effect.
15
A lot of SA optical pairs have thus been combined in molecules16 with a special emphasis on organic ligands working as light-harvesters (S) connected to trivalent narrow band lanthanide emitters (A), a design illustrated in the dinuclear complexes [(hfac)3EuLEu(hfac)3] (Fig. 6a).17 Subsequent optimization of these lanthanide complexes via systematic chemical modifications to reach higher quantum yields (Fig. 6b) has been representing an active field of research in coordination chemistry for several decades.18 In order to extend the possibilities of light-downshifting in molecules, the high-energy photons required to feed the initial excited level can be replaced with the combination of two low-energy photons (Fig. 5b) with the help of non-linear optics which exploits the minor non-linear dependence of the refractive index, a phenomenon discovered by Kerr at the end of the nineteenth century19 and theoretically modeled by Goeppert-Mayer in 1931.20 Its experimental demonstration was delayed until the early 1960s when intense laser excitation beams became available for the induction of second harmonic generation (a second-order NLO process)21 and two-photon absorptions (TPA, a third-order NLO process illustrated in Fig. 5b).22 Spontaneous two-photon emission (STPE, Fig. 5b), also a non-linear optical process,23 offers the advantage of producing two photons of lower energies (quantum cutting), which pushes back the upper limits of the quantum yield in light-downshifting to 200% if light absorption occurs through linear optics. However, these NLO absorption (TPA) and emission (STPE) processes are so weak, at least five to eight orders of magnitude less efficient than related one-photon linear processes,24 that their exploitation in (bio)molecules requires ultra-intense excitation beams using pulsed femtosecond lasers which are difficult to implement in routine applications.25
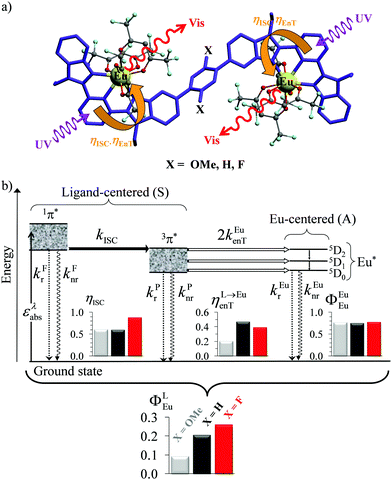 |
| | Fig. 6 (a) Molecular structures and (b) simplified Jablonski diagram for [(hfac)3EuLEu(hfac)3] showing the indirect ligand-centred triplet-mediated sensitization mechanism of the two Eu3+ activators. The photophysical processes are described by first-order rate constants: kFr = ligand fluorescence, kFnr = ligand internal non-radiative conversion, kPr = ligand phosphorescence, kPnr = non-radiative relaxation from the ligand triplet state, kEur = emission of Eu*, kEunr = nonradiative decay of Eu*, kISC = ligand intersystem crossing, and kEuen.tr. = ligand-to-metal energy transfer. Efficiencies of intersystem crossing (ηISC), of energy transfer (ηL→Euen.tr.), of intrinsic quantum yield (ΦEuEu), and global quantum yield (ΦLEu) characterize the antenna effect (solid-state, 293 K). Adapted from ref. 17b. | |
A reasonable alternative for either downconverting one photon of high-energy into two photons of lower energies (maximum quantum yield = 200%, Fig. 7a),14,26 or for upconverting two low-energy photons into one photon of higher energy (maximum quantum yield = 50%, Fig. 7b),27,28 relies on the use of efficient linear optical processes as long as successive electronic transitions can be induced between real electronic states. The required series of real and regularly spaced excited states for performing linear downconversion and upconversion (Fig. 7) is essentially lacking in closed-shell p-block materials (Fig. 2b), roughly satisfied with d-block elements (Fig. 3),27 but nicely fitted with 4f-block trivalent cations (Fig. 4).28
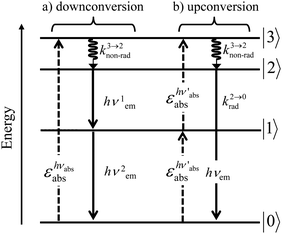 |
| | Fig. 7 Four-level diagram pertinent to an open-shell system showing (a) downconversion and (b) upconversion using linear optics. | |
In order (i) to maximize radiative emission for downconversion and (ii) to extend excited-state lifetimes for upconversion, the intermediate excited levels working as relays should not be quenched by non-radiative relaxation processes, a condition only fulfilled in low-phonon inorganic solids such as oxides, chalcogenides or halides. With this in mind, downconversion and upconversion based on linear optics was mainly implemented in ionic solids or nanoparticles (i.e. ‘nano ionic solids’) doped with trivalent lanthanides.28a,29 Nowadays, these materials enter the domain of practical applications with optimized upconversion quantum yields reaching 12(1)% for Gd2O2S:10%Er3+ and 8.9(7)% for β-NaYF4:25%Er3+,30 while a downconversion quantum yield of 140% was obtained for YF3:Pr3+.31 In this context, trivalent erbium, with its [Xe]4f11 electronic configuration (Fig. 4, right) appeared to be particularly attractive for manipulating the energy of the incident photons using linear optics. Firstly, the lowest 4I13/2 excited state is separated by circa 6000 cm−1 (λ = 1.5 μm) from the 4I15/2 ground state, an ideal energy gap for exploiting erbium in Er-doped fiber amplifiers (EDFAs) for telecommunication since silica optical fibers are transparent at this wavelength.32 Either excitation at 1480 nm to reach a metastable crystal-field sublevel of the Er(4I13/2) excited state, or alternative excitation at 980 nm into the better Er(4I11/2) acceptor level followed by downshifting, appears to be ideal for inducing high-power amplification, which makes these systems competitive with wireless networks.8 One additional advantage of Er3+ comes from its efficient resonant communication with trivalent ytterbium through Yb(2F5/2) → Er(4I11/2) energy transfer processes, a mechanism which allows the use of Yb3+ as a sensitizer (S) for Er3+ working as the activator (A) in SA pairs. With this special design, the low absorbance of Er3+ at 980 nm (Er(4I11/2 ← 4I15/2)) is overcome by the 10-times larger absorption cross-section of Yb3+ at the same wavelength (Yb(2F5/2 ← 2F7/2)). Secondly, trivalent erbium is famous for possessing several emitting levels leading to blue Er(2H11/2 → 4I15/2), green Er(4S3/2 → 4I15/2), red Er(4F9/2 → 4I15/2) and near-infrared Er(4I9/2 → 4I15/2) or Er(4S3/2 → 4I13/2) emissions whenever phonon-activated non-radiative processes are limited to such an extent that knon-rad ≪ krad.28a,32,33 Consequently, Er3+-doped ionic solids and garnets are found among the most popular near-infrared to visible upconverting devices since the initial near-infrared excitation into the Er(4I13/2 ← 4I15/2) band at 1.5 μm in single-doped solids30 or into the Yb(2F5/2 ← 2F7/2) transition at 980 nm in multi-doped Yb/Er solids34 eventually produces upconverted visible light at various wavelengths with 4–12% quantum yields.28–33 Attempts to reduce the size of the ionic materials to reach the nanometric scale compatible with their incorporation into molecular devices or biological organisms drastically increase the surface over volume ratio, and the upconversion efficiency drops as the surface states quench the emission signal.35 For instance, going from the bulk solid (ϕ = 4%) to manufactured 30 nm diameter nanoparticles (ϕ = 0.1%), the multiply-doped β-NaYF4:18%Yb3+–2%Er3+ solid sees its quantum yield reduced by more than one order of magnitude, a drop slightly limited when a passivating shell is deposited onto the surface of the nanoparticles (ϕ = 0.3%).36 Further miniaturization in order to reach the molecular scale in open-shell erbium coordination complexes was thought to be impossible for almost fifty years because the high-energy vibrations/phonons associated with organic ligands produce short excited-state lifetimes, which are not compatible with super-excitation, i.e. the collection of a second photon promoting one excited state into a more energetic level.37
Although it does not fit the criteria for being considered a single molecular process, it is worth mentioning here, for the sake of completeness, the recent revival of interest in sensitized non-coherent upconversion based on the triplet–triplet annihilation of a pair of organic molecules (Fig. 8).38 This mechanism was first reported during the early 1960s39 and has been optimized during the last decade to reach remarkable 16–26% intrinsic upconversion quantum yields compatible with solar cell applications.40 According to the accepted mechanism summarized in Fig. 8,41 closed-shell polyaromatic sensitizing molecules (S) made of light atoms with negligible spin–orbit coupling constants are excited with the help of spin-allowed π* ← π transitions followed by intersystem crossing (ISC) to establish long-lived triplet excited states 3S*. Subsequent intermolecular 3S*/1A → 1S/3A* Dexter-type triplet–triplet energy transfers (TTET) with neighboring acceptors, A, provide the target 3A* excited triplet states, the lifetime of which are long enough to allow diffusion and collisions of the particles. Triplet–triplet annihilation (TTA) between two excited A particles finally produces a mixture of singlet, triplet and quintet excited dimers, in which the 3A* + 3A* → 1A* + 1A pathway leads to the targeted high-energy singlet excited state located on the acceptor. Relaxation of the 1A* state to the ground state is finally accompanied by the emission of a photon of higher energy than those involved in the excitation process, that is, an upconverted emission (Fig. 8).38 Despite its attractive efficiency, the TTA mechanism requires the diffusion and collision of two excited triplet acceptors which limit this methodology to intermolecular processes occurring in solution, rubbery polymeric materials or solid matrices under anaerobic conditions since dioxygen can easily quench triplet excited states. Finally, photobleaching remains a major issue with organic dyes, which is difficult to reconcile with long-term operation periods.
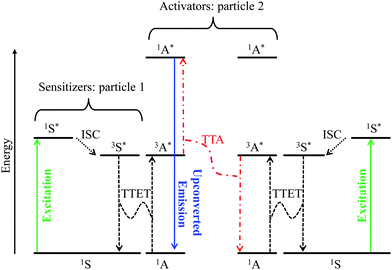 |
| | Fig. 8 Qualitative Jablonski diagram illustrating the sensitized triplet–triplet annihilation (TTA) upconversion process operating in a S/A mixture of adapted polyaromatic molecules. Solid colored arrows indicate transitions in which a photon is involved, while black dashed arrows indicate radiationless processes (ISC = intersystem crossing and TTET = triplet–triplet energy transfer). The alternating dashed-dotted red arrows stand for triplet–triplet annihilation. | |
To summarize, the need for miniaturization in order to reach molecular dimensions and quantum yields compatible with bioanalytical and biomedical applications are currently fitted by downconverting and/or upconverting nanoparticles, but the difficulties linked to their synthetic reproducibility and to their uncontrolled degradation in living organisms are severe limitations. With this in mind, the degradation of the energy of photons in molecules by light-downshifting seems to be a solved problem, but both molecular downconversion and upconversion remain open challenges, for which lanthanide coordination complexes are probably the most promising systems provided that excited-state lifetimes can be significantly improved and/or that some alternative light-conversion mechanism could be discovered.
Erbium coordination complexes for light-conversion using linear optics
Any successful embedding of Er3+ into coordination complexes is correlated with the thermodynamic stabilities of the final edifices, in which organic receptors, often referred to as ligands, are tightly bound to the central metallic cation. Since (i) trivalent 4f-block cations are large and (ii) the 4fn valence electrons are not involved in significant covalent interactions with donor atoms, the coordination chemistry of trivalent lanthanides relies on the use of (pre)organized sequestering multidentate ligands possessing negatively charged donor atoms for maximizing electrostatic metal–ligand interactions. Obviously, Er3+ follows these statements and stable complexes with this cation are formed with polyaminocarboxylates such as EDTA4− and DOTA4−, with acetylacetonates, with anionic polyaromatic phthalocyanins and porphyrins, with calixarenes, with Schiff bases, with quinolinates and even with neutral ligands such as terpyridine to name a few (Fig. 9).42
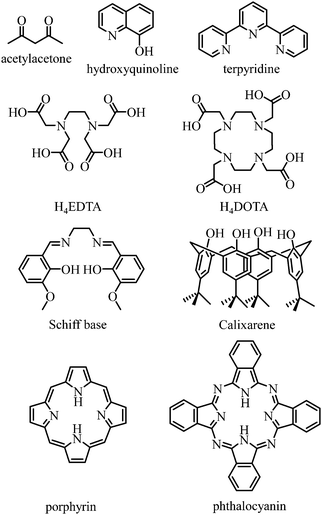 |
| | Fig. 9 Chemical structures of some organic receptors for the efficient complexation of trivalent erbium. | |
According to Choppin's thermodynamic model,43 the ligand and lanthanide partners are initially desolvated, which corresponds to an enthalpically unfavorable, but entropically favored reaction, prior to undergoing hetero-component connection, an enthalpically favorable, but entropically costly reaction. Altogether, the free energy of complexation thus combines opposite contributions which provide enthalpically ‘neutral’ (ΔHtot = ΔHdesolv + ΔHconnect ≤ 0), but entropically positive (ΔStot = ΔSdesolv + ΔSconnect ≫ 0) driving forces in lanthanide coordination chemistry. Moreover, Choppin demonstrated that ΔHdesolv ≃ −TΔSdesolv for the large majority of lanthanide complexes studied in polar solvents, so that the selective fixation of trivalent metals by the organic receptors is ultimately controlled by minor changes in the favorable connection enthalpy (ΔHconnect < 0) along the lanthanide series.44 Trivalent erbium being almost the smallest cation of the lanthanide series, it benefits from maximum electrostatic stabilization, a trend often reinforced by the change in coordination number from CN = 9 to CN = 8 which occurs in the middle of the lanthanide series. This may result in peaks of selectivity around Er3+ when well-programmed receptors are available (Fig. 10).45 Ligand exchange kinetics around Er3+ is also influenced by its small size because ligand replacement in the first coordination sphere follows dissociative pathways, the activation energies of which are maximized at the end of the lanthanide series for complexes possessing the strongest metal–ligand bonds.46 Consequently, the textbook case of water exchange occurring in the first coordination sphere of lanthanide aquo-ions46 corresponds to one of the longest water residence lifetimes for [Er(H2O)8]3+ (kexch = 13.3 × 107 s−1, characteristic residence lifetime 7.5 ns).47 The use of negatively charged multidentate macrocyclic ligands48 or of self-assembled polycyclic receptors49 may extend kinetic inertness around Er3+ to several hours and even weeks. Finally, the short electronic relaxation time of the Er(4I15/2) ground state (0.238 ps)50 combined with its large magnetic anisotropy (Bleaney constant CEr = 33)51 results in paramagnetically shifted NMR signals narrow enough to be easily analysed for the extraction of molecular structures for erbium coordination complexes in solution.52
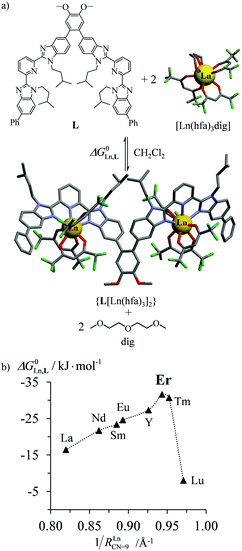 |
| | Fig. 10 (a) Complexation of trivalent lanthanide to a di-tridentate receptor L and (b) selective thermodynamic recognition of erbium.45a 1/RLnCN=9 is the inverse of the ionic radius of nine-coordinate trivalent lanthanides. Color code: C = grey, N = blue, O = red, and F = green. | |
The combination of all these favourable properties makes Er3+-coordination complexes among the most stable, kinetically inert and easily characterized entities along the lanthanide series and it is not surprising that myriads of pertinent examples of such complexes have been reported during the last four decades with potential applications in optics and in magnetism.42,53 In this context, the 4f11 electronic configuration of trivalent erbium is famous for possessing a series of regularly spaced 2S+1LJ excited spectroscopic levels which cover the entire near-infrared (NIR), visible (VIS) and ultra-violet (UV) domains with radiative lifetimes within the millisecond range when the cation is coordinated to oxygen donor atoms in doped solids (Fig. 11) or in molecular complexes, for instance in [Er(D2O)8]3+ where krad(4I13/2 → 4I15/2) = 8.68 ms.54
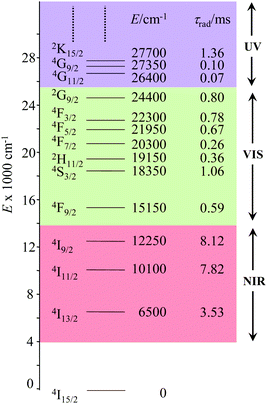 |
| | Fig. 11 Details of the near-infrared, visible, and (low-energy) ultra-violet parts of the energy-level diagram for Er3+ ions doped into yttrium orthoaluminate YAlO3 including calculated radiative lifetimes τrad.56 | |
However, the vast majority of organic ligands used for complexing Er3+ possesses a large distribution of high-energy phonon states mainly associated with O–H, N–H, C–H, C–C, C–N and C–O stretching vibrations, which corresponds to an effective vibrational energy around ℏωeff ≈ 2000 cm−1.37 Under these conditions, the number of phonons n required for bridging two neighboring spectroscopic levels in trivalent erbium never exceeds neff ≈ 2 (see Fig. 11) and eqn (4) predicts that non-radiative relaxation dominates throughout (knr ≫ kr) with no hope for detecting luminescence, except for the weak near-infrared Er(4I13/2 → 4I15/2) emission at 6500 cm−1 (λ ≈ 1.54 μm), which benefits from neff ≥ 3.55 Upon UV or visible ligand excitation, erbium coordination complexes are thus well-known to deliver only one downshifted near-infrared radiative emission around 6500 cm−1 with characteristic lifetimes in the microsecond range and weak intrinsic quantum yields around 0.1% (ϕ = krad/(krad + knon-rad) = τexp/τrad ≈ 5 μs/5 ms = 10−3).42,55 Interestingly, the latter near-infrared emission band matches the third biological window (BW3) where skin and blood are essentially transparent while scattering is negligible. Erbium complexes have therefore attracted considerable interest for working as bioprobes and sensors in living organisms.57 Major efforts were thus made for maximizing the Er(4I13/2 → 4I15/2) emission quantum yield in molecular compounds58 through the minimization of knrvia the replacement of high-energy X–H oscillators (X = C, N, O) located close to the activator with heavier X–D and X–F analogues.59 However, the recent perdeuteration of Lehn's historical cryptates such as [Er(L1)Cl]2+ (Fig. 12a),59e for which the shortest Er⋯H contact distance amounts to 3.28 Å, indeed provided underwhelming experimental Er(4I13/2) excited-state lifetimes (1.8 ≤ τ ≤ 5.7 μs in deuterated acetonitrile) when one considers the synthetic efforts made for producing these sophisticated receptors. These observations are anyhow in line with older reports which mentioned that the lanthanide cations in Lehn's cryptates are not efficiently protected from close interactions with extra solvent molecules and fluorine anions are systematically added in solution for improving the quantum yields of Eu3+ and Tb3+ analogues used as tags in commercial time-resolved fluoroimmunoassays.60 The imidodisphosphinate ligands, designed by Pikramenou and coworkers, provided more appealing results since the shortest Er⋯H contact distance in [Er(L2)3] was extended to 3.53 Å and led to τ(4I13/2) = 6.5 μs for the native (i.e. non-perdeuterated) ligand in non-deuterated acetonitrile (Fig. 12b).59a Upon perfluorination of the aromatic groups in [Er(F20-L2)3], the non-radiative relaxation pathways are significantly reduced and τ(4I13/2) reaches 741 μs in acetonitrile, an impressive increase of the Er(4I13/2) excited-state lifetime by two orders of magnitude.59c A similar trend was obtained by using perfluorothiolate in [Er(L3)3(DME)2] with an exceptional excited-state lifetime of τ(4I13/2) = 2.88 ms measured in the solid state at room temperature (Fig. 12c),61 the longest one reported for an erbium coordination complex to the best of the authors’ knowledge. With these results in mind, one easily understands why the modern design of erbium-containing plastic optical fiber lasers and amplifiers exploits perfluorinated counter-anions and polymers.32
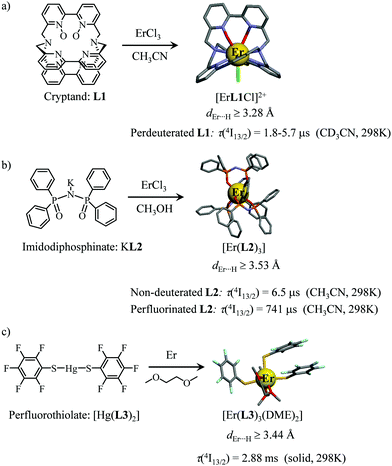 |
| | Fig. 12 Formation and molecular structures of erbium coordination complexes with long Er(4I13/2) excited-state lifetimes obtained upon (a) perdeuteration59e and (b and c) perfluorination59c,61 of the bound ligands (see text). | |
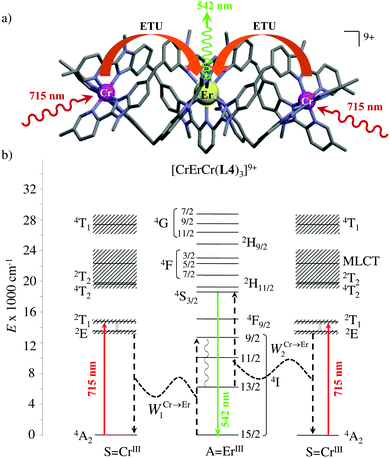
However, the impressive τ(4I13/2) = 2.88 ms found for the molecular complex [Er(L3)3(DME)2] (which can be translated into an intrinsic quantum yield around 50%) despite the presence of close high-energy C–H vibrations belonging to the dimethoxyethane chelates (Fig. 12c),61 forced the authors of this review to deepen their analysis. Taking for granted that recurrent errors in measuring excited-state lifetimes cannot be attributed to the famous main author of ref. 61, we suspect that the surprising inadequacy between the existence of high-energy oscillators located close to the emissive erbium centre and the extremely long Er(4I13/2) excited-state lifetime in [Er(L3)3(DME)2] indeed finds its origin in the combination of (i) a minimum splitting of the J manifolds produced by the very small crystal-field effect (low-coordination numbers, high-symmetry, poorly or non-charged donor atoms) and (ii) the lack of energy matching between the high-energy oscillators of the ligands (no significant vibration in the 1500–2800 cm−1 range) and the average energy gap between the successive 2S+1LJ spectroscopic levels (circa 2000 cm−1) of the erbium complex. Under these circumstances, the lack of resonance conditions predicts that the non-radiative relaxation pathways are reduced to such an extent that the associated photophysical properties in [Er(L3)3(DME)2] will be reminiscent to those of long-lived Er3+-doped low-phonon solids. With this in mind, the complete lack of,37 or extremely weak,62 Er-centred radiative emission reported for the triple-helical [Er(pyridine-2,6-dicarboxylate)3]3− complex upon ligand-centred excitation can be tentatively assigned to the existence of a strong crystal field (six negatively charged carboxylate groups bound to the central metal) responsible for the significant splitting of the J manifolds, combined with a relatively high-energy phonon bath due to the existence of asymmetric/symmetric stretching of the bound carboxylates (∼1600–1700 cm−1). These two parameters may induce very efficient non-radiative relaxation pathways despite the rather long Er⋯H contact distance of 5.37 Å observed in [Er(pyridine-2,6-dicarboxylate)3]3−. Building on this strategy, Piguet, Hauser and coworkers designed a highly protected triple-stranded helicate [GaErGa(L4)3]9+, in which the central erbium is coordinated by nine neutral heterocyclic nitrogen donor atoms arranged in a highly symmetrical tricapped trigonal prismatic organization around the central cation (Fig. 13a).63 The associated crystal field is expected to be small and the non-radiative decay is thus reduced to a sufficient extent so that dual Er-centred light emission indeed occurs in [GaErGa(L4)3]9+ upon UV ligand-centred excitation. The expected downshifted near-infrared Er(4I13/2 → 4I15/2) emission is detected around 1530 nm (τ(4I13/2) = 3.4 μs at 10 K, Fig. 13b), while the unusual (for molecular complexes) green Er(4S3/2 → 4I15/2) emission at 542 nm stands out from the residual ligand-centred fluorescence (τ(4S3/2) = 40 ns at 10 K Fig. 13c).63
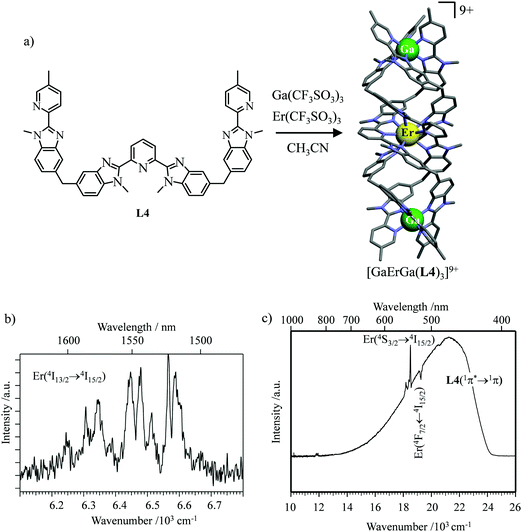 |
| | Fig. 13 (a) Formation and molecular structure of the triple-stranded helicate [GaErGa(L4)]9+, and associated emission spectra in (b) near-infrared and (c) visible domains (λexc = 405 nm, T = 10 K).63 | |
The axial protection brought by the [Ga(benzimidazole-pyridine)3] units in [GaErGa(L4)3]9+ appeared to be not crucial and the related much simpler mononuclear triple helical complex [Er(L5)3]3+ (Fig. 14a) also displayed dual visible/NIR light-downshifting upon ligand-centred sensitization (Fig. 14b left).64 Further replacement of tridentate 2,6-bis(benzimidazol-2-yl)pyridine ligands (L5) with more compact (and more popular) 2,2′;6′,2′′-terpyridine ligands in [Er(terpy)3]3+ is also compatible with the detection of dual light-downshifted emission, the intensity of which is however reduced because the shortest contact distance between the erbium centre from the high-energy C–H oscillators decreases from 3.86 Å in [Er(L5)3]3+ to only 3.42 Å in [Er(terpy)3]3+.
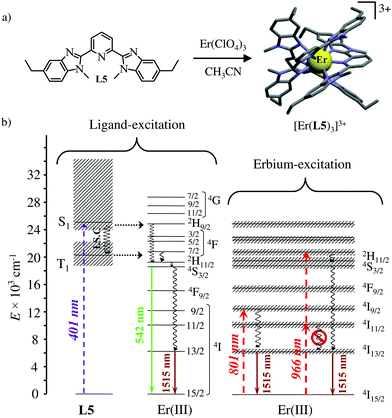 |
| | Fig. 14 (a) Formation and molecular structure of the triple helical complex [Er(L5)3]3+ and (b) Jablonski diagrams summarizing the downshifting processes following ligand-centred (left) or erbium-centred (right) excitations (dashed upward arrows), energy transfers (dotted horizontal arrows), non-radiative multiphonon relaxation (undulating arrows) and radiative emission processes (straight downward arrows).64 | |
Laser excitation directly focused onto the metal-centred Er(4I9/2 ← 4I15/2) transition at 801 nm also provided easily detectable downshifted near-infrared Er(4I13/2 → 4I15/2) luminescence at 1515 nm for both [Er(L5)3]3+ and [Er(terpy)3]3+ (Fig. 14b, centre). More interestingly, the direct excitation of the Er(4I11/2 ← 4I15/2) transition at 966 nm does not induce one photon near-infrared downshifted emission. This implies that the energy splitting of the Er(4I11/2) and Er(4I13/2) manifolds are small enough so that no adapted vibrational phonon is available to fill the exact ΔE = E(4I11/2) − E(4I13/2) = 3750 cm−1 energy gap (Fig. 14b right). Under these conditions, excitation at 966 nm required the successive absorption of two photons for eventually feeding the Er(4I13/2) level and producing downshifted NIR luminescence (Fig. 14b, right).65
Inducing linear light-upconversion at the molecular level: a current challenge
The first attempt to induce upconversion using linear optics in molecular lanthanide complexes can be traced back to Reinhard and Güdel who explored thoroughly the photophysical properties of mononuclear triple-helical [Ln(2,6-dicarboxypyrine)3]3− complexes (Ln = Er, Tm, Yb).37 With the help of a tunable Ti:sapphire laser pumped by an argon ion laser (780–980 nm), they concluded the following: “Non-radiative relaxation processes are dominant also among the f–f excited states in all three systems. The result is that no luminescence could be observed for [Er(pyridine-2,6-dicarboxylate)3]3−, and the luminescence of [Tm(pyridine-2,6-dicarboxylate)3]3− and [Yb(pyridine-2,6-dicarboxylate)3]3− are very weak and short-lived. There is no chance to induce and observe upconversion luminescence in these molecular compounds.” Circumventing the use of the Ti-sapphire intermediate modulator, direct excitation of a poorly characterized thin film of [Er(8-quinolinate)3] using a standard argon laser (λexc = 476.5 nm) was reported in 2003 to indeed give eight different downshifted Er-centred emissions like those found in Er-doped inorganic solids.66 Numerous subsequent studies focused on well-characterized Er-quinolate complexes tried to reproduce this trend, but with no success. Only the planned weak downshifted NIR Er(4I13/2 → 4I15/2) emission around 1520 nm could be systematically detected.55
Nevertheless, physicists and material chemists have more tricks in their bag and massive 109 W cm−2 (= 1 GW cm−2) near-infrared (800–980 nm) laser excitation of a 0.02 M solution of [Er(pyridine-2,6-dicarboxylate)3]3− in D2O indeed showed a weak upconverted signal assigned to Er(4S3/2 → 4I15/2) at 545 nm.67 The use of two simultaneous laser beams with two different excitation wavelengths for exactly fitting the two successive energy gaps separating the Er-centred spectroscopic levels favors linear upconversion, but, under these extreme pump power densities, any attribution of the observed visible emission to excited-state absorption (ESA) mechanisms based on linear optics is only an option because the alternative non-linear optical response becomes competitive and cannot be ruled out. In this context, Sorensen and Faulkner focused a high-power OPO tunable NIR femtosecond laser onto standard lanthanide polycarboxylates68 or even simple Tm3+ solvated in DMSO and they indeed got visible luminescence.69 Interestingly, the latter upconverted signals could be unambiguously assigned as arising from third-order non-linear optical responses (two-photon absorptions) while linear optics was demonstrated to negligibly contribute to the visible luminescence.69 One can conclude that the implementation of the single-centre ESA mechanism (Fig. 15a) seems to be difficult in molecular complexes.
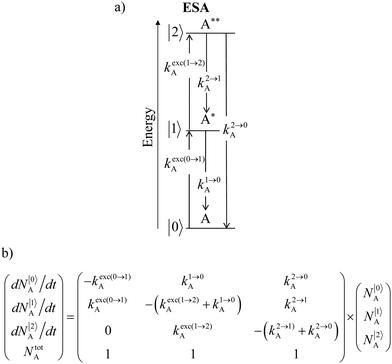 |
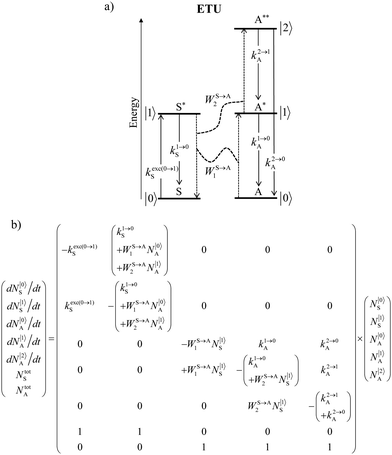
| | Fig. 15 (a) Kinetic diagrams pertinent to linear upconversion operating under non-resonant excitation according to the single-centre excited-state absorption mechanism (ESA) and (b) associated kinetic differential equations combined with mass balance equations. ki→jX stands for the sum of radiative and non-radiative constants responsible for the relaxation of state i to state j occurring on centre X. kexc(i→j)X is the rate constant characterizing the excitation of i to state j occurring on centre X (eqn (9)). N|i〉X is the normalized population density of state i on centre X.70 | |
It is however worth reminding here that in 1966 while working on doped ionic solids, Auzel already proposed some improvements to the ESA mechanism thanks to the use of optimized and independent sensitizers for performing the successive absorption of photons.29a,b Subsequent stepwise energy transfers onto a close activator eventually allows the piling up of the photons required for inducing the target upconverted emission. This closely related mechanism, which exploits two different active centres for performing absorption and emission was originally referred to as APTE (addition de photons par transferts d’énergie).29a It is currently known as ETU for energy transfer upconversion (Fig. 16a).28 A quantitative analysis of the prevalence of ETU over ESA requires to solve the differential equations depicted in Fig. 15b–16b, which model the time-dependent normalized population densities N|i〉X of state i on centre X. Under steady-state (s-s) irradiation, dN|i〉S/dt = 0 and dN|i〉A/dt = 0 and the computed static populations N|2〉A,s-s of the emissive activator levels, which are responsible for the intensity Iup of the upconverted emissions, can be compared for the single-centre excited-state mechanism (ESA, eqn (7)) and for the multi-centre energy transfer upconversion (ETU, eqn (8)).70
| | 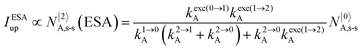 | (7) |
| | 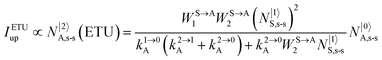 | (8) |
with
| | 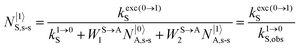 | (9) |
With the help of the pumping rate constant
kexc(i→j)X given in
eqn (10) where
λP is the pump wavelength,
P is the incident pump intensity
, σi→jX is the absorption cross section of the activator-centred
i →
j transition,
h is the Planck constant and
c is the vacuum speed of light,
71 the ratio of the upconverted intensities can be computed in
eqn (11).
| | 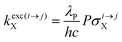 | (10) |
| | 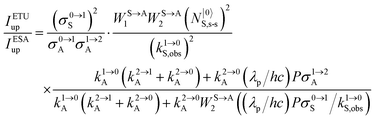 | (11) |
Under reasonable incident pump power densities, for which the major fraction of the activator and sensitizer ions remains in the ground state under steady-state illumination regimes (
i.e. N|0〉A,s-s ≈
NtotA,s-s and
N|0〉S,s-s ≈
NtotS,s-s),
eqn (11) reduces to
eqn (12) where the gain of the ETU mechanism over the ESA mechanism becomes obvious.
28a| | 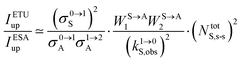 | (12) |
The first ratio in
eqn (12) denotes the advantage brought by the use of sensitizers possessing large absorption cross sections with respect to direct excitation of the poorly absorbing lanthanide activators (
σ0→1S ≫
σi→jA). The second ratio is maximized when two efficient S → A energy transfer processes (
WS→A1 and
WS→A2) are combined with a sensitizer possessing a long lifetime
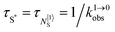
in its excited S* state. The latter sentence is rather contradictory since fast S → A energy transfers will reduce
τS*, which implies some judicious tuning of these interconnected parameters. Finally, the ETU mechanism depends on the square of the concentration of the sensitizer (
NtotS,s-s)
2, which explains the enthusiasm for using co-doped bulk solids and nanoparticles.
14,26,28 Altogether, ETU appeared to be two to three orders of magnitude more efficient than single-centre ESA with a special emphasis on the Yb
3+/Er
3+ pair, where Yb
3+ works as the sensitizer (non-negligible absorption cross section in the near-infrared at 980 nm and long Yb(
2F
5/2) excited-state lifetime) and Er
3+ acts as the activator (regularly spaced excited states). Compared with ionic solids, the introduction of high-energy vibrations (= phonons) in coordination polymers severely reduces the excited-state lifetimes, but
eqn (11) still holds and some weak near-infared to visible energy transfer upconversion (ETU) could be induced in statistically doped Yb
3+/Er
3+ lanthanide organic frameworks (a modern term for lanthanide coordination polymers).
72 Improved upconverted intensities logically resulted from the replacement of high-energy C–H oscillators with less energetic C–F analogues in these polymers.
73,74 However, the statistical distribution of the different centers characterizing these systems limits S → A energy transfer pathways to second-order kinetic processes, which are not compatible with molecular-based mechanisms which requires first-order kinetic treatments.
 |
| | Fig. 16 (a) Kinetic diagrams pertinent to linear upconversion operating under non-resonant excitation according to the multi-centre energy transfer upconversion mechanism (ETU) and (b) associated kinetic differential equations combined with mass balance equations. WS→An are the second-order rate constants for sensitizer-to-activator energy transfers.70 | |
The first successful design of a molecular coordination complex displaying linear upconversion was reported for the trinuclear [CrErCr(L4)]9+ complex (Fig. 17a), in which the ETU mechanism exploits peripheral [CrIIIN6] chromophores as sensitizers for feeding the central [ErIIIN9] activator (Fig. 17b).75 Thanks to the kinetic inertness brought by the wrapped ligand strands, [CrErCr(L4)]9+ could be diluted into isostructural, but optically inactive [GaYGa(L4)]9+ to give solid state solutions exhibiting molecular upconversion in the 10–298 K range. Within a single molecule, the rate constants for the Cr3+-to-Er3+ energy transfers WS→A1 and WS→A2 (Fig. 16) strictly correspond to first-order kinetic processes. This removes the dependence of the upconverted emission intensity IETUup on (NtotS,s-s)2 in eqn (11) and (12). Consequently, the advantage of ETU over ESA in a SnA molecule depends now on the stoichiometric ratio n between the sensitizers and the target activator. When n = 1 in a SA pair, the ETU mechanism requires two successive absorptions on the same sensitizer according to  , where Exc stands for sensitizer excitation and Up-em for upconverted emission. The short lifetime of the SA* excited relay drastically limits the efficiency of linear upconversion in molecular SA pairs.70 When n ≥ 2 in a S2A triad, as designed in [CrErCr(L4)3]9+, the activator-centred ETU mechanism (eqn (13)) is completed by a more efficient sensitizer-centred ETU mechanism (eqn (14)), for which there is no need to wait for a second excitation while the activator is excited.
, where Exc stands for sensitizer excitation and Up-em for upconverted emission. The short lifetime of the SA* excited relay drastically limits the efficiency of linear upconversion in molecular SA pairs.70 When n ≥ 2 in a S2A triad, as designed in [CrErCr(L4)3]9+, the activator-centred ETU mechanism (eqn (13)) is completed by a more efficient sensitizer-centred ETU mechanism (eqn (14)), for which there is no need to wait for a second excitation while the activator is excited.
| | 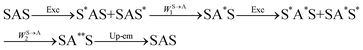 | (13) |
| | 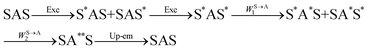 | (14) |
Using long-lived sensitizers, the implementation of the additional mechanism shown in
eqn (14) in a S
2A triad may improve the efficiency of the overall molecular ETU upconversion by one to three orders of magnitude.
63 As a proof of concept, the analogous dinuclear [ErCr(
L6)
3]
6+ complex (
Fig. 18a), which contains only a single sensitizer (Cr
3+) per erbium activator,
i.e. a SA pair, was synthesized for comparison with the S
2A triad implemented in [CrErCr(
L4)]
9+ (
Fig. 17a). NIR-to-green upconverted emission could indeed be detected in [ErCr(
L6)
3]
6+, but reduced in intensity by more than one order of magnitude compared to [CrErCr(
L4)
3]
9+.
63b
 |
| | Fig. 17 (a) Molecular structure of [CrErCr(L4)3]9+ found in the crystal structure of [CrErCr(L4)3](CF3SO3)9 and (b) associated Jablonski diagram showing the energy transfer upconversion (ETU) mechanism induced upon non-resonant excitation. Black dashed arrows indicate radiationless sensitizer-to-activator energy transfer processes and curled arrows stand for non-radiative internal conversion. Red solid arrows correspond to the NIR excitation photons and the green solid arrow stands for the visible upconverted emission.75 | |
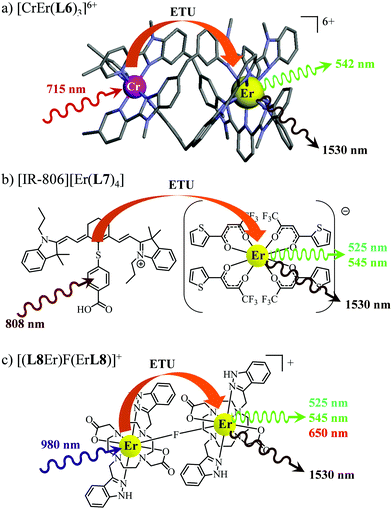 |
| | Fig. 18 Molecular structures, light-downshifting and light-upconversion mechanisms occurring in (a) [CrEr(L6)3]9+,63 (b) [IR-806][Er(L7)4]76 and (c) [(L8Er)F(ErL8)]+.77 | |
This being said, the first-order ETU mechanism implemented in molecules still benefits from the maximization of the ratio σ0→1S/k1→0S,obs predicted in eqn (12), and this parameter has been optimized for improving Er-centred upconversion operating in supramolecular adducts in solution. In [IR-806][Er(L7)4] (Fig. 18b), the use of the organic antennae [IR-806] as the sensitizer maximizes the near-infrared absorption cross section (σ0→1S),76 whereas in [(L8Er)F(ErL8)]+ (Fig. 18c), it is the ‘long-lived’ erbium centre working as the sensitizer which maximizes τ1→0S,obs = 1/k1→0S,obs.77 Although not strictly concerned by this review, which is focused on erbium complexes, it seems to the authors rather unfair to ignore the remarkable work of Charbonnière and coworkers who replaced the central erbium activator in SAS triads with its almost homonymous terbium counterpart to give the trinuclear dimetallic adducts [Tb(YbL9)2] and [Tb(YbL10)2] in deuterated water (Fig. 19).78,79
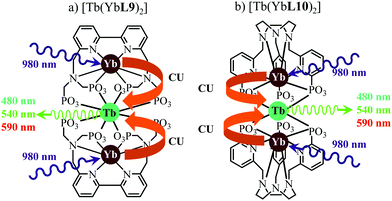 |
| | Fig. 19 Molecular structures and light-upconversion mechanisms occurring for (a) [Tb(YbL9)2] and (b) [Tb(YbL10)2] in solution.78 | |
Obviously, the electronic levels of trivalent terbium (4f8) are completely different from those of trivalent erbium (4f11) and there is no adapted intermediate excited state between the Tb(7F6) ground state and the Tb(5D4) emitting level (Fig. 4) and therefore no possibility for implementing ETU mechanisms. A slightly different upconversion mechanism has thus been invoked, for which the initial collection of low-energy photons onto the Yb3+ sensitizers is followed by cooperative energy transfers. Though some aspects of the theoretical modeling of the latter cooperative upconversion mechanism (CU) are rather analogous to ETU, its efficiency is usually much weaker because it involves quasi-virtual pairs of levels between which transitions have to be described by higher-order perturbations.28a Despite this limitation, Charbonnière and coworkers were able to estimate a quantum yield of Φup = 1.4 × 10−8 for the green emission obtained upon 980 nm excitation of [Tb(YbL10)2] in deuterated water at room temperature (Fig. 19b).78b
Finally, taking advantage of the rare dual visible green (Er(4S3/2 → 4I15/2) at 542 nm) and near-infrared (Er(4I13/2 → 4I15/2) at 1520 nm) downshifted emissions observed upon ligand-based UV excitation of the triple-helical [Er(L5)3]3+ complex (Fig. 14),64 this simple chromophore was further tested for the ultimate miniaturization of linear upconversion occurring in a mononuclear molecular complex according to the ESA mechanism (Fig. 20).65,80 Reasonable (P ≤ 20 W cm2) NIR excitation (801 nm, Er(4I9/2 ← 4I15/2)) of an acetonitrile solution of [Er(L5)3]3+ produced a normalized upconversion quantum yield of Φup = 1.6(3) × 10−8 for the target green Er(4S3/2 → 4I15/2) emission (Fig. 20, bottom left). This value is comparable with that found for the cooperative upconversion operating in the multinuclear [Tb(YbL10)2] complex (Φup ∼ 2 × 1.4 × 10−8 = 2.8 × 10−8) and sets the zero-level for the quantification of molecular upconversion. Interestingly, alternative 966 nm excitation into the Er(4I11/2 ← 4I15/2) transition is not followed by an efficient Er(4I11/2 → 4I13/2) non-radiative relaxation pathway for feeding the ‘long-lived’ intermediate Er(4I13/2) excited relay (Fig. 14b, right), and less-efficient 3-photon and 4-photon processes then become competitive with the 2-photon mechanism (Fig. 20, bottom right).65,80
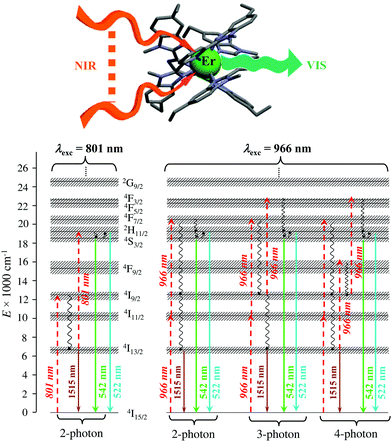 |
| | Fig. 20 Molecular structure and energy diagram summarizing the mechanisms of the Er-centred upconversion processes operating in [Er(L5)3]3+ upon excitation of the Er(4I9/2 ← 4I15/2) transition at 801 nm (left) or of the Er(4I11/2 ← 4I15/2) transition at 966 nm (right). Excitation (dashed upward arrows), non-radiative multiphonon relaxation (downward curled arrows), thermal equilibria (upward curled arrows) and radiative emission processes (straight downward arrows).65,80 | |
Conclusion
The obvious advantages of linear over non-linear optics for efficiently inducing light-upconversion in inorganic materials (ESA and ETU mechanism occurring in doped garnets, ionic solids or nanoparticles) or in closed-shell p-block molecules (via the triplet–triplet annihilation (TTA) upconversion process) are not easily implemented in open-shell d-block or f-block coordination complexes. Only close to negligible upconversion quantum yields have been reported so far for these molecular entities. Firstly, the presence of high-energy oscillators in molecular complexes favors non-radiative relaxation pathways to such an extent that long-lived intermediate excited states working as relays for piling up the successive excitation photons onto the activator are essentially missing. Secondly, the use of sensitizers (S) for maximizing light-absorption prior to exciting the activator (A) in a molecule according to the ETU mechanism requires the synthesis of sophisticated SnA polydiads, which may frighten material chemists and physicists, who are mainly interested in the optical output of these objects. The latter point is all the more true that a major gain in efficiency of ETU over ESA in molecular complexes is only expected when at least two sensitizers are combined with the target activator. Nevertheless, two pioneering groups designed the three complexes [CrErCr(L4)3]9+ (Fig. 17) as well as [Tb(YbL9)2] and [Tb(YbL10)2] (Fig. 19) which fulfill the latter requirement. Since Tb3+ does not possess the favorable organization of the spectroscopic levels found in erbium analogues, only cooperative upconversion (CU) involving virtual pairs operates in the [Tb(YbLk)2] adduct.78b The associated minute quantum yield Φup = 1.4 × 10−8 is therefore analogous to the one observed for single-centre ESA upconversion operating in [Er(L5)3]3+ (Φup = 1.6 × 10−8) and in some analogous triple-helical terpyridine derivatives (3.9 × 10−9 ≤ Φup ≤ 4.6 × 10−9).65 Although no quantum yield was reported for first-order ETU mechanisms operating in [IR-806][Er(L7)4],76 [(L8Er)F(ErL8)]+,77 and [CrErCr(L4)3]9+,70 we however note that a continuous-wave Ti-sapphire incident excitation source was sufficient to induce detectable ETU upconverted Er(4S3/2 → 4I15/2) green emission in [CrErCr(L4)3]9+,75 whereas the same setup, even at higher excitation intensities, failed in inducing a detectable upconverted signal through ESA occurring in [Er(L5)3]3+ (Φup = 1.6 × 10−8). The latter observation confirms that, as for doped inorganic materials, the ETU processes is much more efficient than ESA in molecules and that metal-based molecular upconversion should be now optimized in SnA polydiads with n ≥ 2. The replacement of high-energy OH, CH and NH oscillators with OD, CD, CF and ND analogues is an additional obvious option for bringing further improvement into molecular upconversion, though its synthetic realization is usually challenging. Finally, the deliberate programming of small crystal-field effects in erbium complexes represents a novel track for minimizing multi-phonon non-radiative relaxations and finally improving upconversion.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support from the Swiss National Science Foundation is gratefully acknowledged.
References
- E. R. Scerri, Chem. – Eur. J., 2019, 25, 7410–7415 CrossRef CAS PubMed
 .
.
- D. A. Johnson and A. F. Williams, Chimia, 2019, 73, 144–151 CrossRef CAS
 .
.
- E. R. Scerri, Nature, 2019, 565, 557–559 CrossRef CAS PubMed
 .
.
-
(a) H. B. Klevens and J. R. Platt, J. Chem. Phys., 1949, 17, 470–481 CrossRef CAS
 ;
(b) R. Rieger and K. Mullen, J. Phys. Org. Chem., 2010, 23, 315–325 CAS
;
(b) R. Rieger and K. Mullen, J. Phys. Org. Chem., 2010, 23, 315–325 CAS  .
.
-
B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Application, Wiley-VCH, New York, 2000, pp. 92–144 Search PubMed
 .
.
-
(a) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 753–766 CrossRef CAS
 ;
(b) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS
;
(b) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS  ;
(c) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1956, 11, 864–877 CrossRef CAS
;
(c) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1956, 11, 864–877 CrossRef CAS  .
.
- C.-G. Ma, M. G. Brik, D.-X. Liu, B. Feng, Y. Tian and A. Suchocki, J. Lumin., 2016, 170, 369–374 CrossRef CAS
 .
.
-
J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2016, vol. 50, pp. 141–176 Search PubMed
 .
.
- P. Chen and T. J. Meyer, Chem. Rev., 1998, 98, 1439–1478 CrossRef CAS PubMed
 .
.
-
(a) A. Einstein, Phys. Z., 1917, 18, 121–128 CAS
 ;
(b) S. Strickler and S. J. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS
;
(b) S. Strickler and S. J. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS  ;
(c) J. B. Berks and D. J. Dyson, Proc. R. Soc. London, Ser. A, 1963, 275, 135–148 CrossRef
;
(c) J. B. Berks and D. J. Dyson, Proc. R. Soc. London, Ser. A, 1963, 275, 135–148 CrossRef  .
.
-
J.-C. G. Bünzli and S. V. Eliseeva, in Lanthanide Luminescence: Photophysical, Analytical and Biological Aspects, ed. P. Hänninen and H. Härmä, Springer-Verlag, Berlin Heidelberg, 2010, vol. 7, pp. 1–45 Search PubMed
 .
.
-
(a) L. D. Carlos, R. A. S. Ferreira, V. de Zea Bernidez and S. J. L. Ribeiro, Adv. Mater., 2009, 21, 509–534 CrossRef CAS PubMed
 ;
(b) S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227 RSC
;
(b) S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227 RSC  ;
(c) J.-C. G. Bünzli, A.-S. Chauvin, H. K. Kim, E. Deiters and S. V. Eliseeva, Coord. Chem. Rev., 2010, 254, 2623–2633 CrossRef
;
(c) J.-C. G. Bünzli, A.-S. Chauvin, H. K. Kim, E. Deiters and S. V. Eliseeva, Coord. Chem. Rev., 2010, 254, 2623–2633 CrossRef  .
.
- J. C. del Valle and J. Catalan, Phys. Chem. Chem. Phys., 2019, 21, 10061–10069 RSC
 .
.
-
(a) B. M. van der Ende, L. Aarts and A. Meijerink, Phys. Chem. Chem. Phys., 2009, 11, 11081–11095 RSC
 ;
(b) X. Huang, S. Han, W. Huang and X. Liu, Chem. Soc. Rev., 2013, 42, 173–201 RSC
;
(b) X. Huang, S. Han, W. Huang and X. Liu, Chem. Soc. Rev., 2013, 42, 173–201 RSC  .
.
-
(a)
N. Sabbatini, M. Guardigli and I. Manet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 69–120 Search PubMed
 ;
(b) S. Petoud, Chimia, 2009, 63, 745–752 CrossRef CAS
;
(b) S. Petoud, Chimia, 2009, 63, 745–752 CrossRef CAS  .
.
-
(a) A. Adronov and J. M. J. Fréchet, Chem. Commun., 2000, 1701–1710 RSC
 ;
(b) E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552 CrossRef CAS
;
(b) E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552 CrossRef CAS  ;
(c) A. K. R. Junker, L. R. Hill, A. L. Thompson, S. Faulkner and T. J. Sorensen, Dalton Trans., 2018, 47, 4794–4803 RSC
;
(c) A. K. R. Junker, L. R. Hill, A. L. Thompson, S. Faulkner and T. J. Sorensen, Dalton Trans., 2018, 47, 4794–4803 RSC  .
.
-
(a) J.-F. Lemonnier, L. Guénée, C. Beuchat, T. A. Wesolowski, P. Mukherjee, D. H. Waldeck, K. A. Gogik, S. Petoud and C. Piguet, J. Am. Chem. Soc., 2011, 133, 16219–16234 CrossRef CAS
 ;
(b) J.-F. Lemonnier, L. Babel, L. Guénée, P. Mukherjee, D. H. Waldeck, S. V. Eliseeva, S. Petoud and C. Piguet, Angew. Chem., Int. Ed., 2012, 51, 11302–11305 CrossRef CAS
;
(b) J.-F. Lemonnier, L. Babel, L. Guénée, P. Mukherjee, D. H. Waldeck, S. V. Eliseeva, S. Petoud and C. Piguet, Angew. Chem., Int. Ed., 2012, 51, 11302–11305 CrossRef CAS  .
.
-
(a)
K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2005, vol. 35, pp. 107–272 Search PubMed
 ;
(b)
H. F. Brito, O. M. L. Malta, M. C. F. C. Felinto and E. E. S. Teotonio, The Chemistry of Metal Enolates, ed. J. Zabicky, John Wiley & Sons, Chichester, 2009, vol. 3, pp. 131–184 Search PubMed
;
(b)
H. F. Brito, O. M. L. Malta, M. C. F. C. Felinto and E. E. S. Teotonio, The Chemistry of Metal Enolates, ed. J. Zabicky, John Wiley & Sons, Chichester, 2009, vol. 3, pp. 131–184 Search PubMed  ;
(c) S. Di Pietro, D. Imbert and M. Mazzanti, Chem. Commun., 2014, 50, 10323–10326 RSC
;
(c) S. Di Pietro, D. Imbert and M. Mazzanti, Chem. Commun., 2014, 50, 10323–10326 RSC  ;
(d) A. S. Kalyakina, V. V. Utochnikova, M. Zimmer, F. Dietrich, A. M. Kaczmarek, R. Van Deun, A. A. Vashchenko, A. S. Goloveshkin, M. Nieger, M. Gerhards, U. Sheppers and S. Bräse, Chem. Commun., 2018, 54, 5221–5224 RSC
;
(d) A. S. Kalyakina, V. V. Utochnikova, M. Zimmer, F. Dietrich, A. M. Kaczmarek, R. Van Deun, A. A. Vashchenko, A. S. Goloveshkin, M. Nieger, M. Gerhards, U. Sheppers and S. Bräse, Chem. Commun., 2018, 54, 5221–5224 RSC  .
.
-
(a) J. Kerr, London, Edinburgh Dublin Philos. Mag. J. Sci., 1875, 50, 337–348 CrossRef
 ;
(b) J. Kerr, J. Phys. Theor. Appl., 1879, 8, 414–418 CrossRef
;
(b) J. Kerr, J. Phys. Theor. Appl., 1879, 8, 414–418 CrossRef  .
.
- M. Goeppert-Mayer, Ann. Phys., 1931, 401, 273–294 CrossRef
 .
.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef
 .
.
- W. Kaiser and C. G. B. Garrett, Phys. Rev. Lett., 1961, 7, 229–231 CrossRef CAS
 .
.
-
(a) H. P. Yuen, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 2226–2243 CrossRef
 ;
(b) M. O. Scully, K. Wodkiewicz, M. S. Zubairy, J. Bergou, N. Lu and J. Meyer ter Vehn, Phys. Rev. Lett., 1988, 60, 1832–1835 CrossRef CAS
;
(b) M. O. Scully, K. Wodkiewicz, M. S. Zubairy, J. Bergou, N. Lu and J. Meyer ter Vehn, Phys. Rev. Lett., 1988, 60, 1832–1835 CrossRef CAS  .
.
- C. Andraud and O. Maury, Eur. J. Inorg. Chem., 2009, 4357–4371 CrossRef CAS
 .
.
-
(a) P. Neveu, I. Aujard, C. Benbrahim, T. Le Saux, J.-F. Allemand, S. Vriz, D. Bensimon and L. Jullien, Angew. Chem., Int. Ed., 2008, 47, 3744–3746 CrossRef CAS
 ;
(b) D. K. Sinha, P. Neveu, N. Gagey, I. Aujard, C. Benbrahim-Bouzidi, T. Le Saux, C. Rampon, C. Gauron, B. Goetz, S. Dubruille, M. Baaden, M. Volovitch, D. Bensimon, S. Vriz and L. Jullien, ChemBioChem, 2010, 11, 653–663 CrossRef CAS
;
(b) D. K. Sinha, P. Neveu, N. Gagey, I. Aujard, C. Benbrahim-Bouzidi, T. Le Saux, C. Rampon, C. Gauron, B. Goetz, S. Dubruille, M. Baaden, M. Volovitch, D. Bensimon, S. Vriz and L. Jullien, ChemBioChem, 2010, 11, 653–663 CrossRef CAS  ;
(c) D. Kim, H. G. Ryu and K. H. Ahn, Org. Biomol. Chem., 2014, 12, 4550–4566 RSC
;
(c) D. Kim, H. G. Ryu and K. H. Ahn, Org. Biomol. Chem., 2014, 12, 4550–4566 RSC  ;
(d) T. N. Nguyen, F. M. Ebrahim and K. C. Stylianou, Coord. Chem. Rev., 2018, 377, 259–306 CrossRef CAS
;
(d) T. N. Nguyen, F. M. Ebrahim and K. C. Stylianou, Coord. Chem. Rev., 2018, 377, 259–306 CrossRef CAS  .
.
-
(a) X. Liu and J. Qiu, Chem. Soc. Rev., 2015, 44, 8714–8746 RSC
 ;
(b) M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS
;
(b) M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS  .
.
-
(a) D. R. Gamelin and H. U. Güdel, Acc. Chem. Res., 2000, 33, 235–242 CrossRef CAS
 ;
(b) S. Ye, E.-H. Song and Q.-Y. Zhang, Adv. Sci., 2016, 3, 1600302 CrossRef
;
(b) S. Ye, E.-H. Song and Q.-Y. Zhang, Adv. Sci., 2016, 3, 1600302 CrossRef  .
.
-
(a) F. Auzel, Chem. Rev., 2004, 104, 139–173 CrossRef CAS
 ;
(b) M. Haase and H. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 5808–5829 CrossRef CAS
;
(b) M. Haase and H. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 5808–5829 CrossRef CAS  ;
(c)
J.-C. G. Bünzli and A.-S. Chauvin, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier North Holland, Amsterdam, 2014, vol. 44, pp. 169–281 Search PubMed
;
(c)
J.-C. G. Bünzli and A.-S. Chauvin, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier North Holland, Amsterdam, 2014, vol. 44, pp. 169–281 Search PubMed  ;
(d) G. Liu, Chem. Soc. Rev., 2015, 44, 1635–1652 RSC
;
(d) G. Liu, Chem. Soc. Rev., 2015, 44, 1635–1652 RSC  .
.
-
(a) F. Auzel, C. R. Seances Acad. Sci., Ser. B, 1966, 262, 1016–1019 Search PubMed
 ;
(b) F. Auzel, C. R. Seances Acad. Sci., Ser. B, 1966, 263, 819–821 Search PubMed
;
(b) F. Auzel, C. R. Seances Acad. Sci., Ser. B, 1966, 263, 819–821 Search PubMed  ;
(c) H. Suo, F. Hu, X. Zhao, Z. Zhang, T. Li, C. Duan, M. Yin and C. Guo, J. Mater. Chem. C, 2017, 5, 1501–1507 RSC
;
(c) H. Suo, F. Hu, X. Zhao, Z. Zhang, T. Li, C. Duan, M. Yin and C. Guo, J. Mater. Chem. C, 2017, 5, 1501–1507 RSC  ;
(d) S. Balabjadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121, 13962–13968 CrossRef
;
(d) S. Balabjadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121, 13962–13968 CrossRef  ;
(e) M. Runowski, J. Marciniak, T. Grzyb, D. Przybylska, A. Schylchuck, B. Barszcz, A. Katrusiak and S. Lis, Nanoscale, 2017, 9, 16030–16037 RSC
;
(e) M. Runowski, J. Marciniak, T. Grzyb, D. Przybylska, A. Schylchuck, B. Barszcz, A. Katrusiak and S. Lis, Nanoscale, 2017, 9, 16030–16037 RSC  ;
(f) Z. Wang, J. Chrstiansen, D. Wezendonk, X. Xie, M. A. Van Huis and A. Meijerink, Nanoscale, 2019, 11, 12188–12197 RSC
;
(f) Z. Wang, J. Chrstiansen, D. Wezendonk, X. Xie, M. A. Van Huis and A. Meijerink, Nanoscale, 2019, 11, 12188–12197 RSC  .
.
- R. Martin-Rodriguez, S. Fischer, A. Ivaturi, B. Froehlich, K. W. Krämer, J. C. Goldschmidt, B. S. Richards and A. Meijerink, Chem. Mater., 2013, 25, 1912–1921 CrossRef CAS
 .
.
-
(a) J. L. Sommerdijk, A. Bril and A. W. De Jager, J. Lumin., 1974, 8, 341–343 CrossRef CAS
 ;
(b) W. W. Piper, J. A. DeLuca and F. S. Ham, J. Lumin., 1974, 8, 344–348 CrossRef CAS
;
(b) W. W. Piper, J. A. DeLuca and F. S. Ham, J. Lumin., 1974, 8, 344–348 CrossRef CAS  .
.
-
(a) K. Kuriki, Y. Koike and Y. Okamoto, Chem. Rev., 2002, 102, 2347–2356 CrossRef CAS PubMed
 ;
(b) L. H. Sloof, A. van Blaaderen, A. Polman, G. A. Hebbink, S. I. Klink, F. C. J. M. Van Veggel, D. N. Reinhoudt and J. W. Hofstraat, J. Appl. Phys., 2002, 91, 3955–3980 CrossRef
;
(b) L. H. Sloof, A. van Blaaderen, A. Polman, G. A. Hebbink, S. I. Klink, F. C. J. M. Van Veggel, D. N. Reinhoudt and J. W. Hofstraat, J. Appl. Phys., 2002, 91, 3955–3980 CrossRef  .
.
-
(a) Y. Ding, G. Zhao., J. Chen, Q. Dong, Y. Nakai and T. Tsuboi, J. Lumin., 2011, 131, 1577–1583 CrossRef CAS
 ;
(b) M. T. Berry and P. S. May, J. Phys. Chem. A, 2015, 119, 9805–9811 CrossRef CAS
;
(b) M. T. Berry and P. S. May, J. Phys. Chem. A, 2015, 119, 9805–9811 CrossRef CAS  ;
(c) X. Shang, P. Chen, T. Jia, D. Feng, S. Zhang, Z.-M. Sun and J. Qiu, Phys. Chem. Chem. Phys., 2015, 17, 11481–11489 RSC
;
(c) X. Shang, P. Chen, T. Jia, D. Feng, S. Zhang, Z.-M. Sun and J. Qiu, Phys. Chem. Chem. Phys., 2015, 17, 11481–11489 RSC  ;
(d) M. Runowski, N. Stopikowska, D. Szeremeta, S. Goderski, M. Skwierczynska and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 13389–13396 CrossRef CAS PubMed
;
(d) M. Runowski, N. Stopikowska, D. Szeremeta, S. Goderski, M. Skwierczynska and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 13389–13396 CrossRef CAS PubMed  .
.
- R. Page, K. Schaffers, P. Waide, J. Tassano, S. Payne, W. Krupke and W. Bischel, J. Opt. Soc. Am. B, 1998, 996–1008 CrossRef CAS
 .
.
-
(a) F. Wang, J. Wang and X. Liu, Angew. Chem., Int. Ed., 2010, 49, 7456–7460 CrossRef CAS
 ;
(b) S. Han, R. Deng and X. Liu, Angew. Chem., Int. Ed., 2014, 53, 11702–11715 CrossRef CAS
;
(b) S. Han, R. Deng and X. Liu, Angew. Chem., Int. Ed., 2014, 53, 11702–11715 CrossRef CAS  .
.
- J. C. Boyer and F. C. J. M. van Veggel, Nanoscale, 2010, 2, 1417–1419 RSC
 .
.
- C. Reinhard and H. U. Güdel, Inorg. Chem., 2002, 41, 1048–1055 CrossRef CAS PubMed
 .
.
-
(a) T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS
 ;
(b) J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed
;
(b) J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed  ;
(c) C. Ye, L. Zhou, X.-Y. Wang and Z. Liang, Phys. Chem. Chem. Phys., 2016, 18, 10818–10835 RSC
;
(c) C. Ye, L. Zhou, X.-Y. Wang and Z. Liang, Phys. Chem. Chem. Phys., 2016, 18, 10818–10835 RSC  ;
(d) V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71 CrossRef CAS
;
(d) V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71 CrossRef CAS  .
.
-
(a) C. A. Parker and C. G. Hatchard, Proc. Chem. Soc., 1962, 386–387 CAS
 ;
(b) C. A. Parker, Proc. R. Soc. London, Ser. A, 1963, 276, 125–135 CrossRef CAS
;
(b) C. A. Parker, Proc. R. Soc. London, Ser. A, 1963, 276, 125–135 CrossRef CAS  .
.
- V. Gray, D. Dzebo, M. Abramhamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC
 .
.
- A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332 RSC
 .
.
-
(a)
V. S. Sastri, J.-C. G. Bünzli, V. Ramachandra Rao, G. V. S. Rayudu and J. R. Perumareddi, Modern Aspects of Rare Earths and their Complexes, Elsevier, Amsterdam, 2003 Search PubMed
 ;
(b)
S. Comby and J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2007, vol. 37, pp. 217–470 Search PubMed
;
(b)
S. Comby and J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2007, vol. 37, pp. 217–470 Search PubMed  ;
(c) ed. C. Huand, Rare Eath Coordination Chemistry: Fundamentals and Applications, John Wiley & Sons, Singapore, 2010 Search PubMed
;
(c) ed. C. Huand, Rare Eath Coordination Chemistry: Fundamentals and Applications, John Wiley & Sons, Singapore, 2010 Search PubMed  .
.
-
(a)
G. R. Choppin, in Lanthanide Probes in Life, Chemical and Earth Science, ed. J.-C. G. Bünzli and G. R. Choppin, Elsevier, Amsterdam, 1989, pp. 1–42 Search PubMed
 ;
(b)
G. R. Choppin and E. N. Rizkalla, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, L. Eyring, G. R. Choppin and G. H. Lander, 1994, vol. 18, pp. 559–589 Search PubMed
;
(b)
G. R. Choppin and E. N. Rizkalla, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, L. Eyring, G. R. Choppin and G. H. Lander, 1994, vol. 18, pp. 559–589 Search PubMed  .
.
-
C. Piguet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2015, vol. 47, pp. 209–271 Search PubMed
 .
.
-
(a) L. Babel, T. N. Y. Hoang, L. Guénée, C. Besnard, T. A. Wesolowski, M. Humbert-Droz and C. Piguet, Chem. – Eur. J., 2016, 22, 8113–8123 CrossRef CAS PubMed
 ;
(b) L. Babel, K. Baudet, T. N. Y. Hoang, H. Nozary and C. Piguet, Chem. – Eur. J., 2018, 24, 5423–5433 CrossRef CAS PubMed
;
(b) L. Babel, K. Baudet, T. N. Y. Hoang, H. Nozary and C. Piguet, Chem. – Eur. J., 2018, 24, 5423–5433 CrossRef CAS PubMed  .
.
- L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923–1959 CrossRef CAS PubMed
 .
.
-
(a) C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1988, 27, 1973–1979 CrossRef CAS
 ;
(b) C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1989, 28, 2699–2703 CrossRef CAS
;
(b) C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1989, 28, 2699–2703 CrossRef CAS  .
.
- D. T. Richens, Chem. Rev., 2005, 105, 1961–2002 CrossRef CAS PubMed
 .
.
- D. Zare, Y. Suffren, H. Nozary, A. Hauser and C. Piguet, Angew. Chem., Int. Ed., 2017, 56, 14612–14617 CrossRef CAS PubMed
 .
.
- B. M. Alsaadi, F. J. C. Rossotti and R. J. P. Williams, J. Chem. Soc., Dalton Trans., 1980, 2147–2150 RSC
 .
.
- B. Bleaney, J. Magn. Reson., 1972, 8, 91–100 CAS
 .
.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed
 .
.
- S. Faulkner, S. J. A. Pope and B. P. Burton-Pye, Appl. Spectrosc. Rev., 2005, 40, 1–35 CrossRef CAS
 .
.
- M. H. V. Werts, R. T. F. Jukes and J. W. Verhoeven, Phys. Chem. Chem. Phys., 2002, 4, 1542–1548 RSC
 .
.
- F. Artizzu, M. L. Mercuri, A. Serpe and P. Deplano, Coord. Chem. Rev., 2011, 255, 2514–2529 CrossRef CAS
 .
.
- D. K. Sardar, S. Chandrasekharan, K. L. Nash and J. B. Gruber, J. Appl. Phys., 2008, 104, 023102 CrossRef
 .
.
-
(a) J.-C. G. Bünzli, Chem. Rev., 2010, 110, 2729–2755 CrossRef PubMed
 ;
(b) L.-D. Sun, Y.-F. Wang and C.-H. Yan, Acc. Chem. Res., 2014, 47, 1001–1009 CrossRef CAS PubMed
;
(b) L.-D. Sun, Y.-F. Wang and C.-H. Yan, Acc. Chem. Res., 2014, 47, 1001–1009 CrossRef CAS PubMed  ;
(c) M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed
;
(c) M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed  ;
(d) A. J. Amoroso and S. J. Pope, Chem. Soc. Rev., 2015, 44, 4723–4742 RSC
;
(d) A. J. Amoroso and S. J. Pope, Chem. Soc. Rev., 2015, 44, 4723–4742 RSC  ;
(e) J.-C. G. Bünzli, J. Lumin., 2016, 170, 866–878 CrossRef
;
(e) J.-C. G. Bünzli, J. Lumin., 2016, 170, 866–878 CrossRef  ;
(f) J. Zhou, J. L. Leano Jr., Z. Liu, K.-L. Wong, R.-S. Liu and J.-C. G. Bünzli, Small, 2018, 1801882 CrossRef PubMed
;
(f) J. Zhou, J. L. Leano Jr., Z. Liu, K.-L. Wong, R.-S. Liu and J.-C. G. Bünzli, Small, 2018, 1801882 CrossRef PubMed  .
.
-
(a) A. Mech, A. Monguzzi, F. Meinardi, J. Mezyk, G. Macchi and R. Tubino, J. Am. Chem. Soc., 2010, 132, 4574–4576 CrossRef CAS PubMed
 ;
(b) E. R. Triveldi, S. V. Eliseeva, J. Jankolovits, M. M. Olmstead, S. Petoud and V. L. Pecoraro, J. Am. Chem. Soc., 2014, 136, 1526–1534 CrossRef PubMed
;
(b) E. R. Triveldi, S. V. Eliseeva, J. Jankolovits, M. M. Olmstead, S. Petoud and V. L. Pecoraro, J. Am. Chem. Soc., 2014, 136, 1526–1534 CrossRef PubMed  ;
(c) B. L. Reid, S. Stagni, J. M. Malicka, M. Cocchi, A. N. Sobolev, B. W. Skelton, E. G. Moore, G. S. Hanan, M. I. Ogden and M. Massi, Chem. – Eur. J., 2015, 21, 18354–18363 CrossRef CAS PubMed
;
(c) B. L. Reid, S. Stagni, J. M. Malicka, M. Cocchi, A. N. Sobolev, B. W. Skelton, E. G. Moore, G. S. Hanan, M. I. Ogden and M. Massi, Chem. – Eur. J., 2015, 21, 18354–18363 CrossRef CAS PubMed  ;
(d) Y. Peng, J. X. Xu, H. Lu, R. M. Wilson, M. Motevalli, I. Hernandez, W. P. Gillin, P. B. Wyatt and H. Q. Ye, RSC Adv., 2017, 7, 128–131 RSC
;
(d) Y. Peng, J. X. Xu, H. Lu, R. M. Wilson, M. Motevalli, I. Hernandez, W. P. Gillin, P. B. Wyatt and H. Q. Ye, RSC Adv., 2017, 7, 128–131 RSC  .
.
-
(a) A. P. Bassett, R. Van Deun, P. Nockemann, P. B. Glover, B. M. Kariuki, K. Van Hecke, L. Van Meervelt and Z. Pikramenou, Inorg. Chem., 2005, 44, 6140–6142 CrossRef CAS
 ;
(b) G. Mancino, A. J. Ferguson, A. Beeby, N. J. Long and T. S. Jones, J. Am. Chem. Soc., 2005, 127, 524–525 CrossRef CAS PubMed
;
(b) G. Mancino, A. J. Ferguson, A. Beeby, N. J. Long and T. S. Jones, J. Am. Chem. Soc., 2005, 127, 524–525 CrossRef CAS PubMed  ;
(c) P. B. Glover, A. P. Basset, P. Nockemann, B. M. Kariuki, R. Van Deun and Z. Pikramenou, Chem. – Eur. J., 2007, 13, 6309–6320 CrossRef PubMed
;
(c) P. B. Glover, A. P. Basset, P. Nockemann, B. M. Kariuki, R. Van Deun and Z. Pikramenou, Chem. – Eur. J., 2007, 13, 6309–6320 CrossRef PubMed  ;
(d) L. Song, J. Hu, J. Wang, X. Liu and Z. Zhen, Photochem. Photobiol. Sci., 2008, 7, 689–693 RSC
;
(d) L. Song, J. Hu, J. Wang, X. Liu and Z. Zhen, Photochem. Photobiol. Sci., 2008, 7, 689–693 RSC  ;
(e) C. Doffek, N. Alzakhem, M. Molon and M. Seitz, Inorg. Chem., 2012, 51, 4539–4545 CrossRef CAS
;
(e) C. Doffek, N. Alzakhem, M. Molon and M. Seitz, Inorg. Chem., 2012, 51, 4539–4545 CrossRef CAS  .
.
-
(a)
J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneider Jr and L. Eyring, Elsevier, 1987, vol. 10, pp. 322–394 Search PubMed
 ;
(b)
N. Sabbatini, M. Guardigli and I. Manet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 69–120 Search PubMed
;
(b)
N. Sabbatini, M. Guardigli and I. Manet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 69–120 Search PubMed  ;
(c) J. M. Zwier, H. Bazin, L. Lamarque and G. Mathis, Inorg. Chem., 2014, 53, 1854–1866 CrossRef CAS PubMed
;
(c) J. M. Zwier, H. Bazin, L. Lamarque and G. Mathis, Inorg. Chem., 2014, 53, 1854–1866 CrossRef CAS PubMed  ;
(d)
https://ch.cisbio.eu/terbium-cryptate-labeling-kit-40482
;
(e)
https://ch.cisbio.eu/europium-cryptate-labeling-kit-40385
.
;
(d)
https://ch.cisbio.eu/terbium-cryptate-labeling-kit-40482
;
(e)
https://ch.cisbio.eu/europium-cryptate-labeling-kit-40385
.
- G. A. Kumar, R. E. Riman, L. A. D. Torres, O. B. Garcia, S. Banerjee, A. Kornienko and J. G. Brennan, Chem. Mater., 2005, 17, 5130–5135 CrossRef CAS
 .
.
- B. Zhao, X. Q. Zhao, Z. Chen, W. Shi, P. Cheng, S. P. Yan and D. Z. Liao, CrystEngComm, 2008, 10, 1144–1146 RSC
 .
.
-
(a) Y. Suffren, D. Zare, S. V. Eliseeva, L. Guénée, H. Nozary, T. Lathion, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, J. Phys. Chem. C, 2013, 117, 26957–26963 CrossRef CAS
 ;
(b) D. Zare, Y. Suffren, L. Guénée, S. V. Eliseeva, H. Nozary, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, Dalton Trans., 2015, 44, 2529–2540 RSC
;
(b) D. Zare, Y. Suffren, L. Guénée, S. V. Eliseeva, H. Nozary, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, Dalton Trans., 2015, 44, 2529–2540 RSC  .
.
- B. Golesorkhi, L. Guénée, H. Nozary, A. Fürstenberg, Y. Suffren, S. V. Eliseeva, S. Petoud, A. Hauser and C. Piguet, Chem. – Eur. J., 2018, 24, 13158–13169 CrossRef CAS
 .
.
- B. Golesorkhi, A. Fürstenberg, H. Nozary and C. Piguet, Chem. Sci., 2019, 10, 6876–6885 RSC
 .
.
- H. Suzuki, Y. Nishida and S. Hoshino, Mol. Cryst. Liq. Cryst., 2003, 406, 27/[221]–37/[231] Search PubMed
 .
.
- X. Xiao, J. P. Haushalter and G. W. Faris, Opt. Lett., 2005, 30, 1674–1676 CrossRef CAS PubMed
 .
.
- T. J. Sorensen, O. A. Blackburn, M. Tropiano and S. Faulkner, Chem. Phys. Lett., 2012, 541, 16–20 CrossRef CAS
 .
.
- O. A. Blackburn, M. Tropiano, T. J. Sorensen, J. Thom, A. Beeby, L. M. Bushby, D. Parker, L. S. Natrajan and S. Faulkner, Phys. Chem. Chem. Phys., 2012, 14, 13378–13384 RSC
 .
.
- Y. Suffren, B. Golesorkhi, D. Zare, L. Guénée, H. Nozary, S. V. Eliseeva, S. Petoud, A. Hauser and C. Piguet, Inorg. Chem., 2016, 55, 9964–9972 CrossRef CAS PubMed
 .
.
- M. Pollnau, D. R. Gamelin, S. R. Lüthi and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337–3346 CrossRef CAS
 .
.
-
(a) D. Weng, X. Zheng, X. Chen, L. Li and L. Jin, Eur. J. Inorg. Chem., 2007, 3410–3415 CrossRef CAS
 ;
(b) C.-Y. Sun, X.-J. Zheng, X.-B. Chen and L.-P. Jin, Inorg. Chim. Acta, 2009, 362, 325–330 CrossRef CAS
;
(b) C.-Y. Sun, X.-J. Zheng, X.-B. Chen and L.-P. Jin, Inorg. Chim. Acta, 2009, 362, 325–330 CrossRef CAS  ;
(c) X. Zhang, B. Li, H. Ma, L. Zhang and H. Zhao, ACS Appl. Mater. Interfaces, 2016, 8, 17389–17394 CrossRef CAS PubMed
;
(c) X. Zhang, B. Li, H. Ma, L. Zhang and H. Zhao, ACS Appl. Mater. Interfaces, 2016, 8, 17389–17394 CrossRef CAS PubMed  ;
(d) M. Li, S. Gul, D. Tian, E. Zhou, Y. Wang, Y.-F. Han, L. Yin and L. Huang, Dalton Trans., 2018, 47, 12868–12872 RSC
;
(d) M. Li, S. Gul, D. Tian, E. Zhou, Y. Wang, Y.-F. Han, L. Yin and L. Huang, Dalton Trans., 2018, 47, 12868–12872 RSC  ;
(e) Z. Giedraityte, M. Tuomisto, M. Lastusaari and M. Karppinen, ACS Appl. Mater. Interfaces, 2018, 10, 8845–8852 CrossRef CAS PubMed
;
(e) Z. Giedraityte, M. Tuomisto, M. Lastusaari and M. Karppinen, ACS Appl. Mater. Interfaces, 2018, 10, 8845–8852 CrossRef CAS PubMed  .
.
- T. V. Balashova, A. P. Pushkarev, A. N. Yablonskiy, B. A. Andreev, I. D. Grishin, R. V. Rumyantcev, G. K. Fukin and M. N. Bochkarev, J. Lumin., 2017, 192, 208–210 CrossRef CAS
 .
.
-
(a) I. Hernandez, N. Pathumakanthar, P. B. Wyatt and W. P. Gillin, Adv. Mater., 2010, 22, 5356–5360 CrossRef CAS PubMed
 ;
(b) H. Ye, V. Bogdanov, S. Liu, S. Vajandar, T. Osipowicz, I. Hernandez and Q. Xiong, J. Phys. Chem. Lett., 2017, 8, 5695–5699 CrossRef CAS PubMed
;
(b) H. Ye, V. Bogdanov, S. Liu, S. Vajandar, T. Osipowicz, I. Hernandez and Q. Xiong, J. Phys. Chem. Lett., 2017, 8, 5695–5699 CrossRef CAS PubMed  .
.
-
(a) L. Aboshyan-Sorgho, C. Besnard, P. Pattison, K. R. Kittilstved, A. Aebischer, J.-C. G. Bünzli, A. Hauser and C. Piguet, Angew. Chem., Int. Ed., 2011, 50, 4108–4112 CrossRef CAS PubMed
 ;
(b) L. Aboshyan-Sorgho, M. Cantuel, S. Petoud, A. Hauser and C. Piguet, Coord. Chem. Rev., 2012, 256, 1644–1663 CrossRef CAS
;
(b) L. Aboshyan-Sorgho, M. Cantuel, S. Petoud, A. Hauser and C. Piguet, Coord. Chem. Rev., 2012, 256, 1644–1663 CrossRef CAS  .
.
- I. Hyppänen, S. Lahtinen, T. Ääritalo, J. Mäkelä, J. Kankare and T. Soukka, ACS Photonics, 2014, 1, 394–397 CrossRef
 .
.
- A. Nonat, C. F. Chan, C. Platas-Iglesias, Z. Liu, W.-T. Wong, W.-K. Wong, K.-L. Wong and L. J. Charbonnière, Nat. Commun., 2016, 11978 CrossRef CAS PubMed
 .
.
-
(a) N. Souri, P. Tian, C. Platas-Iglesias, K.-L. Wong, A. Nonat and L. J. Charbonnière, J. Am. Chem. Soc., 2017, 139, 1456–1459 CrossRef CAS
 ;
(b) A. Nonat, S. Bahamyirou, A. Lecointre, F. Przybilla, Y. Mély, C. Platas-Iglesias, F. Camerel, O. Jeannin and L. J. Charbonnière, J. Am. Chem. Soc., 2019, 141, 1568–1576 CrossRef CAS
;
(b) A. Nonat, S. Bahamyirou, A. Lecointre, F. Przybilla, Y. Mély, C. Platas-Iglesias, F. Camerel, O. Jeannin and L. J. Charbonnière, J. Am. Chem. Soc., 2019, 141, 1568–1576 CrossRef CAS  .
.
- L. J. Charbonnière, Dalton Trans., 2018, 47, 8566–8570 RSC
 .
.
- B. Golesorkhi, H. Nozary, L. Guénée, A. Fürstenberg and C. Piguet, Angew. Chem., Int. Ed., 2018, 57, 15172–15176 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Claude
Piguet
and
Claude
Piguet
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range), which prevent very selective color programming and optical addressing. Finally, the promotion of bonding electrons into anti-bonding orbitals alters the stability of the whole molecular edifices, which results in non-negligible optical bleaching through photochemical reactions occurring from reactive excited states upon exposure to light.
000 cm−1 range), which prevent very selective color programming and optical addressing. Finally, the promotion of bonding electrons into anti-bonding orbitals alters the stability of the whole molecular edifices, which results in non-negligible optical bleaching through photochemical reactions occurring from reactive excited states upon exposure to light.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) and vibronic coupling. The resulting intrashell spin-allowed d–d transitions appear as broad bands covering the UV-visible range and only a few spin–flip transitions, cleared from ligand-field effects, may display some thin absorption/emission features.6
000 cm−1) and vibronic coupling. The resulting intrashell spin-allowed d–d transitions appear as broad bands covering the UV-visible range and only a few spin–flip transitions, cleared from ligand-field effects, may display some thin absorption/emission features.6

![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 (Ĥp is the sum of the electric dipole and magnetic dipole perturbation operators) and to the Dirac delta function
ba|2 = 〈φb|Ĥp|φa〉2 (Ĥp is the sum of the electric dipole and magnetic dipole perturbation operators) and to the Dirac delta function 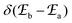 which ensures that the transition occurs with energy conservation.9
which ensures that the transition occurs with energy conservation.9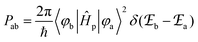
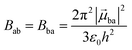
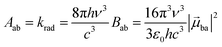
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 led to the well-known selection rules controlling electronic transitions induced by electromagnetic waves. Firstly, the electronic transitions are only allowed when (i) the total spin does not change (spin rule ΔStot = 0) and (ii) the parity of the two incriminated wavefunctions should be inverted (Δl = ±1, 3…) for an electric dipole transition and conserved (Δl = ±0, 2…) for a magnetic dipole transition. Consequently, the intra-shell d ↔ d and f ↔ f transitions are electric-dipole forbidden, but magnetic-dipole allowed. Since the magnetic dipole transitions are three to four orders less intense than their electric dipole counterparts, this results in that intra-shell d ↔ d and f ↔ f are always weak, but they can be enhanced via some specific programming of the transition dipoles |
ba|2 = 〈φb|Ĥp|φa〉2 led to the well-known selection rules controlling electronic transitions induced by electromagnetic waves. Firstly, the electronic transitions are only allowed when (i) the total spin does not change (spin rule ΔStot = 0) and (ii) the parity of the two incriminated wavefunctions should be inverted (Δl = ±1, 3…) for an electric dipole transition and conserved (Δl = ±0, 2…) for a magnetic dipole transition. Consequently, the intra-shell d ↔ d and f ↔ f transitions are electric-dipole forbidden, but magnetic-dipole allowed. Since the magnetic dipole transitions are three to four orders less intense than their electric dipole counterparts, this results in that intra-shell d ↔ d and f ↔ f are always weak, but they can be enhanced via some specific programming of the transition dipoles |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2, for instance by removing the symmetry operator responsible for the parity of the wavefunctions and/or by increasing the energy gaps between the two incriminated levels for maximizing ν = (Eb − Ea)/h in eqn (3). However, transitions between electronic states are not induced by only electromagnetic radiation and non-radiative relaxation processes exist, among which dissipation of energy through vibrational processes plays a crucial role. The temperature-dependent rate constant kvibT for the quenching of a single excited level is described by eqn (4) with the assumption that the deactivating phonons/vibrations involved have all the same energy ħω (n is the number of phonons required to bridge the energy gap ΔE and kvibT=0 is the spontaneous rate at 0 K).11Eqn (4) implies that the phonon-assisted non-radiative quenching essentially depends on the energy gap ΔE between the emissive state and the highest sublevel of its ground, or receiving, multiplet. The smaller this gap, the easier is its closing by non-radiative deactivation processes, for instance through vibrations of high energy such as O–H, N–H, or C–H.
ba|2, for instance by removing the symmetry operator responsible for the parity of the wavefunctions and/or by increasing the energy gaps between the two incriminated levels for maximizing ν = (Eb − Ea)/h in eqn (3). However, transitions between electronic states are not induced by only electromagnetic radiation and non-radiative relaxation processes exist, among which dissipation of energy through vibrational processes plays a crucial role. The temperature-dependent rate constant kvibT for the quenching of a single excited level is described by eqn (4) with the assumption that the deactivating phonons/vibrations involved have all the same energy ħω (n is the number of phonons required to bridge the energy gap ΔE and kvibT=0 is the spontaneous rate at 0 K).11Eqn (4) implies that the phonon-assisted non-radiative quenching essentially depends on the energy gap ΔE between the emissive state and the highest sublevel of its ground, or receiving, multiplet. The smaller this gap, the easier is its closing by non-radiative deactivation processes, for instance through vibrations of high energy such as O–H, N–H, or C–H.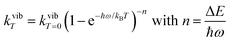
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) ba|2 = 〈φb|Ĥp|φa〉2 through the oscillator strength f (eqn (5), 9n/(n2 + 2)2 is the local electric field correction factor with the refractive index of the medium n,
ba|2 = 〈φb|Ĥp|φa〉2 through the oscillator strength f (eqn (5), 9n/(n2 + 2)2 is the local electric field correction factor with the refractive index of the medium n, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) is the transition wavenumber in cm−1 for εabs in L mol−1 cm−1).12
is the transition wavenumber in cm−1 for εabs in L mol−1 cm−1).12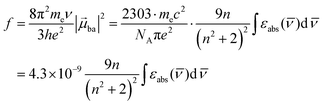
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the barycenter of the transition wavenumber, NA is the Avogadro constant, gGS is the degeneracy of the ground state, and gES is the degeneracy of the excited state).12c
is the barycenter of the transition wavenumber, NA is the Avogadro constant, gGS is the degeneracy of the ground state, and gES is the degeneracy of the excited state).12c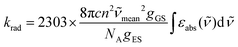









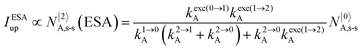
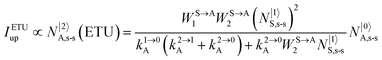
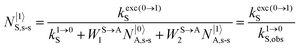
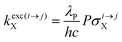
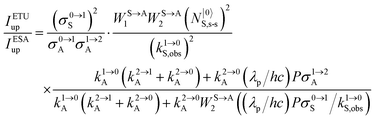
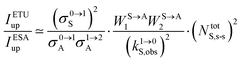
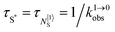 in its excited S* state. The latter sentence is rather contradictory since fast S → A energy transfers will reduce τS*, which implies some judicious tuning of these interconnected parameters. Finally, the ETU mechanism depends on the square of the concentration of the sensitizer (NtotS,s-s)2, which explains the enthusiasm for using co-doped bulk solids and nanoparticles.14,26,28 Altogether, ETU appeared to be two to three orders of magnitude more efficient than single-centre ESA with a special emphasis on the Yb3+/Er3+ pair, where Yb3+ works as the sensitizer (non-negligible absorption cross section in the near-infrared at 980 nm and long Yb(2F5/2) excited-state lifetime) and Er3+ acts as the activator (regularly spaced excited states). Compared with ionic solids, the introduction of high-energy vibrations (= phonons) in coordination polymers severely reduces the excited-state lifetimes, but eqn (11) still holds and some weak near-infared to visible energy transfer upconversion (ETU) could be induced in statistically doped Yb3+/Er3+ lanthanide organic frameworks (a modern term for lanthanide coordination polymers).72 Improved upconverted intensities logically resulted from the replacement of high-energy C–H oscillators with less energetic C–F analogues in these polymers.73,74 However, the statistical distribution of the different centers characterizing these systems limits S → A energy transfer pathways to second-order kinetic processes, which are not compatible with molecular-based mechanisms which requires first-order kinetic treatments.
in its excited S* state. The latter sentence is rather contradictory since fast S → A energy transfers will reduce τS*, which implies some judicious tuning of these interconnected parameters. Finally, the ETU mechanism depends on the square of the concentration of the sensitizer (NtotS,s-s)2, which explains the enthusiasm for using co-doped bulk solids and nanoparticles.14,26,28 Altogether, ETU appeared to be two to three orders of magnitude more efficient than single-centre ESA with a special emphasis on the Yb3+/Er3+ pair, where Yb3+ works as the sensitizer (non-negligible absorption cross section in the near-infrared at 980 nm and long Yb(2F5/2) excited-state lifetime) and Er3+ acts as the activator (regularly spaced excited states). Compared with ionic solids, the introduction of high-energy vibrations (= phonons) in coordination polymers severely reduces the excited-state lifetimes, but eqn (11) still holds and some weak near-infared to visible energy transfer upconversion (ETU) could be induced in statistically doped Yb3+/Er3+ lanthanide organic frameworks (a modern term for lanthanide coordination polymers).72 Improved upconverted intensities logically resulted from the replacement of high-energy C–H oscillators with less energetic C–F analogues in these polymers.73,74 However, the statistical distribution of the different centers characterizing these systems limits S → A energy transfer pathways to second-order kinetic processes, which are not compatible with molecular-based mechanisms which requires first-order kinetic treatments.

 , where Exc stands for sensitizer excitation and Up-em for upconverted emission. The short lifetime of the SA* excited relay drastically limits the efficiency of linear upconversion in molecular SA pairs.70 When n ≥ 2 in a S2A triad, as designed in [CrErCr(L4)3]9+, the activator-centred ETU mechanism (eqn (13)) is completed by a more efficient sensitizer-centred ETU mechanism (eqn (14)), for which there is no need to wait for a second excitation while the activator is excited.
, where Exc stands for sensitizer excitation and Up-em for upconverted emission. The short lifetime of the SA* excited relay drastically limits the efficiency of linear upconversion in molecular SA pairs.70 When n ≥ 2 in a S2A triad, as designed in [CrErCr(L4)3]9+, the activator-centred ETU mechanism (eqn (13)) is completed by a more efficient sensitizer-centred ETU mechanism (eqn (14)), for which there is no need to wait for a second excitation while the activator is excited.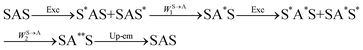
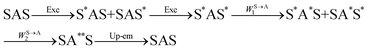




.
.
.
; (b) R. Rieger and K. Mullen, J. Phys. Org. Chem., 2010, 23, 315–325 CAS
.
.
; (b) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS
; (c) Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1956, 11, 864–877 CrossRef CAS
.
.
.
.
; (b) S. Strickler and S. J. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS
; (c) J. B. Berks and D. J. Dyson, Proc. R. Soc. London, Ser. A, 1963, 275, 135–148 CrossRef
.
.
; (b) S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227 RSC
; (c) J.-C. G. Bünzli, A.-S. Chauvin, H. K. Kim, E. Deiters and S. V. Eliseeva, Coord. Chem. Rev., 2010, 254, 2623–2633 CrossRef
.
.
; (b) X. Huang, S. Han, W. Huang and X. Liu, Chem. Soc. Rev., 2013, 42, 173–201 RSC
.
; (b) S. Petoud, Chimia, 2009, 63, 745–752 CrossRef CAS
.
; (b) E. G. Moore, A. P. S. Samuel and K. N. Raymond, Acc. Chem. Res., 2009, 42, 542–552 CrossRef CAS
; (c) A. K. R. Junker, L. R. Hill, A. L. Thompson, S. Faulkner and T. J. Sorensen, Dalton Trans., 2018, 47, 4794–4803 RSC
.
; (b) J.-F. Lemonnier, L. Babel, L. Guénée, P. Mukherjee, D. H. Waldeck, S. V. Eliseeva, S. Petoud and C. Piguet, Angew. Chem., Int. Ed., 2012, 51, 11302–11305 CrossRef CAS
.
; (b) H. F. Brito, O. M. L. Malta, M. C. F. C. Felinto and E. E. S. Teotonio, The Chemistry of Metal Enolates, ed. J. Zabicky, John Wiley & Sons, Chichester, 2009, vol. 3, pp. 131–184 Search PubMed
; (c) S. Di Pietro, D. Imbert and M. Mazzanti, Chem. Commun., 2014, 50, 10323–10326 RSC
; (d) A. S. Kalyakina, V. V. Utochnikova, M. Zimmer, F. Dietrich, A. M. Kaczmarek, R. Van Deun, A. A. Vashchenko, A. S. Goloveshkin, M. Nieger, M. Gerhards, U. Sheppers and S. Bräse, Chem. Commun., 2018, 54, 5221–5224 RSC
.
; (b) J. Kerr, J. Phys. Theor. Appl., 1879, 8, 414–418 CrossRef
.
.
.
.
; (b) M. O. Scully, K. Wodkiewicz, M. S. Zubairy, J. Bergou, N. Lu and J. Meyer ter Vehn, Phys. Rev. Lett., 1988, 60, 1832–1835 CrossRef CAS
.
.
; (b) D. K. Sinha, P. Neveu, N. Gagey, I. Aujard, C. Benbrahim-Bouzidi, T. Le Saux, C. Rampon, C. Gauron, B. Goetz, S. Dubruille, M. Baaden, M. Volovitch, D. Bensimon, S. Vriz and L. Jullien, ChemBioChem, 2010, 11, 653–663 CrossRef CAS
; (c) D. Kim, H. G. Ryu and K. H. Ahn, Org. Biomol. Chem., 2014, 12, 4550–4566 RSC
; (d) T. N. Nguyen, F. M. Ebrahim and K. C. Stylianou, Coord. Chem. Rev., 2018, 377, 259–306 CrossRef CAS
.
; (b) M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS
.
; (b) S. Ye, E.-H. Song and Q.-Y. Zhang, Adv. Sci., 2016, 3, 1600302 CrossRef
.
; (b) M. Haase and H. Schäfer, Angew. Chem., Int. Ed., 2011, 50, 5808–5829 CrossRef CAS
; (c) J.-C. G. Bünzli and A.-S. Chauvin, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier North Holland, Amsterdam, 2014, vol. 44, pp. 169–281 Search PubMed
; (d) G. Liu, Chem. Soc. Rev., 2015, 44, 1635–1652 RSC
.
; (b) F. Auzel, C. R. Seances Acad. Sci., Ser. B, 1966, 263, 819–821 Search PubMed
; (c) H. Suo, F. Hu, X. Zhao, Z. Zhang, T. Li, C. Duan, M. Yin and C. Guo, J. Mater. Chem. C, 2017, 5, 1501–1507 RSC
; (d) S. Balabjadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121, 13962–13968 CrossRef
; (e) M. Runowski, J. Marciniak, T. Grzyb, D. Przybylska, A. Schylchuck, B. Barszcz, A. Katrusiak and S. Lis, Nanoscale, 2017, 9, 16030–16037 RSC
; (f) Z. Wang, J. Chrstiansen, D. Wezendonk, X. Xie, M. A. Van Huis and A. Meijerink, Nanoscale, 2019, 11, 12188–12197 RSC
.
.
; (b) W. W. Piper, J. A. DeLuca and F. S. Ham, J. Lumin., 1974, 8, 344–348 CrossRef CAS
.
; (b) L. H. Sloof, A. van Blaaderen, A. Polman, G. A. Hebbink, S. I. Klink, F. C. J. M. Van Veggel, D. N. Reinhoudt and J. W. Hofstraat, J. Appl. Phys., 2002, 91, 3955–3980 CrossRef
.
; (b) M. T. Berry and P. S. May, J. Phys. Chem. A, 2015, 119, 9805–9811 CrossRef CAS
; (c) X. Shang, P. Chen, T. Jia, D. Feng, S. Zhang, Z.-M. Sun and J. Qiu, Phys. Chem. Chem. Phys., 2015, 17, 11481–11489 RSC
; (d) M. Runowski, N. Stopikowska, D. Szeremeta, S. Goderski, M. Skwierczynska and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 13389–13396 CrossRef CAS PubMed
.
.
; (b) S. Han, R. Deng and X. Liu, Angew. Chem., Int. Ed., 2014, 53, 11702–11715 CrossRef CAS
.
.
.
; (b) J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed
; (c) C. Ye, L. Zhou, X.-Y. Wang and Z. Liang, Phys. Chem. Chem. Phys., 2016, 18, 10818–10835 RSC
; (d) V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71 CrossRef CAS
.
; (b) C. A. Parker, Proc. R. Soc. London, Ser. A, 1963, 276, 125–135 CrossRef CAS
.
.
.
; (b) S. Comby and J.-C. G. Bünzli, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2007, vol. 37, pp. 217–470 Search PubMed
; (c) ed. C. Huand, Rare Eath Coordination Chemistry: Fundamentals and Applications, John Wiley & Sons, Singapore, 2010 Search PubMed
.
; (b) G. R. Choppin and E. N. Rizkalla, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, L. Eyring, G. R. Choppin and G. H. Lander, 1994, vol. 18, pp. 559–589 Search PubMed
.
.
; (b) L. Babel, K. Baudet, T. N. Y. Hoang, H. Nozary and C. Piguet, Chem. – Eur. J., 2018, 24, 5423–5433 CrossRef CAS PubMed
.
.
; (b) C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1989, 28, 2699–2703 CrossRef CAS
.
.
.
.
.
.
.
.
.
.
; (b) L.-D. Sun, Y.-F. Wang and C.-H. Yan, Acc. Chem. Res., 2014, 47, 1001–1009 CrossRef CAS PubMed
; (c) M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed
; (d) A. J. Amoroso and S. J. Pope, Chem. Soc. Rev., 2015, 44, 4723–4742 RSC
; (e) J.-C. G. Bünzli, J. Lumin., 2016, 170, 866–878 CrossRef
; (f) J. Zhou, J. L. Leano Jr., Z. Liu, K.-L. Wong, R.-S. Liu and J.-C. G. Bünzli, Small, 2018, 1801882 CrossRef PubMed
.
; (b) E. R. Triveldi, S. V. Eliseeva, J. Jankolovits, M. M. Olmstead, S. Petoud and V. L. Pecoraro, J. Am. Chem. Soc., 2014, 136, 1526–1534 CrossRef PubMed
; (c) B. L. Reid, S. Stagni, J. M. Malicka, M. Cocchi, A. N. Sobolev, B. W. Skelton, E. G. Moore, G. S. Hanan, M. I. Ogden and M. Massi, Chem. – Eur. J., 2015, 21, 18354–18363 CrossRef CAS PubMed
; (d) Y. Peng, J. X. Xu, H. Lu, R. M. Wilson, M. Motevalli, I. Hernandez, W. P. Gillin, P. B. Wyatt and H. Q. Ye, RSC Adv., 2017, 7, 128–131 RSC
.
; (b) G. Mancino, A. J. Ferguson, A. Beeby, N. J. Long and T. S. Jones, J. Am. Chem. Soc., 2005, 127, 524–525 CrossRef CAS PubMed
; (c) P. B. Glover, A. P. Basset, P. Nockemann, B. M. Kariuki, R. Van Deun and Z. Pikramenou, Chem. – Eur. J., 2007, 13, 6309–6320 CrossRef PubMed
; (d) L. Song, J. Hu, J. Wang, X. Liu and Z. Zhen, Photochem. Photobiol. Sci., 2008, 7, 689–693 RSC
; (e) C. Doffek, N. Alzakhem, M. Molon and M. Seitz, Inorg. Chem., 2012, 51, 4539–4545 CrossRef CAS
.
; (b) N. Sabbatini, M. Guardigli and I. Manet, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier Science, Amsterdam, 1996, vol. 23, pp. 69–120 Search PubMed
; (c) J. M. Zwier, H. Bazin, L. Lamarque and G. Mathis, Inorg. Chem., 2014, 53, 1854–1866 CrossRef CAS PubMed
; (d) https://ch.cisbio.eu/terbium-cryptate-labeling-kit-40482 ; (e) https://ch.cisbio.eu/europium-cryptate-labeling-kit-40385 .
.
.
; (b) D. Zare, Y. Suffren, L. Guénée, S. V. Eliseeva, H. Nozary, L. Aboshyan-Sorgho, S. Petoud, A. Hauser and C. Piguet, Dalton Trans., 2015, 44, 2529–2540 RSC
.
.
.
.
.
.
.
.
.
; (b) C.-Y. Sun, X.-J. Zheng, X.-B. Chen and L.-P. Jin, Inorg. Chim. Acta, 2009, 362, 325–330 CrossRef CAS
; (c) X. Zhang, B. Li, H. Ma, L. Zhang and H. Zhao, ACS Appl. Mater. Interfaces, 2016, 8, 17389–17394 CrossRef CAS PubMed
; (d) M. Li, S. Gul, D. Tian, E. Zhou, Y. Wang, Y.-F. Han, L. Yin and L. Huang, Dalton Trans., 2018, 47, 12868–12872 RSC
; (e) Z. Giedraityte, M. Tuomisto, M. Lastusaari and M. Karppinen, ACS Appl. Mater. Interfaces, 2018, 10, 8845–8852 CrossRef CAS PubMed
.
.
; (b) H. Ye, V. Bogdanov, S. Liu, S. Vajandar, T. Osipowicz, I. Hernandez and Q. Xiong, J. Phys. Chem. Lett., 2017, 8, 5695–5699 CrossRef CAS PubMed
.
; (b) L. Aboshyan-Sorgho, M. Cantuel, S. Petoud, A. Hauser and C. Piguet, Coord. Chem. Rev., 2012, 256, 1644–1663 CrossRef CAS
.
.
.
; (b) A. Nonat, S. Bahamyirou, A. Lecointre, F. Przybilla, Y. Mély, C. Platas-Iglesias, F. Camerel, O. Jeannin and L. J. Charbonnière, J. Am. Chem. Soc., 2019, 141, 1568–1576 CrossRef CAS
.
.
.








