Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilizing cubic γ-Ga2O3:Cr3+ spinel nanocrystals by size confinement into mesoporous silica nanoreactor channels†
Michele
Crozzolin
 a,
Camilla
Belloni
a,
Camilla
Belloni
 a,
Jian
Xu
a,
Jian
Xu
 bc,
Takayuki
Nakanishi
bc,
Takayuki
Nakanishi
 d,
Jumpei
Ueda
e,
Setsuhisa
Tanabe
d,
Jumpei
Ueda
e,
Setsuhisa
Tanabe
 c,
Federico
Dallo
f,
Eleonora
Balliana
c,
Federico
Dallo
f,
Eleonora
Balliana
 g,
Asia
Saorin
g,
Asia
Saorin
 a,
Flavio
Rizzolio
a,
Flavio
Rizzolio
 ah,
Davide
Cristofori
ah,
Davide
Cristofori
 a,
Pietro
Riello
a,
Pietro
Riello
 a,
Alvise
Benedetti
a,
Alvise
Benedetti
 a and
Michele
Back
a and
Michele
Back
 *a
*a
aDepartment of Molecular Sciences and Nanosystems, Ca’ Foscari University of Venice, Via Torino 155, 30172, Mestre – Venezia, Italy. E-mail: michele.back@unive.it
bInternational Center for Young Scientists (ICYS), National Institute of Materials Science (NIMS), Tsukuba, Ibaraki 305-0044, Japan
cGraduate School of Global Environmental Studies, Kyoto University, Yoshida nihonmatsu-cho, Sakyo-ku, Kyoto 606-8501, Japan
dAdvanced Phosphor Group, National Institute of Materials Science (NIMS), Tsukuba, Ibaraki 305-0044, Japan
eGraduate School of Advanced Science and Technology, Japan Advanced Institute of Science and Technology (JAIST), 1-1 Asahidai, Nomi, Ishikawa 923-1292, Japan
fInstitute of Polar Sciences – National Research Council (ISP-CNR), Via Torino 155, 30172, Venezia-Mestre, Venice, Italy
gDepartment of Environmental Sciences, Informatics, Statistics, Ca’ Foscari University of Venice, Scientific Campus – Via Torino 155, 30170 Venezia Mestre, Italy
hPathology Unit, Department of Molecular Biology and Translational Research, Centro di Riferimento Oncologico di Aviano (CRO) IRCCS, via Franco Gallini 2, 33081 Aviano, Italy
First published on 18th June 2024
Abstract
In recent years, Cr3+-activated phosphors have been attracting a lot of interest due to their unique optical features that can be exploited for applications ranging from lasers to optical thermometry, near-infrared (NIR) emitting phosphors for bioimaging and NIR-LEDs, to name a few. Despite the interesting optical properties shown by Cr3+-doped Ga2O3, investigations are limited only to β-Ga2O3 and α-Ga2O3 polymorphs. Using mesoporous silica particles with different pore sizes between 3 nm and 22 nm as nanoreactors, cubic γ-Ga2O3:Cr3+ spinel nanocrystals (NCs) are stabilized through confinement into the mesopores as confirmed by HR-TEM, XRPD and the photoluminescence spectral shape. A detailed spectroscopic investigation in the temperature range between 16 to 500 K allowed extrapolating the fundamental parameters in the framework of the Tanabe–Sugano diagram and comparing the values for Cr3+ in γ-Ga2O3 with the α- and β-phases. In addition, due to the confinement of the NCs into the silica structure, the phase transition to the β-phase, conventionally occurring at about 700 °C, is hindered up to 1000 °C, improving the stability of the γ-Ga2O3 phase.
Introduction
Since the discovery of the ruby laser by Maiman,1 Cr3+-doped crystals have been among the most investigated transition metal ion doped phosphors. The flexibility of the optical properties of Cr3+ ions, arising from the possibility to control the relative energy level position of the low lying 4T2 and 2E excited states through the bond lengths and symmetry of the octahedral site of the host, has led to a huge interest in developing new Cr3+-doped phosphors for a wide variety of applications. Demonstration of the potential of Cr3+ ions in persistent luminescent materials such as spinel ZnGa2O4,2,3 garnets (e.g. Y5Al3−xGaxO124–6) and perovskite LaAlO37 has triggered investigation into their use in biological applications. In addition, Cr3+-activated phosphors were also demonstrated to be particularly promising as luminescent thermometers based on the ratio between the emissions originated from the spin allowed 4T2 → 4A2 and the spin forbidden 2E → 4A2 transitions,8–12 which were proposed for a wide range of temperatures ranging from the cryogenic (CaHfO3:Cr3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13) to high temperatures (ZnGa2O4:Cr3+
13) to high temperatures (ZnGa2O4:Cr3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14). The ability to customize the working temperature range arises from the possibility of modulating the relative energy gap between the 4T2 and 2E states. This modulation is achieved by adjusting the octahedral site through the selection of specific host compositions and structures.15 On the other hand, due to the high stability and efficiency of ruby (α-Al2O3:Cr3+) when used as a pressure sensor in diamond anvil cell experiments all over the world,16–18 Cr3+-doped phosphors were also deeply investigated to discover pressure sensors with higher sensitivities.19–21 More recently, the commercialization of near infrared (NIR) emitting phosphor-converted LEDs based on Cr3+-doped phosphors by Osram, has driven a lot of interest in the development of novel NIR Cr3+-based phosphors characterized by broadband 4T2 emission in weak crystal fields for applications ranging from food and medicine quality monitoring to bioimaging, night vision and plant growth.22–24 From this perspective, the exploration of novel phosphors activated by Cr3+ ions remains highly active.
14). The ability to customize the working temperature range arises from the possibility of modulating the relative energy gap between the 4T2 and 2E states. This modulation is achieved by adjusting the octahedral site through the selection of specific host compositions and structures.15 On the other hand, due to the high stability and efficiency of ruby (α-Al2O3:Cr3+) when used as a pressure sensor in diamond anvil cell experiments all over the world,16–18 Cr3+-doped phosphors were also deeply investigated to discover pressure sensors with higher sensitivities.19–21 More recently, the commercialization of near infrared (NIR) emitting phosphor-converted LEDs based on Cr3+-doped phosphors by Osram, has driven a lot of interest in the development of novel NIR Cr3+-based phosphors characterized by broadband 4T2 emission in weak crystal fields for applications ranging from food and medicine quality monitoring to bioimaging, night vision and plant growth.22–24 From this perspective, the exploration of novel phosphors activated by Cr3+ ions remains highly active.
Gallium oxide (Ga2O3) is emerging as one of the most important materials for a variety of technological applications.24 Ga2O3 is a semiconductor capable of adopting various crystallographic structures, with six different polymorphs known: the stable β-phase and five metastable phases α, γ, δ, ε, and κ.25,26 Among them, β-Ga2O3 has been demonstrated to be a promising host for Cr3+-activated phosphors27–31 and has been investigated for lasing,28 optical thermometry15 and pc-NIR LEDs.32 A detailed spectroscopic investigation on Cr3+ ions in the rhombohedral α-Ga2O3 phase was recently reported, showing a stronger crystal field with respect to β-Ga2O3.15 In addition, a corundum-type α-Ga2O3:Cr3+ system was also proposed as a pressure sensor.33 Al2O3–Ga2O3 and Sc2O3–Ga2O3 solid solutions were also deeply investigated as promising hosts for Cr3+ ions.34,35
The crystalline structure of the γ-Ga2O3 polymorph has been widely investigated and debated due to the complicated defect Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m spinel structure.36–40 γ-Ga2O3 stabilization was also proved in glassy hosts41 showing photocatalytic and catalytic activity.42–44 The defects present in the γ-Ga2O3 spinel structure were exploited to develop size-tuneable luminescent nanocrystals45 and white-light-emitting nanophosphors when coupled through energy transfer with orange-red emitting organic dyes.46 Despite the interest in Ga2O3 polymorphs as hosts for luminescent centres, a detailed investigation on the Cr3+ optical properties in cubic γ-Ga2O3 is still missing.
m spinel structure.36–40 γ-Ga2O3 stabilization was also proved in glassy hosts41 showing photocatalytic and catalytic activity.42–44 The defects present in the γ-Ga2O3 spinel structure were exploited to develop size-tuneable luminescent nanocrystals45 and white-light-emitting nanophosphors when coupled through energy transfer with orange-red emitting organic dyes.46 Despite the interest in Ga2O3 polymorphs as hosts for luminescent centres, a detailed investigation on the Cr3+ optical properties in cubic γ-Ga2O3 is still missing.
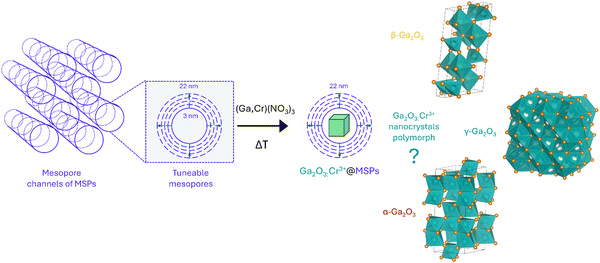
In this study, we investigate the stabilization of Cr3+-doped γ-Ga2O3 nanocrystals (NCs) by taking advantage of the size effect in mesoporous silica particles (MSPs) of different pore sizes. The effects of the size and temperature were investigated by means of a series of physical chemical investigation using XRPD, SEM/HR-TEM, N2 physisorption and TG–DSC analyses. In addition, the photoluminescence (PL) spectral analysis of Cr3+ in the Ga2O3 NCs allowed a detailed spectroscopic investigation to probe the crystalline structure. The HR-TEM analysis confirmed the stabilization of the cubic γ-Ga2O3 spinel structure. Moreover, a detailed investigation of the photoluminescence (PL) and PL excitation (PLE) spectral analysis and the temperature dependence of the PL spectra led to a comparison of the spectroscopic feature of Cr3+ with respect to the β- and α-Ga2O3 polymorphs and to investigations into the effect of the crystal on the 3d3 electrons of Cr3+ in terms of a Tanabe–Sugano diagram and configurational coordinate diagram.
Results and discussion
Stabilizing γ-Ga2O3 polymorphs by size: MSP pore effect
The most common Ga2O3 polymorphs, α, β and γ, exhibit distinct differences in crystal structures and coordination polyhedra with a direct influence on their stability and synthetic methods. The trigonal α-Ga2O3 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) is characterized by a corundum structure with only octahedral GaO6 sites, while β-phase by a monoclinic structure (space group C2/m) with mixed coordination of octahedral GaO6 and tetrahedral GaO4 sites with a ratio 1
c) is characterized by a corundum structure with only octahedral GaO6 sites, while β-phase by a monoclinic structure (space group C2/m) with mixed coordination of octahedral GaO6 and tetrahedral GaO4 sites with a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the cubic γ-phase (space group Fd
1 and the cubic γ-phase (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) mZ) by a defective spinel structure with both octahedral and tetrahedral sites characterized by a high degree of disorder.36–40 The unit cell volume increases by moving from the compact β-Ga2O3 (∼209 Å3) to α-Ga2O3 (∼289 Å3) and finally to the defective γ-Ga2O3 (∼559 Å3).
mZ) by a defective spinel structure with both octahedral and tetrahedral sites characterized by a high degree of disorder.36–40 The unit cell volume increases by moving from the compact β-Ga2O3 (∼209 Å3) to α-Ga2O3 (∼289 Å3) and finally to the defective γ-Ga2O3 (∼559 Å3).
With the aim of investigating suitable sizes to stabilize the cubic γ-Ga2O3 phase, mesoporous silica particles with different mesopores were firstly synthesized as nanoreactors and subsequently the Cr3+-doped Ga2O3 nanocrystals were grown by means of an impregnation procedure followed by thermal treatment (Scheme 1).
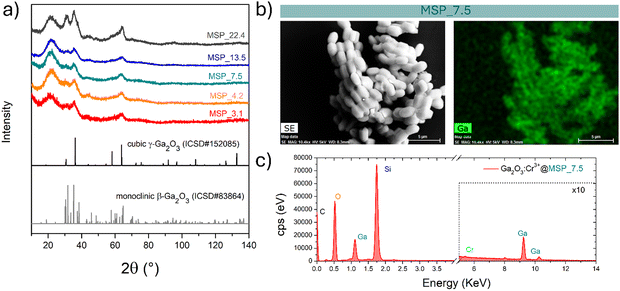
MSPs characterized by five different average pore sizes were firstly prepared as shown in Fig. 1a (labelled as MSP_3.1, MSP_4.2, MSP_7.5, MSP_13.5 and MSP_22.4).
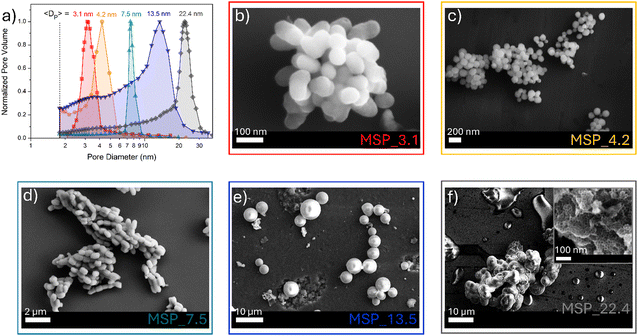 | ||
| Fig. 1 (a) BJH pore size distribution of MSPs and (b)–(f) the corresponding representative FE-SEM images. | ||
Different synthetic procedures were employed to obtain access to MSPs characterized by different pore sizes. Spherical MSNs, with an average pore size of 3.1 nm (Fig. 1b), were obtained following the procedure proposed by Quiao et al.47 Spherical MCM-41 MSNs characterized by a pore size of 4.2 nm were prepared using n-hexane as the swelling agent (Fig. 1c). SBA-15 with average pores of 7.5 nm were synthesized using an aging process in an autoclave at 100 °C for 24 hours without the use of a swelling agent, while SBA-15 characterized by average pore sizes of 13.5 and 22.4 nm were prepared by using trimethylbenzene at different TMB/Pluronic P123 ratios as the swelling agent. The SBA-15 are characterized by typical hexagonal arranged pore structure morphology (Fig. 1d and Fig. S1a and b, ESI†). The conventional tubular shape is lost, and micrometer globular particles are stabilized when a TMB/Pluronic P123 ratio of 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is employed (Fig. 1e and Fig. S1c and d, ESI†). Finally, mesocellular foam with average pore sizes of 22.4 nm were obtained for a TMB/Pluronic P123 ratio of 0.5
1 is employed (Fig. 1e and Fig. S1c and d, ESI†). Finally, mesocellular foam with average pore sizes of 22.4 nm were obtained for a TMB/Pluronic P123 ratio of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 1f and Fig. S1e and f, ESI†). The shape evolution is driven by the TMB/Pluronic P123 ratio due to the effect of TMB on the surfactant packing parameter.48 TMB can be easily dissolved into the PPO core of P123 micelles increasing the volume of the hydrophobic part.49 This change directly influences the micelle shape, described through the geometric model introduced by Israelachvili50 by the packing factor P = V/(a0l), where V is the total volume of the hydrophobic surfactant chain, a0 the effective hydrophilic headgroup size and l is the kinetic surfactant tail length. When the TMB/Pluronic P123 ratio is high (P > 1), the need to decrease the micelle surface-to-volume ratio leads to micellar aggregates with reverse curvature being formed51 and a consequent change in the mesoporous silica structure to mesocellular foam is triggered.
1 (Fig. 1f and Fig. S1e and f, ESI†). The shape evolution is driven by the TMB/Pluronic P123 ratio due to the effect of TMB on the surfactant packing parameter.48 TMB can be easily dissolved into the PPO core of P123 micelles increasing the volume of the hydrophobic part.49 This change directly influences the micelle shape, described through the geometric model introduced by Israelachvili50 by the packing factor P = V/(a0l), where V is the total volume of the hydrophobic surfactant chain, a0 the effective hydrophilic headgroup size and l is the kinetic surfactant tail length. When the TMB/Pluronic P123 ratio is high (P > 1), the need to decrease the micelle surface-to-volume ratio leads to micellar aggregates with reverse curvature being formed51 and a consequent change in the mesoporous silica structure to mesocellular foam is triggered.
The N2 physisorption analysis allows estimating the surface area using the BET technique (Table S1, ESI†) while the pore size distributions and pore volume of the different MSPs were determined using the BJH method (Fig. 1a and Table S1, ESI†). The N2 physisorption hysteresis curves of the MSP samples are shown in Fig. S2 (ESI†).
Subsequently, the MSPs were impregnated with Ga/Cr nitrate precursors using a wet impregnation method by fixing the Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr ratio to obtain a 0.5 at% doping of the Ga sites in the final target product (Ga1.99Cr0.01O3). After that, the system was thermally treated at 900 °C for 2 hours.
Cr ratio to obtain a 0.5 at% doping of the Ga sites in the final target product (Ga1.99Cr0.01O3). After that, the system was thermally treated at 900 °C for 2 hours.
At this stage of the preparation, the XRPD pattern analysis of the samples, shown in Fig. 2a, independently from the pore size, show a pattern similar to that of the γ-Ga2O3 spinel reference, suggesting stabilization of the higher symmetric cubic structure. However, the broadening of the diffraction peaks due to the small crystallites and the amorphous contribution of the MSPs make the assignment not unambiguous.
The effectiveness of the impregnation method is demonstrated by the elemental map of Ga inside the MSPs by means of EDX analysis. As shown in Fig. 2b on the Ga2O3:Cr3+@MSP_7.5 sample, as an example, Ga is homogeneously distributed inside the MSPs. In addition, the EDX spectrum allows us to confirm the Si, Ga and Cr elements are present in the particles. The elemental maps of Ga, Si and O confirmed the effectiveness of the impregnation irrespective to the pore size as evidenced for instance by the elemental maps for Ga2O3@MSP_4.2, Ga2O3@MSP_7.5 and Ga2O3@MSP_13.5 reported in Fig. S3–S5 (ESI†).
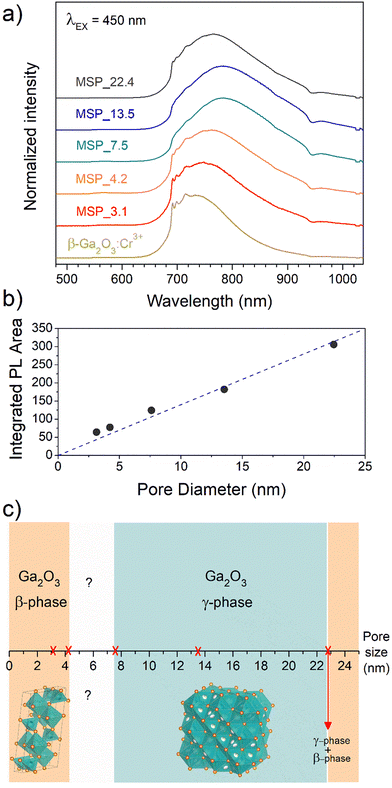
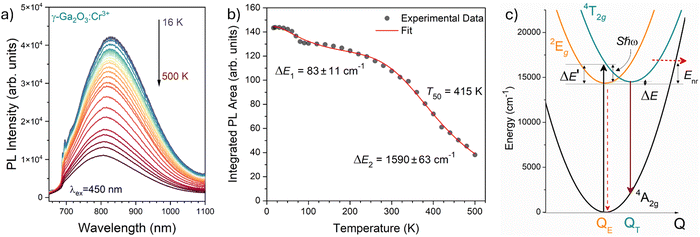
To shed light on the phase assignment, Cr3+ ions can be used as a structural probe. Indeed, the strong effect of the environment on the optical properties of the 3d3 electrons of Cr3+ can be used to probe the stabilized polymorphs. In this way, bulk monoclinic β-Ga2O3:Cr3+ was prepared as a reference. The photoluminescence (PL) spectra of Ga2O3:Cr3+ nanocrystals in Fig. 3a reveal an unexpected behavior showing the stabilization of the γ-Ga2O3 spinel phase for NCs of 7.5 and 13.5 nm, confirming the XRPD analysis, while at smaller sizes the stable monoclinic β-phase is detected. The PL spectrum of the 22.4 nm sample shows the spectral feature of both the β-phase and γ-phase, suggesting a mixture of the polymorphs. Irrespective of the stabilized phase, the integrated PL area increases linearly with the size of the NCs (Fig. 3b) evidencing a major role played by the size on the quenching behavior.
Fig. 3c summarizes the results of the Ga2O3 polymorph stabilization into the mesoporous channels with different size ranges. The stabilization of the cubic γ-Ga2O3 phase can be explain by considering the complex interplay between surface energy and bulk thermodynamic stability along with synthesis conditions. The order of phase stability (based on the formation free energy) for the Ga2O3 polymorphs is β > κ > α > δ > γ.52,53 However, at the nanoscale, the surface to volume ratio increases leading the surface energy playing a significant role in the total energy. On the other hand, high-symmetry phases tend to have lower surface energy making the γ-phase more favorable at small sizes. The stabilization of higher symmetric structures with the decreasing of the size was already demonstrated for many partially covalent compounds such as CdSe,54,55 ZrO2,56 YPO4, BaTiO3, Al2O3, Fe2O3, PbTiO3, PbZrO3, and Bi2CaSr2Cu2O8,57 to name a few. With reduction in particle size, a unit cell expansion up to phase transition was demonstrated for these materials, showing an effect similar to the application of a negative pressure.57
The stabilization of the β-Ga2O3 phase for a size smaller than 4.2 nm confirms the results reported by Fang et al.58 and it could be explained considering that the kinetic barriers that need to be overcome to stabilize different polymorphs can be strongly altered by stress and strain, promoting or hindering the stabilization of metastable polymorphs. The same effect of size dependence stabilization of the γ- and β-phase was also recently demonstrated for ultrathin Ga2O3 nanowires by Wang et al.,59 suggesting that positive or negative strains could inhibit the phase transition to the γ-phase at very small sizes. For sizes larger than about 22 nm, the β-Ga2O3 polymorph is again the more thermodynamically favored.
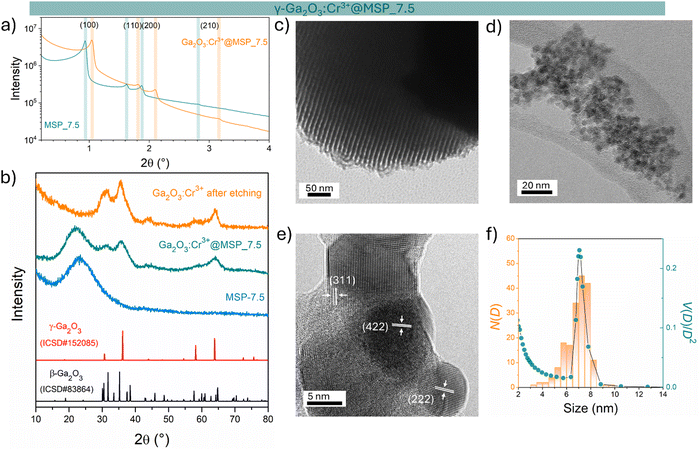
The sample at 7.5 nm was selected as representative of the cubic γ-Ga2O3:Cr3+. As evidenced in Fig. S2 (ESI†) and Fig. 1a, the MSP_7.5 sample is characterized by a type H1 hysteresis loop (IUPAC60) typical of the SBA-15 and a narrow pore size distribution. The XRPD patterns at low angles of the bare MSP_7.5 show the characteristic reflections of the (100), (110) and (200) planes of the p6mm hexagonally arranged cylindrical pores61,62 (Fig. 4a). The well resolved peaks indicate the high degree of hexagonal mesoscopic organization. The intense (100) peak reflects a d spacing of 94 Å, corresponding to a large unit cell parameter a = 10.9 nm. After the Ga2O3 NCs growth into the MSP channels at 900 °C, the p6mm morphology is preserved but the peaks appear at larger 2θ values, with d(100) = 98 Å and a = 9.8 nm. Fig. 4b shows the XRPD at higher angles of the bare SBA-15 MSPs, the SBA-15 MSPs filled with the Ga2O3:Cr3+ nanocrystals after the thermal treatment at 900 °C and the Ga2O3:Cr3+ nanocrystals after the MSP etching by NaOH. Comparison with the Ga2O3 polymorph references evidences the stabilization of the cubic γ-phase. In addition, the theoretical amount of Cr doping was confirmed using ICP-OES analysis. The estimated Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr = 28.62
Cr = 28.62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.18 shows a doping content of 0.6 at%, in good agreement with the theoretical value of 0.5% of the Ga sites (Ga1.99Cr0.01O3).
0.18 shows a doping content of 0.6 at%, in good agreement with the theoretical value of 0.5% of the Ga sites (Ga1.99Cr0.01O3).
The TEM image of the mesoporous silica MSP_7.5 (Fig. 4c) shows the well-organized mesopores, as expected by the pore distribution (Fig. 1a) and the XRPD at low angles (Fig. 4a). Fig. 4d and e and Fig. S6 (ESI†) show the HR-TEM images of the Ga2O3 NCs grown into the mesopores of the MSP_7.5 after the etching process. The HR-TEM analysis (Fig. 4e) provides additional evidence of the stabilization of the cubic γ-Ga2O3 polymorph. The images confirm the high crystalline nature of the Ga2O3 NCs and the investigation of the d-spacing of the families of planes evidenced in the HR-TEM images are unambiguously assigned to the (311), (222), and (422) crystal planes, characteristic of the cubic γ-Ga2O3 polymorph (Table S2, ESI†). The very narrow size distribution of the NCs estimated by TEM (numerical distribution, N(D)dD) shows a mean value of 6.9 ± 1.0 nm in good agreement with the pore size distribution obtained using the BJH method (volumetric distribution, V(D)dD also in this case vary narrow) confirming the stabilization of the γ-Ga2O3 NCs inside the pores of the MSP_7.5 (Fig. 4f). Assuming that the average pore length L is independent of the pore diameter, the two distributions are correlated by 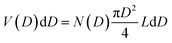 ,63 and the N(D) obtained by TEM is compared with V(D)/D2 obtained by BJH.
,63 and the N(D) obtained by TEM is compared with V(D)/D2 obtained by BJH.
It is worth noting that if the silica is etched from the Ga2O3@MSP system without the use of an ultrasonic bath, this nanocasting method leads to a mesoporous γ-Ga2O3 replica of the SBA-15 (see Fig. S7, ESI†) with potential applications as a support for nanocatalysts or directly as a mesoporous catalyst itself.42,43
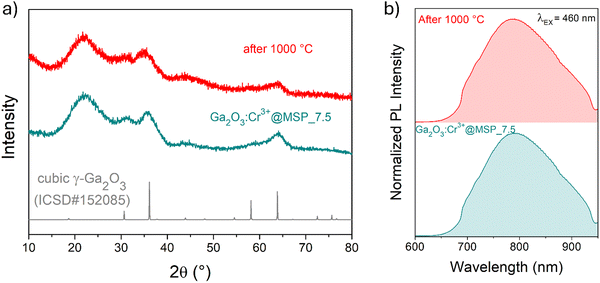
The cubic γ-Ga2O3 spinel phase is well known to undergo a phase transition to the β-phase at high temperature.39,64,65 In order to investigate the effect of the silica structure on the phase stability, the effect of thermal treatment at 1000 °C was studied by comparing the results of TG–DSC analysis with the XRPD and the PL spectral shape after the annealing.
The TG–DSC analysis on the γ-Ga2O3:Cr3+@MSP_7.5 system (Fig. S8, ESI†) evidences the lack of phase transitions in the range explored, up to 1000 °C and the thermal stability of the system. This is also confirmed by the XRPD analysis and the comparison of the PL spectra of the sample after the treatment. As clearly visible in Fig. 5a and b, the γ-phase is kept, suggesting that the phase transformation from γ to β recorded by Castro-Fernandez et al.39 at 550–750 °C for nanocrystals of about 2.5 nm is influenced by the size. Moreover, the silica structure can also play an important role. However, the stability of the γ-Ga2O3 spinel structure up to 1000 °C could be very important for instance for applications in high temperature catalysis.
Spectroscopic investigation and thermal stability of γ-Ga2O3:Cr3+ spinel nanocrystals
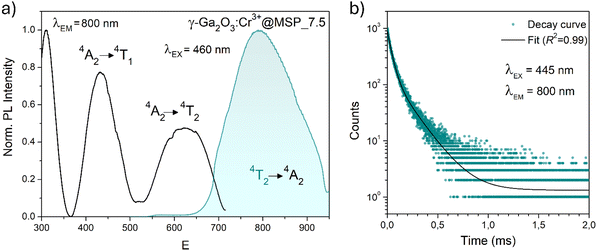
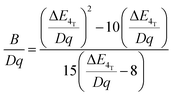
In order to investigate the effect of the local crystal site on the 3d3 electrons of Cr3+, spectroscopic investigation is performed. Fig. 6a shows the PL and PLE spectra of Cr3+ in the cubic γ-Ga2O3 spinel NCs. The PL spectrum is characterized by a broadband centered at about 792 nm and a FWHM of 2785 cm−1 due to the spin allowed 4T2 → 4A2 transition, typical of the weak crystal field materials, while the PLE spectrum is composed by the 4A2 → 4T2 and 4A2 → 4T1 transitions. It is well-known that to better understand the energy levels of transition metal ions in a crystal, the Tanabe–Sugano theory can be employed.66 The crystal field strength 10Dq and the Racah parameters B and C can be directly estimated from the excitation and emission band positions: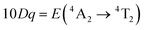 | (1) |
 | (2) |
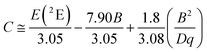 | (3) |
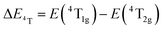 , the difference in energy between the 4T1g and 4T2g states. The energies of the 4A2 → 4T2 and 4A2 → 4T1 transition bands were estimated to be 15
, the difference in energy between the 4T1g and 4T2g states. The energies of the 4A2 → 4T2 and 4A2 → 4T1 transition bands were estimated to be 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 cm−1 and 22
873 cm−1 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 cm−1, respectively. The 10Dq and B parameters are therefore calculated to be 15
831 cm−1, respectively. The 10Dq and B parameters are therefore calculated to be 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 cm−1 and 720 cm−1, respectively, leading to a Dq/B of 2.2. This value is typical of the weak crystal field and smaller than the corresponding values for the rhombohedral α-Ga2O3:Cr3+ (2.9715) and monoclinic β-Ga2O3:Cr3+ (2.5815). In addition, a Stokes shift EStokes of 3247 cm−1 is estimated.
873 cm−1 and 720 cm−1, respectively, leading to a Dq/B of 2.2. This value is typical of the weak crystal field and smaller than the corresponding values for the rhombohedral α-Ga2O3:Cr3+ (2.9715) and monoclinic β-Ga2O3:Cr3+ (2.5815). In addition, a Stokes shift EStokes of 3247 cm−1 is estimated.
The PL decay curve of the spin-allowed 4T2 → 4A2 transition of the γ-Ga2O3:Cr3+ NCs evidences a double-exponential behavior (fitted by 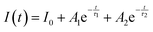 , where τi and Ai are the decay times and the corresponding amplitudes of the decay components) with an average decay time τave = (A1τ12 + A2τ22)/(A1τ1 + A2τ2) of 40 μs. The behaviour of the decay curve may be explained by considering the difference between the crystallographic sites in the core and the surface of the spinel NCs. In fact, for many oxide nanocrystals, it has been demonstrated that decreasing the size leads to a negative pressure at the surface, resulting in a deformation of the unit cell with a relative expansion with respect to the “bulk” core (e.g. MgO, CeO2, Co3O4, Fe3O4, Cu2O, Y2O3 and BaTiO367–71); stronger bonding at the core and a relaxation at the surface.71,72 Therefore, Cr3+ ions could be stabilized in two slightly different octahedral sites of the same γ-phase, at the core and the surface of the NCs, reflecting the bi-exponential behaviour of the decay curve. However, the lifetime estimated is consistent with the conventional microsecond lifetimes of the 4T2 excited state of Cr3+ ions. It is worth noting that recently, Zhao et al. reported a persistent luminescence behaviour in γ-Ga2O3:Cr3+ by co-doping with Ba2+.73
, where τi and Ai are the decay times and the corresponding amplitudes of the decay components) with an average decay time τave = (A1τ12 + A2τ22)/(A1τ1 + A2τ2) of 40 μs. The behaviour of the decay curve may be explained by considering the difference between the crystallographic sites in the core and the surface of the spinel NCs. In fact, for many oxide nanocrystals, it has been demonstrated that decreasing the size leads to a negative pressure at the surface, resulting in a deformation of the unit cell with a relative expansion with respect to the “bulk” core (e.g. MgO, CeO2, Co3O4, Fe3O4, Cu2O, Y2O3 and BaTiO367–71); stronger bonding at the core and a relaxation at the surface.71,72 Therefore, Cr3+ ions could be stabilized in two slightly different octahedral sites of the same γ-phase, at the core and the surface of the NCs, reflecting the bi-exponential behaviour of the decay curve. However, the lifetime estimated is consistent with the conventional microsecond lifetimes of the 4T2 excited state of Cr3+ ions. It is worth noting that recently, Zhao et al. reported a persistent luminescence behaviour in γ-Ga2O3:Cr3+ by co-doping with Ba2+.73
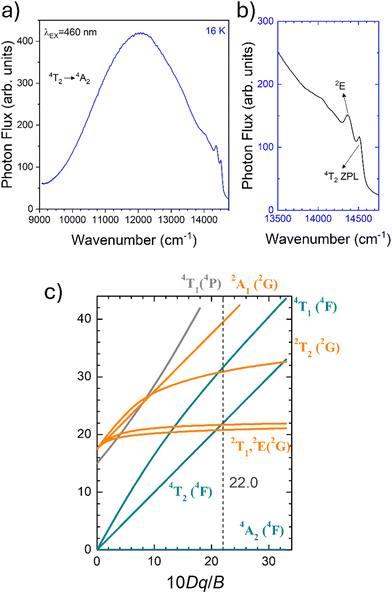
To fairly compare the effect of the environment of different compounds on the Cr3+ electrons, the Tanabe–Sugano diagram calculated for a specific C/B should be considered. To calculate the Racah parameter C, the 2E transition is necessary. However, it is not clearly visible in the RT spectra. The low temperature PL spectrum was measured at 16 K (Fig. 7a). The peaks at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and 14
500 cm−1 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 cm−1 were assigned to the 4T2 zero phonon line (ZPL) and the 2E, respectively (Fig. 7b). With the R-line value, the C parameter was calculated to be 3035 cm−1 and C/B = 4.21. Fig. 7c shows the Tanabe–Sugano diagram calculated for the specific C/B value.
365 cm−1 were assigned to the 4T2 zero phonon line (ZPL) and the 2E, respectively (Fig. 7b). With the R-line value, the C parameter was calculated to be 3035 cm−1 and C/B = 4.21. Fig. 7c shows the Tanabe–Sugano diagram calculated for the specific C/B value.
Fig. S9 (ESI†) shows a comparison of the PL and PLE spectra of Cr3+ in the γ-Ga2O3, β-Ga2O3 and α-Ga2O3 polymorphs, while Table 1 summarizes the main parameters estimated.
By considering the γ-Ga2O3 spinel structure characterized by the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) mZ space group reported by Zinkevich et al.36 (ICDS#152085), a single GaO6 octahedral site with an average 〈Ga–O〉 bond length of 2.0595 Å is present. The trends of the Dq/B parameter along with the Racah parameters B and C and therefore C/B can be explained taking into account the difference in the average 〈Ga–O〉 bond length of the octahedral site of the polymorphs. The weaker the bond (larger average 〈Ga–O〉) the larger the parameter B and the smaller Dq/B and C/B.
mZ space group reported by Zinkevich et al.36 (ICDS#152085), a single GaO6 octahedral site with an average 〈Ga–O〉 bond length of 2.0595 Å is present. The trends of the Dq/B parameter along with the Racah parameters B and C and therefore C/B can be explained taking into account the difference in the average 〈Ga–O〉 bond length of the octahedral site of the polymorphs. The weaker the bond (larger average 〈Ga–O〉) the larger the parameter B and the smaller Dq/B and C/B.
The temperature dependence of the PL spectra was investigated in the 16–500 K range (Fig. 8a). The integrated PL intensity as a function of temperature cannot be reproduced by the simple crossover quenching process described by the Struck and Fonger model.74 As for the case of Eu2+-75,76 or Bi3+-doped77 phosphors, a double quenching barrier model is employed:
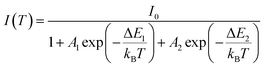 | (4) |
 | ||
| Fig. 8 (a) Temperature dependence of the PL emission spectra of γ-Ga2O3:Cr3+ NCs from 16 to 500 K (T). (b) Temperature dependence of the integrated PL intensity (black dots) and fit (red curve). (c) Configurational coordinate diagram constructed by using eqn (5)–(7). | ||
The two energy barriers can be associated with 2E → 4A2 (ΔE1) and 4T2 → 4A2 (ΔE2) thermal quenching at lower and higher temperatures, respectively. From the fitting curve, the ΔE1 activation energy was estimated to be 83 ± 11 cm−1, in agreement with the small energy difference between the 2E and the 4T2 ZPL (∼135 cm−1) evidenced in Fig. 8b. On the other hand, a value of 1590 ± 63 cm−1 was estimated for the ΔE2 activation energy related to the 4T2 → 4A2 thermal quenching.
In addition, the temperature at which the intensity of the 4T2 → 4A2 transition becomes 50% of that at low temperature, T50, is estimated to be 415 K. Comparing this value with those estimated for the α-Ga2O3:Cr3+ (580 K15) and β-Ga2O3:Cr3+ (480 K15) polymorphs, a clear trend is evidenced. Indeed, the larger the average 〈Ga–O〉 bond length of the octahedral site, the lower the T50.
The energetic distance ΔE′ between 4T2 and 2E electronic manifolds obtained for a fixed position of ligand ions at the minimum energy of the 2E parabola can be calculated as the sum of the energy difference ΔE between the minimum energy of the 4T2 and 2E states and the Sħω = EStokes/2 energy: ΔE′ = E0T − E0E = ΔE + Sħω.78 By considering this lattice relaxation energy Sħω, in the framework of the perturbation approach and adiabatic approximation,9,78 the configurational coordinate diagram is depicted in Fig. 8c by describing the ground state 4A2 and the excited states 2E and 4T2 as single parabolic potential curves79
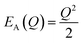 | (5) |
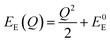 | (6) |
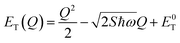 | (7) |
The configurational coordinate diagram confirms the very close position between the 2E and the 4T2 states, in agreement with the Tanabe–Sugano diagram. In addition, the PL spectral features of Cr3+ in the three polymorphs shown in Fig. S9 (ESI†) can be explained through the effect of the crystal field on the 3d3 electrons of Cr3+: the weaker crystal field in γ-Ga2O3 (Dq/B = 2.20) leads to the emission only from 4T2, while the intermediate crystal field in β-Ga2O3 (Dq/B = 2.58) and the stronger field in α-Ga2O3 (Dq/B = 2.97) lead to emissions from both the 4T2 and 2E states, with a relative increase in the spin-forbidden 2E → 4A2 sharp line with respect to the spin-allowed 4T2 → 4A2 broadband as the crystal field increases. This trend can also be understood by considering the average 〈Ga–O〉 bond length of the octahedral GaO6 sites in the three polymorphs reported in Table 1 (the larger the average 〈Ga–O〉, the smaller the Dq/B), in agreement with the multiplet energy level diagram as a function of Cr–O bond length calculated by Ogasawara et al.80 However, while the shift to a weaker crystal field in the Ga2O3 polymorphs leads to a red shift in the spin-allowed 4T2 → 4A2 transition, its thermal quenching becomes more severe, being characterized by a smaller T50.
Conclusions
In conclusion, this study has investigated the stabilization of Cr3+-doped γ-Ga2O3 NCs within mesoporous silica particles of various pore sizes. Through comprehensive physical–chemical analyses including XRPD, SEM/HR-TEM, N2 physisorption, and TG–DSC, the effects of size and temperature on the stabilization process were thoroughly examined. Spectroscopic analyses further elucidated the crystalline structure, confirming the stabilization of the cubic γ-Ga2O3 spinel structure. Moreover, detailed investigations of PL and PLE spectra, alongside temperature dependence studies in the 16–500 K range, provided valuable insights into the spectroscopic characteristics of Cr3+ within the γ-Ga2O3 matrix in the framework of Tanabe–Sugano theory, allowing the design of the configurational coordinate diagram. A comparison of the properties with respect to the β- and α-Ga2O3 polymorphs is provided. Importantly, the use of mesoporous silica particles as nanoreactors effectively stabilized the γ-Ga2O3:Cr3+ NCs, inhibiting the conventional phase transition to the β-phase up to 1000 °C, thus enhancing the stability of the γ-Ga2O3 phase.Experimental
Materials
Chromium nitrate nonahydrate (Cr(NO3)3·9H2O, 99%), cetyltrimethylammonium bromide (C16H33N(CH3)3Br, ≥98%), tetraethyl orthosilicate (Si(OC2H5)4, 98%), ethanol (EtOH, ≥99.97%), methanol (MeOH, ≥99.9%), n-hexane (C6H12, ≥99%), Pluronic P-123 and 1,3,5-trimethylbenzene (C9H12, 98%) were purchased from Sigma-Aldrich. Ammonium hydroxide (NH4OH, 28–30%) and sodium hydroxide (NaOH, 98%) were purchased from Applichem and gallium nitrate hydrate (Ga(NO3)3·xH2O, 98.9%) from Alfa Aesar.All the chemicals were of reagent grade and used without further purification.
Synthesis of MSPs of different pore sizes
MSPs characterized by an average pore size of 3.1 nm (MSP_3.1) were synthesized following the original work reported by Quiao et al.47 The MSNs were synthesized in a flask thermostated at 60 °C using an ionic surfactant for the formation of micelles. 145.2 mL of milliQ water, 5.73 g of cetyltrimethylammonium bromide (CTABr) and 22.8 mL of ethanol are dissolved under vigorous stirring; then 1.25 mL of ammonium hydroxide are added. After about 30 minutes of waiting, 14.6 mL of tetraethoxysilane (TEOS) are added with sustained dripping, then all is left to react for two hours, always with vigorous stirring. Once the synthesis is completed, the MSNs undergo centrifugal deposition cycles at 9000 rpm, elimination of solvent, washing and redispersion by ultrasound in milliQ water until total neutralization of pH. The last washing is carried out in ethanol. After washing, they are placed in an oven at 60 °C overnight to evaporate all the solvent, then they are ground in a mortar and calcined at 550 °C, with a rate of 2 °C min−1 for 6 hours.To prepare MSPs with pores a little larger (MSP_4.2), the procedure described by Ma et al.81 was followed. After solubilization of 0.8 g of CTABr and 3 mL of NaOH 2M in 400 mL of MilliQ water at room temperature, 60 mL of the swelling agent n-hexane was added. After 15 minutes of stirring, the mixture was stopped; then, 4 mL of TEOS were added after separation of the phases. The mixture was stirred again for 5 hours, filtered, washed several times with MeOH and dried at 60 °C overnight. MSNs were then ground in a mortar and calcined at 550 °C, with a rate of 2 °C min−1 for 5 hours.
SBA-15 MSPs with different pore size (MSP_7.5, MSP_13.5 and MSP_22.4) were synthesized following the procedures described in Zhao et al.61,82 and Cao.83 This synthesis was carried out in a 250 mL jacketed flask thermostat at 35 °C. The preparation takes place by dissolving 4 g of Pluronic P123 block copolymer (polyethylene oxide (EO) – polypropylene oxide (PO) – polyethylene oxide (EO) of formula EO20PO70EO20) in 30 mL of milliQ water and 116.5 mL of HCl 2M. At this point, for MSP_13.5 and MSP_22.4, the swelling agent trimethylbenzene (TMB) was added in 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 0.5
1 and 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w ratios, respectively. After 30 minutes, 9 mL of TEOS were added with sustained dripping; then the whole mixture was left to react for 20 hours. The suspension was then placed in hermetically sealed Teflon containers in autoclaves for an aging process in an oven at 100 °C for 24 hours. After cooling to room temperature, the MSNs were washed with deionized water until the pH was neutralized. The last washing was carried out in ethanol. They were then placed in an oven at 100 °C for 6 hours in order to evaporate all the solvent and then calcined in a muffle furnace at 550 °C.
1 w/w ratios, respectively. After 30 minutes, 9 mL of TEOS were added with sustained dripping; then the whole mixture was left to react for 20 hours. The suspension was then placed in hermetically sealed Teflon containers in autoclaves for an aging process in an oven at 100 °C for 24 hours. After cooling to room temperature, the MSNs were washed with deionized water until the pH was neutralized. The last washing was carried out in ethanol. They were then placed in an oven at 100 °C for 6 hours in order to evaporate all the solvent and then calcined in a muffle furnace at 550 °C.
Impregnation method and γ-Ga2O3:Cr3+ NC formation
The precipitation of Ga2O3:Cr3+ NCs into the MSP mesopores was conducted by incipient wetness impregnation at room temperature. The bare MSNs were dispersed in H2O, keeping the mixture under stirring. After 30 minutes, the aqueous solutions of the precursor nitrate salts were added at the appropriate amount to the dispersion with continuous stirring for 2 h. The powder was recovered through the removal of the solvent by means of a rotary evaporator and treated at 900 °C for 2 h.Silica etching
Silica etching was performed by placing the samples under stirring in a 2M NaOH solution for 2 h. After precipitation, the solvent was eliminated and the Ga2O3:Cr3+ NCs were dried at 60 °C overnight.Bulk α-Ga2O3:Cr3+ and β-Ga2O3:Cr3+ references
Gallium nitrate and chromium nitrate solutions were prepared using Ga(NO3)3·nH2O (n = 7–9) (99.9%) and Cr(NO3)3·9H2O (99.9%). The gallium and chromium solutions were stoichiometrically mixed to obtain Ga0.998Cr0.002O3. In order to precipitate the hydroxide, ammonia solution (28%) was dropped into the mixed solution until the pH reached 6, and then kept stirring for 1 h. The obtained precipitate was separated using a centrifuge and washed with water. The washed product was dried at 100 °C for 2 days and the dried powder was finally treated at 500 °C for 12 h and at 1000 °C for 2 h to obtain α-Ga2O3:Cr3+ and β-Ga2O3:Cr3+, respectively.Characterization
Structural and morphological analysis
XRPD measurements at high angles were performed by means of a Philips diffractometer with a PW 1319 goniometer with Bragg–Brentano geometry, equipped with a focusing graphite monochromator and a proportional counter with a pulse-height discriminator. Nickel-filtered Cu Kα radiation and a step-by-step technique were employed (steps of 0.05° in 2θ), with a collection time of 30 s per step. XRPD measurements at low angles were performed by means of an Empyrean Series 3 (Malvern Panalytical) diffractometer equipped with a Cu anode X-ray tube, Bragg–Brentano HD incident-beam optic, and PIXcel3D detector.Size and morphology determination of the nanoparticles and EDS analysis were carried out with a Carl Zeiss Sigma VP Field Emission Scanning Electron Microscope (FE-SEM) equipped with a Bruker Quantax 200 microanalysis detector, with an accelerating voltage from 5 to 20 kV.
The TEM images were taken at 300 kV with a JEOL 3010 instrument with an ultrahigh resolution (UHR) pole-piece (0.17 nm point resolution), equipped with a Gatan slow-scan CCD camera (model 794) and an Oxford Instrument EDS microanalysis detector (model 6636). The powdered samples were dispersed in isopropyl alcohol solution by sonication and then deposited onto a holey carbon film.
Nitrogen adsorption–desorption isotherms were collected at liquid nitrogen temperature using a Micrometrics ASAP 2010 system. Each sample was degassed at 130 °C overnight before the measurements. The Brunauer–Emmett–Teller (BET) equation was used to calculate the specific surface area from the adsorption data and the Barrett–Joyner–Halenda (BJH) model was used to estimate the pore-size distribution from the adsorption branches of the isotherms.
The determination of gallium (Ga) and chromium (Cr) concentrations was conducted using Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES). In the procedure, approximately 10 mg of the sample was transferred into a 50 mL polypropylene (PP) tube. The sample was then subjected to mineralization with 20 mL of aqua regia (a mixture of ultra-pure hydrochloric acid and nitric acid in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) through sonication for 2 hours at 25 °C, using a frequency of 40 kHz at 80% intensity (CP104 model from CEIA, Arezzo). This step was followed by mechanical stirring overnight at 100 rpm (VDRL 711 Opto-lab, Modena). Subsequently, the mineralized sample was diluted to a final volume of 50 mL using Milli-Q water (with a resistivity of 18 MΩ cm) and stored at 4 °C. Prior to analysis, the sample was further diluted twofold with Milli-Q water. Alongside the samples, a procedural blank was also prepared for comparison. The analysis itself was performed on an iCAP 7000 Plus instrument (Thermo Scientific, Bremen), which is equipped with a glass concentric nebulizer and a cyclonic spray chamber made of glass. The detection of Ga and Cr was executed in axial mode, targeting their emission lines at 283.563 nm and 294.364 nm, respectively. Quantification of these elements was achieved through external calibration using mono-elemental standard solutions (provided by UltraScientific, Milan). Five replicates of blanks, standards, and sample measurements were taken and averaged.
1 volume ratio) through sonication for 2 hours at 25 °C, using a frequency of 40 kHz at 80% intensity (CP104 model from CEIA, Arezzo). This step was followed by mechanical stirring overnight at 100 rpm (VDRL 711 Opto-lab, Modena). Subsequently, the mineralized sample was diluted to a final volume of 50 mL using Milli-Q water (with a resistivity of 18 MΩ cm) and stored at 4 °C. Prior to analysis, the sample was further diluted twofold with Milli-Q water. Alongside the samples, a procedural blank was also prepared for comparison. The analysis itself was performed on an iCAP 7000 Plus instrument (Thermo Scientific, Bremen), which is equipped with a glass concentric nebulizer and a cyclonic spray chamber made of glass. The detection of Ga and Cr was executed in axial mode, targeting their emission lines at 283.563 nm and 294.364 nm, respectively. Quantification of these elements was achieved through external calibration using mono-elemental standard solutions (provided by UltraScientific, Milan). Five replicates of blanks, standards, and sample measurements were taken and averaged.
Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) have been performed with a Netzsch STA 409C in air from 30 to 1000 °C at a heating rate of 10 °C min−1. The instrument was purged with a mixture of air and N2 at a 40 mL min−1 flow rate. The analysis was performed with an alumina crucible for compatibility. Alumina was used for internal calibration. Three replicates were performed for each sample. Data were collected with STA Netzsch software.
Spectroscopic measurements and temperature-dependent photoluminescence
PL emission and PLE excitation spectra were obtained using a Horiba–Jobin Yvon Fluorolog 3–21 spectrofluorometer. The photoluminescence spectra were collected by exciting the samples by means of a xenon arc lamp (450 W), selecting the excitation wavelength using a double Czerny–Turner monochromator and collecting with a R928 PMT (Hamamatsu) and a QEPro-XR (Ocean Insight). All spectra were recorded at RT under the same conditions.Time-resolved PL measurements were carried out under excitation at 445 nm using a pulsed SpectraLED (Horiba Scientific) through the Fluorolog-Time Correlated Single Photon Counting system.
The temperature dependence of PL spectra (16–500 K) was investigated with a cryostat (Janis ST-500, Lake Shore Cryotronics., Inc.), exciting with a 450 nm LD and collecting using a Hamamatsu PMA-12 CCD (C10027-02). All the spectra were calibrated using a standard halogen lamp (DH-2000CAL, Ocean Optics) to obtain spectra in the photon flux scale. In addition, the photon flux per constant wavelength interval function, ϕ(λ), is converted to photon flux per energy interval by using the Jacobian transformation.
Author contributions
All authors discussed and contributed to the interpretation of the results and the final manuscript. M. B. conceived the presented idea. M. B., J. X., P. R. and A. B. planned the experiments. M. C., M. B. and A. S. prepared the samples. M. B., M. C., C. B., J. X., T. N., J. U., F. D., E. B. and D. C. carried out the experiments. M. B. supervised the project. A. B., S. T., T. N. and F. R. helped supervise the project. M. B. wrote the manuscript with support from M. C., P. R. and A. B.Data availability
The data supporting this article are provided in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work by M. B. was financially supported by FY2022 JSPS Invitational Fellowships for Research in Japan (S22088) and the CATHENA project funded by the FVG Region POR-FESR 2014-2020 program (CUP: J34I17000010006). This work has benefited from the infrastructural support of the Centre for Trace Analysis (CeTrA) of Ca’ Foscari University through the project IR0000032 – ITINERIS, Italian Integrated Environmental Research Infrastructures System, funded by EU – Next Generation EU, PNRR.The authors acknowledge Mr Tiziano Finotto and Dr Martina Marchiori for the XRPD and absorption/desorption measurements, respectively.
Notes and references
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef
.
- T. Maldiney, A. Bessiere, J. Seguin, E. Teston, S. K. Sharma, B. Viana, A. J. J. Bos, P. Dorenbos, M. Bessodes, D. Gourier, D. Scherman and C. Richard, Nat. Mater., 2014, 13, 418–426 CrossRef CAS PubMed
.
- A. Bessiere, S. K. Sharma, N. Basavaraju, K. R. Priolkar, L. Binet, B. Viana, A. J. J. Bos, T. Maldiney, C. Richard, D. Scherman and D. Gourier, Chem. Mater., 2014, 26, 1365–1373 CrossRef CAS
.
- J. Ueda, P. Dorenbos, A. J. J. Bos, K. Kuroishi and S. Tanabe, J. Mater. Chem. C, 2015, 3, 5642–5651 RSC
.
- Y. Zhuang, Y. Katayama, J. Ueda and S. Tanabe, Opt. Mater., 2014, 36, 1907–1912 CrossRef CAS
.
- J. Xu, J. Ueda, Y. Zhuang, B. Viana and S. Tanabe, Appl. Phys. Express, 2015, 8, 042602 CrossRef
.
- Y. Katayama, H. Kobayashi and S. Tanabe, Appl. Phys. Express, 2015, 8, 012102 CrossRef CAS
.
- M. Back, E. Trave, J. Ueda and S. Tanabe, Chem. Mater., 2016, 28, 8347–8356 CrossRef CAS
.
- M. Back, J. Ueda, M. G. Brik, T. Lesniewski, M. Grinberg and S. Tanabe, ACS Appl. Mater. Interfaces, 2018, 10, 41512–41524 CrossRef CAS PubMed
.
- M. Back, J. Ueda, J. Xu, K. Asami, M. G. Brik and S. Tanabe, Adv. Opt. Mater., 2020, 8, 2000124 CrossRef CAS
.
- A. Kabanski, M. Ptak and D. Stefanska, ACS Appl. Mater. Interfaces, 2023, 15, 7074–7082 CrossRef CAS PubMed
.
- Z. Ristic, V. Dordevic, M. Medic, S. Kuzman, M. G. Brik, Z. Antic and M. D. Dramicanin, Opt. Mater., 2021, 120, 111486 CrossRef
.
- M. Back, J. Ueda, M. G. Brik and S. Tanabe, ACS Appl. Mater. Interfaces, 2020, 12, 38325–38332 CrossRef CAS PubMed
.
- J. Ueda, M. Back, M. G. Brik, Y. Zhuang, M. Grinberg and S. Tanabe, Opt. Mater., 2018, 85, 510–516 CrossRef CAS
.
- M. Back, J. Ueda, H. Nambu, M. Fujita, A. Yamamoto, H. Yoshida, H. Tanaka, M. G. Brik and S. Tanabe, Adv. Opt. Mater., 2021, 9, 2100033 CrossRef CAS
.
- R. A. Forman, G. J. Piermarini, J. D. Barnett and S. Block, Science, 1972, 176, 284–285 CrossRef CAS PubMed
.
- G. J. Piermarini, S. Block, J. D. Barnett and R. A. Forman, J. Appl. Phys., 1975, 46, 2774–2780 CrossRef CAS
.
- H. K. Mao, P. M. Bell, J. W. Shaner and D. J. Steinberg, J. Appl. Phys., 1978, 49, 3276–3283 CrossRef CAS
.
- M. Back, J. Ueda, H. Hua and S. Tanabe, Chem. Mater., 2021, 33, 3379–3385 CrossRef CAS
.
- M. Szymczak, P. Wozny, M. Runowski, M. Pieprz, V. Lavin and L. Marciniak, Chem. Eng. J., 2023, 453, 139632 CrossRef CAS
.
- I. Widmann, G. Kinik, M. Jahnig, R. Glaum, M. Schwarz, C. Wustefeld, D. Johrendt, M. Tribus, C. Hejny, L. Bayarjargal, L. Dubrovinsky, G. Heymann, M. Suta and H. Huppertz, Adv. Funct. Mater., 2024, 2400054 CrossRef
.
- R.-J. Xie, Light: Sci. Appl., 2020, 9, 155 CrossRef PubMed
.
- M. Mao, T. Zhou, H. Zeng, L. Wang, F. Huang, X. Tang and R.-J. Xie, J. Mater. Chem. C, 2020, 8, 1981–1988 RSC
.
- G. N. A. De Guzman, M.-H. Fang, C.-H. Liang, Z. Bao, S.-F. Hu and R.-S. Liu, J. Lumin., 2020, 219, 116944 CrossRef CAS
.
- S. J. Pearton, J. Yang, P. H. CaryIV, F. Ren, J. Kim, M. J. Tadjer and M. A. A. Mastro, Appl. Phys. Rev., 2018, 5, 011301 Search PubMed
.
- R. Roy, V. G. Hill and E. F. Osburn, J. Am. Chem. Soc., 1952, 74, 719 CrossRef CAS
.
- H. H. Tippins, Phys. Rev., 1965, 137, A865 CrossRef
.
- D. Vivien, B. Viana, A. Revcolevschi, J. D. Barrie, B. Dunn, P. Nelson and O. M. Stafsudd, J. Lumin., 1987, 39, 29 CrossRef CAS
.
- C. G. Walsh, J. F. Donegan, T. J. Glynn, G. P. Morgan, G. F. Imbusch and J. P. Remeika, J. Lumin., 1988, 40–41, 103 CrossRef CAS
.
- Y. Tokida and S. Adachi, J. Appl. Phys., 2012, 112, 063522 CrossRef
.
- A. Segure, L. Artus, R. Cuscó, R. Goldhahn and M. Feneberg, Phys. Rev. Mater., 2017, 1, 024604 CrossRef
.
- M.-H. Fang, G. N. A. De Guzman, Z. Bao, N. Majewska, S. Mahlik, M. Grinberg, G. Leniec, S. M. Kaczmarek, C.-W. Yang, K.-M. Lu, H.-S. Sheu, S.-F. Hu and R.-S. Liu, J. Mater. Chem. C, 2020, 8, 11013–11017 RSC
.
- H. Yusa and M. Miyakawa, Inorg. Chem., 2024, 63, 2695–2700 CrossRef CAS PubMed
.
- M.-H. Fang, K.-C. Chen, N. Majewska, T. Lesniewski, S. Mahlik, G. Leniec, S. M. Kaczmarek, C.-W. Yang, K.-M. Lu, H.-S. Sheu and R.-S. Liu, ACS Energy Lett., 2021, 6, 109–114 CrossRef CAS
.
- K.-C. Chen, M.-H. Fang, W.-T. Huang, M. Kaminski, N. Majewska, T. Lesniewski, S. Mahlik, G. Leniec, S. M. Kaczmarek, C.-W. Yang, K.-M. Lu, H.-S. Sheu and R.-S. Liu, Chem. Mater., 2021, 33, 3832–3840 CrossRef CAS
.
- M. Zinkevich, F. M. Morales, H. Nitsche, M. Ahrens, M. Ruehle and F. Aldiger, Z. Metallkd., 2004, 95, 756–762 CrossRef CAS
.
- H. Y. Playford, A. C. Hannon, E. R. Barney and R. I. Walton, Chem. – Eur. J., 2013, 19, 2803–2813 CrossRef CAS PubMed
.
- H. Y. Playford, A. C. Hannon, M. G. Tucker, D. M. Dawson, S. E. Ashbrook, R. J. Kastiban, J. Sloan and R. I. Walton, J. Phys. Chem. C, 2014, 118, 16188–16198 CrossRef CAS
.
- P. Castro-Fernandez, M. V. Blanco, R. Verel, E. Willinger, A. Fedorov, P. M. Abdala and C. R. Müller, J. Phys. Chem. C, 2020, 124, 20578–20588 CrossRef CAS
.
- L. E. Ratcliff, T. Oshima, F. Nippert, B. M. Janzen, E. Kluth, R. Goldhahn, M. Feneberg, P. Mazzolini, O. Bierwagen and C. Wouters,
et al.
, Adv. Mater., 2022, 34, 2204217 CrossRef CAS PubMed
.
- N. V. Golubev, E. S. Ignat’eva, V. N. Sigaev, A. Lauria, L. De Trizio, A. Azarbod, A. Paleari and R. Lorenzi, Phys. Chem. Chem. Phys., 2015, 17, 5141–5150 RSC
.
- R. Lorenzi, N. V. Golubev, E. S. Ignat’eva, V. N. Sigaev, C. Ferrara, M. Acciarri, G. M. Vanacore and A. Paleari, J. Colloid Interface Sci., 2022, 608, 2830–2838 CrossRef CAS PubMed
.
- Z. Yang, L. X. Song, Y. Q. Wang, M. M. Ruan, Y. Teng, J. Xia, J. Yang, S. S. Chen and F. Wang, J. Mater. Chem. A, 2018, 6, 2914–2921 RSC
.
- P. Castro-Fernandez, D. Mance, C. Liu, I. B. Moroz, P. M. Abdala, E. A. Pidko, C. Copéret, A. Fedorov and C. R. Müller, ACS Catal., 2021, 11, 907–924 CrossRef CAS
.
- T. Wang, S. S. Farvid, M. Abulikemu and P. V. Radovanovic, J. Am. Chem. Soc., 2010, 132, 9250–9252 CrossRef CAS PubMed
.
- T. Wang, V. Chirmanov, W. H. M. Chiu and P. V. Radovanovic, J. Am. Chem. Soc., 2013, 135, 14520–14523 CrossRef CAS PubMed
.
- Z. A. Qiao, L. Zhang, M. Guo, Y. Liu and Q. Huo, Chem. Mater., 2009, 21, 3823–3829 CrossRef CAS
.
- C. Xin, N. Zhao, H. Zhan, F. Xiao, W. Wie and Y. Sun, J. Colloid Interface Sci., 2014, 433, 176–182 CrossRef CAS PubMed
.
- T. Lu, X. D. Yao, G. Q. Lu and Y. He, J. Colloid Interface Sci., 2009, 336, 368–373 CrossRef CAS PubMed
.
-
J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 1985 Search PubMed
.
- T. Shimizu, M. Masuda and H. Minamikawa, Chem. Rev., 2005, 105, 1401–1444 CrossRef CAS PubMed
.
- Y. Yoshioka, H. Hayashi, A. Kuwabara, F. Oba, K. Matsunaga and I. Tanaka, J. Phys.: Condens. Matter, 2007, 19, 346211 CrossRef
.
- J. Zhao, J. Byggmastar, H. He, K. Nordlund, F. Djurabekova and M. Hua, npj Comput. Mater., 2023, 9, 159 CrossRef CAS
.
- C. B. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715 CrossRef CAS
.
- D. V. Talapin, A. L. Rogach, A. Kornowski, M. Haase and H. Weller, Nano Lett., 2001, 1, 207–211 CrossRef CAS PubMed
.
- R. C. Garvie, J. Phys. Chem., 1965, 69, 1238–1243 CrossRef CAS
.
- P. Ayyub, V. R. Palkar, S. Chattopadhyay and M. Multani, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6135–6138 CrossRef CAS PubMed
.
- M.-H. Fang, T.-Y. Li, W.-T. Huang, C.-L. Cheng, Z. Bao, N. Majewska, S. Mahlik, C.-W. Yang, K.-M. Lu, G. Leniec, S. M. Kaczmarek, H.-S. Sheu and R.-S. Liu, ACS Energy Lett., 2021, 6, 659–664 CrossRef CAS
.
- J. Wang, X. Guan, H. Zheng, L. Zhao, R. Jiang, P. Zhao, Y. Zhang, J. Hu, P. Li, S. Jia and J. Wang, Nano Lett., 2023, 23, 7364–7370 CrossRef CAS PubMed
.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CrossRef CAS
.
- D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279, 548–552 CrossRef CAS PubMed
.
- M. Kruk, M. Jaroniec, C. H. Ko and R. Ryoo, Chem. Mater., 2000, 12, 1961–1968 CrossRef CAS
.
- G. Sponchia, R. Marin, I. Freris, M. Marchiori, E. Moretti, L. Storaro, P. Canton, A. Lausi, A. Benedetti and P. Riello, J. Nanopart. Res., 2014, 16, 2245 CrossRef
.
- C. Wouters, M. Nofal, P. Mazzolini, J. Zhang, T. Remmele, A. Kwasniewski, O. Bierwagen and M. Albrecht, APL Mater., 2024, 12, 011110 CrossRef CAS
.
- X. Zhang, H. Huang, Y. Zhang, D. Liu, N. Tong, J. Lin, L. Chen, Z. Zhang and X. Wang, ACS Omega, 2018, 3, 14469–14476 CrossRef CAS PubMed
.
- Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766 CrossRef CAS
.
- S.-W. Chan and W. Wang, Mater. Chem. Phys., 2021, 273, 125091 CrossRef CAS
.
- V. Perebeinos, S.-W. Chan and F. Zhang, Solid State Commun., 2002, 123, 295–297 CrossRef CAS
.
- G. Kimmel, A. Sahartov, Y. Sadia, Z. Porat, J. Zabicky and E. Dvir, J. Mater. Res. Technol., 2021, 12, 87–99 CrossRef CAS
.
- C. Beck, K. H. Ehses, R. Hempelmann and C. Bruch, Scr. Mater., 2001, 44, 2127–2131 CrossRef CAS
.
- M. Fukuhara, Phys. Lett. A, 2003, 313, 427–430 CrossRef CAS
.
- M. Leoni, Mater. Sci. Forum, 2004, 443–444, 1–10 CAS
.
- T. Zhao, R. Abdurahman, Q. Yang, R. Aiwaili and X.-B. Yin, J. Mater. Chem. C, 2024, 12, 498–507 RSC
.
- C. W. Struck and W. H. Fonger, J. Appl. Phys., 1971, 42, 4515–4516 CrossRef CAS
.
- P. F. Smet, J. E. Van Haecke, F. Loncke, H. Vrielinck, F. Callens and D. Poelman, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035207 CrossRef
.
- S. Mahlik, K. Wisniewski, M. Grinberg and R. S. Meltzer, J. Phys.: Condens. Matter, 2009, 21, 245601 CrossRef CAS PubMed
.
- M. Back, J. Ueda, J. Xu, K. Asami, L. Amidani, E. Trave and S. Tanabe, J. Phys. Chem. C, 2019, 123, 14677–14688 CrossRef CAS
.
- M. Grinberg and A. Suchoucki, J. Lumin., 2007, 125, 97–103 CrossRef CAS
.
- M. Grinberg and T. Lesniewski, J. Lumin., 2019, 214, 116574 CrossRef CAS
.
- K. Ogasawara, F. Alluqmani and H. Nagoshi, ECS J. Solid State Sci. Technol., 2016, 5, R3191 CrossRef CAS
.
- S. Ma, Y. Wang and Y. Zhu, J. Porous. Mater., 2011, 18, 233–239 CrossRef CAS
.
- D. Zhao, Q. Huo, J. Feng, B. F. Chmelka and G. D. Stucky, J. Am. Chem. Soc., 1998, 120, 6024–6036 CrossRef CAS
.
- L. Cao, T. Man and M. Kruk, Chem. Mater., 2009, 21, 1144–1153 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc01386g |
| This journal is © The Royal Society of Chemistry 2024 |