Understanding and tackling the activity and selectivity issues for methane to methanol using single atom alloys

Abstract

The process for the direct oxidation of methane to methanol is investigated on single atom alloys using density functional theory. A catalyst search is performed across FCC metal single atom alloys. 7 single atom alloys are found as candidates and microkinetic modelling is performed. The activity and selectivity are remarkably improved over that of pure palladium metal, yet remain unideal.

---

The industrial scale conversion of methane to methanol remains to be via syn-gas production, despite ongoing research to find a direct route.¹ There are several issues innate to the reaction that hinder development.

A great variety of oxidation catalysts are available, such as Li-doped MgO.² The simplest class of heterogeneous catalysts, metals, are adept oxidation catalysts.³ Yet, they make poor catalysts for the selective oxidation of methane to methanol due to the indiscriminate oxidation of carbonaceous species. Even if methanol was to form as an intermediate species, it would subsequently be completely oxidised to CO₂.

Clever stepwise approaches to overcome selectivity issues have been developed. The first notable example of overcoming this key issue is the Periana-Catalytica system.⁴ Instead of forming the more reactive methanol product directly, a less reactive methyl bisulphate is first formed. This methyl bisulphate can subsequently be converted into methanol in a secondary step. Another stepwise approach is the implementation of a Cu/Fe zeolite system.^5,6 A pre-reaction oxidation step is required to form the catalytically active metal oxo species. Methane is subsequently activated and oxidised, yet the product remains adsorbed to the metal centre, being unable to be further oxidised. For methanol to be liberated, the catalyst must first be washed with water. For more methanol to be formed, the stepwise process must be restarted. This stepwise nature of the processes restricts the turnover frequency of the catalysts used.

Some developed methane to methanol catalysts offer a non-stepwise approach. These catalysts are often novel materials, such as single atom platinum group metals supported on zeolites⁷ and gold-palladium colloids.⁸ Arguably, these are the most promising form of an industrially viable methane to methanol catalyst as they are non-stepwise systems. Unfortunately, only milli to micromolar amounts of methanol product are typically formed.

For the possibility of further development and intelligent catalyst design, a comprehensive understanding of the methane to methanol system is required with atomic level resolution. This is possible through a theoretical deconstruction of this process, with consideration of important elementary steps and potential avenues for selectivity loss for this system being required. Once key causes of selectivity loss and poor reactivity are identified, a rational catalyst design and search can begin. In this work, the following are considered: (i) deducing the main elementary steps where selectivity is lost for metal systems; (ii) understanding origins of selectivity issues and finding methods for improving them; and (iii) the design and subsequent modelling of efficient single atom alloy catalysts for the methane to methanol process.

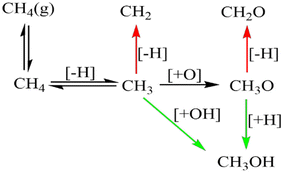
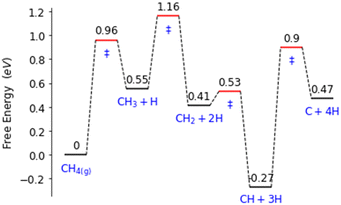
Palladium, a good total oxidation catalyst, is used in this work as an initial theoretical model for studying methanol formation to understand which steps cause significant selectivity loss.⁹ Other surfaces such as platinum are also possible as an initial model.¹⁰ We initially perform DFT calculations to explore key elementary steps involved with the partial oxidation and total oxidation of methane to methanol and CO₂, respectively, on the most dominant Pd(111) surface. Namely, the free energy profiles of C–H bond activation (Fig. 1) and C–O/OH bond formation (Fig. 2) for the carbonaceous species CH_0–4 were calculated. Details of our computational methods can be found in S1 (ESI†).

Fig. 1 Free energy landscape for the activation and subsequent dehydrogenation of methane on the Pd(111) surface. Transition states are denoted with ‘‡’.

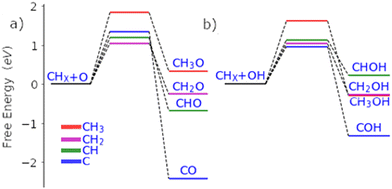Fig. 2 Free energy pathways for the carbon–oxygen coupling steps of all possible surface C₁ species (CH_0-3) with O (a) and OH (b) on the Pd(111) surface.

If methane is to be oxidised, methane must first undergo C–H activation. This is why much focus has been placed on this key elementary step.⁹ However, after methane activation, several reaction pathways are available with a large variety of potential intermediate surface species (Fig. 1 and 2). Ideally for methanol formation, the formed surface methyl species would couple with OH surface species to form methanol directly, as shown in Fig. 2b. Likewise, formed surface methyl species can couple with oxygen to yield a methoxy intermediate as shown in Fig. 2a, which can readily hydrogenate in a quick step to form the methanol product.

Along these ideal pathways, opportunities for unwanted side reactions leading to a loss in selectivity are possible. The formed surface CH₃ species can undergo further dehydrogenation into the other significantly more stable carbonaceous surface species (Fig. 1). We find that surface CH is the most stable species, being 0.81 eV more stable than surface CH₃. CH₂ and C surface species are slightly more stable than the CH₃ species by 0.14 eV and 0.08 eV, respectively. Unfortunately for selectivity purposes, we observe that all CH_X species are more stable than surface CH₃, and this is without consideration for the additional thermodynamic potential from the oxidation of surface hydrogen, which would drive the equilibrium further towards dehydrogenated carbonaceous species. These more stable carbonaceous species would subsequently be oxidised into CO₂, being unlikely to hydrogenate into methanol product under oxidative conditions, following the known dominant pathway for methane total oxidation.¹¹

In addition to being more stable, we also find that the oxidation of other C₁ surface species is also kinetically more accessible compared to the oxidation of CH₃ surface species (Fig. 2). Due to the reasonably strong exergonic nature of most of the oxidation steps of CH_X species, the steps of O and OH coupling with CH_X species can be regarded as largely irreversible with little opportunity for CH_0–2O/CH_0–2OH species to form methanol due to the very low hydrogen surface coverage under oxidative conditions. The final option for surface methyl groups is to simply hydrogenate back to form the methane reactant.

In regard to the significance of specific steps for building a microkinetic model for the selective oxidation of methane to methanol, the following particular steps standout. Firstly, the endergonicity of the free energy change for methane activation should be minimised to ensure greater methyl surface coverage. Secondly, the formation of CH₂ from surface CH₃ should be suppressed. Thirdly, the C–O/OH coupling step for CH₃ with OH/O should be more kinetically accessible to increase the rate of methanol formation. Additionally, further dehydrogenated carbonaceous species on the surface are more reactive than methyl species for C–O/OH coupling, if dehydrogenation of CH₃ occurs to CH₂, the reaction is unlikely to form methanol.

With the aforementioned steps being considered, a microkinetic model can be made (Fig. 3). The formation of surface CH₂ from CH₃, and formaldehyde from CH₃O are modelled as key points of selectivity loss. To reflect the more readily oxidizable nature of other carbonaceous species over CH₃, whilst respecting the reversible nature of CH₃ dehydrogenation and CH₂ hydrogenation, an irreversible step for the immediate removal of CH₂ from the system is modelled. The barrier for this irreversible CH₂ removal step is based on the low effective activation energy of 0.52 eV for the surface CH oxidation with respect to surface CH₂ on Pd(111). For the formaldehyde formation from a surface methoxy species, the actual desorption step is calculated and considered. A total of 15 key elementary steps for methanol formation and selectivity are considered. This is a manageable task in respect to the 35 elementary steps that must be considered for a complete combustion model.

Fig. 3 The reaction pathway considered for a streamlined microkinetic model to reasonably describe the selectivity and reactivity for the selective oxidation of methane to methanol. Steps that are considered as pathways for selectivity loss are marked with red.

The purpose of a streamlined microkinetic model is to minimise the number of steps required to be considered, allowing catalysts proposed by other high throughput parameter search methods to be authenticated. To validate this conjecture, we calculate a complete microkinetic model for the partial oxidation and total oxidation of methane to methanol and CO₂, respectively and compare it to the streamlined microkinetic model (S2, ESI†).

The complete and streamlined microkinetic models give reasonably similar results for both reactivity and selectivity towards methanol formation, with an 11% error for total methanol formation rate and with negligible errors for the total rate of methane consumption (S2, ESI†). As expected for a pure metal, both the selectivity and rate towards methanol production are extremely poor. Effectively, all selectivity loss is found via further dehydrogenation of surface CH₃ (molar fraction of 1.00), with a very minor loss observed via methoxy intermediate dehydrogenation (10⁻⁴). Only extreme trace amounts of methanol are formed (10⁻¹⁸) with respect to over oxidation, also matching the selectivity findings of other microkinetic models.¹¹ Methane adsorption is found to be relatively weak as observed in other work.¹⁰ It should be noted that for a more accurate overall rate of reaction to be calculated, the coverage effect should also be considered.¹²

Pertaining to the oxidation of methane for the pure metal system, we find that the dehydrogenation of CH₃ surface species is the main pathway for methanol selectivity loss. If this step can be made less kinetically favoured, methanol formation would be enhanced. The ensemble effect of pure metals is the dominant reason for further dehydrogenation of activated methane. An example of the removal of this effect is single atom-based catalysts.¹³ Single atom alloys (SAAs), where doped single atoms are part of a host metal surface, are a demonstrated class of catalysts that remove the ensemble effect. The design space is rigid, with the number of single atom alloys related to the number of possible metals selected, giving M²-M possible SAA surfaces.

With this considered, SAAs were chosen as the design space for our catalyst search. FCC group metals were selected to be studied to prevent issues with changing the crystal structure for different SAAs. Ag, Au, Cu, Ir, Ni, Pd, Pt, and Rh were chosen as the periodically contiguous metallic elements for investigation with good alloyability.¹⁴ This offers 56 SAA surfaces and 8 pure metal surfaces to be examined. The most stable (111) surface was chosen. The adsorption energies of CH₃ and CH₂ were calculated for all 64 surfaces (S3, ESI†). If adsorption of CH₃ is stronger on the pure host metal than the single atom alloy site, the SAA is removed from the catalyst search. This is due to the reaction being more likely to take place on the host metal instead of at the SAA site.

The key steps that define a catalyst's performance are the methane activation and surface methyl dehydrogenation. A more favoured methane activation step and a more disfavoured methyl dehydrogenation step are the indicators of a reactive and selective catalyst. Key parameters must be chosen to efficiently approximate the energy barrier for each of these elementary steps. For each of these steps, the explicitly calculated activation energy barriers for pure metal surfaces are related to the adsorption energies of different species (S3, ESI†).

For methane activation, the activation energy was defined as a function of CH₃ adsorption and not the final state CH₃ + H adsorption energy to give a linear relationship (S3.2, ESI†). This is due to a traditional Brønsted–Evans–Polanyi (BEP) relationship not being followed for SAAs.¹⁵ The activation of methane occurs mostly over one atom, whilst the final state involves hydrogen coordination with the dopant atom and two host metals atoms (S3.3, ESI†). Whilst methane activation can typically be described as a function of CH₃ and H adsorption for surface stabilized pathways, logically, this will not be followed for SAAs due to the nature of C–H bond breakage being mainly at the single metal atom that is being activated across. For the dehydrogenation of CH₃ to CH₂, the adsorption of CH₃ and CH₂ are considered. The less favoured the CH₂ formation is with respect to CH₃ formation, the more desirable it is for the C₁ species to remain in the CH₃ state.

Certain cut-off activation energies were selected for the predicted methane activation and CH₃ dehydrogenation energy barriers. This is to limit the number of single atom alloy candidates to a manageable number. For reference, our model of Pd(111) having an activation energy barrier of 0.74 eV, a predicted methane activation energy of 1 eV was selected as the highest predicted barrier as to not restrict CH₃ surface formation. For CH₃ undergoing further dehydrogenation to CH₂, an energy barrier of 0.78 eV is found for our model of Pd(111). Ideally, a barrier over 1 eV will be found for this step to reduce the amount of further dehydrogenated carbonaceous surface species forming.

With these catalyst search restrictions, 7 viable catalysts were found: Ag or Au doped with Ir, Pt, or Rh; and Cu diffusely alloyed with Pt. From a logical standpoint, the catalyst search suggesting these SAAs makes sense. A strongly coordinating metal atom is required for the activation of methane – metals that can readily activate methane in their pure metal state. Regarding the host metals, silver and gold are relatively inert metals that do not strongly adsorb surface species. With CH₂ coordinated to two metal atoms on the surface (unlike CH₃ coordinated only to one), if the host atom is an inert atom, the preference can be driven towards CH₃ being the dominant C₁ surface species.

Throughout the rest of this work, the SAAs will be noted in the form of ‘Dopant–Host’ as in other work.¹³ Ir–Ag and Ir–Au are predicted by the model to have the lowest barriers for methane activation, with very low predicted barriers of 0.39 eV and 0.36 eV, respectively (S4, ESI†). For selectivity against further dehydrogenation of surface CH₃ species, Ir–Ag, Pt–Ag, and Rh–Ag are predicted to have CH₃ dehydrogenation barriers greater than 1.5 eV. However, as the activity and selectivity of a catalyst depends on the concentration of different surface species among other factors, coupled with the inaccuracies of SAAs to be described by BEP-like relationships, explicit calculations of enthalpies and energy barriers are required for each important elementary step. The streamlined microkinetic model (Fig. 3) is calculated for all 7 plausible SAAs catalysts suggested by the catalyst search (S4, ESI†). These results are then compared to the activity and selectivity found for Pd(111).

All of the SAAs are found to be several orders more reactive than Pd(111) (Fig. 4). The most reactive catalyst, Pt–Au, was modelled to have a reactivity that was 10²⁴ times greater than that of palladium metal. It is worth noting that these are the results from the kinetic calculations without coverage effects and to include the coverage effects might significantly reduce the activity difference.¹⁰ The enhanced reactivity of the SAAs is due to surface oxygen not over bonding to the surface, minimizing the C–O bond formation elementary steps. Despite all SAAs having higher rates of methanol production over those found for palladium metal, some of the SAAs selectivities are worse compared to the already bad pure metal surface, namely for Ir–Ag, Pt–Ag, and Pt–Cu. Only one SAA has a somewhat appreciable selectivity towards methanol (Rh–Au), with a selectivity of 0.0015 molar fraction towards methanol. Despite remarkable improvement over the pure metal catalyst, even the best modelled SAA catalyst is not good for the methane to methanol process.

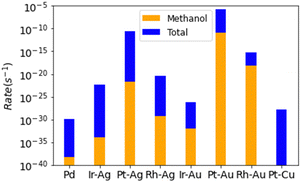Fig. 4 Total rates of reaction for each modelled SAA, with total selectivity towards methanol being reported. Note the logarithmic scale.

For all selected SAAs except Pt–Au, the pathway for selectivity loss is no longer through the dehydrogenation of surface CH₃ seen for palladium. Most of the selectivity loss is through the dehydrogenation of methoxy surface species to formaldehyde. Upon deconstruction of the microkinetic modelling of the trialled SAA catalysts, the main reason for the dehydrogenation of surface methoxy species to formaldehyde, instead of coupling with hydrogen to form methanol, is found to be due to surface coverage limitations (S4, ESI†). Whilst MeO–H coupling on the SAA surfaces have relatively negligible energy barriers and are thermodynamically favoured, so too is the coupling of surface oxygen and hydrogen, to form water. The reason for the poor selectivity observed for the designed SAA catalysts is predominantly due to the poor coverage of hydrogen on the surface under oxidation conditions. One option to counteract this is to introduce a hydrogen source into the system. As seen for surface oxygen, reactive species can abstract hydrogen from water to form surface hydroxyl radicals.^14,16 Water could protonate the CH₃O species, encouraging methanol formation.

The modelled meagre success of Rh–Au as a catalyst is due to the high OH surface coverage instead of O, which is the dominant surface species for all other surfaces. The CH₃–OH coupling, instead of CH₃–O coupling, removes the methoxy surface intermediate that is capable of readily dehydrogenating to formaldehyde. Despite this, there are notable problems with a OH coupling pathway instead of an O coupling pathway. The biggest restricting factor is that OH coupling is calculated to be less facile than O coupling for all modelled surfaces. This kinetic hindrance will always encourage O coupling even if OH is the dominant surface species. Despite this, it has been found in other work that O coupling with CH₃ is inhibited in the aqueous phase, and OH coupling is encouraged.¹⁷ This pushes the argument that whilst these modelled SAA catalysts have poor selectivity in the gas phase, perhaps the reaction taking place in the aqueous phase could allow reasonable selectivity to be observed. This is not possible for pure metal surfaces due to their different dominant pathway for selectivity loss.

In conclusion, we find that SAAs experience unique chemistries distinct from those of pure metal surfaces. However, other important factors also influence the reactivity and selectivity of the surface, such as surface methoxy dehydrogenation to formaldehyde, causing the effectiveness of SAAs as methane to methanol catalysts to be limited in the gas phase. Regardless, their vastly improved reactivities through lowering the energy barrier of the oxidation step also means these SAAs could be used for methane total oxidation. Other factors such as propensity of the dopant single atom to diffuse to the bulk or aggregate should also be considered. Additionally, this work also emphasises that attention should be brought to the importance of streamlined kinetic modelling when considering catalyst searches, instead of simply relying on BEP relationships or the kinetics of a single step, such as C–H activation. Using C–H activation alone would have seriously underrepresented the utility of this novel class of catalysts.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. P. Tomkins, M. Ranocchiari and J. A. van Bokhoven, Acc. Chem. Res., 2017, 50, 418–425.
2. K. Kwapien, J. Paier, J. Sauer, M. Geske, U. Zavyalova, R. Horn, P. Schwach, A. Trunschke and R. Schlögl, Angew. Chem., Int. Ed., 2014, 53, 8774–8778.
3. D. Ciuparu, M. R. Lyubovsky, E. Altman, L. D. Pfefferle and A. Datye, Catal. Rev., 2002, 44, 593–649.
4. R. A. Periana, Science, 1998, 280, 560–564.
5. T. Sheppard, C. D. Hamill, A. Goguet, D. W. Rooney and J. M. Thompson, Chem. Commun., 2014, 50, 11053–11055.
6. V. I. Sobolev, K. A. Dubkov, O. V. Panna and G. I. Panov, Catal. Today, 1995, 24, 251–252.
7. J. Shan, M. Li, L. F. Allard, S. Lee and M. Flytzani-Stephanopoulos, Nature, 2017, 551, 605–608.
8. N. Agarwal, S. J. Freakley, R. U. McVicker, S. M. Althahban, N. Dimitratos, Q. He, D. J. Morgan, R. L. Jenkins, D. J. Willock, S. H. Taylor, C. J. Kiely and G. J. Hutchings, Science, 2017, 358, 223–227.
9. A. A. Latimer, A. Kakekhani, A. R. Kulkarni and J. K. Nørskov, ACS Catal., 2018, 8, 6894–6907.
10. C. Sheldon, J. Paier and J. Sauer, J. Chem. Phys., 2021, 155, 174702.
11. M. Jørgensen and H. Grönbeck, ACS Catal., 2016, 6, 6730–6738.
12. Z. Yao, C. Guo, Y. Mao and P. Hu, ACS Catal., 2019, 9, 5957–5973.
13. M. D. Marcinkowski, M. T. Darby, J. Liu, J. M. Wimble, F. R. Lucci, S. Lee, A. Michaelides, M. Flytzani-Stephanopoulos, M. Stamatakis and E. C. H. Sykes, Nat. Chem., 2018, 10, 325–332.
14. L. Farsi and N. A. Deskins, Phys. Chem. Chem. Phys., 2019, 21, 23626–23637.
15. M. T. Darby, M. Stamatakis, A. Michaelides and E. C. H. Sykes, J. Phys. Chem. Lett., 2018, 9, 5636–5646.
16. F. Xu, I. Fampiou, C. R. O’Connor, S. Karakalos, F. Hiebel, E. Kaxiras, R. J. Madix and C. M. Friend, Phys. Chem. Chem. Phys., 2018, 20, 2196–2204.
17. R. J. Bunting, P. S. Rice, J. Thompson and P. Hu, Chem. Sci., 2021, 12, 4443–4449.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc03183c

---