Palladium-catalysed methoxycarbonylation of ethene with bidentate diphosphine ligands: a density functional theory study

Abstract

Catalytic methoxycarbonylation of ethene with a bidentate tertiary phosphine (DTBPX) and palladium has been explored at the B3PW91-D3/PCM level of density functional theory. Three different pathways for formation of methyl propanoate (MePro) have been studied, namely carbomethoxy (A), ketene (B) and hydride-hydroxyalkylpalladium pathways (C), the latter of which is favoured because it has the lowest overall kinetic barrier. After intermolecular methanolysis, a hydroxyalkylpalladium complex has been characterised on pathway C, which eventually leads to the low overall barrier to produce MePro. The possibility of copolymerisation leading to oligo-/polymers has also been considered. With a computed selectivity of >99% towards the formation of MePro and a reasonably low overall kinetic barrier of 23.0 kcal mol⁻¹, pathway C appears to be the most plausible one. Consistent with experimental data, the overall barrier increases to 30.1 kcal mol⁻¹ for a less bulky bidentate phosphine.

---

Introduction

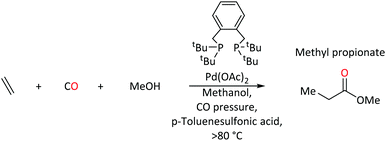
Complexes of palladium are major players in homogeneous catalysis. When equipped with a suitable ligand, palladium acts as an efficient mediator for key transformations within homogenous catalysis e.g. C–C bond formation, migratory insertion and β-hydride elimination.^1–10 Steric and electronic tuning of ligands at the metal center can help to tailor activity and selectivity. Phosphine based ligands are well known to alter electronic and steric profiles of the metal and its surrounding environment,^11,12 which allows Pd(0) and Pd(II) complexes to facilitate a wide range of catalytic reactions. It is usually the electron-donating ability of the phosphorus center, which is modified by the substituents around phosphorus.¹³

Palladium-catalysed ethene methoxycarbonylation with triphenylphosphine ligand is one of many examples that produces methyl propanoate (MePro).¹⁴ MePro is a precursor for methyl methacrylate (MMA), whose polymer, poly(methyl methacrylate), has great industrial importance because of its use in liquid-crystal display screens and touch screen electronics,^15,16 and, more recently, in transparent and lightweight shielding equipment (screens, face coverings).^17–19

On the other hand, under the same reaction conditions, the use of bidentate tertiary phosphines, Ph₂P(CH₂)_n-PPh₂, produces high molecular weight polyketones.²⁰ Reaction rates depend on the length of the backbone spacer between phosphorus atoms of the bidentate species (no reaction when n = 1, maximum rate when n = 3). In contrast, 1,2-bis(di-tert-butylphosphinomethyl)benzene (DTBPX) and 1,3-bis(di-tert-butylphosphino)propane (DTPP) produce MePro, with turnover rates almost 10 times greater than the most efficient oligo-/polymer producing catalysts based on Ph₂P(CH₂)_n-PPh₂ ligands.¹⁴ A Pd catalyst with the DTBPX ligand is used at industrial scale for MePro production (Scheme 1), which is then heterogeneously converted to MMA.^{14–16,21–23}

Scheme 1 Synthesis of methyl propanoate at Pd(P,P) catalyst with DTBPX ligand system.

By using a model diphosphine (specifically, 1,3-diphosphinopropane), DFT calculations at the BP86/6-31G**/SDD level suggested the importance of intermolecular methanolysis following the dissociation of a model monophosphine in order to increase the electrophilicity of the acyl carbon, priming it towards attack.²⁴ Following on from Macgregor's work where it was shown that less geometric disruption at the transition state relative to the prior reactant complex resulted in a lower ΔE^‡,²⁵ Zuidema, through QM/MM calculations, characterised the nature of reductive elimination of organic molecules from palladium–diphosphine complexes.²⁶ However, the atomistic nature of the competing pathways leading to either MePro or oligoketones/polymers, and the reasons for selectivity changes with phosphine ligand bulk, remains unclear.

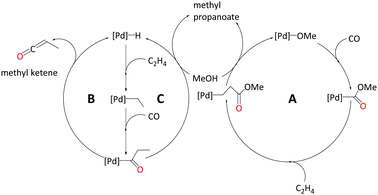
In the current study, we strive to furnish insights into the mechanism(s) operative with these ligands through quantum-chemical modelling of plausible catalytic cycles. We have explored three different pathways to produce MePro catalysed by palladium with the DTBPX ligand, these are: (i) carbomethoxy (pathway A), (ii) ketene (pathway B) and (iii) hydride-hydroxyalkylpalladium pathway (pathway C). The carbomethoxy pathway begins with a Pd–OMe complex. Migratory insertion of carbon monoxide to Pd–OMe produces an ester functionality. The final protonolysis step cleaves off MePro and reproduces Pd–OMe (see Scheme 2, A). We recently identified highly reactive ketene-like intermediates during the formation of MMA at palladium catalyst with P,N-chelating ligands.^27,28 These ketene species undergo rapid alcoholysis leading to the final product. Based on this work, we have characterised a ketene cycle for the production of MePro, which requires an α,β insertion of ethene into the Pd–H bond followed by an α,α insertion of the ethyl group into coordinated carbon monoxide. β-Hydride elimination from acyl group produces a methyl ketene species, which reacts with methanol to produce MePro (see Scheme 2, B). The hydride-hydroxyalkylpalladium cycle is similar to the ketene cycle up until insertion of the ethyl group into coordinated carbon monoxide. An intermolecular methanolysis step closes this cycle by yielding MePro (see Scheme 2, C).

Scheme 2 Mechanistic possibilities explored in this study.

By comparing the energetics of these different routes, we suggest which pathway is most likely to operate under turnover conditions. We then use these insights into the energetically most favourable pathway to rationalise the experimental observation that bulkier ligands produce MePro while under similar conditions the use of a less sterically crowded ligand results in the production of polymers.

Results and discussion

1. Carbomethoxy pathway – A

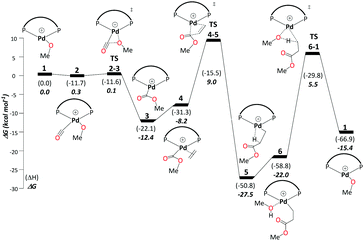
This cycle begins with complex 1, [(P–P)Pd–OMe]⁺, where (P–P) = DTBPX. Carbon monoxide uptake is the first step affording 2 (ΔG_1→2 = −0.3 kcal mol⁻¹). Facile migratory insertion of nucleophilic methoxy into carbon monoxide gives rise to 3 (ΔG_2→3 = −12.1 kcal mol⁻¹ and ΔG^‡_2→3 = 0.4 kcal mol⁻¹). At this stage ethene associates to intermediate 3 in a perpendicular orientation and produces 4 (ΔG_3→4 = 4.2 kcal mol⁻¹). Subsequently, coordinated ethene in 4 rotates to an in-plane mode, whereas the methoxycarbonyl moiety starts to dissociate from Pd to allow ethene insertion viaTS4-5 (ΔG_4→5 = −19.3 kcal mol⁻¹ and ΔG^‡_4→5 = 17.2 kcal mol⁻¹). Methanol uptake to 5 producing 6 is slightly endergonic (ΔG_5→6 = 5.4 kcal mol⁻¹). The final step, protonolysis, yields MePro (ΔG_6→1 = 6.7 kcal mol⁻¹ and ΔG^‡_6→1 = 27.5 kcal mol⁻¹) and regenerates 1 (Scheme 3).

Scheme 3 Carbomethoxy pathway A: free-energy profile [kcal mol⁻¹] relative to Pd–OMe complex 1, with calculations carried out at the B3PW91-D3/ECP2/PCM//B3PW91/ECP1 level of theory using methanol as the model solvent, and terminating at protonolysis with an overall barrier of 32.9 kcal mol⁻¹. Final free energies ΔG and enthalpies (ΔH).

Using the energetic span model of Kozuch and Shaik,^29,30 we have identified complex 5 as the most abundant reaction intermediate (MARI) in this cycle, and TS6-1 (associated with protonolysis) as the highest energy transition state (HETS). Because the resulting overall barrier of 32.9 kcal mol⁻¹ is unsurmountable under the turnover conditions, we can exclude this mechanism. This finding is in agreement with the failure to directly observe intermediates associated with the methoxy cycle in the reaction mixture and with studies conducted specifically on intermediates presumed to be part of the methoxy cycle, which suggest slow protonolysis of the β-chelating ester.³¹

2. Ketene pathway – B

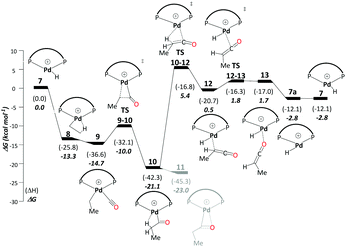
This cycle starts with a Pd hydride complex, [(P–P)Pd–H]⁺ (7). Ethene uptake by complex 7 is rapid and does not have a detectable barrier for hydride transfer to produce ethylpalladium intermediate 8 (ΔG_7→8 = −13.3 kcal mol⁻¹), which is stabilised by a β-agostic interaction. CO uptake by 8 cleaving the β-agostic interaction of the ethyl group has a small but noticeable driving force (ΔG_8→9 = −1.4 kcal mol⁻¹). The subsequent migratory insertion of CO into the Pd–ethyl bond viaTS9-10 leads to Pd-propionyl intermediate, 10, where the β-agostic interaction is restored (ΔG_9→10 = −6.4 kcal mol⁻¹ and ΔG^‡_9→10 = 4.7 kcal mol⁻¹). This β-agostic interaction in 10 facilitates β-H elimination from the propionyl moiety viaTS10-12 (ΔG_10→12 = 20.6 kcal mol⁻¹ and ΔG^‡_10→12 = 26.5 kcal mol⁻¹). 12 is a high-lying intermediate, which bears methyl ketene coordinated to a Pd hydride (see Fig. S1a in the ESI†). Dissociation of methyl ketene proceeds in a stepwise fashion, commencing with an intramolecular rearrangement viaTS12-13 to 13 (ΔG_12→13 = 2.2 kcal mol⁻¹ and ΔG^‡_12→13 = 2.3 kcal mol⁻¹), in which the ketene is coordinated through its O atom. Dissociation of methyl ketene from 13 reproduces the initial hydride complex 7 (ΔG_13→7 = −4.4 kcal mol⁻¹). Methyl ketene is a highly reactive species and, once dissociated from the metal, can rapidly react with the solvent (methanol) to produce MePro (Scheme 4).

Scheme 4 Ketene pathway B: free-energy profile [kcal mol⁻¹] relative to 7, at the B3PW91-D3/ECP2/PCM//B3PW91/ECP1 level of theory using methanol as the model solvent. Final free energies ΔG and enthalpies (ΔH).

The Pd-propionyl intermediate 10 can rearrange to a slightly more stable isomer 11 with an interaction between the carbonyl O atom and Pd (with a metallacyclic character).³² Because this isomer is unreactive on the ketene cycle and has to revert back to 10, it is an off-cycle intermediate. Since it is more stable than 10 by ΔG_10→11 = −1.9 kcal mol⁻¹, 11 has to be included in the energy span analysis, where it is the MARI. HETS is the transition state associated with β-H elimination from the propionyl moiety from 10, TS10-12. This cycle has an overall barrier of 28.4 kcal mol⁻¹, which is lower by 4.5 kcal mol⁻¹ as compared to the overall barrier of the carbomethoxy cycle. The ketene cycle could already be viable under the turnover conditions, albeit with low activity (from Shaik's energy span analysis, a turnover frequency (TOF) of just 1 h⁻¹ would be predicted, see below).

3. Hydride-hydroxyalkylpalladium pathway – C

For an unsolvated hydride mechanism, we calculated a high overall barrier of 38.1 kcal mol⁻¹ (see Scheme S1 in the ESI,† labeled pathway C′). This mechanism involves a methanolysis step where the proton is transferred from coordinated MeOH to the metal. We also explored entry into a reductive elimination pathway via a neutral Pd(0) species following deprotonation. As detailed in the ESI,† this turns out to be not a thermodynamically feasible route and could not account for the differences in experimentally observed product distribution on the basis of ligand bulk.

The “direct” methanolysis steps in the carbomethoxy, ketene and hydride pathways are unfavourable because the proton is transferred via strained four-membered transition states (e.g.TS6-1). Frequently such processes can be assisted through participation of solvent molecules forming longer, less strained relays. Starting from the hydride cycle, we have investigated possible pathways including two and three explicit methanol molecules. We now discuss the most favourable of the pathways with two solvent molecules, which features a new kind of intermediate, a hydroxyalkylpalladium complex.

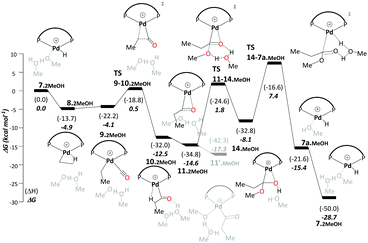
Like the ketene cycle, this pathway starts with a Pd–H complex, 7.2MeOH, with two solvent molecules, where one of these is coordinated to the metal atom. Ethene can displace the coordinated solvent molecule, and like in ketene cycle, we were not able to locate a transition state for formation of the ethylpalladium intermediate 8.2MeOH (ΔG_{7.2MeOH→8.2MeOH} = −4.9 kcal mol⁻¹). Subsequent CO uptake gives rise to 9.2MeOH (ΔG_{8.2MeOH→9.2MeOH} = 0.8 kcal mol⁻¹), which undergoes migratory insertion to form a Pd-propionyl intermediate, 10.2MeOH (ΔG_{9.2MeOH→10.2MeOH} = −8.3 kcal mol⁻¹ and ΔG^‡_{9.2MeOH→10.2MeOH} = 4.6 kcal mol⁻¹). This intermediate, stabilised by a β-agostic interaction, can rearrange to a slightly more stable isomer, 11.2MeOH, with a side-on η²-coordinated carbonyl group (cf.11 in the ketene cycle in Scheme 4). We identified an off-cycle intermediate, 11′.MeOH, where one of the two MeOH molecules is coordinated to the metal atom. Intermediate 11′.MeOH is slightly more stable than 11.2MeOH, by 1.0 kcal mol⁻¹.

Methanolysis, the final step that yields the product, can proceed in a variety of ways. Concomitant with nucleophilic attack of MeOH at the carbonyl group, the H atom of that MeOH eventually needs to be transferred to the metal in order to re-create the Pd hydride catalyst. This can happen in an inter- or intramolecular fashion (i.e. involving MeOH from the bulk or pre-coordinated to the metal, respectively). Many studies support intramolecular methanolysis, with Beller and coworkers recently characterising a pathway for the formation of MePro with an overall barrier of 42.4 kcal mol⁻¹, which was associated with an energetically challenging methanolysis step.³³ This barrier is even higher than the overall barrier that we have calculated for the carbomethoxy pathway (i.e. 32.9 kcal mol⁻¹) and is unsurmountable under the turnover conditions. In our case it transpired that a stepwise transfer of this proton to Pd under formation of a hydroxyalkylpalladium intermediate is more facile (Scheme 5).

Scheme 5 Hydride-hydroxyalkylpalladium pathway C: free energy profile using methanol as the model solvent at the B3PW91-D3/ECP2/PCM level. Energies are in kcal mol⁻¹ relative to 7.2MeOH. Explicit solvent molecules are shown in light grey colour. Final free energies ΔG and enthalpies (ΔH).

The hydroxyalkylpalladium formation step of the pathway starts from intermediate 11.2MeOH, with the characteristics of an intermolecular methanolysis process as methanol molecules do not coordinate directly to palladium (ΔG_{10.2MeOH→11.2MeOH} = −2.1 kcal mol⁻¹). The two methanol molecules associate to the system to afford a six-membered hydrogen bond network involving the alcohol hydroxyl groups and the η²-acyl functionality. A six-membered proton-hopping transition state, TS11-14.MeOH (ΔG_{11.2MeOH→14.MeOH} = 6.4 kcal mol⁻¹ and ΔG^‡_{11.2MeOH→14.MeOH} = 16.3 kcal mol⁻¹), leads to a reactive hydroxyalkylpalladium intermediate, 14.MeOH. The hydrogen of the hydroxy group within this hydroxyalkylpalladium intermediate forms a strong hydrogen bond to the remaining methanol. This explicit methanol acts as a relay viaTS14-7a.MeOH (Fig. 1 and for the reverse direction IRC, please see Fig. S2, ESI†) by pulling the proton from the hydroxyalkylpalladium moiety and delivering its proton to palladium (ΔG_{14.MeOH→7a.MeOH} = −7.2 kcal mol⁻¹ and ΔG^‡_{14.MeOH→7a.MeOH} = 15.6 kcal mol⁻¹). Subsequent additional methanol uptake to 7a.MeOH reproduces 7.2MeOH (ΔG_{7a.MeOH→7.2MeOH} = −13.3 kcal mol⁻¹).

Fig. 1 3D representations of selected transition states. Distances are given in Å. Additional methanol units acting as a relay in this transition state alleviate strain on the P–Pd–P bite angle and facilitate methanolysis.

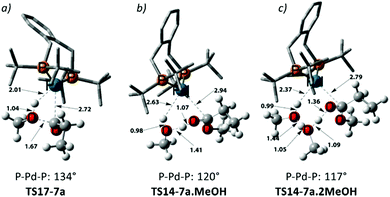
Using the energetic span model of Kozuch and Shaik,^29,30 we have identified 11′.MeOH as the MARI and TS14-7a.MeOH as the HETS. This pathway has an overall barrier of 23.0 kcal mol⁻¹, significantly lower than the other two pathways. For the unsolvated variant of this pathway, pathway C′, formation of an hydroxyalkylpalladium intermediate is not viable, and an intramolecular methanolysis step is involved (via the acyl-methanol complex 17 and TS17-7a) (see Scheme S1, ESI† and Fig. 1a), with the latter being the HETS in this case. Interestingly the P,P bite angle reaches up to 134° in TS17-7a, whereas it is 120° in TS14-7a.MeOH, see Fig. 1a and b. Therefore, the intramolecular methanolysis step in pathway C′ imparts additional strain onto the phosphine chelate ring, rendering the final barrier insurmountably high.

Noting that the energetically unfavourable bite angle strain present in TS17-7a was alleviated by including an extra methanol unit, we explored the effect of adding a further additional explicit solvent molecule to the key intermediates and transition states of pathway C. This was found to reduce the overall barrier to a far more accessible 17.8 kcal mol⁻¹ (see Table S5 in the ESI†) as the P–Pd–P bite angle is reduced to 117° in the corresponding transition state, TS14-7a.2MeOH, ultimately facilitating MePro elimination (see Fig. 1c). This relatively low methanolysis barrier is in agreement with the observation that a complex closely related to 10 (with acetyl instead of propionyl and with trifluoro acetate counterion bonded to Pd) undergoes methanolysis even at temperatures as low as −90 °C (albeit not under turnover, and with a complex product mixture, arguably due to the high concentration under the stoichiometric reaction conditions).³⁴

We have also calculated the overall barrier for the hydride-hydroxyalkylpalladium pathway C with the much less bulky 1,2-bis((dimethylphosphaneyl)methyl)benzene (DMBPX) ligand. Switching from DTBPX to DMBPX, the overall barrier viaTS14-7a.MeOH increases from 23.0 kcal mol⁻¹ to 30.1 kcal mol⁻¹ (Table S5 in ESI†), which would correspond to a reduction of the TOF by a factor of 10⁻⁵ at the experimental temperature. This result is fully consistent with the experimental observation that the large steric bulk of the DTBPX ligand is needed for high activity. The effect of the steric bulk on the overall barrier can be dissected into the effects on the rate-limiting states, viz.:

TS14-7a.MeOH(DTBPX) + C₆H₄(PMe₂)₂ → TS14-7a.MeOH(DMBPX) + C₆H₄(PtBu₂)₂, ΔG = 2.4 kcal mol⁻¹ (1)

11′.MeOH(DTBPX) + C₆H₄(PMe₂)₂ → 11′.MeOH(DMBPX) + C₆H₄(PtBu₂)₂, ΔG = −4.7 kcal mol⁻¹ (2)

Reducing the steric bulk on going from DTBPX to DMBPX stabilizes the MARI notably (eqn (2)), and pushes up the HETS somewhat (eqn (1)), where the steric bulk apparently facilitates product removal (this effect is illustrated in Fig. 2).

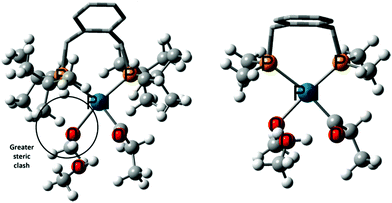Fig. 2 Intermediates 11′MeOH using DTBPX (left) and DMBPX (right) ligands. The enhanced steric clash in DTBPX ligand system is circled.

To summarise this part, we have identified a viable pathway for MePro formation via a hydride-hydroxyalkylpalladium pathway C, with an overall barrier between 17.8 kcal mol⁻¹ to 23.0 kcal mol⁻¹, depending on the number of additional explicit solvent molecules that are included. The resulting computed TOFs (collected in Table S7 in the ESI†) can be compared to the experimental number of 12 000 h⁻¹.¹⁴ Bearing in mind that, like absolute rate constants, absolute TOFs are very difficult to predict quantitatively, it appears that the data for pathway C is in qualitative agreement with experiment, whereas the TOFs evaluated for the other pathways are significantly too low.

3.1 Selectivity between MePro and copolymerisation. As mentioned in the introduction, an important side reaction potentially hampering MePro formation is copolymerisation of the reactants CO and ethene into poly- or oligoketones.^14,20 A characteristic feature of the Pd/DTBPX catalyst is that it yields MePro as the major product with a selectivity of 99.9%.¹⁴ To model this copolymerisation side reaction, we have traced a pathway starting from the Pd-propionyl intermediate 10.2MeOH on pathway C. Ethene uptake by 10.2MeOH producing 15.2MeOH is endergonic by 5.3 kcal mol⁻¹ (see left part of Scheme 6). Formation of the γ-acyl product occurs through ethene insertion into the Pd–acyl bond viaTS15-16.2MeOH. The following CO uptake and migratory insertion affording the intermediate 18.2MeOH (the analogue of 10.2MeOH with growing ketone chain) is strongly exergonic (see Scheme S2 in the ESI†) and occurs with a barrier significantly below TS15-16.2MeOH for ethene insertion.

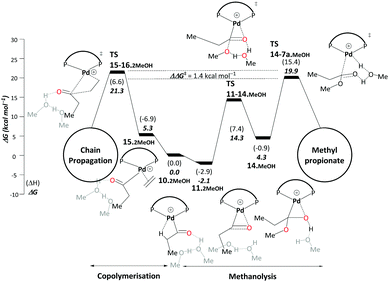Scheme 6 Methanolysis/copolymerisation selectivity: right – pathway C, leading to the production of MePro, left – copolymerisation leading to the formation of oligoketones or polymers. All energies are in kcal mol⁻¹ relative to Pd–acyl complex, 10.2MeOH. Explicit solvent molecules are shown in light grey colour. The ΔΔG^‡ of the selectivity determining transition states increases to 5.4 kcal mol⁻¹ when an additional methanol unit is included (see Scheme S3, ESI†). Final free energies ΔG and enthalpies (ΔH).

The difference between TS15-16.2MeOH and TS14-7a.MeOH on pathway C therefore determines the ratio between MePro and oligoketones or polymers. The resulting free energy difference computed for these models is ΔΔG^‡ = 1.4 kcal mol⁻¹. While inclusion of an additional explicit MeOH molecule stabilises TS14-7a.MeOH, TS15-16.2MeOH is hardly affected as no hydrogen transfer occurs. When adding a second stabilising MeOH an even larger free-energy difference is computed (5.4 kcal mol⁻¹, Scheme S3 in the ESI†), resulting in almost 100% selectivity toward MePro formation, which is in very good agreement with experiment. However, for the less bulky DMBPX, a predicted selectivity of almost 100% towards copolymerisation is computed (see Scheme S4 in the ESI†). This is again fully consistent with experimental observations that reduced steric bulk favours this side reaction.

These results provide further support for pathway C, because not only does it present the lowest overall barrier of all variants studied, but it also readily reproduces the experimentally observed selectivities relating to the ligand dependent switch between chain propagation and terminating methanolysis.

Conclusions

We have studied three pathways for MePro production by a Pd catalyst with the DTBPX ligand system. A carbomethoxy pathway (A) has a prohibitively high overall barrier. A ketene pathway (B) has a slightly lower barrier than pathway A, but both do not account for the experimentally observed catalytic activity under the turnover conditions.

Hydride-hydroxyalkylpalladium pathway (C) has been characterised as a viable pathway towards the production of MePro (Scheme 7). This pathway has a lower overall barrier than all the other pathways studied so far for this system. In this pathway, an intermolecular alcoholysis step involving a reactive hydroxyalkylpalladium intermediate is essential to lower the kinetic barrier via a six-membered transition state. We have also found that explicit solvent molecules are mandatory to estimate the correct energy barriers. Our calculated overall barriers for ligands with less bulky bidentate phosphines are completely consistent with the experimental observations as bulky bidentate phosphines are indispensable for a high catalytic activity.

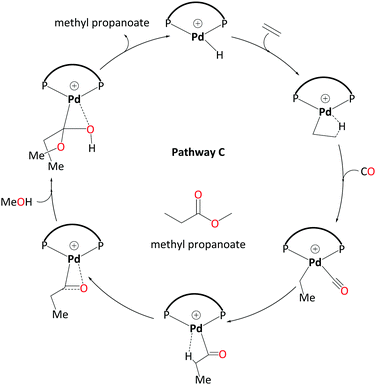Scheme 7 Catalytic cycle for pathway C – involving a hydroxyalkylpalladium complex as emerged from DFT studies. Explicit solvent molecules have been removed.

Furthermore, we have studied the competing copolymerisation reaction at pathway C, which may operate by ethene insertion into the Pd–acyl bond. The difference of energies between selectivity determining transition states is well-matched to experimentally observed selectivity between the formation of oligoketones and MePro on the basis of ligand choice.

In summary, we have for the first time provided detailed computational evidence for a mechanistic scenario, that is broadly compatible with experimental observations, for this industrially important catalytic system. We hope our findings will aid truly rational catalyst design for this and related systems.

Experimental section

The B3PW91^35–37 functional has been used in this study. This hybrid functional has been shown to perform well in modelling a range of reactions involving transition metals.^38–42

All the intermediates and transition states were fully optimised at B3PW91/ECP1, where ECP1 corresponds with the 6-31G** basis set for all non-metal atoms in conjunction with the SDD basis set for the valence electrons of palladium coupled with the equivalent effective core potential for the inner electrons of the transition metal. Analytical harmonic frequency calculations were performed and were used to verify the nature of all possible minima and transition states and to obtain enthalpic and entropic corrections at the standard conditions (298.15 K, 1 bar).

To locate the transition states, potential energy profile scans were performed using suitable constraints at the same level, B3PW91/ECP1. The highest points on the potential energy profiles from the scans were chosen to perform full transition state optimisations, while QST2 and QST3 algorithms⁴³ were also employed. Transition states were confirmed by vibrational analysis and intrinsic reaction coordinate (IRC) calculations.^44,45 An example IRC computation is shown in Fig. S2 (ESI†).

Single point calculations were used to refine the energies of pre-optimised complexes and transition states using the same functional at ECP2 level. ECP2 corresponds to a larger basis set, 6-311+G** for all non-metal atoms, whereas palladium was treated with the same SDD pseudopotential.

A polarisable continuum (PCM)^46–48 was added in the single point calculations with methanol as a solvent, as well as dispersion corrections according to Grimmes's DFT-D3 scheme^49–51 including Becke–Johnson damping.^52,53 When coupled with Grimme's DFT-D3 dispersion correction, B3PW91 also benchmarks well against the explicitly correlated CCSD(T) method,⁵⁴ a highly accurate ab initio reference. The final values of ΔG and ΔH values were calculated as:

ΔG = ΔE + δE_Solv + δE_DFTD3BJ + δE_G (3)

ΔH = ΔE + δE_Solv + δE_DFTD3BJ + δE_H (4)

where δE_G and δE_H are the thermochemical correction terms computed at the B3PW91/ECP1 level, and ΔE, and δE_Solv were computed at the B3PW91-D3BJ/ECP2 level. The Gaussian 09 program⁵⁵ was used to perform all calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank EaStCHEM and the School of Chemistry for support. Computations were carried out on a local Opteron PC cluster maintained by Dr H. Früchtl. The research data supporting this publication can be accessed at https://doi.org/10.17630/058ba909-011e-4c5c-881d-271175acd8df.

Notes and references

1. A. S. K. Hashmi, C. Lothschütz, R. Döpp, M. Rudolph, T. D. Ramamurthi and F. Rominger, Angew. Chem., Int. Ed., 2009, 48, 8243–8246.
2. S. Demir, İ. Özdemir, H. Arslan and D. VanDerveer, J. Organomet. Chem., 2011, 696, 2589–2593.
3. A. Jutand, J. Pytkowicz, S. Roland and P. Mangeney, Pure and Applied Chemistry, 2010, vol. 82, p. 1393.
4. C. Amatore, E. Carre, A. Jutand and M. A. M'Barki, Organometallics, 1995, 14, 1818–1826.
5. A. Flahaut, S. Roland and P. Mangeney, J. Organomet. Chem., 2007, 692, 5754–5762.
6. A. Brennführer, H. Neumann and M. Beller, Angew. Chem., Int. Ed., 2009, 48, 4114–4133.
7. X.-F. Wu, H. Neumann and M. Beller, ChemSusChem, 2013, 6, 229–241.
8. X.-F. Wu, H. Neumann and M. Beller, Chem. Rev., 2013, 113, 1–35.
9. G. M. Roberts, P. J. Pierce and L. K. Woo, Organometallics, 2013, 32, 2033–2036.
10. P. van Leeuwen, Homogeneous Catalysis – Understanding the Art, 2004.
11. S. Otsuka, T. Yoshida, M. Matsumoto and K. Nakatsu, J. Am. Chem. Soc., 1976, 98, 5850–5858.
12. M. Baya, J. Houghton, D. Konya, Y. Champouret, J.-C. Daran, K. Q. Almeida Leñero, L. Schoon, W. P. Mul, A. B. van Oort, N. Meijboom, E. Drent, A. G. Orpen and R. Poli, J. Am. Chem. Soc., 2008, 130, 10612–10624.
13. P. W. N. M. van Leeuwen, P. C. J. Kamer, J. N. H. Reek and P. Dierkes, Chem. Rev., 2000, 100, 2741–2770.
14. W. Clegg, M. R. J. Elsegood, G. R. Eastham, R. P. Tooze, X. L. Wang and K. Whiston, Chem. Commun., 1999, 1877–1878.
15. B. Harris, Ingenia, 2010, 18–23.
16. M. Moukwa, Chem. World, 2010, 50–52.
17. GlobeNewswire, https://www.globenewswire.com/news-release/2020/06/04/2044075/0/en/Amid-the-COVID-19-crisis-and-the-looming-economic-recession-the-Methyl-Methacrylate-MMA-market-worldwide-will-grow-by-a-projected-US-2-5-Billion-during-the-analysis-period.html, (accessed August 2020).
18. Bulletin Line, https://bulletinline.com/2020/05/30/potential-impact-of-covid-19-on-a-latest-research-provides-insights-about-polymethyl-methacrylate-pmma-market/, (accessed August 2020).
19. ICIS, https://www.icis.com/explore/resources/news/2020/07/07/10527405/europe-ethanol-ipa-pmma-sheets-are-bright-spots-in-gloomy-coronavirus-world, (accessed September 2020).
20. E. Drent and P. H. M. Budzelaar, Chem. Rev., 1996, 96, 663–682.
21. W. Clegg, G. R. Eastham, M. R. J. Elsegood, B. T. Heaton, J. A. Iggo, R. P. Tooze, R. Whyman and S. Zacchini, Organometallics, 2002, 21, 1832–1840.
22. G. R. Eastham, R. P. Tooze, M. Kilner, D. F. Foster and D. J. Cole-Hamilton, J. Chem. Soc., Dalton Trans., 2002, 1613–1617.
23. E. Zuidema, C. Bo and P. W. N. M. van Leeuwen, J. Am. Chem. Soc., 2007, 129, 3989–4000.
24. S. M. A. Donald, S. A. Macgregor, V. Settels, D. J. Cole-Hamilton and G. R. Eastham, Chem. Commun., 2007, 562–564.
25. S. A. Macgregor, G. W. Neave and C. Smith, Faraday Discuss., 2003, 124, 111–127.
26. E. Zuidema, P. W. N. M. van Leeuwen and C. Bo, Organometallics, 2005, 24, 3703–3710.
27. S. Ahmad, A. Lockett, T. A. Shuttleworth, A. M. Miles-Hobbs, P. G. Pringle and M. Bühl, Phys. Chem. Chem. Phys., 2019, 21, 8543–8552.
28. S. Ahmad and M. Bühl, Chem. – Eur. J., 2019, 25, 11625–11629.
29. S. Kozuch, S. E. Lee and S. Shaik, Organometallics, 2009, 28, 1303–1308.
30. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
31. J. Liu, B. T. Heaton, J. A. Iggo, R. Whyman, J. F. Bickley and A. Steiner, Chem. – Eur. J., 2006, 12, 4417–4430.
32. A closely related Ni analogue is known, [Ni(tBu₂PC2H₄PtBu₂)(COCH₂tBu)]⁺, CSD refcode YUMQUT: J. J. Curley, K. D. Kitiachvili, R. Waterman and G. L. Hillhouse, Organometallics, 2009, 28, 2568–2571.
33. K. Dong, R. Sang, Z. Wei, J. Liu, R. Dühren, A. Spannenberg, H. Jiao, H. Neumann, R. Jackstell, R. Franke and M. Beller, Chem. Sci., 2018, 9, 2510–2516.
34. P. W. N. M. van Leeuwen, M. A. Zuideveld, B. H. G. Swennenhuis, Z. Freixa, P. C. J. Kamer, K. Goubitz, J. Fraanje, M. Lutz and A. L. Spek, J. Am. Chem. Soc., 2003, 125, 5523–5539.
35. A. D. Becke, J. Chem. Phys., 1996, 54, 1040–1046.
36. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
37. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
38. P. L. Arnold, E. Hollis, G. S. Nichol, J. B. Love, J.-C. Griveau, R. Caciuffo, N. Magnani, L. Maron, L. Castro, A. Yahia, S. O. Odoh and G. Schreckenbach, J. Am. Chem. Soc., 2013, 135, 3841–3854.
39. S. Salman, J.-L. Brédas, S. R. Marder, V. Coropceanu and S. Barlow, Organometallics, 2013, 32, 6061–6068.
40. M. M. Montero-Campillo, A. M. Lamsabhi, O. Mo and M. Yanez, Theor. Chem. Acc., 2013, 132, 1–8.
41. S. K. Ignatov, S. V. Panteleev, S. V. Maslennikov and I. V. Spirina, Russ. J. Gen. Chem., 2012, 82, 1954–1961.
42. L. Wang, Y. Zhang, H. He and J. Zhang, Synth. Met., 2013, 167, 51–63.
43. C. Peng, P. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49–56.
44. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
45. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
46. J. Tomasi, B. Mennucci and E. Cances, THEOCHEM, 1999, 464, 211–226.
47. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
48. A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, Acc. Chem. Res., 2009, 42, 489–492.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
51. T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591.
52. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
53. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
54. M. K. Kesharwani and J. M. L. Martin, Theor. Chem. Acc., 2014, 133, 1–14.
55. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009. The full reference is given in the ESI†.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04454g

---