Open Access Article
Open Access ArticleStructural properties of methanol–water binary mixtures within the quantum cluster equilibrium model†
G.
Matisz
ab,
A.-M.
Kelterer
*c,
W. M. F.
Fabian
d and
S.
Kunsági-Máté
ab
aDepartment of General and Physical Chemistry, University of Pécs, Ifjúság 6, 7624 Pécs, Hungary
bJános Szentágothai Research Center, Ifjúság 20, 7624 Pécs, Hungary
cInstitute of Physical and Theoretical Chemistry, Graz University of Technology, NAWI Graz, Stremayrgasse 9/I, 8010 Graz, Austria. E-mail: kelterer@tugraz.at
dInstitute of Chemistry, University of Graz, NAWI Graz, Heinrichstr. 28, 8010 Graz, Austria
First published on 30th January 2015
Abstract
Density functional theory (B3LYP-D3, M06-2X) has been used to calculate the structures, interaction energies and vibrational frequencies of a set of 93 methanol–water clusters of different type (cubic, ring, spiro, lasso, bicyclic), size and composition. These interaction energies have been used within the framework of the Quantum Cluster Equilibrium Theory (QCE) to calculate cluster populations as well as thermodynamic properties of binary methanol–water mixtures spanning the whole range from pure water to pure methanol. The necessary parameters amf and bxv of the QCE model were obtained by fitting to experimental isobars of MeOH–H2O mixtures with different MeOH content. The cubic and spiro motifs dominate the distribution of methanol–water clusters in the mixtures with a maximum of mixed clusters at x(MeOH) = 0.365. Reasonable agreement with experimental data as well as earlier molecular dynamics simulations was found for excess enthalpies HE, entropies SE as well as Gibbs free energies of mixing GE. In contrast, heat capacities Cp and CEp showed only poor agreement with experimental data.
Introduction
Preferential or selective solvation1–4 of a solute in binary solvent mixtures, where the composition of the solvation shell differs from the composition of the bulk solvent phase, can have significant effects on the physicochemical properties of the solution. The observable differences are obviously in connection with the molecular associations present in the binary solvent mixtures. Several studies can be found in the literature addressing the investigation of binary liquids regarding structural aspects. For instance, in a recent study, Wakisaka published a summary of experimental results5–8 related to the cluster structures possible in binary liquid mixtures of water–MeOH, water–EtOH, water–n-PrOH and water–n-BuOH using fragmentation of liquid droplets and mass spectrometric detection of the ionized clusters.9,10 Solvent relaxation time measurements in mixtures of n-BuOH with MeOH, EtOH, and PrOH indicated a substantial change of the solvation shell at a specific molar fraction of n-BuOH.11 Similarly, measurement of the solvent relaxation time by phase fluorimetry of phenols in binary EtOH–water mixtures resulted in a change from mono- to bi-exponential when the EtOH content exceeded a critical value.12 In view of the importance of such solvent mixtures a detailed understanding of this selective/preferential solvation at an atomic level is essential. Besides experimental investigations quantum chemical calculations also have been used to determine the properties of such clusters formed by different solvent molecules, including e.g. methanol–water clusters up to four-membered rings13 or methanol–benzene clusters.14 Of particular importance for the present investigation are those dealing with water15–17 and/or methanol18–21 clusters addressing mainly the structural properties, binding energies and electronic properties of these clusters. Specifically, rather comprehensive calculations of (MeOH)n clusters with n up to n = 15 using a variety of computational procedures have been carried out by Thakkar and coworkers.21 In addition to methanol clusters those of higher primary alcohols (up to n-hexanol) were treated by Golub et al.19A powerful tool for the description and theoretical modelling of structure and properties of liquids is the quantum cluster equilibrium (QCE) theory22 which is based on quantum chemically calculated cluster/molecular properties and the application of statistical thermodynamics. So far this procedure almost exclusively has been applied to neat liquids, like water,23–34 methanol,28,35–38 ethanol,28,38–41 propan-1-ol,38 butan-1-ol,38 benzyl alcohol,39 2,2-dimethyl-3-ethyl-3-pentanol,39,42 formic acid,43,44 liquid ammonia,27,45,46 phosphine,27 hydrogen sulfide,27N-methylacetamide,47–49 liquid sulfur,50 and liquid hydrogen-fluoride.34,51–53 Recently, in addition to the static thermodynamic description by the QCE model, the kinetics of the hydrogen bond formation and proton transfer in water clusters has been studied by Weinhold.54 To the best of our knowledge, the only binary system for which the QCE model has been applied until now is the water–dimethyl-sulfoxide (DMSO)55 binary mixture. Evidently the reason is not limited interest in binary (or ternary) systems, but rather arise from technical difficulties for a proper description of such mixtures. These include both the approximations inherent in the QCE model, as well as the more complex structure of liquids consisting of more than one component. While in the binary system treated so far by the QCE model one component acts as a hydrogen bond acceptor (DMSO) and the other (water) as donor, in binary mixtures of alcohols or alcohol–water, as used in our previous experimental investigations,11,12 both components can act as hydrogen bond acceptors as well as hydrogen bond donors.
As a first step to a detailed understanding of such binary solvent mixtures in this study we want to present a quantum cluster equilibrium study of the MeOH–water system with different composition ranging from pure water to pure MeOH. We have chosen this system not only as it represents the prototype of binary mixture used in our previous investigations but also since several theoretical modeling studies, mainly by molecular dynamics,56–64 as well as experimental investigations,65–68 have been published.
Moreover, since apparently the QCE model has for the first time been applied to a binary liquid mixture where both components can act as hydrogen bond acceptors and also as hydrogen bond donors, the MeOH–water system presents an important test case for the quantum cluster equilibrium model of such mixtures.
Computational methods
The methanol–water cluster structures have been optimized using the B3LYP density functional69–72 augmented with the D3 dispersion correction73 of Grimme et al. as implemented in the ORCA 2.9.1 program.74 The TZVP basis set75 has been used both for the optimizations and for the vibrational analysis. The intracluster interaction energies (Eint) were determined using the QZVP basis set76 according to eqn (1) and are corrected for the basis set superposition error (BSSE)77| Eint = Ecluster − ∑Emonomers = Ecluster − i·EMeOH − j·EH2O | (1) |
Gibbs free energies of interaction ΔGint were obtained from the BSSE-corrected B3LYP-D3/QZVP interaction energies combined with non-thermal (ZPE) and thermal corrections dGcorr resulting from the TZVP frequency analysis at T = 298.15 K and p = 1 atm. For the rotational partition function the appropriate symmetry numbers (σ = 2 for w1, m2w2r, w4r, m4r, m2w6; σ = 3 for m6r; σ = 4 for w8c and m4w4c; for all other clusters σ = 1) were used.
| ΔGint = Eint(BSSE-QZVP) + [dGcorrcluster − ∑dGcorrmonomers](TZVP) | (2) |
The QCE calculations have been performed using the developer version of the PEACEMAKER 2.0 program (rev. 572) of the research group of Kirchner.33 The extension of the program for binary systems is described in detail in ref. 55. Besides the electronic energy, interaction energy, principal moments of inertia and harmonic vibrational frequencies of clusters, to obtain the statistical thermodynamics data via partition functions, two fitting parameters amf and bxv are used in the QCE theory. The recently developed one-parameter QCE variant so far has only been applied to neat liquids.34
Based on the parameter amf, the interaction energies of each cluster with the surrounding particles/clusters can be defined as an additive term (uint) to the intracluster interaction energies (Eint). The parameter bxv gives the correction for the calculation of the excluded volume Vexcl.
The mean field potential uint in the case of the binary mixture is given by eqn (3), for each cluster individually:
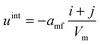 | (3) |
| Vexcl = bxv·Vvdw | (4) |
In the PEACEMAKER program the aforementioned two parameters are sampled with the aims to make agreement between the experimental and the calculated isobars while searching for the phase with the lowest Gibbs energy at the given pressure and temperature. Since only the liquid phase was considered, the mean absolute deviation function was selected in the program for comparison of the calculated and experimental isobars during the sampling process. The experimental isobars were obtained from the Landolt–Börnstein database.68 Both amf and bxv were kept constant over the whole temperature range since there is no provision for a temperature dependence of these two parameters in the PEACEMAKER program.
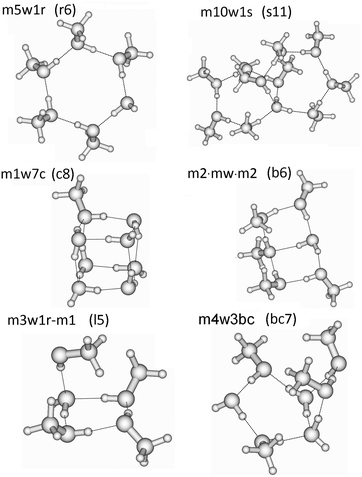
In these QCE calculations it is especially important to provide a representative and comprehensive set of cluster motifs as it has been shown earlier.31 In this study 93 clusters like ring, spiro, book, bicyclic, lasso and cubic structures have been included. The full cluster set (95 including the two monomers) with the naming convention is provided in Table 1 and some representative structures illustrating the notation are presented in Fig. 1. The various structures of the clusters required by the QCE model are denoted as mxwyt where m and w indicate the monomers MeOH (m) and water (w); x and y mean the numbers of the corresponding monomers, and t indicates the cluster type i.e. mon: monomer, dim: dimer, r: monocyclic ring, bc: bicyclic ring, s: spiro cluster31 in which two rings are connected through a common water molecule which establishes four hydrogen-bonds (2 donor and 2 acceptor) towards the two rings; l: lasso, b: book, c: cubic. The ring size of monocyclic clusters (r-type clusters) equals x + y; for spiro cluster besides the total clusters size in parentheses also the numbers of molecules participating in the connected rings are given. For lasso structures in parentheses the numbers of molecules within the ring and of those connected to the ring as well as the points of attachment are given. In the case of seven-membered clusters besides monocyclic rings also bi- and polycyclic structures consisting of a five- and four-membered ring, denoted by bc7(5-4), have been found. Because previously linear chain and lasso structures were found to be less important35,37,38 in the cases of primary alcohols, especially MeOH, within the QCE model only a few of these type of clusters were included. The reason of their smaller contribution originates from the smaller increase (as absolute value) in the interaction energy with the cluster size compared with cyclic structures where the cooperativity effect18,83,84 plays a key role.
| Cluster class | Cluster structure | Number of H-bonds | B3LYP-D3/QZVP | M06-2X/aug-cc-pVTZ | ||||
|---|---|---|---|---|---|---|---|---|
| E int | ΔG298int | ΔG298int/monomer | E int | ΔG298int | ΔG298int/monomer | |||
| a Interaction energies Eint and Gibbs free energies of interaction ΔG298int in kJ mol−1. The M06-2X values for the clusters m8w1s, m8w3s, m9w2s, and m10w1s are based on aug-cc-pVDZ geometries, ZPE, and thermal corrections to ΔGint. | ||||||||
| mon | m1 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| w1 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| dim | m2 | 1 | −24.69 | 16.89 | 8.44 | −24.44 | 14.98 | 7.49 |
| m1w1 | 1 | −21.77 | 12.06 | 6.03 | −20.90 | 13.90 | 6.95 | |
| w1m1 | 1 | −24.39 | 11.67 | 5.84 | −23.83 | 12.92 | 6.46 | |
| w2 | 1 | −21.87 | 11.06 | 5.53 | −21.31 | 13.65 | 6.83 | |
| r3 | m3r | 3 | −75.08 | 19.72 | 6.57 | −72.00 | 15.42 | 5.14 |
| m2w1r | 3 | −73.16 | 16.48 | 5.49 | −71.60 | 17.07 | 5.69 | |
| m1w2r | 3 | −71.16 | 17.29 | 5.76 | −70.96 | 15.62 | 5.21 | |
| w3r | 3 | −69.07 | 17.96 | 5.99 | −70.39 | 17.83 | 5.94 | |
| r4 | m4r | 4 | −133.08 | 17.94 | 4.48 | −121.90 | 1.25 | 0.31 |
| m3w1r | 4 | −130.20 | 13.33 | 3.33 | −121.27 | 6.68 | 1.67 | |
| m2w2r | 4 | −127.46 | 16.78 | 4.19 | −120.71 | 9.98 | 2.49 | |
| m1w3r | 4 | −124.89 | 11.29 | 2.82 | −119.68 | 13.07 | 3.27 | |
| w4r | 4 | −122.36 | 14.70 | 3.68 | −118.77 | 17.15 | 4.29 | |
| r5 | m5r | 5 | −176.80 | 21.49 | 4.30 | −163.32 | 14.30 | 2.86 |
| m4w1r | 5 | −173.36 | 19.23 | 3.85 | −159.68 | 8.05 | 1.61 | |
| m3w2r | 5 | −169.81 | 21.25 | 4.25 | −157.59 | 11.13 | 2.23 | |
| m2w3r | 5 | −165.96 | 22.54 | 4.51 | −155.94 | 18.27 | 3.65 | |
| m1w4r | 5 | −163.26 | 22.90 | 4.58 | −155.59 | 18.62 | 3.72 | |
| w5r | 5 | −160.58 | 20.76 | 4.15 | −154.13 | 22.93 | 4.59 | |
| r6 | m6r | 6 | −217.84 | 35.91 | 5.98 | −200.47 | 0.60 | 0.10 |
| m5w1r | 6 | −214.21 | 35.51 | 5.92 | −198.91 | 6.39 | 1.07 | |
| m4w2r | 6 | −210.60 | 33.30 | 5.55 | −197.35 | 15.34 | 2.56 | |
| m3w3r | 6 | −207.21 | 30.58 | 5.10 | −195.72 | 18.73 | 3.12 | |
| m2w4r | 6 | −203.84 | 32.73 | 5.45 | −194.11 | 24.65 | 4.11 | |
| m1w5r | 6 | −200.76 | 29.77 | 4.96 | −192.28 | 27.35 | 4.56 | |
| w6r | 6 | −197.78 | 30.39 | 5.07 | −190.47 | 31.31 | 5.22 | |
| r7 | m7r | 7 | −261.88 | 42.60 | 6.09 | −242.00 | 29.90 | 4.27 |
| m6w1r | 7 | −257.54 | 40.59 | 5.80 | −240.49 | 34.72 | 4.96 | |
| m5w2r | 7 | −253.78 | 43.01 | 6.14 | −238.75 | 40.97 | 5.85 | |
| m4w3r | 7 | −250.44 | 40.53 | 5.79 | −237.95 | 44.14 | 6.31 | |
| m3w4r | 7 | −245.83 | 42.51 | 6.07 | −234.13 | 48.37 | 6.91 | |
| m2w5r | 7 | −239.41 | 45.81 | 6.54 | −230.56 | 39.58 | 5.65 | |
| m1w6r | 7 | −234.20 | 37.28 | 5.33 | −226.72 | 43.78 | 6.25 | |
| w7r | 7 | −227.96 | 49.45 | 7.06 | −220.17 | 37.24 | 5.32 | |
| bc7(5-4) | m6w1bc | 8 | −263.59 | 42.38 | 6.05 | −242.49 | 34.45 | 4.92 |
| m5w2bc | 8 | −260.87 | 37.81 | 5.40 | −243.50 | 36.35 | 5.19 | |
| m4w3bc | 8 | −255.85 | 37.44 | 5.35 | −241.75 | 41.28 | 5.90 | |
| m3w4bc | 8 | −250.83 | 41.43 | 5.92 | −240.26 | 37.97 | 5.42 | |
| m2w5bc | 9 | −255.42 | 39.40 | 5.63 | −246.11 | 31.00 | 4.43 | |
| m1w6bc | 9 | −251.33 | 36.66 | 5.24 | −244.61 | 36.80 | 5.26 | |
| w7bc | 9 | −247.39 | 34.26 | 4.89 | −241.68 | 38.40 | 5.49 | |
| s5(3-3) | m4w1s | 6 | −145.57 | 52.10 | 10.42 | −140.81 | 32.08 | 6.42 |
| m3w2s | 6 | −143.10 | 51.88 | 10.38 | −140.26 | 34.73 | 6.95 | |
| m2w3s | 6 | −140.95 | 47.91 | 9.58 | −139.93 | 34.67 | 6.93 | |
| m1w4s | 6 | −138.81 | 42.77 | 8.55 | −139.29 | 35.73 | 7.15 | |
| w5s | 6 | −136.99 | 42.51 | 8.50 | −138.93 | 37.01 | 7.40 | |
| s6(3-4) | m5w1s | 7 | −203.39 | 48.52 | 8.09 | −190.70 | 29.28 | 4.88 |
| m4w2s | 7 | −201.22 | 48.74 | 8.12 | −190.35 | 32.49 | 5.41 | |
| m3w3s | 7 | −198.04 | 41.48 | 6.91 | −189.37 | 32.71 | 5.45 | |
| m2w4s | 7 | −195.69 | 41.17 | 6.86 | −188.49 | 30.42 | 5.07 | |
| m1w5s | 7 | −192.80 | 42.76 | 7.13 | −187.71 | 33.78 | 5.63 | |
| w6s | 7 | −190.27 | 43.51 | 7.25 | −186.73 | 38.60 | 6.43 | |
| s9(5-5) | m8w1s | 10 | −357.17 | 55.40 | 6.16 | −327.91 | 46.11 | 5.12 |
| m7w2s | 10 | −352.89 | 57.28 | 6.36 | −325.19 | 49.64 | 5.52 | |
| m6w3s | 10 | −348.04 | 59.15 | 6.57 | −328.16 | 39.34 | 4.37 | |
| m5w4s | 10 | −342.96 | 61.85 | 6.87 | −324.78 | 42.49 | 4.72 | |
| m4w5s | 10 | −339.60 | 60.48 | 6.72 | −319.22 | 37.37 | 4.15 | |
| m3w6s | 10 | −334.50 | 60.68 | 6.74 | −316.61 | 40.36 | 4.48 | |
| m2w7s | 10 | −331.41 | 57.48 | 6.39 | −315.10 | 43.19 | 4.80 | |
| m1w8s | 10 | −328.49 | 53.80 | 5.98 | −313.82 | 49.65 | 5.52 | |
| w9s | 10 | −325.62 | 54.85 | 6.09 | −312.61 | 50.78 | 5.64 | |
| s11(6-6) | m10w1s | 12 | −445.33 | 72.99 | 6.64 | −412.86 | 64.48 | 5.86 |
| m9w2s | 12 | −429.57 | 90.54 | 8.23 | −406.99 | 72.29 | 6.57 | |
| m8w3s | 12 | −424.96 | 93.75 | 8.52 | −395.11 | 52.32 | 4.76 | |
| m7w4s | 12 | −421.45 | 90.79 | 8.25 | −395.51 | 50.19 | 4.56 | |
| m6w5s | 12 | −417.84 | 87.80 | 7.98 | −393.85 | 48.42 | 4.40 | |
| m5w6s | 12 | −413.08 | 88.83 | 8.08 | −389.70 | 46.33 | 4.21 | |
| m4w7s | 12 | −409.66 | 90.71 | 8.25 | −388.05 | 54.69 | 4.97 | |
| m3w8s | 12 | −406.37 | 86.19 | 7.84 | −386.33 | 56.45 | 5.13 | |
| m2w9s | 12 | −407.83 | 76.25 | 6.93 | −391.44 | 57.29 | 5.21 | |
| m1w10s | 12 | −404.44 | 73.24 | 6.66 | −389.72 | 62.27 | 5.66 | |
| w11s | 12 | −401.20 | 74.77 | 6.80 | −388.26 | 66.66 | 6.06 | |
| l5(4-1) | m3w1r-m1 | 5 | −160.57 | 33.92 | 6.78 | −150.76 | 35.86 | 7.17 |
| l6(5-1) | m5r-w1 | 6 | −209.40 | 41.25 | 6.87 | −193.96 | 33.10 | 5.52 |
| l6(4-2) | m3w1r-2m1(1,1) | 6 | −195.04 | 56.63 | 9.44 | −184.46 | 50.15 | 8.36 |
| m3w1r-2m1(1,3) | 6 | −189.89 | 60.69 | 10.11 | −177.78 | 44.24 | 7.37 | |
| b6(4-4) | m2mwm2 | 7 | −220.47 | 27.84 | 4.64 | −204.74 | 21.47 | 3.58 |
| mwmwm2 | 7 | −215.86 | 33.51 | 5.58 | −201.60 | 18.49 | 3.08 | |
| mwmwmw | 7 | −212.42 | 30.65 | 5.11 | −200.34 | 22.54 | 3.76 | |
| w2mwmw | 7 | −210.13 | 26.32 | 4.39 | −199.51 | 23.86 | 3.98 | |
| mww2mw | 7 | −208.13 | 33.47 | 5.58 | −198.48 | 26.23 | 4.37 | |
| w2mww2 | 7 | −207.15 | 27.90 | 4.65 | −198.26 | 26.78 | 4.46 | |
| w2w2w2 | 7 | −202.96 | 31.01 | 5.17 | −196.48 | 31.91 | 5.32 | |
| mww2w2 | 7 | −205.30 | 30.21 | 5.03 | −197.28 | 28.74 | 4.79 | |
| m2w2mw | 7 | −211.51 | 36.48 | 6.07 | −202.07 | 27.86 | 4.64 | |
| m2w2m2 | 7 | −216.05 | 31.16 | 5.19 | −203.55 | 25.13 | 4.19 | |
| c8 | m5w3c | 11 | −331.17 | 24.08 | 3.01 | −307.14 | 30.56 | 3.82 |
| m4w4c | 12 | −341.18 | 17.11 | 2.14 | −319.27 | 21.34 | 2.67 | |
| m3w5c | 12 | −337.67 | 15.94 | 1.99 | −318.44 | 23.83 | 2.98 | |
| m2w6c | 12 | −333.81 | 20.12 | 2.51 | −317.63 | 26.52 | 3.32 | |
| m1w7c | 12 | −330.03 | 20.77 | 2.60 | −316.91 | 28.57 | 3.57 | |
| w8c | 12 | −326.18 | 27.15 | 3.39 | −315.84 | 30.39 | 3.80 | |
| c8-lasso | m4w4c-m1 | 13 | −369.71 | 38.44 | 4.27 | −350.33 | 42.17 | 4.69 |
Because not only the temperature but also the composition dependence of the cluster distribution were planned to be studied, the ring, spiro and cubic clusters were created with all the possible compositions. Hence, starting from pure water clusters, water molecules were successively replaced by methanol molecules with the restriction that the cluster motifs remain unchanged. Therefore, in the case of the spiro clusters one water molecule had to be retained; in the case of the cubic c8 clusters four water molecules are needed to be kept; in case of the ring type clusters, no such restriction applies. The replacements have been carried out according to the previous findings:37 in structures with adjacent MeOH molecules the methyl groups were oriented to different directions (i.e. up–down, respectively). Furthermore, the replacements have been done more or less randomly within the structures, keeping in mind that the appropriate selection of cluster motifs31 (i.e. inclusion of the cubic, the ring and the spiro cluster classes) is more important than the strict placement of the methyl groups or using strictly the putative global minimum structure of a given cluster type. Cartesian coordinates of all clusters optimized with B3LYP-D3/TZVP and M06-2X/aug-cc-pVTZ methods are available as ESI.†
Results and discussion
Values of amf and bxv obtained by fitting to experimental isobars for MeOH–water binary mixtures of different composition [molar fraction x(MeOH)] are summarized in ESI,† Table S1. With increasing methanol molar fraction, the amf value also increases, from 0.19 up to 0.41 J m3 mol−1. At the same time, the fitting becomes less accurate as shown by the increase of the mean absolute error (MAE). Importantly, the ratio of amf/bxv is not constant but shows a parabolic shape. As a consequence, the application of the one-parameter variant of the QCE model to the methanol–water mixture might be problematic.A similar dependence of the quality of the fitting on the composition has also been found for the DMSO–water binary system.30 However, while in DMSO–water the deviation increases with increasing water content, in the MeOH–water mixture the quality of the fit becomes less satisfactory with increasing x(MeOH), i.e. with decreasing water content. For DMSO–water these deviations had been attributed to the rather small clusters used.30 In the present case of MeOH–water not only larger clusters but also a more extensive cluster set has been used.
In the case of neat water the cubic w8c cluster has been shown to dominate at low temperatures,31,32 although neglecting it led to slightly more accurate isobars. To check the importance of this cluster type in binary MeOH–water mixtures, the fitting to experimental isobars has been done with and without these c8 clusters. Experimental isobars of neat water, neat MeOH, and of the 30, 60, 80 w% MeOH–water mixtures and those calculated by the QCE model using B3LYP-D3 results are shown in Fig. 2.
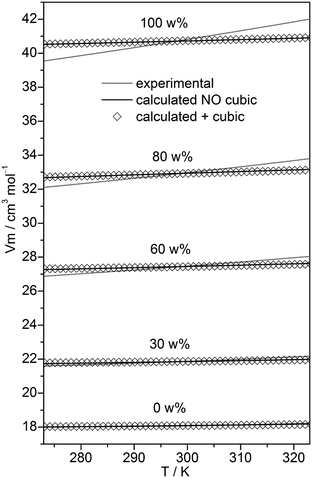 | ||
| Fig. 2 Plot of experimental isobars68 of neat water, neat MeOH and 10, 30, 60, 80 w% MeOH–water mixtures versus those obtained by the QCE model with and without inclusion of the cubic c8 clusters. | ||
Compared with experiment a somewhat too small slope of the isobars – irrespective of the composition – is obtained. As ESI,† Table S2 shows, when cubic c8 clusters are excluded, the values of amf and bxv are only slightly changed. Isobars as well as the values of amf and bxv obtained from M06-2X calculations differ only marginally from those based on B3LYP-D3 calculations (Tables S1 and S2, ESI†).
The quality of the fit only marginally depends on whether cubic clusters are included in the set or not (Fig. 2). The numbers of clusters corresponding to a specific x(MeOH) is shown in ESI,† Fig. S1. Although the number of clusters vary with x, overall the chosen cluster set should allow for a balanced description of the MeOH–water mixture over the whole range of MeOH content.
Based on these optimal parameters amf and bxv in the following, first interaction energies and distribution of the individual clusters considered for the MeOH–water binary mixture will be presented. Second, thermodynamic properties (heat capacities Cp, excess enthalpies, entropies, Gibbs free energies, and volumes of mixing, HE, SE, GE, and VE) derived therefrom will be compared with the corresponding experimental data as well as those obtained from previous calculations (molecular dynamics and Monte Carlo simulations).
Cluster distribution in MeOH–H2O binary mixture
B3LYP-D3 as well as M06-2X interaction energies Eint and Gibbs free energies of interaction ΔG298int for the whole cluster set used in the QCE procedure are presented in Table 1.While interaction energies are strongly negative and approximately correlate with the number of hydrogen bonds, Gibbs free energies of interactions are invariably positive and do not show any correlation with the number of hydrogen bonds.
According to the study of Thakkar et al.21 dispersion-corrected density functionals work reasonably well for MeOH clusters compared with CCSD(T) results. Furthermore, M06-2X/aug-cc-pVDZ interaction energies per molecule of both linear as well as cyclic MeOH clusters were found to be nearly identical to those obtained by MP2/aug-cc-pVTZ calculations.19 In contrast, B3LYP without dispersion corrections resulted in larger deviations.19 Comparison of the present B3LYP-D3/QZVP//TZVP and M06-2X/aug-cc-pVTZ interaction energies with our previous MP2(fc)-CP/6-311++G(d,p) results indicate more negative Eint values but nearly identical trends for both density functionals (Fig. S2, ESI†). Moreover, B3LYP-D3 calculated interaction energies for the full cluster set considered in this paper (Table 1) are in close agreement with the corresponding M06-2X/aug-cc-pVTZ values (R2 = 0.998, Fig. S3, ESI†). Thus, we are confident that the functionals used are appropriate for this study.
The population (based on the B3LYP-D3 calculations) of pure water, pure methanol as well as mixed clusters without further distinction of their composition at three different temperatures (273, 298, and 323 K) is displayed in Fig. 3.
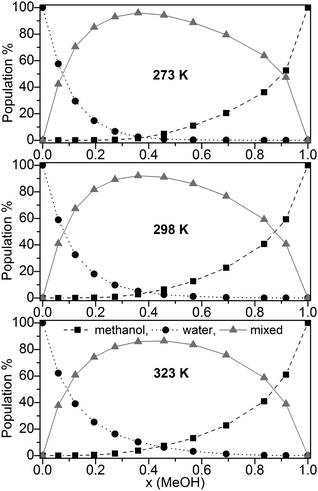 | ||
Fig. 3 Population (%) of ■ pure methanol clusters, ● pure water cluster,  mixed MeOH–water clusters at 273 K, 298 K, and 323 K based on the B3LYP-D3 calculations. mixed MeOH–water clusters at 273 K, 298 K, and 323 K based on the B3LYP-D3 calculations. | ||
Irrespective of the temperature mixed clusters dominate over a wide range of the composition of the binary MeOH-water system (≥60% in the range x(MeOH) = 0.1 to 0.8). Only a slight decrease of the contribution of mixed clusters with increasing temperature is found (Fig. 3). It is interesting to note that NMR relaxation time measurements of MeOH–water mixtures have indicated that at low temperatures Tk < 245 K clusters between the same species prevail while above Tk mixed clusters are preferred.85
Since the lowest temperature considered here (T = 273 K) is well above Tk the predominance of mixed clusters in the intermediate molar fraction region is in line with these experimental findings. Although we have taken into account only clusters up to 11 molecules, our result obtained for the maximum population of mixed clusters at x = 0.365 (273 K) is in line with the mass spectroscopy experiments of Wakisaka.5,8 From these experiments it had been concluded that above x(MeOH) = 0.375 the self-association of alcohol clusters becomes more preferred with increasing x(MeOH).5,8 The gross populations of pure and mixed clusters based on M06-2X/aug-cc-pVTZ calculations are quite similar to those obtained by B3LYP-D3 (Fig. S4, ESI†). The most notable difference concerns mixed clusters which show lower populations over the whole range of x(MeOH) than those based on B3LYP-D3 calculations [<70% (M06-2X) at T = 298 K compared with up to 90% (B3LYP-D3, Fig. 3)]. For DMSO–water binary system a similar distribution of pure water, pure DMSO, and mixed clusters had been found.30 However, the drop and/or rise of the pure clusters is less steep in DMSO–water than in MeOH–water.
For instance, ∼60% pure water clusters at x(DMSO) = 0.2 and ∼60% pure DMSO clusters at x(DMSO) = 0.8 had been calculated30 compared with ∼20% pure water clusters at x(MeOH) = 0.2 and ∼40% pure MeOH clusters at x(MeOH) = 0.8 (Fig. 3). Consequently, the population of the mixed DMSO–water clusters is significantly lower (≤60%)30 than that of mixed MeOH–water clusters.
The population of the various cluster classes irrespective of their composition (based on the B3LYP-D3 calculations) is presented in Fig. 4a (cubic c8 clusters included) and Fig. 4b (populations with cubic c8 clusters neglected).
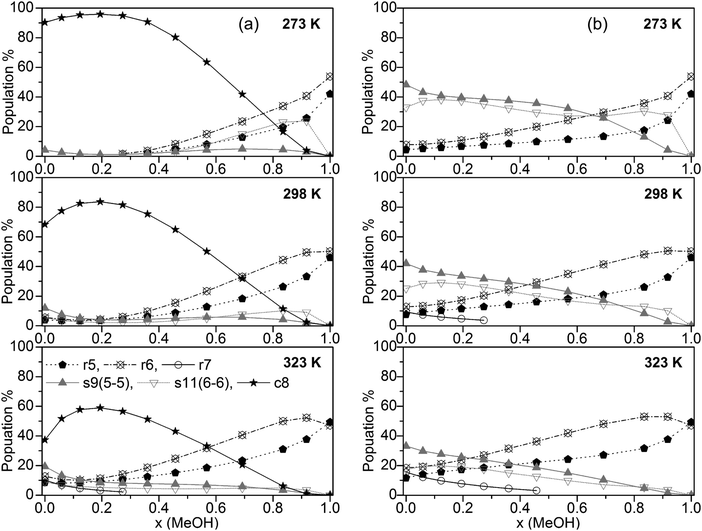 | ||
| Fig. 4 Plot of the population of the cluster classes (a) including and (b) excluding cubic c8 clusters (for clarity, only clusters with populations >10% are shown). | ||
The results in Fig. 4a show that only some of the used clusters are important to consider when including cubic clusters. These are the five- and six-membered monocyclic structures with only one ring, the 8-membered cubic clusters and the s9 and s11 spiro-type clusters. In line with previous findings for neat water32,33 the population of cubic c8 clusters decreases with increasing temperature. Nevertheless, this cluster type by far is dominating up to x(MeOH) = 0.7 (273 K), and x(MeOH) = 0.5 (323 K). Since these clusters contain at least 4 water molecules it is not surprising that at higher MeOH contents their population drops significantly while the populations of monocyclic clusters (r5 and especially r6) where there is no such restriction with respect to the number of water molecules increase substantially at high x(MeOH). The presence of such cyclic structures in liquids capable of forming hydrogen bonds has been corroborated by experimental studies (soft X-ray emission86 and X-ray absorption augmented by DFT calculations87). Especially at lower temperatures the spiro-type cluster s11(6-6) is quite important for mixtures with relatively high MeOH content (maximum of ∼25% at x(MeOH) ∼ 0.8 and T = 273 K, Fig. 4). The populations of s9 spiro type clusters are fairly constant over the whole composition of the MeOH–water mixture at low temperatures; at T = 323 K this cluster type is also populated (10–20%) especially in the water-rich region.
If cubic clusters are neglected in the QCE model (Fig. 4b), the spiro-type clusters s11(6-6) and especially s9(5-5) dominate in the water-rich region at lower temperatures (up to x(MeOH) = 0.6 at T = 273 K); with increasing temperature their contribution decreases from ∼50% (T = 273 K) to ∼35% (T = 323 K) for neat water. Since at least one water molecule is required for the spiro motif, the population steadily decreases with increasing MeOH content. In contrast to spiro clusters, the populations of monocyclic rings (r5 and r6) steadily increase with x(MeOH). As a consequence, neat MeOH is almost exclusively (>90%) composed of five- and six-membered ring clusters. Since cubic clusters require at least four water molecules, this result holds irrespective whether c8 clusters are included or not in the cluster set used to describe the MeOH–water system. Interestingly, seven-membered monocyclic rings r7 are not negligible at higher temperatures and low MeOH content (Fig. 4b).
Populations of individual clusters, i.e. distinguished by composition, are plotted in Fig. 5a (including cubic clusters) and Fig. 5b (neglecting cubic clusters). Dominating clusters are the cubic, spiro (s9 and s11), and ring-type structures while book, lasso and bicyclic clusters are of minor importance. Concerning cubic clusters, for neat water the w8c cluster is by far dominating, ∼70% at T = 273 and 298 K, ∼40% at T = 323 K. With increasing MeOH content the population of this cluster drops quite quickly (∼10% for x(MeOH) = 0.2). In the water-rich region with x(MeOH) < 0.3 the m1w7c structure becomes the dominating cubic cluster with a relatively sharp maximum at x(MeOH) ∼ 0.15. In the intermediate region, x(MeOH) = 0.2 to 0.7 the largest population is obtained for m3w5c and, to a lesser extent, for m4w4c. Especially at lower temperatures (T = 273 and 298 K) and low MeOH content (x(MeOH) = 0.1–0.4) the m2w6c cluster is significantly populated. An increase of the temperature results in a decrease of the populations of these cubic clusters. With respect to spiro-type clusters, in neat water and at very low MeOH content (x ≤ 0.15) only w9s is significantly populated with the population increasing at higher temperatures at the expense of w8c. The only other spiro-type cluster is m10w1s at T = 273 K for x(MeOH) > 0.5 (maximum of 20% at x(MeOH) = ∼0.9). While monocyclic ring structures consisting solely of water molecules (w6r, w7r) are of minor importance (<15% at T = 323 K and even less at lower temperatures), the analogous MeOH clusters m5r and m6r become increasingly important with increasing MeOH content. As mentioned above, neat MeOH can almost exclusively be described by these two cluster types. At T = 323 K the dominant cluster in the region x(MeOH) = 0.6–0.8 is m5w1r. The analogous plot obtained with M06-2X for T = 298 K is shown in Fig. S5 (ESI†). Similar to the B3LYP-D3 results, the dominating cluster types at low MeOH content are the cubic clusters w8c and m1w7c and at high MeOH content the m6r ring structure. In the range x(MeOH) = 0.6–0.9 the cyclic cluster m5w1r is already significantly populated (10–20%) at T = 298 K. Interestingly, in contrast to the B3LYP-D3 results, the five-membered cyclic m5r cluster does not show any substantial population at T = 298 K.
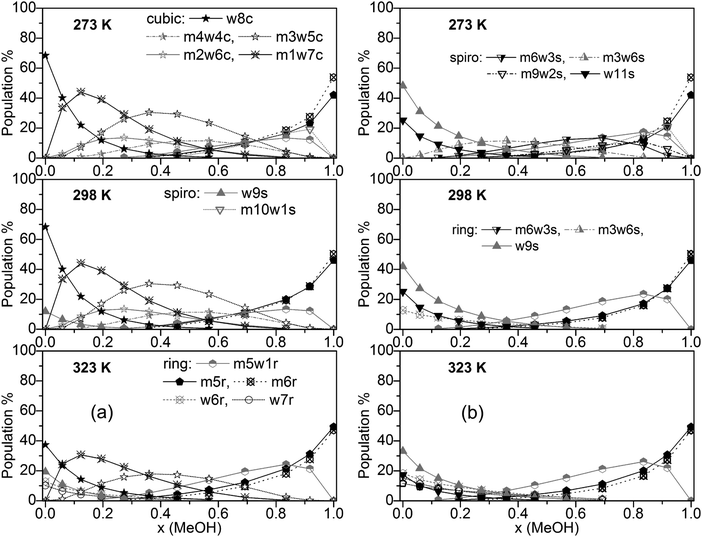 | ||
| Fig. 5 Plot of individual cluster distributions (a) including and (b) excluding cubic c8 clusters (for clarity, only clusters with populations >8% are shown). | ||
Fig. 5b presents cluster populations obtained when cubic clusters are excluded. In the MeOH – rich region (x(MeOH) > 0.8) where cubic clusters are of minor importance, the cluster distribution is quite similar to that obtained with cubic clusters included. The most important contributions are due to the five- and six-membered monocyclic rings m5r, m6r, and m5w1r. Of course, for neat MeOH the population of this latter cluster drops to 0 (Fig. 5b). For neat water and low MeOH content a significant increase of the spiro-type water clusters w9s and w11s can be seen. At higher temperatures the contributions of these clusters decrease in favor of monocyclic rings w6r and w5r (at T = 323 K). This is in agreement with Wakisaka’s results,8 that self-associated clusters are formed predominantly at low molar fraction (water clusters) and high molar fraction (x ≥ 0.375, methanol clusters).
Calculated thermodynamic functions for methanol–water binary liquid mixtures
Based on the QCE calculations, the following thermodynamic functions are available from the canonical partition function according to eqn (22)–(29) in ref. 33 for the different temperatures and compositions: internal energy, enthalpy, entropy, Gibbs free energy, Helmholtz free energy as well as second derivatives of the partition function, like constant pressure and constant volume heat capacities.In Table 2 we compare the experimental excess enthalpies, entropies, and Gibbs free energies of mixing64,65,67,68,88–91 with those calculated by the QCE model as well as those obtained from a molecular dynamics simulation/two-phase thermodynamics (MD/2PT)56 for different compositions of the MeOH–water system.
| x(MeOH) | Exp.67,88, 91 | MD/2PT56 | OPLS/TIP4P64 | QCE B3LYP-D3 | QCE M06-2X | |
|---|---|---|---|---|---|---|
| 0.05 | H E | –0.57 | –0.18 | –0.25 | –0.81 | –0.40 |
| S E | –2.48 | –0.70 | –1.01 | –2.91 | –2.02 | |
| G E | 0.17 | 0.06 | 0.05 | 0.11 | 0.20 | |
| 0.27 | H E | –0.88 | –0.66 | –0.32 | –2.18 | –0.49 |
| S E | –3.93 | –3.31 | –3.42 | –8.44 | –4.25 | |
| G E | 0.29 | 0.37 | 0.70 | 0.42 | 0.78 | |
| 0.54 | H E | –0.79 | –0.82 | –0.32 | –1.67 | –0.17 |
| S E | –3.69 | –3.93 | –3.50 | –7.45 | –3.84 | |
| G E | 0.31 | 0.42 | 0.72 | 0.63 | 0.97 | |
| 0.70 | H E | –0.61 | –0.73 | –0.22 | –1.06 | 0.16 |
| S E | –2.89 | –3.39 | –2.77 | –5.48 | –2.99 | |
| G E | 0.25 | 0.35 | 0.61 | 0.61 | 1.05 | |
The excess enthalpies of mixing HE (eqn (5)) (Fig. 6a) and the excess entropy of mixing SE (eqn (6)) (Fig. 6b) obtained by the QCE calculations with and without inclusion of cubic clusters are plotted against experimental data.89,90
| HE(x) = H(x) − [H(H2Oliq) × (1 − x) + H(MeOHliq) × x] | (5) |
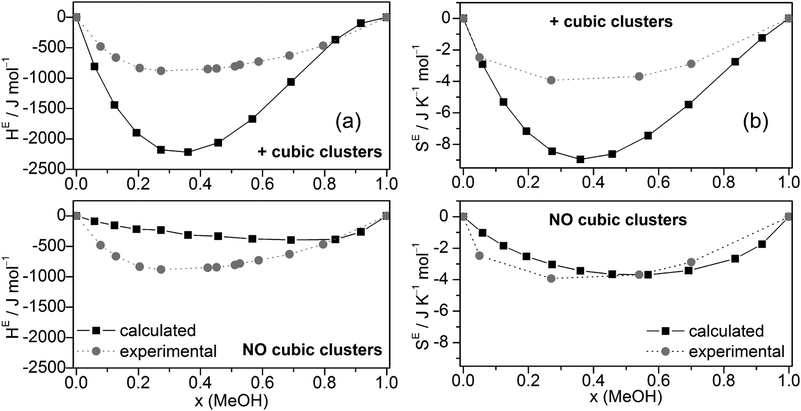 | ||
| Fig. 6 Comparison of experimental and calculated excess enthalpies of mixing HE (a),89,90 excess entropies of mixing SE (b)56 for the full cluster set as well as the cluster set without the cubic c8 clusters at different molar ratios. | ||
The enthalpy values H are taken from the PEACEMAKER output, where H(H2Oliq) and H(MeOHliq) are the values for x = 0.0 and x = 100.0, respectively. Compared with experiment, the values of HE are too negative but the minima of the curves occur approximately at the same molar fraction (x ∼ 0.36). In contrast, MD/2PT56 with the SPC/E model for water (which gave the best results) and even more so OPLS/TIP4P64 calculations resulted in less negative HE values than experiment (Table 2). Neglecting cubic clusters leads to considerably less negative excess enthalpies of mixing HE, i.e. values closer to experiment but with a minimum shifted to much higher MeOH content, x(MeOH) ∼ 0.8 (Fig. 6a). The excess entropy of mixing SE is computed according to eqn (6).
SE(x) = S(x) − [S(H2Oliq) × (1 − x) + S(MeOHliq) × x] + R[x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(x) + (1 − x)ln(1 − x)] ln(x) + (1 − x)ln(1 − x)] | (6) |
Combining HE and SE results to Gibbs free energies of mixing via GE = HE − T·SE. GE values agree relatively well with the experimental data (Fig. 7), although more positive. Compared with the GE values obtained by MD/2PT56 or OPLS/TIP4P64 the corresponding QCE data are more and less, respectively, positive except at x(MeOH) = 0.05 (Table 2).
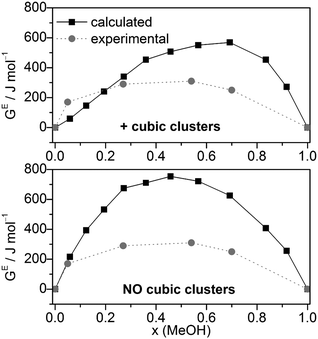 | ||
| Fig. 7 Comparison of experimental56 and calculated excess Gibbs free energies of mixing GE for the full cluster set as well as the cluster set without the cubic c8 clusters at different molar ratios (T = 298 K). | ||
Excess thermochemical quantities of mixing obtained by the QCE model using M06-2X interaction energies and vibrational frequencies show the following (Table 2 and Fig. S6, ESI†): the HE values are less negative than those obtained with B3LYP-D3 or even positive in the methanol rich region (x > 0.7); SE values are in quite good agreement with experimental values especially in the case of the full cluster set. As a consequence, the GE values are more positive than the experimental ones or those calculated by the B3LYP-D3 functional.
The calculated dependence of the excess Gibbs free energy of mixing for the only other binary solvent system treated so far by the QCE model (DMSO–water) closely matches the experimental curve, especially the minimum at x(DMSO) ∼ 0.4. In contrast to MeOH–water, for DMSO–water GE is negative over the whole range of x(DMSO). However, similar to the MeOH–water results, the QCE model yields for DMSO–water also too positive GE values compared with experiment.30
Other quantities which can be compared with experiment are excess volumes of mixing VE (Fig. 8), heat capacities Cp (Fig. 9), and excess heat capacities of mixing CEp (Fig. S7, ESI†). VE and CEp were calculated in analogy to eqn (5). Since the parameter fits have been carried out to get good agreement between experimental and calculated molar volumes (Vm), the calculated VE values agree nearly perfectly with the corresponding experimental data68 as well as those obtained from a Monte Carlo simulation of TIP4P water and OPLS MeOH mixtures.63
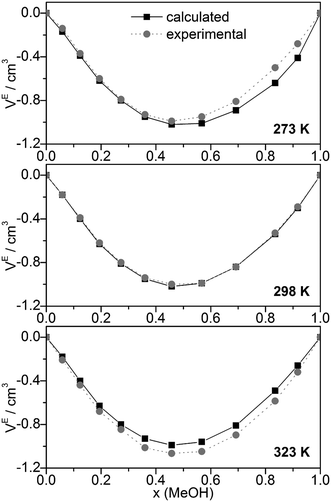 | ||
| Fig. 8 Comparison of experimental68 and calculated excess volumes of mixing VE. | ||
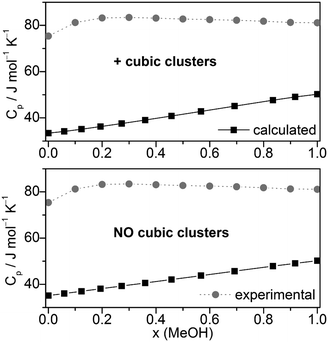 | ||
| Fig. 9 Comparison of experimental67,92,93 and calculated heat capacities Cp at T = 298.15 K. | ||
The heat capacities Cp or the excess heat capacities of mixing CEp are the least satisfactorily reproduced quantities by the QCE calculations, irrespective of whether B3LYP-D3 or M06-2X results were used (Fig. 9, Fig. S7 and S8, ESI†). Such discrepancies had already been noticed in the original QCE publication.23 One possible explanation of this deviation is the application of harmonic oscillator approximation even for the low frequency vibrations. In line with this, the vibrational contribution (Cp,vib) obtained from the vibrational partition function possess the largest amount of contribution to Cp, also in accordance with ref. 33.
Furthermore, it should be considered that the heat capacity is the second derivative of the partition function. Thus it is affected more by the applied approximations in the model than the other first derivative quantities.
Conclusions
The quantum cluster equilibrium model has been applied for the binary mixture of MeOH–water. Structures and interaction energies for a set of 93 clusters of different size, composition as well as class (chain, monocyclic rings, spiro, lasso, bicyclic, cubic) have been calculated by density functional theory (B3LYP-D3/QZVP and M06-2X/aug-cc-pVTZ including counterpoise BSSE corrections). B3LYP-D3 results in somewhat more negative interaction energies but the observed trend closely matches that obtained by M06-2X. The two fitting parameters amf and bxv used in the QCE model were obtained by fitting to experimental isobars of MeOH–water binary mixtures with varying composition. Isobars based on B3LYP-D3 and M06-2X calculations were quite similar. With increasing MeOH content an increasing deviation between calculated and experimental isobars was found. Cluster distributions calculated by the QCE model using either B3LYP-D3 or M06-2X were quite similar with one notable exception: while the monocyclic ring-type clusters m5r and m6r both were found quite significant at high MeOH content with B3LYP-D3, only m6r showed a substantial population (50–100% in the range x(MeOH) = 0.7–1.0) based on M06-2X interaction energies and vibrational frequencies. Cubic c8 cluster structures like w8c or m1w7c were found to dominate at low MeOH content whereas monocyclic ring structures, especially m6r were the most important clusters for x(MeOH) > 0.8. In the intermediate region, x(MeOH) ∼ 0.4 to 0.7 the cubic cluster m3w5c is the dominant species. With increasing temperature the populations of these clusters decrease with a concomitant increase of other cluster populations, e.g. the monocyclic ring structure m5w1r.Compared with experiment the calculated (B3LYP-D3) excess enthalpies of mixing HE of methanol–water are somewhat too negative, those based on M06-2X are less negative and show larger overall deviations from the experimental curve in the methanol rich region. Excess entropies of mixing SE are also too negative with B3LYP-D3 while those based on M06-2X nearly perfectly match the experimental SEvs. x(MeOH) curve. Calculated excess Gibbs free energies of mixing GE by either density functional are more positive than experimental values With respect to previous molecular dynamics simulations of the MeOH–water mixtures,56,64 the QCE model based on B3LYP-D3 calculations consistently results in excess enthalpies HE and especially entropies SE of mixing which are more negative. Excess Gibbs free energies of mixing GE are slightly more positive than the MD/2PT results of Pascal and Goddard56 and slightly less positive than or even equal to the MD results of Tanaka and Gubbins.64 The calculated excess volumes of mixing compare well with experiment. Significant deviations between calculated and experimental heat capacities Cp and excess heat capacity of mixing CEp were found.
Acknowledgements
The computations were run on the Hungarian HPC infrastructure (NIIF Institute, Hungary) and on computational facilities at Karl-Franzens University of Graz and at Graz University of Technology. The authors thank Prof. B. Kirchner and S.B.C. Lehmann for the discussions regarding the PEACEMAKER program. Financial support of the SROP-4.2.2.A-11/1/KONV-2012-0065 project is gratefully acknowledged. The work was also supported by the Scholarship program of the Aktion Österreich-Ungarn.Notes and references
- R. Mecke and H. Kempter, Naturwissenschaften, 1939, 27, 583 Search PubMed
.
-
Y. Marcus, Solvent Mixtures, Properties and Selective Solvation, CRC Press, 2002 Search PubMed
.
- A. Ben-Naim, J. Phys. Chem. B, 2007, 111, 2896 CrossRef CAS PubMed
.
-
C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, Wiley-VCH Verlag, Weinheim, 3rd edn, 2003 Search PubMed
.
- A. Wakisaka and T. Iwakami, J. Mol. Liq., 2014, 189, 44 CrossRef CAS PubMed
.
- A. Wakisaka and K. Matsuura, J. Mol. Liq., 2006, 129, 25 CrossRef CAS PubMed
.
- A. Wakisaka, S. Mochizuki and H. Kobara, J. Solution Chem., 2004, 33, 721 CrossRef CAS
.
- A. Wakisaka, S. Komatsu and Y. Usui, J. Mol. Liq., 2001, 90, 175 CrossRef CAS
.
- A. Wakisaka and T. Ohki, Faraday Discuss., 2005, 129, 231 RSC
.
- A. Wakisaka and Y. Yamamoto, J. Chem. Soc., Chem. Commun., 1994, 2105 RSC
.
- S. Kunsagi-Mate and K. Iwata, Chem. Phys. Lett., 2009, 473, 284 CrossRef CAS PubMed
.
- S. Kunsagi-Mate and K. Iwata, J. Solution Chem., 2013, 42, 165 CrossRef CAS
.
- A. Mandal, M. Prakash, R. M. Kumar, R. Parthasarathi and V. Subramanian, J. Phys. Chem. A, 2010, 114, 2250 CrossRef CAS PubMed
.
- G. Matisz, A.-M. Kelterer, W. M. F. Fabian and S. Kunsagi-Mate, J. Phys. Chem. A, 2011, 115, 10556 CrossRef CAS PubMed
.
- V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. Goddard, J. Chem. Theory Comput., 2009, 5, 1016 CrossRef CAS
.
- R. Wieczorek, L. Haskamp and J. J. Dannenberg, J. Phys. Chem. A, 2004, 108, 6713 CrossRef CAS
.
- R. N. Barnett and U. Landman, J. Phys. Chem. A, 1997, 101, 164 CrossRef CAS
.
- S. L. Boyd and R. J. Boyd, J. Chem. Theory Comput., 2007, 3, 54 CrossRef CAS
.
- P. Golub, I. Doroshenko and V. Pogorelov, Phys. Lett. A, 2014, 378, 1937 CrossRef CAS PubMed
.
- F. C. Hagemeister, C. J. Gruenloh and T. S. Zwier, J. Phys. Chem. A, 1998, 102, 82 CrossRef CAS
.
- S. Kazachenko, S. Bulusu and A. J. Thakkar, J. Chem. Phys., 2013, 138, 224303 CrossRef PubMed
.
- F. Weinhold, J. Chem. Phys., 1998, 109, 367 CrossRef CAS PubMed
.
- F. Weinhold, J. Chem. Phys., 1998, 109, 373 CrossRef CAS PubMed
.
- R. Ludwig and F. Weinhold, J. Chem. Phys., 1999, 110, 508 CrossRef CAS PubMed
.
- R. Ludwig and F. Weinhold, Phys. Chem. Chem. Phys., 2000, 2, 1613 RSC
.
- R. Ludwig and F. Weinhold, Z. Phys. Chem., 2002, 216, 659 CrossRef CAS
.
- R. Ludwig, Phys. Chem. Chem. Phys., 2002, 4, 5481 RSC
.
- P. Borowski, J. Jaroniec, T. Janowski and K. Wolinski, Mol. Phys., 2003, 101, 1413 CrossRef CAS
.
- R. Ludwig, ChemPhysChem, 2007, 8, 938 CrossRef CAS PubMed
.
- A. Lenz and L. Ojamae, J. Chem. Phys., 2009, 131, 134302 CrossRef PubMed
.
- S. B. C. Lehmann, C. Spickermann and B. Kirchner, J. Chem. Theory Comput., 2009, 5, 1640 CrossRef CAS
.
- S. B. C. Lehmann, C. Spickermann and B. Kirchner, J. Chem. Theory Comput., 2009, 5, 1650 CrossRef CAS
.
- B. Kirchner, C. Spickermann, S. B. C. Lehmann, E. Perlt, J. Langner, M. von Domaros, P. Reuther, F. Uhlig, M. Kohagen and M. Brüssel, Comput. Phys. Commun., 2011, 182, 1428 CrossRef CAS PubMed
.
- M. Brüssel, E. Perlt, M. von Domaros, M. Brehm and B. Kirchner, J. Chem. Phys., 2012, 137, 164107 CrossRef PubMed
.
- R. Ludwig, ChemPhysChem, 2005, 6, 1369 CrossRef CAS PubMed
.
- R. Ludwig, ChemPhysChem, 2005, 6, 1376 CrossRef CAS PubMed
.
- G. Matisz, W. M. F. Fabian, A.-M. Kelterer and S. Kunsagi-Mate, THEOCHEM, 2010, 956, 103 CrossRef CAS PubMed
.
- G. Matisz, A.-M. Kelterer, W. M. F. Fabian and S. Kunsagi-Mate, J. Phys. Chem. B, 2011, 115, 3936 CrossRef CAS PubMed
.
- M. Huelsekopf and R. Ludwig, J. Mol. Liq., 2000, 85, 105 CrossRef CAS
.
- R. Ludwig, F. Weinhold and T. C. Farrar, Mol. Phys., 1999, 97, 465 CrossRef CAS
.
- R. Ludwig, F. Weinhold and T. C. Farrar, Mol. Phys., 1999, 97, 479 CrossRef CAS
.
- M. Huelsekopf and R. Ludwig, J. Mol. Liq., 2002, 98, 163 CrossRef
.
- M. A. Wendt, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1998, 109, 5945 CrossRef CAS PubMed
.
- M. J. Hansen, M. A. Wendt and F. Weinhold, Mol. Phys., 2003, 101, 1147 CrossRef CAS
.
- R. Ludwig, F. Weinhold and T. C. Farrar, Ber. Bunsen-Ges., 1998, 102, 197 CrossRef CAS
.
- R. Ludwig, F. Weinhold and T. C. Farrar, Ber. Bunsen-Ges., 1998, 102, 205 CrossRef CAS
.
- R. Ludwig, F. Weinhold and T. C. Farrar, J. Phys. Chem. A, 1997, 101, 8861 CrossRef CAS
.
- R. Ludwig, O. Reis, R. Winter, F. Weinhold and T. C. Farrar, J. Phys. Chem. B, 1998, 102, 9312 CrossRef CAS
.
- M. Huelsekopf and R. Ludwig, Magn. Reson. Chem., 2001, 39, S127 CrossRef CAS
.
- R. Ludwig, J. Behler, B. Klink and F. Weinhold, Angew. Chem., Int. Ed., 2002, 41, 3199 CrossRef CAS
.
- J. Friedrich, E. Perlt, M. Roatsch, C. Spickermann and B. Kirchner, J. Chem. Theory Comput., 2011, 7, 843 CrossRef CAS
.
- C. Spickermann, E. Perlt, M. von Domaros, M. Roatsch, J. Friedrich and B. Kirchner, J. Chem. Theory Comput., 2011, 7, 868 CrossRef CAS
.
- E. Perlt, J. Friedrich, M. von Domaros and B. Kirchner, ChemPhysChem, 2011, 12, 3474 CrossRef CAS PubMed
.
- F. Weinhold, J. Phys. Chem. B, 2014, 118, 7792 CrossRef CAS PubMed
.
- M. Brüssel, E. Perlt, S. B. C. Lehmann, M. von Domaros and B. Kirchner, J. Chem. Phys., 2011, 135, 194113 CrossRef PubMed
.
- T. A. Pascal and W. A. Goddard, J. Phys. Chem. B, 2012, 116, 13905 CrossRef CAS PubMed
.
- L. Vlcek and I. Nezbeda, J. Mol. Liq., 2007, 131, 158 CrossRef PubMed
.
- B. Hribar-Lee and K. A. Dill, Acta Chim. Slov., 2006, 53, 257 CAS
.
- D. P. Geerke and W. F. van Gunsteren, ChemPhysChem, 2006, 7, 671 CrossRef CAS PubMed
.
- D. Gonzalez-Salgado and I. Nezbeda, Fluid Phase Equilib., 2006, 240, 161 CrossRef CAS PubMed
.
- K. Liltorp, P. Westh and Y. Koga, Can. J. Chem., 2005, 83, 420 CrossRef CAS
.
- E. J. W. Wensink, A. C. Hoffmann, P. J. van Maaren and D. van der Spoel, J. Chem. Phys., 2003, 119, 7308 CrossRef CAS PubMed
.
- C. A. Koh, H. Tanaka, J. M. Walsh, K. E. Gubbins and J. A. Zollweg, Fluid Phase Equilib., 1993, 83, 51 CrossRef CAS
.
- H. Tanaka and K. E. Gubbins, J. Chem. Phys., 1992, 97, 2626 CrossRef CAS PubMed
.
- S. W. Cochran, J. C. Holste, K. N. Marsh, B. E. Gammon and K. R. Hall, Fluid Phase Equilib., 1993, 88, 171 CrossRef CAS
.
- S. Z. Mikhail and W. R. Kimel, J. Chem. Eng. Data, 1961, 6, 533 CrossRef CAS
.
- J. M. Simonson, D. J. Bradley and R. H. Busey, J. Chem. Thermodyn., 1987, 19, 479 CrossRef CAS
.
-
C. Synowietz, in 1.1 Introduction, Springer Materials - The Landolt–Börnstein Database, ed. K. Schäfer, http://www.springermaterials.com, DOI: 10.1007/10201852_1 Search PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed
.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS
.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- F. Neese, The ORCA program system, WIREs Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS
.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC
.
- S. F. Boys and F. Bernardi, Mol. Phys., 2002, 100, 65 CrossRef
.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed
.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS PubMed
.
- R. Ludwig, Angew. Chem., Int. Ed., 2001, 40, 1808–1827 CrossRef CAS
.
- G. Z. Han, Y. L. Ding, P. Qian, C. Zhang and W. Song, Int. J. Quantum Chem., 2013, 113, 1511 CrossRef CAS
.
- C. Corsaro, J. Spooren, C. Branca, N. Leone, M. Broccio, C. Kim, S. H. Chen, H. E. Stanley and F. Mallamace, J. Phys. Chem. B, 2008, 112, 10449 CrossRef CAS PubMed
.
- S. Kashtanov, A. Augustson, J. E. Rubensson, J. Nordgren, H. Agren, J. H. Guo and Y. Luo, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 104205 CrossRef
.
- K. R. Wilson, M. Cavalleri, B. S. Rude, R. D. Schaller, T. Catalano, A. Nilsson, R. J. Saykally and L. G. M. Pettersson, J. Phys. Chem. B, 2005, 109, 10194 CrossRef CAS PubMed
.
- R. F. Lama and B. C. Y. Lu, J. Chem. Eng. Data, 1965, 10, 216 CrossRef CAS
.
- L. Abello, J. Chim. Phys. Phys.-Chim. Biol., 1973, 70, 1355 CAS
.
- I. Tomaszkiewicz, S. L. Randzio and P. Gierycz, Thermochim. Acta, 1986, 103, 281 CrossRef CAS
.
- J. A. V. Butler, D. W. Thomson and W. H. Maclennan, J. Chem. Soc., 1933, 136, 674 RSC
.
- M. W. Chase, NIST-JANAF Thermochemical Tables, J. Phys. Chem. Ref. Data, Monograph No. 9, 4th edn, 1998.
- T. S. Khasanshin, T. B. Zykova and S. P. Bunko, High Temp., 1997, 35, 149 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Fitting parameters amf, bxv see Tables S1 (with c8 clusters) and S2 (without c8 clusters). Table S3 ΔG298/H-bond and populations at different molar fraction. Fig. S1 Number of clusters for specific x(MeOH); Fig. S2 Benchmark of methods against MP2 for ring clusters; M06-2X data are shown in Fig. S3 (Eint), S4 (cluster populations), S5 (cluster distributions), S6 (HE, SE, GE), S8 (Cp, CEp), and Fig. S7 (CEp for B3LYP-D3). Cartesian coordinates of all 93 clusters for B3LYP-D3 and M06-2X method as zip file. See DOI: 10.1039/c4cp05836d |
| This journal is © the Owner Societies 2015 |