Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Benchmarking the quadrupolar coupling tensor for chlorine to probe weak-bonding interactions†
Robin
Dohmen
,
Denis
Fedosov
and
Daniel A.
Obenchain
 *
*
Georg-August University, Tammannstraße 6, Göttingen, Germany. E-mail: daniel.obenchain@uni-goettingen.de
First published on 14th December 2022
Abstract
Rotational spectroscopy relies on quantum chemical calculations to interpret observed spectra. Among the most challenging molecules to assign are those with additional angular momenta coupling to the rotation, contributing to the complexity of the spectrum. This benchmark study of computational methods commonly used by rotational spectroscopists targets the nuclear quadrupole coupling constants of chlorine containing molecules and the geometry of its complexes and clusters. For each method, the quality of both structural and electronic parameter predictions is compared with the experimental values. Ab initio methods are found to perform best overall in predicting both the geometry of the complexes and the coupling constants of chlorine with moderate computational cost. This cost can be reduced by combining these methods with density functional theory structure optimization, which still yields adequate predictions. This work constitutes a first step in expanding Bailey's quadrupole coupling data set to encompass molecular clusters. [W. C. Bailey, Calculation of Nuclear Quadrupole Coupling Constants in Gaseous State Molecule, 2019, https://nqcc.wcbailey.net/]
1 Introduction
With the rise of broadband rotational spectroscopy in the last two decades,1,2 the demands for accurate predictions of rotational spectroscopic constants from quantum chemical calculations have increased. More precise calculations are needed to interpret the increasing complexity of molecular targets. The complexity is introduced through an increase in system size, leading to a large conformational space or several angular momenta coupling to the total angular momentum. In addition, below the threshold of molecular mass transferable into the gas-phase, broadband microwave spectroscopy is not size selective. During detection, many impurities and weakly bound complexes containing two or more molecules are observable simultaneously.3The analysis of the large amount of spectroscopic data collected, both in number of spectra and in spectral complexity, can currently be very time consuming. An accurate initial guess of the spectroscopic parameters is valuable because it drastically minimize the time spent on assignment. Accurate theoretical predictions are also valuable for automatic fitting programs,4,5 since it reduces calculation time. The aim of this paper benchmark a number of theoretical methods to test their performance in predicting the complex hyperfine splitting of weakly bound complexes.
In microwave spectroscopy, rotational constants are the fundamental spectroscopic parameters, which are directly related to the geometry of the molecule as they depend on the moments of inertia. This direct link to the mass distribution in the molecule establishes microwave spectroscopy as a powerful tool for determining the molecular structure and underscores the necessity for an accurate prediction of these parameters from theory for assignment. In addition to rotational constants, quantum chemical methods produce predictions for another characteristic important for assignment, the Nuclear Quadrupolar Coupling Constant (NQCC) χij. Provided the target molecule contains one or more quadrupolar nuclei (I > 1/2), such as 14N or 35Cl,6–9 a hyperfine structure is observed that arises from the coupling of the nuclear angular momentum with the molecular angular momentum.10 The coupling is dependent on the intrinsic nuclear quadrupole moment Q and the electronic environment expressed by the Electronic Field Gradient (EFG) qij(i,j = abc).
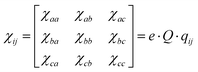 | (1) |
The NQCC χij is experimentally observed in the principal axis system abc based on the construction of the rotational Hamiltonian. Through rotation in the nuclear axis system of the quadrupolar nucleus, the NQCC tensor is transformed to χij(i,j = xyz) by diagonalization. The steepest gradient of the EFG is along the chlorine carbon bond in the nuclear axis system, where this axis is labeled z by convention. To clarify which axis system is used, χabc and χxyz will be used to denote the NQCC in the principal axis system or the nuclear axis frame, respectively.
Bailey et al. performed extensive benchmarking of NQCC11 with a focus on chlorine-containing molecules which are present in many important compounds for chemical industry.12 This is in addition to Bailey's numerous examinations of similar nuclei containing high-spins that are found in rotational spectroscopy studies. Bailey found a linear correlation between NQCC values predicted at the B1LYP/TZV(3df,2p)13,14 level and experimental results of 22 molecules. He established an empirical correction Qeff of the intrinsic nuclear quadrupole moment that acts on the EFG of the molecule. The reference data set encompasses a wide range of chlorine compounds probed with experimental methods that are added sequentially to the data set after the initial publication. The data set is limited exclusively to chlorine-containing monomers, disregarding chlorine-containing species with intermolecular dispersive bonding interactions.
Chlorine containing weakly-bound complexes have been studied experimentally for multiple decades.9,15–33 The data on weakly bound complexes allows one to review the predictive power of quantum chemical calculations for dispersive interactions by utilizing chlorine as a probe for the EFG. The goal is to improve the quantum chemical predictions for non-covalent complexes to assign weak transitions in rotational spectroscopy. Thereby, it is also a step toward the investigation of rarely sampled atoms.
2 Selection of molecular targets
We selected 20 complexes for our data set in this study. Reoccurring substructures such as common monomers or rare gas binding partners appear in multiple structures within the data set. There were several selection parameters that guided the choice of molecular structures to be included in the data set.2.1 Full description of NQCC
From all structures picked from literature, the full description of the NQCC tensor of a quadrupolar nucleus was required, including the off-diagonal elements of the tensor. A full experimental description of the NQCC tensor was required to compare with the computational results. The experimental determination of the full tensor is easier when the number of nonzero off-diagonal elements is low; hence, a number of chosen molecules have symmetry elements.2.2 Gas-phase complex
All chosen structures display non-covalent intermolecular interactions in an effort to expand on Bailey's data set. All are heterodimers and contain only a singular quadrupole of interest. There are a variety of bond strengths in the chosen complexes, from van der Waals interactions to hydrogen bonds and interactions with a weakly covalent character. The data set includes several subgroups with similar monomers for different interactions with organic, inorganic, and metallic bonding partners.These subgroups provide trends within the data set. A large number of structures have chlorine as a component of an organic molecule such as 2-chlorothiophene or CF3Cl which interact with a number of binding partners, mostly small molecules, both organic and inorganic compounds. In particular, CF3Cl has been explored with a number of binding partners offering a wide selection of different interactions with the same system. Another group is argon as a rare gas binding partner to a number of small chlorine compounds such as Cl2 and HCl, uncovering the impact of the covalent environment of chlorine. To further diversify the binding partners, structures containing metals are also included in the data set.34
2.3 Computational cost
To keep the computational cost affordable, the number of complexes with heavy atoms such as Au and Xe was kept to a minimum. The number of atoms was limited by the computational cost and the lowered experimental accessibility of large molecules in the gas-phase, a boundary condition set by the experimental data preexisting in literature.2.4 Chlorine nucleus
This data set is meant to be an extension of Bailey's work, and therefore it is focused exclusively on chlorine as a quadrupolar nucleus. There are also other high-spin nuclei present in selected systems, but at least one chlorine atom was required for inclusion in the benchmarking set.3 Challenges of NQCC benchmarking
When discussing NQCC predictions, there is an inherent overlap with structure that complicates analysis. Geometry, chemical environment, and large amplitude motions all inform quadrupolar coupling constants, both in their inherent changes to the local EFG, and in the projection of the NQCC into the molecular axis system. The reliability of these factors from the calculations is informed by the structure type, specifically the treatment of dispersive complexes compared to that of monomer structures. Overall, dispersive dimers tend to be more floppy and have many local minima on the potential energy surface. A NQCC prediction should be correct for the right reasons. If the optimized structure already has discrepancies from the experimentally observed one, it contaminates the prediction of the EFG and its projection from the nuclear into the principal axis system.This is a particular complication if a single method is used both for structure optimization and for the prediction of the NQCC, as a singular method is not necessarily optimal for both computations. To address this issue, well established methods were used to optimize structures of complexes, and then a variety of methods were used to predict the NQCC of chlorine in these optimized complexes.
An unreliable geometry prediction of dimers is also particularly relevant when it comes to large amplitude motions. Low binding energies compared to covalently bound structures facilitate low energetic barriers for large-amplitude motions. This challenge is not unique to NQCC predictions, but is relevant for dispersive complexes in general. Nevertheless, it is an important factor to consider when approaching NQCC predictions and corrections.
4 Methods and data analysis
To benchmark different quantum chemical methods with preexisting data, we primarily focused on parameters that are directly obtained from experimental microwave spectra and therefore published as observables. We define the unitless MARD (Mean Absolute Relative Deviation) of an observable x for N molecular systems i (see Table 1) with an experimental value xe as follows: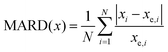 | (2) |
| Structure | A/MHz | B/MHz | C/MHz | χ aa | χ bb | χ cc | χ ab | χ ac | χ bc | Citation |
|---|---|---|---|---|---|---|---|---|---|---|
| a Included in single point calculations. b B not in literature, value for (B + C)/2 given instead. c No parameterization for Ag, Au, Kr, Xe in 6-311++G(d,p) and 6-311++G(2d,2p) basis sets, therefore excluded from MP2 optimization. | ||||||||||
| Ar–ClFa | 0 | 1327.113 | 0 | −140.869 | — | — | 0 | 0 | 0 | 15 |
| Ar–HCla | — | 1678.511b | — | −23.027 | — | — | 0 | 0 | 0 | 16 |
| Ar2–HCla | 1733.857 | 1667.932 | 844.491 | −28.123 | 12.471 | 15.658 | 0 | 0 | 0 | 17 |
| Ar3–HCla | 0 | 843.8974 | 0 | −31.008 | — | — | 0 | 0 | 0 | 18 |
| CF3Cl–Ara | 3373.118 | 988.2529 | 879.5788 | 36.57 | −75.485 | 38.915 | 15.4 | 0 | 0 | 19 |
| CF3Cl–CH3Fa | 21826 | 728.2164 | 702.9987 | −73.3 | 34.05 | 39.25 | 29 | 0 | 0 | 20 |
| CF3Cl–CO2a | 2985.3104 | 890.7548 | 780.1095 | 2.617 | −41.1605 | 38.5435 | 52.89 | 0 | 0 | 21 |
| CF3Cl–DMEa | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738 738 |
595.399 | 565.836 | −76.587 | 39.5235 | 37.0635 | −0.44 | 0 | 0 | 22 |
| CF3Cl–OCH2a | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 295 295 |
787.4896 | 764.373 | −73.91 | 34.695 | 39.215 | 22.96 | 0 | 0 | 23 |
| F2CCFCl–NH3a | 2236.0689 | 1317.19498 | 1219.63324 | −21.817 | −14.4725 | 36.2895 | 55.9 | 10.3 | 12 | 24 |
| Fluorobenzene–HCl | 1863.8635 | 1107.99873 | 918.09242 | −36.6494 | 10.9547 | 25.6947 | 30.48 | 0 | 0 | 25 |
| H2–AgClc | 1588778.3 | 3453.034 | 3443.7141 | −31.608 | 15.232 | 17.384 | 0 | 0 | 0 | 26 |
| H2–AuClc | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209 209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 646 |
3297.117 | 3287.332 | −41.6877 | 18.581 | 23.107 | 0 | 0 | 0 | 9 |
| H2–CuCl | — | 4781.8759b | — | −24.43 | — | — | 0 | 0 | 0 | 27 |
| HCCH–CH2ClFa | 5262.899 | 1546.8071 | 1205.4349 | 28.497 | −65.618 | 37.121 | −22.2007 | 0 | 0 | 28 |
| HCCH–ClHCCF2a | 2671.139543 | 988.154084 | 721.384869 | 36.22802 | −72.54615 | 36.31813 | 20.5876 | 0 | 0 | 29 |
| HCCH–ClHCCH2a | 5679.6182 | 1523.02024 | 1200.10948 | 35.7483 | −67.1371 | 31.3888 | 11.2 | 0 | 0 | 30 |
| HCCH–H2CCFCla | 9147.85663 | 889.015856 | 811.975763 | −70.63491 | 37.3203 | 33.31461 | 12.356 | 0 | 0 | 31 |
| Kr–HClc | 0 | 1200.62374 | 0 | −29.2376 | — | — | 0 | 0 | 0 | 32 |
| Xe–HClc | 0 | 989.26113 | 0 | −34.67 | — | — | 0 | 0 | 0 | 33 |
For errors the standard deviation of the MARD is calculated.
ORCA 4.2.135–37 was chosen for all quantum chemical calculations, as it is widely used through open access and offers customization of the basis sets.38–40
Most of the methods were chosen due to their prevalence among rotational spectroscopists such as B3LYP41–43 and its D344–46 and D447–49 dispersion corrected extensions with Becke–Johnson damping.45,46,50 The prevalence of the double hybrid functional B2PLYP51 similarly justifies its inclusion. B1LYP14,41,52 was chosen for comparison with Bailey's studies. B97M-D3BJ53 is a meta-GGA functional chosen to compare with hybrid functionals based on previous studies.49,54 MP2 is also a popular method among rotational spectroscopists for structure predictions and serves as an ab initio method comparison with moderate computational cost.55
The basis sets used for DFT and meta-GGA methods are the def2 basis sets def2-TZVPD and def2-TZVPPD,56–59 a very common all-purpose basis set. To compare with another basis with an improved description of core electrons, which potentially has an impact on the shielding effect of the quadrupolar nucleus by the electrons, x2c-TZVPP-2c60 and x2c-TZVPP-s61 are included. An exception is B1LYP, where VTZ(3df,2d)62–72 was used to compare with Bailey's calculations. For the MP2 calculations 6-311++G(d,p) and 6-311++G(2d,2p)64–69 basis sets where used to compare basis sets of different sizes. ORCA's integrated basis sets were used unless the basis was unavailable, then the basis set was downloaded from Basis Set Exchange.38–40
4.1 Optimization
The geometries of all the structures in the benchmark set were optimized with the methods mentioned above. An exception are the heavy atom containing complexes, which were excluded from MP2 optimizations in the absence of parameterization of the basis set for Au, Ag, Kr and Xe. In addition to geometry, the EFG of chlorine was calculated for the optimized structure.4.2 Single point calculations
It proved difficult to compare the computational results for the NQCC independently of the structural predictions. Several methods yielded inaccurate geometries, displaying relative deviations beyond 10% for structural parameters, which is generally unsuitable for fitting and auto-fitting when hyperfine splitting is also present. Therefore, single point calculations were performed on select pre-optimized structures to obtain predictions of the NQCC based on different starting geometries. While this approach cannot negate the inherent link between geometry and EFG, predictions of the NQCC based on a common geometry share the same systematic error through structural distortion, hence a relative comparison of EFG predictions between methods is possible. This is the same methodology prescribed by Bailey that we now extend to complexes.Single point calculations was performed for select geometries optimized at the levels of B3LYP/def2-TZVPPD, B3LYP-D3(BJ)/def2-TZVPPD, and B3LYP-D3(BJ)/x2c-TZVPPall-2c. These structures were chosen to keep the scope limited within the B3LYP hybrid functional group, as these calculations provided a large range of quality in their respective geometry optimizations with respect to structure. As these methods were used for the optimization in this part of the study, each method was subsequently used as a single point calculation method on the other two optimized structures. For example, a single point calculation was done with B3LYP/def2-TZVPPD on the optimized geometry at the B3LYP-D3(BJ)/def2-TZVPPD level. This was done for completeness of the comparison. For these geometries, a mix of calculations were used. In keeping with the previous standards, the NQCC was determined with a single point calculation using B1LYP/TZV(3df,2p) according to Bailey,62 which includes transforming the raw EFG tensor to the NQCC tensor using both the nuclear quadrupole moment Q from the literature and Bailey's corrected Qeff. For each of the three optimized geometries, B3LYP/def2-TZVPPD. Lastly, CCSD(T)/cc-pVQZ73–76 was chosen to compare with a high-level ab initio method. The treatment of all geometries was repeated in these single point calculations, regardless of the quality of the predicted structure, with the exception of many electron systems. As CCSD(T)77,78 is a very expensive method, Ag, Au, Cu, Kr, Xe and fluorobenzene were excluded from this sub-test set, as the computational cost was too high (see Table 1).
5 Results
5.1 Optimization results and interpretation
To assess performance in benchmarking, an estimated behaviour from other test sets is advantageous. For rotational constants, a back correction to experimental ground state B0 from equilibrium values Be of −1(±1)% is expected for monomers and −1(±3)% for hydrogen bonded dimers.80 Currently, this is the highest possible accuracy that can be expected with the approximations in place for the rotational constant estimation.For χij, the distinction between the NQCC in the nuclear axis frame and principle axis system has to be made. No previous study has rigorously investigated dispersive dimers, but Bailey corrected Qeff by 0.1 ± 0.9% for 35Cl containing monomers.
5.2 Geometry
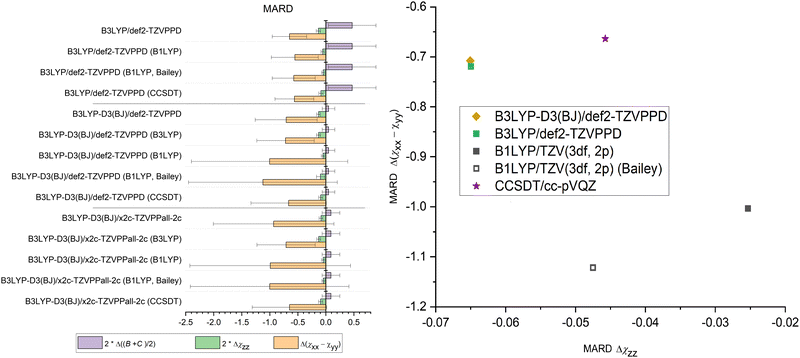
The methods in Fig. 1 are compared with the experiment with three key observables: (B + C)/2 as structural parameter and the diagonal elements of NQCC χij in both the nuclear axis system and the principal axis system to probe the electronic description. The sign of the MARD values determined by the definition the χxyz axis system for chlorine, its steepest gradient along the z-axis is negative in all cases.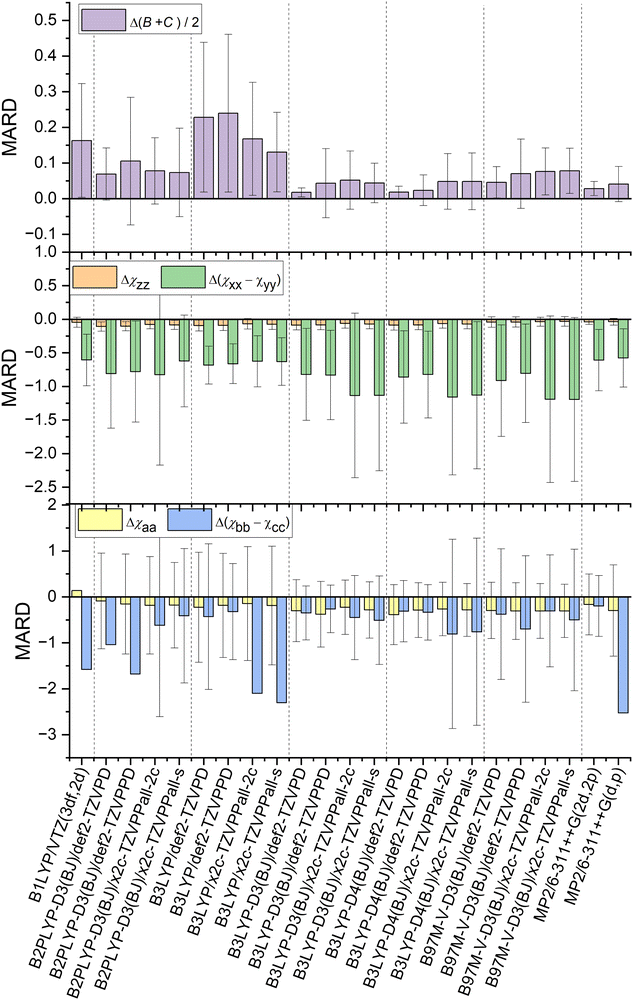 | ||
| Fig. 1 Comparison of MARD of NQCC and geometry predictions made by examined combinations of methods and basis sets after optimization. Error bars were omitted when the values were to large for a readable depiction. The values can be found in the ESI† (Tables S1–S5) in the dataverse.79 | ||
The DFT hybrid functionals like B1LYP and B3LYP show large discrepancies between predicted geometries and experimental structures when omitting Grimme's dispersion correction and Becke–Johnson damping as demonstrated by the large MARD for (B + C)/2. This is expected behavior, as long-range dispersive interactions are underestimated by theory and lead to distortion in geometry for the dimer data set governed by dispersion.45
Reliable structural data with mean relative deviations below <4%80 are provided by B3LYP-D3/def2-TZVPD, B3LYP-D4/def2-TZVPD, B3LYP-D4/def2-TZVPPD, and MP2/6-311++G(2d,2p) calculations. Overall, B3LYP-D3/def2-TZVPD and B3LYP-D4/def2-TZVPD performed best among all methods in predicting rotational constants, demonstrating no significant differences beyond the methods precision between D3 and D4 dispersion corrections. A close second is MP2/6-311++G(2d,2p) in archiving quality geometric predictions. However, it is important to note that a precise prediction is not expected, as we are comparing equilibrium structure calculations with the ground state structure observed in experiments. Nevertheless, spectroscopists have reliably used these methods for conformational assignment, and the benchmark data presented here confirm once more that these methods provide a robust description of weakly bound complexes at moderate computational costs.54,81–83 With a shift to flexible systems with internal motions, this mismatch in comparisons needs to be carefully considered in a case-by-case method.
5.3 χ xyz
Direct comparison of the nuclear quadrupole moment is best done in the nuclear axis frame xyz. The steepest gradient of NQCC along the axis of the chlorine covalent bond χzz is described with reasonable precision by all methods. The best predictions for this parameter are provided by B97M-V-D3 and MP2 calculations, with these methods producing the same quality of predictions. In contrast, the double hybrid functional B2PLYP performs worst among the methods discussed. It is also remarkable that B1LYP/VTZ (3df,2d) outperforms most other methods, despite the lack of dispersion corrections. As (B + C)/2 demonstrates, the geometry is distorted and does not agree with the experimental findings, bringing the reliability of the prediction of NQCC into question. Among the basis sets, the x2c basis set always outperformed the def2 basis sets independent of the method.The description of the quadrupole tensor orthogonal to the bond axis Δ(χxx − χyy) is less accurate than for χzz. As the NQCC tensor is traceless, χxx and χyy are of similar magnitude in most of the chlorine compounds selected. For this reason, the difference Δ(χxx − χyy) leads to higher relative errors compared to χzz. Indeed, the non-dispersion corrected B3LYP and B1LYP methods outperform other DFT hybrid functional approaches with Grimme corrections in predicting Δ(χxx − χyy). Due to inaccurate geometry predictions, this is most likely due to the much larger error spread and error compensation. Therefore, it is important to view the Δ(χxx − χyy) predictions in conjunction with χzz and (B + C)/2, to ensure that the NQCC description is correctly described and not just by chance. The method that strikes that balance best with a single optimization is MP2/6-311++G(2d,2p), as this method performs the best in predicting the NQCC while simultaneously occupying fourth place for geometry predictions among the methods tested here, suggesting that the electronic description of the EFG is reliable.
The difference between D3 and D4 for B3LYP is minor, they have almost identical NQCC MARDs, as the test set lacks ionic species, the characteristic D4 improves over D3.47Fig. 1 indicates that overall B1LYP produces better predictions of NQCC than other DFT methods despite the imperfect structure obtained by optimization, which is discussed in another section.
The basis set has a significant impact on the description of NQCC. The x2c basis set is an all-electron basis that was fit using NMR parameters. NMR data were chosen specifically to improve the shielding constants for inner electrons.60,61 This approach can theoretically affect NQCC if the description of the core potential for chlorine is inadequate. In contrast to expectations, the x2c basis set does not outperform the def2 basis set for the description of quadupole coupling. While χzz is comparatively well described, the errors in Δ(χxx − χyy) rise compared to the Karlsruhe def2 basis set. Overall, the relative error of Δ(χxx − χyy) is much larger than that of χzz, thereby making this parameter less reliable in judging the overall quality of the prediction of the NQCC tensor. As a result, the x2c basis sets still outperform the def2 basis sets for DFT calculations. However, MP2 with a 6-311++G(2d,2p) basis set still overall provides the most reliable predictions of the entire set of methods.
5.4 χ abc
Although NQCC χxyz in the nuclear axis system provides insight into the electronic description of the nucleus, for the purpose of fitting a spectrum, χabc is required, which is the projection of χ into the principal axis system of the molecule. An accurate description of the geometry and the EFG is important to prevent distortion of the NQCC tensor. However, methods that fail to optimize geometry sufficiently, such as B1LYP and B3LYP without dispersion correction, have poorer precision than others, such as B3LYP-D3. It resulted in the omission of error bars in Fig. 1 to enhance legibility, which can be found in the ESI.† The non-dispersion corrected methods yield slightly better MARD for χaa with lower precision, but as with the Grimme corrected counterpart of the B3LYP methods, it lacks precision.When comparing ab initio MP2 methods, the importance of the basis set is highlighted. The addition of diffuse functions to the basis set results in robuster NQCC predictions in the molecular axis frame. Therefore, among the methods tested, MP2/6-311++G(2d,2p) is the best choice among the methods tested if only a single calculation is performed, if the basis set can be computationally afforded.
5.5 Single point calculation
As described in Section 4.2, connect geometries optimized at different levels of theory to the same single point calculations. Therefore, B1LYP/TZV(3df,2p), CCSD(T)/cc-pVQZ, B3LYP/def2-TZVPPD, B3LYP-D3(BJ)/def2-TZVPPD, and B3LYP-D3(BJ)/x2c-TZVPPall-2c levels of theory were used to calculated the NQCC from the geometries optimized at the B3LYP/def2-TZVPPD, B3LYP-D3(BJ)/def2-TZVPPD, and B3LYP-D3(BJ)/x2c-TZVPPall-2c level of theory. The data for the latter three methods is included in the supplement.79 Structures which could not be treated with CCSD(T) due to computational cost had to be excluded, which yields 14 comparable dimers remain in the single point data set.Omitting B3LYP dispersion corrections does not have a significant effect on the prediction of NQCC, since the coupling is primarily dependent on the description of the electronic environment. The impact of dispersion correction on this calculation is diminished by other computational decisions, such as the choice of basis sets, which is illustrated in Fig. 2. Comparison of B3LYP and B3LYP-D3 indicates that B3LYP did not accurately predict χ for the right reason, as suggested in Fig. 1. Instead, the low NQCC MARD is caused by error compensation between the distorted geometry and an inaccurate description of the nuclear environment.
Despite the inaccuracies in optimization discussed above, B1LYP/TZV(3df,2p) outperforms all other methods in describing χzz, albeit prediction for (χxx − χyy) contains the largest errors compared to B3LYP-D3/def2-TZVPPD and CCSD(T)/cc-pVQZ. Employing Qeff to transform the EFG according to eqn (1) fails to correct the NQCC, as it breaks down when applied to dimers.
The CCSD(T) results improve the prediction of χ compared to B3LYP, although it is still outperformed by B1LYP in terms of χzz. The ab initio method performs best for (χxx − χyy). This result was a surprise, as CCSD(T) is often praised as the gold standard in computational chemistry. It can likely be attributed to the basis set cc-pVQZ used in the CCSD(T) calculation, which is not augmented with diffuse functions compared to the TZV(3df,2p) employed for the B1LYP calculation. More benchmarking needs to be done to confirm this hypothesis. It demonstrates the importance of the basis set, as in this case a chosen DFT method with a large basis set can compete with CCSD(T) calculations in accuracy to predict the local EFG.
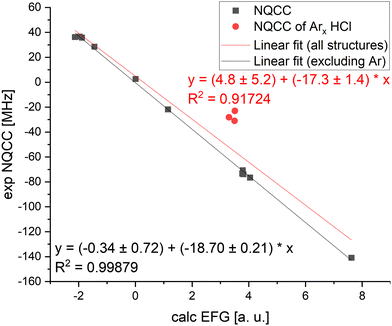
5.6 NQCC correlation
To directly compare the electronic description around the nucleus, selected geometries pre-optimized with B3LYP-D3/def2-TZVPPD were used to determine the EFG at the level of B1LYP/TZV(3df,2p) and plotted against the experimental values of NQCC. This is following Bailey's method of optimizing the geometry with one's preferred method and calculating the EFG using B1LYP/TZV(3df,2p) to apply an empirical correction factor. When correlating the calculated EFG and the experimental NQCC values, the data spread is much more pronounced compared to Bailey's monomers, as the geometry of dimers are generally harder to predict (see Chapter 3). Additionally, the dimer data set is smaller, with 14 comparable systems which had existing basis set parameterisation for all atoms, while Bailey included 22 systems in his correlation. When applying a linear fit, we derive a value of eQeff/h = −17.3 ± 1.4 MHz a.u.−1 for 35Cl compared to Bailey's eQeff/h = −19.166 ± 0.021 MHz a.u.−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 Bailey's values suggests shielding of chlorine nucleus as the effective quadrupole moment Qeff = − 81.568 ± 0.091 mb is smaller than the literature value of Q = − 81.65 ± 0.80 mb. Therefore, the calculations underestimate the electronic interactions with the quadrupole moment. This effect ostensibly is enhanced in complexes, where the effective quadrupole moment is −73.4 ± 5.9 mb, but may have influence from other sources, as we suggest below.
62 Bailey's values suggests shielding of chlorine nucleus as the effective quadrupole moment Qeff = − 81.568 ± 0.091 mb is smaller than the literature value of Q = − 81.65 ± 0.80 mb. Therefore, the calculations underestimate the electronic interactions with the quadrupole moment. This effect ostensibly is enhanced in complexes, where the effective quadrupole moment is −73.4 ± 5.9 mb, but may have influence from other sources, as we suggest below.
A major issue for correlating prediction and experiment is that fundamental approximations made by optimizing equilibrium structures cause much larger errors in loosely bound systems and in more rigid monomers. This is particularly apparent in the argon–HCl complexes, which show a large deviation from the linear fit in Fig. 3. The average ground state structure deviates greatly from the equilibrium geometry due to large amplitude motion.16 For cases such as this where the equilibrium structure is an insufficient approximation, Qeff as a single correction parameter falls short. When Ar complexes are excluded from linear regression, the effective quadrupole moments in the data set can be determined to be Qeff = −79.6 ± 0.9 mb. This is a significant improvement of the fit, but, the fact that simple calculations become less reliable still holds true for this data set, and using this correction factor for the NQCC for other systems still requires a chemical understanding in case the approximations of the calculations break down. In that case, a larger benchmarking set is required to determine Qeff for similar cases, which probably requires the definition of individual Qeff for complexes dominated by the same effects. Grouping the complexes in this data set and investigating them separately has been done, where the Arx–HCl complexes show the most pronounced deviations, but the experimental data set is very limited (see Fig. SF1, ESI†). Alternatively, calculations with less approximation and higher time investment, such as vibrational calculations, might be used to treat these cases. In either case, simply using Bailey's Qeff determined from monomers for complexes is a fallacy.
Returning to our large shift of Qeff = −73.4 ± 5.9 mb compared to Bailey's value Qeff = −81.568 ± 0.091 mb, Bailey's reasoning that inner-core electron shielding effects explain the shift in monomers is more clear. In our study of complex NQCC, we now connect the large contribution of revs. r0 differences in geometry to the NQCC prediction. Ultimately, we cannot disentangle the contributions of either from the effective quadrupole moment of −73.4 ± 5.9 mb, and must conclude that both contribute. The large shift in the complexes does suggest a significant contribution from structural difference between equilibrium and ground state geometries.
6 Conclusion
In this work, the quantum chemical predictions for NQCC were compared to the experimental spectroscopic results to determine the best performing methods to obtain initial guesses for future fitting efforts of spectroscopic data.The primary focus was on established methods for structure determination, with MP2 and dispersion corrected B3LYP-D3(BJ) and B3LYP-D4 performing best, proving their status as robust methods for geometry optimization. To reliably obtain accurate predictions for the NQCC, MP2/6-311++G(2d,2p) as an ab initio method outperformed all DFT methods when requiring both reliable geometry and NQCC predictions with a single calculation. We showed that Bailey's empirical correction of chlorine monomers is not applicable for dimers. An empirical correction factor based on the accessible dimer data set was defined by pre-optimization of the geometry and calculation of the NQCC at B1LYP/TZV(3df,2p) level. It is at the user's discretion if the correction is applicable, because flexible systems with large amplitude motions or energetically close conformers require computational treatment of these phenomena to improve the NQCC predictions.
Future work on this project would broaden the variety of methods employed, in particular, more different ab initio methods for comparison, since MP2 performed well compared to DFT methods. An important step would be the further investigation flexible cases such as the argon complexes featured in this study with a more expensive anharmonic treatment to improve the NQCC. The experimental data set should be extended to include different quadrupolar nuclei, such as nitrogen, boron, bromine, and iodine. These extended data sets present a challenge in that they are typically harder to analyze and have fewer examples in the literature. The benefit of extending to these data sets to bromine and iodine is that they are more likely to have full, experimentally determined quadrupole coupling tensors due to the larger Q values of the nuclei.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the BENCh Research Training Group (DFG-389479699/GRK2455) for funding this project.84 This work used the Scientific Compute Cluster at GWDG, the joint data center of Max Planck Society for the Advancement of Science (MPG) and University of Göttingen.References
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- G. B. Park and R. W. Field, J. Chem. Phys., 2016, 144, 200901 CrossRef PubMed.
- D. P. Tabor, R. Kusaka, P. S. Walsh, E. L. Sibert and T. S. Zwier, J. Phys. Chem. Lett., 2015, 6, 1989–1995 CrossRef CAS PubMed.
- E. J. Riffe, S. T. Shipman, S. A. Gaster, C. M. Funderburk and G. G. Brown, J. Phys. Chem. A, 2019, 123, 1091–1099 CrossRef CAS PubMed.
- N. A. Seifert, I. A. Finneran, C. Perez, D. P. Zaleski, J. L. Neill, A. L. Steber, R. D. Suenram, A. Lesarri, S. T. Shipman and B. H. Pate, J. Mol. Spectrosc., 2015, 312, 13–21 CrossRef CAS.
- W. C. Bailey, J. Mol. Spectrosc., 2001, 209, 57–59 CrossRef CAS.
- L. A. Surin, I. V. Tarabukin, S. Schlemmer, A. A. Breier, T. F. Giesen, M. C. McCarthy and A. van der Avoird, Astrophys. J., 2017, 838, 27 CrossRef.
- K. P. Nair, S. Herbers, W. C. Bailey, D. A. Obenchain, A. Lesarri, J. U. Grabow and H. V. L. Nguyen, Spectrochim. Acta, Part A, 2021, 247, 119120 CrossRef CAS PubMed.
- D. A. Obenchain, D. S. Frank, H. M. Pickett and S. E. Novick, J. Chem. Phys., 2017, 146, 204302 CrossRef PubMed.
- W. Gordy and R. L. Cook, Microwave molecular spectra, Wiley, 1984, p.929 Search PubMed.
- W. C. Bailey, J. Mol. Struct., 2001, 195–201 CrossRef CAS.
- K. Naumann, Pest Manage. Sci., 2000, 56, 3–21 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. J. Harris, S. E. Novick, W. Klemperer and W. E. Falconer, J. Chem. Phys., 1974, 61, 193–197 CrossRef CAS.
- S. E. Novick, P. Davies, S. J. Harris and W. Klemperer, J. Chem. Phys., 1973, 59, 2273 CrossRef CAS.
- T. D. Klots, C. Chuang, R. S. Ruoff, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1987, 86, 5315–5322 CrossRef CAS.
- T. D. Klots, R. S. Ruoff, C. Chuang, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1987, 87, 4383–4387 CrossRef CAS.
- L. Evangelisti, Q. Gou, G. Feng and W. Caminati, Chem. Phys. Lett., 2016, 653, 1–4 CrossRef CAS.
- Q. Gou, L. Spada, E. J. Cocinero and W. Caminati, J. Phys. Chem. Lett., 2014, 5, 1591–1595 CrossRef CAS PubMed.
- Y. Zheng, S. Herbers, Q. Gou, W. Caminati and J. U. Grabow, J. Phys. Chem. Lett., 2021, 12, 3907–3913 CrossRef CAS PubMed.
- L. Evangelisti, G. Feng, Q. Gou, J. U. Grabow and W. Caminati, J. Phys. Chem. A, 2014, 118, 579–582 CrossRef CAS PubMed.
- Q. Gou, G. Feng, L. Evangelisti, M. Vallejo-López, L. Spada, A. Lesarri, E. J. Cocinero and W. Caminati, Chem. – Eur. J., 2015, 21, 4148–4152 CrossRef CAS PubMed.
- Q. Gou, L. Spada, Y. Geboes, W. A. Herrebout, S. Melandri and W. Caminati, Phys. Chem. Chem. Phys., 2015, 17, 7694–7698 RSC.
- M. E. Sanz, S. Antolínez, J. L. Alonso, J. C. López, R. L. Kuczkowski, S. A. Peebles, R. A. Peebles, F. C. Boman, E. Kraka and D. Cremer, J. Chem. Phys., 2003, 118, 9278–9290 CrossRef CAS.
- G. S. Grubbs, D. A. Obenchain, H. M. Pickett and S. E. Novick, J. Chem. Phys., 2014, 141, 114306 CrossRef PubMed.
- H. M. Pickett, D. A. Obenchain, G. S. Grubbs II and S. E. Novick, Observation of moderate strength interaction of hydrogen with a coinage metal halide: The rotational spectrum and structure of the para-H2-CuCl and ortho-H2-CuCl complexes, 2013.
- L. F. Elmuti, R. A. Peebles, S. A. Peebles, A. L. Steber, J. L. Neill and B. H. Pate, Phys. Chem. Chem. Phys., 2011, 13, 14043–14049 RSC.
- H. O. Leung and M. D. Marshall, J. Phys. Chem. A, 2020, 124, 1382–1389 CrossRef CAS PubMed.
- H. O. Leung, M. D. Marshall and F. Feng, J. Phys. Chem. A, 2013, 117, 13419–13428 CrossRef CAS PubMed.
- H. O. Leung, M. D. Marshall and D. D. Grimes, J. Chem. Phys., 2011, 134, 034303 CrossRef PubMed.
- A. E. Barton, T. J. Henderson, P. R. Langirdge-Smith and B. J. Howard, Chem. Phys., 1980, 45, 429–438 CrossRef CAS.
- M. R. Keenan, L. W. Buxton, E. J. Campbell, T. J. Balle and W. H. Flygare, J. Chem. Phys., 1980, 73, 3523–3529 CrossRef CAS.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- E. F. Valeev, Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions, 2017, http://libint.valeyev.net/, version 2.7.1.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- I. Y. Zhang, J. Wu and X. Xu, Chem. Commun., 2010, 46, 3057–3070 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Rahman Allouche, J. Comput. Chem., 2012, 32, 174–182 CrossRef PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- M. Bursch, E. Caldeweyher, A. Hansen, H. Neugebauer, S. Ehlert and S. Grimme, Acc. Chem. Res., 2019, 52, 258–266 CrossRef CAS PubMed.
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1997, 274, 242–250 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 74111 CrossRef PubMed.
- P. Kraus and I. Frank, J. Phys. Chem. A, 2018, 122, 4894–4901 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 0–11 CrossRef CAS PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705 CrossRef CAS PubMed.
- Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664 RSC.
- W. C. Bailey, Calculation of Nuclear Quadrupole Coupling Constants in Gaseous State Molecule, http://nqcc.wcbailey.net/.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- J. P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021 CrossRef CAS.
- L. A. Curtiss, M. P. McGrath, J. P. Blaudeau, N. E. Davis, R. C. Binning and L. Radom, J. Chem. Phys., 1995, 103, 6104–6113 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- P. M. Gill, B. G. Johnson, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1992, 197, 499–505 CrossRef CAS.
- G. W. Spitznagel, T. Clark, P. von Ragué Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 Search PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 99, 3730–3737 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910 CrossRef CAS.
- R. Dohmen, D. Fedosov and D. A. Obenchain, GRO.data, 2022.
- S. Oswald and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 18799 RSC.
- F. Xie, X. Ng, N. A. Seifert, J. Thomas, W. Jäger and Y. Xu, J. Chem. Phys., 2018, 149, 224306 CrossRef PubMed.
- Y. Jin, T. Lu and G. Feng, Phys. Chem. Chem. Phys., 2020, 22, 28339 RSC.
- P. Pinacho, A. Krin, C. Pérez, S. Zinn, J. C. López, S. Blanco and M. Schnell, Phys. Chem. Chem. Phys., 2018, 20, 15635–15640 RSC.
- R. Mata and M. Suhm, BENCh RTG, 2022, https://www.uni-goettingen.de/en/587836.html.
Footnote |
| † Electronic supplementary information (ESI) available: Files and data basis of the plots can be accessed digitally at https://doi.org/10.25625/VMY3WD. See DOI: https://doi.org/10.1039/d2cp04067k |
| This journal is © the Owner Societies 2023 |