Mechanistic study on the reaction of pinB-BMes₂ with alkynes based on experimental investigation and DFT calculations: gradual change of mechanism depending on the substituent

Abstract

Transition metal-free direct and base-catalyzed 1,2-diborations of arylacetylenes using pinB-BMes₂ provided a syn/anti-isomeric mixture of diborylalkenes. The kinetic analysis showed that the reaction rate and isomer ratio were affected by reaction conditions and substituents on the aryl ring. DFT calculations indicated that direct addition proceeded via the interaction of acetylene-π with the BMes₂ fragment. In contrast, for the base-catalyzed diboration, the previously isolated sp²–sp³ diborane and borataallene were confirmed as stable intermediates by calculations. The whole reaction pathways can be divided into the Bpin-migration and deprotonation steps, where the borataallene should be considered as a common intermediate. It should be noted that the deprotonation step is reversible and affords the kinetically less favoured isomer under the thermodynamic conditions. As a result, the composition of isomeric products, in the base-catalyzed diboration, is attributed to the small difference of activation barriers between direct and base-catalyzed systems.

---

Introduction

Transition metal-mediated diboration of alkynes to produce diborylalkene is useful to construct tri- and tetra-substituted alkenes in a controlled manner.¹ In the first report on platinum-mediated diboration of alkynes,² a plausible mechanism was proposed, which consisted of the oxidative addition of the B–B bond of a diborane(4) reagent to Pt, insertion of the alkyne to the Pt–B bond, and B–C bond-forming reductive elimination with experimental observation of a diborylplatinum complex as an intermediate. This observation initiated subsequent mechanistic studies, including isolation of catalytically active intermediates and kinetic analysis.³ Thus, the reaction mechanism of transition metal-mediated diboration of alkynes has been well-established.

In addition to metal-mediated reactions, transition metal-free diborations of alkynes have been reported. The first example was reported for the reaction of acetylene with B₂F₄ or B₂Cl₄ to produce bis(dihaloboryl)ethylene in 1959 (Scheme 1),⁴ whose four-centered transition state was recently proposed by DFT calculations.⁵ Two seminal reactions, alkoxide-catalyzed diboration of alkenes⁶ and phosphine-catalyzed β-boration of electron-deficient alkenes,⁷ induced the next evolution of the diboration of alkynes using a Lewis base as a catalyst.^8,9 These reactions involve the formation of sp²–sp³ intermediates via the coordination of the Lewis base to the diborane(4) reagent.¹⁰ Apart from the development of the base-catalyzed diboration of alkynes, two electrophilic diboration reactions of alkynes were recently reported (Scheme 2). The reaction of tetraaryldiborane(4) with 1-pentyne furnished diborated alkenes as an isomeric mixture (Scheme 2a).¹¹ The computational study proposed η¹-coordinated alkyne complexes as transition states for 1,1- and 1,2-diboration reactions.¹² We reported the reaction of pinB-BMes₂ (1)¹³ with terminal and internal alkynes resulting in the formation of diborylalkenes (Scheme 2b).¹⁴ It should be noted that the latter reaction with terminal alkynes could also be catalyzed by using ⁿBuLi as an external base, affording different product distributions depending on the reaction conditions.

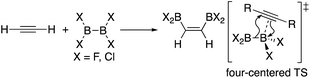Scheme 1 Electrophilic diboration of alkynes by using B₂X₄.

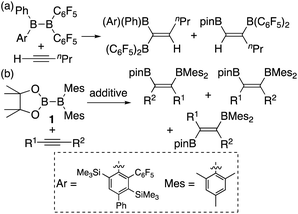Scheme 2 Electrophilic diboration of alkynes by using electron-deficient aryl-substituted diborane(4)s.

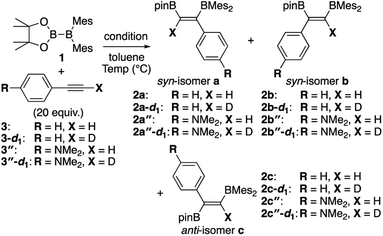
In our recent contribution towards the diboration of phenylacetylene derivatives (Scheme 2b) by using pinB-BMes₂,¹⁴ we used three different conditions; A: simple mixing of the substrate and reagent without any additive, B: ⁿBuLi-catalyzed diboration, and C: ⁿBuLi-catalyzed diboration in the presence of a catalytic amount of DME. Considering the formation of three isomers, we tentatively propose a mechanism (Scheme 3) consisting of a concerted pathway through alkyne-coordinating transition states TS2a and TS2b (direct addition pathway) and a stepwise pathway through two intermediates 4(solv)_n and 5(solv)_n (base-catalyzed pathway), which were independently isolated and structurally characterized.

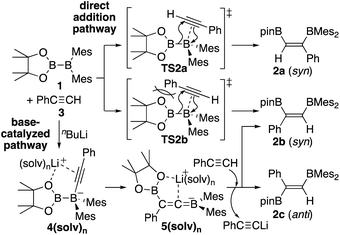Scheme 3 Proposed mechanism for direct and base-catalyzed diboration of phenylacetylene by using pinB-BMes₂.

Although the anti-selectivity of the reaction in Scheme 2(b) is remarkable, it was very difficult to understand the substituent effect toward the selectivity for each isomer and reaction rate. Some of the representative results with three phenylacetylene derivatives 3, 3′, and 3′′ in the previous report are summarized in Table 1. These results provide the following eight trends: (i) an electron-poor R substituent (run 2 vs. run 1) lengthened the reaction time and gave a similar selectivity to that in run 1, (ii) an electron-rich R substituent (run 3 vs. run 1) accelerated the reaction and changed the selectivity toward isomer b; (iii) the ⁿBuLi-catalyzed reaction (run 4 vs. run 1) was accelerated with selectivity toward isomer b; (iv) lower temperature for the ⁿBuLi-catalyzed reaction (run 5 vs. run 4) changed the selectivity toward isomer c; (v) reaction in THF solvent can accelerate reaction even under lower temperature (run 6 vs. run 4) with selectivity toward isomer c; (vi) ⁿBuLi/DME-catalyzed reaction (run 7 vs. run 4) was further accelerated with a change in the selectivity toward isomer c; (vii) an electron-poor R substituent under ⁿBuLi/DME-catalyzed conditions (run 8 vs. run 7) decelerated the reaction but the selectivity was retained; (viii) an electron-rich R substituent under ⁿBuLi/DME-catalyzed conditions (run 9 vs. run 7) accelerated the reaction with lower selectivity. One can expect that the base-catalyzed reactions under condition B or C (runs 4–9 in Table 1) involve the direct addition pathway, in which an electron-rich substituent would increase the reaction rate, as a background reaction, in addition to the base-catalyzed pathway. In this paper, we report a detailed experimental study with kinetic analysis and theoretical study with DFT calculations to understand the mechanism of the diboration reaction using pinB-BMes₂ (1).

Table 1 Direct and base-catalyzed diboration of alkynes with 1, extracted from the previous work¹⁴

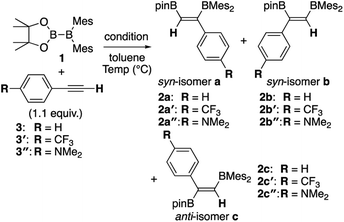
Run	Condition^a/solvent	Alkyne	Temp. (°C)	Time (h)	Yield^b (%)
					a	b	c
a Condition A: 1.0 equiv. of 1 (0.4 M), 1.1 equiv. of alkyne. Condition B: 1.0 equiv. of 1 (0.2 M), 1.1 equiv. of alkyne, 15 mol% of ^nBuLi. Condition C: 1.0 equiv. of 1 (0.4 M), 1.1 equiv. of alkyne, 3 mol% of ^nBuLi and DME. b NMR yield. c 0.2 M toluene solution of 1. d Not isolated, but tentatively characterized by NMR spectral analysis.
1	A/toluene^c	3	100	37	69	30
2^c	A/toluene	3′	100	59	69	16
3	A/toluene	3′′	100	6	24	76
4	B/toluene	3	100	17	10	61	8
5	B/toluene	3	40	42	14	9	58
6	B/THF	3	70	19	21	7	56
7	C/toluene^c	3	100	3	16	9	67
8	C/toluene	3′	100	8	18	6	59
9	C/toluene	3′′	100	1.5	13	41	27^d

---

Results and discussion

Kinetic study with deuterium labeling

To confirm the relationship among the substituent, the reaction order of 1, reaction rate, and change of selectivity toward the three isomers a, b, and c, we performed the kinetic analysis of the diboration of terminal alkynes (3, 3-d₁, 3′′, and 3′′-d₁) with 1 under the direct (A) and base/DME-catalyzed (C) conditions (Table 2). The concentration of 1 was monitored by ¹H NMR spectroscopy in the presence of excess amount of alkyne to establish a pseudo-first-order reaction. After the reaction was complete, the decay of 1 under each condition was fitted to confirm the first order reaction and to evaluate the observed rate constant, k_obs. The yields of the resulting isomers a–c were determined from the integral ratio between the products and internal standard. In run 1 of Table 2, the rate constant for the reaction of 1 with 3 at 100 °C in toluene (same condition as run 1 of Table 1) was estimated as 7.64 ± 0.14 × 10⁻⁴ (s⁻¹) with reproducibility of the isomeric ratio (a : b = 64% : 32%), which is similar to that in run 1 of Table 1. Changing the solvent to C₆D₆ and a lower reaction temperature due to its lower boiling point (run 2) decreased the reaction rate but the isomeric ratio was comparable to that in run 1. Heating 1 with 3-d₁ (run 3) gave a slightly larger rate constant than that in run 2, leading to an inverse kinetic isotope effect of 0.93. This result indicates that the reaction involves a concerted pathway with change of hybridization at the acetylenic C–H in the alkyne substrate.¹⁵ Reaction of 1 with 3′′ (run 4) afforded a larger rate constant than those in runs 2 and 3, indicating the acceleration of the reaction by the introduction of the electron-donating substituent. Simultaneously, the selectivity toward isomer b was observed. The reaction with 3′′-d₁ (run 5) afforded a slightly smaller rate constant and similar isomeric ratio in comparison with those in run 4, providing a positive KIE of 1.16. Under the base-catalyzed condition C, the reaction of 3 (run 6) gave a comparable rate constant and isomeric ratio to those obtained in run 2. The reaction of 3-d₁ (run 7) exhibited a smaller rate constant and different selectivity toward the isomer a in comparison to those in run 5, leading to a positive KIE of 1.32. In the reaction of 3′′ (run 8), the rate constant is larger than that in run 2, but smaller than that in run 4, with a moderate selectivity toward isomer b. The reaction of 3′′-d₁ gave a similar rate constant with isomer b as the major product (run 9), offering a KIE of 0.99.

Table 2 Kinetic analysis of direct or base-catalyzed diboration of alkynes by using 1

Run	Condition^a/solvent	Alkyne	Temp. (°C)	k obs [×10^−4 s^−1]	KIE^c	Yield^d (%)
						a	b	c
a Condition A: 50 μmol of 1, 500 μL solvent, 50 μmol of phenanthrene (internal standard); condition C: 50 μmol of 1, 10 mol% of ^nBuLi and DME, 550 μL solvent, 65 μmol of phenanthrene (internal standard). b Determined by monitoring the decay of 1 with 1st order kinetic analysis. c KIE: kinetic isotope effect = kH/kD. d ^1H NMR yield with 1,3,5-trimethoxybenzene as an internal standard (see details in the ESI).
1	A/tol-d8	3	100	7.64 ± 0.14	—	64	32	—
2	A/C6D6	3	70	1.474 ± 0.002	—	65	28	—
3	A/C6D6	3-d1	70	1.591 ± 0.003	0.93	70	28	—
4	A/C6D6	3′′	70	8.81 ± 0.07	—	19	74	2
5	A/C6D6	3′′-d1	70	7.62 ± 0.06	1.16	21	76	3
6	C/C6D6	3	70	1.48 ± 0.06	—	36	14	40
7	C/C6D6	3-d1	70	1.120 ± 0.003	1.32	48	16	29
8	C/C6D6	3′′	70	7.86 ± 0.04	—	18	69	5
9	C/C6D6	3′′-d1	70	7.95 ± 0.06	0.99	19	73	5

---

Elucidation of the reaction mechanism by DFT calculations

In order to elucidate the reaction mechanism, DFT calculations were performed. We first compared the experimentally observed structures with the DFT-calculated structures to see the accuracy of the calculation method. We then studied the direct diboration reaction. Finally, the results of our DFT calculations for the reaction mechanisms of the ⁿBuLi-initiated stoichiometric reaction and catalytic diboration are presented.

Suitability of the calculation method

We performed calculations with full geometry optimization at the B3LYP-D3/6-31G(d,p) level of theory (see the ESI† for the computational details). All the structural parameters of the starting diborane(4) 1, the two previously isolated intermediates 4(thf)₂ and 5(thf)₂, which were generated by the reaction of 1 with lithium phenylacetylide and subsequent heating,¹⁴ were well reproduced by DFT calculations (Fig. 1), suggesting that the computational method should give reasonable results.

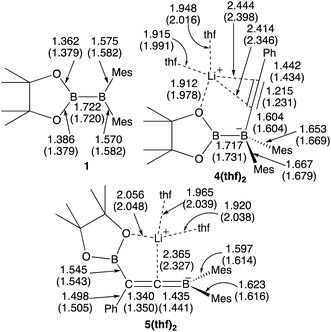Fig. 1 Comparison between the experimental and calculated (in parentheses) structures of 1, 4(thf)₂, and 5(thf)₂. All the bond distances are given in Å.

Reaction mechanism for the diboration of alkynes in the absence of a base in comparison with the experimental kinetic study

The calculated energy profiles for the direct diboration reactions of phenylacetylene (3) and phenylacetylene-d₁ (3-d₁) with diborane(4) 1 under the condition A are illustrated in Fig. 2(a). All the calculated transition states show a simple coordination of the alkyne π-bond to the electron-deficient boron center of the BMes₂ group [Fig. 2(b)–(e)]. The direct diboration of phenylacetylene kinetically favors the transition state TS_1-2a over TS_1-2b (with the reaction barrier of 26.73 kcal mol⁻¹versus 28.4 kcal mol⁻¹), and that of phenylacetylene-d₁ favors TS_1-2a-d₁ over TS_1-2b-d₁ (with the reaction barrier of 26.65 kcal mol⁻¹versus 28.2 kcal mol⁻¹), consistent with the experimental findings regarding the major and minor products in runs 2 and 3 of Table 2. A slightly lower TS_1-2b-d₁ (26.65 kcal mol⁻¹) than TS_1-2b (26.73 kcal mol⁻¹) would contribute a small inverse KIE, which was observed in the experiment (runs 2 and 3 in Table 2). These results seem consistent with the common notion that an inverse KIE is normally observed for a process involving a change from C(sp) to C(sp²).¹⁵ The calculated energy barriers are over 26.0 kcal mol⁻¹ and the calculated reaction energies gained are more than 39.0 kcal mol⁻¹, showing that all the reactions are irreversible and the regioselectivity of the reaction is kinetically controlled. It should be noted that the four-centered structures of the transition states in Fig. 2 are similar to those calculated for direct (non-catalyzed) haloboration¹⁶ and diboration^5,12 of alkenes and alkynes. Confirmed by intrinsic reaction coordinate (IRC) calculations, the migration of the pinB group to an alkyne carbon proceeds in a concerted fashion, which is consistent with the first order kinetics as was observed in the experiments. Apparently, the orientation of alkyne coordination determines the regioselectivity of the reactions, with the phenyl substituent pointing towards the pinB moiety in diborane being less favored in both cases, indicating that the steric repulsion between pinB and phenyl substituents controlled the selectivity.

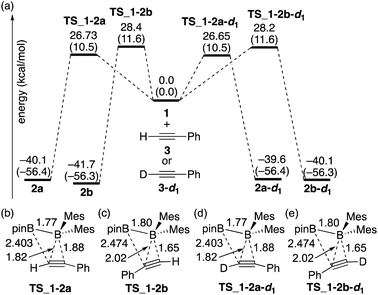Fig. 2 (a) Energy profiles calculated for the direct diboration reactions of 3 and 3-d₁ with 1. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. (b)–(e) Structures of the calculated transition states. Selected bond distances are shown in Å.

The direct diboration of 4-dimethylaminophenylacetylene 3′′ and its deuterated derivative 3′′-d₁ with 1 was also examined as illustrated in Fig. 3(a). Similar to Fig. 2, all the calculated transition states have a four-centered structure [Fig. 3(b)–(e)]. The experimentally observed opposite selectivity (run 4 vs. run 2, Table 2) for the formation of isomer 2b′′ could be reproduced by DFT calculations with a lower-energy transition state of TS_1-2b′′versusTS_1-2a′′ (with the reaction barrier of 25.1 kcal mol⁻¹versus 28.1 kcal mol⁻¹). It should be noted that TS_1-2b′′ is lower in energy than TS_1-2a, which is also consistent with the faster reaction rate with 3′′ than with 3. Transition states TS_1-2a′′-d₁ and TS_1-2b′′-d₁ for the deuterium-labeled substrates were calculated to be almost the same as TS_1-2a′′ and TS_1-2b′′ respectively, offering a small KIE value (runs 4 and 5).

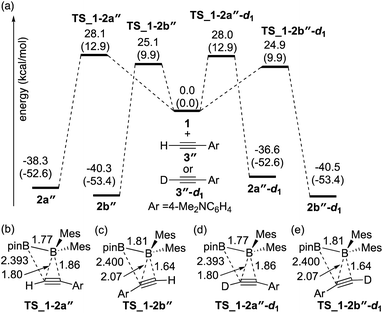Fig. 3 (a) Energy profiles calculated for the direct diboration reactions of 3′′ and 3′′-d₁ with 1. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. (b)–(e) Structures of the calculated transition states. Selected bond distances are shown in Å.

Reaction mechanism for the diboration of phenylacetylene in the presence of a base

Evaluation of coordinating solvent. Next, we estimated the mechanism of the diboration of phenylacetylene 3 with 1 under the conditions B and C. We believe PhC≡CLi (6), generated from phenylacetylene and ⁿBuLi in situ, is the active species that initiates the reactions. Since the coordination environment of a lithium cation depends on the reaction conditions, we first considered how 6 is coordinated to various potential ligands such as the solvent THF and toluene, additive DME, and reactant 1. We calculated the binding energies of 6 with the different potential ligands mentioned above. Binding energies of all the potential ligands are summarized in Scheme 4. The calculation results show that the two diborane(4) 1 molecules in 6(1)₂, three THF molecules in 6(thf)₃, and two DME molecules in 6(dme)₂ coordinate to the lithium center with similar stabilizing energy. In contrast, benzene (representing the actual solvent toluene) is a very poor ligand for the lithium center in 6(C₆H₆)₂. On the basis of these calculation results, we will consider (i) the use of the diborane(4) reagent 1 as the ligand for the lithium center in the absence of additives and (ii) the use of the solvent THF or additive DME as the ligand when they were employed.

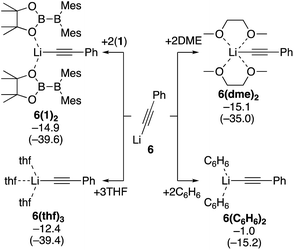Scheme 4 Binding energies of various ligands to PhC≡CLi (6). The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹.

Reaction mechanism for the base-catalyzed diboration of phenylacetylene (coordinating ligand: diborane(4) 1 = with no ethereal additive)

The first half of the reaction: migration of the Bpin group which is the rate-determining step. We conducted DFT calculations where the coordinating ligand to Li⁺ is diborane(4) 1. As shown in the energy profile (Fig. 4), 6(1)₂ undergoes an exothermic PhC≡C⁻ migration from the lithium center to the BMes₂ boron center with a small barrier of 5.3 kcal mol⁻¹, giving 4(1). From 4(1), there are two pathways [paths A (red) and B (blue)] involving a pinB migration leading to the formation of a common intermediate 5(1). Path A consists of the following three steps: (a) a B–B bond cleavage to furnish 1,1-diborylalkeneyllithium 7(1)via a ‘1,2-metalate shift’ of alkynylborate,¹⁷ (b) migration of the pinB group as an intramolecular nucleophilic attack of alkenyllithium to give borataallene 5a(1), in which the Li⁺ is coordinated to an oxygen atom from the Bpin moiety and a phenyl ring, and (c) migration of the Li⁺ cation from the phenyl ring to the allenic carbon atom to form the common intermediate 5(1),¹⁸ which is a species similar to the experimentally isolated 5(thf)₂ reported in the previous work.¹⁴ Thus, path A involves two-step migrations of the Bpin substituent. On the other hand, path B consists of two steps: (a) exchange of a ligand coordinating to the Li⁺ from the alkyne to mesityl ring resulting in the formation of 4a(1), and (b) a nucleophilic 1,3-migration of the pinB group to a benzylic carbon atom to afford the common intermediate 5(1). Our calculations show that these two pathways have comparable reaction barriers, with path A [24.8 kcal mol⁻¹viaTS_4(1)–7(1)] being slightly more favorable than path B [25.9 kcal mol⁻¹viaTS_4a(1)–5(1)]. It should be noted that paths A and B here are slightly faster than the direct addition pathway (26.73 kcal mol⁻¹) shown in Fig. 2.

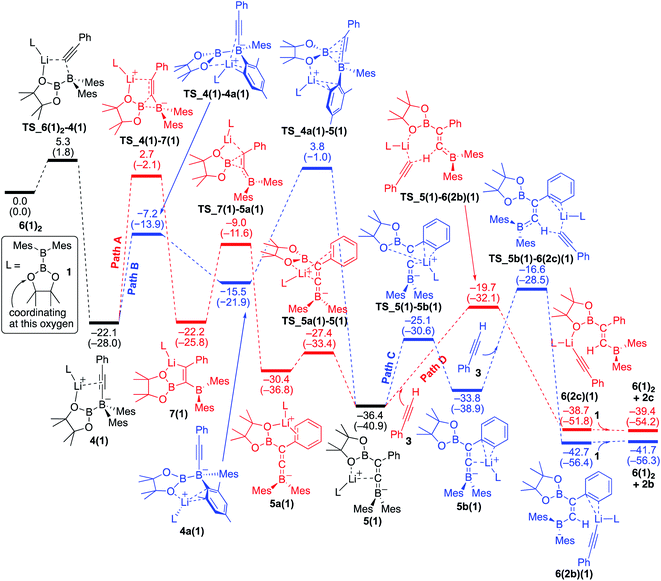Fig. 4 Energy profiles calculated for the base-catalyzed diboration of phenylacetylene with 1 initiated from 6(1)₂ in the presence of 1 as the coordinating molecule to the Li⁺ cation. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. Thermodynamically favorable pathways before and after the common intermediate 5(1) are colored in red.

The second half of the reaction: deprotonation of the acetylene substrate. From the common intermediate 5(1), two independent pathways [paths C (blue) and D(red)], which respectively give syn- and anti-isomers 2b and 2c as the products, were found with activation energies of 19.8 and 16.7 kcal mol⁻¹. Path C contains the following two steps: (a) migration of the Li⁺ from the oxygen atom of the Bpin group to the phenyl ring to furnish 5b(1), and (b) deprotonation of 3, which is coordinating with lithium, by the allenic carbon of 5b(1) resulting in the formation of 6(2b)(1). The subsequent ligand exchange of 6(2b)(1) with 1 affords the product 2b and regenerates 6(1)₂ to realize the catalytic cycle. Path D also includes a similar deprotonation of Li⁺-coordinating 3 by the allenic carbon atom of 5(1) to give 6(2c)(1). The subsequent ligand exchange of 6(2c)(1) with 1 affords the product 2c and regenerates 6(1)₂. Considering the energy profiles shown in Fig. 4, we see that the rate-determining step of the reaction corresponds to the pinB migration from 4(1)via path A with a barrier of 24.8 kcal mol⁻¹ at the transition state TS_4(1)–7(1).

Reversibility of the deprotonation step that contributes to the selectivity toward the products syn-2b and anti-2c. The selectivity towards the formation of 2b and 2c is controlled by the deprotonation steps. Under the reaction conditions, the backward reaction of path D is energetically accessible [19.0 kcal mol⁻¹, from 6(2c)(1) to 5(1)]. Therefore, in the later stage of the catalytic process where the concentration of 1 decreased, this backward reaction and subsequent path C would contribute to produce the syn-product 2b. These calculation results regarding the kinetic and thermodynamic preference are consistent with the experimental observations that 2c is the major product when the reaction is conducted at 40 °C (Table 1, run 5), while 2b becomes the major product when the reaction temperature is set to 100 °C (Table 1, run 4).

Reaction mechanism for the base-catalyzed diboration of alkynes (coordinating ligand: THF)

We also performed calculations for the reaction of diborane 1 in THF solvent. The energy profiles calculated are shown in Fig. 5. The starting compound 6(1)(thf)₂ undergoes exothermic alkynyl migration with a small barrier of 2.4 kcal mol⁻¹ to give 4(thf)₂, which was directly characterized by the single-crystal X-ray diffraction analysis.¹⁴ In a similar manner shown in Fig. 4 with 1 as the ligand, two similar pathways were found [paths A (blue) and B (red)]. However, in the case of Fig. 5 with THF as a ligand, the 1,3-migration of pinB via path B (25.9 kcal mol⁻¹) is kinetically more favorable than the 1,2-migration of pinB via path A (26.7 kcal mol⁻¹). The results are consistent with the experimental observation that 4(thf)₂ was formed at low temperature, and further heating at higher temperature converted 4(thf)₂ to 5(thf)₂.¹⁴ From the common intermediate 5(thf)₂, path D providing the anti-product 2c is kinetically favored by 7.2 kcal mol⁻¹ with a smaller activation energy (19.3 kcal mol⁻¹) viaTS_5(thf)₂–6(2c)(thf)₂ than path C providing the syn-product 2b. The isomerization from 2c to 2bvia the common intermediate 5(thf)₂ and the transition state TS_5b(thf)₂–6(2b)(thf)₂ requires a slightly higher energy of 26.5 kcal mol⁻¹ in comparison with that (22.1 kcal mol⁻¹) in Fig. 4, suggesting a better product selectivity toward anti-isomer 2c in run 6 (vs. runs 4 in Table 1).

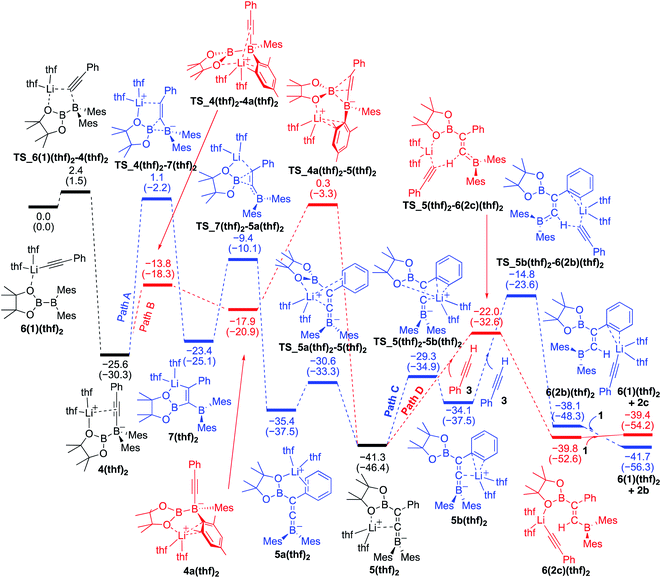Fig. 5 Energy profiles calculated for the base-catalyzed diboration of phenylacetylene with 1 initiated from 6(1)(thf)₂ in the presence of THF as the coordinating molecule to the Li⁺ cation. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. Thermodynamically favorable pathways are colored in red.

Reaction mechanism for the base-catalyzed diboration of phenylacetylene (coordinating ligand: DME)

We then considered the situation in which the additive DME acts as a ligand. The corresponding energy profiles calculated on the basis of the mechanisms given are shown in Fig. 6. The property of the obtained energy profile for DME as a ligand in Fig. 6 is almost identical to that of Fig. 5, except that the rate determining barrier [23.7 kcal mol⁻¹, which is calculated as the difference between 4(dme) and TS_4a(dme)–5(dme) in path B] is lower than those in Fig. 4 and 5. In other words, DME enhances the reaction rate, consistent with the experimental observation as described in run 7 (vs. run 4) of Table 1. The rate enhancement is attributed to the relatively lower isomerization energy from 4(dme) to 5(dme) which contributes to the overall energy barrier of path B. The bidentate DME ligands can stabilize the lithium cation to a greater extent than the monodentate ligand 1 and THF, which gives a higher nucleophilicity to the Bpin group and a smaller isomerization energy between intermediates 4a(dme) and 5(dme), and lowers the reaction barrier. Thus, the use of DME as an additive can improve the product selectivity, consistent with the experimental observation.

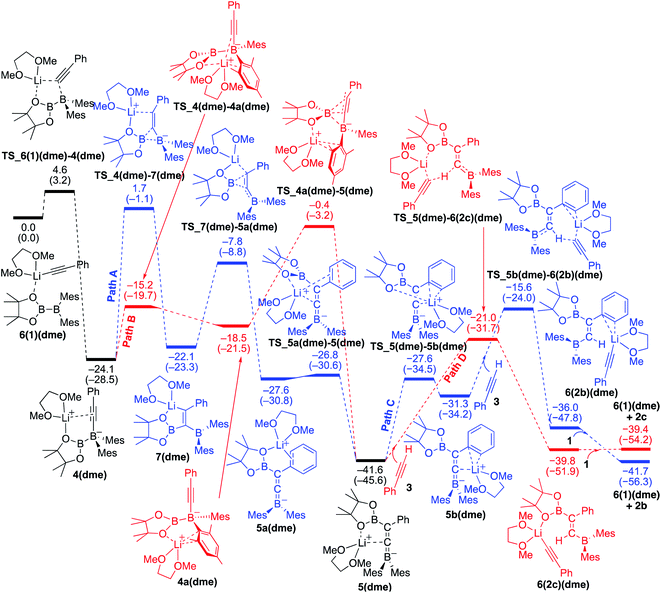Fig. 6 Energy profiles calculated for the base-catalyzed diboration of phenylacetylene with 1 initiated from 6(1)(dme) in the presence of DME as the coordinating molecule to the Li⁺ cation. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. Thermodynamically favorable pathways are colored in red.

Comparison of energy profiles for the base-catalyzed diboration of phenylacetylene, 4-dimethylaminophenylacetylene, and their deuterium-labeled derivatives (coordinating ligand: DME)

To understand the results of kinetic experiments in runs 6–9 of Table 2 under base-catalyzed conditions, additional calculations were performed. In runs 6 and 7 of Table 2, deuterium labeling of phenylacetylene led to a slower reaction rate, which was reproduced by DFT calculations for the reaction of the common intermediate 5(dme) with deuterated phenylacetylene 3-d₁ as shown in Fig. 7. The results regarding the kinetic and thermodynamic preference are the same as those in Fig. 6, where path D giving product 2c-d₁ is kinetically favored by 5.3 kcal mol⁻¹ than path C giving 2b-d₁. Path D in Fig. 7 with 3-d₁ requires a slightly higher activation barrier of 21.5 kcal mol⁻¹ than that in Fig. 6 with 3 (20.6 kcal mol⁻¹), supporting the experimentally obtained positive KIE value. In runs 8 and 9 in Table 2, the reaction rates were almost the same with a KIE value of 0.99 and the selectivities for isomers a–c were comparable to each other which were similar to those in runs 4 and 5. The DFT calculations for the reaction between the intermediate 5(dme) and 3′′-d₁ result in the kinetic preference of 2c′′-d₁ (path D) to 2b′′-d₁ (path C) by 4.4 kcal mol⁻¹ (Fig. 8). However, experimentally, no significant KIE was observed. Given the rate-determining activation energy of 23.7 kcal mol⁻¹ in Fig. 6 is close to that of TS_1-2b′′-d₁ in Fig. 3 and a lower concentration of catalytically active species for the base-catalyzed condition (10 mol% ⁿBuLi and DME were used), the direct diboration of 1 with excess amount of 3′′-d₁ is dominant and affords 2b′′-d₁ as the major product for runs 8 and 9 in Table 2 even in the presence of catalytic amounts of ⁿBuLi and DME.

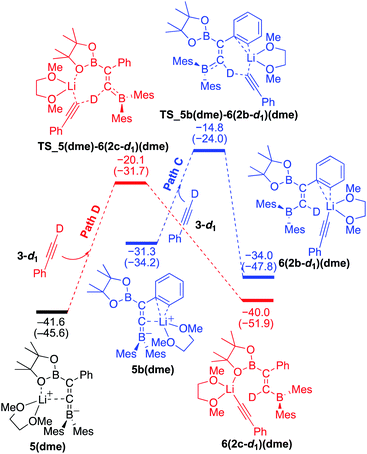Fig. 7 Energy profiles calculated for the paths C and D in the base-catalyzed diboration of phenylacetylene-d₁ with 1 initiated from the common intermediate 5(dme) (same as Fig. 6) in the presence of DME as the coordinating molecule to the Li⁺ cation. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. Thermodynamically favorable pathways are colored in red.

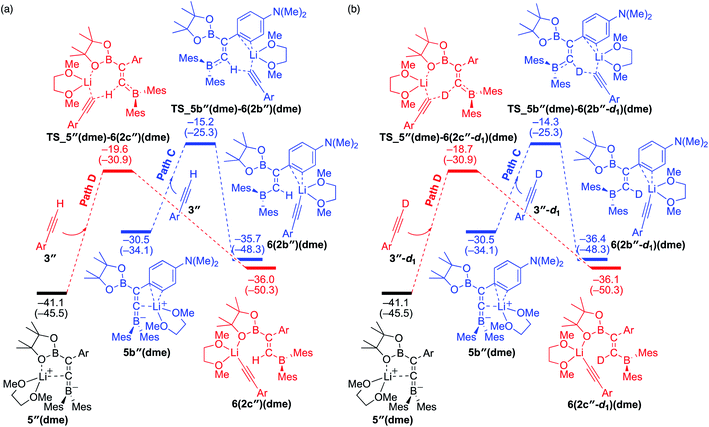Fig. 8 Energy profiles calculated for the paths C and D in the base-catalyzed diboration of 3′′ (a) and 3′′-d₁ (b) with 1 initiated from the common intermediate 5′′(dme) in the presence of DME as the coordinating molecule to the Li⁺ cation. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹. Thermodynamically favorable pathways are colored in red.

Origin of the product distribution in the base-catalyzed diboration of phenylacetylene (Table 1)

Summarizing the results obtained by DFT calculations, distribution of the isomeric products in the diboration of alkynes by using 1 could be clearly explained by a combination of the direct addition pathway and the base-catalyzed pathway as illustrated in Scheme 5. The DFT calculations indicated that the former reaction affords only 2a and 2b [Scheme 5(a)], where the minor product 2b is thermodynamically more stable, consistent with the irreversible nature of this step. While the base-catalyzed pathway furnished only 2b and 2c [Scheme 5(b)], the backward reaction from 2c to 2b reflects their relative thermodynamic stability. Therefore, the isomeric mixture of 2a–c as results of runs 4–9 in Table 1 is expected to originate from both pathways. The composition of the isomeric mixture was also controlled by the difference in the activation barriers for the protonation steps of the borataallene intermediate 5(solv)_n and the relative rate of their backward isomerization as confirmed by our DFT calculations.

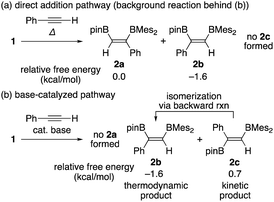Scheme 5 Possible products 2a, 2b, and 2c for the two pathways, relative free energies for each product, and backward isomerization from 2c to 2b.

Conclusions

Reaction mechanisms of the transition-metal free direct addition pathway and base-catalyzed pathway in the diborations of arylacetylenes using pinB-BMes₂ were experimentally and theoretically investigated. For the direct addition pathway, the more Lewis acidic BMes₂ fragment pulls acetylene to be pyramidalized, followed by migration of the pinB fragment to afford syn-adducts 2a and 2b. These results indicate that the high Lewis acidity of diborane(4) is the key point for the direct diboration of alkynes. In the presence of ⁿBuLi as the base-catalyst, intramolecular 1,3- and/or 1,2-boryl anion migrations take place to afford a common borataallene intermediate, which is converted to syn/anti-adducts 2b and 2c. It should be noted that the kinetically favoured isomer 2c can be converted to 2b in the backward reaction. Our experimental and theoretical studies suggest that the reaction barriers of direct addition and base-catalyzed pathways can be controlled by reaction conditions and substituents of arylacetylenes. This knowledge would contribute to further development of selective diboration reactions.

Data availability

All experimental procedures, analytical data, computational methods, and associated Cartesian coordinates are provided as the ESI.

Author contributions

LW and CK equally contributed this work. ZL and MY conceived the project. CK and SM conducted all experiments. LW and KHL conducted all DFT calculations. ZL and MY wrote the manuscript. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was financially supported by Grants-in-Aid for Scientific Research (A) (B) (MEXT KAKENHI grants 17H01191 and 21H01915) as well as by the Research Grants Council of Hong Kong (HKUST16302418). Parts of the theoretical calculations were carried out using resources of the Research Center for Computational Science, Okazaki (Japan).

Notes and references

1. (a) T. Ishiyama and H. Miyaura, J. Synth. Org. Chem., Jpn., 1999, 57, 503–511; (b) T. Ishiyama and N. Miyaura, J. Organomet. Chem., 2000, 611, 392–402; (c) T. Ishiyama and N. Miyaura, Chem. Rec., 2004, 3, 271–280; (d) J. Takaya and N. Iwasawa, ACS Catal., 2012, 2, 1993–2006.
2. T. Ishiyama, N. Matsuda, N. Miyaura and A. Suzuki, J. Am. Chem. Soc., 1993, 115, 11018–11019.
3. (a) R. T. Baker, J. C. Calabrese, S. A. Westcott, P. Nguyen and T. B. Marder, J. Am. Chem. Soc., 1993, 115, 4367–4368; (b) C. N. Iverson and M. R. Smith, J. Am. Chem. Soc., 1995, 117, 4403–4404; (c) T. Ishiyama, N. Matsuda, M. Murata, F. Ozawa, A. Suzuki and N. Miyaura, Organometallics, 1996, 15, 713–720; (d) G. Lesley, P. Nguyen, N. J. Taylor, T. B. Marder, A. J. Scott, W. Clegg and N. C. Norman, Organometallics, 1996, 15, 5137–5154; (e) C. N. Iverson and M. R. Smith, Organometallics, 1996, 15, 5155–5165.
4. (a) P. Ceron, A. Finch, J. Frey, J. Kerrigan, T. Parsons, G. Urry and H. I. Schlesinger, J. Am. Chem. Soc., 1959, 81, 6368–6371; (b) C. Chambers and A. K. Holliday, J. Chem. Soc., 1965, 3459–3462; (c) R. W. Rudolph, J. Am. Chem. Soc., 1967, 89, 4216–4217.
5. C. Pubill-Ulldemolins, E. Fernández, C. Bo and J. M. Brown, Org. Biomol. Chem., 2015, 13, 9619–9628.
6. A. Bonet, C. Pubill-Ulldemolins, C. Bo, H. Gulyás and E. Fernández, Angew. Chem., Int. Ed., 2011, 50, 7158–7161.
7. C. Pubill-Ulldemolins, A. Bonet, H. Gulyas, C. Bo and E. Fernandez, Org. Biomol. Chem., 2012, 10, 9677–9682.
8. (a) Y. Nagashima, K. Hirano, R. Takita and M. Uchiyama, J. Am. Chem. Soc., 2014, 136, 8532–8535; (b) A. Morinaga, K. Nagao, H. Ohmiya and M. Sawamura, Angew. Chem., Int. Ed., 2015, 54, 15859–15862; (c) K. Nagao, H. Ohmiya and M. Sawamura, Org. Lett., 2015, 17, 1304–1307; (d) N. Miralles, R. Alam, K. J. Szabó and E. Fernández, Angew. Chem., Int. Ed., 2016, 55, 4303–4307; (e) T. Ohmura, Y. Morimasa and M. Suginome, Chem. Lett., 2017, 46, 1793–1796; (f) A. Verma, R. F. Snead, Y. Dai, C. Slebodnick, Y. Yang, H. Yu, F. Yao and W. L. Santos, Angew. Chem., Int. Ed., 2017, 56, 5111–5115; (g) S. Peng, G. Liu and Z. Huang, Org. Lett., 2018, 20, 7363–7366.
9. A related organosulfide-catalyzed diboration of alkyne under irradiation of light was reported by Ogawa, in which a thiyl radical was proposed as a key intermediate; see, A. Yoshimura, Y. Takamachi, L.-B. Han and A. Ogawa, Organosulfide-Catalyzed Diboration of Terminal Alkynes under Light, Chem.–Eur. J., 2015, 21, 13930–13933.
10. R. D. Dewhurst, E. C. Neeve, H. Braunschweig and T. B. Marder, Chem. Commun., 2015, 51, 9594–9607.
11. F. Ge, X. Tao, C. G. Daniliuc, G. Kehr and G. Erker, Angew. Chem., Int. Ed., 2018, 57, 14570–14574.
12. G. Kehr and G. Erker, Chem. Commun., 2012, 48, 1839–1850.
13. (a) H. Asakawa, K.-H. Lee, Z. Lin and M. Yamashita, Nat. Commun., 2014, 5, 4245; (b) H. Asakawa, K.-H. Lee, K. Furukawa, Z. Lin and M. Yamashita, Chem.–Eur. J., 2015, 21, 4267–4271; (c) Y. Katsuma, H. Asakawa, K.-H. Lee, Z. Lin and M. Yamashita, Organometallics, 2016, 35, 2563–2566; (d) Y. Katsuma, H. Asakawa and M. Yamashita, Chem. Sci., 2018, 9, 1301–1310.
14. C. Kojima, K.-H. Lee, Z. Lin and M. Yamashita, J. Am. Chem. Soc., 2016, 138, 6662–6669.
15. E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006.
16. C. Wang and M. Uchiyama, Eur. J. Org. Chem., 2012, 2012, 6548–6554.
17. (a) M. T. Lee, M. B. Goodstein and G. Lalic, J. Am. Chem. Soc., 2019, 141, 17086–17091; (b) P. Binger and R. Köster, Tetrahedron Lett., 1965, 6, 1901–1906; (c) P. Binger and R. Köster, Synthesis, 1973, 1973, 309–311; (d) P. Binger and R. Köster, J. Organomet. Chem., 1974, 73, 205–210; (e) P. Binger and R. Köster, Synthesis, 1974, 1974, 350–351; (f) A. Pelter, C. Subrahmanyam, R. J. Laub, K. J. Gould and C. R. Harrison, Tetrahedron Lett., 1975, 16, 1633–1636; (g) A. Pelter, K. J. Gould and C. R. Harrison, Tetrahedron Lett., 1975, 16, 3327–3330; (h) A. Pelter, T. W. Bentley, C. R. Harrison, C. Subrahmanyam and R. J. Laub, J. Chem. Soc., Perkin Trans. 1, 1976, 2419–2428; (i) A. Pelter, K. J. Gould and C. R. Harrison, J. Chem. Soc., Perkin Trans. 1, 1976, 2428–2434; (j) J. Hooz and R. Mortimer, Tetrahedron Lett., 1976, 17, 805–808; (k) R. Koster, Pure Appl. Chem., 1977, 49, 765–789; (l) J. Hooz and R. D. Mortimer, Can. J. Chem., 1978, 56, 2786–2788; (m) A. Pelter and M. E. Colclough, Tetrahedron Lett., 1986, 27, 1935–1938; (n) A. Pelter and M. Eamon Colclough, Tetrahedron, 1995, 51, 811–828; (o) J. Gerard and L. Hevesi, Tetrahedron, 2001, 57, 9109–9121.
18. It should be noted that the reactivity of borataallene where the carbon atom has a nucleophilicity seems to be similar to that of borataalkene species. See: R. J. Maza, J. J. Carbó and E. Fernández, Adv. Synth. Catal., 2021, 363, 2274–2289.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02863d

‡ These authors contributed equally to this work.

---