Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advances in half-Heusler alloys for thermoelectric power generation
Robert J.
Quinn
 and
Jan-Willem G.
Bos
and
Jan-Willem G.
Bos
 *
*
Institute of Chemical Sciences and Centre for Energy Storage and Recovery, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: j.w.g.bos@hw.ac.uk
First published on 13th September 2021
Abstract
Half-Heusler alloys are leading candidate materials for large scale thermoelectric power generation. In the past decade, substantial improvements have been made to the established n-types based on XIVNiSn, and exciting new p-types based on XVFeSb and ZrCoBi have been discovered. This has been achieved through careful experimental work and by increased fundamental insight. In particular, advances in materials synthesis and compositional optimisation guided by empirical modelling have been key to extracting more performance from half-Heuslers alloys. This review summarises recent progress for the main classes of half-Heusler alloys, including their fundamental electronic and thermal properties, processing, and thermoelectric performance. It also incorporates some of the expanding body of work focused on translating materials performance (zT > 1 at 773 K is now routinely possible) into generator devices.
1. Introduction
The world is currently undergoing a transition from an energy economy based on non-renewable fossil fuels to a system making use of a range of renewable generators including solar panels, wind turbines and hydroelectric plants, supplemented by nuclear energy.1 While major changes are taking place in terms of primary energy generation, work on improving the overall efficiency of the world's energy infrastructure is important, which can be achieved by improving electricity transmission, improving device efficiency, and recovering waste energy lost as heat. Thermoelectric generators (TEG's) turn a temperature gradient into an electrical current, allowing waste heat to converted back into electricity.2–7 The widespread application of TEG's would lead to a reduction in the energy production required by primary generators. TEG's can also be used as primary generators, in scenarios where maintenance is difficult, or a long lifetime is required.2–7TEG's have temperature ranges in which they operate most effectively, due to the underlying material properties.8 The only commercial TEGs based on Bi2Te3 for example operate well from 300–500 K, but their effectiveness begins to decrease at higher temperatures. For application involving higher temperatures a different material is required, such as PbTe and GeTe used in the Mars Perseverance rover. However, for large scale terrestrial applications, other requirements such as elemental abundance and cost are important.9,10 Other factors are scalability of materials processing, mechanical properties, temperature stability, matching n- and p-type compositions and ease of electrical and thermal contacting within the TEG devices.4
Of all investigated bulk thermoelectric materials, the half-Heusler (HH) alloys hit most of these target criteria.11–16 In terms of outright performance, they are characterised by good electrical properties, making them suitable for power generation application, and are only held back by relatively high lattice thermal conductivities, which limit the overall heat to electricity conversion efficiency. Due to their good compromise between engineering properties and TE performance, HH alloys have received significant attention as potential thermoelectric materials. Initial investigations into these materials started in the late 1990s and identified n-type and p-type phases based on XIVNiSn and XIVCoSb (XIV = Ti, Zr and Hf) as the most promising compositions.17–29 However, the difficulty in getting reproducible results and pushing zT above one meant that other materials systems, in particular skutterudites and tellurides gained more prominence.6,7
For designing and quantifying the potential of a thermoelectric material, the figure of merit (zT) is used:3
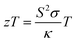 | (1) |
The performance of a material is fundamentally determined by its electronic and phonon bandstructures. Another metric which describes this balance is the quality factor (B), originally established in works by Goldsmid, Chasmar and Stratton:30–32
 | (2) |
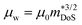 , where μ0 is the carrier mobility in the limit of zero carrier concentration and
, where μ0 is the carrier mobility in the limit of zero carrier concentration and 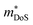 is the density of states effective mass. B gives a measure of the quality of a thermoelectric material independent of the requirement to optimise the carrier concentration n.30
is the density of states effective mass. B gives a measure of the quality of a thermoelectric material independent of the requirement to optimise the carrier concentration n.30
Having a large zT is not the only metric that needs to be considered when selecting a good thermoelectric material, and it has been noted that a reduction in zT to improve the power output can be beneficial.33–35 A singular focus on zT ignores the importance of S2σ for power generation, and on this metric the HH alloys are leading. As discussed below the HH alloys have intrinsic fairly large κl values, and in terms of the quality factor, B, their good performance derives from the large μw. This contrasts with many chalcogenides where high B values are driven by glass-like κl values.6
Up to 2014, the main research focus was on developing n-type materials based on XIVNiSn and p-type materials based on XIVCoSb. This involved developing strategies for alloying and carrier doping and resulted in zT ∼ 1 and zT ∼ 0.7 at 773 K for the n-types and p-types respectively.14 Grain size reduction through high energy ball milling was also established as a route to lower κl but was found to require small average grain sizes 0.2–0.3 μm to be effective.14,36,37 The other route for optimisation that gained interest in the early 2010s was the use of phase segregation to embed favourable micro- and nanostructures for reduction of κl. This focused in particular on segregation of X-site elements (Ti, Zr and Hf)38–40 and excess metals, leading to incorporation of full-Heusler domains.41–45
Recent advances include the rise of p-type compositions XVFeSb (XV = V, Nb and Ta) and ZrCoBi, each with zT > 1 at 773 K.46–48 It also includes the widespread use of single parabolic band (SPB) and Callaway modelling,15 coupled to first principles calculations, which have placed understanding of the HH alloys on a much firmer footing. This manuscript will review these main recent developments and will conclude with a brief overview of the integration of HH materials into working TEGs, which is attracting more and more interest.
This review is structured into 3 main sections. Section 2 will discuss general structural and processing aspects, and fundamental electronic and thermal properties of HH alloys. Section 3 gives an overview of key recent materials developments for the main classes of HH alloys. Section 4 gives a brief overview of incorporation into TEG devices.
2. General trends in half-Heusler materials
This section will describe some of the general trends in HH materials. This is focused on crystal structure and compositions, an overview of observed zT and temperature-averaged zTav values and general trends in electronic and thermal properties of these materials.2.1. Crystal structure
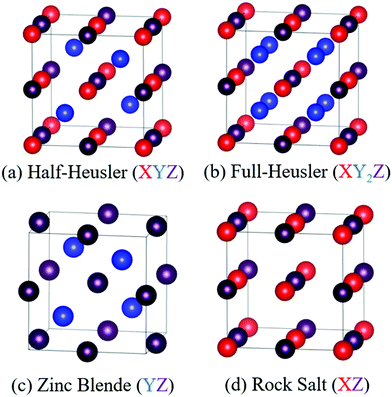
HH alloys have a typical composition XYZ, where X is an early transition metal (Sc, Ti, V groups), Y is a late transition metal (Fe, Co, Ni groups) and Z is a heavy main group metal (typically Sn or Sb, occasionally Ge, Pb or Bi).49 The structure can be described as a combination of zinc blende (YZ) and rock-salt (XZ) structures, with a F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (216) cubic space group, as shown in Fig. 1.49,50 HH materials with a valence electron count of 18 are semiconducting, as each element has either a filled or empty valence shell. For example in TiNiSn, the formal oxidation states are Ti4+ (3d0), Ni0 (3d10) and Sn4− (5s25p6) and in NbFeSb, they are Nb5+ (4d0), Fe2− (3d10) and Sb3− (5s25p6). Hence, each element has an empty/full shell and the oxidation states are balanced, signalling a stable composition.49–51 Similarly, one can consider the electronic structure to be related to III–V semiconductors, with an 18 electron [YZ]n− zinc blende sublattice charge balanced by the electropositive metal Xn+.49 This electron counting does not fully guarantee a semiconducting state, with HH phases with higher average atomic number sometimes found to be semimetallic (e.g. HfCoSb), due to the closing of the band gap.19 It should also be noted that d-orbitals from the X and Y metals form the dominant contributions to the valence and conduction band,49 so the simple Zintl-model, with separate ionic Xn+ and covalent [YZ]n− substructures, does not fully capture the chemical bonding.52 First principles calculations confirm that the crystal structure is stabilised by strong covalent bonding in the YZ sublattice but also by stabilisation linked to the “ionic” XZ rock-salt sublattice,24,27 where (intuitively) site inversion would carry a large electrostatic penalty. Defect energy calculations confirm this picture with X/Z and Y/Z site inversion being costly, and the lowest energy defect generally being occupancy of the interstitial tetrahedral site.27,53–56 Full occupancy of the interstitial site leads to the XY2Z full-Heusler structure as shown in Fig. 1. As indicated by defect energy calculations, inversion of X and Y is uncommon (e.g. <1% in XIVNiSn),57 but there is evidence that this occurs for V0.8CoSb and VFeSb,58,59 where V/Fe and V/Co are (almost) adjacent in the periodic table and hence likely to have similar site preferences.
3m (216) cubic space group, as shown in Fig. 1.49,50 HH materials with a valence electron count of 18 are semiconducting, as each element has either a filled or empty valence shell. For example in TiNiSn, the formal oxidation states are Ti4+ (3d0), Ni0 (3d10) and Sn4− (5s25p6) and in NbFeSb, they are Nb5+ (4d0), Fe2− (3d10) and Sb3− (5s25p6). Hence, each element has an empty/full shell and the oxidation states are balanced, signalling a stable composition.49–51 Similarly, one can consider the electronic structure to be related to III–V semiconductors, with an 18 electron [YZ]n− zinc blende sublattice charge balanced by the electropositive metal Xn+.49 This electron counting does not fully guarantee a semiconducting state, with HH phases with higher average atomic number sometimes found to be semimetallic (e.g. HfCoSb), due to the closing of the band gap.19 It should also be noted that d-orbitals from the X and Y metals form the dominant contributions to the valence and conduction band,49 so the simple Zintl-model, with separate ionic Xn+ and covalent [YZ]n− substructures, does not fully capture the chemical bonding.52 First principles calculations confirm that the crystal structure is stabilised by strong covalent bonding in the YZ sublattice but also by stabilisation linked to the “ionic” XZ rock-salt sublattice,24,27 where (intuitively) site inversion would carry a large electrostatic penalty. Defect energy calculations confirm this picture with X/Z and Y/Z site inversion being costly, and the lowest energy defect generally being occupancy of the interstitial tetrahedral site.27,53–56 Full occupancy of the interstitial site leads to the XY2Z full-Heusler structure as shown in Fig. 1. As indicated by defect energy calculations, inversion of X and Y is uncommon (e.g. <1% in XIVNiSn),57 but there is evidence that this occurs for V0.8CoSb and VFeSb,58,59 where V/Fe and V/Co are (almost) adjacent in the periodic table and hence likely to have similar site preferences.
2.2. Synthesis
HH materials are intermetallic compounds and are usually prepared from elemental precursors, which span a range of melting points, e.g. 1855 °C for Zr and 232 °C for Sn. Given the presence of refractory elements, melting has historically been the favoured route for initial reaction. Most frequently this is done by arc-melting of elemental pieces in an argon atmosphere, although levitation melting has become more common in recent years.60,61 The main advantage of levitation melting is that the sample does not touch the sample environment (usually a Cu plate in arc melting) and the presence of eddy currents that improve the homogeneity of the melt.48,60 Arc-melting has been noted to contain different microstructures in different sections of the final ingot.62 A linked practical advantage of melt-based routes is that larger elemental pieces can be used avoiding issues with surface oxidation that can be significant in powder metallurgy. Nevertheless, powder-based routes can give good performing samples, but care has to be taken with precursors, and the lower temperatures also place limitations on grain growth.59,63,64 Other means of achieving reaction include microwave synthesis and self-propagating combustion synthesis.65–69After initial reaction it is common to anneal the sample, typically between 900–1000 °C, to equilibrate the sample and increase homogeneity. In the past couple of years however, what may be called ‘out-of-equilibrium’ processing has gained much prominence. Here, melting is followed by ball milling and rapid consolidation at high temperature and under applied pressure, often using spark plasma sintering (SPS), but no long duration heating is used.47,48,70,71 This can be a favourable route that maintains embedded nanostructures that would be annealed out at high temperatures.72 In some instances, most notably for ZrCoBi, the melting step is removed altogether, leading to an efficient synthetic protocol.48 Compared to the initial literature of the early 2000s, ball milling after HH phase formation has gained prominence and is now nearly always used. Reasons include promoting sample homogeneity and achieving a good particle size distribution that facilitates consolidation into dense ingots, whilst very small grain sizes are also beneficial for κl reduction.36,37 Using direct mechanical alloying of elemental precursors has been found to narrow the grain size distribution in a range of HH materials,73 with HH and FH alloys forming during the milling stage.48,73,74 Ball milling needs to be carried out under an inert atmosphere, including the handling of the resulting fine powders, to protect the high surface area samples from oxidation.
Whether or not there is an annealing stage, all samples need to be in a highly dense form before property measurement. While samples can be cut from a melted piece with high density,75,76 it is more common for the powdered sample to be consolidated using either hot-pressing or SPS, with much of the improvement in thermoelectric performance in recent years arising due to more careful consolidation of samples. In particular, SPS has become more prominent and enables very rapid densification.77,78 In conventional hot pressing, uniaxial pressure is applied to the sample in a graphite die which is heated indirectly, for example using an induction coil.79 SPS applies a current directly through the graphite die, allowing for much more rapid heating of the sample. In some methods, such as flash-SPS, very short consolidation times on the order of minutes are possible.80,81 The choice of pressing method is expected to have an effect on the properties of the sample, with literature comparisons in other material systems showing significant differences in optical, thermal and mechanical properties.82–84
2.3. Electronic transport properties
HH thermoelectric materials are small band gap semiconductors, with calculated band gaps typically ranging between 0.5–1 eV.85 The conduction band minimum typically lies at the X-point, while the valence band will either exist at the Γ-point or the L-point, and in some cases, both can be effectively degenerate, as illustrated for the ZrCoBi system (Fig. 2). In addition, the W-point can sometimes be close to the other valence band maxima. From this perspective, p-type materials have a larger potential for band-engineering to improve the thermoelectric properties, as degenerate band extrema allow for an increase in the density of states effective mass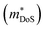 :
: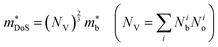 | (3) |
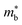 is the band effective mass. Paradoxically, for good electronic performance a large
is the band effective mass. Paradoxically, for good electronic performance a large 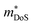 is desirable for large S, but a low
is desirable for large S, but a low 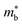 is desirable for high σ. On balance a smaller
is desirable for high σ. On balance a smaller 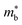 is better overall, yielding large μw.86
is better overall, yielding large μw.86
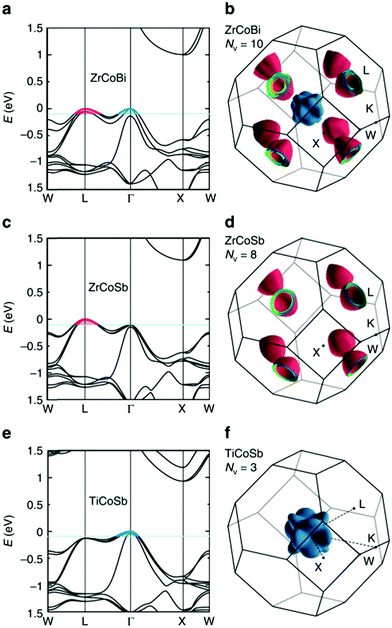 | ||
| Fig. 2 First principles electronic bandstructures of XCoSb half-Heusler materials (including spin–orbit coupling contributions). As shown in (a) and (b), p-type doped ZrCoBi is expected to have carriers from the doubly degenerate L-point and Γ-point, leading to a substantial total degeneracy NV = 10. This is larger than many high-performance p-type half-Heusler phases, which have only L-point holes (NV = 8), such as ZrCoSb as shown in (c) and (d). By contrast, TiCoSb only has carriers from the triply degenerate Γ-point (NV = 3) as shown in (e) and (f) and is experimentally found to have the lowest power factor, S2σ. Reproduced from Zhu et al. Nature Communications, 2018.48 | ||
As shown in Table 1, 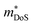 for HH materials can be quite large, in some cases exceeding 10 me, with
for HH materials can be quite large, in some cases exceeding 10 me, with 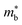 typically between 1.5–3.0 me, which requires large amounts of doping to reach optimal nH up to orders of magnitude of 1020–1021 cm−3. HH materials typically have μH on the order of 10 cm2 V−1 s−1, with examples of single crystal ZrNiSn as large as 70 cm2 V−1 s−1 and Ta0.81CoSb with μH as low as 1.4 cm2 V−1 s−1.59,87 Here, nH and μH are the carrier concentration and mobility from Hall measurements.
typically between 1.5–3.0 me, which requires large amounts of doping to reach optimal nH up to orders of magnitude of 1020–1021 cm−3. HH materials typically have μH on the order of 10 cm2 V−1 s−1, with examples of single crystal ZrNiSn as large as 70 cm2 V−1 s−1 and Ta0.81CoSb with μH as low as 1.4 cm2 V−1 s−1.59,87 Here, nH and μH are the carrier concentration and mobility from Hall measurements.
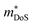 , in electron mass units) obtained from Hall data as outlined in Appendix A. Here, Nb is the number of bands at the valence or conduction band extrema, N0 is the number of equivalent points in the Brillouin zone and Nv is the total valley degeneracy
, in electron mass units) obtained from Hall data as outlined in Appendix A. Here, Nb is the number of bands at the valence or conduction band extrema, N0 is the number of equivalent points in the Brillouin zone and Nv is the total valley degeneracy
| Type | Point | N b | N o | N v | m b | Ref. | ||
|---|---|---|---|---|---|---|---|---|
a Based on 19 electron NbCoSb with potentially larger Nb in the defective Nb0.8CoSb composition.
b Cu interstitials may increase band degeneracy at the conduction band.
c Data suggests a higher Nv for this sample, see Section 3.5.
d Data suggests that 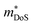 increases with Sn substitution, as discussed in Section 3.2. increases with Sn substitution, as discussed in Section 3.2.
|
||||||||
| V0.8+δCoSb | n | X | 3 | 10.0 | 59 | |||
| Nb0.8+δCoSb | n | X | 2a | 3 | 6 | 7.7 | 2.33 | 183 and 188 |
| Ta0.8+δCoSb | n | X | 3 | 5.9 | 59 | |||
| Zr0.5Hf0.5Co1−xNixSb | n | X | 1 | 3 | 3 | 6.0 | 2.88 | 142 and 234 |
| Zr1−xHfxCoSb | n | X | 1 | 3 | 3 | 6.5 | 3.13 | 93 |
| Ti0.9−xHfxTa0.1CoSb | n | X | 1 | 3 | 3 | 9.1 | 4.37 | 143 |
| ZrNi1+xSn | n | X | 1 | 3 | 3 | 3.0 | 1.44 | 114 and 235 |
| TiNi1+xSn1−ySb | n | X | 1 | 3 | 3 | 2.8 | 1.35 | 175 and 235 |
| Ti0.5Zr0.25Hf0.25NiCuxSn | n | X | 1b | 3 | 3 | 4.1 | 1.97 | 64 and 235 |
| Zr1−xHfxNiSn0.985Sb0.015 | n | X | 1 | 3 | 3 | 2.8 | 1.35 | 4 and 235 |
| Ti1−xTaxNi0.92Sn | n | X | 1 | 3 | 3c | 4.5 | 2.16 | 71 and 235 |
| NbCoSn1−xSb | n | X | 2 | 3 | 6 | 6.1 | 1.85 | 197 and 198 |
| ZrCo1−xPdxBi | n | X | 1 | 3 | 3 | 4.4 | 2.12 | 126 |
| ZrCo1−xNixBi | n | X | 1 | 3 | 3 | 7.0 | 3.37 | 86 |
| Ta1−xTixFeSb | p | L | 2 | 4 | 8 | 9.0 | 2.25 | 47 |
| Nb1−xHfxFeSb | p | L | 2 | 4 | 8 | 6.9 | 1.73 | 113 and 121 |
| (V0.6Nb0.4)1−xTixFeSb | p | L | 2 | 4 | 8 | 10.0 | 2.50 | 119 |
| ZrCoBi1−xSnx (x = 0.2) | p | L/Γ | 2/2 | 4/1 | 10 | 13d | 2.80 | 48 and 86 |
| Ti1−xHfxCoSb0.85Sn0.15 | p | L/Γ | 2/3 | 4/1 | 11 | 10.7 | 2.16 | 75 and 234 |
| Zr1−xHfxCoSb0.8Sn0.2 | p | L | 2 | 4 | 8 | 12.5 | 3.13 | 92 |
As collection of Hall data has become more frequent, so have detailed investigations into the dominant carrier scattering mechanisms. For semiconductors at low doping concentrations (nH < 1017 cm−3) μH is expected to be limited by ionised impurity (II) scattering, which has a characteristic μH ∼ T1.5 behaviour.88 At high doping concentration (nH > 1018 cm−3), II scattering is minimal due to screening from the high number of charge carriers, and it is common to find scattering by phonons (acoustic phonon scattering; APS) to be dominant. This has a characteristic μH ∼ T−1.5 temperature dependence for semiconductors and μH ∼ T−1 in the metallic limit.88 A final intrinsic effect is alloy scattering (AS) due to size difference between alloying elements, with similar nH dependence to APS but a different characteristic μH ∼ T−0.5 dependence.89,90 AS has been identified as the dominant carrier scattering mechanism in a number of HH phases,91,92 with recent work indicating that this can be minimised by using alloying elements with similar sizes (minimising lattice strain).93 In other systems, the data suggests a dominant APS dependence, with the large S2σ in HH materials attributed to a fundamentally weak coupling of electrons with acoustic phonons, leading to high μ in spite of large 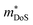 .94
.94
Electronic transport can also be affected by “extrinsic” scattering contributions arising from the materials microstructure.95 In particular, the impact of grain boundary (GB) resistances has attracted much recent interest.96–98 The most successful electronic transport models treat these materials as two-phase composites with bulk and GB phase contributions. The GB phase is usually modelled as a tunnel barrier (due to charge depletion in the GB region), accurately reproducing σ(T) in a range of thermoelectrics, including Mg3Sb2 and SrTiO3.96,97 GB scattering is particularly relevant for p-type NbFeSb with a very sensitive processing dependence of S2σ, caused by changes in σ(T)99 (also Section 3.1). It has also been observed in p-type ZrCoSb, where GB scattering is found to be substantial for low nH and small grain sizes (Section 3.4).100
The recent availability of ZrNiSn single crystals has enabled in-depth investigation of the electronic properties. This includes collection of ARPES data on ZrNiSn that revealed a large intrinsic band gap ∼0.66 eV, comparable to DFT values (∼0.5 eV) and unlike the ∼0.15 eV values usually found from transport data due to in-gap states resulting from interstitial Ni.101 A comparison of single crystal and polycrystalline ZrNiSn1−ySby samples reveals a complex carrier scattering phase diagram. With increasing nH a crossover from II and GB scattering to APS and AS occurs near 300 K, whilst at high temperature the transition is from polar optical (PO) phonon scattering to APS and AS. These transitions occur near nH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3–5
3–5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
× ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1020
1020![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−3 and are a consequence of the effective screening of II, GB and PO scattering at higher carrier concentrations.87
cm−3 and are a consequence of the effective screening of II, GB and PO scattering at higher carrier concentrations.87
2.4. Thermal transport properties
Compared to other state-of-the art thermoelectric materials, which benefit from ultralow (<1 W m−1 K−1) κ,102,103 the HH family of materials typically have large S2σ and relatively high κ values. This is partly due to large κl as outlined above, but also due to large electronic (κel) values, consistent with the large reported S2σ values of these materials. Within the HH thermoelectric literature, experimental κl(T) data is typically treated using the Debye–Callaway model to describe the temperature dependence, with κl(T) defined as:91,104,105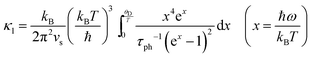 | (4) |
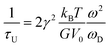 | (5) |
| Composition | Source | a HH (Å) | v l (m s−1) | v t (m s−1) | v s (m s−1) | Θ D (K) | γ | κ Umklappl (W m−1 K−1) | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| VFeSb | DFT | 5.769 | 5773 | 2974 | 3330 | 393 | 1.90 | 19.7 | 236 |
| NbFeSb | AC | 5.950 | 5597 | 3099 | 3452 | 396 | 1.65 | 32.9 | 123 |
| TaFeSb | AC | 5.938 | — | — | 2907 | 334 | — | — | 47 |
| TaFeSb | DFT | 5.950 | 5115 | 2818 | 3140 | 360 | 1.64 | 33.4 | 113 |
| TiCoBi | DFT | 6.033 | 4775 | 2736 | 3039 | 343 | 1.53 | 29.9 | 125 |
| ZrCoBi | AC | 6.188 | 4613 | 2558 | 2849 | 314 | 1.64 | 23.2 | 48 |
| HfCoBi | DFT | 6.194 | 4155 | 2353 | 2617 | 288 | 1.57 | 24.6 | 125 |
| TiCoSb | AC | 5.882 | 5691 | 3230 | 3591 | 416 | 1.56 | 35.6 | 141 |
| ZrCoSb | AC | 6.070 | 5488 | 3144 | 3493 | 392 | 1.53 | 37.9 | 141 |
| HfCoSb | AC | 6.039 | 4703 | 2709 | 3008 | 340 | 1.51 | 34.1 | 141 |
| TiNiSn | AC | 5.930 | 5426 | 3062 | 3406 | 392 | 1.58 | 29.0 | 237 |
| ZrNiSn | AC | 6.110 | 5498 | 3149 | 3498 | 390 | 1.53 | 37.4 | 237 |
| HfNiSn | Mech. | 6.080 | 4191 | 2503 | 2770 | 311 | 1.38 | 31.4 | 238 |
| V0.8+δCoSb | AC | 5.795 | 5437 | 2902 | 3242 | 381 | 1.78 | 21.0 | 191 |
| Nb0.8+δCoSb | AC | 5.902 | 5581 | 2987 | 3336 | 385 | 1.77 | 26.2 | 183 |
| Ta0.8+δCoSb | MP-31459 | 5.969 | 4650 | 2323 | 2607 | 297 | 2.00 | 12.8 | 239 and 240 |
| NbCoSn | DFT | 5.946 | 5625 | 3016 | 3368 | 386.09 | 1.762 | 26.7 | 196 |
| TaCoSn | DFT | 5.948 | 4955 | 2761 | 3077 | 352.30 | 1.6268 | 31.6 | 196 |
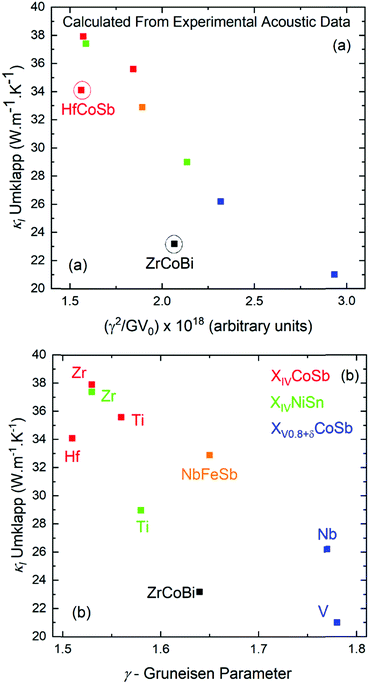 | ||
| Fig. 3 Plots of calculated lattice thermal conductivity (κl) at 300 K (see Section 2.4), assuming the presence of only Umklapp scattering (i.e. for the defect free parent materials), versus (a) the variables determining the magnitude of Umklapp scattering and (b) the acoustic Grüneisen parameter. HfCoSb and ZrCoBi have lower κl due to low vs (see Table 2). | ||
As the scattering rate, τU−1 increases, κl is expected to decrease, which is illustrated well in Fig. 3a, with the outliers being ZrCoBi and HfCoSb due to their low θD. TaFeSb also has low θD and is another outlier, but is not included in Fig. 3, since only the average velocity of sound was reported.47 In the plot of κlvs. γ in Fig. 3b, there is a larger spread due to lower vt for TiNiSn and V0.8+δCoSb (yielding a larger γ) versus their second row analogues. This is ultimately corrected for by a larger G, giving a relatively smooth dependence in Fig. 3a. Naturally these values only represent an upper limit for κl, and the measured experimental values don’t get close to 40 W m−1 K−1. Within the Debye–Callaway model, phonon scattering can be expected to arise due to grain boundaries, the existence of point defects and electron–phonon interactions. Even small effects can have a large effect on κl. In ZrNiSn for example, introducing a point defect scattering term Γ = 0.02 is enough to reduce κl from 37 W m−1 K−1 to 17 W m−1 K−1, which is the value expected from a 2% Hf impurity (which is typical in commercial elemental Zr). Small amounts of interstitials are also sufficient to embed this amount point defect disorder and have been linked to strongly suppressed κl values in XIVNiSn and XIVCoSb systems.63,114
In addition to κl, HH thermoelectrics usually have significant κel, due to the large carrier concentrations and bipolar transport at high temperatures. The total κel is given by:115
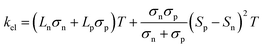 | (6) |
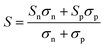 | (7) |
2.5. Overview of materials efficiency: zT and zTavg
The most commonly used metric to quantify the thermoelectric performance of a single material is the materials figure of merit (zT). A larger zT is expected to translate into higher efficiency in a thermoelectric device. However, a more appropriate metric of performance is the temperature average of zT over the gradient the TEG operates under. For this review we have used the following equation:117,118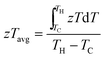 | (8) |
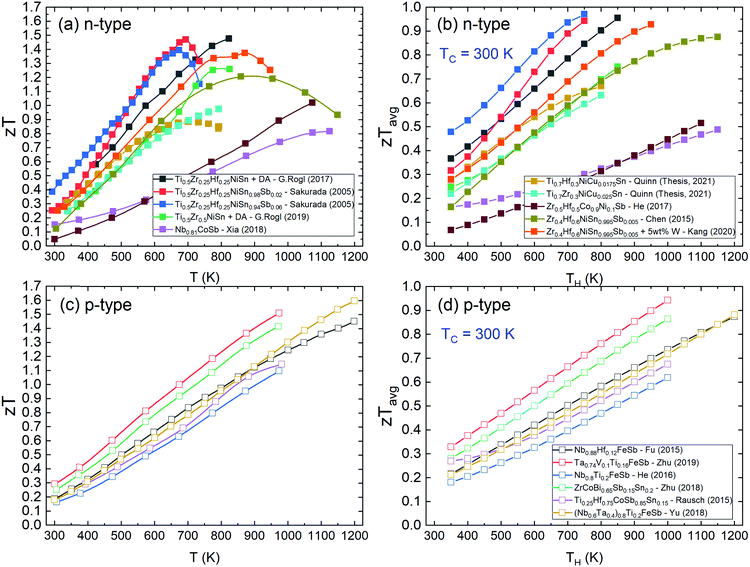 | ||
| Fig. 4 Literature zT values of the best n-type and p-type half-Heusler thermoelectric materials. Panels (a) and (b) show zT and the average zTavg of n-type samples as a function of temperature.142,148,172,174,179,183,191,242 Panels (c) and (d) show zT and the average zTavg of p-type samples.47,48,75,120,121 XNiSn systems have large low temperature zT, but their increase slows above 800 K due to onset of bipolar transport linked to the relatively small band gap. | ||
The best p-type samples all show a gradual increase in zT at least up to 1200 K, at their best achieving zT ∼ 1.5. The overall lower zT for the p-types means that where zTavg would approach 1 at 800 K for the best n-type materials, it takes until 1200 K to reach similar zTavg for p-type HH phases. From Fig. 4c and d, it is clear that the p-type XIVCoSb materials have been overtaken rapidly by the new wave of ZrCoBi and XVFeSb systems.
3. Recent developments in half-Heusler materials
In the following an overview of the main recent materials development will be given, starting with the new p-type materials, followed by good n-types and then other compositions of interest.3.1. XVFeSb (XV = V, Nb and Ta) (p-type)
In 2014, promising p-type thermoelectric properties were reported for (V0.6Nb0.4)1−xTixFeSb, with moderately large S2σ around 3 mW m−1 K−2 and quite small κl below 3 W m−1 K−1, yielding peak zT900K = 0.8 for x = 0.2.119 The good performance in this series was attributed to large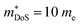 and consequently large S(T), combined with significant X-site alloy point defect scattering suppressing κl. This ‘heavy hole’ behaviour is the main characteristic of the XVFeSb family (and for the other p-type HH materials) and arises due to a doubly degenerate L-point valence band maxima with Nv = 8 (Table 1).119,120 Consequently, high doping levels between 1021–1022 cm−3 are required to optimise the thermoelectric performance at high temperatures, which was not achieved in this initial report. It only took one year for the same group to report zT1200K = 1.5 for the composition Nb0.88Hf0.12FeSb.121 This material removes all V from the system, resulting in a decrease in
and consequently large S(T), combined with significant X-site alloy point defect scattering suppressing κl. This ‘heavy hole’ behaviour is the main characteristic of the XVFeSb family (and for the other p-type HH materials) and arises due to a doubly degenerate L-point valence band maxima with Nv = 8 (Table 1).119,120 Consequently, high doping levels between 1021–1022 cm−3 are required to optimise the thermoelectric performance at high temperatures, which was not achieved in this initial report. It only took one year for the same group to report zT1200K = 1.5 for the composition Nb0.88Hf0.12FeSb.121 This material removes all V from the system, resulting in a decrease in  to 6.9 me reducing the doping required to reach the optimal S2σ, with the increased μH resulting in a near doubling of S2σ to between 5–6 mW m−1 K−2. In addition to p-type doping the material, Hf substitution introduces X-site alloy point defect scattering, maintaining low κl. Further success was found in TaFeSb, for which the composition Ta0.74V0.1Ti0.16FeSb uses the same approach of combined carrier doping and phonon scattering using Ti, with a small fraction of V used to further suppress κl and push zT973K from 1.39 to 1.52.47 The largest peak zT reported for XVFeSb materials comes from the (Nb1−xTax)0.8Ti0.2FeSb series, with both x = 0.36 and 0.4 reaching zT1200K = 1.6,48 As can be seen in Fig. 4c however, the magnitude of zT is lower for the (Nb1−xTax)0.8Ti0.2FeSb series closer to room temperature (leading to a lower zTavg in Fig. 4d), perhaps due to the weaker mass disorder provided by Nb.
to 6.9 me reducing the doping required to reach the optimal S2σ, with the increased μH resulting in a near doubling of S2σ to between 5–6 mW m−1 K−2. In addition to p-type doping the material, Hf substitution introduces X-site alloy point defect scattering, maintaining low κl. Further success was found in TaFeSb, for which the composition Ta0.74V0.1Ti0.16FeSb uses the same approach of combined carrier doping and phonon scattering using Ti, with a small fraction of V used to further suppress κl and push zT973K from 1.39 to 1.52.47 The largest peak zT reported for XVFeSb materials comes from the (Nb1−xTax)0.8Ti0.2FeSb series, with both x = 0.36 and 0.4 reaching zT1200K = 1.6,48 As can be seen in Fig. 4c however, the magnitude of zT is lower for the (Nb1−xTax)0.8Ti0.2FeSb series closer to room temperature (leading to a lower zTavg in Fig. 4d), perhaps due to the weaker mass disorder provided by Nb.
Perhaps the most impressive feature of this family is the ability to achieve extremely large S2σ between 5–6 mW m−1 K−1 over a wide temperature range.46–48,121–123 As first reported in 2016, careful processing allows for S2σ300K > 10 mW m−1 K−2 to be achieved in Nb0.95Ti0.05FeSb, using a hot pressing temperature of 1100 °C to eliminate the parasitic electrical resistance from grain boundary scattering observed with lower pressing temperatures, as illustrated in Fig. 5.99 This was later also demonstrated for the analogous systems with Zr and Hf dopants.123 In addition to the very large S2σ, the κl(T) achieved in Ta0.74V0.1Ti0.16FeSb is extremely low for a HH material, starting at κl,300K = 2.3 W m−1 K−1 decreasing to κl,300K = 1.6 W m−1 K−1, with mass disorder from Ti/V substitution proving to be effective at suppressing κl.47
 | ||
| Fig. 5 The effect of hot-pressing temperature on the electronic properties of Nb0.95Ti0.05FeSb. As seen in (a) hot-pressing at 1100 °C leads to over double the power factor, S2σ at 300 K, relative to pressing at 950 °C. As illustrated in (b) this enhancement arises due to an increase in σ300K, attributed to the elimination of grain boundary scattering of charge carriers. Reproduced from He et al. PNAS, 2016.99 | ||
A range of synthetic routes have been used to prepare XVFeSb HH materials. The initial reports on (V0.6Nb0.4)1−xTixFeSb and Nb1−xHfxFeSb used levitation melting, mechanical milling, SPS and a short annealing step at a low temperature of 750 °C.119,121 The TaFeSb based samples were prepared directly from the elements using ball milling (in a shaker mill), followed by direct current hot-pressing (similar to SPS) for only two minutes at 850 °C, with no subsequent annealing step.47 This report does not establish whether the HH phase forms during the milling step, or whether reaction takes place during hot pressing with the assistance of finely dispersed powder precursors. In spite of the well documented benefit on σRT of a 1100 °C densification temperature for Nb1−xTixFeSb (Fig. 5), highly doped Ta1−xTixFeSb samples seem to suffer no detriment from the relatively low 850 °C pressing temperature (although x < 0.06 samples seem to suffer from grain boundary effects).47 This suggests that these systems have a different grain boundary chemistry. Note that due to the higher melting point of Ta compared to Nb, a priori smaller grain sizes and a more pronounced impact on σRT might have been expected. However, this does not appear to be the case. To conclude, the XVFeSb materials are blessed with naturally excellent electronic properties and thermal transport, which can be easily suppressed using well established mass disorder techniques.
3.2. ZrCoBi (p-type)
In 2018, ZrCoBi0.65Sb0.15Sn0.2 was reported to have the then largest zT973K = 1.42 for any p-type HH phase.48 This composition benefits from a large Nv = 10, which arises due to degenerate Γ and L (Table 1) valence band maxima, which is an inherent property of the stoichiometric ZrCoBi phase (Fig. 2). This convergence translates to large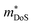 , with the reported Hall data suggesting that
, with the reported Hall data suggesting that 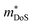 increases from around 9 me to 13 me with Sn substitution up to x = 0.2 in the ZrCoBi1−xSnx solid solution (Table 1).48,86 A combination of Sn and Sb alloying is successful in suppressing κl and optimising the carrier concentration, with the parent composition already having a markedly lower κl than many HH phases due to the high mass of Bi and a low velocity of sound, vs (Table 2). As was the case for TaFeSb,47 the ZrCoBi samples were prepared via ball milling the constituent elements and then direct current hot pressing for 5 minutes at 900 °C.48 In this report the HH phase was found to form directly after the milling step. No further experimental work has emerged on p-type XIVCoBi materials since, although two separate computational investigations of XIVCoBi materials also find near degenerate Γ and L point valence band maxima in TiCoBi and HfCoBi.124,125 It was discovered, however, that n-type ZrCoBi is also a promising thermoelectric material, reaching zT973K = 1 for ZrCo0.9Ni0.1Bi0.85Sb0.15, again utilising a ball-milling to pressing synthetic protocol.86 As before Bi/Sb alloying is used to suppress κl, but interestingly Co/Ni alloying also reduces κl significantly, despite minimal expected mass and strain differences. The reported
increases from around 9 me to 13 me with Sn substitution up to x = 0.2 in the ZrCoBi1−xSnx solid solution (Table 1).48,86 A combination of Sn and Sb alloying is successful in suppressing κl and optimising the carrier concentration, with the parent composition already having a markedly lower κl than many HH phases due to the high mass of Bi and a low velocity of sound, vs (Table 2). As was the case for TaFeSb,47 the ZrCoBi samples were prepared via ball milling the constituent elements and then direct current hot pressing for 5 minutes at 900 °C.48 In this report the HH phase was found to form directly after the milling step. No further experimental work has emerged on p-type XIVCoBi materials since, although two separate computational investigations of XIVCoBi materials also find near degenerate Γ and L point valence band maxima in TiCoBi and HfCoBi.124,125 It was discovered, however, that n-type ZrCoBi is also a promising thermoelectric material, reaching zT973K = 1 for ZrCo0.9Ni0.1Bi0.85Sb0.15, again utilising a ball-milling to pressing synthetic protocol.86 As before Bi/Sb alloying is used to suppress κl, but interestingly Co/Ni alloying also reduces κl significantly, despite minimal expected mass and strain differences. The reported 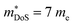 is quite large considering the low band degeneracy of the X-point, suggesting a large mb, consistent with the reported low mobility. In the previous year n-type ZrCo1−xPdxBi was reported with substantially lower zT, due to a combination of significantly larger κl and a much lower
is quite large considering the low band degeneracy of the X-point, suggesting a large mb, consistent with the reported low mobility. In the previous year n-type ZrCo1−xPdxBi was reported with substantially lower zT, due to a combination of significantly larger κl and a much lower 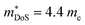 .126 The samples in this report were prepared using arc-melting, ball-milling and rapid uniaxial hot-pressing.
.126 The samples in this report were prepared using arc-melting, ball-milling and rapid uniaxial hot-pressing.
3.3. XIVCoSb (XIV = Ti, Zr and Hf) (p-type)
Before the rapid emergence of the high zT p-type XVFeSb and ZrCoBi materials, XIVCoSb materials were by far the most promising candidate p-type HH phases. zT1073K = 1.0 had been achieved for Ti0.2Hf0.8CoSb0.8Sn0.2 in 2012, with the same achieved in a 2013 follow up report on Ti0.12Zr0.44Hf0.44CoSb0.8Sn0.2, with both utilising X-site alloying and milling to suppress κl.127,128 Once again, these p-type compositions benefit from high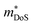 due to the doubly degenerate L-point valence band maximum (Table 1), although S2σ did not exceed 3.0 mW m−1 K−2 in these materials, with a fundamentally low μH in this system. The modest S2σ is a serious drawback for these compositions, as there are few clear-cut ways to improve the electronic properties and zT, whereas a range of strategies are available to suppress κl. In 2015 zT was pushed up to 1.15 at 973 K for the composition Ti0.25Hf0.75CoSb0.85Sn0.15, by optimising nH and X-site alloying, with phase segregation into Ti-rich and Hf-rich regions credited with further suppression of κl.75 Another important detail in this paper is while
due to the doubly degenerate L-point valence band maximum (Table 1), although S2σ did not exceed 3.0 mW m−1 K−2 in these materials, with a fundamentally low μH in this system. The modest S2σ is a serious drawback for these compositions, as there are few clear-cut ways to improve the electronic properties and zT, whereas a range of strategies are available to suppress κl. In 2015 zT was pushed up to 1.15 at 973 K for the composition Ti0.25Hf0.75CoSb0.85Sn0.15, by optimising nH and X-site alloying, with phase segregation into Ti-rich and Hf-rich regions credited with further suppression of κl.75 Another important detail in this paper is while 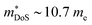 remains largely constant in the Ti1−xHfxCoSb solid solution, μH is around 3 times lower in TiCoSb than HfCoSb, which makes the expensive element Hf key to high performance.75 Studies into the stability of the phase segregation revealed both zT and microstructure to remain unchanged upon repeated temperature cycling.129,130 Another drawback of TiCoSb is that it appears to be more susceptible to oxidation than other HHs.131–137
remains largely constant in the Ti1−xHfxCoSb solid solution, μH is around 3 times lower in TiCoSb than HfCoSb, which makes the expensive element Hf key to high performance.75 Studies into the stability of the phase segregation revealed both zT and microstructure to remain unchanged upon repeated temperature cycling.129,130 Another drawback of TiCoSb is that it appears to be more susceptible to oxidation than other HHs.131–137
Since 2015, there hasn’t been any increase in zT in the p-type XVCoSb materials, although work on these materials continues.138,139 An extensive investigation into the Zr1−xHfxCoSb1−ySny system determined that the temperature dependence of hole mobility is consistent with alloy scattering (μH ∼ T−0.5), in stark contrast to the XVFeSb materials, which have temperature dependences consistent with acoustic phonon scattering.92
The above reports generally make use of arc-melting to react elemental pieces, although a 2021 report eliminated the melting step, simply ball-milling elemental precursors and hot-pressing at 1000 °C.140 This study equalled the record with zT975K = 1.1 for this family with the composition Ti0.4Hf0.6CoSb0.83Sn0.17, with suppressed κl and S2σ.140 While this is a positive result, it also illustrates that κl can’t be suppressed further using Ti without also suppressing the electronic performance.
3.4. XIVCoSb (XIV = Ti, Zr and Hf) (n-type)
The XIVCoSb materials are unusual in that good zT values are possible in both n- and p-type doped compositions. The n-type materials have the X-point conduction band minimum shared amongst all 18 electron HH phases (Fig. 2). Despite the fact that XIVCoSb materials have long been known to be intrinsically n-type,141 reports on competitive zT have only emerged in the last 4–5 years.93,142 Initially, Ni substitution was used to dope Zr0.5Hf0.5CoSb, with zT1073K = 1 achieved in Zr0.5Hf0.5Co0.9Ni0.1Sb, with moderate S2σ vales exceeding 3.25 mW m−1 K−2 and once again suppressed κl due to X-site alloying.142 A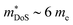 was confirmed in subsequent reports on other n-type compositions, with (Zr1−xHfx)1−yNbyCoSb having
was confirmed in subsequent reports on other n-type compositions, with (Zr1−xHfx)1−yNbyCoSb having 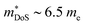 .93,100 Although the Nb doped materials don’t exceed zT = 1, the initial report used Callaway analysis to show that the X-site alloying in these materials suppresses κl without causing any reduction in μH. This is consistent with the earlier observation that minimising the size mismatch between dopant/alloying elements helps maintain good μH values,93 whilst mass disorder effectively reduces κl. These studies have also shown that n-type TiCoSb is substantially more promising than its p-type counterpart,139 with the composition Ti0.6Hf0.3Ta0.1CoSb reaching zT973K = 0.9.143
.93,100 Although the Nb doped materials don’t exceed zT = 1, the initial report used Callaway analysis to show that the X-site alloying in these materials suppresses κl without causing any reduction in μH. This is consistent with the earlier observation that minimising the size mismatch between dopant/alloying elements helps maintain good μH values,93 whilst mass disorder effectively reduces κl. These studies have also shown that n-type TiCoSb is substantially more promising than its p-type counterpart,139 with the composition Ti0.6Hf0.3Ta0.1CoSb reaching zT973K = 0.9.143
A subsequent study on (Hf0.3Zr0.7)0.94Nb0.06CoSb established that σ300K can be heavily suppressed by grain boundary scattering, introduced by intense ball-milling used to reduce grain size.100 This leads to semiconducting behaviour near 300 K, while at high temperatures degenerate semiconducting behaviour is observed. Hence, as was seen for NbFeSb, care must be taken when processing HH phases to prevent grain boundary scattering of charge carriers. At present all n-type XIVCoSb materials reported use a melting, milling and pressing procedure, but this may simply reflect the novel nature of these compositions and a lack of detailed processing studies.
3.5. XIVNiSn (XIV = Ti, Zr and Hf) (n-type)
The XIVNiSn compositions are very much the original HH thermoelectric,17,18,20,21,24–27,144–147 with the 2005 report of zT700K = 1.5 driving a significant amount of interest in HH thermoelectrics.148 As shown in Fig. 4, zT values from this report have never been fully matched, contrary to the expected evolution of material optimisation, which sees a gradual increase in zT over the years.The XIVNiSn phases have some unique properties relative to the other HH alloys. The XIVNiSn materials have the lowest reported 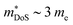 amongst the high zT materials, which arises due to a combination of low Nv = 3 and low
amongst the high zT materials, which arises due to a combination of low Nv = 3 and low 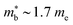 (Table 1). This means that lower doping levels are required to optimise S2σ, and in several instances the best performance comes for ∼1–2% atomic substitution,148–150 contrasting with 15–20% required for the p-types.
(Table 1). This means that lower doping levels are required to optimise S2σ, and in several instances the best performance comes for ∼1–2% atomic substitution,148–150 contrasting with 15–20% required for the p-types.
An additional factor to consider is the interstitial site and the full-Heusler XNi2Sn phase.41–44,54,57,71,72,151–166 The interstitial site is the vacant 8-coordinate (tetrahedral coordination to X and Z) site in the material (sometimes referred to as the Wyckoff 4d or tetrahedral site), which is fully occupied in the FH structure (Fig. 1).49 Even stoichiometric XIVNiSn materials commonly form with a few percent occupation of the interstitial site, with an XIV/Sn binary phase formed to compensate.41,43,45,57,72,160 Preparing compositions with intentional metal excess, XIVNi1+xSn is possible, although there is a limit to x, past which a FH phase begins to form.151,154,155 Both interstitial Ni acting as point defects or FH nanoinclusions have been claimed to be useful for scattering phonons.63,72 The pursuit of FH nanoinclusions was a major focus for XIVNiSn investigations in the early 2010s.14 The presence of interstitial Ni is also cited as reducing the observed electronic band gap.71,116
The approach which was able to reduce κl the most used a convoluted synthetic protocol consisting of arc-melting, induction-melting, annealing, an undisclosed “densification aid”, ball-milling and finally hot-pressing.172 This work also aimed to exploit X-site phase segregation by initial heating above the spinodal line and subsequent heat treatment just below to force nanoscale segregation. However, the paper itself does not provide direct microscopy confirmation. Nevertheless, the composition Ti0.5Zr0.25Hf0.25NiSn (+DA) was reported to have a very low κl ∼ 1.8 W m−1 K−1 at 300 K, while maintaining a large S2σ, enabling zT823K = 1.5.172 Outside of this report, the group is able to consistently achieve zT800K > 1 with the assistance of a “densification aid” that is considered to improve electrical contacting of the grains.173,174 In the composition Ti0.5Zr0.5NiSn for example, the addition of the “densification aid” increases S2σ at 700 K from ∼2.5 W m−1 K−2 to ∼4 W m−1 K−2, and coupled to a low κl this enables zT > 1.174
Property measurements have confirmed the significance of interstitials on the thermoelectric properties, with excess Ni suppressing κl by up to 70% in the TiNi1+xSn and ZrNi1+xSn system.72,160,161,175 Callaway analysis demonstrates that Ni/Cu interstitials have a similar impact to vacancies with additional disorder contribution due to bond formation.63,160 For the Ti1−xTaxNi0.92Sn system, the intentional Ni deficiency (with the aim of obtaining stoichiometric TiNiSn) leads to an increase in both κl and μH, with the improved electronic properties leading to a net increase in zT (Fig. 6).71 At low temperatures, the Ni deficiency leads to a substantial increase in σ, while at higher temperatures S is enhanced, leading to a minimum of 35% increase in S2σ(T) across the entire temperature range.
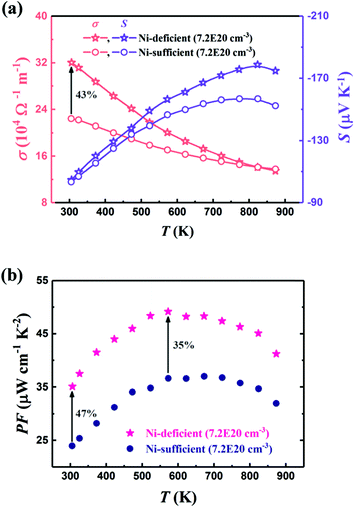 | ||
| Fig. 6 The effect of nominal Ni deficiency in the Ti1−xTaxNi1−δSn system, in samples with identical carrier concentration, nH. As seen in (a), nominal Ni deficiency causes a substantial increase in μH at 300 K and enhances S(T) at high temperatures. This leads to a significant increase in power factor, S2σ as seen in (b). Reproduced from Ren et al. 2019, Advanced Electronic Materials.71 | ||
Using appropriate processing, excess Ni can also be stabilised as FH (nano)inclusions in the HH matrix, acting an extrinsic source of phonon and electron scattering. Chai et al. reported success in preparing composite ZrNi1.1Sn with significantly improved thermoelectric properties relative to the stoichiometric composition, attributed largely to a dispersion of nanoscale FH inclusions.44,72,153,167 DTA analysis suggested the FH phases ‘dissolve’ into the HH matrix above 800 °C, and reform with a smaller domain size when cooled.72 These nanoscale FH inclusions suppress κl by up to 40%, leading to a ∼40% increase in zTmax from 0.54 to 0.75, compared to the first heating cycle. In addition to these melt-based routes, the Poudeu group has reported extensively on nanocomposite HH samples prepared using a high-temperature solid-state route.42,156,157 Carrier filtering was reported to improve S2σ and reductions in κl were observed, with a highest zT = 0.8 at 800 K.
Recently it was found that W nanoinclusions are highly effective in reducing κl by 20% while simultaneously enhancing S2σ by up to 33%. Hf0.6Zr0.4NiSn0.99Sb0.01 + 5 wt% W has peak zT773K = 1.4.179 This would seem to be a successful implementation of the nanoinclusion effect (i.e. carrier filtering and reductions in κl) that had been previously considered to be possible with nanoscale FH inclusions. The introduction of W in these samples was achieved by ball milling W nanoparticles into premade HH samples, followed by SPS for densification. The cycling stability was confirmed for 10 cycles up to 1073 K, suggesting the composition is sufficiently stable for application.
While 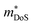 in ZrNiSn and HfNiSn have been well established as being close to 3.0 me, the value for TiNiSn based materials is less clear.114 Data on Sb-doped TiNi1+xSn samples from 2018 show a similar
in ZrNiSn and HfNiSn have been well established as being close to 3.0 me, the value for TiNiSn based materials is less clear.114 Data on Sb-doped TiNi1+xSn samples from 2018 show a similar 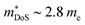 , which seems to be robust up to 700 K.175 Data from high performance Ti1−xTaxNi0.92Sn samples however are more consistent with
, which seems to be robust up to 700 K.175 Data from high performance Ti1−xTaxNi0.92Sn samples however are more consistent with 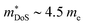 .71 Given that both reports place μH between 20–30 cm2 V−1 s−1 at room temperature, there does not appear to be a significant increase in
.71 Given that both reports place μH between 20–30 cm2 V−1 s−1 at room temperature, there does not appear to be a significant increase in 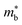 (which would lead to a significant decrease in μH). Considering eqn (3), the increase in
(which would lead to a significant decrease in μH). Considering eqn (3), the increase in 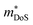 should be attributed to an increase in Nv. Our reported data on TiNiCu0.075Sn, which uses interstitial Cu to n-type dope the material, gives a relatively large values of ∼5.5 me.63 Similarly Hall data for the Ti0.5Zr0.25Hf0.25NiCuySn series conform to
should be attributed to an increase in Nv. Our reported data on TiNiCu0.075Sn, which uses interstitial Cu to n-type dope the material, gives a relatively large values of ∼5.5 me.63 Similarly Hall data for the Ti0.5Zr0.25Hf0.25NiCuySn series conform to 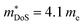 , including the undoped sample.64 Some data in the Ti1−xHfxNiSn1−ySby series also suggests
, including the undoped sample.64 Some data in the Ti1−xHfxNiSn1−ySby series also suggests 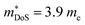 .180 While the large
.180 While the large 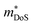 in the Ti1−xTaxNi0.92Sn system was not addressed, first principles calculations on the interstitial Cu-doped materials suggest the appearance of a second conduction band minimum in the electronic bandstructure, supporting the idea that the increase in
in the Ti1−xTaxNi0.92Sn system was not addressed, first principles calculations on the interstitial Cu-doped materials suggest the appearance of a second conduction band minimum in the electronic bandstructure, supporting the idea that the increase in 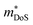 is caused by to an increase in Nv.64
is caused by to an increase in Nv.64
Given the high volume of publications on the XIVNiSn system, a number of protocols outside of melting, ball-milling and hot-pressing/SPS exist, with TiNiSn being the target of most experimentation. Microwave synthesis has reported for TiNiSn, achieving a peak zT740K = 0.45.65 In 2019 Zilber et al. successfully grew TiNiSn single crystals from a Sn flux, with lower nH and larger S than typically reported in polycrystalline samples.181 Similarly ZrNiSn1−ySby crystals can be grown and extracted by centrifuging, with improved μH compared to high quality polycrystalline samples.87
Self-propagating synthesis for exothermic processes allows for the heat produced from initial reaction to drive the reaction to completion, as has been demonstrated for ZrNiSn.66,69 In a custom pressing setup, the heat released from the reaction (initiated by Tungsten electrode) was enough to densify the pellet, with a Tmax = 1668 K achieved by the self-propagating reaction.66
The large literature pool also allows for comparisons to be made in how the HH phases form, which is important when planning microstructure and defects. ZrNiSn and HfNiSn are known form congruently from the molten state, while TiNiSn prefers to form the TiNi2Sn FH phase.155,176,177 Similarly TiNiSn decomposes when heated above 1450 K. The rapid solidification achieved by melt-spinning is claimed to be able to suppress formation of TiNi2Sn from the molten state.182 It remains the case that melting, milling and hot-pressing/SPS give the best thermoelectric performance.
Overall, for the XIVNiSn compositions, it remains challenging to optimise the thermoelectric properties. This is related to the tendency for significant deviations from nominal stoichiometry, phase segregation and the small electronic bandgap, which leads to significant bipolar transport at high temperatures. Elimination of interstitial Ni is desirable as this would increase the electronic bandgap, hence reducing the minority carrier conduction and improving the high temperature zT.
3.6. XV0.8CoSb (XV = V, Nb and Ta) (n-type)
Perhaps the most significant recent discovery for the n-type HH materials is promising thermoelectric performance in the nominally 19 electron XVCoSb compositions.59,183–188 As a stoichiometric phase, these materials are expected to be metallic with the possibility of ferromagnetism.189 In 2016, the material VCoSb was synthesised with S(T) significantly larger than what is typical of a fully metallic sample, although nH was quite large at ∼1.6 × 1022 cm−3.185 The properties of this phase and the subsequently investigated NbCoSb and TaCoSb phases were discovered to be due to X-site vacancies,187,188 which reduce the overall electron count without depleting electronic states in the valence band, which is easily understood through the valence electron counting Xn+[YZ]n− description introduced earlier. To reach a theoretically semiconducting state one would need to reach the composition XV0.8CoSb (Fig. 7). Each of the XVCoSb phases forms with a different vacancy fraction, with the V phase forming preferentially as V0.87CoSb, the Nb phase as Nb0.85CoSb, while the Ta phase forms close to being ‘fully’ vacant at Ta0.81CoSb.59nH is dependent on the vacancy fraction as has been demonstrated for the Nb0.8+δCoSb system,183 so V0.87CoSb is highly degenerate while Ta0.81CoSb is close to being a semiconductor.59 There is some level of control that can be achieved, as demonstrated in Nb0.8+δCoSb, which can be doped between 0.5–6.5 × 1021 cm−3 by varying the nominal vacancy fraction.183 One complication to doping control is the dependence of δ on the annealing temperature.190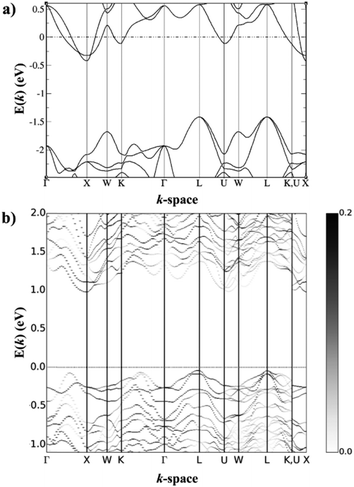 | ||
Fig. 7 Calculated electronic band structures of (a) 19 electron NbCoSb and (b) 18 electron Nb0.8CoSb. NbCoSb is metallic, although the gap in the lower energy states is typical of semiconducting half-Heusler materials, with an L-point valence band maximum and an X-point conduction band minimum. Nb0.8CoSb contains these features but has additional conduction band states at the U-point, which could be responsible for the increased  compared to NbCoSn. Reproduced from Zeier et al. 2017, Chemistry of Materials.188 compared to NbCoSn. Reproduced from Zeier et al. 2017, Chemistry of Materials.188 | ||
Relative to the XIVNiSn materials, 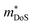 for these materials is quite large, ranging from 10 me for V0.87CoSb to 5.9 me for Ta0.81CoSb (Table 1).59,183,191 The lower magnitude of μH (∼4 cm2 V−1 s−1 for Nb0.8+δCoSb) may point to an increase in
for these materials is quite large, ranging from 10 me for V0.87CoSb to 5.9 me for Ta0.81CoSb (Table 1).59,183,191 The lower magnitude of μH (∼4 cm2 V−1 s−1 for Nb0.8+δCoSb) may point to an increase in 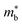 , but calculated bandstructures for both NbCoSb and Nb0.8CoSb suggests more bands can contribute than the singly degenerate X-point minimum that is commonly observed (Fig. 7).188 Assuming a doubly degenerate conduction band as shown in Table 1,
, but calculated bandstructures for both NbCoSb and Nb0.8CoSb suggests more bands can contribute than the singly degenerate X-point minimum that is commonly observed (Fig. 7).188 Assuming a doubly degenerate conduction band as shown in Table 1, 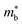 for Nb0.8+δCoSb is calculated to be ∼2.33 me, which is a large value compared to n-type XIVNiSn.
for Nb0.8+δCoSb is calculated to be ∼2.33 me, which is a large value compared to n-type XIVNiSn.
One unusual behaviour in this family is the very low κl in V0.87CoSb below 2 W m−1 K−1, which would expected to be larger than the Nb and Ta phases due its lower formula mass.59,191 The relative acoustic behaviour of the V0.8+δCoSb and Nb0.8+δCoSb materials have been confirmed to be similar, with no significant effect caused by vacancies observed through experiment, which would point to a reduced κl, with measured vs in the Nb0.8+δCoSb varying by no more than ±2% between 0 < δ < 0.2.183,191 As of yet there is no clear explanation for this extremely low value. One can note that the experimental acoustic properties point to a large γ for these materials (Table 2), which correlates with strong Umklapp scattering and low κl as shown in Fig. 3. One structural feature of interest in these phases is the potential ordering of the XV site vacancies.192–195 Over large distances the vacancies are disordered, but at the nanoscale the vacancies are short-range ordered (SRO), offering a route to reduce κL.192 Furthermore, Monte Carlo simulated vacancy ordering coupled to DFT supercell calculations points to widening of the electronic CBM (increase in 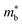 ) relative to the ordered Nb0.8CoSb and the presence of Co-defect states in the band gap, with electron diffraction simulations confirming existence of SRO in real samples.195 A more detailed discussion on the vacancy ordering in these materials can be found in the 2021 review by Xia et al.12
) relative to the ordered Nb0.8CoSb and the presence of Co-defect states in the band gap, with electron diffraction simulations confirming existence of SRO in real samples.195 A more detailed discussion on the vacancy ordering in these materials can be found in the 2021 review by Xia et al.12
The majority of reports on the XV0.8CoSb materials have utilised a similar synthetic protocol, with melted elemental pieces being optionally ball-milled and then consolidated by hot-pressing/SPS.183,184 However, a powder route consisting of solid-state reaction and hot pressing achieves similar performance.59 Finally, a recent report on V0.855Ti0.1CoSb used a direct ball milling and consolidation approach and achieved zT values larger than other reported V0.8+δCoSb samples.191 This suggests that for the group V based materials, these relatively straightforward powder based routes may be more feasible than for XIVNiSn, where the best performing samples are invariably prepared using melting routes.
3.7. Other HH phases
The best performing new and existing materials have been described above, but exploration of new phases has turned up some interesting results. One recent HH family which has emerged is the XVCoSn (XV = Nb and Ta) phases, which are intrinsically n-type materials.187,196–198 The bandstructure of NbCoSn appears contain a doubly degenerate X-point conduction band minimum, giving Nv = 6, which appears to be partially responsible for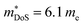 in the NbCoSn1−xSbx series (Table 1).197,198 At present the largest zT is found for X-site alloying between Nb and Ta, yielding zT1000K = 0.75 for Nb0.4Ta0.6CoSn0.94Sb0.06.196 Better low temperature performance has been observed when using Pt as both n-type dopant and phonon scatterer in NbCo0.95Pt0.05Sn, due to the large mass difference between Co and Pt.197 While it would be useful to use V for X-site alloying, the VCoSn phase does not appear to readily form.131 While there have been reports of the phase being observed by powder diffraction, the evidence presented is less than convincing.199,200 It has been suggested that this composition is difficult to reach through normal processing routes, but might be made through non-equilibrium processes.201 Finally, p-type doping has also been demonstrated using scandium doping in Nb1−xScxCoSn, however these samples have relatively poor performance, with the largest zT879K = 0.13 reported for Nb0.95Sc0.05CoSn.202
in the NbCoSn1−xSbx series (Table 1).197,198 At present the largest zT is found for X-site alloying between Nb and Ta, yielding zT1000K = 0.75 for Nb0.4Ta0.6CoSn0.94Sb0.06.196 Better low temperature performance has been observed when using Pt as both n-type dopant and phonon scatterer in NbCo0.95Pt0.05Sn, due to the large mass difference between Co and Pt.197 While it would be useful to use V for X-site alloying, the VCoSn phase does not appear to readily form.131 While there have been reports of the phase being observed by powder diffraction, the evidence presented is less than convincing.199,200 It has been suggested that this composition is difficult to reach through normal processing routes, but might be made through non-equilibrium processes.201 Finally, p-type doping has also been demonstrated using scandium doping in Nb1−xScxCoSn, however these samples have relatively poor performance, with the largest zT879K = 0.13 reported for Nb0.95Sc0.05CoSn.202
An established family of HH alloys that has recently gained renewed interest are the RNiSb phase (R = lanthanide, Sc).203–206 As synthesised, these materials are p-type and are characterised by spontaneous Ni deficiency (as much as 15%).207 They also have small band gaps (Eg ∼ 0.3 eV), leading to substantial bipolar transport at low temperatures, ultimately limiting the maximum achievable zT values. A large study comparing R = Sc, Dy, Ho, Er, Tm and Lu, confirmed the intrinsic p-type behaviour with semiconductor like S(T) and ρ(T).205 Typical peak S2/ρ = 1–1.5 mW m−1 K−2 for the RNiSb materials with highest reported zT ∼ 0.3 at 650 K.205,208,209 Careful analysis of the bipolar transport, suggested much higher electron than hole mobilities.204 Subsequent attempts at n-type doping exploiting Te in ScNiSb1−xTex yielded large S2/ρ = 4 mW m−1 K−2, demonstrating the potential of n-type RNiSb systems. Substitution of Te is also correlated to an increasing 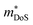 , providing another example of the significant impact of a doping element on the underlying bandstructure.206 No zT values were reported, but the chemical flexibility for substitution on the X site and potential to manipulate the Ni deficiency (concentration and potentially SRO through heat treatment), suggest that these materials are promising for further exploration.
, providing another example of the significant impact of a doping element on the underlying bandstructure.206 No zT values were reported, but the chemical flexibility for substitution on the X site and potential to manipulate the Ni deficiency (concentration and potentially SRO through heat treatment), suggest that these materials are promising for further exploration.
Another interesting development is the exploration of “double HH” phases, which combine an equal mixture of 17 electron and 19 electron HH phases.112 For example the model material proposed in 2019 was [TiFeSb]0.5[TiNiSb]0.5, each of which forms a HH-like phase independently. Experimental realisation of [TiFeSb]1−x[TiNiSb]x was successful, showing that VEC < 18 were p-type and VEC > 18 were n-type as would be expected, and that isoelectronic alloying using Hf could be used to reduce κl.210 Some unusual points emerged, such as the large reduction in κl just above and below x = 0.5 and massive apparent 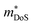 values up to 23.8 me, which was later confirmed by a separate group.211 The emergence of defective HH phases and double-HH phases has provided an extended range of potential compositions to explore, which has allowed for the application of computational screening, beyond the common style of reporting the first principles properties of stoichiometric XYZ HHs.112,212 The emergence of these phases coincide with the development of effective band structure techniques, that allow supercell bandstructures to be compared to stoichiometric parent phases.213,214
values up to 23.8 me, which was later confirmed by a separate group.211 The emergence of defective HH phases and double-HH phases has provided an extended range of potential compositions to explore, which has allowed for the application of computational screening, beyond the common style of reporting the first principles properties of stoichiometric XYZ HHs.112,212 The emergence of these phases coincide with the development of effective band structure techniques, that allow supercell bandstructures to be compared to stoichiometric parent phases.213,214
4. Recent developments in half-Heusler thermoelectric generators
There has been an increased research effort in recent years aimed at implementing HH materials into TEG modules and systems.215–219 It is now more common for “materials” studies to include work on prototype devices,121,122,179 while an increasing number of manuscripts are dedicated to electrical and thermal contacting of HH materials.220–224 Most of this published work is from research institutions but there has been industrial work producing HH materials and generators, most notably from GMZ energy in the USA, and the Isabellen Hutte Heusler company and Vacuum Schmelzen in Germany. A vital aspect in translating materials to TEG performance is the electrical and thermal contacting. In particular, the requirements for electrical contacting are strict in order to maintain as much of the intrinsic performance of the HH materials. The effective zT for a “contacted” material is given by:4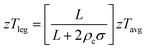 | (9) |
| n-/p-type materials | # couples (dimensions mm3) | zT (n/p-type@T/K) | Power density (W cm−2)/(ΔT/K) | Efficiency (%) | Ref. |
|---|---|---|---|---|---|
| a Surface area of module, not TE material. b This study covers a range of leg lengths and surface areas, showing the inverse correlation between efficiency and power density. | |||||
| Large-scale melt XIVNiSn/XIVCoSb | 7 (2.5 × 2.5 × 3) | 0.8/0.5@773 K | 3.2 (525 K) | 5 | 215 |
| Milled nano-XIVNiSn/XIVCoSb | 1 (1.8 × 1.8 × 2) | 1.0/0.9@773 K/973 K | 5.3 (500 K) | 7 | 216 and 241 |
| 28 (1 module) | 4.0 (500 K) | — | |||
| 400 modules | 2.8 (500 K) | 2.1 | |||
| Self-propagating XIVNiSn/XIVCoSb | 8 | 1.0/0.9@773/973 K | 2.4 (680 K)ab | 8 | 217 |
| 1.7 (680 K) | 9.5 | ||||
| XIVNiSn/XVFeSb | 8 | 1.0/1.0@973/1200 K | 2.1 (655 K)a | 8.3 | 218 |
| XIVNiSn/XVFeSb | 1 | 1.0/1.0@773/973 K | 6.2 (500 K) | — | 122 |
| XIVNiSn/XVFeSb | 1 (1.5 × 1.5 × 2.4) | 1.0/1.0@773/973 K | 8.6 (570 K) | 6.2 | 224 |
| TiNiSn/XVFeSb | 18 (1.75 × 1.75 × 4.0) | 0.4/0.4@873 K | 3.1 (575 K) | — | 219 |
One of the first papers to address upscaling and device manufacture originated from the Fraunhofer Institute in 2014.215 This work used vacuum melting and casting to prepare kilogram scale ingots of optimal n-type Zr0.4Hf0.6NiSn0.98Sb0.02 and p-type Zr0.5Hf0.5NiSb0.8Sn0.2. The HH materials had zT ∼ 0.8 (n-type) and ∼0.5 (p-type) at 773 K, respectively. TEG modules containing 7 n/p-couples were fabricated using Cu contacts and a brazing process. These were exposed to repeated thermal cycling up to 873 K and thermal shock without degradation of performance. The power density was 3.2 W cm−2 (area of thermoelectric) from a 527 K gradient, with the cold side near room temperature. The efficiency was estimated to be ∼5% with an average TEG module ZT ∼ 0.4.
Zhang et al. demonstrated a 1 kW TEG for use in automotive applications.216 The HH materials used were based on milled nanostructured XIVNiSn and XIVCoSb with zT = 1 (773 K) and zT = 0.9 (973 K), respectively. The production process and different stages in the TEG module development are illustrated in Fig. 8. A Ag–Cu brazing alloy was used to bond the legs directly to the Cu leads through heating in vacuum at 825 °C. Unicouple generators produced 5.3 W cm−2 (500 K gradient), while a module consisting of 28 couples generated 4 W cm−2 (500 K gradient). The reduced power density of the module is caused by parasitic losses, attributed to thermal losses between the inert atmosphere steel encapsulation and TEG device (Fig. 8). The final TEG that was embedded in the exhaust stream of a heavy-duty vehicle used an impressive number of 400 TEG modules and could generate 1 kW electrical output (power density ∼2.8 W cm−2) with a 2.1% heat-to-electricity efficiency (340 K gradient, with an average 823 K exhaust temperature).
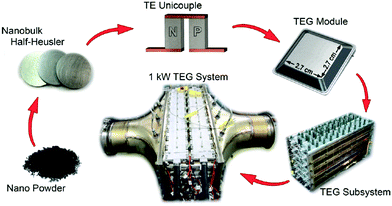 | ||
| Fig. 8 Schematic illustrating upscaling of half-Heusler materials production, electrical contacting, TEG module and incorporation of TEG subsystem into exhaust stream of a heavy vehicle. Reproduced from Zhang et al. 2015, Energy Conversion and Management.216 | ||
Reflecting the development of the new p-type compositions, a shift has occurred towards XVFeSb as the counterpart to XIVNiSn. The initial materials development study by Fu et al. reported a power density ∼2 W cm−2 from an 8 couple TEG module (650 K gradient).121 A subsequent study geared towards improving the device performance yielded a measured 2.1 W cm−2 power density and 8.3% efficiency from a 655 K gradient.218 Simulations as part of this work suggest a maximum efficiency of 10.5% is possible, but this would only be possible at with a reduction of power density. The work reporting ultrahigh 300 K power factors in NbFeSb translates to a very large TEG power density ∼20 W cm−2 (500 K gradient), albeit measured on a single contacted bar of material (and not in a TEG geometry).99 TaFeSb shows similar high power densities based on measurement of a single leg.47 Further work on NbFeSb in a unicouple device using a high-performance XIVNiSn composition as the n-type, enables a device power density of 6.2 W cm−2 (500 K gradient), outperforming a comparable unicouple device with a XIVCoSb p-type leg (5.5 W cm−2).122 Furthermore, the NbFeSb material used in that study did not contain Hf and is hence only about 1/6 of the cost of the alternative XIVCoSb p-types (typical 30–70% Hf on the X-site), offering a significant cost saving. Subsequent improvements in device contacting and geometry enabled a power density 8.6 W cm−2 at 6% efficiency under a 570 K gradient.224 This is a clear demonstration that the outstanding performance of NbFeSb can be translated to working TEG devices.
Self-propagating synthesis is a promising route to produce large quantities of materials that has recently been applied to HH materials.67,68 Using this processing, 200 gram batches of Zr0.5Hf0.5NiSn0.985Sb0.015 and Zr0.5Hf0.5CoSb0.8Sn0.2 were prepared and consolidated using conventional hot pressing.217 These were then fabricated into TEG modules containing 8 unicouple pairs. This study covered a range of leg geometries, where the ratio of leg height over area (L/A) can be used to favour either efficiency (increase L/A) or power density (decrease L/A). Limiting measured values in a 680 K gradient are ∼2.4 W cm−2 (∼8% efficiency) and ∼1.7 W cm−2 (9.5% efficiency). Simulations suggest an upper limit of ∼3.1 W cm−2 and 10.5% for the power density and efficiency, respectively.217 However, it is worth noting that the performance of these modules is limited by relatively large contact resistances, ∼30 μΩ cm−2 for both n- and p-type legs. A final noteworthy study focused on TiNiSn (hence avoiding the use of Hf) as the n-type material and NbFeSb as the p-type. Despite a low zT873K ∼ 0.4 for both n- and p-types, a fabricated TEG with 16 pairs showed a respectable power density of ∼3.1 W cm−2 from a 575 K gradient, reflecting the large S2σ of the HHs.219
5. Conclusions
Significant progress has been made in the development of HH thermoelectrics with the emergence of new high-performing p-type materials based on XVFeSb and ZrCoBi, and further development of existing n-types based on XIVNiSn. Application of these materials in TEG modules has led to the demonstration of promising power outputs and efficiencies. Looking ahead there are a number of areas that deserve attention. Further work on translating materials into TEGs is needed, including underpinning work on electrical and thermal contacting and stability studies. A related area is the development of scalable synthetic routes to mass produce HH alloys with good performance. These more applied activities should be underpinned by further materials development work as there continues to be significant potential for further improvements. One area of interest is the elimination of parasitic effects, for example grain boundary resistances, enabling the intrinsic materials performance to be extracted. Another area is new design concepts, in particular building on the much-improved understanding of the electronic structure,225–227 and the emergence of new classes of more complex HH alloy compositions.112 The complex HH alloys behave opposite to the conventional XYZ compositions: they have low thermal conductivities but also relatively poor power factors. Uniting large power factors and low thermal conductivities remains the key challenge in HH materials development. The largely harmonic bonding limits the strength of phonon–phonon scattering, leaving structural disorder as the most plausible route to achieve low κl. A possible interesting route is to focus on grain boundary engineered composite samples, where the boundary region is exploited to suppress phonon transmission and reduce κl. This has been demonstrated for graphene decorated skutterudites and titanium oxides,228,229 whilst dislocation networks have been exploited in Bi2Te3.230 In principle, these approaches can be applied to HH alloys, and the key challenge is to find appropriate additives and processing routes to manipulate the microstructure. In terms of homogenous materials, advances might come from the design of materials with favourable bandstructures, enabling large power factors at lower doping levels, hence limiting the electronic thermal conductivity.227 One possible route to enhance S without affecting σ is the introduction of resonant states, leading to a “spike” in the electronic density of states. This concept has been explored for XIVNiSn with some evidence of a favourable impact on the power factor and thermoelectric performance.231,232 As already remarked, the similar conduction band structures for XYZ HH compositions limits opportunities for band engineering in the n-types. In the p-types, there is more diversity and hence more opportunity for bandstructure engineering. ZrCoBi and NbFeSb are both systems that naturally benefit from large valley and orbital degeneracies. Alloying has been widely explored to reduce the lattice thermal conductivity but can also lead to substantially different bandstructures. Recent work using unfolded supercell calculations has shown that new bands can emerge in substituted HH compositions (e.g. in vacancy systems,170 for interstitials58 and complex compositions233) and this is another possible route for performance improvements. This is an area where theory could lead experiments by identifying new compositions with promising electronic bandstructures.To conclude, great progress has been made over the past decade, driven by improvements in materials preparation and through better understanding from first principles and semi-empirical modelling. Many avenues of research remain open for exploration in the future and some of these will undoubtedly lead to better materials performance. The current generation of materials is already good enough for niche applications in thermoelectric waste heat recovery. Improved performance, or increased penalties for carbon emissions, may lead to increased industrial interest for large scale application in thermoelectric power generation.
Author contributions
RJQ undertook the data analysis based on the literature and drafted figures and tables. JWGB supervised the work and acquired funding. Both authors contributed to writing the article.Conflicts of interest
There are no conflicts of interest to declare.Appendix A – supplemental equations
DFT computational papers will typically report the bulk (B) and shear (G) moduli, from elastic tensors (Cij). The crystallographic density (ρ) is simply obtained following a sufficiently converged geometry optimisation of the unit cell. The longitudinal (vl) and transverse (vt) can be expressed as:243,244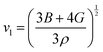 | (S1) |
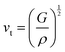 | (S2) |
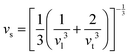 | (S3) |
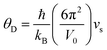 | (S4) |
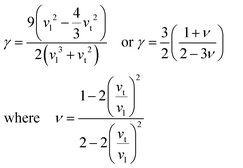 | (S5) |
Within the SPB model, HH materials are typically treated with acoustic phonon scattering as the dominant carrier scattering mechanism. For clarity, the SPB model uses the following equations with only acoustic phonon scattering:91,248
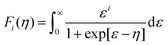 | (S6) |
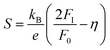 | (S7) |
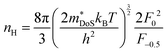 | (S8) |
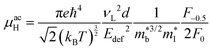 | (S9) |
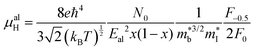 | (S10) |
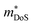 is typically determined from a series of samples at fixed temperature by plotting S vs. nH in a Pisarenko plot and fitting for a fixed
is typically determined from a series of samples at fixed temperature by plotting S vs. nH in a Pisarenko plot and fitting for a fixed 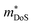 , although a single datapoint can be used. The weighted mobility (μw) is a measure of the fundamental mobility of a material independent of nH and can be defined as:248,249
, although a single datapoint can be used. The weighted mobility (μw) is a measure of the fundamental mobility of a material independent of nH and can be defined as:248,249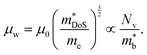 | (S11) |
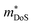 . A relationship compatible with S(T) and σ(T) is expressed as:249
. A relationship compatible with S(T) and σ(T) is expressed as:249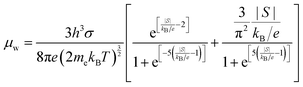 | (S12) |
Acknowledgements
The EPSRC (EP/N01717X/1) and Leverhulme Trust (RPG-2020-177) for funding and Heriot-Watt University is for a James Watt Scholarship for RJQ.References
- W. Gong, M. Yadav and A. J. Jacobson, MRS Online Proc. Libr., 2009, 1126, 807 Search PubMed.
- Thermoelectric Energy Conversion, ed. R. Funahashi, Woodhead Publishing, 2021 Search PubMed.
- Materials, preparation, and characterization in thermoelectrics, ed. D. M. Rowe, CRC Press, Boca Raton, 2012 Search PubMed.
- W. Liu, Q. Jie, H. S. Kim and Z. Ren, Acta Mater., 2015, 87, 357–376 CrossRef CAS.
- D. Champier, Energy Convers. Manage., 2017, 140, 167–181 CrossRef.
- X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515 CrossRef CAS PubMed.
- T. J. Zhu, Y. T. Liu, C. G. Fu, J. P. Heremans, J. G. Snyder and X. B. Zhao, Adv. Mater., 2017, 29, 1605884 CrossRef PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Chem. Mater., 2013, 25, 2911–2920 CrossRef CAS.
- S. K. Yee, S. LeBlanc, K. E. Goodson and C. Dames, Energy Environ. Sci., 2013, 6, 2561–2571 RSC.
- J.-W. G. Bos, in Thermoelectric Energy Conversion, ed. R. Funahashi, Woodhead Publishing, 2021, pp. 125–142 Search PubMed.
- K. Xia, C. Hu, C. Fu, X. Zhao and T. Zhu, Appl. Phys. Lett., 2021, 118, 140503 CrossRef CAS.
- S. Chen and Z. Ren, Mater. Today, 2013, 16, 387–395 CrossRef CAS.
- J. W. G. Bos and R. A. Downie, J. Phys.: Condens. Matter, 2014, 26, 433201 CrossRef PubMed.
- T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588 CrossRef.
- S. J. Poon, J. Phys. D: Appl. Phys., 2019, 52, 493001 CrossRef CAS.
- B. A. Cook, G. P. Meisner, J. Yang and C. Uher, International Conference on Thermoelectrics, ICT, Proceedings, IEEE, 1999, pp. 64–67.
- C. Uher, J. Yang, S. Hu, D. T. Morelli and G. P. Meisner, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8615–8621 CrossRef CAS.
- Y. Xia, S. Bhattacharya, V. Ponnambalam, A. L. Pope, S. J. Poon and T. M. Tritt, J. Appl. Phys., 2000, 88, 1952–1955 CrossRef CAS.
- J. Toboła and J. Pierre, J. Alloys Compd., 2000, 296, 243–252 CrossRef.
- S. Bhattacharya, A. L. Pope, R. T. Littleton IV, T. M. Tritt, V. Ponnambalam, Y. Xia and S. J. Poon, Appl. Phys. Lett., 2000, 77, 2476 CrossRef CAS.
- Y. Xia, V. Ponnambalam, S. Bhattacharya, A. L. Pope, S. J. Poon and T. M. Tritt, J. Phys.: Condens. Matter, 2001, 13, 77–89 CrossRef CAS.
- S. R. Culp, J. W. Simonson, S. J. Poon, V. Ponnambalam, J. Edwards and T. M. Tritt, Appl. Phys. Lett., 2008, 93, 022105 CrossRef.
- S. Ogut and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10443–10453 CrossRef CAS PubMed.
- H. Hohl, A. P. Ramirez, C. Goldmann, G. Ernst, B. Wölfing and E. Bucher, J. Phys.: Condens. Matter, 1999, 11, 1697–1709 CrossRef CAS.
- P. Larson, S. D. Mahanti, S. Sportouch and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15660–15668 CrossRef CAS.
- P. Larson, S. D. Mahanti and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 12754–12762 CrossRef CAS.
- Q. Shen, L. Chen, T. Goto, T. Hirai, J. Yang, G. P. Meisner and C. Uher, Appl. Phys. Lett., 2001, 79, 4165–4167 CrossRef CAS.
- Y. Kawaharada, K. Kurosaki, H. Muta, M. Uno and S. Yamanaka, J. Alloys Compd., 2004, 377, 312–315 CrossRef CAS.
- Y. Pei, H. Wang and G. J. Snyder, Adv. Mater., 2012, 24, 6125–6135 CrossRef CAS PubMed.
- H. J. Goldsmid, Proc. Phys. Soc., London, Sect. B, 1954, 67, 360–363 CrossRef.
- R. P. Chasmar and R. Stratton, J. Electron. Control, 1959, 7, 52–72 CrossRef CAS.
- D. Narducci, Appl. Phys. Lett., 2011, 99, 102104 CrossRef.
- D. Nemir and J. Beck, J. Electron. Mater., 2010, 39, 1897–1901 CrossRef CAS.
- W. Liu, H. S. Kim, Q. Jie and Z. Ren, Scr. Mater., 2016, 111, 3–9 CrossRef CAS.
- X. Yan, G. Joshi, W. Liu, Y. Lan, H. Wang, S. Lee, J. W. Simonson, S. J. Poon, T. M. Tritt, G. Chen and Z. F. Ren, Nano Lett., 2011, 11, 556–560 CrossRef CAS PubMed.
- G. Joshi, X. Yan, H. Z. Wang, W. S. Liu, G. Chen and Z. F. Ren, Adv. Energy Mater., 2011, 1, 643–647 CrossRef CAS.
- M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868–1872 RSC.
- R. A. Downie, D. A. MacLaren and J. W. G. Bos, J. Mater. Chem. A, 2014, 2, 6107–6114 RSC.
- S. Populoh, M. H. Aguirre, O. C. Brunko, K. Galazka, Y. Lu and A. Weidenkaff, Scr. Mater., 2012, 66, 1073–1076 CrossRef CAS.
- H. Hazama, M. Matsubara, R. Asahi and T. Takeuchi, J. Appl. Phys., 2011, 110, 063710 CrossRef.
- J. P. A. Makongo, D. K. Misra, X. Y. Zhou, A. Pant, M. R. Shabetai, X. L. Su, C. Uher, K. L. Stokes and P. F. P. Poudeu, J. Am. Chem. Soc., 2011, 133, 18843–18852 CrossRef CAS PubMed.
- J. E. Douglas, C. S. Birkel, M. S. Miao, C. J. Torbet, G. D. Stucky, T. M. Pollock and R. Seshadri, Appl. Phys. Lett., 2012, 101, 183902 CrossRef.
- Y. W. Chai and Y. Kimura, Acta Mater., 2013, 61, 6684–6697 CrossRef CAS.
- R. A. Downie, D. A. MacLaren, R. I. Smith and J. W. G. Bos, Chem. Commun., 2013, 49, 4184–4186 RSC.
- W. Silpawilawan, S.-A. Tanuslip, Y. Ohishi, H. Muta and K. Kurosaki, Phys. Status Solidi A, 2020, 217, 2000419 CrossRef CAS.
- H. T. Zhu, J. Mao, Y. W. Li, J. F. Sun, Y. M. Wang, Q. Zhu, G. N. Li, Q. C. Song, J. W. Zhou, Y. H. Fu, R. He, T. Tong, Z. H. Liu, W. Y. Ren, L. You, Z. M. Wang, J. Luo, A. Sotnikov, J. M. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. F. Ren, Nat. Commun., 2019, 10, 270 CrossRef PubMed.
- H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 16032 CrossRef CAS.
- S. Anand, K. Xia, V. I. Hegde, U. Aydemir, V. Kocevski, T. Zhu, C. Wolverton and G. J. Snyder, Energy Environ. Sci., 2018, 11, 1480–1488 RSC.
- K. Tolborg and B. B. Iversen, Chem. Mater., 2021, 33, 5308–5316 CrossRef CAS.
- A. Page, C. Uher, P. F. Poudeu and A. Van Der Ven, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174102 CrossRef.
- K. Kirievsky, Y. Gelbstein and D. Fuks, J. Solid State Chem., 2013, 203, 247–254 CrossRef CAS.
- D. T. Do, S. D. Mahanti and J. J. Pulikkoti, J. Phys.: Condens. Matter, 2014, 26, 275501 CrossRef PubMed.
- Y. G. G. Yu, X. W. Zhang and A. Zunger, Phys. Rev. B, 2017, 95, 085201 CrossRef.
- R. A. Downie, S. A. Barczak, R. I. Smith and J. W. G. Bos, J. Mater. Chem. C, 2015, 3, 10534–10542 RSC.
- D. A. Ferluccio, B. F. Kennedy, S. A. Barczak, S. R. Popuri, C. Murray, M. Pollet and J. W. G. Bos, J. Phys.: Energy, 2021, 3, 035001 Search PubMed.
- D. A. Ferluccio, J. E. Halpin, K. L. Macintosh, R. J. Quinn, E. Don, R. I. Smith, D. A. Maclaren and J. W. G. Bos, J. Mater. Chem. C, 2019, 7, 6539–6547 RSC.
- M. Biesuz, T. Saunders, D. Ke, M. J. Reece, C. Hu and S. Grasso, J. Mater. Sci. Technol., 2021, 69, 239–272 CrossRef.
- J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313 CrossRef.
- T. Nagase, K. Mizuuchi and T. Nakano, Entropy, 2019, 21, 483 CrossRef CAS PubMed.
- S. A. Barczak, J. E. Halpin, J. Buckman, R. Decourt, M. Pollet, R. I. Smith, D. A. MacLaren and J.-W. G. Bos, ACS Appl. Mater. Interfaces, 2018, 10, 4786–4793 CrossRef CAS PubMed.
- S. A. Barczak, R. J. Quinn, J. E. Halpin, K. Domosud, R. I. Smith, A. R. Baker, E. Don, I. Forbes, K. Refson, D. A. MacLaren and J. W. G. Bos, J. Mater. Chem. A, 2019, 7, 27124–27134 RSC.
- C. S. Birkel, W. G. Zeier, J. E. Douglas, B. R. Lettiere, C. E. Mills, G. Seward, A. Birkel, M. L. Snedaker, Y. Zhang, G. J. Snyder, T. M. Pollock, R. Seshadri and G. D. Stucky, Chem. Mater., 2012, 24, 28 Search PubMed.
- T. Hu, W. Cao, D. Yang, Y. Yan, Y. Cao, T. Zhang, X. Su, W. Liu, P. Poudeu-Poudeu and X. Tang, Scr. Mater., 2019, 165, 140–144 CrossRef CAS.
- X. Su, F. Fu, Y. Yan, G. Zheng, T. Liang, Q. Zhang, X. Cheng, D. Yang, H. Chi, X. Tang, Q. Zhang and C. Uher, Nat. Commun., 2014, 5, 4908 CrossRef CAS PubMed.
- Y. Xing, R. Liu, Y.-Y. Sun, F. Chen, K. Zhao, T. Zhu, S. Bai and L. Chen, J. Mater. Chem. A, 2018, 6, 19470–19478 RSC.
- T. Hu, D. Yang, X. Su, Y. Yan, Y. You, W. Liu, C. Uher and X. Tang, ACS Appl. Mater. Interfaces, 2018, 10, 864–872 CrossRef CAS PubMed.
- N. S. Chauhan, S. Bathula, B. Gahtori, S. D. Mahanti, A. Bhattacharya, A. Vishwakarma, R. Bhardwaj, V. N. Singh and A. Dhar, ACS Appl. Mater. Interfaces, 2019, 11, 47830–47836 CrossRef CAS PubMed.
- W. Ren, H. Zhu, J. Mao, L. You, S. Song, T. Tong, J. Bao, J. Luo, Z. Wang and Z. Ren, Adv. Electron. Mater., 2019, 5, 1900166 CrossRef.
- Y. W. Chai, T. Oniki and Y. Kimura, Acta Mater., 2015, 85, 290–300 CrossRef CAS.
- S. V. Pedersen, J. R. Croteau, N. Kempf, Y. Zhang, D. P. Butt and B. J. Jaques, J. Solid State Chem., 2020, 285, 121203 CrossRef CAS.
- A. Novitskii, I. Serhiienko, A. Nepapushev, A. Ivanova, T. Sviridova, D. Moskovskikh, A. Voronin, H. Miki and V. Khovaylo, Intermetallics, 2021, 133, 107195 CrossRef CAS.
- E. Rausch, B. Balke, J. M. Stahlhofen, S. Ouardi, U. Burkhardt and C. Felser, J. Mater. Chem. C, 2015, 3, 10409–10414 RSC.
- E. Rausch, B. Balke, S. Ouardi and C. Felser, Phys. Chem. Chem. Phys., 2014, 16, 25258–25262 RSC.
- Z. A. Munir and M. Ohyanagi, J. Mater. Sci., 2021, 56, 1–15 CrossRef CAS.
- K. Chen, C. Nuttall, E. Stefanaki, K. Placha, R. Tuley, K. Simpson, J. W. G. Bos and M. J. Reece, Scr. Mater., 2021, 191, 71–75 CrossRef CAS.
- A. D. LaLonde, T. Ikeda and G. J. Snyder, Rev. Sci. Instrum., 2011, 82, 025104 CrossRef PubMed.
- M. Yu, S. Grasso, R. Mckinnon, T. Saunders and M. J. Reece, Advances in Applied Ceramics, Taylor and Francis Ltd, 2017, vol. 116, pp. 24–60 Search PubMed.
- F. Gucci, T. G. Saunders, B. Srinivasan, F. Cheviré, D. A. Ferluccio, J. W. G. Bos and M. J. Reece, J. Alloys Compd., 2020, 837, 155058 CrossRef CAS.
- C. Chlique, G. Delaizir, O. Merdrignac-Conanec, C. Roucau, M. Dollé, P. Rozier, V. Bouquet and X. H. Zhang, Opt. Mater., 2011, 33, 706–712 CrossRef CAS.
- X. Wei, C. Back, O. Izhvanov, C. Haines and E. Olevsky, Materials, 2016, 9, 577 CrossRef PubMed.
- R. Yamanoglu, I. Daoud and E. A. Olevsky, Powder Metall., 2018, 61, 178–186 CrossRef CAS.
- M. T. Dylla, A. Dunn, S. Anand, A. Jain and G. J. Snyder, Research, 2020, 2020, 1–8 CrossRef PubMed.
- H. Zhu, J. Mao, Z. Feng, J. Sun, Q. Zhu, Z. Liu, D. J. Singh, Y. Wang and Z. Ren, Sci. Adv., 2019, 5, eaav5813 CrossRef PubMed.
- Q. Ren, C. Fu, Q. Qiu, S. Dai, Z. Liu, T. Masuda, S. Asai, M. Hagihala, S. Lee, S. Torri, T. Kamiyama, L. He, X. Tong, C. Felser, D. J. Singh, T. Zhu, J. Yang and J. Ma, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- S. S. Li, in Semiconductor Physical Electronics, ed. S. S. Li, Springer, New York, 2006, pp. 211–245 Search PubMed.
- J. W. Harrison and J. R. Hauser, Phys. Rev. B: Solid State, 1976, 13, 5347–5350 CrossRef CAS.
- H. Wang, A. D. LaLonde, Y. Pei and G. J. Snyder, Adv. Funct. Mater., 2013, 23, 1586–1596 CrossRef CAS.
- H. Xie, H. Wang, Y. Pei, C. Fu, X. Liu, G. J. Snyder, X. Zhao and T. Zhu, Adv. Funct. Mater., 2013, 23, 5123–5130 CrossRef CAS.
- C. Hu, K. Xia, X. Chen, X. Zhao and T. Zhu, Mater. Today Phys., 2018, 7, 69–76 CrossRef.
- Y. Liu, C. Fu, K. Xia, J. Yu, X. Zhao, H. Pan, C. Felser and T. Zhu, Adv. Mater., 2018, 30, 1800881 CrossRef PubMed.
- J. W. Zhou, H. T. Zhu, T. H. Liu, Q. C. Song, R. He, J. Mao, Z. H. Liu, W. Y. Ren, B. L. Liao, D. J. Singh, Z. F. Ren and G. Chen, Nat. Commun., 2018, 9, 1721 CrossRef PubMed.
- J. Y. W. Seto, J. Appl. Phys., 1975, 46, 5247–5254 CrossRef CAS.
- J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434 RSC.
- J. Y. Cao, D. Ekren, Y. D. Peng, F. Azough, I. A. Kinloch and R. Freer, ACS Appl. Mater. Interfaces, 2021, 13, 11879–11890 CrossRef CAS PubMed.
- S. R. Popuri, R. Decourt, J. A. McNulty, M. Pollet, A. D. Fortes, F. D. Morrison, M. S. Senn and J. W. G. Bos, J. Phys. Chem. C, 2019, 123, 5198–5208 CrossRef CAS.
- R. He, D. Kraemer, J. Mao, L. Zeng, Q. Jie, Y. C. Lan, C. H. Li, J. Shuai, H. S. Kim, Y. Liu, D. Broido, C. W. Chu, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13576–13581 CrossRef CAS PubMed.
- Q. Qiu, Y. Liu, K. Xia, T. Fang, J. Yu, X. Zhao and T. Zhu, Adv. Energy Mater., 2019, 9, 1803447 CrossRef.
- C. Fu, M. Yao, X. Chen, L. Z. Maulana, X. Li, J. Yang, K. Imasato, F. Zhu, G. Li, G. Auffermann, U. Burkhardt, W. Schnelle, J. Zhou, T. Zhu, X. Zhao, M. Shi, M. Dressel, A. V. Pronin, G. J. Snyder and C. Felser, Adv. Sci., 2020, 7, 1902409 CrossRef CAS PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557 CrossRef CAS PubMed.
- A. Petersen, S. Bhattacharya, T. M. Tritt and S. J. Poon, J. Appl. Phys., 2015, 117, 035706 CrossRef.
- J. Zou and A. Balandin, J. Appl. Phys., 2001, 89, 2932 CrossRef CAS.
- P. Hermet and P. Jund, J. Alloys Compd., 2016, 688, 248–252 CrossRef CAS.
- J. Shiomi, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104302 CrossRef.
- G. Ding, G. Y. Gao and K. L. Yao, J. Phys. D: Appl. Phys., 2015, 48, 235302 CrossRef.
- A. Katre, J. Carrete and N. Mingo, J. Mater. Chem. A, 2016, 4, 15940–15944 RSC.
- S. N. H. Eliassen, A. Katre, G. K. H. Madsen, C. Persson, O. M. Lovvik and K. Berland, Phys. Rev. B, 2017, 95, 045202 CrossRef.
- M. Schrade, K. Berland, S. N. H. Eliassen, M. N. Guzik, C. Echevarria-Bonet, M. H. Sørby, P. Jenuš, B. C. Hauback, R. Tofan, A. E. Gunnæs, C. Persson, O. M. Løvvik and T. G. Finstad, Sci. Rep., 2017, 7, 13760 CrossRef PubMed.
- S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238 CrossRef CAS.
- G. A. Naydenov, P. J. Hasnip, V. K. Lazarov and M. I. J. Probert, J. Phys.: Mater., 2019, 2, 035002 CAS.
- R. He, T. Zhu, Y. Wang, U. Wolff, J.-C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood, Z. Liu, L. Feng, N. P. Rodriguez, G. J. Snyder, J. C. Grossman, K. Nielsch and G. Schierning, Energy Environ. Sci., 2020, 13, 5165–5176 RSC.
- Thermal Conductivity: Theory, Properties and Applications, ed. T. M. Tritt, Kluwer Academic, New York, 2004 Search PubMed.
- J. Schmitt, Z. M. Gibbs, G. J. Snyder and C. Felser, Mater. Horiz., 2015, 2, 68–75 RSC.
- H. S. Kim, W. Liu and Z. Ren, Energy Environ. Sci., 2017, 10, 69–85 RSC.
- G. J. Snyder and A. H. Snyder, Energy Environ. Sci., 2017, 10, 2280–2283 RSC.
- C. Fu, T. Zhu, Y. Pei, H. Xie, H. Wang, G. J. Snyder, Y. Liu, Y. Liu and X. Zhao, Adv. Energy Mater., 2014, 4, 1400600 CrossRef.
- C. Fu, T. Zhu, Y. Liu, H. Xie and X. Zhao, Energy Environ. Sci., 2015, 8, 216–220 RSC.
- C. G. Fu, S. Q. Bai, Y. T. Liu, Y. S. Tang, L. D. Chen, X. B. Zhao and T. J. Zhu, Nat. Commun., 2015, 6, 8144 CrossRef PubMed.
- G. Joshi, R. He, M. Engber, G. Samsonidze, T. Pantha, E. Dahal, K. Dahal, J. Yang, Y. C. Lan, B. Kozinsky and Z. F. Ren, Energy Environ. Sci., 2014, 7, 4070–4076 RSC.
- A. Tavassoli, F. Failamani, A. Grytsiv, G. Rogl, P. Heinrich, H. Müller, E. Bauer, M. Zehetbauer and P. Rogl, Acta Mater., 2017, 135, 263–276 CrossRef CAS.
- H. Ma, C.-L. Yang, M.-S. Wang, X.-G. Ma and Y.-G. Yi, J. Phys. D: Appl. Phys., 2019, 52, 255501 CrossRef CAS.
- G. Surucu, M. Isik, A. Candan, X. Wang and H. H. Gullu, Phys. B, 2020, 587, 412146 CrossRef CAS.
- D. Zhao, M. Zuo, L. Bo and Y. Wang, Materials, 2018, 11, 728 CrossRef PubMed.
- X. Yan, W. Liu, H. Wang, S. Chen, J. Shiomi, K. Esfarjani, H. Wang, D. Wang, G. Chen and Z. Ren, Energy Environ. Sci., 2012, 5, 7543–7548 RSC.
- X. Yan, W. Liu, S. Chen, H. Wang, Q. Zhang, G. Chen and Z. Ren, Adv. Energy Mater., 2013, 3, 1195–1200 CrossRef CAS.
- E. Rausch, B. Balke, S. Ouardi and C. Felser, Energy Technol., 2015, 3, 1217–1224 CrossRef CAS.
- E. Rausch, M. V. Castegnaro, F. Bernardi, M. C. M. Alves, J. Morais and B. Balke, Acta Mater., 2016, 115, 308–313 CrossRef CAS.
- M. Asaad, J. Buckman, R. I. Smith and J. W. G. Bos, RSC Adv., 2016, 6, 56511–56517 RSC.
- O. Appel, S. Cohen, O. Beeri, N. Shamir, Y. Gelbstein and S. Zalkind, Materials, 2018, 11, 2296 CrossRef PubMed.
- A. Berche and P. Jund, Intermetallics, 2018, 92, 62–71 CrossRef CAS.
- R. W. H. Webster, J. E. Halpin, S. R. Popuri, J. W. G. Bos and D. A. MacLaren, APL Mater., 2019, 7, 013206 CrossRef.
- H. B. Kang, U. Saparamadu, A. Nozariasbmarz, W. J. Li, H. T. Zhu, B. Poudel and S. Priya, ACS Appl. Mater. Interfaces, 2020, 12, 36706–36714 CrossRef CAS PubMed.
- R. W. H. Webster, M. T. Scott, S. R. Popuri, J. W. G. Bos and D. A. MacLaren, Appl. Surf. Sci., 2020, 512, 145649 CrossRef CAS.
- K. Galazka, S. Populoh, L. Sagarna, L. Karvonen, W. J. Xie, A. Beni, P. Schmutz, J. Hulliger and A. Weidenkaff, Phys. Status Solidi A, 2014, 211, 1259–1266 CrossRef CAS.
- M. Asaad, J. Buckman and J. W. G. Bos, Metals, 2018, 8, 935 CrossRef CAS.
- M. Asaad, J. Buckman, R. I. Smith and J. W. G. Bos, J. Solid State Chem., 2019, 276, 181–189 CrossRef CAS.
- I. Ioannou, P. S. Ioannou, A. Delimitis, Y. Gelbstein, I. J. Giapintzakis and T. Kyratsi, J. Alloys Compd., 2021, 858, 158330 CrossRef CAS.
- T. Sekimoto, K. Kurosaki, H. Muta and S. Yamanaka, Mater. Trans., 2006, 47, 1445–1448 CrossRef CAS.
- R. He, H. Zhu, J. Sun, J. Mao, H. Reith, S. Chen, G. Schierning, K. Nielsch and Z. Ren, Mater. Today Phys., 2017, 1, 24–30 CrossRef.
- R. F. Wang, S. Li, W. H. Xue, C. Chen, Y. M. Wang, X. J. Liu and Q. Zhang, Rare Met., 2021, 40, 40–47 CrossRef CAS.
- J. Pierre, R. V. Skolozdra, Y. K. Gorelenko and M. Kouacou, J. Magn. Magn. Mater., 1994, 134, 95–105 CrossRef CAS.
- J. Tobola, J. Pierre, S. Kaprzyk, R. V. Skolozdra and M. A. Kouacou, J. Phys.: Condens. Matter, 1998, 10, 1013–1032 CrossRef CAS.
- F. G. Aliev, N. B. Brandt, V. V. Moshchalkov, V. V. Kozyrkov, R. V. Skolozdra and A. I. Belogorokhov, Z. Phys. B: Condens. Matter, 1989, 75, 167–171 CrossRef CAS.
- F. G. Aliev, V. V. Kozyrkov, V. V. Moshchalkov, R. V. Scolozdra and K. Durczewski, Z. Phys. B: Condens. Matter, 1990, 80, 353–357 CrossRef CAS.
- S. Sakurada and N. Shutoh, Appl. Phys. Lett., 2005, 86, 1–3 CrossRef.
- C. Yu, T.-J. Zhu, R.-Z. Shi, Y. Zhang, X.-B. Zhao and J. He, Acta Mater., 2009, 57, 2757–2764 CrossRef CAS.
- L. Chen, S. Gao, X. Zeng, A. Mehdizadeh Dehkordi, T. M. Tritt and S. J. Poon, Appl. Phys. Lett., 2015, 107, 041902 CrossRef.
- R. A. Downie, R. I. Smith, D. A. MacLaren and J. W. G. Bos, Chem. Mater., 2015, 27, 2449–2459 CrossRef CAS.
- X. Li, P. Yang, Y. Wang, Z. Zhang, D. Qin, W. Xue, C. Chen, Y. Huang, X. Xie, X. Wang, M. Yang, C. Wang, F. Cao, J. Sui, X. Liu and Q. Zhang, Research, 2020, 2020, 1–9 Search PubMed.
- Y. W. Chai and Y. Kimura, Appl. Phys. Lett., 2012, 100, 033114 CrossRef.
- C. S. Birkel, J. E. Douglas, B. R. Lettiere, G. Seward, N. Verma, Y. C. Zhang, T. M. Pollock, R. Seshadri and G. D. Stucky, Phys. Chem. Chem. Phys., 2013, 15, 6990–6997 RSC.
- J. E. Douglas, C. S. Birkel, N. Verma, V. M. Miller, M. S. Miao, G. D. Stucky, T. M. Pollock and R. Seshadri, J. Appl. Phys., 2014, 115, 043720 CrossRef.
- Y. F. Liu, P. Sahoo, J. P. A. Makongo, X. Y. Zhou, S. J. Kim, H. Chi, C. Uher, X. Q. Pan and P. F. P. Poudeu, J. Am. Chem. Soc., 2013, 135, 7486–7495 CrossRef CAS PubMed.
- J. P. A. Makongo, D. K. Misra, J. R. Salvador, N. J. Takas, G. Y. Wang, M. R. Shabetai, A. Pant, P. Paudel, C. Uher, K. L. Stokes and P. F. P. Poudeu, J. Solid State Chem., 2011, 184, 2948–2960 CrossRef CAS.
- J. E. Douglas, P. A. Chater, C. M. Brown, T. M. Pollock and R. Seshadri, J. Appl. Phys., 2014, 116, 163514 CrossRef.
- E. E. Levin, F. Long, J. E. Douglas, M. L. C. Buffon, L. K. Lamontagne, T. M. Pollock and R. Seshadri, Materials, 2018, 11, 903 CrossRef PubMed.
- S. A. Barczak, J. Buckman, R. I. Smith, A. R. Baker, E. Don, I. Forbes and J. W. G. Bos, Materials, 2018, 11, 536 CrossRef PubMed.
- H. H. Xie, H. Wang, C. G. Fu, Y. T. Liu, G. J. Snyder, X. B. Zhao and T. J. Zhu, Sci. Rep., 2014, 4, 6888 CrossRef CAS PubMed.
- Y. T. Liu, H. H. Xie, C. G. Fu, G. J. Snyder, X. B. Zhao and T. J. Zhu, J. Mater. Chem. A, 2015, 3, 22716–22722 RSC.
- K. S. Kim, Y. M. Kim, H. Mun, J. Kim, J. Park, A. Y. Borisevich, K. H. Lee and S. W. Kim, Adv. Mater., 2017, 29, 1702091 CrossRef PubMed.
- H. J. Lee, K. H. Lee, L. Fu, G. Han, H. S. Kim, S. I. Kim, Y. M. Kim and S. W. Kim, Acta Mater., 2019, 180, 97–104 CrossRef CAS.
- M. N. Guzik, M. Schrade, R. Tofan, P. A. Carvalho, K. Berland, M. H. Sorby, C. Persson, A. E. Gunnaes and B. C. Hauback, CrystEngComm, 2019, 21, 3330–3342 RSC.
- A. Berche and P. Jund, Materials, 2018, 11, 868 CrossRef PubMed.
- Y. Kimura and Y. W. Chai, JOM, 2015, 67, 233–245 CrossRef CAS.
- A. Page, A. Van der Ven, P. F. P. Poudeu and C. Uher, J. Mater. Chem. A, 2016, 4, 13949–13956 RSC.
- O. Appel and Y. Gelbstein, J. Electron. Mater., 2014, 43, 1976–1982 CrossRef CAS.
- M. Schwall and B. Balke, Materials, 2018, 11, 649 CrossRef PubMed.
- M. N. Guzik, C. Echevarria-Bonet, M. D. Riktor, P. A. Carvalho, A. E. Gunnæs, M. H. Sørby and B. C. Hauback, Acta Mater., 2018, 148, 216–224 CrossRef CAS.
- G. Rogl, P. Sauerschnig, Z. Rykavets, V. V. Romaka, P. Heinrich, B. Hinterleitner, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2017, 131, 336–348 CrossRef CAS.
- M. Gürth, G. Rogl, V. V. Romaka, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2016, 104, 210–222 CrossRef.
- G. Rogl, K. Yubuta, V. V. Romaka, H. Michor, E. Schafler, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2019, 166, 466–483 CrossRef CAS.
- Y. Tang, X. Li, L. H. J. Martin, E. Cuervo Reyes, T. Ivas, C. Leinenbach, S. Anand, M. Peters, G. J. Snyder and C. Battaglia, Energy Environ. Sci., 2018, 11, 311–320 RSC.
- M. Gurth, A. Grytsiv, J. Vrestal, V. V. Romaka, G. Giester, E. Bauer and P. Rogl, RSC Adv., 2015, 5, 92270–92291 RSC.
- P. Sauerschnig, A. Grytsiv, J. Vrestal, V. V. Romaka, B. Smetana, G. Giester, E. Bauer and P. Rogl, J. Alloys Compd., 2018, 742, 1058–1082 CrossRef CAS.
- S. A. Barczak, PhD thesis, Heriot-Watt University, 2018.
- H. B. Kang, B. Poudel, W. Li, H. Lee, U. Saparamadu, A. Nozariasbmarz, M. G. Kang, A. Gupta, J. J. Heremans and S. Priya, Mater. Today, 2020, 36, 63–72 CrossRef CAS.
- K. Sung Kim, Y.-M. Kim, H. Mun, J. Kim, J. Park, A. Y. Borisevich, K. Hyoung Lee, S. Wng Kim, K. S. Kim, Y.-M. Kim, H. Mun, S. W. Kim, J. Kim, J. Park, A. Y. Borisevich and K. H. Lee, Adv. Mater., 2017, 29, 1702091 CrossRef PubMed.
- T. Zilber, S. Cohen, D. Fuks and Y. Gelbstein, J. Alloys Compd., 2019, 781, 1132–1138 CrossRef CAS.
- F. Aversano, A. Ferrario, S. Boldrini, C. Fanciulli, M. Baricco and A. Castellero, J. Mater. Eng. Perform., 2018, 27, 6306–6313 CrossRef CAS.
- K. Xia, Y. Liu, S. Anand, G. J. Snyder, J. Xin, J. Yu, X. Zhao and T. Zhu, Adv. Funct. Mater., 2018, 28, 1705845 CrossRef.
- L. Huang, R. He, S. Chen, H. Zhang, K. Dahal, H. Zhou, H. Wang, Q. Zhang and Z. Ren, Mater. Res. Bull., 2015, 70, 773–778 CrossRef CAS.
- H. Zhang, Y. Wang, L. Huang, S. Chen, H. Dahal, D. Wang and Z. Ren, J. Alloys Compd., 2016, 654, 321–326 CrossRef CAS.
- L. H. Huang, Q. Y. Zhang, Y. M. Wang, R. He, J. Shuai, J. J. Zhang, C. Wang and Z. F. Ren, Phys. Chem. Chem. Phys., 2017, 19, 25683–25690 RSC.
- D. A. Ferluccio, R. I. Smith, J. Buckman and J. W. G. Bos, Phys. Chem. Chem. Phys., 2018, 20, 3979–3987 RSC.
- W. G. Zeier, S. Anand, L. Huang, R. He, H. Zhang, Z. Ren, C. Wolverton and G. J. Snyder, Chem. Mater., 2017, 29, 1210–1217 CrossRef CAS.
- K. Kaczmarska, J. Pierre, J. Beille, J. Tobola, R. V. Skolozdra and G. A. Melnik, J. Magn. Magn. Mater., 1998, 187, 210–220 CrossRef CAS.
- S. Anand, K. Xia, T. Zhu, C. Wolverton and G. J. Snyder, Adv. Energy Mater., 2018, 8, 1801409 CrossRef.
- S. Li, F. Bai, R. Wang, C. Chen, X. Li, F. Cao, B. Yu, J. Sui, X. Liu, Z. Ren and Q. Zhang, Ann. Phys., 2020, 532, 1900440 CrossRef CAS.
- K. Y. Xia, P. F. Nan, S. H. Tan, Y. M. Wang, B. H. Ge, W. Q. Zhang, S. Anand, X. B. Zhao, G. J. Snyder and T. J. Zhu, Energy Environ. Sci., 2019, 12, 1568–1574 RSC.
- P. Nan, K. Wu, Y. Liu, K. Xia, T. Zhu, F. Lin, J. He and B. Ge, Nanoscale, 2020, 12, 21624–21628 RSC.
- N. Roth, T. J. Zhu and B. B. Iversen, IUCrJ, 2020, 7, 673–680 CrossRef CAS PubMed.
- S. Tan, P. Nan, K. Xia, H. Yang, T. Zhu, B. Ge and W. Zhang, J. Phys. Chem. C, 2021, 125, 1125–1133 CrossRef CAS.
- S. Li, H. Zhu, J. Mao, Z. Feng, X. Li, C. Chen, F. Cao, X. Liu, D. J. Singh, Z. Ren and Q. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 54 Search PubMed.
- F. Serrano-Sánchez, T. Luo, J. Yu, W. Xie, C. Le, G. Auffermann, A. Weidenkaff, T. Zhu, X. Zhao, J. A. Alonso, B. Gault, C. Felser and C. Fu, J. Mater. Chem. A, 2020, 8, 14822–14828 RSC.
- R. He, L. Huang, Y. Wang, G. Samsonidze, B. Kozinsky, Q. Zhang and Z. Ren, APL Mater., 2016, 4, 104804 CrossRef.
- C. S. Lue, Y. Oner, D. G. Naugle and J. H. Ross, IEEE Trans. Magn., 2001, 37, 2138–2140 CrossRef CAS.
- S. Hooshmand Zaferani, A. Darebaghi, S.-J. Hong, D. Vashaee and R. Ghomashchi, Energies, 2020, 13, 1459 CrossRef.
- H. Shi, W. Ming, D. S. Parker, M. H. Du and D. J. Singh, Phys. Rev. B, 2017, 95, 195207 CrossRef.
- R. Yan, W. Xie, B. Balke, G. Chen and A. Weidenkaff, Sci. Technol. Adv. Mater., 2020, 21, 122–130 CrossRef CAS PubMed.
- I. Wolańska, K. Synoradzki, K. Ciesielski, K. Załęski, P. Skokowski and D. Kaczorowski, Mater. Chem. Phys., 2019, 227, 29–35 CrossRef.
- K. Ciesielski, K. Synoradzki, I. Veremchuk, P. Skokowski, D. Szymański, Y. Grin and D. Kaczorowski, Phys. Rev. Appl., 2020, 14, 054046 CrossRef CAS.
- K. Ciesielski, K. Synoradzki, I. Wolańska, P. Stachowiak, L. Kepiński, A. Jeżowski, T. Toliński and D. Kaczorowski, J. Alloys Compd., 2020, 816, 152596 CrossRef CAS.
- K. Ciesielski, I. Wolańska, K. Synoradzki, D. Szymański and D. Kaczorowski, Phys. Rev. Appl., 2021, 15, 044047 CrossRef CAS.
- T. Harmening, H. Eckert and R. Pöttgen, Solid State Sci., 2009, 11, 900–906 CrossRef CAS.
- K. Kawano, K. Kurosaki, T. Sekimoto, H. Muta and S. Yamanaka, Appl. Phys. Lett., 2007, 91, 062115 CrossRef.
- K. Kawano, K. Kurosaki, H. Muta and S. Yamanaka, J. Appl. Phys., 2008, 104, 013714 CrossRef.
- Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29, 1905044 CrossRef CAS.
- Q. Wang, X. Li, C. Chen, W. Xue, X. Xie, F. Cao, J. Sui, Y. Wang, X. Liu and Q. Zhang, Phys. Status Solidi A, 2020, 217, 2000096 CrossRef CAS.
- S. Guo, Z. Liu, Z. Feng, T. Jia, S. Anand, G. J. Snyder and Y. Zhang, J. Mater. Chem. A, 2020, 8, 23590–23598 RSC.
- V. Popescu and A. Zunger, Phys. Rev. Lett., 2010, 104, 236403 CrossRef PubMed.
- V. Popescu and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085201 CrossRef.
- K. Bartholomé, B. Balke, D. Zuckermann, M. Köhne, M. Müller, K. Tarantik and J. König, J. Electron. Mater., 2014, 43, 1775–1781 CrossRef.
- Y. L. Zhang, M. Cleary, X. W. Wang, N. Kempf, L. Schoensee, J. Yang, G. Joshi and L. Meda, Energy Convers. Manage., 2015, 105, 946–950 CrossRef.
- Y. F. Xing, R. H. Liu, J. C. Liao, Q. H. Zhang, X. G. Xia, C. Wang, H. Huang, J. Chu, M. Gu, T. J. Zhu, C. X. Zhu, F. F. Xu, D. X. Yao, Y. P. Zeng, S. Q. Bai, C. Uher and L. D. Chen, Energy Environ. Sci., 2019, 12, 3390–3399 RSC.
- J. J. Yu, Y. F. Xing, C. L. Hu, Z. J. Huang, Q. Y. Qiu, C. Wang, K. Y. Xia, Z. Y. Wang, S. Q. Bai, X. B. Zhao, L. D. Chen and T. J. Zhu, Adv. Energy Mater., 2020, 10, 2000888 CrossRef CAS.
- D. Landmann, Y. L. Tang, B. Kunz, R. Huber, D. Widner, P. Rickhaus, R. N. Widmer, H. R. Elsener and C. Battaglia, J. Appl. Phys., 2019, 126, 085113 CrossRef.
- J. J. Shen, Z. Y. Wang, J. Chu, S. Q. Bai, X. B. Zhao, L. D. Chen and T. J. Zhu, ACS Appl. Mater. Interfaces, 2019, 11, 14182–14190 CrossRef CAS PubMed.
- Z. J. Huang, L. Yin, C. L. Hu, J. J. Shen, T. J. Zhu, Q. Zhang, K. Y. Xia, J. Z. Xin and X. B. Zhao, J. Mater. Sci. Technol., 2020, 40, 113–118 CrossRef.
- Z. Y. Wang, C. G. Fu, K. Y. Xia, F. Liu, X. B. Zhao and T. J. Zhu, ACS Appl. Mater. Interfaces, 2021, 13, 7317–7323 CrossRef CAS PubMed.
- A. Nozariasbmarz, U. Saparamadu, W. J. Li, H. B. Kang, C. Dettor, H. T. Zhu, B. Poudel and S. Priya, J. Power Sources, 2021, 493, 229695 CrossRef CAS.
- D. Black, L. Schoensee, J. Richardson, T. Vleisides, N. Kempf, D. Z. Wang, Z. F. Ren and Y. L. Zhang, ACS Appl. Energy Mater., 2018, 1, 5986–5992 CrossRef.
- P. Graziosi, C. Kumarasinghe and N. Neophytou, J. Appl. Phys., 2019, 126, 155701 CrossRef.
- C. Kumarasinghe and N. Neophytou, Phys. Rev. B, 2019, 99, 195202 CrossRef CAS.
- P. Graziosi and N. Neophytou, J. Phys. Chem. C, 2020, 124, 18462–18473 CrossRef CAS.
- P. A. Zong, R. Hanus, M. Dylla, Y. S. Tang, J. C. Liao, Q. H. Zhang, G. J. Snyder and L. D. Chen, Energy Environ. Sci., 2017, 10, 183–191 RSC.
- Y. Lin, M. T. Dylla, J. J. Kuo, J. P. Male, I. A. Kinloch, R. Freer and G. J. Snyder, Adv. Funct. Mater., 2020, 30, 1910079 CrossRef CAS.
- S. I. Kim, K. H. Lee, H. A. Mun, H. S. Kim, S. W. Hwang, J. W. Roh, D. J. Yang, W. H. Shin, X. S. Li, Y. H. Lee, G. J. Snyder and S. W. Kim, Science, 2015, 348, 109–114 CrossRef CAS PubMed.
- J. W. Simonson, D. Wu, W. J. Xie, T. M. Tritt and S. J. Poon, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235211 CrossRef.
- L. Chen, Y. Liu, J. He, T. M. Tritt and S. J. Poon, AIP Adv., 2017, 7, 065208 CrossRef.
- S. Guo, Z. Liu, Z. Feng, T. Jia, S. Anand, G. J. Snyder and Y. Zhang, J. Mater. Chem. A, 2020, 8, 23590–23598 RSC.
- H. Joshi, D. P. Rai, A. Laref and R. K. Thapa, Mater. Res. Express, 2019, 6, 066307 CrossRef CAS.
- M. Zahedifar and P. Kratzer, Phys. Rev. B, 2018, 97, 035204 CrossRef CAS.
- B. Kong, B. Zhu, Y. Cheng, L. Zhang, Q. X. Zeng and X. W. Sun, Phys. B, 2011, 406, 3003–3010 CrossRef CAS.
- H. Muta, T. Yamaguchi, K. Kurosaki and S. Yamanaka, International Conference on Thermoelectrics, ICT, Proceedings, 2005, vol. 2005, pp. 339–342.
- G. Rogl, A. Grytsiv, M. Gürth, A. Tavassoli, C. Ebner, A. Wünschek, S. Puchegger, V. Soprunyuk, W. Schranz, E. Bauer, H. Müller, M. Zehetbauer and P. Rogl, Acta Mater., 2016, 107, 178–195 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- M. De Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. K. Ande, S. Van Der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Sci. Data, 2015, 2, 1–13 Search PubMed.
- G. Joshi and B. Poudel, J. Electron. Mater., 2016, 45, 6047–6051 CrossRef CAS.
- R. J. Quinn, PhD thesis, Heriot-Watt University, 2021.
- L. Kinsler, Fundamentals of Acoustics, Wiley, Hoboken, NJ, 4th edn, 2000 Search PubMed.
- M. Razeghi, Fundamentals of Solid State Engineering, Springer, New York, NY, 3rd edn, 2009 Search PubMed.
- V. N. Belomestnykh, Tech. Phys. Lett., 2004, 30, 91–93 CrossRef CAS.
- Q. Chen and B. Sundman, Acta Mater., 2001, 49, 947–961 CrossRef CAS.
- D. S. Kim, H. L. Smith, J. L. Niedziela, C. W. Li, D. L. Abernathy and B. Fultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 14307 CrossRef.
- A. F. May and G. J. Snyder, in Materials, Preparation, and Characterization in Thermoelectrics, ed. D. M. Rowe, 2012, pp. K1–K18 Search PubMed.
- G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |