Open Access Article
Open Access ArticleAntiaromatic non-alternant heterocyclic compounds as molecular wires†
Edmund
Leary
 *a,
Carlos
Roldán-Piñero
*a,
Carlos
Roldán-Piñero
 b,
Rocío
Rico-Sánchez-Mateos
b and
Linda A.
Zotti
b,
Rocío
Rico-Sánchez-Mateos
b and
Linda A.
Zotti
 *bc
*bc
aFundación IMDEA Nanociencia, E-28049 Madrid, Spain. E-mail: edmund.leary@imdea.org
bDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain. E-mail: linda.zotti@uam.es
cCondensed Matter Physics Center (IFIMAC) and Instituto Nicolás Cabrera (INC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
First published on 22nd February 2024
Abstract
We have theoretically studied the electron-transport properties of a family of molecular junctions containing the non-alternant antiaromatic pentalene moiety stabilised with various 5-membered heterocycles. For this purpose, we used a combination of density functional theory and Green's function techniques. We have focussed on dithieno derivatives to understand if the relative position of the heteroatom influences the transport properties as significantly as it does the degree of antiaromaticity. We found that the heteroatom position does significantly affect the shape of the transmission curves, but there is no correlation between the degree of antiaromaticity and the magnitude of the transmission at the Fermi level. Overall, we find that this behaviour is well-modelled by tight-binding calculations and the graphical prediction scheme. On the other hand, curly arrow rules fail for certain isomers, regardless of the degree of antiaromaticity. Reasons for this discrepancy are discussed.
Introduction
Antiaromatic compounds have generated a lot of interest in the field of molecular electronics over recent years.1–7 They typically display high-energy π-systems, low-lying triplet states and reduced HOMO–LUMO gaps. This, on the one hand, makes them chemically less stable. For molecular electronics, however, these properties are expected to improve conductance by lowering the energy barrier for electrons to traverse the molecule.8,9 Furthermore, Breslow and Foss10 also considered that when an antiaromatic molecule is connected to a pair of metallic electrodes, there would be an additional drive to distort the π-system away from the initial antiaromatic state. This would then lead to a more favourable conjugation pathway between the terminal anchor groups compared to aromatic analogues. This make antiaromatic compounds potentially significantly advantageous over analogous aromatic compounds, where smaller compounds could be designed with the conductance properties of larger, more extended π-systems. The reduced HOMO–LUMO gaps will also lead to more accessible energy levels, which should have a positive effect upon both conductance and thermopower, which is important for creating the next generation of thermoelectric devices based on molecules.The relationship between aromaticity/antiaromaticity and conductance, however, is still under debate10–13 and more comparative studies are needed. Aromaticity has been linked to conductance suppression, whilst antiaromaticity is, conversely, suspected to have a positive impact. Inclusion of purely antiaromatic units into the backbone of a molecular wire is, unsurprisingly, extremely challenging due to inherent chemical instability. Synthetic routes to stable molecular wires have been achieved via the use of phenyl ring fusion.14 Examples include biphenylene (stabilised cyclobutadiene),3,15 dibenzopentalene (DBP)8 and indenofluorene7 wires. Norcorrole, which is an antiaromatic analogue of porphyrin, has also been studied in the context of molecular junctions.2 The trade-off with benzene annulation is that it typically decreases the degree of antiaromaticity to achieve the greater stability. This can be rationalised by considering the main resonance contributors, which favour aromaticity in the benzene rings and disfavour antiaromaticity in the core. This, unfortunately, limits the potential benefits when compared to purely aromatic analogues.
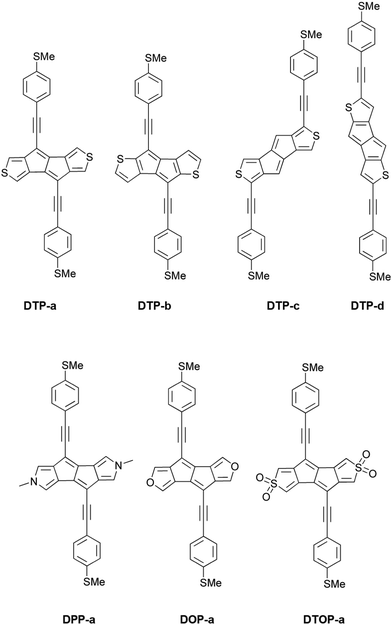
Recently, several groups have reported the synthesis of dithieno[a,e]pentalenes (DTPs), where instead of phenyl annulation, thiophene rings are used to stabilise the pentalene core.16–18 Usuba et al.19 showed that, depending on the isomer, this led to preservation of the strongly antiaromatic character of the parent pentalene core whilst at the same time being thermally stable, avoiding the need for sterically-bulky substituents. Several isomers of DTP were synthesised and studied, in particular a pentalene with thiophenes fused at the 3 and 4 thiophene carbons (as shown in Fig. S1a of the ESI†) and another at the 2 and 3 carbons (Fig. S1b, ESI†).19 Anisotropy of the induced current density (ACID), iso-chemical shielding surface ICSS and nucleus independent chemical shift (NICS(1)zz) calculations have all shown that 2,3-fusion results in much greater antiaromaticity within the central pentalene compared to 3,4 fusion, as well as compared to dibenzopentalene (DBP). Electrochemical studies also showed that 2,3 fusion leads to a much smaller HOMO–LUMO gap compared to DBP. This behaviour can again be rationalized in terms of the dominant resonance contributors which, in the case of 2,3 fusion, place the double bonds at the a and e positions of the pentalene (i.e. along the bonds adjoining the thiophene rings). Similarly, a correlation has been shown between the bond order of fused arenes attached to indacene cores and the paratropicity strength of the central antiaromatic unit.14 The key point is that this preserves the aromaticity of the thiophenes whilst simultaneously giving a formally 8 π-electron pentalene core, which displays strong antiaromaticity. These results inspired us to investigate theoretically a variety of DTP compounds as potential molecular wires in single-molecule junctions in order to determine if changing the antiaromaticity of the core also significantly influences transport.
We have previously explored several isomers of DBP, both experimentally and theoretically,8 in which we found the 5,10-substituted isomer (where the substitution refers to the position of the thioanisole acetylene anchor groups about the DBP group) to have a slightly greater conductance compared to the purely aromatic and similarly sized anthracene compound. The 3,6 isomer, however, had a much lower conductance as a result of destructive quantum interference (DQI) between HOMO and LUMO. DQI appears because of the specific position of the linker groups about the central unit.20 Constructive quantum interference (CQI) typically leads to higher conductances compared to DQI, but it produces lower Seebeck coefficients if the Fermi level lies towards the centre of the HOMO–LUMO gap where the energy dependence of the transmission is low. The steeper energy dependence of the transmission for DQI is also expected to increase on/off ratios obtained by applying a gate/bias voltage.21–23
In this study, our goal was to assess the theoretical transport properties of a selection of molecular wires containing different isomers of DTP, and to explore the effect of changing the linker group connectivity at the core. In particular, we have focussed on isomers that have already been shown in the literature, but we have also expanded the study to include additional isomers not yet isolated experimentally. In addition, we have studied the effect of changing the heterocycle from thiophene to oxazole and pyrrole in order to see if further tuning is feasible by modifying the aromaticity of the annulating ring. Another goal was to compare the outcome of the charge transport calculations with ‘rule of thumb’ methods like graphical-based schemes and ‘curly arrow’ rules (CARs) to determine if the main features of the transmission spectra (i.e. the presence of CQI or DQI within the HOMO–LUMO gap) can be predicted without expensive calculations.
Computational details
The electronic and geometrical structures of the compounds in the gas phase as well as in the metal–molecule–metal junctions were obtained by density functional theory (DFT) using the Turbomole code.24 A def-SVP basis set25 and BP86 functional26 were employed. The electron-transport properties were then obtained by Green's function techniques in the spirit of the Landauer formalism.27 For selected cases, the HOMO–LUMO gap was corrected via the DFT+Σ procedure.28,29 The NICS calculations were carried out using Gaussian 09,30 using a B3LYP/6-31G(d)31 level of theory. More details about the geometry optimization as well as the NICS calculations are reported in the ESI.†Results and discussion
Gas-phase properties of dithieno compounds
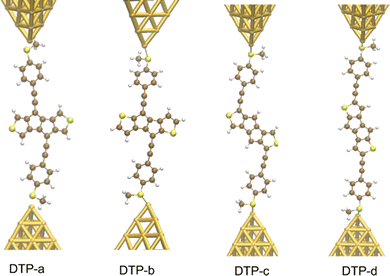
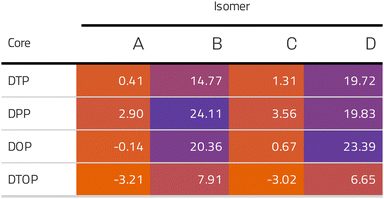
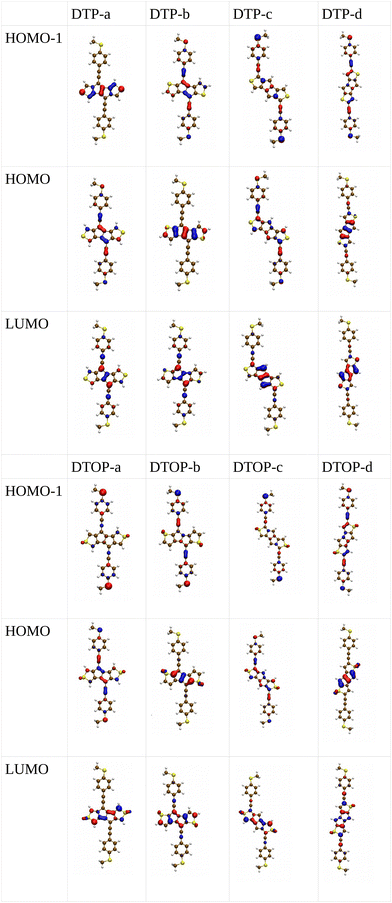
Inspired by the results of Usuba et al.,19 we studied the conducting properties of molecular wires incorporating the aforementioned DTP groups as central units (shown in Fig. 1). In order to consider plausible molecular structures for potential single-molecule conductance measurements (e.g. break-junction techniques), we designed junctions in which this central unit is connected to two gold clusters via two –C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ph–SMe (thioanisole acetylene) groups. The use of these groups is common in single-molecule conductance studies as they give rise to the formation of clear conductance plateaus in the measurements. The corresponding metal–molecule–metal junctions are shown in Fig. 2. We have principally considered two different isomers of the DTP core following Usubas work, fusion via the 2,3 carbons of the thiophene ring as well as fusion via the 3,4 carbons. Based on these two isomers, we further considered two different connectivities of the linker groups, either to the pentalene core or to the thieno rings. Overall, this gives rise to four different compounds as shown schematically in Fig. 1. Note that we focussed our work on compounds based on the isomers studied in ref. 19, which do not include all possible isomers. We extended our study to include other isomers that could potentially be synthesized at a later date (see Fig. S6 in the ESI,† for the curves obtained for some of the possible alternative isomers). We carried out NICS calculations in order to evaluate the degree of aromaticity/antiaromaticity in each compound. The details, as well as a table of the values, are provided in the ESI.† In Fig. 3, we report the values for the inner rings in a colour-coded table. For each isomer, the thiophene rings have negative chemical shifts (not shown in Fig. 3, but which can be found in Section 4 of the ESI†), indicating they remain aromatic in all cases. The degree of aromaticity is, however, smaller in molecules DTP-b and DTP-d as seen by the slightly less-negative values. The central 5-membered rings, on the other hand, all show positive chemical shifts, indicating they have antiaromatic character. The b and d isomers, however, show much higher chemical shifts than a and c. Both observations tell us that 2,3 fusion to the outer thiophene ring produces much stronger antiaromaticity within the pentalene core, which is in good agreement with the work of Usuba. The chemical shift of the central 5-membered ring in DTP-d is greater than in DTP-b, which suggests the position of the anchor groups also modulates the antiaromaticity to some extent. We note that the HOMO is more spatially delocalised in DTP-d compared to DTP-b, extending to the acetylene groups (Fig. 6). Attaching the anchor groups to the outer thiophene rings thus affords a compound with greater central antiaromaticity as well as better overall delocalisation in HOMO and LUMO levels.
C–Ph–SMe (thioanisole acetylene) groups. The use of these groups is common in single-molecule conductance studies as they give rise to the formation of clear conductance plateaus in the measurements. The corresponding metal–molecule–metal junctions are shown in Fig. 2. We have principally considered two different isomers of the DTP core following Usubas work, fusion via the 2,3 carbons of the thiophene ring as well as fusion via the 3,4 carbons. Based on these two isomers, we further considered two different connectivities of the linker groups, either to the pentalene core or to the thieno rings. Overall, this gives rise to four different compounds as shown schematically in Fig. 1. Note that we focussed our work on compounds based on the isomers studied in ref. 19, which do not include all possible isomers. We extended our study to include other isomers that could potentially be synthesized at a later date (see Fig. S6 in the ESI,† for the curves obtained for some of the possible alternative isomers). We carried out NICS calculations in order to evaluate the degree of aromaticity/antiaromaticity in each compound. The details, as well as a table of the values, are provided in the ESI.† In Fig. 3, we report the values for the inner rings in a colour-coded table. For each isomer, the thiophene rings have negative chemical shifts (not shown in Fig. 3, but which can be found in Section 4 of the ESI†), indicating they remain aromatic in all cases. The degree of aromaticity is, however, smaller in molecules DTP-b and DTP-d as seen by the slightly less-negative values. The central 5-membered rings, on the other hand, all show positive chemical shifts, indicating they have antiaromatic character. The b and d isomers, however, show much higher chemical shifts than a and c. Both observations tell us that 2,3 fusion to the outer thiophene ring produces much stronger antiaromaticity within the pentalene core, which is in good agreement with the work of Usuba. The chemical shift of the central 5-membered ring in DTP-d is greater than in DTP-b, which suggests the position of the anchor groups also modulates the antiaromaticity to some extent. We note that the HOMO is more spatially delocalised in DTP-d compared to DTP-b, extending to the acetylene groups (Fig. 6). Attaching the anchor groups to the outer thiophene rings thus affords a compound with greater central antiaromaticity as well as better overall delocalisation in HOMO and LUMO levels.
Following this, we analyzed the Mulliken charges which revealed a positive charge on the pentalene in DTP-a and DTP-c (+0.3 and +0.8 respectively) as opposed to slightly negative charges found in DTP-b and DTP-d (−0.08 and −0.13 e, respectively). This supports the results of the NICS calculations, which shows again that the main formal resonance contributors can be used to explain the trends in antiaromaticity. DTP-a and DTP-c formally have two double bonds within the pentalene core, whereas DTP-b and DTP-d would have four, according to their Lewis structures. In other words, DTP-a and DTP-c should have a lower electron density in the pentalene core whereas DTP-b and DTP-d should have higher density. Furthermore, the DFT-calculated energy positions of the HOMO and LUMO of each compound (shown in Fig. S2 of the ESI†) show that the gaps of DTP-a and DTP-c are significantly larger than DTP-b and DTP-d. This agrees with the NICS analysis showing that DTP-a and DTP-c have overall lower antiaromaticity compared to DTP-b and DTP-d, where the antiaromaticity of the parent pentalene is much better preserved.
Transport properties of dithienopentalene compounds
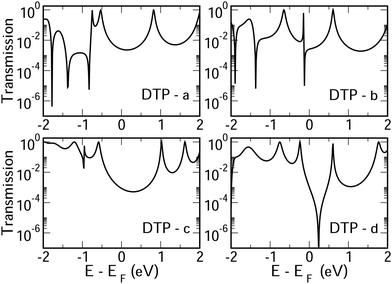
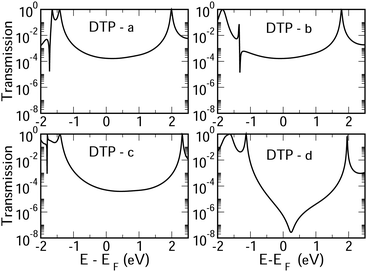
In Fig. 4, we show the transmission as a function of energy for DTP-a–d. In all cases, the Fermi level is found to be closer to the HOMO than the LUMO, and the influence of the position of the thiophene–sulfur on the transmission profile is highly significant. Despite junctions a and b having the same connection between the central core and the linker groups, the frontier orbitals give rise to Lorentzian resonances in a, whereas a resonance–antiresonance pair appears just below the Fermi level in b. This feature is due to a Fano-type interference which is known to appear when there is an orbital strongly decoupled from the leads (the HOMO, in this case, see Fig. 6). We also observe that the energy difference between the HOMO and LUMO-derived levels in b parallels the gas-phase properties (Fig. S2, ESI†) and is much less than in a. This is clearly due to the significantly greater degree of antiaromaticity at the core of DTP-b, but, as can be seen in Fig. 4, the strongly decoupled level and the presence of a sharp Fano resonance at the energy of the HOMO does not result in a boost in transmission.Junction c, as for a, also produces Lorentzian-shaped resonances. Junction d, on the other hand, produces an antiresonance in the middle of the gap arising from DQI. This can be explained by applying the symmetry and parity rules reported in ref. 32, in which interference appears in the presence of so-called “forbidden” connections which, in turn, correspond to configurations in which the sign of the product of the molecular expansion coefficients related to the input and output (I/O) sites is the same for both HOMO and LUMO. This is indeed the case for the two orbitals in junction d (see Fig. 6).
It is now interesting to test if this behaviour is predictable from molecular topology schemes, which do not require lengthy quantum chemical calculations. We first turned to the method proposed by O'Driscoll and Bryce,33 which is based on arrow-pushing between I/O (known as “curly-arrow rules”, CARs) which further stems from work by Hosoya34 and Stuyver.35 It is essentially derived from valence-bond theory. For a detailed description of this method, please see Section 9 of the ESI.†
CARs predict CQI for each molecule (i.e.DTP-a–d), but clearly this is at odds with some of the isomers (see ESI,† Section 9 for curly-arrow schemes). Compounds DTP-a and DTP-c indeed show straightforward CQI around the Fermi level, thus agreeing with CARs. On the other hand, our results for DTP-b show that the localised HOMO gives rise to a Fano resonance which has a minor contribution to transport at the Fermi level, which drops even further after applying a HOMO–LUMO gap correction (necessary for addressing the gap underestimation resulting from the use of the DFT-GGA approach, see ESI,† for further details). The greatest discrepancy, however, comes with DTP-d, which is dominated by DQI regardless of whether the HOMO–LUMO gap is corrected or not (gap-corrected curves are given in Fig. 8). It has been shown that the behaviour of certain non-alternant hydrocarbons, such as azulene and fulvalene, appear to contradict CARs.36–38 A similar “breakdown” was also suggested for certain cross-conjugated species39 which have been shown to display much higher conductances than would otherwise be expected.40 A modification to the rules can, however, be applied which redraws the bonds to generate zwitterions, generally leading to better agreement. For DTP-d, however, we do not believe this is justifiable as, unlike azulene, no significant zwitterionic forms are expected due to the symmetry of the molecule. Furthermore, CARs clearly state that “if the donor lone pair can be delocalised onto the acceptor using curly arrows, CQI is expected”.33 This means that, as defined, both basic and extended CARs cannot account for the presence of the strong anti-resonance in DTP-d. The question is why CARs appear to make correct predictions for DTP-a and DTP-c but fail for DTP-b and, mostly strongly, in the case of DTP-d. The most obvious difference between the two sets of isomers is the degree of antiaromaticity. As we discussed in the previous section, our NICS calculations show that DTP-a and DTP-c are essentially non-aromatic within the 5-membered rings (NICS values of 0.41 ppm and 1.31 ppm respectively). DTP-b and DTP-d, on the other hand, have much more positive values (14.77 ppm and 19.72 ppm respectively), making them strongly antiaromatic. The difference in the resulting shape of the HOMO in the two sets is significant. The HOMO in DTP-a and DTP-c contains two lobes within the pentalene core located where the double bonds can be expected from the Lewis structures (Fig. 6). Crucially, the sign of the wavefunction changes between the two nodes for the HOMO but not for the LUMO, meaning that CQI will ensue, in line with CARs. In this way, the molecules behave more like a chain of alternating single-double/triple bonds. For DTP-b and DTP-d, the HOMO contains several lobes within the pentalene core, with one spanning the C7–C14 bond (using the IUPAC nomenclature for fused compounds, see Fig. S1 for the full labelling, ESI†) across the central bond. This means that at the positions of the anchor groups in DTP-d, the wavefunction of the HOMO does not change sign. As the sign also still does not change for the LUMO, DQI is thus obtained between HOMO and LUMO. The formal position of the central double bonds in the Lewis drawings of DTP-b and DTP-d is, however, the same as for DTP-a and DTP-c. This is the reason CARs thus breakdown in this case as it is clear one cannot treat the C7–C14 bond in the same way for DTP-a/c and DTP-b/d. We note that the HOMO and HOMO−1 levels in DTP-a and DTP-c are, essentially, reversed in DTP-b and DTP-d. In DTP-a and DTP-c, delocalisation along this central C7–C14 bond provides effective coupling between the two anchor groups and gives rise to CQI. Such effective delocalisation has been demonstrated in the 5,10-connected dibenzopentalene (i.e. with anchor groups situated at the same relative positions around the pentalene core as in the a and b isomers) which we reported previously showing high conductance.8 In DTP-b and DTP-d, the C7–C14 bond cannot be considered as part of the conjugation path due to the behaviour of the wavefunction. The inversion of HOMO/HOMO−1 and the molecular orbital shape are clearly levels of detail beyond which curly arrows can deal with. The table in Fig. 5 summarizes the appearance of CQI and DQI for each compound. This includes the isomers DTP-e and DTP-f, which are studied and discussed in detail in Section 6 of the ESI.† Interestingly, contrary to the trend in isomers DTP-a to d, here the DFT-based transmission curve of the weakly-antiaromatic DTP-e does not agree with CARs, but for the strongly antiaromatic DTP-f, it does. For DTP-e, the agreement can be resolved by implementing the extended version of CARs (ECAR-2, Fig. S11 of Section 9 in the ESI†) which suggests the DQI is shifted away from the HOMO–LUMO gap. For further discussion, please see Sections 6 and 7 in the ESI.† On the other hand, the agreement of DTP-f can be understood because there is no potential conjugation path through the DTP core via any series of bonds, neither via the periphery of the pentalene nor via the central transannular bond.
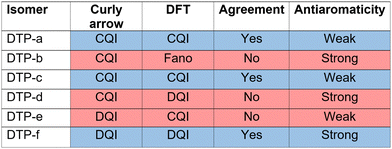 | ||
| Fig. 5 Schematic summary of the appearance of CQI or DQI for each DTP isomer and corresponding degree of antiaromaticity. For the structures of DTP-e and DTP-f, see Section 6 of the ESI.† The CAR prediction given here is based on the basic version. | ||
To delve deeper into the behaviour of DTPa–d, we calculated the transmission curves using a tight-binding (TB) model and compared the results with the DFT-derived curves. We set the carbon onsite energies to 0 eV, and we used a value of −2.9 eV for sulphur sites (for further details please see Section 5 of the ESI†). In summary, the results closely match those of the DFT calculations in each case, reproducing the CQI in DTP-b and DTP-c, the Fano resonance at the position of the HOMO in DTP-c and the large antiresonance about the Fermi level in DTP-d. The TB approach, however, allows us to modify the connections arbitrarily, which can now help us to form a more complete picture of what is happening, particularly, in DTP-d. We simulated the effect of removing specific bonds within the pentalene core (structure 2, Fig. S8 in the ESI†), which is effectively done by setting the couplings between the adjacent atomic sites to zero. After cutting bonds 9 and 10 (i.e. between C6–C7 and C13–C14), the same formal conjugation pathway is mantained from one side of the DTP to the other, but it breaks the formally 8-π cyclic pentalene core. Interestingly, this modified structure loses the antiresonance and shows only CQI between HOMO and LUMO. This is rational because this new structure would be equivalent to two thiophene rings in which the 2 and 2′ positions (of the thiophenes) are joined via a butadiene group with the linkers in the 5 and 5′ positions (n.b. 2,5 connected thiophenes have been shown typically to yield CQI13). In this modified structure, the core is transformed from non-alternant to alternant and also becomes non-aromatic. We also simulated the effect of cutting the central bond of the pentalene core (i.e. C7–C14, structure 3 of Fig. S8, ESI†). Cutting this bond changes the CARs prediction from CQI to DQI, as we formally prevent conjugation via the C7–C14 bond, and the result now matches what we find in the calculated transmission curve. The fact now that DTP-d and the modified structure 3 both display DQI between HOMO and LUMO (albeit at slightly different energies) whereas structure 2 yield CQI is confirmation that CARs cannot be applied to (at least) DTP compounds with strongly antiaromatic cores. These observations prove that there is no conjugation pathway via the C7–C14 bond when the DTP core is strongly antiaromatic.
We further checked to see if DTP-d adopts a biradical electronic configuration, which may change the prediction from the CAR scheme. We did not find any clear evidence for the presence of radicals in the calculations.
Subsequently, we applied the graphical rules as put forward by Markussen, Stadler and Thygesen41 (MST) for predicting DQI/CQI to DTP-d. For a detailed explanation of the rules, see ref. 23, 38 and 41. As with CARs, these rules aim to predict the appearance of interference features in the transmission spectrum by drawing a series of diagrams on top of the molecular skeletal structure within the Hückel theory. Additionally, the energetic positions of the interference features can also be predicted. The result of applying these rules to DTP-d gave 48 diagrams (see Section 10 of the ESI†), each of them contributing to a third-order equation (eqn (1)). This large equation contains four parameters: coupling terms for double and single C–C bonds (t1 and t2) and C–S bond (tS) and the S on-site energy (the on-site energy for C having been set to zero). For all parameters, the same values as those employed in the tight-binding model were employed. The unknown variable in this equation is the energetic position of the interference. We found the solution coincided well with the position predicted by the tight-binding and DFT-based transport calculations. Clearly, the (MST) graphical method, which is very convenient for small molecules, is much more cumbersome for larger compounds like those explored in the present study. Nevertheless, the fact that it leads to the appearance of the same DQI feature found in DFT and tight binding confirms our theoretical approach and shows that this method should return the correct prediction of CQI/DQI regardless of whether the molecule is alternant/non-alternant or antiaromatic.
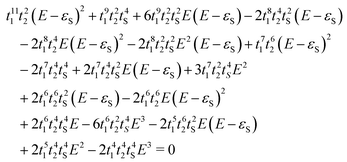 | (1) |
Comparing dithieno with N-methylpyrrolo and furyl analogues
In the following section we will discuss the effect changing the heteroatom in the five-membered rings has upon transport. As far as we are aware, only DTPs have been synthesised and previously studied. Here, we have expanded the study to include N-methylpyrrolo and furyl-stabilised pentalene (DPP and DOP respectively), which we have done by replacing the S atoms in the thienopentalenes with N-CH3 and O atoms respectively. This gives a further four isomers per heteroatom (see Fig. 1 for sketches of the isomers). Furthermore, we also investigated the effect of oxidation of the thienyl groups in DTP which we did by adding two O atoms per S atom to give a thiophene S,S-dioxide unit (DTOP). This dramatically changes the π-system which may, therefore, be a useful way to switch the conductance of the molecules experimentally. Our NICS calculations show that regardless of the heteroatom, the outer heterocyclic ring remains aromatic in almost all cases, except for DTP-b, where the results suggest the ring is essentially non-aromatic. Much greater variation is found for the inner five-membered rings. For the a and c structures, the inner rings are typically non-aromatic to mildly antiaromatic (DTP, DPP and DOP). For DTOP, the inner rings are mildly aromatic. For b and d structures, the inner rings are antiaromatic in all cases, however, the antiaromaticity is much more pronounced for DTP/DPP/DOP than for DTOP. Between DTP, DPP and DOP, the pyrrole and furyl-stabilised compounds typically show the largest NICS values, with highest being about 24 ppm for both DPP-b and DOP-d. Typically, thiophene shows greater aromatic character than pyrrole, which in turn is more aromatic than furan (which is based on a number of factors including resonance energy,11 NICS values and isotropic shieldings42,43). The lower aromaticity in DPP and DOP could be a result of more localised double bonds at the edge between inner and outer five-membered rings, which in turn promotes greater antiaromaticity within the pentalene core. This further reduces the HOMO–LUMO gaps in DPP and DOP compared to DTP.In Fig. 7, we show the transmission curves obtained for all heterocyclic isomers. For the a-structures, the most striking difference lies in the energy alignment of the frontier orbitals. With respect to DTP, in the case of DPP, all levels are shifted upwards in energy, whilst for DTOP they are shifted downwards. For DOP the levels are located at similar energies. This behaviour is consistent with the gas-phase trend (Fig. S2, ESI†) and is most likely related to the different electron-withdrawing (SO2) and electron-donating (NCH3) character of these substituents. In addition, an interesting effect arises for DPP-a. Unlike the other three cases, the corresponding curve shows an interference feature (Fano resonance) immediately below the Fermi level. This corresponds to the gas-phase HOMO−1 which, in the junction, overtakes the HOMO to become the actual frontier molecular-based orbital. This inversion is favoured by their proximity in energy. Along with what we have previously discussed about CARs and predicting DQI, this is another demonstration of how the appearance and form of interference features in transmission curves cannot easily be predicted in such compounds based on considerations of the gas-phase orbitals alone.
For the b-structures, we found that the Fano feature associated with the HOMO is closer to the Fermi level for DPP and DOP with respect to DTP, but is further away and broader for DTOP. This suggests a larger coupling of the HOMO with the electrodes for DTOP which is a consequence of a slightly higher delocalization of this level compared to the other compounds (see Section 3 of the ESI†).
Turning to the c structures, the trend in the orbital energies is similar to the a and b structures, and no major differences appear in the transmission close to the Fermi level between DTP, DPP and DOP, where the midgap behaviour is dominated by the Lorentzian curves. Interestingly, an interference feature now appears in the case of DTOP. This is intriguing as, once again, the formal Lewis bonding pattern in the cores of DTP-c and DTOP-c is the same. To gain insight, we analyzed the gas phase orbitals of these compounds. In Fig. 6, we show the frontier orbitals for DTP-c and DTOP-c. The HOMOs for both DTP-c and DTOP-c are very similar, with the only obvious difference being extra density on the oxygen atoms of DTOP-c. The LUMOs, on the other hand, are substantially different. The LUMO of DTP-c is similar to the LUMOs in DPP and DOP (see Fig. S4 in the ESI†) and does not change parity from one end of the molecule to the other. The LUMO of DTOP, on the other hand, does change parity, and as the HOMO also changes parity, this produces DQI. Further analysis shows that the LUMO+1 in DTOP-c is spatially very similar to the LUMO of DTP-c. Likewise, the LUMO+1 of DTP-c is also very similar to the LUMO of DTOP-c, although there is some more variation. It appears, therefore, that thiophene oxidation reorders the LUMO and LUMO+1 in the reduced molecule (i.e. relative to DTP) to become the LUMO+1 and LUMO respectively in DTOP, which is the origin of the DQI. It is worth noting that the energies of the LUMO and LUMO+1 in DTOP-c are very similar in the gas phase (insert values) and slightly diverge when the molecule is inside the junction. This implies that if these levels in DTOP-c had inverted, as we saw in the case of the HOMO/HOMO−1 in DPP-a, then CQI would have prevailed. This underlines that trying to predict the appearance of CQI/DQI will be nearly impossible for compounds in which the HOMO/HOMO−1 or LUMO/LUMO+1 are close in energy in the gas phase, potentially swapping order in the junction. Finally, we also observe that, in general, the c-structures produce slightly broader HOMO-related resonances than for the a-structures (i.e. where the heteroatoms are in the same positions). As discussed earlier, this suggests that conjugation is favoured when the CC–Ph–SMe groups are attached to the outer heterocyclic rings rather than to the pentalene core. In terms of transmission at the Fermi level, this offsets the slight increase in the distance between the anchor groups.
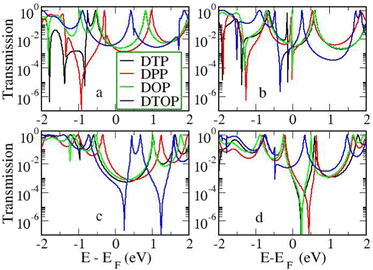 | ||
| Fig. 7 Transmission as a function of energy for all heterocycles and heteroatom/linker group positions. | ||
Moving finally to the d-structures, DPP and DOP show the same destructive interference as for DTP, although the dip lies at higher energy for DPP. Interestingly, DTOP again behaves differently, and the DQI dip is replaced by a narrow Fano resonance. It arises from the significant decoupling of the HOMO from the leads (see Fig. 6), which also has a different spatial distribution compared to DTP-d. The spatial distribution of the LUMO is also different for DTOP-d, but the parity at the anchor groups remains the same. The HOMO−1 of both compounds is very similar and the parity means that CQI (between the HOMO−1 and the LUMO) prevails at the Fermi level. Oxidation of DTP to DTOP, thus, offers a dramatic change in conductance (roughly a factor 10 from Fig. 5) and at the same time a change in the sign of the slope of the transmission curve (which changes the sign of the thermovoltage generated in response to an applied temperature gradient). We note that this behaviour is robust even after opening the HOMO–LUMO gap. This suggests that DTP-d could form the basis of a molecular switch/sensor where both conductance and thermovoltage could be turned on or off in dramatic fashion. Comparing DTP/DPP/DOP c and d structures, we imagine that the d-structures would be better to take advantage of the reduced HOMO–LUMO gaps to form high-conductance molecular wires that can also produce a significant thermovoltage. The b-structures all show Fano resonances which, due to their narrow profile, are unlikely to make a significant contribution to transport at the Fermi level. The d-structures, on the other hand, all give DQI between HOMO and LUMO, but, due to the narrowness of the gap, the conductance should not be as negatively affected as it is for an oligo(phenylene ethynylene) which has a much wider gap.44 We stress that despite the inaccuracies originating from the use of DFT-GGA, these conclusions are robust as they hold also after correcting the HOMO–LUMO gap (Fig. 8). Whilst the gap correction shifts the interference feature of the b-structures to lower energies, this would not be the case for the d-structures, for which the antiresonance dip remains close to the Fermi level.
We will now summarise the findings and present an unified picture of the underlying reasons for the mixed agreement between the DFT-based transmission curves and the predictions based on curly arrow/valence bond level of theory. Firstly, for all non/weakly-antiaromatic compounds (where we refer to the properties only within the pentalene core) curly arrow rules agree with the DFT results. For this subset of compounds, when CARs predict CQI, DFT also predicts CQI (as is the case for DTP-a and DTP-c). This shows that despite having non-bipartite lattice structures (i.e. being non-alternant) the normal rules of conjugation still hold. On the other hand, for the weakly antiaromatic DTP-e (analysed in the ESI†) CARs predict DQI, but the DFT level of theory gives CQI within the HOMO–LUMO gap. This discrepancy can, however, be explained using the known heteroatom effect which alters the interference pattern between HOMO and LUMO. This has been observed in numerous compounds such as meta-connected fluorenones and pyridines.40,45 Turning to the strongly antiaromatic compounds, we were unable to find structures in which DQI does not dominate, or in which one of the frontier orbitals is not highly-localised. In DTP-b, the HOMO is strongly localized on the DTP core, and is therefore weakly-coupled to the electrodes (i.e. there is negligible HOMO weight on the anchor groups). This produces a Fano resonance at the energy of the HOMO, with the transmission at the Fermi level being, instead, due to a convolution of the LUMO with the HOMO−1. In this situation, CARs cannot account for the decoupling of the HOMO from the electrodes. In the case of DTP-d, which is also strongly antiaromatic in the core, CARs predict CQI, yet DQI is found by DFT and tight-binding procedures. We have shown, however, that if the only way to draw a conjugation path from an anchor group to the other (i.e. to connect donor and acceptor groups placed at the sites of the original anchor groups around the core) using curly arrows is via the central C7–C14 bond (i.e. the bond between adjacent 5-membered cyclopentadiene rings) then CARs will fail. This can be explained due to the shape of the HOMO which has a single lobe spanning the bonds C1–C14–C7–C8 (i.e. spanning the sites of the formal double bonds at C1–C14 and C7–C8 through the C14–C7 transannular bond). In this case, these formal double bonds do not behave as they would in a linearly conjugation alkene, where the sign of the wavefunction changes between adjacent double bonds. Instead, in the strongly antiaromatic DTP-d (and DTP-b) there is no sign change, and thus there is no conjugation path. Taken with the symmetry of the LUMO, this is the physical origin of the DQI within the HOMO–LUMO gap. If one prohibits drawing curly arrows through the C14–C7 bond, then there is no way to connect D and A which, for DTP-d, restores agreement between CARs and DFT, but this detail cannot be accounted for looking only at the Lewis structure. The other strongly antiaromatic compound we have investigated, DTP-f (ESI,† Section 6), also gives rise to DQI in the DFT-based transmission curve, but this time both DFT and CARs agree. This is because there is no conjugation path through the molecule to connect the anchor group sites, neither around the perifery of the molecule or via the C14–C7 transannular bond. This highlights the clear limitations to the application of simple representations of molecular structure in making accurate transport predictions. Our picture also explains why the Lewis structures adequately explain the difference in the degree of antiaromaticity within the pentalene core between the various isomers, despite CARs failing. This is because the idea of antiaromaticity only considers delocalisation of bonds around the periphery of the cyclic system. For transport, however, the transannular bond becomes important, which changes substantially between weakly and strongly antiaromatic isomers.
Conclusions
In summary, we have studied electron transport in a family of antiaromatic, non-alternant heterocyclic molecular wires built upon pentalene core using DFT and Green's function techniques. The degree of antiaromaticity at the core was modulated by changing the position of the heteroatom as well as its type. We investigated thieno, N-methylpyrrolo and furyl-stabilised pentalene as well as the effect of changing the linker group position. In general, there was no correlation between the degree of antiaromaticity within the pentalene and the magnitude of the transmission at the Fermi level. Instead, we found that all strongly antiaromatic compounds either gave rise to destructive interference within the HOMO–LUMO gap, resulting in low transmission, or a narrow Fano resonance due to the strongly-decoupled HOMO level. On the other hand, the isomers with mild antiaromaticity typically, but not exclusively, showed constructive interference inside the HOMO–LUMO gap. The difference between the transmission profile of the mildly antiaromatic compounds versus the strongly antiaromatic compounds appears to be due to inversion of the HOMO and HOMO−1. The symmetry of the HOMO when the molecule is strongly antiaromatic either prevents this orbital from significantly hybridising with the anchor groups or gives rise to destructive quantum interference, depending on the anchor group position. For the strongly antiaromatic DTP cores examined, there seems to be no way to place the anchor groups in a symmetric fashion in order to avoid DQI.We compared our results with tight-binding calculations as well as graphical predictions, which both give good agreement with the DFT-based results. On the other hand, the valence-bond derived curly-arrow rules for predicting the nature of interference within the HOMO–LUMO gap fail for some, although not all, strongly-aromatic compounds. This can be put down to the failure of this approach to recognise that the double bonds are no longer linearly conjugated via the central transannular bond of pentalene when the molecule becomes strongly antiaromatic. This raises the question of whether CARs fail for other strongly antiaromatic structures, which will be the subject of future investigations. In the case of mildly antiaromatic cores, however, the central pentalene can be reliably modelled using the curly-arrow approach. We found that oxidising the thiophenes to thiophene-S,S-dioxides is a promising way to switch both conductance and thermopower in dramatic fashion. We have discussed the optimum structure for such a switch. The studied molecules show interesting effects which merit further investigation. We thus hope that our results inspire others to synthesize and measure their conductance properties.
Data availability statement
The Cartesian coordinates of the optimized structures for all gold-molecule-gold junctions studied in this work can be found at https://doi.org/10.21950/BLB9NR.Author contributions
E. L. and L. A. Z. conceived the project, designed the calculations, wrote the manuscript and supervised the work. R. R.-M. and L. A. Z. carried out the DFT-based calculations. E. L. carried out the tight-binding calculations. C. R.-P. performed the graphical-method analysis. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Spanish MICIN for the María de Maeztu Programme for Units of Excellence in R&D (grant No. CEX2018-000805-M). Financial support from MCIN/AEI/10.13039/501100011033 is acknowledged by L. A. Z. (grant PID2021-125604NB-I00), E. L. (PID2021-127964NB-C21). We also thank the Universidad Autónoma de Madrid and the Comunidad de Madrid (grants No. SI3/PJI/2021-00191). E. L. thanks the Comunidad de Madrid Atracción de Talento grant 2019-T1/IND-16384. IMDEA Nanociencia acknowledges support from the ‘Severo Ochoa’ Programme for Centres of Excellence in R&D (CEX2020-001039-S).Notes and references
- C. Hong, J. Baltazar and J. D. Tovar, Eur. J. Org. Chem., 2022, e202101343 CrossRef CAS.
- S. Fujii, S. Marqués-González, J.-Y. Shin, H. Shinokubo, T. Masuda, T. Nishino, N. P. Arasu, H. Vázquez and M. Kiguchi, Nat. Commun., 2017, 8, 15984 CrossRef CAS PubMed.
- M. Gantenbein, X. Li, S. Sangtarash, J. Bai, G. Olsen, A. Alqorashi, W. Hong, C. J. Lambert and M. R. Bryce, Nanoscale, 2019, 11, 20659–20666 RSC.
- P. P. Kalapos, P. J. Mayer, T. Gazdag, A. Demeter, B. Oruganti, B. Durbeej and G. London, J. Org. Chem., 2022, 87, 9532–9542 CrossRef CAS PubMed.
- N. P. Arasu and H. Vázquez, ChemPhysChem, 2021, 22, 864–869 CrossRef CAS PubMed.
- P. Seitz, M. Bhosale, L. Rzesny, A. Uhlmann, J. S. Wössner, R. Wessling and B. Esser, Angew. Chem., 2023, 135, e202306184 CrossRef.
- R. Casares, A. Martínez-Pinel, S. Rodríguez-González, I. R. Márquez, L. Lezama, M. T. González, E. Leary, V. Blanco, J. G. Fallaque, C. Díaz, F. Martín, J. M. Cuerva and A. Millán, J. Mater. Chem. C, 2022, 10, 11775–11782 RSC.
- M. Schmidt, D. Wassy, M. Hermann, M. T. González, N. Agräit, L. A. Zotti, B. Esser and E. Leary, Chem. Commun., 2021, 57, 745–748 RSC.
- A. A. Deniz, K. S. Peters and G. J. Snyder, Science, 1999, 286, 1119–1122 CrossRef CAS PubMed.
- R. Breslow and F. W. Foss, J. Phys.: Condens. Matter, 2008, 20, 374104 CrossRef.
- W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920 CrossRef CAS PubMed.
- M. Gantenbein, L. Wang, A. A. Al-Jobory, A. K. Ismael, C. J. Lambert, W. Hong and M. R. Bryce, Sci. Rep., 2017, 7, 1794 CrossRef PubMed.
- Y. Yang, M. Gantenbein, A. Alqorashi, J. Wei, S. Sangtarash, D. Hu, H. Sadeghi, R. Zhang, J. Pi, L. Chen, X. Huang, R. Li, J. Liu, J. Shi, W. Hong, C. Lambert and M. Bryce, J. Phys. Chem. C, 2018, 122, 14965–14970 CrossRef CAS.
- C. K. Frederickson, L. N. Zakharov and M. M. Haley, J. Am. Chem. Soc., 2016, 138, 16827–16838 CrossRef CAS PubMed.
- S. Schneebeli, M. Kamenetska, F. Foss, H. Vazquez, R. Skouta, M. Hybertsen, L. Venkataraman and R. Breslow, Org. Lett., 2010, 12, 4114–4117 CrossRef CAS PubMed.
- Z. U. Levi and T. D. Tilley, J. Am. Chem. Soc., 2009, 131, 2796–2797 CrossRef CAS PubMed.
- A. Konishi, T. Fujiwara, N. Ogawa, Y. Hirao, K. Matsumoto, H. Kurata, T. Kubo, C. Kitamura and T. Kawase, Chem. Lett., 2010, 39, 300–301 CrossRef CAS.
- J. Wu, Y. Chen, J. Liu, Z. Pang, G. Li, Z. Lu, Y. Huang, A. Facchetti and T. J. Marks, J. Mater. Chem. C, 2022, 10, 2724–2731 RSC.
- J. Usuba, M. Hayakawa, S. Yamaguchi and A. Fukazawa, Chem. – Eur. J., 2021, 27, 1638–1647 CrossRef CAS PubMed.
- C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888 RSC.
- L. A. Zotti, E. Leary, M. Soriano, J. C. Cuevas and J. J. Palacios, J. Am. Chem. Soc., 2013, 135, 2052–2055 CrossRef CAS PubMed.
- L. A. Zotti, Appl. Sci., 2021, 11, 4828 CrossRef CAS.
- L. A. Zotti and E. Leary, Phys. Chem. Chem. Phys., 2020, 22, 5638–5646 RSC.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004 CrossRef.
- S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482 CrossRef CAS PubMed.
- M. J. Frisch et al. Computer Code GAUSSIAN09, Revision C.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- K. Yoshizawa, T. Tada and A. Staykov, J. Am. Chem. Soc., 2008, 130, 9406–9413 CrossRef CAS PubMed.
- L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 1103–1123 RSC.
- H. Hosoya, Curr. Org. Chem., 2015, 19, 293–310 CrossRef CAS.
- T. Stuyver, S. Fias, F. De Proft and P. Geerlings, J. Phys. Chem. C, 2015, 119, 26390–26400 CrossRef CAS.
- L. J. ODriscoll, S. Sangtarash, W. Xu, A. Daaoub, W. Hong, H. Sadeghi and M. R. Bryce, J. Phys. Chem. C, 2021, 125, 17385–17391 CrossRef CAS PubMed.
- J. Xia, B. Capozzi, S. Wei, M. Strange, A. Batra, J. R. Moreno, R. J. Amir, E. Amir, G. C. Solomon, L. Venkataraman and L. M. Campos, Nano Lett., 2014, 14, 2941–2945 CrossRef CAS PubMed.
- K. G. L. Pedersen, A. Borges, P. HedegÅrd, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2015, 119, 26919–26924 CrossRef CAS.
- J. Alqahtani, H. Sadeghi, S. Sangtarash and C. J. Lambert, Angew. Chem., Int. Ed., 2018, 57, 15065–15069 CrossRef CAS PubMed.
- A. Alanazy, E. Leary, T. Kobatake, S. Sangtarash, M. T. González, H.-W. Jiang, G. R. Bollinger, N. Agräit, H. Sadeghi, I. Grace, S. J. Higgins, H. L. Anderson, R. J. Nichols and C. J. Lambert, Nanoscale, 2019, 11, 13720–13724 RSC.
- T. Markussen, R. Stadler and K. S. Thygesen, Phys. Chem. Chem. Phys., 2011, 13, 14311–14317 RSC.
- S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893–1898 CAS.
- K. E. Horner and P. B. Karadakov, J. Org. Chem., 2013, 78, 8037–8043 CrossRef CAS PubMed.
- R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672 CrossRef CAS PubMed.
- X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc04266a |
| This journal is © The Royal Society of Chemistry 2024 |