Open Access Article
Open Access ArticleThe adhesion capability of Staphylococcus aureus cells is heterogeneously distributed over the cell envelope†
Christian
Spengler‡
 a,
Erik
Maikranz‡
a,
Erik
Maikranz‡
 b,
Bernhard
Glatz
c,
Michael Andreas
Klatt§
b,
Bernhard
Glatz
c,
Michael Andreas
Klatt§
 ad,
Hannah
Heintz
ad,
Hannah
Heintz
 a,
Markus
Bischoff
a,
Markus
Bischoff
 e,
Ludger
Santen
b,
Andreas
Fery
e,
Ludger
Santen
b,
Andreas
Fery
 cf and
Karin
Jacobs¶
cf and
Karin
Jacobs¶
 *a
*a
aExperimental Physics, Saarland University, Center for Biophysics, 66123 Saarbrücken, Germany. E-mail: k.jacobs@physik.uni-saarland.de
bTheoretical Physics, Saarland University, Center for Biophysics, 66123 Saarbrücken, Germany
cInstitute of Physical Chemistry and Physics of Polymers, Leibniz Institute of Polymer Research, 01069 Dresden, Germany
dDepartment of Physics, Princeton University, Jadwin Hall, Princeton, NJ 08544-0001, USA
eInsitute of Medical Microbiology and Hygiene, Saarland University, Center for Biophysics, 66421 Homburg/Saar, Germany
fPhysical Chemistry of Polymer Materials, Technical University Dresden, 01062 Dresden, Germany
First published on 16th October 2023
Abstract
Understanding and controlling microbial adhesion is a critical challenge in biomedical research, given the profound impact of bacterial infections on global health. Many facets of bacterial adhesion, including the distribution of adhesion forces across the cell wall, remain poorly understood. While a recent ‘patchy colloid’ model has shed light on adhesion in Gram-negative Escherichia coli cells, a corresponding model for Gram-positive cells has been elusive. In this study, we employ single cell force spectroscopy to investigate the adhesion force of Staphylococcus aureus. Normally, only one contact point of the entire bacterial surface is measured. However, by using a sine-shaped surface and recording force-distance curves along a path perpendicular to the rippled structures, we can characterize almost a hemisphere of one and the same bacterium. This unique approach allows us to study a greater number of contact points between the bacterium and the surface compared to conventional flat substrata. Distributed over the bacterial surface, we identify sites of higher and lower adhesion, which we call ‘patchy adhesion’, reminiscent of the patchy colloid model. The experimental results show that only some cells exhibit particularly strong adhesion at certain locations. To gain a better understanding of these locations, a geometric model of the bacterial cell surface was created. The experimental results were best reproduced by a model that features a few (5-6) particularly strong adhesion sites (diameter about 250 nm) that are widely distributed over the cell surface. Within the simulated patches, the number of molecules or their individual adhesive strength is increased. A more detailed comparison shows that simple geometric considerations for interacting molecules are not sufficient, but rather strong angle-dependent molecule-substratum interactions are required. We discuss the implications of our results for the development of new materials and the design and analysis of future studies.
Infections caused by bacterial biofilms are a major healthcare problem.1–3 These biofilms can be found both on natural surfaces, e.g. in the nasal4 and oral5 cavity, as well as on artificial surfaces, such as the exterior of prostheses, catheters and other medical devices.6–9 In this context, Staphylococcus aureus (S. aureus) is an important human pathogen,10,11 which is capable of forming biofilms with increased resistance to antibiotic treatment12 and the bodys own immune system.13 Consequently, S. aureus can cause various diseases,14 such as superficial skin disease, sepsis, endocarditis and pneumonia and numerous implant-associated infections.10 Since the formation of a biofilm begins with the attachment of single bacterial cells, understanding and controlling bacterial adhesion to solid surfaces is an urgent challenge in biomedical research.
Previous studies demonstrated that S. aureus cells adhere by tethering cell wall macromolecules, the number of which varies greatly depending on the properties of the underlying substrate.15,16 The number and properties of individual tethering molecules define the adhesive strength,17 and by length fluctuations, the molecules can overcome certain degrees of surface roughness.18 For the secretion and deposition of adhesins on the S. aureus cell wall, different mechanisms have been unraveled.19 In particular, it has been shown that protein A is secreted very selectively near the septum and then built into the cell wall.20 In another study, however, accumulation of protein A was also observed in additional areas of the cell wall and differences in the frequency and density of these clusters depending on the growth phase could be detected.21 In the same study, clustering was also observed for clumping factor A (ClfA), the size of which, but not the frequency, was growth phase-dependent.21 Atomic force microscopy (AFM) has been used in many studies to find specific interactions between functionalized probes and certain proteins at the cell wall.22–27 While in these studies, ClfA and B as well as the fibronectin-binding protein A (FnbpA) have not been found to be distributed in distinct clusters,23–25 it has been found that the collagen-binding protein (Cna) in S. aureus26 and Serine-aspartate repeat-containing protein G (SdrG) in Staphylococcus epidermis27 show a cluster-like distribution. Furthermore, a recent study utilizing DNA-PAINT, showed that in S. aureus the density of fibronectin-binding proteins is so small, that their interaction with flat surfaces is limited to the binding of single heterogeneously distributed molecules28||. Recently, mechanisms that can lead to protein clustering in lipid membranes have been deciphered by single-molecule atomic force microscopy.29 However, the question of how the overall adhesion capability of S. aureus or other Gram-positive cells is distributed over the cell surface has not yet been answered. For Gram-negative Escherichia coli (E. coli) cells, it has been found recently that this species adheres to glass surfaces by adhesive patches on their cell wall, and that the number of patches defines the adhesive strength.30 However, Gram-positive S. aureus cells have a very different cell wall composition and cell division behavior than E. coli cells, and it has been shown that the size of the contact area between cell and surface does not correlate with its adhesive strength. In particular it has been shown that the size of the contact area of different strains is largely comparable while they may differ vastly in terms of adhesive strengths.17
The aim of this study is to record the distribution of adhesive forces across a hemisphere of the bacterial envelope. We use single cell force spectroscopy (SCFS) to determine the adhesive force. Normally, SCFS is only able to assess a single point of contact between the bacterium and the support material. However, with a sine-shaped structured surface, force-distance curves perpendicular to the ripples can be recorded and it is possible to map the adhesive force over the lower half of S. aureus. The sine-shaped substrata consisted of polydimethylsiloxane (PDMS) with a periodicity slightly above the size range of the bacterial diameter (see Fig. 1). These surfaces were formed by a controlled wrinkling process, which allowed patterning in a scalable manner and has been applied in various studies.31–33 The experimental data show that the adhesion strength at a given position is quite consistent over the course of several measurements, but can fluctuate widely for different cell wall positions depending on the individual cell. For a better understanding of the data, Monte Carlo (MC) simulations have been performed and a recently developed adhesion model15 was extended to include curved surfaces and angle-dependent molecule-substrata interactions. In addition, a geometric model of a bacterial surface was developed to illustrate the distribution of highly adhesive patches on a cell wall, which would lead to comparable SCFS mapping data. These results are important for the fabrication of new materials and the design of more precise models to describe bacterial adhesion.
1 Results and discussion
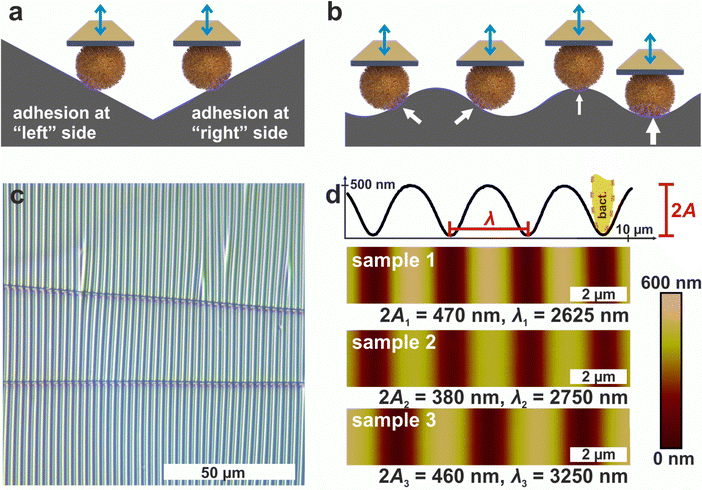
1.1 Periodically wrinkled PDMS surfaces as suitable substrates
Since AFM-based force-distance curves can only be recorded by a vertical movement of a bacterial probe, surfaces providing flanks with slopes of suitable absolute values in positive and negative direction are required to measure the adhesion at different positions of the cell surface by SCFS (see Fig. 1a). Moreover, a substrate with a continuous transition from positive to negative local slopes would allow to probe not only two points, but also intermediate positions (see Fig. 1b). These requirements can be met by wrinkled PDMS surfaces, which are shown in Fig. 1c and d.31,32The optical micrograph shows that the wrinkled PDMS substrate has quite a homogeneous wrinkle structure over a large area, which is only rarely disrupted by cracks in the material (see Fig. 1c). To characterize the surface topography in all dimensions, the wrinkled PDMS was analyzed via topographical AFM (see Fig. 1d). For our experiments, we used three different PDMS samples, which were produced with slightly varying parameters. Fig. 1d shows AFM images of all samples. In addition, a scan line recorded on sample 1 is depicted, in which the specific wrinkling parameters, wavelength λ and amplitude A, are defined. All samples have a very homogeneous surface structure: Locally and parallel to the trenches, the surface is very smooth with a root mean square roughness calculated parallel to the trenches (i.e. in y-direction in Fig. 1) below 5 nm. Perpendicular to the trenches, all surfaces feature a nearly sinusoidal periodicity that results in a vigorously homogeneous surface and a high symmetry within its repetitive structuring. The wavelengths and amplitudes of the periodic structures are such that the curvature of the S. aureus cells matches the one in the trenches of the wrinkled PDMS surfaces, as sketched in Fig. 1d. Therefore, the wrinkled PDMS surfaces are a well-suited substrate to determine the adhesion force of S. aureus cells at different locations on the cell wall by SCFS.
1.2 Periodic adhesion patterns of S. aureus on wrinkled PDMS – construction of adhesion profiles
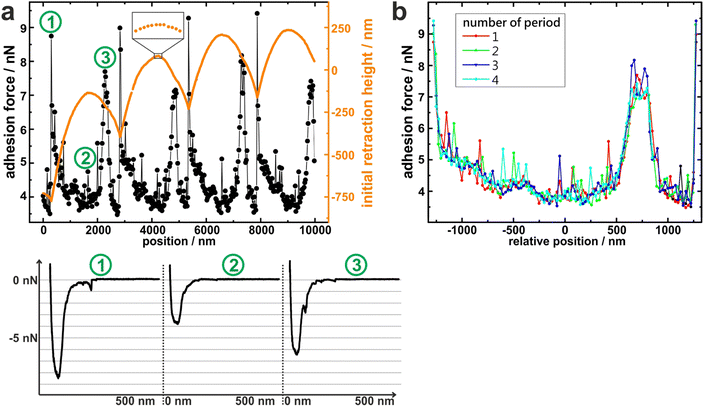
To measure the adhesion of S. aureus cells at different positions relative to the periods of the wrinkled PDMS surfaces, the substrates were mounted in a way that the trenches on the surfaces were parallel to the y-direction of the AFM scan area. Correct positioning was verified by scanning the surface before performing SCFS experiments. (An inclination of up to 1° was accepted, otherwise the sample was repositioned.)Then, several hundred force-distance curves were recorded with one and the same single cell while the x-position between each two consecutive curves was changed by a constant value (of 20–30 nm). From every curve, the adhesion force and the z-height at which the retraction began (termed “initial retraction height”) were determined, and the results are shown in Fig. 2a for one exemplary cell.
The graph of the initial retraction heights (orange data in Fig. 2a) has a distinct periodicity which reflects the surface topography. Notably, it does not have the same curve form as the AFM scans in Fig. 1d. The reason for this is that the AFM tip that scanned the surface had a tip radius of approximately 20 nm while the force-distance curves were recorded with an attached bacterial cell that features a much wider radius (approx. 500 nm). Hence, the cell – in contrast to the tip – cannot exactly follow the surface topography, especially not in the trenches of the surface (For an explanatory sketch, see Fig. S1 in the ESI†). In addition, the AFM has a certain vertical drift that causes a linear offset in the orange data in Fig. 2a. Nevertheless, the data reproduce the surface periodicity very well and can be used to extract the position of each force-distance curve in relation to the periodic structures of the substrate. All recorded force-distance curves (three of which are exemplary shown in Fig. 2a) have a similar parabola-like shape, suggesting that a rather high number of cell wall molecules is responsible for adhesion on every position of the wrinkled PDMS.15 Notably, the recorded adhesion forces show a periodicity with the same wavelength as the initial retraction heights: For example, the graph of the adhesion forces has local maxima at x = 200 nm, 2800 nm, 5200 nm, and 7800 nm, each of which nicely corresponds to a minimum in the initial retraction height data. Next, the recorded adhesion forces were subdivided relative to the periodicity and plotted accordingly, as shown in Fig. 2b. In this graph, the recorded adhesion forces inside each period show clearly the same dependence on the surfaces’ topography. This allows us to meaningful average over the results from different periods and construct mean adhesion curves in respect to the surface periodicity (see Fig. 3). These are called adhesion profiles hereinafter and allow us to characterize the adhesion in detail in the next paragraph.
1.3 Individual adhesion profiles of experimentally tested cells
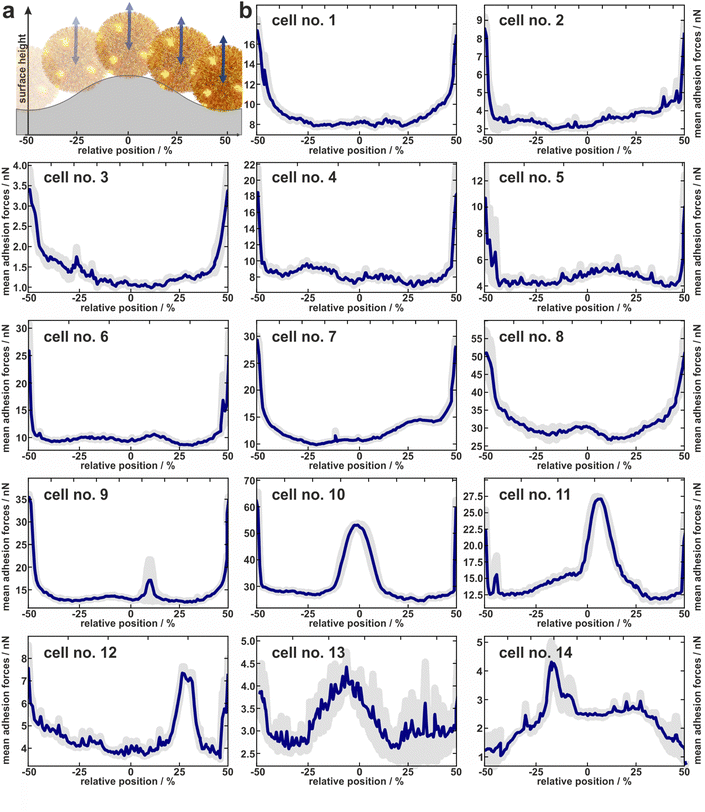
In total, the adhesion profiles for 14 individual S. aureus cells were construed as described in the previous paragraph. The beginning and end of the x-axes refer to the minima of the surface (“trenches”) while the middle corresponds to the local maxima (“hills”) as shown in Fig. 3a.Cells no. 1–12 show comparatively high adhesion forces at the minima of the surface. Between these maxima, the mean adhesion forces are up to a factor of three smaller but feature local maxima that are more or less pronounced depending on the individual cell.
For example, cell no. 1–8 show a bathtub-like adhesion profile with only small local maxima. These profiles are asymmetric around the surfaces’ hill (Fadh(x) ≠ Fadh(−x)), though the surface topography (reflected by the initial retraction heights of 2a) is highly symmetrical. In contrast, cells no. 9–14 feature very pronounced local maxima between the maxima of the curves. The adhesion forces determined on the shoulders or on the top of the wrinkled PDMS surface correspond to the adhesion forces on a flat PDMS sample.
Notably, the existence of local maxima or their relative size does not depend on the measured mean adhesion forces (i.e. the mean value of the measured adhesion forces on every position). In other words, cells with rather low overall adhesive strength can have distinct positions with relatively high adhesion (e.g. cell no. 13), while other cells with a rather strong overall adhesion do not show these positions (e.g. cell no. 6). The cells no. 13 and no. 14, for instance, even do not show the highest adhesion in the minima of the surface. Apparently, the adhesion strength of their highly adhesive positions on the cell wall surpasses the effect of increased contact area-enhanced stronger adhesion in the periods minima.
To summarize, the measured adhesion forces of the tested cells not only show often distinct local maxima in the surfaces’ minima, but sometimes enhanced adhesion capabilities outside these minima. Furthermore, even for adhesion profiles without additional peaks, i.e. outside the surfaces minima, the profiles are asymmetric within a period. Hence the adhesion capabilities are clearly heterogeneously distributed over the cell envelope. In order to interpret the profiles, it is important to note that we do not necessarily measure the same adhesion forces on the wrinkled surface as we would on a flat substrate: By moving along the surface, not only the location of the bacterial surface area that can contribute to the adhesion force changes, but also its size. Furthermore, since the cantilever with the bacterial cell moves only in a vertical direction, the direction of the cells movement relative to the local normal direction of the surface changes for different positions within one period. Since the mechanic properties of the involved macromolecules during elongation under different angles are unknown, it is not straightforward to correct the measured values for this geometric effect and thus directly determine the distribution of adhesins on the cell wall. Therefore, we attempted to disentangle the contributions of the varying bacterial surface area from the mechanical stretching by comparing the experimentally measured data with simulations, as described in the next section.
1.4 Disentangling the origin of the adhesion profiles
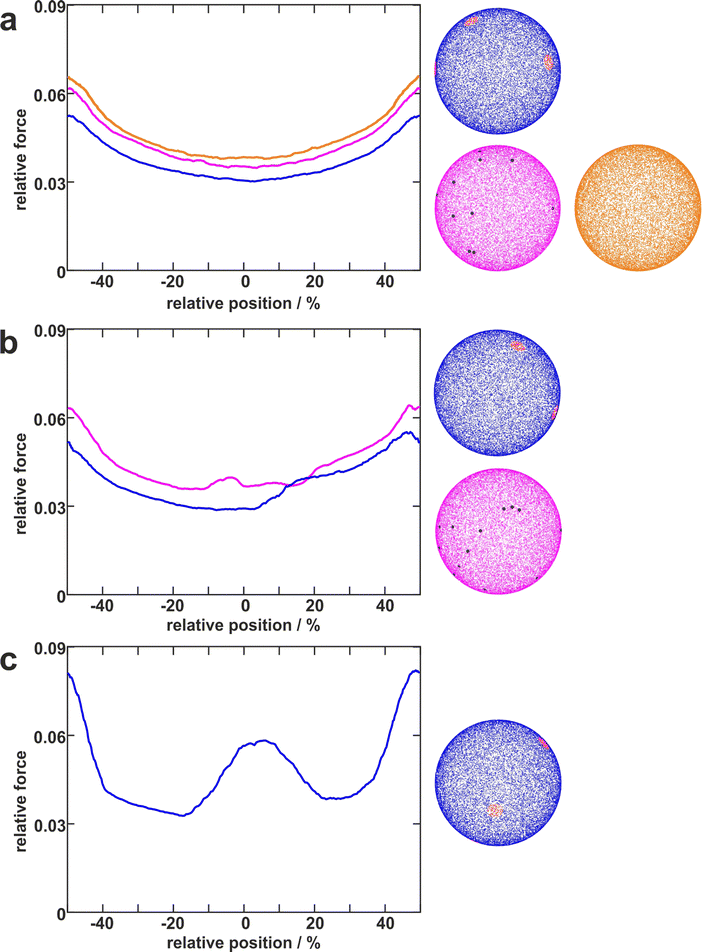
To disentangle the influence of a varying bacterial surface area from the influence of distinct mechanical stretching of macromolecules, we simulated the bacteria as hard spheres on which adhesive molecules are distributed. Since the adhesion process of S. aureus is governed by the collective response of individual macromolecules to stretching,15,16,34 whose mechanical properties, e.g. length, and stiffness, are heterogeneous and can lead to macroscopically nonlinear behavior in SCFS experiments,34 we used the model published by Maikranz et al.15 and extended it to curved surfaces (see ESI†). Most importantly we included the possibility for an angle-dependent molecule-substratum interaction, which are typically associated with complex protein mixtures. To estimate the bacterial surface area that can interact with the surface, we used a rather simple geometric model, where adhesive molecules are modelled as rods of fixed length that protrude outward the bacterial cell wall that is modelled as a hard sphere. After the cell is brought into tangential contact at position x above the surface, the relative adhesive strength is calculated from the molecules intersecting with the surface (each molecule might also have a different adhesiveness, for details, see Materials and methods section and ESI†). In essence, the geometric model describes, in the limit of many uniform distributed macromolecules, the fraction of the bacterial surface area that is able to contribute to the adhesion (see Fig. S2 for how this depends on the number of macromolecules, ESI†). Hence, the geometric model does not provide the correct force scale but relative values.As in the experiments all models showed the maximal obtained adhesion in the surfaces trench, which then decreased towards the surfaces’ maximum. Note, however, that for varying properties of the macromolecules the maximal adhesion force is not necessarily realized (see Fig. S6, ESI†). A comparison of the geometric model and the thermally fluctuating molecules in the absence of angle-dependent interactions show that although the geometric model produced smoother curves, the overall shapes and relative magnitudes of the profiles obtained from both models were the same (see Fig. 5). Thus, both models displayed rather parabola-like profiles instead of the experimentally observed bathtub. However, if we consider angle-dependent interactions, a bathtub-like adhesion profile was recovered. The influence of the angle-dependence is emphasised by rescaling into the adhesion force in the geometric model by the magnitude of the local surface normal (see Fig. 5). This leads to a smaller extend of the plateau in the adhesion profile. Hence the interaction of individual macromolecules with the local surface potential is expressed in the length of the plateau. However, none of the considered models reproduced the magnitude of the reduction in adhesion forces to about 50%.
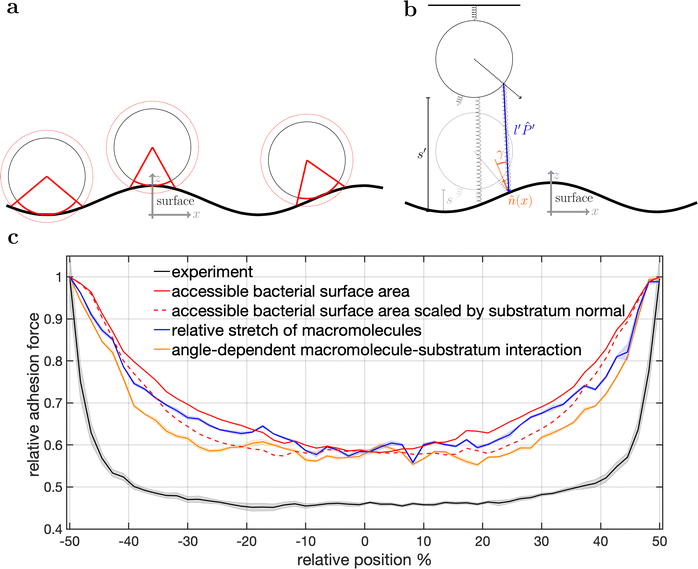 | ||
| Fig. 5 Model schematics and resulting mean adhesion profiles. (a) Illustration of the varying bacterial surface area that is able to interact with the surface when a certain interaction range indicated by the dashed line is assumed. (b) Illustration of the stretch tethered macromolecules experience when the bacterium is retracted and an illustration of the possible angle-dependent macromolecule-substratum interaction. (c) Resulting adhesion profiles normalized by the maximal adhesion force. For the simulation results we averaged over 5 repetitions of 5 distinct bacteria, while for the experimental mean adhesion profile we averaged cells 1–8 in Fig. 2b. Note that only angle-dependent macromolecule-substratum interaction reproduce a constant profile along large distances of the surface. | ||
To understand the reduced magnitude, we tracked in the model not only the total force experienced by the bacterium but also its spatial origin (see Fig. S8, ESI†). This analysis (for a discussion of the results see the ESI†) revealed that inside the surfaces minimum mostly molecules pointing perpendicular to the surfaces periodicity contribute to the adhesion force. While outside the surfaces minimum the molecules pointing along the trench contribute probably the most to the adhesion. A naive attempt to exploit this feature by introducing a cut-off angle for the molecule-substratum interaction lead for small cut-offs to a marginal extension of the adhesion plateau but not to a reduction in adhesion force (see Fig. S8, ESI†). In fact, larger cut-offs led only away from the surfaces maximum to a reduction in adhesion forces such that no bathtub-like profile was recovered. Hence, more complicated molecule-substratum interactions should be considered. However, since our model considers the bacterium as a rigid sphere, the influence of deformations and elliptical shape were not considered. While these effects, as well as neglected substratum deformations, are considered to be secondary factors, a true evaluation of the angle-dependence requires the repetition of SCFS experiments, whereby the bacteria are retracted at an angle to the surface. This, however, requires a specialised experimental set-up and is beyond the scope of this work.
2. Conclusions
We investigated the adhesion capability of S. aureus cells to a periodically structured surface by single-cell force spectroscopy to measure how the strength of adhesion depends on the position relative to a structured surface. We found that the adhesion of bacteria is not only cell-specific (as shown before (15, 17)), but also depends on the position on the cell envelope. Simulations reproducing the experimental results revealed the importance of angle-dependent interactions, and gave information about the distribution of the adhesion capability on the cell wall: Our data show a large reduction of adhesion forces outside of the surfaces minimum but also that S. aureus cells can have highly adhesive patches. Depending on the probed cell, these patches have different properties: While the experimental results for some cells suggest a rather high number (up to 30) of independent patches with diameters of about 50 nm, other cells must have fewer distinct patches (about 5–6 patches, some of which have a distance of at least 850 nm to neighbouring patches) with a larger diameter of about 250 nm.Hence, our results for coccal-shaped Gram-positive S. aureus cells nicely complement the patchy colloid model of adhesion for rod-shaped Gram-negative E. coli cells by Vissers et al.30 Their experiments show that E. coli cells have distinct patches on their surface and that the number of these patches defines adhesive strength of a cell; if no patches exist, a cell hardly adheres. However, our results – together with former studies – lead to a slightly different notion for S. aureus cells: Since the force-distance curves on all positions of the surface look similar, namely parabola-like, S. aureus cells seem to have many adhesive molecules at almost every position of the cell wall, but the strength of adhesion has maxima at certain locations.15
At these points, not necessarily the number of molecules is maximal, but rather their individual properties lead to maximum adhesive strength.17 Although we do not determine the origin of the adhesive patches, the angle-dependence of the interaction suggests molecules with complex 3d structures, like, proteins as the source. Furthermore, the simulated patchy spheres (see Fig. 4) are quite similar to the electron micrographs showing the distribution of protein A and Clumping factor A in the publication of Harris et al.21 Other candidates for the origin of the adhesive patches might be Cna and/or FnbpA, since both are multifunctional adhesins and cluster in nanometer-sized domains on the S. aureus cell wall.26,35 However, we cannot answer the question, whether the adhesive patches are “hot spots” where many adhesins occur together, whether there are several clusters, each containing only one type of adhesin, or whether the combination of different adhesive molecules with certain mechanical properties renders a given position at the cell wall highly adhesive.
Moreover, we cannot resolve if cells that do not show very distinct maxima in the adhesion profiles do not have any patches, or if – by chance – none of the patches come in contact to the surface. Along this line, it might be possible that only one half of the cell, for example the part that was newly synthesized during cell division, has patches of high adhesion capability.36,37 This is an exciting subject for further studies, in which adhesion measurements on structured surfaces could be combined with fluorescent labelling techniques.38 In that way, it will be possible to correlate the prevalence of certain proteins and/or former division planes with the adhesion capability of the investigated cells. Alternatively or in addition to this, extracellular vesicles formed and temporary retained on the S. aureus cell surface might contribute to this phenomenon.39,40
Our findings have consequences for science and material development: in future experiments and especially when designing models for simulations, the cells should not be regarded as rather uniform colloids, but as objects with heterogeneous surface properties. For instance, Duffadar and Davis showed that the adhesion behaviour of silica beads is affected by a patchy surface,41 suggesting that bacteria with patchy adhesion properties may also be able to orient themselves in the flow prior to adhesion. Finally, these differences in adhesive properties should be considered in the design of new antibacterial materials for the reduction of infections. In particular, the large reduction of adhesion forces outside the surfaces trenches, caused by an angle-dependent substratum interaction, could be exploited to reduce adhesion.
3 Material and methods
3.1 Production of the wrinkled surfaces
PDMS was prepared by mixing the pre-polymer and curing agent of a Dow Corning Sylgard 184 PDMS Kit in 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, curing it at RT for 24 h followed by a thermal treatment of 4 h at 80 °C under ambient conditions. Slabs of 4.5 cm × 1.0 cm were cut out, cleaned with Milli-Q water and dried with nitrogen. The slabs were clamped in a custom-made stretching-device and strained uniaxially to 5–10% of their initial length. Afterwards the slabs were placed in a low-pressure RF-plasma chamber and treated for 120–300 s with a H2-plasma at 800 W. Eventually the pre-strain is released, revealing opaque colored wrinkles on the PDMS topside.31
1 ratio, curing it at RT for 24 h followed by a thermal treatment of 4 h at 80 °C under ambient conditions. Slabs of 4.5 cm × 1.0 cm were cut out, cleaned with Milli-Q water and dried with nitrogen. The slabs were clamped in a custom-made stretching-device and strained uniaxially to 5–10% of their initial length. Afterwards the slabs were placed in a low-pressure RF-plasma chamber and treated for 120–300 s with a H2-plasma at 800 W. Eventually the pre-strain is released, revealing opaque colored wrinkles on the PDMS topside.31
3.2 Bacterial cultures
S. aureus cells, strain SA113, from a deep-frozen stock culture were plated on blood agar for one day and a fresh plate was used no longer than a week. The day before the experiments, one colony from the plate was transferred into 5 ml of tryptic soy broth (TSB) and cultured for 16 h at 37 °C under agitation (150 rpm). To get cells in exponential growth phase, at the day of the experiments, 40 μL of the overnight culture were transferred into 4 ml of fresh TSB and cultured for 2.5 h at 37 °C under agitation (150 rpm). From this final culture, 1 ml was washed three times with sterile phosphate buffered saline (PBS) at an acceleration of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g. The cells in PBS were stored at 4 °C and used no longer than 6 h.
000 g. The cells in PBS were stored at 4 °C and used no longer than 6 h.
3.3 Single-cell force spectroscopy
As described in the publication of Thewes et al., using a micromanipulator (Narishige Group, Tokyo, Japan), single bacterial cells were immobilized on tipless cantilevers (MLCT-0-F with nominal spring constants of 0.03 N m−1 from Bruker, Santa Barbara), which were beforehand coated with polydopamine.42 With these bacterial probes, single-cell force spectroscopy measurements were performed using a Bioscope Catalyst (Bruker) at room temperature in PBS (pH 7.3, ionic strength 0.1728 mol L−1). Force-distance curves were performed with a ramp size of 800 nm and a velocity of 800 nm s−1. The force trigger, i.e. the maximal force with which the cell is pressed onto the substrate prior to immediate retraction, was set to 300 pN. With every cell, some hundreds (between 400 and 500) of consecutive curves were recorded in a straight line with a constant lateral distance (of 20 nm, 25 nm, or 30 nm; called x-offset hereinafter) between consecutive curves on one of the three PDMS samples. Hence, force measurements on 4–5 equivalent positions in different periods were recorded. No systematic change in the adhesion behavior, such as a decreasing adhesive strength due to cell fatigue, could be observed even after 500 curves. The direction of this straight line was perpendicular to the trenches in the wrinkled PDMS samples with a deviation of less than 1°. For every probed cell, the parameters of the experiment (number of curves, x-offset, underlaying PDMS sample) are given in Table S1 in the ESI.†3.4 Analysis
From every recorded force-distance curve, a baseline was first subtracted, and the adhesion force was determined as the minimum force that occurred during retraction of the cantilever. In addition, the z-position of the instruments height sensor at the beginning of the retraction was recorded, and also corrected for a linear baseline shift caused by a drift of the AFM piezo. The adhesion forces and the positions where the retraction of the cantilever started were plotted against the corresponding x-offset and the periodicity was determined automatically as follows: The curves of the initial retraction heights were searched for peaks in negative direction (denoting the valleys of the surface). The positions of these peaks were used to divide the calculated adhesion forces into sections that correspond to the different periods of the surface. Since the wavelength of the periodicity can locally vary and since it does not necessarily fit a multiple of the x-offset, the data for each period were slightly shifted in x-direction, so that each period has the same size.3.5 Simulations
To obtain an estimate of the distribution of adhesive molecules on the bacterial cell wall, we used two types of models:We investigated homogeneous as well as patchy distributions of adhesive capabilities. A random, homogeneous distribution of rods on the cell surface was realized by placing rods with identical weight randomly on the sphere (independently and uniformly distributed). We either uniformly distribute 50.000 molecules and compare the results of the thermally fluctuating macromolecules with the geometric model. Or, to obtain complete spatial randomness, the number of rods follow a Poisson distribution.43 Adhesive patches have been produced by placing clusters of fixed radial extension (spherical caps) onto a homogeneous distribution. Inside these clusters the adhesive strength was increased by either placing additional rods inside the cluster or by giving all rods inside a cluster a larger adhesive weight. These clusters have been realized in two different ways: (i) Clusters via random position: A Poisson distributed number of spherical caps with constant radii (125 nm) were placed at random positions. Note that different clusters might overlap. (ii) Clusters via random sequential adsorption (RSA)44: In each adsorption step, a spherical cap with constant radius (125 nm) and a constant “radius of repulsion” (850 nm) was randomly positioned on the spheres surface. The position of the following spherical caps was only accepted if their “radii of repulsion” did not overlap with previously placed caps. The RSA process was stopped after 1000 runs, i.e. when with a high probability no additional spherical caps could be added.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the German Research Foundation (DFG) for funding within the context of the Collaborative Research Center SFB 1027 (projects B1 and B2). K. J. and C. S. acknowledge funding from the DFG the project JA 905/6. M. A. K. acknowledges funding by the Princeton University Innovation Fund for New Ideas in the Natural Sciences and support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the SPP 2265, under grant numbers ME 1361/16-1, WI 5527/1-1, and LO 418/25-1, as well as by the Volkswagenstiftung via the Experiment Project “Finite Projective Geometry.” A. F. and B. G. acknowledge funding from the DFG project number FE 600/20-1. K. J. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) priority program SPP 2265 under grant number JA 905/8-1 and DFG large instrument funding under grant number INST 256/542-1 FUGG (project number 449375068) as well as funding within the Max Planck School Matter to Life supported by the German Federal Ministry of Education and Research (BMBF) in collaboration with the Max Planck Society.References
- T. Bjarnsholt, APMIS, 2013, 121, 1–58 CrossRef PubMed.
- L. Hall-Stoodley, J. W. Costerton and P. Stoodley, Nat. Rev. Microbiol., 2004, 2, 95–108 CrossRef CAS PubMed.
- K. S. Park, C.-H. Huang, K. Lee, Y.-E. Yoo, C. M. Castro, R. Weissleder and H. Lee, Sci. Adv., 2016, 2, e1600300 CrossRef.
- C. M. Liu, L. B. Price, B. A. Hungate, A. G. Abraham, L. A. Larsen, K. Christensen, M. Stegger, R. Skov and P. S. Andersen, Sci. Adv., 2015, 1, e1400216 CrossRef PubMed.
- D. Berger, A. Rakhamimova, A. Pollack and Z. Loewy, High-Throughput, 2018, 7, 24 CAS.
- C. R. Arciola, D. Campoccia and L. Montanaro, Nat. Rev. Microbiol., 2018, 16, 397 CrossRef CAS.
- E. D. Austin, S. B. Sullivan, S. Whittier, F. D. Lowy and A.-C. Uhlemann, Open Forum Infect. Dis., 2016, ofw072 CrossRef.
- M. D. Feldman, A. J. Petersen, L. S. Karliner and J. A. Tice, Gen. Intern. Med. J., 2008, 23, 57–63 CrossRef.
- A. J. Tande and R. Patel, Clin. Microbiol. Rev., 2014, 27, 302–345 CrossRef.
- F. D. Lowy, N. Engl. J. Med., 1998, 339, 520–532 CrossRef CAS PubMed.
- M. K. Suresh, R. Biswas and L. Biswas, Int. J. Med. Microbiol., 2019, 309, 1–12 CrossRef CAS PubMed.
- N. Høiby, T. Bjarnsholt, M. Givskov, S. Molin and O. Ciofu, Int. J. Antimicrob. Agents, 2010, 35, 322–332 CrossRef PubMed.
- H.-C. Flemming and J. Wingender, Nat. Rev. Microbiol., 2010, 8, 623–633 CrossRef CAS.
- S. Y. Tong, J. S. Davis, E. Eichenberger, T. L. Holland and V. G. Fowler, Clin. Microbiol. Rev., 2015, 28, 603–661 CrossRef CAS PubMed.
- E. Maikranz, C. Spengler, N. Thewes, A. Thewes, F. Nolle, P. Jung, M. Bischoff, L. Santen and K. Jacobs, Nanoscale, 2020, 12, 19267–19275 RSC.
- N. Thewes, A. Thewes, P. Loskill, H. Peisker, M. Bischoff, M. Herrmann, L. Santen and K. Jacobs, Soft Matter, 2015, 11, 8913–8919 RSC.
- C. Spengler, N. Thewes, P. Jung, M. Bischoff and K. Jacobs, Nanoscale, 2017, 9, 10084–10093 RSC.
- C. Spengler, F. Nolle, J. Mischo, T. Faidt, S. Grandthyll, N. Thewes, M. Koch, F. Müller, M. Bischoff and M. A. Klatt, et al. , Nanoscale, 2019, 11, 19713–19722 RSC.
- O. Schneewind and D. M. Missiakas, Gram-positive Pathog., 2019, 592–598 CAS.
- A. C. DeDent, M. McAdow and O. Schneewind, J. Bacteriol., 2007, 189, 4473–4484 CrossRef CAS PubMed.
- L. G. Harris, S. Foster and R. G. Richards, et al. , Eur. Cell Mater., 2002, 4, 100 CrossRef.
- V. Prystopiuk, C. Feuillie, P. Herman-Bausier, F. Viela, D. Alsteens, G. Pietrocola, P. Speziale and Y. F. Dufrêne, ACS Nano, 2018, 12, 3609–3622 CrossRef CAS.
- P. Vitry, C. Valotteau, C. Feuillie, S. Bernard, D. Alsteens, J. A. Geoghegan and Y. F. Dufrêne, mBio, 2017, 8, e01748–17 CrossRef CAS.
- P. Herman-Bausier, C. Labate, A. M. Towell, S. Derclaye, J. A. Geoghegan and Y. F. Dufrêne, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5564–5569 CrossRef CAS PubMed.
- P. Herman-Bausier, S. El-Kirat-Chatel, T. J. Foster, J. A. Geoghegan and Y. F. Dufrêne, mBio, 2015, 6, e00413–15 CrossRef CAS PubMed.
- P. Herman-Bausier, C. Valotteau, G. Pietrocola, S. Rindi, D. Alsteens, T. J. Foster, P. Speziale and Y. F. Dufrêne, mBio, 2016, 7, e01529–16 CrossRef CAS.
- P. Herman, S. El-Kirat-Chatel, A. Beaussart, J. A. Geoghegan, T. J. Foster and Y. F. Dufrêne, Mol. Microbiol., 2014, 93, 356–368 CrossRef CAS PubMed.
- H. Khateb, R. S. Sørensen, K. Cramer, A. S. Eklund, J. Kjems, R. L. Meyer, R. Jungmann and D. S. Sutherland, ACS Nano, 2022, 16, 10392–10403 CrossRef CAS PubMed.
- J. Strasser, R. N. de Jong, F. J. Beurskens, J. Schuurman, P. W. Parren, P. Hinterdorfer and J. Preiner, ACS Nano, 2019, 14, 2739–2750 CrossRef PubMed.
- T. Vissers, A. T. Brown, N. Koumakis, A. Dawson, M. Hermes, J. Schwarz-Linek, A. B. Schofield, J. M. French, V. Koutsos and J. Arlt, et al. , Sci. Adv., 2018, 4, eaao1170 CrossRef PubMed.
- B. A. Glatz and A. Fery, Soft Matter, 2019, 15, 65–72 RSC.
- A. Schweikart and A. Fery, Microchim. Acta, 2009, 165, 249–263 CrossRef CAS.
- Y. Yu, C. Ng, T. A. Koönig and A. Fery, Langmuir, 2019, 35, 8629–8645 CrossRef CAS PubMed.
- S. Ostvar and B. D. Wood, Langmuir, 2016, 32, 5213–5222 CrossRef CAS PubMed.
- C. Valotteau, V. Prystopiuk, G. Pietrocola, S. Rindi, D. Peterle, V. De Filippis, T. J. Foster, P. Speziale and Y. F. Dufrêne, ACS Nano, 2017, 11, 2160–2170 CrossRef CAS PubMed.
- R. D. Turner, E. C. Ratcliffe, R. Wheeler, R. Golestanian, J. K. Hobbs and S. J. Foster, Nat. Commun., 2010, 1, 1–9 Search PubMed.
- R. Wheeler, S. Mesnage, I. G. Boneca, J. K. Hobbs and S. J. Foster, Mol. Microbiol., 2011, 82, 1096–1109 CrossRef CAS PubMed.
- B. M. Saraiva, M. Sorg, A. R. Pereira, M. J. Ferreira, L. C. Caulat, N. T. Reichmann and M. G. Pinho, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- E.-Y. Lee, D.-Y. Choi, D.-K. Kim, J.-W. Kim, J. O. Park, S. Kim, S.-H. Kim, D. M. Desiderio, Y.-K. Kim and K.-P. Kim, et al. , Proteomics, 2009, 9, 5425–5436 CrossRef CAS PubMed.
- H. Im, S. Lee, S. A. Soper and R. J. Mitchell, Mol. BioSyst., 2017, 13, 2704–2714 RSC.
- R. D. Duffadar and J. M. Davis, J. Colloid Interface Sci., 2008, 326, 18–27 CrossRef CAS PubMed.
- N. Thewes, P. Loskill, C. Spengler, S. Hümbert, M. Bischoff and K. Jacobs, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 140 CrossRef PubMed.
- G. Last and M. Penrose, Lectures on the Poisson process, Cambridge University Press, 2017, vol. 7 Search PubMed.
- S. N. Chiu, D. Stoyan, W. S. Kendall and J. Mecke, Stochastic geometry and its applications, John Wiley & Sons, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01045g |
| ‡ These authors contributed equally to this work. |
| § Institut für KI Sicherheit, Deutsches Zentrum für Luft- und Raumfahrt (DLR), Wilhelm-Runge-Straße 10, 89081 Ulm, Germany; Institut für Materialphysik im Weltraum, Deutsches Zentrum für Luft- und Raumfahrt (DLR), 51170 Köln, Germany; Department of Physics, Ludwig-Maximilians-Universität, Schellingstraße 4, 80799 Munich, Germany. |
| ¶ Max Planck School Matter to Life, 69120 Heidelberg, Germany. |
| || We acknowledge that at low densities it is difficult to meaningfully define heterogeneously distributed. |
| This journal is © The Royal Society of Chemistry 2024 |