Enhancing enantioselectivity in chiral metal organic framework fluorescent sensors

Abstract

The straightforward identification of enantiomers is of large importance to applications in the pharmaceutical, food and agricultural industries. We report the incorporation of two ligands containing the 1,1′-binaphthyl (BINOL) core with axial chirality and D-camphoric acid containing point chirality into Zn(II) metal–organic framework (MOF) chiral fluorescence sensors. The Zn(II) MOFs displayed outstanding enantioselectivity as chiral fluorescent sensors with an exceptional enantiomeric ratio (ER) of 3.92 which is amongst the highest values reported, along with excellent accuracy for the determination of enantiomeric excess in unknown samples. The role of complementary void shapes, a chiral co-ligand and hydrogen bonding interactions between the guest and sensors are explored.

---

Introduction

The detection of chirality in biological and chemical systems is of fundamental importance given its prevalence in nature.¹ The determination of chirality and enantiopurity in molecules is particularly important for the pharmaceutical, agricultural and food industries due to the possible adverse effects of the wrong enantiomer upon biological systems. The ratios and/or presence of specific enantiomers are additionally useful for the detection of diseases including cancer, renal disorders, and brain injuries.² The detection of chirality is difficult due to the very similar physical properties of a pair of enantiomers which only differ in their 3D orientation in space; an enantiomer can only be detected in the presence of other chiral systems or in the presence of plane-polarised light.

Techniques involving column chromatography, in particular HPLC with a chiral stationary phase, have dominated the detection of chiral molecules.³ HPLC however has several drawbacks including the cost and the need for specialised instrumentation requiring careful optimisation with different chiral analytes. A faster, more accessible, and simpler method for differentiating between a pair of enantiomers is the use of optical techniques including fluorescence which provide faster data acquisition, require simpler instrumentation and are more user friendly.^4–6

Supramolecular systems including metal–organic frameworks (MOFs) and coordination polymers (CPs) are particularly amenable as fluorescent chiral sensors due to their tuneable nature and potential chiral voids.^5,7 The chiral voids may be engineered to ensure shape complementarity with non-covalent interactions to ensure strong binding of the target chiral analyte to the sensor.⁸ The voids may facilitate preconcentration of the chiral analyte, enabling detection at very low analyte concentrations.⁹ Despite the large potential for the development of MOFs as fluorescent chiral sensors, only a handful of studies have been reported.^5,9–18 A challenge facing MOF-based fluorescent chiral sensors is engendering a high degree of enantioselectivity in interactions with enantiomeric pairs.

One of the most versatile systems that have emerged for application as chiral fluorescent sensors is 1,1′-binaphthyl (BINOL) which contains axial chirality due to hindered rotation of its naphthyl rings about the aryl–aryl bond.^19,20 The aromatic naphthyl rings bestow fluorescent properties that can be tuned by variation of the substituents on the BINOL core.²⁰ To the best of our knowledge, only two examples of BINOL CPs and MOFs as fluorescent chiral sensors exist.^9,12 The first report on [Cd₂(tbtb)(H₂O)₂]·6.5DMF·3EtOH [tbtb-H₄ = (R)-2,2′-dihydroxy-1,1′-binaphthyl-4,4′,6,6′-tetrakis(4-benzoic acid); DMF = N,N′-dimethylformamide] was effective as an enantioselective fluorescence sensor for amino alcohols, with a high enantiomeric ratio (ER) of 3.12 obtained for 2-amino-3-methyl-1-butanol.⁹

The second example was a Zn(II) MOF previously reported from our group, [Zn₃((S)-L₁)(tma)₂(DMF)₃]·2DMF ((S)-L₁ = (S)-4,4′-dipyridyl-2,2′-diethoxy-1,1′-binaphthalene, H₃tma = trimesic acid) as a fluorescent chiroptical sensor effective towards a range of carboxylic acids, amino alcohols, amines and amino acids, with particular enantioselectivity towards Mosher's acid with an ER of 2.23.¹² The Zn(II) MOF was successfully used to determine the enantiomeric excess (ee) of unknown solutions – albeit with a large error at higher ee's. We rationalised that changing the achiral trimesic acid co-ligand for a chiral co-ligand such as D-camphoric acid (which contains point chirality) may induce higher enantioselectivity in our Zn(II) MOF fluorescence sensor due to the additional source of chirality.

Herein, we present the synthesis of two isostructural BINOL-containing Zn(II) MOFs, [Zn((S)-L₁)(D-cam)₂]·4.9DMF·2.8H₂O (1-OEt) ((S)-L₁ = (S)-4,4′-(2,2′-diethoxy-[1,1′-binaphthalene]-4,4′-diyl)dipyridine) and [Zn((S)-L₂)(D-cam)₂] (1-OH) ((S)-L₂ = (S)-4,4′-(2,2′-dialcohol-[1,1′-binaphthalene]-4,4′-diyl)dipyridine), and assess their ability as chiroptical fluorescent sensors towards Mosher's acid. Both 1-OH and 1-OEt exhibit outstanding ERs which are among the highest values currently known for MOF-based chiral fluorescent sensors. The role of hydrogen bonding, the additional point chirality of the D-camphoric co-ligand and the hourglass shape of the void will be discussed in terms of their impact upon the enantioselectivity of the MOF. The ability of 1-OH to determine the ee of unknown solutions was quantified through the construction of a calibration curve.

Results and discussion

Synthesis and structure

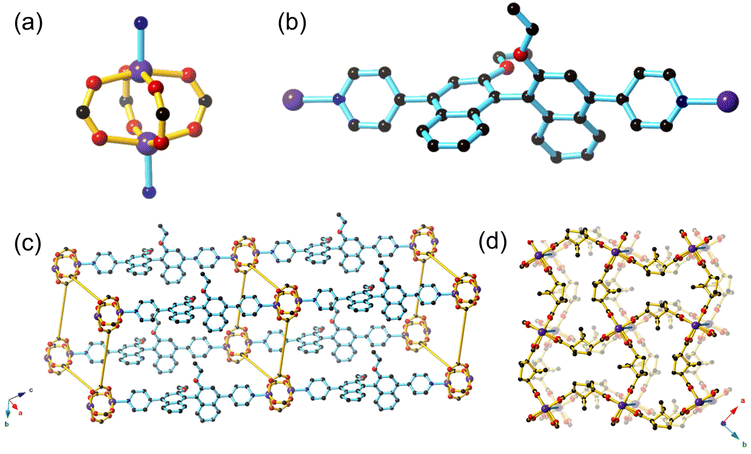
[Zn((S)-L₁)(D-cam)₂]·4.9DMF·2.8H₂O (1-OEt) ((S)-L₁ = (S)-4,4′-(2,2′-diethoxy-[1,1′-binaphthalene]-4,4′-diyl)dipyridine, D-cam = D-camphoric acid) and [Zn((S)-L₂)(D-cam)₂] (1-OH) ((S)-L₂ = (S)-4,4′-(2,2′-dialcohol-[1,1′-binaphthalene]-4,4′-diyl)dipyridine) were synthesised by heating (S)-L₁ or (S)-L₂ with D-camphoric acid in DMF at 80 °C overnight to yield the isostructural frameworks of 1-OEt and 1-OH, respectively as pale yellow crystals.

1-OEt contains a zinc paddlewheel node where two Zn(II) ions are each linked by four dicarboxylate ligands in a monodentate manner (Fig. 1a). The Zn(II) ion features a square pyramidal coordination sphere containing four equatorial O-donors from four distinct dicarboxylate ligands and one axial N-donor from (S)-L₁. Typical bond distances of 2.012(4)–2.034(4) Å for Zn(II)–N and 2.012(2)–2.097(2) Å for Zn(II)–O are observed. The axial chirality in (S)-L₁ is clearly shown through the orthogonal orientation of the two naphthyl rings in the ligand (Fig. 1b). The chiral (S)-L₁ ligand is coordinated through the axial position of the Zn(II) paddlewheel enabling the square grid 2D sheet containing Zn(II) paddlewheels and dicarboxylate ligands to be extended into three dimensions, forming a framework with pcu topology (Fig. 1c). The neighbouring 2D sheets are separated by approximately ∼19 Å; a distance that approximately corresponds to the length of the (S)-L₁ ligand (free ligand length is 15.772 Å) coordinated to the Zn(II) centres. 1-OEt does not exhibit any structural interpenetration due to the hourglass shape of the channels formed by the D-cam co-ligands where the distance at the central waist of the hourglass channels (2.127 Å) is too short to allow the (S)-L₁ ligand to pass through (Fig. 1d).

Fig. 1 Structure of the Zn(II) paddlewheel framework 1-OEt in this study, depicting (a) the Zn(II) paddlewheel node, (b) structure of (S)-L₁ showing the axial chirality of the BINOL moiety, (c) the pcu 3D structure where the D-cam co-ligands are shown as yellow rods and (d) the hourglass shaped pores formed by the Zn(II) paddlewheels and D-cam co-ligands, as viewed from the c axis. Atom depictions are as follows: carbon = black, oxygen = red, nitrogen = blue, zinc = purple. Hydrogens have been omitted for clarity.

Strong intermolecular interactions must be engendered to ensure effective association between the BINOL core of the ligand and potential chemical analytes in sensing. The 1-OH framework contains the (S)-L₂ ligand featuring unprotected hydroxyl groups that should enable hydrogen bonding interactions between the framework and chiral guests. Despite our best efforts, a satisfactory single crystal structure solution was unable to be resolved due to the poor diffraction quality of the crystals. However, the powder XRD of 1-OH indicates that it is isostructural to 1-OEt (ESI, Fig. S3†). The (S)-L₂ ligand therefore links the 2D sheets containing zinc paddlewheel nodes and D-cam together through coordination in the axial position in an analogous manner to (S)-L₁ in 1-OEt. Most importantly, the hydroxy binding sites from (S)-L₂ will be pointing into the pores of 1-OH, analogous to the ethoxy groups from (S)-L₁ in 1-OEt, which will allow interaction of guest molecules with the 1,1′-binapthyl moiety. The FT-IR spectrum of 1-OH is similar to 1-OEt, with the notable difference of a broad absorption at 3332 cm⁻¹, indicative of the ν_OH stretch (ESI, Fig. S5 and 6†).

The lack of interpenetration in 1-OEt enables an overall accessible void space of 43.8%. The thermal gravimetric analysis (TGA) of 1-OEt and 1-OH are similar, displaying a moderate mass loss below 140 °C (1-OEt: 14%, 1-OH: 22%) corresponding to the liberation of DMF and water molecules present in the framework voids before decomposition occurs above 350 °C (ESI, Fig. S7–9†). The larger mass loss for 1-OH may be attributed to the lower steric bulk of the hydroxy group in 1-OH when compared to the ethoxy group in 1-OEt resulting in a larger accessible volume.

Photophysical properties

The photophysical properties of 1-OH and 1-OEt were characterised by UV/vis absorption spectroscopy and fluorescence spectrophotometry to evaluate their suitability for fluorescence-based sensing experiments. Crystals of both compounds were soaked in acetonitrile overnight, then filtered, washed, and manually crushed before being suspended in acetonitrile to prepare stock suspensions with the frameworks at effective concentrations of 10 μM. These framework suspensions absorb strongly in the UV region: 1-OH displays three absorption maxima at 229 nm, 302 nm, and 344 nm (ESI, Fig. S10†), while 1-OEt absorbs at 233 nm, 305 nm, and 349 nm (ESI, Fig. S11†). The three-band absorption profile common to both frameworks matches those of similar BINOL-based structures,^12,21 and is assigned to organic π–π* transitions. The isostructural frameworks of 1-OH (ESI, Fig. S12–14†) when excited at 229 nm, 302 nm, and 344 nm and 1-OEt (ESI, Fig. S15–17†) when excited at 229 nm, 305 nm and 349 nm feature similar emission spectra. 1-OH emits at 415 nm, with a second, weaker emission band at 780 nm while 1-OEt emits at 428 nm and 800 nm. The emission of both 1-OH and 1-OEt correspond to the strong emissions of BINOL-based systems in the range of 350–450 nm.^12,20

Fluorescence quenching experiments

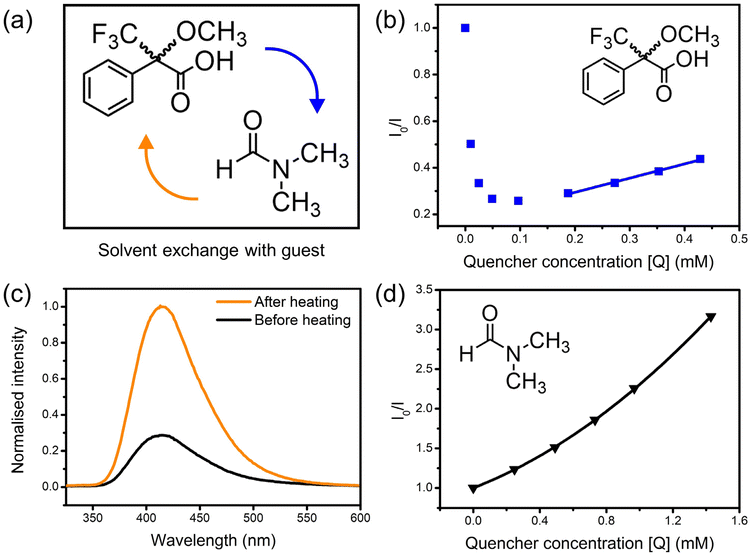
Mosher's acid was chosen as a chiral analyte to test the sensing ability of 1-OH and 1-OEt towards chiral guest species via fluorescence quenching studies (Fig. 2a). Mosher's acid is commonly used as a chiral derivatising agent for the NMR elucidation of chiral species.^22,23 This analyte is ideal for enantioselective sensing studies,¹² as the compound possesses multiple binding sites capable of non-covalent interactions with a host framework, such as carboxylic acid and trifluoromethyl functionalities suitable for hydrogenbonding and a phenyl ring for π–π stacking. The CF₃ moiety adds considerable steric bulk about the compound's chiral centre, which can be exploited to enforce greater enantioselectivity within the confines of a porous material.

Fig. 2 (a) Exchange of residual N,N-dimethylformamide (DMF) solvent with chiral guest Mosher's acid; (b) Stern–Volmer plot showing the fluorescence enhancement, then quenching, by (R)-Mosher's acid of 1-OH without heating to remove residual DMF (linear fit shown for 0.2–0.5 mM); (c) fluorescence spectra of 1-OH as a suspension in acetonitrile before and after heating at 60 °C for 1 hour; (d) Stern–Volmer plot of the fluorescence quenching of 1-OH by DMF. In all cases, λ_ex = 229 nm.

Solutions of the (R)-enantiomer of Mosher's acid were added to suspensions of 1-OH to probe the framework's fluorescence response. The resulting changes in fluorescence intensity of the 415 nm emission peak were measured via fluorescence spectrophotometry. Unexpectedly, the emission of 1-OH was enhanced upon addition of the analyte (Fig. 2b). The fluorescence intensity continued increasing until the analyte reached a critical concentration of 0.1–0.2 mM, after which the intensity decreased again, then followed linear Stern–Volmer quenching behaviour up to 0.6 mM. The Mosher's acid guest was likely exchanging with the small amount of residual DMF solvent molecules inside the framework which was quenching the fluorescence of 1-OH. The emission intensity of 1-OH decreased once the concentration of Mosher's acid was high enough to have exchanged out most DMF solvent molecules.

The crystals of 1-OH were heated at 60 °C to verify the role of DMF in quenching the fluorescence of 1-OH prior to suspension in acetonitrile. Heating of 1-OH successfully removed residual DMF solvent molecules as observed through FT-IR spectroscopy (ESI, Fig. S18†) and fluorescence spectrophotometry (Fig. 2c). DMF was reintroduced to the suspension after heating of 1-OH resulting in fluorescence quenching, confirming the role of DMF in the fluorescence behaviour of the system (Fig. 2d). The upward trend in the Stern–Volmer plot is suggestive of combined static and dynamic quenching mechanisms.

Enantioselective sensing studies

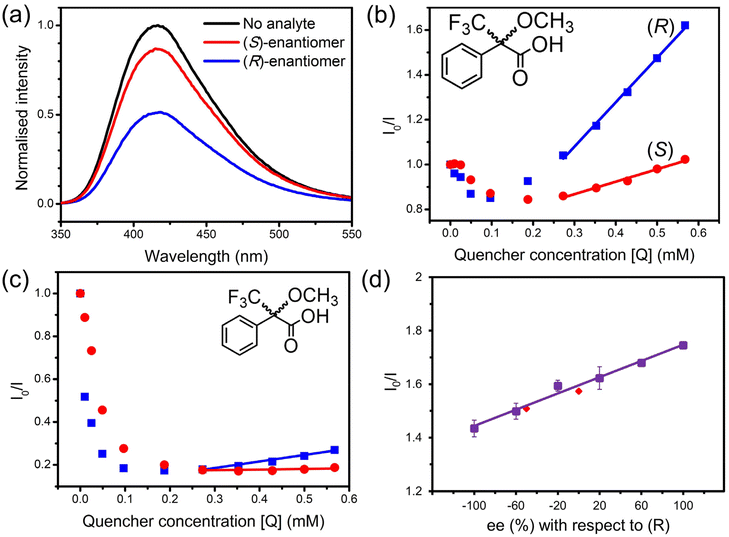
Both enantiomers of Mosher's acid were used in fluorescence quenching experiments to assess the enantiomeric recognition ability of 1-OH and 1-OEt. Enantiopure solutions of either (R)-Mosher's acid or (S)-Mosher's acid were added incrementally to suspensions of 1-OH and 1-OEt following heating of the framework to eliminate as much residual DMF as possible.

A marked difference was observed in the quenching response of 1-OH towards the enantiomers of Mosher's acid, where the response was over four times stronger for (R)-Mosher's acid than that of (S)-Mosher's acid at the same concentration (Fig. 3a). A higher population of (R)-Mosher's acid may be present within the channels of 1-OH, due to complementarity between the orientation of the analyte and the stereospecific pore environments of the MOF resulting in the differences in fluorescence quenching.

Fig. 3 (a) Fluorescence spectra of 1-OH (λ_ex = 229 nm) before and after the addition of the enantiomers of Mosher's acid at quencher concentration of 0.57 mM; Stern–Volmer plots following the quenching of (b) 1-OH (λ_ex = 229 nm) and (c) 1-OEt (λ_ex = 233 nm) by the enantiomers of Mosher's acid; (d) calibration plot for the quenching of 1-OH by racemic mixtures of Mosher's acid at different enantiomeric excess values with respect to the (R)-enantiomer (λ_ex = 229 nm). (S)-Mosher's acid is represented by red lines, and (R)-Mosher's acid by blue lines in all figures.

The quenching behaviour of (R) and (S)-Mosher's acid on 1-OH was approximately linear in the analyte concentration range of 0.2–0.6 mM (Fig. 3b). The linearity of the quenching response allowed each quenching response to be mapped to the linear Stern–Volmer equation: I₀/I = K_SV[Q] + 1 (where I₀ is the initial fluorescence intensity of 1-OH; I is the intensity after addition of the quencher; K_SV is the Stern–Volmer constant; and [Q] is the concentration of the quencher).²⁴ The gradient of the linear fit for each enantiomer could be approximated as the Stern–Volmer constant, K_SV, relating to the quenching strength of the analyte. The average K_SV constant for (R)-Mosher's acid was 1.21 × 10³ M⁻¹, while (S)-Mosher's acid was 0.32 × 10³ M⁻¹. The enantioselectivity ratio (ER) can then be calculated using the two K_SV constants, representing the enantioselectivity of the quenching process. The average ER value for the quenching of 1-OH by Mosher's acid was calculated to be 3.92 ± 0.38. To our knowledge, this is the highest of such values reported in the literature to date for MOF-based fluorescent sensing systems (Table 1).

Table 1 A list of selected CPs and MOFs with enantioselective fluorescence-based sensing functions with the enantioselectivity ratio (ER) values for given chiral analytes

Framework^a	Chiral analyte(s)	ER	Ref.
a See cited references for detailed framework and ligand structures.
[Zn2(S-L2)(D-cam)2]·0.5DMF·10H2O (1-OH)	Mosher's acid	3.92	This work
[Zn2(S-L1)(D-cam)2]·4.9DMF·2.8H2O (1-OEt)	Mosher's acid	3.72	This work
[Cd(L)(4,4′-bpy)]·DMA·5H2O	Penicillamine	3.60	10
[Zn4(L)2(μ4-H2O)(TBSC)]·3DMF·MeOH·6H2O	Alaninol	3.27	11
MIL-53-C1	Quinine/quinidine	3.26	17
	Hydroquinidine/hydroquinine	1.57	17
	Cinchonine/cinchonidine	1.16	17
[Cd2(L)(H2O)2]·6.5DMF·3EtOH	2-Amino-3-methyl-1-butanol	3.12	9
MIL-53-C2	Quinine/quinidine	2.51	17
	Hydroquinidine/hydroquinine	1.84	17
	Cinchonine/cinchonidine	1.93	17
[Zn3(S-L1)(tma)2(DMF)3]·2DMF	Mosher's acid	2.23	12
[Cu2(D-cam)2(4,4′-bpy)]	α-Ethylbenzylamine	2.02	11
UiO-66-C	Quinine/quinidine	2.01	17
	Hydroquinidine/hydroquinine	1.69	17
	Cinchonine/cinchonidine	1.21	17
[Zr6O4(OH)5(BTC)2(HCOO)5(H2O)]	Tryptophan	1.53	13
[(CH3)2NH2]1/2[Zn2(adenine)(TATAB)O1/4]·6.5DMF·4H2O	Cinchonine/cinchonidine	1.40	14
MIL-125-NH2-C	Quinine/quinidine	1.36	17
	Hydroquinidine/hydroquinine	1.18	17
	Cinchonine/cinchonidine	1.13	17
[(CH3)2NH2][Cd(bpdc)3/2]·2DMA	Quinine/quinidine	1.20	15

---

A suspension of 1-OEt in acetonitrile was also treated with solutions of Mosher's acid to assess the role of hydrogenbonding upon fluorescence quenching (Fig. 3c). The presence of the ethoxy group in 1-OEt precludes hydrogen bonding from occurring between the BINOL moiety and the Mosher's acid guest. A direct comparison of the impact of hydrogen bonding can be made between 1-OEt and 1-OH as these frameworks are isostructural. 1-OEt showed similar quenching behaviour to 1-OH, including the initial enhancement by Mosher's acid up to 0.20–0.35 mM and subsequent quenching. This was unexpected as 1-OEt is unable to form hydrogenbonds with residual DMF solvent molecules. The similar behaviour of 1-OEt to 1-OH suggests fluorescence quenching primarily occurs due to the complementary shape and size of the pore environment towards DMF rather than hydrogen-bonding ability. 1-OEt did, however, display weaker enhancement upon the addition of Mosher's acid than 1-OH, suggesting hydrogen bonding does have a minor impact on the interaction of the chiral analyte with the framework.

As with 1-OH, the quenching responses for 1-OEt and the enantiomers of Mosher's acid were mapped to the linear Stern–Volmer equation in applicable concentration ranges (0.4–0.6 mM) (Fig. 3c). For 1-OEt, the K_SV constants of (R)-Mosher's acid and (S)-Mosher's acid were 0.39 × 10³ M⁻¹ and 0.11 × 10³ M⁻¹, respectively. The ER value for the quenching of 1-OEt by Mosher's acid is calculated to be 3.72 – a lower value than that of 1-OH, but still an impressive result as an enantioselective chiral MOF-based sensor, with 1-OEt only second to 1-OH.

While 1-OH does boast higher enantioselectivity than 1-OEt, the enhancement of the ER value attributed to the increased hydrogen-bonding ability of (S)-L₂ is slight. This suggests that the strength of the hydrogenbonds formed with an analyte needs to be considered together with the shape and size complementarity between the pore environment and the chiral guest. The total network accessible surface area was calculated to be 957.48 mŲ/cmų using a nitrogen probe radius of 3.314 Å with the “Pore analysis” function in Mercury (ESI, Table S3†). The pore limiting diameter was determined to be 4.15 Å and the maximum pore diameter to be 7.25 Å. Mosher's acid is approximately 6.1 Å along its longest axis, and ∼3.0 Å along the short axis, which are highly complementary in size to the calculated pore dimensions, enabling a perfect fit between host and guest and thus resulting in heightened stereospecificity in sensing.

The framework 1-OH was investigated as a quantitative chiral sensor due to its higher ER value. The ability of 1-OH to determine the ee from an unknown mixture was evaluated by initially constructing a calibration curve from −100% ee to +100% ee (Fig. 3d). The calibration curve was constructed using six different (R) and (S) ratios, and each measurement repeated three times. Two randomly selected racemic ratios were tested to validate the calibration; the fluorescence responses of ee at −50% and 0% with respect to the (R)-enantiomer were obtained from the calibration curve with values of −51.5% and −1.6%, respectively. The excellent similarity of the ee values determined from the calibration curve demonstrate the ability of 1-OH to discriminate between the enantiomers of Mosher's acid. Of particular note is the higher accuracy achieved by 1-OH for the determination of the ee value for an unknown mixture when compared to the previously reported Zn(II) BINOL MOF, [Zn₃(S-L₁)(tma)₂(DMF)₃]·2DMF¹² which shows more than a 20% deviation. The increased accuracy of 1-OH may be attributed to the greater enantioselectivity of the framework where the higher ER value enables a larger gradient in the calibration curve and thus greater accuracy.

Time-resolved fluorescence measurements

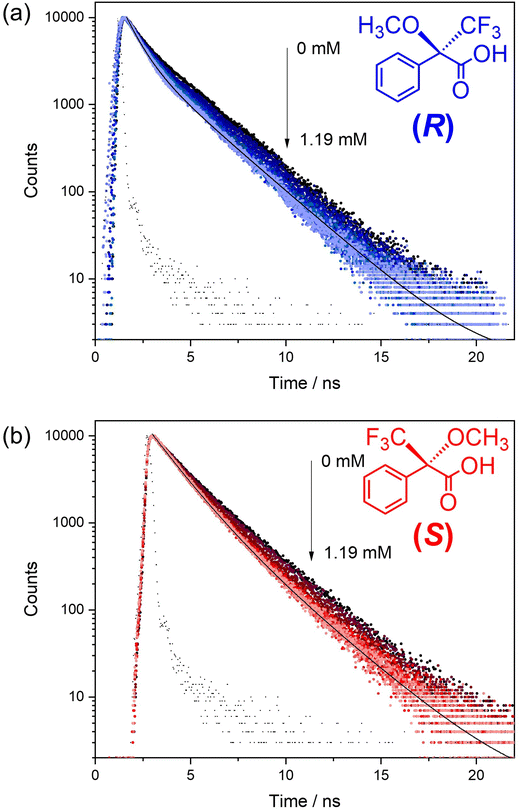
Time-resolved fluorescence experiments were conducted to study the quenching mechanism of 1-OH in more detail (Fig. 4 and ESI, Tables S4, 5†). The capacity of both (R) and (S)-Mosher's Acid to quench the fluorescence of the BINOL fluorophore in framework 1-OH was determined by comparing the fluorescence decay time of the fluorophore alone to the fluorophore in the presence of increasing concentrations of (R) and (S)-Mosher's acid (Fig. 5). In both cases, the fluorescence decay timescale of the fluorophore slightly decreases as the concentration of the enantiomer increases. However, double exponential global analyses of the decay curves (ESI, Tables S4 and 5†) reveal that for both (R) and (S)-Mosher's Acid, any decrease in the average emission decay time is due to a change in the weighting (α) of the two separate lifetimes associated with the fluorophore rather than a decrease in the actual lifetimes (τ). This indicates that the quenching of the BINOL fluorophore by Mosher's Acid is not dynamic, but rather a static process.²⁵ The differences in the strength of interaction between the enantiomers of Mosher's acid and frameworks 1-OH and 1-OEt may therefore be due to the formation of a weaker emissive host–guest complex for the (S)-enantiomer.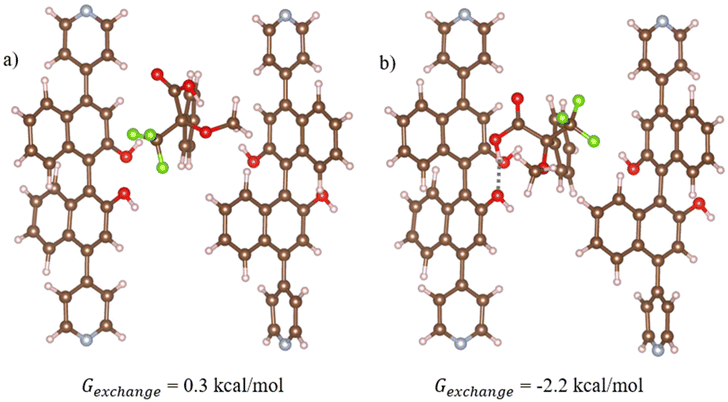

Fig. 4 Fluorescence decay curves for the BINOL fluorophore in acetonitrile alone (10 mM) and in the presence of an increasing concentration of (a) (R)-Mosher's Acid or (b) (S)-Mosher's Acid. The fluorescence was recorded using l_ex = 300 nm and λ_em = 416 nm. The solid black line is the fit and the black data points the instrument response function (IRF).

Fig. 5 Optimised geometries of the most stable structures for (a) (R)- and (b) (S)-Moshers acid interacting with 1-OH. In this structure, 1-OH is represented using cluster model 1 which is vertically aligned with the z axis relative to the periodic structure (refer to Fig. S1a†). Hydrogen bonds are shown in dotted grey, where atom depictions are as follows: carbon = grey, hydrogen = white, oxygen = red, nitrogen = teal, fluorine = green.

Previous studies of the fluorescence decays of MOF chiral sensors in the presence of analytes have elucidated a static quenching process for L- and D-penicilliamine,¹⁰ dynamic quenching for L- and D-tryptophan¹³ and multiple quenching (both dynamic and static) for quinine and quinidine.¹⁵ The mechanism of fluorescence quenching therefore appears to be highly variable and dependent upon the chiral MOF sensor and the analytes used.

Computational studies – host–guest interactions and the position of guests in voids

Density Functional Theory (DFT) simulations with cluster models were used to study the interactions between Mosher's acid and 1-OH. Details of the calculations including the development of the cluster models are provided in Computational approach. Across our tests of Mosher's acid with the four cluster models used to simulate 1-OH, the most stable structures for both (R) and (S) isomers of Mosher's acid are found for cluster model 1 (Fig. 5). In this cluster, the OH in the BINOL groups of (S)-L₁ are in closest proximity to the void space that Mosher's acid occupies in our simulations. As a result, these alcohol groups provide potential hydrogen bonding sites between 1-OH and Mosher's acid. In addition, π–π stacking interactions between the aromatic BINOL groups and Mosher's acid are also possible. (S)-Mosher's acid has a more favourable exchange reaction free energy with the acetonitrile solvent (Fig. 5b, G_exchange = −2.2 kcal mol⁻¹) than (R)-Mosher's acid (Fig. 5a, G_exchange = 0.3 kcal mol⁻¹). This difference can be attributed to the formation of hydrogen bonds between the carboxylic group of (S)-Mosher's acid and the OH group of the BINOL ligand (hydrogen bond length = 1.8 Å, Fig. 5b). (R)-Mosher's acid does not form these hydrogen bonds. Interestingly, neither isomer shows π–π stacking interactions in its most stable structure. As discussed in the ESI,† we trialled initial configurations that favoured π–π stacking; in the case of (R)-Mosher's acid all structures optimised to give geometries with no such interactions; for (S)-Mosher's acid we found optimised structures with π–π stacking but these were not as stable as the structure in Fig. 5b which has a hydrogen bonding interaction. Overall, our results show that (S)-Mosher's acid forms a stronger interaction with 1-OH when compared to (R)-Mosher's acid. This is in contrast with experimental results showing that (R)-Mosher's acid exhibits greater quenching behaviour. This leads to the conclusion that the quenching behaviour of the 1-OH is driven more by the chirality and complementary fit of the pore channels for the enantiomers of Mosher's acid than the strength of the interactions between Mosher's acid and 1-OH.

Discussion

Two major factors are believed to contribute to the high enantioselectivity of 1-OH; the confined hourglass void environment and hydrogen bonding in the framework. The observations from experimental results and computational calculations indicate that the enantioselectivity of 1-OH and 1-OEt is predominantly driven by the complementary and confined void environments within the framework structure. While hydrogen bonding does play a role in enhancing the enantioselectivity of 1-OH, the increase is slight when compared to 1-OEt. The enantioselectivity in 1-OH and 1-OEt arises due to the complementary void size and chemistry with the Mosher's acid guest, which contrasts with previous MOF chiral sensors whose function was predominately attributed to non-covalent interactions between the MOF and the chiral analyte. These non-covalent interactions included hydrogen bonding and π–π stacking for the sensing of enantiomers of quinine and quinidine,¹⁵ cinchonine and cinchonidine,¹⁴L- and D-penicillamine¹⁰ and L- and D-tryptophan.¹³

The two sources of chirality inside the voids of 1-OH and 1-OEt – axial chirality from the BINOL-based (S)-L₁ or (S)-L₂ ligands and point chirality from the D-cam co-ligands – together generate inner-framework channels with enhanced stereospecificity. The chiral centres in the D-cam co-ligand do not possess functional groups likely to form hydrogenbonds or undergo other non-covalent interactions with a chiral analyte. As a result, D-cam is unlikely to compete with (S)-L₁ or (S)-L₂ for guest binding and would only complement the enantioselectivity of these interactions.

The role of the additional source of point chirality from the D-cam co-ligands in enhancing the enantioselectivity of the system was explored by conducting Stern–Volmer fluorescence quenching experiments with 1-OH containing a racemic L₂ (rac-L₂) (ESI, Fig. S20 and 21†). [Zn₂(rac-L₂)(D-cam)₂]·0.5DMF·10H₂O (rac-1-OH) was treated with (R)- or (S)-Mosher's acid to reveal that even in the absence of enantiopure BINOL, rac-1-OH exhibited enantioselectivity (ESI, Fig. S20†). The Stern Volmer plots of rac-1-OH yielded K_SV constants of 1.68 × 10³ M⁻¹ for (R)-Mosher's acid and 0.90 × 10³ M⁻¹ for (S)-Mosher's acid to obtain an ER of 1.86 (ESI, Fig. S21†). When compared to 1-OH (ER = 3.92), rac-1-OH showed a significant decrease in enantioselective efficiency in the absence of enantiopure BINOL, implying that the chirality of BINOL and D-cam constructively influence the enantiomeric response toward Mosher's acid. Including secondary sources of chirality in a framework may therefore be a beneficial strategy to consider in the design of future chiral materials.

Conclusion

The introduction of additional sources of chirality to yield confined voids with high enantioselectivity is a powerful design strategy in the development of MOF-based chiral sensors. 1-OEt and 1-OH are Zn(II)-based MOFs containing both axial chirality from BINOL and point chirality from the D-cam co-ligand resulting in exceptional ERs of 3.72 and 3.92, respectively. The 1-OH framework is an effective and accurate quantitative chiral fluorescence sensor with excellent agreement between the actual and calculated ee values. The accuracy achieved for 1-OH can be attributed to its high ER, which enables a greater differential between ee values to be achieved in the construction of the calibration curve. The confined and complementary voids in 1-OH had a larger effect when compared with hydrogen bonding interactions upon fluorescence quenching with the enantiomers of Mosher's acid.

Experimental

General experimental

All chemicals commercially obtained were used without further purification unless otherwise stated. Rac-4,4′-dibromo-2,2′-binaphthol,²⁶ (S)-4,4′-dibromo-2,2′-binaphthol²⁶ and Pd(PPh₃)₄²⁷ were synthesised according to literature procedures. Fourier Transform Infrared spectra were measured on an ATR Bruker Alpha spectrometer between 4000–400 cm⁻¹ with 4 cm⁻¹ resolution and 32 scans and normalised as absorbance spectra. Thermal gravimetric analysis (TGA) was conducted on a Mettler Toledo TGA/SDTA851 instrument using aluminium crucibles as sample holders under high purity nitrogen. Typical analysis involved heating the sample up to 450 °C with a temperature increment of 5 °C min⁻¹. Microanalysis was carried out at the Chemical Analysis Facility – Elemental Analysis Service in the Department of Chemistry and Biomolecular Science at Macquarie University, Australia. Powder diffraction data were collected on an XtaLAB Synergy diffractometer employing CuKα at λ = 1.5418 Å. PXRD patterns from single crystal structures were calculated using Mercury v.4.0. Absorption and emission experiments were performed with quartz cuvettes containing suspensions in acetonitrile; UV/vis absorption spectra were recorded on an Agilent Cary 60 UV-Vis spectrophotometer, and fluorescence spectra were recorded on an Agilent Cary Eclipse Fluorescence spectrophotometer.

Synthesis of frameworks

[Zn((S)-L₁)(D-cam)₂]·4.9DMF·2.8H₂O (1-OEt). A solution of 4,4′-(2,2′-diethoxy-[1,1′-binaphthalene]-4,4′-diyl)dipyridine ((S)-L₁) (7.4 mg, 0.015 mmol), D-camphoric acid (6.5 mg, 0.03 mmol) and Zn(NO₃)₂·6H₂O (8.9 mg, 0.03 mmol) in DMF (3 mL) was heated at 85 °C for 10 hours. The reaction mixture was cooled to room temperature, filtered, and washed with DMF (5.0 mL) to obtain pale yellow plate crystals (8.7 mg, 42%). IR (ATR): 3065, 2929, 1669, 1632, 1589, 1385, 1342, 1219, 1088, 1030, 845, 767, 658, 509, 443 cm⁻¹. Elemental analysis (%): calc'd for [Zn₂C₅₄H₅₆N₂O₁₀]·4.9DMF·2.8H₂O: C 57.77, H 6.76, N 6.74; found: C 57.78, H 6.55, N 6.74.

[Zn((S)-L₂)(D-cam)₂]·6DMF (1-OH). A mixture of 4,4′-(2,2′-dialcohol-[1,1′-binaphthalene]-4,4′-diyl)dipyridine ((S)-L₂) (3.3 mg, 0.0075 mmol), Zn(NO₃)₂·6H₂O (3.9 mg, 0.013 mmol), and D-camphoric acid (2.6 mg, 0.013 mmol) in DMF (1.5 mL) was heated at 85 °C for three days. The reaction mixture was cooled to room temperature before being washed with DMF, then filtered and dried to afford brown plate crystals of 1-OH (2.3 mg, 26%). IR (ATR): 3332, 3066, 2966, 1611, 1579, 1545, 1459, 1403, 1366, 1321, 1220, 1067, 1030, 950, 841, 785, 765, 680, 610, 517, 443 cm⁻¹. Elemental analysis (%): calc'd for [Zn₂C₅₀H₄₈N₂O₁₀]·0.5DMF·10H₂O: C 52.16, H 6.14, N 2.98; found: C 52.41, H 5.20, N 2.95.

Crystallography

Single crystal X-ray diffraction data was collected on a Rigaku Oxford Diffraction Synergy-S diffractometer equipped with CuKα radiation. In general, single crystals were transferred directly from the mother liquor into immersion oil and placed under a stream of nitrogen at 100 K or 240 K. Crystal structures were solved by direct methods using the program SHELXT²⁸ and refined using a full matrix least-squares procedure based on F² (SHEXL),²⁹ within the Olex2³⁰ GUI program. In structures containing disordered solvent molecules that could not be satisfactorily modelled, the solvent mask routine in Olex2 was used.³¹

Fluorescence quenching experiments

Crystals of the framework (1-OH or 1-OEt) were washed with acetonitrile and dried under vacuum with heating at 60 °C, manually crushed in a mortar and pestle and suspended in acetonitrile (10 mL) at an effective concentration of 5 × 10⁻⁴ M. Acetonitrile was chosen as the MOF structure was stable in acetonitrile (Fig. S4†), whilst the Mosher's acid analyte displayed good solubility in the solvent. Small 0.5 mL aliquots of the 5 × 10⁻⁴ M stock solution were then further diluted with acetonitrile (24.5 mL) to yield stock suspensions at an effective concentration of 1 × 10⁻⁵ M. All suspensions were sonicated for a minimum of 10 minutes to ensure even dispersion of particulates. Stock suspensions were stored away from direct sources of light.

The 5 × 10⁻⁴ M stock suspension was used for UV/vis absorption experiments. For recording of fluorescence spectra, 3 mL of the 1 × 10⁻⁵ M stock suspension of 1-OH or 1-OEt was dispensed into a quartz cuvette. The fluorescence spectrometer excitation wavelength was set to 229 nm, with a UV29 filter inserted to eliminate second and third harmonic scattered light signals. Chiral analytes were prepared as acetonitrile solutions at 3 mM, then added to the cuvette in increments of 10–500 μL until total analyte concentration in the cell reached 0.5 mM. Fluorescence spectra were recorded after each incremental addition of the analyte, with measurements consistently taken four minutes apart. Samples in the cuvette were shaken between fluorescence measurements to maintain an even dispersion of the framework within the suspension.

Stern–Volmer analysis was conducted by plotting the fluorescence intensity of the 415 nm peak in each emission spectrum against the increasing concentration of chiral analytes. Enantioselectivity ratios were calculated by approximating the gradient of the linear fit for each quenching plot to the Stern–Volmer constant K_SV. Calibration experiments with Mosher's acid were conducted with racemic samples of the analyte at a total concentration of 0.3 mM within the cuvette. Three linear calibration plots were generated, then averaged by calculating the mean fluorescence intensity at each ee value. Error bars represent the highest standard deviation observed for the mean fluorescence intensity. ‘Unknown’ samples of Mosher's acid were prepared at a known ee, then added to suspensions of the framework as normal so that the resulting fluorescence intensity could be inserted into the equation of the linear fit for the calibration plot to determine the ee value.

Steady-state photophysical measurements

UV-vis absorption spectra were acquired using a UV-visible spectrophotometer (CARY 50 Bio, Varian). Steady-state fluorescence spectra were acquired on a spectrofluorimeter (Varian Eclipse) using an excitation wavelength of 300 nm.

Time-correlated single-photon counting (TCSPC) measurements

Solution samples were excited with a mode-locked and cavity-dumped Ti/sapphire laser (Coherent Mira 900F/APE PulseSwitch) pumped by a Coherent Verdi-10 DPSS Nd:YVO4 laser. The laser output (900 nm, 5.4 MHz repetition rate) was frequency-tripled to provide an excitation wavelength of 300 nm. The fluorescence was collected using a lens after first passing through an emission polarisation analyser set at the magic angle, then a monochromator (Andor Kymera 193i) and detected using a hybrid photomultiplier tube (Becker & Hickl, HPM-100-07-C). The individual fluorescence decay curves were recorded using the time-correlated single-photon counting technique. Synchronization of the laser pulses was achieved by feeding the detector output through a nanosecond delay box and constant fraction discriminator (Tennelec TC455) as the stop signal for the time-to amplitude converter (Ortec model 457). The fluorescence decay parameters were extracted from the decay profiles using nonlinear least square iterative reconvolution software (FAST, Edinburgh Instruments Ltd) and a global analysis.

Computational approach

All calculations with the 1-OH cluster models and the chiral isomers of Moshers acid were carried out using the ORCA software package (version 5.0.3)³² and Kohn–Sham DFT^33,34 with the RIJCOSX approximation.³⁵ Geometry optimisations were performed using the PBE functional³⁶ with D3BJ^37,38 dispersion corrections with the def2-SVP^39,40 basis set on all atoms. A GGA functional was a necessary choice due to the large number of atoms. Frequency calculations were performed to verify that optimized structures are true minima and the results of these calculations were also used to calculate thermochemical corrections and calculate free energies. Energies were refined via single point energy calculations using the ωB97x-D3BJ^41,42 hybrid functional with the def2-TZVP⁴³ basis set on all atoms. Solvation effects due to the acetonitrile solvent were accounted for using the implicit SMD solvation model.⁴⁴ Solvation corrections were calculated by reoptimizing the structures with implicit solvation and performing single point energy refinement calculations.

We modelled 1-OH using cluster models. The use of cluster models is common for the study of MOFs with quantum chemistry tools⁴⁵ as this reduces the computational time required for a calculation to run while allowing the use of more accurate methods relative to periodic simulations. The use of cluster models in this study is further justified given that the binding of the Moshers acid guests is likely localized on the BINOL sites of the MOF and thus a full account of the periodic structure is not needed. Four different cluster models were extracted from the 1-OEt crystal structure and the OEt moieties were replaced with OH groups to model 1-OH. More details on the cluster model design are provided in the ESI.† The interaction strength (G_exchange) between the Moshers acid guests and the MOF was assessed based on the reaction free energy for the exchange of a solvent molecule bound to the MOF with a Moshers acid guest:

G_exchange = (G_mof+guest + G_acn) − (G_mof+acn + G_guest) (1)

where G_mof+guest refers to the Gibbs free energy of Moshers acid bound to 1-OH, G_mof+acn refers to the Gibbs free energy of acetonitrile bound to 1-OH, G_acn refers to the Gibbs free energy of an isolated acetonitrile solvent molecule, and G_guest refers to the Gibbs free energy of an isolated Moshers acid guest molecule. Details on the free energy calculations are provided in the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was conducted by the Australian Research Council Centre of Excellence in Exciton Science (project number CE170100026) and funded by the Australian Government. We are grateful for the computational resources and services from the National Computational Infrastructure (NCI), provided by the Australian government and the computational cluster Katana supported by the Research Technology Services at UNSW Sydney.

References

1. W. Ma, L. Xu, L. Wang, C. Xu and H. Kuang, Chirality-Based Biosensors, Adv. Funct. Mater., 2019, 29, 1805512.
2. Y. Liu, Z. Wu, D. W. Armstrong, H. Wolosker and Y. Zheng, Detection and analysis of chiral molecules as disease biomarkers, Nat. Rev. Chem., 2023, 7, 355–373.
3. H.-L. Qian, S.-T. Xu and X.-P. Yan, Recent Advances in Separation and Analysis of Chiral Compounds, Anal. Chem., 2023, 95, 304–318.
4. X. Zhang, J. Yin and J. Yoon, Recent Advances in Development of Chiral Fluorescent and Colorimetric Sensors, Chem. Rev., 2014, 114, 4918–4959.
5. S. Thoonen and C. Hua, Chiral Detection with Coordination Polymers, Chem. – Asian J., 2021, 16, 890–901.
6. A. Hubber and C. Hua, Chiral Metal-Organic Frameworks with Spectroscopic Methods: Towards Chemical Sensor Devices, Chem. – Eur. J., 2024, e202400071.
7. H. M. Tay, N. Kyratzis, S. Thoonen, S. A. Boer, D. R. Turner and C. Hua, Synthetic strategies towards chiral coordination polymers, Coord. Chem. Rev., 2021, 435, 213763.
8. M. Ma, J. Chen, H. Liu, Z. Huang, F. Huang, Q. Li and Y. Xu, A review on chiral metal–organic frameworks: synthesis and asymmetric applications, Nanoscale, 2022, 14, 13405–13427.
9. M. M. Wanderley, C. Wang, C.-D. Wu and W. Lin, A Chiral Porous Metal–Organic Framework for Highly Sensitive and Enantioselective Fluorescence Sensing of Amino Alcohols, J. Am. Chem. Soc., 2012, 134, 9050–9053.
10. Q. Zhang, M. Lei, F. Kong and Y. Yang, A water-stable homochiral luminescent MOF constructed from an achiral acylamide-containing dicarboxylate ligand for enantioselective sensing of penicillamine, Chem. Commun., 2018, 54, 10901–10904.
11. X. Zhao, E. T. Nguyen, A. N. Hong, P. Feng and X. Bu, Chiral Isocamphoric Acid: Founding a Large Family of Homochiral Porous Materials, Angew. Chem., Int. Ed., 2018, 57, 7101–7105.
12. S. Thoonen, H. M. Tay and C. Hua, A chiral binaphthyl-based coordination polymer as an enantioselective fluorescence sensor, Chem. Commun., 2022, 58, 4512–4515.
13. S. Li, Y. Zhou and B. Yan, Zirconium Metal Organic Framework-Based Hybrid Sensors with Chiral and Luminescent Centers Fabricated by Postsynthetic Modification for the Detection and Recognition of Tryptophan Enantiomers, Inorg. Chem., 2022, 61, 9615–9622.
14. Z. Han, K. Wang, Y. Guo, W. Chen, J. Zhang, X. Zhang, G. Siligardi, S. Yang, Z. Zhou, P. Sun, W. Shi and P. Cheng, Cation-induced chirality in a bifunctional metal-organic framework for quantitative enantioselective recognition, Nat. Commun., 2019, 10, 5117.
15. T.-Y. Liu, X.-L. Qu and B. Yan, A sensitive metal–organic framework nanosensor with cation-introduced chirality for enantioselective recognition and determination of quinine and quinidine in human urine, J. Mater. Chem. C, 2020, 8, 14579–14586.
16. Z. Han, M. Wang, K. Wang, P. Cheng and W. Shi, A Bifunctional Coordination-Chain-Based Hydrogen-Bonded Framework for Quantitative Enantioselective Sensing, Chem. – Eur. J., 2023, 29, e202301892.
17. Z. Han, K. Wang, M. Wang, T. Sun, J. Xu, H.-C. Zhou, P. Cheng and W. Shi, Tailoring chirality and porosity in metal-organic frameworks for efficient enantioselective recognition, Chem, 2023, 9, 2561–2572.
18. Z. Han, K. Wang, H.-C. Zhou, P. Cheng and W. Shi, Preparation and quantitative analysis of multicenter luminescence materials for sensing function, Nat. Protoc., 2023, 18, 1621–1640.
19. F. Yu, Y. Chen, H. Jiang and X. Wang, Recent advances of BINOL-based sensors for enantioselective fluorescence recognition, Analyst, 2020, 145, 6769–6812.
20. L. Pu, Enantioselective Fluorescent Sensors: A Tale of BINOL, Acc. Chem. Res., 2012, 45, 150–163.
21. T. Tsuboi, Z.-F. An, Y. Nakai, J. Yin, R.-F. Chen, H.-F. Shi and W. Huang, Photophysical properties of chirality: Experimental and theoretical studies of (R)- and (S)-binaphthol derivatives as a prototype case, Chem. Phys., 2013, 412, 34–40.
22. J. M. Chong and R. Loewith, A Convenient Preparation of (±)-α-Methoxy-α-trifluoromethylphenylacetic Acid (Mosher's Acid), Synth. Commun., 1993, 23, 2145–2150.
23. T. Kusumi, T. Fukushima, I. Ohtani and H. Kakisawa, Elucidation of the absolute configurations of amino acids and amines by the modified mosher's method, Tetrahedron Lett., 1991, 32, 2939–2942.
24. K. A. Paterson, J. Arlt and A. C. Jones, Dynamic and static quenching of, 2-aminopurine fluorescence by the natural DNA nucleotides in solution, Methods Appl. Fluoresc., 2020, 8, 025002.
25. M. Toprak, Fluorescence study on the interaction of human serum albumin with Butein in liposomes, Spectrochim. Acta, Part A, 2016, 154, 108–113.
26. M. W. A. MacLean, T. K. Wood, G. Wu, R. P. Lemieux and C. M. Crudden, Chiral Periodic Mesoporous Organosilicas: Probing Chiral Induction in the Solid State, Chem. Mater., 2014, 26, 5852–5859.
27. D. R. Coulson, L. C. Satek and S. O. Grim, in Inorganic Syntheses, John Wiley & Sons, Inc., 2007, pp. 121–124,  DOI:10.1002/9780470132449.ch23.
28. G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
29. G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
30. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
31. P. Van Der Sluis and A. L. Spek, BYPASS: an effective method for the refinement of crystal structures containing disordered solvent regions, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201.
32. F. Neese, Software update: The ORCA program system—Version, 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
33. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871.
34. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
35. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the, 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
38. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
39. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
40. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
41. N. Mardirossian and M. Head-Gordon, ωB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
42. A. Najibi and L. Goerigk, The Nonlocal Kernel in van der Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ωB97M-V Approaches, J. Chem. Theory Comput., 2018, 14, 5725–5738.
43. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
44. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
45. J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Electronic Structure Modeling of Metal–Organic Frameworks, Chem. Rev., 2020, 120, 8641–8715.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic and structural details, continuous shape analysis, powder XRD, thermal gravimetric analysis, ATR-FTIR spectra, additional absorption and emission spectra and additional computational approach details. CCDC 2341663 and 2341664. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi00760c

---