Open Access Article
Open Access ArticleNearly three-dimensional Dirac fermions in an organic crystalline material unveiled by electron spin resonance†
Ryuhei
Oka
a,
Keishi
Ohara
ab,
Naoya
Tajima
c,
Toshihiro
Shimada
 d and
Toshio
Naito
d and
Toshio
Naito
 *abe
*abe
aGraduate School of Science and Engineering, Ehime University, Matsuyama 790-8577, Japan. E-mail: tnaito@ehime-u.ac.jp
bResearch Unit for Development of Materials Development for Efficient Utilization and Storage of Energy (E-USE), Ehime University, Matsuyama 790-8577, Japan
cDepartment of Physics, Toho University, Funabashi, Chiba 274-8510, Japan
dGraduate School of Engineering, Hokkaido University, Kita 13, Nishi 8, Kita-ku, Sapporo 060-8628, Japan
eGeodynamics Research Center (GRC), Ehime University, Matsuyama 790-8577, Japan
First published on 1st November 2023
Abstract
Materials containing Dirac fermions (DFs) have unique electronic properties, and have been extensively studied. Electron spin resonance revealed that α-ET2I3 (ET = bis(ethylenedithio)-tetrathiafulvalene) at 1 bar contained a nearly three-dimensional DFs above ∼100 K coexisting with standard fermions. The close charge-transfer ET–I3 interactions account for temperature-sensitive three-dimensional (3D) band structures and temperature-independent resistivity behaviour. As 3D band structures cannot be depicted in a four-dimensional space, the analysis method proposed herein provides a general way to present important and easy-to-understand information of such band structures that cannot be obtained otherwise.
Introduction
Recently, a quantum state of matter called topological material has garnered considerable attention from a wide range of materials scientists.1–7 There are many types of topological materials known to date. All of their unique physical properties originate from Dirac fermions (DFs) located around the Fermi levels and governing the electrical, magnetic, and optical properties, instead of the standard fermions (SFs) of electrons or holes in common materials. The SFs transform to DFs when they are accommodated in linearly dispersive parts of bands called Dirac cones (Fig. 1).8 To understand the mechanism of such intriguing physical properties, the direct observation of DFs with their characteristic electronic properties is important. However, the direct observation is demanding, partly because some require high pressure (∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bar, for example) to realise such band structures,9–16 and partly because the direct observation of the band structures requires an extremely high accuracy (e.g., a few meV) in energy. However, for observation, most measurements require larger energy of perturbation than a few meV and are performed at high temperatures (Ts) to allow significant thermal excitation, both of which often prevent the unambiguous observation of the ground states of the DF systems. These experimental restrictions practically narrow down the available powerful tools for observation, such as angle-resolved photoemission spectroscopy (ARPES) and scanning tunnelling microscopy/spectroscopy (STM/STS) at extremely low Ts (a few Kelvins or lower, for example).17,18 Both observations are surface-sensitive and require an ultra-high vacuum, where the samples (single crystals) should be cleaved to expose atomically clean surfaces prior to the observation.
000 bar, for example) to realise such band structures,9–16 and partly because the direct observation of the band structures requires an extremely high accuracy (e.g., a few meV) in energy. However, for observation, most measurements require larger energy of perturbation than a few meV and are performed at high temperatures (Ts) to allow significant thermal excitation, both of which often prevent the unambiguous observation of the ground states of the DF systems. These experimental restrictions practically narrow down the available powerful tools for observation, such as angle-resolved photoemission spectroscopy (ARPES) and scanning tunnelling microscopy/spectroscopy (STM/STS) at extremely low Ts (a few Kelvins or lower, for example).17,18 Both observations are surface-sensitive and require an ultra-high vacuum, where the samples (single crystals) should be cleaved to expose atomically clean surfaces prior to the observation.
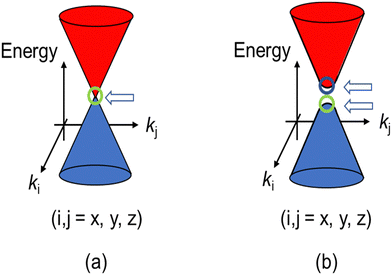 | ||
| Fig. 1 (a) Schematic band structure of the Dirac cones. A close view of the band structure of a typical DF system, a zero-gap semiconductor, around a Weyl point indicated by the arrow. (b) Dirac cones with round apexes and with an energy gap between two Weyl points. The cases (a) and (b) correspond to m = 0 and m ≠ 0, respectively in eqn (1). The energy gap between the two cones in (b) equals 2mc2 (a “mass gap”). | ||
Meanwhile, some organic charge-transfer (CT) salts have been studied in terms of the DFs.19–38 They include α-D2I3 (D = ET = bis(ethylenedithio)-tetrathiafulvalene, STF = bis(ethylenedithio)-diselenadithiafulvalene, and BETS = bis(ethylenedithio)-tetraselenafulvalene: Scheme 1).
In 2007–2008, the high-pressure phase (≥12 kbar) of α-ET2I3 was established as a DF system called zero-gap semiconductor (ZGS; Fig. 1(a)).19–30 Recently, it has been argued that the related salts, α-STF2I331–35 and α-BETS2I3,31,36–38 are also close to or belong to ZGSs based mainly on the band calculations. Their apparent advantage over other DF systems is that the DFs can be observed as bulk properties, such as electrical resistivity without any demanding pre-treatment for observation. The bulk properties originate from internal parts of condensed matters, which are protected to be intact by their own surfaces. Furthermore, the bulk sample can contain three-dimensional (3D) DF systems, which nanosheets such as graphene cannot contain. The difference in the system dimension generally provides qualitatively different physical properties.39–41 However, most work on the organic DFs thus far has been focused on the two-dimensional (2D) ZGSs, which is the same feature that graphene and related nanosheets possess. Except for a limited range of Ts, the electronic states of α-D2I3 at 1 bar remain rather unexplored, as they were speculated to be less relevant to ZGS. However, lack of experimentally detailed and systematic information on the electronic structures at 1 bar in these materials leaves important questions unanswered. For example, in previous papers, many molecular conductors were classified as ZGSs exclusively based on the T-independent resistivity (TIR) except for the calculated band structures, as if the observation of TIR should be the necessary and sufficient condition. However, there is no explanation as to why α-ET2I3 in the metallic phase (at 1 bar and T > 135 K) exhibits identical resistivity behaviour (the TIR) with that in the ZGS state of the same material (P ≥ 12 kbar). Additionally, there is no explanation as to why most Weyl points in molecular conductors are located at general points in the reciprocal space, which are not associated with high symmetries for allowing the degeneracy between the two bands. These unanswered questions make it unclear which behaviour should be associated with the ZGS states. In our previous study, we proposed T-dependent band structures of α-D2I3 (ET = ET and BETS) (296–30 K) based on a first-principles calculation, and established their validity by comparing them with the observed electrical, magnetic, and optical properties.42 Based on the study, we clarified that the carrier systems in these salts contain two kinds of fermions: SFs at the Fermi surfaces and DFs at different parts of the same bands with linear dispersions like Dirac cones. It should be noted that it never means that α-ET2I3 should be a ZGS at 1 bar, but means that it is a semiconductor with a separated pair of “round-apex Dirac cones” in the insulating phase (Fig. 1(b)). As a part of the thermally excited fermions (electrons and holes) that are located at the linear dispersive parts of the cones at some T range, they behave as DFs. With varying T at 1 bar, the band structures vary qualitatively and the dominant carrier system crosses over between the two kinds of fermions. The relationship between the two kinds of fermions in Fig. 1(a) and (b) is described by eqn (1),
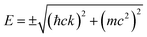 | (1) |
Electron spin resonance (ESR) enables us direct observation of such DFs, distinguishing them from the coexisting SFs as different spin systems. Therefore, using ESR, the single crystals of α-D2I3 at 1 bar are the sample of choice for the observation of DFs, including how they originate from SFs or vice versa. In this work, we examined the ESR spectra of the single crystals of α-ET2I3 concerning magnetic-field-angle (θ)- and T-dependencies, which have unveiled the nearly 3D behaviour of DFs in this salt above ∼100 K.
Results and discussion
The discussion thus far is qualitatively valid for three-dimensionally at any T and 1 bar in α-ET2I3 (Fig. 2). Thus, the molecular orbitals of the ET cations and I3 anions are mixed in a complicated manner to form conduction and valence bands of α-ET2I3. This situation makes the discussion on the electronic properties more comprehensive based on the band structure compared to the crystal structure. Therefore, firstly, we will relate the conduction behaviour to the band structure features shared by the kakc (Fig. 2) and kakb (Fig. S1, ESI†) spaces, and then refer to supplementary features based on the crystal structure (Fig. 3). We will not repeat similar discussion on the band structures in the kakb space (Fig. S1, ESI†), which are qualitatively similar to those in the kakc space (Fig. 2). However, the band structure contains developing Dirac cones and narrowly recognisable Weyl points in the kakb space, whilst the Dirac cones merged into a nodal line in the kakc space. Thus, hereafter, we will refer to these Dirac-cone-related features as “linearly dispersive parts in the bands”. At 296 K, the conducting properties are governed by two kinds of fermions mobile in a nearly 3D way (Fig. 2 and Fig. S1, ESI†): SFs (electrons at the Fermi surface in the 3D bands) and DFs (thermally excited electrons and holes at the linearly dispersive parts in the 3D bands). At 150 K, the Fermi level intersects with the top of the linearly dispersive parts of the second HOMO band in both kakb (Fig. S1, ESI†) and kakc spaces (Fig. 2), which means that the 3D DFs dominate the conduction at ∼150 K. A metal (high-T phase)–insulator (low-T phase) (M–I) transition occurs at 135 K in α-ET2I3. This causes the Fermi surface and the SFs to disappear simultaneously, and causes energy gaps to appear. The M–I transition allows for distinguishing the SFs and DFs in α-ET2I3. At 100 K, there are energy gaps of a few meV at the linearly dispersive parts in the kakb space (Fig. S1, ESI†), which means that no SFs contribute to the conduction in the ab plane. On the other hand, the Fermi level intersects the lower band still at 100 K in the kakc space (Fig. 2), which contradicts with the observed resistivity behaviour (Fig. 4). This inconsistency is probably attributable to stronger electron correlation20,26,29,30 or a larger change in the effective charge of ET (0.5 − δ)42 than our calculation estimated. Consistently, the temperature dependence of resistivity (‖b) slightly varies at T ≤ 90–100 K (Fig. 4). The value of δ is T-dependent because it depends on the ET–I3 CT interactions, which are based on a chemical equilibrium and thus are also T-dependent.42 The assumption that the insulating (charge ordered) phase in α-ET2I3 (T < 135 K) is not a simple band insulator is qualitatively consistent with the observed T-dependent activation energy in this phase.9 Accordingly, thermally excited electrons and holes through the band gap around the linearly dispersive parts serve as carriers and behave as DFs at ∼100 K.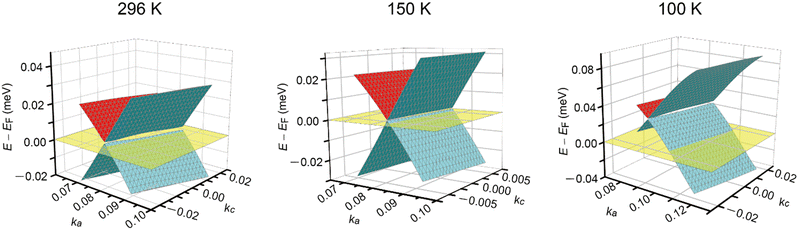 | ||
| Fig. 2 Band structures near the Fermi level EF in α-ET2I3 at 1 bar and 296, 150, and 100 K in the kakc space. At each T, the Fermi level is shown by the half-transparent yellow plane. The green (front)/red (back) and blue (front)/green (back) curved surfaces respectively show a part of the top and the second HOMO bands. The corresponding figure (the band structures in the kakb space at 296, 150, and 100 K) is shown in Fig. S1 in the ESI,† which also shows linearly dispersive parts in the band structure. | ||
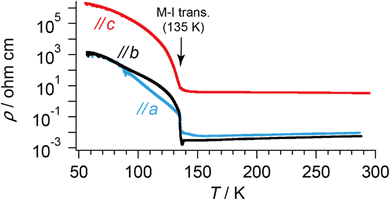 | ||
| Fig. 4 T-dependent electrical resistivities of α-ET2I3 along each crystallographic axis. The values are identical at T ≈ 60–90 K along the a- and b-axes. | ||
The crystal structure of α-ET2I3 is shown in Fig. 3.42,43 The unit cell contains three (more precisely, two halves and a whole) independent ET species and two (halves of) independent I3 species. At the M–I transition (TMI = 135 K), the space group changes between P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (a high-T, metallic phase) and P1 (a low-T, insulating phase). There are two key features in the crystal structure, which are indispensable to uniquely realize the nearly 3D DFs. Firstly, the ET radical cations form 2D conduction sheets in the ab planes. Such network makes this salt a narrowly metallic conductor. Here, the phrase “a narrowly metallic conductor” is important. It indicates that the salt unambiguously belongs to the metals because it has a Fermi surface (Fig. 2 and Fig. S1, ESI†), satisfying the definition of metals. This is corroborated by the T-dependence of the resistivity ρ, dρ/dT > 0, which is characteristic to the metals. However, the Fermi surface is extremely small (Fig. 2 and Fig. S1, ESI†), which indicates the metallic band structure should be unstable. This is also corroborated by the extremely small T-dependence of ρ in the metallic phase (dρ/dT ≈ 0 at T ≥ 135 K at any direction in the unit cell) (Fig. 4), a conducting property also close to that of an insulator (dρ/dT < 0). This underlying metal-instability promotes the Dirac-cone-like band structure formation, when the net charge of the ET cations changes by T-variation as explained next. Secondly, there are CT interactions between ET+0.5 and I3− species, which vary the net charge of the ET cations (ET+0.5 → ET(0.5 − δ)+, δ ≠ 0), as follows. Firstly, they cause electron-doping from the I3 anions to the ET cations. Then, they affect the metal-phase (in)stability, as they directly change the band filling and the Fermi energy. The electrical conduction is mainly based on the close ET–ET interactions in the ab planes supported by π–π overlaps between the highest occupied molecular orbitals (HOMOs) of ET. They are also singly occupied molecular orbitals (SOMOs) of ET, dominating the electronic properties. Furthermore, the ET–I3 interactions extend the conduction pathway to the third direction (along the c-axis), which make the materials narrowly 3D metallic conductors as evidenced by the resistivity measurements (Fig. 4). Consistent with the abovementioned structural features, α-ET2I3 exhibited TIR-like ρ (dρ/dT ≈ 0) along the a-, b-, and c-axis at 300–135 K, which is an intermediate behaviour between metals (dρ/dT > 0) and insulators (dρ/dT < 0). However, this electrical behaviour does not necessarily indicate that the system belongs to the ZGSs, which also generally exhibit TIR in wide T ranges. Instead, the calculated band structure (Fig. 2) and the observed ESR spectra account for the observed electrical behaviour: α-ET2I3 at 1 bar has a closely related 3D band structure to ZGS at 1 bar (Fig. 1(b)) and TIR is a result of the combined contributions from SFs and DFs. The ratio of contributions varies with T in a complicated manner, which is revealed by the ESR analyses below.
(a high-T, metallic phase) and P1 (a low-T, insulating phase). There are two key features in the crystal structure, which are indispensable to uniquely realize the nearly 3D DFs. Firstly, the ET radical cations form 2D conduction sheets in the ab planes. Such network makes this salt a narrowly metallic conductor. Here, the phrase “a narrowly metallic conductor” is important. It indicates that the salt unambiguously belongs to the metals because it has a Fermi surface (Fig. 2 and Fig. S1, ESI†), satisfying the definition of metals. This is corroborated by the T-dependence of the resistivity ρ, dρ/dT > 0, which is characteristic to the metals. However, the Fermi surface is extremely small (Fig. 2 and Fig. S1, ESI†), which indicates the metallic band structure should be unstable. This is also corroborated by the extremely small T-dependence of ρ in the metallic phase (dρ/dT ≈ 0 at T ≥ 135 K at any direction in the unit cell) (Fig. 4), a conducting property also close to that of an insulator (dρ/dT < 0). This underlying metal-instability promotes the Dirac-cone-like band structure formation, when the net charge of the ET cations changes by T-variation as explained next. Secondly, there are CT interactions between ET+0.5 and I3− species, which vary the net charge of the ET cations (ET+0.5 → ET(0.5 − δ)+, δ ≠ 0), as follows. Firstly, they cause electron-doping from the I3 anions to the ET cations. Then, they affect the metal-phase (in)stability, as they directly change the band filling and the Fermi energy. The electrical conduction is mainly based on the close ET–ET interactions in the ab planes supported by π–π overlaps between the highest occupied molecular orbitals (HOMOs) of ET. They are also singly occupied molecular orbitals (SOMOs) of ET, dominating the electronic properties. Furthermore, the ET–I3 interactions extend the conduction pathway to the third direction (along the c-axis), which make the materials narrowly 3D metallic conductors as evidenced by the resistivity measurements (Fig. 4). Consistent with the abovementioned structural features, α-ET2I3 exhibited TIR-like ρ (dρ/dT ≈ 0) along the a-, b-, and c-axis at 300–135 K, which is an intermediate behaviour between metals (dρ/dT > 0) and insulators (dρ/dT < 0). However, this electrical behaviour does not necessarily indicate that the system belongs to the ZGSs, which also generally exhibit TIR in wide T ranges. Instead, the calculated band structure (Fig. 2) and the observed ESR spectra account for the observed electrical behaviour: α-ET2I3 at 1 bar has a closely related 3D band structure to ZGS at 1 bar (Fig. 1(b)) and TIR is a result of the combined contributions from SFs and DFs. The ratio of contributions varies with T in a complicated manner, which is revealed by the ESR analyses below.
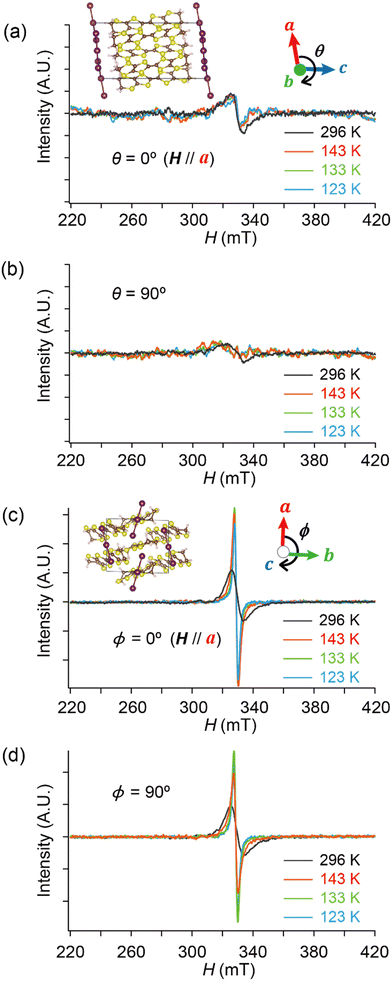
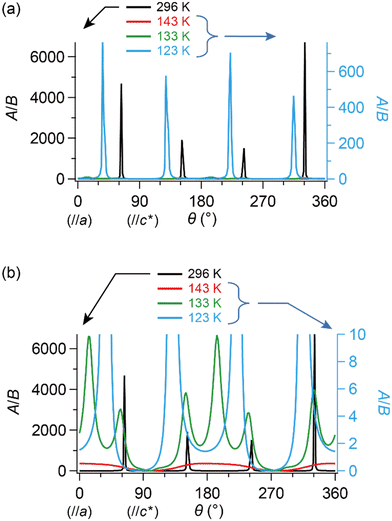
Based on these structural and electrical properties, we discuss the ESR spectra mainly around TMI = 135 K, as most noticeable changes in ESR are expected around TMI to distinguish the SFs and DFs. The anisotropy was examined by rotating the single crystal around the b-axis from the a-axis (θ = 0°) toward the c-axis (θ ≈ 98°), or around the c-axis from the a-axis (ϕ = 0°) toward the b-axis (ϕ ≈ 91°) (Fig. 5 and 6). On rotating the single crystal around the b-axis, it should be noted that the ESR signals were weak and noisy independent of T and θ (Fig. 5(a) and (b)). The spectral measurements with rotation around the c-axis did not suffer from such weak intensities (Fig. 5(c) and (d)). This is not only because of the anisotropy in the resistivity (Fig. 4), but also because of complicated hyperfine (and possibly superhyperfine) structures (Fig. 6(a)) originating from each nuclear spin I = 5/2 on the four magnetically inequivalent iodine atoms in the unit cell. The hyperfine interactions split a single peak into many fine peaks.‡ In other words, to corroborate the ET–I3 CT interactions, the b-axis rotation is the most favourable experimental condition for observing the spins on the I3 anions.
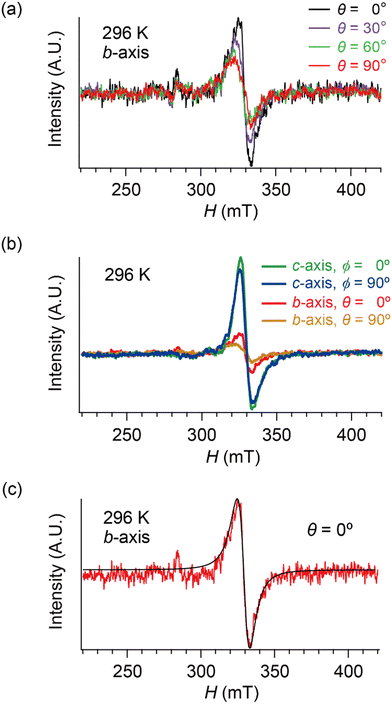 | ||
| Fig. 6 Selected ESR spectra of α-ET2I3 (single crystal, 296 K). (a) Angle-dependence, θ = 0, 30, 60 and 90°, when the sample was rotated around the b-axis. (b) Comparison of the ESR spectra between different orientations (θ or ϕ) and between different rotation axes (b- or c-axes). (c) H‖a-axis (θ = 0°) when the sample was rotated around the b-axis. Red and black curves show the observed and best-fit spectra, respectively. For the parameters of the simulated spectra, see Tables S1–S8 (ESI†). All the spectra in (b) were measured using the same single crystal under the identical measurement conditions, except for the crystal setting orientation. | ||
Hereafter, we will discuss details of the main peak at ∼330 mT (g = 2.006) observed when the sample was rotated around the b-axis (Fig. 5(a) and 6(c)). We will not repeat similar discussion on the spectra with the c-axis rotation (Fig. S2, ESI†), as the spectra with the b-axis rotation include necessary information for the following discussion. The lineshape and intensity were hardly dependent on T, and minimally affected by the M–I transition (Fig. 5(a)). However, they depended on the magnetic-field (H)-angle θ (Fig. 6(a)), where θ = 0° corresponded to the H‖a-axis. When H was perpendicular to the ab planes (θ = 90°: Fig. 6(b)), the main peak was evidently less intensive than that of θ = 0° (Fig. 6(a)). Our previous study indicated that there are CT interactions between ET and I3 in α-ET2I3 with leaving spins on the I3 anions.42 Considering the arrangement of the I3 anions in the unit cell (Fig. 3), the b-axis rotation includes the widest range of angles (∼0 to ∼90°) between the averaged principal axis of the I3 anions and H. Accordingly, the ESR spectra with the b-axis rotation should contain peaks assigned to the unpaired electrons on the iodine atoms in the I3(1−δ)− (0 < δ < 1) anions. The nuclear spins on the inequivalent four iodine atoms in the two I3 anions produce many highly complicated hyperfine and superhyperfine structures.‡,§ Most of them may not be distinguished from noises. Accordingly, the main peak at ∼330 mT should be an envelope of overlapped peaks of the delocalised spins.‡§ Although the delocalised spins in α-ET2I3 form a single spin system, the ESR peaks can be classified into three types based on the temporal locations of the spins during the resonance and based on the type of fermions: the signals assigned to the spins on the I3 anions, those assigned to the SFs on the ET cations, and those assigned to the DFs on the ET cations. When the spins are on the I3 anions, the finely split complicated peaks prevented the distinguishing of the type of fermions. Suggested by the observation of hyperfine structures, the spins on the I3 anions exhibit more localised character than the other two types. Thus, they are more easily saturated under the high power radiation (P) of microwaves during ESR measurements than the other two types of spins.42 Thus, above a certain value of Psat, we can approximately suppress most hyperfine structures and resonance peaks assigned to the spins on the I3 anions. In our previous work,42 we found Psat ≅ 9 mW. In fact, the broad peak at ∼330 mT under the measurement conditions in this study (P = 9 mW) was consistently deconvoluted in two peaks as shown below (Fig. 7 and 8). The intensity, lineshape, and g-value of the main peak were less dependent on θ than those of related organic conductors,44,45 which indicates that the spin system is more isotropic around the b-axis than it appears from the crystal structure (Fig. 3). As the b-axis rotation includes both directions of the H‖ and H⊥ab planes (2D conduction sheets), the spin system is close to 3D rather than 2D. It has recently revealed that α-ET2I3 also contains a 3D Dirac fermion system at high pressures.46,47 Both experimental46 and theoretical47 studies corroborated that an interlayer coupling (ET–I3-interaction) opens the energy gap between the Dirac cones as in Fig. 1(b), which is consistent with the present study. As the interlayer coupling is T-independent unless the crystal structure drastically changes, the energy gap between the Dirac cones remains through phase transitions, which is also consistent with the calculated band structures (Fig. 2). The main peak remained below the M–I transition TMI (135 K). The T-(in)dependence indicates that the major origin of the peak is the DFs at least at 123 K (the lowest T of measurements in this study) ≤ T < 135 K (TMI). Because the band gap around where the Fermi surface was in the metallic phase is ∼75–85 meV (≈ 1000 K) in the insulating phase (T < 135 K),42,48 the contribution from thermally excited electrons and holes through this band gap, which are the SFs, can be ignored.
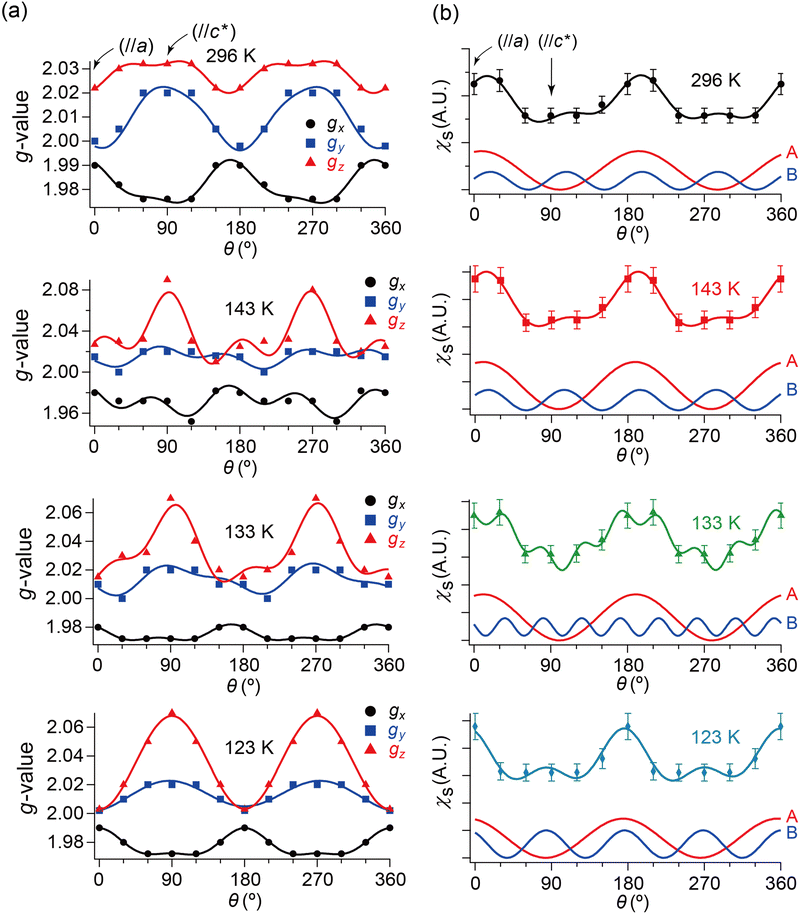 | ||
| Fig. 7 θ- and T-dependencies of (a) g-values and (b) spin susceptibility χs of the ESR spectra when the single crystal was rotated around the b-axis. In each panel of (a), the three curves consist of the data from the simulated spectra with the best-fitting curves using eqn (2). Although the unit of angle θ was radian in the fitting, it is described in degree in this figure. The subscripts x, y and z of the g-values approximately indicate the following directions: (x, y) ≈ (a, b) or (b, a), and z ≈ c-axis. Whether (x, y) ≈ (a, b) or (b, a) could not be determined based on the ESR data. In each panel of (b), the bottom two curves indicate the fitting components to the top curve corresponding to the first (A) and second (B) terms in eqn (2), respectively. The obtained parameters are summarised in Tables S9–S16 (ESI†). | ||
 | ||
| Fig. 8 θ- and T-dependencies of the ratio of amplitudes in components A and B in eqn (2), A/B, which approximately correlates with the number ratio between SFs and DFs, NSF/NDF. The single crystal was rotated around the b-axis, where θ = 0° corresponds to H‖a-axis. (a) Entire and (b) enlarged view. It should be noted that both curves corresponding to 143 K (red) and 133 K (green) almost overlap with the horizontal axis in (a). Although the unit of angle θ was radian in the fitting, it is described in degree in this figure. | ||
Next, we will distinguish the two spin systems: the SFs at the Fermi surfaces and the DFs at the linearly dispersive parts of the 3D bands. Using eqn (2), the fitting-analyses of the obtained ESR spectra revealed the angle (θ/rad) dependencies of spin susceptibility χs(θ) and g-values g(θ).49 Although the unit of angle θ was radian in the fitting, it is described in degree in the following figures (Fig. 7 and 8) for simplicity. χs(θ) and gi(θ) (i = x, y, and z) are based on the simulated spectra to exclude possible overlapped irrelevant peaks and noise. The parameters for the simulated spectra are summarised in Tables S1–S8 (ESI†).
χs(θ) or gi(θ) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(aθ + δ1) + B sin2(aθ + δ1) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(bθ + δ2) + C (i = x, y, z) sin2(bθ + δ2) + C (i = x, y, z) | (2) |
First, we will discuss g(θ) in Fig. 7(a). If g(θ) is ideally 2D:
| gy(θ) = gx(θ + π/2) | (3) |
Then, based on eqn (2) and (3),
gx(θ) + gy(θ) = g0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + g0 θ + g0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = g0. θ = g0. | (4) |
Next, we will discuss χs(θ) in Fig. 7(b). After deconvolution using eqn (2), it should be noted that the relationship between χs(θ) and the amplitude at θ in each component (A or B) is indicated by eqn (5) and (6), respectively.
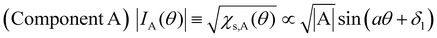 | (5) |
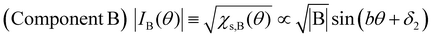 | (6) |
Here, we will make a brief comment on the consistency between g(θ) (Fig. 7(a)) and χs(θ) (Fig. 7(b)) regarding the local rotation symmetries of DFs and SFs. In the metallic phase (296–133 K), the complicated θ-dependences in both g(θ) and χs(θ) are consistent with each other in that they both exhibit nearly twofold rotation symmetries. The onefold symmetry of SFs derived from χs(θ) at 296–123 K is almost twofold symmetry based on the calculated band structures around the Fermi surfaces (Fig. 2 and Fig. S1, ESI†). Thus, the SFs (component A) contribution to g(θ) should be approximately twofold like that of the DFs (ccomponent B), which was observed at 296–123 K as an overlap pattern of two waves with twofold symmetries with different phase shifts (Fig. 7(a) and Tables S9–S11, ESI†). Particularly at 123 K, the contribution of the SFs to g(θ) and χs(θ) are negligible compared with the (thermally activated) DFs because of the M–I transition, as is discussed below.
A nearly 3D band structure based on the ET–ET and ET–I3 interactions is obtained by combining our present (Fig. 2, the kakc space) and previous42 (Fig. S1, ESI† the kakb space) band structures, and is supported by the observed 3D metallic T-dependence of the resistivity (Fig. 4).
Now, we clarify how DFs revolve with the band reshaping and temperature variation. As a coarse approximation, here we assume that the relaxation times in the ESR of SFs and DFs should be comparable to each other.|| Then, one can roughly estimate the ratio between the numbers of SFs and DFs at T and θ based on the amplitudes of the two components, A and B (Fig. 8). At 296 K (the metallic phase) and 123 K (the insulating phase), the SFs (corresponding to A) dominate in number, but only in limited directions (Fig. 8(a)). Fig. 8(a) and (b) show that the DFs increase with decreasing T. At 143 K, the DFs become comparable to the SFs in number (A/B ≈ 1) at practically all θ (Fig. 8(b)). This indicates that the DFs form a 3D system in the kakbkc space, considering the b-axis rotation includes both directions of H‖and H⊥ab planes (2D conduction sheets). The value of θ where A/B becomes maximum, θmax, clearly shifts with T. This manifests how the SFs turn into the DFs: the DFs continuously increase with decreasing T and with change of the band structure. The transformation between DFs and SFs exhibited complicated T-dependence. In the middle of the M–I transition (133 K: green curves in Fig. 8(b)), the carrier system exhibited both features of θ-dependence in A/B at 296 K (black) and 143 K (red). This is noteworthy, as the θ-dependence at 296 K (black) was once averaged out at 143 K (red) and reproduced at 133 K (green). Finally, the values of θmax are different between 296 K and 123 K, although the rotation symmetry is retained (Fig. 8(a) and (b)). Such complicated T-dependence of the band structure is explained as follows. The entire band structure is cooperatively governed by the ET–ET and ET–I3 interactions at 296–123 K. Additionally, the number of carriers is T-dependent, but always small at all Ts in this salt, whether they are SFs or DFs. Thus, to lower the Gibbs energy of the electronic and lattice system, the interactions deform the smallest part of the band to be a cone or similar shapes toward the lower energy, where the carriers are accommodated. The number of carriers depends on T-sensitive ET–I3 CT interactions. Such a subtle balance in energy based on the chemical equilibrium in the ET–I3-redox reaction in the solid state is responsible for causing the observed complicated T-dependence and three-dimensionality in the “DF-SF equilibrium”.
In summary, the coexisting components A and B at 296–123 K revealed by the ESR spectra demonstrated that the nearly 3D DFs are present at 296–123 K. The complicated T- and θ-dependencies of the two components are consistent with our band calculations indicating the T-dependent formation of the DFs.
Experimental
Selected information on materials, methods, and calculations are described below. Other details are described in ESI.†Materials
The single crystals were prepared following the reported procedure.42,43 Prior to the physical property measurements, all single crystals were checked by the X-ray oscillation photographs in terms of the crystal quality and orientation of crystallographic axes.Band structure calculation
The electronic band structures were calculated using the Vienna Ab initio Simulation Package (VASP),50 similarly to our previous work.42 The PBE functional51 was used along with the augmented plane wave method. Crystal structures derived from the X-ray diffraction experiments in our previous work42 were used, and no structure optimization was performed. The structure at 150 K was provided by Prof. H. Sawa (Nagoya University, Japan). The atomic parameters used in the calculation are submitted as cif files in ESI.†Electrical resistivity measurements
The electrical resistivities along the a-, b- and c-axes of the α-ET2I3 single crystals were measured by a standard four-probe method, where the four electrical leads were attached to align along the crystallographic axes. For the c-axis resistivity measurements, either side of the most developed face (the ab plane) of the platelet crystals was attached with two leads, and the constant current flew from one side to the other. Carbon paste and gold wires (15 μm in the diameter) were used as the electrical contacts. A commercially available VTI cryostat (CRYOGENIC) inserted with a homemade probe was used. The current source and the voltameter were Model 6221 AC and DC Current Source (KEITHLEY) and Model 2182A Nanovoltmeter (KEITHLEY), respectively.ESR spectra measurements
The ESR spectra of the X band (9.3 GHz) were measured using the single crystals of α-D2I3 at 120–300 K with the JEOL JES-FA100. The single crystal was mounted on a Teflon piece settled with a minimal amount of Apiezon N grease, and sealed in a 5 mm-diameter quartz sample tube in a low-pressure (∼20 mmHg) helium atmosphere. The background signals were measured prior to the sample measurement under conditions identical to those of the samples, and the resultant spectra were subtracted from the raw sample spectra. The microwave power, Q-values, time constant, sweep time, modulation, and its amplitude were 9 mW, 4700–8200, 0.03 s, 1 min, 100 kHz, and 2 mT, respectively. Here, the Q-values are the factors indicating the resonance specification of the cavity, and are defined as the ratio between the energy stored in the cavity and that consumed inside the cavity. The magnetic field was corrected by a Gauss meter (JEOL NMR Field Meter ES-FC5) at the end of every measurement. The temperature was controlled using a continuous flow-type liquid N2 cryostat with a digital temperature controller (JEOL). The temperature variation did not exceed ± 0.5 K during the field sweep. The cooling rate was −10 K min−1. No hysteretic behaviour was observed in the ESR spectra between the heating and cooling processes.Conclusions
Generally, the conducting properties are qualitatively sensitive to the dimension of the electronic systems. Additionally, the DF systems of any dimension (2D or 3D) often exhibit conducting behaviour that SFs do not exhibit under any condition. Using ESR, we identified nearly 3D DF systems underlying in α-ET2I3 at 1 bar. Additionally, the ratio between the numbers of SF and DF anisotropically depends on T. The crystalline materials with well-defined stoichiometries containing DFs are scarce, let alone the 3D DFs. Even more scarce are the fermions, which sensitively and reversibly transform themselves between DFs and SFs by varying T at 1 bar: a practical condition enabling various experiments. This work has established that α-ET2I3 has both features: a nearly 3D fermion system with a well-defined stoichiometry, being reversibly interconvertible between SFs and DFs by varying T at 1 bar. Such a flexible character of the electronic system is an evident advantage of conducting materials based on the weak van der Waals interactions, namely the organic conductors. The findings here will accelerate both theoretical and experimental studies on the DFs and their characteristic electronic properties.Author contributions
T. N. contributed to the conceptualization, resources, funding acquisition, project administration, supervision, methodology, original draft writing, review, and editing. K. O. contributed to the formal analysis and resources. R. O., T. S. and N. T. performed the investigation and validation. R. O., N. T., T. S. and T. N. collaborated in the visualization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Prof. H. Sawa (Nagoya University) for providing the atomic coordinates of α-ET2I3 at 150 K. We would like to acknowledge the assistance provided by Dr S. Mori and Ms R. Konishi (ADRES, Ehime University) in the X-ray structural analyses. This work was partially funded by a Grant-in-Aid for Challenging Exploratory Research (18K19061) and a Grant-in-Aid for Scientific Research (B) (22H02034) of JSPS, the Iketani Science and Technology Foundation (ISTF; 0331005-A), the Research Grant Program of the Futaba Foundation, CASIO Science Promotion Foundation, an Ehime University Grant for Project for the Promotion of Industry/University Cooperation, and the Canon Foundation (Science and Technology that Achieve a Good Future).Notes and references
- W. Ko, Z. Gai, A. A. Puretzky, L. Liang, T. Berlijn, J. A. Hachtel, K. Xiao, P. Ganesh, M. Yoon and A.-P. Li, Adv. Mater., 2023, 35, 2106909 CrossRef CAS.
- J. Liu and T. Hesjedal, Adv. Mater., 2023, 35, 2102427 CrossRef CAS.
- S. Jana, A. Bandyopadhyay, S. Datta, D. Bhattacharya and D. Jana, J. Phys.: Condens. Matter, 2022, 34, 053001 CrossRef CAS PubMed.
- M. M. Sharma, P. Sharma, N. K. Karn and V. P. S. Awana, Supercond. Sci. Technol., 2022, 35, 083003 CrossRef.
- J.-X. Yin, B. Lian and M. Z. Hasan, Nature, 2022, 612, 647 CrossRef CAS PubMed.
- Y. Lei, T. Zhang, Y.-C. Lin, T. Granzier-Nakajima, G. Bepete, D. A. Kowalczyk, Z. Lin, D. Zhou, T. F. Schranghamer, A. Dodda, A. Sebastian, Y. Chen, Y. Liu, G. Pourtois, T. J. Kempa, B. Schuler, M. T. Edmonds, S. Y. Quek, U. Wurstbauer, S. M. Wu, N. R. Gravin, S. Das, S. P. Dash, J. M. Redwing, J. A. Robinson and M. Terrones, ACS Nanosci. Au, 2022, 2, 450 CrossRef CAS PubMed.
- H. Xue, Y. Yang and B. Zhang, Nat. Rev. Mater., 2022, 7, 974 CrossRef.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef CAS.
- N. Tajima, S. Sugawara, M. Tamura, Y. Nishio and K. Kajita, J. Phys. Soc. Jpn., 2006, 75, 051010 CrossRef.
- N. Tajima, S. Sugawara, M. Tamura, R. Kato, Y. Nishio and K. Kajita, EPL, 2007, 80, 47002 CrossRef.
- N. Tajima, R. Kato, S. Sugawara, Y. Nishio and K. Kajita, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 033401 CrossRef.
- K. Kajita, Y. Nishio, N. Tajima, Y. Suzumura and A. Kobayashi, J. Phys. Soc. Jpn., 2014, 83, 072002 CrossRef.
- N. Tajima, Crystals, 2018, 8, 126 CrossRef.
- T. Tani, N. Tajima and A. Kobayashi, Crystals, 2019, 9, 212 CrossRef CAS.
- R. Kobara, S. Igarashi, Y. Kawasugi, R. Doi, T. Naito, M. Tamura, R. Kato, Y. Nishio, K. Kajita and N. Tajima, J. Phys. Soc. Jpn., 2020, 89, 113703 CrossRef.
- T. Naito, Crystals, 2021, 11, 838 CrossRef CAS.
- N. P. Amitage, E. J. Mele and A. Vishwanath, Rev. Mod. Phys., 2018, 90, 015001 CrossRef.
- I. Crassee, R. Sankar, W.-L. Lee, A. Akrap and M. Orlita, Phys. Rev. Mater., 2018, 2, 120302 CrossRef CAS.
- A. Kobayashi, Y. Suzumura and H. Fukuyama, J. Phys. Soc. Jpn., 2008, 77, 064718 CrossRef.
- M. Hirata, K. Ishikawa, K. Miyagawa, K. Kanoda and M. Tamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125133 CrossRef.
- Y. Suzumura and A. Kobayashi, J. Phys. Soc. Jpn., 2011, 80, 104701 CrossRef.
- Y. Suzumura and A. Kobayashi, Crystals, 2012, 2, 266 CrossRef CAS.
- M. Monteverde, M. O. Goerbig, P. Auban-Senzier, F. Navarin, H. Henck, C. R. Pasquier, C. Mézière and P. Batail, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245110 CrossRef.
- K. Miyagawa, Y. Sata, T. Taniguchi, M. Hirata, D. Liu, M. Tamura and K. Kanoda, J. Phys. Soc. Jpn., 2016, 85, 073710 CrossRef.
- G. Matsuno, Y. Omori, T. Eguchi and A. Kobayashi, J. Phys. Soc. Jpn., 2016, 85, 094710 CrossRef.
- M. Hirata, K. Ishikawa, K. Miyagawa, M. Tamura, C. Berthier, D. Basko, A. Kobayashi, G. Matsuno and K. Kanoda, Nat. Commun., 2016, 7, 12666 CrossRef CAS PubMed.
- D. Liu, K. Ishikawa, R. Takehara, K. Miyagawa, M. Tamura and K. Kanoda, Phys. Rev. Lett., 2016, 116, 226401 CrossRef PubMed.
- R. Beyer, A. Dengl, T. Peterseim, S. Wackerow, T. Ivek, A. V. Pronin, D. Schweitzer and M. Dressel, Phys. Rev. B, 2016, 93, 195116 CrossRef.
- M. Hirata, K. Ishikawa, G. Matsuno, A. Kobayashi, K. Miyagawa, M. Tamura, C. Berthier and K. Kanoda, Science, 2017, 358, 1403 CrossRef CAS PubMed.
- M. Hirata, A. Kobayashi, C. Berthier and K. Kanoda, Rep. Prog. Phys., 2021, 84, 036502 CrossRef CAS.
- K.-I. Hiraki, S. Harada, K. Arai, Y. Takano, T. Takahashi, N. Tajima, R. Kato and T. Naito, J. Phys. Soc. Jpn., 2011, 80, 014715 CrossRef.
- T. Naito, R. Doi and Y. Suzumura, J. Phys. Soc. Jpn., 2020, 89, 023701 CrossRef.
- T. Naito and R. Doi, Crystals, 2020, 10, 270 CrossRef CAS.
- T. Naito and Y. Suzumura, Crystals, 2022, 12, 346 CrossRef CAS.
- Y. Suzumura and T. Naito, J. Phys. Soc. Jpn., 2022, 91, 064701 CrossRef.
- D. Ohki, K. Yoshimi and A. Kobayashi, Phys. Rev. B, 2020, 102, 235116 CrossRef CAS.
- T. Tsumuraya and Y. Suzumura, Eur. Phys. J. B, 2021, 94, 17 CrossRef CAS.
- S. Kitou, T. Tsumuraya, H. Sawahata, F. Ishii, K.-I. Hiraki, T. Nakamura, N. Katayama and H. Sawa, Phys. Rev. B, 2021, 103, 035135 CrossRef CAS.
- T. Naito and Y. Fukuda, Phys. Chem. Chem. Phys., 2022, 24, 4147 RSC.
- S. Das and V. Jayaraman, Prog. Mater. Sci., 2014, 66, 112 CrossRef CAS.
- M. Dressel, Naturwissenschaften, 2007, 94, 527 CrossRef CAS PubMed.
- T. Naito, R. Oka, K. Ohara, K. Konishi, I. Yamane and T. Shimada, Magnetochemistry, 2023, 9, 153 CrossRef.
- K. Bender, I. Hennig, D. Schweitzer, K. Dietz, H. Endres and H. J. Keller, Mol. Cryst. Liq. Cryst., 1984, 108, 359 CrossRef CAS.
- T. Sugano, G. Saito and M. Kinoshita, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 117 CrossRef CAS PubMed.
- E. L. Venturini, L. J. Azevedo, J. E. Schirber, J. M. Williams and H. H. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 2819 CrossRef CAS PubMed.
- N. Tajima, Y. Kawasugi, T. Morinari, R. Oka, T. Naito and R. Kato, J. Phys. Soc. Jpn., 2022, 92, 013702 CrossRef.
- T. Morinari, J. Phys. Soc. Jpn., 2021, 90, 104709 CrossRef.
- T. Ivek, B. Korin-Hamzić, O. Milat, S. Tomić, C. Clauss, N. Drichko, D. Schweitzer and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 165128 CrossRef.
- T. Nakamura, T. Nobutoki, T. Takahashi, G. Saito, H. Mori and T. Mori, J. Phys. Soc. Jpn., 1994, 63, 4110 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2012, 7, 11 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, the calculated band structure in the kakb plane (Fig. S1), angle- and temperature-dependencies in the ESR spectra (Fig. S2), the parameters for the simulated ESR spectra (Tables S1–S16). See DOI: https://doi.org/10.1039/d3ma00619k |
| ‡ For example, if the two crystallographically independent I3 anions can be assumed to be identical in the hyperfine interactions and thus there are only two hyperfine constants regarding the I3 anions, a single peak could be split into 65 peaks at most. If there are more kinds of hyperfine constants or if there are interactions between nuclear spins on the I atoms, additional peak splitting (super-hyperfine structures) occurs in the spectra, which makes each signal even more difficult to identify. Because of this complexity and many unidentified peaks, quantitative analyses like spectrum simulation were not performed. |
| § The obtained g-values and linewidths are not consistent with those reported in ref. 44. As the observed spectra and other details on the ESR of α-ET2I3 are not described in their paper, the reason for inconsistency is not known. |
| ¶ It should be noted that the local symmetries at particular points in the band structure are independent of the crystallographic symmetry (the space group). |
| || Generally, the ESR signal intensity is not simply proportional to the number of unpaired electrons, when the signal originates from different kinds of electrons with different relaxation times. The Dirac electrons are generally considered to exhibit unusual short relaxation times in linearly dispersive parts of bands around the Fermi energies. However, it should not be assumed that they also exhibit unusual short relaxation times when they are photoexcited to parabolic or cosine bands across band gaps. They may behave as SFs in such non-linearly dispersive bands. Thus, our assumption on the relaxation times of DFs and SFs in ESR should be examined via further studies in the future. |
| This journal is © The Royal Society of Chemistry 2024 |