Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling the complex speciation of halozincate ionic liquids using X-ray spectroscopies and calculations†
J. M.
Seymour
 a,
E.
Gousseva
a,
F. K.
Towers Tompkins
a,
L. G.
Parker
a,
N. O.
Alblewi
a,
C. J.
Clarke
a,
E.
Gousseva
a,
F. K.
Towers Tompkins
a,
L. G.
Parker
a,
N. O.
Alblewi
a,
C. J.
Clarke
 b,
S.
Hayama
c,
R. G.
Palgrave
b,
S.
Hayama
c,
R. G.
Palgrave
 d,
R. A.
Bennett
d,
R. A.
Bennett
 a,
R. P.
Matthews
a,
R. P.
Matthews
 *e and
K. R. J.
Lovelock
*e and
K. R. J.
Lovelock
 *a
*a
aDepartment of Chemistry, University of Reading, Reading, UK. E-mail: k.r.j.lovelock@reading.ac.uk
bSchool of Chemistry, University of Nottingham, Nottingham, UK
cDiamond Light Source, Harwell, UK
dDepartment of Chemistry, University College London, UK
eSchool of Health, Sport and Bioscience, University of East London, UK. E-mail: R.Matthews3@uel.ac.uk
First published on 9th April 2024
Abstract
Using a combination of liquid-phase X-ray spectroscopy experiments and small-scale calculations we have gained new insights into the speciation of halozincate anions in ionic liquids (ILs). Both core and valence X-ray photoelectron spectroscopy (XPS) experiments were performed directly on the liquid-phase ILs, supplemented by Zn 1s X-ray absorption near edge structure (XANES) spectroscopy. Density functional theory (DFT) calculations were carried out on both 1− and 2− halozincate anions, in both a generalised solvation model SMD (Solvation Model based on Density) and the gas phase, to give XP spectra and total energy differences; time-dependent DFT was used to calculate XANES spectra. Speciation judgements were made using a combination of the shape and width of the experimental spectra, and visual matches to the calculated spectra. For 2− halozincate anions, excellent matches were found between the experimental and calculated XP spectra, clearly showing that only 2− halozincate anions were present at all zinc halide mole fractions, x, studied. At specific values of x (0.33, 0.50, 0.60) only one halozincate anion was present; equilibria of different halozincate anions at those values of x were not observed. All findings show that chlorozincate anion and bromozincate anion speciation matched at the same x. Based on the results, predictions are made of the halozincate anion speciation for all values of x up to 0.67. Caution is advised when using differences in calculated total energies obtained from DFT to judge halozincate anion speciation, even when the SMD was employed, as predictions based on total energy differences did not always match the findings from the experimental and calculated spectra. Our findings clearly establish that the combination of high-quality experimental data from multiple spectroscopies and a wide range of calculated structures are essential to have high confidence in halozincate anion speciation identification.
1. Introduction
Halozincate ionic liquids (ILs), formed by ZnHal2 (Hal = halide) added to a halide anion-containing IL (eqn (1), e.g. 1-octyl-3-methylimidazolium chloride, [C8C1Im]Cl),1 have potential applications as catalysts,2 in zinc electrodeposition,3–5 in zinc batteries,6–8 extraction/separation9–13 and preparing antibacterial surfaces.14,15 The variation in speciation (i.e., zinc anions present in solution) with increasing mole fraction of ZnHal2, x, in halozincate ILs potentially allows fine control of both properties (e.g. mass transport) and reactivity (e.g. catalysis, electrodeposition). Lewis acidity and thermal stability increase with increasing x,16,17 and anion–cation interaction strength and cost decrease with increasing x.17–19 Both monomeric and oligomeric halometallate anions can be formed for ZnHal2 + [C8C1Im]Hal, with oligomeric halometallate anions composed of multinuclear metals and bridging halides; oligomeric halometallate anions are not formed for all halometallate ILs, e.g. FeCl2 + Cl−, which forms a solid precipitate at x > 0.33.20 The primary halide ligand studied has been chloride,1 with some focus on bromide. The combination of appealing properties and the ability to tune those properties by varying the composition through sensible choices of both x and halide identity makes halozincates particularly attractive.| (ZnHal2)x + ([C8C1Im]Hal)(1−x) | (1) |
Understanding halozincate speciation is crucial, as it allows informed selection of x and halide. The option to test all x and halide combinations to find the optimum composition for a particular application is not feasible, given the large range of possible x and more than one possible halide. Furthermore, calculated dissociation energies suggest that terminal and bridging halides in halozincate anions have different Zn–Hal bond strengths,17 demonstrating that knowledge of speciation is crucial for interpretation of reactivity data in particular. For example, knowledge of speciation would enable determination of both catalytic and electrodeposition mechanisms, allowing the design of better catalysts and optimisation of reactivity.
Zn is spectroscopically quiet,21 with a dearth of techniques available that probe liquid-phase speciation. Spectroscopies that are suitable for open-shell halometallate complexes are unsuitable for probing halozincate anion speciation, e.g. electron paramagnetic resonance (EPR) and UV-VIS spectroscopy. Indirect methods have been used to study zinc speciation, e.g. bulk property measurements. Mass spectrometry has been widely used, although questions have been raised about the suitability of using both gas-phase and solid-phase techniques to probe liquid-phase speciation,1,22 especially since most 2− halometallate anions are unstable in the gas phase due to strong electrostatic repulsion of the excess electrons.23 Raman spectroscopy, core X-ray photoelectron spectroscopy (XPS), X-ray absorption near edge structure (XANES) spectroscopy and extended X-ray absorption fine structure (EXAFS) have been recommended as the best techniques for probing halozincate speciation.1 Furthermore, calculated anion total energy differences from small-scale density functional theory (DFT) calculations have been used to judge speciation for halobismuthate anions (Gibbs free energies were used)24 and halozincate anions (sum of electronic and zero-point energies were used, although the values were given as dissociation energies).17 A full comparison of spectroscopic and calculated structures has not yet been made for halozincate anions, especially the consideration of both 1− and 2− halozincate anions (see Fig. 1 for 2− halozincate anions and ESI Fig. S1† for 1− halozincate anions).
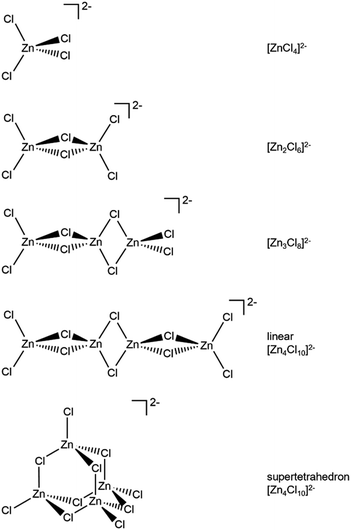 | ||
| Fig. 1 2− chlorozincate structures. Bromozincate anions would be the same apart from Br replacing Cl. See ESI Fig. S1† for 1− chlorozincate structures. | ||
For Zn2+ cations, there is no ligand field stabilisation energy, so the coordination number is primarily determined by the size of the coordinating ligands.25 Zinc is usually tetrahedrally coordinated (although in aqueous solution Zn2+ is coordinated to six water molecules),26 which is expected to be driven by the four vacant orbitals of the Zn2+ cation (4s + 4p3).27 Therefore, one would expect the same coordination number for all chlorozincate anions and the same coordination number for all bromozincate anions, i.e., for all values of x. A strong case has been made based on Raman spectroscopy and core XPS that halozincate anions are always 2−.16,18 However, a case was made using gas-phase mass spectrometry that 1−chlorozincate anions were always formed.28–30 Two pertinent observations can be made. Firstly, no one has claimed to have found both 1− and 2− chlorozincate anions for the same sample, indicating essentially two separate groups of findings. Secondly, when calculations were performed on 1− anions it would appear that 2− halozincate anions were not considered, so these calculations should not be used to judge speciation. Therefore, the speciation of halozincate ILs at different values of x remains an open question.
To quote the excellent review by Swadźba-Kwaśny and co-workers: “The defining characteristic of chlorometallates is the presence of complex anionic equilibria”.1 For halometallate ILs it is possible to form just one halometallate anion at certain values of x (e.g. for halozincates at x = 0.50 it is possible to form just [Zn2Cl6]2−) but equilibria of more than one halozincate anion may also form at these values of x (e.g. at x = 0.50 [Zn2Cl6]2− and [ZnCl3]− or [ZnCl4]2− and [Zn3Cl8]2− could potentially form). For AlCl3 + Cl− multiple chloroaluminate anions have been found at one value of x, e.g. at x = 0.67 both [Al2Cl7]− and [Al3Cl10]− (Fig. 8b),1,31 demonstrating that an equilibrium occurs; an excellent summary for AlCl3 + Cl− is given in ref. 1.
The speciation for x = 0.50 is still not settled; does 2 × ZnCl2 + 2 × Cl− form [Zn2Cl6]2− or 2 × [ZnCl3]−?22 Using extended X-ray absorption fine structure (EXAFS) data at x = 0.50, the coordination number of Zn was 2.9,32 suggesting the formation of [ZnCl3]−. Both fast atom bombardment and electrospray ionisation mass spectrometry studies came to the same conclusion of [ZnCl3]− speciation.28,30 Conversely, Raman spectroscopy and core XPS concluded that [Zn2Cl6]2− was the species at x = 0.50.16,18 Calculations have been performed on both [ZnCl3]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33,34 and [Zn2Cl6]2−.17
33,34 and [Zn2Cl6]2−.17
The speciation for x = 0.67 is also still not settled; does 4 × ZnCl2 + 2 × Cl− form [Zn4Cl10]2− or 2 × [Zn2Cl5]−?22 Using extended X-ray absorption fine structure (EXAFS) data at x = 0.67, the coordination number of Zn was found to be 2.6,32 suggesting the formation of [Zn2Cl5]− with two terminal Cl and one bridging Cl for both Zn centres. Using fast atom bombardment mass spectrometry at x = 0.67, a range of 1− anions was observed: [ZnCl3]−, [Zn2Cl5]−, [Zn3Cl7]− and high-mass clusters.28,29 Electrospray ionisation mass spectrometry experiments reported for x > 0.50 showed [Zn3Cl7]− was present.30 Furthermore, [Zn2Cl5]− was assumed to be the anion in ammonia absorption experiments underpinning their use in absorption refrigerators and heat pumps.13 Conversely, Raman spectroscopy concluded that [Zn4Cl10]2− was the species at x = 0.67.16 In the solid state, a supertetrahedron, [Zn4I10]2−, has been found.35 Calculations have been performed on both [Zn2Cl5]− (with three bridging Cl and one terminal Cl on both Zn centres)36 and [Zn4Cl10]2−.17
Given that both [ZnCl3]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30,32 and [ZnCl4]2−
30,32 and [ZnCl4]2−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16,18,37 are apparently stable, the speciation for x = 0.33 is also not settled; does 1 × ZnCl2 + 2 × Cl− form [ZnCl4]2− or 1 × [ZnCl3]− + 1 × Cl−?22 An interesting property of chlorozincates is that the Lewis acidity (measured using the Gutmann–Beckett method) has a step change at x = 0.33, which indicates a change in speciation at x = 0.33.16
16,18,37 are apparently stable, the speciation for x = 0.33 is also not settled; does 1 × ZnCl2 + 2 × Cl− form [ZnCl4]2− or 1 × [ZnCl3]− + 1 × Cl−?22 An interesting property of chlorozincates is that the Lewis acidity (measured using the Gutmann–Beckett method) has a step change at x = 0.33, which indicates a change in speciation at x = 0.33.16
It is still unclear whether multiple halozincate anions exist in equilibrium at one value of x where it is possible that just one anion forms. For halozincates, mass spectrometry at x = 0.67 suggested an equilibrium of [ZnCl3]−, [Zn2Cl5]−, [Zn3Cl7]− and high-mass clusters,29 but this finding is doubtful given the concerns over the reliability of mass spectrometry for halozincate speciation.22
Element-specific electronic structures can be probed using core XPS and XANES; a major advantage for studying halozincate speciation is the ability to study more than one element, i.e., both zinc and the halide can be studied independently. Core-state-specific binding energies, EB, from XPS can capture the presence of different electronic environments,38–40 including for chlorozincates.18 XANES can also be used to determine the structure using core state to unoccupied valence state absorption energies.41 The ratio of peak areas from core XPS gives the relative abundance of each of those species, as there is no selection rule for core XPS at the same edge for the same element, e.g. two Cl 2p3/2 peaks in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio means a 3
2 ratio means a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of those two Cl-containing species. XPS can be a surface-sensitive technique, but for ILs studied using laboratory XPS (i.e., at hν = 1486.6 eV) and under a normal emission angle, signals reflect bulk IL composition, i.e., no surface sensitivity has been observed.42 Spin–orbit coupling for any orbital that is not an s orbital (e.g. Zn 2p, Cl 2p, Br 3d) contributes two components for each electronic environment in a sample in a predictable peak area ratio and peak splitting, e.g. for Cl 2p the peak area ratio is 2
2 ratio of those two Cl-containing species. XPS can be a surface-sensitive technique, but for ILs studied using laboratory XPS (i.e., at hν = 1486.6 eV) and under a normal emission angle, signals reflect bulk IL composition, i.e., no surface sensitivity has been observed.42 Spin–orbit coupling for any orbital that is not an s orbital (e.g. Zn 2p, Cl 2p, Br 3d) contributes two components for each electronic environment in a sample in a predictable peak area ratio and peak splitting, e.g. for Cl 2p the peak area ratio is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with ΔEB (Cl 2p3/2 − Cl 2p1/2) = 1.60 eV. The timescales of XPS photoemission and XANES are both fs,43 meaning nuclear motion during the core photoemission/photoexcitation process will not contribute to energy differences; if more than one halozincate species is in equilibrium in the IL, both species will contribute to the spectra and the major challenge for detection is sufficient energy separation of the contributions from different halozincate species. For XPS, the core-state peak full width at half maximum (FWHM) is dependent on the core state studied (each core state has a fixed width contribution due to lifetime broadening44), instrumental factors (which are very similar for modern XPS apparatus), vibrational contributions, and the sample speciation.45–48 Molecules and ions in liquids give significantly larger measured FWHM values than metal single crystals such as Pt due to their greater disorder.49 On a microscopic level, there are a range of different solvation environments for Cl− solvated by [C8C1Im]+ in the liquid phase, and these different solvation environments contribute to the XPS FWHM;19 on a macroscopic level, [C8C1Im]Cl and [C8C1Im]Br both present one halide electronic environment in the liquid phase. Bridging and terminal chlorine atoms have been observed using XPS for both halometallate solids50 and chlorozincate anions in ILs.18 Valence XPS has not been used to probe halometallate speciation for ILs to date.24
1 with ΔEB (Cl 2p3/2 − Cl 2p1/2) = 1.60 eV. The timescales of XPS photoemission and XANES are both fs,43 meaning nuclear motion during the core photoemission/photoexcitation process will not contribute to energy differences; if more than one halozincate species is in equilibrium in the IL, both species will contribute to the spectra and the major challenge for detection is sufficient energy separation of the contributions from different halozincate species. For XPS, the core-state peak full width at half maximum (FWHM) is dependent on the core state studied (each core state has a fixed width contribution due to lifetime broadening44), instrumental factors (which are very similar for modern XPS apparatus), vibrational contributions, and the sample speciation.45–48 Molecules and ions in liquids give significantly larger measured FWHM values than metal single crystals such as Pt due to their greater disorder.49 On a microscopic level, there are a range of different solvation environments for Cl− solvated by [C8C1Im]+ in the liquid phase, and these different solvation environments contribute to the XPS FWHM;19 on a macroscopic level, [C8C1Im]Cl and [C8C1Im]Br both present one halide electronic environment in the liquid phase. Bridging and terminal chlorine atoms have been observed using XPS for both halometallate solids50 and chlorozincate anions in ILs.18 Valence XPS has not been used to probe halometallate speciation for ILs to date.24
In this article, we report a comprehensive study of the speciation of halozincate anions in ILs. We intend to primarily answer four questions. (i) What is the speciation at specific values of x where only one halozincate anion may be present? (ii) What contribution does an equilibria of different halozincate anions play in speciation? (iii) Can small-scale DFT calculations capture halozincate speciation? (iv) What is the effect of chloro versus bromo ligands for halozincate speciation? We answer these questions using a combination of core XPS, valence XPS, Zn 1s high-energy resolution fluorescence detected (HERFD)-XANES spectroscopy, DFT calculations for XPS (both core and valence) and total energies, and time-dependent DFT calculations for Zn 1s XANES spectroscopy. We performed calculations for both 2− and 1− halozincate anions.
2. Methods
2.1. Experimental
XP spectra for 20 ILs are used in this paper. Core and valence XP spectra were published for 16 ILs in the ESI of ref. 51 and for three ILs in the ESI of ref. 19. XP spectra are published for the first time for x = 0.43 where (ZnCl2)x + ([C8C1Im]Cl)(1−x). EB(core) values for all 20 ILs are published for the first time here (ESI Table S4†).The halozincate IL samples (∼1 drop) were mounted between two pieces of Kapton tape and were kept in place by a plastic O-ring. We used the Si (111) monochromator crystal cut to select the incident energy.52 Zn 1s HERFD-XANES measurements were taken using the I20 X-ray emission spectrometer52 equipped with three Ge (555) analyser crystals, set at an emission energy of 9572 eV to capture the Kβ1,3 (3p → 1s) X-ray emission.53 The spectrometer was calibrated using a Zn foil, measuring the Kβ1,3 line with the incident energy tuned +100 eV from the Zn 1s absorption edge. HERFD-XANES measurements offer better spectral resolution than conventional XANES and are ideally suited for probing unoccupied states.54
We emphasise that all XPS and XANES measurements discussed in this article were made at room temperature.
2.2. Calculations
DFT calculations were performed using Gaussian 16 (version C.01).55 All zinc halide structures were optimised under no symmetry constraints and confirmed as minima via vibrational analysis employing the long-range corrected ωB97XD functional56–59 in combination with the quadruple zeta def2-QZVPP basis set (see ESI† Section 12 for comparisons to data calculated using the triple zeta def2-TZVPP basis set). Several of the initial starting structures were taken from previous work.17 To account for solvent effects, the SMD (Solvation Model based on Density) was used, specifically the [C4C1Im][PF6] parameters (relative permittivity, εr, = 11.40; refractive index, n, = 1.4090; surface tension, γ, = 0.266 cal mol−1 Å2; Abraham basicity, β, = 0.216).60 Moreover, optimisation convergence criteria were set to 10−11 on the density matrix and 10−9 on the energy matrix, and the numerical grid was improved from the default using the keywords (int=SuperFineGrid) which gives a pruned (optimised) grid of 250 radial shells and 974 angular points per shell. Vibrational frequencies and zero-point vibrational energy corrections (ZPE) were attained using the harmonic approximation.The procedure to convert calculated EB results into calculated XP spectra is explained in ESI Section 4.† Spin–orbit coupling contributions were added for Cl 2p, Br 3d and Zn 2p, with the parameters given in ESI Table S3.†
Single-point calculations were computed using ORCA (v 5.0.3).61 The electronic structure was calculated with time-dependent DFT for Zn 1s XANES, using the ωB97X-D3BJ functional,62 the ZORA-def2-QZVPP basis set59 and the SARC/J auxiliary basis set.58 Scalar relativistic effects were taken into account by applying the zeroth-order regular approximation (ZORA).63 In all cases, electric-dipole, magnetic-dipole, and quadrupole contributions were allowed in the spectral calculations. Time-dependent DFT calculations were performed with the Tamm–Dancoff approximation (TDA) applied. For the XANES calculation, the Zn 1s orbital was excited into all virtual unoccupied molecular orbitals to mimic the Zn 1s K-edge XANES. Calculated XANES spectra were shifted by −8.9 eV to align with the experimental absorption energies. All XANES spectra were generated by convoluting the computed energies and oscillator strengths with Gaussian functions with a full width at half maximum (FWHM) of 2.5 eV.
2.3. Fitting/analysis
All experimental XP spectra were fitted using CasaXPS™ software.64 Fitting was carried out using a Shirley background and GL30 line shapes (70% Gaussian, 30% Lorentzian). The peak constraints used are outlined in the ESI Section 2.† Relative sensitivity factors from ref. 65 were used to ensure the experimentally-derived stoichiometries matched the nominal stoichiometries.All XPS EB(core,exp.) were shifted relative to EB(Calkyl 1s, exp.) = 285.00 eV, as is standard for ILs.51,66,67
In some cases, calculated XP spectra were shifted in EB to give the best visual match; EB shifts used are given in the figure captions. Calculated Zn 1s XANES spectra were shifted −8.9 eV in energy, which has been found to give excellent matches to experimental XANES spectra.68
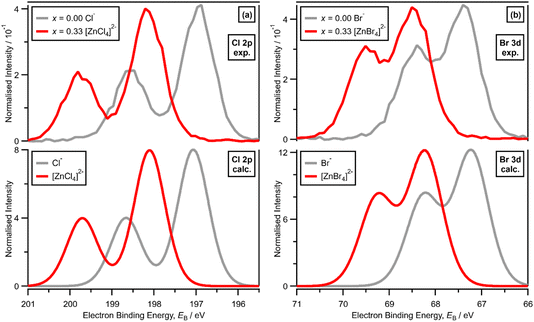
XPS of [C8C1Im]Cl, i.e., x = 0.00 with Cl− solvated by [C8C1Im]+, gives one experimental Cl electronic environment in the Cl 2p core XP spectrum, which manifests as two peaks due to spin–orbit coupling; ΔEB(Cl 2p3/2 − Cl 2p1/2) = 1.60 eV and the peak area ratio for Cl 2p3/2 to Cl 2p1/2 is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 2a). The same occurs for [C8C1Im]Br, where XPS gives one experimental Br electronic environment in the Br 3d core XP spectrum (Fig. 2b); ΔEB(Br 3d5/2 − Br 3d3/2) = 1.04 eV and the peak area ratio for Br 3d5/2 to Br 3d3/2 is 3
1 (Fig. 2a). The same occurs for [C8C1Im]Br, where XPS gives one experimental Br electronic environment in the Br 3d core XP spectrum (Fig. 2b); ΔEB(Br 3d5/2 − Br 3d3/2) = 1.04 eV and the peak area ratio for Br 3d5/2 to Br 3d3/2 is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Fig. 2c). On a macroscopic level, [C8C1Im]Cl and [C8C1Im]Br both present one halide electronic environment in the liquid phase with FWHM values of ∼0.90 eV and ∼0.85 eV, respectively (ESI Table S5†). Therefore, we use the Cl 2p XP spectrum for [C8C1Im]Cl and the Br 3d XP spectrum for [C8C1Im]Br as our baseline for judging one halide electronic environment in the liquid phase.
2 (Fig. 2c). On a macroscopic level, [C8C1Im]Cl and [C8C1Im]Br both present one halide electronic environment in the liquid phase with FWHM values of ∼0.90 eV and ∼0.85 eV, respectively (ESI Table S5†). Therefore, we use the Cl 2p XP spectrum for [C8C1Im]Cl and the Br 3d XP spectrum for [C8C1Im]Br as our baseline for judging one halide electronic environment in the liquid phase.
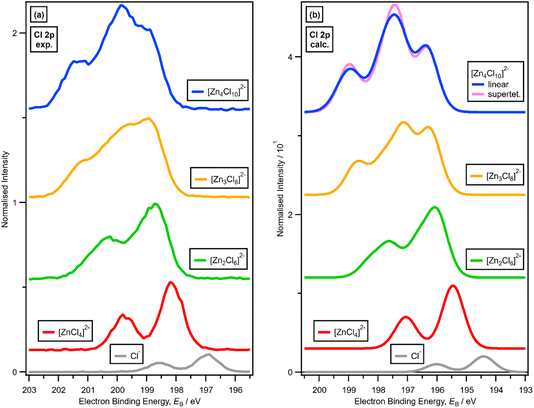
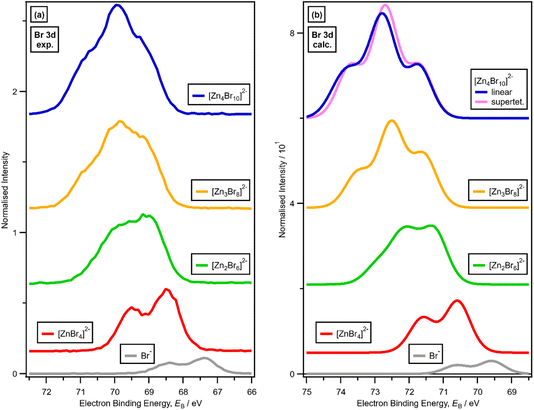
3. Results
3.1. Speciation at x = 0.33: 1 × ZnHal2 + 2 × Hal− forms [ZnHal4]2−
For x = 0.00 and x = 0.33 the experimental and calculated Cl 2p XPS results match both in terms of EB differences and FWHM (Fig. 2a), which indicates that all four Cl atoms are equivalent for x = 0.33. The core XPS makes clear that there are four terminal chlorides in each [ZnCl4]2− anion, with no other anion species detectable, i.e., no Cl−, [Zn2Cl6]2− or [ZnCl3]−. Therefore, anion speciation for x = 0.33 is [ZnCl4]2−. The same results are found for x = 0.33 with Br; the experimental and calculated Br 3d spectra match for x = 0.00 and x = 0.33, both in terms of EB differences and FWHM (Fig. 2b). Therefore, anion speciation for x = 0.33 is [ZnBr4]2−. Our results match well to findings from Raman spectroscopy and EXAFS,16,18,37 and demonstrate that the gas-phase [ZnCl3]− speciation observed using mass spectrometry30,32 does not match the liquid-phase speciation.3.2. Speciation at x = 0.50: 2 × ZnHal2 + 2 × Hal− forms [Zn2Hal6]2− and not 2 × [ZnHal3]−
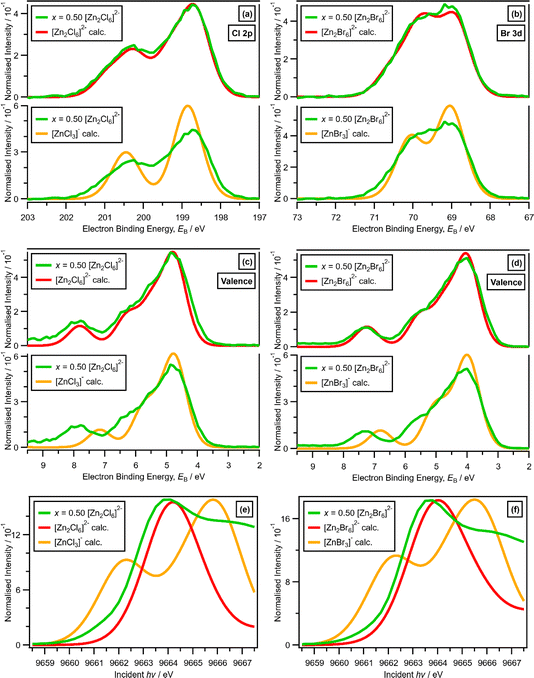
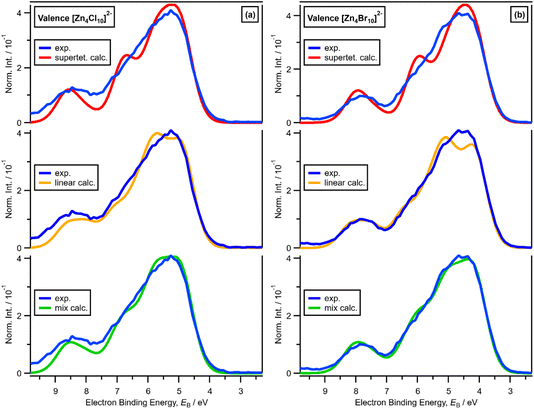
For x = 0.50, i.e., 2 × ZnHal2 + 2 × Hal−, more than one halide electronic environment exists for both Cl and Br, as the Cl 2p and Br 3d photoemission profiles for x = 0.50 do not visually match the shape of the Cl 2p and Br 3d XP spectra, respectively (Fig. 2), confirming that there is more than one halide environment for x = 0.50. Therefore, at x = 0.50 the speciation cannot be [ZnHal3]− only (with no [Zn2Cl6]2−), as [ZnHal3]− would give a single halide environment in Cl 2p/Br 3d XPS. The visual match of experimental and calculated core and valence XPS for both Cl and Br for the experimental x = 0.50 versus calculated [Zn2Hal6]2− are almost perfect (Fig. 3a to d). The core XPS makes clear that there are two bridging and four terminal halides in each [Zn2Hal6]2− anion (which in an ideal structure has D2h symmetry), matching the speciation found using Raman spectroscopy.16 Furthermore, the visual match of experimental and calculated core and valence XPS for both Cl and Br for the experimental x = 0.50 versus [ZnHal3]− are relatively poor (Fig. 3a to d). Moreover, the experimental Zn 1s XANES spectroscopy results for x = 0.50 for both Cl and Br match well to the calculated Zn 1s XANES spectroscopy results for [Zn2Hal6]2− and very poorly to [ZnHal3]− (Fig. 3e and f). Therefore, the [ZnCl3]− speciation proposed from gas-phase mass spectrometry results28,30 does not reflect the liquid-phase speciation. Overall, our results show definitively that x = 0.50 (i.e., 2 × ZnCl2 + 2 × Cl−) gives [Zn2Cl6]2− and not 2 × [ZnCl3]−.3.3. Speciation at x = 0.67: 4 × ZnHal2 + 2 × Hal− forms linear and supertetrahedral [Zn4Hal10]2−
x = 0.67, i.e., 2 × ZnHal2 + 1 × Hal−, gave more than one halide electronic environment, as the Cl 2p (and Br 3d) results for x = 0.67 do not match the Cl 2p (and Br 3d) results for x = 0.00 (Fig. 6a and 7a). Furthermore, the visual matches of experimental and calculated core and valence XPS for both Cl and Br for the experimental x = 0.67 versus [Zn4Hal10]2− (both for the linear form with D2h symmetry and the supertetrahedral form with Td symmetry, Fig. 1) are good (Fig. 4, Fig. 6 and 7), matching a finding from Raman spectroscopy of linear [Zn4Cl10]2−.16 The core XPS makes clear that there are six bridging and four terminal halides in each [Zn4Hal10]2− anion (ESI Fig. S7d and S12d†). Therefore, a structure that has been suggested in the literature,36 [Zn2Cl5]− with three bridging Cl atoms between the two Zn atoms and one terminal Cl atom on each Zn atom (ESI Fig. S1†), is certainly not present, confirmed by the visual mismatch between experimental and calculated XP spectra (both core Cl 2p and valence, ESI Fig. S22 and S23†). Furthermore, [Zn2Cl5]− with two bridging Cl atoms between the two Zn atoms, two terminal Cl atom on one Zn atom, and one terminal Cl atom on one Zn atom could not be optimised using DFT calculations. However, the core XPS is not suitable for distinguishing contributions from the linear and supertetrahedral forms. The visual matches of experimental and calculated valence XPS for both Cl and Br for the experimental x = 0.67 versus [Zn4Hal10]2− are good (Fig. 4, top and middle). However, the calculated valence XPS for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 combination of the linear and supertetrahedral forms gives an even better visual match (Fig. 4, bottom) than the valence XPS results for the individual linear and supertetrahedral forms (Fig. 4, top and middle). The uncertainty in the 1
1 combination of the linear and supertetrahedral forms gives an even better visual match (Fig. 4, bottom) than the valence XPS results for the individual linear and supertetrahedral forms (Fig. 4, top and middle). The uncertainty in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is relatively large, but we are confident that the speciation for x = 0.67 is not only one species. Overall, we found good evidence that two species are present for x = 0.67, linear and supertetrahedral [Zn4Cl10]2−, in approximately a 1
1 ratio is relatively large, but we are confident that the speciation for x = 0.67 is not only one species. Overall, we found good evidence that two species are present for x = 0.67, linear and supertetrahedral [Zn4Cl10]2−, in approximately a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, with no evidence for the presence of 1− anions such as [ZnCl3]−, [Zn2Cl5]− and [Zn3Cl7]− observed using mass spectrometry and found from EXAFS data.28–30,32
1 ratio, with no evidence for the presence of 1− anions such as [ZnCl3]−, [Zn2Cl5]− and [Zn3Cl7]− observed using mass spectrometry and found from EXAFS data.28–30,32
3.4. Speciation at x = 0.33, 0.50, 0.60 for halozincates: one anion present
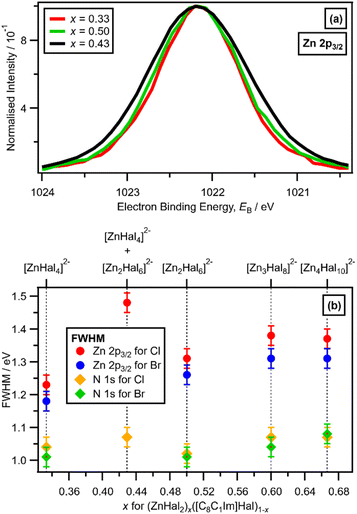
Results from Section 3.1 for x = 0.33 and Section 3.2 for x = 0.50 all point towards there being only one species present, [ZnCl4]2− and [Zn2Cl6]2−, respectively. Results from Section 3.3 show that there were two anions present for x = 0.67, linear and supertetrahedral [Zn4Hal10]2−. For x = 0.43, it is impossible for there to be only one anion present; two anions must be present, predicted to be a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of [ZnCl4]2− and [Zn2Cl6]2−.
1 ratio of [ZnCl4]2− and [Zn2Cl6]2−.
A larger FWHM (Zn 2p3/2) for x = 0.43 was clearly observed, relative to x = 0.33 and x = 0.50 (with Cl ligands), when the Zn 2p3/2 XP spectra are set at the same EB (Zn 2p3/2) and normalised to the same peak intensity to make visual judgements of the FWHM relatively easy (Fig. 5a). The FWHM (Zn 2p3/2) obtained from peak fitting (Fig. 5b) gave the same results as the visual assessment of the peak FWHM (Fig. 5a). The order of FWHM (Zn 2p3/2) (and FWHM (Zn 2p1/2), ESI Fig. S24†) for x was: 0.33 < 0.50 < 0.60 ≈ 0.67 < 0.43 (Fig. 5b). Therefore, the FWHM (Zn 2p3/2) was far larger for x = 0.43 when two species were definitely present than all other values of x (Fig. 5b). For x = 0.43 and x = 0.67, two anions were present for both solutions, but the FWHM (Zn 2p3/2) was substantially larger for x = 0.43 than x = 0.67, because the two anions present for x = 0.67 (linear and supertetrahedral [Zn4Cl10]2−) were more similar than the two anions present for x = 0.43 ([ZnCl4]2− and [Zn2Cl6]2−).
There is a very good match of experimental and calculated XPS for both EB (Cl 2p) and XP spectral shape as x increased for Cl-containing ILs (Fig. 6); the same observations hold for EB (Br 3d) as x increased for Br-containing ILs (Fig. 7). These findings provide more evidence that one halozincate anion exists at certain values of x.
These observations confirm that one halozincate anion was present for x = 0.33, x = 0.50 and x = 0.60, which are [ZnHal4]2−, [Zn2Hal6]2− and [Zn3Hal8]2−, respectively (Fig. 8a). Furthermore, at x = 0.67 only [Zn4Hal10]2− is present, most likely a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or similar combination of linear and supertetrahedral [Zn4Hal10]2−. This finding contrasts with results for AlCl3 + Cl−,1 where multiple anions were proposed where there was the potential to form only one anion, e.g. x = 0.67 (Fig. 8b).
1 or similar combination of linear and supertetrahedral [Zn4Hal10]2−. This finding contrasts with results for AlCl3 + Cl−,1 where multiple anions were proposed where there was the potential to form only one anion, e.g. x = 0.67 (Fig. 8b).
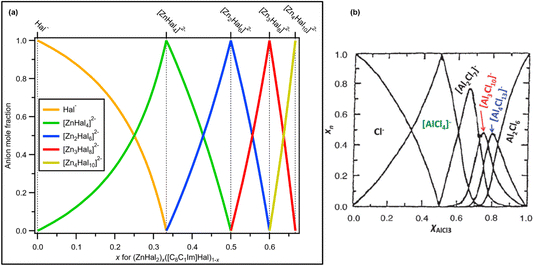 | ||
| Fig. 8 (a) Mole fraction of anion products plotted against mole fraction of zinc halide starting material for mixtures of ZnHal2 and [C8C1Im]Hal. Values for x = 0.00, x = 0.33, x = 0.50, x = 0.60 and x = 0.67 are known; anion product speciation at other values of x is calculated. (b) Mole fraction of anion products plotted against mole fraction of aluminium chloride starting material for mixtures of AlCl3 and [C2C1Im]Hal (at 200 °C, calculated from a thermodynamic model; taken with permission from ref. 1, original data from ref. 69). | ||
3.5. Chlorozincate and bromozincate speciation match at all values of x
All the data presented so far in this article (Figure 2 to 7) show that chlorozincate and bromozincate ILs have the same anion speciation at any value of x. One last piece of evidence is that both the experimental and calculated valence XPS for each value of x studied have the same spectral features, i.e., the anion(s) present for each value of x has the same bonding and therefore the same speciation whether the ligands are Cl or Br (ESI Fig. S25†). For example, at x = 0.33 there are clearly three groups of features for both chlorozincate and bromozincate (ESI Fig. S25a and d†), i.e., the bonding and therefore the speciation was the same: [ZnHal4]2−. The same feature comes at an EB value that is ∼0.7 eV lower in the experimental valence XPS for bromozincate anions compared to the chlorozincate anions (ESI Fig. S25a and c†), and at an EB value that is ∼1.0 eV lower in the calculated valence XPS for bromozincate anions compared to the chlorozincate anions (ESI Fig. S25d and f†).3.6. Halozincate speciation: discussion
All our experimental evidence, backed up by calculations, shows that only 2− halozincate anions occur in the liquid phase up to x = 0.67 (Fig. 8a). For certain values of x only one anion formed within our detection limit (estimated to be 1% of the main species): x = 0.33 ([ZnHal4]2−), x = 0.50 ([Zn2Hal6]2−) and x = 0.60 ([Zn3Hal8]2−) (Fig. 8a), demonstrating that any equilibria with other anions is very much towards the halozincate anions listed here. Our liquid-phase findings using X-ray spectroscopy contrast strongly to findings from gas-phase mass spectrometry, where equilibria of multiple halozincate anions were observed.29 Clearly, mass spectrometry is an inadequate technique for studying speciation of halozincate anions in ILs,22 and probably for all anions with a formal negative charge of 2− or larger. For x = 0.67, only one anion composition was found but with two different isomers, supertetrahedral and linear [Zn4Hal10]2− (Fig. 8a), suggesting that an equilibrium occurred for x = 0.67. We expect that the same trend will continue for larger values of x as ZnHal2 does not form stable neutral dimers (unlike AlCl3 [ref. 1 and 69]), e.g. at x = 0.714 we predict only [Zn5Cl12]2− would form. Overall, there are specific turning points in the halozincate speciation.For all values of x, at least up to x = 0.60, there are definitely two 2− halozincate anions present for all non-turning-point values of x (i.e., all x values apart from x = 0.33, x = 0.50 and x = 0.60, Fig. 8a). It is tough to use X-ray spectroscopy to judge the exact halozincate speciation for x away from the turning-point x values, as demonstrated by the Cl 2p XPS data for x = 0.43 (ESI Section 2†). However, given the fact we have these turning-point x values, we expect that at 0.33 < x < 0.67 the speciation can be predicted to be a combination of the expected ratios of halozincate anions (Fig. 8a). For example, x = 0.556 would give 1 × [Zn2Cl6]2− + 1 × [Zn3Cl8]2−, x = 0.538 would give 2 × [Zn2Cl6]2− + 1 × [Zn3Cl8]2− and x = 0.571 would give 1 × [Zn2Cl6]2− + 2 × [Zn3Cl8]2− (Fig. 8a).
IL Lewis acidity (measured using the Gutmann–Beckett method) has a step change at x = 0.33,16 which matches the change in speciation above x = 0.33 with the appearance of [Zn2Cl6]2−. Furthermore, the Lewis acidity shows no significant step changes with relatively gentle increases when x was increased to above x = 0.50 or above x = 0.60,16 even though we know new halozincate anions appear above those x values. Therefore, the presence of bridging Zn–Hal bonds appears to be essential for high halozincate Lewis acidity. Zinc centres with four halide bonds do not appear capable of increasing their coordination number to allow the bonding of the Lewis basic probe, triethylphosphine oxide (TEPO), as [ZnCl4(OH2)]2− and [ZnBr4(OH2)]2− are calculated to be thermodynamically unstable species.70–72 Therefore, for halozincate anions the TEPO probe would have to bind to a zinc centre after the breaking of a Zn–Hal bond. We propose that bridging Zn–Hal bonds dissociate more readily than terminal Zn–Hal bonds, meaning that halozincate anions with bridging Zn–Hal bonds have higher Lewis acidity than [ZnHal4]2−. The smaller changes in Lewis acidity as x increased above 0.33 were likely due to a combination of bridging Zn–Hal bonds being easier to dissociate for larger halozincate anions (apart from supertetrahedral [Zn4Hal10]2− we expect) and changes in the electronic structure.
Thermal stability increases with increasing x,17 which can be related principally to metal-complex speciation. It has been proposed that the presence of free Hal− ions is required for thermal decomposition of halozincate ILs.17 Hence, thermal stability shows a significant increase from x = 0.00 to x = 0.33, where only [ZnCl4]2− and no free Hal− ions are present.17 Thermal stability continues to increase with increasing x beyond x = 0.33, indicating that the presence of halozincate anions with a bridging Hal leads to increased thermal stability, likely due to the greater energy barrier to forming free Hal− anions.
The viscosity of halozincate ionic liquids is larger than their haloaluminate equivalents.29 This greater viscosity is very likely linked to the speciation, i.e., the differences in charge of the anions [ZnnHal2n+2]2− and [AlnHal3n+1]−. In general, ILs with 2− halometallate anions have stronger electrostatic interactions with organic cations than 1− halometallate anions, although that is not true across all halometallate anions.18,19
To fully understand many of the properties of halometallate-containing ILs, e.g. anion redox properties, both the speciation and the electronic structure need to be considered. The electronic structure of halozincate anions will be considered in a separate publication.73
For some applications, e.g. catalysis, trace amounts of an unexpected halozincate anion could make data interpretation very challenging indeed. The chances of making an IL with only one value of x is expected to be extremely challenging. Commercial ZnCl2 often contains traces of hydroxide, even those sold as anhydrous,74 meaning that the composition a researcher intends to make may not quite occur.
3.7. Attempting to use differences in calculated total energies to predict speciation
The introduction of an SMD provides an adequate description/approximation of the surrounding solvent environment without actually explicitly including cations and additional anions. This is a big bonus, especially as it allows for the use of large basis sets (as in this case).In the gas phase, total energies from calculations strongly suggest that 1− anions are massively more stable than 2− anions (ESI Table S6†). For example, 2 × [ZnCl3]− + 2 × Cl− are far more stable in the gas phase than 2 × [ZnCl4]2− (ESI Table S6†). Firstly, this finding is in complete contrast to our liquid-phase experimental speciation. Secondly, this finding also strongly indicates why anion speciation from mass spectrometry techniques is unlikely to match liquid-phase speciation, as gas-phase stability must be a strong factor in the halozincate anions observed in the mass spectrometry.
For calculations using the SMD, there are a number of examples where the halozincate anion speciation predicted by the calculated total energies does not match our experimental findings according to ΔG (Table 1): (i) for x = 0.33, 1 × [ZnCl3]− + 1 × Cl− is considerably more stable than 2 × [ZnCl4]2−, and 1 × [ZnBr3]− + 1 × Br− is the same stability as 2 × [ZnBr4]2−; (ii) for x = 0.50, 2 × [ZnHal3]− is considerably more stable than 1 × [Zn2Hal6]2− for both Cl and Br ligands; (iii) for x = 0.67, 1 × supertetrahedral [Zn4Hal10]2− is considerably more stable than 1 × linear [Zn4Hal10]2− for both Cl and Br ligands; (iv) for x = 0.60, 1 × [Zn2Hal6]2− + 1 × supertetrahedral [Zn4Hal10]2− is more stable than 2 × [Zn3Hal8]2−. Of these mismatches of experimental data and calculated total energy differences, numbers (i), (ii) and (iv) in our list above are the ones that make us doubt the reliability of using calculated total energy differences to judge anion speciation, as we have very high confidence in our experimental measurements of anion speciation for x = 0.33, x = 0.50 and x = 0.60. For mismatch (iii) listed above, we are less confident of our experimental measurements of anion speciation for x = 0.67.
| ZnHal2 mole fraction, x | Reactants | Possible anionic speciesa | ΔE/kJ mol−1 | ΔG/kJ mol−1 |
|---|---|---|---|---|
| a Experimental speciation given in bold in this column. | ||||
| 0.33 | 4 × Cl− + 2 × ZnCl2 | 2 × [ZnCl 4 ] 2 − | ||
| 2 × Cl− + 1 × [Zn2Cl6]2− | 45 | 35 | ||
| 2 × Cl− + 2 × [ZnCl3]− | 45 | −24 | ||
| 0.33 | 4 × Br− + 2 × ZnBr2 | 2 × [ZnBr 4 ] 2 − | ||
| 2 × Br− + 1 × [Zn2Br6]2− | 31 | 32 | ||
| 2 × Br− + 2 × [ZnBr3]− | 57 | 4 | ||
| 0.43 | 4 × Cl− + 3 × ZnCl2 | 1 × [ZnCl 4 ] 2 − + 1 × [Zn 2 Cl 6 ] 2 − | ||
| 1 × Cl− + 1 × [ZnCl3]− + 1 × [Zn2Cl6]2− | 22 | −12 | ||
| 1 × Cl− + 3 × [ZnCl3]− | 22 | −71 | ||
| 0.50 | 4 × Cl− + 4 × ZnCl2 | 2 × [Zn 2 Cl 6 ] 2 − | ||
| 1 × [ZnCl4]2− + 1 × [Zn3Cl8]2− | 33 | 32 | ||
| 4 × [ZnCl3]− | 0 | −118 | ||
| 0.50 | 4 × Br− + 4 × ZnBr2 | 2 × [Zn 2 Br 6 ] 2 − | ||
| 1 × [ZnBr4]2− + 1 × [Zn3Br8]2− | 36 | 27 | ||
| 4 × [ZnBr3]− | 53 | −57 | ||
| 0.60 | 4 × Cl− + 6 × ZnCl2 | 2 × [Zn 3 Cl 8 ] 2 − | ||
| 1 × [Zn2Cl6]2− + 1 × linear [Zn4Cl10]2− | 13 | 21 | ||
| 1 × [Zn2Cl6]2− + 1 × supertetrahedral [Zn4Cl10]2− | −30 | −17 | ||
| 0.60 | 4 × Br− + 6 × ZnBr2 | 2 × [Zn 3 Br 8 ] 2 − | ||
| 1 × [Zn2Br6]2− + 1 × linear [Zn4Br10]2− | 17 | 18 | ||
| 1 × [Zn2Br6]2− + 1 × supertetrahedral [Zn4Br10]2− | −25 | −20 | ||
| 0.67 | 2 × Cl− + 4 × ZnCl2 | 1 × linear [Zn 4 Cl 10 ] 2 − | ||
| 1 × supertetrahedral [Zn 4 Cl 10 ] 2 − | −44 | −38 | ||
| 2 × [Zn2Cl5]− | 61 | 10 | ||
| 0.67 | 2 × Br− + 4 × ZnBr2 | 1 × linear [Zn 4 Br 10 ] 2 − | ||
| 1 × supertetrahedral [Zn 4 Br 10 ] 2 − | −41 | −38 | ||
It is clear from the calculations that by total energy differences the supertetrahedral [Zn4Hal10]2− is judged as far more stable than the linear [Zn4Hal10]2−. It is possible that the calculated total energy differences are simply unreliable in this case. It could also be that kinetic contributions are important here, that the supertetrahedral [Zn4Hal10]2− takes a relatively large amount of energy to form. Such discussions are beyond the scope of our calculations.
Two different energy values (at least) have been used for judging halozincate speciation: Gibbs free energies, ΔG, and the sum of electronic and zero-point energies, ΔE (Table 1). If only total energy differences were used to judge speciation, different conclusions would be drawn if either ΔG or ΔE were used (Table 1). For example, for x = 0.33, ΔG predicts that 2 × [ZnCl3]− + 2 × Cl− is more stable than 2 × [ZnCl4]2−, whereas the reverse is true using ΔE (Table 1) and also our conclusions from experimental data. Overall, it is clear that ΔE is better for judging speciation than ΔG (Table 1), as ΔE predicts speciation that matches experimental data more often than ΔG. However, neither ΔE nor ΔG match experimental speciation at all values of x (Table 1), demonstrating that total energy differences obtained from small-scale DFT calculations should be treated with caution when judging speciation of halozincate anions, and most likely all halometallate anions.
There are two reasons for this mismatch of speciation from experimental and calculated total energy differences. Firstly, the relative permittivity we are using is not correct; it is likely too low. We expect total energy differences from ΔG values will be very sensitive to the solvation environment, in our case the choice of the relative permittivity used for the SMD. We estimate that the relative permittivity needs to be set to ∼40 (rather than the value of 11.4 that we have used as standard here) for ΔG to predict x = 0.33 that 2 × [ZnCl4]2− is more stable than 2 × [ZnCl3]− + 2 × Cl− (ESI Table S6†). Secondly, the local structures around the halozincate anions are important for energetics. When using lone anions in an SMD, specific anion–cation interactions are clearly not included in the calculations, and these interactions may be important for capturing true total energy differences. A major drawback for capturing these specific anion–cation interactions is at least two cations would be required for each 2− halozincate anion to achieve charge neutrality, and even larger clusters may be needed, which would be prohibitively expensive, especially with the DFT methods used in this article.
Overall, we have demonstrated that using anion total energies from small-scale DFT calculations (used, for example, for halobismuthate anions24) is not suitable as a standalone method for determining liquid phase halozincate speciation. Experimental data, ideally from both core and valence XPS and at times backed up by XANES spectroscopy, is required to have high confidence in judging anion speciation for halometallate ILs.
Attempts have been made to use calculated total energies (which can be used to calculate dissociation energies) to judge halozincate anion thermal stability.17 Our work suggests that ΔE and not ΔG would be far better placed to judge thermal stability.
4. Conclusions
We have undertaken a comprehensive study of the speciation of halozincate anions in ILs using a combination of core XPS, valence XPS, Zn 1s XANES spectroscopy, DFT calculations for XPS and total energies, and time-dependent DFT calculations for XANES spectroscopy. We believe this is the first study that considers both 1− and 2− halozincate anions from a computational perspective. We have demonstrated that at specific values of the zinc halide mole fraction, x, only one halozincate anion was present, and the equilibria of different halozincate anions at those values of x do not occur to any significant level. Furthermore, we have made predictions of the speciation for all values of x up to 0.67. Small-scale DFT calculations were used in conjunction with experimental X-ray spectroscopy data to capture halozincate speciation, but we advise caution when using differences in calculated total energies to judge halozincate speciation. Lastly, we demonstrated that speciation for chlorozincates and bromozincates was the same at any particular value of x.Our findings prove that high-quality data from multiple spectroscopies and calculations are essential to have high confidence in halozincate anion speciation identification. Moreover, our methodology can be used to identify the speciation of any halometallate anion, which is especially important for the many spectroscopically quiet closed-shell metals, e.g. Ga, In, and Bi. Furthermore, our methodology of using the core XPS peak FWHM to judge speciation will be suitable for halometallates that are capable of expanding their coordination number, e.g. In (we have shown here [ESI Fig. S26 and S27†] that 1 × InCl3 + 1 × Cl− forms exclusively (at our detection limit) [InCl4]− as there is one Cl electronic environment, the same as Cl−). ILs with more than one metal cation present have been shown to have complex speciation,75 which our methods will also be suitable for. Lastly, catalysis using halometallate ILs is often run above room temperature; there are great challenges determining speciation in such cases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
KRJL acknowledges support from a Royal Society University Research Fellowship (URF\R\150353 and URF\R\211005). JMS acknowledges support from a Royal Society University Research Fellowship Enhancement Award (RGF\EA\180089). EG acknowledges support from a Royal Society Research Grant for Research Fellows (RGF\R1\180053). LGP and FKTT acknowledge support from a Royal Society Research Fellows Enhanced Research Expenses (RF\ERE\210061). NOA acknowledges the Saudi Culture Bureau. We acknowledge Diamond Light Source for time on Beamline I20 under Proposals SP24305, SP28565 and SP30597. Prof. Gosia Swadźba-Kwaśny is thanked for helpful discussion.References
- J. Estager, J. D. Holbrey and M. Swadźba-Kwaśny, Chem. Soc. Rev., 2014, 43, 847–886 RSC.
- K. Li, H. Choudhary and R. D. Rogers, Curr. Opin. Green Sustainable Chem., 2018, 11, 15–21 CrossRef.
- A. P. Abbott and K. J. McKenzie, Phys. Chem. Chem. Phys., 2006, 8, 4265–4279 RSC.
- Z. Liu, T. Cui, T. Q. Lu, M. S. Ghazvini and F. Endres, J. Phys. Chem. C, 2016, 120, 20224–20231 CrossRef CAS.
- A. P. Abbott, G. Frisch and K. S. Ryder, in Annual Review of Materials Research, ed. D. R. Clarke, Annual Reviews, Palo Alto, 2013, vol. 43, pp. 335–358 Search PubMed.
- C. Zhang, J. Holoubek, X. Y. Wu, A. Daniyar, L. D. Zhu, C. Chen, D. P. Leonard, I. A. Rodriguez-Perez, J. X. Jiang, C. Fang and X. Ji, Chem. Commun., 2018, 54, 14097–14099 RSC.
- X. Y. Wu, Y. K. Xu, C. Zhang, D. P. Leonard, A. Markir, J. Lu and X. L. Ji, J. Am. Chem. Soc., 2019, 141, 6338–6344 CrossRef CAS PubMed.
- T. S. Zhang, Y. Tang, S. Guo, X. X. Cao, A. Q. Pan, G. Z. Fang, J. Zhou and S. Q. Liang, Energy Environ. Sci., 2020, 13, 4625–4665 RSC.
- X. C. Chen, D. D. Song, C. Asumana and G. R. Yu, J. Mol. Catal. A: Chem., 2012, 359, 8–13 CrossRef CAS.
- L. H. Zhang, J. Y. Wang, Y. L. Sun, B. Jiang and H. W. Yang, Chem. Eng. J., 2017, 328, 445–453 CrossRef CAS.
- Z. Q. Zhang, F. Wang, H. H. Nie, T. Zhou, G. D. Zhang, X. F. Wang, M. Cui and Y. Z. Li, J. Sol-Gel Sci. Technol., 2017, 82, 827–833 CrossRef CAS.
- W. Chen, S. Q. Liang, Y. X. Guo and D. W. Tang, Energy Convers. Manage., 2014, 85, 13–19 CrossRef CAS.
- W. Chen, S. Q. Liang, Y. X. Guo, X. H. Gui and D. W. Tang, Fluid Phase Equilib., 2013, 360, 1–6 CrossRef CAS.
- K. S. Lovejoy, C. A. Corley, E. K. Cope, M. C. Valentine, J. G. Leid, G. M. Purdy, J. S. Wilkes, A. T. Koppisch and R. E. Del Sesto, Cryst. Growth Des., 2012, 12, 5357–5364 CrossRef CAS.
- H. B. Halima, T. Zwingelstein, V. Humblot, B. Lakard and L. Viau, ACS Appl. Mater. Interfaces, 2023, 15, 33382–33396 CrossRef CAS PubMed.
- J. Estager, P. Nockemann, K. R. Seddon, M. Swadźba-Kwaśny and S. Tyrrell, Inorg. Chem., 2011, 50, 5258–5271 CrossRef CAS PubMed.
- C. J. Clarke, H. Baaqel, R. P. Matthews, Y. Y. Chen, K. R. J. Lovelock, J. P. Hallett and P. Licence, Green Chem., 2022, 24, 5800–5812 RSC.
- A. W. Taylor, S. Men, C. J. Clarke and P. Licence, RSC Adv., 2013, 3, 9436–9445 RSC.
- E. Gousseva, F. K. Towers Tompkins, J. M. Seymour, L. G. Parker, C. J. Clarke, R. G. Palgrave, R. A. Bennett, R. Grau-Crespo and K. R. J. Lovelock, J. Phys. Chem. B, 2024, 128, 5030–5043 CrossRef CAS PubMed.
- S. Csihony, H. Mehdi and I. T. Horváth, Green Chem., 2001, 3, 307–309 RSC.
- J. E. Penner-Hahn, Coord. Chem. Rev., 2005, 249, 161–177 CrossRef CAS.
- M. Swadźba-Kwaśny, RSC Adv., 2017, 7, 51907–51909 RSC.
- T. Waters, X. B. Wang and L. S. Wang, Coord. Chem. Rev., 2007, 251, 474–491 CrossRef CAS.
- R. Rowe, K. R. J. Lovelock and P. A. Hunt, J. Chem. Phys., 2021, 155, 014501 CrossRef CAS PubMed.
- A. Krężel and W. Maret, Arch. Biochem. Biophys., 2016, 611, 3–19 CrossRef PubMed.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 2000, 122, 11146–11153 CrossRef CAS.
- R. R. Roe and Y. P. Pang, J. Mol. Model., 1999, 5, 134–140 CrossRef CAS.
- S. I. Hsiu, J. F. Huang, I. W. Sun, C. H. Yuan and J. Shiea, Electrochim. Acta, 2002, 47, 4367–4372 CrossRef CAS.
- A. P. Abbott, G. Capper, D. L. Davies and R. Rasheed, Inorg. Chem., 2004, 43, 3447–3452 CrossRef CAS PubMed.
- V. Lecocq, A. Graille, C. C. Santini, A. Baudouin, Y. Chauvin, J. M. Basset, L. Arzel, D. Bouchu and B. Fenet, New J. Chem., 2005, 29, 700–706 RSC.
- S. Takahashi, L. A. Curtiss, D. Gosztola, N. Koura and M. L. Saboungi, Inorg. Chem., 1995, 34, 2990–2993 CrossRef CAS.
- Y. Zou, H. J. Xu, G. Z. Wu, Z. Jiang, S. M. Chen, Y. Y. Huang, W. Huang and X. J. Wei, J. Phys. Chem. B, 2009, 113, 2066–2070 CrossRef CAS PubMed.
- W. H. Wu, Y. X. Lu, Y. T. Liu, H. Y. Li, C. J. Peng, H. L. Liu and W. L. Zhu, J. Phys. Chem. A, 2014, 118, 2508–2518 CrossRef CAS PubMed.
- F. Parveen, T. Patra and S. Upadhyayula, New J. Chem., 2018, 42, 1423–1430 RSC.
- P. H. Fourcroy, D. Carre and J. Rivet, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3160–3162 CrossRef.
- D. K. Mishra, G. Gopakumar, G. Pugazhenthi, C. Rao, S. Nagarajan and T. Banerjee, J. Phys. Chem. A, 2021, 125, 9680–9690 CrossRef CAS PubMed.
- A. P. Abbott, J. C. Barron, G. Frisch, S. Gurman, K. S. Ryder and A. F. Silva, Phys. Chem. Chem. Phys., 2011, 13, 10224–10231 RSC.
- K. R. J. Lovelock, I. J. Villar-Garcia, F. Maier, H. P. Steinrück and P. Licence, Chem. Rev., 2010, 110, 5158–5190 CrossRef CAS PubMed.
- K. R. J. Lovelock and P. Licence, in Ionic Liquids UnCOILed: Critical Expert Overviews, ed. K. R. Seddon and N. V. Plechkova, Wiley, Oxford, 2012, ch. 8, pp. 251–282 Search PubMed.
- H. P. Steinrück, Phys. Chem. Chem. Phys., 2012, 14, 5010–5029 RSC.
- M. L. Baker, M. W. Mara, J. J. Yan, K. O. Hodgson, B. Hedman and E. I. Solomon, Coord. Chem. Rev., 2017, 345, 182–208 CrossRef CAS PubMed.
- F. Maier, T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, P. S. Schulz, P. Wasserscheid and H. P. Steinrück, Phys. Chem. Chem. Phys., 2010, 12, 1905–1915 RSC.
- P. A. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703–740 CrossRef.
- J. L. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- Surface Analysis by Auger and X-Ray Photoelectron Spectroscopy, ed. D. Briggs and J. T. Grant, IM Publications, Manchester, 2003 Search PubMed.
- Surface Analysis: the Principal Techniques, ed. J. C. Vickerman and I. S. Gilmore, John Wiley & Sons, Chichester, 2009 Search PubMed.
- P. S. Bagus, E. S. Ilton and C. J. Nelin, Surf. Sci. Rep., 2013, 68, 273–304 CrossRef CAS.
- E. Gousseva, S. D. Midgley, J. M. Seymour, R. Seidel, R. Grau-Crespo and K. R. J. Lovelock, J. Phys. Chem. B, 2022, 126, 10500–10509 CrossRef CAS PubMed.
- J. Liu, H. Zhang, Y. M. Li and Z. Liu, J. Phys. Chem. B, 2018, 122, 10600–10606 CrossRef CAS PubMed.
- R. A. Walton, Coord. Chem. Rev., 1976, 21, 63–91 CrossRef CAS.
- J. M. Seymour, E. Gousseva, A. I. Large, C. J. Clarke, P. Licence, R. M. Fogarty, D. A. Duncan, P. Ferrer, F. Venturini, R. A. Bennett, R. G. Palgrave and K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2021, 23, 20957–20973 RSC.
- S. Hayama, G. Duller, J. P. Sutter, M. Amboage, R. Boada, A. Freeman, L. Keenan, B. Nutter, L. Cahill, P. Leicester, B. Kemp, N. Rubies and S. Diaz-Moreno, J. Synchrotron Radiat., 2018, 25, 1556–1564 CrossRef CAS PubMed.
- S. Hayama, R. Boada, J. Chaboy, A. Birt, G. Duller, L. Cahill, A. Freeman, M. Amboage, L. Keenan and S. Diaz-Moreno, J. Phys.: Condens. Matter, 2021, 33, 284003 CrossRef CAS PubMed.
- P. Glatzel, M. Sikora, G. Smolentsev and M. Fernandez-Garcia, Catal. Today, 2009, 145, 294–299 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Journal, 2016.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- V. S. Bernales, A. V. Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122–9129 CrossRef CAS PubMed.
- F. Neese and W. Interdiscip, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS PubMed.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- N. Fairley, V. Fernandez, M. Richard-Plouet, C. Guillot-Deudon, J. Walton, E. Smith, D. Flahaut, M. Greiner, M. Biesinger, S. Tougaard, D. Morgan and J. Baltrusaitis, Appl. Surf. Sci. Adv., 2021, 5, 100112 CrossRef.
- C. Kolbeck, M. Killian, F. Maier, N. Paape, P. Wasserscheid and H. P. Steinrück, Langmuir, 2008, 24, 9500–9507 CrossRef CAS PubMed.
- T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem.–Eur. J., 2010, 16, 9018–9033 CrossRef CAS PubMed.
- I. J. Villar-Garcia, E. F. Smith, A. W. Taylor, F. L. Qiu, K. R. J. Lovelock, R. G. Jones and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 2797–2808 RSC.
- L. G. Parker, F. K. Towers Tompkins, J. M. Seymour, N. O. Alblewi, E. Gousseva, M. R. Daw, S. Hayama, R. P. Matthews, A. A. E. Fouda, J. D. Elliott, C. D. Smith and K. R. J. Lovelock, 2024, in preparation.
- H. A. Øye, M. Jagtoyen, T. Oksefjell and J. S. Wilkes, in Molten Salt Chemistry and Technology, ed. M. Chemla, D. Devilliers and M. Vogler, 1991, vol. 73, pp. 183–189 DOI:10.4028/b-1Utg6H.
- O. G. Parchment, M. A. Vincent and I. H. Hillier, J. Phys. Chem., 1996, 100, 9689–9693 CrossRef CAS.
- C. C. Pye, C. R. Corbeil and W. W. Rudolph, Phys. Chem. Chem. Phys., 2006, 8, 5428–5436 RSC.
- C. C. Pye, S. M. Black and W. W. Rudolph, J. Solution Chem., 2011, 40, 1932–1954 CrossRef CAS.
- L. G. Parker, F. K. Towers Tompkins, J. M. Seymour, E. Gousseva, N. O. Alblewi, C. A. Borrill, C. J. Clarke, S. Hayama, R. Seidel, D. Céolin, R. H. Temperton, R. P. Matthews, C. D. Smith and K. R. J. Lovelock, 2024, in preparation.
- S. B. Pillai, R. J. Wilcox, B. G. Hillis, B. P. Losey and J. D. Martin, J. Phys. Chem. B, 2022, 126, 2265–2278 CrossRef CAS PubMed.
- T. M. Laher and C. L. Hussey, Inorg. Chem., 1983, 22, 3247–3251 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00029c |
| This journal is © The Royal Society of Chemistry 2024 |