Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of carbene formation in the reaction of methane with the tantalum cation in the gas phase†
Marcel
Meta
 a,
Maximilian E.
Huber
a,
Maximilian E.
Huber
 a,
Maurice
Birk
a,
Maurice
Birk
 a,
Martin
Wedele
a,
Milan
Ončák
a,
Martin
Wedele
a,
Milan
Ončák
 b and
Jennifer
Meyer
b and
Jennifer
Meyer
 *a
*a
aRPTU Kaiserslautern-Landau, Fachbereich Chemie und Forschungszentrum OPTIMAS, Erwin-Schrödinger Str. 52, 67663 Kaiserslautern, Germany. E-mail: jennifer.meyer@chem.rptu.de; Fax: +49 631 205 2750; Tel: +49 631 205 4211
bUniversität Innsbruck, Institut für Ionenenphysik und Angewandte Physik, Technikerstr. 25, 6020 Innsbruck, Austria
First published on 20th May 2024
Abstract
The controlled activation of methane has drawn significant attention throughout various disciplines over the last few decades. In gas-phase experiments, the use of model systems with reduced complexity compared to condensed-phase catalytic systems allows us to investigate the intrinsic reactivity of elementary reactions down to the atomic level. Methane is rather inert in chemical reactions, as the weakening or cleavage of a C–H bond is required to make use of methane as C1-building block. The simplest model system for transition-metal-based catalysts is a mono-atomic metal ion. Only a few atomic transition-metal cations activate methane at room temperature. One of the most efficient elements is tantalum, which forms a carbene and releases molecular hydrogen in the reaction with methane: Ta+ + CH4 → TaCH2+ + H2. The reaction takes place at room temperature due to efficient intersystem crossing from the quintet to the triplet surface, i.e., from the electronic ground state of the tantalum cation to the triplet ground state of the tantalum carbene. This multi-state reactivity is often seen for reactions involving transition-metal centres, but leads to their theoretical treatment being a challenge even today. Chemical reactions, or to be precise reactive collisions, are dynamic processes making their description even more of a challenge to experiment and theory alike. Experimental energy- and angle-differential cross sections allow us to probe the rearrangement of atoms during a reactive collision. By interpreting the scattering signatures, we gain insight into the atomistic mechanisms and can move beyond stationary descriptions. Here, we present a study combining collision energy dependent experimentally measured differential cross sections with ab initio calculations of the minimum energy pathway. Product ion velocity distributions were recorded using our crossed-beam velocity map imaging experiment dedicated to studying transition-metal ion molecule reactions. TaCH2+ velocity distributions reveal a significant degree of indirect dynamics. However, the scattering distributions also show signatures of rebound dynamics. We compare the present results to the oxygen transfer reaction between Ta+ and carbon dioxide, which we recently studied.
1 Introduction
Methane CH4 as a major natural carbon feedstock is currently primarily used as fuel, but methane is also a valuable C1-feedstock for the chemical industry as natural oil resources diminish over the next few decades. However, the effective chemical conversion of methane comes with the challenge of selective activation and chemical modification of methane. CH4 is chemically rather inert, with one of the strongest C–H bonds, i.e., a bond dissociation energy (BDE) of 4.5 eV.1 Additionally, it has no dipole moment, no appreciable quadrupole moment, a very low polarizability (2.593 Å3),1 and an ionization energy of 12.6 eV.2 All this makes methane practically inert in chemical reactions and necessitates the use of catalysts for economical chemical transformations. Herein lies the challenge of selectivity: at least one chemical bond in most reaction products is more reactive than the C–H bond in methane, which makes the selective activation of methane an ongoing field of research across various disciplines of chemistry.3–7 If we very crudely sort the studies by objective, we can classically sort them either as improving on catalyst performance or on understanding the molecular processes happening during elementary reactions. Separating out individual influences or molecular mechanisms in a condensed-phase environment is challenging due to the high complexity of the catalyst material, many participating reactants and the reaction conditions.7,8 This necessitates the design and use of model systems in well controlled environments to single out elementary reaction steps and investigate the properties of the catalyst as a function of the chosen conditions. One way to negate the influence of an environment is to not have one in the first place, that is to move the reaction into the gas phase. Small clusters present one possible model system for heterogeneous catalysts and have been explored since the early days of cluster chemistry.9–14 To achieve better control over the composition of the cluster, ionic clusters are used, and by means of mass spectrometry the composition can be easily determined. Numerous techniques have been used to study the activation of methane by transition-metal clusters covering the periodic table.3–5,15–20 It has been found that the elements of the 5d series are particularly reactive, down to the smallest possible model system: the mono-cation M+.15,21–25 While the ion, due its high charge density, is commonly more reactive than the corresponding condensed phase of the element, it allows us to concentrate on the intrinsic reactivity of the element towards methane. Hence, the mono-cation presents the ultimate single-site catalyst.18The reaction of methane with the mono-cations of the 5d series is highly efficient and the thermal rates are close to, or on the order of, the collision rate.15,21,22,26,27 At low collision energies, the main product channel is a species with the formal composition [M,C,2H]+ and molecular hydrogen H2. Thermodynamic arguments and recent spectroscopic investigations showed that the carbene M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 is the favoured isomer compared to the carbyne H–M–CH+.25 In the case of tantalum, the carbene structure has no C2v symmetry but is slightly distorted due an agostic interaction between one of the hydrogen atoms and the tantalum cation.
CH2 is the favoured isomer compared to the carbyne H–M–CH+.25 In the case of tantalum, the carbene structure has no C2v symmetry but is slightly distorted due an agostic interaction between one of the hydrogen atoms and the tantalum cation.
| Ta+ + CH4 → TaCH2+ + H2 | (1) |
| Ta+ + CD4 → TaCD2+ + D2 | (2) |
Here, we present reactive scattering experiments using a crossed-beam 3D velocity map imaging set-up. This experimental technique allows us to gain insights into the energy- and angle-differential cross sections (DCS) of a reactive collision.28–32 While the integral cross section, thermal reaction rate, structures of reaction products, and partly intermediates have been thoroughly investigated, direct experimental investigations into the dynamics of reactions (1) and (2) are missing. A reactive collision is an intrinsically dynamic process, and information on the dynamics of a reaction can be extracted from the DCS that is otherwise hidden or very hard to extract.30–35 By interpreting the experimental velocity distributions with respect to the product ion speed and scattering angle, we can identify dynamic fingerprints. These encode information on the atomic-level rearrangement during the reaction, and on energy partitioning between the translational and internal degrees of freedom. Today, studies on the dynamics of ion molecule reactions by reactive scattering experiments are possible.36–42 In the early 2000s, Weisshaar and co-workers investigated the reaction dynamics of transition-metal ions with hydrocarbon molecules using crossed-beam imaging. However, the experiment focused on cobalt and nickel cations in reactions with C3–C4-hydrocarbons.43,44 The chemistry is dominated by the activation, that is cleavage, of the C–C bond and not the C–H bond. Early work by Armentrout and co-workers investigating integral cross sections of reactions between transition-metal ions and methane CH4, molecular hydrogen H2, and small hydrocarbon molecules with a C2 backbone showed that the reactivity of methane much more resembles that of molecular hydrogen than that of the longer-chain hydrocarbon molecules.12,45,46 A recent study by us revealed that the activation of carbon dioxide CO2 by the tantalum cation is dominated by indirect dynamics despite the reaction rate being close to the collision rate47 and the reaction being exothermic by more than 2 eV. We found a near constant kinetic energy release and that about 60% of the available energy is partitioned into internal degrees of freedom. We postulated that the reaction is trapped in the entrance well and that either the submerged barrier or the crossing point from the quintet to the triplet state is acting as an efficient bottleneck.47 This shows again that experiments are important because chemical intuition and interpretations of stationary properties alone can be misleading47,48 and underestimate the influences exerted by submerged barriers.49 The mentioned multi-state reactivity is an accepted phenomenon in transition-metal chemistry.50 If the reaction on the electronic ground state is associated with a high barrier, intersystem crossing (ISC) can occur and quite efficiently. ISC is, for example, assumed to happen with nearly unit probability for the heavy 5d elements. Similar to the reaction Ta+ + CO2 → TaO+ + CO, the reaction with methane forming the carbene is only possible at room temperature assuming ISC.22 The efficiency of carbene formation in reaction (1) is similar to that of TaO+ being formed in the oxygen atom transfer reaction. Reaction (1), however, is far less exothermic, and one might consider it even thermoneutral (see Fig. 1). Furthermore, the carbene formation is chemically much more evolved because it requires the cleavage of two C–H bonds and the subsequent formation of two new bonds and the release of molecular hydrogen from the tantalum ion. The mechanism resembles a classic two-step process of organometallic chemistry: (1) oxidative addition by insertion of the tantalum ion into a C–H bond followed by migration of a second H-atom to the metal centre and (2) reductive elimination of molecular hydrogen from the metal centre.51–53
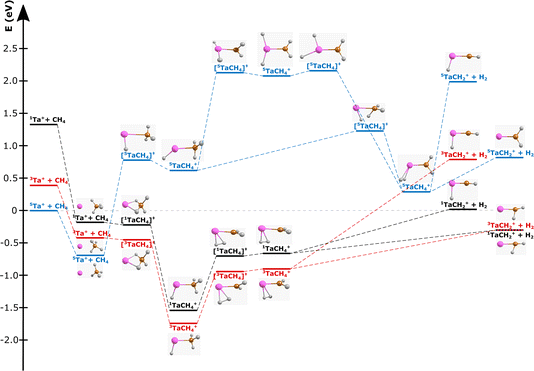 | ||
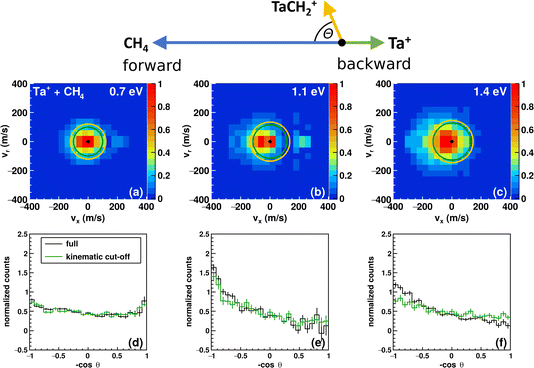
| Fig. 1 Reaction pathway for Ta+ + CH4 → TaCH2+ + H2 with structures of the stationary points along the reaction coordinate (i.e., for the pre-reaction complex (entrance channel), intermediates and post-reaction complexes, as well as the transition states) for the quintet surface (blue), triplet (red) and singlet (black). (Elements are denoted as follows: Ta = pink, carbon = orange, and hydrogen = white; structural data can be found in the ESI†). Energies are given in electron volts relative to the isolated ground-state reactants 5Ta+ + CH4. The given reaction energy of E(5Ta+) = −0.3 eV and energy splitting between 5Ta+ and 3Ta+ are used for calculating the kinematic cut-offs displayed in Fig. 2. Calculated at the CCSD(T)//B3LYP level (for details, see Methods). The energy of the transition states below the local minima is induced through the zero-point energy correction. The reaction pathway including transition states of lower importance is given in Fig. S1.† | ||
Here, we present energy- and angle-differential cross sections as a function of collision energy for reaction (1), measured by velocity mapping the TaCH2+ product ion. The reaction is dominated by product ions isotropically scattered around the centre-of-mass, which is a fingerprint of indirect dynamics. However, we observe more anisotropy in the angular distributions than in the reaction with Ta+ + CO2, which hints at some more direct dynamics contributing. The velocity distributions and derived integrated angular and energy distributions are not as clear regarding their interpretation as for Ta+ + CO2, with some of the scattering signal found outside the energy range defined by the so-called kinematic cut-off. The experiments are complemented by ab initio calculations of the minimum energy path of reaction (1) for three spin multiplicities (quintet/triplet/singlet) of the tantalum cation Ta+. We will first briefly introduce the experimental and theoretical methods used in the present study. The results section will begin with a discussion of the minimum energy pathway and is followed by the experimental results on the title reaction and a comparison to Ta+ + CD4. We will finish with a discussion of the recent results in comparison to the oxygen atom transfer reaction with CO2 and conclude with an outlook on future experiments.
2 Methods
2.1 Experiment
In this experiment, we combine crossed beams with 3D velocity map imaging.40,54,55 We generate an ion beam with a home-built laser vaporization source.56,57 The second harmonic of an Nd:YAG laser (532 nm, 20 Hz, ≈ 4 mJ per pulse (5 × 107 W cm−2)) is focused on a rotating tantalum target. The ions in the produced plasma are extracted by a synchronized transverse helium pulse (8 bar of helium, 40 μs) into the interaction region of the source. The ion beam passes through an expansion channel (61 mm length, 2 mm diameter) where the ions undergo about 104 collisions with helium before expanding into the high vacuum (approx. 5 × 10−6 mbar in operation).47 So far, we have no direct control over the electronic states of the produced tantalum cations. However, it is assumed that no significant amounts of electronically excited tantalum cations are produced, as the formation of electronically excited tantalum cations is not only energetically demanding, but also statistically disadvantaged.2,47 The conditions of the ion source are adjusted in such a way that tantalum cations are generated and the formation of ionic tantalum clusters is suppressed at the same time. The ion beam passes through an aperture before it is focused by several Einzel lenses and deflectors, and finally transferred to the interaction region of the velocity map imaging spectrometer. In this process, the energy of the ion beam and to some degree its angle can be adjusted. The ion beam is characterised by velocity mapping. In the interaction zone, the ion beam is crossed with a neutral beam generated using a home-built piezo valve.58 Pure CH4 is expanded and enters the interaction zone through a skimmer. The molecular beam can be characterized in a similar way to the ion beam; the ionization of the neutral beam takes place by non-resonant electron impact ionization. The two beams are crossed at an angle of ≈150° and the resulting product ions are then accelerated perpendicularly in the direction of the time- and position-sensitive detector unit. The detector unit consists of a combination of microchannel plates and a phosphor screen with a camera to record the position of ion impact, as well as a photo multiplier tube to record the time of arrival. All three velocity components can then be extracted from the measured data sets in such a way that the Newton sphere can finally be reconstructed.54 The analysis of the recorded data is based on an established routine from Wester and co-workers.40,54,59 The recovered 3D Newton spheres are visualized in 2D representations, where the velocity distributions of the product ions are represented as 2D histograms using the velocity component vx and the radial velocity vr (which is obtained from the velocity components vz and vy). An integration of the original distributions over the solid angle or the energy gives the 1D histograms, which are normalized to the unit area if not stated otherwise.2.2 Theory
Minima and transition states along the Ta+ + CH4 reaction pathway were optimized employing density functional theory (DFT) with the B3LYP functional and the aug-cc-pVTZ basis set on C and H, and the ECP60MDF_AVTZ basis set on Ta.60 To obtain more accurate electronic energies, single-point recalculation at the coupled cluster level, CCSD(T), with the same basis set was performed, employing the zero-point energy correction as obtained at the DFT level. This approach was shown to work reasonably well for the [TaCO2]+ system.47 Further benchmarking is provided in the ESI,† including comparison to multi-reference calculations and a comparison of Ta–H. Armentrout and co-workers also did benchmarking for reactants and/or products participating in the present reaction.22,61 To make sure that the lowest-lying solution of the electronic Schrödinger equation was obtained in the given spin multiplicity, wave-function stabilization was performed prior to every single-reference calculation. Single-reference calculations were performed in the Gaussian quantum chemical program,62 and multi-reference ones in Molpro.63–653 Results and discussion
The carbene TaCH2+ formation is the dominant reaction pathway for methane with 5d transition-metal cations. A conceivable reaction all the way to the carbide TaC+ is endothermic by more than 3 eV. Three spin states have been considered by us for reaction (1): quintet, triplet and singlet. The respective structures and energies of the stationary points are shown in Fig. 1. If we look at the product ion TaCH2+, the energies of the triplet and singlet states are indistinguishable from each other. The whole reaction pathways for the triplet (red trace) and singlet (black trace) states go in parallel, while the quintet (blue trace) follows a somewhat different pathway. The reaction of 5Ta+ with methane is associated with a barrier of almost 1.5 eV, whereas starting from the triplet state 3Ta+ (or singlet state 1Ta+), the reaction shows all the features common to an exothermic gas phase ion molecule reaction with all transition states submerged relative to the free reactants. Intersystem crossing (ISC) has to occur before the first transition state on the quintet surface for the reaction to efficiently happen at room temperature (Fig. 1). The crossing is only reasonably possible in the vicinity of the first triplet transition state, which is related to the formation of the first hydrogen–tantalum bond. Crossing to the singlet surface is possible but unlikely because it lies higher in energy and can be assumed to have a lower crossing probability compared to crossing to the triplet surface because two spin flips are required. The crossing to the triplet surface is the commonly assumed pathway and 3[HTaCH3]+ is formed as an intermediate.22,66–68 Subsequently, a second hydrogen atom moves to the tantalum atom which leads to [H2TaCH2]+, from which molecular hydrogen is eliminated. Two isomers are possible for the [Ta,C,2H]+ product but the carbene [TaCH2]+ is the lower energy isomer compared to the carbyne [HTaCH]+. Preferential carbene formation for [TaCH2]+ has also been spectroscopically confirmed.25Here, we present angle- and energy-differential cross sections for the title reaction (reaction (1)) from which we can gain insight into the dynamics of the carbene formation. We studied the reaction as a function of relative collision energy (0.7 eV, 1.1 eV and 1.3 eV). The product ion velocity distributions together with the integrated angular distributions are given in Fig. 2.
At the lowest investigated relative collision energy, we observe an isotropic distribution of the TaCH2+ around the center-of-mass (Fig. 2a). This velocity distribution is a common signature for indirect dynamics.29 In this atomistic mechanism, the reactants form a long-lived complex, whose lifetime outlasts several rotational periods. The complex subsequently decays statistically in all spatial directions. During the complex’s lifetime, kinetic energy can be efficiently redistributed into rotational and vibrational modes of molecular products, here TaCH2+ and H2. This specific symmetric signature has already been observed in other ion-molecule reactions36,47,69,70 and is usually associated with small impact parameter collisions and efficient transfer of angular momentum of the collision into rotational angular momentum of molecular products.29–31 The isotropic scattering becomes even more obvious in the integrated angular distribution, which shows a constant scattering probability for the whole scattering range (see black trace in Fig. 2d). It is apparent that events can be found outside the velocity space defined by the kinematic cut-off. The kinematic cut-offs are depicted by the green and orange rings superimposed onto the scattering distributions and give the maximum possible product kinetic energy taking energy and momentum conservation into account given that the experiments are conducted under single-collision conditions. The available energy is defined by the relative collision energy Erel, (possible) internal energy of the reactants and the energy freed or consumed by the reaction, which we refer to as reaction exothermicity Eexo. Here, we use the reaction exothermicity as shown in Fig. 1. Experimental uncertainties for the product ion velocities (and energies) are derived by Gaussian error propagation based on the energy and angular spread of the reactant beams.54 A graphical representation of the errors superimposed onto the velocity distributions at the kinematic cut-off is shown in Fig. S5.† If the relative collision energy is increased, some changes in the reaction dynamics can be observed. An asymmetry in the velocity distribution of the product ions emerges. It is also obvious that an even greater fraction of events can be found outside the kinematic cut-off. At 1.3 eV relative collision energy, the majority of events are scattered within the forward hemisphere, that is the initial direction of the neutral beam. An asymmetric velocity distribution is a sign of a direct atomistic mechanism. Taking the kinematics into account, namely a much heavier ion (m(Ta+) = 181 amu) compared to the neutral reactant (m(CH4) = 16 amu), scattering of TaCH2+ into the forward hemisphere means that the tantalum ion turns around. We observe what is generally termed as direct rebound. However, the majority of events are still scattered isotropically, especially within the kinematic-cut off (see green histograms in Fig. 2d–f).
The integrated kinetic energy distributions do not significantly differ from each other as function of relative collision energy (see Fig. 3 and S3†). The distributions just broaden with increasing collision energy. As discussed above, the absolute kinetic energy of the product ion TaCH2+ is very small due to the high mass difference of both products (m(TaCH2+) = 195 amu and m(H2) = 2 amu) and the required momentum conservation. The corresponding internal energy Eint distributions are given in Fig. S2 and S3.† The distributions slightly shift towards larger values with increasing collision energy indicating that at least part of the additional collision energy is partitioned into ro-vibrational excitation of either TaCH2+ or H2. Due to the experimental uncertainty, we will not discuss the energy partitioning in more detail.
| Erel + Eexo = Ekin(TaCH2+) + Ekin(H2) + Eint | (3) |
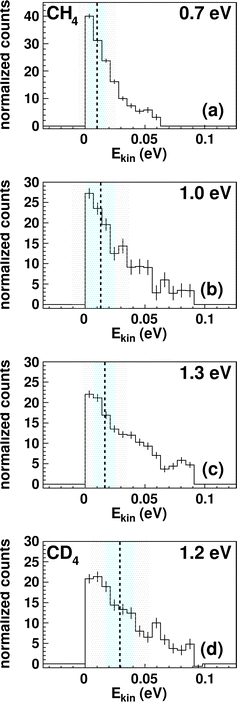 | ||
| Fig. 3 Kinetic energy Ekin distributions for TaCH2+ (a–c) and TaCD2+ (d). The energy resolution is calculated using Gaussian error propagation from the energy and angular spread of the reactant beams.54 The ± 1σ-error interval is given by the light blue area and the ± 2σ-error interval by the grey one. The distributions extend beyond the kinematic cut-offs given by energy and momentum conservation with respect to the relative collision energy Erel and the reaction exothermicity Eexo. In other words, this means that an unavailable amount of energy is converted into kinetic energy.71 Possible explanations are missing contributions to the energy balance, for example, electronically excited states of Ta+ contributing or the internal energy of CH4. The relative contributions of events scattered within the kinematic cut-off and the two shown error-intervals are given in Table 1. | ||
The trend in the velocity distribution towards the forward hemisphere for TaCH2+ in the reaction with methane (reaction (1)) was not expected by us. To further exclude systematic errors, we therefore decided to carry out the reaction at the highest investigated relative collision energy with fully deuterated methane CD4 (Fig. 4). This sounds trivial but gives us a product ion TaCD2+ with a mass-to-charge ratio m/z of 197, which makes gating our detector with respect to the time-of-flight trace a little less challenging (see Table S1†). Fig. 4 shows the differential cross section for reactions (1) and (2) at a comparable relative collision energy. Similar scattering signatures are observed for TaCH2+ and TaCD2+. This suggests that both reactions proceed by a very similar mechanism. This is in line with our expectations, since the dominant scattering signature is indirect and therefore most likely statistical regarding the energy partitioning. In addition, the chemical properties of the reactants do not significantly change upon going from CH4 to CD4.
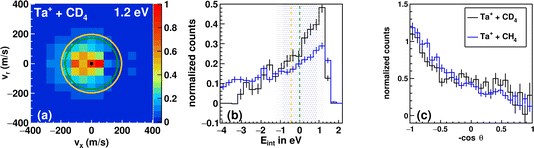 | ||
| Fig. 4 Differential cross section of the reaction between Ta+ + CD4 at 1.2 eV (a). Kinematic cut-offs (green: 5Ta+; orange: 3Ta+ are superimposed and calculated using the exothermicities given in Fig. 1. (b) Integrated internal energy distributions for the reaction with CD4 in black and CH4 in blue together with the ±1σ-error illustrated as a shaded area around the kinematic cut-off of the ground-state reaction (CD4 in blue and CH4 in grey), which is given as the vertical line (green). The ±1σ-error is derived from Gaussian error propagation of the energy and angular spread of the reactant beams.54 (c) The integrated angular distribution for the reaction with CD4 in black and CH4 in blue. | ||
The integrated angular distributions for reactions with CH4 and CD4 (Fig. 4c) confirm the impression from the velocity distributions. The distribution of the internal energy Eint in the reaction with CD4 is very similar to the one in the reaction with CH4 and seems to be slightly narrower, i.e., with less events outside the kinematic cut-off (see Table 1). The general forms of the distribution for both reactions hardly differ from each other. Minor deviations can of course be due to differences in kinematics, but also to isotope effects. However, the experiments with d4-methane confirm the observations made with methane. The kinematic cut-off for reaction (2) is calculated using the reaction exothermicity for Ta+ + CH4 corrected for the zero-point energy contribution of ≈+0.10 eV.
| Relative collision energy (eV) | ||||
|---|---|---|---|---|
| 0.7 | 1.0 | 1.3 | 1.2 (CD4) | |
| v kc(TaCH2+) (m s−1) | 102 | 115 | 128 | 169 |
| 1σ-error vkc(TaCH2+) (m s−1) | 37 | 52 | 35 | 72 |
| f kc/% | 33 | 36 | 39 | 54 |
| f kc+1σ/% | 58 | 50 | 61 | 84 |
| f kc+2σ/% | 81 | 66 | 81 | ≈100 |
We observed a large amount of events scattered outside the kinematic cut-off. We discuss these events below, including why a majority of these events can be explained by the experimental uncertainties. The fraction of events scattered with the kinematic cut-off and the ±1σ and ±2σ-interval defined by the error of the product ion velocity are presented in Table 1. The fractions for the respective intervals are on the order of what to theoretically expect. Comparing the error to the product ion velocity in absolute numbers for the reactions with H2 and D2 at comparable relative collision energies, we see that although the error is on the same order, the fraction of events found within the kinematic cut-off is significantly higher in the case of CD4. The present reactions suffer from unfortunate kinematics, i.e., a high mass difference between the two product species. A similar observation of a significant number of events scattered outside the ±2σ-interval has been seen before in ion-molecule reactive scattering experiments.71 Additionally, the tantalum ion is very heavy compared to the neutral reactant, and the uncertainties of the reactant ion beam are larger than the ones of the molecular beam of the neutral reactants. Thus, a careful adjustment and monitoring of the ion-beam performance is required. An example of this effect is given in the ESI (Fig. S4).†
Events found outside the expected scattering range could also be due to a missing contribution to the energy balance (eqn (3)), which puts the kinematic cut-off at the wrong value. The presence of electronically excited states of Ta+ seems to be the most obvious source of additional energy for the present reaction. The first electronically excited state is a triplet about 0.4 eV above the ground state.2 The kinematic-cut off for this potential reactant state is indicated by the orange circles in Fig. 2a–c. We do not assume contributions from this state to be a significant source for the high velocity events found. Firstly, as can be seen, the velocity spacing between the kinematic cut-offs is small (≈20 m s−1). Secondly, in a previous study, we gave an upper limit of about 20% contribution of the first electronically excited triplet. Here, we used similar source conditions (He backing pressure, laser power, timings) as for recording the Ta+ + CO2 data47 and we recorded the data with a break in between measurements and two different piezo valves in the ion source and observed similar signatures in the velocity distributions. We should also keep in mind that the spin–orbit manifold of the quintet spans 0.8 eV and significantly overlaps with the manifold of the first triplet state. Another contribution to the energy balance could be internal excitation of the methane. However, we consider methane to have little or no vibrational excitation given our source conditions and for it to be rotationally cold.
Besides the arguments related to the energy balance, a different product channel could be the source of events found outside the expected range. A different center-of-mass combined with a different exothermicity leads to scattering observed in a different area. To account for the observed events, we would need (a) a more favourable mass ratio of the two products and (b) an exothermic reaction. For the reaction Ta+ + CH4/CD4, the carbene formation is the lowest energy channel, and up to 2 eV relative collision energy no other product channels were observed in guided ion beam experiments.22 The first product to appear is TaH+, which we would not have been able to detect due to the mass difference of 1 amu. The conceivable formation of the carbide TaC+ is beyond the energy range of the present experiment because TaC+ formation is endothermic by more than 3.2 eV. We do not see any evidence in the time-of-flight trace for higher-mass products. We, therefore, conclude that we do not have a second product channel contributing. Another possibility to consider is that we do have a different reactant ion or neutral reactant present. We expand a pure CH4 beam with the CH4 used from the gas cylinder. The carbene formation is highly efficient, i.e., on the order of 10% of the collision rate. Any contamination would have to be present in the interaction region at the timing of the crossing of the two beams, at a density plus cross section to compete with methane. This is highly unlikely and we exclude this possibility. We saw no evidence of cluster formation in the expansion. A contamination to the ion beam at the levels needed is also unlikely. The small time-of-flight differences between the reactant and product ion makes us sensitive to contamination (see Table S1† for TOF-values). The ion beam is orders of magnitudes more intense than the product ion signal. We set the amplification for scattering experiments to single-ion counting mode. The most likely ‘contaminations' from the source are TaO+ and TaC+. If we have any traces of these present, and so far we only saw TaO+, we cannot run a scattering experiment. The TaO+ could always be traced back to leaks in the gas lines after maintenance of the source. The stability of the ion beam is key for our reactive scattering experiments. We expect that the addition of an ion trap into the ion beam path will help with the long-term stability of the ion beam.
3.1 Comparison to Ta+ + CO2
This study investigated the reaction between tantalum cations and methane at three different relative collision energies up to approximately 1.3 eV. Initially, an isotropic distribution around the center-of-mass is observed, which gains some forward contribution as the relative collision energy increases. At low relative collision energy, we observe scattering signatures that are very similar to the experimental velocity distributions for the reaction between tantalum cations and carbon dioxide (reaction (4)).47 For the oxygen atom transfer, a slight asymmetry towards the forward hemisphere in the velocity distribution of the TaO+ was observed only at 2.0 eV collision energy. This trend is more obvious for the reaction with methane, with an onset at much lower collision energies. At this point, it is interesting to discuss the chemical and physical differences between carbon dioxide and methane.| Ta+ + CO2 → TaO+ + CO | (4) |
It is obvious that only four atoms are involved in the reaction with CO2, whereas six atoms are involved in the reaction with methane. Reaction (1) is much more complex and will be a major challenge for theory, especially for quantum theory. In both reactions (reactions (1) and (4)), diatomic neutral products are formed and a double bond to the tantalum cation is formed. At first glance this indicates a similarity, but the chemistry of both reactions is very different. The long-range interaction between Ta+ and CO2 is dominated by the charge-quadrupole term and steers the reactants into a co-linear pre-reaction complex.47,72 During the reaction, the geometry shifts over to a bent configuration, potentially allowing for torque between TaO+ and CO to occur. The data of Meta et al. shows that most of the available energy is transferred into internal degrees of freedom of the products, which means into vibrational and rotational modes of TaO+ and/or CO.47 Reaction (1) is chemically much more complicated. The bond between the two hydrogen atoms to the carbon atom must first be broken while Ta–H bonds are formed. These are cleaved when the H–H bond is formed to release molecular hydrogen H2. The experimental data also indicate that the available energy is not exclusively transferred into internal energy, but that a substantial part goes into the kinetic energies of the reaction products, although we have to tread carefully here. We now want to speculate on why the more complex and less exothermic chemical transformation seems to slightly favour direct dynamics. The central carbon atom in CH4 is partially negatively charged due to its slightly higher electronegativity relative to hydrogen. This is a difference compared to CO2, for which the negative charge is more centred on oxygen atoms. In contrast to CO2, methane also has no appreciable quadrupole moment, which makes the charge-induced dipole interaction the leading term for the long-range potential. The well depth of the pre-reaction complex [TaCH4]+ is similar to that of [TaCO2]+, but the barrier to the first transition state (3TS) is lower in the case of Ta+ + CH4 and associated with less structural rearrangement. This might result in a better coupling of translation to the reaction coordinate compared to reaction (4). Even though more atoms are involved and more bonds are cleaved, formed and rearranged, the overall geometry changes at the carbon atom appear not as pronounced for Ta+ + CH4 as for Ta+ + CO2 when crossing over the first transition state. The crossing is followed by a second H-abstraction, which needs about 1 eV for the intermediate [HTaCH3]+ to transfer a second hydrogen atom to the tantalum and is followed by H2 formation. Once the second H-atom is abstracted, the surface is rather flat and not associated with another barrier that could act as a bottle-neck. All of the above arguments are speculative and could be answered by trajectory simulations that are not available yet.
4 Conclusions
We presented energy- and angle-differential cross sections for the reaction Ta+ + CH4 → TaCH2+ + H2 as a function of collision energy. The dynamics of the reaction are dominated by an indirect complex-mediated mechanism that allows for efficient partitioning of energy into internal degrees of freedom. The present reaction shows a little more direct character compared to the oxygen atom transfer reaction Ta+ + CO2 → TaO+ + CO. For both systems, the direct mechanism leads to scattering into the forward hemisphere due to a direct rebound, that is turn-around of the tantalum indicative of a head-on collision. The experimental velocity distributions extend beyond the kinematic cut-off defined by the energy balance of the collision: relative collision energy, internal energy of Ta+ and CH4, and reaction exothermicity. The majority of events found outside the kinematic cut-off fall into the ±2σ-interval defined by the uncertainty of the product ion velocity distribution. If we are missing contributions to the energy balance, from which we derive the kinematic cut-off, the most obvious missing candidates are (1) an electronically excited state of Ta+ or (2) calculations not being converged despite the high level employed here. We will further address these open questions by investigating another transition metal, having a more detailed look into the source conditions, and by further testing different levels of theory. The theoretical description of open-shell transition-metal species is notoriously difficult due to the strong multi-reference character and thus we need further collaborations between experiment and theory. A final answer might be given by comparison with trajectory simulations. The present data set will be subject to further scrutiny from ourselves, for example, by repeating experiments at lower collision energy with CD4 once the ion trap is built in. The design follows that of the imaging experiment developed by the Wester group.69 While we do not expect the intrinsic velocity spread of the ion beam to reduce significantly below the current values for individual measurements, we expect a better long-term stability in the central velocity of the beam and the angular spread. These two points lead to an uncertainty in the centre-of-mass of the collision, which is known to generally be the main error in reactive ion molecule scattering.The carbene TaCH2+ presents a reactive carbon centre that can readily undergo further reactions. For example, it is known that platinum or iridium cations can undergo reactions with more than one methane molecule.24,73–75 In the next step, we will modify our crossed-beam imaging experiment by including a radio-frequency ion trap into the ion beam path, similar to the instrument operated by the Wester group.54,76 Reactive carbon species will be formed in situ in the ion trap77 and transferred into the interaction region of the velocity map imaging spectrometer. We aim for [M–CH3]+ and [MCH2]+ carbon species to investigate whether C–C coupling reactions occur with small hydrocarbons such as methane or ethylene. These reactions are postulated to proceed via cyclic transition states, but if they occur via a step-wise or concerted mechanism is still debated. Our aim is to contribute to this debate by exploring the dynamics of C–C coupling reactions.
Author contributions
M. M., M. E. H., M. B. and M. W. carried out the crossed-beam experiments and analysed the data; M. O. performed and analyzed the quantum chemical calculations; J. M. supervised and devised the experiment; M. M., M. O. and J. M. prepared the manuscript, J. M. and M. O. coordinated the study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. M. thanks the Deutsche Forschungsgemeinschaft DFG (Project number 500279291) for support of this project. M. M. acknowledges support by the DFG through the SFB TRR88/3MET. The computational results presented have been achieved using the HPC infrastructure LEO of the University of Innsbruck. M. M., M. B., M. W. and J. M. acknowledge and thank Roland Wester and Björn Bastian for providing the data analysis software package for the reactive scattering data. We thank Roland Wester, Nicholas S. Shuman and Shaun G. Ard for valuable discussions of the presented results. We thank Roland Wester, Nicholas S. Shuman, Shaun G. Ard and Hua Guo for valuable discussions of the presented results.Notes and references
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 84th edn, 2003 Search PubMed.
- ed. A. Kramida, Y. Ralchenko, J. Reader, and N. I. S. T. A. S. D Team, http://physics.nist.gov/asd/.
- H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 10096–10115 CrossRef CAS PubMed.
- J. Roithová and D. Schröder, Chem. Rev., 2010, 110, 1170–1211 CrossRef.
- J. Roithová and J. M. Bakker, Mass Spectrom. Rev., 2022, 41, 513–528 CrossRef PubMed.
- A. Hu, J.-J. Guo, H. Pan and Z. Zuo, Science, 2018, 361, 668 CrossRef CAS PubMed.
- M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017, 56, 16464–16483 CrossRef CAS PubMed.
- H. Arakawa, M. Aresta, J. N. Armor, M. A. Barteau, E. J. Beckman, A. T. Bell, J. E. Bercaw, C. Creutz, E. Dinjus, D. A. Dixon, K. Domen, D. L. DuBois, J. Eckert, E. Fujita, D. H. Gibson, W. A. Goddard, D. W. Goodman, J. Keller, G. J. Kubas, H. H. Kung, J. E. Lyons, L. E. Manzer, T. J. Marks, K. Morokuma, K. M. Nicholas, R. Periana, L. Que, J. Rostrup-Nielson, W. M. H. Sachtler, L. D. Schmidt, A. Sen, G. A. Somorjai, P. C. Stair, B. R. Stults and W. Tumas, Chem. Rev., 2001, 101, 953–996 CrossRef CAS PubMed.
- K. K. Irikura and J. L. Beauchamp, J. Am. Chem. Soc., 1991, 113, 2769–2770 CrossRef CAS.
- M. M. Kappes and R. H. Staley, J. Phys. Chem., 1981, 85, 942–944 CrossRef CAS.
- M. M. Kappes and R. H. Staley, J. Am. Chem. Soc., 1981, 103, 1286–1287 CrossRef CAS.
- P. B. Armentrout and J. L. Beauchamp, Acc. Chem. Res., 1989, 22, 315–321 CrossRef CAS.
- G. Albert, C. Berg, M. Beyer, U. Achatz, S. Joos, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 1997, 268, 235–241 CrossRef CAS.
- J. C. Weisshaar, Acc. Chem. Res., 1993, 26, 213–219 CrossRef CAS.
- P. B. Armentrout, Mass Spectrom. Rev., 2022, 41, 606–626 CrossRef CAS.
- H. Schwarz, Isr. J. Chem., 2014, 54, 1413–1431 CrossRef CAS.
- A. Fielicke, Chem. Soc. Rev., 2023, 52, 3778–3841 RSC.
- D. K. Bohme and H. Schwarz, Angew. Chem., Int. Ed., 2005, 44, 2336–2354 CrossRef PubMed.
- S. M. Lang and T. M. Bernhardt, Phys. Chem. Chem. Phys., 2012, 14, 9255–9269 RSC.
- K. R. Asmis and A. Fielicke, Top. Catal., 2018, 61, 1–2 CrossRef CAS.
- A. Shayesteh, V. V. Lavrov, G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2009, 113, 5602–5611 CrossRef CAS PubMed.
- L. G. Parke, C. S. Hinton and P. B. Armentrout, J. Phys. Chem. C, 2007, 111, 17773–17787 CrossRef CAS.
- R. Wesendrup and H. Schwarz, Angew. Chem., Int. Ed., 1995, 34, 2033–2035 CrossRef CAS.
- O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, J. Phys. Chem. A, 2016, 120, 6216–6227 CrossRef CAS PubMed.
- V. J. F. Lapoutre, B. Redlich, A. F. G. van der Meer, J. Oomens, J. M. Bakker, A. Sweeney, A. Mookherjee and P. B. Armentrout, J. Phys. Chem. A, 2013, 117, 4115–4126 CrossRef CAS PubMed.
- J. Lengyel, N. Levin, M. Ončák, K. Jakob, M. Tschurl and U. Heiz, Chem. - Eur. J., 2022, 29, e202203259 CrossRef.
- J. F. Eckhard, T. Masubuchi, M. Tschurl, R. N. Barnett, U. Landman and U. Heiz, J. Phys. Chem. A, 2021, 125, 5289–5302 CrossRef CAS PubMed.
- Y. Lee, Science, 1987, 236, 793 CrossRef CAS.
- D. R. Herschbach, Angew. Chem., Int. Ed., 1987, 26, 1221–1243 CrossRef.
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, 2009 Search PubMed.
- Tutorials in Molecular Reaction Dynamics, ed. M. Brouard and C. Vallance, RSC Publishing, 2012 Search PubMed.
- X. Yang, D. C. Clary and D. M. Neumark, Chem. Soc. Rev., 2017, 46, 7481–7482 RSC.
- P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355 CrossRef CAS.
- K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111 CrossRef CAS PubMed.
- E. Carrascosa, J. Meyer and R. Wester, Chem. Soc. Rev., 2017, 46, 7498–7516 RSC.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemueller and R. Wester, Science, 2008, 319, 183–186 CrossRef CAS.
- J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333–353 CrossRef CAS PubMed.
- L. Pei, E. Carrascosa, N. Yang, S. Falcinelli and J. M. Farrar, J. Phys. Chem. Lett., 2015, 6, 1684–1689 CrossRef CAS.
- M.-M. He, J. Hu, C.-X. Wu, Y. Zhi and S. X. Tian, J. Phys. Chem. A, 2020, 124, 3358–3363 CrossRef CAS.
- J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977–981 CrossRef CAS.
- G. Zhang, D. Lu, Y. Ding, L. Guan, S. Han, H. Guo and H. Gao, Nat. Chem., 2023, 15, 1255–1261 CrossRef CAS PubMed.
- D. Swaraj, T. Michaelsen, A. Khan, F. Zappa, R. Wild and R. Wester, Mol. Phys., 2024, 122, e2194455 CrossRef.
- E. L. Reichert and J. C. Weisshaar, J. Phys. Chem. A, 2002, 106, 5563–5576 CrossRef CAS.
- S. S. Yi, E. L. Reichert, M. C. Holthausen, W. Koch and J. C. Weisshaar, Chem.–Eur. J., 2000, 6, 2232–2245 CrossRef CAS PubMed.
- P. B. Armentrout, Science, 1991, 251, 175–179 CrossRef CAS.
- D. Schroeder, H. Schwarz, D. E. Clemmer, Y. Chen, P. B. Armentrout, V. I. Baranov and D. K. Boehme, Int. J. Mass Spectrom. Ion Processes, 1997, 161, 175–191 CrossRef CAS.
- M. Meta, M. E. Huber, T. Michaelsen, A. Ayasli, M. Ončák, R. Wester and J. Meyer, J. Phys. Chem. Lett., 2023, 14, 5524–5530 CrossRef CAS PubMed.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151–156 CrossRef CAS PubMed.
- H. Song and H. Guo, ACS Phys. Chem. Au, 2023, 3, 406–418 CrossRef CAS PubMed.
- D. Schroeder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145 CrossRef CAS.
- C. Elschenbroich, Orgonametallchemie, Springer Vieweg, 6th edn, 2008 Search PubMed.
- F. Breher, in Organometallverbindungen, ed. R. L. K. James, E. Huheey and E. A. Keiter, deGruyter, 2014, ch. 15, pp. 757–939 Search PubMed.
- M. Lersch and M. Tilset, Chem. Rev., 2005, 105, 2471–2526 CrossRef CAS PubMed.
- R. Wester, Phys. Chem. Chem. Phys., 2014, 16, 396–405 RSC.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- D. Proch and T. Trickl, Rev. Sci. Instrum., 1989, 60, 713–716 CrossRef CAS.
- V. E. Bondybey and J. H. English, J. Chem. Phys., 1981, 74, 6978–6979 CrossRef CAS.
- D. Gerlich, G. Jerke, U. Mueck and U. Person, Schnelles Ventil zur Erzeugung sehr kurzer Gasimpulse, Internal Document Physics Department, Freiburg University, Germany, 1990, http://www.tu-chemnitz.de/physik/ION/Technology Search PubMed.
- S. Trippel, M. Stei, R. Otto, P. Hlavenka, J. Mikosch, C. Eichhorn, A. Lourderaj, J. Zhang, W. L. Hase, M. Weidemüller and R. Wester, J. Phys.: Conf. Ser., 2009, 194, 012046 CrossRef.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- C. S. Hinton, F. Li and P. Armentrout, Int. J. Mass Spectrom., 2009, 280, 226–234 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, a Package of Ab Initio Programs (Version 2012), see: http://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, I. Miller, F. Thomas, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- E. Sicilia, G. Mazzone, A. Pérez-González, J. Pirillo, A. Galano, T. Heine and N. Russo, Phys. Chem. Chem. Phys., 2017, 19, 16178–16188 RSC.
- K. K. Irikura, I. Goddard and A. William, J. Am. Chem. Soc., 1994, 116, 8733–8740 CrossRef CAS.
- N. Sändig and W. Koch, Organometallics, 1997, 16, 5244–5251 CrossRef.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534–538 CrossRef CAS PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969 CrossRef CAS PubMed.
- B. Bastian, T. Michaelsen, J. Meyer and R. Wester, Astrophys. J., 2019, 878, 162 CrossRef CAS.
- C. Heinemann, J. Schwarz and H. Schwarz, Chem. Phys. Lett., 1995, 247, 611–613 CrossRef CAS.
- O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, Int. J. Mass Spectrom., 2019, 435, 78–92 CrossRef CAS.
- F. J. Wensink, N. Roos, J. M. Bakker and P. B. Armentrout, Inorg. Chem., 2022, 61, 11252–11260 CrossRef CAS PubMed.
- J. Kozubal, T. Heck and R. B. Metz, J. Phys. Chem. A, 2020, 124, 8235–8245 CrossRef CAS PubMed.
- R. Otto, J. Xie, J. Brox, S. Trippel, M. Stei, T. Best, M. R. Siebert, W. L. Hase and R. Wester, Faraday Discuss., 2012, 157, 41–57 RSC.
- E. Carrascosa, M. Stei, M. A. Kainz and R. Wester, Mol. Phys., 2015, 113, 3955 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1: reaction coordinate for Ta+ + CH4 including stationary points of lower importance. Fig. S2: internal energy distributions. Fig. S3: direct comparison of internal and TaCH2+ energy distributions and mean values of the respective distributions. Fig. S4: velocity distribution for Ta+ + CH4 at Erel ≈ 1.0 eV for selected reactant ion velocity subsets. Fig. S5: graphical error representation of product ion velocity distribution. Table S1: time-of-flight values for species of interest. Table S2: benchmarking relative energies (in eV) for three multiplicities in [TaCH4]+. Table S3: benchmarking of reaction energies (in eV) including Ta–H and Ta–C bonds. Cartesian coordinates and energies for optimized structures for Ta+ + CH4. See DOI: https://doi.org/10.1039/d3fd00171g |
| This journal is © The Royal Society of Chemistry 2024 |