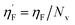Predictive binary mixture toxicity modeling of fluoroquinolones (FQs) and the projection of toxicity of hypothetical binary FQ mixtures: a combination of 2D-QSAR and machine-learning approaches†
Received
12th October 2023
, Accepted 21st November 2023
First published on 22nd November 2023
Abstract
All sorts of chemicals get degraded under various environmental stresses, and the degradates coexist with the parent compounds as mixtures in the environment. Antibiotics emerge as an additional concern due to the bioactive nature of both the parent compound and degradation products and their combined exposure to the environment. Therefore, environmental risk assessment of antibiotics and their degradation products is very much necessary. In this direction, we made use of in silico new approach methodologies (NAMs) and machine-learning algorithms. In this study, we have developed a robust and predictive mixture-quantitative structure–activity relationship (QSAR) model with promising quality and predictability (internal: MAETrain = 0.085, QLOO2 = 0.849, external: MAETest = 0.090, and QF12 = 0.859) for predicting the toxicity of the mixtures of a class of antibiotics and their degradation products. To obtain the predictive model, toxicity data of 78 binary fluoroquinolone mixtures in E. coli (endpoint: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/IC50 in molar) have been utilized. We have used only 0D–2D descriptors to efficiently encode the structural features of mixture components without any additional complexities. The optimization of the class of mixture descriptors has been performed in this study by using three different mixing rules (linear combination of molecular contributions, the squared molecular contributions, and the norm of molecular contributions). Different machine-learning approaches namely, random forest (RF), ada boost, gradient boost (GB), extreme gradient boost (XGB), support vector machine (SVM), linear support vector machine (LSVM), and ridge regression (RR) have been employed here apart from the conventional partial least squares (PLS) regression to optimize the modeling approach. A rigorous validation protocol has been used for assessing the goodness-of-fit, robustness, and external predictability of the models. Finally, the toxicity of possible untested mixtures of different photodegradation products of fluoroquinolones has been predicted using the best model reported in this study.
1/IC50 in molar) have been utilized. We have used only 0D–2D descriptors to efficiently encode the structural features of mixture components without any additional complexities. The optimization of the class of mixture descriptors has been performed in this study by using three different mixing rules (linear combination of molecular contributions, the squared molecular contributions, and the norm of molecular contributions). Different machine-learning approaches namely, random forest (RF), ada boost, gradient boost (GB), extreme gradient boost (XGB), support vector machine (SVM), linear support vector machine (LSVM), and ridge regression (RR) have been employed here apart from the conventional partial least squares (PLS) regression to optimize the modeling approach. A rigorous validation protocol has been used for assessing the goodness-of-fit, robustness, and external predictability of the models. Finally, the toxicity of possible untested mixtures of different photodegradation products of fluoroquinolones has been predicted using the best model reported in this study.
Environmental significance
In this study, we have developed machine learning-based mixture QSAR models from the toxicity data of the binary mixtures of fluoroquinolones in E. coli. Fluoroquinolones are one of the major classes of antibiotics that have been used for a long time and found in different environmental compartments along with their degradation products. However, their mixture toxicity is mostly unknown. Thus, an approach of mixture toxicity assessment has been made in light of the in silico predictive modeling approach. This study will help us to understand the mixture effect of FQs and their degradation products and will also provide knowledge about the toxicity prediction of untested FQ mixtures.
|
1. Introduction
Antibiotics are one of the widely used pharmaceuticals that are found in the environment due to improper waste management in households, hospitals, industrial setups, etc.1–3 This widespread presence of antibiotics in the environment is a major cause of environmental pollution and associated biohazards.1,4 They adversely affect various environmental ecosystems and lower organisms5,6 and also facilitate the development of bacterial resistance.7 Besides the parent compounds, transformation products are also causes of great concern. Most of the chemicals get degraded in the environment and make different degradation products; antibiotics are also not exempted from this natural process.8 On top of this, the antibiotics undergo various transformation reactions during discharge through the wastewater treatment plants in industrial setups, and thus, produce different homologous substances.9 Therefore, a soup of multiple chemicals is released into the environment instead of a single chemical. If we carefully explore the scientific literature, many articles prove the simultaneous presence of different antibiotics and their degradates in the environment.10,11 It should not be taken for granted that the degradation products are less active than the parent compounds; they may retain their bioactive nature instead and may produce enhanced activity in some cases.12,13 The interactive effects such as response addition and synergism play crucial roles in the combined activity, and thus, enhanced toxic action is seen even at a suboptimal concentration of both parent antibiotics and their degradation products.14,15 Therefore, the assessment of mixture toxicity should be a primary objective in the environmental risk assessment. The major chemical regulatory agencies thoroughly investigate the probable environmental risk of individual antibiotics as well as their mixtures,16 but the degradation products are mostly overlooked, although they are a potential cause of environmental threat and should be accounted for in the environmental risk assessment process.
The toxicity analysis of degradation products is largely unexplored due to obvious reasons. The degradation products from different structural analogues can be formed throughout the lifecycle of any chemicals, and it is very complex to identify, isolate, and analyse these by experimentation. The assessment of the combined toxicity among different degradation products or among parent compounds and their degradation products is a far more tricky process because there are no actual traces of the number of such combinations and their compositions. The in silico new approach methodologies (NAMs) such as quantitative structure–activity relationship (QSAR), read-across predictions, etc. can be effectively used in a situation like this where the experimentation is very troublesome. The QSAR models can be developed by correlating the already existing experimental toxicity data with the computationally derived structural and physicochemical descriptors (independent variables of chemicals) and then, can be further used for toxicity prediction. One of the major advantages of such QSAR models over experimentation is the ability to predict the toxicity of an infinite number of combinations without physical formulation; the mixtures must fall under the domain of applicability of the developed model to get a reliable prediction. Both the QSAR and read-across have been employed in many previous studies for the toxicity predictions of individual toxicants17–19 as well as chemical mixtures.20–23 Chemical regulatory agencies such as the US-Environmental Protection Agency (US-EPA), European Chemicals Agency (ECHA), Australian Industrial Chemical Introduction Scheme (AICIS), etc. and legislations such as the European Union's Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH) also encourage the use of such computational approaches for environmental risk assessment and data gap filling.24,25
Among various antibiotics, fluoroquinolones are widely used, and thus, they are often detected in different environmental compartments (wastewater streams, wastewater receiving rivers, etc.) in the ng L−1 to mg L−1 range.26,27 Fluoroquinolones (FQs) get degraded during wastewater treatment in industrial setups and different environmental stresses like sunlight and heat can also affect the integrity of the molecules after disposal.28–30 Although the basic quinolone ring is stable enough to tolerate environmental stresses, the side chains can be easily broken. Therefore, there are high chances of combined effects developed from fluoroquinolone mixtures towards lower environmental species which should be identified. Many research groups have previously worked on fluoroquinolone degradates and their toxicity, but most of the time they got the combined toxic effects without sufficient knowledge about the combination of substances.8,28,31 Wang et al. have published an article in the recent past where they reported an in silico toxicity model for predicting the toxicity of photodegradation products of fluoroquinolones.32 The molecular docking-based energy descriptors have been used to model the mixture toxicity, and they claimed the mixture effects to be mostly additive in the case of fluoroquinolones. However, these descriptors are not simple and reproducible, and there are uncertainties about the use of molecular docking-based descriptors due to the lack of knowledge on the exact mechanism of toxicity mediation. Therefore, there is scope to explore the topic in light of the machine-learning algorithms and to develop more efficient predictive models with simple, reproducible, and easily interpretable descriptors.
In the present work, we have developed well-validated mixture-QSAR models from the existing toxicity data of fluoroquinolone mixtures in Escherichia coli.32E. coli is one of the resident bacteria present in the lower intestine of warm-blooded animals including human beings and it has several beneficial effects.33,34 Therefore, it is a good marker to assess the detrimental effects of fluoroquinolone mixtures towards gut microbiota. Different machine-learning algorithms have been employed with the conventional partial least squares (PLS) regression to optimize the modeling method. We have also optimized the mixing rule for mixture descriptor calculation in this study. To avoid exhaustive calculations, simple, interpretable, and reproducible 0D–2D descriptors have been used. The models have been validated employing the strict validation protocol suggested by the Organization for Economic Co-operation and Development (OECD).35 The probable degradation products of the fluoroquinolones have been identified from the literature. Based on this, the hypothetical binary mixtures have been generated from the degradation products, and their parent compounds and their combined toxicities have been predicted using the newly developed QSAR model. Mostly the freely available software tools have been used to model the toxicity which makes this work cost-effective.
2. Materials and methods
2.1. Toxicity data collection
We have collected a toxicity dataset of 78 binary fluoroquinolone mixtures from the recently published article of Wang et al.32 and have used these for toxicity modeling. The log(1/IC50) values (on the molar scale) have been taken as the endpoint of this study where IC50 is defined as the median inhibitory concentration of binary mixtures in E. coli. The mixtures were prepared from 13 different fluoroquinolone antibiotics namely ciprofloxacin (CIP), danofloxacin (DAN), enoxacin (ENO), enrofloxacin (ENR), levofloxacin (LEV), marbofloxacin (MAR), moxifloxacin (MOX), norfloxacin (NOR), ofloxacin (OFL), orbifloxacin (ORB), pefloxacin (PEF), sarafloxacin (SAR), and sparfloxacin (SPA). All of these component chemicals have been tabulated along with their 2D structures and experimental toxicity data [log(1/IC50)] in Table S1 of the ESI.† According to the report of Wang et al.,32 equitoxic amounts of component chemicals were mixed to obtain the desired mixtures and then used for generating the toxicity data; we have tabulated the compositions (same as those collected) of these 78 binary mixtures in Table S2 of the ESI.† The IC50s of the studied mixtures were determined by using a logistically fitted concentration–inhibition curve. The growth inhibition of E. coli was determined by comparing the optical density of inoculated lysogeny broth (LB) before and after the addition of sample mixtures. The bacterial strain of E. coli was inoculated in a sterile LB medium and cultured at 37 °C for toxicity assay. The optical density of the LB medium was tested using a Multiskan™ FC Microplate Photometer (Thermo-Fisher Scientific, USA).
2.2. Mixture descriptor calculation
In any mixture-QSAR model, each mixture is considered as an individual data point represented by the unique structural features that are numerically encoded in the mixture descriptors. Generally, molecular descriptors are defined as “the final result of a logical and mathematical procedure which transforms chemical information encoded within a symbolic representation of a molecule into a useful number or the result of some standardized experiments”;36 however, mixture descriptors are different from the individual molecular descriptors. Computation of a mixture descriptor is a two-step process where the molecular descriptors of the mixture components are computed first. In the next step, the mixture descriptors are calculated from the structural information of the component chemicals and their corresponding concentration or mass ratio. Different mixing rules are found in the literature for calculating the mixture descriptors among which a linear combination of molecular contributions is mostly used. In a linear combination, the mixture effect is assumed to be additive; however, the mixture components may also produce supra-additive/sub-additive responses due to biological interactions namely, synergism and antagonism, respectively. Qin et al.37 have enlisted numerous mixing rules apart from the linear combination of molecular contributions among which the norm of molecular contributions38 and square molecular contributions39 is most prominent. Therefore, to consider the probable additive, supra-additive, and sub-additive mixture effects, we have employed the linear combination of molar contributions, the square molar contributions, and the norm of molar contributions respectively in the present work. These three mixing rules have been presented in the following eqn (1)–(3):| | | Mixing rule 1 = linear combination of molecular contributions = Σ(pi × xi) | (1) |
| | | Mixing rule 2 = square molecular contributions = (Σ(pi × xi))2 | (2) |
| | 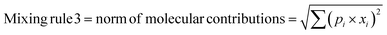 | (3) |
where pi and xi are the mole fraction and descriptor values, respectively, of the ith component. The sum of mole fractions of all component chemicals should be 1. We have used only 0D–2D descriptors to make it simple and easily interpretable. Nine classes of 0D–2D descriptors namely constitutional indices, molecular properties, ring descriptors, connectivity index, electro-topochemical atom indices, functional group counts, atom-centred fragments, atom-type E-state indices, and 2D atom pairs (total descriptor count = 2400) have been computed from the AlvaDesc software40 and accordingly pretreated to omit the redundant descriptors (descriptors with the same values and descriptors with strong inter-correlation). Finally, three classes of pretreated mixture descriptors (363 descriptors in each class) have been obtained by using a Java-based software tool “Mixture-Desc-Calc v1.0” (freely available online: https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home?pli=1).
2.3. Dataset division and optimization of the mixing rule
Ideally, the QSAR models should be developed with the available experimental data and then validated with an external experimental dataset. However, the availability of such experimental data is very limited, and therefore, the complete dataset gets divided into training and test sets to serve the purpose. The training data points are used for model development, whereas the test data points are separately employed for external validation. Here in this study, we have developed QSAR models using 75% of the total data, and the rest have been used to test the developed model (as the test set). There are many reported research studies in the literature where well-validated QSAR models were obtained with 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 training-test divisions.21,22,41 Both the response-based (sorted-activity-based division) and descriptor-based (Euclidean distance-based division and Kennard-Stone division) division techniques have been applied to get the optimum division. The division has been performed using the “Dataset Division GUI” version 1.2 tool (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/), and nine different training-test division sets have been obtained (4 seeds of sorted activity-based divisions, 4 seeds of Euclidean distance-based divisions, and 1 Kennard-Stone division) for each descriptor matrix; therefore a total of 27 division sets were generated.
25 training-test divisions.21,22,41 Both the response-based (sorted-activity-based division) and descriptor-based (Euclidean distance-based division and Kennard-Stone division) division techniques have been applied to get the optimum division. The division has been performed using the “Dataset Division GUI” version 1.2 tool (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/), and nine different training-test division sets have been obtained (4 seeds of sorted activity-based divisions, 4 seeds of Euclidean distance-based divisions, and 1 Kennard-Stone division) for each descriptor matrix; therefore a total of 27 division sets were generated.
For optimizing the mixing rule and selecting the best division set, we have employed the “Double Cross-Validation v2.0” (DCV) tool42 (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/) and have developed preliminary genetic algorithm-based multiple linear regression (GA-MLR) models from each of the 27 training sets for the respective mixing rule. Another round of data pretreatment has been carried out (using “dataPreTreatmentTrainTest v1.0” tool; freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/) before starting the preliminary GA-MLR modeling for removing the redundant descriptors generated after division. The preliminary models have been validated in the same tool (“Double Cross-Validation v2.0”) and validation metrics such as R2, QLOO2, MAETrain95%, QF12, and MAETest95% have been calculated. To optimize the best mixing rule, the averages of the above-mentioned metrics have been calculated, and based on the average values, the optimum mixing rule has been selected. To avoid any division bias and to make the criteria more robust, we have used the mean of the validation metrics of the preliminary models obtained from 9 different training-test pairs as the determination criteria of optimum mixing rule selection. After optimization of the mixing rule, we have compared the balance of internal and external validation metrics of different division sets under the optimized mixing rule, and based on that, the best division was selected. The mixing rule-wise computed validation metrics for each division have been tabulated in Table S3 of the ESI†.
2.4. Feature selection and model development
A multi-layered algorithm has been adopted in this study for extracting valuable structural features for modeling. The most suitable descriptor combination has been finalized by comparing the determination coefficient (R2) and cross-validated correlation coefficient (QLOO2) values of all possible subsets of descriptors. Generally in the regression-based model, a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is maintained between the number of training data points and the number of modeled descriptors; the same rule has been followed here too and the combinations with minimum descriptors have been prioritized. We have generated all possible subsets from the descriptor pool using “BestSubsetSelection v2.1” tool. However, all possible subset selection is computationally very exhaustive and it needs a lot of time to compute the validation metrics of the MLR models developed from the descriptor combinations. Thus, a pool reduction is carried out (from 138 descriptors to 40 descriptors) before all possible subset selections. The initial pool reduction has been commenced by a genetic algorithm (GA) (using the “Genetic algorithm v4.1” tool; available from http://teqip.jdvu.ac.in/QSAR_Tools/) in this study. The important descriptors have been taken into the reduced pool based on the R2 and QLOO2 values of the incoming descriptor combinations.
1 ratio is maintained between the number of training data points and the number of modeled descriptors; the same rule has been followed here too and the combinations with minimum descriptors have been prioritized. We have generated all possible subsets from the descriptor pool using “BestSubsetSelection v2.1” tool. However, all possible subset selection is computationally very exhaustive and it needs a lot of time to compute the validation metrics of the MLR models developed from the descriptor combinations. Thus, a pool reduction is carried out (from 138 descriptors to 40 descriptors) before all possible subset selections. The initial pool reduction has been commenced by a genetic algorithm (GA) (using the “Genetic algorithm v4.1” tool; available from http://teqip.jdvu.ac.in/QSAR_Tools/) in this study. The important descriptors have been taken into the reduced pool based on the R2 and QLOO2 values of the incoming descriptor combinations.
After selecting the best descriptor combination, we have performed the final regression analysis by using a PLS algorithm by employing the “PLS_single_Y v1.0” tool (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/). The PLS is the generalized form of MLR that can handle strongly correlated and colinear data too.43 In the PLS algorithm, latent variables (LVs) are computed from the descriptors and they take part in the regression analysis, unlike MLR. We have optimized the number of latent variables (LVs) by comparing the calculated x-variances after incorporating each incoming LV. Finally, a PLS model has been obtained with the optimum number of LVs from the selected descriptors.
2.5. Machine-learning models
Machine learning (ML) is the science of programming computers so that they can learn from the existing data and use that knowledge to solve future assignments more efficiently.44 Its applications span across different sectors including regulatory decision-making and in silico predictive modeling also. The computers are trained by using the significant patterns of large data against a specific learning algorithm, and then that learning experience is used for predicting the corresponding properties of query compounds. Based on the learning algorithm, ML methods are categorised into three major classes, namely supervised learning, unsupervised learning, and reinforcement. Supervised and unsupervised ML are trained by using labelled and unlabelled data, respectively.45 Reinforcement is different from these two and it is trained by the feedback (either reward or penalty) of the performed action.45,46 In the present study, we have applied supervised machine learning by employing algorithms like random forest (RF),47 ada boost,48 gradient boosting (GB),48 extreme gradient boosting (XGB),49 linear support vector machine (LSVM),50 support vector machine (SVM),47 and ridge regression (RR),48,51 to develop a regression model.
Generally, different models are trained by a specific ML algorithm for a dataset and the best one is selected based on the performance. However, there may be some possibilities for further improvement of the model, and to do so, tuning of hyperparameters is carried out. In this study, we have employed our in-house Python-based tool “Optimization and Cross-validation v1.0” (available online: https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/machine-learning-model-development-guis?pli=1) for tuning the hyperparameters for all the ML algorithms. The GridSearhCV and negative mean squared error have been used as the optimizing algorithm and the scoring function, respectively, in this study. The same training set containing the scaled matrix of previously identified descriptors and endpoint values has been used for hyperparameter optimization. After obtaining the optimized setting, the ML models have been developed using the Python-based “Machine Learning Regression v1.0” tool (available online: https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/machine-learning-model-development-guis?pli=1). For obtaining further details of the ML method used, one may consult the article published by Pore et al.52 The same standardized training and test sets have been used for all ML-based models [standardized/scaled value = (original value − mean of the respective column)/standard deviation of the same column; training set means have been used for the scaling of both training and test sets] as used for the PLS model development. The entire modeling process has been schematically represented in the following Fig. 1.
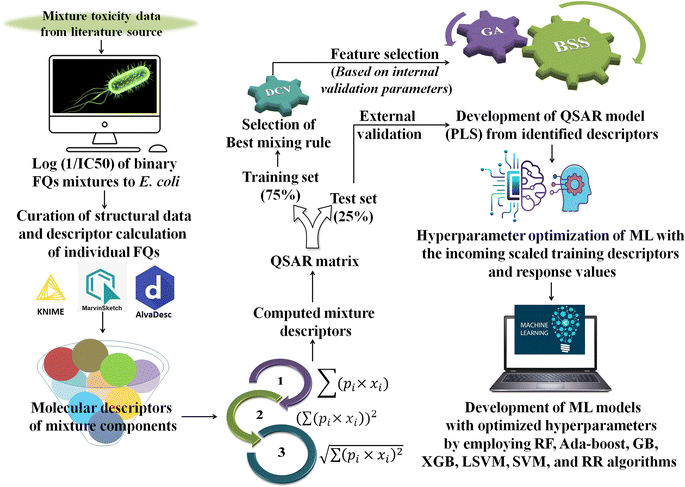 |
| | Fig. 1 Schematic representation of the entire modeling process [*FQs = fluoroquinolones, DCV = double cross-validation, GA = genetic algorithm, BSS = best subset selection, ML = machine learning, PLS = partial least squares, RF = random forest, GB = gradient boost, XGB = extreme gradient boost, LSVM = linear support vector machine, SVM = support vector machine (non-linear), and RR = ridge regression]. | |
2.6. Statistical validation
Statistical validation is an inevitable part of any predictive modeling. As per OECD guideline 4, the QSAR model should be a good fit with the training data, sufficiently robust and externally predictive. Thus, to comply with the norm, we have computed several internal and external validation metrics for assessing the quality of developed models in this study. The internal validation metrics such as the determination coefficient (R2), adjusted R2 (RAdj2), cross-validated correlation coefficient (QLOO2), and mean absolute error of the training set (MAETrain) have been computed from the training data, whereas external validation metrics such as the external correlation coefficient (QF12, QF22, QF32), mean absolute error of the test set (MAEtrain) and concordance correlation coefficient (CCC) have been computed with the test data. The determination coefficients (R2 and/or RAdj2) are the measurement parameters of goodness of fit, mean absolute errors (MAETrain or MAETest) are the measures of error of predictions, and the external correlation coefficients (QF12, QF22, and QF32) are the measures of the external predictability of the model. The cross-validated correlation coefficient (QLOO2) is measured for adjudging the robustness of the statistical model. The difference between QLOO2 and R2 is a marker of robustness and this difference should ideally be a smaller one for a robust model. The threshold limits for external validation metrics (QF12/QF22/QF32 ≥ 0.5) along with internal validation metrics (R2/RAdj2 ≥ 0.6, QLOO2 ≥ 0.5) have been mentioned as per the criterion of Golbaikh and Tropsha for defining the statistical quality of the regression-based models.53,54 The concordance correlation coefficient (CCC) measures the deviation between the regression line and the concordance line (line passing through the origin); therefore, it is a measure of both precision and accuracy. Any value of CCC > 0.85 indicates the reliability of the developed model.55 The important validation metrics which are used in this study have been computed by using the following mathematical eqn (4)–(11):| | 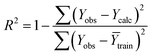 | (4) |
| | 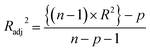 | (5) |
| | 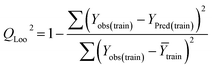 | (6) |
| |  | (7) |
| | 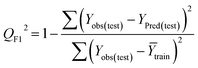 | (8) |
| | 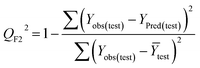 | (9) |
| | 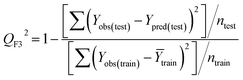 | (10) |
| | 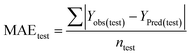 | (11) |
In this study, we have also performed the Y-randomization test to ensure that the developed QSAR models are not the result of any chance correlation. The validation in Y-randomization is accomplished by permuting the response values (Y) 100 times with respect to the X matrix, which remains unchanged. The Y-randomization test has been performed using “SIMCA-P software”56 in this study. As per the protocol, the acceptable value of R2 and Q2 intercepts of the Y-randomization plot must be below 0.2 and 0.05, respectively.
2.7. Toxicity prediction of the binary mixture dataset designed from parent FQs and their degradates: use of the PRI tool
As found in the literature, the chemical species get degraded under open sunlight and other environmental stresses.8 There are many instances where photodegradation/chemical degradation of FQs has been reported in the literature.57,58 As we are mostly focused on the environmental aspects of FQs, we have concentrated on the photodegradation products only. Sturini et al.,8 Babić et al.,59 Ye et al.,31 and Ou et al.28 reported different photodegradation pathways of FQs which are graphically represented in Fig. 2 by taking ciprofloxacin as a prototype compound. Reductive halogenation at the 6th position, hydroxy substitution at the 6th position, and hydroxy addition at the 2nd position are the important transformation reactions that may take place under UV light in the quinolone ring whereas, H-elimination, oxidation, and photolysis are the important transformation reactions that may take place at the ring attached at 7th position of quinolone. We have not considered any reaction where the structural integrity of the core quinolone ring of FQ (important for the toxic response of FQs) is compromised. We have designed a hypothetical mixture dataset from nine parent FQs (ciprofloxacin, danofloxacin, enoxacin, enrofloxacin, levofloxacin, marbofloxacin, norfloxacin, pefloxacin, and sarafloxacin) and their corresponding degradation products as the component chemicals of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 binary mixtures. All possible combinations of components (45 mixtures) have been considered for each FQ. The composition of all the hypothetical mixtures is tabulated in Table S4 of the ESI.†
50 binary mixtures. All possible combinations of components (45 mixtures) have been considered for each FQ. The composition of all the hypothetical mixtures is tabulated in Table S4 of the ESI.†
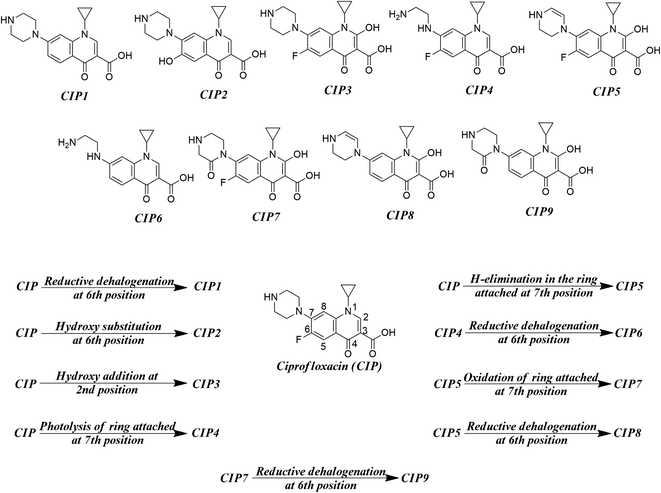 |
| | Fig. 2 Different transformation reactions (UV light-mediated) and the probable photodegradation degradation products. | |
The 2D structures of all degradation products have been made in MarvinSketch software with explicit hydrogen addition and proper aromatization and then subjected to the AlvaDesc software for descriptor calculation. The mixture descriptors have been computed from the computed descriptors (modeled descriptors) of individual components by employing the linear combination of molecular contribution in a similar manner as discussed in the previous “mixture descriptor calculation” section. Finally, the “prediction reliability indicator” (PRI) tool (available online: http://teqip.jdvu.ac.in/QSAR_Tools/) has been employed for the prediction of mixture toxicity and the reliability of the predictions as well. This tool was developed by Roy et al.60 and predicts the toxicity of untested mixtures using the developed model and also categorizes the reliability of the predicted responses into ‘good’, ‘moderate’, and ‘poor’, depending upon the composite score. The reliability of predictions obtained from the PRI tools is essentially based on three sets of principles i.e., “(1) mean absolute error of prediction (leave-one-out) of a query compound from the 10 closest training compounds; (2) applicability domain in terms of similarity, by using the standardization approach; (3) closeness of predicted values to the mean of the observed response of training set compounds”. This tool also provides the applicability domain status of the untested mixtures based on the Euclidean distance analysis of query mixtures with the training set mixtures.
3. Results and discussion
3.1. Optimized mixing rule and best division
We have optimized the mixing rule based on the statistical quality of the preliminary GA-MLR models developed with 9 sets of division obtained from the descriptor matrix of each mixing rule. The computed validation metrics (R2, QLOO2, MAETrain95%, QF12, and MAETest95%) of each model have been tabulated in Table S3 of the ESI.† We have taken the average of validation metrics from all the divisions. Among the three mixing rules, the linear combination of molecular contributions has shown the best average metric values (R2 = 0.883, QLOO2 = 0.853, MAETrain95% = 0.085, QF12 = 0.827, and MAETest95% = 0.091), and therefore, it has been selected as the optimum mixing rule for mixture descriptor calculation in this study. To select the best division, we have compared the performance metrics of GA-MLR models obtained from mixing rule 1. It has been observed that the 2nd seed of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 activity-based division (4-2 ABD) yielded a model with the most balanced performance (R2 = 0.874, QLOO2 = 0.842, MAETrain95% = 0.087, QF12 = 0.837, and MAETest95% = 0.088). Thus, we have proceeded to the feature selection step with 4-2 ABD.
25 activity-based division (4-2 ABD) yielded a model with the most balanced performance (R2 = 0.874, QLOO2 = 0.842, MAETrain95% = 0.087, QF12 = 0.837, and MAETest95% = 0.088). Thus, we have proceeded to the feature selection step with 4-2 ABD.
3.2. Partial least squares (PLS) regression model and validation
As discussed in the section “2.4. Feature selection and model development”, all possible subset selection has been employed to identify the best descriptor combination from the reduced pool of 40 descriptors. Six descriptors namely H-047, Eta_F_A, nR03, F05[C-O], nBnz, and MLOGP2 have been identified as the most prominent descriptors for the prediction of toxicity of fluoroquinolone mixtures. We have moved forward with these six descriptors and developed the QSAR model using the PLS algorithm. To optimise the number of LVs, a PLS regression has been run with the MINITAB software61 and the X-variances of each incoming LV have been noted (see Table S5 of the ESI†). With 5 LVs, the maximum X-variance has been extracted (X-variance = 0.948) from the descriptor matrix, and therefore, final PLS regression has been performed with 5 LVs. It should be noted that the number of LVs in PLS must be lower than the number of descriptors; otherwise, the PLS model will be converted to an MLR equation. The developed PLS model has been shown in the following eqn (12) along with the computed validation metrics-| | | Log (1/IC50) = −1.09774 + 0.1092 × H-047 + 8.10906 × Eta_F_A + 1.50499 × nR03 − 0.11551 × F05[C-O] − 0.33295 × nBnz − 0.144 × MLOGP2 | (12) |
n
Train = 59, R2 = 0.882, RAdj2 = 0.868, QLOO2 = 0.849, MAETrain = 0.085, 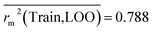 , Δr2m(Train, LOO) = 0.123, RMSEC = 0.108;
, Δr2m(Train, LOO) = 0.123, RMSEC = 0.108;
n
Test = 19, QF12 = 0.859, QF22 = 0.858, QF32 = 0.873, MAETest = 0.090, 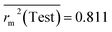 , Δr2m(Test) = 0.089; CCC = 0.927, RMSEP = 0.112.
, Δr2m(Test) = 0.089; CCC = 0.927, RMSEP = 0.112.
The developed model is statistically sound and externally predictive as evidenced by the high computed validation metric values (above 0.8) such as R2, RAdj2,QLOO2, QF12, QF22, and QF32. The error metrics of both training and test sets (such as MAETrain and RMSEC and MAETest and RMSEP) are on the lower side (below 0.15) which signifies the reliability of predictions. There is a very minute difference (0.033) between the determination coefficient (R2) and the cross-validated correlation coefficient (QLOO2), which is an indicator of the robustness of the model. The computed values of rm2 metrics are also in the acceptable range. We have computed the CCC of the developed model and its higher value (CCC = 0.927) represents the proximity of the regression line and the concordance line (line passing through the origin of the observed vs. predicted scatter plot) of the developed model; therefore, the accuracy and precision of the predicted responses have been acknowledged. We have shown the observed vs. predicted scatter plot in the following Fig. 3A where the least scattering and uniform distribution of the training and test data points have been observed surrounding the line passing through the origin. The score plot obtained using the SIMCA-P software indicates the uniform representations of the training data points from all the quadrants of the ellipse (Fig. 3B). We have run the Y-randomization test using SIMCA-P software to cut down the possibility of chance correlation. The R2 and Q2 intercepts of the Y-randomization plot have been computed and the resultant Y-randomization plot is given in the following Fig. 3C. These R2 and Q2 intercept values (R2 = 0.0069 and Q2 = −0.577) have not crossed the threshold limit which indicates the statistical soundness of the model and affirms that it is not the result of any chance correlation.
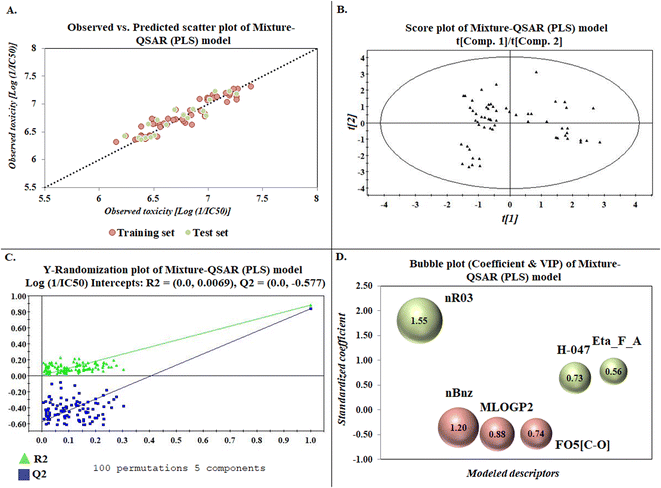 |
| | Fig. 3 Graphical representations [(A) observed vs. predicted toxicity scatter plot, (B) score plot, (C) Y-randomization plot, and (D) bubble plot (coefficient & VIP)]. | |
To know the contributory effect and order of importance of the modeled descriptors, we have derived the standardized regression coefficients and the VIP scores using SIMCA-P software. The variable importance in projection (VIP) scores are the numerical values which portray the variable importance of individual descriptors towards the modeled endpoint. After arranging the descriptors in descending order of the VIP scores and giving them the number of importance (1 to 6), we plotted them against the respective standardized coefficient in a bubble plot (Fig. 3D). The number of importance and the standardized coefficient have been plotted in the bubble plot along the X-axis and Y-axis, respectively, where the bubbles' radii represent the VIP scores of the respective descriptors. As per the bubble plot, nR03 and nBnz are the most important descriptors with VIP scores > 1. Among the 6 descriptors, nR03, H-047, and Eta_F_A are the positively contributory descriptors (represented by green colour in Fig. 3D), whereas nBnz, MLOGP2, and F05[C-O] are the negatively contributory descriptors (represented by red colour in Fig. 3D).
3.3. Machine learning models and the result of validation
To get the best possible predictions from ML, we first optimized the hyperparameter settings of different ML algorithms using the scaled training set. The optimized settings for different ML approaches are given in Table S6 of the ESI.† Finally, we got the ML-derived predictions using RF, AdaBoost, GB, XGB, SVM, LSVM, and RR algorithms. The validation metrics have been computed and tabulated in the following Table 1. Among these seven different ML algorithms, the model derived by extreme gradient boost (XGB) has the most balanced performance. The high R2 (0.885) and QLOO2 (0.858) values, and the minute difference between them (0.027) confirm the goodness of fit and robustness, respectively. In contrast, the high value of external correlation coefficients (QF12 = 0.858, QF22 = 0.857, and QF32 = 0.872) indicates the good external predictability of the model. The error metrics such as MAETrain (0.267) and MAETest (0.279) are also on the lower side. Togo et al., recently published an explainable artificial intelligence (XAI) study for the prediction of developmental toxicity of 585 chemicals, where they reported the XGB-based ML model to be the most efficient and interpretable model.62 One point may be noted here that the machine-learning algorithms may cause model overfitting, and hence, rigorous cross-validation must be performed. The difference between the determination coefficient (R2) and cross-validated correlation coefficient (QLOO2) should be checked (the difference should be minimal) with the conventional validation metrics.
Table 1 Computed validation metrics obtained from the predictions of ML models
| Metrics |
RF |
AdaBoost |
GB |
XGB |
SVM |
LSVM |
RR |
|
MAE and RMSEp values based on standardized input values.
|
|
R
2
|
0.786 |
0.907 |
0.996 |
0.885 |
0.917 |
0.877 |
0.881 |
|
Q
LOO
2
|
0.657 |
0.648 |
0.619 |
0.858 |
0.713 |
0.844 |
0.852 |
| MAETrain |
0.349 |
0.240 |
0.053 |
0.267 |
0.198 |
0.263 |
0.271 |
| RMSEC |
0.458 |
0.302 |
0.064 |
0.336 |
0.286 |
0.348 |
0.343 |
|
Q
F1
2
|
0.772 |
0.769 |
0.701 |
0.858 |
0.838 |
0.838 |
0.847 |
|
Q
F2
2
|
0.770 |
0.767 |
0.698 |
0.857 |
0.837 |
0.837 |
0.845 |
|
Q
F3
2
|
0.794 |
0.791 |
0.730 |
0.872 |
0.854 |
0.854 |
0.862 |
| MAETesta |
0.345 |
0.355 |
0.391 |
0.279 |
0.284 |
0.287 |
0.284 |
| CCC |
0.859 |
0.867 |
0.839 |
0.925 |
0.906 |
0.910 |
0.918 |
| RMSEPa |
0.450 |
0.453 |
0.515 |
0.355 |
0.379 |
0.379 |
0.369 |
We have compared the XGB-derived ML model and the PLS model based on their overall performance. Both of these models have almost similar goodness of fit, robustness, and external predictability. However, the PLS model has shown the least errors of predictions (MAETrain = 0.085 and MAETest = 0.090) as compared to the XGB-derived ML model (MAETrain = 0.267 and MAETest = 0.279). Therefore, in terms of the overall performance, the PLS model has been chosen as the best one.
3.4. Insights of modeled descriptors
As we have stated earlier, six 2D descriptors namely, H-047, Eta_F_A, nR03, F05[C-O], nBnz, and MLOGP2 have been identified by using the best subset selection algorithm and then modeled using PLS regression in this study. We have discussed the contributions of each descriptor in the coming section following their order of importance towards the studied endpoint. The structural features defined by the identified descriptors have been showcased in the following Fig. 4.
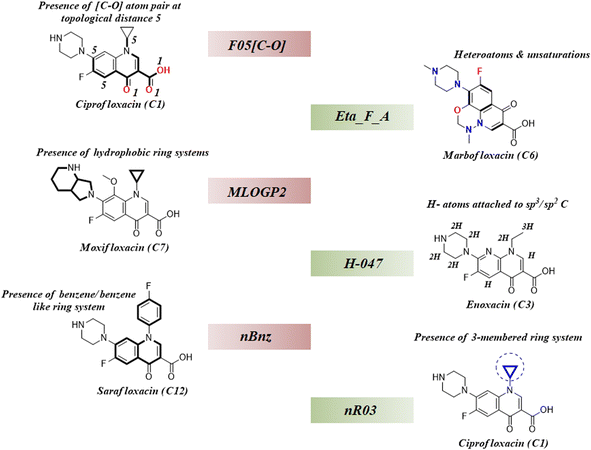 |
| | Fig. 4 Structural representation of modelled descriptors (green blocks: positive contributory descriptors and red blocks = negative contributory descriptors). | |
3.4.1. nR03 descriptor.
nR03 is the most important and positive contributing descriptor of this study. It belongs to the class of ‘ring descriptor’ and represents the number of three-membered ring systems in the molecule. It has been observed that the presence of the 3-membered ring in the mixture component potentiates mixture toxicity. For better understanding, we have compared a set of mixtures with structural representation in Fig. S1 of the ESI.† The most toxic mixture [mixture M12: log(1/IC50) = 7.4] of this data set consists of the cyclopropyl ring containing the components ciprofloxacin and sparfloxacin which enhance the mixture toxicity by a considerable amount. In contrast, the mixture of enoxacin and norfloxacin (mixture M28) is devoid of the 3-membered ring system, and thus, it is found to be the least toxic (mixture M28: log(1/IC50) = 6.16) among all the training data points.
3.4.2. nBnz descriptor.
nBnz is the next important descriptor, which indicates the number of benzene or benzene-like ring systems in a molecule. It is a negative contributing descriptor that seems to decrease the mixture toxicity. We have comparatively analysed two mixtures (M56 and M22) with different toxicities [log(1/IC50): M56 = 7.17; M22 = 7.27] in Fig. S2 of the ESI.† It has been observed that the comparatively less toxic mixture M56 contains marbofloxacin (mole fraction = 0.4) and sarafloxacin (mole fraction = 0.6) as the mixture components, and the more toxic mixture M22 contains danofloxacin (mole fraction = 0.61) and sarafloxacin (mole fraction = 0.39) as the mixture components. Sarafloxacin has a 4-fluorobenzyl substitution on the nitrogen of the central quinolone ring, and it is a constant component of both the mixtures. However, it constitutes 60% of mixture M56 and 39% of mixture M22. Among the variable components, marbofloxacin constitutes 40% of mixture M56, and it has a 6-membered fused ring attached to the central quinolone. In contrast, danofloxacin of mixture M22 constitutes 61% of the mixture and contains a cyclopropyl ring in its structure (cyclopropyl ring helps to increase toxicity). Due to the presence of more benzene-like ring systems attached to the central quinolone ring, less toxic mixture M56 has a greater nBnz value (1.6) than the more toxic counterpart mixture M22 (nBnz = 1.39). This comparative analysis clearly justifies the negative contributory effect of the descriptor nBnz and also establishes the positive contributory effect of the descriptor nR03.
3.4.3. MLOGP2 descriptor.
The next important descriptor is the molecular property MLOGP2, which negatively affects the endpoint prediction in this study. MLOGP2 is the squared Moriguchi octanol–water partition coefficient which indicates the lipophilicity of chemicals. Generally, the lipophilic chemicals become more toxic due to the easy transportation in the cell through the lipid bi-layers; however, the increase has a limit. Roy et al. reported the parabolic relationship between lipophilicity and cellular toxicity where they showed a continuous decrease in toxicity after reaching the peak level with a continuous increase in lipophilicity.63 Besides this, Wang et al. identified the π–π stacking interaction and hydrogen bonding interaction as the most important mechanisms for toxic action of fluoroquinolones in a docking study.32 Therefore, it has been established that the lipophilicity is not increasing the toxicity here. We have comparatively analysed the studied mixtures also in Fig. S2 of the ESI.† A more lipophilic mixture M27 (MLOGP2 = 4.014) is found to be less toxic [log(1/IC50) = 6.25] than a comparatively less lipophilic mixture M05 [MLOGP2 = 2.331; log(1/IC50) = 7.28] which justifies the negative contributory effect of MLOGP2 towards the toxic endpoint of this study.
3.4.4. F05[C-O] descriptor.
F05[C-O] is a 2D-atom pair descriptor which represents the frequency of [C-O] atom pairs present at topological distance 5 in a molecule. Its negative regression coefficient indicates an inverse correlation between the toxic endpoint and the descriptor value. We have carefully analysed the components of two different mixtures (M59 and M12) presented in Fig. S2 of the ESI.† It has been observed that the atom pair [C-O] at topological distance 5 mostly represents the central quinolone ring. Therefore, a greater value of this descriptor corresponds to the attachment of extra ring systems to the central quinolone as seen in Fig. S2 of the ESI,† and this structural deviation of the main quinolone ring is detrimental to the toxicity. Mixture M59 has a greater descriptor value (F05[C-O] = 12.04) and comparatively less toxicity [log(1/IC50) = 6.69] than mixture M12 with a lower descriptor value (F05[C-O] = 8.0) and comparatively more toxicity [log(1/IC50) = 7.4]. These observations justify the negative contributory effect of F05[C-O] towards the studied endpoint in E. coli.
3.4.5. H-047 descriptor.
H-047 is the penultimate descriptor as per the descending order of importance (see Fig. 2D). This atom-centered fragment descriptor is a measure of H-atoms attached to the sp3/sp2 carbons in a molecule. Its positive regression coefficient indicates the linear correlation between the descriptor value and the toxicity. Mixtures from the studied dataset also align with this trend. For example, a mixture of enoxacin and norfloxacin (mixture M28) has a lower H-047 value (11.47) as well as toxicity [log(1/IC50) = 6.16] as compared to the mixture of ciprofloxacin and marbofloxacin (mixture M05) which has a greater H-047 value (13.08) and toxicity [log(1/IC50) = 7.28]. In Fig. S1 of the ESI,† we have analysed the structural components of both mixtures M28 and M05 for a better understanding of the descriptor.
3.4.6. Eta_F_A descriptor.
Eta_F_A is a 1st generation electro-topochemical atom (ETA) index descriptor which positively contributes towards the prediction of the studied endpoint [log(1/IC50)] to E. coli. It is a measure of heteroatoms and unsaturation present relative to the overall size of a molecule. According to the published report of Roy et al., Eta_F_A 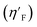 is calculated by employing the following formula64
is calculated by employing the following formula64
where ηF is the functionality index which estimates the unsaturation and heteroatoms of a molecule, whereas Nv is the total number of non-hydrogen atoms present in a molecule. For a better understanding of the descriptor, we have compared two studied mixtures (M7 and M57) in Fig. S1 of the ESI.† Mixture M7 is composed of ciprofloxacin and norfloxacin as the component chemicals, whereas mixture M57 contains marbofloxacin and sparfloxacin. The unsaturation count of both these mixtures is the same; however, mixture M57 bears more heteroatoms (8 N, 3 F, and 1 O) than mixture M7 (6 N and 2 F). Generally, the presence of electronegative atoms influences the formation of intermolecular H-bonds with the amino acid residues of the cellular receptor/protein and therefore increases the toxic potential.32 A similar observation has been proven in this study also. The mixture toxicity is increased from lower heteroatom containing mixture M7 [Eta_F_A = 0.938; log(1/IC50) = 6.34] to greater heteroatom containing mixture M57 [Eta_F_A = 0.999; log(1/IC50) = 7.24].
3.5. Applicability domain analysis
The applicability domain (AD) is the theoretical region in descriptor space where the model-derived predictions become reliable.65 The reliable predictions of all chemicals cannot be derived from a single model and that is why the knowledge of AD should be provided with a newly developed model. OECD also suggests the same as a form of OECD principle 3 (a defined domain of applicability).35 To comply with the norm, we have also analyzed the domain of applicability of the developed PLS-based mixture QSAR model in this study. The DModX (distance to the model in X-space) approach has been employed in SIMCA-P software to derive the AD of the PLS model. We have given the AD plots in Fig. S3 of the ESI.† No outliers have been found (in both training and test sets) at a 99% confidence interval (D-Crit value = 0.00999898) which again strengthens the performance claim of the new model.
3.6. Predicted responses of untested mixtures and the result of reliability analysis
We have predicted the toxicity of 405 hypothetical mixtures (designed from the parent FQs and their probable photodegradation products) with the developed PLS model employing the PRI tool. The predicted responses are tabulated in Table S7 of the ESI† along with their respective reliability of prediction and AD status. The toxicity of 354 mixtures (87.41%), 42 mixtures (10.37%), and 9 mixtures (2.22%) has been predicted respectively with “good”, “moderate”, and “poor” reliability. Among these mixtures, 86.67% fall under the domain of applicability of the developed PLS model, whereas 13.33% of mixtures have been identified as outliers. This analysis once again proved the efficiency of the developed model for predicting the toxicity of untested mixtures. We have also graded the response as highly toxic and less toxic after keeping the observed response of prototype FQ ciprofloxacin [log(1/IC50) = 7.30 mol L−1] as the threshold. According to this grading procedure, 19.75% of mixtures have been classified as highly toxic, whereas the rest have come under the less toxic category.
4. Comparison of models
We have compared the modeling approaches as well as the performance metrics of this study with those in a previously published work by Wang et al.32 The same toxicity dataset was used in both of these studies; however, we have changed the training-test division in the current work. All the models have been developed with 59 training compounds in this study, unlike the 63 training compounds used in the previous work. Besides this, more efficient PLS regression and ML-based modeling approaches have been used in this study instead of the simple linear regression of the previous model. As per the reported validation metrics by Wang et al., the previous linear regression was a robust model with sufficient goodness of fit and moderate external predictability (Table 2). The present study has achieved better performance in all aspects of the previous model. Both the PLS and XGB models have shown better R2 (PLS = 0.882 ans XGB = 0.885), QLOO2 (PLS = 0.849 and XGB = 0.858), and QF12 (PLS = 0.859 and XGB = 0.858) values than the previous model (R2 = 0.824, QLOO2 = 0.778 and QF12 = 697). The difference between R2 and QLOO2 (an indicator of robustness) is less in the PLS (0.882 − 0.849 = 0.033) and XGB (0885 − 0.858 = 0.027) models of this study as compared to the linear regression model (0.824 − 0.778 = 0.046) of the previous work. Based on the unstandardized error values of the XGB model, it clearly outperforms the linear regression of the previous work (XGB-unstandardized: RMSEC = 0.106, RMSEP = 0.112; linear regression: RMSEC = 0.135, and RMSEP = 0.156). The PLS-based regression model also outperforms the previously reported linear regression in both the errors (PLS: RMSEC = 0.108 and RMSEP = 0.112). Above all, the present models (PLS and ML) have been developed with simple and easily reproducible 0D–2D descriptors which make the model easily transferable as compared to the linear regression model obtained from the molecular docking-based energy descriptors (docking energy descriptor calculation involves non-reproducible and less transferable steps i.e., energy minimization and conformational analysis of the 3D structures of molecules). Finally, as a part of this work, we have also analyzed the effect of the structural features as well as the mole fraction of each component on the toxicity of E. coli which helps the reader to graphically understand the additive nature of the studied mixtures.
Table 2 Comparative assessment of the performance of the present models (PLS and XGB) with the previous work
| Criteria and metrics of comparison |
Linear regression model of previous work by Wang et al.32 |
PLS-based regression model of the present work |
XGB-based regression model of the present work |
| Dataset size |
n
Train = 63, nTest = 15 |
n
Train = 59, nTest = 19 |
n
Train = 59, nTest = 19 |
| Modeled descriptors used |
Molecular docking-based energy descriptor |
2D descriptors |
2D descriptors |
| Type of mixtures |
Additive |
Additive |
Additive |
|
R
2
|
0.824 |
0.882 |
0.885 |
|
Q
LOO
2
|
0.778 |
0.849 |
0.858 |
| RMSEC |
0.135 |
0.108 |
0.106 (unstandardized) |
|
Q
F1
2
|
0.697 |
0.859 |
0.858 |
| RMSEP |
0.156 |
0.112 |
0.112 (unstandardized) |
5. Conclusion
The present work represents the development of QSAR models for toxicity prediction of FQ mixtures in E. coli and the use of different linear and non-linear machine learning algorithms for model development. The models were made only with the binary mixtures' toxicity data. The conventional PLS algorithm and the XGB-based ML approach have shown promising efficiency in mixture toxicity prediction. We have successfully applied three different mixing rules to compute the mixture descriptors in this study and the linear combination of molecular contributions (additive effect) has been identified as the best one. Our model outperforms the previous one in terms of goodness of fit, robustness, and external predictivity. The use of 2D-structural descriptors made the model quite simple, reproducible, and easily transferable as compared to its more complicated counterparts. Six different 2D-structural features have been identified which successfully demonstrate the effect of structural features on mixture toxicity of FQs. The presence of a tricyclic ring on the 1st N of quinolone and a greater number of heteroatoms and unsaturation in the mixture component can be detrimental to environmental safety. In contrast, the lipophilicity and the presence of more benzene/benzene-like ring structures in the mixture component can reduce the greater toxic effect. The toxic effect of different photodegradation products on mixture toxicity has also been assessed in this study. We have predicted the toxicity of 405 hypothetical mixtures (binary) which are empirically designed from 9 FQs and their corresponding photodegradation products. Among these 405 mixtures, 19.75% have shown a higher risk of being toxic towards E. coli. This result strengthens the claim of efficient prediction of real untested/new mixtures without the physical synthesis using 2D-QSAR and ML-based models. Thus, these in silico modeling approaches can be efficiently used in the decision-making of chemical regulatory agencies in the near future. However, this projection cannot cover the entire chemical domain of the FQs and their different degradation products which makes us bound to perform more exhaustive work towards diverse ecological species for better risk assessment. Besides the toxicological perspectives, these in silico approaches can be used for predicting the chances of degradation by taking physical parameters such as pKa/pKb (dissociation constants) as independent variables. This is another important path which needs to be explored exhaustively in the near future.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Mainak Chatterjee sincerely acknowledges the financial assistance of All India Council for Technical Education (AICTE-New Delhi) as a form of National Doctoral Fellowship.
References
- K. Kümmerer, Antibiotics in the Aquatic Environment – A Review – Part I, Chemosphere, 2009, 75, 417–434, DOI:10.1016/J.CHEMOSPHERE.2008.11.086.
- D. Álvarez-Muñoz, S. Rodríguez-Mozaz, A. L. Maulvault, A. Tediosi, M. Fernández-Tejedor, F. Van den Heuvel, M. Kotterman, A. Marques and D. Barceló, Occurrence of Pharmaceuticals and Endocrine Disrupting Compounds in Macroalgaes, Bivalves, and Fish from Coastal Areas in Europe, Environ. Res., 2015, 143, 56–64, DOI:10.1016/j.envres.2015.09.018.
- W. Xiong, Y. Sun, T. Zhang, X. Ding, Y. Li, M. Wang and Z. Zeng, Antibiotics, Antibiotic Resistance Genes, and Bacterial Community Composition in Fresh Water Aquaculture Environment in China, Microb. Ecol., 2015, 70, 425–432, DOI:10.1007/s00248-015-0583-x.
- K. Kümmerer, The Presence of Pharmaceuticals in the Environment Due to Human Use – Present Knowledge and Future Challenges, J. Environ. Manage., 2009, 90, 2354–2366, DOI:10.1016/j.jenvman.2009.01.023.
- N. Martins, R. Pereira, N. Abrantes, J. Pereira, F. Gonçalves and C. R. Marques, Ecotoxicological effects of ciprofloxacin on freshwater species: data integration and derivation of toxicity thresholds for risk assessment, Ecotoxicology, 2012, 21, 1167–1176, DOI:10.1007/s10646-012-0871-x.
- K. Kümmerer, Antibiotics in the Aquatic Environment – A Review – Part II, Chemosphere, 2009, 75, 435–441, DOI:10.1016/j.chemosphere.2008.12.006.
- Y. Yang, W. Song, H. Lin, W. Wang, L. Du and W. Xing, Antibiotics and Antibiotic Resistance Genes in Global Lakes: A Review and Meta-Analysis, Environ. Int., 2018, 116, 60–73, DOI:10.1016/j.envint.2018.04.011.
- M. Sturini, A. Speltini, F. Maraschi, L. Pretali, E. N. Ferri and A. Profumo, Sunlight-induced degradation of fluoroquinolones in wastewater effluent: photoproducts identification and toxicity, Chemosphere, 2015, 134, 313–318, DOI:10.1016/j.chemosphere.2015.04.081.
- X. Guo, Z. Yan, Y. Zhang, X. Kong, D. Kong, Z. Shan and N. Wang, Removal mechanisms for extremely high-level fluoroquinolone antibiotics in pharmaceutical wastewater treatment plants, Environ. Sci. Pollut. Res., 2017, 24, 8769–8777, DOI:10.1007/s11356-017-8587-3.
- L. Jiang, X. Hu, D. Yin, H. Zhang and Z. Yu, Distribution and seasonal variation of antibiotics in the Huangpu River, Shanghai, China, Chemosphere, 2011, 82, 822–828, DOI:10.1016/j.chemosphere.2010.11.028.
- C. Li, J. Chen, J. Wang, Z. Ma, P. Han, Y. Luan and A. Lu, Occurrence of antibiotics in soils and manures from greenhouse vegetable production bases of Beijing, China and an associated risk assessment, Sci. Total Environ., 2015, 521–522, 101–107, DOI:10.1016/j.scitotenv.2015.03.070.
- S. Achermann, V. Bianco, C. B. Mansfeldt, B. Vogler, B. A. Kolvenbach, P. F. X. Corvini and K. Fenner, Biotransformation of sulfonamide antibiotics in activated sludge: The formation of pterin-conjugates leads to sustained risk, Environ. Sci. Technol., 2018, 52, 6265–6274, DOI:10.1021/acs.est.7b06716.
- D. M. Cwiertny, S. A. Snyder, D. Schlenk and E. P. Kolodziej, Environmental designer drugs: When transformation may not eliminate risk, Environ. Sci. Technol., 2014, 48, 11737–11745, DOI:10.1021/es503425w.
- S. Kar and J. Leszczynski, Is intraspecies QSTR model answer to toxicity data gap filling: Ecotoxicity modeling of chemicals to avian species, Sci. Total Environ., 2020, 738, 139858, DOI:10.1016/j.scitotenv.2020.139858.
- X. Zou, Z. Lin, Z. Deng, D. Yin and Y. Zhang, The joint effects of sulfonamides and their potentiator on Photobacterium phosphoreum: differences between the acute and chronic mixture toxicity mechanisms, Chemosphere, 2012, 86, 30–35, DOI:10.1016/j.chemosphere.2011.08.046.
- O. Nicolotti, E. Benfenati, A. Carotti, D. Gadaleta, A. Gissi, G. F. Mangiatordi and E. Novellino, REACH and in silico methods: an attractive opportunity for medicinal chemists, Drug Discov. Today, 2014, 19, 1757–1768, DOI:10.1016/j.drudis.2014.06.027.
- Y. Hao, T. Fan, G. Sun, F. Li, N. Zhang, L. Zhao and R. Zhong, Environmental toxicity risk evaluation of nitroaromatic compounds: machine learning driven binary/multiple classification and design of safe alternatives, Food Chem. Toxicol., 2023, 170, 113461, DOI:10.1016/j.fct.2022.113461.
- S. Chen, G. Sun, T. Fan, F. Li, Y. Xu, N. Zhang, L. Zhao and R. Zhong, Ecotoxicological QSAR study of fused/non-fused polycyclic aromatic hydrocarbons (FNFPAHs): assessment and priority ranking of the acute toxicity to Pimephales promelas by QSAR and consensus modeling methods, Sci. Total Environ., 2023, 876, 162736, DOI:10.1016/j.scitotenv.2023.162736.
- F. Li, T. Fan, G. Sun, L. Zhao, R. Zhong and Y. Peng, Systematic QSAR and IQCCR modelling of fused/non-fused aromatic hydrocarbons (FNFAHs) carcinogenicity to rodents: reducing unnecessary chemical synthesis and animal testing, Green Chem., 2022, 24, 5304–5319, 10.1039/D2GC00986B.
- M. Chatterjee and K. Roy, Chemical similarity and machine learning-based approaches for the prediction of aquatic toxicity of binary and multicomponent pharmaceutical and pesticide mixtures against Aliivibrio fischeri, Chemosphere, 2022, 308, 136463, DOI:10.1016/j.chemosphere.2022.136463.
- M. Chatterjee and K. Roy, “Data fusion” quantitative read-across structure–activity-activity relationships (q-rasaars) for the prediction of toxicities of binary and ternary antibiotic mixtures toward three bacterial species, J. Hazard. Mater., 2023, 459, 132129, DOI:10.1016/j.jhazmat.2023.132129.
- R. Paul, M. Chatterjee and K. Roy, First report on soil ecotoxicity prediction against Folsomia candida using intelligent consensus predictions and chemical read-across, Environ. Sci. Pollut. Res., 2022, 29, 88302–88317, DOI:10.1007/s11356-022-21937-w.
- P. Kumar, A. Kumar and D. Singh, CORAL: development of a hybrid descriptor based QSTR model to predict the toxicity of dioxins and dioxin-like compounds with correlation intensity index and consensus modelling, Environ. Toxicol. Pharmacol., 2022, 93, 103893, DOI:10.1016/j.etap.2022.103893.
- A. B. Raies and V. B. Bajic, silico toxicology: Computational methods for the prediction of chemical toxicity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 147–172, DOI:10.1002/wcms.1240.
- S. Klatte, H. C. Schaefer and M. Hempel, Pharmaceuticals in the environment – a short review on options to minimize the exposure of humans, animals and ecosystems, Sustainable Chem. Pharm., 2017, 5, 61–66, DOI:10.1016/j.scp.2016.07.001.
- R. Gothwal and Shashidhar, Occurrence of high levels of fluoroquinolones in aquatic environment due to effluent discharges from bulk drug manufacturers, J. Hazard., Toxic Radioact. Waste, 2017, 21, 05016003, DOI:10.1061/(ASCE)HZ.2153-5515.0000346.
- A. S. Oberoi, Y. Jia, H. Zhang, S. K. Khanal and H. Lu, Insights into the fate and removal of antibiotics in engineered biological treatment systems: a critical review, Environ. Sci. Technol., 2019, 53, 7234–7264, DOI:10.1021/acs.est.9b01131.
- H. S. Ou, J. S. Ye, S. Ma, C. H. Wei, N. Y. Gao and J. Z. He, Degradation of ciprofloxacin by UV and UV/H2O2 via multiple-wavelength ultraviolet light-emitting diodes: Effectiveness, intermediates and antibacterial activity, Chem. Eng. J., 2016, 289, 391–401, DOI:10.1016/j.cej.2016.01.006.
- M. I. Vasquez, E. Hapeshi, D. Fatta-Kassinos and K. Kümmerer, Biodegradation potential of ofloxacin and its resulting transformation products during photolytic and photocatalytic treatment, Environ. Sci. Pollut. Res., 2013, 20, 1302–1309, DOI:10.1007/s11356-012-1096-5.
- X. Wei, J. Chen, Q. Xie, S. Zhang, L. Ge and X. Qiao, Distinct photolytic mechanisms and products for different dissociation species of ciprofloxacin, Environ. Sci. Technol., 2013, 47, 4284–4290, DOI:10.1021/es400425b.
- J. S. Ye, J. Liu, H. S. Ou and L. L. Wang, Degradation of ciprofloxacin by 280 nm ultraviolet-activated persulfate: Degradation pathway and intermediate impact on proteome of Escherichia coli, Chemosphere, 2016, 165, 311–319, DOI:10.1016/j.chemosphere.2016.09.031.
- D. Wang, Q. Ning, J. Dong, B. W. Brooks and J. You, Predicting mixture toxicity and antibiotic resistance of fluoroquinolones and their photodegradation products in Escherichia coli, Environ. Pollut., 2020, 262, 114275, DOI:10.1016/j.envpol.2020.114275.
- J. N. V. Martinson and S. T. Walk, Escherichia coli residency in the gut of healthy human adults, EcoSal Plus, 2020, 9, 10–1128, DOI:10.1128/ecosalplus.esp-0003-2020.
- J. N. V. Martinson, N. V. Pinkham, G. W. Peters, H. Cho, J. Heng, M. Rauch, S. C. Broadaway and S. T. Walk, Rethinking gut microbiome residency and the enterobacteriaceae in healthy human adults, ISME J., 2019, 13, 2306–2318, DOI:10.1038/s41396-019-0435-7.
-
OECD, Validation of (Q)SAR Models – OECD, https://www.oecd.org/chemicalsafety/risk-assessment/validationofqsarmodels.htm, accessed 30 September 2023 Search PubMed.
-
V. Consonni and R. Todeschini, Molecular descriptors, in Recent Advances in QSAR Studies. Challenges and Advances in Computational Chemistry and Physics, ed. T. Puzin, J. Leszczynski and M. Cronin, Springer, 2010, DOI:10.1007/978-1-4020-9783-6_3.
- L. T. Qin, Y. H. Chen, X. Zhang, L. Y. Mo, H. H. Zeng and Y. P. Liang, QSAR prediction of additive and non-additive mixture toxicities of antibiotics and pesticide, Chemosphere, 2018, 198, 122–129, DOI:10.1016/j.chemosphere.2018.01.142.
- T. Gaudin, P. Rotureau and G. Fayet, Mixture descriptors toward the development of quantitative structure-property relationship models for the flash points of organic mixtures, Ind. Eng. Chem. Res., 2015, 54, 6596–6604, DOI:10.1021/acs.iecr.5b01457.
- D. A. Saldana, L. Starck, P. Mougin and B. Rousseau, Prediction of flash points for fuel mixtures using machine learning and a novel equation, Energy Fuels, 2013, 27, 3811–3820, DOI:10.1021/ef4005362.
-
A. Mauri, AlvaDesc: a tool to calculate and analyze molecular descriptors and fingerprints, in Methods in Pharmacology and Toxicology, ed. K. Roy, Humana Press Inc., New York, 2020, pp. 801–820, DOI:10.1007/978-1-0716-0150-1_32.
- S. Ghosh, M. Chatterjee and K. Roy, Predictive quantitative read-across structure–property relationship modeling of the retention time (log tR) of pesticide residues present in foods and vegetables, J. Agric. Food Chem., 2023, 71, 9538–9548, DOI:10.1021/acs.jafc.3c01438.
- K. Roy and P. Ambure, The “Double Cross-Validation” software tool for MLR QSAR model development, Chemom. Intell. Lab. Syst., 2016, 159, 108–126, DOI:10.1016/j.chemolab.2016.10.009.
- S. Wold, M. Sjöström and L. Eriksson, PLS-regression: a basic tool of chemometrics, Chemom. Intell. Lab. Syst., 2001, 58, 109–130, DOI:10.1016/S0169-7439(01)00155-1.
- J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Applications of machine learning in drug discovery and development, Nat. Rev. Drug Discovery, 2019, 18, 463–477, DOI:10.1038/s41573-019-0024-5.
- M. I. Jordan and T. M. Mitchell, Machine learning: Trends, perspectives, and prospects, Science, 2015, 349, 255–260, DOI:10.1126/science.aaa8415.
- I. H. Sarker, Machine learning: Algorithms, real-world applications and research directions, SN Comput. Sci., 2021, 2, 1–21, DOI:10.1007/s42979-021-00592-x.
-
R. J. Chase, D. R. Harrison, G. M. Lackmann and A. McGovern, A Machine Learning Tutorial for Operational Meteorology, Part II: Neural Networks and Deep Learning, Weather Forecast, 2023, pp. 1271–1293, DOI:10.1175/waf-d-22-0187.1.
-
A. Geron, Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, O'Reilly
Media, Inc., USA, 2019 Search PubMed.
-
T. Chen and C. Guestrin, XGBoost: a scalable tree boosting system, in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, pp. 785–794, DOI:10.1145/2939672.2939785.
- R. Burbidge, M. Trotter, B. Buxton and S. Holden, Drug design by machine learning: support vector machines for pharmaceutical data analysis, Comput. Chem., 2001, 26, 5–14, DOI:10.1016/S0097-8485(01)00094-8.
- G. C. McDonald, Ridge regression, Wiley Interdiscip. Rev. Comput. Stat., 2009, 1, 93–100, DOI:10.1002/wics.14.
- S. Pore, A. Banerjee and K. Roy, Machine learning-based q-RASPR modeling of power conversion efficiency of organic dyes in dye-sensitized solar cells, Sustainable Energy Fuels, 2023, 7, 3412–3431, 10.1039/d3se00457k.
-
K. Roy, S. Kar and R. N. Das, Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press, 2015, DOI:10.1016/C2014-0-00286-9.
- K. Roy and I. Mitra, On various metrics used for validation of predictive QSAR models with applications in virtual screening and focused library design, Comb. Chem. High Throughput Screening, 2011, 14, 450–474, DOI:10.2174/138620711795767893.
- N. Chirico and P. Gramatica, Real external predictivity of qsar models: How to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient, J. Chem. Inf. Model., 2011, 51, 2320–2335, DOI:10.1021/ci200211n.
-
Z. Wu, D. Li, J. Meng and H. Wang, Introduction to SIMCA-P and its application, in Handbook of Partial Least Squares, ed. V. Esposito Vinzi, W. Chin, J. Henseler and H. Wang, Springer, Berlin, Heidelberg, 2010, pp. 757–774, DOI:10.1007/978-3-540-32827-8_33.
- M. Rusch, A. Spielmeyer, H. Zorn and G. Hamscher, Degradation and transformation of fluoroquinolones by microorganisms with special emphasis on ciprofloxacin, Appl. Microbiol. Biotechnol., 2019, 103, 6933–6948, DOI:10.1007/s00253-019-10017-8.
- H. Zhang and C. H. Huang, Oxidative transformation of fluoroquinolone antibacterial agents and structurally related amines by manganese oxide, Environ. Sci. Technol., 2005, 39, 4474–4483, DOI:10.1021/es048166d.
- S. Babić, M. Periša and I. Škorić, Photolytic degradation of norfloxacin, enrofloxacin and ciprofloxacin in various aqueous media, Chemosphere, 2013, 91, 1635–1642, DOI:10.1016/j.chemosphere.2012.12.072.
- K. Roy, P. Ambure and S. Kar, How precise are our quantitative structure–activity relationship derived predictions for new query chemicals?, ACS Omega, 2018, 3, 11392–11406, DOI:10.1021/acsomega.8b01647.
-
Data Analysis, Statistical & Process Improvement Tools | Minitab, 2004, https://www.minitab.com/en-us/, accessed 2023-04-05 Search PubMed.
- M. V. Togo, F. Mastrolorito, F. Ciriaco, D. Trisciuzzi, A. R. Tondo, N. Gambacorta, L. Bellantuono, A. Monaco, F. Leonetti, R. Bellotti, C. D. Altomare, N. Amoroso and O. Nicolotti, TIRESIA: an explainable artificial intelligence platform for predicting developmental toxicity, J. Chem. Inf. Model., 2023, 63, 56–66, DOI:10.1021/acs.jcim.2c01126.
- J. Roy, P. Kumar Ojha, E. Carnesecchi, A. Lombardo, K. Roy and E. Benfenati, First report on a classification-based QSAR model for chemical toxicity to earthworm, J. Hazard. Mater., 2020, 386, 121660, DOI:10.1016/j.jhazmat.2019.121660.
- K. Roy and G. Ghosh, Introduction of extended topochemical atom (ETA) indices in the valance electron mobile (VEM) environment as tools for QSAR/QSPR studies, Internet Electron. J. Mol. Des., 2003, 2, 599–620 Search PubMed.
- D. Gadaleta, G. F. Mangiatordi, M. Catto, A. Carotti and O. Nicolotti, Applicability domain for QSAR models: Where theory meets reality, Int. J. Quant. Struct. Relat., 2016, 1, 45–63, DOI:10.4018/IJQSPR.2016010102.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  and
Kunal
Roy
and
Kunal
Roy
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/IC50 in molar) have been utilized. We have used only 0D–2D descriptors to efficiently encode the structural features of mixture components without any additional complexities. The optimization of the class of mixture descriptors has been performed in this study by using three different mixing rules (linear combination of molecular contributions, the squared molecular contributions, and the norm of molecular contributions). Different machine-learning approaches namely, random forest (RF), ada boost, gradient boost (GB), extreme gradient boost (XGB), support vector machine (SVM), linear support vector machine (LSVM), and ridge regression (RR) have been employed here apart from the conventional partial least squares (PLS) regression to optimize the modeling approach. A rigorous validation protocol has been used for assessing the goodness-of-fit, robustness, and external predictability of the models. Finally, the toxicity of possible untested mixtures of different photodegradation products of fluoroquinolones has been predicted using the best model reported in this study.
1/IC50 in molar) have been utilized. We have used only 0D–2D descriptors to efficiently encode the structural features of mixture components without any additional complexities. The optimization of the class of mixture descriptors has been performed in this study by using three different mixing rules (linear combination of molecular contributions, the squared molecular contributions, and the norm of molecular contributions). Different machine-learning approaches namely, random forest (RF), ada boost, gradient boost (GB), extreme gradient boost (XGB), support vector machine (SVM), linear support vector machine (LSVM), and ridge regression (RR) have been employed here apart from the conventional partial least squares (PLS) regression to optimize the modeling approach. A rigorous validation protocol has been used for assessing the goodness-of-fit, robustness, and external predictability of the models. Finally, the toxicity of possible untested mixtures of different photodegradation products of fluoroquinolones has been predicted using the best model reported in this study.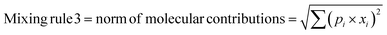
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 training-test divisions.21,22,41 Both the response-based (sorted-activity-based division) and descriptor-based (Euclidean distance-based division and Kennard-Stone division) division techniques have been applied to get the optimum division. The division has been performed using the “Dataset Division GUI” version 1.2 tool (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/), and nine different training-test division sets have been obtained (4 seeds of sorted activity-based divisions, 4 seeds of Euclidean distance-based divisions, and 1 Kennard-Stone division) for each descriptor matrix; therefore a total of 27 division sets were generated.
25 training-test divisions.21,22,41 Both the response-based (sorted-activity-based division) and descriptor-based (Euclidean distance-based division and Kennard-Stone division) division techniques have been applied to get the optimum division. The division has been performed using the “Dataset Division GUI” version 1.2 tool (freely available online: http://teqip.jdvu.ac.in/QSAR_Tools/), and nine different training-test division sets have been obtained (4 seeds of sorted activity-based divisions, 4 seeds of Euclidean distance-based divisions, and 1 Kennard-Stone division) for each descriptor matrix; therefore a total of 27 division sets were generated.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is maintained between the number of training data points and the number of modeled descriptors; the same rule has been followed here too and the combinations with minimum descriptors have been prioritized. We have generated all possible subsets from the descriptor pool using “BestSubsetSelection v2.1” tool. However, all possible subset selection is computationally very exhaustive and it needs a lot of time to compute the validation metrics of the MLR models developed from the descriptor combinations. Thus, a pool reduction is carried out (from 138 descriptors to 40 descriptors) before all possible subset selections. The initial pool reduction has been commenced by a genetic algorithm (GA) (using the “Genetic algorithm v4.1” tool; available from http://teqip.jdvu.ac.in/QSAR_Tools/) in this study. The important descriptors have been taken into the reduced pool based on the R2 and QLOO2 values of the incoming descriptor combinations.
1 ratio is maintained between the number of training data points and the number of modeled descriptors; the same rule has been followed here too and the combinations with minimum descriptors have been prioritized. We have generated all possible subsets from the descriptor pool using “BestSubsetSelection v2.1” tool. However, all possible subset selection is computationally very exhaustive and it needs a lot of time to compute the validation metrics of the MLR models developed from the descriptor combinations. Thus, a pool reduction is carried out (from 138 descriptors to 40 descriptors) before all possible subset selections. The initial pool reduction has been commenced by a genetic algorithm (GA) (using the “Genetic algorithm v4.1” tool; available from http://teqip.jdvu.ac.in/QSAR_Tools/) in this study. The important descriptors have been taken into the reduced pool based on the R2 and QLOO2 values of the incoming descriptor combinations.
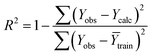
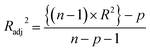
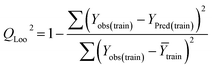

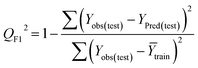
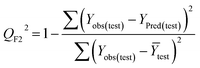
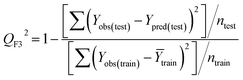
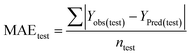
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 binary mixtures. All possible combinations of components (45 mixtures) have been considered for each FQ. The composition of all the hypothetical mixtures is tabulated in Table S4 of the ESI.†
50 binary mixtures. All possible combinations of components (45 mixtures) have been considered for each FQ. The composition of all the hypothetical mixtures is tabulated in Table S4 of the ESI.†

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 activity-based division (4-2 ABD) yielded a model with the most balanced performance (R2 = 0.874, QLOO2 = 0.842, MAETrain95% = 0.087, QF12 = 0.837, and MAETest95% = 0.088). Thus, we have proceeded to the feature selection step with 4-2 ABD.
25 activity-based division (4-2 ABD) yielded a model with the most balanced performance (R2 = 0.874, QLOO2 = 0.842, MAETrain95% = 0.087, QF12 = 0.837, and MAETest95% = 0.088). Thus, we have proceeded to the feature selection step with 4-2 ABD.
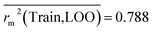 , Δr2m(Train, LOO) = 0.123, RMSEC = 0.108;
, Δr2m(Train, LOO) = 0.123, RMSEC = 0.108;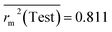 , Δr2m(Test) = 0.089; CCC = 0.927, RMSEP = 0.112.
, Δr2m(Test) = 0.089; CCC = 0.927, RMSEP = 0.112.

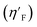 is calculated by employing the following formula64
is calculated by employing the following formula64