 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy harnessing and storage from surface switching with a ferroelectric electrolyte†
Maria Helena
Braga
 abc
abc
aEngineering Physics Department, Engineering Faculty, University of Porto, R. Dr. Roberto Frias, s/n, 4200-465 Porto, Portugal. E-mail: mbraga@fe.up.pt
bLAETA – INEGI, Institute of Science and Innovation in Mechanical and Industrial Engineering, R. Dr. Roberto Frias 400, 4200-465 Porto, Portugal
cMatER, Materials for Energy Research, Engineering Faculty, University of Porto, 4200-465 Porto, Portugal
First published on 5th April 2024
Abstract
In the quest for innovative energy solutions suitable for mobile, stationary and digital applications, ferroelectric topological insulators (FETIs)1 emerge as promising candidates. These materials combine topologically protected states with spontaneous and switchable polarization. This study reveals emergent phenomena in FETI-electrolytes through experiments and simulations, specifically in the A3–2xBaxClO family (where A = Li, Na or K, and x = 0 or 0.005). Here, it is shown that surface oscillations of the potential (V), temperature, and mass may synchronize with the bulk's oscillations, and be harnessed and stored in the form of electrical energy either in a sole FETI or in a battery-type cell presenting a panoply of applications from wireless batteries to transistors, memories, sensors, and selective catalysts.
The work of Kotwal et al. has, both theoretically and experimentally with an integrated circuit, demonstrated that in active systems composed of nonlinear electronic circuits, topologically robust edge modes can be autonomously initiated.2 This finding is significant as it illustrates these systems' natural formation and self-organization of topological wave patterns. The latter brings us back to Prigogine's dissipative structures and their adaptation to topological amplifiers fabricated with Josephson junctions (JJs), nano-mechanical oscillators, or trapped ions3 which are precisely what we show herein with (1) a sole sample of Na2.99Ba0.005ClO and two battery cells, (2) a double layer pouch Zn/Na2.99Ba0.005ClO/Cu and (3) a coaxial Al/K2.99Ba0.005ClO/Cu (mesh). Any external force did not actuate the samples and devices; they were either set to a thermogravimetric (TGA) experiment (samples) or set to discharge with an external material resistor with a Rext of 1 or 1.8 kΩ, enabling the potentiostat to work solely as a voltmeter associated with a thermocouple placed over an electrical insulator on the battery cells’ surface.
Within the topological domain,2 the boundary nodes exhibit a weak connection to the bulk, mirroring the behavior of somewhat isolated van der Pol vdP oscillators, as depicted in Fig. 1a. This scenario is influenced by the locally active injection of energy, destabilizing the nodes' rest state. Consequently, the boundary nodes are nudged towards a stable limit cycle (phase portrait in Fig. 1a). In contrast, nodes located within the bulk are strongly interconnected with their neighbours (thick lines). This leads to dynamics that are distinctly non-topological and characteristic of the bulk. These dynamics bear a resemblance to intensely nonlinear relaxation oscillations, diverging from the behavior observed at the boundaries (Fig. 1b). Fig. 1c shows the electrical equivalent circuit that best suits the results in Fig. 1d and e. Herein, the vdP-FitzHugh Nagumo feedback circuit4,5 was used to describe the Zn(−)/Na2.99Ba0.005ClO (FETI)/Cu(+) battery cell.
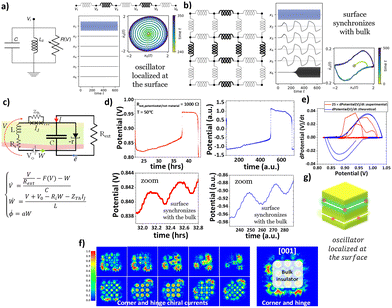 | ||
Fig. 1 Experiments and theory showing high-frequency topological edge self-activated modes inducing slow synchronized bulk oscillations that will then activate the edge at the converse surface end: (a) the one-dimensional equivalent circuit,1 (b) the 2D equivalent circuit1 representing the surface and bulk oscillators, (c) the equivalent circuit simulating the Zn/Na2.99Ba0.005ClO/Cu battery cell behaving very similarly to (b). (d) Experiments (red) with the Zn/Na2.99Ba0.005ClO/Cu battery cell matching simulations (blue) for the surface (bottom) and the bulk (top) with (![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) , Ẇ, , Ẇ, ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) ) = (2(V + 0.02V2 − V3 − W)), 0.004 (0.5 + V − 0.01W + 2(sin 25ϕ + sin 250ϕ)), 0.08W for initial values (0.1,0,0.1), using the Runge–Kutta method (ESI†). (e) Phase plot of (d). (f) Vortices in the electron localization function (ELF) by DFT simulations of (Na3ClO)27 [001] cube-surface slices. ELF = 1 and ELF = ½ corresponding to the localized and electron gas. (g) 3D adaptation from (f) representing the FETI. ) = (2(V + 0.02V2 − V3 − W)), 0.004 (0.5 + V − 0.01W + 2(sin 25ϕ + sin 250ϕ)), 0.08W for initial values (0.1,0,0.1), using the Runge–Kutta method (ESI†). (e) Phase plot of (d). (f) Vortices in the electron localization function (ELF) by DFT simulations of (Na3ClO)27 [001] cube-surface slices. ELF = 1 and ELF = ½ corresponding to the localized and electron gas. (g) 3D adaptation from (f) representing the FETI. | ||
When a direct current (DC) potential (V) is applied across a JJ, an alternating current (AC) supercurrent flows through the junction. Therefore, the circuit element transforming the DC into an AC is an equivalent JJ, as referred to previously. Fig. 1d shows an example of the experimental potential difference on the terminals of Rext of 1 kΩ when connected to the Zn/Na2.99Ba0.005ClO (FETI)/Cu battery cell set to discharge at 50 °C. The zoomed-in view of the plots corresponding to surface oscillation of the bulk is shown below in Fig. 1d; in other words, the experimental two-level system is dimensionally consistent with the theoretical solution of the equivalent circuit at both levels. The electrons at the surface of the FETI tunnel go back and forth from the FETI to and from the negative electrode (Zn). The number of electrons oscillating at the surface in Fig. 1d is Nē ≈ 1016 ē ≈ 1015 ē cm−2 ≈ 1016 ē cm−3; double the number of Josephson arrays in series. However, not all the electrons tunnel back to the surface of the FETI, which manifested in the increased potential of the surface oscillation baseline.6 Therefore, electrons will accumulate on the negative electrode until a catastrophic jump7 up in the potential (V) takes place corresponding to resonance at the bulk level as observed. The battery cell self-charges while oscillating at multilevel (surface and bulk) for 200 h (ESI†).
The current8 and temperature9 do not vary their baseline upon the jump in potential (V), likely indicating that it is a resonance, a synchronization response, and not the formation of a new phase. Added to the latter idea is that both surface and bulk oscillations, including jumps, result from the same nonlinear equation. Therefore, catastrophic jumps7 seem not to correspond to a phase transition but to relaxation oscillations.
The plot of Fig. 1d (zoomed-in view) corresponds to surface effects; the Shapiro steps are observed as stripes equally distant from each other in the ESI,† corresponding to a potential difference of 0.76 mV with a correlation factor of R-square = 0.9995. The corresponding f(Shapiro stepNa2.99Ba0.005ClO) value is 0.34 THz (upper limit of the microwave electromagnetic spectrum). The number of electrons corresponding to each Shapiro step is Nē,step ≈ 1014 ē cm−2 ≈ 1015 ē cm−3 calculated using 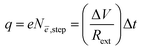 . The phase portrait in Fig. 1e shows a similar surface–bulk interaction to the topoelectrical phase portrait in Fig. 1b for the experimental potential (V) difference and simulations of Fig. 1d, as expected. The electron localization function (ELF) simulated for (Na3ClO)27 using DFT10 on a cubic surface at 37 °C (Fig. 1f) shows how the ferroelectric becomes negatively charged by mediating the impact of the Na+-cations that attract two electrons each, forming corner, hinge vortex loops, allowing the latter Cooper pair to conduct through the edges and surface of the electrolyte as predicted in ref. 11 for planar junctions or layered superconductors4,12–14 and subsequently, as proposed herein, synchronizing with the bulk. It is hypothesized that the localized states shown in Fig. 1f are Moiré lattices due to the polarization of the FETI manifested in discrete states shown in the phase portraits and Poincaré maps in Fig. 2 and 3. In Fig. 1g, a TI phenomenon is proposed at the surface of the FETI shown in Fig. 1f. While Fig. 1 reflects the effects of the surface and bulk electronic conduction under the impact of the negative nonlinear resistance due to the ferroelectric character of the electrolyte, Fig. 2 shows the surface thermal effects—the thermal states of a system that is periodically driven,15 as Floquet's theory describes. The concept is especially relevant to nonequilibrium statistical mechanics. In a periodically driven system, energy absorption from the driving field can lead to a steady-state distribution of Floquet states, which can be described by an effective temperature, even if the system is not in thermal equilibrium in the conventional sense. In a battery cell, a FETI-electrolyte is subjected to an electric field due to the difference in chemical potentials between the electrodes and the electrolyte, necessitating the equalization of their electrochemical potentials. The latter electric field causes the polarization of the ferroelectric-electrolyte to change, and this variation in polarization leads to a temperature variation, without any heat exchange with the surroundings. This effect is adiabatic16 and is designated as adiabatic electrocaloric.
. The phase portrait in Fig. 1e shows a similar surface–bulk interaction to the topoelectrical phase portrait in Fig. 1b for the experimental potential (V) difference and simulations of Fig. 1d, as expected. The electron localization function (ELF) simulated for (Na3ClO)27 using DFT10 on a cubic surface at 37 °C (Fig. 1f) shows how the ferroelectric becomes negatively charged by mediating the impact of the Na+-cations that attract two electrons each, forming corner, hinge vortex loops, allowing the latter Cooper pair to conduct through the edges and surface of the electrolyte as predicted in ref. 11 for planar junctions or layered superconductors4,12–14 and subsequently, as proposed herein, synchronizing with the bulk. It is hypothesized that the localized states shown in Fig. 1f are Moiré lattices due to the polarization of the FETI manifested in discrete states shown in the phase portraits and Poincaré maps in Fig. 2 and 3. In Fig. 1g, a TI phenomenon is proposed at the surface of the FETI shown in Fig. 1f. While Fig. 1 reflects the effects of the surface and bulk electronic conduction under the impact of the negative nonlinear resistance due to the ferroelectric character of the electrolyte, Fig. 2 shows the surface thermal effects—the thermal states of a system that is periodically driven,15 as Floquet's theory describes. The concept is especially relevant to nonequilibrium statistical mechanics. In a periodically driven system, energy absorption from the driving field can lead to a steady-state distribution of Floquet states, which can be described by an effective temperature, even if the system is not in thermal equilibrium in the conventional sense. In a battery cell, a FETI-electrolyte is subjected to an electric field due to the difference in chemical potentials between the electrodes and the electrolyte, necessitating the equalization of their electrochemical potentials. The latter electric field causes the polarization of the ferroelectric-electrolyte to change, and this variation in polarization leads to a temperature variation, without any heat exchange with the surroundings. This effect is adiabatic16 and is designated as adiabatic electrocaloric.
 | ||
| Fig. 2 Electrochemical and thermal (pyro) self-cycling of an Al/K2.99Ba0.005ClO composite/Cu (mesh) coaxial structural battery.16 (a) The zoomed-in view of an electrochemical cycle: charge for 3 min, at 1.3 V, followed by a discharge set for 24 h with a Rext of 1.8 Ω performed after the cell was set to discharge with the same Rext for 340 h (ESI†). (b) A periodic temperature vs. potential curve with two characteristic oscillations with slightly different frequencies, highlighting the phase shift between the temperature and potential. (c) Schematic representation of the Floquet-thermal FETI. (d) The phase plot of the temperature in (a) showing coherent Floquet thermal states also observed in the corresponding Poincaré map in (e), as expected; sd1 and sd2 are the radii of the confidence ellipse. (f) The phase portrait of the potential highlighting surface oscillations with dislocation of the system's equilibria from 0.59 to 0.76 V corresponding to self-charge. (g) and (h) Coherent states at all scales in the Poincaré maps corresponding to the potential in (a) and (f). | ||
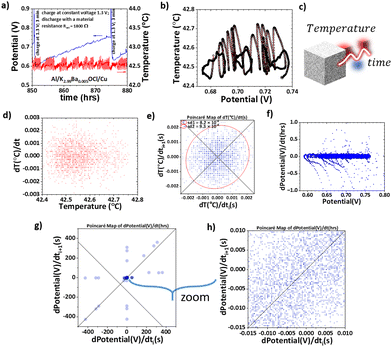
 | ||
| Fig. 3 Piezoelectric effects in the Na2.99Ba0.005ClO FETI obtained with TGA. (a) Photograph of the TGA's hanging platinum sample holder and crucible containing the Na+-FETI. (b) Mechanical equivalent circuit of an actuator representing the Na2.99Ba0.005ClO FETI that by spontaneous polarization and surface conduction autogenerates a potential across the surface leading to self-oscillations represented by (c) corresponding to the vdP active topoelectric node in ref. 1 that to highlight the quantum coherence in the FETI is substituted by (d) that contains a JJ stack instead of an inductor Lii. (e) A 3D nanoparticle of (Na3ClO)27 where the light blue represents the surface localized edge electrons which give rise to electrical fields that generate sample vibrations. (f) Schematics for the mechanical surface waves in the FETI. (g) The self-excited mechanical surface displaced waves corresponding to beats (left) at the glass transition; while showing pulses from 33 °C to 46 °C (right) similar to ‘Shapiro’ steps. (h) The phase plot of the sample's weight. (i) The beats from (g) in detail in blue after applying a high pass filter. (j) Coherent Floquet piezoelectric states in the correspondent Poincaré map. | ||
The cell tested in Fig. 2 is an Al/K2.99Ba0.005ClO/Cu coaxial structural battery17 that was set to cycle with a Rext of 1.8 kΩ after being set to discharge with the same load for 340 h (ESI†). The electrochemical cycle comprised a 3 minute charge at 1.3 V and a 24 hour discharge at a constant resistance of 1.8 kΩ. Fig. 2a and b show the temperature advanced by 10 min from the potential (V). Fig. 2c shows a hypothetical illustration for the Floquet-thermal phenomena at the surface of a FETI. The temperature-dependent phase plot in Fig. 2d and the Poincaré map in Fig. 2e demonstrate coherence at the macro level. Discrete states are expected for Floquet-thermal states.18Fig. 2f demonstrates that the system energy levels, reflected in the potential (V) of the cell, changed over time but not as expected when set to discharge with a material resistor. The cell not only self-cycles but overall self-charges17 (Fig. 2a). The phase plot in Fig. 2f shows the surface oscillations with apparent displacement of the system's surface energy levels over time, from 0.59 to 0.76 V. The phase plot of the surface-bulk is very similar to the one in Fig. 1b,2 although it reflects a displacement of the system's surface energy levels over time corresponding to an overall self-charge.
The Poincaré map captures the system's state at discrete time intervals, typically one period apart. The Poincaré maps in Fig. 2e, g and h, conversely to Fig. S2 ESI,† show discrete states corresponding to coherence at the macro level as expected for Floquet-thermal states.18 It is hypothesized that the discrete patterns in Fig. 2d and e are Moiré lattices, as pointed out before. The latter can lead to various emergent phenomena, including changes in the electronic band structure – the emergence of flat bands where electrons are localized (Fig. 1f) –superconductivity, correlated insulating states, and even magnetism. These effects result from the altered interactions between electrons due to the new periodic potential that, in the present FETI, is likely imposed by the ferroelectric spontaneous polarization, causing the atomic lattice to show two slightly mismatched sublattices as shown in simulated structures of A3ClO (A = Na and K) in ref. 17.
In Fig. 3, the mechanical surface oscillations are demonstrated for a Na2.99Ba0.005ClO FETI single sample of approximately 11 mg when tested using TGA (Fig. 3a). These mechanical vibrations that translate into oscillations of the weight of the sample are due to the piezoelectric character of the FETI. A similar sample was also analyzed with differential scanning calorimetry (DSC) to understand how the sample's transitions affect its piezoelectric behavior. The piezoelectric behavior of the FETI is affected by the variation of the electric field at the surface of the sample due to the topologically protected oscillations; in other words, the DC field that is transformed into an AC in the JJ planes triggers not only a Floquet-thermal, but also a Floquet-piezoelectric behavior in the FETI. The mechanical equivalent circuit is represented in Fig. 3b and is an actuator circuit. Therefore, it is comprehensible that the electrical circuits (Fig. 3c and d) used previously in Fig. 1a and c for unfolding the electrical properties of a FETI in a battery cell also describe the piezoelectric properties. In the latter, the features due to the chemical potential (V) difference imposed by the presence of the electrodes (V0), Ri, and external resistance Rext are not included as the sample is isolated in an alumina crucible in the sample holder of the TGA. In Fig. 3e and f, the (Na3ClO)27 3D simulated ELF inspired the schematics hypothesizing a FETI showing Floquet-piezoelectric behavior.
The Na2.99Ba0.005ClO FETI may be synthesized as a glassy material that undergoes a glass transition approximately at 46 °C into a supercooled liquid.16 The transition is also associated with the material's relaxation times, the time it takes for ferroelectric dipoles to rearrange themselves. Below Tg, these relaxation times are so long that dipolar rearrangement is effectively almost frozen, while above Tg, they decrease significantly, allowing for dipolar mobility. The latter is perhaps why, below 33 °C, no piezoelectric behavior is observed in Na2.99Ba0.005ClO set to be analyzed using a TGA (Fig. 3a and g). Between 33 and 46 °C, small amplitude oscillations are observed like their correspondent in Fig. 1d (zoomed-in view); between 46 and 52 °C, no oscillations are detected; from 52 to 63 °C beats corresponding to two frequencies ω1 = 11.56 s−1 and ω2 = 8.44 s−1 and temperature differences ΔT1 = 0.045 °C and ΔT2 = 0.062 °C are visible (Fig. 3i). Above 63 °C, the displaced oscillations are still observed, but the amplitude is much smaller than from 52 to 63 °C. It is worth mentioning that we have shown in ref. 16 that 36 and 56 °C are relative and absolute internal potential energy minima, while 46 °C is a relative maximum. These temperatures may have their equivalents in the TGA experiment (33, 46, and 52 °C), therefore indicating that the minimum in the potential energy leads to oscillations and the maximum to their collapse.
In Fig. 3g (right), the zoomed-in view shows periodic oscillations between 33 and 46 °C, similar to those lent in Fig. 1d (zoomed-in view); each oscillation shows steps similar to the Shapiro step in Fig. 1d (zoomed-in view), although not as defined. Fig. 3h shows two limit circles centered at 100.080 and 100.108%, indicating topologic periodic behavior as shown in Fig. 1a and 2b. The phase plot in Fig. 3h gives rise to a lattice-like structure in the Poincaré map (Fig. 3 j), which implies that the system is stable around the periodic orbits represented by the points on the lattice. Small perturbations to the system's initial conditions will likely result in trajectories that remain close to these periodic orbits rather than diverging away. This stability is an essential feature for understanding the robustness of the system's behavior under small disturbances, which is a “fingerprint” of a topologic insulator and recurrent (as shown in Fig. 2e, h and 3j). By applying a high pass filter, the beats become clearer. The maximum force exerted on the TGA sample holder is ΔFmax = 0.045 μN (Fig. 3g), corresponding to a pressure of ΔPmax = 0.017 N m2. Relating the previous ΔPmax = 0.017 N m2 with the thickness of the sample t ≈ 1.6 mm, and the Shapiro steps in Fig. 1d with ΔVShapiro = 0.76 mV, the piezoelectric coefficient is d = 0.25 pC N−1 using g = ΔVShapiro/(ΔPmaxt), where g is the piezoelectric voltage constant; the piezoelectric stress constant (d) is d = gε0, where ε0 is the permittivity of free space considering that the JJs are interatomic planes. Nevertheless, the real relative permittivity of Na2.99Ba0.005ClO is ≈108 in the temperature range of 33–63 °C, depending on the polarization and thermal history of the sample,16 which means that the piezoelectric coefficient might be much higher, up to d = 2.5 × 107 pC N−1. The value d = 0.25 pC N−1 is within the typical range for piezoelectric materials, although on the lower end. Notably, the periodic potential difference is self-induced even if the material is isolated in an insulating Al2O3 alumina crucible (Fig. 3a).
In ref. 19, the authors predict and simulate topologic acoustics in a two-dimensional acoustic topological insulator composed of discrete rigid solid cylinders surrounded by a cylindrical fluid-filled region in a stationary fluid matrix, separated from the fluid in the cylindrical region. In fact, the latter simulated material may give clues for the morphology and piezoelectric phenomena at the surface of the Na2.99Ba0.005ClO (FETI) sample during the glass transition. The acoustic system in their study is said to behave like a “zero-field quantum Hall” system20 and is periodic in the unit cell. The latter model agrees with the discrete character of the Poincaré map in Fig. 3j.
The manifestations of the latter periodic states, all evolving from the auto-induced topological currents, lead to self-charge, opening a panoply of unforeseen applications beyond energy harvesting and storage. This unique combination of properties opens a plethora of potential futuristic applications beyond A+-batteries (A = Li, Na, and K): (1) energy harvesting, (2) wireless low-power self-sustained devices, (3) quantum computing, (4) sensors and actuators,21 (5) non-volatile memories, (6) novel transistors, and (7) selective catalysts among others. Remembering Prigogine's findings:22 “In an unstable complex system, small islands of coherence have the potential to change the whole system.”
This project was funded by the FCT UIDP/50022/2020 Emerging Technologies–LAETA and PTDC/QUI-ELT/2593/2021 and by the European Union – NextGeneration EU and Agenda NGS – New Generation Storage, nr. C644936001-00000045, investment project nr. 58, financed by the Recovery and Resilience Plan (PRR). The author acknowledges Eng. Adão Araújo from Norleq and the MatER affiliates for their support.
Conflicts of interest
There are no conflicts to declare.References
- B. M. Gomes, J. F. R. Moutinho and M. H. Braga, J. Mater. Chem. A, 2024, 12, 690–722 RSC.
- T. Kotwal, F. Moseley, A. Stegmaier, S. Imhof, H. Brand, T. Kießling, R. Thomale, H. Ronellenfitsch and J. Dunkel, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2106411118 CrossRef CAS PubMed.
- Á. Gómez-León, T. Ramos, A. González-Tudela and D. Porras, Quantum, 2023, 7, 1016 CrossRef.
- R. FitzHugh, Bull. Math. Biophys., 1955, 17, 257–278 CrossRef.
- J. Nagumo, S. Arimoto and S. Yoshizawa, Proc. IRE, 1962, 50, 2061–2070 Search PubMed.
- T. F. Q. Larson, L. Zhao, E. G. Arnault, M.-T. Wei, A. Seredinski, H. Li, K. Watanabe, T. Taniguchi, F. Amet and G. Finkelstein, Nano Lett., 2020, 20, 6998–7003 CrossRef CAS PubMed.
- K. Hirai, M. Iwai and T. Ushio, IEEE Trans. Autom. Control, 1981, 26, 601–603 CrossRef.
- M. H. Braga, Materials, 2021, 14, 2398 CrossRef CAS PubMed.
- M. Valente, S. M. Silva and M. H. Braga, Heliyon, 2023, 9, e15063 CrossRef CAS PubMed.
- Products, (accessed 13 January 2024) https://www.materialsdesign.com/products.
- G. R. Berdiyorov, M. V. Milošević, F. Kusmartsev, F. M. Peeters and S. Savel’ev, Sci. Rep., 2018, 8, 2733 CrossRef CAS PubMed.
- X. Y. Jin, J. Lisenfeld, Y. Koval, A. Lukashenko, A. V. Ustinov and P. Müller, Phys. Rev. Lett., 2006, 96, 177003 CrossRef CAS PubMed.
- A. Dienst, E. Casandruc, D. Fausti, L. Zhang, M. Eckstein, M. Hoffmann, V. Khanna, N. Dean, M. Gensch, S. Winnerl, W. Seidel, S. Pyon, T. Takayama, H. Takagi and A. Cavalleri, Nat. Mater., 2013, 12, 535–541 CrossRef CAS PubMed.
- B. Liu, M. Först, M. Fechner, D. Nicoletti, J. Porras, T. Loew, B. Keimer and A. Cavalleri, Phys. Rev. X, 2020, 10, 011053 CAS.
- M. Cao, X. Wang, W. Cao, X. Fang, B. Wen and J. Yuan, Small Weinh. Bergstr. Ger., 2018, 14, e1800987 CrossRef PubMed.
- M. Carvalho Baptista, H. Khalifa, A. Araújo, B. A. Maia, M. Souto and M. H. Braga, Adv. Funct. Mater., 2023, 33, 2212344 CrossRef CAS.
- F. Danzi, M. Valente, S. Terlicka and M. H. Braga, APL Mater., 2022, 10, 031111 CrossRef CAS.
- A. Rubio-Abadal, M. Ippoliti, S. Hollerith, D. Wei, J. Rui, S. L. Sondhi, V. Khemani, C. Gross and I. Bloch, Phys. Rev. X, 2020, 10, 021044 CAS.
- Z. Yang, F. Gao, X. Shi, X. Lin, Z. Gao, Y. Chong and B. Zhang, Phys. Rev. Lett., 2015, 114, 114301 CrossRef PubMed.
- F. D. M. Haldane, Phys. Rev. Lett., 1988, 61, 2015–2018 CrossRef CAS PubMed.
- Z.-L. Hou, X. Ma, J. Zhang, C. Li, Y. Wang and M. Cao, Small, 2022, 18, 2205624 CrossRef CAS PubMed.
- I. Prigogine and I. Stengers, Order Out of Chaos: Man's New Dialogue with Nature, Bantam Books, 1984 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc00414k |
| This journal is © The Royal Society of Chemistry 2024 |
