Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying electrochemical losses in perovskite solar cells†
Tulus
 ab,
Junke
Wang
ab,
Junke
Wang
 c,
Yulia
Galagan
c,
Yulia
Galagan
 cd and
Elizabeth
von Hauff
cd and
Elizabeth
von Hauff
 *aef
*aef
aPhysics of Energy, Department of Physics & Astronomy, Faculty of Sciences, Vrije Universiteit Amsterdam, 1081 HV, Amsterdam, The Netherlands. E-mail: elizabeth.von_hauff@tu-dresden.de
bResearch Center for Advanced Materials, National Research & Innovation Agency (BRIN), Jakarta, 10340, Indonesia
cTNO – Solliance, 5656 AE, Eindhoven, The Netherlands
dNational Taiwan University, Department of Materials Science and Engineering, Taipei, 106, Taiwan
eFaculty of Electrical and Computer Engineering, Technical University of Dresden, Dresden, Germany
fFraunhofer Institute for Organic Electronics, Electron Beam and Plasma Technology (FEP), Dresden, Germany
First published on 31st January 2023
Abstract
We quantify electrochemical losses in perovskite solar cells (PSCs) based on methylammonium lead triiodide (MAPbI3) films with impedance analysis. We focus on the characteristic signatures of impedance spectra taken from PSCs, in particular the negative capacitance hook widely observed in the low frequency regime. We elucidate the underlying physical origin for the negative capacitance by applying a generalized equivalent circuit model (ECM) for PSCs that accounts for fast electrical dynamics resulting in high frequency (HF) signatures due to electronic processes, and much slower electrochemical dynamics that result in low frequency (LF) signatures in the spectra. We observe relaxation times faster than 10−6 s in the HF regime that can be attributed to electrical dynamics, while relaxation times longer than 10−3 s in the LF regime that are consistent with electrochemical dynamics. The voltage-dependence and timescales of the electrochemical dynamics are consistent with MA+ and I− migration in the MAPbI3 absorber layer. At higher applied voltages, we observe a highly non-linear response from the PSC which is consistent with irreversible chemical changes in the MAPbI3 absorber. We demonstrate how ECM modelling combined with the analysis of ECM fit quality is a useful approach for in situ monitoring and quantitative diagnosis of loss mechanisms in PSC.
1. Introduction
Metal halide perovskite solar cells (PSCs) are an emerging technology that has demonstrated unprecedented increases in power conversion efficiencies (PCE) over the last decade.1–6 Advances in PSC device performance have been achieved via the optimization of fabrication protocols, new compositions, and stabilization of the perovskite absorber layer.7,8 PSCs have good potential to become an efficient and low-cost thin-film photovoltaic (PV) technology.7–10 The current record efficiency of PSC are over 25%.11–15 Reduction in charge carrier recombination, which fundamentally limits the fill factor (FF) and the open-circuit voltage (Voc), is necessary to increase PSCs efficiency towards the thermodynamic limit.7–9,16–19 However, the performance of even state-of-the-art PSC are ultimately limited by losses at the device interfaces,7,11,16,20–22 and therefore more efforts are required to understand interfacial losses during device operation.Methylammonium (MA) lead triiodide (CH3NH3PbI3) – or MAPbI3 – is a perovskite absorber layer that was widely used in the first generation of PSC.1,23–25 From all the single-halide absorber layers i.e. MAPbI3, MAPbBr3, MAPbCl3, FAPbI3 (FA: Formamidinium), FAPbBr3 and FAPbCl3; MAPbI3 has the most appropriate bandgap for photovoltaic energy conversion, as Br and Cl-based absorber layers have larger bandgaps and therefore comparatively reduced light harvesting potential.26–28 In this context, MAPbI3 and FAPbI3 may be the most promising PSC absorbers for PV applications.8,29 However, FAPbI3 has been reported to have poor structural stability at room temperature, and can crystallize either into a photo-inactive, non-perovskite hexagonal δ-phase (yellow phase) or a photoactive perovskite α-phase (black phase), which is sensitive to solvents or humidity.30 In the case of MAPbI3, instability of the absorber layer has been linked to the thermally unstable and reactive MA+ ion31,32 as well as to the mobile I− ion.5,26–28 While the larger ionic radius of Br− in MAPbBr3 absorbers results in better stability, this stability comes at the cost of a less optimal bandgap for PV energy conversion.26,27
In early studies, MAPbI3 films were produced from a solution of methylammonium iodide (MAI) and lead(II) iodide (PbI2) using a two-step deposition process that yielded low quality films with pinholes.9,33,34 Advances in the processing and understanding of MAPbI3 film formation has resulted in more stable films.18,33 Recent studies demonstrated that one-step deposition that does not incorporate anti-solvent, but does include trace amounts of water, yields larger perovskite crystals with less defects,35 resulting in higher quality films.34–37 While mixed cation, mixed halide PSC have yielded the best efficiency and stability results to date,11,38–41 processing single cation, single halide PSC is more straightforward for industrially-relevant fabrication protocols and up-scaling.6,7,9,10,42,43 In this study, we focus on the well-known PSC system MAPbI3, fabricated with an optimized one-step process.9,34,36,44
The instability of PSC has been linked to the mixed conduction of ionic and electrical carriers in the perovskite absorber, including ion accumulation at the device interfaces.45–49 These electrochemical dynamics can be detrimental to PSC stability, as they result in charge rearrangement and therefore a change in the electrostatic environment in the absorber layer.45–49 This, in turn, impacts the electrical dynamics, i.e. charge transport and recombination, in the solar cell.45
In this study, we applied impedance spectroscopy (IS) to identify and quantify electrochemical losses in PSC based on MAPbI3, as the physical interpretation of the low frequency features in the IS spectra of these devices remains unclear.50–52 We investigate MAPbI3 fabricated using an optimized one-step process in a standard device architecture,34,36,44,45,53–55 as a model system. We used photoluminescence spectroscopy (PL) and X-ray diffraction analysis (XRD) to confirm the structure and quality of the MAPbI3 film. We then applied IS combined with a generalized equivalent circuit model (ECM) analysis45,56 that allows us to distinguish between electrical and electrochemical dynamics in the PSC. From the ECM we are able to estimate the dielectric constant of the MAPbI3 layer, and quantify the timescales of the electrochemical dynamics. We apply a Kramers–Kronig analysis to analyze the quality of the ECM fit in order to elucidate the nature of the loss processes in the PSC.
2. Result
2.1. MAPbI3 film structure
We fabricated MAPbI3 films according to the optimized one-step protocol in the Experimental section. To verify the quality of the films, we performed XRD to confirm the crystallinity, and optical studies with PL spectroscopy to confirm the low defect density in the films. Fig. 1(a) shows XRD pattern of the MAPbI3 perovskite film on glass. We observe prominent peaks that are consistent with the MAPbI3 crystal structure at 2θ = 14° (110), 28° (220) and 43° (330), respectively.34–36,44Fig. 1(b) shows the PL (red line); and absorption properties (blue line), of MAPbI3 film on glass after thermal annealing, respectively. We observed a sharp peak in the PL spectrum at 1.60 eV (773 nm) corresponding to bandgap energy of MAPbI3, which is consistent with previous reports34,35,44 as well as with the absorption spectrum. We note that the bandgap of our MAPbI3 perovskite films are narrower (1.60 eV) than that of MAPbI3 fabricated via a two-step deposition (1.50 eV).57,58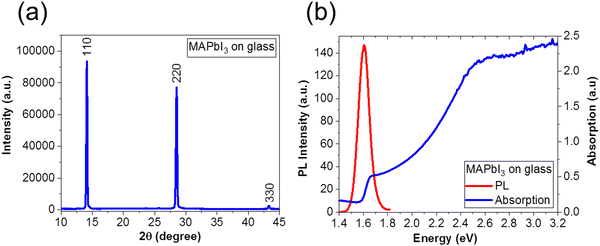 | ||
| Fig. 1 (a) XRD pattern and (b) PL (red line) and absorption (blue line) spectra of a MAPbI3 film on glass substrate. | ||
2.2. Solar cells characteristics
PSCs were fabricated with the planar structure: ITO/TiO2/MAPbI3/Spiro-OMeTAD/Au. The TiO2 serves as an electron transport layer (ETL) and the spin-cast Spiro-OMeTAD layer serves as the hole transport layer (HTL) in the device. A total of 28 devices were fabricated and measured for this study. Fig. 2(a) is a schematic of the solar cell architecture investigated in this study, and Fig. 2(b) shows the current density–voltage (J–V) characteristics of the champion PSC in the dark (black) and under standard AM 1.5 illumination before (blue) and after (red) light soaking. We depict the reverse scan here. The PSC was subjected to light soaking (2 minutes) immediately before the J–V measurement. We note a slight change in the solar cell parameters after light soaking. The PCE of the champion cells increased from 16.71% to 17.45%, the Voc increased from 980.42 mV to 1025.27 mV, and the FF increased from 77.89% to 78.10% after light soaking. The short-circuit current density (Jsc) however decreases slightly after light soaking from 21.88 mA cm−2 of 21.79 mA cm−2.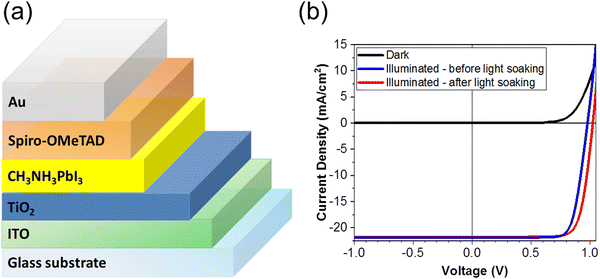 | ||
| Fig. 2 (a) Schematic of the PSC architecture, (b) the J–V characteristics of the PSC under dark (blue), and under standard AM 1.5 illumination before (blue) and after (red) light soaking. | ||
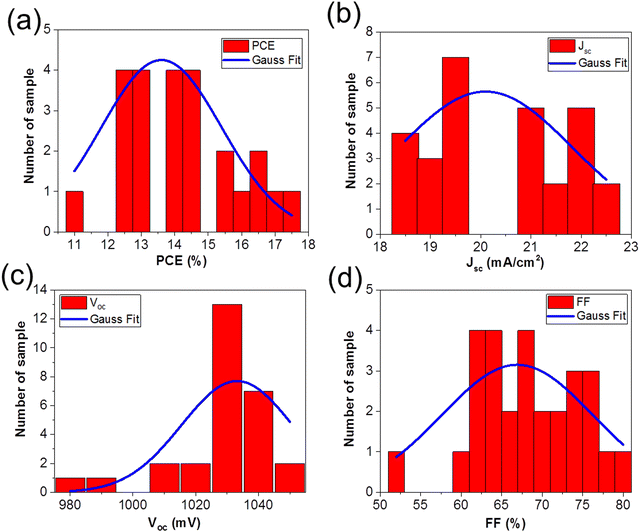
Fig. 3 shows the solar cells parameters from the 28 solar cells measured, and the data were fit with a Gaussian to extract the mean values as well as the standard deviation in the solar cell parameters: (a) PCE = 13.60% ± 3.61%, (b) Jsc = 20.09 mA cm−2 ± 3.47 mA cm−2, (c) Voc = 1033.16 mV ± 35.25 mV, and (d) FF = 66.92% ± 18.62%. Table 1 summarizes the solar cell parameters from the champion cell before and after light soaking, as well as the mean values from the 28 devices.
The change in Voc, FF, and Jsc upon light soaking are consistent with reports of light induced trap filling21,59,60 or curing59,61,62 at the perovskite/TiO2 interface.
| Sample | Condition | V oc (mV) | J sc (mA cm−2) | FF (%) | PCE (%) |
|---|---|---|---|---|---|
| Champion cell | Before light soaking | 980.42 | 21.88 | 77.89 | 16.71 |
| After light soaking | 1025.27 | 21.79 | 78.1 | 17.45 | |
| Average from 28 devices | After light soaking | 1033.16 ± 35.25 | 20.09 ± 3.47 | 66.92 ± 18.62 | 13.60 ± 3.61 |
2.3. Quantifying electrochemical dynamics in MAPbI3 PSC
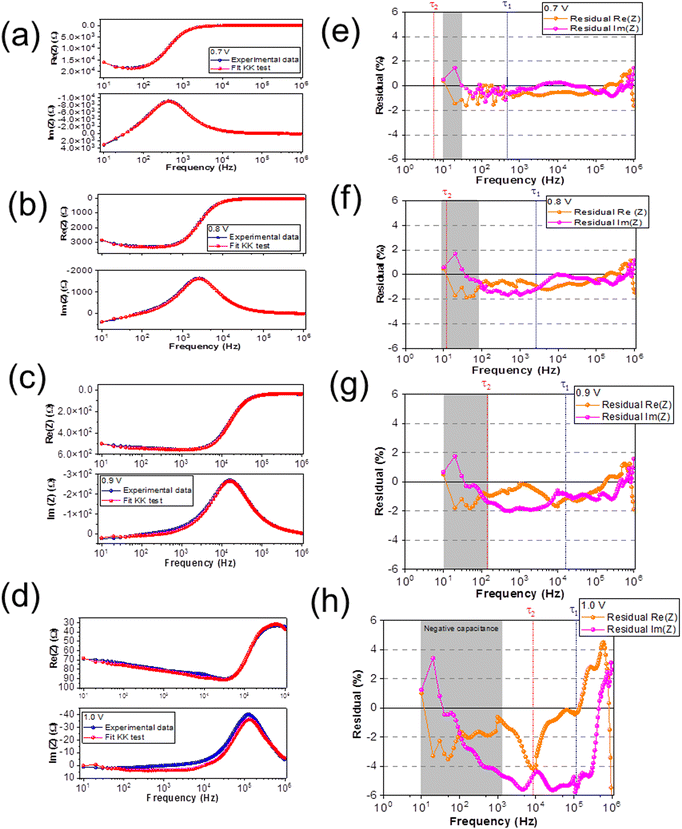
During an IS measurement, the PSC is subject to an external bias and often illumination over many minutes. It is therefore generally challenging to obtain reliable IS data sets45,63,64 from PSC under these conditions, except at Voc. Therefore, we specifically chose to investigate the IS from the PSC in the dark as a function of the external applied voltage. This allowed us to study and quantify the voltage-dependence of electrochemical dynamics in the PSC under controlled conditions, and to isolate these effects from more complex photo-activated (and irreversible) dynamics in the device.We investigated the IS at applied DC voltage offsets of 0.7 V, 0.8 V, 0.9 V, and 1.0 V. Fig. 4 shows the Nyquist plots of the experimental data (blue) and fits at voltages of (a) 0.7 V, (b) 0.8 V, (c) 0.9 V and (d) 1.0 V. The Nyquist plots display the characteristic form for PSC: a high frequency (HF) semicircle and a low frequency (LF) feature, including hooks and/or tails.45,50,51,65 Specifically, our data reveal a LF negative capacitance (see ESI† in Fig. S1(c)). The HF dynamics are attributed to fast electrical dynamics, such as transport and recombination, in the PSC. The reported timescales of these electrical dynamics are highly comparable in PSC devices, independently of the composition of the absorber layer or ETL and HTL materials. In contrast, the slower LF dynamics, attributed to electrochemical dynamics, and are strongly dependent on the quality and stability of the materials and interfaces in the PSC.45,56 Strictly speaking, the HF and LF dynamics are interdependent in PSC, as the rearrangement of the ionic species in the PSC influences the electrostatic environment in the absorber layer and therefore changes the electrical transport dynamics in the device.46,66 However, electrical dynamics are orders of magnitude faster than electrochemical dynamics, and therefore the HF and LF signatures are separated by several orders of magnitude in the IS frequency spectrum. This means that the IS from the PSC can be modelled with a general ECM comprised of two independent, serially connected resistor–capacitor (RC) elements to account for the HF and LF dynamics.45
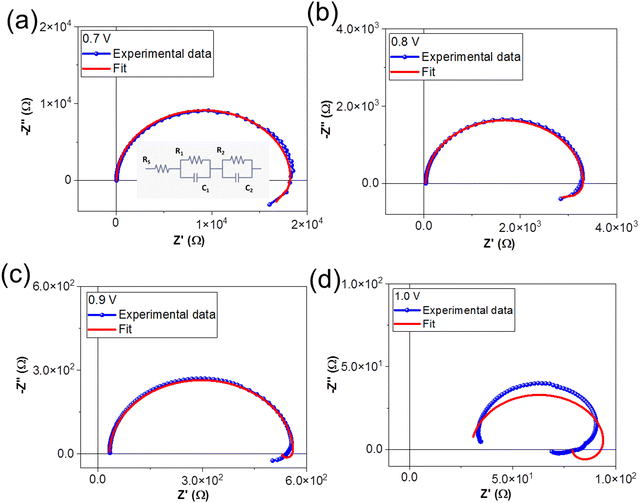 | ||
| Fig. 4 Nyquist plots of experimental data and ECM fits at (a) 0.7 V, (b) 0.8 V, (c) 0.9 V and (d) 1.0 V. The ECM used to fit the data is shown in the inset of (a). | ||
We fit the IS data using the generalized ECM shown in the inset of Fig. 4(a), where RS accounts for the series resistance, R1C1 accounts for the HF dynamics, and R2C2 accounts for the LF electrochemical dynamics. The time constant (τ) of the RC element (τ = R.C) corresponds to the relaxation times of the dynamics. We note that the ECM fits the IS data measured at DC voltages of 0.7 V, 0.8 V and 0.9 V, but that the fits are very poor for spectra taken at 1.0 V. The values of the circuit elements from the ECM are summarized in Table 2.
| DC offset (V) | R S (Ω) | R 1 (Ω) | C 1 (F) | R 2 (Ω) | C 2 (F) |
|---|---|---|---|---|---|
| 0.7 | 42.47 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446.0 446.0 |
178.42 × 10−8 | −7321.00 | −3.89 × 10−6 |
| 0.8 | 37.14 | 3280.0 | 183.98 × 10−8 | −751.70 | −1.76 × 10−5 |
| 0.9 | 33.58 | 529.3 | 189.68 × 10−8 | −33.19 | −3.32 × 10−5 |
| 1.0 | 29.95 | 68.9 | 198.68 × 10−8 | −19.92 | −9.29 × 10−7 |
We discuss the voltage-dependence of the series resistance, RS, followed by the HF response R1C1 and the respective timescale τ1, and finally the LF response, R2C2 and the respective timescale τ2.
We attribute the decrease in the series resistance RS with applied voltage to changes in the electrical properties of the TiO2 due to current flow, i.e. trap filling.59,60
The HF circuit element R1C1 models the cumulative electrical dynamics in the PSC, and it is not possible to elucidate individual dynamics associated with transport and recombination processes. This assumption relies, on one hand, results from recent studies that combined electrical characterization and modelling to show that time and frequency-resolved electrical characterization (such as IS) cannot directly access electrical dynamics in the PSC, but instead probe the change in the electrical transport resulting from slower electrochemical dynamics that change the electrostatic environment during the measurement.46,47,66 Secondly, it is based on the fact that the geometric capacitance (Cgeo) of the PSC, as the lowest capacitance in series, dominates at high frequencies, thereby making it impossible to de-convolute individual dynamics.45 It should be noted, however, that changes in R1C1 in response to voltage, illumination, and more specifically, in response to environmental stress are useful for monitoring PSC performance.51 Therefore, R1 is an effective resistance that contains all of the electrical contributions (transport, recombination) to resistance at high frequencies. We exploit the fact that Cgeo dominates C1 to estimate the relative permittivity (ε) of the perovskite absorber layer according to
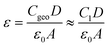 | (1) |
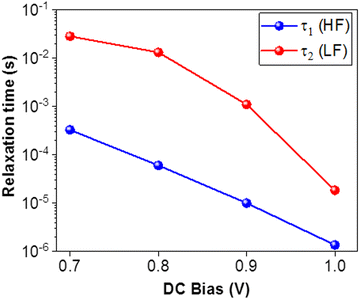
The LF circuit element R2C2 models the slower electrochemical dynamics in the PSC. We note that both R2 and C2 are negative for all voltages, corresponding to the negative capacitive tail observed in the Nyquist plots. Negative resistances are correlated with processes that promote current flow, while negative capacitances occur when the AC current response leads the AC voltage excitation, i.e. capacitive discharge. This behavior is consistent with the neutralization of trap states in the PSC and/or improved band bending at the device interface,45 and has been very frequently observed at high voltage in organometal tri-halide PSCs based on MAPbI3 and MAPbBr3.65 Analogously to R1, R2 decreases with voltage. However, R2 is more than an order of magnitude lower than R1 at each applied voltage and the values are negative. The C2 values are also negative, and are between one and three orders of magnitude larger than C1. In contrast to the other circuit elements, C2 does not follow any clear trend with applied voltage (see ESI† in Fig. S3(a and b)). The LF time constant τ2 is positive and larger than the HF time constant τ1 (consistent with the slower dynamics), and decreases with applied voltage. At 1.0 V, τ1 = 1.37 × 10−6 s and τ2 = 1.85 × 10−5 s, and at this point, the timescales of the HF and LF dynamics become comparable. We observed that there is no longer obtain a linear response in the IS from the PSC at higher applied voltages.
The migration of I− and MA+ ions in MAPbI3,68 as well as the formation of PbI268,69 and PbI6 in MAPbI3 films deposited on TiO2 substrates35,61,62,70 has been widely reported. This results in transient behavior of the electrical properties of MAPbI3 PSC, which has been correlated with voltage-dependent variations in local ionic concentration.59,64,68 Under open circuit conditions, the MA+ ions accumulate at the ETL, while the I− ions accumulate at the HTL, while under applied forward bias, MA+ ions drift away from the HTL interface, while the negatively charged I− ions drift away from the ETL, respectively. Futscher et al.68 performed temperature-dependent transient ion drift measurements on MAPbI3 PSC and found that the concentration of MA+ ions is generally one order of magnitude higher than the concentration of I− ions, and reported transients associated with MA+ on the order of seconds, depending on the fabrication of the PSC while I− transients are faster (less than ms) and comparable between different MAPbI3 PSC. Additionally, the sensitivity of MAPbI3 absorber layers to moisture has been widely reported.35,36,71 While trace amounts of water35 and water vapor71 introduced either via the precursors or during post processing of the MAPbI3 layer can impact crystal size and quality, liquid water can promote the chemical degradation of the absorber,36,71 resulting in the formation of PbI2. Our XRD results do not indicate the formation of PbI2 and our measurements were performed under an N2 atmosphere. Therefore, we do not expect water-induced degradation in our samples, although we cannot fully exclude the impact of trace amounts of water introduced over the precursors on the LF signature.
In order to understand the LF dynamics in more detail, we apply a Kramers–Kronig (KK) check. Generally, KK checks are applied to confirm the quality of the IS spectra for analysis and modelling.64,72–74 IS spectra must satisfy the basic criteria of linearity, stability, causality, and finiteness, however the slow electrochemical dynamics can impact both stability and causality during the measurement leading to deviations from the ideal linear response. We exploit deviations from the KK relations in our IS data in order to elucidate the underlying nature of the LF dynamics at different applied voltages. Specifically, we examine the frequency-dependence of the residuals from the KK test to identify the timescales at which the KK relations deviate from the expected linear behavior. The KK fit is performed by fitting the spectra with a linear series of RC elements, typically between 5–20. The number of RC elements in the circuit is increased until a good fit is achieved, and the residuals indicate the difference between the fit and the experimental data. The rationale behind this approach is that KK-compliant IS data can be fit with an infinite chain of RC elements. However, the ECM used for the KK fit does not necessarily have any relevance for the physical interpretation, as it is likely over-dimensioned.63 As a rule of thumb, residuals < 0.5% are accepted in the literature to indicate good agreement between experiment and the KK fit.50,63,64
Fig. 6(a–d) shows the experimental data (blue) and the KK fit (red) of Re(Z) and Im(Z) versus frequency at a DC bias of 0.7 V, 0.8 V, 0.9 V, and 1.0 V, respectively. Fig. 6(e–h) show the residuals from the KK fit versus frequency; at DC bias of 0.7 V, 0.8 V, 0.9 V, and 1.0 V, respectively. The orange data represents the residual from Re(Z) and the pink data represents the residual from Im(Z), respectively. The frequencies that correspond to the relaxation times (τ1 and τ2 shown in Fig. 5) are marked with a vertically dashed line in each spectrum (HF (blue) and LF (red)), while the highlighted (gray) region corresponds to the frequency range where the negative capacitive tail is observed in the Nyquist plot.
We observe reasonable agreement between the experimental data and the KK fits for DC biases of 0.7 V, 0.8 V, and 0.9 V (<2%), except at 1.0 V (>2%), which is consistent with the poor fit of the ECM at 1.0 V. We classify the offsets in the KK residuals into four different frequency regimes. At low frequencies (101 Hz ≤ f ≥ 102 Hz, corresponding to timescales between 10−3–10−2 s), we observe a constant offset in the residuals at all applied voltages that increases in magnitude with increasing voltage. At low-intermediate frequencies (102 Hz ≤ f > 104 Hz, corresponding to timescales between 10−5–10−3 s), we observe the emergence of a further voltage-dependent offset in the residuals at voltages of 0.8 V and higher. At high-intermediate frequencies (f ≈ 105 Hz, corresponding to timescales around 10−6 s), we observe a weakly voltage-dependent offset that overlaps strongly with lower and higher frequency offsets at increasing voltage. Finally at high frequencies (f > 105 Hz, corresponding to timescales lower than 10−6 s), we observe a large offset that we attribute to the capacitive effects of the cables, which is consistent with the literature.63
The timescales associated with the low and low-intermediate frequency offset in the KK-residuals (f < 103 Hz) are consistent with timescales of ionic transport,45 and more specifically these timescales are comparable to values reported for MA+ (s) and I− (ms) ion migration in MAPbI3 PSC,68 respectively. This interpretation is consistent with results from a recent report from Reichert, et al.75 who applied transient electrical studies to identify the activation energies of distinct interfacial defect states related to the voltage-dependent migration of MA+ and I− ions, as well as a reports on the voltage-dependent kinetics associated with ion/vacancy surface interactions.65
The concentration of MA+ ions is higher than I− ions and the transport of MA+ slower than I− ions, therefore we expect the MA+ ions dominate the LF signature in the IS data. The negative capacitive hook observed in the Nyquist plot as well as the τ2 values are within this LF range, indicating that the LF dynamics are dominated by ionic, specifically MA+ migration. However, we note that the LF dynamics are a convolution of all ionic dynamics, including the diffusion coefficients, concentrations, and activation energies. This is consistent with the lack of clear voltage-dependence we observe in C2, as the voltage-dependence of LF combines the independent contributions of the MA+ and I− ionic distributions. The high-intermediate frequency regime corresponds to timescales on the order of 10−5 s, which has been attributed in the literature to electrode polarization and carrier detrapping.45,50 Since we are examining KK-residuals, i.e. deviations from the linear response, we are more confident about attributing the dynamics in this frequency range to electrode polarization due to ion migration. While ionic transport may generally be reversible, the IS measurements are performed under a constant applied DC offset bias. Therefore, ion migration (which is much slower than electrical transport) behaves as an irreversible process and leads to the KK residuals in the corresponding frequency regime. Finally, we note that the poor ECM fit and significant offsets in the KK-residuals at an applied DC bias offset of 1.0 V may be due to the limited linear response of the PSC in the current–voltage characteristics at such high applied voltages. Additionally, the formation of PbI2 has been reported in MAPbI2 at high applied biases.69
The analysis of the KK-residuals appears to offer detailed insight into frequency-dependence of electrochemical loss processes, as these generally result in a non-linear IS response. In the case of multiple electrochemical processes, such as ion migration, chemical reactions, electrode polarization, with overlapping frequency responses, the KK residuals may offer insight to guide ECM analysis.
We identify and quantify electrochemical dynamics in MAPbI3 PSC using IS studies combined with a universal ECM. The HF and LF dynamics are ubiquitously separated by several orders of magnitude in the frequency spectrum in PSC, enabling a robust fitting procedure to distinguish electrical and electrochemical processes. We show how the HF response can be analyzed to extract accurate values for the PSC permittivity. Analysis of the LF dynamics reveals detailed insight into loss processes in the PSC, specifically ionic dynamics which we attribute to MA+ and I− migration in the MAPbI3 absorber layers. The KK-residuals, which are generally used as an indication of the quality of IS data, can be used to shed light on the timescale and the nature of the electrochemical dynamics. We show how the voltage and frequency dependence of the residuals can offer more detailed information than the Nyquist plot on specific slow and/or irreversible dynamics related to losses in the PSC. Our approach represents a fast and straightforward method for screening and evaluating materials and fabrication procedures on PSC stability and lifetime.
3. Experimental section
3.1. Solar cells fabrication
In general the formation of the MAPbI3 can be described by the following reaction:34
| PbX2 + 3CH3NH3I → CH3NH3PbI3 + 2CH3NH3X | (2) |
3.2. J–V characterization
The J–V measurements were performed in the dark and under standard AM 1.5 illumination (100 mW cm−2) with a solar simulator in an N2 environment. The J–V scan were conducted start from 1.2 V to −1 V. Light soaking was applied for 2 minutes before J–V scan under illumination. The sample mask which of 0.038 cm2, 0.089 cm2, 0.249 cm2, and 0.805 cm2 active areas were used on the J–V measurement under illumination, respectively. The active areas of the every samples without masked consisting of 0.09 cm2, 0.16 cm2, 0.36 cm2, and 1.0 cm2, respectively.3.3. Impedance spectroscopy
IS measurements were performed using an GSTAT302N (Autolab, Metrohm) with an impedance analyzer (FRA3M). We performed the IS measurement on the solar cells device in the dark at DC bias of 0.7 V, 0.8 V, 0.9 V and 1.0 V. The impedance measurement was conducted from 1 MHz to 10 Hz using the AC voltage amplitude of 20 mV.3.4. PL spectroscopy
PL measurements of perovskite were conducted at 470 nm of excitation wave length, with parameters of excitation filters from 335–620 nm and the emission filters from 550–1100 nm, respectively.Author contributions
All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Tulus acknowledges the National Research and Innovation Agency (BRIN), the Republic of Indonesia for the scholarship Program for Research and Innovation in Science and Technology (RISET-Pro) World Bank Loan No. 8245-ID. Tulus, Elizabeth von Hauff and Yulia Galagan acknowledge the COST Action Stable Next Generation Photovoltaics (Grant No. MP1307) for support.References
- J. Y. Kim, J. W. Lee, H. S. Jung, H. Shin and N. G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef CAS PubMed.
- M. Saliba, O. M. Bakr, N. Pradhan, M. Kuno and P. V. Kamat, ACS Energy Lett., 2019, 4, 3036–3038 CrossRef.
- Y. Zhou and M. Saliba, ACS Energy Lett., 2021, 6, 2750–2754 CrossRef CAS.
- K. M. Yeom, S. U. Kim, M. Y. Woo, J. H. Noh and S. H. Im, Adv. Mater., 2020, 32, 2002228 CrossRef CAS PubMed.
- J. Liang and Y. B. Qi, Mater. Today Nano, 2021, 16, 100143 CrossRef CAS.
- J. Jeong, M. Kim, J. Seo, H. Lu, P. Ahlawat, A. Mishra, Y. Yang, M. A. Hope, F. T. Eickemeyer, M. Kim, Y. J. Yoon, I. W. Choi, B. P. Darwich, S. J. Choi, Y. Jo, J. H. Lee, B. Walker, S. M. Zakeeruddin, L. Emsley, U. Rothlisberger, A. Hagfeldt, D. S. Kim, M. Grätzel and J. Y. Kim, Nature, 2021, 592, 381–385 CrossRef CAS PubMed.
- J. Chen, D. He and N. G. Park, Sol. RRL, 2022, 6, 2100767 CrossRef CAS.
- N. G. Park, Adv. Energy Mater., 2019, 1903106, 1–14 Search PubMed.
- S. I. Seok, M. Grätzel and N. G. Park, Small, 2018, 14(20), 1–17 CrossRef PubMed.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- M. Kim, J. Jeong, H. Lu, T. K. Lee, F. T. Eickemeyer, Y. Liu, I. W. Choi, S. J. Choi, Y. Jo, H. B. Kim, S. I. Mo, Y. K. Kim, H. Lee, N. G. An, S. Cho, W. R. Tress, S. M. Zakeeruddin, A. Hagfeldt, J. Y. Kim, M. Grätzel and D. S. Kim, Science, 2022, 375, 302–306 CrossRef CAS PubMed.
- E. J. Juarez-Perez and M. Haro, Science, 2020, 368(6497), 1309 CrossRef CAS PubMed.
- H. Lu, A. Krishna, S. M. Zakeeruddin, M. Gratzel and A. Hagfeldt, iScience, 2020, 23(101359), 1–14 Search PubMed.
- Y. Chen, S. Tan, N. Li, B. Huang, X. Niu, L. Li, M. Sun, Y. Zhang, X. Zhang, C. Zhu, N. Yang, H. Zai, Y. Wu, S. Ma, Y. Bai, Q. Chen, F. Xiao, K. Sun and H. Zhou, Joule, 2020, 4(9), 1961–1976 CrossRef CAS.
- J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y. K. Kim, C. S. Moon, N. J. Jeon, J. P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Nature, 2021, 590(2), 587–593 CrossRef CAS PubMed.
- D. Luo, R. Su, W. Zhang, Q. Gong and R. Zhu, Nat. Rev. Mater., 2019, 5, 44–60 CrossRef.
- J. F. Guillemoles, T. Kirchartz, D. Cahen and U. Rau, Nat. Photonics, 2019, 13(8), 501–505 CrossRef CAS.
- A. Sharenko and M. F. Toney, J. Am. Chem. Soc., 2016, 138, 463–470 CrossRef CAS PubMed.
- L. K. Ono, S. F. Liu and Y. Qi, Angew. Chem., Int. Ed., 2020, 59, 6676–6698 CrossRef CAS PubMed.
- E. M. Hutter, J. J. Hofman, M. L. Petrus, M. Moes, R. D. Abellon, P. Docampo and T. J. Savenije, Adv. Energy Mater., 2017, 7, 1602349 CrossRef.
- Tulus, S. Olthof, M. Marszalek, A. Peukert, L. A. Muscarella, B. Ehrler, O. Vukovic, Y. Galagan, S. C. Boehme and E. Von Hauff, ACS Appl. Energy Mater., 2019, 2(5), 3736–3748 CrossRef CAS.
- P. Schulz, D. Cahen and A. Kahn, Chem. Rev., 2019, 119(5), 3349–3417 CrossRef CAS PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- Y. Wu, F. Xie, H. Chen, X. Yang, H. Su, M. Cai, Z. Zhou, T. Noda and L. Han, Adv. Mater., 2017, 29, 1701073 CrossRef PubMed.
- L. Mcgovern, M. H. Futscher, L. A. Muscarella and B. Ehrler, J. Phys. Chem. Lett., 2020, 11, 7127–7132 CrossRef CAS PubMed.
- T. B. Song, Q. Chen, H. Zhou, C. Jiang, H. H. Wang, Y. M. Yang, Y. Liu, J. You and Y. Yang, J. Mater. Chem. A, 2015, 3, 9032–9050 RSC.
- Q. Lin, A. Armin, R. Chandra, R. Nagiri, P. L. Burn and P. Meredith, Nat. Photonics, 2015, 9, 106–112 CrossRef CAS.
- M. A. Green and S. P. Bremner, Nat. Mater., 2017, 16(1), 23–34 CrossRef PubMed.
- J. W. Lee, D. H. Kim, H. S. Kim, S. W. Seo, S. M. Cho and N. G. Park, Adv. Energy Mater., 2015, 5, 1501310 CrossRef.
- S. H. Turren-Cruz, A. Hagfeldt and M. Saliba, Science, 2018, 362, 449–453 CrossRef CAS PubMed.
- J. Wei, Q. Wang, J. Huo, F. Gao, Z. Gan, Q. Zhao and H. Li, Adv. Energy Mater., 2021, 11, 2002326 CrossRef CAS.
- J. B. Patel, R. L. Milot, A. D. Wright, L. M. Herz and M. B. Johnston, J. Phys. Chem. Lett., 2016, 7, 96–102 CrossRef CAS PubMed.
- W. Zhang, M. Saliba, D. T. Moore, S. K. Pathak, M. T. Horantner, T. Stergiopoulos, S. D. Stranks, G. E. Eperon, J. A. Alexander-Webber, A. Abate, A. Sadhanala, S. Yao, Y. Chen, R. H. Friend, L. A. Estroff, U. Wiesner and H. J. Snaith, Nat. Commun., 2015, 6(6142), 1–10 CAS.
- B. Conings, A. Babayigit, T. Vangerven, J. D'Haen, J. Manca and H. G. Boyen, J. Mater. Chem. A, 2015, 3, 19123–19128 RSC.
- L. Ling, S. Yuan, P. Wang, H. Zhang, L. Tu, J. Wang, Y. Zhan and L. Zheng, Adv. Funct. Mater., 2016, 26, 5028–5034 CrossRef CAS.
- M. Alsari, O. Bikondo, J. Bishop, M. Abdi-Jalebi, L. Y. Ozer, M. Hampton, P. Thompson, M. T. Horantner, S. Mahesh, C. Greenland, J. E. Macdonald, G. Palmisano, H. J. Snaith, D. G. Lidzey, S. D. Stranks, R. H. Friend and S. Lilliu, Energy Environ. Sci., 2018, 11, 383–393 RSC.
- D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hörantner, A. Haghighirad, N. Sakai, L. Korte, B. Rech, M. B. Johnston, L. M. Herz and H. J. Snaith, Science, 2016, 351(6269), 151–155 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, K. Domanski, J. Y. Seo, A. Ummadisingu, S. M. Zakeeruddin, J.-P. Correa-Baena, W. R. Tress, A. Abate, A. Hagfeldt and M. Gratzel, Science, 2016, 354(6309), 206–209 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J. Y. Seo, K. Domanski, J. P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9(6), 1989–1997 RSC.
- S. Mahesh, J. M. Ball, R. D. J. Oliver, D. P. Mcmeekin, B. Johnston and H. J. Snaith, Energy Environ. Sci., 2020, 13, 258–267 RSC.
- H. Li and W. Zhang, Chem. Rev., 2020, 120, 9835–9950 CrossRef CAS PubMed.
- H. J. Snaith, Nat. Mater., 2018, 17, 372–376 CrossRef CAS PubMed.
- E. L. Unger, A. R. Bowring, C. J. Tassone, V. Pool, A. Gold-Parker, R. Cheacharoen, K. H. Stone, E. T. Hoke, M. F. Toney and M. D. McGehee, Chem. Mater., 2014, 26(24), 7158–7165 CrossRef CAS.
- E. von Hauff and D. Klotz, J. Mater. Chem. C, 2022, 10(2), 742–761 RSC.
- G. Y. Kim, A. Senocrate, T. Y. Yang, G. Gregori, M. Grätzel and J. Maier, Nat. Mater., 2018, 17, 445–449 CrossRef CAS PubMed.
- F. Ebadi, N. Taghavinia, R. Mohammadpour, A. Hagfeldt and W. Tress, Nat. Commun., 2019, 10(1574), 1–9 CAS.
- J. Lim, M. T. Horantner, N. Sakai, J. M. Ball, S. Mahesh, N. K. Noel, Y. H. Lin, J. B. Patel, D. P. McMeekin, M. B. Johnston, B. Wenger and H. J. Snaith, Energy Environ. Sci., 2019, 12(1), 169–176 RSC.
- B. Hailegnaw, N. S. Sariciftci and M. C. Scharber, Phys. Status Solidi A, 2020, 217, 2000291 CrossRef CAS.
- D. Klotz, Electrochem. Commun., 2019, 98(11), 58–62 CrossRef CAS.
- A. J. Riquelme, K. Valadez-Villalobos, P. P. Boix, G. Oskam, I. Mora-Seró and J. A. Anta, Phys. Chem. Chem. Phys., 2022, 24(26), 15657–15671 RSC.
- R. S. Sanchez, V. Gonzalez-Pedro, J. W. Lee, N. G. Park, Y. S. Kang, I. Mora-Sero and J. Bisquert, Phys. Chem. Lett., 2014, 5(13), 2357–2363 CrossRef CAS PubMed.
- J. Seo, J. H. Noh and S. I. Seok, Acc. Chem. Res., 2016, 49(3), 562–572 CrossRef CAS PubMed.
- M. Grätzel, Nat. Mater., 2014, 13(9), 838–842 CrossRef PubMed.
- W. Nie, J. C. Blancon, A. J. Neukirch, K. Appavoo, H. Tsai, M. Chhowalla, M. A. Alam, M. Y. Sfeir, C. Katan, J. Even, S. Tretiak, J. J. Crochet, G. Gupta and A. D. Mohite, Nat. Commun., 2016, 7(11574), 1–9 Search PubMed.
- Tulus, L. A. Muscarella, Y. Galagan, S. C. Boehme and E. von Hauff, Electrochim. Acta, 2022, 433, 141215 CrossRef CAS.
- H. S. Kim, C. R. Lee, J. H. Im, K. B. Lee, T. Moeh, A. Marchioro, S. J. Moon, R. H. Baker, J. H. Yum, J. E. Moser, M. Gratzel and N. G. Park, Sci. Rep., 2012, 2(591), 1–7 Search PubMed.
- W. J. Scheideler, N. Rolston, O. Zhao, J. Zhang and R. H. Dauskardt, Adv. Energy Mater., 2019, 1803600 CrossRef.
- T. Leijtens, G. E. Eperon, S. Pathak, A. Abate, M. M. Lee and H. J. Snaith, Nat. Commun., 2013, 4(2885), 1–8 Search PubMed.
- B. Ecker, H. Egelhaaf, R. Steim, J. Parisi and E. von Hauff, J. Phys. Chem. C, 2012, 116, 16333–16337 CrossRef CAS.
- Y. Lu, Z. Si, H. Liu, Y. Ge, J. Hu, Z. Zhang, X. Mu, K. Selvakumar and M. Sui, Chem. – Eur. J., 2021, 27, 3729–3736 CrossRef CAS PubMed.
- A. Alberti, I. Deretzis, G. Pellegrino, C. Bongiorno, E. Smecca, G. Mannino, F. Giannazzo, G. G. Condorelli, N. Sakai, T. Miyasaka, C. Spinella and A. La Magna, Chem. Phys. Chem., 2015, 16, 3064–3071 CrossRef CAS PubMed.
- E. von Hauff, J. Phys. Chem. C, 2019, 123, 11329–11346 CrossRef CAS.
- D. Klotz, G. Tumen-ulzii, C. Qin, T. Matsushima and C. Adachi, RSC Adv., 2019, 9, 33436–33445 RSC.
- A. O. Alvarez, R. Arcas, C. A. Aranda, L. Bethencourt, E. Mas-Marzá, M. Saliba and F. Fabregat-Santiago, J. Phys. Chem. Lett., 2020, 11, 8417–8423 CrossRef CAS PubMed.
- Z. S. Wang, F. Ebadi, B. Carlsen, W. C. H. Choy and W. Tress, Small Methods, 2020, 4, 2000290 CrossRef CAS.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, APL Mater., 2019, 7, 010901 CrossRef.
- M. H. Futscher, J. M. Lee, L. McGovern, L. A. Muscarella, T. Wang, M. I. Haider, A. Fakharuddin, L. Schmidt-Mende and B. Ehrler, Mater. Horiz., 2019, 6, 1497–1503 RSC.
- Y. Yuan, Q. Wang, Y. Shao, H. Lu, T. Li, A. Gruverman and J. Huang, Adv. Energy Mater., 2016, 6, 1501803 CrossRef.
- S. Thampy, B. Zhang, K. H. Hong, K. Cho and J. W. P. Hsu, ACS Energy Lett., 2020, 5(4), 1147–1152 CrossRef CAS.
- A. M. A. Leguy, Y. Hu, M. Campoy-Quiles, M. I. Alonso, O. J. Weber, P. Azarhoosh, M. van Schilfgaarde, M. T. Weller, T. Bein, J. Nelson, P. Docampo and Piers R. F. Barnes, Chem. Mater., 2015, 27, 3397–3407 CrossRef CAS.
- M. Schönleber and E. Ivers-Tiffée, Electrochem. Commun., 2015, 58, 15–19 CrossRef.
- M. Schönleber, D. Klotz and E. Ivers-Tiffée, Electrochim. Acta, 2014, 131, 20–27 CrossRef.
- B. A. Boukamp, J. Electrochem. Soc., 1995, 142(6), 1885–1894 CrossRef CAS.
- S. Reichert, Q. An, Y. W. Woo, A. Walsh, Y. Vaynzof and C. Deibe, Nat. Commun., 2020, 11, 6098 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc03486g |
| This journal is © The Royal Society of Chemistry 2023 |