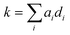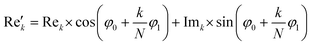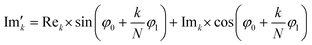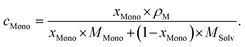A user-guide for polymer purification using dialysis†
Timo
Schuett
 ab,
Ilya
Anufriev
ab,
Patrick
Endres
ab,
Steffi
Stumpf
ab,
Ivo
Nischang
ab,
Ilya
Anufriev
ab,
Patrick
Endres
ab,
Steffi
Stumpf
ab,
Ivo
Nischang
 ab,
Stephanie
Hoeppener
ab,
Stephanie
Hoeppener
 ab,
Stefan
Zechel
ab,
Ulrich S.
Schubert
ab,
Stefan
Zechel
ab,
Ulrich S.
Schubert
 *ab and
Robert
Geitner
*ab and
Robert
Geitner
 *c
*c
aLaboratory of Organic and Macromolecular Chemistry (IOMC), Friedrich Schiller University Jena, Humboldtstr. 10, 07743 Jena, Germany. E-mail: ulrich.schubert@uni-jena.de
bJena Center for Soft Matter (JCSM), Friedrich Schiller University Jena, Philosophenweg 7, 07743 Jena, Germany
cInstitute for Chemistry and Bioengineering, Technical University Ilmenau, Weimarer Str. 32, 98693 Ilmenau, Germany. E-mail: robert.geitner@tu-ilmenau.de
First published on 12th November 2022
Abstract
Dialysis diffusion kinetics are investigated via in situ NMR spectroscopy for numerous different raw polymeric solutions to result in a general guideline for polymer purification using dialysis. In several approaches, a polymer was on purpose contaminated with its respective monomer, regenerated conducting conventional dialysis and monitored online utilizing in situ NMR spectroscopy. Consequently, polymer type and molar mass, monomer type, molar mass cut-off of the dialysis tubing and type of solvent were varied resulting in 29 different purification approaches and over 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 NMR-spectra. As a result, several major parameters were identified affecting the purification process significantly such as the chosen solvent, viscosity and alpha value. On the contrary, parameters such as dialysis tubing molar mass cut-off and molar mass of the polymer did not affect the purification in a significant manner. Furthermore, physical properties such as density, viscosity, alpha value, and dipole moment of the ingredients were combined in a principal component analysis in order to identify the most important parameters.
000 NMR-spectra. As a result, several major parameters were identified affecting the purification process significantly such as the chosen solvent, viscosity and alpha value. On the contrary, parameters such as dialysis tubing molar mass cut-off and molar mass of the polymer did not affect the purification in a significant manner. Furthermore, physical properties such as density, viscosity, alpha value, and dipole moment of the ingredients were combined in a principal component analysis in order to identify the most important parameters.
Introduction
Polymers are utilized in a wide range of applications and influence nearly every aspect of human life. For instance, in medicine1 and aeronautics2,3 high performance polymers are required. Such polymers can be synthesized by various methods. However, prior to utilization, the synthesized polymer has to be purified to remove contaminations such as unreacted monomer or toxic solvent residuals in nearly all cases.4 A commonly applied technique for polymer purification is precipitation of the raw polymer in a non-solvent.5 Notwithstanding, the effort of precipitation is relatively high, since typically several iterative precipitation steps are required to achieve a high purity.6 Furthermore, not every polymer can be precipitated easily within solvents of choice.4 Another efficient technique for polymer purification is preparative size exclusion chromatography (SEC).7,8 However, the effort and time required for this technique is even much higher compared to precipitation, if not performed in an automated manner.9Alternatively, dialysis represents a powerful tool for polymer purification, requiring less human effort and typically resulting in high purities.10–12 Furthermore, the high amount of required solvent can be diminished by utilizing optimized setups and parameters.13 However, many parameters are not investigated in detail up to now and, consequently, the most important settings are not known and rely on educated guessing. Additionally, most commercially available dialysis tubings are produced and certified for applications in and with water, but not for organic solvents.14 Nevertheless, the utilization of dialysis techniques is also possible in a variety of organic solvents and these were already applied frequently for polymer purification.15 The materials of the tubing are prone to swelling in organic solvents which unavoidably leads to different purification results due to varying pore sizes, a situation that has not been addressed so far.
In situ reaction monitoring is an efficient tool for kinetic investigations and real-time control of reactions.16 Application of semi-automated scripts can increase the data output or preparation of numerous samples without significant human interaction,17 and hence, lead to more precise results. Furthermore, by construction of a feedback-based self-optimizing system, in situ characterization devices such as a nuclear magnetic resonance (NMR)-spectrometer,18,19 an infrared (IR)-spectrometer,17 a gas chromatographic device20,21 or a UV-Vis-spectrometer22 can send a trigger signal after completion of the respective analysis task, i.e., reaction or purification, to the operator, to finish or continue with the next step of the reaction.16,23,24
Prior to this study, we developed a semi-automated dialysis system25 and investigated the best performance parameters via in situ NMR spectroscopy in regard to solvent flow, volume, and starting concentration for the purification of poly(methyl methacrylate) (PMMA) in tetrahydrofuran (THF).13 Furthermore, we also tested the new setup in fully automated operation mode26 and for nanoparticle purification successfully.14
In the present study, we investigate in detail a variation of the polymer chemistry and the respective monomer type, the polymer molar mass, the dialysis tubing molar mass cut-off limit, and the solvent. The aim is investigating the kinetics of the purification to provide a general guidance for polymer purification using dialysis and to reveal the most governing parameters of this type of polymer purification.
Results and discussion
Prior to this study, we investigated that there is no solvent exchange required to reach the detection limit of the NMR-spectrometer regarding the monomer contaminations when starting with 20 mL of a 0.5 M solution of PMMA and methyl methacrylate (MMA) in THF and 250 mL of surrounding solvent in the dialysis system.13 Consequently, we continued this study by utilizing the same parameters, but varying the polymer chemistry and monomer type, the dialysis tubing, and the solvent. Specifically, we investigated three common polymer types, PMMA (P1 and P2), polystyrene (PS) (P3 and P4) and poly(poly(ethylene glycol) methyl ether methacrylate) (Poly(PEGMEMA)) (P5 and P6) featuring two different molar masses with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (P1, P3 and P5) and 30
000 g mol−1 (P1, P3 and P5) and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 (P2, P4 and P6) for each polymer. All polymers were synthesized via reversible addition–fragmentation chain transfer (RAFT) polymerization, since this technique allows the synthesis of defined polymers with enhanced molar mass control.27 Details about the characterization of the polymers can be found in the Experimental section as well as in the ESI.†
000 g mol−1 (P2, P4 and P6) for each polymer. All polymers were synthesized via reversible addition–fragmentation chain transfer (RAFT) polymerization, since this technique allows the synthesis of defined polymers with enhanced molar mass control.27 Details about the characterization of the polymers can be found in the Experimental section as well as in the ESI.†
Moreover, we investigated the influence of the molar mass cut-off of the dialysis tubing, utilizing two different dialysis tubings based on regenerated cellulose with a cut-off of 1 kDa and 8 kDa, respectively. Finally, the effect of three different solvents on the dialysis process was investigated: THF as a polar standard solvent in polymer purification utilizing dialysis,28 toluene as a non-polar solvent, and chloroform as a halogenated solvent.
Each polymer was mixed with its respective monomer to investigate the purification kinetic during the dialysis process via in situ NMR-spectroscopy. Every experiment and its respective parameters are summarized in Table 3. An example of the measured kinetic profiles and fits can be seen in Fig. 1.
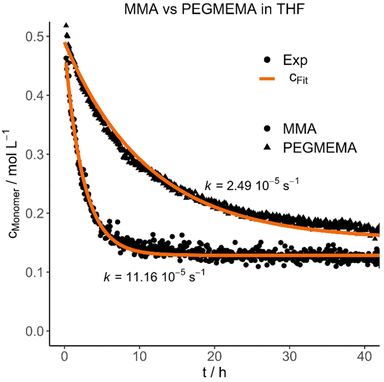 | ||
| Fig. 1 Selected experimental concentration decays and fits highlighting the difference between MMA and PEGMEMA diffusion in THF. | ||
The purification velocity in dependence of different parameters is shown in Fig. 2. The correlation of all investigated parameters with each other is presented in the ESI† as a pairs plot.29 The solvent has a significant influence on the kinetic of the dialysis (Fig. 2a). THF as standard solvent for polymer purification using dialysis28 results in the fastest purification velocity for every monomer (D1–D12), whereas toluene shows a significantly slower velocity (D13–D24). In chloroform, there is no visible diffusion through the membrane (D25–D27). Even after 14 days, there was no difference in the monomer concentration detectable (D25). The certified molar mass cut-off values given by the supplier are determined utilizing defined proteins in water-based surroundings. In detail, a dialysis tubing's cut-off size is defined by retaining 90% of the inserted macromolecules of respective molar mass after 17 hours.30 However, the cellulose membrane presumably shows a different swelling behaviour in organic solvents. THF promotes the lowest swelling, whereas toluene induces formation of very small pores and chloroform results in completely closed pores due to material swelling. Consequently, the diffusion through the membrane slows down, the smaller the pores are.
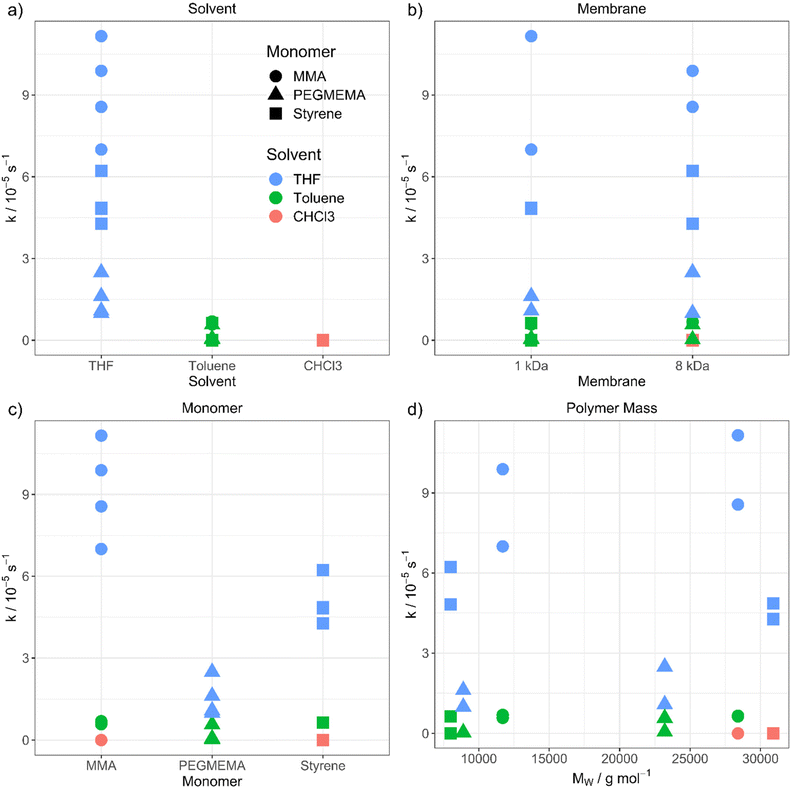 | ||
| Fig. 2 Purification velocity in dependency of (a) the solvent, (b) the pore size of the membrane, (c) the type of monomer and (d) the molecular weight of the polymer. | ||
However, changing the dialysis tubing to a higher molar mass cut-off value is not influencing the purification velocity (Fig. 2b). The cut-off was changed from 1 (D1–D6 and D13–D18) to 8 kDa (D7–D12 and D19–D27) resulting in nearly identical results, thus, the pore size differences in organic solvents seem to be smaller than in aqueous solution. There is still a very low or no diffusion through the membrane when toluene (D19–D24) and chloroform (D25–D27) were utilized. Consequently, choosing a dialysis tubing with a higher cut-off value does not compensate for the solvent swelling effect of the materials and pore closure of the membrane. The pores of the dialysis tubing close completely even at a much higher cut-off value. We utilized a maximum pore size of 8 kDa to ensure, that no polymer is diffusing through the membrane due to its size independently from the type of solvent. Dialysis tubings made from cellulose are available with molar mass cut-offs from 0.5 to 100 kDa.31 Changing to a higher cut-off value could accelerate the purification velocity. However, the cut-off value in the organic solvent needs to be smaller than the polymer size to separate the monomer from the polymer successfully.
Furthermore, the monomer has an influence on the diffusion velocity (Fig. 2c). Regarding the measurements in THF (D1–D12), MMA shows the fastest diffusion rate (D1–D2 and D7–D8), followed by styrene (D3–D4 and D9–D10) and PEGMEMA (D5–D6 and D11–D12). The purifications in toluene (MMA: D13–D14 and D19–D20, styrene: D15–D16 and D21–D22 and PEGMEMA: D17–D18 and D23–D24) resulted in the same tendency with a smaller difference in the diffusion velocities.
Moreover, we investigated the influence of the polymer size on the diffusion velocity with two different molar masses (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and 30
000 g mol−1 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) for each polymer, due to the increasing viscosity of the polymeric solution with increasing molar mass of the polymer and the resulting slower diffusion. Regarding comparable datasets, there is no dependency between the purification velocity and the molar mass of the polymer. (for, e.g., PMMA in THF (Fig. 2d, green dots) shows lower purification velocity for lower molar mass polymer compared to styrene in THF (Fig. 2d, green squares) which results in a faster purification velocity for a lower mass polymer). As can be seen from Fig. 2, the solvent and monomer type have by far the strongest impact on the kinetic of the diffusion process. The question that arises is the physicochemical explanation for these findings. To understand the underlying mechanism, we transformed the qualitative variables, e.g., solvent, to quantitative physicochemical descriptors. Therefore, the four investigated parameters (solvent, monomer type, polymer molar mass and membrane cut-off) resulted in 11 descriptors, which are solution dynamic viscosity, ν, solution density σ, solvent density, σSolv, monomer density, σMono, solvent molar mass, MSolv, monomer molar mass, MMono, polymer molar mass, MPolym, alpha values, α (which describes the hydrodynamic volume of a polymer in a specific solvent according to the Mark–Houwink equation32), solvent dipole moment, μSolv, monomer dipole moment, μMono and membrane cut-off, MCO. All physical data is shown in the ESI.†
000 g mol−1) for each polymer, due to the increasing viscosity of the polymeric solution with increasing molar mass of the polymer and the resulting slower diffusion. Regarding comparable datasets, there is no dependency between the purification velocity and the molar mass of the polymer. (for, e.g., PMMA in THF (Fig. 2d, green dots) shows lower purification velocity for lower molar mass polymer compared to styrene in THF (Fig. 2d, green squares) which results in a faster purification velocity for a lower mass polymer). As can be seen from Fig. 2, the solvent and monomer type have by far the strongest impact on the kinetic of the diffusion process. The question that arises is the physicochemical explanation for these findings. To understand the underlying mechanism, we transformed the qualitative variables, e.g., solvent, to quantitative physicochemical descriptors. Therefore, the four investigated parameters (solvent, monomer type, polymer molar mass and membrane cut-off) resulted in 11 descriptors, which are solution dynamic viscosity, ν, solution density σ, solvent density, σSolv, monomer density, σMono, solvent molar mass, MSolv, monomer molar mass, MMono, polymer molar mass, MPolym, alpha values, α (which describes the hydrodynamic volume of a polymer in a specific solvent according to the Mark–Houwink equation32), solvent dipole moment, μSolv, monomer dipole moment, μMono and membrane cut-off, MCO. All physical data is shown in the ESI.†
Using these 11 descriptors, di, a multiple linear regression was performed utilizing response factors, ai, to explain the observed diffusion rate constant, k.
As expected, some descriptors such as MSolv had a larger influence than others. Thus, the next step was to investigate, which of the descriptors could be neglected without lowering the regression accuracy. For this purpose, a generalized linear model with stepwise feature selection was applied. The idea behind this algorithm is to optimize the performance of the model by only using those descriptors, which significantly improve the model's accuracy. The metric applied here was the Akaike information criterion (AIC).33 Using this feature selection approach, it was found that σ, α, MSolv, σMono, and MMono together best explain k, while minimizing the number of descriptors. Most importantly this finding shows that the polymer only has an indirect impact on the diffusion kinetic via the solution viscosity and its shape. Furthermore, the membrane cut-off does not influence the kinetic in the present experiments. Descriptors belonging to the solvent and monomer are present in this optimized linear model. It is challenging to pinpoint the reason why, for example, the molar mass of the solvent is included while the dipole moment is excluded. We believe that this is not a physical phenomenon but its rather rooted in the construction of the qualitative descriptions. In our case, MSolv is inversely proportional to the polarity (e.g., THF has the lowest molar mass and the highest polarity in our study), acts as a surrogate for the solvent type and is sufficient to represent it in the model building process. Leaving out MSolv from the stepwise feature selection process leads to its replacement by σSolv and μSolv. This finding strengthens the surrogate explanation. Therefore, it is not the molar mass of the solvent alone that is important but rather the combination of features each solvent brings into the dialysis process. The same interpretation is also valid for the monomer.
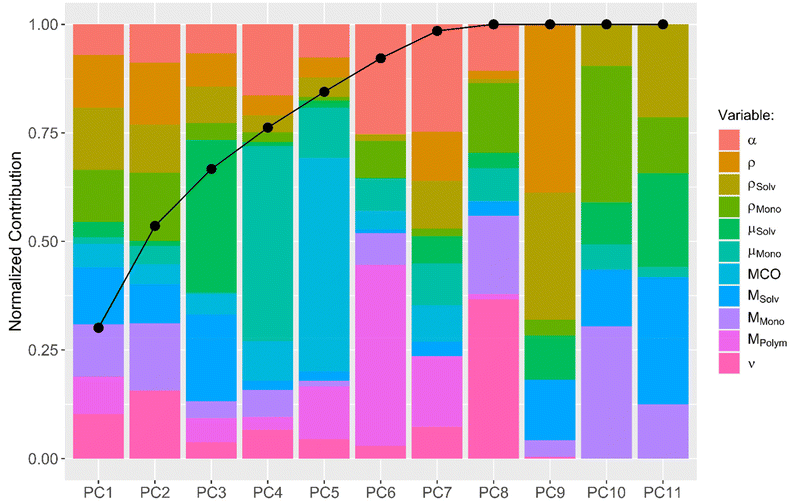
A more sophisticated analysis also includes the interaction of the descriptors with one another. One can imagine that, e.g., the use of solvents with large dipole moments in combination with monomers with large dipole moments results in fast diffusion processes. To explore the possibility that not one descriptor alone but a combination of multiple descriptors together leads to a conclusive explanation of the observed diffusion kinetics, a principal component analysis (PCA) was performed. A PCA combines multiple input descriptors together to best describe the variance found in the dataset.34 The bar plot displayed in Fig. 3 shows to which extend each of the original descriptors contributes to the calculated principal components (PCs). The connected dots in Fig. 3 furthermore indicate the cumulative proportion of the standard deviations explained by each PC. PC1 explains 30.1% of the standard deviation found in the dataset, while PC2 explains 23.5%. PC1–PC7 together explain 98.5% of the variance found, indicating that PC8–PC11 can be neglected without compromising the quality of the dataset.
Subsequently, a generalized linear model with stepwise feature selection was applied, again, in order to analyze which of the PCs can be left out of the linear model to explain the diffusion kinetic. None of the utilized PCs can be left out and the best model is the one which uses the descriptive value of all 7 PCs.
In conclusion, there is no single variable, neither original quantitative descriptor, nor PC that describes the diffusion kinetic completely on its own. Some parameters are more effective than others but overall, there is a strong interaction of the individual parameters. Thus, the dialysis process is still affected by a large number of variables and needs further investigations. E.g., the swelling behavior of the dialysis tubing materials and reduction in pore sizes in the respective solvent, for, e.g., is a parameter, required for a better understanding of the dialysis process. We started a first approach to visualize the pores utilizing freeze drying of the tubing, to preserve the swollen state and subsequent scanning electron microscopy (SEM). The images are shown in the ESI.† However, the resolution was not sufficient to identify single pores.
Additionally, we investigated the swelling degree by weighing swollen membranes in the respective solvent and comparing them to the dried membrane. All experiments and results are listed in Table S2† of the ESI.† The mass of the membranes swollen in water increased the most (150%, W1–W3), while the lowest increase was detected in THF and chloroform (W4–W6 and W10–W12, each 7%). The mass of the membranes stored in toluene increased about 18% (W7–W9). It has to be considered that THF and chloroform have the lowest boiling points and, therefore, evaporate fastest. Furthermore, the density of the solvent is important, which is the highest in chloroform. However, regarding the investigated aspects, the results do not follow any correlation regarding the purification velocity in dialysis. Consequently, the characterization of the pores of the dialysis membranes require additional investigations.
Finally, we would like to show the practical application of the results presented in two different experiments. For this purpose, we purified a RAFT reaction conducted in DMF (P7), stopped after 11 hours (46% conversion), to simulate an incomplete reaction with a high concentration of impurities (D29). The concentration decays and fits of both impurities DMF and MMA are shown in Fig. 4a, resulting in an efficient purification within 8 hours for this system. Additionally, both contaminations have nearly the same diffusion velocity (kDMF = 18.5 10−5 s−1, kMMA = 19.9 10−5 s−1).
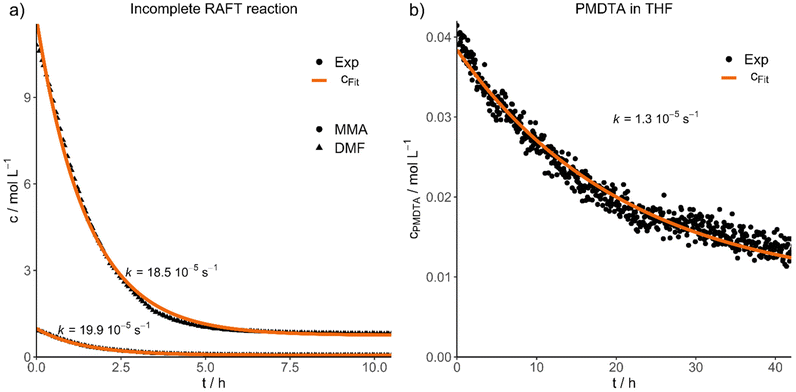 | ||
| Fig. 4 Experimental concentration decays and fits of (a) an incomplete RAFT reaction, monitoring the diffusion of DMF and MMA impurities and (b) PMDTA in THF. | ||
Moreover, we investigated the influence of dialysis on the molar mass by SEC analysis of P7 directly after the synthesis (before purification) and after purification. The elugrams are shown in the ESI (Fig. S13†). The raw polymeric solution reveals a low molar mass (Mn = 6000 g mol−1) and a high dispersity was observed (Đ = 1.44). Moreover, the elugram indicates two shoulders, revealing a heterogeneous molar mass distribution. However, the purification increased the molar mass (Mn = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 g mol−1) by simultaneously decreasing the dispersity (Đ = 1.25) and almost eliminating the shoulders. Due to the long duration of purification, the reaction may still proceed in the dialysis tubing, resulting in a higher molar mass. Furthermore, light could have affected the polymeric solution, and oligomers could have diffused through the dialysis membrane in addition to the monomer.
200 g mol−1) by simultaneously decreasing the dispersity (Đ = 1.25) and almost eliminating the shoulders. Due to the long duration of purification, the reaction may still proceed in the dialysis tubing, resulting in a higher molar mass. Furthermore, light could have affected the polymeric solution, and oligomers could have diffused through the dialysis membrane in addition to the monomer.
In the second application experiment, we investigated the purification of an atom transfer radical polymerization (ATRP) reaction by mixing PMMA and N,N,N′,N′′,N′′-pentamethyldiethylenetriamine (PMDTA) in THF and by following the diffusion of the ligand (D28, Fig. 4b). The purification is considerably slower compared to the RAFT purification (D29) and was not finished completely even after 42 hours. However, the impurity concentration decreased to about one third of the starting concentration during this time.
Both experiments highlight the analytical capabilities of low field NMR spectrometers to track even unknown impurities.
Experimental section
Materials and methods
All chemicals were used as received from TCI, Sigma Aldrich, Alfa Aesar, VWR, Thermo Fisher Scientific and Acros Organics if not otherwise stated. Dimethylformamide (DMF) was dried over a molecular sieve (3 Å) under nitrogen atmosphere. To remove the stabilizer from the monomer (methyl methacrylate (MMA), styrene, poly(ethylene glycol) methyl ether methacrylate (PEGMEMA)), stabilized monomer was passed over an AlOx column (neutral AlOx, obtained from Molekula). The dialysis tubing was purchased from Spectrum Labs (Spectra/PorTM, pre-wetted tubing, 3.5 kDa, d = 34 mm) and rinsed with the respective solvent before use.The dynamic and kinematic viscosities, ηdyn and ηkin, were evaluated using a microviscometer operating with a capillary ball combination system (AMVn, Anton Paar, Graz, Austria). The ball times in polymer solutions, tc, and in solvents, t0, together with densities were used to calculate viscosities. Density measurements were carried out by using a DMA 4100 M densimeter (Anton Paar, Graz, Austria). All measurements were conducted at a temperature of T = 20 °C. Alpha values were used from the literature.35
Size exclusion chromatography (SEC) was performed on the following setup: Shimadzu with CBM-20A (system controller), DGU-14A (degasser), LC-20AD (pump), SIL-20AHT (auto sampler), CTO-10AC vp (oven), SPD-20A (UV detector), RID-10A (RI detector), PSS SDV guard/1000 Å/1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å (5 μm particle size) chloroform/isopropanol/triethyl-amine [94/2/4] with 1 mL min−1 at 40 °C and poly(methyl methacrylate) as standard for P1–P2 and P5–P6 and poly(styrene) as standard for P3–P4.
000 Å (5 μm particle size) chloroform/isopropanol/triethyl-amine [94/2/4] with 1 mL min−1 at 40 °C and poly(methyl methacrylate) as standard for P1–P2 and P5–P6 and poly(styrene) as standard for P3–P4.
Nuclear magnetic resonance (NMR) spectra of the synthesized polymers were acquired by using a Bruker AC 300 (300 MHz) spectrometer at 298 K. The deuterium signal of the utilized solvent was used as an internal reference.
Scanning electron microscopy (SEM) imaging was performed with a Sigma VP Field Emission Scanning Electron Microscope (Carl-Zeiss AG, Germany) using the InLens detector with an accelerating voltage of 4 kV. The samples were coated with a thin layer of platinum via sputter coating (CCU-010 HV, Safematic, Zizers, Switzerland) before the measurement.
In situ NMR spectra were recorded using a benchtop 43 MHz Spinsolve NMR spectrometer (Magritek, Germany) running on Spinsolve version 1.18.1. As advised by the manufacturer, the spectrometer was shimmed repeatedly using 10% D2O in H2O. A glass capillary from the same manufacturer was inserted into the spectrometer to pump the sample solution through the NMR spectrometer with a flow rate of 1.5 mL min−1. One 1H NMR spectrum in the form of a free induction decay (FID) was recorded every five minutes (in case of toluene or THF as solvent) or every 15 minutes (for chloroform as solvent) with a pulse length of 8.6 μs, a total acquisition time of 15 s, an acquisition delay of 20 s and a dwell time of 200 μs. This results in 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 data points spread across an interval from −52.77 to 65.32 ppm. An additional shim on sample was performed every 15 minutes (for toluene and THF as solvent) and every 30 minutes (for chloroform as solvent). The time for measurements in THF was at least two days, for toluene at least three days, and for chloroform at least seven days. The schematic representation of the measurement scripts can be found in the ESI.†
768 data points spread across an interval from −52.77 to 65.32 ppm. An additional shim on sample was performed every 15 minutes (for toluene and THF as solvent) and every 30 minutes (for chloroform as solvent). The time for measurements in THF was at least two days, for toluene at least three days, and for chloroform at least seven days. The schematic representation of the measurement scripts can be found in the ESI.†
Synthetic procedures
The polymer synthesis was performed according to the literature.25 RAFT-polymerizations (P1–P7). Solutions of the initiator (azobisisobutyronitrile, AIBN), chain-transfer-agent (P1–P2, P5–P7: 2-cyano-2-propylbenzodithioat (CPDB), P3–P4: S,S-dibenzyl trithiocarbonate (DBTTC)) and monomer (P1–P2, P7: PMMA, P3–P4: PS and P5–P6: P(PEGMEMA)) in DMF were prepared with different [M]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA]
[CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] ([ ] = concentration, M = monomer, CTA = RAFT-agent, I = initiator) ratios in a round bottom flask. After closing the reaction vessel with a septum, the reaction mixture was degassed by flushing with nitrogen for 30 minutes. The solution polymerizations were carried out in a pre-heated oil-bath at 70 °C for 11 h (P7) or 17 h (P1–P6). All amounts and volumes are listed in Table 1. The respective polymers were obtained after dialysis in THF (5 × 600 mL, solvent exchange after 24 h) and after drying in vacuo. The obtained molar masses (number-average Mn and weight-average Mw) are summarized in Table 2.
[I] ([ ] = concentration, M = monomer, CTA = RAFT-agent, I = initiator) ratios in a round bottom flask. After closing the reaction vessel with a septum, the reaction mixture was degassed by flushing with nitrogen for 30 minutes. The solution polymerizations were carried out in a pre-heated oil-bath at 70 °C for 11 h (P7) or 17 h (P1–P6). All amounts and volumes are listed in Table 1. The respective polymers were obtained after dialysis in THF (5 × 600 mL, solvent exchange after 24 h) and after drying in vacuo. The obtained molar masses (number-average Mn and weight-average Mw) are summarized in Table 2.
| Number | Polymer type | Monomer | CTA | [M]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA] [CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [I] [I] |
m(monomer) [g] | m(CTA) [mg] | M(AIBN) [mg] | V(DMF) [mL] |
|---|---|---|---|---|---|---|---|---|
| P1 | PMMA | MMA | CPDB | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
80 | 1415 | 262 | 400 |
| P2 | PMMA | MMA | CPDB | 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
40 | 177 | 33 | 200 |
| P3 | PS | Styrene | DBTTC | 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
150 | 837 | 118 | 360 |
| P4 | PS | Styrene | DBTTC | 5000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
150 | 84 | 12 | 360 |
| P5 | P(PEGMEMA) | PEGMEMA | CPDB | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
50 | 2213 | 411 | 50 |
| P6 | P(PEGMEMA) | PEGMEMA | CPDB | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
100 | 885 | 164 | 100 |
| P7 | PMMA | MMA | CPDB | 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25 |
100 | 1105 | 205 | 499 |
| Polymer | M n [g mol−1] | M w [g mol−1] | Đ |
|---|---|---|---|
| P1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.19 |
| P2 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.31 |
| P3 | 8000 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.35 |
| P4 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.36 |
| P5 | 8900 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
1.22 |
| P6 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.17 |
| P7 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.25 |
P1: 1H NMR (300 MHz, CDCl3, δ): 0.78 (3H), 0.95 (2H), 3.53 (3H) ppm.
P2: 1H NMR (300 MHz, CDCl3, δ): 0.78 (3H), 0.95 (2H), 3.53 (3H) ppm.
P3: 1H NMR (300 MHz, CDCl3, δ): 1.49 (2H), 1.73–2.06 (1H), 6.29–6.92 (m, 2H), 6.93–7.43 (m, 3H) ppm.
P4: 1H NMR (300 MHz, CDCl3, δ): 1.48 (2H), 1.73–2.06 (1H), 6.32–6.90 (2H), 6.92–7.38 (3H) ppm.
P5: 1H NMR (300 MHz, CDCl3, δ): 0.86 (3H), 1.03 (2H), 3.51–3.81 (50H), 4.09 (3H) ppm.
P6: 1H NMR (300 MHz, CDCl3, δ): 0.84 (3H), 1.00 (2H), 3.47–3.81 (50H), 4.06 (3H) ppm.
Dialysis experiments
The dialysis experiments were adapted from literature.13 A stock solution was prepared by mixing the respective polymer with the corresponding monomer (MMA, styrene or PEGMEMA) in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the solvent (THF, toluene or chloroform) to prepare a 0.5 M monomer solution. For each experiment, 20 mL of this solution was filled into a dialysis tubing (1 kDa or 8 kDa, d = 34 mm), which was fixed at the cap of the dialysis system. For analysis, the solution located inside the dialysis tubing was continuously pumped in a loop through the benchtop NMR spectrometer and back into the dialysis tubing. All experiments are summarized in Table 3.
1 and the solvent (THF, toluene or chloroform) to prepare a 0.5 M monomer solution. For each experiment, 20 mL of this solution was filled into a dialysis tubing (1 kDa or 8 kDa, d = 34 mm), which was fixed at the cap of the dialysis system. For analysis, the solution located inside the dialysis tubing was continuously pumped in a loop through the benchtop NMR spectrometer and back into the dialysis tubing. All experiments are summarized in Table 3.
| Solvent | Cut-off dialysis tubing [kDa] | MMA | Styrene | PEGMEMA | ||||
|---|---|---|---|---|---|---|---|---|
| P1 (10 kDa) | P2 (30 kDa) | P7 (10 kDa) | P3 (10 kDa) | P4 (30 kDa) | P5 (10 kDa) | P6 (30 kDa) | ||
| a N,N,N′,N′′,N′′-Pentamethyldiethylenetriamine was added as additional impurity. | ||||||||
| THF | 1 | D1 | D2 | D29 | D3/D28 | D4 | D5 | D6 |
| 8 | D7 | D8 | — | D9 | D10 | D11 | D12 | |
| Toluene | 1 | D13 | D14 | — | D15 | D16 | D17 | D18 |
| 8 | D19 | D20 | — | D21 | D22 | D23 | D24 | |
| Chloroform | 1 | — | — | — | — | — | — | — |
| 8 | — | D25 | — | — | D26 | — | D27 | |
The stock solution of D28 was prepared by mixing PS (P3, 1.05 g) and PMDTA (130 mg, 0.75 mmol) in 20 mL THF.
NMR spectra pre-processing and kinetic fits
The NMR pre-processing and kinetic fits were adapted from the literature.13 The entire data analysis process was done using R (4.1.2).36 The R package caret37 was used for model building and the R packages ggplot2,38 GGally,39 and gridExtra40 were utilized to create the figures.First the NMR FID was drift corrected by using 5% of the data points recorded at the end of the acquisition period to calculate a mean value, which was subtracted from all FID values. The kth data point from the FID was multiplied with an exponential apodization function featuring a frequency of W = 1 Hz.
| e−πWkΔt |
Subsequently, the FID was zero filled by adding 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 zeros to the end of the FID resulting in 65
768 zeros to the end of the FID resulting in 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 data points, which enables the extraction of all recorded information according to the Nyquist–Shannon sampling theorem.41–44 Finally, the complex conjugate of the processed FID was Fourier transformed using a Fast Fourier Transformation algorithm.45,46 The resulting NMR spectrum was phase corrected using the phase correction angles φ0 and φ1 as well as the following equations.
536 data points, which enables the extraction of all recorded information according to the Nyquist–Shannon sampling theorem.41–44 Finally, the complex conjugate of the processed FID was Fourier transformed using a Fast Fourier Transformation algorithm.45,46 The resulting NMR spectrum was phase corrected using the phase correction angles φ0 and φ1 as well as the following equations.
where k = 0, …, N − 1; Rek and Imk are the real and imaginary components of the kth data point,
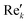 and
and 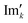 are the new components after correction and N is the total number of points. φ0 and φ1 were manually determined for each measurement series using the graphical user interface of MestReNova (14.2.3–29
are the new components after correction and N is the total number of points. φ0 and φ1 were manually determined for each measurement series using the graphical user interface of MestReNova (14.2.3–29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241).47 Finally, the NMR spectra were referenced to the respective residual solvent signal (THF: 1.85; toluene: 2.09; chloroform: 7.26 ppm), were cropped to the region of interest between −20 and 14 ppm, and the frequency axis as well as all spectra were interpolated to 0.001 ppm intervals. Afterwards, the NMR spectra were baseline corrected using a SNIP algorithm48,49 (iterations = 200, order = 2) and the spectra were normalized to the area of the respective solvent signal (THF: 0.88–2.18; toluene: 1.86–2.34; chloroform: 6.81–7.70 ppm).
241).47 Finally, the NMR spectra were referenced to the respective residual solvent signal (THF: 1.85; toluene: 2.09; chloroform: 7.26 ppm), were cropped to the region of interest between −20 and 14 ppm, and the frequency axis as well as all spectra were interpolated to 0.001 ppm intervals. Afterwards, the NMR spectra were baseline corrected using a SNIP algorithm48,49 (iterations = 200, order = 2) and the spectra were normalized to the area of the respective solvent signal (THF: 0.88–2.18; toluene: 1.86–2.34; chloroform: 6.81–7.70 ppm).
The preprocessed NMR spectra were analyzed by integrating the respective monomer signal (MMA: 5.26–5.70; PEGMEMA: 5.87–6.33; styrene: 5.26–5.70 ppm) or impurity signal (DMF: 7.40–8.40, PMDTA: 2.38–2.45 ppm). The PMDTA signal was background corrected due to its proximity to the much larger THF signal. The monomer signals, stemming from one of the alkenyl protons were considered good indicators for the monomer concentration inside the sample solution. The PMDTA signal belongs to the eight methylene protons, while the DMF signal can be assigned to the formyl proton.
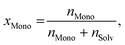
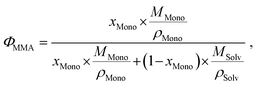
As usual in NMR-spectroscopy, the peak area provides the ratio of the monomer alkenyl proton to the solvent protons previously used to normalize the NMR spectra. The molar ratio, xMono, extracted by NMR spectroscopy can be transformed into a monomer concentration, cMono, according to the following equations:
| ρM = ΦMono × ρMono + (1 − ΦMono) × ρSolv, |
It is important to note that this transformation is valid and only exact when a binary mixture of monomer and solvent is studied and no interactions between monomer and solvent, which alter the density of either component, occur. It is still a very good approximation, when the respective polymer is present in solution as it should not alter the density of the solution in a significant manner nor interact with either species significantly.
The kinetic analysis was based on Fick's law, which describes the temporal and spatial evolution of cMono.50 In all experiments the area of the dialysis membrane over which diffusion can occur was kept constant. Thus, the following equation can be utilized to describe cMono in the sample volume:
| cMono = cMono,0 × e−kt + cMono,Eq |
As the real initial monomer concentration is unknown due to an unavoidable delay between the insertion of the sample solution into the setup and the start of the NMR measurements the initial concentration in the sample solution was assumed to be the monomer concentration extracted by the first NMR measurement. Thus, even a delay between the sample insertion and the start of the NMR measurements is correctly reflected in the data analysis approach.
Model building
The model building and kinetic fits were adapted from the literature.13 For the initial multiple linear regression using the solution viscosity ν, solution density σ, solvent density σSolv, monomer density σMono, solvent molar mass MSolv, monomer molar mass MMono, polymer molar mass MPolym, alpha values α, solvent dipole moment μSolv, monomer dipole moment μMono, and membrane cut-off MCO, a generalized linear model was built. For the subsequent feature selection, a generalized linear model with stepwise feature selection based on Akaike's information criterion (AIC) was employed.33 The feature selection was tested by adding and omitting features from the fitting process to avoid a potential bias which might occur when building up a suitable model from a pool of parameters compared to reducing the complexity of a given model by feature removal. The model performance was validated by 10-fold cross-validation. For the PCA the dataset was initially centered and scaled to avoid the dominance of one descriptor due to its larger range of values. The resulting PCs were also used to fit a generalized linear model with stepwise feature selection, as described in the main text. The fitting and validation process was identical to the one used for the original 11 descriptors.Swelling degree experiments
Small slices of dialysis membranes (1 kDa) were cut, dried over night at 30 °C, and weighted afterward. Subsequently, each slice was stored under solvent (H2O, THF, toluene or CHCl3) over night, shaken to remove excess of solvent from the surface, and weighted again. Each experiment was performed three times. The results of the swelling degree experiments are listed in Table S2.†Conclusions
Within this study deep insight into polymer purification using dialysis is given. Utilizing a standard dialysis setup, connected to a benchtop NMR spectrometer, we investigated dialysis purification kinetics of three different polymer chemistries and their respective monomers, two molar masses of each polymer chemistry, three standard solvents, and two different dialysis molar mass cut-off values, resulting in a total of 27 dialysis approaches and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 NMR spectra.
000 NMR spectra.
Furthermore, we investigated the influence of the physical properties of the investigated substances and analysed all parameters in a principal components analysis to determine the main parameters affecting the dialysis process.
As a result of the membrane swelling behavior, the solvent has a major influence affecting the pore structure of the dialysis tubing. In case of THF, it results in fast purification, a slower process in toluene, and no apparent diffusion in chloroform. Moreover, the utilized polymer and its respective monomer are affecting the system, with MMA as fast, styrene as medium and PEGMEMA as slow diffusing components. However, the molar mass of the polymer and an increase in the dialysis tubing molar mass cut-off had no influence on the purification velocity within the range tested.
Finally, also physical properties, such as the alpha value, viscosity, density, and dipole moment of the ingredients have an influence on the purification process. Consequently, the overall most important parameters for the dialysis efficiency and velocity are the type and polarity of the solvent and the monomer used.
In conclusion, we developed a general guideline on which setup, solvent and monomers should be utilized to achieve a fast purification as basis for further investigations. Based on the current experiments, the derived general guidelines for users of dialysis for polymer purification are:
(i) Choose a polar, non-halogenated solvent (e.g., THF or water)
(ii) If possible, choose a small, polar monomer (e.g., MMA)
(iii) To the best of our knowledge the dialysis tubing cut-off and the polymer size have no influence on the purification within the range tested.
Author contributions
Conceptualization, T. S., R. G. and S. Z.; experiments, T. S., I. A., P. E., S. H. and S. S.; data evaluation, R. G., T. S., P. E. and S. Z.; writing – original draft preparation, T. S.; writing – review and editing, S. Z., R. G., I. N., I. A., S. H., S. S., and U. S. S.; supervision, S. Z., I. N., and U. S. S.; project administration, U. S. S.; funding acquisition, U. S. S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Thüringer Aufbaubank (TAB) (2021 FGI 0005) and the Thuringian Ministry of Economic Affairs, Science and Digital Society (TMWWdG) (CEEC-01/2020) for financial support. The TOC figure was created with BioRender.com. The SEM facilities of the Jena Center for Soft Matter (JCSM) were established with a grant from the German Research Council (DFG).References
- B. D. Fairbanks, P. A. Gunatillake and L. Meagher, Adv. Drug Delivery Rev., 2015, 91, 141–152 CrossRef CAS.
- A. Lefeuvre, S. Garnier, L. Jacquemin, B. Pillain and G. Sonnemann, Resour., Conserv. Recycl., 2017, 125, 264–272 CrossRef.
- A. Gloria, D. Ronca, T. Russo, U. D'Amora, M. Chierchia, R. De Santis, L. Nicolais and L. Ambrosio, J. Appl. Biomater. Biomech., 2011, 9, 151–163 CAS.
- C. A. Barson, J. C. Bevington and B. J. Hunt, Eur. Polym. J., 1996, 32, 1055–1059 CrossRef CAS.
- J. Kimmig, T. Schuett, A. Vollrath, S. Zechel and U. S. Schubert, Adv. Sci., 2021, 8, 2102429 CrossRef CAS PubMed.
- G. Moad, D. H. Solomon, S. R. Johns and R. I. Willing, Macromolecules, 1984, 17, 1094–1099 CrossRef CAS.
- B. G. G. Lohmeijer and U. S. Schubert, Angew. Chem., Int. Ed., 2002, 41, 3825–3829 CrossRef CAS PubMed.
- M. Chiper, M. A. R. Meier, J. M. Kranenburg and U. S. Schubert, Macromol. Chem. Phys., 2007, 208, 679–689 CrossRef CAS.
- J. Lawrence, S.-H. Lee, A. Abdilla, M. D. Nothling, J. M. Ren, A. S. Knight, C. Fleischmann, Y. Li, A. S. Abrams, B. V. K. J. Schmidt, M. C. Hawker, L. A. Connal, A. J. McGrath, P. G. Clark, W. R. Gutekunst and C. J. Hawker, J. Am. Chem. Soc., 2016, 138, 6306–6310 CrossRef CAS PubMed.
- C. H. H. Neufeld and C. S. Marvel, J. Polym. Sci., Part A: Polym. Chem., 1966, 4, 2907–2908 CrossRef CAS.
- I. Perevyazko, A. Vollrath, S. Hornig, G. M. Pavlov and U. S. Schubert, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 3924–3931 CrossRef CAS.
- A. I. Mufula and E. W. Neuse, J. Inorg. Organomet. Polym. Mater., 2011, 21, 511–526 CrossRef CAS.
- T. Schuett, R. Geitner, S. Zechel and U. S. Schubert, Macromolecules, 2021, 54, 9410–9417 CrossRef CAS.
- A. De San Luis, M. Kleinsteuber, T. Schuett, S. Schubert and U. S. Schubert, J. Colloid Interface Sci., 2021, 612, 628–638 CrossRef.
- K. Verstraete, A.-L. Buckinx, N. Zaquen and T. Junkers, Macromolecules, 2021, 54, 3865–3872 CrossRef CAS.
- V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264 RSC.
- P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., Int. Ed., 2021, 60, 8139–8148 CrossRef CAS.
- C. Botha, J. Höpfner, B. Mayerhöfer and M. Wilhelm, Polym. Chem., 2019, 10, 2230–2246 RSC.
- J. Hopfner, K. F. Ratzsch, C. Botha and M. Wilhelm, Macromol. Rapid Commun., 2018, 39, 1700766 CrossRef PubMed.
- G. Falony, A. Verschaeren, F. D. Bruycker, V. D. Preter, K. Verbeke, F. Leroy and L. D. Vuyst, Appl. Environ. Microbiol., 2009, 75, 5884–5892 CrossRef CAS.
- R. Hoogenboom, M. W. M. Fijten, C. H. Abeln and U. S. Schubert, Macromol. Rapid Commun., 2004, 25, 237–242 CrossRef CAS.
- D. Salley, G. Keenan, J. Grizou, A. Sharma, S. Martin and L. Cronin, Nat. Commun., 2020, 11, 2771 CrossRef CAS PubMed.
- V. Dragone, V. Sans, A. B. Henson, J. M. Granda and L. Cronin, Nat. Commun., 2017, 8, 15733 CrossRef PubMed.
- J. M. Granda, L. Donina, V. Dragone, D. L. Long and L. Cronin, Nature, 2018, 559, 377–381 CrossRef CAS.
- T. Schuett, J. Kimmig, S. Zechel and U. S. Schubert, Polymers, 2020, 12, 2095 CrossRef CAS.
- T. Schuett, J. Kimmig, S. Zechel and U. S. Schubert, Polymers, 2022, 14, 292 CrossRef CAS PubMed.
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- T. Schuett, M. Wejner, J. Kimmig, S. Zechel, T. Wilke and U. S. Schubert, Polymers, 2022, 14, 361 CrossRef CAS PubMed.
- J. W. Emerson, W. A. Green, B. Schloerke, J. Crowley, D. Cook, H. Hofmann and H. Wickham, J. Comput. Graph. Stat., 2013, 22, 79–91 CrossRef.
- P. Haney, K. Herting and S. Smith, Separation characteristics of dialysis membranes, https://www.thermofisher.com/de/de/home/life-science/protein-biology/protein-biology-learning-center/protein-biology-resource-library/protein-biology-application-notes/separation-characteristics-dialysis-membranes.html#/legacy=https://www.piercenet.com, (accessed 10/11/2022).
- https://www.fishersci.de/shop/products/spectrum-spectra-por-biotech-cellulose-ester-ce-dialysis-membrane-tubing-28/p-2387504 , (accessed 10/11/2022).
- A. Goldberg, W. Hohenstein and H. Mark, J. Polym. Sci., 1947, 2, 503–510 CrossRef CAS.
- J. Ding, V. Tarokh and Y. Yang, IEEE Signal Process. Mag., 2018, 35, 16–34 Search PubMed.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer Handbook, Wiley, Chichester, New York, 4th edn, 2004 Search PubMed.
- R. C. Team, R: A language and environment for statistical computing. R foundation for statistical computing, Vienna, Austria, 2020 Search PubMed.
- J. W. M. Kuhn, S. Weston, A. Williams, C. Keefer, A. Engelhardt, T. Cooper, Z. Mayer, B. Kenkel, R Core Team, M. Benesty, R. Lescarbeau, A. Ziem, L. Scrucca, Y. Tang, C. Candan and T. Hunt, caret: Classification and Regression Training, R package version 6.0-90, 2019 Search PubMed.
- H. Wickham, ggplot2: Elegant graphics for data analysis, Springer-Verlag, New York, 2016 Search PubMed.
- B. Schloerke, D. Cook, J. Larmarange, F. Briatte, M. Marbach, E. Thoen, A. Elberg, O. Toomet, J. Crowley, H. Hofmann and H. Wickham, GGally: Extension to ‘ggplot2′, R package version 2.1.2, 2021 Search PubMed.
- B. Auguie, gridExtra: Miscellaneous functions for “Grid” graphics, 2017 Search PubMed.
- J. M. Whittaker, Proc. Edinb. Math. Soc., 1928, 1, 169–176 CrossRef.
- V. A. Kotelnikov, Procs. of the first all-union conference on the technological reconstruction of the communications sector and low-current engineering, 1933, pp. 1–19 Search PubMed.
- H. Nyquist, Trans. Am. Inst. Electron. Ing., 1928, 47, 617–644 Search PubMed.
- C. E. Shannon, Proc. IRE, 1949, 37, 10–21 Search PubMed.
- W. C. James and W. T. John, Math. Comput., 1965, 19, 297–301 CrossRef.
- M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216–231 Search PubMed.
- Mestrelab, MestReNova, Mestrelab Research S. L., Santiago de Compostela, Spain, 2015 Search PubMed.
- C. G. Ryan, E. Clayton, W. L. Griffin, S. H. Sie and D. R. Cousens, Nucl. Instrum. Methods Phys. Res., Sect. B, 1988, 34, 396–402 CrossRef.
- M. Morhac, Peaks: Peaks, R package version 0.2, 2008 Search PubMed.
- A. Fick, Ann. Phys., 1855, 170, 59–86 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2py00972b |
| This journal is © The Royal Society of Chemistry 2023 |