Microfluidic viscometer by acoustic streaming transducers†
Ruoyu
Jiang‡
 a,
Paul
Yoo‡
a,
Paul
Yoo‡
 a,
Abhinand M.
Sudarshana
a,
Abhinand M.
Sudarshana
 a,
Emma
Pelegri-O'Day
c,
Sandeep
Chhabra
c,
Marissa
Mock
c and
Abraham P.
Lee
a,
Emma
Pelegri-O'Day
c,
Sandeep
Chhabra
c,
Marissa
Mock
c and
Abraham P.
Lee
 *ab
*ab
aBiomedical Engineering, University of California, Irvine, CA 92697, USA
bMechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
cAmgen Research, Biologics Therapeutic Discovery, 1 Amgen Center Drive, Thousand Oaks, California 91320, USA
First published on 25th April 2023
Abstract
Measurement of fluid viscosity represents a huge need for many biomedical and materials processing applications. Sample fluids containing DNA, antibodies, protein-based drugs, and even cells have become important therapeutic options. The physical properties, including viscosity, of these biologics are critical factors in the optimization of the biomanufacturing processes and delivery of therapeutics to patients. Here we demonstrate an acoustic microstreaming platform termed as microfluidic viscometer by acoustic streaming transducers (μVAST) that induces fluid transport from second-order microstreaming to measure viscosity. Validation of our platform is achieved with different glycerol content mixtures to reflect different viscosities and shows that viscosity can be estimated based on the maximum speed of the second-order acoustic microstreaming. The μVAST platform requires only a small volume of fluid sample (∼1.2 μL), which is 16–30 times smaller than that of commercial viscometers. In addition, μVAST can be scaled up for ultra-high throughput measurements of viscosity. Here we demonstrate 16 samples within 3 seconds, which is an attractive feature for automating the process flows in drug development and materials manufacturing and production.
Introduction
Precise measurement of viscosity is critical to characterize and determine fluidic behavior. In many biomedical applications, viscosities of therapeutic proteins or monoclonal antibody (mAb) solutions are routinely monitored to ensure drug developability.1 Viscous mAb solutions are not suitable for subcutaneous injection and are also difficult to produce and process during manufacturing.2,3 Since often highly concentrated monoclonal antibody drugs are needed to maximize therapeutic efficacy, viscosity becomes a limiting factor when designing the dosing concentrations for patient injection. In a clinical setting, blood viscosity increases blood coagulation and continuous monitoring of blood viscosity is crucial for routine clinical tests such as the activated clotting time (ACT), the thrombin clotting time (TCT) and thromboelastography (TEG).4,5 Traditional viscometers, such as cone and plate, falling ball, and capillary sensing, are generally used to measure fluid viscosities.6,7 However, most of the conventional viscometers are extremely bulky, and require precise balance such as perfectly leveled flatbed to avoid error in the results.8,9 These techniques typically require large sample volumes on the order of milliliters and time-consuming data acquisition and sample handling steps. In the event of early drug screening, such as engineered mAb drug solutions during optimization, producing large quantities of drug candidates is not feasible. Furthermore, most conventional approaches to viscosity measurement are limited to measuring one sample at a time, further reducing throughput. Therefore, it is desirable to develop high throughput viscometers that consume minimal sample volumes while measuring multiple samples within one system.With the help of the recent development of microfluidic technologies, various approaches have been introduced to measure fluid viscosity at the micro-scale and can be categorized as whether a given pressure is applied or a given flow rate is applied externally to induce fluid transport to correlate with viscosity. Viscometers based on capillary-pressure-driven principle have been used as a pressure driven method to measure the traveling speed of the liquid head within a polydimethylsiloxane (PDMS) or paper-based channel to correlate with liquid viscosity.10–12 Although this method requires a very small amount of liquid, the meniscus is sensitive to the channel wetting condition, and the resulting measurement is prone to distortion. Another pressure-driven approach is to use a microcantilever and analyze the responses of the cantilever under resonance vibrations.13–15 Viscosities can be extracted by tracking the vibrational particle/liquid movements via droplet vibration. However, like previously mentioned capillary viscometers, these methods require complex calculations/derivation and are limited by wetting conditions of the surface. A droplet-based microfluidic system is a common type of flow rate driven approach that can be used to continuously measure fluid viscosity.16 The velocity of the droplets when entering the constriction channel can be correlated with fluid viscosity and volume ratio of oil to droplets can also be used to measure viscosity ranges.17–21 These methods require complicated calibration and have limitations in viscosity ranges and types of fluids such as non-Newtonian fluids. Li et al. developed another system to measure viscosity by droplet length.22 Under constant pressure, the viscosity of both Newtonian and non-Newtonian fluids can be measured under such system and the measurement needs as low as 1 μL volume. Nevertheless, the system lacks in sensitivity and can only distinguish samples that possess large range of viscosity differences rather than samples that share close viscosities (e.g. 4 and 5 cP). Additionally, diffusion microfluidic viscometers have also been developed to measure the diffusive motion of tracer particles to quantify fluid viscosity using Stokes–Einstein–Sutherland relation. They require low sample volume and offer high sensitivity in measurement.23–25 However, the choice of the probe sizes and unwanted interaction between probes and liquid material need to be considered.26
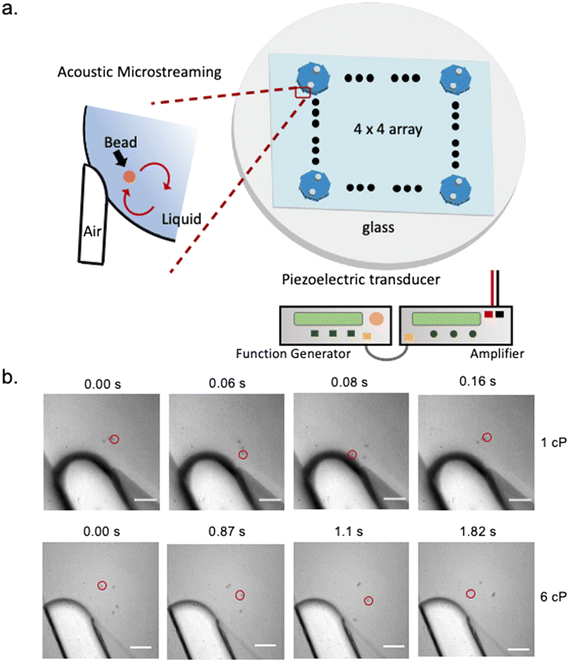
Acoustic-based microfluidics offers high particle controllability and low sample volume requirement to address the challenges above and has been reported for precise spatial and temporal particle manipulation such as translation, rotation, mixing, trapping, and sorting.27,28 Specifically, localized acoustic microstreaming generated from oscillating bubbles has been used to achieve multimodal control over the object orientations and the magnitude of the object moving velocity and its position can be controlled by the acoustic voltage and frequency.29–31 In this work, we present a microfluidic platform termed microfluidic viscometer by acoustic microstreaming transducers (μVASTs) consisting of 16 independent wells, with each well capable of measuring the viscosity of different fluids using volumes as low as 1.2 μL, and each well containing 8 lateral cavity acoustic transducers (LCATs). LCATs are dead-end side channels that produce microstreaming patterns at the air–liquid interface powered by an activated piezoelectric transducer (PZTs). To minimize the fluid volume while maximizing the number of measured samples, a well-shaped design is incorporated (Fig. 1a). Using this design, we show that micrometer beads can be trapped within the microstreaming vortices with traveling velocities near the air–liquid interface precisely that correlate with a wide range of viscosities (1–50 cP). At low Reynolds number and Stokes flow regime we demonstrate that the bead velocity is in inverse relationship with the fluid viscosity (Fig. 1b).26,32,33
When beads are traveling within the microstreaming vortices, the μVASTs can continuously record bead velocity over 3 seconds and a regression model is constructed (R2 = 0.96) correlating fluid viscosity to bead velocities. By measuring the bead velocities, it is practical to estimate viscosities of other types of fluids based on a regression model. We further demonstrate the device's accuracy in sample fluids such as bovine serum albumin (BSA) and dextran under different concentrations, and our estimated viscosities match well with those from cone-and-plate viscometers. Overall, this work demonstrates a high-throughput, highly precise, and portable microfluidic viscometer platform for the measurement of a wide range of viscosities that has broad applications toward point-of-care testing, blood tests, and antibody/protein therapy.
Materials and methods
Microfluidic chip fabrication
In this study, devices were fabricated using the standard soft lithography process on a 4 inch silicon wafer. Channel layer was spin coated with SU-8 2075 (MicroChem, USA) at 500 rpm for 10 s, followed by 2150 rpm for 30 s to obtain 100 μm height. SU-8 molds were soft baked at 65 °C for 5 min and 95 °C for 15 min and cooled for 3 min. They were exposed and patterned by ultraviolet light at 23 s with a chrome mask (Front Range, USA). The wafer was then post exposure baked at 65 °C for 5 min and 95 °C for 10 min. While the wafer is submerged in the developer solution, a sonicator was used for 40 s to remove unexposed photoresist. The molds were then cure baked at 150 °C for 10 min. μVAST devices were fabricated with the polymer polydimethylsiloxane (PDMS) and Sylgard 184 silicone elastomer curing agent and base (Dow Corning, USA) at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11.5 ratio and poured on the mold. After setting at room temperature overnight, the PDMS channel was peeled off and bonded to the glass by oxygen plasma treatment. The bonded devices were placed on a hotplate at 90 °C overnight.
11.5 ratio and poured on the mold. After setting at room temperature overnight, the PDMS channel was peeled off and bonded to the glass by oxygen plasma treatment. The bonded devices were placed on a hotplate at 90 °C overnight.
Liquid sample preparation
Liquid samples with different viscosities ranging from ∼1 to 50 cPs were prepared from glycerol–PBS (without Ca2+ and Na+) (STEMCELL, Canada) mixtures of different mixing ratios according to manufacture protocol. Polystyrene (Spherotech, USA) beads with diameters of 5 μm were mixed with glycerol as the final solution for the microfluidic viscometer device. Bovine serum albumin (Sigma, A1900) was weighed and dissolved completely in 1 mL water before each experiment. The dextrans (MW 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) were obtained from Sigma Co. (St. Louis, MO) (produced by Leuconostoc mesenteroides) and dissolved in water as wt/wt percentage. Viscosity results for BSA and dextran using cone and plate rheometer were collected from literature.34,35
000) were obtained from Sigma Co. (St. Louis, MO) (produced by Leuconostoc mesenteroides) and dissolved in water as wt/wt percentage. Viscosity results for BSA and dextran using cone and plate rheometer were collected from literature.34,35
Experimental setup
This setup was placed onto an upright microscope for analysis. A high-speed camera (Phantom v310, Vision Research Inc., USA) was used to record videos of the motion of polystyrene beads (Degradex, USA) in the viscometer. The videos were recorded at a frame rate of 1000 frames per second to study bead motion in high temporal resolutions. This was particularly important in capturing the velocity changes at the air–liquid interface of LCATs in the device. For the experiments studying air–liquid interface oscillation amplitude and periodicity, the video frame rate was increased to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps due to the rapid oscillation of the interface. To generate the acoustic energy field, a square wave signal of 50.2 kHz was delivered to the PZT using a function generator (Agilent Technologies, USA). The function generator was coupled with a power amplifier (Micromechatronics, Inc., USA) to read out the specific voltages used in the experiments. Acoustic streaming velocity distribution of particles was analyzed using the PIVLab toolbox in Matlab.36
000 fps due to the rapid oscillation of the interface. To generate the acoustic energy field, a square wave signal of 50.2 kHz was delivered to the PZT using a function generator (Agilent Technologies, USA). The function generator was coupled with a power amplifier (Micromechatronics, Inc., USA) to read out the specific voltages used in the experiments. Acoustic streaming velocity distribution of particles was analyzed using the PIVLab toolbox in Matlab.36
Image processing
Fiji37 was used to visualize the particle movement and to perform most of the image processing and analyses. Particle traveling distance was measured using Fiji and velocity is calculated as: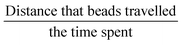 . The frame rate used for calculating maximum streaming speed is 1000 frames per second.
. The frame rate used for calculating maximum streaming speed is 1000 frames per second.
Results
We have previously established acoustic microstreaming platform used for rapid bead/cell trapping, separation, mixing and pumping applications.38–41 Operations of the LCATs rely on oscillation of trapped microbubbles in lateral slanted dead-end side channels to generate a first order oscillatory flow at the air–liquid interface.41–44 The first order oscillatory flow induces a second order streaming flow that consists of an open microstreaming flow and a closed loop microstreaming vortex. The dead-end side channels were designed to have a 15° slanted angle so that the microstreaming generates the maximum flow speed that traps particles.42,45 The velocity of the acoustic microstreaming (u) is generated due to the first order oscillation flow from the oscillating air–liquid interface given by:32,46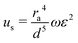 | (1) |
| Fdrag = 6πμrbub | (2) |
Eqn (1) and (2) suggests positive correlation between the oscillation of the air–liquid interface and the microstreaming velocity: larger oscillation amplitude of the air–liquid interface leads to higher microstreaming velocity and lower amplitude leads to lower microstreaming velocity. We selected beads size (∼5 μm) and low bead concentrations (3–10 beads per vortex) to minimize bead-to-bead interference so that velocity of the microbead approaches the velocity of the acoustic microstreaming under low Reynolds number (us ≈ up).32 Hence, at low Reynolds number and Stokes flow regime, each position of a given acoustic microstreaming pattern produces a drag force that dictates the bead velocity is in inverse relationship with the fluid viscosity. That is, higher viscosity leads to lower microbead speed and lower viscosity leads to higher particle speed (Fig. 1a).
Characterization of first-order oscillation flow and second order acoustic microstreaming
A 1 mL glycerol–PBS mixture was prepared and 5 μm beads were added to have the final concentration 3 × 105 beads per mL (original bead stock to sample volume ratio: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
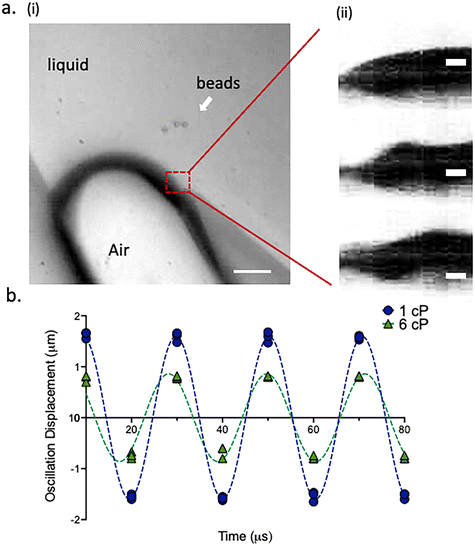
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000). A 1.2 μL aliquot of each sample fluid was then injected into the μVAST device via the inlet. Air–liquid interfaces were formed due to priming of the aqueous solution. The angles of the dead-end side channels were approximately 19°, slightly different from previously reported straight 15° channel angel due to the circular and round shape of the reported design47 (Fig. S1†). Fig. 2a demonstrates the oscillation patterns of the air–liquid interface, the oscillating amplitudes and frequency under different viscosities. The static air–liquid interface showed no sign of oscillation when PZT was not excited and its oscillation motion behaved in a sinusoidal fashion when PZT was excited.
1000). A 1.2 μL aliquot of each sample fluid was then injected into the μVAST device via the inlet. Air–liquid interfaces were formed due to priming of the aqueous solution. The angles of the dead-end side channels were approximately 19°, slightly different from previously reported straight 15° channel angel due to the circular and round shape of the reported design47 (Fig. S1†). Fig. 2a demonstrates the oscillation patterns of the air–liquid interface, the oscillating amplitudes and frequency under different viscosities. The static air–liquid interface showed no sign of oscillation when PZT was not excited and its oscillation motion behaved in a sinusoidal fashion when PZT was excited.
Furthermore, all eight air–liquid interfaces within one well were excited to oscillate with the same pattern (Fig. S2†). It is shown that higher viscosity fluid (50% glycerol mixture) generated from glycerol–PBS mixture causes air–liquid interface to oscillate much less compared with the oscillation displacement generated from the lower viscosity fluid (1× PBS without glycerol) (Fig. 2b). Interface oscillation amplitude is directly proportional to applied voltage and inversely proportional to viscosity (Fig. S3†). The inverse relationship between oscillation amplitude and viscosity is especially apparent as voltage increases. At each voltage level, solutions of higher viscosity displayed lower interface oscillation amplitudes than solutions of lower viscosity. These amplitude differences typically increased at higher voltages. Therefore, applying a high voltage, such as 20 V, may facilitate the differentiation of fluids by viscosity. The general trend of amplitude versus voltage was similar between the solutions, demonstrating the consistency in the relationship between amplitude and viscosity (Fig. S4†). The correlation between fluid viscosity and oscillation amplitude suggests that viscosity resists the motion of the interface. However, the changes in fluid viscosity did not affect the frequency of the oscillation. These results show at a fundamental level how fluid viscosity affects oscillation amplitude of the air–liquid interface, which ultimately determines the formation of the acoustic microstreaming pattern in the μVAST chamber.
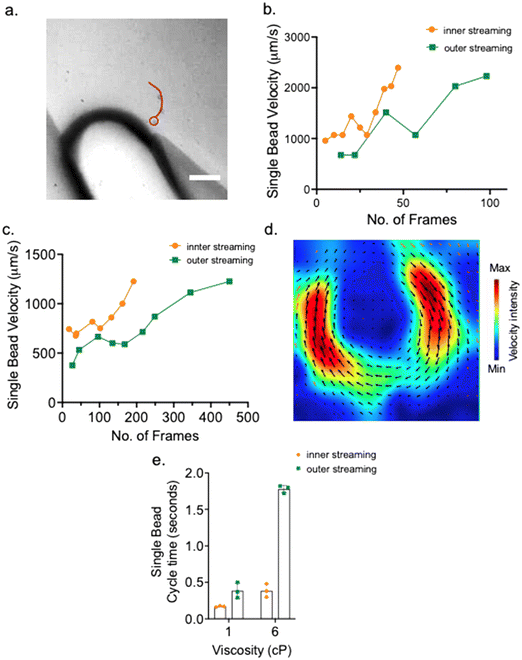
The high-speed Phantom camera was used to capture the movement of beads within the acoustic microstreaming vortices. The movement of the beads was tracked frame by frame and used the distances traveled between each frame divided by the time interval (Fig. 3a and S5†). Calculations were paused when beads encountered the air–liquid interface (Fig. 3a, red circle), since the dark contrast prevented us from conducting an accurate reading of the particle speed. We profiled the single bead velocity from the point further away from the air–liquid interface to regions close to the interface at the sharp tip. Fig. 3b showed that beads travelled much faster under 1 cP fluid (0% glycerol mixture with 1× PBS) compared with the beads from 6 cP (50% glycerol mixture) fluid (Fig. 3c). Furthermore, the velocity profile showed more fluctuation at regions farther away from the air–liquid interface and particle speed tended to vary (Fig. 3b). In contrast, when beads moved near the air–liquid interface (approximately 30–40 μm away), the speeds were consistently increasing without variation. Furthermore, particles located in the inner streaming have similar speed compared with particles located in the outer streaming traces when they move near the air–liquid interface (Fig. 3b and c). Therefore, we selected this region near the air–liquid interface to track the particle speed and correlate with fluid viscosity. Particle image velocimetry (PIV) confirms our single particle tracking within the acoustic microstreaming and near the air–liquid interface appears to have maximum streaming speed of the complete one cycle indicated by the red intensity of traveling speed (Fig. 3d).
Since the particle speed reflects the relative value of the fluid viscosity, beads traveled faster in low viscosity fluids and took less time to complete one cycle within the acoustic microstreaming. Higher viscosity fluids required beads to spend more time to travel one cycle of the acoustic microstreaming (Fig. 3e).
Estimation of fluid viscosity using acoustic microstreaming
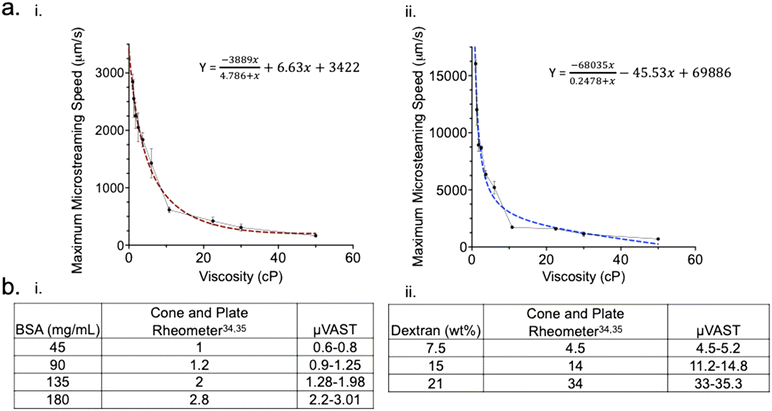
We investigated particle velocity measurement from glycerol–PBS mixture to verify our device's ability to measure fluid viscosity. In this experiment, PBS–glycerol mixture containing 5 μm beads that have the same volume (1.2 ± 0.2 μL) but viscosity values ranging from 1 to 50 cP were tested. The sample and beads preparation and viscosity measurement processes are described in the methods section. The experiment was performed at room temperature. First, the sample liquid was gently injected into inlet of the μVAST array to form hydrophobic air–liquid interfaces at the dead-end side channels. Bead movements were captured using high-speed camera as noted above.Fig. 4a and b show the maximum microstreaming speed of beads from 1 cP to 50 cP using different percentages of PBS–glycerol mixture at 4 Vp–p and 8 Vp–p respectively. When the PZT actuator was applied, the oscillation of the air–liquid interface was instantaneously excited to generate acoustic microstreaming where speed decreased with increasing viscosity of the fluid. The bead speeds were estimated to reflect the microstreaming speed as mentioned previously. The beads speed were obtained across a wide range of viscosities, with speed apparently exponentially decreasing as a function of viscosity. As we increased the input acoustic voltage from 4 Vp–p to 8 Vp–p, the acoustic microstreaming speed also increased. Bead velocity also decreased as a function of viscosity in a similar pattern under 8 Vp–p. We then conducted regression models to these two voltage conditions and fitted our speed with an exponential decay function (y = (y0 − plateau) × exp(−K × t)), as shown Fig. 4a and b. The best fitted values of K were 0.165 and 0.317 for the 4 Vp–p and 8 Vp–p and the R-squared were 0.96 and 0.94, respectively. The viscosity of other sample fluids such as BSA and dextran were also obtained by plotting the relationship between the bead maximum speed and fluid viscosity. Because the correlation of bead maximum speed at the air–liquid interface under 4 Vp–p generated higher equation fitness (0.96 vs. 0.94), we used this voltage condition to test BSA and dextran. Fig. 4c and d show viscosity measurement for BSA at 45, 90, 135 and 180 mg ml−1 and dextran at 7.5, 15 and 21 wt%. The results show that our estimated values align closely with those of the reported values from cone and plate rheometers.34,35
Discussion
In this paper, we presented an acoustic microstreaming platform, μVAST, for rapid viscosity measurement and addressed several key limitations of traditional viscometers. One critical challenge to measure viscosity is the requirement of large volumes of sample fluids. μVASTs only require 1.2 μL of fluid sample to conduct viscosity measurement while traditional cone-and-plate viscometers require more than 100 μL in volume. Other miniaturized viscometers available on the market, such as the Honeybun released in 2022 by Unchained Labs©, which requires 35 μL of sample, still needs nearly 30 times more sample than μVASTs.Furthermore, another advantage of μVASTs is its throughput, as many paralleled samples can be measured without laborious instrument loading in individual capillaries. Further, each μVAST measurement is rapid since multiple beads velocities can be collected within 3–5 s regardless of viscosity values. For comparison, the Honeybun takes 1 minute per sample at <10 cP but needs up to 8 min to measure more viscous samples, which limits measurement throughput. Although the Honeybun can measure 10 samples per device and it is one of the highest numbers of paralleled samples reported from a viscometer, μVASTs can measure 16 independent samples per chip and can easily be scaled up to a 24 well or 48 well system that requires less than 1 μL of fluid samples.
In addition to practical advantages as a tool for viscosity measurement, μVAST devices also provide a versatile platform to study the physics of fluids. It should also be noted that the maximum streaming speed examined in this study is different from the maximum streaming velocity defined at the boundary layer.48,49 As the viscosity of the fluid increases, the boundary layer thickness also increases; this layer has a thickness of 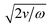 , where ν and ω are the kinematic viscosity of the fluid and angular frequency of the acoustic wave.50,51 Therefore, our measurement region was not directly at the boundary layer interface of the air–liquid interface. Furthermore, the microfluidic device has been designed and validated for Newtonian liquids. Since the viscosity of Newtonian fluids does not vary with applied shear rate, the pressure generated from acoustic microstreaming does not affect the viscosity measurement, which enables consistent measurement of the bead streaming speed. Conversely, the apparent viscosity depends on the applied shear rate for non-Newtonian fluids,52 which is proportional to the amount of shear that the acoustic streaming generates. Thus, by varying the input acoustic power as shown in Fig. 4b, μVASTs have the potential to decipher the relationship between the fluid viscosity and the applied shear rate.
, where ν and ω are the kinematic viscosity of the fluid and angular frequency of the acoustic wave.50,51 Therefore, our measurement region was not directly at the boundary layer interface of the air–liquid interface. Furthermore, the microfluidic device has been designed and validated for Newtonian liquids. Since the viscosity of Newtonian fluids does not vary with applied shear rate, the pressure generated from acoustic microstreaming does not affect the viscosity measurement, which enables consistent measurement of the bead streaming speed. Conversely, the apparent viscosity depends on the applied shear rate for non-Newtonian fluids,52 which is proportional to the amount of shear that the acoustic streaming generates. Thus, by varying the input acoustic power as shown in Fig. 4b, μVASTs have the potential to decipher the relationship between the fluid viscosity and the applied shear rate.
Uniform dispersion of the beads in the μVASTs is important in determining the bead traveling speed, as uneven distribution within the sample liquid greatly affects the measurement accuracy. In the experiments at high viscosities (>15 cP), we found the beads do not mix uniformly in the solution, resulting in high concentrations near the air–liquid interface, making it challenging to localize single beads. On the other hand, low bead concentrations in this region results in insufficient data from small numbers of slow-traveling beads. To avoid this problem, the beads should be carefully mixed with PBS buffer and then mixed with glycerol to produce more uniform distributions.
Conclusion
In conclusion, we developed an acoustic microstreaming method to measure viscosity requiring low volumes of sample fluids. The proposed microfluidic platform had 16 independent μVAST chambers to maximize the number of samples that can be measured. With acoustic microstreaming, the oscillation of the air–liquid interface and the speed of the beads following the fluid streaming patterns were investigated. We show that the oscillation amplitudes of the first order oscillation decreased in high viscosity fluids. Thus, the second order microstreaming velocity also decreased and the relationship between the particle speed within the microstreaming and the fluid viscosity can be correlated. Finally, we demonstrate that the viscosity of small volume fluids, ranging from 0% to 78% glycerol mixture (1 to 50 calculated cP), can be estimated from the maximum streaming speed of beads near the air–liquid interface. The proposed method to measure viscosity requires a sample volume of approximately 1.2 μL, which is 30-fold lower than commercial viscometers.14 Moreover, the number of samples that can be measured on a single chip is 16 and future chips could be designed to accommodate even more independent wells. The operation procedure and the viscometer set-up are simple and does not require complex tubing or external syringe pumps to initiate fluid movement. We envision the μVAST viscometer can be broadly used in many applications such as antibody/protein manufacturing, point-of-care testing, blood tests or other applications in the characterization of complex fluids.Author contributions
R. J., P. B. Y. and A. P. L. designed experiments. R. J., P. B. Y., A. M. S. conducted microfluidic device design validation, characterization, and investigation; R. J., P. B. Y. wrote the manuscript. E. P.-O., S. C. and M. M. mentored and edited manuscript. A. P. L. supervised and edited the manuscript.Conflicts of interest
R. J., A. M. S., P. B. Y. and A. P. L. are inventors of US patent application related to this work.Acknowledgements
The authors would like to acknowledge support from the National Science Foundation and the industrial members of the Center for Advanced Design and Manufacturing of Integrated Microfluidics (NSF I/UCRC award number IIP-1841509).References
- A. C. Anselmo, Y. Gokarn and S. Mitragotri, Nat. Rev. Drug Discovery, 2019, 18, 19–40 CrossRef CAS PubMed.
- J. Jezek, M. Rides, B. Derham, J. Moore, E. Cerasoli, R. Simler and B. Perez-Ramirez, Adv. Drug Delivery Rev., 2011, 63, 1107–1117 CrossRef CAS PubMed.
- J. S. Kingsbury, A. Saini, S. M. Auclair, L. Fu, M. M. Lantz, K. T. Halloran, C. Calero-Rubio, W. Schwenger, C. Y. Airiau, J. Zhang and Y. R. Gokarn, Sci. Adv., 2020, 6, eabb0372 CrossRef CAS PubMed.
- G. J. Despotis and L. T. Goodnough, Ann. Thorac. Surg., 2000, 70, S20–S32 CrossRef CAS PubMed.
- E. W. Davie, K. Fujikawa and W. Kisiel, Biochemistry, 1991, 30, 10363–10370 CrossRef CAS PubMed.
- F. Ciornei, S. Alaci, D. Amarandei, L. Irimescu, I. Romanu and L. Acsinte, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 174, 012041 Search PubMed.
- P. Singh, K. Sharma, I. Puchades and P. B. Agarwal, Sens. Actuators, A, 2022, 338, 113456 CrossRef CAS.
- A. Manz, D. J. Harrison, E. M. J. Verpoorte, J. C. Fettinger, A. Paulus, H. Lüdi and H. M. Widmer, J. Chromatogr. A, 1992, 593, 253–258 CrossRef CAS.
- S. B. Puneeth, M. B. Kulkarni and S. Goel, Eng. Res. Express, 2021, 3, 022003 CrossRef.
- A. Grupi and A. P. Minton, Anal. Chem., 2012, 84, 10732–10736 CrossRef CAS PubMed.
- N. Srivastava and M. A. Burns, Lab Chip, 2006, 6, 744–751 RSC.
- I. Jang, K. E. Berg and C. S. Henry, Sens. Actuators, B, 2020, 319, 128240 CrossRef CAS.
- B. A. Bircher, R. Krenger and T. Braun, Sens. Actuators, B, 2016, 223, 784–790 CrossRef CAS.
- T.-V. Nguyen, M.-D. Nguyen, H. Takahashi, K. Matsumoto and I. Shimoyama, Lab Chip, 2015, 15, 3670–3676 RSC.
- K. Fukada and S. Shiratori, RSC Adv., 2016, 6, 38475–38480 RSC.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- S. E. Mena, Y. Li, J. McCormick, B. McCracken, C. Colmenero, K. Ward and M. A. Burns, Biomicrofluidics, 2020, 14, 014109 CrossRef CAS PubMed.
- W. Zeng and H. Fu, Phys. Fluids, 2020, 32(4), 042002 CrossRef CAS.
- H. Chen, J. Man, Z. Li and J. Li, ACS Appl. Mater. Interfaces, 2017, 9, 21059–21064 CrossRef CAS PubMed.
- E. Livak-Dahl, J. Lee and M. A. Burns, Lab Chip, 2013, 13, 297–301 RSC.
- J. Carneiro, J. B. L. M. Campos and J. M. Miranda, Chem. Eng. Sci., 2019, 195, 442–454 CrossRef CAS.
- Y. Li, K. R. Ward and M. A. Burns, Anal. Chem., 2017, 89, 3996–4006 CrossRef CAS PubMed.
- P. Arosio, K. Hu, F. A. Aprile, T. Müller and T. P. J. Knowles, Anal. Chem., 2016, 88, 3488–3493 CrossRef CAS PubMed.
- P. Arosio, T. Müller, L. Rajah, E. V. Yates, F. A. Aprile, Y. Zhang, S. I. A. Cohen, D. A. White, T. W. Herling, E. J. De Genst, S. Linse, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, ACS Nano, 2016, 10, 333–341 CrossRef CAS PubMed.
- K. M. Schultz and E. M. Furst, Lab Chip, 2011, 11, 3802–3809 RSC.
- S. Gupta, W. S. Wang and S. A. Vanapalli, Biomicrofluidics, 2016, 10, 043402–043402 CrossRef PubMed.
- C. Chen, Y. Gu, J. Philippe, P. Zhang, H. Bachman, J. Zhang, J. Mai, J. Rufo, J. F. Rawls, E. E. Davis, N. Katsanis and T. J. Huang, Nat. Commun., 2021, 12, 1118 CrossRef CAS PubMed.
- P. Zhang, H. Bachman, A. Ozcelik and T. J. Huang, Annu. Rev. Anal. Chem., 2020, 13, 17–43 CrossRef CAS PubMed.
- Y. Gao, M. Wu, Q. Luan, I. Papautsky and J. Xu, Lab Chip, 2022, 22, 805–813 RSC.
- J. Zhang, S. Yang, C. Chen, J. H. Hartman, P.-H. Huang, L. Wang, Z. Tian, P. Zhang, D. Faulkenberry, J. N. Meyer and T. J. Huang, Lab Chip, 2019, 19, 984–992 RSC.
- W. Zhang, B. Song, X. Bai, L. Jia, L. Song, J. Guo and L. Feng, Lab Chip, 2021, 21, 4760–4771 RSC.
- D. Ahmed, A. Ozcelik, N. Bojanala, N. Nama, A. Upadhyay, Y. Chen, W. Hanna-Rose and T. J. Huang, Nat. Commun., 2016, 7, 11085 CrossRef CAS PubMed.
- P. A. Janmey, P. C. Georges and S. Hvidt, in Methods in Cell Biology, Academic Press, 2007, vol. 83, pp. 1–27 Search PubMed.
- F. Carrasco, E. Chornet, R. P. Overend and J. Costa, J. Appl. Polym. Sci., 1989, 37, 2087–2098 CrossRef CAS.
- S. Yadav, S. Shire and D. Kalonia, Pharm. Res., 2011, 28, 1973–1983 CrossRef CAS PubMed.
- W. Thielicke and R. Sonntag, J. Open Res. Softw., 2021, 9(1), 12 CrossRef.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- M. Aghaamoo, Y.-H. Chen, X. Li, N. Garg, R. Jiang, J. T.-H. Yun and A. P. Lee, Adv. Sci., 2022, 9, 2102021 CrossRef CAS PubMed.
- N. Garg, T. M. Westerhof, V. Liu, R. Liu, E. L. Nelson and A. P. Lee, Microsyst. Nanoeng., 2018, 4, 17085 CrossRef CAS.
- R. Jiang, S. Agrawal, M. Aghaamoo, R. Parajuli, A. Agrawal and A. P. Lee, Lab Chip, 2021, 21, 875–887 RSC.
- M. V. Patel, I. A. Nanayakkara, M. G. Simon and A. P. Lee, Lab Chip, 2014, 14, 3860–3872 RSC.
- A. R. Tovar, M. V. Patel and A. P. Lee, Microfluid. Nanofluid., 2011, 10, 1269–1278 CrossRef CAS.
- P. Marmottant and S. Hilgenfeldt, Nature, 2003, 423, 153–156 CrossRef CAS PubMed.
- P. Marmottant and S. Hilgenfeldt, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9523–9527 CrossRef CAS PubMed.
- A. R. Tovar and A. P. Lee, Lab Chip, 2009, 9, 41–43 RSC.
- D. L. Miller, J. Acoust. Soc. Am., 1988, 84, 1378–1387 CrossRef CAS PubMed.
- N. Garg, D. Boyle, A. Randall, A. Teng, J. Pablo, X. Liang, D. Camerini and A. P. Lee, Lab Chip, 2019, 19, 1524–1533 RSC.
- N. F. Läubli, J. T. Burri, J. Marquard, H. Vogler, G. Mosca, N. Vertti-Quintero, N. Shamsudhin, A. deMello, U. Grossniklaus, D. Ahmed and B. J. Nelson, Nat. Commun., 2021, 12, 2583 CrossRef PubMed.
- N. F. Läubli, M. S. Gerlt, A. Wüthrich, R. T. M. Lewis, N. Shamsudhin, U. Kutay, D. Ahmed, J. Dual and B. J. Nelson, Anal. Chem., 2021, 93, 9760–9770 CrossRef PubMed.
- C. Chen, S. P. Zhang, Z. Mao, N. Nama, Y. Gu, P.-H. Huang, Y. Jing, X. Guo, F. Costanzo and T. J. Huang, Lab Chip, 2018, 18, 3645–3654 RSC.
- M. Wiklund, R. Green and M. Ohlin, Lab Chip, 2012, 12, 2438–2451 RSC.
- F. Del Giudice, G. D'Avino, F. Greco, I. De Santo, P. A. Netti and P. L. Maffettone, Lab Chip, 2015, 15, 783–792 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00101f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |