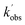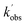Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental, theoretical, and astrochemical modelling investigation of the gas-phase reaction between the amidogen radical (NH2) and acetaldehyde (CH3CHO) at low temperatures†
Kevin M.
Douglas
 *a,
Lok Hin Desmond
Li
*a,
Lok Hin Desmond
Li
 a,
Catherine
Walsh
a,
Catherine
Walsh
 b,
Julia H.
Lehman
b,
Julia H.
Lehman
 c,
Mark A.
Blitz
c,
Mark A.
Blitz
 ad and
Dwayne E.
Heard
ad and
Dwayne E.
Heard
 *a
*a
aSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK. E-mail: k.m.douglas@leeds.ac.uk; d.e.heard@leeds.ac.uk
bSchool of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK
cSchool of Chemistry, University of Birmingham, Edgbaston, B15 2TT, UK
dNational Centre for Atmospheric Science (NCAS), University of Leeds, Leeds, LS2 9JT, UK
First published on 3rd April 2023
Abstract
The first experimental study of the low-temperature kinetics of the gas-phase reaction of NH2 with acetaldehyde (CH3CHO) has been performed. Experiments were carried out using laser-flash photolysis and laser-induced fluorescence spectroscopy to create and monitor the temporal decay of NH2 in the presence of CH3CHO. Low temperatures relevant to the interstellar medium were achieved using a pulsed Laval nozzle expansion. Rate coefficients were measured over the temperature and pressure range of 29–107 K and 1.4–28.2 × 1016 molecules per cm3, with the reaction exhibiting a negative temperature dependence and a positive pressure dependence. The yield of CH3CO from the reaction has also been determined at 67.1 and 35.0 K, by observing OH produced from the reaction of CH3CO with added O2. Ab initio calculations of the potential energy surface (PES) were combined with Rice–Rampsberger–Kessel–Marcus (RRKM) calculations to predict rate coefficients and branching ratios over a broad range of temperatures and pressures. The calculated rate coefficients were shown to be sensitive to the calculated density of states of the stationary points, which in turn are sensitive to the inclusion of hindered rotor potentials for several of the vibrational frequencies. The experimentally determined rate coefficients and yields have been used to fit the calculated PES, from which low-pressure limiting rate coefficients relevant to the ISM were determined. These have been included in a single-point dark cloud astrochemical model, in which the reaction is shown to be a potential source of gas-phase CH3CO radicals under dark cloud conditions.
1. Introduction
An active field of astrochemical research remains the understanding of the reaction mechanisms for the formation of complex organic molecules (COMs), which are molecules observed in space containing carbon with at least 6 atoms.1 Since the early 1960s, the development of ground based radio astronomy has led to a rapid rate of detection of COMs with a wide range of functional groups in the interstellar medium (ISM).2 The detection of COMs at very high spatial resolution in cold objects suggests a gas-phase route to their formation rather than just via a pure surface-grain chemistry mechanism.3 However, the mechanisms for forming many gas-phase COMs are still unknown, with both gas-phase and grain-surface (via non-thermal desorption) routes possible.The formation of biomolecules such as amino acids from COMs under pre-biotic conditions has attracted much interest.4 Amino acids such as glycine (NH2CH2COOH), which has been observed in the coma of a comet,5 are building blocks for proteins, which are essential components of all living systems. The peptide bond (NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) the plays a key role in the linking of amino acids into peptide chains and proteins, and contains all the components necessary for the formation of nucleic polymers under prebiotic conditions.6 However, only two molecules containing this bond have been observed in space, formamide (NH2CHO),7 and acetamide (NH2C(O)CH3).8
O) the plays a key role in the linking of amino acids into peptide chains and proteins, and contains all the components necessary for the formation of nucleic polymers under prebiotic conditions.6 However, only two molecules containing this bond have been observed in space, formamide (NH2CHO),7 and acetamide (NH2C(O)CH3).8
In a previous paper9 we investigated the low-temperature kinetics of the gas-phase reaction between the amidogen radical (NH2) and formaldehyde (CH2O) as a possible source of interstellar formamide. In this paper, we have performed an experimental and theoretical study of the kinetics of the reaction of NH2 with acetaldehyde, the next aldehyde in the homologous series after formaldehyde, for which there are three energetically favourable channels (ΔH calculated in this study, see Section 4):
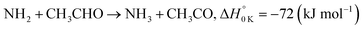 | (R1a) |
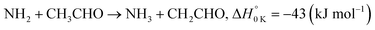 | (R1b) |
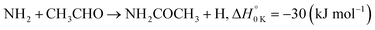 | (R1c) |
Reaction (R1) therefore, is both a potential source of gas-phase organic radicals (CH3CO and CH2CHO via reactions (R1a) and (R1b), respectively), and of acetamide (NH2COCH3, via reaction (R1c)), the largest interstellar molecule with a peptide bond that has so far been observed in space.8 We present measurements of rate coefficients for the reaction of NH2 and CH3CHO in the range 29–107 K, using a pulsed laser photolysis-laser induced fluorescence (PLP-LIF) technique coupled with a Laval nozzle to achieve the low temperatures relevant to the ISM. We also report an experimental measurement of the absolute branching yield for reaction (R1a) generating NH3 + CH3CO products at 35 K and 67 K. We also performed a theoretical investigation of the reaction using ab initio methods to calculate the potential energy surface, and used reaction rate theory to calculate both rate coefficients and product branching ratios over the temperature range 20–400 K. These kinetic data are then incorporated into a single point dark cloud astronomical model to assess the impact of the newly determined rate coefficients. A more detailed introduction to the low-temperature kinetics of gas-phase reactions, to the astrochemistry of acetamide, and to the related reaction between NH2 and formaldehyde, is given in the ESI in Section S1.†
2. Methodology
2.1 Experimental study
The use of a Laval nozzle expansion coupled with a PLP-LIF technique has been employed by this group to study a range of low temperature neutral–neutral reactions, including reactions of OH with unsaturated hydrocarbons10 and VOCs,11–141CH2 (singlet methylene) with atmospheric gases and hydrocarbons,15,16 CH with CH2O,17 and NH2 with CH2O.9 In the current study, we employ the same technique to study the low temperature reaction of NH2 with CH3CHO. As the experimental apparatus employed in the current and previous studies has been discussed in detail elsewhere,10–13 only a very brief overview is given here, with additional details given in the ESI in Section S2.†The low temperatures employed in this study were obtained by the isentropic expansion of a gas mixture from a high pressure reservoir to a low pressure chamber through a Laval nozzle, producing a thermalized low temperature gas flow that is stable for several centimetres from the nozzle exit. A set of 4 nozzles were used during the experiments to achieve flow temperatures of between 29 and 107 K. The density and temperature profile of the flows were characterized by impact pressure measurements, and the temperature of several of the uniform flows was confirmed by rotationally resolved LIF spectroscopy.15,17
The gas mixture introduced to the reservoir consists primarily of an inert bath gas (Ar (99.9995%, BOC), He (99.9995%, BOC), or N2 (99.9995%, BOC)), together with smaller amounts of the NH2 precursor (NH3 (99.98%, BOC)), the CH3CHO co-reagent (Sigma-Aldrich, ≥99.0%), and CH4 (99.995%, BOC). These reagent and bath gases were combined in the required quantities in a mixing manifold using calibrated mass flow controllers (MFCs; MKS Instruments). Both the bath gases and the CH4 were introduced as pure gases, while the NH3 was introduced as a dilute mixture of ∼10% in Ar. The dilute NH3 flow typically accounted for less than 0.2% of the total flow, resulting in ∼0.02% NH3 present in the gas expansions. The CH3CHO co-reagent was introduced by entraining CH3CHO vapour in a flow of the bath gas passing through a glass bubbler (a modified Dreschel bottle) containing CH3CHO liquid. By measuring the pressure of the bath gas over the CH3CHO, the concentration of CH3CHO entrained in the gas flow was determined via its known vapour pressure,18 and confirmed by UV absorption spectroscopy (see ESI Section S2†).
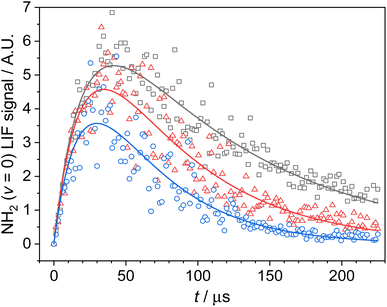
NH2 radicals were generated from the PLP of NH3 at 213 nm (Reaction (R2)) by the 5th harmonic of a Nd:YAG laser (Quantel Q-Smart 850), with a typical pulse energy of ∼10 mJ. NH2 radicals were observed by time-resolved LIF spectroscopy, probing the A2A1 (0,9,0) ← X2B1 (0,0,0) transition near 597.7 nm (ref. 19 and 20) using the output of a Nd:YAG pumped dye laser (a Quantel Q-smart 850 pumping a Sirah Cobra-Stretch). The non-resonant fluorescence at ∼620 nm was collected via a series of lenses through an optical filter (Semrock Brightline interference filter, λmax = 620 nm, fwhm = 14 nm), and observed by a temporally gated channel photomultiplier (CPM; PerkinElmer C1952P), mounted at 90° to both laser beams. The temporal evolution of the LIF signal was recorded by varying the time delay between the photolysis and probe lasers. A typical time-resolved LIF profile (Fig. 1) consisted of 165 delay steps and resulted from the average or between 5 and 15 individual delay scans.
| NH3 + ℏν (213 nm) → NH2 + H | (R2) |
Photolysis of NH3 produces both ground and vibrationally excited NH2,20,21 and as a consequence of this the profiles of NH2 (v = 0) exhibit a growth resulting from the relaxation of vibrationally excited NH2 (see Fig. 1). As kinetics measurements are limited by the dynamic time of the low temperature expansions, it was important that this relaxation was as efficient as possible, in order to maximise the time in which we could observe the loss of NH2 (v = 0). As such, CH4, which has been shown to efficiently relax NH2 (v > 0),9 was added to our gas flows.
Experiments looking at the dimerization of CH3CHO at low temperatures were conducted using the same experimental apparatus as described above. CH3CHO was observed by probing the 3(n,π*) A3A′′ ← X1A′ transition at 308.0 nm,22 using the frequency doubled output of a Nd:YAG pumped dye laser (same system as described above with a BBO doubling crystal). The non-resonant fluorescence at λ > 390 nm was discriminated using a long pass Perspex filter.
Some additional experiments were also carried out observing the production of OH radicals from the reaction of CH3CO with O2(R4), in order to obtain the yield of CH3CO produced from reaction (R1) (via channel (R1a)). As a part of these experiments, the temporal removal of OH by CH3CHO, both with and without O2 present, was also recorded, with the OH produced by the PLP of tert-butyl hydrogen peroxide ((CH3)3COOH; tBuOOH). These experiments were all conducted using the same experimental apparatus as described above. The tBuOOH precursor was introduced in the same method as the CH3CHO co-reagent, by entraining its vapour in a flow of bath gas passing through a bubbler containing tBuOOH liquid (Alfa-Aesar, 70% aqueous solution). The concentration of tBuOOH in our low temperature flows was estimated using its known vapour pressure at room temperature, and confirmed by UV absorption spectroscopy (see ESI Section S2†). OH radicals were observed by probing the A2 Σ+ (v′ = 0) ← X2 Π (v′′ = 0) transition at ∼307.9 nm, using the laser system as described above. The resonant fluorescence was collected using a gated photomultiplier tube, in which the scattered laser probe light was gated out, fitted with an interference filter centred at 308.5 nm (Barr Associates, fwhm = 5 nm).
2.2 Theoretical calculations
All ab initio electronic structure calculations were carried out using the Gaussian 09 programme.23 Geometric structures of the stationary points involved (reactants, products, and intermediates including adducts, pre-reaction complexes (PRCs), and transition states (TSs)) were optimised at the M062X/aug-cc-pVTZ level of theory,24–27 using the ultrafine integration grids in Gaussian. Rotational constants, harmonic vibrational frequencies, and zero-point energies (ZPEs) were obtained from the same level of theory. TSs were found to have only one imaginary vibrational frequency, while for the reactants, products and intermediates, all of the vibrational frequency values were positive. ZPEs obtained from the harmonic frequencies were corrected with a scaling factor of 0.956 for M062X/aug-cc-pVTZ.28 Intrinsic reaction coordinate (IRC) calculations were performed for all the TSs identified to verify their linkage with the respective local minima on the PES. More accurate single-point energy values were obtained at the CCSD(T)/aug-cc-pVTZ level29,30 upon the optimised structures. RRKM calculations were performed using the Master Equation Solver for the Multi-Energy Well Reactions (MESMER) program.313. Results
3.1 Kinetics
Typical NH2 (v = 0) LIF temporal profiles produced following the PLP of NH3 can be seen in Fig. 1. As can be seen from these profiles there is an initial growth in the NH2 signal, with no instant signal observed. As discussed above, this growth in the NH2 (v = 0) signal is due to relaxation of vibrationally excited NH2 produced following the photolysis of NH3. Although the growth of the NH2 (v = 0) signal is not strictly a single exponential growth (due to the presence of several vibrationally excited states relaxing down), we were able to fit the NH2 traces satisfactorily treating the growth as a single process: | (R3) |
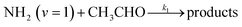 | (R1) |
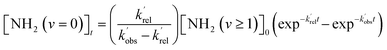 | (E1) |
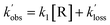 | (E2) |
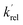 and
and 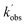 are the pseudo-first-order rate coefficients for the reactions producing and removing NH2 (v = 0), [NH2 (v ≥ 1)]0 is the initial amount of NH2 (v ≥ 1) produced following photolysis of NH3 that is subsequently relaxed down to NH2 (v = 0), and
are the pseudo-first-order rate coefficients for the reactions producing and removing NH2 (v = 0), [NH2 (v ≥ 1)]0 is the initial amount of NH2 (v ≥ 1) produced following photolysis of NH3 that is subsequently relaxed down to NH2 (v = 0), and 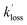 is the total rate coefficient for other loss processes of NH2 (v = 0), such as diffusion out of the probe laser beam volume. Eqn (E1) was fitted to the NH2 (v = 0) temporal profiles, and the parameters
is the total rate coefficient for other loss processes of NH2 (v = 0), such as diffusion out of the probe laser beam volume. Eqn (E1) was fitted to the NH2 (v = 0) temporal profiles, and the parameters 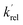 ,
, 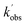 , and [NH2 (v ≥ 1)]0 extracted. As can be seen from Fig. 1, the NH2 traces are satisfactorily fit using a biexponential function, indicating the validity of treating the growth of the NH2 (v = 0) signal as a single process. Plotting
, and [NH2 (v ≥ 1)]0 extracted. As can be seen from Fig. 1, the NH2 traces are satisfactorily fit using a biexponential function, indicating the validity of treating the growth of the NH2 (v = 0) signal as a single process. Plotting 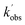 vs. [CH3CHO] should then yield a straight line (eqn (E2)), with a gradient equal to the bimolecular rate constant, k1, and intercept
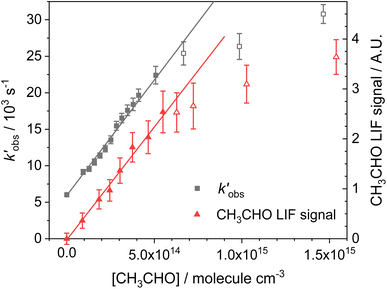
vs. [CH3CHO] should then yield a straight line (eqn (E2)), with a gradient equal to the bimolecular rate constant, k1, and intercept 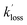 . An example of such a bimolecular plot can be seen in Fig. 2. As can be seen from Fig. 2, in some of our bimolecular plots we observe a curvature in the
. An example of such a bimolecular plot can be seen in Fig. 2. As can be seen from Fig. 2, in some of our bimolecular plots we observe a curvature in the 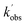 values at high [CH3CHO], which we attribute to the formation of CH3CHO dimers in our low temperature flows. Depending on the reactivity of the dimer with NH2 compared to the monomer, the bimolecular plots may curve upwards or downwards, or display no curvature if the dimer removes NH2 at exactly twice the rate as the monomer. In order to help identify at which CH3CHO concentration significant amounts of dimers form, experiments were carried out monitoring the relative concentration of CH3CHO in the flow via laser-induced fluorescence as a function of the [CH3CHO] added (see Fig. 2). In regions in which little or no dimerization is occurring, the amount of CH3CHO monomer present in the flow will increase linearly with the [CH3CHO] added; as such the CH3CHO LIF signal will increase linearly (closed red triangles in Fig. 2). However, in regions in which CH3CHO dimerization is occurring, the amount of CH3CHO monomer present in the flows will actually be less than the [CH3CHO] added, and as such the CH3CHO LIF signal will begin to curve over with increasing [CH3CHO] (open red triangles in Fig. 2). These dimerization experiments were carried out for each low temperature uniform flow employed in this study. When determining the bimolecular rate coefficient, k1, from a bimolecular plot, only data in the linear region below the CH3CHO concentration at which dimers formed were used (solid black squares in Fig. 2). As can be seen from Fig. 2, both the bimolecular plot and the dimerization plot exhibit the same shape with increasing [CH3CHO] and are in good agreement on the concentration at which CH3CHO dimers begin to form (above 6 × 1014 molecules per cm3).
values at high [CH3CHO], which we attribute to the formation of CH3CHO dimers in our low temperature flows. Depending on the reactivity of the dimer with NH2 compared to the monomer, the bimolecular plots may curve upwards or downwards, or display no curvature if the dimer removes NH2 at exactly twice the rate as the monomer. In order to help identify at which CH3CHO concentration significant amounts of dimers form, experiments were carried out monitoring the relative concentration of CH3CHO in the flow via laser-induced fluorescence as a function of the [CH3CHO] added (see Fig. 2). In regions in which little or no dimerization is occurring, the amount of CH3CHO monomer present in the flow will increase linearly with the [CH3CHO] added; as such the CH3CHO LIF signal will increase linearly (closed red triangles in Fig. 2). However, in regions in which CH3CHO dimerization is occurring, the amount of CH3CHO monomer present in the flows will actually be less than the [CH3CHO] added, and as such the CH3CHO LIF signal will begin to curve over with increasing [CH3CHO] (open red triangles in Fig. 2). These dimerization experiments were carried out for each low temperature uniform flow employed in this study. When determining the bimolecular rate coefficient, k1, from a bimolecular plot, only data in the linear region below the CH3CHO concentration at which dimers formed were used (solid black squares in Fig. 2). As can be seen from Fig. 2, both the bimolecular plot and the dimerization plot exhibit the same shape with increasing [CH3CHO] and are in good agreement on the concentration at which CH3CHO dimers begin to form (above 6 × 1014 molecules per cm3).
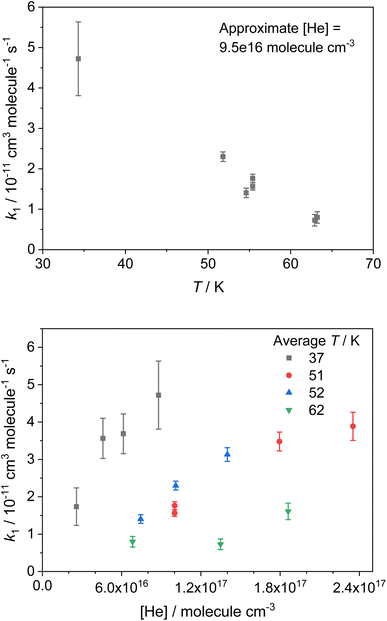
The bimolecular rate coefficients for the reaction of NH2 with CH3CHO (R1) determined in this study are presented in Table 1. The errors reported are the 1σ confidence intervals of the linear least squares fits of the bimolecular plots. A selection of these results recorded using He as a bath gas are shown in Fig. 3. Presenting only those rate coefficients collected in a particular bath gas and at the same approximate pressure, it can be seen that the reaction exhibits a clear negative temperature dependence over the temperature range investigated (see Fig. 3 top panel and Fig. S3†). By presenting the rate coefficients collected at the same approximate temperature (from the same nozzle) and again in the same bath gas, it can also be seen that the reaction exhibits a strong positive pressure dependence over the pressure range investigated (see Fig. 3 bottom panel and Fig. S4†). Both the negative T dependence and the positive P dependence are indicative of reactions with a pre-reaction complex on their potential energy surface (PES; see Fig. 7). There have been no previous studies of the reaction between NH2 and CH3CHO at low temperatures, and only one study at higher temperatures, over the temperature range 297–543 K, conducted using an isothermal discharge flow system.34 These high temperature rate coefficients are compared with our theoretically determined rate coefficients in Section 4, and in Fig. S13.†
| Nozzle | Gas | ∼T /K | T /K | Densityb/1016 molecules per cm3 | k 1 /10−11 cm3 per molecule per s |
|---|---|---|---|---|---|
| a Average T of the low temperature flows for a particular nozzle and a particular gas. b Uncertainties in each value of T and density are ±1σ (the standard deviation) of the measured T and density along the axis of the Laval expansion. c Uncertainties reported at the 1σ level for the linear least-squares fitting of the pseudo-first-order coefficients as a function of [CH3CHO]. | |||||
| 1 | Ar | 31 | 34.2 ± 3.0 | 2.1 ± 0.3 | 3.77 ± 0.61 |
| 30.3 ± 2.7 | 3.4 ± 0.4 | 5.82 ± 0.45 | |||
| 28.7 ± 2.6 | 6.2 ± 0.8 | 10.7 ± 1.9 | |||
| He | 37 | 42.2 ± 5.4 | 2.6 ± 0.5 | 1.74 ± 0.50 | |
| 37.2 ± 3.1 | 4.6 ± 0.6 | 3.56 ± 0.54 | |||
| 35.0 ± 2.8 | 6.1 ± 0.7 | 3.69 ± 0.53 | |||
| 34.3 ± 3.4 | 8.8 ± 1.3 | 4.72 ± 0.91 | |||
| N2 | 66 | 70.0 ± 2.7 | 1.4 ± 0.1 | 0.25 ± 0.27 | |
| 67.1 ± 2.1 | 2.5 ± 0.2 | 0.84 ± 0.38 | |||
| 67.1 ± 2.1 | 2.5 ± 0.2 | 1.53 ± 0.33 | |||
| 64.6 ± 2.0 | 4.5 ± 0.3 | 0.92 ± 0.39 | |||
| 62.9 ± 2.4 | 6.4 ± 0.6 | 2.80 ± 0.31 | |||
| 2 | Ar | 45 | 52.2 ± 2.9 | 6.2 ± 0.5 | 3.17 ± 0.09 |
| 47.0 ± 2.8 | 11.2 ± 1.0 | 4.37 ± 0.41 | |||
| 41.6 ± 1.6 | 28.2 ± 1.6 | 9.88 ± 0.90 | |||
| 39.3 ± 2.7 | 16.5 ± 1.7 | 8.46 ± 0.37 | |||
| He | 51 | 55.4 ± 3.8 | 10.0 ± 1.0 | 1.76 ± 0.10 | |
| 55.4 ± 3.8 | 10.0 ± 1.0 | 1.56 ± 0.09 | |||
| 50.9 ± 1.9 | 17.9 ± 1.0 | 3.48 ± 0.25 | |||
| 47.6 ± 1.5 | 23.5 ± 1.2 | 3.89 ± 0.38 | |||
| N2 | 83 | 89.9 ± 2.5 | 4.2 ± 0.3 | 0.72 ± 0.10 | |
| 84.4 ± 2.8 | 7.4 ± 0.6 | 0.57 ± 0.22 | |||
| 80.5 ± 2.9 | 13.0 ± 1.2 | 2.57 ± 0.31 | |||
| 78.4 ± 2.9 | 17.7 ± 1.6 | 1.43 ± 0.42 | |||
| 3 | Ar | 45 | 47.9 ± 4.3 | 6.2 ± 0.8 | 4.89 ± 0.11 |
| 44.4 ± 4.3 | 11.2 ± 1.6 | 9.95 ± 0.91 | |||
| 43.3 ± 4.3 | 15.9 ± 2.3 | 11.6 ± 0.7 | |||
| He | 52 | 54.6 ± 4.0 | 7.4 ± 0.8 | 1.4 ± 0.12 | |
| 51.8 ± 3.7 | 10.1 ± 1.1 | 2.3 ± 0.12 | |||
| 49.6 ± 3.9 | 14 ± 1.6 | 3.13 ± 0.18 | |||
| N2 | 89 | 92.9 ± 6.6 | 5.3 ± 0.9 | 0.17 ± 0.05 | |
| 87.4 ± 6.4 | 9.1 ± 1.7 | 0.92 ± 0.18 | |||
| 85.6 ± 6.0 | 12.7 ± 2.2 | 1.14 ± 0.18 | |||
| 4 | Ar | 55 | 59.4 ± 7.4 | 8.8 ± 1.6 | 3.7 ± 0.21 |
| 54.2 ± 7.9 | 15.0 ± 3.2 | 6.28 ± 0.59 | |||
| 52.4 ± 7.8 | 20.5 ± 4.5 | 9.69 ± 0.61 | |||
| He | 62 | 63.2 ± 6.2 | 6.8 ± 0.9 | 0.80 ± 0.14 | |
| 62.9 ± 5.7 | 13.5 ± 1.9 | 0.73 ± 0.14 | |||
| 60.0 ± 6.2 | 18.6 ± 2.9 | 1.61 ± 0.22 | |||
| N2 | 101 | 106.7 ± 8.6 | 7.6 ± 7.6 | 0.42 ± 0.04 | |
| 99.5 ± 9.8 | 12.7 ± 3.1 | 0.21 ± 0.03 | |||
| 97.0 ± 9.7 | 17.7 ± 4.3 | 0.21 ± 0.08 | |||
3.2 NH2 (v > 0) removal
The strong pressure dependence of reaction (R1), which at certain temperatures and with certain bath gases exhibited an almost 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relationship between rate coefficient and pressure, was slightly unexpected, and indicated that the reaction is firmly within the low-pressure region over the pressures investigated (1.4–28.2 × 1016 molecules per cm3). In contrast, the reaction between OH and CH3CHO, which has also been studied at low temperatures, does not exhibit any pressure dependence over the temperature and pressure range of 21–106 K and 1–20 × 1016 molecules per cm3, respectively.35 One method for estimating the high-pressure limit of a reaction is the proxy method,36,37 in which the loss of vibrationally excited NH2 with CH3CHO is measured. Here, the assumption is made that following the formation of the collision complex, the excess vibrational energy in the NH2 is rapidly redistributed among the many other modes in the complex, and any NH2 formed following dissociation of the complex is in v = 0. Thus, the proxy method provides an estimate of the capture rate coefficient for complex formation, which can be used as the inverse Laplace transform (ILT) parameters for the initial association reaction of NH2 with CH3CHO in our MESMER calculations (Section 4).
1 relationship between rate coefficient and pressure, was slightly unexpected, and indicated that the reaction is firmly within the low-pressure region over the pressures investigated (1.4–28.2 × 1016 molecules per cm3). In contrast, the reaction between OH and CH3CHO, which has also been studied at low temperatures, does not exhibit any pressure dependence over the temperature and pressure range of 21–106 K and 1–20 × 1016 molecules per cm3, respectively.35 One method for estimating the high-pressure limit of a reaction is the proxy method,36,37 in which the loss of vibrationally excited NH2 with CH3CHO is measured. Here, the assumption is made that following the formation of the collision complex, the excess vibrational energy in the NH2 is rapidly redistributed among the many other modes in the complex, and any NH2 formed following dissociation of the complex is in v = 0. Thus, the proxy method provides an estimate of the capture rate coefficient for complex formation, which can be used as the inverse Laplace transform (ILT) parameters for the initial association reaction of NH2 with CH3CHO in our MESMER calculations (Section 4).
Rate coefficients for the removal of NH2 (v = 0, x, 0) with CH3CHO, where x = 0–4 and represents vibrational excitement of the v2 bending mode in NH2, are presented in Fig. 4 and Table 2, together with the transitions and wavelengths employed.21,38 In experiments monitoring removal of NH2 (v = 1–4), no CH4 was added to the low temperature flows, and a Perspex filter was used to collect the fluorescence and cut out the scattered laser light from the 213 nm photolysis pulse. As can be seen from Fig. 4 and Table 2, removal of vibrationally excited NH2 by CH3CHO is significantly faster than removal of ground state NH2, with higher vibrational levels appearing to be removed faster than lower vibrational levels. However, the rate coefficient does appear to be reaching a limit (the high-pressure limit) at high v; at 37.2 K in He this limit is practically reached by v = 1, and appears around 4 × 10−10 cm3 per molecule per s (assessed visually), while at 67.1 K in N2 the limit is not reached until around v = 2 or 3, and appears to be around 3.5 × 10−10 cm3 per molecule per s. These results suggest that for the NH2 + CH3CHO system, only at the lowest temperatures are the initial collision complexes long-lived enough to ensure complete redistribution of the excess vibrational energy from the NH2 species into the complex, and that at higher temperatures some complexes may dissociate before this has happened. Thus, proxy method estimations of the high-pressure limit for other systems carried out looking at the removal of v = 1 only, may underestimate the true limit. However, as the results at 67.1 K in N2 show, the redistribution of energy from higher vibrational states appears to be faster, suggesting the high-pressure limit may still be estimated by looking at removal from successively higher vibrational levels. The slightly larger high-pressure limit at 37.2 K suggests a small negative temperature dependence in the initial association reaction between NH2 and CH3CHO.
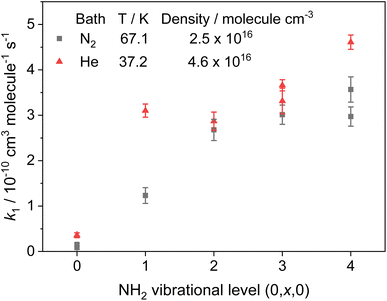 | ||
| Fig. 4 Rate coefficients for the removal of NH2 (v = 0–4) with CH3CHO. Grey squares; T = 67.1 K, [N2] = 2.5 × 1016 molecules per cm3. Red triangles; T = 37.2 K, [He] = 4.6 × 1016 molecules per cm3. | ||
| v 2 | Transitiona | λ/nm |
k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b/×10−10 cm3 per molecule per s b/×10−10 cm3 per molecule per s |
|
|---|---|---|---|---|
In N2 at 67.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c K c K |
In He at 37.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d K d K |
|||
| a A 2A1 ← X2B1 transition. b Uncertainties reported at the 1σ level for the linear least-squares fitting of the pseudo-first-order coefficients as a function of [CH3CHO]. c Collected using nozzle 1 at T = 67.1 K and [N2] = 2.5 × 1016 molecules per cm3. d Collected using nozzle 1 at T = 37.2 K and [He] = 4.6 × 1016 molecules per cm3. | ||||
| 0 | 0,9,0 ← 0,0,0 | 597.7 | 0.08 ± 0.04 | 0.54 ± 0.05 |
| 0.15 ± 0.03 | — | |||
| 1 | 0,11,0 ← 0,1,0 | 591.1 | 1.23 ± 0.18 | 3.1 ± 0.15 |
| 2 | 0,12,0 ← 0,2,0 | 607.2 | 2.68 ± 0.23 | — |
| 608.4 | — | 2.87 ± 0.2 | ||
| 3 | 0,13,0 ← 0,3,0 | 628.9 | 3.01 ± 0.21 | 3.31 ± 0.28 |
| 627.4 | — | 3.66 ± 0.12 | ||
| 4 | 0,16,0 ← 0,4,0 | 611.0 | 3.57 ± 0.28 | 4.61 ± 0.16 |
| 616.8 | 2.97 ± 0.21 | — | ||
3.3 OH/CH3CO yields
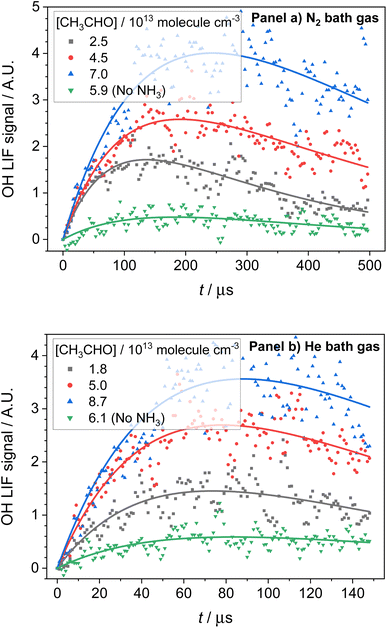
OH LIF profiles produced following the photolysis of NH3 in the presence of both CH3CHO and O2 are presented in Fig. 5. The OH observed is the result of CH3CO, the product of reaction (R1a), reacting with O2 to produce OH (R4):| CH3CO + O2 → OH + co-products | (R4) |
As the experiments were carried out under pseudo-first-order conditions (i.e. [NH2] ≪ [CH4], [CH3CHO], and [O2]), the growth and loss of the OH signal can be described by a bi-exponential function of the form:
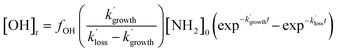 | (E3) |
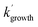 and
and 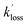 are the pseudo-first-order rate coefficients for the reactions producing and removing OH, [NH2]0 is the initial amount of NH2 produced following PLP of NH3, and fOH is the observed OH fluorescence signal, or OH yield (note, the reaction of CH3CO + O2 can also lead to other products). As OH itself reacts with CH3CHO (R5), its primary loss is the sum of (R5) and diffusional losses. Although the OH profiles are not strictly bi-exponential in nature, as the growth of the OH signal is the result of series of subsequent reactions (vibrational relaxation of
are the pseudo-first-order rate coefficients for the reactions producing and removing OH, [NH2]0 is the initial amount of NH2 produced following PLP of NH3, and fOH is the observed OH fluorescence signal, or OH yield (note, the reaction of CH3CO + O2 can also lead to other products). As OH itself reacts with CH3CHO (R5), its primary loss is the sum of (R5) and diffusional losses. Although the OH profiles are not strictly bi-exponential in nature, as the growth of the OH signal is the result of series of subsequent reactions (vibrational relaxation of 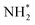 by CH4(R3), reaction of NH2 with CH3CHO to form CH3CO (R1a), and reaction of CH3CO with O2 to form OH (R4)), they could be satisfactorily fit using eqn (E3), and the parameters
by CH4(R3), reaction of NH2 with CH3CHO to form CH3CO (R1a), and reaction of CH3CO with O2 to form OH (R4)), they could be satisfactorily fit using eqn (E3), and the parameters 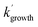 ,
, 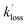 , and fOH extracted.
, and fOH extracted.
The OH yields themselves do not give the yield for CH3CO production from reaction (R1). To do this requires two additional pieces of knowledge; the first is an understanding of how many OH radicals have been produced relative to the initial number of NH2 radicals produced, while the second is an understanding of the yield of OH from the reaction of CH3CO with O2 (ϕOH; R4). The second can be determined by measuring the rate coefficient for the removal of OH by CH3CHO (R5) both with and without O2 present.39,40 In the experiments with O2 present, CH3CO formed by reaction (R5) will react with O2, with a fraction regenerating OH (R4). If the concentration of O2 is great enough such that the reaction between CH3CO and O2 is fast compared to the OH + CH3CHO reaction (i.e.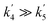 ), then the OH removal will be determined by the fraction of (R5) that does not regenerate OH. As such, the reduction in the bimolecular rate coefficient for OH loss with CH3CHO in the presence of O2, kO2, as compared to without O2, kno O2, gives the OH yield:
), then the OH removal will be determined by the fraction of (R5) that does not regenerate OH. As such, the reduction in the bimolecular rate coefficient for OH loss with CH3CHO in the presence of O2, kO2, as compared to without O2, kno O2, gives the OH yield:
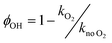 | (E4) |
| OH + CH3CHO → CH3CO, + other products | (R5) |
Experiments monitoring the loss of OH by CH3CHO, both with and without O2 present, were carried out at T = 67.1 K in N2 bath gas. OH LIF traces collected in these experiments (see Fig. S5†) could be fit with a single exponential loss in order to obtain the observed pseudo-first-order loss rate, 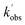 . Bimolecular plots obtained by plotting
. Bimolecular plots obtained by plotting 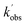 vs. [CH3CHO] can be seen in Fig. 6, in which the clear reduction in the bimolecular rate coefficient with O2 can be seen. With no O2 present, we obtain a value of k5(no O2) = (9.81 ± 0.57) × 10−11 cm3 per molecule per s. This rate coefficient is in good agreement with a recent literature study of the low temperature reaction of OH with C3HCHO, in which they obtain a rate coefficient of (1.25 ± 0.13) × 10−10 cm3 per molecule per s at T = 64 K.35 With O2 present, we obtain a value of k5(O2) = (5.4 ± 4.2) × 10−12 cm3 per molecule per s, giving a value of ϕOH = 0.94 ± 0.05.
vs. [CH3CHO] can be seen in Fig. 6, in which the clear reduction in the bimolecular rate coefficient with O2 can be seen. With no O2 present, we obtain a value of k5(no O2) = (9.81 ± 0.57) × 10−11 cm3 per molecule per s. This rate coefficient is in good agreement with a recent literature study of the low temperature reaction of OH with C3HCHO, in which they obtain a rate coefficient of (1.25 ± 0.13) × 10−10 cm3 per molecule per s at T = 64 K.35 With O2 present, we obtain a value of k5(O2) = (5.4 ± 4.2) × 10−12 cm3 per molecule per s, giving a value of ϕOH = 0.94 ± 0.05.
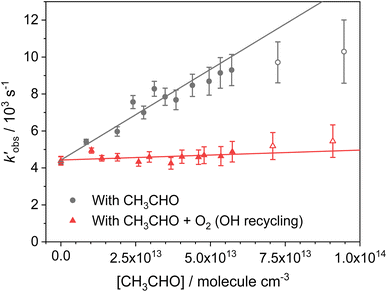 | ||
Fig. 6 Bimolecular plot of 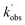 vs. [CH3CHO] for the reaction between OH + CH3CHO (R5). Grey circles; OH loss with only CH3CHO present. Red triangles; OH loss with both CH3CHO and O2 present. Curvature of the grey circles at [CH3CHO] above 7 × 1013 molecules per cm3 indicates significant dimer formation, with the linear fits obtained only using data points below this. vs. [CH3CHO] for the reaction between OH + CH3CHO (R5). Grey circles; OH loss with only CH3CHO present. Red triangles; OH loss with both CH3CHO and O2 present. Curvature of the grey circles at [CH3CHO] above 7 × 1013 molecules per cm3 indicates significant dimer formation, with the linear fits obtained only using data points below this. | ||
To address the first issue in determining the yield for CH3CO production from (R1), that is understanding how many OH radicals have been produced relative to the initial number of NH2 radicals produced, we used the following procedure. In these experiments, we are photolyzing a known amount of NH3 to produce NH2 radicals, which go on to form a number of OH radicals which we observe using LIF. Using both the concentration and absorption cross section of NH3 we are able to estimate the number of NH2 radicals produced in our system. This calculation also requires the energy of the photolysis laser, however as this is kept constant in our experiments, this will later cancel out in our calculations and can be ignored. To put the OH signal we observe on an absolute scale, we then calibrate our OH LIF signal in a separate experiment by photolyzing a known amount of tBuOOH under the same conditions and using the same photomultiplier settings. Again, as we know both the concentration and absorption cross section of tBuOOH, we can determine the number of OH radicals present in our system giving us our OH LIF signal. In this manner we can determine a ratio of how many OH radicals we observe compared to the initial number of NH2 radicals produced. In these calculations we account for the reduction in the initial NH3 concentration in our system due to removal by CH3CHO, and for the non-unity conversion of CH3CO to OH by O2. Using this method, we have determined CH3CHO yields from reaction (R1) (i.e. the branching ratio for reaction (R1a)) to be 0.029 ± 0.014 at T = 67.1 K and [N2] = 2.50 × 1016 molecules per cm3, and 0.026 ± 0.008 at T = 35.0 K and [He] = 6.14 × 1016 molecules per cm3. A more detailed account of how we determined these CH3CO yields is given in the ESI in Section S6.†
4. Discussion
4.1 Ab initio calculations of the PES
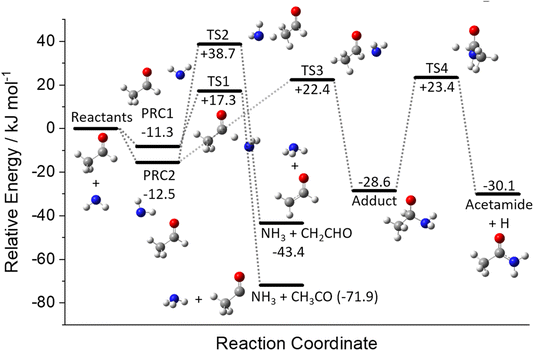
A schematic of the full PES for the reaction between NH2 and CH3CHO can be seen in Fig. 7. The energies given are at the CCSD(T) level of theory and include ZPEs calculated at the M062x level. The optimised structures of the stationary points are given in Fig. S7 in the ESI,† together with the full molecular properties in Tables S8–S10.† As can be seen from Fig. 7, the reaction initially proceeds via the formation of one of two pre-reaction complexes (PRCs; labelled PRC1 and PRC2 in Fig. 7). PRC1, in which the NH2 moiety is located over the acetyl H/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O end of the acetaldehyde, is linked to the formation of the acetyl H-abstraction products NH3 + CH3CO via TS1 (+17.3 kJ mol−1). PRC2, in which the NH2 moiety is located above the methyl/C
O end of the acetaldehyde, is linked to the formation of the acetyl H-abstraction products NH3 + CH3CO via TS1 (+17.3 kJ mol−1). PRC2, in which the NH2 moiety is located above the methyl/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O end of the acetaldehyde, is linked to two product channels; the methyl H-abstraction channel products NH3 + CH2CHO via TS2 (+38.7 kJ mol−1), and the addition–elimination channel products acetamide + H. The acetamide + H product channel requires the initial formation of a bound adduct from PRC2 via TS3 (+22.4 kJ mol−1), followed by the elimination of an H atom to form products via TS4 (+23.4 kJ mol−1). As both the H-abstraction channels involve the transfer of an H-atom, quantum mechanical tunnelling is likely to play a role at low temperatures.
O end of the acetaldehyde, is linked to two product channels; the methyl H-abstraction channel products NH3 + CH2CHO via TS2 (+38.7 kJ mol−1), and the addition–elimination channel products acetamide + H. The acetamide + H product channel requires the initial formation of a bound adduct from PRC2 via TS3 (+22.4 kJ mol−1), followed by the elimination of an H atom to form products via TS4 (+23.4 kJ mol−1). As both the H-abstraction channels involve the transfer of an H-atom, quantum mechanical tunnelling is likely to play a role at low temperatures.
There have been no previous theoretical investigations into the reaction between NH2 and CH3CHO; however, the reaction between NH2 and formaldehyde (CH2O) has been studied.9,41–44 As expected, considering the similarity between the two systems, the PESs for the two reactions resemble each other remarkably well, in both the depth of the PRCs (where mentioned) and the heights of the barriers; the only significant difference is the additional methyl-H abstraction channel present in the case of NH2 + CH3CHO.
4.2 Rate theory calculations using MESMER
Using the calculated NH2 + CH3CHO PES surface given in Fig. 7, rate coefficients and branching ratios for the reaction over a wide range of temperatures and pressures have been calculated using the MESMER program.31 The inverse Laplace transform (ILT) parameters for the association reaction of NH2 with acetaldehyde, which take the form of a modified Arrhenius function A(T/300)n (with the activation energy being set to zero), were adjusted to give good agreement to the high pressure limits determined in Section 3.1, with the values A = 2.5 × 10−10 cm3 per molecule per s and n = −0.25 used. Initial calculations carried out using the full PES have shown that the acetamide + H product channel (R1c) is predicted to be a very minor channel at all temperatures and pressures (over the range 20–400 K and 1 × 1011 to 1 × 1024 molecules per cm3). Indeed, at a pressure of [Ar] = 1 × 1016 molecules per cm3, the channel (R1c) only accounts for 0.1% of the product yield at 400 K, and decreases with decreasing temperature, becoming insignificant below ∼150 K (see ESI Fig. S11†). This is due to the relatively high barrier to adduct formation (TS3, 22.4 kJ mol−1) effectively turning off this channel at low temperatures as there is no coordinate for H-atom tunnelling under this barrier. As such, for the MESMER calculations discussed below, a simplified PES was used, in which the channel (R1c) was excluded (see ESI Fig. S12†).Rate coefficients predicted by MESMER using the surface given in Fig. S12† and at a pressure of 1 × 1017 molecules per cm3, are compared with our experimental data collected at a similar pressure in Fig. S13.† As can be seen from Fig. S13,† the experimental rate coefficients are significantly faster than those predicted by MESMER, by around 2 orders of magnitude. However, both the experimental and MESMER rate coefficients show a strong positive pressure dependence and a negative temperature dependence. This T and P dependence is the result of the formation of the weakly bound pre-reaction complexes on the PES. As the pressure is increased, there is more chance for the excess energy in the incoming reactants to be removed by collisions and for stabilization into the potential well to occur, while at the same time as the temperature is lowered, the rate of dissociation of the PRCs back to products will also decrease, increasing the effective loss rate of the reactants. Looking at species time profiles produced by MESMER, it can be seen that on the timescales of our experiments, as the reactants are lost we see significant population of the PRCs, which eventually go on to form products on longer timescales via quantum mechanical tunnelling. Thus, the fast removal rates of NH2 we observe in our experiments correspond to the population of the PRCs. How MESMER calculates the stabilization of the reactants into the PRC wells is dependent on the description of the molecular parameters of the species involved in the reaction scheme, and in particular how these affect the density of states of the reactants and adducts. The significantly smaller rate coefficients predicted by MESMER compared to experiment suggest an underestimation in the calculation of the density of states of the PRCs as compared to the reactants.
The approximation of the harmonic oscillator was used for the vibrational frequencies in the calculation of the density of states. However, a few vibrational frequencies may be better represented by the hindered rotor (HR) approximation. Typically, treating low frequency vibrations as HRs increases the density of states. Fig. S14† shows all the rotations described with the HR approach. HR potentials were constructed through an ab initio calculation of a relaxed scan of the energy as the dihedral angle respective to the rotation is changed, with steps of 5°. A partial structure optimization was performed at the end of every step, until a 360° coverage was obtained. Both PRCs have 3 hindered rotors; rotation of the methyl group around the C–C bond, rotation of the terminal N–H around bond 7, and rotation of the N around bond 9 (see Fig. S14† for bond labels). For the hindered rotors around bond 9, we were only able to obtain a potential around ∼180° of the dihedral when carrying out a relaxed scan, due to the O–H–N angle approaching linearity and causing difficulties in the representation of the dihedral in Gaussian. However, by carrying out a fixed scan an approximation of the potential around the full 360° was obtained. Surprisingly, the treatment of the rotations around bonds 4 and 7 as HRs, rather than harmonic vibrations, results in a marginal increase in the density of states in the PRCs. However, the treatment of the rotation around bond 9 as a HR does increase the density of states, especially for PRC2. This increase in the density of states results in around a 3 fold increase in the rate coefficients predicted by MESMER (between 20 and 100 K and at [Ar] = 1 × 1017 molecules per cm3), bringing them closer to the experimental values (see Fig. S13†).
In order to obtain better agreement between the experimental and calculated rate coefficients, we have used MESMER to fit the experimental data by adjusting the well depths of the PRCs. In these calculations, we include the HR potentials and use the reduced NH2 + CH3CHO PES (excluding channel (R1c), Fig. S12†), and the errors of the experimental rate coefficients were set to 20% (or kept as the experimental error if >20%). In order to reduce the computational expense when fitting the experimental data, rather than allowing the ZPEs of each PRC well to be varied independently, we set the ZPE of PRC2 to be defined from the ZPE of PRC1 minus 1.2 kJ mol−1. In this manner we keep the absolute difference in energy between the two PRCs, while allowing the ZPEs of both to move up and down in tandem during the fitting.
The best fit to the experimental rate coefficients was obtained by moving the ZPEs of the PRCs down by 9.5 kJ mol−1, to −20.8 and −22.0 kJ mol−1 for PRCs 1 and 2, respectively. The χ2 parameter of the fit reduces from 856 (20.4 per point) using the original ZPEs down to 177 (4.2 per point) with the new values. Table S15† compares the experimental and calculated rate coefficients determined using these new values, and gives the % difference between the two. There is reasonable agreement between the rate coefficients, with an average difference of 20% for those using He as the bath, 30% using Ar, and 55% using N2. The larger % difference using N2 as a bath gas is likely the result of the larger errors in the experimental rate coefficients, which are on the lower edge of what we can reasonably measure in our experiments. This increase of 9.5 kJ mol−1 in the well depths of the PRCs is rather large. Typically, CCSD(T) calculations would be expected to be accurate to within 5 kJ mol−1, so an adjustment of almost double this suggests either some sort of systematic error or interference in the experimental results, or some error in the description and treatment of the species in the calculation. Possible sources of error in the experimental results which have been discussed above, are in the acetaldehyde concentrations in our experiments, and in the possible formation of acetaldehyde dimers. Our acetaldehyde concentrations are confirmed using UV absorption spectroscopy, and furthermore we obtain a rate coefficient for OH + CH3CHO in good agreement with another study.35 Regarding dimers, as we are able to directly monitor the fluorescence from acetaldehyde we are able to determine at what [CH3CHO] significant dimers begin to form, and ensure we only determine rate coefficients below this value where the second order plot is entirely linear. Another possible source of error is due to secondary chemistry in our experiments, such as from the removal of NH2 with a photolysis product of CH3CHO. However we deem this unlikely, as the cross-section for CH3CHO at 213 nm is ∼5 × 10−22 cm−2,45 over 3 orders of magnitude smaller than for NH3 at 213 nm, meaning that even at the highest CH3CHO concentrations in our experiments we would expect a ratio of NH2 to CH3CHO photolysis products of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Possible sources of error in the MESMER calculations likely lie in the description of the HRs, in particular the HR relating to rotation around bond 9 in both PRCs. The magnitude and shape of the potential for this HR has been shown to have a strong effect on the calculated density of states of the PRCs, and as such the calculated rate coefficients are sensitive to this potential. Thus, this study highlights the importance of improved computational methods in calculating low frequency vibrational frequencies and hindered rotor potentials.
1. Possible sources of error in the MESMER calculations likely lie in the description of the HRs, in particular the HR relating to rotation around bond 9 in both PRCs. The magnitude and shape of the potential for this HR has been shown to have a strong effect on the calculated density of states of the PRCs, and as such the calculated rate coefficients are sensitive to this potential. Thus, this study highlights the importance of improved computational methods in calculating low frequency vibrational frequencies and hindered rotor potentials.
In addition to fitting the rate coefficients, we are also able to fit the experimentally determined yields for CH3CO. As discussed above, at the temperatures and pressures in our experimental setup, the loss of NH2 that we observe in our experiments is primarily due to the formation of the PRCs (and in particular PRC2), which on timescales significantly longer than our experiments will go on to form products (both channels (R1a) and (R1b)). However, as observed in our experiments, some CH3CO is formed on the same timescale as NH2 is lost, which for convenience we will call instant CH3CO. This instant CH3CO can be thought of as the CH3CO produced from well-skipping, and is sensitive to the height of the acetyl H-abstraction transition state (TS1). Thus, we are able to fit the height of TS1 to the experimentally determined CH3CO yields. This is crucially important for understanding the astrochemical implications of this reaction, as the height of TS1 greatly affects the low-pressure limiting rate coefficient, which is the relevant value for interstellar environments where there is no collisional stabilisation of the pre-reactive complex. As in the case of fitting the ZPEs of the PRCs, we have kept the absolute difference in the ZPEs of the TSs for the two H-abstraction channels constant, by defining the ZPE of TS2 from the ZPE of TS1 plus 21.4 kJ mol−1, while allowing the ZPEs of both to move up and down in tandem during the fitting. When entering the CH3CO yields to be fit into MESMER, the timescale for the yield must also be entered to ensure we are fitting to the instant CH3CO, rather than the final CH3CO yield. This timescale must be also be consistent with the excess reagent concentration entered in the model.
Table S16† compares the calculated instant CH3CO yields to the experimental values following fitting of the ZPEs of the H-abstraction TSs (TS1 and TS2) to the experimental data. The best fit to the experimental yields is obtained by moving the ZPEs of the H-abstraction TSs down by 0.9 kJ mol−1, to 16.4 and 37.8 kJ mol−1 for TSs 1 and 2, respectively. This small change in the heights of the H-abstraction TSs is well within the expected error of the calculated CCSD(T) energies.
Using the ZPEs of the PRCs and TSs obtained by fitting to the experimental data, we have calculated rate coefficients and branching ratios over a wide range of temperatures and pressures. Fig. 8 gives the low-pressure limiting rate coefficients which are applicable to the interstellar medium, while the rate coefficients over the full T and P range, which may be applicable to other high-pressure environments, can be seen in Fig. S17 in the ESI.† At the low-pressure limit, the only product channel open is the CH3CO + NH3 channel (R1a). Looking at Fig. 8, a turn around in the rate can be seen at around 200 K; above this temperature we see a small positive temperature dependence, whereas below this temperature we see a strong negative temperature dependence. This sharp increase in the rate coefficient at low temperatures is the result of the PRC wells on the PES, which are sufficiently long-lived at low temperatures to allow the H-atom to quantum-mechanically tunnel through the aldehydic H-abstraction barrier (TS1) to products. This mechanism has been reported previously for a range of low temperature H-abstraction reactions involving OH and oxygenated volatile organic compounds,11–13,35 and for NH2 + CH2O.9 Although the product channel (R1b), producing CH2CHO + NH3, also involves the transfer of an H atom and can occur by quantum mechanical tunnelling, due to the significantly larger barrier to methyl H-abstraction (TS2, 21.4 kJ mol−1 higher than TS1), and a similar imaginary frequency, the tunnelling rate through TS2 is insignificant when compared to the tunnelling rate through TS1. As such, the only products at the low-pressure limit are CH3CO + NH3(R1a). The unique shape of the low-pressure limiting rate coefficient for (R1) does not allow for the parameterization of the data over the whole temperature range using a single modified Arrhenius equation. Instead, the data above and below 170 K were parameterized, giving (see red and blue solid lines in Fig. 8: units are cm3 per molecule per s; errors are the 1σ level of a least squares fit to the data):
k(NH2+CH3CH![[O with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_004f_20d1.gif) NH3+CH3CO) (20 ≤ T/K ≤ 170) = (7.23 ± 0.64) × 10−16 × (T/300)(−2.56±0.15) × exp[(22.0±7.8)/T] NH3+CH3CO) (20 ≤ T/K ≤ 170) = (7.23 ± 0.64) × 10−16 × (T/300)(−2.56±0.15) × exp[(22.0±7.8)/T] |
k(NH2+CH3CH![[O with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_004f_20d1.gif) NH3+CH3CO) (170 ≤ T/K ≤ 400) = (9.99 ± 1.49) × 10−18 × (T/300)(9.70±0.17) × exp[(1944±44)/T] NH3+CH3CO) (170 ≤ T/K ≤ 400) = (9.99 ± 1.49) × 10−18 × (T/300)(9.70±0.17) × exp[(1944±44)/T] |
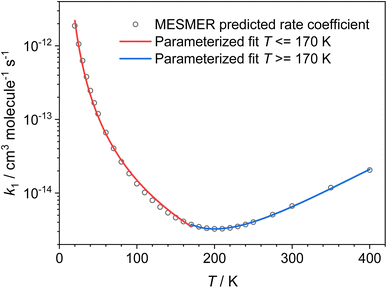 | ||
| Fig. 8 Low-pressure limiting rate coefficients for the reaction between NH2 + CH3CHO → NH3 + CH3CO (R1a) calculated by MESMER, using the PRC and TS energies determined by fitting to the experimental data (see text for details). | ||
These new rate coefficients will be submitted to the Kinetic Database for Astrochemistry (KIDA),46 and the UMIST Database for Astrochemistry (UdFA).47
4.3 Astrochemical implications
To assess the astrophysical implications of the measured rate constant, we ran a single-point dark cloud astrochemical model with a temperature of 10 K, a gas number density of 104 cm−3, and a cosmic-ray ionisation rate of 1.3 × 10−17 s−1. We assume that the cloud has a high visual extinction and is fully shielded from any external sources of UV radiation. We ran four variants of the model with different assumptions for the chemistry: (i) a gas-phase only model using the network from Walsh et al.48 with updates as described in Douglas et al.,15 (ii) a gas–grain model with the same chemistry, (iii) a gas-phase only model including the new reaction and rate constant measured in this work, and (iv) a gas–grain model including the same update. We find that the abundance of the reactants, NH2 and CH3CHO, and that of one of the products, NH3, are not significantly affected when the new reaction is included in the network. However, we do see a non-negligible effect on the gas-phase abundance of the radical, CH3CO, as shown in Fig. 9. In scenario (i), there are no efficient gas-phase routes to form this radical in the Walsh et al.48 network and its abundance is effectively zero. When gas–grain chemistry is included (scenario (ii); red solid line in Fig. 9), the abundance increases to ∼10−26 to 10−24 with respect to H nuclei density; however, this range is still considered negligible. In this gas–grain model, the only source of gas-phase CH3CO is via cosmic-ray-induced photodesorption from the ice phase. Radicals such as CH3CO are efficiently hydrogenated in the ice even at 10 K, and so have a very short life-time on the surface and hence reach a negligible gas-phase abundance only. When the new reaction studied here is included in the gas-phase only model (scenario (iii); blue dotted line in Fig. 9), the abundance of CH3CO increases from ∼10−20 to 10−18 with production driven solely by the included reaction. Finally, when gas–grain chemistry is included together with the new reaction studied here (scenario (iv); blue solid line in Fig. 9), the abundance of CH3CO increases further, to the arguably non-negligible range of 10−14 to 10−12 with respect to H nuclei density beyond a time of 106 years. This is driven by the more efficient production of gas-phase CH3CHO in the gas–grain model, for which the abundance is boosted by two orders of magnitude when grain-surface processes are included. The steady-state fractional abundance reached for gas-phase CH3CO (∼10−12) is approaching the threshold at which molecules become potentially observable in interstellar environments. For example, the methoxy radical, CH3O, has been observed towards several dense cores, with an estimated fractional abundance of ∼10−12 to 10−11 with respect to H nuclei density.49–51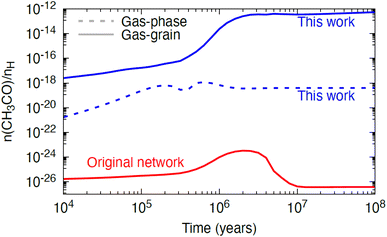 | ||
| Fig. 9 The abundance of gas-phase CH3CO with respect to hydrogen nuclei density as a function of time, a dark cloud model using three different variants of the chemical network from Walsh et al.48 with: one using the gas–grain network from Walsh et al.48 with the rate constants from Douglas et al.15 (red solid line), one using a gas-phase only network including the gas-phase reaction studied in this work (NH2 + CH3CHO; dotted blue line), and one using a gas–grain network including the reaction studied in this work (solid blue line). | ||
The model results for a dark cloud shown here, suggest that, whilst the NH2 + CH3CHO reaction is not a dominant loss mechanism for either reactant, nor a dominant production mechanism for NH3, it is a potential production route for the gas-phase radical, CH3CO, at least under dark cloud conditions. We leave exploration of the impact of this reaction on the chemistry in other astrophysical environments to future work. The gas-phase chemistry of organic radicals, such as CH3CO, remains poorly constrained. A search of KIDA,46 suggested only two gas-phase reactions forming this radical under astrophysical conditions (C2H3 + O and OH + H2C3O),52,53 and no gas-phase destruction reactions.
5. Conclusions
The reaction between NH2 and CH3CHO has been investigated experimentally over the temperature and pressure range 29–107 K and 1.4–28.2 × 1016 molecules per cm3, using a PLP-LIF technique. The low temperatures relevant to the ISM were achieved by a pulsed Laval nozzle expansion. Over the temperatures and pressures investigated, the reaction was shown to have a negative temperature dependence and a positive pressure dependence. Yields for the production of the CH3CO product from the reaction were determined at 67.1 and 35.0 K, by monitoring the production of OH from the reaction of CH3CO with O2. The full PES for the NH2 + CH3CHO system was determined using electronic structure calculations, and these combined with RRKM theory to obtain rate coefficients and branching ratios over a broad range of temperatures and pressures. The calculated rate coefficients have been shown to be sensitive to the inclusion of hindered rotor (HR) potentials in the rate theory calculations. In particular, the magnitude and shape of the HR potentials for the PRCs have been shown to have a strong effect on the calculated density of states of the PRCs, and as such the calculated rate coefficients are sensitive to this. Species time profiles produced by these calculations indicate that on the timescales of our experiments, the loss of NH2 we observe is primarily due to the formation of the PRCs, and in particular PRC2, which on timescales significantly longer than our experiments will go on to form products (both channels (R1a) and (R1b)). However, as observed in our experiments, some CH3CO is formed on the same timescale as NH2 is lost; this instant CH3CO can be thought of as the CH3CO produced from well-skipping, and is sensitive to the height of the acetyl H-abstraction transition state (TS1). The experimentally determined rate coefficients and yields have been used to fit the calculated PES, from which low-pressure liming rate coefficients relevant to the ISM have been determined. These low-pressure limiting rate coefficients have been included in a single point dark cloud astronomical model, in which the reaction is shown to be a potential source of CH3CO radicals under dark cloud conditions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for the Science and Technology Facilities Council (STFC) for funding of this work under grant number ST/T000287/1. CW further acknowledges financial support from UKRI research and innovation grant number MR/T040726/1.References
- E. Herbst and E. F. van Dishoeck, Complex Organic Interstellar Molecules, in Annual Review of Astronomy and Astrophysics, ed. R. Blandford, J. Kormendy and E. van Dishoeck, 2009, vol. 47, pp. 427–480 Search PubMed.
- B. A. McGuire, Astrophys. J. Suppl., 2022, 259, 30 CrossRef.
- A. I. Vasyunin and E. Herbst, Astrophys. J., 2013, 769, 34 CrossRef.
- S. A. Sandford, M. Nuevo, P. P. Bera and T. J. Lee, Chem. Rev., 2020, 120, 4616–4659 CrossRef CAS PubMed.
- K. Altwegg, H. Balsiger, A. Bar-Nun, J. J. Berthelier, A. Bieler, P. Bochsler, C. Briois, U. Calmonte, M. R. Combi and H. Cottin, et al. , Sci. Adv., 2016, 2, e1600285 CrossRef PubMed.
- R. Saladino, C. Crestini, S. Pino, G. Costanzo and E. Di Mauro, Phys. Life Rev., 2012, 9, 84–104 CrossRef PubMed.
- R. H. Rubin, G. W. Swenson, R. C. Benson, H. L. Tigelaar and W. H. Flygare, Astrophys. J., 1971, 169, L39 CrossRef CAS.
- J. M. Hollis, F. J. Lovas, A. J. Remijan, P. R. Jewell, V. V. Ilyushin and I. Kleiner, Astrophys. J., 2006, 643, L25–L28 CrossRef CAS.
- K. M. Douglas, D. I. Lucas, C. Walsh, N. A. West, M. A. Blitz and D. E. Heard, Astrophys. J., 2022, 937, L16 CrossRef.
- S. E. Taylor, A. Goddard, M. A. Blitz, P. A. Cleary and D. E. Heard, Phys. Chem. Chem. Phys., 2008, 10, 422–437 RSC.
- R. L. Caravan, R. J. Shannon, T. Lewis, M. A. Blitz and D. E. Heard, J. Phys. Chem. A, 2015, 119, 7130–7137 CrossRef CAS PubMed.
- J. C. Gomez Martin, R. L. Caravan, M. A. Blitz, D. E. Heard and J. M. C. Plane, J. Phys. Chem. A, 2014, 118, 2693–2701 CrossRef CAS PubMed.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745–749 CrossRef CAS PubMed.
- R. J. Shannon, R. L. Caravan, M. A. Blitz and D. E. Heard, Phys. Chem. Chem. Phys., 2014, 16, 3466–3478 RSC.
- K. Douglas, M. A. Blitz, W. H. Feng, D. E. Heard, J. M. C. Plane, E. Slater, K. Willacy and P. W. Seakins, Icarus, 2018, 303, 10–21 CrossRef CAS.
- K. M. Douglas, M. A. Blitz, W. Feng, D. E. Heard, J. M. C. Plane, H. Rashid and P. W. Seakins, Icarus, 2019, 321, 752–766 CrossRef CAS.
- N. A. West, T. J. Millar, M. Van de Sande, E. Rutter, M. A. Blitz, L. Decin and D. E. Heard, Astrophys. J., 2019, 885, 134 CrossRef CAS.
- S. Bull, I. Seregrennaja and P. Tsherbakora, Khim. Prom., 1963, 7, 507–509 Search PubMed.
- R. A. Copeland, D. R. Crosley and G. P. Smith, In laser-induced fluorescence spectroscopy of NCO and NH2 in atmospheric pressure flames, in Symposium (International) on Combustion, Elsevier, 1985, pp. 1195–1203 Search PubMed.
- V. M. Donnelly, A. P. Baronavski and J. R. McDonald, Chem. Phys., 1979, 43, 271–281 CrossRef CAS.
- K. Yamasaki, A. Watanabe, T. Kakuda, A. Itakura, H. Fukushima, M. Endo, C. Maruyama and I. Tokue, J. Phys. Chem. A, 2002, 106, 7728–7735 CrossRef CAS.
- P. Limão-Vieira, S. Eden, N. J. Mason and S. V. Hoffmann, Chem. Phys. Lett., 2003, 376, 737–747 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database, http://cccbdb.nist.gov/.
- R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581 CrossRef CAS.
- J. A. Pople, R. Krishnan, H. B. Schlegel and J. S. Binkley, Int. J. Quantum Chem., 1978, 14, 545–560 CrossRef CAS.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- K. H. Gericke, L. M. Torres and W. A. Guillory, J. Chem. Phys., 1984, 80, 6134–6140 CrossRef CAS.
- T.-X. Xiang, K.-H. Gericke, L. M. Torres and W. A. Guillory, Chem. Phys., 1986, 101, 157–163 CrossRef CAS.
- W. Hack, H. Kurzke, P. Rouveirolles and H. G. Wagner, Ber. Bunsen-Ges. Phys. Chem., 1986, 90, 1210–1219 CrossRef CAS.
- S. Blazquez, D. Gonzalez, E. M. Neeman, B. Ballesteros, M. Agundez, A. Canosa, J. Albaladejo, J. Cernicharo and E. Jimenez, Phys. Chem. Chem. Phys., 2020, 22, 20562–20572 RSC.
- D. H. Jaffer and I. W. M. Smith, Faraday Discuss. Chem. Soc., 1979, 67, 212–220 RSC.
- M. Quack and J. Troe, Ber. Bunsen-Ges. Phys. Chem., 1975, 79, 170–183 CrossRef CAS.
- R. A. Copeland, D. R. Crosley and G. P. Smith, Symp. (Int.) Combust., [Proc.], 1985, 20, 1195–1203 CrossRef.
- N. U. M. Howes, J. P. A. Lockhart, M. A. Blitz, S. A. Carr, M. T. Baeza-Romero, D. E. Heard, R. J. Shannon, P. W. Seakins and T. Varga, Phys. Chem. Chem. Phys., 2016, 18, 26423–26433 RSC.
- L. Onel, L. Thonger, M. A. Blitz, P. W. Seakins, A. J. C. Bunkan, M. Solimannejad and C. J. Nielsen, J. Phys. Chem. A, 2013, 117, 10736–10745 CrossRef CAS PubMed.
- V. Barone, C. Latouche, D. Skouteris, F. Vazart, N. Balucani, C. Ceccarelli and B. Lefloch, Mon. Not. R. Astron. Soc.: Lett., 2015, 453, L31–L35 CrossRef CAS.
- Q. S. Li and R. H. Lü, J. Phys. Chem. A, 2002, 106, 9446–9450 CrossRef CAS.
- L. Song and J. Kästner, Phys. Chem. Chem. Phys., 2016, 18, 29278–29285 RSC.
- F. Vazart, D. Calderini, C. Puzzarini, D. Skouteris and V. Barone, J. Chem. Theory Comput., 2016, 12, 5385–5397 CrossRef CAS PubMed.
- H. Keller-Rudek, G. K. Moortgat, R. Sander and R. Sörensen, Earth System Science Data, 2013, 5, 365–373 CrossRef.
- V. Wakelam, E. Herbst, J. C. Loison, I. W. M. Smith, V. Chandrasekaran, B. Pavone, N. G. Adams, M. C. Bacchus-Montabonel, A. Bergeat and K. Beroff, et al. , Astrophys. J. Suppl., 2012, 199, 21 CrossRef.
- D. McElroy, C. Walsh, A. J. Markwick, M. A. Cordiner, K. Smith and T. J. Millar, Astron. Astrophys., 2013, 550, A36 CrossRef.
- C. Walsh, H. Nomura and E. van Dishoeck, Astron. Astrophys., 2015, 582, A88 CrossRef.
- J. Cernicharo, N. Marcelino, E. Roueff, M. Gerin, A. Jiménez-Escobar and G. M. Muñoz Caro, Astrophys. J., 2012, 759, L43 CrossRef.
- I. Jiménez-Serra, A. I. Vasyunin, P. Caselli, N. Marcelino, N. Billot, S. Viti, L. Testi, C. Vastel, B. Lefloch and R. Bachiller, Astrophys. J., 2016, 830, L6 CrossRef.
- A. Megías, I. Jiménez-Serra, J. Martín-Pintado, A. I. Vasyunin, S. Spezzano, P. Caselli, G. Cosentino and S. Viti, Mon. Not. R. Astron. Soc., 2022, 519, 1601–1617 CrossRef.
- J.-C. Loison, M. Agúndez, N. Marcelino, V. Wakelam, K. M. Hickson, J. Cernicharo, M. Gerin, E. Roueff and M. Guélin, Mon. Not. R. Astron. Soc., 2016, 456, 4101–4110 CrossRef CAS PubMed.
- J.-C. Loison, M. Agúndez, V. Wakelam, E. Roueff, P. Gratier, N. Marcelino, D. N. Reyes, J. Cernicharo and M. Gerin, Mon. Not. R. Astron. Soc., 2017, 470, 4075–4088 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00046j |
| This journal is © The Royal Society of Chemistry 2023 |