Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Noncovalent bonding assessment by pair distribution function†
Lucy K.
Saunders
 ,
Daniel
Irving
,
Daniel
Irving
 ,
Philip A.
Chater
,
Philip A.
Chater
 and
Maria
Diaz-Lopez
and
Maria
Diaz-Lopez
 *
*
Diamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot OX11 0DE, UK. E-mail: maria.diaz-lopez@neel.cnrs.fr
First published on 11th January 2023
Abstract
Noncovalent interactions are essential in the formation and properties of a diverse range of materials. However, reliably identifying noncovalent interactions remains challenging using conventional methods such as X-ray diffraction, especially in nanocrystalline, poorly crystalline or amorphous materials which lack long-range lattice periodicity. Here, we demonstrate the accurate determination of deviations in the local structure and tilting of aromatic rings during the temperature-induced first order structural transition in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct of 4,4′-bipyridinium squarate (BIPY:SQA) from the low temperature form HAZFAP01 to high temperature HAZFAP07 by X-ray pair distribution function. This work demonstrates how pair distribution function analyses can improve our understanding of local structural deviations resulting from noncovalent bonds and guide the development of novel functional materials.
1 adduct of 4,4′-bipyridinium squarate (BIPY:SQA) from the low temperature form HAZFAP01 to high temperature HAZFAP07 by X-ray pair distribution function. This work demonstrates how pair distribution function analyses can improve our understanding of local structural deviations resulting from noncovalent bonds and guide the development of novel functional materials.
1. Introduction
Although noncovalent interactions including hydrogen-bonding, π–π stacking, electrostatic interactions, and van der Waals interactions are weak compared to covalent bonding, they play a vital role in the formation, physical properties and chemical processes of functional materials.1–10 Noncovalent interactions have been utilized in the development of functional materials,11–13 for tailoring crystallization,14–16 and the study of host–guest interactions.17–19 Reliably identifying noncovalent interactions is crucial in the understanding and development of novel functional materials. This article studies the noncovalent interactions in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct of 4,4′-bipyridinium squarate (BIPY:SQA) as a function of temperature by diffraction methods. BIPY:SQA exhibits colour-change properties as a function of external stimuli, thus presenting potential as a multi-mode sensor.20,21 We note that other techniques such as nuclear magnetic resonance (NMR), infrared, ultraviolet-visible, and Raman spectroscopies are used to characterize noncovalent interactions. However, these techniques are limited by the spatial resolution, and signal-to-noise ratio of the spectra. The results can therefore be ambiguous, and typically noncovalent interactions can only be partially resolved even when different spectroscopy techniques are combined.
1 adduct of 4,4′-bipyridinium squarate (BIPY:SQA) as a function of temperature by diffraction methods. BIPY:SQA exhibits colour-change properties as a function of external stimuli, thus presenting potential as a multi-mode sensor.20,21 We note that other techniques such as nuclear magnetic resonance (NMR), infrared, ultraviolet-visible, and Raman spectroscopies are used to characterize noncovalent interactions. However, these techniques are limited by the spatial resolution, and signal-to-noise ratio of the spectra. The results can therefore be ambiguous, and typically noncovalent interactions can only be partially resolved even when different spectroscopy techniques are combined.
This article will focus on Bragg and Pair Distribution Function (PDF) methods and introduce the strengths and limitations of these methods in the determination of non-covalent interactions.
1.1. How we detect non-covalent bonds with X-ray crystallography
Single-crystal diffraction data can reveal a wealth of atomic-level structural information. The experiment yields a 3D map of electron density from which the atomic positions and crystal structure are determined. Once a structure is obtained, non-covalent interaction between molecules can then be identified either by considering molecular geometry alongside van der Waals radii of neighbouring atoms or detected in the electron density map and its derivatives, either obtained following a charge density analysis of the diffraction data22,23 or from quantum mechanical calculations on the determined crystal structure.24–26There has been a continual push to study ever smaller crystals at ever higher resolution. Synchrotron facilities offer tunable, high intensity focused X-ray sources which are often coupled with fast, sensitive detectors. Laboratory instrumentation has advanced significantly in recent years, notably via microsource X-ray tubes and CCD or solid-state detectors. In spite of significant advances, X-ray single crystal diffraction of the quality required to resolve subtle features requires relatively large (>5 × 5 × 5 μm3) and well-ordered crystals, and the size required for neutron single crystal diffraction is often orders of magnitude larger.
Growing large crystals suitable for single crystal diffraction can be challenging and time-consuming. A significant quantity of pure material is required, and it may be necessary to test a wide range of conditions before a suitable set is found, potentially resulting in an expensive undertaking. These factors can complicate, or even prohibit structure determination by single crystal diffraction. In the area of pharmaceuticals, where intermolecular interactions play a significant role, there is an increasing trend towards exploiting active pharmaceutical ingredients that do not form well-ordered single crystals as these tend to have greater solubility and therefore bioavailability.
Alternatively, powder diffraction can be used to gain structural insights from powdered (microcrystalline) samples where larger crystals are not available. However, structure determination from powder data is considerably more challenging and typically limited to small lattices, as peak overlap in the one-dimensional pattern makes structure determination difficult. Fortunately, structure determination has advanced considerably through the development of the direct-space strategy for structure solution.27 Nonetheless, the noncovalent interactions resolved from powder diffraction data are often ambiguous, owing to the large number of symmetry restraints that are often required in structure refinement.
Neutrons can be more advantageous than X-ray diffraction methods to accurately locate hydrogen positions. Naturally abundant hydrogen has a detrimentally large incoherent scattering that is typically avoided by deuteration prior to neutron diffraction experiments. However, deuterated samples oftentimes have a different performance28,29 (and significantly higher cost) than their hydrogenated counterparts which can pose a significant added challenge to these experiments.
1.2. Assessment of noncovalent interactions by PDF
Traditional crystallography relies on the periodicity of the lattice and is insensitive to subtle changes of the local structure that could entail interesting changes in the properties of materials, even when there is no change in the periodicity of the lattice (i.e., the average structure). Alternatively, we could recover the information on the local structure embedded in the diffuse scattering of polycrystalline materials, disregarded in conventional crystallography, by total scattering (the combined analysis of diffuse and Bragg scattering).The Fourier transform of total scattering data gives the pair distribution function or PDF, which is the only probe sensitive to all length scales from local- to meso- to long-range ordering that can provide bulk average information on the atomic positions with high accuracy.30
Total scattering is defined in terms of correlation functions and several definitions of these functions exist which have been covered in ref. 31. The G(r) function yields the probability of finding a pair of atoms separated by a distance r:
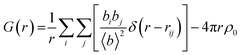 | (1) |
Experimentally, the PDF can be calculated by the Fourier transformation of the normalized coherent scattering or S(Q) as:
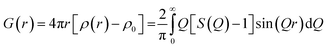 | (2) |
Whilst treating the data in this manner, the whole diffraction pattern including both Bragg reflections and diffuse scattering is used to obtain G(r). Note that S(Q) can only be measured over a finite Q-range and the integration of G(r) is over 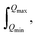 leading to the formation of termination ripples with a wavelength of ∼2π/Qmax in the Fourier transform. If experimentally accessible, Qmax is adjusted to a value where the distinct scattering signal has disappeared. Since the signal in S(Q) dies off due to thermal and static disorder, total scattering data is ideally measured up to a Qmax greater than 3/〈〈u2〉〉1/2, where 〈u2〉 is the atomic mean square displacement. X-ray PDF data of organic samples are typically processed with a Qmax of around 20 Å−1, even when higher Qmax are experimentally accessible, due to the damping of the form factor with increasing Q which is especially pronounced for lighter elements. The PDFs of neutron data having Q-independent scattering lengths can be processed to higher Qmax of around 40 Å−1.
leading to the formation of termination ripples with a wavelength of ∼2π/Qmax in the Fourier transform. If experimentally accessible, Qmax is adjusted to a value where the distinct scattering signal has disappeared. Since the signal in S(Q) dies off due to thermal and static disorder, total scattering data is ideally measured up to a Qmax greater than 3/〈〈u2〉〉1/2, where 〈u2〉 is the atomic mean square displacement. X-ray PDF data of organic samples are typically processed with a Qmax of around 20 Å−1, even when higher Qmax are experimentally accessible, due to the damping of the form factor with increasing Q which is especially pronounced for lighter elements. The PDFs of neutron data having Q-independent scattering lengths can be processed to higher Qmax of around 40 Å−1.
In order to obtain the S(Q) from an as-collected diffraction pattern, all of the incoherent and inelastic contributions (Compton, fluorescence in the case of X-rays, Placzcek scattering in the case of neutrons) as well as the signals which do not derive from the sample (sample holder(s), air scattering, etc.) need to be removed. These corrections are performed through a combination of subtraction of additional background measurements (empty sample holder, etc.), and computation of other contributions from the sample or ad hoc corrections to account for these, and user-friendly programs are available which can calculate the PDF from experimental data. Some of the most routinely used software for obtaining PDFs are GudrunN32 and PDFGetN33 for neutron scattering data and GudrunX and PDFgetX3 (ref. 34) for X-ray scattering data.
The general approach to obtaining a powder diffraction pattern suitable for PDF analysis consists of using high-energy monochromatic radiation over a wide Q range (to access high Qmax) with high counting statistics and maintaining a constant and low background to facilitate the data corrections. Due to the decrease in the scattering intensity with increasing Q, especially in X-rays, sufficiently high counting statistics at high Q-values need to be collected to avoid random noise at high Q that will give rise to artefacts in the derived PDF.
Most PDF studies in the literature deal with inorganic materials. However, more recently, the number of organic materials investigated by PDF has rapidly risen, driven by the growing interest of the pharmaceutical industry in amorphous formulations with higher bioavailability than the crystalline versions.35 Noncovalent interactions can be more readily understood from the analysis of the distribution of distances in true atomistic models of the local structure.36,37 Recent PDF investigations have demonstrated quantitative and structural investigations even on amorphous and nanostructured organic materials,38,39 and have been able to identify pre-crystallisation products.40 New methodology has even enabled local-structure solution of organic compounds from scratch by a fit to PDF data, without prior knowledge of lattice parameters and space group.41
PDF analyses of powdered samples allowed us to indirectly infer the presence and change of H-bond connectivity. Although H-bonds cannot be directly observed from the X-ray data, the presence of H-bonds results in different tilts and rotation of the carbon rings that give rise to differences in the meso-structures that can be identified by PDF. With a judicious set of structural constraints and restraints, the presence of H-bonds can be inferred and characterised.
2. Experimental
2.1. Synthesis
A crystalline sample of BIPY:SQA was prepared by dissolving separately equimolar (2.5 mmol) quantities of each component in minimum volumes of H2O whilst stirring and heating to 60 °C. The solutions were mixed and left to crystallise on cooling to room temperature. Yellow ochre needles of BIPY:SQA were formed in solution after 24 hours and were extracted and dried using Buchner funnel vacuum filtration. The precipitate was ground to a powder and loaded into a 1 mm diameter Kapton capillary for X-ray PDF (XPDF) measurements.2.2. Data acquisition
Total scattering measurements were performed on the I15-1 XPDF beamline at the Diamond Light Source (UK) using high energy X-rays with a wavelength of 0.189578 Å. The BIPY:SQA powdered samples were prepared in Kapton capillaries, and measurements of the empty capillaries were used as background contributions during XPDF calculations.The 300–500 K data collections were carried out using two PerkinElmer detectors; one at ∼20 cm from the sample for XPDF data collections and one at ∼80 cm for Bragg data collections. The data collections took approximately 15 min at each temperature.
The relative geometry of the capillaries and the detectors was calibrated with Si standards and the collected 2D data was processed into 1D diffraction patterns using the DAWN software.42
2.3. Data processing and analysis
Total scattering data was corrected and normalized with the GudrunX software43 using a Qmax of 20 Å−1. Combined Rietveld and XPDF refinements were performed using the TOPAS software.44 The Bragg data of the XPDF detector was jointly refined with XPDF data using a single instrumental resolution function for both data sets.45 Standard uncertainties in atomic positions were estimated by the bootstrap method as implemented in TOPAS.462.4. Structural refinement
The experimental Bragg and XPDF data were jointly fitted using the TOPAS software (TOPAS Academic Version 6)44 using the published crystallographic models as a starting point.Each peak in the PDF represents an atom–atom distance and they have a width which is determined from sample contributions based on the relative thermal motion of the atom–atom pair and displacements of atoms from their average position, as well as instrumental/processing effects such as from the finite Q range that is used in the Fourier transform. The peaks at low r are systematically sharper than the peaks in the high-r regions due to the correlated motion of atoms. In molecular compounds, the width of the PDF peaks is vastly different for pairs of atoms in the same molecule bonded by strong and rigid covalent bonds versus atoms located in two different molecules held by less strong electrostatic interactions, H-bonds or even by only van der Waals interactions. This discrepancy in peak widths from inter- and intra-molecular distances presents a special challenge when modelling the PDF data from molecular solids over a wide range of r.
In this work, an r-dependent peak width method was used to fit the short (rcut), medium (rlo) and long r-range in the XPDF, accounting for only intra-molecular, both intra- and inter-molecular and only inter-molecular distances, and the PDF of a sphere was used to scale between the thermal parameter values refined for the medium and high r for uncorrelated atomic motions as implemented in the ‘beq_rcut_rlo_spherical’ macro in Topas v6 and v7.44,45 To decrease the number of refined parameters, the thermal parameters in the rcut region and the radius of the sphere were constrained to be the same for all atoms.
The starting models for the BIPY:SQA system were taken from crystal structures deposited in the Cambridge Structural Database47 with reference codes HAZFAP01 and HAZFAP07 and are the reported low- and high-temperature phases, respectively, for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 system.20,48 The CSD was additionally mined to obtain expected ranges for certain 4,4′-bipyridine and squaric acid parameters which were then used as limits in the BIPY:SQA refinements. The search criteria included crystal structures containing either mono- or di-protonated 4,4′-bipyridine molecules and mono- or di-anions of squaric acid molecules. Search parameters included all bond distances, ring or square centroid to atom distances for the BIPY and SQA molecules, respectively, and ∠CCCC 4,4′-bipyridine ring torsion angles. The atomic coordinates of the pyridyl and squaric acid ligands were refined using rigid body constraints in order to minimise the number of refinable parameters, and a single set of isotropic thermal parameters was refined for the same atoms in a group. A total of six parameters were refined for each rigid body: three rotations + three translations. A total of seven thermal parameters were refined to model atomic correlated motions: one thermal parameter to fit the short r-range of intramolecular distances, two thermal parameters for each molecule to fit the medium r-range of both intra- and inter-molecular distances and four thermal parameters (one for each atom) to fit the long r-range accounting for only inter-molecular distances, and the Bragg data.
1 system.20,48 The CSD was additionally mined to obtain expected ranges for certain 4,4′-bipyridine and squaric acid parameters which were then used as limits in the BIPY:SQA refinements. The search criteria included crystal structures containing either mono- or di-protonated 4,4′-bipyridine molecules and mono- or di-anions of squaric acid molecules. Search parameters included all bond distances, ring or square centroid to atom distances for the BIPY and SQA molecules, respectively, and ∠CCCC 4,4′-bipyridine ring torsion angles. The atomic coordinates of the pyridyl and squaric acid ligands were refined using rigid body constraints in order to minimise the number of refinable parameters, and a single set of isotropic thermal parameters was refined for the same atoms in a group. A total of six parameters were refined for each rigid body: three rotations + three translations. A total of seven thermal parameters were refined to model atomic correlated motions: one thermal parameter to fit the short r-range of intramolecular distances, two thermal parameters for each molecule to fit the medium r-range of both intra- and inter-molecular distances and four thermal parameters (one for each atom) to fit the long r-range accounting for only inter-molecular distances, and the Bragg data.
3. Results and discussion
The slow evaporative crystallisation of 4,4′-bipyridine and squaric acid from aqueous solution forms yellow-ochre single crystals of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
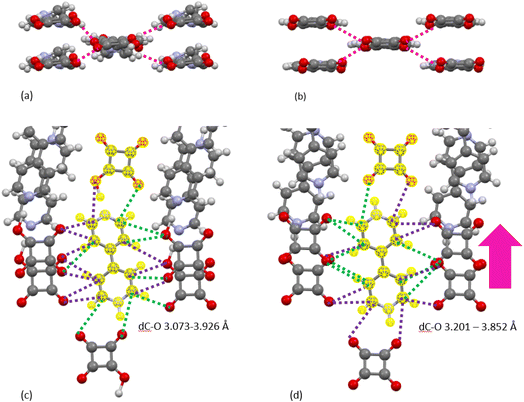
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct (BIPY:SQA) of the two components present in their monoprotonated forms and crystallised in space group P21/n (see Fig. 1).48 The crystal structure of BIPY:SQA is known to be sensitive to the external environment, exhibiting proton transfer events and structural transitions as a function of applied temperature and pressure20 and electric fields21 which are coupled to colour changes along the yellow-orange-red spectrum and have been determined using single crystal X-ray diffraction (SCXRD), powder X-ray and neutron diffraction, and optical and infrared spectroscopy.49
1 adduct (BIPY:SQA) of the two components present in their monoprotonated forms and crystallised in space group P21/n (see Fig. 1).48 The crystal structure of BIPY:SQA is known to be sensitive to the external environment, exhibiting proton transfer events and structural transitions as a function of applied temperature and pressure20 and electric fields21 which are coupled to colour changes along the yellow-orange-red spectrum and have been determined using single crystal X-ray diffraction (SCXRD), powder X-ray and neutron diffraction, and optical and infrared spectroscopy.49
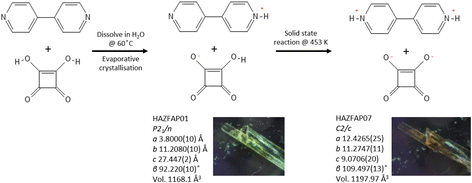 | ||
Fig. 1 Schematic showing the preparation of the BIPY:SQA 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct and its temperature dependent behaviour, undergoing a solid-state reaction at 453 K. 1 adduct and its temperature dependent behaviour, undergoing a solid-state reaction at 453 K. | ||
Here, we explore the temperature dependent behaviour of BIPY:SQA using XPDF. SCXRD measurements indicate a single-crystal to single-crystal first order transition on heating to 453 K, changing from structure HAZFAP01 (ref. 48) (The Cambridge Structural Data base (CSD)47 reference code) in space group P21/n to HAZFAP07 (ref. 20) in space group C2/c. Changes in unit cell volume (1168.1 Å3 to 1197.97 Å3) and molecular planarities (the co-planarity of the 4,4′-bipyridinium rings increases following a change in the ∠CCCC torsion angle from 22.65° to 0.25°) were also observed. The neutron powder diffraction study by Martins et al.20 found a higher transition temperature of above 488 K and additionally identified the transfer of the second acid proton during the transition to form a di-protonated 4,4′-bipyridinium.
XPDF measurements to observe the temperature dependent behaviour of BIPY:SQA were mapped along the heating profile at 300, 350, 400, 450, 470, 480, 490 and 500 K. A visual inspection of the PDF patterns at each temperature indicates the most significant change to be occurring between 470 and 480 K (see Fig. S1 and S2†).
Structural refinements against the XPDF data identify 480 K as the temperature at which the room temperature structure (CSD refcode HAZFAP01) no longer fits the data. Instead, the high temperature structure (HAZFAP07) achieves the better refinement. Compared with previous studies, we identify the transition temperature range to be higher than in the single crystal XRD study (occurring at ca. 453 K) and slightly lower than in the corresponding PXRD study (493 K). In the XPDF refinements, the 4,4′-bipyridinium ring ∠CCCC torsion angle reduces, from 28.2° to 0.0°, following the transition; this is in agreement with what has previously been found but with a slightly larger starting torsion angle of the BIPY rings (HAZFAP01 ∠CCCC 22.65°). A second protonation event of the BIPY molecule is also stable in the refinement. Structural refinements either side of the transition, i.e., between 300 and 470 K and between 480 K and 500 K show no significant structural changes, confirming the nature of the temperature induced phase transition to be first order, occurring in a one-step mechanism between 470 and 480 K.
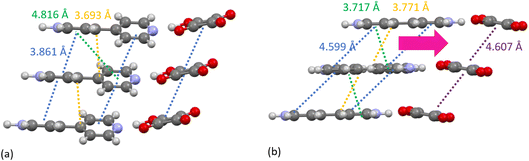
The temperature induced structural transition is most evident in the XPDF in the region of 3–5 Å, see Fig. 2. For molecular organic crystals such as those containing carbon, nitrogen, oxygen, sulphur and halides, 3–5 Å is the region most characteristic of weaker, but structurally important, non-covalent interactions, when considering the sum of the van der Waals radii of these atoms50 and molecular separation in π–π stacks.51–53 Breaking the XPDF down further into its partials, the most intense peaks in the 3 to 5 Å region are those corresponding to C–O (3–4 Å) and C–C atomic separations (3.5–5 Å). The peak for C–C distances redistributes, becoming less intense just below 4 Å and broadening above 4 Å. The opposite effect is seen for the C–O distances where the broad peak at 3–4 Å redistributes over a narrower range, becoming more intense at <3.5 Å and <3.9 Å.
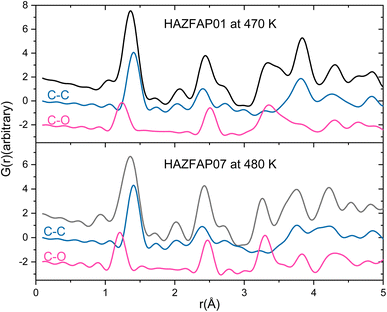 | ||
| Fig. 2 Simulated XPDF of BIPY:SQA models refined against PDF and Bragg data with C–C and C–O partials indicated at 470 K and 480 K. | ||
A specific contact search in CCDC Mercury™54 within a distance range of 3–4 Å between C and O atoms for the 470 K structure highlighted contacts between aromatic C–H groups and squarate oxygen atoms between molecules in the same and different molecular planes. These identified contacts equate to electrostatic weak C–H⋯O hydrogen bonding interactions.55 Using van der Waals criteria, only C–H⋯O interactions with C–O donor–acceptor distances of less than 3.22 Å would be classified as weak hydrogen bonds. However, longer C–O donor–acceptor distances (up to 4.0 Å) involving C–H donors and O atom acceptors are frequently included in the weak C–H⋯O hydrogen bond category and as such will also be considered here.55–58
It is worth noting that the hydrogen bond angle (∠CHO) is also found to be important in assessing weak C–H⋯O hydrogen bonds but as it requires accurate determination of H-atom positions, it is beyond the scope of this discussion.59
As seen in the XPDF, between 470 and 480 K, the partials for the C–O separations adjust and the broad range splits with the majority occupying a narrower distance range <3.5 Å with a few occupying longer separations at <3.9 Å. In the structures, the changes in C–O separations correspond to adjustments in space of the BIPY aromatic C–H groups relative to the squarate oxygen atoms. A shift in the position of the squarate molecules relative to the neighbouring BIPY molecule occurs, becoming more adjacent to a single BIPY ring at 480 K rather than straddling both BIPY rings, as is the case at 470 K. The BIPY rings also increase in co-planarity (∠CCCC torsion reduces to 0.0°), leading to a greater co-planarity with the local environment (see Fig. 3a and b) and a change in orientation of the aromatic C–H groups relative to the acid molecules. These two effects lead to a shortening of some weak C–H⋯O interactions, whilst lengthening others (see Fig. 3c and d, green and purple dashed lines). Overall, the C–O distance range narrows from 3.073–3.926 Å at 470 K to 3.201–3.852 Å at 480 K whilst there are a greater number of C–O distances in the region of 3.2–3.4 Å at 480 K, in agreement with the narrowing and increase in intensity of this region in the PDF. Examining the 470 and 480 K refined structures and considering weak C–H⋯O hydrogen bonds that fall within van der Waals criteria (dC⋯O < 3.22 Å), there is an overall elongation of these interactions over a narrower distance range from dC⋯O of 3.073–3.188 Å at 470 K to 3.196–3.201 Å at 480 K. This effect additionally contributes to the narrowing of the C–O partial at <3.5 Å. The observed adjustment in structure as a function of temperature may be a result of the change in charge of the BIPY aromatic rings following a second proton transfer event at 480 K to give two, overall, positively charged rings that will interact more similarly and attractively with the local environment.
A specific contact search in CCDC Mercury™54 within a distance range of 3.5 to 5 Å (as indicated by the C–C partials) between C atoms for the 470 K structure highlighted π–π contacts between molecules in BIPY:SQA stacks (Fig. 4a) and interatomic separations (C–C) between adjacent stacks. Following the temperature induced transition, 4,4′-bipyridine molecules become more planar whilst molecular overlap within both BIPY and SQA stacks decreases. The SQA molecules rotate (by 16°) whilst BIPY centroids shift from being overlapped in a head–head arrangement at 470 K to a head to tail arrangement at 480 K. This is as found previously and results in a shift of the C–C separations to longer distances, as observed in the C–C XPDF partials. Examining specific distances, the BIPY dC10⋯C7 increases from 3.693(6) Å at 470 K to 3.771(4) Å at 480 K whilst the SQA dC⋯C is dC1A⋯C2A 3.861(11) Å at 470 K versus dC1A⋯C1A 4.607(12) Å at 480 K.
Following the temperature induced structural transition and the second proton transfer event, the number of N⋯O hydrogen bonds reduces from two symmetry independent interactions of different types (N+–H⋯O−versus O–H⋯N) with differing N⋯O donor–acceptor distances (dN⋯O 2.551(7) Å and 2.702(10) Å) at 470 K to one symmetry independent N+–H⋯O− charge assisted hydrogen bond with a mid-range donor–acceptor distance of dN⋯O− 2.64(4) Å at 480 K. Reflecting this change, the N–O partial in the hydrogen bonding region of 2.5 to 3.0 Å becomes sharper within the region of 2.6 Å at 480 K (see Fig. S3†).
In the previous study by Martins et al.,20 they identified how the pattern of non-covalent intermolecular contacts was essentially unchanged following the phase transition. This is generally the case in the refined structures presented here, however, the XPDF data more clearly highlights the subtle differences in the non-covalent interactions as a function of temperature within this pattern. In the same study by Martins et al., theoretical plane wave basis set calculations showed that the second proton transfer event occurring with increasing temperature is strongly disfavoured in the gas phase and as such, in the solid-state, crystal packing and non-covalent interactions have an important compensating or facilitating role. In related proton disorder systems, intermolecular contacts around the disorder site appear to tune the extent of disorder occurring.60 The multi temperature XPDF measurements of BIPY:SQA clearly capture the intermolecular region compensating as the structure evolves with temperature, as observed in the 3 to 5 Å section of the pattern. XPDF analysis is therefore highlighted as a new, flexible and effective technique to probe the non-covalent interactions, which is able to quickly identify the length scale at which the structure is affected through comparison of data as well as providing complimentary structural data which is sensitive to local atomic arrangements.
4. Conclusions
In summary, we have used XPDF analysis to detect changes in the non-covalent interactions following a previously reported temperature-induced first order structural transition in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct of 4,4′-bipyridinium squarate from the low temperature form HAZFAP01 to high temperature HAZFAP07. This study was motivated by the knowledge that the transition is accompanied by changes in the inter-planar separation but where the overall pattern of non-covalent interactions is described as being maintained. A good fit to the XPDF data was obtained using published models as a starting point and implementing r-dependent thermal parameters to model more accurately the peak width evolution of intra-molecular and inter-molecular distances.
1 adduct of 4,4′-bipyridinium squarate from the low temperature form HAZFAP01 to high temperature HAZFAP07. This study was motivated by the knowledge that the transition is accompanied by changes in the inter-planar separation but where the overall pattern of non-covalent interactions is described as being maintained. A good fit to the XPDF data was obtained using published models as a starting point and implementing r-dependent thermal parameters to model more accurately the peak width evolution of intra-molecular and inter-molecular distances.
Through the XPDF analysis, we observe that the second protonation event of the 4,4′-bipyridinium, alongside an increase in molecular co-planarity which occurs during the temperature-induced transition, primarily affects the molecular interaction at atomic distances between 3 and 5 Å. Specific insight is found by considering the atomic partials where a narrower distribution of the C⋯O distances in the high temperature form corresponds to an adjustment in the non-covalent weak C–H⋯O hydrogen bonds following the increase in positive charge of the di-protonated 4,4′-bipyridinium molecule. Here we add to the knowledge that there are subtle differences within the overall pattern of non-covalent interactions following the structural transition.
The use of the XPDF technique has allowed us to probe more easily the non-covalent interactions, allowing us to quickly identify the length scale at which the structure is affected. This has implications for in situ studies for easy identification of material response to an external probe source. We envision that the in situ measurements of non-covalent interactions during crystallisation reactions are likely to become more common thanks to the planned improvements to synchrotron sources, detector technologies and sample environment design. One such development is a liquid flow cell which has been designed for the study of in situ crystallisation and synthesis experiments on the I15-1 beamline. The basis of this sample environment is using liquid pumps, to inject solutions into a capillary-type chamber where X-rays can penetrate and therefore scattering data can be acquired. Using such methodology allows the user to control the mixing, flow rates and ultimately the crystallisation under similar mixing conditions to those used in a laboratory. This will allow one to probe the prenucleation, nucleated and solidified structures all within one experiment. Observing the local structures of molecules as they crystallise will offer new insights into how non-covalent bonding impacts the crystallisation outcome.
Author contributions
We highlight joint first coauthorship of L. K. Saunders (LKS) and M. Diaz-Lopez (MDL) who had significant shared data curation and investigation roles with MDL taking the lead in conceptualisation of the study and writing the original draft and LKS for writing – review and editing. MDL and LKS are credited for formal analysis, methodology, validation and visualisation. Daniel Irving participated in the data acquisition and discussions in the in situ methodology. Philip A. Chater is credited for writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Diamond Light Source for access to beamline I15-1 (proposal cm31137-2).References
- M. Y. Jin, Q. Zhen, D. Xiao, G. Tao, X. Xing, P. Yu and C. Xu, Nat. Commun., 2022, 13, 3276 CrossRef CAS PubMed.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640 RSC.
- F. Hibbert and J. Emsley, Hydrogen Bonding and Chemical Reactivity, 1990, vol. 26 Search PubMed.
- X. Lucas, A. Bauzá, A. Frontera and D. Quiñonero, Chem. Sci., 2016, 7, 1038 RSC.
- L. E. Hatcher, E. J. Bigos, M. J. Bryant, E. M. MacCready, T. P. Robinson, L. K. Saunders, L. H. Thomas, C. M. Beavers, S. J. Teat, J. Christensen and P. R. Raithby, CrystEngComm, 2014, 16, 8263 RSC.
- N. Walshe, M. Crushell, J. Karpinska, A. Erxleben and P. McArdle, Cryst. Growth Des., 2015, 15, 3235 CrossRef CAS.
- S. P. Anthony, S. Varughese and S. M. Draper, Chem. Commun., 2009, 7500 RSC.
- M. C. Etter, M. Zia-Ebrahimi, Z. Urbañczyk-Lipkowska and T. W. Panunto, J. Am. Chem. Soc., 1990, 112, 8415 CrossRef CAS.
- S. Ghosh, A. Mondal, M. S. R. N. Kiran, U. Ramamurty and C. M. Reddy, Cryst. Growth Des., 2013, 13, 4435 CrossRef CAS.
- E. J. Carrington, S. F. Dodsworth, S. van Meurs, M. R. Warren and L. Brammer, Angew. Chem., Int. Ed., 2021, 60, 17920 CrossRef CAS PubMed.
- J. Zhou, S. Lin, H. Zeng, J. Liu, B. Li, Y. Xu, X. Zhao and G. Chen, Mater. Horiz., 2020, 7, 2936 RSC.
- M. J. Bryant, J. M. Skelton, L. E. Hatcher, C. Stubbs, E. Madrid, A. R. Pallipurath, L. H. Thomas, C. H. Woodall, J. Christensen, S. Fuertes, T. P. Robinson, C. M. Beavers, S. J. Teat, M. R. Warren, F. Pradaux-Caggiano, A. Walsh, F. Marken, D. R. Carbery, S. C. Parker, N. B. McKeown, R. Malpass-Evans, M. Carta and P. R. Raithby, Nat. Commun., 2017, 8, 1800 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and S. Ishibashi, Chem. Sci., 2018, 9, 425 RSC.
- M. K. Corpinot and D. K. Bučar, Cryst. Growth Des., 2019, 19, 1426 CrossRef CAS.
- A. R. Klapwijk, E. Simone, Z. K. Nagy and C. C. Wilson, Cryst. Growth Des., 2016, 16, 4349 CrossRef CAS.
- J. W. Li, S. H. Zhang, R. J. Gou, G. Han and M. H. Chen, J. Cryst. Growth, 2019, 507, 260 CrossRef CAS.
- H. Choi, Y. H. Oh, S. Park, S. S. Lee, H. Bin Oh and S. Lee, Sci. Rep., 2022, 12, 8169 CrossRef CAS PubMed.
- P. Kasprzycki, P. Kopycki, A. Listkowski, A. Gorski, C. Radzewicz, D. J. S. Birch, J. Waluk and P. Fita, Phys. Chem. Chem. Phys., 2020, 22, 17117 RSC.
- H. Wahl, D. A. Haynes and T. Le Roex, CrystEngComm, 2015, 17, 1549 RSC.
- D. M. S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall, R. M. Ibberson, K. Knight, S. Moggach, M. Brunelli and C. A. Morrison, J. Am. Chem. Soc., 2009, 131, 3884 CrossRef CAS PubMed.
- L. K. Saunders, H. H.-M. Yeung, M. R. Warren, P. Smith, S. Gurney, S. F. Dodsworth, I. J. Vitorica-Yrezabal, A. Wilcox, P. V. Hathaway, G. Preece, P. Roberts, S. A. Barnett and D. R. Allan, J. Appl. Crystallogr., 2021, 54, 1349 CrossRef CAS PubMed.
- M. Pyziak, J. Pyziak, M. Hoffmann and M. Kubicki, Cryst. Growth Des., 2015, 15, 5223 CrossRef CAS.
- A. Krawczuk and P. Macchi, Chem. Cent. J., 2014, 8, 68 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- R. Laplaza, F. Peccati, R. A. Boto, C. Quan, A. Carbone, J. P. Piquemal, Y. Maday and J. Contreras-García, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1497 CAS.
- A. J. Edwards, C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Faraday Discuss., 2017, 203, 93 RSC.
- B. M. Kariuki, H. Serrano-González, R. L. Johnston and K. D. M. Harris, Chem. Phys. Lett., 1997, 280, 189 CrossRef CAS.
- Z. Tun, R. J. Nelmes, W. F. Kuhs and R. F. D. Stansfield, J. Phys. C: Solid State Phys., 1988, 21, 245 CrossRef CAS.
- A. Franz, D. M. Többens, F. Lehmann, M. Kärgell and S. Schorr, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 267 CrossRef CAS PubMed.
- T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks, Structural Analysis of Complex Materials, Pergamon, 2012 Search PubMed.
- D. A. Keen, J. Appl. Crystallogr., 2001, 34, 172 CrossRef CAS.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714 CrossRef CAS.
- P. F. Peterson, M. Gutmann and T. Proffen, J. Appl. Crystallogr., 2000, 33, 1192 CrossRef CAS.
- P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560 CrossRef.
- A. Schittny, J. Huwyler and M. Puchkov, Drug Delivery, 2020, 27, 110 CrossRef CAS PubMed.
- M. W. Terban and S. J. L. Billinge, Chem. Rev., 2022, 122, 1208 CrossRef CAS PubMed.
- A. Pallipurath, B. Evans, A. Pugejs, P. A. Chater and S. L. M. Schroeder, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.12905840.v1.
- T. Davis, M. Johnson and S. J. L. Billinge, Cryst. Growth Des., 2013, 13, 4239 CrossRef CAS.
- S. J. L. Billinge, Pharm. Res., 2015, 10, 2473 CAS.
- M. W. Terban, E. Y. Cheung, P. Krolikowski and S. J. L. Billinge, Cryst. Growth Des., 2016, 16, 210 CrossRef CAS.
- C. Schlesinger, S. Habermehl and D. Prill, J. Appl. Crystallogr., 2021, 54, 776 CrossRef CAS PubMed.
- J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day, M. Drakopoulos, M. W. Gerring, M. L. Hart, O. V Magdysyuk, S. Michalik, A. Smith, C. C. Tang, N. J. Terrill, M. T. Wharmby and H. Wilhelm, J. Appl. Crystallogr., 2017, 50, 959 CrossRef CAS PubMed.
- A. K. Soper, GudrunN and GudrunX: Programs for Correcting Raw Neutron and X-Ray Total Scattering Data to Differential Cross Section, 2012 Search PubMed.
- A. A. Coelho, Topas-Academic, Version 6, 2016 Search PubMed.
- P. A. Chater, 2022, https://github.com/pachater/topas.
- B. Efron and R. Tibshirani, Stat. Sci., 1986, 1, 54 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- M. T. Reetz, S. Höger and K. Harms, Angew. Chem., Int. Ed. Engl., 1994, 33, 181 CrossRef.
- Z. Ma, J. Li, C. Liu, C. Sun and M. Zhou, Sci. Rep., 2017, 7, 4677 CrossRef PubMed.
- S. Alvarez, Inorg. Mater., 2014, 37, 871 Search PubMed.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191 RSC.
- L. Krivosudský and E. Rakovsky, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, m267 CrossRef PubMed.
- J. C. Hargis, E. Vöhringer-Martinez, H. L. Woodcock, A. Toro-Labbé and H. F. Schaefer, J. Phys. Chem. A, 2011, 115, 2650 CrossRef CAS PubMed.
- C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226 CrossRef CAS PubMed.
- G. R. Desiraju, Nature, 1962, 195, 68 CrossRef.
- T. Steiner, Crystallogr. Rev., 2003, 9, 177 CrossRef CAS.
- P. R. Mallinson, K. Woźniak, C. T. Smith and K. L. McCormack, J. Am. Chem. Soc., 1997, 119, 11502 CrossRef CAS.
- U. Koch, P. L. A. Popelier, L. Road and C. Cb, J. Phys. Chem., 1995, 99, 9747 CrossRef CAS.
- D. Z. Veljković, G. V. Janjić and S. D. Zarić, CrystEngComm, 2011, 13, 5005 RSC.
- A. O. F. Jones, N. Blagden, G. J. McIntyre, A. Parkin, C. C. Seaton, L. H. Thomas and C. C. Wilson, Cryst. Growth Des., 2013, 13, 497 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2fd00159d |
| This journal is © The Royal Society of Chemistry 2023 |