Compositional influence of local and long-range polarity in the frustrated pyrochlore system Bi2−xRExTi2O7 (RE = Y3+,Ho3+)†
Owen
Bailey
a,
Samra
Husremovic
a,
Madison
Murphy
a,
Jason
Ross
a,
Joyce
Gong
a,
Daniel
Olds
 b and
Geneva
Laurita
b and
Geneva
Laurita
 *a
*a
aBates College Department of Chemistry and Biochemistry, Bates College, Lewiston, ME, USA. E-mail: glaurita@bates.edu
bNational Synchrotron Light Source-II, Brookhaven National Laboratory, Upton, NY, USA
First published on 31st May 2022
Abstract
Structural distortions such as cation off-centering are frustrated in the pyrochlore structure due to the triangular arrangement of cations on the pyrochlore lattice. This geometric constraint inhibits a transition from a paraelectric to a ferroelectric phase in the majority of pyrochlore oxide materials. Few pyrochlore materials can overcome this frustration and exhibit polar crystal structures, and unraveling the origin of such leads to the understanding of polarity in complex materials. Herein we hypothesize that frustration on the pyrochlore lattice can be relieved through A-site doping with rare earth cations that do not possess stereochemically active lone pairs. To assess if frustration is relieved, we have analyzed cation off-centering in various Bi2−xRExTi2O7 (RE = Y, Ho) pyrochlores through neutron and X-ray total scattering. Motivated by known distortions from the pyrochlore literature, we present our findings that most samples show local distortions similar to the β-cristobalite structure. We additionally comment on the complexity of factors that play a role in the structural behavior, including cation size, bond valence, electronic structure, and magnetoelectric interactions. We posit that the addition of magnetic cations on the pyrochlore lattice may play a role in an extension of the real-space correlation length of electric dipoles in the Bi-Ho series, and offer considerations for driving long-range polarity on the pyrochlore lattice.
1 Introduction
The study of polar materials for electronic applications has been dominated by oxides that crystallize in the perovskite structure.1 Oxides with this structure demonstrate high temperature stability, ease of preparation, and versatility of chemical substitution on the cation sites. Literature on the perovskite structure is vast and mechanisms that control its polarity are well understood;2–4 as such, it is also understood that the most efficient and highest performing perovskites are lead (Pb)-based, due to the Pb cation's lone pair stereochemical activity, which often enhances the second order Jahn–Teller (SOJT) activity of other cations in the system.5 Pb-based perovskite structures are currently found in many electronic devices for a variety of applications that are ubiquitous throughout many fields, from electronics to medical fields to military applications.6 This presents a clear problem through Pb's known toxicity and subsequent regulations,7,8 guiding motivation for a new class of lead-free materials with similar or better efficiencies than the highest performing perovskites available.The pyrochlore structure A2B2O7 is importantly similar to the perovskite structure in its high diversity of possible cation substitutes, ease of preparation, and high temperature stability.9 This structure plays a role in properties of wide variety, including superconductivity,10 metal-to-insulator transitions,11,12 and ferroelectricity.13–19 As such, study into Pb-free pyrochlores may provide alternate materials for similar applications as the Pb-based perovskites, allowing for the phase-out of Pb-containing components.
Similar to the perovskite structure, the pyrochlore structure has two types of cations, defined as A and B. However, the more complex pyrochlore structure has two crystallographically distinct oxygen sites, and the formula is often written as A2B2O6O’ to indicate this. The structure consists of two interpenetrating corner-shared metal oxide networks of A2O’ chains and B2O6 corner-shared octahedra.9 Due to the three-dimensional triangular lattice of the interpenetrating cation networks, geometric frustration occurs with cation off-centering and electrical dipoles are unable to align coherently over long length scales. While this behavior is desirable for high dielectric constant materials,20 the lack of correlated displacements prevents piezo- or ferroelectric behavior. Combined SOJT distortion effects between the A-site s2 and B-site d0 cations play an important role in the long-range polarity in perovskites materials, and would suggest this might lead to long range polarity in pyrochlores, but geometric frustration tends to dominate and the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure is often maintained crystallographically down to low temperatures.
m structure is often maintained crystallographically down to low temperatures.
The arrangement of cations on the triangular pyrochlore lattice leads to a wealth of interesting physical phenomena influenced by geometric frustration. Coherent off-centering of the A-site cation can be frustrated on the rigid pyrochlore lattice, preventing the ferroelectric-paraelectric phase transition in the majority of pyrochlore oxide materials. A few pyrochlore materials overcome this frustration and exhibit ferroelectricity, such as the highly studied Cd2Nb2O7 and related compounds,21–23 Ho2Ti2O7,24 and epitaxially strained La2Zr2O7.17 While there are only a few examples of crystallographically polar pyrochlores, there are many stable compositions that have cations which possess the electronic configurations necessary to promote structural distortions. Therefore, it is crucial to study these materials on a local and crystallographic scale to assess the existence of local distortions, which can then be further probed in an effort to realize long-range polarity.
Bi2Ti2O7 in particular holds high promise for long range polarity, as it is chemically analogous to the prototypical ferroelectric perovskite PbTiO3, containing both lone pair- and SOJT-active cations. Additionally, DFT calculations indicate that there are lattice instabilities present in this structure that are consistent with a ferroelectric ground state, and the reason it exhibits as a frustrated structure is the propensity for disorder on the pyrochlore lattice.25 In the ideal pyrochlore structure the A-site cation is found on the fixed 16c Wyckoff site; however, in Bi2Ti2O7, studies find that the Bi cation is statically off-centered towards the TiO6 octahedra into one of the variable 96-fold Wyckoff sites.26–30 Due to the aforementioned geometric frustration, cation off-centering leads to a charge-ice arrangement at lower temperatures instead of a coherent, polar phase.31 Thus, the triangular octahedral arrangement of the lone pair cation A = Bi3+ inhibits the material from achieving long-range polarity.
In an attempt to alleviate geometric frustration and achieve long-range polarity, herein we study the intricacies of the pyrochlore structure through stoichiometric substitution of rare earth cations onto the A-site of Bi2Ti2O7. Smaller rare earth cations like yttrium and holmium are appropriate substitutions, as they have no associated lone pair and crystallize in the pyrochlore structure when B = Ti4+.32,33 To approach our question, we have analyzed the local structure and the correlation length of cation off-centering in the substituted pyrochlores Bi2−xRExTi2O7 (RE = Y3+ and Ho3+) through neutron and X-ray total scattering to assess the local and average cation off-centering over various length scales. We find that all pyrochlores studied herein are locally distorted beyond the cubic crystallographic structure, and the correlation length is the longest in the sample with the smallest Ho3+ substitution. This work contributes towards our understanding of the origin of structural distortions in pyrochlore materials, which steps us closer to being able to induce polarity in this promising class of materials.
2 Experimental
2.1 Sample preparation and characterization
All samples were prepared by direct reaction of relevant oxide powders (Bi2O3, 99.999%, Alfa Aesar; TiO2, 99.995%, Alfa Aesar; Y2O3, 99.995%, Alfa Aesar; Ho2O3, 99.995%, STREM Chemicals). Powders were ground with a mortar and pestle, pressed into pellets, and placed in alumina crucibles. All samples were heated at 600 °C to prevent volatilization of bismuth, then heated for 72 hours to final temperatures between 1050–1200 °C. Samples with higher bismuth content were heated to the lower temperatures, while samples with less or no bismuth content were heated to the higher temperatures, and details on the heating for each sample can be found in the ESI.† Samples were reground and re-pressed between any subsequent heatings.Initial sample characterization was performed at Bates College with a Rigaku Miniflex-II to verify phase purity. Samples were further characterized by high resolution synchrotron powder X-ray scattering data obtained from the 11-BM-B beamline at Argonne National Laboratory's Advanced Photon Source (λ = 0.412682 Å) and the Pair-Distribution Function (PDF) beamline at the National Synchrotron Light Source II (NSLS-II) (λ = 0.1671 Å). Powders were loaded into kapton capillaries for X-ray scattering experiments. Powder neutron scattering data were collected from the Spallation Neutron Source's NOMAD diffractometer at Oak Ridge National Laboratory. Powders were loaded into vanadium cans, with data collected at 2 K and 300 K. The reciprocal-space data were analyzed using the Rietveld method through GSAS II.34 X-ray PDF data were obtained using the program PDFgetX335 with a Qmax = 22 Å−1. Neutron PDF data were obtained utilizing the Mantid software framework36,37 with a Qmax between 29 and 31.4 Å−1. Qmax values were chosen to balance between resolution and termination ripples in the reduced data for each sample. Least-squares refinement of PDF data was performed using PDFGUI.38 Crystal structures were visualized using the VESTA software suite.39 Conversions between the high-symmetry Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and low-symmetry subgroups were performed using the Bilbao Crystallographic Server.40–42
m and low-symmetry subgroups were performed using the Bilbao Crystallographic Server.40–42
3 Results
Previous crystallographic analysis on the stoichiometric end members Y2Ti2O7,43 Bi2Ti2O7,44 and Ho2Ti2O724 indicate the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at room temperature. After successfully synthesizing compounds in the Bi2−xRExTi2O7 (RE = Y3+ [x = 0.5, 1.0, and 2.0], Ho3+ [x = 0.5, 1.5, and 2.0]) series, average structural analysis against neutron and X-ray scattering indicates the Fd
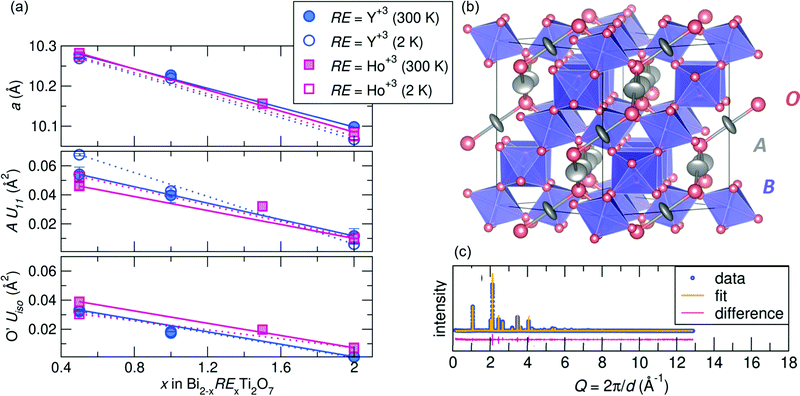
m structure at room temperature. After successfully synthesizing compounds in the Bi2−xRExTi2O7 (RE = Y3+ [x = 0.5, 1.0, and 2.0], Ho3+ [x = 0.5, 1.5, and 2.0]) series, average structural analysis against neutron and X-ray scattering indicates the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure is a good description of the data at room temperature and 2 K, with Rw values at or less than 10% for all samples. A summary of the refined variables from the joint neutron and X-ray Rietveld analysis can be found in the ESI† Tables S1 and S2. As illustrated in Fig. 1a top panel, the samples all follow a linear decreasing trend with rare earth substitution. This follows Vegard's Law and given the ionic radii of each cation (Bi3+ =1.17 Å, Y3+ = 1.019 Å, and Ho3+ =1.015 Å in an 8-coordinate site45,46) indicates a solid solution can be formed between the various end members. Various site occupancy refinements were attempted, and there was no evidence of bismuth deficiency or antisite defects of Ti on the A-site. The refinements indicated for all samples that the A-site cation is best modeled with anisotropic atomic displacement parameters (ADPs, modeled as Uani or Uiso), and the U11 term increases with increasing bismuth content (Fig. 1a middle panel). Elevated ADPs on the A-site were accompanied by elevated isotropic ADPs on the O' site (Fig. 1a bottom panel). An attempt to model the O' ADPs anisotropically was conducted, but the refined values remained isotropic. The shape of the displacement ellipsoids can be found in Fig. 1b, illustrating the pancake-like displacements of the A-site cation perpendicular to the A–O' bond. Enlarged ADPs on both the A and O' site indicate a large amount of structural disorder in the form of atomic off-centering from the ideal site, and because these enlarged values persist at low temperatures, the disorder is likely static rather than dynamic.
m structure is a good description of the data at room temperature and 2 K, with Rw values at or less than 10% for all samples. A summary of the refined variables from the joint neutron and X-ray Rietveld analysis can be found in the ESI† Tables S1 and S2. As illustrated in Fig. 1a top panel, the samples all follow a linear decreasing trend with rare earth substitution. This follows Vegard's Law and given the ionic radii of each cation (Bi3+ =1.17 Å, Y3+ = 1.019 Å, and Ho3+ =1.015 Å in an 8-coordinate site45,46) indicates a solid solution can be formed between the various end members. Various site occupancy refinements were attempted, and there was no evidence of bismuth deficiency or antisite defects of Ti on the A-site. The refinements indicated for all samples that the A-site cation is best modeled with anisotropic atomic displacement parameters (ADPs, modeled as Uani or Uiso), and the U11 term increases with increasing bismuth content (Fig. 1a middle panel). Elevated ADPs on the A-site were accompanied by elevated isotropic ADPs on the O' site (Fig. 1a bottom panel). An attempt to model the O' ADPs anisotropically was conducted, but the refined values remained isotropic. The shape of the displacement ellipsoids can be found in Fig. 1b, illustrating the pancake-like displacements of the A-site cation perpendicular to the A–O' bond. Enlarged ADPs on both the A and O' site indicate a large amount of structural disorder in the form of atomic off-centering from the ideal site, and because these enlarged values persist at low temperatures, the disorder is likely static rather than dynamic.
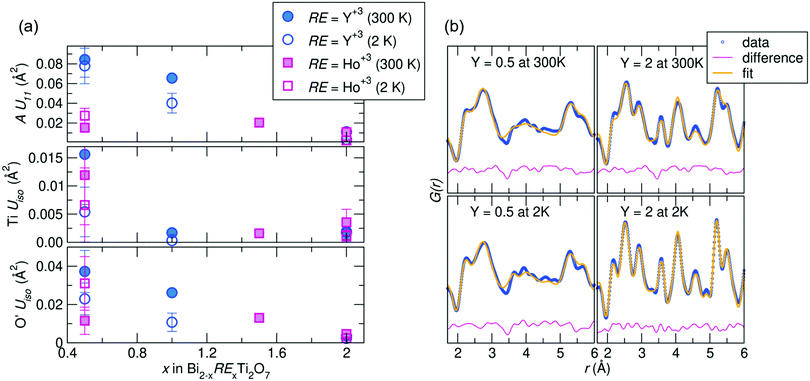
Joint Rietveld analysis of our samples against the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group indicates that this model may not completely describe the structure, from both the elevated ADPs and somewhat high Rw values. This hints at underlying disorder, which may be better described on a local scale. Thus to further understand this disorder, local structural analysis through the neutron pair distribution function (NPDF) was performed on the samples at 300 K and 2 K. NPDF has the advantage of amplifying oxygen scattering and providing contrast between the A-site cations and Ti (due to its negative scattering length) and can provide insight into the local bonding environment of the cations. Results of the refined ADPs from fits against the Fd
m space group indicates that this model may not completely describe the structure, from both the elevated ADPs and somewhat high Rw values. This hints at underlying disorder, which may be better described on a local scale. Thus to further understand this disorder, local structural analysis through the neutron pair distribution function (NPDF) was performed on the samples at 300 K and 2 K. NPDF has the advantage of amplifying oxygen scattering and providing contrast between the A-site cations and Ti (due to its negative scattering length) and can provide insight into the local bonding environment of the cations. Results of the refined ADPs from fits against the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model over 1–6 Å and fits from the highest and lowest Y-substituted samples are shown in Fig. 2. It can be observed that the ADPs for all atoms in the system increase with increasing bismuth content, with a noticeable increase in the Uiso of Ti4+ in the Ho3+/Y3+ = 0.5 samples. Upon substitution with RE cations, the ADPs of the Ti4+ decrease significantly, but are still within the physically reasonable range between 0.001–0.004 Å2. The difference curves, shown in pink in Fig. 2b, reveal areas of the PDF that are not well described by the Fd
m model over 1–6 Å and fits from the highest and lowest Y-substituted samples are shown in Fig. 2. It can be observed that the ADPs for all atoms in the system increase with increasing bismuth content, with a noticeable increase in the Uiso of Ti4+ in the Ho3+/Y3+ = 0.5 samples. Upon substitution with RE cations, the ADPs of the Ti4+ decrease significantly, but are still within the physically reasonable range between 0.001–0.004 Å2. The difference curves, shown in pink in Fig. 2b, reveal areas of the PDF that are not well described by the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure. While the Y3+= 2.0 sample is generally better fit by the average structure, there are still areas of significant deviation indicated by the difference curve, such as between 3 and 4 Å at 300 K. This suggests the local structure of each sample can be described through lower symmetry models that better describe the distortions than as disordered about the ideal crystallographic sites.
m structure. While the Y3+= 2.0 sample is generally better fit by the average structure, there are still areas of significant deviation indicated by the difference curve, such as between 3 and 4 Å at 300 K. This suggests the local structure of each sample can be described through lower symmetry models that better describe the distortions than as disordered about the ideal crystallographic sites.
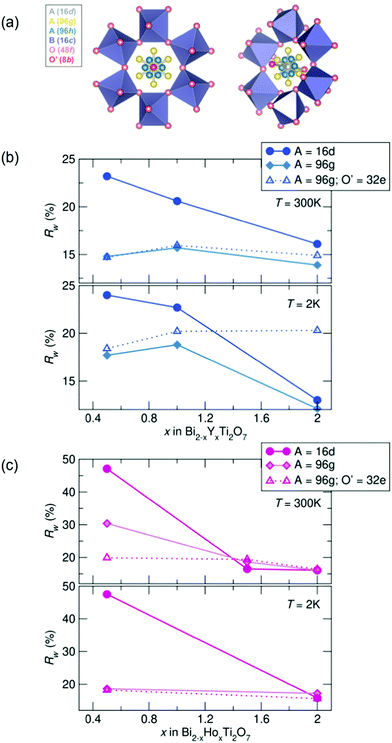
To investigate the nature of the cation disorder in the samples, various split-site models can be employed that lower the site symmetry of the atoms while retaining the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Off-centering of the A-site cation into the 96 g and the O' cation in the 32 e site (a variable site between the 16 d and 8 b sites) has been described and reported in Bi2Ti2O7,26–30,47 and these two split-site models were compared to the disordered 16 d model for each sample. The split-site models improve the fit to the data (indicated by lower Rw values, illustrated in Fig. 3), particularly with higher bismuth content. All yttrium samples at both temperatures show the lowest Rw values with the A-site cation modeled in the 96 g position at 300 K and 2 K. All holmium samples at 2 K are better modeled with A = in the 96 g site and O′ = in the 32 e, as well as with the highest bismuth content at 300 K. However, the disordered 16 d model better describes the samples with higher holmium content at 300 K. While the split-sites more accurately model our structure, correlations are not fully captured, particularly in the samples with the highest bismuth content. Additionally, the holmium samples show elevated Rw values across the series in comparison to the yttrium samples, suggesting lower symmetry models may more appropriately describe the local structure of each sample.
m space group. Off-centering of the A-site cation into the 96 g and the O' cation in the 32 e site (a variable site between the 16 d and 8 b sites) has been described and reported in Bi2Ti2O7,26–30,47 and these two split-site models were compared to the disordered 16 d model for each sample. The split-site models improve the fit to the data (indicated by lower Rw values, illustrated in Fig. 3), particularly with higher bismuth content. All yttrium samples at both temperatures show the lowest Rw values with the A-site cation modeled in the 96 g position at 300 K and 2 K. All holmium samples at 2 K are better modeled with A = in the 96 g site and O′ = in the 32 e, as well as with the highest bismuth content at 300 K. However, the disordered 16 d model better describes the samples with higher holmium content at 300 K. While the split-sites more accurately model our structure, correlations are not fully captured, particularly in the samples with the highest bismuth content. Additionally, the holmium samples show elevated Rw values across the series in comparison to the yttrium samples, suggesting lower symmetry models may more appropriately describe the local structure of each sample.
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m is one of the highest-symmetry space groups (no. 227), and as such, there is the potential for various symmetry-lowering distortions that can be derived from group-subgroup relationships. Lowering the symmetry to F
m is one of the highest-symmetry space groups (no. 227), and as such, there is the potential for various symmetry-lowering distortions that can be derived from group-subgroup relationships. Lowering the symmetry to F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m allows for in/out ordering of the O’ site, and was successfully used to model the O’/vacancy ordering in the pyrochlore Pb2Ru2O6.5, allowing for long range correlation of the lone pairs associated with Pb2+.48 However, our diffraction analysis does not indicate the presence of O' site vacancies. To model in/out ordering of the cations, space group symmetry was lowered to P
3m allows for in/out ordering of the O’ site, and was successfully used to model the O’/vacancy ordering in the pyrochlore Pb2Ru2O6.5, allowing for long range correlation of the lone pairs associated with Pb2+.48 However, our diffraction analysis does not indicate the presence of O' site vacancies. To model in/out ordering of the cations, space group symmetry was lowered to P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, which allows for two positions of the A (and B) site metals, and can be used to model and in/out ordering of either cation site. Alternative to the in/out model is distortions similar to that found in the β-cristobalite structure, which has been suggested for a variety of pyrochlores including Bi2Ti2O7.26,49 The β-cristobalite P43212 (enantiomer to P41212) is the highest symmetry space group that allows for the cation tetrahedra to rotate in all three directions while only having one symmetrically equivalent A (and B) cation site. We additionally considered the Ima2 space group that is the reported ferroelectric structure of Cd2Nb2O7.21–23,50,51 However, our analysis with this space group resulted in a large number correlated parameters and large errors on refined variables, indicating that is an unrealistic model and thus is not presented in our comparison.
3m, which allows for two positions of the A (and B) site metals, and can be used to model and in/out ordering of either cation site. Alternative to the in/out model is distortions similar to that found in the β-cristobalite structure, which has been suggested for a variety of pyrochlores including Bi2Ti2O7.26,49 The β-cristobalite P43212 (enantiomer to P41212) is the highest symmetry space group that allows for the cation tetrahedra to rotate in all three directions while only having one symmetrically equivalent A (and B) cation site. We additionally considered the Ima2 space group that is the reported ferroelectric structure of Cd2Nb2O7.21–23,50,51 However, our analysis with this space group resulted in a large number correlated parameters and large errors on refined variables, indicating that is an unrealistic model and thus is not presented in our comparison.
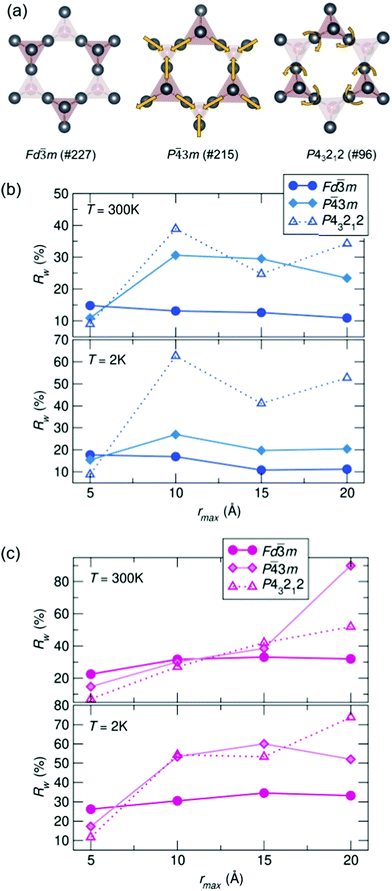
To compare potential local distortions in our pyrochlore samples, NPDF data for each sample was fit from 1.5–6 Å against three candidate models: the best-fitting cubic model from analysis presented in Fig. 3, the in/out P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m structure, and the β-cristobalite P43212 structure. The Rw values as a function of yttrium and holmium content at 300 and 2 K are presented in Fig. 4. It can be seen that for nearly all samples a lower symmetry structure provides the lowest Rw value and thus better description of the structure. A summary of the best fitting space group and corresponding Rw values for each sample can be found in Table 1 and the corresponding fits of the best two candidate models can be found in the ESI,† Fig. S1.
3m structure, and the β-cristobalite P43212 structure. The Rw values as a function of yttrium and holmium content at 300 and 2 K are presented in Fig. 4. It can be seen that for nearly all samples a lower symmetry structure provides the lowest Rw value and thus better description of the structure. A summary of the best fitting space group and corresponding Rw values for each sample can be found in Table 1 and the corresponding fits of the best two candidate models can be found in the ESI,† Fig. S1.
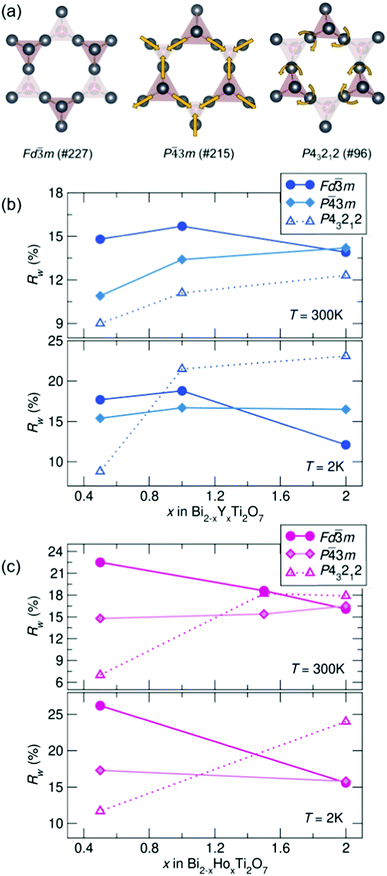 | ||
| Fig. 4 (a) Distortions of the A-site cations in the various structural models. Rw as a function of x in Bi2−x RExTi2O7 for (b) RE = Y and (c) RE = Ho (NPDF, NOMAD, SNS). | ||
| REx | Y0.5 | Y1 | Y2 | Ho0.5 | Ho1.5 | Ho2 |
|---|---|---|---|---|---|---|
| 300 K | P43212 | P43212 | P43212 | P43212 |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
P43212 |
| R w | 9.0% | 11.1% | 12.3% | 19.8% | 15.4% | 17.9% |
| 2 K | P43212 |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
P43212 | — | P43212 |
| R w | 8.8% | 16.7% | 11.1% | 10.3% | — | 24.0% |
While neutron scattering has the benefit of amplifying oxygen scattering and providing contrast between the A-site cations and Ti, many of the stronger oxygen correlations obscure some of the near-neighbor interactions between the cations in the system. To investigate the M–M correlations in the highest-Bi content samples, joint fits of the neutron and X-ray PDFs were performed against the candidate models over a range of 1–6 Å, illustrated in the ESI,† Fig. S2. It can be seen that the cristobalite model continues to be the best description of the neutron data, but the fits to the X-ray data are variable and not as conclusive based on the models. This suggests that the data may better be fit through independently treating the TiO6 and A–O' networks, or that a large-box modeling approach that incorporates additional local data such as XAFS or Raman may be needed to fully describe the distortions. This is outside of the scope of the current manuscript, but even so, it can be concluded that of the models considered, the cristobalite type distortion best describes the local structure of these two samples.
To understand the length of real-space correlation of the locally distorted models, box-car fits of the NPDF data were performed for each sample against the structures obtained from the local fits. Box-car fits are performed at a set increment (in our case over 5 Å) with an increasing rmin and rmax (0–5 Å, 5–10 Å, etc.). The Rw values for Ho3+/Y3+ = 0.5 as a function of rmax can be found in Fig. 5, and the corresponding plots for the other samples in the ESI,† Fig. S3 and S4. It can be seen that for most samples the cubic structure becomes the best model past 5 Å; however, in the Ho3+ = 0.5 sample, the structure is still best described by the β-cristobalite P43212 structure at 10 Å (with an Rw values that is 4% lower than the other two models), indicating the correlation between off-centered cations persists farther in real-space than in the other samples.
4 Discussion
There is a wealth of literature surrounding the analysis of Bi2Ti2O7, Y2Ti2O7, and Ho2Ti2O7, and understanding the behavior of the end members can provide important context for the observed behavior of the solid solutions. Detailed X-ray44 and neutron26 studies on stoichiometric Bi2Ti2O7 indicate movement of the Bi cation into the 96 g or 96 h site and the O′ anion off of its ideal 8 b site to the variable 32 e site, which is corroborated by our observations that the split-site cubic models result in a better fit for all samples, most significantly in the samples with the highest bismuth content. The neutron study additionally reported a cristobalite-type distortion of the Bi–O′ network, showing evidence that there was some degree of near-neighbor Bi–Bi ordering, with a preference for 180 degree alignment. This work revealed a cooperative cristobalite-type correlation of the O'Bi4 tetrahedral sub-network through the rotation of these units. Our current work suggests that this cristobalite-type distortion is maintained at room temperature across the Bi–Y solid solution, but there may be a rearrangement of A-site cation local ordering upon cooling when the yttrium content increases to x = 1 and above. We also see a cristobalite distortion at room and low temperature for the lowest holmium content in the Bi-Ho solid solution, but the room temperature data indicates a preference for in/out ordering or complete disorder (modeled by the cubic structure) with increasing holmium content.In addition to the magnitude of the ADPs, the shape of the ellipsoids from crystallographic analysis can provide insight into the nature of the underlying disorder. Pancake-like ellipsoids suggest movement of cations perpendicular to the A-O' bond, which indicates tetrahedral sub-unit rotation/tilting as seen in the cristobalite structure versus in/out ordering, which would be evidenced by rod-like ellipsoids on the tetrahedral vertices of the O'A4 sub-units. Closer examination of the diffraction data supports this finding as well. The appearance of the 442 reflection suggests static β-cristobalite disorder due to A or B cation displacements, and is not an allowed peak in the symmetric cubic structure with the cations on the ideal 16 d and 16 c sites.44 Our RE = Y3+ samples at 300 K show a weak reflection in the 442 position of the synchrotron data (shown in the ESI,† Fig. S5), indicating displacements consistent with the local cristobalite observations. However, these reflections, while assigned intensity, are not strong enough to influence the overall fit metrics of the diffraction data, and Rietveld fits against the P43212 space group did not yield significant statistical improvements in the fits. Therefore, it is likely that the long range structure of Y2Ti2O7 (and the other Y-substituted samples) has cristobalite distortions that average out to be very small distortions from the ideal positions in the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at room temperature.
m structure at room temperature.
The large amount of structural disorder due to lone-pair effects is further evidenced in the physical properties of pyrochlore materials. Previous specific heat measurements on A2Ti2O7 (A = Bi, Y) pyrochlores show elevated values at lower temperatures when the A-site cation is the lone-pair-bearing Bi3+, suggesting static disorder that is not present in the Y3+ analog.52
Spectroscopic studies28,53 provide ample evidence for local distortions on both the TiO6 and Bi–O′ networks in Bi2Ti2O7, and further suggests the influence of the two networks on each other, corroborated with previous vibrational studies of other rare earth titanate pyrochlore.54 A combination of Raman and IR spectroscopy reveals several Bi–O stretching and Bi–O′–Bi bending motions, combined to suggest a large amount of displacive disorder on both the Bi and O' site. These works provided additional evidence of Ti displacements through the observation of Ti–O stretching modes, and suggests this can be found in several rare earth titanates with increasing frequency as the radius of the A-site cation decreases. We do see an elevated U11 for Ti4+ in the most local fits of all samples, which decreases upon cooling, suggesting there is local dynamic disorder of Ti4+ at room temperature. Together, this supports our observations of a locally distorted structure for all of our samples, regardless of the presence of a lone pair cation. This may additionally explain why Ho3+, which is slightly smaller than Y3+ (and much smaller than Bi3+) exhibits a more distorted local environment that persists to longer correlation lengths in the Ho3+ = 0.5 sample.
Ho2Ti2O7 has garnered a significant amount of attention due to the unpaired f-electrons associated with the Ho3+ cation. This has been a large area of interest in terms of magnetic phenomena, particularly given the frustrated nature of the spins on the pyrochlore lattice that gives rise to spin ice behavior at lower temperatures. In addition to magnetic properties, this material has been investigated as a multiferroic given the potential for the interaction of magnetic (associated with Ho3) and electrical (associated with the SOJT Ti4+) dipoles. Previous work on single crystals55 and powders24 of Ho2Ti2O7 indicated an observed ferroelectric transition with a small polarization at approximately 23 K. Previous structural work has indicated that the was no observable change from cubic symmetry through the transition, and pose that the nature of the structural distortion through the observed ferroelectric transition is related to local disorder on both oxygen sites,56 which they supported with the observation of O'– A–O′ and O–A–O bending modes through IR spectroscopy in other pyrochlores.57,58 It should be noted that this structural study was performed with X-ray radiation, which is not as sensitive to oxygen positions, but the work provides valuable information on the evolution of the lattice parameters upon cooling. Further work on the existence of ferroelectric transitions in Ho2Ti2O7 report that a first ferroelectric transition around 60 K (polycrystalline) to 28 K (single crystal) are structural in origin,59 while a second transition at 23 K (polycrystalline) is due to the magnetic nature of the material.24 Raman studies on Ho2Ti2O7 and related titanate pyrochlores59 indicate distortions in the TiO6 network through the observations of O–Ti–O bending and Ti–O stretching, showing distortions in this material are primarily related to the Ti cation and the variable 48 f oxygen position. In the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure the O 48 f position x = 0.3125 for a perfect octahedron around the Ti cation. This value is greater than 0.32 for all of our samples (See ESI,† Tables S1 and S2), indicating distorted TiO6 octahedra. It has been suggested that the local electrical dipole in Ho2Ti2O7 is related to the existence of a magnetic monopole that arises due to the spin ice nature of the material.60 Several studies have emerged that investigate the role of the magnetic spins on structural distortions,24,55,61–64 and it is clear that this relationship plays an important role in the lower local symmetry observed in Ho2Ti2O7.
m structure the O 48 f position x = 0.3125 for a perfect octahedron around the Ti cation. This value is greater than 0.32 for all of our samples (See ESI,† Tables S1 and S2), indicating distorted TiO6 octahedra. It has been suggested that the local electrical dipole in Ho2Ti2O7 is related to the existence of a magnetic monopole that arises due to the spin ice nature of the material.60 Several studies have emerged that investigate the role of the magnetic spins on structural distortions,24,55,61–64 and it is clear that this relationship plays an important role in the lower local symmetry observed in Ho2Ti2O7.
Recent work by Trump et al. suggests that local distortions are inherent to all pyrochlores,65 and is driven by the ionic radius ratio of the A/B cations. This study focuses primarily on zirconate pyrochlores, and suggests that a β-cristobalite local structure is adopted to accommodate for overbonding of the A site cation. The cristobalite structure results in octahedral rotation versus bond elongation or compression, and this motion satisfies valence of the A-site cation when in a compressed environment. A bond valence argument has also been presented in the context of Bi2Ti2O7,66 suggesting that the underbonded nature of Bi3+ in the 16 d site is the primary driver of lone pair driven off-centering of the Bi3+ perpendicular to the A–O' bond. For our samples, the Ho and Y end members are overbonded (bond valence sums, BVS, between 3.04 and 3.07), and this overbonding increases upon cooling. This supports the need for octahedral rotations enabled by the cristobalite structure to relieve this overbonding. All of our bismuth-containing samples have underbonded A-site cations (BVS between 2.63 and 2.97), and while the BVS still increases with cooling, these samples remain underbonded. This supports our observations of bismuth off-centering, and the observation of locally distorted sites. The driving force for distortion varies across the solid solution (overbonding in the pure Y and Ho samples that prompts octahedral twisting, underbonding in the Bi samples that drives lone-pair enabled off-centering), but nonetheless results in local distortions for all samples.
If we consider the existing literature together, we can begin to understand the nature of the distortions in our two solid solutions. Starting with the work by Trump et al.,65 we can make an assumption that all pyrochlores should have an underlying local distortion, which we do indeed see locally for most samples. It should be noted that we chose three test case models for the nature of the local distortions, and in several cases the relatively high Rw s (above 10% in the NPDF fits) suggest that the local symmetry is even lower than our chosen models, and this is further supported by the difficulty of describing the joint XPDF and NDPF with these models. We can think about the drivers of structural distortions in terms of the three end members of our solid solutions: Y2Ti2O7 is the simplest, which in addition to the underlying distortion has a SOJT active Ti4+ cation on the B site; Ho2Ti2O7 has both of these drivers, with an additional magnetoelectric factor that can drive distortions; Bi2Ti2O7 has the combined SOJT nature of Ti4+ and the lone pair associated with Bi3+. With this in mind, we can begin to explain the observations from Fig. 4 and Table 1: with increasing Bi3+ content, local distortions are more prevalent, and are better described by the P43212 cristobalite model. The only sample that is best described locally by the cubic model is the one with the fewest drivers for distortion (Y2Ti2O7), and it should be noted that the Rw value is larger than 10%, indicating that a different structural model than those considered here would be a better structural description. The nature of the distortions changes with Bi3+ content, and in general, samples with the highest Bi3+ content favor the cristobalite model, whereas middle and low-bismuth compositions tend to favor the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m in/out model. This is particularly true in the holmium samples, which may be more strongly influenced by the local ordering of magnetic dipoles on the triangular pyrochlore lattice. This magnetoelectric influence may also play a role on the observed correlation length behavior: while all samples in the Bi–Y series become much better described by the cubic models past an rmax of 5 Å, the holmium-containing samples show a longer correlation length (up to 10 Å) for Bi1.5Ho0.5Ti2O7 and much closer Rw values for the in/out and cubic models at all length scales (see ESI,† Fig. S3 and S4). While the drivers for atomic displacements mostly lead to frustration that quickly averages out to a cubic disordered mid- and long-range structure, the influence of magnetic dipoles on the lattice coupled to electric dipoles may play a role manipulating long-range polarity on the pyrochlore lattice.
3m in/out model. This is particularly true in the holmium samples, which may be more strongly influenced by the local ordering of magnetic dipoles on the triangular pyrochlore lattice. This magnetoelectric influence may also play a role on the observed correlation length behavior: while all samples in the Bi–Y series become much better described by the cubic models past an rmax of 5 Å, the holmium-containing samples show a longer correlation length (up to 10 Å) for Bi1.5Ho0.5Ti2O7 and much closer Rw values for the in/out and cubic models at all length scales (see ESI,† Fig. S3 and S4). While the drivers for atomic displacements mostly lead to frustration that quickly averages out to a cubic disordered mid- and long-range structure, the influence of magnetic dipoles on the lattice coupled to electric dipoles may play a role manipulating long-range polarity on the pyrochlore lattice.
5 Conclusions
Here we present detailed structural analysis based on neutron and X-ray total scattering for samples in the series Bi2−xRExTi2O7 (RE = Y3+, Ho3+) at room temperature and 2 K. This work helps elucidate the nature of local distortions as a function of the A-site cation at these two discreet temperatures, and analysis of any transition states between these temperatures will provide a more complete picture of the structural evolution upon cooling. With this in mind, our group has recently performed a series of X-ray scattering measurements of these and related samples, and a detailed analysis of various X-ray techniques on titanate pyrochlores is a subject of a forthcoming manuscript.The structural behavior of pyrochlores is considerably complex, as the structure is prone to underlying distortions and site disorder. The known SOJT and lone-pair drivers of ferroelectric distortions in perovskite materials lead to frustration in favor of a correlated polar phase in most pyrochlores, but the addition of magnetic dipoles to the lattice may help stabilize the correlation of electronic dipoles. While this does not account for the ferroelectric behavior observed in the highly-studied Cd2Nb2O7 pyrochlore, this offers an additional factor to include in the search for polar pyrochlore materials. Our work illustrates the complex interplay between size, bond valence, electronic, and magnetoelectric contributions to structural distortions on the pyrochlore lattice, and offers insight into real-space-dependent correlations across various pyrochlore compositions. This contributes to the broader literature of pyrochlore materials towards the realization of new polar pyrochlore materials.
Author contributions
O. B. contributed to resources, methodology, investigation, formal analysis, visualization, writing – original draft. S. H. and M. M. contributed to resources, investigation, and formal analysis. J. R. and J. G. contributed to resources and formal analysis. D. O. contributed to investigation, software, and writing – review & editing. G. L. contributed to conceptualization, funding acquisition, methodology, project administration, supervision, formal analysis, visualization, writing – original draft, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Bates College internal funding and the National Science Foundation (NSF) through DMR 1904980. This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. G. L. would additionally like to thank Hayden Evans for useful discussions. This research used the Pair Distribution Function (PDF) beamline of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DE-SC0012704.Notes and references
- H. D. Megaw, Acta Crystallogr., 1954, 7, 187–194 CrossRef CAS
.
-
H. Megaw, Ferroelectricity in Crystals, Methuen, London, 1957 Search PubMed
.
- V. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS
.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS
.
- D. Payne, R. Egdell, A. Walsh, G. Watson, J. Guo, P.-A. Glans, T. Learmonth and K. Smith, Phys. Rev. Lett., 2006, 96, 157403 CrossRef CAS PubMed
.
- L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 1–14 Search PubMed
.
- B. Hailegnaw, S. Kirmayer, E. Edri, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 1543–1547 CrossRef CAS PubMed
.
- U. S. E. P. Agency, Lead Laws and Regulations, 2021, https://www.epa.gov/lead/lead-laws-and-regulations.
- M. Subramanian, G. Aravamudan and G. S. Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef CAS
.
- R. Jin, J. He, S. McCall, C. Alexander, F. Drymiotis and D. Mandrus, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 180503 CrossRef
.
- Z. Porter, E. Zoghlin, S. Britner, S. Husremovic, J. P. Ruff, Y. Choi, D. Haskel, G. Laurita and S. D. Wilson, Phys. Rev. B, 2019, 100, 054409 CrossRef CAS
.
- G. Laurita, D. Puggioni, D. Hickox-Young, J. M. Rondinelli, M. W. Gaultois, K. Page, L. K. Lamontagne and R. Seshadri, Phys. Rev. Mater., 2019, 3, 095003 CrossRef CAS
.
- W. R. Cook and H. Jaffe, Phys. Rev., 1953, 89, 1297–1298 CrossRef CAS
.
- X. W. Dong, K. F. Wang, S. J. Luo, J. G. Wan and J. M. Liu, J. Appl. Phys., 2009, 106, 104101 CrossRef
.
- D. Liu, L. Lin, M. F. Liu, Z. B. Yan, S. Dong and J.-M. Liu, J. Appl. Phys., 2013, 113, 17D901 CrossRef
.
- D. Bernard, J. Lucas and L. Rivoallan, Solid State Commun., 1976, 18, 927–930 CrossRef CAS
.
- S. Saitzek, Z. Shao, A. Bayart, A. Ferri, M. Huvé, P. Roussel and R. Desfeux, J. Mater. Chem. C, 2014, 2, 4037 RSC
.
- M. Kimura, S. Nanamatsu, T. Kawamura and S. Matsushita, Jpn. J. Appl. Phys., 1974, 13, 1473–1474 CrossRef CAS
.
- T. M. McQueen, D. V. West, B. Muegge, Q. Huang, K. Noble, H. W. Zandbergen and R. J. Cava, J. Phys.: Condens. Matter, 2008, 20, 235210 CrossRef CAS PubMed
.
- B. Melot, E. Rodriguez, T. Proffen, M. Hayward and R. Seshadri, Mater. Res. Bull., 2006, 41, 961–966 CrossRef CAS
.
- W. Cook and H. Jaffe, Phys. Rev., 1952, 88, 1426 CrossRef CAS
.
- D. Bernard, J. Pannetier and J. Lucas, Solid State Commun., 1975, 334, 328 CrossRef
.
- G. Laurita, D. Hickox-Young, S. Husremovic, J. Li, A. W. Sleight, R. Macaluso, J. M. Rondinelli and M. A. Subramanian, Chem. Mater., 2019, 31, 7626–7637 CrossRef CAS
.
- X. Dong, K. Wang, S. Luo, J. Wan and J.-M. Liu, J. Appl. Phys., 2009, 106, 104101 CrossRef
.
- C. J. Fennie, R. Seshadri and K. M. Rabe, arXiv preprint arXiv:0712.1846, 2007.
- D. P. Shoemaker, R. Seshadri, A. L. Hector, A. Llobet, T. Proffen and C. J. Fennie, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144113 CrossRef
.
- D. P. Shoemaker, A. Llobet, M. Tachibana and R. Seshadri, J. Phys.: Condens. Matter, 2011, 23, 315404 CrossRef PubMed
.
- C. Turner, P. M. Johns, E. M. Thatcher, D. Tanner and J. C. Nino, J. Phys. Chem. C, 2014, 118, 28797–28803 CrossRef CAS
.
- B. Brooks Hinojosa, A. Asthagiri and J. C. Nino, Appl. Phys. Lett., 2011, 99, 082903 CrossRef
.
- J. R. Esquivel-Elizondo, B. B. Hinojosa and J. C. Nino, Chem. Mater., 2011, 23, 4965–4974 CrossRef CAS
.
- R. Seshadri, Solid State Sci., 2006, 8, 259–266 CrossRef CAS
.
- A. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453–480 CrossRef CAS
.
- O. Knop, F. Brisse and L. Castelliz, Can. J. Chem., 1969, 47, 971–990 CrossRef CAS
.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS
.
- P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef
.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS
.
- D. Olds, C. N. Saunders, M. Peters, T. Proffen, J. Neuefeind and K. Page, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 293–307 CrossRef CAS PubMed
.
- C. L. Farrow, P. Juhas, J. W. Liu, D. B. Bryndin, E. S. J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS
.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, G. Ivantchev, S. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr., 2006, 221, 15–27 CAS
.
- M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., 2006, A62, 115–128 CrossRef CAS PubMed
.
- M. Suganya, K. Ganesan, P. Vijayakumar, A. S. Gill, R. Ramaseshan and S. Ganesamoorthy, Scr. Mater., 2020, 187, 227–231 CrossRef CAS
.
- A. L. Hector and S. B. Wiggin, J. Solid State Chem., 2004, 177, 139–145 CrossRef CAS
.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., 1969, B25, 925 CrossRef
.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751 CrossRef CAS
.
- M. Tachibana, H. Kawaji and T. Atake, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064103 CrossRef
.
- D. P. Shoemaker, A. Llobet, M. Tachibana and R. Seshadri, J. Phys.: Condens. Matter, 2011, 23, 315404 CrossRef PubMed
.
- B. A. Trump, S. M. Koohpayeh, K. J. T. Livi, J.-J. Wen, K. E. Arpino, Q. M. Ramasse, R. Brydson, M. Feygenson, H. Takeda, M. Takigawa, K. Kimura, S. Nakatsuji, C. L. Broholm and T. M. McQueen, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed
.
- T. Malcherek, U. Bismayer and C. Paulmann, J. Phys.: Condens. Matter, 2010, 22, 205401 CrossRef CAS PubMed
.
- M. Fischer, T. Malcherek, U. Bismayer, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014108 CrossRef
.
- B. C. Melot, R. Tackett, J. O’Brien, A. L. Hector, G. Lawes, R. Seshadri and A. P. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224111 CrossRef
.
- D. Arenas, L. Gasparov, W. Qiu, J. Nino, C. H. Patterson and D. Tanner, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 214302 CrossRef
.
- M. Vandenborre, E. Husson, J. Chatry and D. Michel, J. Raman Spectrosc., 1983, 14, 63–71 CrossRef CAS
.
- D. Liu, L. Lin, M. Liu, Z. Yan, S. Dong and J.-M. Liu, J. Appl. Phys., 2013, 113, 17D901 CrossRef
.
- P. K. Yadav, M. Tolkiehn and C. Upadhyay, J. Phys. Chem. Solids, 2019, 134, 201–208 CrossRef CAS
.
- J. C. Nino, M. T. Lanagan, C. A. Randall and S. Kamba, Appl. Phys. Lett., 2002, 81, 4404–4406 CrossRef CAS
.
- S. Kamba, V. Porokhonskyy, A. Pashkin, V. Bovtun, J. Petzelt, J. C. Nino, S. Trolier-McKinstry, M. T. Lanagan and C. A. Randall, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 054106 CrossRef
.
- M. Maczka, M. Sanjuán, A. Fuentes, L. Macalik, J. Hanuza, K. Matsuhira and Z. Hiroi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214437 CrossRef
.
- D. Khomskii, Nat. Commun., 2012, 3, 1–5 Search PubMed
.
- D. Dai and M.-H. Whangbo, Inorg. Chem., 2005, 44, 4407–4414 CrossRef CAS PubMed
.
- J. Clancy, J. Ruff, S. Dunsiger, Y. Zhao, H. Dabkowska, J. Gardner, Y. Qiu, J. Copley, T. Jenkins and B. Gaulin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014408 CrossRef
.
- R. A. Borzi, F. A. Gómez Albarracn, H. D. Rosales, G. L. Rossini, A. Steppke, D. Prabhakaran, A. Mackenzie, D. C. Cabra and S. A. Grigera, Nat. Commun., 2016, 7, 1–8 Search PubMed
.
- K. Baroudi, B. D. Gaulin, S. H. Lapidus, J. Gaudet and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 024110 CrossRef
.
- B. A. Trump, S. M. Koohpayeh, K. J. T. Livi, J.-J. Wen, K. E. Arpino, Q. M. Ramasse, R. Brydson, M. Feygenson, H. Takeda, M. Takigawa, K. Kimura, S. Nakatsuji, C. L. Broholm and T. M. McQueen, Nat. Commun., 2018, 9, 2619.
- D. P. Shoemaker, R. Seshadri, M. Tachibana and A. L. Hector, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 064117 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Details of synthesis temperatures, refined crystallographic data tables at 300 K and 2 K, local fits of the NDPF data against the best two structural models, joint fits of the XPDF and NPDF data at 100 K, boxcar fits of the Y3+ = 1.0, 2.0 and Ho3+ = 1.5, 2.0, highlight of the 442 reflection in the synchrotron diffraction data for the RE = Y3+. See DOI: https://doi.org/10.1039/d2tc01328b |
| This journal is © The Royal Society of Chemistry 2022 |