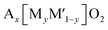Open Access Article
Open Access ArticleActive material and interphase structures governing performance in sodium and potassium ion batteries
Eun Jeong
Kim
 a,
P. Ramesh
Kumar
a,
Zachary T.
Gossage
a,
P. Ramesh
Kumar
a,
Zachary T.
Gossage
 a,
Kei
Kubota†
a,
Kei
Kubota†
 ab,
Tomooki
Hosaka
ab,
Tomooki
Hosaka
 ab,
Ryoichi
Tatara
ab,
Ryoichi
Tatara
 ab and
Shinichi
Komaba
ab and
Shinichi
Komaba
 *ab
*ab
aDepartment of Applied Chemistry, Tokyo University of Science, 1-3 Kagurazaka, Shinjuku, Tokyo 162-8601, Japan. E-mail: komaba@rs.tus.ac.jp
bElements Strategy Initiative for Catalysts and Batteries (ESICB), Kyoto University, 1-30 Goryo-Ohara, Nishikyo-ku, Kyoto 615-8245, Japan
First published on 18th May 2022
Abstract
Development of energy storage systems is a topic of broad societal and economic relevance, and lithium ion batteries (LIBs) are currently the most advanced electrochemical energy storage systems. However, concerns on the scarcity of lithium sources and consequently the expected price increase have driven the development of alternative energy storage systems beyond LIBs. In the search for sustainable and cost-effective technologies, sodium ion batteries (SIBs) and potassium ion batteries (PIBs) have attracted considerable attention. Here, a comprehensive review of ongoing studies on electrode materials for SIBs and PIBs is provided in comparison to those for LIBs, which include layered oxides, polyanion compounds and Prussian blue analogues for positive electrode materials, and carbon-based and alloy materials for negative electrode materials. The importance of the crystal structure for electrode materials is discussed with an emphasis placed on intrinsic and dynamic structural properties and electrochemistry associated with alkali metal ions. The key challenges for electrode materials as well as the interface/interphase between the electrolyte and electrode materials, and the corresponding strategies are also examined. The discussion and insights presented in this review can serve as a guide regarding where future investigations of SIBs and PIBs will be directed.
1. Introduction
Burgeoning environmental issues stemming from societal dependence on fossil fuels necessitate a major shift toward new energy production, storage, and utilization technologies. While energy production from solar and wind appears promising and virtually unlimited compared with fossil fuels, its implementation requires significant improvements in energy storage for proper delivery. Electrochemical energy storage systems, such as rechargeable batteries and electric double layer capacitors, have received considerable attention as a potential solution to deal with the growing energy demand without increasing our carbon footprint. Among developed energy storage systems, lithium ion batteries (LIBs) have remained at the forefront since their first commercialization in 1991, and continue to expand their applications from portable consumer electronics toward transportation and powering the grid.1 However, applying LIBs in these more demanding sectors has increased concerns on the scarcity of lithium sources.2 In addition, other raw materials used in LIBs, e.g. Co, Ni, Cu, etc., face environmental and ethical challenges including their concentration within limited regions of the world.3 Such conditions are accelerating the discovery of novel alternatives for electrochemical energy storage, including sodium ion batteries (SIBs) and potassium ion batteries (PIBs), to compete with and/or compensate for the LIB market.4–12SIBs and PIBs have seen rapid development in recent years, partially drawing from their likeness to LIBs where they can show similar energy storage mechanisms and are composed of analogous cell components.4,6,7 For example, they can be constructed using insertion materials and carbon-based materials for the positive and negative electrodes, respectively, a standard porous separator made of glassy fiber or polymer, and a fluorophosphate, carbonate ester electrolyte (Fig. 1). However, utilizing Na+ and K+ as ionic carriers results in distinct coordination preferences in the electrode materials, different interactions with the electrolyte, and unique properties for their solid electrolyte (SEI) and cathode electrolyte interphases (CEI).4,13 These differences result in limitations and benefits when preparing a battery based on Li+, Na+ or K+, indicating they are not directly interchangeable. Instead, their unique physical properties, as summarized in Table 1, directly impact their performance.
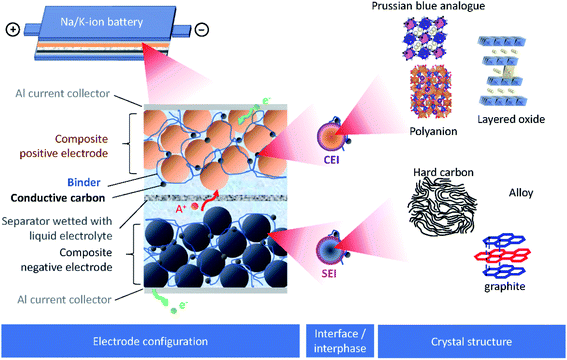 | ||
| Fig. 1 Schematic presentation of SIBs or PIBs showing the electrode configuration, the interface/interphase between the electrode and electrolyte, and the crystal structure of electrode materials. | ||
| Li+ | Na+ | K+ | |
|---|---|---|---|
| Relative atomic mass | 6.94 | 22.99 | 39.10 |
| Mass to charge ratio | 6.94 | 22.99 | 39.10 |
| Shanon's ionic radius (Å) with six-fold coordination14 | 0.76 | 1.02 | 1.38 |
| Stokes radius (Å) in PC15 | 4.8 | 4.6 | 3.6 |
| Limiting molar ionic conductivity in PC (S cm2 mol−1)15 | 8.3 | 9.1 | 15.2 |
| Desolvation energy in PC (kJ mol−1)16 | 215.8 | 158.2 | 119.2 |
| E° vs. SHE (V) in aqueous solution | −3.04 | −2.71 | −2.93 |
| E° vs. Li/Li+ (V) in PC | 0 | 0.23 | −0.09 |
| Melting point of metal (°C) | 180.5 | 97.8 | 63.4 |
| Crust abundance (mass%) | 0.0017 | 2.3 | 1.5 |
Based on Faraday's law, the lower mass to charge ratio delivers the higher gravimetric capacity for a cell. In this respect, electrode materials containing Na+ and K+ would seem to show lower capacity than Li+ counterparts. Actually, the delivered capacity is determined by the total mass of the electrode material including the framework which generally governs a larger portion of the active material mass compared to the carrier ion. For example, the theoretical capacity of KCoO2 is 206 mA h g−1, equivalent to 75% of LiCoO2 (274 mA h g−1). This physical property becomes determinant only in the specific positive electrode cases, where the carrier ion makes up a large portion of the active material mass, but not the case of negative electrodes such as carbon and alloys.
Aside from adding mass, the framework further plays a key role in the stability of the electrode during operation. With reference to positive electrode materials, the amount of extractable alkali metal ions (A+) is strongly correlated with the stability of the framework upon extraction of A+, which often restrains upper cut-off voltage, delivering much less than the theoretical capacity. Structural integrity is also key to negative electrode materials such as common graphite and alloys, which rely on a crystalline structure to accommodate A+ insertion. Large volume changes can result in loss of capacity and can disrupt key SEI structures. Maintaining the framework and interphase structures is an important task to provide batteries with reliable behavior and high cyclability.
Improving rate capabilities is another important target for the next generation of batteries. The smaller Stokes radii of K+ and Na+ compared with Li+ (Fig. 2) result from their coordination with solvent/electrolyte species and their transfer at the SEI.15 The large ionic radius of K+ produces a relatively low surface charge density, namely classified as weak Lewis acid, resulting in weaker interactions between K+ and solvent molecules. This has been demonstrated experimentally with K+ in propylene carbonate (PC), showing the highest limiting molar ionic conductivity and implying the fastest diffusion rate.15 Likewise, Na+ represents a weaker Lewis acidity than Li+, implying faster diffusion and a smaller activation energy of Na+ transfer at the SEI formed in PC.17 In addition, DFT calculations show that the desolvation energy of both Na+ and K+ is smaller than that of Li+ in several aprotic solvents.16 Kinetics of A+ transfer at the interphase between the electrode and electrolyte is strongly linked to this desolvation energy as shown in LIBs.18,19 Altogether, these results suggest promising rate performance capabilities for Na+ and K+ systems.
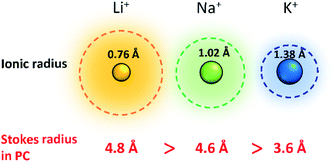 | ||
| Fig. 2 Comparison of Shannon's radii and Stokes radii in PC for Li+, Na+ and K+ ions. Adopted with permission from ref. 4. Copyright 2020 American Chemical Society. | ||
Operating voltage is a critical factor in determining the energy density of a battery, which is defined by the difference in potential between negative and positive electrodes. To achieve high energy densities, a high and low operating potential is desired for the positive and negative electrodes, respectively. When an alkali metal is used as the negative electrode, the standard electrode potential (E°) of alkali metal determines the lowest potential. In this respect, Li/Li+ shows the lowest standard electrode potential, E°, in aqueous electrolytes. However, in PC, the E° of K/K+ was calculated to be −0.09 V vs. Li/Li+,20 and thereafter, experimentally confirmed for multiple carbonate ester solvents by our group.21,22 Taking this into consideration, PIBs possibly have a wide potential window which is advantageous to achieve higher energy density than LIBs under certain conditions. As seen in Fig. 3, the voltage window of a PIB widens compared to either LIBs or SIBs in PC-based electrolytes, assuming that the anodic limit of the electrolyte is consistent for all systems. It is worth noting that the operating voltage is also limited by electrolyte stability and passivation. Therefore, the formation of a reliable SEI and CEI becomes important to prevent continuous reduction and oxidation of the electrolyte by inhibiting direct electron transfer between the electrode and the electrolyte. In general, the SEI and CEI should prevent solvent breakdown and permeability while enabling fast ionic conductivity and mechanical stability.13 Development of electrolytes with high oxidation and reduction resistance as well as understanding the interface between the electrode and electrolyte are indispensable to achieve high-voltage SIBs and PIBs.
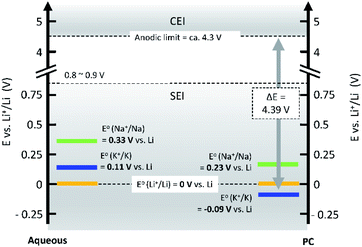 | ||
| Fig. 3 Comparison of standard electrode potentials, E°, of alkali metals in aqueous (left), and PC (right) solutions. | ||
Other important points in the development of high-performance SIBs and PIBs are safety and cost. Considering commercial graphite-based LIBs, the potential of graphite continuously increases upon deep discharge and reaches above 3 V (vs. Li/Li+), eventually causing Cu oxidation and Cu plating onto the positive electrode.23–25 The consequences of extreme discharge yield not only capacity fade but also severe thermal hazards. In contrast, SIBs and PIBs can use an Al current collector for the negative electrode since Al foil does not undergo alloying reactions with Na and K.21 This bypasses such issues related to deep discharge in graphite-based LIBs and can reduce the weight and cost of the battery, permitting 0 V storage and/or transportation in the case of SIBs.23–25 Aside from graphite, the interest for using large capacity alkali metals as negative electrode materials brings about other safety concerns. For one, these metals are highly reactive posing potential fire and explosion hazards. The metal plating reactions can lead to dendrite formation as often occurs at overcharged states, and this can lead to shorting and thermal runaway.26–28 Furthermore, plated Na and K metals can react with the electrolyte relatively easily compared with Li metal, leading to redissolution into the electrolyte.29,30 Significant research efforts have been exploring ways to minimize and prevent dendrite formation through electrolyte and interphase engineering.
The performance of SIBs and PIBs still needs to be enhanced for practical application beyond LIBs. Parameters including capacity, available voltage range, rate capability, cycle life, energy efficiency, and temperature range are important criteria to make SIBs and PIBs competitive. Here, we consider the strong correlations between these parameters and the impact of electrode material structure on the interaction with each A+, the associated advantages as well as limitations, and the role of interphase structures between the electrode material and electrolyte. Of note, among the new chemistries such as Li–air, Li–S, Mg, and Ca batteries that have been considered as beyond LIB technologies, SIBs are the closest to reach the maturation stage, having given birth to companies such as Faradion in the UK, Novasis in the USA, Tiamat in France, and so on. Furthermore, systematic studies of three different A+ ions and their electrochemistry are expected to provide synergistically deeper understanding and accelerate development of PIBs, taking advantage of low Lewis acidity and weak ionic interaction of K+.
In this review, we will first focus on positive electrode materials for SIBs and PIBs, classified as layered oxides, polyanion materials, and Prussian blue analogues (PBAs). In the section of layered oxides, polymorphs of layered oxides and their evolution upon cycling will be explained, followed by the discussion on different electrochemical features including charge/discharge curves, capacity, working voltage, and cyclability as a function of A+. Thereafter, we will examine binary transition metal systems which present peculiar properties including transition metal ordering and oxygen redox activity. The benefits of binary and ternary transition metal systems for electrochemical performance derived from the reversible/stable crystal structure, fast kinetics, and stable interface will be described as well. In the following section on polyanion materials, we will discuss how the covalency of bonds between the redox active metal and ligand influences the operating potential of polyanion compounds. Important compounds are grouped based on their structure types, and their electrochemical properties are examined, highlighting the effects of different A+. Furthermore, the influences of ligand type and symmetry for polyhedral groups are described in the sub sections. After that, material design of PBAs for SIBs and PIBs will be discussed based on their crystal and electronic structures, which are varied by transition metal species, crystal water, insertion ions, and crystal defects.
In the second half of this review, we will discuss carbon-based materials and alloy compounds as negative electrode materials, as well as the interphase that occurs at the negative electrode. In carbon-based materials, we will describe the different types of carbon electrodes and their impact on the energy storage mechanism with each of the A+. The limitations of graphitic materials with Na+ and K+ ions, and methods for improving their energy storage capabilities through incorporation of more functional binders and concepts of co-solvent intercalation will be detailed. Thereafter, we will discuss efforts toward preparing hard and soft carbons for application in SIBs and PIBs. The impact of the precursor and preparation method will be described as well as the assumed mechanisms for different types of non-graphitic carbons. For alloy materials, we will briefly focus on their benefits and current challenges. Lastly, the importance of interphase studies will be reviewed, highlighting the different characteristics of interphases with each of A+.
2. Layered oxides for positive electrode materials
Lithium layered oxides have been the most widely used class of positive electrode materials in LIBs since their commercialization in 1991 using LiCoO2 as a positive electrode material. With the success of lithium layered oxides and the superior properties of layered oxides over other chemistries, e.g. their low formula weight, sodium and potassium analogues have been extensively investigated since the 1980s.312.1. Polymorphs of layered oxides
Classification proposed by Delmas et al. has been widely used to describe layered oxides with the AxMO2 (A = alkali metal and M = transition metal(s)) formula.31 The layered oxides are built up of MO2 slabs of edge-sharing MO6 octahedra and A+ ions occupying interlayer spaces. Depending on the various oxygen stacking sequences along the c-axis, they can be categorized into groups including O3, P3, P2 and O2, as illustrated in Fig. 4. The letter indicates the coordination environment of A+ and the number corresponds to the number of transition metal layers in a hexagonal unit cell. When the hexagonal lattice is distorted, the prime symbol (′) is added between the alphabet and the number while the number of MO2 is counted in a pseudohexagonal unit cell.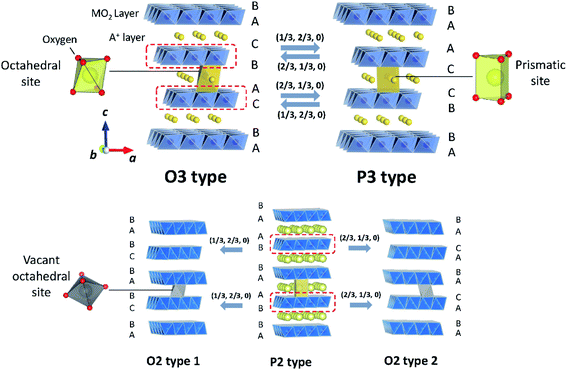 | ||
| Fig. 4 Crystal diagrams of O3, P3, P2 and O2 type layered oxides. The MO2 slabs are shown in blue. A+ and vacancies in A+ layers are shown in yellow and grey, respectively. Adopted with permission from ref. 8. Copyright 2014 American Chemical Society. | ||
In the O3 type structure, A+ ions occupy octahedral sites between MO2 slabs with AB CA BC oxygen stacking and three MO2 slabs are included in a hexagonal unit cell as seen in Fig. 4. Layered oxide materials commonly applied in commercialized LIBs such as LiCoO2, LiNi0.8Co0.15Al0.05O2 and LiNi1/3Mn1/3Co1/3O2 adopt the O3 type with a space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, also referred to as α-NaFeO2 type. To the best of our knowledge, LiMO2 compounds, prepared by solid state synthesis, only crystallize in O3 type among the four groups described above because of the small ionic radius of Li+. It is worth noting that there are other structure types such as γ-LiFeO2 type, in which Li+ and transition metal cations are ordered, and β-NaMnO2 type known as a corrugated (zig-zag) layer type.32–34 In the O3 type LixMO2, cationic mixing is often observed due to the similar radius size between Li+ and transition metal ion(s). In contrast, larger A+ such as Na+ and K+ show a large variety of transition metals adopting the O3 type structure without cation mixing.9 When Jahn–Teller active elements such as Mn3+ (3d4 in high spin) or Ni3+ (3d7 in low spin) consist of O3 type layered oxides, elongation or shortening of M–O bonds of MO6 octahedra induces the cooperative Jahn–Teller effect. The macroscopic distortion of hexagonal symmetry results in the compounds adopting a monoclinic lattice with the C2/m space group in the O′3 type structure, which is observed for NaMnO2 (ref. 35) and NaNiO2.36 Note that NaxCoO2 also crystallizes in the O′3 structure with a slightly deficient Na content.37
m, also referred to as α-NaFeO2 type. To the best of our knowledge, LiMO2 compounds, prepared by solid state synthesis, only crystallize in O3 type among the four groups described above because of the small ionic radius of Li+. It is worth noting that there are other structure types such as γ-LiFeO2 type, in which Li+ and transition metal cations are ordered, and β-NaMnO2 type known as a corrugated (zig-zag) layer type.32–34 In the O3 type LixMO2, cationic mixing is often observed due to the similar radius size between Li+ and transition metal ion(s). In contrast, larger A+ such as Na+ and K+ show a large variety of transition metals adopting the O3 type structure without cation mixing.9 When Jahn–Teller active elements such as Mn3+ (3d4 in high spin) or Ni3+ (3d7 in low spin) consist of O3 type layered oxides, elongation or shortening of M–O bonds of MO6 octahedra induces the cooperative Jahn–Teller effect. The macroscopic distortion of hexagonal symmetry results in the compounds adopting a monoclinic lattice with the C2/m space group in the O′3 type structure, which is observed for NaMnO2 (ref. 35) and NaNiO2.36 Note that NaxCoO2 also crystallizes in the O′3 structure with a slightly deficient Na content.37
In the P3 type structure, the number of MO2 slabs in a hexagonal unit cell with the R3m space group is three and A+ ions occupy trigonal prismatic sites between MO2 slabs with the AB BC CA array of oxygen packing along the c-axis. In contrast to LiMO2, NaxMO2 and KxMO2 can crystallize in P3 or P′3 type structures in as-synthesized materials due to their larger ionic radii. In the case of NaxMO2, P3 type is preferred when x < 0.5. Removal of alkali metal ions from the O3 type structure in general induces a structural change to the P3 structure through gliding of MO2 slabs without breaking of M–O bonds (Fig. 4). OP2 type is also reported as an intergrowth structure between O3 and P3 types upon charge/discharge. In an ideal OP2 structure, two types of A+ layers, O type and P type layers, are alternately stacked along the c-axis.38
The P2 type structure is favored for alkali metal deficient compositions, and therefore found for NaxMO2 (0.6 < x < 0.7) and KxMO2 where A+ ions occupy trigonal prismatic sites between MO2 layers with AB BA oxygen array stacking along the c-axis. In the P2 type structure, there are two MO2 slabs in a hexagonal unit cell with the space group of P63/mmc. The P2 phase transforms into the O2 phase upon extraction of A+ by gliding MO2 slabs. The gliding ideally occurs either (1/3, 2/3, 0) or (2/3, 1/3, 0) vector, leading to O2 type 1 or O2 type 2, respectively (Fig. 4).39 The formation of intermediate structure OP4 proceeds upon charge as well. An ideal OP4 type has prismatic and octahedral A+ layers, piled up alternately along the c-axis and two types of O2 layers are alternately stacked as octahedral A+ layers.38
The different polymorphs influence electrochemical performance. In reference to capacity, O3 type compounds deliver higher initial charge capacity due to the high concentration of A+ ions compared to A+ deficient phases (P2 or P3). On the other hand, A+ ions in prismatic sites enable the realization of larger reversible extraction of A+ from the structure and faster diffusion compared to those in octahedral sites. The absence of tetrahedral sites in P2 or P3 type structures prevents migration of transition metal ions from MO2 slabs to A+ layers and permits direct A+ migration to neighboring face-shared prismatic sites.
Table 2 summarizes structure types of AxMO2 (A = Li, Na or K, M = a single 3d transition metal and Rh, x ≤ 1) obtained from direct synthesis methods, not including the ion-exchange step, with a single 3d transition metal and Rh. As mentioned above, the size of A+ governs the structure of as-prepared materials, and therefore LixMO2 with the smallest Li+ crystallizes in the O3 structure which is a most thermodynamically stable phase. In contrast, KxMO2 and NaxMO2 can crystallize in P type structures. In particular, Na+ with an intermediate radius size permits a large variety of phases, drawing scientific interest.
| Atomic numberM (M = 3d metal and Rh) | 21Sc | 22Ti | 23V | 24Cr | 25Mn | 26Fe | 27Co | 28Ni | 29Cu | 45Rh |
|---|---|---|---|---|---|---|---|---|---|---|
| LixMO2 | — | — | O3 | O3 | — | — | O3 | O3 | — | O3 |
| NaxMO2 | O3 | O3 | O3 | O3 | O′3 | O3 | O3/O′3 | O′3 | O′3 | O3 |
| P′3 | P′3 | |||||||||
| P2/P′2 | P2 | |||||||||
| KxMO2 | O3 | — | — | O3/O′3 | — | — | — | O3 | ||
| P3/P′3 | P3/P′3 | P3 | ||||||||
| P′2 | P2/P′2 | P2 |
2.2. Different electrochemical features of AxMO2
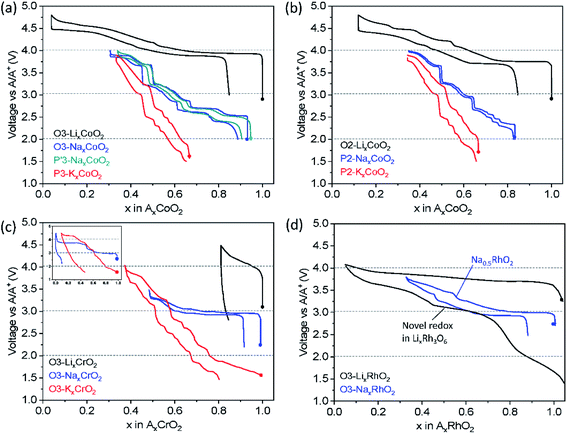
Fig. 5a shows charge/discharge profiles of AxCoO2 adopting the O3 or P(′)3 structure. O3 type NaxCoO2 shows a significantly lower operating voltage compared to that of LiCoO2. Given that both compounds are composed of Co with octahedral coordination and adopt the same O3 phase, the site energy of A+ and the coordination and bond lengths of A–O and M–O seem to be comparable. The lower working voltage in NaxCoO2 can be attributed to the changes in the redox energy of Co3+/4+. According to a paper by Goodenough et al., stronger covalent mixing of Co–O in the Na system raises Co–O antibonding orbital energy, and thus stronger Na+–Na+ repulsion increases the Co–O bond length, particularly at a higher Na+ content, rendering lower voltage than the counterpart in the Li system.40 In the same vein, P2 type NaxCoO2 and KxCoO2 display a lower voltage than O2 type LiCoO2 (Fig. 5b) due to more covalent Co–O bonds, weaker Lewis acidity of Na+ or K+ and stronger Na+–Na+ or K+–K+ repulsion than those related to Li+.
Another striking difference depending on the A+ ion is the charge/discharge voltage profile upon galvanostatic cycling: LiCoO2 exhibits smooth curves whereas the stepwise voltage profile is observed in NaxCoO2 and KxCoO2 regardless of the initial crystal structure type. The unique stepwise voltage curves are attributed to the A+-vacancy ordering for the peculiar A+ concentration such as 3/4, 5/8, 2/3, 4/7, 1/2, 1/3, etc.41–44 The voltage jumps are related to the formation of a highly stable phase in a narrow A+ concentration range surrounded by biphasic regimes that display voltage plateaus. During continuous changes in the concentration of A+ in AxCoO2, an AxCoO2 single-phase is feasible, resulting in slopy voltage curves. Clear voltage jumps are evidenced at the well-known compositions of P2 type Na1/2CoO2 and Na2/3CoO2 (ref. 41) (Fig. 5b) and the phase transformation from O3 to O′3 for NaxCoO2 results in the voltage plateau at 2.5 V (Fig. 5a).37
When a certain amount of Na+ ions are extracted, Na+ in NaxCoO2 favors prismatic sites,37,45 leading to similar voltage curve evolution as shown in O3 and P′3 type NaxCoO2 (Fig. 5a). The analogous voltage profiles in the range of x ≤ 2/3 in P′3 and P2 type NaxCoO2 (Fig. 5a and b, respectively) upon extraction/insertion of Na+ are probably due to fast and liquid-like Na+ diffusion in P′3 and P2 types and weaker interaction between Na+ and CoO2 slabs having a wider interlayer distance than those of O3 type. The comparable voltage curves for P3 and P2 type KxCoO2 (Fig. 5a and b, respectively) can be explained in the same way.
As shown in Fig. 5c, LiCrO2 shows unsatisfactory electrochemical performance with notable irreversible capacity on the first cycle irrespective of particle size.47,48 The main reason for the inferior discharge capacity is related to the irreversible structural change in the voltage range of 3.0–4.5 V (vs. Li/Li+). During delithiation of LiCrO2, oxidized Cr4+ (3d2) tends to undergo the disproportionation reaction, forming Cr3+ (3d3) and Cr6+ (3d0). Besides, the interlayer distance in LiCrO2 matches well with that in tetrahedral CrO42−, which can be a driving force to migrate Cr4+ (3d2) into the interstitial tetrahedral sites in Li layers in an irreversible disproportionation manner.47 Using high angle annular dark field (HAADF) scanning transmission electron microscopy (STEM) and DFT calculation, the Cr migration from transition metal layers to Li layers on the surface and the increased Li diffusion barrier are shown, which are responsible for the unsatisfactory electrochemical reactivity.48
In contrast to LiCrO2, NaCrO2 delivers a reasonable discharge capacity of ca. 110 mA h g−1, corresponding to 0.43 Na+ intercalation between 2.2 and 3.6 V (vs. Na/Na+). In this voltage range, the compound undergoes O3–O′3–P′3 phase transformation with two biphasic regimes while 0.52 Na+ is deintercalated. The structural evolution is reversible, leading to decent cycling performance.49,50 When the upper cut-off voltage is extended to 4.5 V (vs. Na/Na+), extremely small capacity is delivered on the first discharge. This is due to irreversible Cr migration induced by further phase transformation to O′3 beyond 3.6 V – in the O′3 phase vacant tetrahedral sites are formed by Na+ extraction where oxidized Cr cations favorably migrate from their original transition metal layers, eventually the migrated Cr cations move to vacant octahedral sites and become pinned.51 In addition, the significant voltage jump from 3.3 to 3.65 V (vs. Na/Na+) shown at x = 1/2 in NaxCrO2 (Fig. 5c inset) originates from the Na+-vacancy ordering, which is not observed in the counterpart of Li+.52
In the case of KCrO2, the stepwise voltage profile is more pronounced than the counterpart of Na+ which represents a more complex phase transition. In situ XRD reveals the complex phase transition with the sequence of O3–O′3–P′3–P3–P′3–P3–O3 in the voltage range of 1.5–4.0 V (vs. K/K+). This is probably attributed to the strong K+–K+ repulsion that requires several intermediate phases to minimize the K+–K+ repulsive interaction. The phase changes during charge are almost reversible except for the fact that the initial O3 phase is not recovered. Sluggish kinetics of K+ is considered reason for the incomplete intercalation. As observed in NaCrO2, once KCrO2 is charged to 4.5 V, an additional plateau at around 4.3 V is found and significantly reduced discharge capacity is delivered (Fig. 5c inset) because the amorphous-like phase formed at the end of charge to 4.5 V lasts until the following discharge to 1.5 V.46
In the case of O3 type NaRhO2, the charge/discharge profiles are reversible in the voltage range of 2.5–3.8 V (vs. Na/Na+) and a voltage jump is distinct when the Na+ content is about 0.5 as shown in Fig. 5d. No phase transformation is observed until removal of a Na+ content of 0.67 (charge to 3.8 V (vs. Na/Na+)), different from NaCoO2 in which gliding of CoO2 results in P(′)3 type phases upon desodiation.55 In addition, cation migration is expected to be prevented due to the increased covalency of Rh–O bonds using 5d electrons compared to that of 3d metal, Co–O.
From the above discussion by comparing charge/discharge profiles of AxCoO2, AxCrO2 and AxRhO2, we can understand that (i) larger A+ tends to exhibit more notable stepwise load curves, (ii) dynamic structural evolution is more complex with larger A+, (iii) the transformed phase at the end of charge dictates the reversibility of the structural transition, and (iv) using 4d or 5d transition metals might suppress MO2 gliding upon extraction/insertion of A+. From the practical points of view, layered oxides with a single metal, AxMO2, deliver generally limited capacity in Na and K cells. This drives spontaneously the research on layered oxides towards introducing multiple elements in transition metal layers.
2.3. Ordering in transition metal layers
Multiple elements in transition metal layers have been investigated as the electrochemical characteristics in the systems are significantly different from single transition metal systems, often resulting in enhanced performance. Thereby, we focus on binary and ternary systems in SIBs and PIBs here. In particular, transition metal ordering is often observed in binary systems (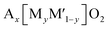 where square brackets represent transition metal layers). The differences in ionic radii as well as the valence between two cations composed of transition metal layers is believed to be a driving force to form the ordering. Honeycomb ordering is the most known in layered oxides where a cation (M) is surrounded by six cations (M′) and gives rise to the √3a × √3a superlattice. The ribbon superstructure is another ordering observed in the Li–Mn binary system where Li+ ions separate ribbons composed of four Mn cations. The two different types of transition metal ordering are presented in Fig. 6a and b. In binary systems with adjacent transition metals, most of the compounds exhibit a disordered phase except for Na2/3[Ni1/3Mn2/3]O2 (ref. 56) in which Ni2+ is a center of the honeycomb superlattice. The honeycomb ordering between Ni and Mn seems to induce a stronger coupling between MO2 layers, preventing the intercalation of water. In contrast, when Co is substituted for Ni, Mn3+ cations are formed and the superlattice of Ni(Co)–Mn ordering is suppressed, leading to a hydrophilic character.56 Among layered oxides for PIBs, K2/3[Te1/3Ni2/3]O2 (ref. 57) is an interesting example having the honeycomb ordering. These transition metal ordered materials often have unique features such as moisture/air stability and oxygen redox activity.
where square brackets represent transition metal layers). The differences in ionic radii as well as the valence between two cations composed of transition metal layers is believed to be a driving force to form the ordering. Honeycomb ordering is the most known in layered oxides where a cation (M) is surrounded by six cations (M′) and gives rise to the √3a × √3a superlattice. The ribbon superstructure is another ordering observed in the Li–Mn binary system where Li+ ions separate ribbons composed of four Mn cations. The two different types of transition metal ordering are presented in Fig. 6a and b. In binary systems with adjacent transition metals, most of the compounds exhibit a disordered phase except for Na2/3[Ni1/3Mn2/3]O2 (ref. 56) in which Ni2+ is a center of the honeycomb superlattice. The honeycomb ordering between Ni and Mn seems to induce a stronger coupling between MO2 layers, preventing the intercalation of water. In contrast, when Co is substituted for Ni, Mn3+ cations are formed and the superlattice of Ni(Co)–Mn ordering is suppressed, leading to a hydrophilic character.56 Among layered oxides for PIBs, K2/3[Te1/3Ni2/3]O2 (ref. 57) is an interesting example having the honeycomb ordering. These transition metal ordered materials often have unique features such as moisture/air stability and oxygen redox activity.
 | ||
| Fig. 6 Structural diagrams of (a) honeycomb and (b) ribbon ordering in the transition metal layers and (c) charged Na0.67[Mg0.28Mn0.72]O2 (Na0[Mg0.28Mn0.72]O2 adopting O2 type), highlighting a local oxygen environment coordinated octahedrally by two Mn and one Mg from the transition metal layer and three vacancies from the Na layer. Reprinted with permission from Springer Nature Customer Service Centre GmbH: Springer Nature, Nature Chemistry, ref. 60 copyright 2018. (d) Schematic charge/discharge curves of Li-rich and Na-rich layered oxides. Reprinted with permission from Springer Nature Customer Service Centre GmbH: Springer Nature, Nature, ref. 77 copyright 2019 (e) In-plane Mn migration (arrows) required to form O2 molecules (orange ellipses) in the transition metal layers of charged honeycomb ordered Na0.75[Li0.25Mn0.75]O2 and ribbon ordered Na0.6[Li0.2Mn0.8]O2. Reprinted with permission from Springer Nature Customer Service Centre GmbH: Springer Nature, Nature, ref. 73 copyright 2019. | ||
 .
To enhance the electrochemical activity of the AMO2 electrode, reversible redox of Mn+/m+ and O2−/(2−δ)− couples can be combined and has been investigated to date.58Table 3 summarizes the compounds not only having transition metal ordering but also exhibiting oxygen redox in the case of A = Na and K. Extensive theoretical studies together with experimental support have been carried out to explain the oxygen redox mechanism in layered oxides. Ceder and co-workers report that unhybridized O 2p orbitals, derived from the specific 180° Li–O–Li configurations in Li-rich layered oxides (one Li in transition metal layers and the other in Li layers), are responsible for the activation of the oxygen redox process.59 This mechanism can explain the oxygen redox activity in sodium layered oxides containing Li+ in transition metal layers. In the presence of specific Li–O–Na configurations, the energy level of orphaned O 2p orbitals is relatively higher than that of hybridized transition metal orbitals which trigger oxygen redox. In a similar vein, oxygen redox in the Mg–Mn binary systems can be attributed to the ionic Mg–O bonds that allow the O 2p orbitals to place at the top of the valence band upon extraction of Na+.60
.
To enhance the electrochemical activity of the AMO2 electrode, reversible redox of Mn+/m+ and O2−/(2−δ)− couples can be combined and has been investigated to date.58Table 3 summarizes the compounds not only having transition metal ordering but also exhibiting oxygen redox in the case of A = Na and K. Extensive theoretical studies together with experimental support have been carried out to explain the oxygen redox mechanism in layered oxides. Ceder and co-workers report that unhybridized O 2p orbitals, derived from the specific 180° Li–O–Li configurations in Li-rich layered oxides (one Li in transition metal layers and the other in Li layers), are responsible for the activation of the oxygen redox process.59 This mechanism can explain the oxygen redox activity in sodium layered oxides containing Li+ in transition metal layers. In the presence of specific Li–O–Na configurations, the energy level of orphaned O 2p orbitals is relatively higher than that of hybridized transition metal orbitals which trigger oxygen redox. In a similar vein, oxygen redox in the Mg–Mn binary systems can be attributed to the ionic Mg–O bonds that allow the O 2p orbitals to place at the top of the valence band upon extraction of Na+.60
| Composition | Ionic radii M/M′ (Å) in six-fold coordination | Ordering type | Oxygen redox activity | Lattice oxygen loss | Voltage hysteresis |
|---|---|---|---|---|---|
| Na[Li1/3Mn2/3]O2 (ref. 69) | 0.76/0.53 | Honeycomb | Active | O2 evolution | Significant |
| Na0.75[Li0.25Mn0.75]O2 (ref. 73) | 0.76/0.53 | Honeycomb | Active | Suppressed | Significant |
| Na0.6[Li0.2Mn0.8]O2 (ref. 73 and 76) | 0.76/0.53 | Ribbon | Active | Suppressed | Suppressed |
| Na2/3[Mg0.28Mn0.72]O2 (ref. 60) | 0.72/0.53 | Honeycomb | Active | Suppressed | Significant |
| Na[Na1/3Ru2/3]O2 (ref. 61) | 1.02/0.62 | Honeycomb | Active | Suppressed | Suppressed |
| Na[Na1/3Ir2/3]O2 (ref. 62) | 1.02/0.625 | Honeycomb | Active | Suppressed | Suppressed |
| Na2/3[Ni1/3Mn2/3]O2 (ref. 63–66) | 0.69/0.53 | Honeycomb | Active/inactive | O2 evolution/suppressed | Suppressed |
| K2/3[Te1/3Ni2/3]O2 (ref. 57) | 0.69/0.97 | Honeycomb | Active | — | Suppressed |
In the case of Na[Na1/3Ru2/3]O2, the honeycomb ordered phase is essential to trigger oxygen redox because the short O–O bonds are created only in the ordered phase, which raises unhybridized O 2p orbitals nearby the Fermi level. The honeycomb ordering is maintained between cationic vacancies and Ru cations after 1/3 Na+ extraction from the transition metal layers of [Na1/3Ru2/3]O2 slabs and leads to cooperative distortion, producing shorter O–O bonds.61 Similarly, the shorter O–O bonds are formed in the honeycomb ordered Na[Na1/3Ir2/3]O2 upon desodiation, featuring oxygen redox.62 Moreover, the stronger overlapping between Ir 5d and O 2p orbitals allows oxygen redox to trigger in the earlier charge state than the 4d Ru case – oxygen redox is activated after removal of 0.5 Na+ and 1 Na+ in the Na–Ir and Na–Ru binary systems, respectively.
Oxygen participation in the charge compensation mechanism in P2-type Na2/3[Ni1/3Mn2/3]O2 was first proposed by Lee et al.63 based on the electronic structure and density of state (DOS) calculation. However, whether oxygen redox is triggered or lattice oxygen loss dominates in the high voltage region is still under debate.64–66
Little investigation on oxygen redox has been performed in potassium layered oxides. Masesse et al. showed the participation of oxide anions in K2/3Te1/3Ni2/3O2via strong hybridization between Ni 3d and O 2p orbitals.57 Theoretical and experimental studies reveal that O 2p orbitals are in the vicinity of the Fermi level and reversible formation of ligand holes in O 2p bands during the first cycle.
Although oxygen redox represents a strategy to enhance the capacity of layered oxides via using cumulative cationic and anion redox processes, irreversible oxidation of the oxide anion, also referred to as lattice oxygen loss via O2 evolution, and the voltage hysteresis between oxidation and reduction processes are major drawbacks for better application.
In the case of Na-rich layered oxides with a 4d or 5d metal such as Na[Na1/3Ru2/3]O2 and Na[Na1/3Ir2/3]O2, ordering in the Na–Ru and Na–Ir slabs, respectively, becomes more pronounced upon desodiation, which is induced by the cooperative effect for maximizing the coulombic attraction between Na+ and transition metal vacancies and minimizing the coulombic repulsion between Na+ and Ru5+ or Ir5+. This leads to the reversible phase transition O3–O1–O′1 upon cycling and provides a rigid structure to stabilize oxygen redox without lattice oxygen loss.70
Recently, the importance of ordering in transition metal layers to alleviate the voltage hysteresis associated with cation migration has been reported by investigation of two compounds having a similar composition but adopting different transition metal ordering: honeycomb ordered Na0.75[Li0.25Mn0.75]O2 and ribbon ordered Na0.6[Li0.2Mn0.8]O2.73 In the honeycomb superlattice, Mn migration, primarily in-plane, forms vacancies that accommodate O2 molecules and the honeycomb ordering is lost upon charge. During discharge, the trapped O2 molecules in the bulk are reduced and Li+ returns to transition metal layers. However, the Li+ ions occupy the sites where Mn is displaced rather than their original sites. The discharge voltage for this process is much lower, leading to voltage hysteresis. On the other hand, the in-plane Mn migration in the ribbon superstructure is less likely than in the honeycomb superlattice because multiple Mn displacements via already filled sites are necessary in the former as shown in Fig. 6e. Thereby, the ribbon type ordering provides narrow polarization of oxygen redox, which is also revealed in the Li-rich system.78
For the compounds based on 4d or 5d metals, large delocalization of 4d or 5d orbitals permits a larger overlap with O 2p orbitals than 3d metals. This leads to a strong covalent character of M–O bonds that suppresses transition metal migration to interlayers, as observed in Na[Na1/3Ru2/3]O2,61,70 Na[Na1/3Ir2/3]O2 (ref. 62) and Li[Li1/3Ir2/3]O2.79 Additionally, the well maintained honeycomb superstructure upon desodiation as mentioned above is attributed to the absence of voltage hysteresis.
Given the examples above, transition metal ordering plays an important role in not only activating oxygen redox but also stabilizing its electrochemical activity via suppressing lattice oxygen loss and/or voltage hysteresis. To exploit these advantages, the design of materials should be coupled with development of ultra-high-resolution XAS and RIXS to explain the complete mechanism of oxygen redox. Furthermore, a stable electrolyte at very high voltage should be considered for accurate understanding without interference from parasitic electrolyte reactions.
2.4. Binary and ternary systems for improved electrochemical performance
Designing binary and ternary system materials has been one of the strategies to enhance electrochemical performance in SIBs and PIBs as reversible and stable crystal structures both in bulk and in local and sufficient kinetics strongly depend on the composed elements. In parallel, surface modification to stabilize the interface between the electrolyte and electrode material and decreasing the primary particle size have been widely applied to achieve satisfactory performance. In the current section, P2 type Na2/3[Ni1/3Mn2/3]O2 is selected as a model compound for SIBs to examine the role of an additional substitution and its influence on electrochemical properties since this compound has been considered as a possible candidate for positive electrode materials due to not only its high operating voltage (around 3.8 V vs. Na/Na+) and capacity (ca. 173 mA h g−1) but also its air stability that is an intrinsic advantage for mass production.39 As relatively fewer systematic studies have been carried out for layered oxides in PIBs, some examples exhibiting excellent performance are discussed, underlining the benefits of binary and ternary systems.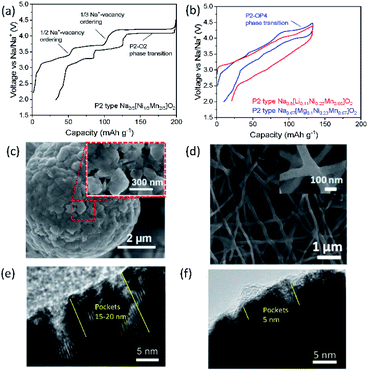 | ||
| Fig. 7 Typical charge/discharge curves for (a) P2 type Na2/3[Ni1/3Mn2/3]O2 and (b) Na0.8[Li0.12Ni0.22Mn0.66]O2 and Na0.67[Mg0.1Ni0.23Mn0.67]O2 in red and blue, respectively. SEM images showing (c) secondary particles assembled by primary nanoparticles in P2 type K0.65[Fe0.5Mn0.5]O2. Reprinted with permission from ref. 88. Copyright 2018 John Wiley and Sons, and (d) interconnected P3 type K0.7[Fe0.5Mn0.5]O2 nanowires. Reprinted with permission from ref. 89. Copyright 2017 American Chemical Society. TEM images of (e) P2 type Na2/3[Ni1/3Mn2/3]O2 and (f) P2 type Na2/3[Al1/18Ni11/36Mn23/36]O2 after 10 cycles in 2.0–4.5 V (vs. Na/Na+). (e) and (f) are adopted with permission from ref. 90. Copyright 2018 John Wiley and Sons. | ||
Using P2 type Na2/3[Ni1/3Mn2/3]O2 as a starting material, P2 type K0.75[Ni1/3Mn2/3]O2 is prepared using electrochemical ion-exchange by Myung and co-workers.85 After 20 cycles, ion-exchange is completed where the honeycomb ordering is expected to be retained and a larger interlayer distance is found due to larger K+. In contrast to Na2/3[Ni1/3Mn2/3]O2, there is no phase transformation to the O2 phase when K0.75[Ni1/3Mn2/3]O2 is charged to 4.3 V (vs. K/K+) because the formation of O2 is predicted to occur below 1.5 V and beyond 4.3 V (vs. K/K+) based on the computational studies. Therefore, a solid-solution reaction happens during cycling in the voltage range of 1.5–2.3 V with a voltage step due to the presence of ordering with a K+ content of 1/2 in P2 type K0.75[Ni1/3Mn2/3]O2. This leads to satisfactory cycling performance, retaining 86% of the initial capacity after 300 cycles at 20 mA g−1.
3. Polyanion compounds
While layered oxides have significant precedence in research and as commercial materials, they suffer from stacking modification with slab gliding or irreversible structural transformation when the number of extracted A+ is high. In contrast, polyanionic materials provide long-term structural stability and high thermal stability, which are their major advantages despite weight penalty. Polyanionic compounds possess an open framework structure consisting of MOx (M = transition metals) and (XOx)n (X = P, S, As, Si, Mo, or W) polyanionic groups. This 3D structure offers not only structural and thermal stabilities but also a large interstitial space to accommodate larger A+ during insertion reactions. In addition, the nature of the polyanionic groups permits tuning Mn+/(n+1)+ redox potentials, which represents a way to enhance the working voltage for positive electrode materials. There are so many types of polyanionic compounds due to the diversity of their composition and structure, and it is possible to fine-tune their electrochemical properties such as capacity, rate capability, and operating potential.In layered oxides, the selection of transition metals predominantly affects the working potential of the electrode and the cell voltage. In the same vein, the type of transition metal is essential to achieve high electrode-potential in polyanionic compounds. In addition to that, polyanionic compounds crystalize into many more structural types. Thereby, polyanionic compounds provide many more numerous ways to adjust the Mn+/(n+1)+ redox potential, which is highly correlated mainly with the transition metals and structural types. Depending on the structural type, the ionicity/covalency of the M–O bonds in the MOx polyhedron is varied. The three most important structural factors are (i) the type of ligand, (ii) the presence and number of oxygen atoms that are simultaneously shared by all MOx, XOx, and AOx polyhedra, called as commonly shared oxygen hereafter, and (iii) the sharing mode between adjacent MOx–MOx and the position of the ligand introduced into MOx.
As shown in Fig. 8a, the ligands include not only XOx oxyanionic groups but also –F− or –OH− that are more electronegative than –O2−. When XOx is coordinated to M, the higher electronegativity of the oxyanionic groups increases the ionic character of M–O bonds, significantly raising the Mn+/(n+1)+ redox potential as a primary inductive effect.93 The order of their electronegativity is (SiO4)4− < (BO3)3− < (PO4)3− < (P2O7)4− < (C2O4)2− < (SO4)2−, determined by the electronegativity of Si, B, P, C, and S which is 1.9, 2.04, 2.19, 2.55, and 2.58, respectively. Therefore, (SO4)2− containing polyanionic compounds exhibit a higher redox potential as long as other parameters, e.g. the valency of the redox center and the sharing mechanism, are comparable. Replacing oxygen with a highly electronegative anion, referred to as Y from now on, such as F− (3.98) and OH− (3.44) in the MOx polyhedron is also shown to raise the ionic character of M–O bonds and the Mn+/(n+1)+ redox potential.
The second major factor is the presence and the number of commonly shared oxygen (Fig. 8b), which raises the Mn+/(n+1)+ redox potential as the secondary inductive effect.94 When an A+ ion is coordinated to the oxygen commonly shared by both the MOx and XOx polyhedra, the ionic character of M–O bonds further increases. This extra effect beyond the primary inductive effect is called the secondary inductive effect. The higher number of the commonly shared oxygen increases the ionicity of M–O bonds.95 Of note, the number of commonly shared oxygen is normalized by the number of transition metals to avoid the effect of unit cell size throughout the section. Similarly, the electropositivity (low electronegativity close to zero) of A+ would affect the secondary inductive effect.
The third major factor of the positional effects is categorized into three: sharing types between two adjacent MOx polyhedra (Fig. 8c), sharing types between MOx and XOx polyhedra (Fig. 8d), and configuration types of substituted Y (Fig. 8e). First, the sharing types between MOx affect the distance between two neighboring M: M-to-M distance. In the edge- or face-sharing, the M-to-M distance is shorter than in the corner-sharing, which promotes symmetry change through the shifting of the M position systematically from its original position to reduce electrostatic repulsion between Mn+ and Mn+. The changes in the symmetry, namely distortion of MOx, lower the energy of antibonding molecular orbitals, leading to a higher Mn+/(n+1)+ redox potential.94 The effect of sharing type between MOx and XOx on the redox potential is also significant. When the MO6 shares the edge, face, or corner with the XO4, cationic repulsion between M and X increases the ionic character of M–O bonds in MO6, resulting in increased redox potentials. This effect is also more pronounced in edge- or face-sharing than corner-sharing. When two O atoms in MOx are substituted by a more electronegative element Y such as F and OH, two configurations exist based on the position of the substituted element. In the cis-configuration the substituted elements exist at an angle of Y–M–Y about 90° in the polyhedron, whereas in the trans-configuration, the Y–M–Y angle is approximately 180° (Fig. 8e). The cis-configuration tends to alter the symmetry of the polyhedron more significantly than the trans-configuration. For example, the MO4F2 octahedron with cis-configurated F has asymmetrical charge distribution compared to the MO4F2 octahedron with trans-configurated F. This asymmetrical charge distribution and the strong interaction between F–F in the cis-configuration leads to high distortion in the MO4F2 octahedron.96 As a result, the cis-configurated octahedron delivers a higher Mn+/(n+1)+ redox potential compared to the trans-configurated octahedron. Sometimes, the cis-configurated substituted elements are part of the edge- or face-sharing between two adjacent polyhedra. In this case, the effect of repulsion between two metals (M–M or M–X) on the redox potential is minor.94
In the following sections, we will review important polyanionic compounds classified by structure types, focusing on how the nature of transition metal affects electrochemical performance as well as how the ionicity/covalency of the M–O bonds in the MOx polyhedron influences the Mn+/(n+1)+ redox potential by presenting important examples.
3.1. Olivine related and amorphous types
To date, the most successful polyanionic material is triphylite LiFePO4 with its successful application in LIBs. LiFePO4 has an olivine-like structure based on a distorted oxygen hexagonal closed packing. However, unlike olivine Mg2SiO4 where Mg occupies both 4a and 4c octahedral sites (Fig. 9b), Li+ and Fe2+ ions separately occupy the 4a and 4c sites, respectively (Fig. 9a). LiFePO4 has a one-dimensional Li+ diffusion path along the b-axis.97 Despite its attractive properties such as high redox potential and excellent cycling stability, LiFePO4 shows key drawbacks, including low intrinsic electronic conductivity and anti-site defect formation that significantly impede Li+ diffusion.98,99 Various synthetic approaches have been employed to overcome the low electronic conductivity nature,100e.g. making composites using carbonaceous materials (carbon, graphite, carbon nanotube, etc.), metal particle dispersion on the surface, and doping of supervalent cations (Zn4+, Nb5+, Ti4+, Mg2+, Al3+). To enhance the Li+ diffusion, nanosizing is one of the strategies. As per previous reports, when the same concentration of Li/Fe anti-site defects is present, the nano-size LiFePO4 shows less trapped Li+ compared to the micron-size one, reducing the possibility of Li+ diffusion tunnel blocking.101 The nano-sized LiFePO4 may enhance its properties, but low electrode tap density significantly reduces the volumetric energy density. Lithiophilite LiMnPO4 also has a triphylite-type structure having distinctive Li+ and Mn2+ sites (Fig. 9c). The redox potential driven by Mn2+/3+ (4.1 V vs. Li/Li+) is higher than that of Fe2+/3+ (3.43 V vs. Li/Li+), but LiMnPO4 is a highly insulating material with a bandgap of 2 eV, and has structural instability in a fully charged state. During the charge, oxidation of Mn2+ generates Mn3+ (high spin) which is Jahn–Teller active in the MnO6 octahedra. Asymmetrical distribution of electron density leads to elongation of bonds between Mn3+ and ligands in the z-direction, called Jahn–Teller distortion. Due to the cooperative distortion of the MnO6 octahedron in Mn(III)PO4, the one-dimensional Li+ diffusion path shrinks, which is unfavorable for the subsequent lithiation process.102,103 Although triphylite-type LiCoPO4 and LiNiPO4 provide higher redox potentials, the lack of a stable electrolyte in the high voltage region hinders their practical application. In addition, Ni3+ has a high spin configuration in the NiO6 octahedron that has a strong Jahn–Teller distortion, hindering the one-dimensional Li+ diffusion path.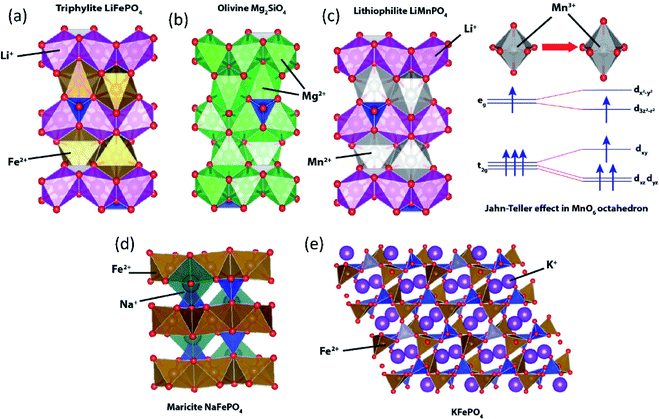 | ||
| Fig. 9 Structural illustration of (a) triphylite LiFePO4, (b) olivine Mg2SiO4, (c) lithiophilite LiMnPO4 with an inset showing Jahn–Teller distortion in MnO6, (d) maricite NaFePO4, and (e) KFePO4. | ||
Since the successful application of LiFePO4, its counterparts have been extensively investigated in SIBs. Similar to triphylite LiFePO4, maricite NaFePO4 also has an olivine-like structure. However, Na+ and Fe2+ ions occupy 4c and 4a octahedral sites, respectively (Fig. 9d), and the positions of the A+ and Fe2+ are opposite to those of the triphylite. In the maricite-type structure, parallel FeO6 chains are formed by FeO6 octahedral edge-sharing, and the PO4 tetrahedron connects three parallel FeO6 chains, which restrict the migration of Na+.104 Interestingly, it has been demonstrated that maricite NaFePO4 is transformed to amorphous FePO4 upon the first charge, which allows Na+ to hop between adjacent sites with lower activation energy along the b-axis.105 Triphylite-type NaFePO4 can be obtained by electrochemical or chemical ion exchange from triphylite LiFePO4 and this material delivers a discharge capacity of 154 mA h g−1,106 comparable to that of the amorphous compound.
In the case of KFePO4, synthesized by a solid-state reaction, it contains units of FeO4 tetrahedral groups linked by corner-sharing with another FeO4 and PO4 tetrahedral groups (Fig. 9e), different from the olivine-related types (triphylite and maricite types).107 KFePO4 (space group of P21/n) delivers very low capacity (20 mA h g−1) with a slopy voltage profile, indicating an unfavorable crystal structure for K+ extraction/insertion reactions. Recently, it has been reported that amorphous FePO4 and amorphous KFePO4 deliver 160 mA h g−1 and 90 mA h g−1, respectively, in PIBs.108 Once K+ inserted into the amorphous FePO4, it becomes a crystalline monoclinic KFe2(PO4)2 phase delivering a high reversible capacity.109 In 2018, our group demonstrated the K+ storage ability of the delithiated triphylite FePO4/C composite. The FePO4/C composite shows a very stable capacity of 120 mA h g−1 with a mid-point discharge voltage (corresponding to the voltage at SOC = 50%, Table 4) of 2.3 V (vs. K/K+).110 But, it shows very slopy charge/discharge curves, indicating that insertion of larger K+ into FePO4 lowers its crystallinity, accompanied by irreversible transformation into the phase with insufficient ionic diffusivity.
| Structure type | Material | Space group | Redox couple | Sharing mechanism between two neighbouring TM polyhedra | No. of commonly shared oxygen atoms | SIB/PIB | Mid-point discharge voltage | Theoretical (*)/initial experimental capacity (mA h g−1) | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Oc = MO6 octahedron; Te = MO4 tetrahedron; Sp = MO5 square pyramid; TeX = XO4 tetrahedron; Oc-cor-Oc = corner sharing two MO6 octahedra; Oc-cor[F]-Oc = F atom in the corner sharing bond between two octahedra; Oc-ed-Oc = edge sharing two MO6 octahedra. * Numbers of alkali metal ions were used for theoretical capacity calculation. | |||||||||
| Olivine and amorphous | NaFePO4 | Pnma | Fe2+/3+ | Oc-ed-Oc | 4 | SIB | 2.8 | 154 (1Na)/150 | 106 |
| Amorphous-FePO4 | — | Fe2+/3+ | — | — | SIB | 2.4 | 177 (1Na)/154 | 109 | |
| Amorphous-FePO4 | — | Fe2+/3+ | — | — | PIB | 2.5 | 177 (1K)/156 | 109 | |
| Hematiite-FePO4 | Pnma | Fe2+/3+ | Oc-ed-Oc | — | PIB | 2.3 | 177 (1K)/120 | 110 | |
| Amorphous-KFePO4 | — | Fe2+/3+ | — | — | PIB | 2.5 | 141 (1K)/90 | 108 | |
| NASICON | Na3V2(PO4)3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
V3+/4+ | Oc-cor-TeX-cor-Oc | 6 | SIB | 3.4 | 118 (2Na)/115 | 116 |
| Na3V2(PO4)3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
V2+/3+ | Oc-cor-TeX-cor-Oc | 6 | PIB | 1.4 | 113 (2K)/100 | This work | |
| K3V2(PO4)3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
V3+/4+ | Oc-cor-TeX-cor-Oc | 6 | PIB | 3.7 | 101 (2K)/80 | 119 | |
| NaTi2(PO4)3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
Ti3+/4+ | Oc-cor-TeX-cor-Oc | 6 | SIB | 2.1 | 133 (2Na)/130 | 120 | |
| NaFe2PO4(SO4)2 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
Fe2+/3+ | Oc-cor-TeX-cor-Oc | 3 | SIB | 3.1 | 100 (2Na)/90 | 123 | |
| Tavorite and triplite | NaVPO4F | I 4/mmm | V3+/4+ | Oc-cor-TeX-cor-Oc | 4 | SIB | 3.8 | 143 (2Na)/133 | 131 |
| NaFeSO4F | P21/c | Fe2+/3+ | Oc-cor[F]-Oc | 3 | SIB | 3.55 | 138 (1Na)/75 | 135 | |
| KTiOPO4 type | KTiOPO4 | Pna21 | Ti3+/4+ | Oc-cor-Oc | 3.5 | PIB | 0.8 | 135 (1K)/130 | 139 |
| KVOPO4 | Pna21 | V4+/5+ | Oc-cor-Oc | 3.5 | PIB | 3.95 | 133 (1K)/84 | 142 | |
| KVPO4F | Pna21 | V3+/4+ | Oc-cor[F]-Oc | 4 | PIB | 4.05 | 131 (1K)/92 | 142 | |
| KTiPO4F | Pna21 | Ti3+/4+ | Oc-cor[F]-Oc | 4 | PIB | 3 | 133 (1K)/97 | 144 | |
| KFeSO4F | Pna21 | Fe3+/4+ | Oc-cor[F]-Oc | 3 | PIB | 3.6 | 127 (1K)/111 | 145 | |
| Alluaudite | Na0.67FePO4 | C2/c | Fe2+/3+ | Oc-ed-Oc | 4 | SIB | 2.5 | 154 (1Na)/143 | 147 |
| Na2Fe2(SO4)3 | C2/c | Fe2+/3+ | Oc-ed-Oc | 4 | SIB | 3.8 | 120 (2Na)/102 | 148 | |
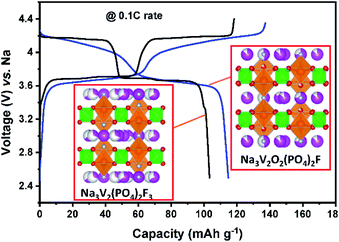
| Others | Na3V2(PO4)2F3 | Cmcm | V3+/4+ | Oc-cor[F]-Oc | 4 | SIB | 3.75 | 128 (2Na)/114 | 152 |
| Na3V2(PO4)2F3 | Cmcm | V3+/4+ | Oc-cor[F]-Oc | 4 | PIB | 3.7 | 128 (2Na)/100 | 154 | |
| Na3V2O2x(PO4)2F3−2x | Cmcm | V3+/4+ | Oc-cor[F]-Oc | 4 | SIB | 3.6 | 130 (2Na)/125 | 153 | |
| Na3V2O2x(PO4)2F3−2x | Cmcm | V3+/4+ | Oc-cor[F]-Oc | 4 | PIB | 3.8 | 130 (2Na)/118 | 154 | |
| Na2FeP2O7 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Fe2+/3+ | Oc-cor-TeX-cor-Oc | 5 | SIB | 2.9 | 97 (2Na)/84 | 157 | |
| Na2FeP2O7 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Fe2+/3+ | Oc-cor-TeX-cor-Oc | 5 | PIB | 2.8 | 97 (2Na)/77 | 159 | |
| Na2MnP2O7 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Mn2+/3+ | Oc-cor-TeX-cor-Oc | 5 | SIB | 3.4 | 93 (2Na)/80 | 160 | |
| Na2CoP2O7 | Pna21 | Co2+/3+ | Te-cor-TeX-cor-Te | 4 | SIB | 4 | 96 (2Na)/78 | 161 | |
| Na4Fe3(PO4)2(P2O7) | Pn21a | Fe2+/3+ | Oc-cor-Sp | 3 | SIB | 3.1 | 129 (3Na)/100 | 165 | |
| Na4Fe3(PO4)2(P2O7) | Pn21a | Fe2+/3+ | Oc-cor-Sp | 3 | PIB | 2.8 | 129 (3Na)/118 | 165 | |
| KVP2O7 | P21/c | V3+/4+ | Oc-cor-TeX-cor-Oc | 5 | PIB | 4.5 | 101 (1K)/60 | 170 | |
3.2. NASICON type
Na1+xZr2SixP3−xO12 is a promising sodium super ion conductor, so-called NASICON.111 The general formula of NASICON type compounds is AxM2(XO4)3, where A is the alkali metal, alkaline earth metal, or vacancy, M is any of the trivalent, tetravalent, or pentavalent transition metal alone or in combination, and X is one of P, S, Si, or As.112 The valence of transition metals is varied between divalent and pentavalent to realize charge neutrality in the compounds. The NASICON type structure (Fig. 10a) consists of a three-dimensional network made up of MO6 octahedra sharing all their corners with XO4 tetrahedra and vice versa to form so-called lantern units (M2(XO4)3). The lantern units are aligned parallel to each other, offering a free space for A+ migration, and the number of commonly shared oxygen of six.113 Despite the high value, its effect on redox potential is negligible because the MO6 octahedron shares its six ligand (O) commonly with other polyhedral groups, and thereby the covalency of six M–O bonds is equal. NASICON type materials have been promising electrode materials due to their high ionic conductivity and structural stability. However, their low-activity polarons for electron transfer due to the absence of direct contact between MO6 octahedra leads to low electronic conductivity.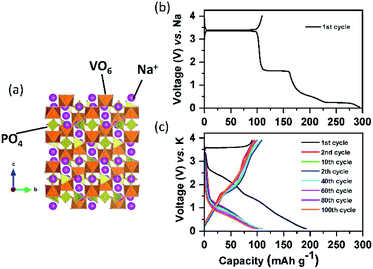 | ||
| Fig. 10 (a) Structural diagram of Na3V2(PO4)3; charge/discharge curves of the carbon coated Na3V2(PO4)3 composite in the (b) SIB and (c) PIB. | ||
Since lithium vanadium phosphate, Li3V2(PO4)3 (LVP) is the first positive electrode material applied to LIBs among the NASICON type compounds, its electrochemical behaviors will be compared to those of Na and K counterparts. LVP displays a voltage plateau at around 3.7 V (vs. Li/Li+) based on the V3+/4+ redox potential, corresponding to a two-phase transition between the compositions of Li3V2(PO4)3 and LiV2(PO4)3.114,115 Sodium vanadium phosphate, Na3V2(PO4)3 (NVP) exhibits exactly the same reaction with a flat voltage plateau at about 3.4 V (vs. Na/Na+), corresponding to the reactions from Na3V2(PO4)3 to NaV2(PO4)3 and vice versa.116 Inspired by NVP, potassium vanadium phosphate, K3V2(PO4)3 (KVP), has been studied by a few research groups117,118 and is usually prepared by the sol–gel reaction. In contrast to the NVP case, asymmetric charge/discharge profiles are observed. Upon depotassiation, KVP delivers a capacity of 55 mA h g−1 (about half of its theoretical capacity), with reaction from K3V2(PO4)3 to K1.5V2(PO4)3, which is reversible, and its mid-point discharge voltage is 3.7 V (vs. K/K+). During potassiation, extra K+ can be inserted into the K3V2(PO4)3 using the V2+/3+ redox couple, forming the final composition of K4V2(PO4)3 and its mid-point discharge voltage is 1.4 V (vs. K/K+).119 Our group studied a Na-based carbon-coated NVP composite in both the NIB and PIB. As shown in Fig. 10b, NVP shows three flat voltage plateaus on the first cycle, corresponding to three different two-phase reactions during sodiation in the voltage window of 3.9–0.05 V (vs. Na/Na+). In contrast, NVP shows no clear plateaus upon potassiation between 3.9 and 0.05 V (vs. K/K+) (Fig. 10c). Although the exact exchange mechanism between Na+ and K+ upon depotassiation is under investigation, the sloping voltage profiles upon potassiation imply that K+ can insert into the structure due to the large enough empty space. From comparison between the first and second cycle, there is a high irreversible capacity due to the electrolyte decomposition in the first discharge and therefore in the second cycle onwards less K+ is reversibly inserted into the NVP structure. Similar to A3V2(PO4)3, ATi2(PO4)3 (A = Li and Na) compounds, adopting the NASICON structure, are also electrochemically active in LIBs and SIBs based on the Ti3+/4+ redox couple of 2.4 V (vs. Li/Li+) and 2.1 V (vs. Na/Na+). As a characteristic of NASICON type compounds, NaTi2(PO4)3 also shows an excellent 3D open crystal structure, leading to superior A+ migration.120
There are only two NASICON type sulfates reported for alkali metal ion battery applications: Fe2(SO4)3 and NaFe2PO4(SO4)2. The former one contains no A+ at the pristine state, but Li+ and Na+ can be inserted and extracted reversibly in the LIB and SIB, respectively. It is shown that the maximum insertion is restrained to about 1 Li+ and 0.6 Na+ per Fe2(SO4)3.121 Both, Fe2(SO4)2 and NaFe2PO4(SO4)2 demonstrate the same average Fe2+/3+ redox potential of 3.1 V (vs. Na/Na+).122,123 Even though high electronegativity (SO4)2− may increase the Fe–O bond ionicity, all the six oxygens of FeO6 participate in primary and secondary inductive effects, and thereby the resultant effect of (SO4)2− on the redox centre is insignificant in the NASICON phase. This is different from the cases in the alluaudite phase that will be discussed later. NaFe2PO4(MoO4)2 is another example having the Fe2+/3+ redox couple (2.5 V vs. Na/Na+) and crystallizing in the NASICON type structure. Astonishingly, NaFe2PO4(MoO4)2 has high electronic conductivity due to the formation of Mo 4d orbitals at the bottom of the conduction band, which results in the formation of electronically connective MoO4 groups in this compound.124 Despite the general trend of low electronic conductivity for NASICON type compounds, the NASICON structure offers a rich ability for chemical substitution, which can be an effective way to increase the working voltage of the positive electrodes as shown in Na2TiV(PO4)3, Na3FeV(PO4)3, Na4MnV(PO4)3, Na3MnZr(PO4)3, and Na3MnTi(PO4)3.112,125 In addition, various methods such as carbon coating and reducing the particle size have been shown to improve the electronic conductivity, eventually providing satisfactory electrochemical properties.100,126
3.3. Tavorite and triplite types
Tavorite is a type of structure for polyanion compounds with a general formula of AMXO4Y (A = Li, Na, K; M = Fe, V, Mn, Ti; X = P, S; Y = OH, O, F). The Y atoms are coordinated to M to form the trans-coordinated MO4F2 octahedron and infinite [Y–MO4–Y–MO4–] chains, and XO4 tetrahedra connect to these chains to form a 3D network as well as channels for A+ diffusion. The number of commonly shared oxygen by MO4F2, AOX, and XO4 polyhedral groups is three in the tavorite structured materials. Tavorite-type phosphates such as LiFePO4F127 and LiFePO4OH have been studied as positive electrode materials for LIBs. Unlike the materials mentioned above, the Fe ions in these phosphate materials are initially trivalent, and the electrochemical test generally starts from lithiation. These materials show an average lithiation potential of 2.7 and 2.6 V (vs. Li/Li+),128 respectively, via Fe2+/3+ reduction. Comparing the redox potentials of LiFePO4F and LiFePO4OH, it is clear that the relatively high electronegativity of F provides a slightly higher redox potential in a given structure. Vanadium based tavorite LiVPO4F and NaVPO4F are also reported as high-capacity positive electrode materials. LiVPO4F and NaVPO4F deliver an average voltage of 4.3 V (vs. Li/Li+) and 3.8 V (vs. Na/Na+), respectively. In particular, the high working voltage in NaVPO4F can be explained by the primary inductive effect of F and the four commonly shared oxygen.129–131LiFeSO4F is an interesting material as it can crystallize in either tavorite or triplite type, as shown in Fig. 11a and b, respectively. An interesting point is that triplite LiFeSO4F shows a higher voltage of 3.9 V (vs. Li/Li+) than that of tavorite LiFeSO4F (3.6 V vs. Li/Li+) and the voltage is the highest among Fe-based polyanion compounds reported. This particularly high voltage relies on its crystal structure. In the triplite LiFeSO4F, two F atoms are arranged into a FeO4F2 octahedron in a cis-coordination, and are shared by two adjacent FeO4F2 octahedra to form a shared F–F edge.94 Furthermore, the number of the commonly shared oxygen is three, while the tavorite type has two commonly shared oxygen. The voltage increase in triplite LiFeSO4F is directly related to the cis-configurations of the F in FeO4F2, not because of the strong Fe3+–Fe3+ repulsive interactions in the edge-sharing mechanism.132,133 Preliminary electrochemical properties of tavorite type NaFeSO4F are reported, and 55% of the theoretical capacity is achieved with a plateau near 3.55 V (vs. Na/Na+).134 The Na+ migration energy in NaFeSO4F is ca. 0.9 eV; higher than the Li+ migration energy of 0.4 eV in LiFeSO4F. The difference is due to the size effect of A+ in the same structure – small size Li+ favors the 3D pathway in LiFeSO4F while larger size Na+ mobility takes place within the 1D channels in NaFeSO4F.135
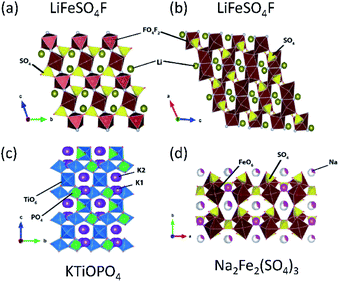 | ||
| Fig. 11 Typical compounds representing (a) tavorite, (b) triplite, (c) KTiOPO4, and (d) alluaudite types. | ||
3.4. KTiOPO4 type
The KTiOPO4 structure comprises a three-dimensional framework of MO4Y2 octahedra and XO4 tetrahedra with a formula of AMXO4Y. The corner-sharing MO4Y2–MO4Y2 octahedra form infinite chains along the bc plane, and A+ ions are located in the channels (Fig. 11c), providing extraordinary mobility of K+ ions: high ionic conductivity around 10−4 S cm−1 at room temperature.136 Hence, this structural type is attractive for designing electrode materials for alkali metal ion batteries.137,138 Even though the KTiOPO4 structure has four commonly shared oxygens, the covalency of Ti–O bonds slightly decreases due to the distortion in the octahedron induced by cis- and trans-configurated oxygen compared to other frameworks. KTiOPO4 itself demonstrates a mid-point discharge voltage of 0.8 V (vs. K/K+) via the Ti3+/4+ redox reaction, thereby being unsuitable for a positive electrode material despite a discharge capacity of 135 mA h g−1.139 Replacing V for Ti in the same structure enables the V4+/5+ redox couple to be used as shown in LiVOPO4, NaVOPO4, and KVOPO4 with the mid-point discharge voltage of 3.9 V (vs. Li/Li+),140 3.5 V (vs. Na/Na+),141 and 3.95 V (vs. K/K+).142 In particular, the KTiOPO4 type materials are attractive for PIBs, and one of the promising materials is KVPO4F. This compound shows a wider open framework than KVOPO4, assembled by corner-sharing V3+O4F2 octahedra and PO4 tetrahedra, lowering the activation energy of K+.143 In addition, its average high mid-point discharge voltage of 4.05 V (vs. K/K+) is due to the highly electronegative F atoms. KTiPO4F shows cis- and trans-configuration effects since two different TiO4F2 octahedra exist as a result of the F configuration within the TiO4F2 octahedra: one with cis-configurated F and another with trans-configurated F. The Ti3+/4+ redox in trans-configurated TiO4F2 octahedra is reflected in the lower slopy plateau at 2.9 V (vs. K/K+) while that in cis-configurated octahedra shows a plateau around 3.5 V (vs. K/K+).144 Similar influence is observed in KFeSO4F, i.e., Fe2+/3+ redox potential at 3.5 and 4.1 V (vs. K/K+) originating from the trans- and the cis-configuration of F, respectively.1453.5. Alluaudite type
Alluaudite type compounds have the general formula of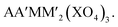 The structure consists of infinite chains of edge-sharing MO6 and M'O6 octahedra, and XO4 tetrahedra link these chains to form a 3D architecture with two tunnels where the A and A′ ions are located (Fig. 11d). So far, only one alluaudite structured material has been reported for LIBs, i.e., Li0.67FePO4, prepared by the soft chemical ion-exchange method.146 Its redox potential of Fe2+/3+ is lower (3.0 vs. Li/Li+) than that of triphylite LiFePO4 (3.4 vs. Li/Li+) probably due to the less localized charge in Fe as a result of edge-sharing of all FeO6 octahedra, and the reduced inductive effect due to the corner-sharing between FeO6 and PO4 in the alluaudite.146 In SIBs, the alluaudite type Na0.67FePO4/CNT composite electrode delivers a discharge capacity of 143 mA h g−1 based on the Fe2+/3+ redox reaction (2.5 V vs. Na/Na+) and exhibits stable cyclability.147 Yamada et al. reported that the alluaudite type Na2Fe2(SO4)3 demonstrates the redox potential of Fe2+/3+ at 3.8 V (vs. Na/Na+) and fast kinetics, which draws much attention for the low-cost Fe-based sulfates for SIBs.148 Another alluaudite type Fe-based sulfate is Na2Fe(SO4)2 (can be described as Na3Fe1.5(SO4)3) that displays a high operating voltage of around 3.6 V (vs. Na/Na+) based on the Fe2+/3+ redox couple as well as superior thermal stability (around 580 °C).149 These alluaudite type sulfate compounds show higher voltage compared to the NASICON type NaxFe2(SO4)3 due to the more covalent Fe–O bonds originating from the six equal corner sharing mechanism between FeO6–SO4 polyhedra and four commonly shared oxygens.121
The structure consists of infinite chains of edge-sharing MO6 and M'O6 octahedra, and XO4 tetrahedra link these chains to form a 3D architecture with two tunnels where the A and A′ ions are located (Fig. 11d). So far, only one alluaudite structured material has been reported for LIBs, i.e., Li0.67FePO4, prepared by the soft chemical ion-exchange method.146 Its redox potential of Fe2+/3+ is lower (3.0 vs. Li/Li+) than that of triphylite LiFePO4 (3.4 vs. Li/Li+) probably due to the less localized charge in Fe as a result of edge-sharing of all FeO6 octahedra, and the reduced inductive effect due to the corner-sharing between FeO6 and PO4 in the alluaudite.146 In SIBs, the alluaudite type Na0.67FePO4/CNT composite electrode delivers a discharge capacity of 143 mA h g−1 based on the Fe2+/3+ redox reaction (2.5 V vs. Na/Na+) and exhibits stable cyclability.147 Yamada et al. reported that the alluaudite type Na2Fe2(SO4)3 demonstrates the redox potential of Fe2+/3+ at 3.8 V (vs. Na/Na+) and fast kinetics, which draws much attention for the low-cost Fe-based sulfates for SIBs.148 Another alluaudite type Fe-based sulfate is Na2Fe(SO4)2 (can be described as Na3Fe1.5(SO4)3) that displays a high operating voltage of around 3.6 V (vs. Na/Na+) based on the Fe2+/3+ redox couple as well as superior thermal stability (around 580 °C).149 These alluaudite type sulfate compounds show higher voltage compared to the NASICON type NaxFe2(SO4)3 due to the more covalent Fe–O bonds originating from the six equal corner sharing mechanism between FeO6–SO4 polyhedra and four commonly shared oxygens.121
3.6. Other types
Sodium vanadium oxyfluoride phosphates, Na3V2O2x(PO4)2F3−2x (0 ≤ x ≤ 1),150,151 have been gaining much attention since the successful implementation of Na3V2(PO4)2F3 in Tiamat's prototype SIB cells. In the structure of the Na3V2O2x(PO4)2F3−2x family, MO4F2 octahedra are corner-shared via their trans-configurated F and form a M2O8F3 octahedron dimer. This dimer is bridged by PO4 tetrahedra, building a 3D framework and offering Na+ migration channels along the a and b-axes. The number of the commonly shared oxygen is four. All compounds in this family have three Na+ ions occupying two different sites: two fully filled Na(1) sites and two half-filled Na(2) sites. Even though one can see two main voltage plateaus at 3.6 V and 4.1 V in the charge–discharge curves, precise mechanistic studies reveal more voltage plateaus and very complicated reactions, which include the multiple redox processes of vanadium ions through vanadium's disproportionation (2V4+ → V3+ + V5+) and simultaneous extraction/insertion of Na+ from/into the both sites (Fig. 12).152 The phase evolution is rather complicated: three biphasic reactions of Na3V2(PO4)2F3–Na2.4V2(PO4)2F3, Na2.4V2(PO4)2F3–Na2.2V2(PO4)2F3, and Na2.2V2(PO4)2F3–Na2V2(PO4)2F3 in the lower voltage region and two biphasic and one monophasic reactions of Na2V2(PO4)2F3–Na1.8V2(PO4)2F3, NayV2(PO4)2F3 (1.8 < y < 1.3), and Na1.3V2(PO4)2F3–NaV2(PO4)2F3 in the higher voltage region during the charging process.153 Recently, our group observed excellent electrochemical properties of the Na3V2O2x(PO4)2F3−2x/MWCNT composite in K cells. The composite electrode delivers an initial discharge capacity of 118 mA h g−1 at 13 mA g−1 with a mid-point discharge voltage of 3.8 V (vs. K/K+). During the first charge, two Na+ ions are extracted from Na3V2O2x(PO4)2F3−2x and form NaV2O2x(PO4)2F3−2x. The remaining one Na+ is exchanged with K+ during subsequent discharge, producing K3V2O2x(PO4)2F3−2x. Once K3V2O2x(PO4)2F3−2x is formed insertion/extraction of K+ take place reversibly, maintaining K3V2O2x(PO4)2F3−2x at the end of 4th discharge.154In 2010, Yamada and co-workers successfully developed a new polyanionic group, pyrophosphate (P2O7)4− to increase the Mn+/(n+1)+ redox potential.155 They have reported the electrochemical and structural characteristics of new pyrophosphate compounds A2MnP2O7 (A = Li and Na; M = Fe, Mn and Co) synthesized by a conventional solid–state reaction. In α-Li2FeP2O7 (space group of P21/n), FeO6 octahedra and FeO5 pyramids are connected in an edge-sharing manner. The redox potential of Fe in the FeO5 pyramid is affected by the commonly shared oxygen atoms and more attractive interaction between Fe and O atoms in FeO5 than in FeO6 delivers a higher redox potential of Fe2+/3+. Based on the calculation, 3.9 V (vs. Li/Li+) is anticipated, however the experimental redox voltage is 3.5 V (vs. Li/Li+) due to structural rearrangement related to Fe migration.156 In SIBs, β-Na2FeP2O7 (space group of P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) shows two different voltage plateaus at 2.9 V and 2.5 V (vs. Na/Na+), because of two distinct constituent Fe sites.157,158 Na2FeP2O7 also shows K+ storage ability with a mid-point discharge voltage of 2.8 V (vs. K/K+), however huge polarization and a slopy voltage plateau are observed due to the size of K+.159 As expected, replacing Fe with Mn or Co provides a higher mid-point discharge voltage, which is shown in Na2MnP2O7 with 3.4 V (vs. Na/Na+)160 and Na2CoP2O7 with 4.0 V (vs. Na/Na+).161 Na2CoP2O7 adopts a layered structure where each of four O in a CoO4 tetrahedron is linked with four of the surrounding PO4 units to form [Co(P2O7)]22 layers parallel to 〈001〉 and stacked alternately with a layer of Na. In this layered structure, Na2CoP2O7 demonstrates mid-point discharge voltage at 4.0 V (vs. Na/Na+) via Co2+/3+. This difference might be explained by the less ionic character of Co–O bonds in the tetrahedral coordination.162
) shows two different voltage plateaus at 2.9 V and 2.5 V (vs. Na/Na+), because of two distinct constituent Fe sites.157,158 Na2FeP2O7 also shows K+ storage ability with a mid-point discharge voltage of 2.8 V (vs. K/K+), however huge polarization and a slopy voltage plateau are observed due to the size of K+.159 As expected, replacing Fe with Mn or Co provides a higher mid-point discharge voltage, which is shown in Na2MnP2O7 with 3.4 V (vs. Na/Na+)160 and Na2CoP2O7 with 4.0 V (vs. Na/Na+).161 Na2CoP2O7 adopts a layered structure where each of four O in a CoO4 tetrahedron is linked with four of the surrounding PO4 units to form [Co(P2O7)]22 layers parallel to 〈001〉 and stacked alternately with a layer of Na. In this layered structure, Na2CoP2O7 demonstrates mid-point discharge voltage at 4.0 V (vs. Na/Na+) via Co2+/3+. This difference might be explained by the less ionic character of Co–O bonds in the tetrahedral coordination.162
Mixed phosphates of Na4M3(PO4)2(P2O7) using M2+/3+ have emerged as promising positive electrode materials for NIBs, which are unique frameworks only obtained in the Na system using direct synthetic methods. In particular, cost effective Fe-containing Na4Fe3(PO4)2(P2O7) shows low volume change during desodiation/sodiation (<4%) via a one-phase reaction and superior thermal stability.163,164 The trivial volume variation is attributed to the P2O7 bitetrahedron that is able to rotate and distort to accommodate the structural change in the desodiated phase of NaFe3(PO4)2(P2O7) in a reversible way.165 The replacement of Fe with Co166 or Ni167 raises the M2+/3+ redox potential from 3.2 to 4.5 or 4.8 V (vs. Na/Na+), respectively. However, electrochemical performances of Na4Co3(PO4)2(P2O7) and Na4Ni3(PO4)2(P2O7) are not as good as Na4Fe3(PO4)2(P2O7), and the Co containing compound exhibits complex phase transformation upon charge including four biphasic and a solid-solution reactions.168,169
Park et al. carried out computation studies to propose suitable high voltage polyanionic compounds for PIBs.170 They found seven electrochemically active pyrophosphate compounds (KCrP2O7, KFeP2O7, KTiP2O7, KVP2O7, KMoP2O7, K2(VO)3(P2O7)2, and K2MnP2O7). Among these, redox potentials of KCrP2O7 and KFeP2O7 are suggested to be beyond the stability window of common electrolytes. Experimentally, KVP2O7 is shown to deliver 60% of its theoretical capacity (based on V3+/4+) with a mid-point discharge voltage of 4.5 V (vs. K/K+).170 Structural investigation reveals that KVP2O7 crystallizes in the monoclinic phase in which VO6 octahedral groups corner-share with the P2O7 diphosphate group and have one-dimensional diffusion pathways along the 〈001〉 direction. The monoclinic KVP2O7 undergoes reversible phase transformation into triclinic (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) K0.4VP2O7 at the fully depotassiated state.
) K0.4VP2O7 at the fully depotassiated state.
Overall, polyanionic compounds deliver a high redox potential along with high structural stability, and in consequence high energy density and higher thermal stability related to battery safety. However, they have inherently low electronic conductivity and should be prepared along with different carbonaceous materials to provide efficient electron conduction paths in the composite electrode.
4. Prussian blue analogues
As discussed in the previous polyanion compound section, open structures are preferable for the electrochemical insertion of larger A+ such as Na+ and K+. Among the various 3D framework materials, open-channel hexacyanometallate compounds, also known as PBAs, have been studied as Li+,171 Na+,172 and K+173–175 insertion hosts. Generally, Prussian blue (KxFe[Fe(CN)6]y) is well known as a traditional pigment. Although it comprises cyanide, it is not toxic because of the extraordinary stability of the [Fe(CN)6]4−/3− complex. Various PBAs containing different metals have also been reported. The chemical formula of PBAs is represented as AxM1[M2(CN)6]y·nH2O (0 ≤ x ≤ 2, y ≤ 1), where A is typically an alkali metal, and M1 and M2 can be various metals such as Ti, V, Cr, Fe, Co, Ni, Cu, and Zn. AxM1[M2(CN)6]y·nH2O is abbreviated as M1M2–PBA or AM1M2–PBA for simplicity hereafter.Fig. 13a and b illustrate a typical crystal structure of A0M1[M2(CN)6] and A2M1[M2(CN)6], respectively. PBAs have 3D open-frameworks in which M1N6 and M2C6 octahedra are linked via cyano ligands.176 The framework structure provides an open 3D channel available for mobile metal diffusion, which is suitable for the diffusion of large ions. Another feature of PBAs is the different spin states of the transition metals in the M1N6 and M2C6 octahedra, which is explained by the ligand field theory. For transition metals such as Fe and Mn, the high-spin (HS) M1 is located in the M1N6 octahedron, while the low-spin (LS) M2 is located in the M2C6 octahedron owing to their respective weak N-coordinated and strong C-coordinated ligand fields.177 PBAs usually have the [M2(CN)6]n− anion vacancy in the framework as shown in Fig. 13c. In addition, the framework contains two kinds of crystal water, i.e., interstitial water in the interstitial site and coordinated water bound to M1 metal next to the anion vacancy (Fig. 13c).
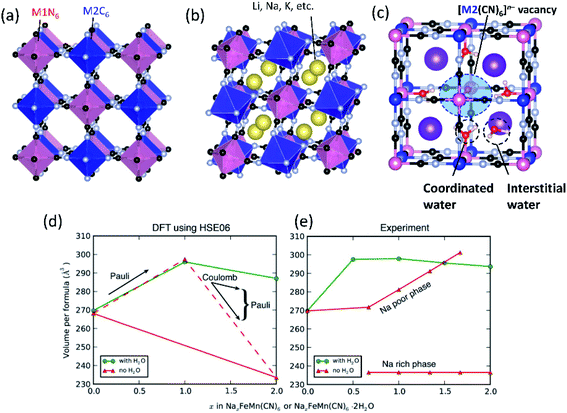 | ||
| Fig. 13 Crystal structures of (a) A0M1[M2(CN)6] and (b) A2M1[M2(CN)6], where A is an alkali metal, and M1 and M2 can be various metals. The blue and pink polyhedra represent M1N6 and M2C6, while the yellow spheres represent alkali metals. (a) and (b) are reproduced with permission from ref. 4. Copyright 2020 American Chemical Society. (c) Structure of the domain with the [M2(CN)6]n− vacancy, where oxygen and hydrogen atoms of interstitial and coordinated water are represented as red and pale pink spheres, respectively. Volume change comparison of NaMnFe–PBA between (d) theory and (e) experiment. In the DFT results, the solid lines represent the average volume of the formula unit in the crystal under equilibrium conditions. The dashed red line is out of equilibrium, in which the half-filled Na structure, slightly above the convex hull, is assumed to be formed. In the experimental results, the volume of the Na poor and rich phases is determined separately, and the value of x is an average of these two phases. (d) and (e) are reproduced with permission from ref. 176. Copyright 2015 American Chemical Society. | ||
Typical PBAs whose alkali metal content is ≤ 1.5 per formula possess a cubic structure (space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) in which all the octahedra are arranged linearly (Fig. 13a). On the other hand, the octahedra rotate cooperatively in the alkali metal-rich phase, resulting in monoclinic (space group of P21/n) or rhombohedral (typically the space group of R
m) in which all the octahedra are arranged linearly (Fig. 13a). On the other hand, the octahedra rotate cooperatively in the alkali metal-rich phase, resulting in monoclinic (space group of P21/n) or rhombohedral (typically the space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ; Fig. 13b) structures. For example, Na-rich phases have monoclinic structures when water molecules are in the interstitial site (interstitial water), while dehydrated Na-rich PBAs have rhombohedral structures whose lattice volume per formula is smaller than that of the monoclinic phase.176,178 This structural change is explained by Song et al. using experiments and DFT calculations as follows. Fig. 13d and e compare the calculated and experimental volume of the NaMnFe–PBA crystal with or without interstitial H2O at different Na contents. The DFT calculation shows that the volume of the Na-free structure is essentially the same with and without interstitial H2O. In the fully sodiated state, the volume of the hydrated phase is larger than that of the desodiated phase. The calculation results are found to be in quantitative agreement with the experimental data (Fig. 13e). The volume reduction of the dehydrated structure indicates that there is a strong coulombic interaction between the intercalated Na+ and the host framework. On the other hand, the presence of interstitial H2O in the lattice suppresses the lattice contraction due to the strong Pauli repulsion. Similar to the Na-poor PBAs adopting a cubic phase, K-poor PBAs have a cubic structure. However, K-rich PBAs have monoclinic structures, regardless of the presence of interstitial H2O.174,175,179,180 This phenomenon is explained by the large ionic radius of K+, which increases the Pauli repulsion in the lattice and prevents lattice shrinkage,178 and the formation of a monoclinic phase with a larger lattice volume than that of the rhombohedral phase. Furthermore, most K-rich PBAs contain significantly less interstitial water174,175,179 than Na-rich PBAs, which typically contain about 2 mol interstitial water per formula unit.178 These facts indicate that K+ and water molecules rarely occupy the interstitial sites of the PBAs simultaneously, because of the limited interstitial space formed by the [Fe(CN)6] vacancy.
; Fig. 13b) structures. For example, Na-rich phases have monoclinic structures when water molecules are in the interstitial site (interstitial water), while dehydrated Na-rich PBAs have rhombohedral structures whose lattice volume per formula is smaller than that of the monoclinic phase.176,178 This structural change is explained by Song et al. using experiments and DFT calculations as follows. Fig. 13d and e compare the calculated and experimental volume of the NaMnFe–PBA crystal with or without interstitial H2O at different Na contents. The DFT calculation shows that the volume of the Na-free structure is essentially the same with and without interstitial H2O. In the fully sodiated state, the volume of the hydrated phase is larger than that of the desodiated phase. The calculation results are found to be in quantitative agreement with the experimental data (Fig. 13e). The volume reduction of the dehydrated structure indicates that there is a strong coulombic interaction between the intercalated Na+ and the host framework. On the other hand, the presence of interstitial H2O in the lattice suppresses the lattice contraction due to the strong Pauli repulsion. Similar to the Na-poor PBAs adopting a cubic phase, K-poor PBAs have a cubic structure. However, K-rich PBAs have monoclinic structures, regardless of the presence of interstitial H2O.174,175,179,180 This phenomenon is explained by the large ionic radius of K+, which increases the Pauli repulsion in the lattice and prevents lattice shrinkage,178 and the formation of a monoclinic phase with a larger lattice volume than that of the rhombohedral phase. Furthermore, most K-rich PBAs contain significantly less interstitial water174,175,179 than Na-rich PBAs, which typically contain about 2 mol interstitial water per formula unit.178 These facts indicate that K+ and water molecules rarely occupy the interstitial sites of the PBAs simultaneously, because of the limited interstitial space formed by the [Fe(CN)6] vacancy.
Based on the features of PBAs described above, the material design of PBAs is achieved by varying transition metal species, the amount of crystal water, the type and content of alkali metals, and the number of anion vacancies. The varied transition metals result in a wide variety of redox potentials on Na+ and K+ insertion. Among the reported PBAs, A2Mn[Fe(CN)6] and A2Fe[Fe(CN)6] have attracted attention because of their high reversible capacity and suitable high potential based on Fe2+/3+ and Mn2+/3+ redox.175,177,178,181–183Fig. 14a shows the charge–discharge curves of K2Mn[Fe(CN)6] (KMnFe–PBA) and K2Fe[Fe(CN)6] (KFeFe–PBA) in K cells.175 KFeFe–PBA shows two voltage plateaus at around 3.3 and 3.8 V, which are attributed to HS Fe2+/3+ and LS Fe2+/3+, respectively.177 As shown in Fig. 14b, in the half-discharged state (K1Fe(III)[Fe(II)(CN)6]) the high redox voltage of LS Fe2+/3+ is due to the stable electronic state (t2g)6 and low energy level of the t2g orbital caused by the large ligand field splitting. KMnFe–PBA shows two voltage plateaus at ca. 3.8 and 4.1 V. The plateau at ca. 3.8 V is attributed to LS Fe2+/3+, whereas the higher voltage plateau at ca. 4.1 V is attributed to HS Mn2+/3+ (Fig. 14). The higher redox potential of HS Mn2+/3+ in K2Mn[Fe(CN)6] than HS Fe2+/3+ in K2Fe[Fe(CN)6] results in a higher working potential of K2Mn[Fe(CN)6] than that of K2Fe[Fe(CN)6]. The correlation between the redox potential and transition metals is quite similar to Na cases. Thus, K2Mn[Fe(CN)6] and Na2Mn[Fe(CN)6] are promising materials in terms of their high redox potential for the positive electrode in a full cell.
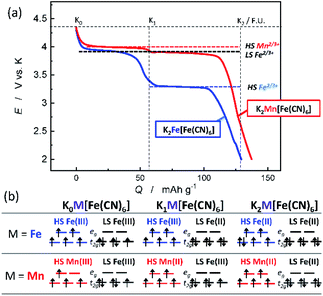 | ||
| Fig. 14 (a) Typical discharge curves of KFeFe–PBA and KMnFe–PBA in K cells. (b) Electronic structures of KxM[Fe(CN)6], where x = 0, 1, 2, and M = Fe or Mn. | ||
In addition to the transition metal species, the effects of interstitial water, alkali metal species, and anion vacancies on Na+ and K+ insertion have been investigated. In 2015, Song et al. reported a significant impact of interstitial water of NaMnFe–PBA on electrochemical properties.178Fig. 15a and b show the charge/discharge curves of hydrated NaMnFe–PBA (Na1.89Mn[Fe(CN)6]0.97·1.87H2O) and dehydrated (Na1.89Mn[Fe(CN)6]0.97) in Na cells. The hydrated sample exhibits two slopy voltage plateaus in the range of 3.17–3.45 and 3.5–3.8 V, whereas the dehydrated sample shows a single clear plateau around 3.5 V. Soft XAS reveals that the Fe and Mn redox reactions in hydrated electrodes are separated to the lower and higher voltage plateaus, respectively. In contrast, mixed Fe and Mn redox in the same voltage range is found for the dehydrated system.184 Since the t2g orbital of C-coordinated LS Fe2+ has a low energy level due to the strong ligand field, the LS Fe2+/3+ exhibits a relatively high redox potential in the case of the dehydrated sample. Thus, the redox potential of LS Fe2+/3+ is competitive with that of HS Mn2+/3+, eventually generating a single potential merged from the two potentials in the dehydrated NaMnFe–PBA. In contrast, the existence of interstitial water is believed to dilute the strong ligand field, resulting in a gap between the redox potentials of Fe2+/3+ and Mn2+/3+.184 The structural change caused by the interstitial water would also affect the change in the redox potential. Although hydrated NaMnFe–PBA shows a smaller volume change of about 10% during the charge/discharge process than dehydrated NaMnFe–PBA (ca. 27%), the release of crystal water into the electrolyte and the structural change to the dehydrated phase could lead to capacity degradation. Future studies would clarify the effects of volume change and crystal water release on the capacity degradation to develop long-life PBA materials for SIBs. In contrast to the significant effect of interstitial water of Na–PBAs, the interstitial water has no significant influence on the electrochemical performance of KMnFe–PBA in K half-cells,180 which could be due to the fact that the large K+ and water molecules hardly occupy the same interstitial sites of the PBA simultaneously.
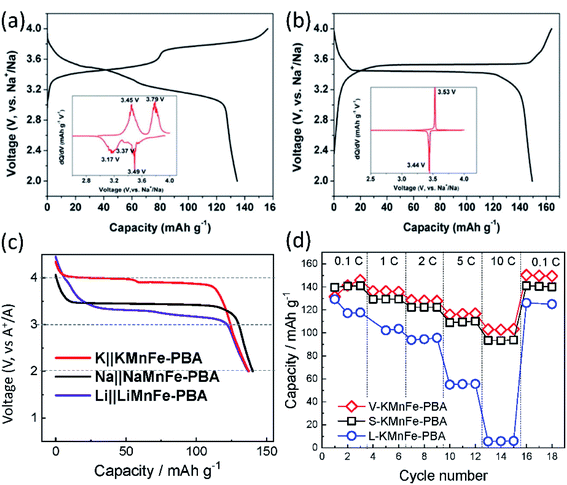 | ||
| Fig. 15 Initial charge/discharge profiles of (a) hydrated NaMnFe–PBA and (b) dehydrated NaMnFe–PBA. Differential versus voltage (dQ/dV) plots are shown in the insets (a) and (b) are reproduced with permission from ref. 178. Copyright 2015 American Chemical Society. (c) Galvanostatic discharge curves of LixMn[Fe(CN)6]y (LiMnFe–PBA), NaxMn[Fe(CN)6]y (NaMnFe–PBA), and K1.75Mn[Fe(CN)6]0.93 (KMnFe–PBA) in nonaqueous Li, Na, and K cells, respectively. (d) Variations of discharge capacity of S-KMnFe–PBA, L-KMnFe–PBA, and V-KMnFe–PBA. The electrodes were charged at 0.1C (15.5 mA g−1) and discharged at different discharge current densities. Reproduced with permission from ref. 188. Copyright 2021 Wiley-VCH. | ||
Since the open-framework structure of PBAs suits reversible storage of different cations, including Li+, Na+, and K+, we compare the electrochemical properties of different A+ insertions in nonaqueous electrolytes. Fig. 15c summarizes the charge/discharge curves of LixMn[Fe(CN)6]y (LiMnFe–PBA), NaxMn[Fe(CN)6]y (NaMnFe–PBA), and K1.75Mn[Fe(CN)6]0.93 (KMnFe–PBA) in the Li, Na, and K cells, respectively. The NaMnFe–PBA and KMnFe–PBAs were synthesized by a simple precipitation method. On the other hand, LiMnFe–PBA was synthesized via electrochemical ionic exchange in the K cell because it is hardly obtained via a simple precipitation method. Fig. 15c illustrates that LiMnFe–PBA, NaMnFe–PBA, and KMnFe–PBA deliver similar discharge capacities of 137, 140, and 137 mA h g−1, respectively. The Mn–Fe-based PBAs exhibit average discharge voltages of 3.3, 3.4 (3.7 V vs. Li), and 3.8 V (3.7 V vs. Li) in the Li, Na, and K cells, respectively. The specific energy densities of LiMnFe–PBA, NaMnFe–PBA, and KMnFe–PBA were 446, 472, and 521 W h kg−1 in the Li-, Na-, and K-metal cells, respectively. These results indicate that PBAs are promising electrode materials, especially for high-energy density SIBs and PIBs.
The effect of anion vacancies on Na+ insertion performance has been extensively studied, and several studies prove that anion-vacancy free (stoichiometric) Na–PBAs demonstrate larger capacity and better capacity retention in the repeated cycles than the nonstoichiometric Na–PBAs with anion vacancies.177,183,185 This larger reversible capacity is attributed to a larger fraction of redox-active Fe in [Fe(CN)6] vacancy-free samples.183 Similar to Na–PBAs, a previous study shows that K–PBAs with few anion vacancies exhibit a large reversible capacity.186 Additionally, it has been suggested that the anion vacancies promote the diffusion of K+.187,188 To fully understand the effect of anion vacancies on the K+ insertion, independent control of the number of anion vacancies and particle size is essential. This is because these two factors generally have a strong negative correlation, i.e., samples with a small particle size have many anion vacancies and vice versa. Thus, our group synthesized three KMnFe–PBAs whose particle size and the number of anion vacancies are varied by employing precipitation synthesis with addition of a suitable amount of chelate agent and the Na/K ion exchange route.188 The chemical composition of the three samples, small (S)-, large (L)-, and anion-vacant (V)-KMnFe–PBAs, are estimated to be K1.9Mn[Fe(CN)6]1.0, K1.8Mn[Fe(CN)6]0.99□0.01, and Na0.10K1.6Mn[Fe(CN)6]0.85□0.15, respectively after drying at 200 °C. The particle size of S-KMnFe–PBA ranges in 100–200 nm, whereas the particle size of L- and V-KMnFe–PBA is approximately 1–2 μm. Thus, the effects of particle size and anion vacancies are investigated by comparing S-KMnFe–PBA with L-KMnFe–PBA and L-KMnFe–PBA with V-KMnFe–PBA, respectively. Fig. 15d displays the variation in discharge capacities at different discharge rates from 0.1 to 10C and a constant charge rate at 0.1C. The V-KMnFe–PBA electrode demonstrates superior rate performance to L-KMnFe–PBA and is competitive with that of S-KMnFe–PBA, consisting of much smaller particles. The superior rate performance of V-KMnFe–PBA is attributed to the enhanced K+ diffusion in the lattice with anion vacancies based on the galvanostatic intermittent titration technique measurements and DFT calculation results.188 These results prove that the appropriate number of anion vacancies promotes K+ insertion into PBAs, which is different from the sodium case.
Overall, PBAs are potential positive electrode materials for SIBs and PIBs because of their relatively high gravimetric energy density based on the Fe2+/3+ and Mn2+/3+ redox and good rate and cycle performance. As a Chinese company, CATL, announced the commercialization of SIBs using PBA as the positive electrode material in July 2021, practical development is expected to be accelerated based on the development of advanced SIB/PIB materials.
5. Carbon-based negative electrode materials
5.1. Types of carbon applied for batteries
While significant effort is being made towards improving and understanding positive electrode material performance for emerging SIBs and PIBs, researchers are also approaching better performance for negative electrode materials. As with positive electrode materials, the structure is key to the interaction with different A+ and not all electrode materials are equally suitable for Li+, Na+ and K+ ions.21,189–192 In this section, we discuss carbon-based negative electrode materials which continue to be heavily explored due to their wide array of structure and morphological variability, continued application in modern day LIBs, and promising performance within both SIBs and PIBs.191,193,194 Aside from being made of an abundant and sustainable material,195,196 carbon-based negative electrode materials take advantage of multiple features including low cost, good chemical stability, high conductivity, and large specific surface area.8,191,193 Carbon materials applied in batteries include a variety of structures ranging in dimensionality (e.g. 3D, 2D), order (e.g. long or short range ordering), and heteroatom doping (e.g. N or O adatoms). Among highly ordered carbons, the most common material is based on graphite (Fig. 16a), a negative electrode material extensively applied in commercial LIBs.191,197 Graphitic carbons are based on a 3D crystalline structure with layered domains of sp2-hybridized carbon (graphene) that typically follows hexagonal AB stacking (a.k.a. Bernal stacking or 2H) for synthetic graphite;198,199 though alternative stacking, e.g. ABC or rhombohedral (3R), is also found for multi-layered graphene and natural graphite.200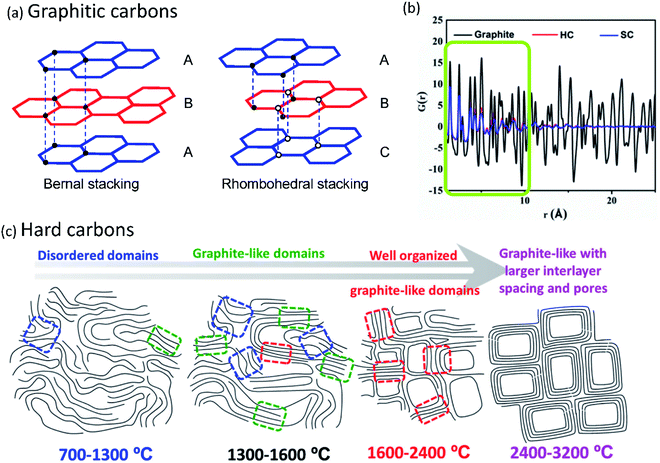 | ||
| Fig. 16 Structural differences for graphitic and hard carbons. (a) Structure and stacking of graphite. (b) Neutron total scattering showing short- and long-range ordering in different forms of carbon. Reprinted with permission from ref. 272. Copyright 2017 American Chemical Society. (c) Structure of hard carbons prepared with increasing temperature. | ||
The other most common carbon-based electrode materials being applied and explored for battery applications are those based on hard carbons. Unlike graphite, hard carbons do not display a long-range periodic structure in plane or along the stacking direction (Fig. 16b). The name ‘hard carbons’ for these materials derives from their often observed mechanical hardness and original patent,201 though they can be relatively soft when prepared under low-temperature conditions. More appropriately, hard carbons can be labelled as non-graphitizable; they do not change to a graphite structure even at very high temperatures (e.g. 3000 °C) as demonstrated long ago in the studies of Rosalind Franklin.202 Many of the structural features found in hard carbons including amorphous regions (sp3) with randomly aligned sp2 graphitic microdomains, pore structures, and defect content, are directly impacted by the preparation temperature (Fig. 16c). In contrast, ‘soft carbons’ have a structure which enables greater mobility in the carbon atoms to rearrange into graphite at temperatures between 1500 and 3000 °C. Preparation of soft carbons under low temperature preparation shows some similar features to hard carbons and can even form hard carbons when heated under an oxygen environment.
The structure of carbon-based materials heavily determines the energy storage mechanism and thus understanding relationships between the structure and performance becomes essential for improving their performance inside batteries. In the following sections, we outline the main progress with different types of carbon-based anode materials applied in LIBs, SIBs and PIBs, discuss their limitations, and highlight research efforts to push these materials to higher performance.
5.2. Graphitic electrodes for Li+, Na+, and K+
Graphite remains one of the most common anode materials for LIBs191,197 and also is a promising candidate for PIBs.4,21,192,203,204 The graphite structure features weak van der Waals bonding in the vertical direction between the graphene sheets producing an average interlayer spacing of approximately 3.35 Å. When the graphite electrode is charged, the layers are filled by the intercalated alkali metal atoms (A) (Fig. 17a) and the interlayer spacing increases to accommodate the insertion, as confirmed with in situ/operando XRD methods.7,205–208 This process follows a staging mechanism where alkali metal atoms order within domains in the graphite crystal structure and initially are accompanied by empty layers between the A-filled regions forming a series of stages or graphite intercalation compounds (A-GICs), e.g. KC36, KC24, KC8.21,203,209 The stage-number signifies the number of layers in between the A layers, e.g. stage-4 has three empty layers between the subsequent A-filled layers within a four graphene layer domain. Moving from Li to the much larger K leads to an increase in the interlayer distance upon intercalation and some differences in the staging process (Fig. 17a).21,205 The increased A size also impacts the distance between adjacent A atoms relative to the surrounding carbon atoms,210 and this leads to a lower number of intercalated A from LiC6 with a theoretical capacity of 372 mA h g−1 to KC8 with a capacity near 279 mA h g−1.21,203 Ultimately, the matching of the graphite structure to the intercalated A and chemical affinities are key to the electrochemical (de)intercalation process, where interactions of graphite with A energetically compete with A-to-A and A-to-solvent interactions. The mismatch in structure leads to unfavorable thermodynamic interactions between graphite and Na and poor capacity access during cycling (Fig. 17b), though Na+ is smaller in ionic radius than K+.210–213 Na-GICs have a lower energetic stability and their calculated formation potentials are shown to be below that of sodium metal.211–215 As such, most research efforts have focused on applying graphite with K+ and Li+ for better cyclability and capacity access.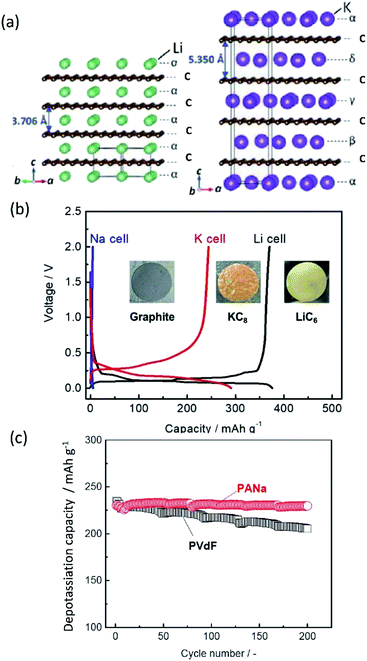 | ||
| Fig. 17 Comparison of Li, Na and K interaction in the graphite electrode. (a) Difference in inter-layer distance and ordering of alkali metal atoms within the lattice for stage-1 Li-GIC (LiC6) and K-GIC (KC8). The organization of Li atoms in subsequent layers is identical, denoted as alpha, while K atoms organize into 4 unique layers with offset positions relative to graphite, denoted as α, β, γ, and δ. C represents a graphene layer. (b) Charge/discharge curves in a K-cell with graphite. Reprinted with permission from ref. 7. Copyright 2018 John Wiley and Sons. (c) Comparison of binder impact on graphite cycling between poly(vinylidene fluoride) (PVDF) and sodium polyacrylate (PANa). (a) and (c) are reproduced with permission from ref. 205. Copyright 2021, Royal Society of Chemistry. | ||
Considering the volume expansion that occurs within graphite during A+ insertion, the role of the binder becomes vital in maintaining the electrode structure during cycling.5,216–218 In general, the binder is a polymeric material that functions by adhering the electrode particles together with the current collector; while at the same time, enabling flow of A+ and solvent molecules to/from the bulk electrolyte. At times, binders also incorporate conductive additives, especially for poorly conductive materials, e.g. oxides used as positive electrodes. Commercial binders include polyvinylidene fluoride (PVDF), carboxyl methylcellulose (CMC), and styrene-butadiene rubber (SBR).216 As seen in Fig. 17c, the choice of binder can significantly impact the capacity retention of the electrodes during cycling.219 Binders become even more important when considering large increases in interlayer distance, as in the K+ case, and for some of the emerging high capacity negative electrode materials which undergo more significant volume changes during cycling, e.g. Si, P, etc.216,217,220,221 Also, the binder choice can have a direct impact on the forming interphase structures on carbon-based electrodes.222–225 Recent efforts have pushed to better understand the role of the binder, improve its preparation, and provide more functionality beyond acting as a glue, such as interphase stabilization and inherent conductivity.216,226–228 Ultimately, the role of the binder remains somewhat overlooked, though it seems to play an important role in achieving higher performance.
In addition, solvated Na+ ions can interact favorably and form stable intercalation compounds with graphite when their insertion is accompanied by co-intercalating solvent molecules. The reversible formation of these structures, known as ternary graphite intercalation compounds (t-GICs), was first pioneered in the work by Jache and Adelhelm.229 It is reported that t-GICs can be formed in a diglyme electrolyte (Fig. 18a) showing reversible insertion of Na+ with a structure of Na(diglyme)2C20 and capacity close to 100 mA h g−1 at 0.1C for 1000 cycles. These solvated Na+ ions are much larger than the native Na+, resulting in expansion of the interlayer spacing to very large distances (>10 nm) to accommodate the Na(diglyme)2 insertion (Fig. 18b).230,231 To date, several ether solvents have been demonstrated to reversibly co-intercalate with Na+ (Fig. 18c).230,232,233 The co-intercalation process occurs due to a high Na-solvent solvation energy which maintains a stable Na-solvent structure during insertion.230,234 In a Na-ion full cell like graphite/Na+-diglyme/NaMO2, asymmetric reactions of co-intercalation and solvent-free intercalation at graphite and NaMO2 electrodes, respectively, will cause a change in diglyme concentration in the electrolyte, which may be an issue for stable battery operation. Recent research efforts have focused on improving the binder to accommodate this breathing process of large expansion and shrinkage and on manipulation of the material interlayer spacing.235,236 Likewise, Li+ and K+ can form t-GICs.229,237–239 While all three A+ ions show similar initial capacities, the cyclability of Li+t-GICs tends to be unstable due to the strong interactions between graphite and Li+ resulting in separation and free solvent that remains in the graphite structure.237,240 On the other hand, both Na+ and K+t-GICs show good cyclability at high rates. Nevertheless, ether-based electrolytes remain limited in their application toward actual batteries due to their narrow voltage windows compared with carbonate ester-based electrolytes.
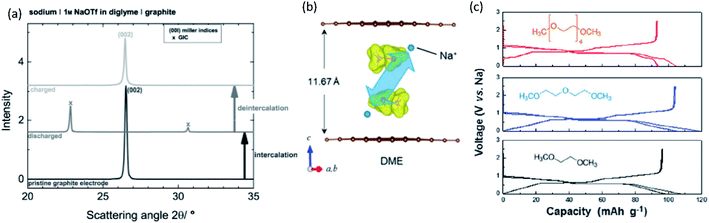 | ||
| Fig. 18 Na+ intercalation into graphite via solvent co-intercalation. (a) Diffraction patterns of graphite electrodes in 1 M sodium triflate (NaOTf) in diglyme. Bottom: pristine graphite electrode, middle: charged to 0.01 V (vs. Na/Na+), top: discharged to 3.0 V (vs. Na/Na+). Reprinted with permission from ref. 229. Copyright 2014 John Wiley and Sons. (b) Structure of co-intercalated Na+ in dimethyl ether (DME). (c) Na+ co-intercalation with graphite during charge/discharge in ether-based solvents of varying chain length; tetraethylene glycol dimethyl ether (red), diethylene glycol dimethyl ether (blue), and dimethoxyethane (black). (b) and (c) reproduced from ref. 230. Copyright 2015, Royal Society of Chemistry. | ||
5.3. Hard carbon electrodes for Li+, Na+, and K+
Hard carbons are promising alternatives to graphite with improved compatibility with Na+.189,241,242 They have already been applied as commercialized negative electrodes in LIBs and continue to be used for high power applications.243 Currently, hard carbons are the negative electrodes of choice and only materials likely to be commercialized for SIBs due to their promising electrochemical properties including: a low working potential, high capacity, good cycling stability;8,10,190 and their preparation from environmentally friendly, low cost sources.244–246While graphitic carbons mostly rely on (de)intercalation to store energy, hard carbons show a more complex mechanism involving multiple presumed ion storage modes.194,247–249 Depending on the hard carbon structure, the overall charge/discharge response may result from cumulative reactions including: (i) adsorption/desorption to heteroatom, edge and defect structures, (ii) (de)intercalation processes and (iii) pore-filling.189,194,249 The (de)intercalation process involves insertion into layered structures of the hard carbon that tends to display greater disorder and interlayer spacing than graphite.247,248,250 The A+ adsorption process involves cations adsorbing at edge sites and defects within the pore structure.249,251 Depending on the adsorption site, A+ adsorption can either irreversibly trap A+ ions or enable rapid A+ migration.251 The pore-filling process involves adsorption and gradual filling of the pore structures with A+ leading to high capacities >400 mA h g−1.252,253
As seen in Fig. 19a, the electrochemical behavior for this complex mechanism can be broken down into different regions.253,254 An initial sloping region (red part of the curve) is attributed to adsorption on defects in the pore wall and at edge sites, and A+ intercalation into defective graphite-like domains.253 As such, this process is highly dependent on the amount and type of defects in the material. Thereafter, the plateau region involves intercalation into graphitic domains or the formation of island-shaped clusters in the pore wall (blue part of the curve) followed by eventual A+ filling of the pore structure (green part of the curve).194,255 To account for observed electrochemical behaviors for various hard carbons, multiple mechanisms incorporating these reactions have been proposed including: adsorption-pore filling,249 adsorption-intercalation250 and intercalation-pore filling or the “house of cards” model.247,248 Considering the vast number of hard carbons that have been explored some materials may show different mechanisms or predominant reactions that are dependent on their structure and energetics for each process.193,241,242
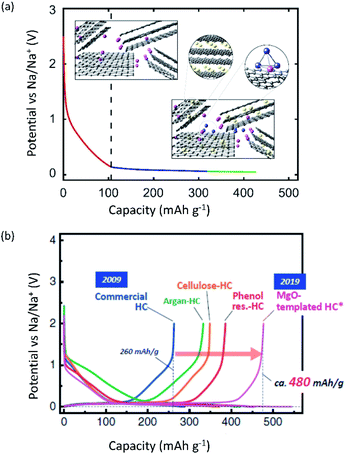 | ||
| Fig. 19 Impact of the carbon structure on capacity. (a) Proposed alkali ion storage mechanism of hard carbon electrodes. Reprinted with permission from Springer Nature Customer Service Centre GmbH: Springer Nature, npj Computational Materials, ref. 253. Copyright 2021. (b) Cycling behavior of hard carbons prepared with different precursors. Reproduced from ref. 256. | ||
The structure and performance are highly impacted by the preparation precursors and temperature as presented in Fig. 19b.256 Hard carbons for battery applications are typically prepared through a complex carbonization process involving chemical pre-treatment steps followed by thermal–driven reactions including decomposition of organic materials and σ-bond rearrangement.241,244 During carbonization, small molecules are removed from the structure including H2O, CO2 and N2 leading to extensive porosity, low apparent desnsity, low particle density, and low bulk powder density.202,257,258 Interestingly, the prepared hard carbon material tends to maintain much of its original microstructure and morphology based on the parent material. At the same time, very different hard carbon end products with unique structural and morphological properties can be obtained from the same parent material depending on how the hard carbon is prepared.257,259–261 The final product can be considered a combination of distorted graphene-like nanosheets and fullerenic structures, with edges, defect/heteroatom substitutions, and closed and/or open pores.262,263 The graphene-type layers are stacked randomly in a turbostratic structure that cannot be unfolded or flattened and contain a wide size-range of voids and pores.262 The exact nature of these structures can greatly impact electrode performance. Having open structures can enable greater electrolyte penetration leading to high irreversible charge capacities and SEI formation. Materials with large pores may inhibit the effectiveness of the pore-filling mechanism. Not all defect adsorption sites are highly reversible, so the type and amount will impact electrochemical performance. Overall, the structure of hard carbons can vary substantially, and no single model should be expected to cover all of the possible hard carbon structures, and thus characterization is essential for understanding the origin of high performance or issues with the material.
Recent efforts to further improve the capacity and cyclability of hard carbons have focused on template-synthesis methods.264,265 Template synthesis involves the incorporation of inorganic materials, such as MgO,265 zeolites266 or silica,267 which act to control the pore structure during synthesis. As discussed above, micro- and nano-pores can accommodate A+ clusters252 leading to high capacities with Na+ (>400 mA h g−1).264,268 Recently, our group reported novel hard carbon materials that were synthesized via a MgO template technique and demonstrated a reversible capacity of 478 mA h g−1 at 25 mA g−1.264 As seen in Fig. 20a–c, the structure of the hard carbon is prepared by tuning the size and concentration of the MgO templates through using mixtures of Mg gluconate (Glu) and glucose (Glc). The compounds were mixed by dry mechanical mixing and freeze–drying methods, Fig. 20a, showing distinct electrochemical behavior (Fig. 20d). The freeze–drying aided in dispersion of the Mg Glu and suppressed its crystallization. Our methods demonstrated the potential for optimizing and improving hard carbon behavior through exploring various synthetic routes. The structure of the pores is not fully understood, yet higher capacities may still be attainable as we come to understand the optimization of this mechanism.
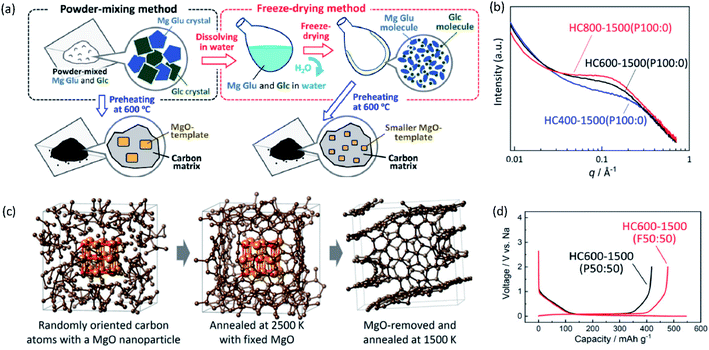 | ||
Fig. 20 Improving the pore structure in hard carbons through template-synthesis. (a) Schematic of the preparation methods for template-based synthesis for hard carbons. (b) Small-angle X-ray scattering of magnesium gluconate-based hard carbons prepared with different preheating temperatures; 400 °C (blue), 600 °C (black) and 800 °C (red). (c) First-principles molecular dynamic calculations of MgO/carbon composite structures and MgO-removed. Brown, orange, and red spheres represent carbon, magnesium, and oxygen atoms, respectively. (d) Charge–discharge profile for hard carbons prepared with 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 molar ratio (Mg Glu 50 molar ratio (Mg Glu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mg Glc) for powder mixing (P) or freeze–drying (F) methods with preheating at 600 °C, acid treatment, and post-heating at 1500 °C. (a)–(d) are reprinted with permission from ref. 264. Copyright 2021 John Wiley and Sons. Mg Glc) for powder mixing (P) or freeze–drying (F) methods with preheating at 600 °C, acid treatment, and post-heating at 1500 °C. (a)–(d) are reprinted with permission from ref. 264. Copyright 2021 John Wiley and Sons. | ||
5.4. Other carbon materials
With the vast variety of carbon materials there are other carbon structures being explored for battery applications. Like hard carbons, soft carbons can also be prepared with a structure and mechanism dependent on preparation conditions.269 These materials show more graphitic character and take advantage of heteroatom doping to give them distinctly different microstructures and energy storage behaviors from hard carbon or graphite.194,270–273 Soft carbons contain significant sp2 carbon and layers with interlayer distances greater than that found in natural graphite enabling (de)intercalation even for Na+.202,272 In 1991, soft carbons were used as the negative electrode materials in Sony's first-generation of LIBs,243 and their energy storage mechanism has been investigated.194,272,274 They tend to show some irreversible character with expansion and A+ remaining in the structure after charging. Still, they show relatively fast kinetics and long cycle-lifetimes at high rates.273,275 For SIBs, soft carbons can potentially present higher capacities than graphite while taking advantage of some of the aspects of hard carbons. Our knowledge on the potential for soft carbons remains limited due to the much fewer studies compared with hard carbons and graphite. Perhaps, we will see some exciting materials being developed in the near future toward SIBs and PIBs.Yet other carbon allotropes include a wide variety of nanoscale and thin layered structures such as graphene.276 Such graphene materials show higher Li+ storage capacity than graphite,277 and upon doping they can show promising results for Na+ and K+ storage.278,279
6. Alloy materials
As discussed in the previous section, carbon-based negative electrode materials provide the capacity to store A+ in the interlayers or nanopores of the carbon structure. In this section, we introduce active materials that can store A+via alloying reactions. In LIBs, Si280 forms metastable crystalline phases such as Li12Si7, Li14Si6, Li13Si4, Li15Si4, and Li22Si5.281 Hereafter, electrochemical lithium insertion into Si forming these silicides, which are compounds correctly, not alloys, is regarded as an alloying reaction for simplicity. When the metastable phases are formed, the alloying reaction proceeds via complex combination of amorphization and recrystallization.282 Since the study of the electrochemical performance of various alloy materials and alloying mechanisms has been exhaustively explained in the literature,280,283–289 we will focus our discussion on the most promising alloy materials in SIBs and PIBs.One of the advantages of alloy materials is delivering extremely high capacity due to their superior ability to accommodate multiple A atoms in the matrix structure compared to topotactic insertion materials290 as shown in Fig. 214,221,291–297 where the theoretical gravimetric and volumetric capacities of alloy materials in Li, Na, and K systems are compared.
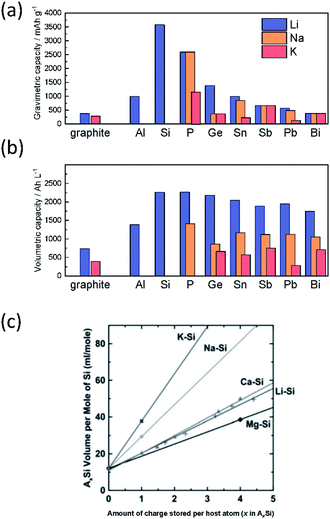 | ||
| Fig. 21 Theoretical (a) gravimetric and (b) volumetric capacities of selected alloy materials for LIBs, SIBs, and PIBs. The volumetric capacities were calculated at the fully charged state. (a) and (b) are adopted with permission from ref. 4. Copyright 2020 American Chemical Society. (c) Volume of AxSi per mole of Si plotted as a function of the charge stored. Reproduced with permission from ref. 303. Copyright IOP Publishing. | ||
With reference to the gravimetric capacity (Fig. 21a), Si is known to be the most promising alloy material for LIBs owing to its high gravimetric capacity (4200 mA h g−1 for Li4.4Si and 3580 mA h g−1 for Li3.75Si).280 NaSi and KSi are recognized as the most alkali metal-rich silicide phases in Na and K systems, respectively, being expected to deliver 954 mA h g−1.298 However, to the best of our knowledge, the electrochemical formation of NaSi and KSi in the SIB and PIB has not hitherto been reported.4 Similar to Si, other group-14 elements (Ge, Sn, and Pb) are known to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 alloys with alkali metals. Although the reaction mechanism and final discharge products were different among various alloys, the corresponding theoretical capacities for Na+ and K+ are generally lower than those for Li+ due to the increased weight of the alkali metal (Li < Na < K).298 However, it is worth noting that the Na–Sn alloy shows lower reaction voltage compared with the Li–Sn case, which could increase the energy density of SIBs when used as a negative electrode.299 While Na-rich Na15Sn4 formation (847 mA h g−1) was reported in the Na cell, only KSn formation (226 mA h g−1) was confirmed in K cells.300 Regarding group-15 elements (P, Sb, and Bi), alkali metal-rich phases are formed, for example, Li3P and Na3P (2597 mA h g−1), Li3Sb, Na3Sb and K3Sb (660 mA h g−1), and Li3Bi, Na3Bi, and K3Bi (385 mA h g−1).4 For phosphorus based alloys, alkali metal rich Li3P and Na3P can be formed in Li and Na cells, however, only KP301 or K4P3
1 alloys with alkali metals. Although the reaction mechanism and final discharge products were different among various alloys, the corresponding theoretical capacities for Na+ and K+ are generally lower than those for Li+ due to the increased weight of the alkali metal (Li < Na < K).298 However, it is worth noting that the Na–Sn alloy shows lower reaction voltage compared with the Li–Sn case, which could increase the energy density of SIBs when used as a negative electrode.299 While Na-rich Na15Sn4 formation (847 mA h g−1) was reported in the Na cell, only KSn formation (226 mA h g−1) was confirmed in K cells.300 Regarding group-15 elements (P, Sb, and Bi), alkali metal-rich phases are formed, for example, Li3P and Na3P (2597 mA h g−1), Li3Sb, Na3Sb and K3Sb (660 mA h g−1), and Li3Bi, Na3Bi, and K3Bi (385 mA h g−1).4 For phosphorus based alloys, alkali metal rich Li3P and Na3P can be formed in Li and Na cells, however, only KP301 or K4P3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 302 can be formed in the K cell, where the detailed reaction mechanism for KxP formation is still unclear.
302 can be formed in the K cell, where the detailed reaction mechanism for KxP formation is still unclear.
In addition to the gravimetric capacity, volumetric capacity is an important factor, and it should be discussed with respect to the volume at the fully charged state. Fig. 21b shows the volumetric capacities calculated based on the expanded volume.4,303 In general, the molar volume of K in K compounds tends to be higher because of the larger ionic radius of K+ than that of Na+ and Li+. Therefore, the volumetric capacity of K-alloy materials is lower than that of Li-and Na-alloy materials. For example, Sb shows the same theoretical gravimetric capacity in Li, Na, and K cells, but their volumetric capacities calculated with fully alloying volume are 1890, 1120, and 760 A h L−1 in the Li, Na, and K cells, respectively.
Not only the higher capacity but also relatively low reaction potential of alloy materials is beneficial for negative electrode materials, leading to the increase in the cell voltage and eventually increasing the energy density of the cell. However, the electrode suffers from a large volume change during charge and discharge. As a result, the alloy-based electrode is physically pulverized through repeated volume expansion/shrinkage during cycling.304,305 The interfacial resistance between the electrode and the electrolyte continuously increases due to the repetitive decomposition reaction of the electrolyte on the newly formed charged alloy surface in every charge cycle. Fig. 21c shows the volume expansion of the alkali metal-Si alloys as a function of the alkali metal content.298 The volumes of the materials increase monotonically with increasing alkali metal content, and the volume expansion increases in the order of Li < Na < K. This large volume change destroys the electrode structure and triggers side reactions such as continuous decomposition of the electrolyte, leading to a decrease in capacity, accompanied by electrical isolation of active materials.
To reduce the detrimental effects of volume expansion, core–shell306–308 or thin platelets materials,309 highly elastic binders,310–315 and nanosized particulates316 are used, when employing alloy-based materials. Particularly, nanoparticles are widely used to prevent degradation of the electrode structure during battery cycling.280,317,318 It is well known that the use of nanosized Si for LIBs enables the suppression of pulverization by continuous volume change.280,315,319–321 However, nanoparticles are industrially expensive and a hazard to health, requiring complicated preparation methods. In addition, the use of nanoparticles cannot completely suppress the continuous electrolyte decomposition on the surface of the active materials because a new surface is still formed in every cycle through repetitive expansion/shrinkage.304 The formation of the new surface cannot be prevented by solely modifying the active material architecture. To control the continuous growth of the surface decomposition layer, two methods have been investigated: (i) the use of functional binders to coat the active material surface and form a passivation layer;219,315,322–324 and (ii) design of the electrolyte with appropriate solvents, salts, and additives to control the decomposition reaction of the electrolyte.304,325–329 The surface reaction of the active material is strongly affected by the components of the electrolyte. As shown in Fig. 22, the cycling performance is significantly affected by the electrolyte components, such as salts and organic solvents.304 With regard to the Na–Bi alloy system, the PF6− anion shows superior capacity retention compared with that of ClO4− and CF3SO3− (TfO−) anions (Fig. 22a). Additionally, the ether-based solvent shows higher retention than the carbonate ester solvent (Fig. 22b). Similar behavior can be observed in the K–Bi alloy system as shown in Fig. 22c and d, where the ether-based electrolyte shows superior capacity retention compared with carbonate solvents. This is because continuous electrolyte decomposition occurs on the new surface formed in every charging cycle, and pulverization of the macroparticles occurs due to volume expansion, as shown in Fig. 22e. Therefore, a major challenge lies in passivating the repeatedly exposed new surface by using a functional binder or additive, or by appropriate electrolyte design, in order to use an alloy-based anode with extremely high reversible capacity.
 | ||
| Fig. 22 Comparative performance of alloy materials in Na cells filled with different electrolytes. Cycling performance of Bi in (a) 1.0 M NaPF6, NaCF3SO3 or NaClO4 in DME and in (b) 1.0 M NaPF6 in DME, EC/DEC, or PC, respectively. Inset in the panel (a) is the SEM images of the microsized Bi particles. (c) Cycling performance and (d) coulombic efficiency of Bi in K cells filled with 1.0 M KPF6, in DME or PC. (e) Alloying reaction model: behaviors of alloying electrode materials in the incompatible electrolyte upon cycling (a–e) are reprinted with permission from ref. 304. Copyright 2020 American Chemical Society. | ||
7. Interphases on positive and negative electrodes
As highlighted in the sections of negative electrode materials, interphases between the electrode and the electrolyte significantly impact battery performance.330–332 The interphases represent highly complex, multiphase structures that control the flux of A+ carrier ions to and from the electrolyte before A+ ions interact with the electrodes' bulk structure.332–334 As such, these structures directly influence the rate performance of batteries and improving their chemistry is essential for attaining higher rates. Further, the formation of interphase structures, especially at the negative electrode, is crucial for attaining high voltage batteries.332,335 Only a few studies reported electrolytes that showed no apparent SEI formation and instead likely involved solvent co-intercalation.336 In general, the lack of an interphase on the negative electrode leads to continuous electrolyte degradation during charging and would not effectively store energy.Though the SEI has been extensively studied within LIBs, interphase chemistry is also a well-known phenomenon in high-voltage SIBs and PIBs.337,338 However, compared with our knowledge on the properties of bulk electrodes, these interphases are much less understood due to their thin and complex composition, fluctuation across the lifetime of the battery, heterogeneity across the electrode surfaces,339 and strong dependence on the electrolyte composition.332,335,340,341 Because of their multi-phase and dynamic nature, it becomes essential to conduct in situ or operando analyses.342,343 Through various materials characterization techniques, understanding of the SEI components,344,345 their reactivity and formation,346,347 and their A+ content and transfer properties are being revealed.348–350
To date, most research has focused on better comprehending the behavior of the SEI that occurs at negative electrodes. The SEI forms when electrons at the negative electrode surface meet and reduce electrolyte species, solvent molecules, or electrolyte additives in a cascade of complex reactions.351–353 These reactions heavily depend on the content of the electrolyte, electrochemical conditions, electrode surface, temperature, and so on. In the electrolyte, the cations can coordinate with the solvent molecules or anions (depending on electrolyte concentration),354,355 and this can result in changes in thermodynamics and oxidation/reduction stability.356,357 Generally, most of this chemistry occurs during initial cycles and results in the nanoscale film with a compact inorganic layer, consisting mainly of metal fluorides, oxides and carbonates, and a mostly organic, outer layer of more alkyl carbonates, semicarbonates, and polymers.332,353 However, the thickness of this interphase can change with cycling and is heavily dependent on the electrolyte.341 Further, concentrated electrolytes tend to show interphases that are anion-derived producing predominantly inorganic passivating structures.358,359
The SEI impacts battery performance in multiple ways including the initial capacity loss, self-discharge behavior, voltage efficiency, cycle life and safety. Since it is desirable to have low potentials for the negative electrodes to achieve a high voltage for the battery, this generally always leads to interface chemistry that occurs during the initial charging of the battery; that is an irreversible component. In the case of graphite and other uncharged electrodes, this leads to consumption of some of the positive electrode material capacity and some of the electrolyte content. Therefore, having a large irreversible loss during the first charging step is undesirable since it would require an additional positive active material and less efficient utilization. The electrolyte components and additives can have a significant impact on this first cycle coulombic efficiency and subsequent cycle life.340,360,361 Metals and other negative electrode in their charged state can continue to react with the electrolyte if not effectively covered with an SEI, leading to undesirable self-discharge, further electrolyte consumption and a decrease in coulombic efficiency.341,353 Lastly, the SEI directly impacts plating reactions and potential for dendrite formation; therefore, it can play an important role in maintaining battery safety in developing metal and air batteries.362–365
While significant work has been done regarding Li+ (Li-SEI), only a limited number of papers have focused on the interphases that occur in SIBs and PIBs with most focusing on characterization of the SEI composition, morphology and structure. As with other components of the electrolyte, the kind and concentration of A+ ions impact the reduction stability of the electrolyte and the SEI formation. The Li-SEI tends to show stable SEI components with greater polymerization and crosslinking, while Na-SEI components tend to show poorer stability and higher solubility.366,367 In addition, the K-SEI can show incomplete coverage leading to higher likelihood of plating.368 A comparison of the SEI on hard carbons conducted by our group indicates that 1 M Li+, Na+ and K+ (bis(fluorosulfonyl)imide) (FSI−) electrolytes show differences in initial reversible capacity/coulombic efficiency and structural compositions based on XPS and time-of-flight secondary ion mass spectrometry (TOF-SIMS) analyses.4 Specifically, these results show that the overall organic and inorganic contents in the Li and K cells are more significant than the Na cell, suggesting a thinner Na-SEI in agreement with other studies.367 The K-SEI shows unique anion-derived chemical components and a relatively small amount of KF,4 strongly contrasting with LiF which is thought to play a key role in Li-SEI function.369 In terms of distribution across the SEI, TOF-SIMS further indicates that only the Li-SEI shows organic and inorganic content at the outer layer of the SEI, while the Na and K cells show mainly inorganic components.4 Interestingly, utilizing a preformed Li-SEI for applications in a K electrolyte has shown improved cycling, further emphasizing differences in the properties of the formed SEI.368 Altogether these results suggest different formation mechanisms, structures and stabilities for the Li-, Na-, and K-SEI with dramatically diverse results even when using analogous electrolytes.
In terms of performance, symmetrical cells and impedance measurements show that the equivalent Na- and K-SEIs display poorer ionic conductivity compared with Li, leading to polarization even at low current densities.370 Localized measurements further indicate higher Li+ uptake during SEI formation and more rapid passivation.371 This likely derives from not only the overall interphase structure, but the individual components which can show different properties. For example, theoretical studies have indicated significant differences in ion-transfer capabilities of NaF compared with LiF while metal carbonates and oxides can attain faster ion-transfer rates.372 Likewise, the observed stability of the SEI toward dissolution also derives from the individual components as solubility for Li, Na, and K salts is known to vary drastically and depends on the solvent. When considering practical batteries, research also shows that the Li-SEI chemistry has greater stability toward extreme operating temperatures.373 Understanding these individual components and their synergistic interactions remains quite complex, but is still an important goal toward obtaining high-performance batteries.4,374
In general, improving the interphase chemistry focuses on two main strategies: engineering of the electrolyte, through concentration and additive approaches, and artificial interphases, where a preformed structure is prepared before constructing a battery. Toward electrolyte engineering, vinylene carbonate (VC) and fluoroethylene carbonate (FEC) are two widely explored additives applied for improving LIBs.375,376 In PIBs, FEC can show mixed effects toward the positive and negative electrodes360,377 and at different additive concentrations.378 Therefore, modifications cannot be easily generalized across different battery systems.379 Still, the use of electrolyte additives can improve polarization, change the reaction products, and inhibit electrolyte degradation during cycling.365,380 Another option is engineering of the interphase directly with the so-called artificial SEI381,382 or alternatively through direct modification of the electrode structure that interacts with the forming SEI.383,384 An artificial SEI generally refers to an interphase structure formed on the surface of the negative electrode through various means before cycling or assembly of the battery. Artificial SEIs have been widely explored for Li and Na metals including the use of Al2O3, graphene, carbon nanotubes, and polymers, to list a few.381,382 Comparatively, less work has focused on highly reactive K metal anodes.380,385 Due to their highly reducing potentials, artificial SEIs can be electrochemically prepared on such alkali metal electrodes under spontaneous conditions.385,386 Harnessing this chemistry could lead to interesting interphase properties before the electrodes make contact with the electrolyte. It seems that both additive and interphase engineering can provide benefits toward battery performance and safety, thus determining optimal conditions from both could be very useful for future battery concepts.
Though they have received much less attention, the CEI structure and processes may also play an important role in battery stability and achieving high voltage batteries as decomposition of the electrolyte at LIB cathodes is a well-known occurrence.387,388 Recently, Scipioni et al. used atom probe tomography to examine the CEI layers on LiMn2O4. Their results indicated a mixed nanometer-thick, layered-mosaic structure consisting of an inner layer of MnxOy and MnFx and an outer network made of LiF, Li2O and organic components, e.g. polycarbonates.330 Likewise, interfacial chemistry involving Co atoms was revealed on LiCoO2 showing some link to electrocatalytic behavior of the transition metal oxide and battery degradation,389 and other reports have indicated that the CEI can continuously grow with cycling, storage time and temperature.387 CEI chemistry is also known to occur on cathode materials for SIBs92,390 and PIBs,391 though significantly less knowledge has been acquired on these structures. Much remains unknown about the prevalence of the CEI or its importance in SIB and PIB operations, but future studies will reveal further details for achieving better performance.
8. Conclusions
We have reviewed promising positive (layered oxides, polyanion materials, and PBAs) and negative electrode (graphitic carbon, hard carbon, soft carbon, and alloy) materials for SIBs and PIBs, focusing on the crystal structure and interfacial phenomena.Characteristics of Na+ provide a large variety of structure types and the appropriate selection of substitutional elements in transition metal layers enables not only the enhancement of electrochemical performance but also activates oxygen redox in the case of layered oxides. As a result, layered oxides are in leading positions for positive electrode materials in SIBs. In contrast, layered oxides with larger K+ often suffer from structural instability with consecutive phase transitions and deliver inferior capacity in PIBs. Cation permutation either in the transition or alkali metal layers is one of the strategies to overcome those disadvantages. Alternatively, polyanion materials and PBAs are favorable choices since the 3D framework structure provides decent channels and interstitial sites for large K+ diffusion and insertion/extraction, respectively. In addition, high working voltage driven by tuning the covalency of M–O bonds is one of the advantages for open-framework materials for both SIBs and PIBs.
With reference to negative electrode materials, Na+ and K+ show distinctive features with graphite, the most commonly used carbon-based electrode material in LIBs. In the case of Na+, the unfavorable thermodynamic interaction with the graphite results in no stable intercalation compounds. In contrast, graphite is promising for PIBs although the number of intercalated K+ ions is lower than that of Li+. Using co-intercalating solvent molecules also enables the formation of stable intercalation compounds for both Na+ and K+. This further opens possibilities for graphite application even for SIBs.
Hard carbons are the most promising for SIBs and meet the philosophy of SIBs: environmentally friendly preparation methods and low-cost sources. Depending on the synthetic conditions of hard carbons including precursors, temperatures, and templates, their structure is rather complex and diverse. This simultaneously necessitates the incorporation of multiple mechanisms to elucidate observed electrochemical behaviors.
Alloy materials are attractive due to their superior gravimetric and volumetric capacities. However, the volume change during charge/discharge produces mechanical stress, rapidly leading to the electrochemical pulverization of active materials. In addition, new portions of metal surface are exposed to the electrolyte at each charge, which promotes continuous electrolyte degradation and impedes stabilization of the SEI. Two promising methods to overcome the issues related to the volume change include the use of functional binders and the design of appropriate electrolytes.
Those strategies spontaneously stress the importance of comprehending the exclusive SEI features observed in SIBs and PIBs, e.g. unstable and soluble SEI components in the electrolyte and poor ionic conductivity. Since the SEI formation mechanism highly depends on the electrolyte such as its concentration and composition, the design of the electrolyte formulation is critical. Moreover, in situ/operando characterization is much preferred to understand the SEI properties, but these measurements under realistic conditions are still challenging. Few studies have been carried out for the CEI although a stable CEI would expand the selection of transition metal as well as the use of oxygen redox for positive electrode materials. As the lower Lewis acidity of Na+ and K+ might allow fast ionic diffusion in the electrolyte and the interphase, comprehensive studies on the SEI and CEI would further shed insights on the rate capability for SIBs and PIBs.
A global push to reduce fossil fuel reliance will create a massive market for energy storage. For stationary applications where cost, safety, ease of maintenance, reliability, and lifetime are more important than size and weight, SIBs can be competitive against LIBs in the near term based on their current state of development. The practical application of PIBs necessities further improvement of their electrochemical performance and decent safety strategies. However, as evidenced by recent intensive studies on PIBs, PIBs are also promising next generation battery candidates. From a scientific point of view, research on the development of SIBs and PIBs should be approached in a multidisciplinary way to understand rather complex phenomena involved in electrode materials, electrolytes, electrolyte additives, and functional binders.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was partly funded by the MEXT program “ESICB” (Grant No. JPMXP0112101003), the JST through A-STEP program (Grant No. JPMJTS1611), the CONCERT-Japan program, CREST (Grant No. JPMJCR21O6), NEDO (JPNP20004), and JSPS KAKENHI (Grant No. JP20H02849, JP20K05690, JP21K14724, and JP21K20561). Schematic illustrations of the crystal structures were drawn using the program VESTA.392References
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278 CrossRef CAS.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef.
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. Fu, Joule, 2017, 1, 229–243 CrossRef.
- T. Hosaka, K. Kubota, A. S. Hameed and S. Komaba, Chem. Rev., 2020, 120, 6358–6466 CrossRef CAS PubMed.
- S. Komaba, Electrochemistry, 2019, 19-16-E2677 Search PubMed.
- S. Komaba, Chem. Lett., 2020, 49, 1507–1516 CrossRef CAS.
- K. Kubota, M. Dahbi, T. Hosaka, S. Kumakura and S. Komaba, Chem. Rec., 2018, 18, 459–479 CrossRef CAS PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- K. Kubota, Electrochemistry, 2020, 88, 507–514 CrossRef CAS.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- J. Y. Hwang, S. T. Myung and Y. K. Sun, Adv. Funct. Mater., 2018, 28, 1802938 CrossRef.
- H. Kim, J. C. Kim, M. Bianchini, D. H. Seo, J. Rodriguez-Garcia and G. Ceder, Adv. Energy Mater., 2018, 8, 1702384 CrossRef.
- G. G. Eshetu, G. A. Elia, M. Armand, M. Forsyth, S. Komaba, T. Rojo and S. Passerini, Adv. Energy Mater., 2020, 10, 2000093 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- Y. Matsuda, H. Nakashima, M. Morita and Y. Takasu, J. Electrochem. Soc., 1981, 128, 2552 CrossRef CAS.
- M. Okoshi, Y. Yamada, S. Komaba, A. Yamada and H. Nakai, J. Electrochem. Soc., 2016, 164, A54 CrossRef.
- F. Sagane, T. Abe, Y. Iriyama and Z. Ogumi, J. Power Sources, 2005, 146, 749–752 CrossRef CAS.
- Y. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, Langmuir, 2009, 25, 12766–12770 CrossRef CAS PubMed.
- F. Sagane, T. Abe and Z. Ogumi, J. Phys. Chem. C, 2009, 113, 20135–20138 CrossRef CAS.
- Y. Marcus, Pure Appl. Chem., 1985, 57, 1129–1132 CrossRef CAS.
- S. Komaba, T. Hasegawa, M. Dahbi and K. Kubota, Electrochem. Commun., 2015, 60, 172–175 CrossRef CAS.
- T. Hosaka, S. Muratsubaki, K. Kubota, H. Onuma and S. Komaba, J. Phys. Chem. Lett., 2019, 10, 3296–3300 CrossRef CAS PubMed.
- A. Rudola, C. J. Wright and J. Barker, Energy Mater. Adv., 2021, 1–12 Search PubMed.
- A. Rudola, A. J. Rennie, R. Heap, S. S. Meysami, A. Lowbridge, F. Mazzali, R. Sayers, C. J. Wright and J. Barker, J. Mater. Chem. A, 2021, 9, 8279–8302 RSC.
- N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain and Y. Chen, J. Phys.: Energy, 2021, 3, 031503 CAS.
- Z. Guo, J. Zhu, J. Feng and S. Du, RSC Adv., 2015, 5, 69514–69521 RSC.
- B. Song, I. Dhiman, J. C. Carothers, G. M. Veith, J. Liu, H. Z. Bilheux and A. Huq, ACS Energy Lett., 2019, 4, 2402–2408 CrossRef CAS.
- W. Lu, C. M. López, N. Liu, J. T. Vaughey and A. Jansen, J. Electrochem. Soc., 2012, 159, A566 CrossRef CAS.
- N. Xiao, W. D. McCulloch and Y. Wu, J. Am. Chem. Soc., 2017, 139, 9475–9478 CrossRef CAS PubMed.
- H. Kondou, J. Kim and H. Watanabe, Electrochemistry, 2017, 85, 647–649 CrossRef CAS.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS.
- R. Kanno, T. Shirane, Y. Inaba and Y. Kawamoto, J. Power Sources, 1997, 68, 145–152 CrossRef CAS.
- T. Shirane, R. Kanno, Y. Kawamoto, Y. Takeda, M. Takano, T. Kamiyama and F. Izumi, Solid State Ionics, 1995, 79, 227–233 CrossRef CAS.
- L. Hoffmann and R. Hoppe, Z. Anorg. Allg. Chem., 1977, 430, 115–120 CrossRef CAS.
- J.-P. Parant, R. Olazcuaga, M. Devalette, C. Fouassier and P. Hagenmuller, J. Solid State Chem., 1971, 3, 1–11 CrossRef CAS.
- E. Chappel, M. Nunez-Regueiro, G. Chouteau, O. Isnard and C. Darie, Eur. Phys. J. B, 2000, 17, 615–622 CrossRef CAS.
- C. Delmas, J.-J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3, 165–169 CrossRef.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef CAS PubMed.
- Z. Lu and J. Dahn, J. Electrochem. Soc., 2001, 148, A1225 CrossRef CAS.
- J. B. Goodenough, K. Mizushima and T. Takeda, Jpn. J. Appl. Phys., 1980, 19, 305 CrossRef.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80 CrossRef CAS PubMed.
- J. L. Kaufman and A. Van der Ven, Phys. Rev. Mater., 2019, 3, 015402 CrossRef CAS.
- M. Y. Toriyama, J. L. Kaufman and A. Van der Ven, ACS Appl. Energy Mater., 2019, 2, 2629–2636 CrossRef CAS.
- Y. Hironaka, K. Kubota and S. Komaba, Chem. Commun., 2017, 53, 3693–3696 RSC.
- Y. Lei, X. Li, L. Liu and G. Ceder, Chem. Mater., 2014, 26, 5288–5296 CrossRef CAS.
- H. Kim, D.-H. Seo, A. Urban, J. Lee, D.-H. Kwon, S.-H. Bo, T. Shi, J. K. Papp, B. D. McCloskey and G. Ceder, Chem. Mater., 2018, 30, 6532–6539 CrossRef CAS.
- S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358 CrossRef CAS.
- Y. Lyu, L. Ben, Y. Sun, D. Tang, K. Xu, L. Gu, R. Xiao, H. Li, L. Chen and X. Huang, J. Power Sources, 2015, 273, 1218–1225 CrossRef CAS.
- S. Komaba, T. Nakayama, A. Ogata, T. Shimizu, C. Takei, S. Takada, A. Hokura and I. Nakai, ECS Trans., 2009, 16, 43 CrossRef CAS.
- Y.-N. Zhou, J.-J. Ding, K.-W. Nam, X. Yu, S.-M. Bak, E. Hu, J. Liu, J. Bai, H. Li and Z.-W. Fu, J. Mater. Chem. A, 2013, 1, 11130–11134 RSC.
- K. Kubota, I. Ikeuchi, T. Nakayama, C. Takei, N. Yabuuchi, H. Shiiba, M. Nakayama and S. Komaba, J. Phys. Chem. C, 2015, 119, 166–175 CrossRef CAS.
- N. Yabuuchi, I. Ikeuchi, K. Kubota and S. Komaba, ACS Appl. Mater. Interfaces, 2016, 8, 32292–32299 CrossRef CAS PubMed.
- A. Mendiboure, H. Eickenbusch, R. Schöllhorn and G. S. Rao, J. Solid State Chem., 1987, 71, 19–28 CrossRef CAS.
- D. Mikhailova, O. M. Karakulina, D. Batuk, J. Hadermann, A. M. Abakumov, M. Herklotz, A. A. Tsirlin, S. Oswald, L. Giebeler and M. Schmidt, Inorg. Chem., 2016, 55, 7079–7089 CrossRef CAS PubMed.
- L. Verger, M. Guignard and C. Delmas, Inorg. Chem., 2019, 58, 2543–2549 CrossRef CAS PubMed.
- Z. Lu and J. Dahn, Chem. Mater., 2001, 13, 1252–1257 CrossRef CAS.
- T. Masese, K. Yoshii, Y. Yamaguchi, T. Okumura, Z.-D. Huang, M. Kato, K. Kubota, J. Furutani, Y. Orikasa and H. Senoh, Nat. Commun., 2018, 9, 1–12 CrossRef CAS PubMed.
- M. Zhang, D. A. Kitchaev, Z. Lebens-Higgins, J. Vinckeviciute, M. Zuba, P. J. Reeves, C. P. Grey, M. S. Whittingham, L. F. Piper and A. Van der Ven, Nat. Rev. Mater., 2022, 1–19 Search PubMed.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697 CrossRef CAS PubMed.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin and M. A. Pérez-Osorio, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- B. M. De Boisse, G. Liu, J. Ma, S.-i. Nishimura, S.-C. Chung, H. Kiuchi, Y. Harada, J. Kikkawa, Y. Kobayashi and M. Okubo, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- A. J. Perez, D. Batuk, M. Saubanère, G. Rousse, D. Foix, E. Mccalla, E. J. Berg, R. Dugas, K. HW van den Bos and M.-L. Doublet, Chem. Mater., 2016, 28, 8278–8288 CrossRef CAS.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC.
- K. Dai, J. Mao, Z. Zhuo, Y. Feng, W. Mao, G. Ai, F. Pan, G. Liu and W. Yang, Nano Energy, 2020, 74, 104831 CrossRef CAS.
- Y. Zhang, M. Wu, J. Ma, G. Wei, Y. Ling, R. Zhang and Y. Huang, ACS Cent. Sci., 2020, 6, 232–240 CrossRef CAS PubMed.
- C. Cheng, S. Li, T. Liu, Y. Xia, L.-Y. Chang, Y. Yan, M. Ding, Y. Hu, J. Wu and J. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 41304–41312 CrossRef CAS PubMed.
- R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Robers and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300 CrossRef.
- K. Dai, J. Wu, Z. Zhuo, Q. Li, S. Sallis, J. Mao, G. Ai, C. Sun, Z. Li and W. E. Gent, Joule, 2019, 3, 518–541 CrossRef CAS.
- Q. Wang, S. Mariyappan, G. Rousse, A. V. Morozov, B. Porcheron, R. Dedryvère, J. Wu, W. Yang, L. Zhang and M. Chakir, Nat. Mater., 2021, 20, 353–361 CrossRef CAS PubMed.
- B. M. de Boisse, M. Reynaud, J. Ma, J. Kikkawa, S.-i. Nishimura, M. Casas-Cabanas, C. Delmas, M. Okubo and A. Yamada, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund and C.-J. Sun, Nat. Mater., 2019, 18, 256–265 CrossRef CAS PubMed.
- W. E. Gent, K. Lim, Y. Liang, Q. Li, T. Barnes, S.-J. Ahn, K. H. Stone, M. McIntire, J. Hong and J. H. Song, Nat. Commun., 2017, 8, 1–12 CrossRef CAS PubMed.
- R. A. House, U. Maitra, M. A. Perez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters and K.-J. Zhou, Nature, 2020, 577, 502–508 CrossRef CAS PubMed.
- K. Du, J. Zhu, G. Hu, H. Gao, Y. Li and J. B. Goodenough, Energy Environ. Sci., 2016, 9, 2575–2577 RSC.
- X. Rong, J. Liu, E. Hu, Y. Liu, Y. Wang, J. Wu, X. Yu, K. Page, Y.-S. Hu and W. Yang, Joule, 2018, 2, 125–140 CrossRef CAS.
- E. J. Kim, P. A. Maughan, E. N. Bassey, R. J. Clément, L. A. Ma, L. C. Duda, D. Sehrawat, R. Younesi, N. Sharma, C. P. Grey and A. R. Armstong, Adv. Energy Mater., 2021, 2102325 Search PubMed.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef CAS PubMed.
- R. A. House, G. J. Rees, M. A. Pérez-Osorio, J.-J. Marie, E. Boivin, A. W. Robertson, A. Nag, M. Garcia-Fernandez, K.-J. Zhou and P. G. Bruce, Nat. Energy, 2020, 5, 777–785 CrossRef CAS.
- E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák and G. Van Tendeloo, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- Y. Yoda, K. Kubota, H. Isozumi, T. Horiba and S. Komaba, ACS Appl. Mater. Interfaces, 2018, 10, 10986–10997 CrossRef CAS PubMed.
- J. Xu, D. H. Lee, R. l. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS.
- G. Singh, N. Tapia-Ruiz, J. M. Lopez del Amo, U. Maitra, J. W. Somerville, A. R. Armstrong, J. Martinez de Ilarduya, T. Rojo and P. G. Bruce, Chem. Mater., 2016, 28, 5087–5094 CrossRef.
- N. Tapia-Ruiz, W. M. Dose, N. Sharma, H. Chen, J. Heath, J. W. Somerville, U. Maitra, M. S. Islam and P. G. Bruce, Energy Environ. Sci., 2018, 11, 1470–1479 RSC.
- H. Yoshida, N. Yabuuchi, K. Kubota, I. Ikeuchi, A. Garsuch, M. Schulz-Dobrick and S. Komaba, Chem. Commun., 2014, 50, 3677–3680 RSC.
- J. H. Jo, J. U. Choi, Y. J. Park, Y. H. Jung, D. Ahn, T. Y. Jeon, H. Kim, J. Kim and S. T. Myung, Adv. Energy Mater., 2020, 10, 1903605 CrossRef CAS.
- P.-F. Wang, H.-R. Yao, X.-Y. Liu, Y.-X. Yin, J.-N. Zhang, Y. Wen, X. Yu, L. Gu and Y.-G. Guo, Sci. Adv., 2018, 4, eaar6018 CrossRef PubMed.
- J. U. Choi, J. Kim, J.-Y. Hwang, J. H. Jo, Y.-K. Sun and S.-T. Myung, Nano Energy, 2019, 61, 284–294 CrossRef CAS.
- T. Deng, X. Fan, J. Chen, L. Chen, C. Luo, X. Zhou, J. Yang, S. Zheng and C. Wang, Adv. Funct. Mater., 2018, 28, 1800219 CrossRef.
- X. Wang, X. Xu, C. Niu, J. Meng, M. Huang, X. Liu, Z. Liu and L. Mai, Nano Lett., 2017, 17, 544–550 CrossRef CAS PubMed.
- K. Kubota, S. Kumakura, Y. Yoda, K. Kuroki and S. Komaba, Adv. Energy Mater., 2018, 8, 1703415 CrossRef.
- U.-H. Kim, S.-T. Myung, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2017, 2, 1848–1854 CrossRef CAS.
- J. Alvarado, C. Ma, S. Wang, K. Nguyen, M. Kodur and Y. S. Meng, ACS Appl. Mater. Interfaces, 2017, 9, 26518–26530 CrossRef CAS PubMed.
- A. Gutierrez, N. A. Benedek and A. Manthiram, Chem. Mater., 2013, 25, 4010–4016 CrossRef CAS.
- M. Ben Yahia, F. Lemoigno, G. Rousse, F. Boucher, J.-M. Tarascon and M.-L. Doublet, Energy Environ. Sci., 2012, 5, 9584–9594 RSC.
- B. C. Melot, D. O. Scanlon, M. Reynaud, G. Rousse, J.-N. Chotard, M. Henry and J.-M. Tarascon, ACS Appl. Mater. Interfaces, 2014, 6, 10832–10839 CrossRef CAS PubMed.
- P. Kubacek and R. Hoffmann, J. Am. Chem. Soc., 1981, 103, 4320–4332 CrossRef CAS.
- S. Adams, J. Solid State Electrochem., 2010, 14, 1787–1792 CrossRef CAS.
- K.-Y. Park, I. Park, H. Kim, H.-d. Lim, J. Hong, J. Kim and K. Kang, Chem. Mater., 2014, 26, 5345–5351 CrossRef CAS.
- C. A. J. Fisher, V. M. Hart Prieto and M. S. Islam, Chem. Mater., 2008, 20, 5907–5915 CrossRef CAS.
- T. V. S. L. Satyavani, A. Srinivas Kumar and P. S. V. Subba Rao, Engineering Science and Technology, an International Journal, 2016, 19, 178–188 CrossRef.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123–4127 CrossRef CAS PubMed.
- C. Delacourt, L. Laffont, R. Bouchet, C. Wurm, J. B. Leriche, M. Morcrette, J. M. Tarascon and C. Masquelier, J. Electrochem. Soc., 2005, 152, A913 CrossRef CAS.
- L. F. J. Piper, N. F. Quackenbush, S. Sallis, D. O. Scanlon, G. W. Watson, K. W. Nam, X. Q. Yang, K. E. Smith, F. Omenya, N. A. Chernova and M. S. Whittingham, J. Phys. Chem, C, 2013, 117, 10383–10396 CrossRef CAS.
- M.-y. Zheng, Z.-y. Bai, Y.-W. He, S. Wu, Y. Yang and Z.-Z. Zhu, ACS Omega, 2020, 5, 5192–5201 CrossRef CAS PubMed.
- J. Kim, D.-H. Seo, H. Kim, I. Park, J.-K. Yoo, S.-K. Jung, Y.-U. Park, W. A. Goddard Iii and K. Kang, Energy Environ. Sci., 2015, 8, 540–545 RSC.
- C. Berlanga, I. Monterrubio, M. Armand, T. Rojo, M. Galceran and M. Casas-Cabanas, ACS Sustainable Chem. Eng., 2020, 8, 725–730 CrossRef CAS.
- O. V. Yakubovich, W. Massa and O. V. Dimitrova, Z. Anorg. Allg. Chem., 2005, 631, 2445–2449 CrossRef CAS.
- I. Sultana, M. M. Rahman, S. Mateti, N. Sharma, S. Huang and Y. Chen, Batteries Supercaps, 2020, 3, 450–455 CrossRef CAS.
- V. Mathew, S. Kim, J. Kang, J. Gim, J. Song, J. P. Baboo, W. Park, D. Ahn, J. Han, L. Gu, Y. Wang, Y.-S. Hu, Y.-K. Sun and J. Kim, NPG Asia Mater., 2014, 6, e138 CrossRef CAS.
- T. Hosaka, T. Shimamura, K. Kubota and S. Komaba, Chem. Rec., 2019, 19, 735–745 CrossRef CAS PubMed.
- J. B. Goodenough, H. Y. P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS.
- R. Rajagopalan, Z. Zhang, Y. Tang, C. Jia, X. Ji and H. Wang, Energy Storage Materials, 2021, 34, 171–193 CrossRef.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552–6591 CrossRef CAS PubMed.
- S. Patoux, C. Wurm, M. Morcrette, G. Rousse and C. Masquelier, J. Power Sources, 2003, 119–121, 278–284 CrossRef CAS.
- S. C. Yin, H. Grondey, P. Strobel, M. Anne and L. F. Nazar, J. Am. Chem. Soc., 2003, 125, 10402–10411 CrossRef CAS PubMed.
- X. Zhang, X. Rui, D. Chen, H. Tan, D. Yang, S. Huang and Y. Yu, Nanoscale, 2019, 11, 2556–2576 RSC.
- X. Wang, C. Niu, J. Meng, P. Hu, X. Xu, X. Wei, L. Zhou, K. Zhao, W. Luo, M. Yan and L. Mai, Adv. Energy Mater., 2015, 5, 1500716 CrossRef.
- J. Han, G.-N. Li, F. Liu, M. Wang, Y. Zhang, L. Hu, C. Dai and M. Xu, Chem. Commun., 2017, 53, 1805–1808 RSC.
- L. Zhang, B. Zhang, C. Wang, Y. Dou, Q. Zhang, Y. Liu, H. Gao, M. Al-Mamun, W. K. Pang, Z. Guo, S. X. Dou and H. K. Liu, Nano Energy, 2019, 60, 432–439 CrossRef CAS.
- C. Delmas, A. Nadiri and J. L. Soubeyroux, Solid State Ionics, 1988, 28–30, 419–423 CrossRef.
- S.-C. Chung, J. Ming, L. Lander, J. Lu and A. Yamada, J. Mater. Chem. A, 2018, 6, 3919–3925 RSC.
- S.-F. Li, X.-K. Hou, Z.-Y. Gu, Y.-F. Meng, C.-D. Zhao, H.-X. Zhang and X.-L. Wu, New J. Chem., 2021, 45, 4854–4859 RSC.
- R. Essehli, A. Alkhateeb, A. Mahmoud, F. Boschini, H. Ben Yahia, R. Amin and I. Belharouak, J. Power Sources, 2020, 469, 228417 CrossRef CAS.
- Y. Wu, Z. Cao, L. Song and J. Gao, ACS Appl. Mater. Interfaces, 2021, 13, 48865–48871 CrossRef CAS PubMed.
- P. Ramesh Kumar, A. Kheireddine, U. Nisar, R. A. Shakoor, R. Essehli, R. Amin and I. Belharouak, J. Power Sources, 2019, 429, 149–155 CrossRef CAS.
- U. Ahmadu, in Advanced Sensor and Detection Materials, 2014, pp. 265–308 Search PubMed.
- B. L. Ellis, T. N. Ramesh, W. N. Rowan-Weetaluktuk, D. H. Ryan and L. F. Nazar, J. Mater. Chem., 2012, 22, 4759–4766 RSC.
- N. R. Khasanova, O. A. Drozhzhin, D. A. Storozhilova, C. Delmas and E. V. Antipov, Chem. Mater., 2012, 24, 4271–4273 CrossRef CAS.
- E. Boivin, J.-N. Chotard, T. Bamine, D. Carlier, P. Serras, V. Palomares, T. Rojo, A. Iadecola, L. Dupont, L. Bourgeois, F. Fauth, C. Masquelier and L. Croguennec, J. Mater. Chem. A, 2017, 5, 25044–25055 RSC.
- E. Boivin, J.-N. Chotard, M. Ménétrier, L. Bourgeois, T. Bamine, D. Carlier, F. Fauth, C. Masquelier and L. Croguennec, J. Phys. Chem, C, 2016, 120, 26187–26198 CrossRef CAS.
- M. Ling, Z. Lv, F. Li, J. Zhao, H. Zhang, G. Hou, Q. Zheng and X. Li, ACS Appl. Mater. Interfaces, 2020, 12, 30510–30519 CrossRef CAS PubMed.
- N. Recham, J. N. Chotard, L. Dupont, C. Delacourt, W. Walker, M. Armand and J. M. Tarascon, Nat. Mater., 2010, 9, 68–74 CrossRef CAS PubMed.
- S. Lee and S. S. Park, J. Phys. Chem, C, 2014, 118, 12642–12648 CrossRef CAS.
- R. Tripathi, T. N. Ramesh, B. L. Ellis and L. F. Nazar, Angew. Chem., Int. Ed., 2010, 49, 8738–8742 CrossRef CAS PubMed.
- R. Tripathi, G. R. Gardiner, M. S. Islam and L. F. Nazar, Chem. Mater., 2011, 23, 2278–2284 CrossRef CAS.
- N. E. Novikova, N. I. Sorokina, I. A. Verin, O. A. Alekseeva, E. I. Orlova, V. I. Voronkova and M. Tseitlin, Crystals, 2018, 8, 283 CrossRef.
- S. S. Fedotov, A. S. Samarin and E. V. Antipov, J. Power Sources, 2020, 480, 228840 CrossRef CAS.
- S. S. Fedotov, A. S. Samarin, V. A. Nikitina, D. A. Aksyonov, S. A. Sokolov, A. Zhugayevych, K. J. Stevenson, N. R. Khasanova, A. M. Abakumov and E. V. Antipov, J. Mater. Chem. A, 2018, 6, 14420–14430 RSC.
- P. R. Kumar, K. Kubota, D. Igarashi and S. Komaba, J. Phys. Chem, C, 2021, 125, 24823–24830 CrossRef CAS.
- K. L. Harrison and A. Manthiram, Chem. Mater., 2013, 25, 1751–1760 CrossRef CAS.
- G. He, A. Huq, W. H. Kan and A. Manthiram, Chem. Mater., 2016, 28, 1503–1512 CrossRef CAS.
- K. Chihara, A. Katogi, K. Kubota and S. Komaba, Chem. Commun., 2017, 53, 5208–5211 RSC.
- J. Ding, Y.-C. Lin, J. Liu, J. Rana, H. Zhang, H. Zhou, I.-H. Chu, K. M. Wiaderek, F. Omenya, N. A. Chernova, K. W. Chapman, L. F. J. Piper, S. P. Ong and M. S. Whittingham, Adv. Energy Mater., 2018, 8, 1800221 CrossRef.
- S. S. Fedotov, N. D. Luchinin, D. A. Aksyonov, A. V. Morozov, S. V. Ryazantsev, M. Gaboardi, J. R. Plaisier, K. J. Stevenson, A. M. Abakumov and E. V. Antipov, Nat. Commun., 2020, 11, 1484 CrossRef CAS PubMed.
- N. Recham, G. Rousse, M. T. Sougrati, J.-N. Chotard, C. Frayret, S. Mariyappan, B. C. Melot, J.-C. Jumas and J.-M. Tarascon, Chem. Mater., 2012, 24, 4363–4370 CrossRef CAS.
- J. Kim, H. Kim, I. Park, Y.-U. Park, J.-K. Yoo, K.-Y. Park, S. Lee and K. Kang, Energy Environ. Sci., 2013, 6, 830–834 RSC.
- W. Huang, J. Zhou, B. Li, L. An, P. Cui, W. Xia, L. Song, D. Xia, W. Chu and Z. Wu, Small, 2015, 11, 2170–2176 CrossRef CAS PubMed.
- P. Barpanda, G. Oyama, S.-i. Nishimura, S.-C. Chung and A. Yamada, Nat. Commun., 2014, 5, 4358 CrossRef CAS PubMed.
- W. Pan, W. Guan, S. Liu, B. B. Xu, C. Liang, H. Pan, M. Yan and Y. Jiang, J. Mater. Chem. A, 2019, 7, 13197–13204 RSC.
- P. R. Kumar, Y. H. Jung, C. H. Lim and D. K. Kim, J. Mater. Chem. A, 2015, 3, 6271–6275 RSC.
- P. R. Kumar, Y. H. Jung, J. E. Wang and D. K. Kim, J. Power Sources, 2016, 324, 421–427 CrossRef CAS.
- M. Bianchini, F. Fauth, N. Brisset, F. Weill, E. Suard, C. Masquelier and L. Croguennec, Chem. Mater., 2015, 27, 3009–3020 CrossRef CAS.
- M. Bianchini, N. Brisset, F. Fauth, F. Weill, E. Elkaim, E. Suard, C. Masquelier and L. Croguennec, Chem. Mater., 2014, 26, 4238–4247 CrossRef CAS.
- P. R. Kumar, K. Kubota, Y. Miura, M. Ohara, K. Gotoh and S. Komaba, J. Power Sources, 2021, 493, 229676 CrossRef CAS.
- S.-i. Nishimura, M. Nakamura, R. Natsui and A. Yamada, J. Am. Chem. Soc., 2010, 132, 13596–13597 CrossRef CAS PubMed.
- T. Ye, P. Barpanda, S.-i. Nishimura, N. Furuta, S.-C. Chung and A. Yamada, Chem. Mater., 2013, 25, 3623–3629 CrossRef CAS.
- P. Barpanda, T. Ye, S.-i. Nishimura, S.-C. Chung, Y. Yamada, M. Okubo, H. Zhou and A. Yamada, Electrochem. Commun., 2012, 24, 116–119 CrossRef CAS.
- P. Barpanda, G. Liu, C. D. Ling, M. Tamaru, M. Avdeev, S.-C. Chung, Y. Yamada and A. Yamada, Chem. Mater., 2013, 25, 3480–3487 CrossRef CAS.
-
R. Gond, S. Singh, S. P. Vanam, V. Pralong and P. Barpanda, In Situ X-Ray Diffraction and Alkali Ion (A
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li, Na, K) Intercalation Behavior of Na2FeP2O7 Pyrophosphate, Singapore, 2021 Search PubMed.
Li, Na, K) Intercalation Behavior of Na2FeP2O7 Pyrophosphate, Singapore, 2021 Search PubMed. - Y. Niu, Y. Zhang and M. Xu, J. Mater. Chem. A, 2019, 7, 15006–15025 RSC.
- H. Kim, C. S. Park, J. W. Choi and Y. Jung, Angew. Chem., Int. Ed., 2016, 55, 6662–6666 CrossRef CAS PubMed.
- P. Barpanda, M. Avdeev, C. D. Ling, J. Lu and A. Yamada, Inorg. Chem., 2013, 52, 395–401 CrossRef CAS PubMed.
- H. Kim, I. Park, D.-H. Seo, S. Lee, S.-W. Kim, W. J. Kwon, Y.-U. Park, C. S. Kim, S. Jeon and K. Kang, J. Am. Chem. Soc., 2012, 134, 10369–10372 CrossRef CAS PubMed.
- H. Kim, I. Park, S. Lee, H. Kim, K.-Y. Park, Y.-U. Park, H. Kim, J. Kim, H.-D. Lim and W.-S. Yoon, Chem. Mater., 2013, 25, 3614–3622 CrossRef CAS.
- B. Senthilkumar, C. Murugesan, K. Sada and P. Barpanda, J. Power Sources, 2020, 480, 228794 CrossRef CAS.
- M. Zarrabeitia, M. Jauregui, N. Sharma, J. C. Pramudita and M. Casas-Cabanas, Chem. Mater., 2019, 31, 5152–5159 CrossRef CAS.
- H. Zhang, I. Hasa, D. Buchholz, B. Qin, D. Geiger, S. Jeong, U. Kaiser and S. Passerini, NPG Asia Mater., 2017, 9, e370 CrossRef CAS.
- P. R. Kumar, H. B. Yahia, I. Belharouak, M. T. Sougrati, S. Passerini, R. Amin and R. Essehli, J. Solid State Electrochem., 2020, 24, 17–24 CrossRef CAS.
- P. R. Kumar, R. Essehli, H. B. Yahia, R. Amin and I. Belharouak, RSC Adv., 2020, 10, 15983–15989 RSC.
- W. B. Park, S. C. Han, C. Park, S. U. Hong, U. Han, S. P. Singh, Y. H. Jung, D. Ahn, K.-S. Sohn and M. Pyo, Adv. Energy Mater., 2018, 8, 1703099 CrossRef.
- N. Imanishi, T. Morikawa, J. Kondo, R. Yamane, Y. Takeda, O. Yamamoto, H. Sakaebe and M. Tabuchi, J. Power Sources, 1999, 81–82, 530–534 CrossRef CAS.
- Y. Lu, L. Wang, J. Cheng and J. B. Goodenough, Chem. Commun., 2012, 48, 6544 RSC.
- A. Eftekhari, J. Power Sources, 2004, 126, 221–228 CrossRef CAS.
- L. Xue, Y. Li, H. Gao, W. Zhou, X. Lü, W. Kaveevivitchai, A. Manthiram and J. B. Goodenough, J. Am. Chem. Soc., 2017, 139, 2164–2167 CrossRef CAS PubMed.
- X. Bie, K. Kubota, T. Hosaka, K. Chihara and S. Komaba, J. Mater. Chem. A, 2017, 5, 4325–4330 RSC.
- P. Xiao, J. Song, L. Wang, J. B. Goodenough and G. Henkelman, Chem. Mater., 2015, 27, 3763–3768 CrossRef CAS.
- L. Wang, J. Song, R. Qiao, L. A. Wray, M. A. Hossain, Y. D. Chuang, W. Yang, Y. Lu, D. Evans, J. J. Lee, S. Vail, X. Zhao, M. Nishijima, S. Kakimoto and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2548–2554 CrossRef CAS PubMed.
- J. Song, L. Wang, Y. Lu, J. Liu, B. Guo, P. Xiao, J.-J. Lee, X.-Q. Yang, G. Henkelman and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2658–2664 CrossRef CAS PubMed.
- J. Liao, Q. Hu, Y. Yu, H. Wang, Z. Tang, Z. Wen and C. Chen, J. Mater. Chem. A, 2017, 5, 19017–19024 RSC.
- P. A. Morozova, I. A. Trussov, D. P. Rupasov, V. A. Nikitina, A. M. Abakumov and S. S. Fedotov, Crystals, 2021, 11, 895 CrossRef CAS.
- Y. Lu, L. Wang, J. Cheng and J. B. Goodenough, Chem. Commun., 2012, 48, 6544–6546 RSC.
- L. Wang, Y. Lu, J. Liu, M. Xu, J. Cheng, D. Zhang and J. B. Goodenough, Angew. Chem., 2013, 52, 1964–1967 CrossRef CAS PubMed.
- Y. You, X.-L. Wu, Y.-X. Yin and Y.-G. Guo, Energy Environ. Sci., 2014, 7, 1643 RSC.
- J. Wu, J. Song, K. Dai, Z. Zhuo, L. A. Wray, G. Liu, Z.-x. Shen, R. Zeng, Y. Lu and W. Yang, J. Am. Chem. Soc., 2017, 139, 18358–18364 CrossRef CAS PubMed.
- Y. You, X. Yu, Y. Yin, K.-W. Nam and Y.-G. Guo, Nano Res., 2014, 8, 117–128 CrossRef.
- L. Deng, J. Qu, X. Niu, J. Liu, J. Zhang, Y. Hong, M. Feng, J. Wang, M. Hu and L. Zeng, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed.
- M. Ishizaki, H. Ando, N. Yamada, K. Tsumoto, K. Ono, H. Sutoh, T. Nakamura, Y. Nakao and M. Kurihara, J. Mater. Chem. A, 2019, 7, 4777–4787 RSC.
- T. Hosaka, T. Fukabori, H. Kojima, K. Kubota and S. Komaba, ChemSusChem, 2021, 14, 1166–1175 CrossRef CAS PubMed.
- K. Kubota, S. Shimadzu, N. Yabuuchi, S. Tominaka, S. Shiraishi, M. Abreu-Sepulveda, A. Manivannan, K. Gotoh, M. Fukunishi and M. Dahbi, Chem. Mater., 2020, 32, 2961–2977 CrossRef CAS.
- M. Dahbi, N. Yabuuchi, K. Kubota, K. Tokiwa and S. Komaba, Phys. Chem. Chem. Phys., 2014, 16, 15007–15028 RSC.
- G. Wang, M. Yu and X. Feng, Chem. Soc. Rev., 2021, 50, 2388–2443 RSC.
- J. Zhang, L. Lai, H. Wang, M. Chen and Z. X. Shen, Mater. Today Energy, 2021, 100747 CrossRef CAS.
- L. Zhang, W. Wang, S. Lu and Y. Xiang, Adv. Energy Mater., 2021, 11, 2003640 CrossRef CAS.
- D. Cheng, X. Zhou, H. Hu, Z. Li, J. Chen, L. Miao, X. Ye and H. Zhang, Carbon, 2021, 182, 758–769 CrossRef CAS.
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- G. Haxel, Rare earth elements: critical resources for high technology, US Department of the Interior, US Geological Survey, 2002 Search PubMed.
- R. Marom, S. F. Amalraj, N. Leifer, D. Jacob and D. Aurbach, J. Mater. Chem., 2011, 21, 9938–9954 RSC.
- J. D. Bernal, Proc. R. Soc. London, Ser. A, 1924, 106, 749–773 CAS.
- P. Trucano and R. Chen, Nature, 1975, 258, 136–137 CrossRef CAS.
- A. Yacoby, Nat. Phys., 2011, 7, 925–926 Search PubMed.
- MOTIG, Manufacture of hard carbon, US Pat., US338542A, 1886, USA, Utility patent Search PubMed.
- R. E. Franklin, Proc. R. Soc. London, Ser. A, 1951, 209, 196–218 CAS.
- Z. Jian, W. Luo and X. Ji, J. Am. Chem. Soc., 2015, 137, 11566–11569 CrossRef CAS PubMed.
- S. Dhir, S. Wheeler, I. Capone and M. Pasta, Chem, 2020, 6, 2442–2460 CAS.
- H. Onuma, K. Kubota, S. Muratsubaki, W. Ota, M. Shishkin, H. Sato, K. Yamashita, S. Yasuno and S. Komaba, J. Mater. Chem. A, 2021, 9, 11187–11200 RSC.
- J. C. Pramudita, V. K. Peterson, J. A. Kimpton and N. Sharma, Powder Diffr., 2017, 32, S43–S48 CrossRef.
- L. Fan, R. Ma, Q. Zhang, X. Jia and B. Lu, Angew. Chem., 2019, 131, 10610–10615 CrossRef.
- T. Ohzuku, Y. Iwakoshi and K. Sawai, J. Electrochem. Soc., 1993, 140, 2490 CrossRef CAS.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Chem. Soc. Rev., 2019, 48, 4655–4687 RSC.
- M. S. Dresselhaus and G. Dresselhaus, Adv. Phys., 1981, 30, 139–326 CrossRef CAS.
- H. Moriwake, A. Kuwabara, C. A. J. Fisher and Y. Ikuhara, RSC Adv., 2017, 7, 36550–36554 RSC.
- Y. Liu, B. V. Merinov and W. A. Goddard, Proc. Natl. Acad. Sci. U.S.A., 2016, 113, 3735–3739 CrossRef CAS PubMed.
- O. Lenchuk, P. Adelhelm and D. Mollenhauer, Phys. Chem. Chem. Phys., 2019, 21, 19378–19390 RSC.
- K. Nobuhara, H. Nakayama, M. Nose, S. Nakanishi and H. Iba, J. Power Sources, 2013, 243, 585–587 CrossRef CAS.
- Y. Okamoto, J. Phys. Chem. C, 2014, 118, 16–19 CrossRef CAS.
- F. Zou and A. Manthiram, Adv. Energy Mater., 2020, 10, 2002508 CrossRef CAS.
- W. Zhang, M. Dahbi and S. Komaba, Curr. Opin. Chem. Eng., 2016, 13, 36–44 CrossRef.
- P.-F. Cao, G. Yang, B. Li, Y. Zhang, S. Zhao, S. Zhang, A. Erwin, Z. Zhang, A. P. Sokolov and J. Nanda, ACS Energy Lett., 2019, 4, 1171–1180 CrossRef CAS.
- S. Komaba, N. Yabuuchi, T. Ozeki, K. Okushi, H. Yui, K. Konno, Y. Katayama and T. Miura, J. Power Sources, 2010, 195, 6069–6074 CrossRef CAS.
- S. Komaba, N. Yabuuchi, T. Ozeki, Z.-J. Han, K. Shimomura, H. Yui, Y. Katayama and T. Miura, J. Phys. Chem. C, 2012, 116, 1380–1389 CrossRef CAS.
- N. Yabuuchi, Y. Matsuura, T. Ishikawa, S. Kuze, J.-Y. Son, Y.-T. Cui, H. Oji and S. Komaba, ChemElectroChem, 2014, 1, 580–589 CrossRef.
- K. Ui, D. Fujii, Y. Niwata, T. Karouji, Y. Shibata, Y. Kadoma, K. Shimada and N. Kumagai, J. Power Sources, 2014, 247, 981–990 CrossRef CAS.
- T. Zhang, I. de Meatza, X. Qi and E. Paillard, J. Power Sources, 2017, 356, 97–102 CrossRef CAS.
- S. Komaba, T. Ozeki and K. Okushi, J. Power Sources, 2009, 189, 197–203 CrossRef CAS.
- S. Komaba, K. Okushi, T. Ozeki, H. Yui, Y. Katayama, T. Miura, T. Saito and H. Groult, Electrochem. Solid-State Lett., 2009, 12, A107 CrossRef CAS.
- D. Bresser, D. Buchholz, A. Moretti, A. Varzi and S. Passerini, Energy Environ. Sci., 2018, 11, 3096–3127 RSC.
- V. A. Nguyen and C. Kuss, J. Electrochem. Soc., 2020, 167, 065501 CrossRef CAS.
- Y. Ma, J. Ma and G. Cui, Energy Storage Materials, 2019, 20, 146–175 CrossRef.
- B. Jache and P. Adelhelm, Angew. Chem., 2014, 126, 10333–10337 CrossRef.
- H. Kim, J. Hong, G. Yoon, H. Kim, K.-Y. Park, M.-S. Park, W.-S. Yoon and K. Kang, Energy Environ. Sci., 2015, 8, 2963–2969 RSC.
- M. Goktas, C. Bolli, E. J. Berg, P. Novak, K. Pollok, F. Langenhorst, M. V. Roeder, O. Lenchuk, D. Mollenhauer and P. Adelhelm, Adv. Energy Mater., 2018, 8, 1702724 CrossRef.
- H. Kim, J. Hong, Y. U. Park, J. Kim, I. Hwang and K. Kang, Adv. Funct. Mater., 2015, 25, 534–541 CrossRef CAS.
- Z.-L. Xu, G. Yoon, K.-Y. Park, H. Park, O. Tamwattana, S. J. Kim, W. M. Seong and K. Kang, Nat. Commun., 2019, 10, 1–10 CrossRef PubMed.
- G. Yoon, H. Kim, I. Park and K. Kang, Adv. Energy Mater., 2017, 7, 1601519 CrossRef.
- I. Escher, Y. Kravets, G. A. Ferrero, M. Goktas and P. Adelhelm, Energy Technol., 2021, 9, 2000880 CrossRef CAS PubMed.
- Y. J. Kim, S. Pyo, S. Kim and W.-H. Ryu, Carbon, 2021, 175, 585–593 CrossRef CAS.
- H. Kim, G. Yoon, K. Lim and K. Kang, Chem. Commun., 2016, 52, 12618–12621 RSC.
- L. Li, L. Liu, Z. Hu, Y. Lu, Q. Liu, S. Jin, Q. Zhang, S. Zhao and S. L. Chou, Angew. Chem., 2020, 132, 13017–13024 CrossRef.
- A. P. Cohn, N. Muralidharan, R. Carter, K. Share, L. Oakes and C. L. Pint, J. Mater. Chem. A, 2016, 4, 14954–14959 RSC.
- S. C. Jung, Y.-J. Kang and Y.-K. Han, Nano Energy, 2017, 34, 456–462 CrossRef CAS.
- X. Dou, I. Hasa, D. Saurel, C. Vaalma, L. Wu, D. Buchholz, D. Bresser, S. Komaba and S. Passerini, Mater. Today, 2019, 23, 87–104 CrossRef CAS.
- D. Saurel, B. Orayech, B. Xiao, D. Carriazo, X. Li and T. Rojo, Adv. Energy Mater., 2018, 8, 1703268 CrossRef.
- Y. Nishi, Chem. Rec., 2001, 1, 406–413 CrossRef CAS PubMed.
- X. Dou, I. Hasa, M. Hekmatfar, T. Diemant, R. J. Behm, D. Buchholz and S. Passerini, ChemSusChem, 2017, 10, 2668–2676 CrossRef CAS PubMed.
- E. M. Lotfabad, J. Ding, K. Cui, A. Kohandehghan, W. P. Kalisvaart, M. Hazelton and D. Mitlin, ACS Nano, 2014, 8, 7115–7129 CrossRef CAS PubMed.
- H. Hou, X. Qiu, W. Wei, Y. Zhang and X. Ji, Adv. Energy Mater., 2017, 7, 1602898 CrossRef.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271 CrossRef CAS.
- S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Adv. Funct. Mater., 2011, 21, 3859–3867 CrossRef CAS.
- P. Bai, Y. He, X. Zou, X. Zhao, P. Xiong and Y. Xu, Adv. Energy Mater., 2018, 8, 1703217 CrossRef.
- S. Qiu, L. Xiao, M. L. Sushko, K. S. Han, Y. Shao, M. Yan, X. Liang, L. Mai, J. Feng and Y. Cao, Adv. Energy Mater., 2017, 7, 1700403 CrossRef.
- C. Chen, Z. Wang, B. Zhang, L. Miao, J. Cai, L. Peng, Y. Huang, J. Jiang, Y. Huang and L. Zhang, Energy Storage Materials, 2017, 8, 161–168 CrossRef.
- J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Chem. Commun., 2016, 52, 12430–12433 RSC.
- Y. Youn, B. Gao, A. Kamiyama, K. Kubota, S. Komaba and Y. Tateyama, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- J. M. Stratford, A. K. Kleppe, D. S. Keeble, P. A. Chater, S. S. Meysami, C. J. Wright, J. Barker, M.-M. Titirici, P. K. Allan and C. P. Grey, J. Am. Chem. Soc., 2021, 143, 14274–14286 CrossRef CAS PubMed.
- Y. Morikawa, S. i. Nishimura, R. i. Hashimoto, M. Ohnuma and A. Yamada, Adv. Energy Mater., 2020, 10, 1903176 CrossRef CAS.
- A. Kamiyama, K. Kubota and S. Komaba, presented in part at The 46th Annual Meeting of the Carbon Society of Japan, 2019 Search PubMed.
- B. Zhang, C. M. Ghimbeu, C. Laberty, C. Vix-Guterl and J. m. Tarascon, Adv. Energy Mater., 2016, 6, 1501588 CrossRef.
- J. J. Kipling, J. N. Sherwood, P. V. Shooter and N. R. Thompson, Carbon, 1964, 1, 315–320 CrossRef CAS.
- Y. Li, M. P. Paranthaman, K. Akato, A. K. Naskar, A. M. Levine, R. J. Lee, S.-O. Kim, J. Zhang, S. Dai and A. Manthiram, J. Power Sources, 2016, 316, 232–238 CrossRef CAS.
- A. M. Navarro-Suarez, D. Saurel, P. Sanchez-Fontecoba, E. Castillo-Martinez, J. Carretero-González and T. Rojo, J. Power Sources, 2018, 397, 296–306 CrossRef CAS.
- H. Yamamoto, S. Muratsubaki, K. Kubota, M. Fukunishi, H. Watanabe, J. Kim and S. Komaba, J. Mater. Chem. A, 2018, 6, 16844–16848 RSC.
- Z. Li, C. Bommier, Z. S. Chong, Z. Jian, T. W. Surta, X. Wang, Z. Xing, J. C. Neuefeind, W. F. Stickle and M. Dolgos, Adv. Energy Mater., 2017, 7, 1602894 CrossRef.
- P. J. F. Harris, Crit. Rev. Solid State Mater. Sci., 2005, 30, 235–253 CrossRef CAS.
- A. Kamiyama, K. Kubota, D. Igarashi, Y. Youn, Y. Tateyama, H. Ando, K. Gotoh and S. Komaba, Angew. Chem., Int. Ed., 2021, 60, 5114–5120 CrossRef CAS PubMed.
- T. Morishita, T. Tsumura, M. Toyoda, J. Przepiórski, A. W. Morawski, H. Konno and M. Inagaki, Carbon, 2010, 48, 2690–2707 CrossRef CAS.
- T. Kyotani, Z. Ma and A. Tomita, Carbon, 2003, 41, 1451–1459 CrossRef CAS.
- R. Ryoo, S. H. Joo and S. Jun, J. Phys. Chem. B, 1999, 103, 7743–7746 CrossRef CAS.
- Q. Meng, Y. Lu, F. Ding, Q. Zhang, L. Chen and Y.-S. Hu, ACS Energy Lett., 2019, 4, 2608–2612 CrossRef CAS.
- Y. Qi, Y. Lu, F. Ding, Q. Zhang, H. Li, X. Huang, L. Chen and Y. S. Hu, Angew. Chem., Int. Ed., 2019, 58, 4361–4365 CrossRef CAS PubMed.
- B. Cao, H. Liu, B. Xu, Y. Lei, X. Chen and H. Song, J. Mater. Chem. A, 2016, 4, 6472–6478 RSC.
- Y. Xu, C. Zhang, M. Zhou, Q. Fu, C. Zhao, M. Wu and Y. Lei, Nat. Commun., 2018, 9, 1–11 CrossRef PubMed.
- Z. Jian, C. Bommier, L. Luo, Z. Li, W. Wang, C. Wang, P. A. Greaney and X. Ji, Chem. Mater., 2017, 29, 2314–2320 CrossRef CAS.
- D. Ni, W. Sun, Z. Wang, Y. Bai, H. Lei, X. Lai and K. Sun, Adv. Energy Mater., 2019, 9, 1900036 CrossRef.
- J. R. Dahn, T. Zheng, Y. Liu and J. Xue, Science, 1995, 270, 590–593 CrossRef CAS.
- W. Luo, Z. Jian, Z. Xing, W. Wang, C. Bommier, M. M. Lerner and X. Ji, ACS Cent. Sci., 2015, 1, 516–522 CrossRef CAS PubMed.
- J. Ni and Y. Li, Adv. Energy Mater., 2016, 6, 1600278 CrossRef.
- E. Yoo, J. Kim, E. Hosono, H.-s. Zhou, T. Kudo and I. Honma, Nano Lett., 2008, 8, 2277–2282 CrossRef CAS PubMed.
- S. Gong and Q. Wang, J. Phys. Chem. C, 2017, 121, 24418–24424 CrossRef CAS.
- C. Ling and F. Mizuno, Phys. Chem. Chem. Phys., 2014, 16, 10419–10424 RSC.
- X. Zuo, J. Zhu, P. Müller-Buschbaum and Y.-J. Cheng, Nano Energy, 2017, 31, 113–143 CrossRef CAS.
- H. Okamoto, J. Phase Equilib. Diffus., 2009, 30, 118–119 CrossRef CAS.
- M. R. Zamfir, H. T. Nguyen, E. Moyen, Y. H. Lee and D. Pribat, J. Mater. Chem. A, 2013, 1, 9566 RSC.
- W.-J. Zhang, J. Power Sources, 2011, 196, 13–24 CrossRef CAS.
- M. Lao, Y. Zhang, W. Luo, Q. Yan, W. Sun and S. X. Dou, Adv. Mater., 2017, 29, 1700622 CrossRef PubMed.
- I. Sultana, M. M. Rahman, Y. Chen and A. M. Glushenkov, Adv. Funct. Mater., 2018, 28, 1703857 CrossRef.
- K. Yang, X. Zhang, K. Song, J. Zhang, C. Liu, L. Mi, Y. Wang and W. Chen, Electrochim. Acta, 2020, 337, 135783 CrossRef CAS.
- J. Zhang, K. Song, L. Mi, C. Liu, X. Feng, J. Zhang, W. Chen and C. Shen, J. Phys. Chem. Lett., 2020, 11, 1435–1442 CrossRef CAS PubMed.
- S. Zhou, J. Lan, K. Song, Z. Zhang, J. Shi and W. Chen, FlatChem, 2021, 28, 100259 CrossRef CAS.
- K. Song, J. Liu, H. Dai, Y. Zhao, S. Sun, J. Zhang, C. Qin, P. Yan, F. Guo and C. Wang, Chem, 2021, 7, 2684–2694 CAS.
- C.-M. Park, J.-H. Kim, H. Kim and H.-J. Sohn, Chem. Soc. Rev., 2010, 39, 3115 RSC.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- S. Komaba, Y. Matsuura, T. Ishikawa, N. Yabuuchi, W. Murata and S. Kuze, Electrochem. Commun., 2012, 21, 65–68 CrossRef CAS.
- M. Dahbi, N. Yabuuchi, K. Kubota, K. Tokiwa and S. Komaba, Phys. Chem. Chem. Phys., 2014, 16, 15007–15028 RSC.
- K. Kubota and S. Komaba, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS.
- I. Abe, T. Horiba, Y. Abe, K. Hida, T. Matsuyama, S. Yasuno and S. Komaba, J. Electrochem. Soc., 2020, 167, 110513 CrossRef CAS.
- M. Dahbi, N. Yabuuchi, M. Fukunishi, K. Kubota, K. Chihara, K. Tokiwa, X.-F. Yu, H. Ushiyama, K. Yamashita, J.-Y. Son, Y.-T. Cui, H. Oji and S. Komaba, Chem. Mater., 2016, 28, 1625–1635 CrossRef CAS.
- M. Obrovac, L. Christensen, D. B. Le and J. R. Dahn, J. Electrochem. Soc., 2007, 154, A849 CrossRef CAS.
- T. T. Tran and M. N. Obrovac, J. Electrochem. Soc., 2011, 158, A1411 CrossRef CAS.
- Y. Lee, H. Lim, S.-O. Kim, H.-S. Kim, K. J. Kim, K.-Y. Lee and W. Choi, J. Mater. Chem. A, 2018, 6, 20383–20392 RSC.
- I. Sultana, T. Ramireddy, M. M. Rahman, Y. Chen and A. M. Glushenkov, Chem. Commun., 2016, 52, 9279–9282 RSC.
- I. Sultana, M. M. Rahman, T. Ramireddy, Y. Chen and A. M. Glushenkov, J. Mater. Chem. A, 2017, 5, 23506–23512 RSC.
- J. Ruan, F. Mo, Z. Long, Y. Song, F. Fang, D. Sun and S. Zheng, ACS Nano, 2020, 14, 12222–12233 CrossRef CAS PubMed.
- T. T. Tran and M. Obrovac, J. Electrochem. Soc., 2011, 158, A1411 CrossRef CAS.
- L. Zhou, Z. Cao, W. Wahyudi, J. Zhang, J.-Y. Hwang, Y. Cheng, L. Wang, L. Cavallo, T. Anthopoulos, Y.-K. Sun, H. N. Alshareef and J. Ming, ACS Energy Lett., 2020, 5, 766–776 CrossRef CAS.
- A. K. Chan, R. Tatara, S. Feng, P. Karayaylali, J. Lopez, I. E. L. Stephens and Y. Shao-Horn, J. Electrochem. Soc., 2019, 166, A1867–A1874 CrossRef CAS.
- S. Sim, P. Oh, S. Park and J. Cho, Adv. Mater., 2013, 25, 4498–4503 CrossRef CAS PubMed.
- X.-Y. Zhou, J.-J. Tang, J. Yang, J. Xie and L.-L. Ma, Electrochim. Acta, 2013, 87, 663–668 CrossRef CAS.
- Y. S. Jung, K. T. Lee and S. M. Oh, Electrochim. Acta, 2007, 52, 7061–7067 CrossRef CAS.
- M. Saito, K. Nakai, T. Yamada, T. Takenaka, M. Hirota, A. Kamei, A. Tasaka and M. Inaba, J. Power Sources, 2011, 196, 6637–6643 CrossRef CAS.
- I. Kovalenko, B. Zdyrko, A. Magasinski, B. Hertzberg, Z. Milicev, R. Burtovyy, I. Luzinov and G. Yushin, Science, 2011, 334, 75–79 CrossRef CAS PubMed.
- J. Song, M. Zhou, R. Yi, T. Xu, M. L. Gordin, D. Tang, Z. Yu, M. Regula and D. Wang, Adv. Funct. Mater., 2014, 24, 5904–5910 CrossRef CAS.
- B. Koo, H. Kim, Y. Cho, K. T. Lee, N.-S. Choi and J. Cho, Angew. Chem., 2012, 124, 8892–8897 CrossRef.
- M.-H. Ryou, J. Kim, I. Lee, S. Kim, Y. K. Jeong, S. Hong, J. H. Ryu, T.-S. Kim, J.-K. Park, H. Lee and J. W. Choi, Adv. Mater., 2013, 25, 1571–1576 CrossRef CAS PubMed.
- N. S. Hochgatterer, M. R. Schweiger, S. Koller, P. R. Raimann, T. WöHrle, C. Wurm and M. Winter, Electrochem. Solid-State Lett., 2008, 11, A76 CrossRef CAS.
- T. Mochizuki, S. Aoki, T. Horiba, M. Schulz-Dobrick, Z.-J. Han, S. Fukuyama, H. Oji, S. Yasuno and S. Komaba, ACS Sustainable Chem. Eng., 2017, 5, 6343–6355 CrossRef CAS.
- H. Li, Electrochem. Solid-State Lett., 1999, 2, 547 CrossRef CAS.
- W.-R. Liu, Z.-Z. Guo, W.-S. Young, D.-T. Shieh, H.-C. Wu, M.-H. Yang and N.-L. Wu, J. Power Sources, 2005, 140, 139–144 CrossRef CAS.
- J. R. Szczech and S. Jin, Energy Environ. Sci., 2011, 4, 56–72 RSC.
- M. Murase, N. Yabuuchi, Z.-J. Han, J.-Y. Son, Y.-T. Cui, H. Oji and S. Komaba, ChemSusChem, 2012, 5, 2307–2311 CrossRef CAS PubMed.
- S. Komaba, N. Yabuuchi, T. Ozeki, Z.-J. Han, K. Shimomura, H. Yui, Y. Katayama and T. Miura, J. Phys. Chem. C, 2012, 116, 1380–1389 CrossRef CAS.
- M. Fukunishi, N. Yabuuchi, M. Dahbi, J.-Y. Son, Y. Cui, H. Oji and S. Komaba, J. Phys. Chem. C, 2016, 120, 15017–15026 CrossRef CAS.
- P. Parikh, M. Sina, A. Banerjee, X. Wang, M. S. D'Souza, J.-M. Doux, E. A. Wu, O. Y. Trieu, Y. Gong, Q. Zhou, K. Snyder and Y. S. Meng, Chem. Mater., 2019, 31, 2535–2544 CrossRef CAS.
- A. Miranda, K. Sarang, B. Gendensuren, E.-S. Oh, J. Lutkenhaus and R. Verduzco, Mol. Syst. Des. Eng., 2020, 5, 709–724 RSC.
- T. R. Martin, R. T. Pekarek, J. E. Coyle, M. C. Schulze and N. R. Neale, J. Mater. Chem. A, 2021, 9, 21929–21938 RSC.
- L. Chen, K. Wang, X. Xie and J. Xie, J. Power Sources, 2007, 174, 538–543 CrossRef CAS.
- C. Xu, F. Lindgren, B. Philippe, M. Gorgoi, F. Björefors, K. Edström and T. Gustafsson, Chem. Mater., 2015, 27, 2591–2599 CrossRef CAS.
- S. Dalavi, P. Guduru and B. L. Lucht, J. Electrochem. Soc., 2012, 159, A642–A646 CrossRef CAS.
- V. Etacheri, O. Haik, Y. Goffer, G. A. Roberts, I. C. Stefan, R. Fasching and D. Aurbach, Langmuir, 2012, 28, 965–976 CrossRef CAS PubMed.
- Y. Jin, N.-J. H. Kneusels, P. C. M. M. Magusin, G. Kim, E. Castillo-Martínez, L. E. Marbella, R. N. Kerber, D. J. Howe, S. Paul, T. Liu and C. P. Grey, J. Am. Chem. Soc., 2017, 139, 14992–15004 CrossRef CAS PubMed.
- R. Scipioni, D. Isheim and S. A. Barnett, Appl. Mater. Today, 2020, 20, 100748 CrossRef.
- W. Li, A. Dolocan, P. Oh, H. Celio, S. Park, J. Cho and A. Manthiram, Nat. Commun., 2017, 8, 1–10 CrossRef PubMed.
- E. Peled and S. Menkin, J. Electrochem. Soc., 2017, 164, A1703 CrossRef CAS.
- P. Verma, P. Maire and P. Novák, Electrochim. Acta, 2010, 55, 6332–6341 CrossRef CAS.
- E. Peled, J. Electrochem. Soc., 1979, 126, 2047 CrossRef CAS.
- E. Markevich, G. Salitra and D. Aurbach, ACS Energy Lett., 2017, 2, 1337–1345 CrossRef CAS.
- H. Kim, K. Lim, G. Yoon, J. H. Park, K. Ku, H. D. Lim, Y. E. Sung and K. Kang, Adv. Energy Mater., 2017, 7, 1700418 CrossRef.
- J. Song, B. Xiao, Y. Lin, K. Xu and X. Li, Adv. Energy Mater., 2018, 8, 1703082 CrossRef.
- H. Wang, D. Zhai and F. Kang, Energy Environ. Sci., 2020, 13, 4583–4608 RSC.
- H. Bülter, F. Peters, J. Schwenzel and G. Wittstock, Angew. Chem., Int. Ed., 2014, 53, 10531–10535 CrossRef PubMed.
- T. Hosaka, T. Matsuyama, K. Kubota, S. Yasuno and S. Komaba, ACS Appl. Mater. Interfaces, 2020, 12, 34873–34881 CrossRef CAS PubMed.
- Y. Lei, D. Han, J. Dong, L. Qin, X. Li, D. Zhai, B. Li, Y. Wu and F. Kang, Energy Storage Materials, 2020, 24, 319–328 CrossRef.
- A. M. Tripathi, W.-N. Su and B. J. Hwang, Chem. Soc. Rev., 2018, 47, 736–851 RSC.
- J. Hui, Z. T. Gossage, D. Sarbapalli, K. Hernandez-Burgos and J. Rodríguez-López, Anal. Chem., 2018, 91, 60–83 CrossRef PubMed.
- J. Z. Olson, P. K. Johansson, D. G. Castner and C. W. Schlenker, Chem. Mater., 2018, 30, 1239–1248 CrossRef CAS.
- F. Shi, P. N. Ross, G. A. Somorjai and K. Komvopoulos, J. Phys. Chem. C, 2017, 121, 14476–14483 CrossRef CAS.
- A. v. Cresce, S. M. Russell, D. R. Baker, K. J. Gaskell and K. Xu, Nano Lett., 2014, 14, 1405–1412 CrossRef CAS PubMed.
- M. Steinhauer, M. Stich, M. Kurniawan, B.-K. Seidlhofer, M. Trapp, A. Bund, N. Wagner and K. A. Friedrich, ACS Appl. Mater. Interfaces, 2017, 9, 35794–35801 CrossRef CAS PubMed.
- J. L. L. Lopez and P. J. Grandinetti, J. Mater. Chem. A, 2018, 6, 231–243 RSC.
- Z. T. Gossage, J. Hui, Y. Zeng, H. Flores-Zuleta and J. Rodríguez-López, Chem. Sci., 2019, 10, 10749–10754 RSC.
- Z. J. Barton, J. Hui, N. B. Schorr and J. Rodríguez-López, Electrochim. Acta, 2017, 241, 98–105 CrossRef CAS.
- D. Aurbach, B. Markovsky, I. Weissman, E. Levi and Y. Ein-Eli, Electrochim. Acta, 1999, 45, 67–86 CrossRef CAS.
- G. G. Eshetu, S. Grugeon, H. Kim, S. Jeong, L. Wu, G. Gachot, S. Laruelle, M. Armand and S. Passerini, ChemSusChem, 2016, 9, 462–471 CrossRef CAS PubMed.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood III, Carbon, 2016, 105, 52–76 CrossRef CAS.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- B. Ravikumar, M. Mynam and B. Rai, J. Phys. Chem. C, 2018, 122, 8173–8181 CrossRef CAS.
- X. Chen, H. R. Li, X. Shen and Q. Zhang, Angew. Chem., Int. Ed., 2018, 57, 16643–16647 CrossRef CAS PubMed.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed.
- J. Wang, Y. Yamada, K. Sodeyama, E. Watanabe, K. Takada, Y. Tateyama and A. Yamada, Nat. Energy, 2018, 3, 22–29 CrossRef CAS.
- K. Takada, Y. Yamada, E. Watanabe, J. Wang, K. Sodeyama, Y. Tateyama, K. Hirata, T. Kawase and A. Yamada, ACS Appl. Mater. Interfaces, 2017, 9, 33802–33809 CrossRef CAS PubMed.
- X. Bie, K. Kubota, T. Hosaka, K. Chihara and S. Komaba, J. Mater. Chem. A, 2017, 5, 4325–4330 RSC.
- J. Patra, H.-T. Huang, W. Xue, C. Wang, A. S. Helal, J. Li and J.-K. Chang, Energy Storage Materials, 2019, 16, 146–154 CrossRef.
- B. Liu, J.-G. Zhang and W. Xu, Joule, 2018, 2, 833–845 CrossRef CAS.
- B. Lee, E. Paek, D. Mitlin and S. W. Lee, Chem. Rev., 2019, 119, 5416–5460 CrossRef CAS PubMed.
- H. Wang, D. Yu, X. Wang, Z. Niu, M. Chen, L. Cheng, W. Zhou and L. Guo, Angew. Chem., 2019, 131, 16603–16607 CrossRef.
- H. Zhang, G. G. Eshetu, X. Judez, C. Li, L. M. Rodriguez-Martínez and M. Armand, Angew. Chem., Int. Ed., 2018, 57, 15002–15027 CrossRef CAS PubMed.
- R. Mogensen, D. Brandell and R. Younesi, ACS Energy Lett., 2016, 1, 1173–1178 CrossRef CAS.
- M. Moshkovich, Y. Gofer and D. Aurbach, J. Electrochem. Soc., 2001, 148, E155 CrossRef CAS.
- J. Hui, N. B. Schorr, S. Pakhira, Z. Qu, J. L. Mendoza-Cortes and J. Rodríguez-López, J. Am. Chem. Soc., 2018, 140, 13599–13603 CrossRef CAS PubMed.
- J. Tan, J. Matz, P. Dong, J. Shen and M. Ye, Adv. Energy Mater., 2021, 11, 2100046 CrossRef CAS.
- M. Hess, Electrochim. Acta, 2017, 244, 69–76 CrossRef CAS.
- Y. Zeng, Z. T. Gossage, D. Sarbapalli, J. Hui and J. Rodríguez-López, ChemElectroChem, 2022, 9, e202101445 CrossRef CAS.
- H. Yildirim, A. Kinaci, M. K. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2015, 7, 18985–18996 CrossRef CAS PubMed.
- R. A. Adams, A. Varma and V. G. Pol, J. Power Sources, 2019, 410, 124–131 CrossRef.
- M. Li, J. Lu, X. Ji, Y. Li, Y. Shao, Z. Chen, C. Zhong and K. Amine, Nat. Rev. Mater., 2020, 5, 276–294 CrossRef CAS.
- A. L. Michan, B. S. Parimalam, M. Leskes, R. N. Kerber, T. Yoon, C. P. Grey and B. L. Lucht, Chem. Mater., 2016, 28, 8149–8159 CrossRef CAS.
- S. S. Zhang, J. Power Sources, 2006, 162, 1379–1394 CrossRef CAS.
- J. Liao, Q. Hu, Y. Yu, H. Wang, Z. Tang, Z. Wen and C. Chen, J. Mater. Chem. A, 2017, 5, 19017–19024 RSC.
- S. U. Yoon, H. Kim, H.-J. Jin and Y. S. Yun, Appl. Surf. Sci., 2021, 547, 149193 CrossRef CAS.
- U. Purushotham, N. Takenaka and M. Nagaoka, RSC Adv., 2016, 6, 65232–65242 RSC.
- T. Hosaka, T. Fukabori, T. Matsuyama, R. Tatara, K. Kubota and S. Komaba, ACS Energy Lett., 2021, 6, 3643–3649 CrossRef CAS.
- R. Xu, X.-B. Cheng, C. Yan, X.-Q. Zhang, Y. Xiao, C.-Z. Zhao, J.-Q. Huang and Q. Zhang, Matter, 2019, 1, 317–344 CrossRef.
- W. Liu, P. Liu and D. Mitlin, Adv. Energy Mater., 2020, 10, 2002297 CrossRef CAS.
- Y. Wan, K. Song, W. Chen, C. Qin, X. Zhang, J. Zhang, H. Dai, Z. Hu, P. Yan and C. Liu, Angew. Chem., Int. Ed., 2021, 60, 11481–11486 CrossRef CAS PubMed.
- X. Wang, L. Fu, R. Zhan, L. Wang, G. Li, M. Wan, X.-L. Wu, Z. W. Seh, L. Wang and Y. Sun, ACS Appl. Mater. Interfaces, 2021, 13, 13354–13361 CrossRef CAS PubMed.
- H. Wang, J. Hu, J. Dong, K. C. Lau, L. Qin, Y. Lei, B. Li, D. Zhai, Y. Wu and F. Kang, Adv. Energy Mater., 2019, 9, 1902697 CrossRef CAS.
- N. Xiao, J. Zheng, G. Gourdin, L. Schkeryantz and Y. Wu, ACS Appl. Mater. Interfaces, 2019, 11, 16571–16577 CrossRef CAS PubMed.
- K. Edstroem, T. Gustafsson and J. O. Thomas, Electrochim. Acta, 2004, 50, 397–403 CrossRef CAS.
- K. Nie, Y. Hong, J. Qiu, Q. Li, X. Yu, H. Li and L. Chen, Front. Chem., 2018, 6, 616 CrossRef CAS PubMed.
- D. Takamatsu, Y. Koyama, Y. Orikasa, S. Mori, T. Nakatsutsumi, T. Hirano, H. Tanida, H. Arai, Y. Uchimoto and Z. Ogumi, Angew. Chem., Int. Ed., 2012, 51, 11597–11601 CrossRef CAS PubMed.
- L. Mu, X. Feng, R. Kou, Y. Zhang, H. Guo, C. Tian, C. J. Sun, X. W. Du, D. Nordlund and H. L. Xin, Adv. Energy Mater., 2018, 8, 1801975 CrossRef.
- X. Zhang, Y. Yang, X. Qu, Z. Wei, G. Sun, K. Zheng, H. Yu and F. Du, Adv. Funct. Mater., 2019, 29, 1905679 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Present address: Battery Materials Analysis Group, Center for Green Research on Energy and Environmental Materials (GREEN), National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan |
| This journal is © The Royal Society of Chemistry 2022 |